OTSU-UCAN: An OTSU-Based Integrated Satellite–Terrestrial Information System for 6G in Vehicle Navigation

Abstract

One of the bottlenecks hindering the applications (e.g., vehicle navigation) of blockchain–UCAN is privacy. A sharded blockchain can protect vehicle data to a certain extent. However, unbalanced shard loads lead to low throughput and poor feature extraction in blockchain–UCAN. This paper proposes an optimal image binarization method (OTSU-GK) to enhance image features and reduce the amount of uploaded data, thereby improving throughput. Specifically, OTSU-GK uses a Gaussian kernel method where the parameters are optimized using grid search to improve the calculation of the threshold. Additionally, we have designed a Node Load Score (NLS)-based sharding blockchain, which considers the number of historical transactions, transaction types, transaction frequency, and other metrics to balance the sharding loads and further improve throughput. The experimental results show that OTSU-GK improves by 74.3%, 58.7%, and 83% in SSIM, RMSE/MAE/AER, and throughput. In addition, it reduces IL by 70.3% compared to other methods.

1. Introduction

UCAN (User-centric Access Network) is a de-cellular network with a universal architecture for unified management and flexible organization of diverse APs on various platforms to provide on-demand and consistent services for users Chen et al. [1]. UCAN is fit for 6G scenarios to provide user-centric services by integrating the UCAN architecture into a wide-area network. For example, the satellite-based base stations in UCAN provide backhaul services to moving-based stations, e.g., vehicles. Unfortunately, the privacy of vehicle data (e.g., track information) is undermined since all data is placed on one public blockchain, which is accessible to all nodes on the chain. To solve this problem, a sharding blockchain divides the entire blockchain into multiple shards so that nodes can only access the data of the shard they are on. Thus, data privacy is protected to some extent. However, the image feature extraction in navigation system and the throughput problem of the sharding blockchain, in turn, reduce the efficiency of the whole navigation system.

In a navigation system, images collected from cameras are embedded images. There are many challenges in processing embedded images, such as increasing resolution and frame rates while operating at low power Bailey [2]. Image binarization is a fundamental technique that simplifies images to two colours, reducing data complexity, highlighting image features, and enhancing processing efficiency. Recently, researchers have proposed a variety of binarization methods.

However, these methods fails in the scenario of blockchain–UCAN due to the computational limitations and resource constraints. Therefore, a new UCAN framework is needed to satisfy the requirements of both feature extraction and a sharding blockchain. In this paper, we propose an OTSU-UCAN (ref. Figure 1) by combining two novel OTSU-GK and NLS-Chain techniques. Specifically, color figures collected from the vehicles are binarized by OTSU-GK, where a Gaussian kernel is used to enhance the feature extraction. Grey images are then uploaded to access points (APs) to save storage space. Conversely, AP data is evaluated using the Node Load Score, which takes into account historical transactions, transaction types, and frequency. Finally, the nodes are assigned to different shards according to their targets. The main contributions of this paper are summarized as follows:

• OTSU-GK: The OTSU-GK is a new adaptive thresholding approach, which integrates a Gaussian kernel. The parameters of the Gaussian kernel are optimized through grid search to enhance threshold calculation. OTSU-GK provides a new solution in the field of image binarization.
• Node Load Score-based (NLS) sharding blockchain: We propose a blockchain segmentation method based on node load scoring to segment blockchain nodes by predicting the number of transactions of each node in the next epoch and calculating the corresponding transaction load scoring, which reflects the node’s transaction load, with the aim of achieving load balancing between segments.
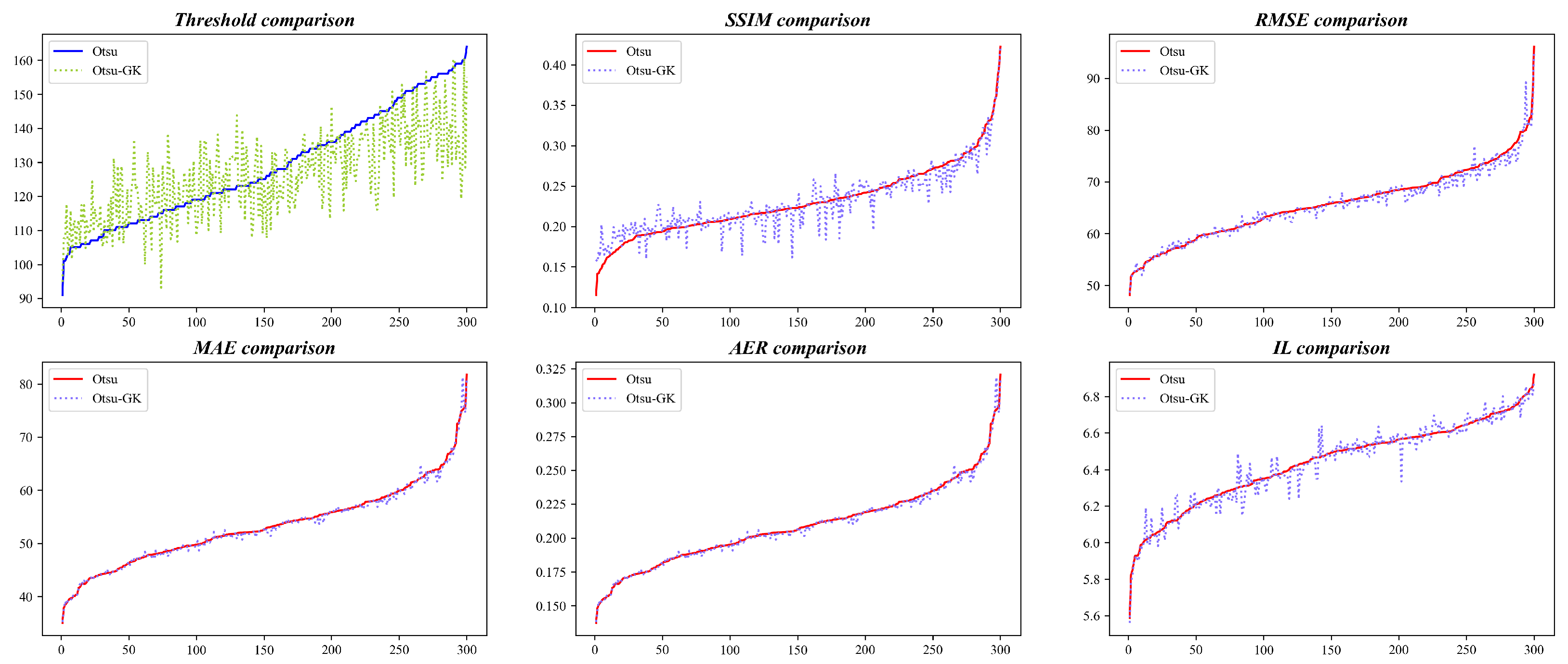
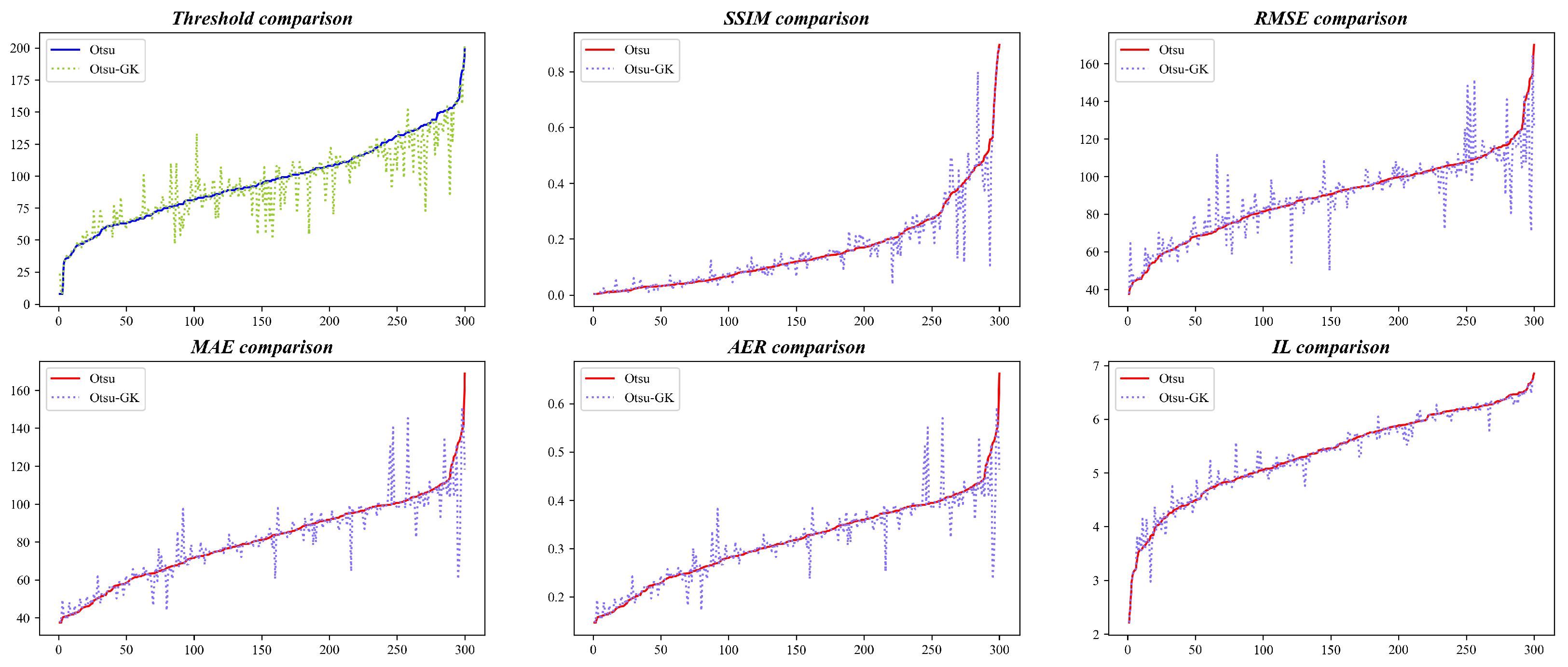
• Significant Performance Improvement: Compared to the traditional OTSU method, OTSU-GK shows approximately 50% improvement in SSIM (Structural Similarity), RMSE (root mean square error), and IL (information loss). This indicates that OTSU-GK performs better in image processing, thereby supporting the advancement of embedded image processing.
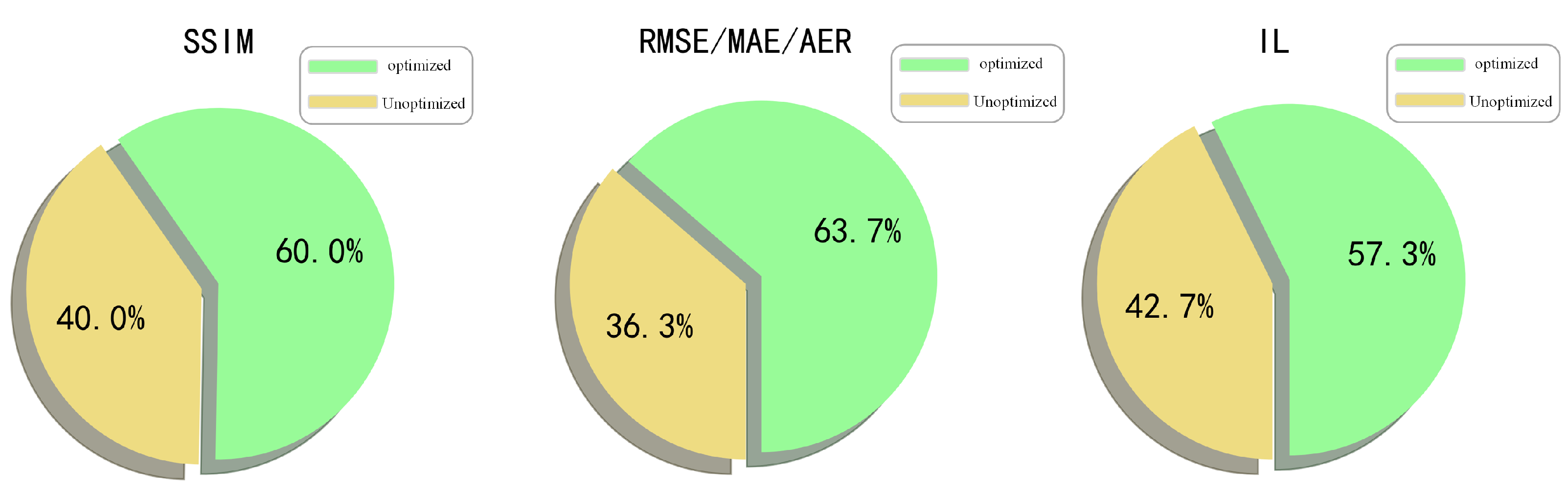
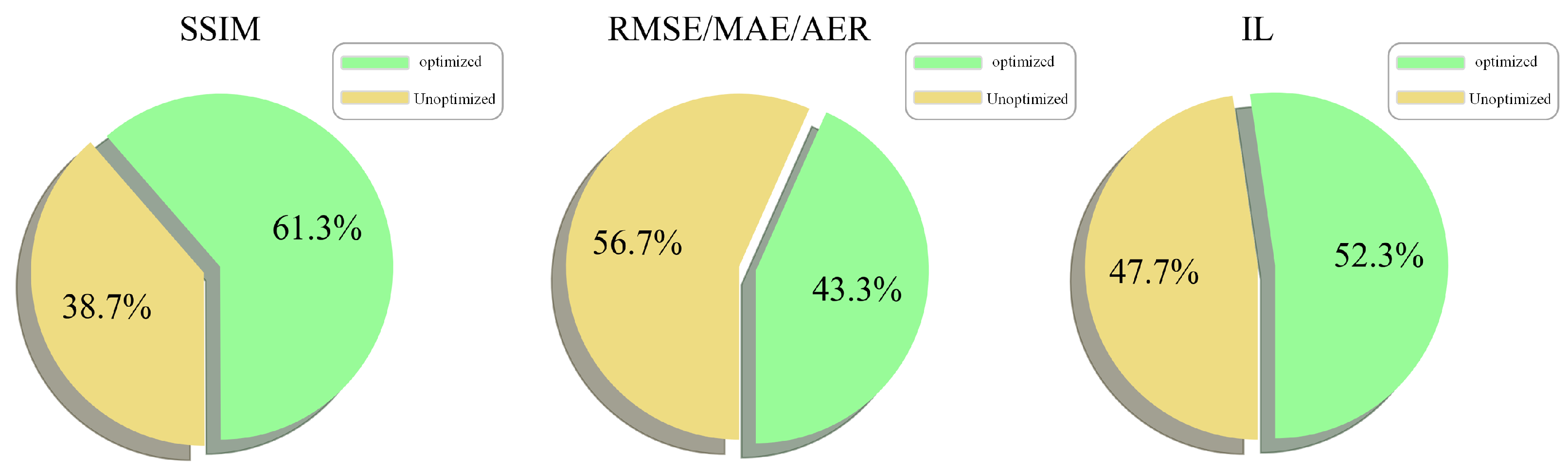
• Effectiveness of Parameter Optimization: Ablation experiments confirm the effectiveness of parameter optimization through grid search. When compared to methods with non-optimized parameters, OTSU-GK demonstrates a 14.3% increase in the SSIM metric and a 13% reduction in the IL metric on the KITTI dataset, which indicates that the process of optimizing parameters significantly enhances the performance of OTSU-GK.

2. Related Work

2.1. Image Binarization

Currently, image binarization methods include fixed threshold methods, adaptive threshold methods, and deep learning approaches. The fixed threshold method [3] involves setting a fixed threshold to categorize image pixels into foreground and background. This method relies on a fixed threshold for binarization, which requires manual intervention for threshold selection and exhibits limited adaptability.

Adaptive thresholding methods are proposed to dynamically calculate the threshold by considering local image characteristics. Yang et al. [4] optimized the OTSU method by utilizing the relationship between pixel grayscale values and cumulative pixel count changes, which further enhanced the performance of the OTSU method. Zhang et al. [5] proposed a new adaptive threshold segmentation method based on image sharpness evaluation, which aims to accurately find a reasonable threshold for improving image segmentation performance. Lin et al. [6] introduced an improved decision-based adaptive threshold median filter (IDBATMF) for denoising salt-and-pepper noise in fingerprint images. Pan et al. [7] proposed a method for single image dehazing and segmentation based on the dark channel prior (DCP) and adaptive thresholding, which improved target recognition efficiency. Rehman et al. [8] developed a new image enhancement method by combining adaptive thresholding methods.

The Gaussian kernel assigns higher weights to the central regions of the image by applying a weighted average to the threshold matrix after image segmentation. This effectively adapts to the uneven illumination and local contrast variations commonly found in in-vehicle images. This processing enhances the structural features of the image, thereby directly optimizing binarization performance, manifested as improved SSIM and reduced IL. Kim et al. [9] applied Gaussian weighting to Transformers, which was intended to enhance their performance. Chen et al. [10] proposed a Gaussian mixture model, which was designed to fully exploit point cloud information. Suryowati et al. [11] employed fixed and adaptive Gaussian kernel weighting functions for geographic weighted regression modeling, which was used to analyze maternal mortality rates. Basteri & Trevisan [12] initialized neural networks with random Gaussian parameters, which aimed to investigate how the sizes of hidden and output layers affect the Gaussian behavior of the network.

2.2. Optimization Methods of Hyperparameters

Hyperparameter optimization holds significant importance in the field of computer image processing, with its primary aim being the enhancement of model performance through the adjustment of model hyperparameters. Indeed, the configuration of hyperparameters directly influences the performance of the model [13], making it an essential step in the training process. Common methods for hyperparameter optimization include Bayesian optimization, genetic algorithms, and grid search. In short, Bayesian optimization [14] employs probabilistic models to guide the selection of hyperparameters, continuously updating the model to identify the optimal hyperparameters, which demonstrates notable efficiency and accuracy. Conversely, genetic algorithms [15] simulate the process of natural selection, incorporating operations such as crossover and mutation to interactively improve parameter configurations, thereby achieving hyperparameter optimization. Each of these methods has distinct characteristics, which can be chosen based on specific needs to attain the ultimate model performance.

Furthermore, grid search provides significant advantages due to its systematic and comprehensive nature, allowing it to explore all possible parameter combinations and thereby ensure the identification of a global optimum. Consequently, for embedded image processing, employing grid search to determine the optimal parameters for fitting Gaussian kernel parameters in the training set represents a highly effective approach.

2.3. Sharding Blockchain

Elastico [16] is proposed to divide the blockchain into different shards, each with an independent consensus mechanism to process part of the transactions separately. However, since Elastico adopts the PBFT (Practical Byzantine Fault Tolerance) consensus mechanism, it suffers from the problem of slow transaction validation when processing transactions. Omniledger [17] adopts the ByzCoin consensus mechanism as an improved version of PBFT but still faces the problem of performance limitation when processing large-scale transactions. Pyramid [18] proposes a hierarchical sharding blockchain system that can complete the verification of cross-shard transactions within one round of consensus, which improves the speed of the system in processing large-scale transactions. However, Pyramid uses random sharding and does not consider load balancing among nodes. LB-Chain [19] proposes a sharding method with shard load balancing, which migrates accounts from a high-load shard to a low-load shard through an account migration algorithm; however, LB-Chain does not consider the security of the system.

3. Method

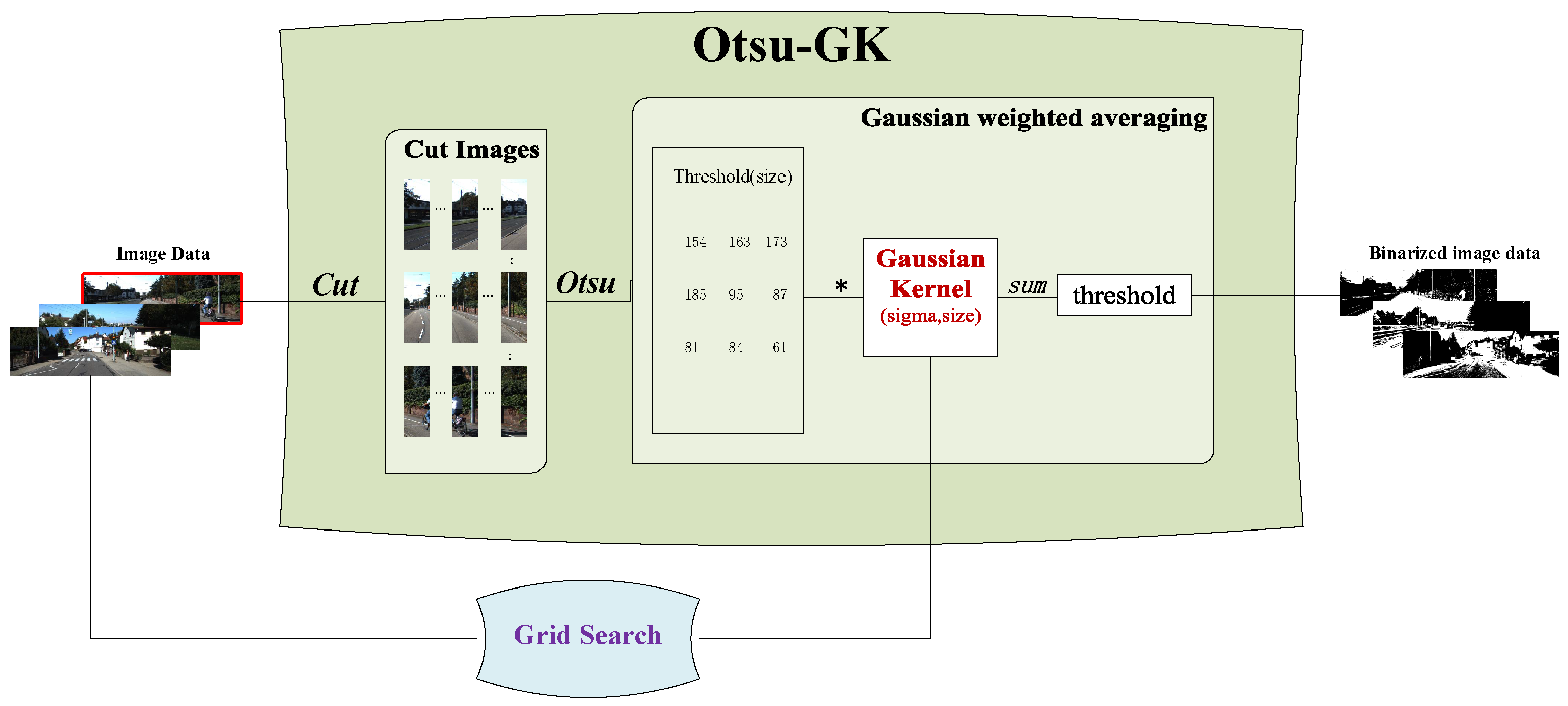
3.1. Framework of OTSU-GK

The framework of OTSU-GK is illustrated in Figure 1 and consists of three core modules: Grid Search, Cut Images, and Gaussian Kernel Average.

• Grid Search: We employ grid search for hyperparameter tuning, specifically to optimize the two hyperparameters of the Gaussian kernel, sigma ($\sigma$) and size, which determine the number of cut images (see Section 3.2 for details).
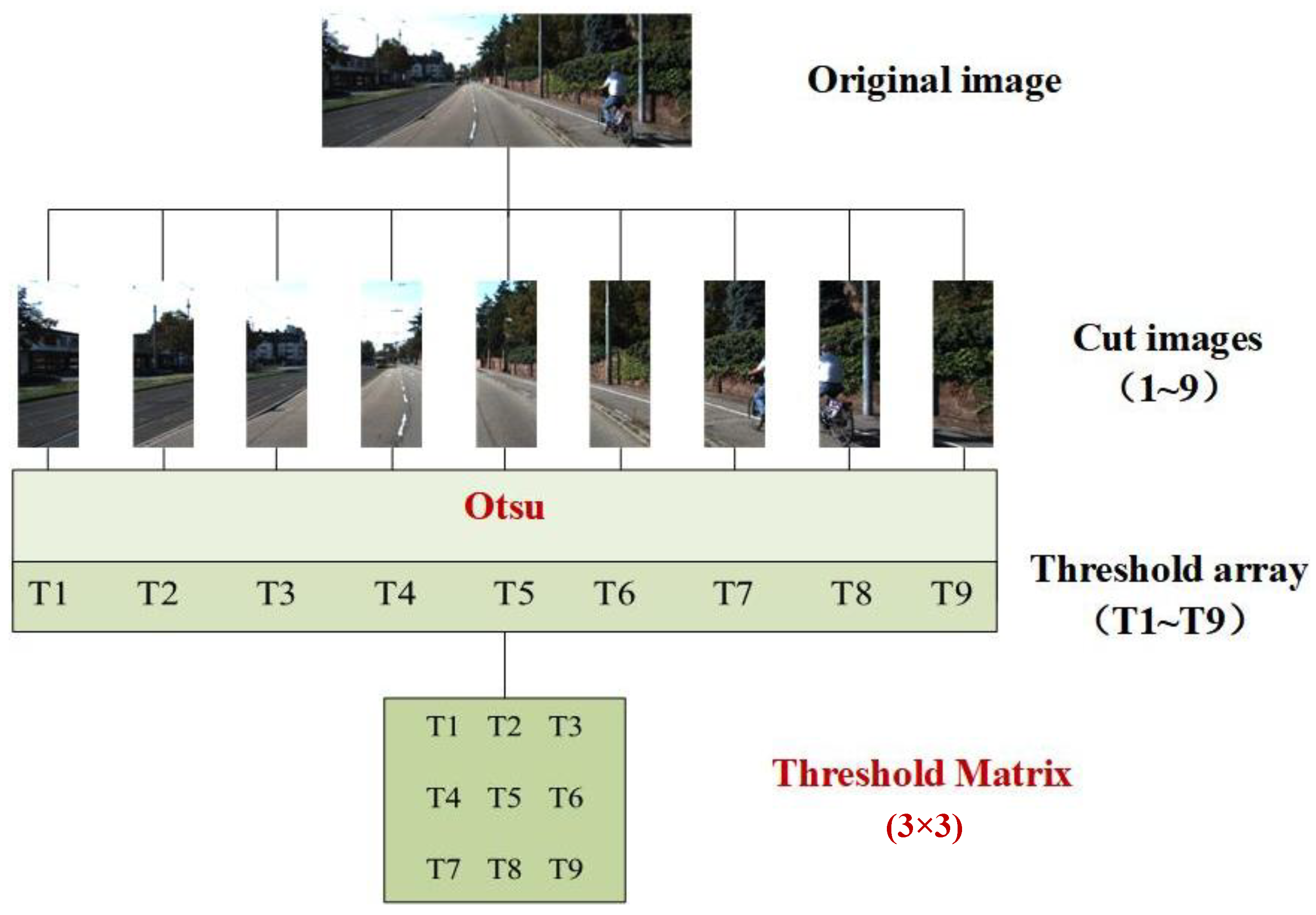
• Cut Images: We select original images from the dataset and perform proportional slicing from left to right. OTSU thresholding is then applied to each sliced image, resulting in a corresponding threshold matrix (see Section 3.3 for details).
• Gaussian Kernel Average: The Gaussian kernel performs matrix multiplication with the threshold matrices generated from the cut images. The resulting matrix is summed to determine the final threshold value for the original image, which is then used for binarization (see Section 3.4 for details).

3.2. Grid Search

Grid search ensures the identification of the optimal model configuration by systematically exploring all possible hyperparameter combinations. In this work, it is used to optimize the Gaussian kernel parameters: sigma ($\sigma$) and size.

The algorithm defines a set of predefined ranges and steps for each hyperparameter, evaluates each combination using a scoring function, and selects the one with the best performance. This exhaustive search guarantees that the most suitable parameter set is identified within the given range. The pseudocode of the grid search algorithm for OTSU-GK is presented in Algorithm 1.

Algorithm 1 Grid search for hyperparameter tuning

1: procedure GridSearch($\sigma$-range, $size$-range) 2:     $\mathit{\text{best\_score}}\leftarrow 0$ 3:     $\mathit{\text{best\_params}}\leftarrow (\mathrm{None},\mathrm{None})$ 4:     for $\sigma$ in $\sigma$-range do 5:         for $size$ in $size$-range do 6:            $score\leftarrow \text{evaluate\_params}(\sigma ,size)$ 7:            if $score>\mathit{\text{best\_score}}$ then 8:                $\mathit{\text{best\_score}}\leftarrow score$ 9:                $\mathit{\text{best\_params}}\leftarrow (\sigma ,size)$ 10:            end if 11:         end for 12:     end for 13:     return $\mathit{\text{best\_params}}$, $\mathit{\text{best\_score}}$ 14: end procedure

During the experiment, we randomly select 300 images from the dataset for testing, and 20% of them are used for parameter evaluation. The range of sigma is set from 0.5 to 6.0, divided into 10 equal intervals. The size of the Gaussian kernel ranges from 3 to 7, considering only odd values (i.e., 3, 5, and 7) to maintain symmetry. For the abnormal images (entirely black or entirely white images) that appear after image segmentation, we do not apply OTSU thresholding. Instead, we set their threshold to a default value (such as the global image threshold or the average of adjacent slices) or directly exclude the slice from the threshold matrix. This ensures the threshold matrix does not contain extreme outliers.

In the evaluate_params function, we normalize the evaluation metrics, including SSIM, MAE, and information loss (IL). For metrics where higher values indicate better performance (e.g., SSIM), we directly aggregate their scores. For those where lower values are better (e.g., MAE and IL), we subtract their normalized scores. The final score is flexibly adjusted based on experimental objectives to ensure optimal Gaussian kernel parameter selection.

3.3. Cut-Image Generation

Once the Gaussian kernel hyperparameters $(\sigma ,\mathit{size})$ have been obtained by grid search (Algorithm 1), OTSU-GK segments the original image into $\mathit{size}\times \mathit{size}$ equal-width (or equal-height) tiles starting from the left-most column. Each tile is processed independently by classical OTSU thresholding, yielding one threshold per tile. The resulting thresholds are then laid out row-wise to form a $\mathit{size}\times \mathit{size}$ threshold matrix $\mathbf{T}$ that will later be convolved with the Gaussian kernel.

Figure 2 illustrates the cutting procedure for $\mathit{size}=3$; the original image is partitioned into nine non-overlapping sub-images, The asterisks denote matrix multiplication and the corresponding threshold matrix is

$$\mathbf{T}=\left[\begin{array}{ccc}{t}_{11}& t_{12}& t_{13}\\ t_{21}& t_{22}& t_{23}\\ t_{31}& t_{32}& t_{33}\end{array}\right],t_{ij}=\mathtt{OTSU}\left({\mathrm{tile}}_{ij}\right).$$

3.4. Experimental Settings

3.4.1. Cut Images

The Gaussian kernel is selected since it smooths noise and enhances image features through distance-weighted processing, which is particularly crucial for in-vehicle image processing. In OTSU-GK, the Gaussian kernel is applied to the thresholding matrix, effectively integrating local features across different image regions. This avoids detail loss caused by a single threshold, thereby improving binarization performance (as evidenced by enhancements in SSIM and IL metrics). After obtaining the Gaussian kernel hyperparameters ($\sigma ,size$) through grid search, OTSU-GK segments the original image based on the value of $size$. Specifically, the image is segmented with equal-width or equal-height cuts starting from the left side of the original image, resulting in $size\times size$ cut images. Subsequently, each cut image is processed individually using OTSU to generate thresholds. These thresholds are then arranged sequentially to form a matrix of $size\times size$ thresholds. For example, with $size=3$, the process of generating cut images is illustrated in Figure 3.

3.4.2. Gaussian Kernel Average

Gaussian weighted average is a method that assigns weights to data points based on their distance from a central point, with closer points receiving higher weights. This technique is commonly used in signal processing, image processing, and data analysis to smooth out noise and emphasize important features. The Gaussian weighted average algorithm first defines a Gaussian function of the form. The formula for a Gaussian function is as follows, where $\mu$ represents the mean of the Gaussian function and $\sigma$ represents the standard deviation, which controls the center point of the function and the width of the function:

$$f\left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}{e}^{-{\displaystyle \frac{{(x-\mu )}^2}{2{\sigma }^2}}}$$

(1)

When using the Gaussian function, it is necessary to input the parameters $\sigma$ and $size$ into the function. To better understand the distribution of the Gaussian kernel, we set different values for $\sigma$ and $size$ and illustrated the characteristics of the Gaussian kernel through heatmaps, as shown in Figure 3.

In OTSU-GK, the threshold matrix generated from cut images is combined with the Gaussian kernel matrix, which is used for matrix multiplication. This operation, which performs the smoothing and adjustment of the threshold values, ultimately yields the threshold of the original image.

4. NLS-Chain: NLS Sharding Blockchain

We construct a high-TPS sharding blockchain system named NLS-Chain to address the low throughput of traditional sharded blockchain systems. NLS-Chain predicts the number of transactions for each node in the upcoming epoch and computes a Node Load Score (NLS) based on this prediction. By sharding nodes according to their NLS, the system achieves inter-shard load balance and significantly improves overall TPS. The framework of NLS-Chain is illustrated in Figure 4.

4.1. Prediction of the Number of Node Transactions

In the transaction prediction phase, we construct a GRU-based sequence prediction method [20] to forecast the number of transactions for each node in the next epoch. The prediction result is used as the basis for calculating the NLS. In fact, GRU contains one input layer, one output layer, and five hidden layers. The length of the input layer depends on the length of the transaction sequence. Algorithm 2 details the generation of the transaction sequence. First, input the raw data and step size. Then create two empty lists to store the input sequence and output labels. Use a for loop to control the data length and prevent out-of-bounds access, adding data to the empty lists one item at a time. Finally, output the lists as the transformed data format. Use the output of Algorithm 2 as input for the GRU prediction model. Train the model using 2/3 of the data as the training set, and use the remaining 1/3 as the test set to evaluate the model’s accuracy. Five hidden layers are connected sequentially to process time series data, with their units controlled by gates to regulate information flow. The output layer is typically a fully connected layer that processes and extracts features from the GRU layer’s outputs, mapping them to the output space via activation functions to produce the final prediction results (e.g., transaction sequences).

Transaction sequences generated by GRU are subsequently fed into a large language model (LLM) for further processing, with the Transformer serving as the core component of the LLM. The Transformer employs an attention mechanism to enhance the model’s ability to capture relationships between different parts of a transaction sequence, enabling it to better understand contextual information and improve its processing capabilities.

Algorithm 2 The generation of a transaction sequence

1: procedure Generation($data$, $\mathit{\text{seq\_length}}$) 2:     X, Y=[], [] 3:     for i in $step$ $length$ do 4:         $X.append\left(data\right[i+\mathit{\text{seq\_length}}\left]\right)$ 5:         $Y.append\left(data\right[i+\mathit{\text{seq\_length}}\left]\right)$ 6:     end for 7:     return $np.array\left(X\right)$, $np.array\left(Y\right)$ 8: end procedure

We first convert the raw transaction data into sequence format using a create_sequence function. This function splits the data into fixed-length input sequences and corresponding target values. The process is controlled by a loop to avoid out-of-bounds access, and the resulting sequences are stored in lists for model input.

The converted data is then fed into the GRU model, which is trained using the Adam optimizer. Adam calculates both the first-order moment (mean) and the second-order moment (uncentered variance) of the gradients and applies bias correction to prevent small initial updates. After training, the model is evaluated using Mean Squared Error (MSE), which measures the average squared difference between predicted and actual values. A lower MSE indicates better model fitting. We train the model for 30 epochs and validate its performance on both training and validation datasets.

4.2. Sharding Method Based on NLS

We propose a Node Load Score (NLS)-based sharding method to achieve transaction load balancing across shards. At the beginning of each epoch, nodes are reassigned to shards based on their NLS. A higher NLS indicates stronger transaction processing capability and a better resource configuration, while a lower NLS suggests limited capacity. Our method considers both the NLS and its volatility to determine the optimal shard assignment for each node.

The NLS algorithm is designed for a sharded blockchain system based on node reputation to enhance blockchain scalability. The specific process is as follows: First, a node reputation assessment method is designed. This method combines the number of node transactions predicted by a transaction prediction model with the node’s historical transaction behavior to form a node reputation score. Initial sharding is performed based on node reputation scores before each iteration period. Next, to address load balancing among nodes, a polling mechanism dynamically adjusts node assignments to minimize load disparities between shards, adapting to dynamic node changes. Note that although NLS handles dynamic changes between nodes, these changes refer specifically to shifts in on-chain nodes across different shards. The current work does not account for sudden alterations in node behavior patterns; future research will explore scenarios where dynamic shifts in node behavior patterns impact reputation.

NLS Calculation

We use a weighted scoring method to calculate the NLS for each node. The score is derived from three main factors: predicted transaction volume, node stability, and historical performance. The formula is given in Equation (2):

$${\mathrm{NLS}}_i={\mathrm{Weight}}_p·Q_p+{\mathrm{Weight}}_s·Q_s+{\mathrm{Weight}}_h·Q_h$$

(2)

Here, $Q_p$: Quantized predicted transaction volume (0–1), output from the GRU model. $Q_s$: Quantized node stability, including online time, response time, sync status, error rate, and resource availability. $Q_h$: Quantized historical performance, including success rate, transaction efficiency, verification accuracy, participation, and violation records. ${\mathrm{Weight}}_p+{\mathrm{Weight}}_s+{\mathrm{Weight}}_h=1$: Weight coefficients balancing the contribution of each factor.

$Weigh{t}_p$, $Weigh{t}_s$, and $Weigh{t}_h$ represent the weighting coefficients for predicted transaction volume, node stability, and historical performance, respectively, with $Weigh{t}_p+Weigh{t}_s+Weigh{t}_h$ = 1. Specifically, $Weigh{t}_p$ denotes predicted transaction volume, indicating the node’s projected transaction count over the next epoch. $Weigh{t}_s$ measures node stability, encompassing uptime, response time, synchronization status, error rate, and resource availability. $Weigh{t}_h$ reflects historical performance, including success rate, transaction efficiency, validation accuracy, node participation, and past violation records. Each factor $Q_{\ast }$, where ∗ denotes p, s, and h, respectively, is computed as a weighted average of its sub-indicators, as shown in Equation (3):

$$Q_{\ast }=\sum _{k=1}^K{w}_k·x_k,\mathrm{with}\sum _{k=1}^K{w}_k=1$$

(3)

$x_k$ is the normalized value of the k-th sub-indicator and $w_k$ is its corresponding weight. All sub-indicators are normalized to the range [0, 1] to ensure consistency and comparability.

After calculating each node’s NLS, nodes must be periodically re-sharded based on this score. Additionally, to guarantee high throughput and low latency across epochs, nodes are periodically re-sharded according to their freshly computed NLS. The sharding problem is formulated as minimizing the sum of squared deviations between each shard’s aggregated NLS and the global average NLS. The objective is to minimize the squared difference between each shard’s total node transaction load and the shard’s average transaction load. The squared term ensures that load discrepancies exert a greater influence on the inter-shard load distribution, thereby incentivizing the optimization process to reduce these differences.

4.3. NLS-Chain: Load-Balanced Sharding via NLS

To guarantee high throughput and low latency across epochs, nodes are periodically re-sharded according to their freshly computed Node Load Score (NLS). The sharding problem is cast as the minimization of the sum of squared deviations between each shard’s aggregated NLS and the global average NLS. The quadratic term penalizes large imbalances more severely than a linear criterion, thus encouraging a tight load distribution.

4.3.1. Optimization Objective

Let $\mathcal{S}=\{1,\dots ,S\}$ be the set of shards, $\mathcal{N}=\{1,\dots ,N\}$ be the set of nodes, ${\lambda }_j^t\in [0,1]$ be the NLS of node j at epoch t (computed via Equation (2)), and $x_{ij}^t\in \{0,1\}$ indicate whether node i is assigned to shard j at epoch t. The total NLS of shard j is $Su{m}_j^t$ (ref. Equation (4)) and the ideal average NLS per shard is $Av{g}^t$ (ref. Equation (5)).

$${\mathrm{Sum}}_j^t=\sum _{i\in \mathcal{N}}{\lambda }_i^t{x}_{ij}^t,$$

(4)

$${\mathrm{Avg}}^t={\displaystyle \frac{1}{S}}\sum _{j\in \mathcal{S}}{\mathrm{Sum}}_j^t={\displaystyle \frac{1}{S}}\sum _{i\in \mathcal{N}}{\lambda }_i^t.$$

(5)

$$\underset{\{x_{ij}^t\}}{min}\sum _{j\in \mathcal{S}}{\left({\mathrm{Sum}}_j^t-{\mathrm{Avg}}^t\right)}^2\mathrm{subject}\mathrm{to}\sum _{j\in \mathcal{S}}{x}_{ij}^t=1\forall i\in \mathcal{N}$$

(6)

Equation (6) is a convex quadratic assignment problem and an exact solution is NP-hard for large N. NLS-Chain therefore employs a fast greedy heuristic:

• Sort nodes by descending ${\lambda }_i^t$;
• Round-robin assignment to obtain equal-sized shards;
• Iteratively migrate the node that yields the largest marginal reduction in (6) until no improvement is possible.

The heuristic converges within 5–10 iterations and scales linearly with N.

4.3.2. Throughput Evaluation

Table 1. Comparison of average TPS.

Shard Size	Random	LB-Chain	NLS-Chain
4	276	323	392
8	477	512	670
16	612	713	873
32	895	1362	1955

summarizes the average TPS achieved under increasing shard counts. NLS-Chain consistently outperforms both random sharding and LB-Chain [19], delivering up to $2.2\times$ higher throughput when $S=32$.

5. Experiment

We conduct experiments on three public datasets: Set12, KITTI, and DOTA [21]. Set12 is a standard benchmark for image denoising and restoration; KITTI is widely used in autonomous driving and robotics; and DOTA provides richly annotated aerial images suitable for binarization tasks. In the experiment, all datasets from SET12 (12 grayscale images, including Lena, Cameraman, House, Pepper, Fishstar, Monarch, Airplane, Parrot, Barbara, Ship, Man, and Couple) and the left color images from the Road/Lane Detection Evaluation 2013 dataset in KITTI are selected as algorithm application data. The data is collected from various real-world environments such as urban areas, rural landscapes, and highways. From the DOTA-V1.0 dataset, 300 images are randomly selected by category as algorithm application data, primarily including baseball diamond, tennis court, basketball court, track field, harbor, bridge, large vehicle, small vehicle, helicopter, roundabout, soccer field, and swimming pool.

Five metrics are adopted to quantify similarity and discrepancy: SSIM, RMSE, MAE, AER, and IL. Note that, in this paper, OTSU-GK is primarily employed for image binarization to enhance feature extraction, rather than for pixel-level classification. Therefore, metrics such as SSIM and RMSE, instead of precision and recall, are used to measure the similarity between the binarized image and either the original image or the expected image.

5.1. Results of OTSU-GK

To justify the optimization of OTSU in OTSU-GK, we first compare three adaptive thresholding strategies on Set12.

Table 2. Adaptive thresholding results on Set12. * Higher is better; all others prefer lower values.

Method	SSIM *	RMSE	MAE	AER	IL
OTSU	0.5230	90.10	80.04	0.314	6.156
MEAN	0.1903	123.53	108.05	0.424	6.066
GAUSSIAN	0.1748	127.91	112.37	0.441	6.092

shows that plain OTSU obtains the highest SSIM and the lowest RMSE, MAE, AER, and IL. It is therefore selected as the baseline for subsequent Gaussian kernel enhancement.

We next randomly sample 300 images from KITTI and DOTA to evaluate OTSU-GK. KITTI: SSIM improves by 74.3% and RMSE/MAE/AER by 58.7%, and IL is reduced by 70.3% (Figure 5 and Figure 6). DOTA: SSIM improves by 61.3% and RMSE/MAE/AER by 43.3%, and IL is reduced by 52.3% (Figure 7 and Figure 8). The consistent gains demonstrate that the Gaussian kernel average preserves structural details while suppressing noise. Test results on the KITTI and DOTA datasets show improvements in the Structural Similarity Index (SSIM) of 60% and 61.3%, respectively, indicating enhanced preservation of structural information in processed images and visual quality closer to the original images. Root mean square error (RMSE)/Mean Absolute Error (MAE)/Average Error Rate (AER) improved by 63.7% and 43.3%, respectively, reflecting enhanced pixel-level reconstruction accuracy and significantly reduced discrepancies between algorithm outputs and target images. The information loss metric improved by 57.3% and 52.3%, proving that the optimized algorithm more effectively preserves the original information and detailed features of the image. The synergistic improvement in these metrics collectively validates the effectiveness of the proposed algorithmic enhancements across three dimensions: perceptual quality, numerical accuracy, and information integrity.

5.2. Ablation Study

We further verify the contribution of each component on KITTI. OTSU-GK denotes the basic Gaussian kernel enhancement; OTSU-GK* denotes the version whose kernel parameters ($\sigma$, size) are optimized by grid search. The asterisks in

Table 3. Ablation results on KITTI.

Method	SSIM ↑	RMSE ↓	IL ↓
OTSU-GK	+60.0%	+63.7%	+57.3%
OTSU-GK *	+74.3%	+58.7%	+70.3%

represent the algorithms with parameters optimized through grid search. From Table 3, grid search brings an extra 14.3% SSIM boost and 13% IL reduction, confirming the necessity of systematic hyperparameter tuning. It should be noted that the row for the OTSU method in Table 3 is blank: the optimization rates of the other two methods for the column attribute indicators are calculated relative to OTSU (with OTSU as the baseline), so no numerical values are provided for the OTSU row. The step size of the grid search in the experiment ensures global exploration while keeping computational overhead manageable, with a low risk of discretization. This is because finer step sizes (e.g., $\sigma$ step size of 0.1) did not yield significant performance improvements in preliminary experiments. Note that the smoothing property of the Gaussian kernel reduces abrupt changes at image boundaries through a weighted average threshold matrix, thereby preserving edge continuity. As weights decay with distance, adjacent image thresholds are fused, minimizing boundary artifacts.

5.3. Throughput of NLS-Chain

We implement a prototype of NLS-Chain in Python 3.9 under PyCharm (https://www.jetbrains.com/pycharm/). The simulation comprises 500 geographically distributed nodes that communicate via the Gossip protocol; transaction generation and block validation are driven by SimPy. The test-bed is an Intel i7-8550U machine with 8 GB RAM; inter-node bandwidth is set to 35 Mbps with full-mesh connectivity.

We measure steady-state TPS over 50 epochs while varying the number of shards $S\in \{4,8,16,32\}$. Figure 9 reports both average TPS and 95th-percentile TPS (after discarding the top/bottom 5% outliers). NLS-Chain consistently surpasses the two baselines:

• Random: Nodes and transactions are randomly assigned to shards.
• LB-Chain: It predicts node traffic via LSTM and re-shards through account migration.

As summarized in

Table 4. Average TPS vs. shard count (500 nodes).

Shards	Random	LB-Chain	NLS-Chain
4	276	323	392
8	477	512	670
16	612	713	873
32	895	1362	1955

, NLS-Chain delivers up to 83% higher average TPS than LB-Chain when $S=32$, while maintaining linear scalability with the number of shards.

6. Conclusions

We present OTSU-UCAN, a unified framework for secure and efficient vehicle navigation in 6G satellite–terrestrial networks. OTSU-GK enhances embedded image binarization via a Gaussian kernel weighted threshold, while NLS-Chain guarantees privacy-preserving, load-balanced sharding with up to 83% TPS gain. Future work will explore adaptive kernel selection and dynamic re-sharding intervals to further boost performance. In addition, future works will also include exploring adaptive step size strategies to optimize search efficiency.