Fully-Cascaded Spatial-Aware Convolutional Network for Motion Deblurring

Abstract

Motion deblurring is an ill-posed, challenging problem in image restoration due to non-uniform motion blurs. Although recent deep convolutional neural networks have made significant progress, many existing methods adopt multi-scale or multi-patch subnetworks that involve additional inter-subnetwork processing (e.g., feature alignment and fusion) across different scales or patches, leading to substantial computational cost. In this paper, we propose a novel fully-cascaded spatial-aware convolutional network (FSCNet) that effectively restores sharp images from blurry inputs while maintaining a favorable balance between restoration quality and computational efficiency. The proposed architecture consists of simple yet effective subnetworks connected through a fully-cascaded feature fusion (FCFF) module, enabling the exploitation of diverse and complementary features generated at each stage. In addition, we design a lightweight spatial-aware block (SAB), whose core component is a channel-weighted spatial attention (CWSA) module. The SAB is integrated into both the FCFF module and skip connections, enhancing feature fusion by enriching spatial detail representation. On the GoPro dataset, FSCNet achieves 33.01 dB PSNR and 0.962 SSIM, delivering comparable or higher accuracy than state-of-the-art methods such as HINet, while reducing model size by nearly 80%. Furthermore, when the GoPro-trained model is evaluated on three additional benchmark datasets (HIDE, REDS, and RealBlur), FSCNet attains the highest average PSNR (29.53 dB) and SSIM (0.903) among all compared methods. This consistent cross-dataset superiority highlights FSCNet’s strong generalization and robustness under diverse blur conditions, confirming that it achieves state-of-the-art performance with a favorable performance–complexity trade-off.

1. Introduction

In practical computer vision applications, the observed images or videos are often blurred due to camera moves, object moves, and light changes [1,2,3]. Specifically, due to camera shaking, quickly moving objects, and low shutter speed, motion blur commonly occurs. Motion blur leads to low-quality images and information loss, such as object boundaries, texture details, and image colors. Thus, image deblurring is a fundamental task in computer vision [4,5].

In recent years, image deblurring approaches based on deep convolutional neural networks (CNNs) have been increasingly studied. Early attempts focus on employing CNNs to estimate the motion-blur kernel [5,6]. Despite effectiveness in deblurring images with simple blur kernels, these methods cannot effectively tackle complex non-uniform blurs caused by multiple factors, such as moving objects, camera shaking, and depth variations, which often occur in real-world scenarios. To address this challenge, recently methods [7,8,9,10,11,12,13,14,15,16,17,18,19] exploit end-to-end CNN models to generate sharp images from blurry images caused by complex motion blurs. These methods typically adopt the encoder–decoder CNN architecture, in which encoders are used to extract primary contextual information of latent blurry images and decoders are then exploited to recover sharp images.

Although these methods have strengths in preserving contextual details for motion deblurring, they also lose a lot of substantial spatial details due to the decreased receptive field of encoders [20]. Many recent deblurring networks attempt to address this limitation by implementing two types of structures: multi-scale structure and multi-patch structure (according to the input), as shown in Figure 1a and Figure 1b, respectively. Both types of structures endeavor to employ the diversity and complementarity of the features obtained from multiple sub-networks to achieve better deblurring results.

Multi-scale methods [7,8,9,10,11] enhance the diversity of extracted features by changing the scale of the input image. Differently, multi-patch methods [12,13,14] enrich the extracted features by slicing the input blurry image into multiple patches. Both schemes yield better deblurring results than traditional networks.

However, both multi-scale and multi-patch networks still have the following shortcomings. (1) The scaling process from a blurry image to a low-resolution image in multi-scale methods leads to the spatial information loss, especially for the edges of objects. (2) The partitioned patches in multi-patch methods result in discontinuous contextual information, which may degrade the quality of the resultant sharp images [21]. (3) Most of the multi-scale and multi-patch networks aim at, in principle, changing the input image to produce diverse features for better deblurring, but neglect the diverse yet complementary features generated from different sub-networks. (4) Although multi-scale and multi-patch networks rely on additional processing for multiple scales or patches to extract more representative features and enhance performance, they inevitably increase computational complexity.

After revising the merits and limitations of existing deblurring methods, we propose a novel and efficient fully-cascaded spatial-aware convolutional network (namely FSCNet) for motion deblurring. Our network is able to effectively restore sharp images from blurry images while maintaining relatively low computational complexity. It has the following advantages over existing methods.

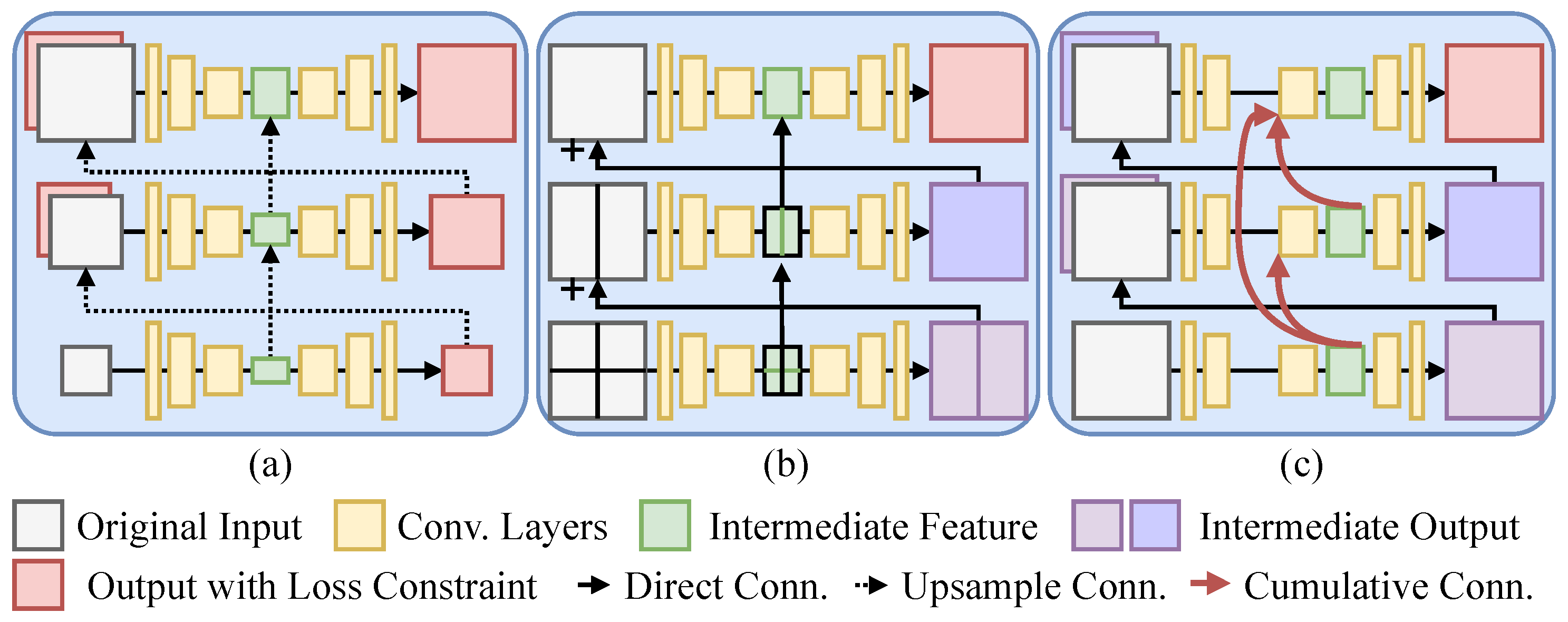
• We design a simple yet effective deblurring network with invariant-scale inputs. This network consists of multi-stage sub-networks, which process input images without downscaling them or splitting them into patches, as shown in Figure 1c. Moreover, we fully cascade all sub-networks (rather than only two adjacent ones) to enable each higher-level sub-network to progressively reuse features from all lower-level sub-networks.
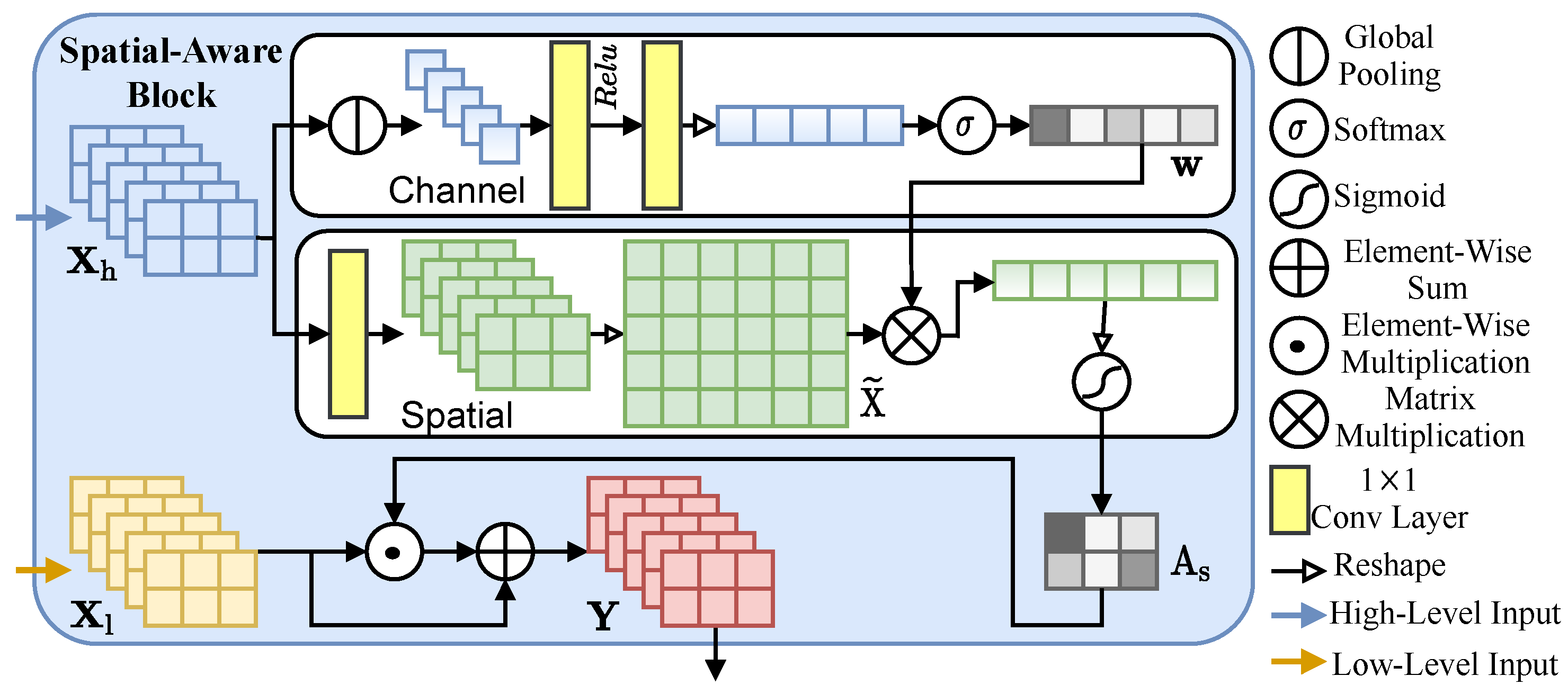
• We devise a lightweight spatial-aware block (SAB) that incorporates a novel channel-weighted spatial attention (CWSA) mechanism, which adopts a channel-weighted summation instead of the conventional channel pooling. SAB enhances the extraction and representation of spatial features. When integrated into both the fully-cascaded feature fusion (FCFF) and skip connections, SAB facilitates more effective feature fusion and spatial detail compensation, thereby further improving deblurring performance.
• We conduct extensive experiments on four representative datasets to evaluate the performance of the proposed FSCNet. Experimental results demonstrate that our method outperforms the state-of-the-art (SOTA) methods while maintaining a favorable performance–complexity trade-off.

2. Related Work

This section reviews the related deblurring methods, with a particular focus on those based on convolutional networks.

2.1. End-to-End Deblurring Driven by Convolutional Networks

In end-to-end image processing methods, a multi-stage strategy has long been a prevalent design paradigm, enabling progressive refinement of features and mitigating the difficulty of direct mapping from degraded to high-quality images. This is a trend that was later exemplified in tasks like forgery detection [22,23,24] and image enhancement [25,26]. Early end-to-end deblurring methods followed this established trend, also leveraging multi-stage designs to address motion blur. These works primarily focused on bridging the mapping gap between blurred and sharp images through structural optimizations, with multi-scale modeling and parameter sharing being two core optimization directions.

Beyond architectural design, a key characteristic of end-to-end methods lies in their training data paradigm: most rely on sharp images and artificially synthesized blurred images for training. This has long been a mainstream approach, given the scarcity of real blurry images paired with their sharp ground-truths for supervised learning.

Nah et al. [7] generated a dataset with pixel-aligned sharp and blur image pairs by utilizing high-speed cameras and neighborhood fusion techniques in the temporal domain, and proposed a multi-scale deblurring CNN model for mimicking conventional coarse-to-fine optimization methods. However, each scale of this network adopts independent parameters, resulting in a large model size. Moreover, Tao et al. [8] presented a scale-recurrent network to reduce the model size and improved the training stability by sharing network parameters at different scales. In addition, Gao et al. [10] proposed a deblurring scheme based on a general and effective parameter-sharing scheme with an integration with a nested skip connection structure.

Beyond multi-scale design, multi-patch modeling has also emerged as an effective way to boost end-to-end performance. For example, Zhang et al. [12] devised a deep hierarchical multi-patch model by exploiting the deblurring cues at different scales. Cho et al. [16] proposed a multi-input multi-output U-net to achieve an excellent image deblurring effect by considering the strategy from the coarse grain to fine grain.

However, among these end-to-end methods, those with cascaded structures (often referred to as “partial cascades”) only reuse features between adjacent stages, failing to fully exploit contextual information from all lower levels. Additionally, with the demand for real-time deblurring, recent works (e.g., LNNet [27]) have focused on lightweight end-to-end architectures, but often sacrificed deblurring accuracy for lightweight design. These gaps (limited feature reuse in partial cascades, trade-off between accuracy and efficiency) motivate our fully-cascaded design, which aims to balance comprehensive feature reuse and model compactness.

2.2. Attention-Enhanced Deblurring in Convolutional Networks

The attention mechanism has been widely and successfully applied to high-level vision tasks, such as image classification [28,29], detection [30,31], and segmentation [32,33]. Its core advantage, which is the ability to adaptively highlight discriminative features, has driven its extension to low-level vision tasks, particularly image deblurring [9,11,13,15], where it helps focus on blur-relevant regions or features to enhance restoration quality.

Early attention-based deblurring methods focused on either region-specific or non-local feature modeling. For example, Shen et al. [9] developed a three-branch framework that targets foreground human blur, background blur, and global blur respectively, and they equipped it with a human-aware attention module to prioritize deblurring of visually critical human regions. Purohit et al. [15] further explored non-local dependencies by leveraging self-attention to capture pixel-wise correlations across spatial locations, though this approach introduces high computational complexity. Building on these efforts, advanced methods have refined attention designs for more comprehensive feature modeling. Suin et al. [13] proposed a hybrid approach that integrates global channel attention and adaptive local spatial filters as relatively independent components, aiming to balance global context and local details. Complementing this work, Liu et al. [11] focused on high-frequency information such as edges and textures, which are key elements degraded by motion blur, and designed a high-frequency attention module to enhance the reconstruction of such fine-grained features.

Despite these advancements, most attention-based deblurring methods suffer from two critical limitations: they either rely on complex gating mechanisms, which increase inference latency, or they fail to model the mutual dependence between channel and spatial dimensions, which results in suboptimal feature refinement. To address these issues, we do not use self-attention due to its high computational complexity and propose a channel-weighted spatial attention (CWSA) module. By fusing channel importance weights directly into spatial attention generation, CWSA captures the interplay between channel and spatial dimensions while maintaining low computational complexity, which enables seamless integration into our fully-cascaded network.

3. Methodology

This section provides an overview of the overall network architecture, multi-stage sub-networks, fully-cascaded feature fusion (FCFF) module, spatial-aware block (SAB) incorporating the channel-weighted spatial attention (CWSA), and the adopted loss function.

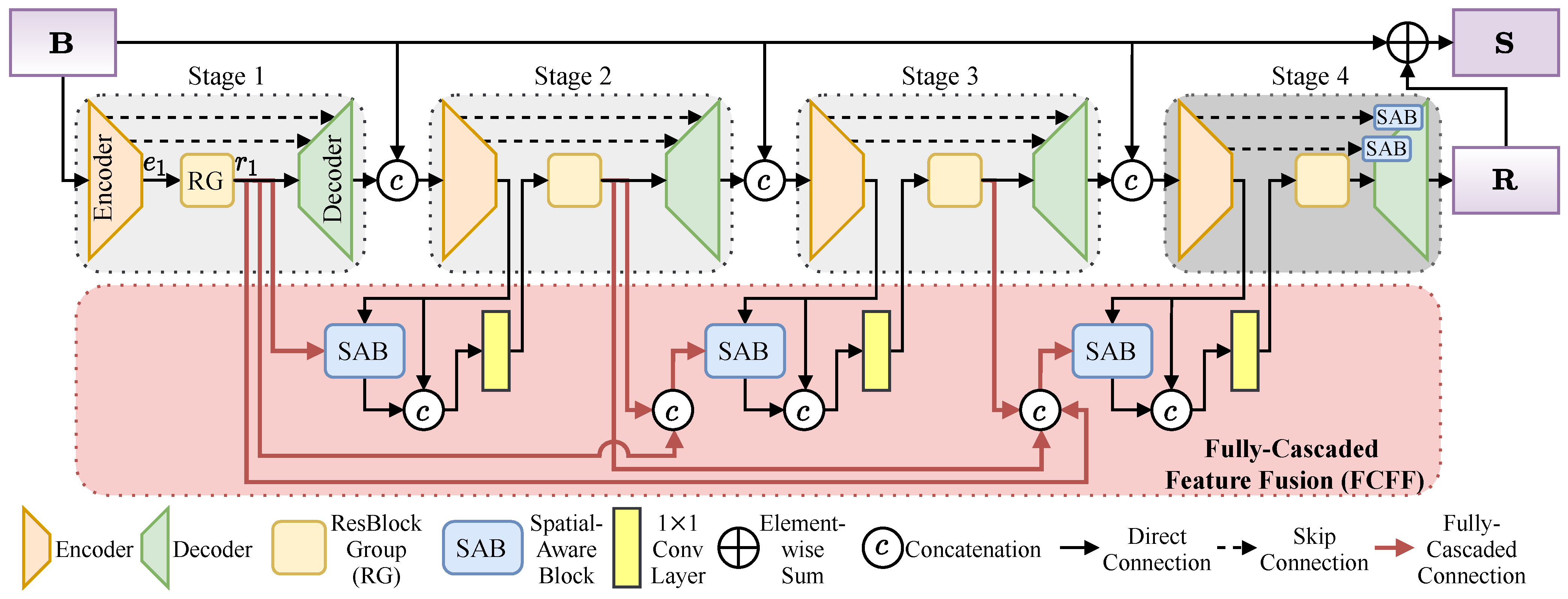
3.1. Overview

The architecture of the proposed FSCNet is illustrated in Figure 2. It consists of four sub-networks, representing four stages, which cumulatively process deblurring features of blurry images. Particularly, each stage has direct access to the original input blurry image $\mathbf{B}$. In each sub-network, the encoder transforms (i.e., conducts downsampling) the input data into intermediate features with smaller sizes and exploits more channels to capture both contextual and spatial features. The decoder then recovers (i.e., it performs upsampling) these features to obtain the output $\mathbf{R}$, which is then added to the input $\mathbf{B}$ to obtain the sharp image $\mathbf{S}$.

In contrast to existing multi-scale and multi-patch architectures [8,10,12,13], sub-networks in our FSCNet process blurry images without downscaling the original inputs or splitting them into smaller regions (i.e., patches). As a result, both edge information and continuous contextual details are well preserved (see Section 3.2). More importantly, a fully-cascaded network is designed to connect all sub-networks (unlike connecting only two adjacent sub-networks in most of the existing methods) so as to propagate the transmission of diverse yet complementary deblurring information across the entire network. Thereafter, fully-cascaded sub-networks can reuse the refined features acquired from other sub-networks, consequently enriching the deblurring features (see Section 3.3). Furthermore, we design an SAB that is implemented with a novel channel-weighted spatial attention. The integration of SAB with the fully-cascaded network can further enhance the fusion of deblurring features by offering more spatial details (see Section 3.4).

Notably, the base architecture of FSCNet, featuring a multi-stage framework with invariant-scale input processing, already provides high deblurring performance while maintaining moderate computational complexity (see Section 4.2.2). The invariant-scale strategy eliminates redundant operations inter-subnetwork associated with multi-scale and multi-patch processing, allowing this architecture to achieve strong restoration capability without excessive computation. Building upon this efficient design, FCFF and SAB are integrated to further enhance feature fusion and spatial detail representation. Integrating FCFF and SAB on the GoPro dataset improves PSNR by 0.23 dB with only a 0.42% increase in FLOPs (see Section 4.2.2). These results demonstrate that FSCNet improves deblurring performance through a systematically efficient design: the base architecture effectively reduces redundant computation, and the lightweight modules provide incremental gains at negligible computational cost, together achieving a favorable performance–complexity trade-off compared with conventional multi-scale or multi-patch architectures.

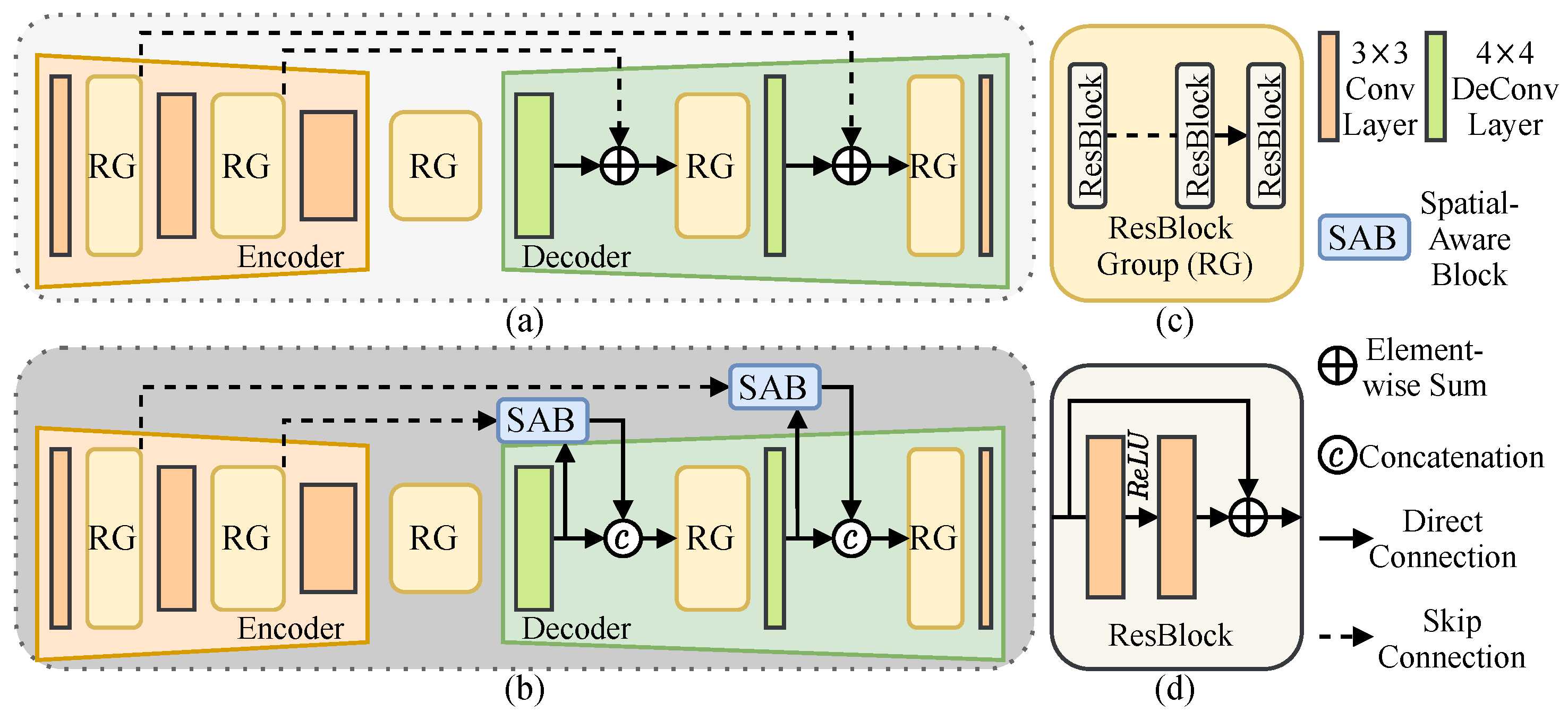
3.2. Multi-Stage Sub-Networks

The multi-stage sub-networks are connected by the fully-cascaded feature fusion module. Figure 3 elaborates on the detailed design of the sub-network at each stage. Particularly, each sub-network consists of an encoder and a decoder. Each encoder consists of three convolution layers and two ResBlock groups (RGs). Each decoder consists of two deconvolution layers, one convolution layer, and two RGs. Each RG consists of n ResBlocks. To achieve a balance between efficiency and performance, we choose $n=7$ in our experiments. In the encoder, the first convolution layer processes the input into 32 feature maps. The second and third convolution layers conduct downsampling to halve their inputs and then output 64 and 128 feature maps, respectively. In the decoder, these two deconvolution layers conduct upsampling to double the size of their inputs and then output 64 and 32 feature maps, respectively. The last convolution layer transforms its input into a three-channel image with the same resolution as the original input. For each RG, the number of input channels is the same as that of the output channels of the previous layer. We use skip connections to connect the encoder with the decoder in each sub-network so as to transmit more image details to the decoder, thereby improving the deblurring performance [20].

Each stage except for the last stage adopts the identical sub-network as depicted in Figure 3a. The last stage adopts a distinct sub-network in Figure 3b by introducing (i) SABs to skip connections and (ii) concatenation operations. Such a design preserves more spatial features by refining the low-level features from the encoder. Moreover, the introduction of SABs to skip connections further enhances the extraction of spatial features. This design is beneficial to image restoration since more spatial features are used to restore sharp images, especially important for the last stage, which directly outputs the final result.

3.3. Fully-Cascaded Feature Fusion

In our framework, we design a fully-cascaded feature fusion (FCFF) module to reuse the refined features across different sub-networks by connecting each sub-network. The architecture of FCFF is shown at the bottom of Figure 2.

We denote the output of the encoder of i-th sub-network by $e_i$. Meanwhile, ${\mathcal{R}}_i$ denotes the ResBlock group between the encoder and the decoder of the i-th sub-network, and $r_i$ denotes the output of ${\mathcal{R}}_i$. In particular, for the sub-network at Stage 1, we have $r_1={\mathcal{R}}_1\left(e_1\right)$. Regarding the subsequent i-th ($i>1$) sub-network, the input of ${\mathcal{R}}_i$ includes the output $e_i$ of the current encoder and outputs $(r_1,\dots ,r_{i-1})$ of all previous sub-networks. Moreover, we introduce SAB, denoted as ${\mathcal{F}}_{\mathrm{SAB}}$ (explained in Section 3.4), to use the features obtained by the subsequent stage to refine the features extracted at the preceding stages. Consequently, for the i-th ($i>1$) sub-network, we have

$$r_i={\mathcal{R}}_i\left(f_{\mathrm{conv}}^i\left[e_i,{\mathcal{F}}_{\mathrm{SAB}}(e_i,[r_1,\dots ,r_{i-1}])\right]\right),$$

(1)

where $[·]$ denotes the concatenation operation. Note that we concatenate multiple inputs of ${\mathcal{R}}_i(·)$ in Equation (1) into a single tensor and use a $1\times 1$ convolution (i.e., $f_{\mathrm{conv}}^i$) to unify the number of channels of this tensor to 128.

3.4. Spatial-Aware Block

To enhance the extraction of features, especially for spatial features, we design a lightweight SAB to refine the extracted spatial features. As shown in Figure 4, our SAB contains two inputs: a high-level feature map ${\mathbf{X}}_{\mathrm{h}}\in {\mathbb{R}}^{C\times H\times W}$ and a low-level feature map ${\mathbf{X}}_{\mathrm{l}}\in {\mathbb{R}}^{C\times H\times W}$, where C and $H\times W$ denote the number of channels and the spatial dimension, respectively.

In SAB, the spatial attention mechanism plays an important role in deciding which key regions to focus on. Instead of using general channel pooling [28] to produce the attention mask, we propose a channel-weighted spatial attention that uses the channel-weighted sum to reduce the channel dimension to 1, i.e., combines different weights of channel and spatial dimensions to produce the spatial attention mask. Since the higher-level features contain more accurate contextual features, we utilize the high-level feature map ${\mathbf{X}}_{\mathrm{h}}$ to dominate CWSA.

Figure 4 depicts the working flow of SAB. First, for the input hight-level feature map ${\mathbf{X}}_{\mathrm{h}}$, we compute the channel weights $\mathbf{w}$ of the feature map. We then conduct the matrix multiplication on both $\mathbf{w}$ and the reshaped feature map $\tilde{\mathrm{X}}$ to obtain the attention of each position. Finally, we use the sigmoid function to normalize the above attention to obtain the final attention mask ${\mathrm{A}}_{\mathrm{s}}$.

We present the detailed derivation of ${\mathrm{A}}_{\mathrm{s}}$ as follows. First, we rewrite ${\mathbf{X}}_{\mathrm{h}}$ as ${\mathbf{X}}_{\mathrm{h}}=[{\mathrm{X}}_1,{\mathrm{X}}_2\dots ,{\mathrm{X}}_C]$, and use ${\mathrm{X}}_c\in {\mathbb{R}}^{H\times W}$ to denote the c-th channel of ${\mathbf{X}}_{\mathrm{h}}$. Meanwhile, we use ${\mathrm{X}}_c(i,j)$ to represent the value of ${\mathrm{X}}_c$ at position $(i,j)$. To aggregate the spatial information and compute the channel weights, we adopt the global average pooling to compress the spatial dimension of the input feature map and generate a global average-pooled feature $\mathbf{z}\in {\mathbb{R}}^{C\times 1}$. Let $\mathbf{z}=[{\mathrm{z}}_1,{\mathrm{z}}_2\dots ,{\mathrm{z}}_C]$, then the c-th element of $\mathbf{z}$ is defined as

$${\mathrm{z}}_c={\mathcal{F}}_{\mathrm{GAP}}\left({\mathrm{X}}_c\right)={\displaystyle \frac{1}{H\times W}}\sum _{i=1}^H\sum _{j=1}^W{\mathrm{X}}_c(i,j),$$

(2)

where ${\mathcal{F}}_{\mathrm{GAP}}(·)$ is the global average pooling function.

Then, we perform two $1\times 1$ convolution operations (i.e., $f_{{\mathrm{conv}}_1}$ and $f_{{\mathrm{conv}}_2}$) on the feature $\mathbf{z}$ to learn a nonlinear interaction between channels. The channel-wise statistic $\mathbf{s}\in {\mathbb{R}}^C$ can be obtained by

$$\mathbf{s}=f_{{\mathrm{reshape}}_1}\left(f_{{\mathrm{conv}}_1}\left(ReLU\left[f_{{\mathrm{conv}}_2}\left(\mathbf{z}\right)\right]\right)\right),$$

(3)

where the tensor-reshape operation $f_{{\mathrm{reshape}}_1}$ changes the shape of the output from $C\times 1$ to $1\times C$. Moreover, we employ the following softmax function to normalize $\mathbf{s}$ and get the channel weights $\mathbf{w}\in {\mathbb{R}}^C$:

$$w_c={\displaystyle \frac{\exp \left(s_c\right)}{{\sum }_{c=1}^C\exp \left(s_c\right)}},$$

(4)

where $w_c$ and $s_c$ are the c-th element of $\mathbf{w}$ and $\mathbf{s}$, respectively. The channel weights indicate the impact of the c-th channel on the whole channels.

Next, we transform the input feature map ${\mathbf{X}}_{\mathrm{h}}$ into a new feature space $\tilde{\mathrm{X}}\in {\mathbb{R}}^{C\times HW}$. In particular, a $1\times 1$ convolution operations $f_{{\mathrm{conv}}_3}$ is performed on ${\mathbf{X}}_{\mathrm{h}}$. Thus, we have

$$\tilde{\mathrm{X}}=f_{{\mathrm{reshape}}_2}\left(f_{{\mathrm{conv}}_3}\left({\mathbf{X}}_{\mathrm{h}}\right)\right),$$

(5)

where the tensor-reshape operation $f_{{\mathrm{reshape}}_2}$ transforms the shape of the output from $C\times H\times W$ to $C\times HW$.

Finally, we conduct the matrix multiplication operation on the channel weights $\mathbf{w}$ and the new feature map $\tilde{\mathrm{X}}$. The nonlinear activation function sigmoid is used to obtain the final spatial attention mask ${\mathrm{A}}_{\mathrm{s}}$:

$${\mathrm{A}}_{\mathrm{s}}=\mathrm{sigmoid}\left(f_{{\mathrm{reshape}}_3}(\mathbf{w}\otimes \tilde{\mathrm{X}})\right),$$

(6)

where ⊗ denotes the matrix multiplication. The tensor-reshape operation $f_{{\mathrm{reshape}}_3}$ can transform the shape of calculation results from $1\times HW$ to $H\times W$. Analyzing Equations (4)–(6), we know that the attention mask ${\mathrm{A}}_{\mathrm{s}}$ contains the information on both spatial and channel dimensions. In particular, ${\mathrm{A}}_{\mathrm{s}}$ presents the spatial attention mask of feature map ${\mathbf{X}}_{\mathrm{h}}$ with the impact of each channel.

We use the attention mask ${\mathrm{A}}_{\mathrm{s}}$ to re-calibrate the low-level feature ${\mathrm{X}}_{\mathrm{l}}$ so as to finally output $\mathbf{Y}={\mathrm{X}}_{\mathrm{l}}+{\mathrm{X}}_{\mathrm{l}}\odot {\mathrm{A}}_{\mathrm{s}}$, where ⊙ is the element-wise multiplication. For convenience, let $\mathbf{Y}={\mathcal{F}}_{\mathrm{SAB}}({\mathbf{X}}_{\mathrm{h}},{\mathbf{X}}_{\mathrm{l}})$ and ${\mathrm{A}}_{\mathrm{s}}={\mathcal{F}}_{\mathrm{SP}}\left({\mathbf{X}}_{\mathrm{h}}\right)$, the equation of $\mathbf{Y}$ can be rewritten as follows:

$${\mathcal{F}}_{\mathrm{SAB}}({\mathbf{X}}_{\mathrm{h}},{\mathbf{X}}_{\mathrm{l}})={\mathbf{X}}_{\mathrm{l}}+{\mathbf{X}}_{\mathrm{l}}\odot {\mathcal{F}}_{\mathrm{SP}}\left({\mathbf{X}}_{\mathrm{h}}\right).$$

(7)

In SAB, the computational complexity depends on $\left(1,C\right)\times \left(C,HW\right)$ matrix multiplication in Equation (6) and has a complexity of $\mathcal{O}\left(CHW\right)$. Thus, the proposed SAB is computationally lightweight while it can effectively enhance the restoration of sharp images. Experimental results in Section 4.2 will demonstrate the effectiveness of our SAB.

3.5. Loss Function

Our FSCNet follows the idea of residual learning [34], which does not directly predict the restored sharp image $\mathbf{S}$ but predicts the residual image $\mathbf{R}$. We then add the resulting image $\mathbf{R}$ to the original blurred image $\mathbf{B}$ to obtain the sharp image $\mathbf{S}$, i.e., $\mathbf{S}=\mathbf{R}\oplus \mathbf{B}$. In particular, we only use the loss function at the output of the last stage. Rather than using the mean square error (MSE) function, we use a more robust Charbonnier penalty function [35] to approximate the ground-truth image $\mathbf{G}$ successively. Finally, we establish the loss function of our FSCNet as follows:

$$\mathcal{L}=\sqrt{{(\mathbf{R}\oplus \mathbf{B}-\mathbf{G})}^2+{\epsilon }^2},$$

(8)

where $\epsilon$ is the penalty coefficient chosen as $0.001$.

4. Experiments

This section first presents the key implementation details of our FSCNet, then compares its deblurring performance with that of state-of-the-art methods and, finally, conducts an ablation study to validate the effectiveness of the network’s key components.

4.1. Experimental Settings

Dataset: We mainly adopt four representative datasets: GoPro [7], HIDE [9], REDS [36], and RealBlur [37] datasets in our experiments. The GoPro dataset consists of 3214 pairs of blurred and clean images extracted from 33 captured sequences. The HIDE dataset is generated from 31 high-fps (frames per second) videos that consist of realistic outdoor scenes with various numbers, poses, and appearances of humans at various distances. The REDS dataset is generated from 300 videos at 120 fps, synthesizing blurry frames by merging subsequent frames. All images of the RealBlur dataset are captured from the camera in raw and JPEG formats. These geometrically aligned image pairs are divided into two categories: RealBlur-R generated by raw images, and RealBlur-J generated by JPEG images. We follow the same configurations as [7] and the model is trained with 2103 image pairs from the GoPro [7] dataset. For testing, we use 1111 image pairs from the GoPro [7], 2025 image pairs from the HIDE [9], 3000 image pairs from the deblurring validation set of REDS [36], and 980 image pairs from the RealBlur-R [37] dataset, and 980 image pairs from the RealBlur-J [37] dataset. The images in the GoPro, HIDE, and REDS datasets have a uniform resolution of 1280 × 720 pixels, whereas the RealBlur dataset contains images with varying resolutions, with heights ranging from 736 to 769 pixels and widths ranging from 652 to 675 pixels.

Implementation Details: We implement FSCNet (the source code are available at: https://github.com/CaiGuoHS/FSCNet, accessed on 30 September 2025) using the PyTorch library on a single NVIDIA Tesla V100 GPU, and train it for 3000 epochs with a batch size of 8. We employ the Adam optimizer with ${\beta }_1=0.9$, ${\beta }_2=0.999$, and a weight decay coefficient of $\lambda ={10}^{-8}$. The learning rate is scheduled using a combination of gradual warmup and cosine annealing: it linearly increases from 0 to ${10}^{-4}$ during the first three epochs and then decays from ${10}^{-4}$ to ${10}^{-6}$ via cosine annealing [38]. To alleviate overfitting during training, we apply several targeted data augmentation techniques to preprocess the training dataset: specifically, input images are first randomly rotated by 90 degrees, 180 degrees, 270 degrees, and 360 degrees; we then perform gamma correction on the images and adjust the color saturation using a random saturation factor within $(0.5,1.5]$. Finally, the processed images are randomly cropped by $256\times 256$ pixels. To ensure compatibility with the model, which requires input dimensions to be multiples of 8, images from the GoPro, HIDE, and REDS datasets are directly used since their resolutions already meet this requirement. In contrast, RealBlur images with varying resolutions are adjusted using edge padding to satisfy the dimensional constraint.

Evaluation Metric: To ensure fair and consistent evaluations, we define the core metrics adopted throughout both ablation and comparative experiments as follows. For deblurring performance, we use the peak signal-to-noise ratio (PSNR, in dB) and structural similarity index (SSIM, ranging from 0 to 1), both computed as the average over all restored test images of each dataset, where higher values indicate better consistency with the sharp ground truth. For model efficiency, we report the model size (in MB, reflecting storage overhead), the number of floating-point operations (FLOPs, in G, estimated using a $3\times 256\times 256$ input to quantify theoretical complexity), and the inference time (in ms, averaged over $3\times 720\times 1280$ images on a single NVIDIA Tesla V100 GPU, with torch.cuda.synchronize() applied to prevent PyTorch 1.8.0 asynchronous timing errors).

4.2. Ablation Study

To verify the impact of FSCNet’s key configurations on performance and computational complexity, we conduct systematic ablation experiments. All ablation experiments are performed on the GoPro dataset.

4.2.1. Impact of the Number of Stacked ResBlocks in RG

As the core structural parameter of the ResBlock Group (RG), the number of stacked ResBlocks directly determines the model’s basic feature extraction capability and computational overhead, making it the primary factor affecting the performance-complexity trade-off. We therefore first validate this variable by constructing FSCNet variants with different ResBlock counts: FSCNet-R2, FSCNet-R3, FSCNet-R4, FSCNet-R5, FSCNet-R6, FSCNet-R7, FSCNet-R8, corresponding to RGs by stacking 2, 3, 4, 5, 6, 7, and 8 ResBlocks.

As shown in

Table 1. Quantitative results of ResBlock number in RG on the GoPro test set.

Models	PSNR	SSIM	Model Size	FLOPs	Inference Time
FSCNet-R2	31.72	0.951	23.10 MB	67.05 G	171 ms
FSCNet-R3	32.23	0.955	31.91 MB	98.55 G	228 ms
FSCNet-R4	32.48	0.958	40.73 MB	130.05 G	287 ms
FSCNet-R5	32.75	0.960	49.54 MB	161.55 G	346 ms
FSCNet-R6	32.83	0.960	58.36 MB	193.05 G	405 ms
FSCNet-R7	33.01	0.962	67.18 MB	224.54 G	461 ms
FSCNet-R8	33.03	0.962	75.99 MB	256.04 G	523 ms

, the results reveal a clear trend: With the increase in ResBlock count, model performance (PSNR/SSIM) steadily improves. It rises from 31.72 dB/0.951 (FSCNet-R2) to 33.01 dB/0.962 (FSCNet-R7), as more ResBlocks enhance the model’s ability to capture fine-grained image features. However, when the number exceeds 7 (i.e., FSCNet-R8), the performance gain becomes negligible. PSNR only increases by 0.02 dB and SSIM remains unchanged at 0.962, while model size grows from 67.2 MB to 76.0 MB (an increase of 13%) and FLOPs rise from 224.54 G to 256.04 G (an increase of 14%). This leads to significant efficiency loss without meaningful performance improvement. Thus, we select 7 ResBlocks in RG as the optimal configuration for FSCNet, as it achieves the best balance between deblurring performance and computational efficiency.

4.2.2. Effectiveness of the Base Architecture, FCFF, and SAB

To verify the effectiveness of FSCNet’s core components, including the multi-stage invariant-scale input base architecture, the fully-cascaded feature fusion (FCFF) module, and the spatial-aware block (SAB). We then consider the following five models, four controlled variants (M1–M4) and the complete FSCNet, as defined below.

• M1: Base architecture only, without FCFF and all SAB modules; represents the efficient invariant-scale input foundation.
• M2: M1 combined with FCFF (without SABs); used to assess the contribution of FCFF on the base framework.
• M3: M2 with additional SABs applied to the last stage; used to evaluate the individual effect of the last-stage SABs.
• M4: M1 integrated with FCFF (with SABs); used to verify SAB’s role in feature fusion.
• FSCNet: M1 integrated with FCFF (with SABs) and last-stage SABs; represents the full configuration.

In particular, M1 demonstrates that the base architecture itself achieves strong performance by adopting subnetworks with invariant-scale input processing. This design avoids the need for redundant multi-scale or multi-patch operations while still capturing key image features, allowing the base architecture to deliver high deblurring capability without extra complexity. Even without any enhancement modules, it reaches 32.78 dB PSNR and 0.960 SSIM (

Table 2. Effectiveness evaluation of the Base Architecture, FCFF, and SAB in FSCNet.

Models	FCFF	FCFF with SABs	Last Stage with SABs	PSNR	SSIM	Model Size	FLOPs
M1	✗	✗	✗	32.78	0.960	66.00 MB	223.60 G
M2	✔	✗	✗	32.91	0.961	66.60 MB	224.20 G
M3	✔	✗	✔	32.96	0.961	66.64 MB	224.34 G
M4	✔	✔	✗	32.98	0.961	67.13 MB	224.41 G
FSCNet	✔	✔	✔	33.01	0.962	67.18 MB	224.54 G

✗ denotes the module is excluded. ✔ denotes the module is included.

), which is already comparable to top-performing networks such as HINet [17] in our comparative experiments (see Section 4.3.1). This confirms that M1 provides a strong and efficient foundation capable of achieving state-of-the-art (SOTA) performance without auxiliary modules.

Building on M1, M2 integrates FCFF (without SABs) and brings a 0.13 dB PSNR improvement with only a 0.60 G increase in FLOPs (approximately +0.27%), demonstrating its effectiveness in aggregating cross-stage features with minimal cost. Introducing SAB further enhances performance: M3 builds on M2’s FCFF (without SABs) and achieves a 0.05 dB PSNR improvement by only adding last-stage SABs, with a 0.14 G increase in FLOPs (+0.06%), while M4, which embeds SABs within FCFF, yields an additional 0.07 dB PSNR gain with a 0.21 G increase in FLOPs (+0.09%). These results confirm that SAB consistently contributes to performance improvement through two integration strategies, either applied independently at the last stage or embedded within FCFF, both requiring only marginal computational overhead.

Overall, the complete FSCNet achieves the most balanced trade-off between restoration quality and efficiency, surpassing the base model (M1) by 0.23 dB in PSNR with merely a 0.94 G (+0.42%) increase in FLOPs. These findings validate the systematic efficiency of FSCNet: the base architecture that adopts invariant-scale input processing effectively avoids redundant computation, FCFF enables efficient multi-stage feature interaction, and SAB refines spatial representation. Together, these components achieve a favorable balance between performance and computational complexity.

4.2.3. Validation of CWSA in SAB

To validate the effectiveness of the proposed CWSA, we compare it with another spatial attention mechanism integrated into SAB. Specifically, using FSCNet as the baseline, we replace the CWSA in its SAB with the Convolutional Block Attention Module (CBAM) [28], a classical module that sequentially applies channel and spatial attention, where the spatial attention is derived through simple channel pooling. This replacement forms a comparative variant designed to isolate the impact of attention design. The essential difference lies in how spatial attention is generated: unlike CBAM’s sequential channel–spatial design with pooling, the proposed SAB combines channel and spatial information by generating attention through a channel-weighted summation.

Table 3. Comparison between CWSA and CBAM when used in SAB.

Models	PSNR	SSIM	Model Size	FLOPs
SAB uses CBAM	32.60	0.959	66.66 MB	224.21 G
SAB uses CWSA	33.01	0.962	67.18 MB	224.54 G

summarizes the quantitative results of these two variants on the GoPro test set. As shown in Table 3, when CWSA is adopted in SAB, FSCNet outperforms the CBAM-based variant by 0.41 dB in PSNR. This performance gain comes with only marginal increases in FLOPs (from 224.21 G to 224.54 G), confirming the efficiency of the proposed attention mechanism.

Figure 5 visualizes the attention masks generated by CBAM and CWSA, with the corresponding blurred input image included for reference. As illustrated, the attention map from the CBAM-based SAB appears more dispersed and fails to focus on the key blurred regions of the image (e.g., the cars at the bottom). In contrast, the attention map produced by the proposed CWSA-based SAB is more concentrated and aligns well with salient edge structures and heavily blurred areas, exhibiting an attention distribution consistent with regions that require restoration. This visual comparison indicates that, unlike CBAM’s channel pooling, which averages feature responses across channels, CWSA considers the varying contributions of individual channels, resulting in finer-grained and more accurate spatial attention inference.

4.3. Performance Comparisons

We compare our method with the SOTA methods [8,10,11,12,13,15,16,17]. For fairness, all comparative experimental results are obtained by executing the source code and pre-trained models on a single NVIDIA Tesla V100 GPU server. Since the authors [13,15] did not release the source code, the evaluation results of their methods were cited from the original papers or evaluated from the released deblurred images.

4.3.1. Quantitative Evaluations

Table 4. Quantitative results on the GoPro [7].

Models	GoPro
	PSNR	SSIM	Model Size	FLOPs	Inference Time
SRNDeblur [8]	30.20	0.933	32.26 MB	536.93 G	672 ms
Gao et al. [10]	30.96	0.942	46.46 MB	471.36 G	575 ms
DMPHN [12]	31.39	0.948	86.90 MB	128.80 G	765 ms
RADN [15]	31.82	0.953	-	-	-
Liu et al. [11]	31.85	0.951	108.33 MB	280.46 G	625 ms
Suin et al. [13]	32.02	0.953	-	-	-
MIMO-UNet [16]	32.44	0.957	64.59 MB	150.11 G	359 ms
HINet [17]	32.77	0.959	354.71 MB	153.52 G	256 ms
FSCNet (Ours)	33.01	0.962	67.18 MB	224.54 G	461 ms

presents the quantitative evaluation results on the GoPro [7] dataset. Our FSCNet achieves the highest PSNR (33.01 dB) and SSIM (0.962) among all compared methods. The second-best HINet [17] achieves approximately 1.8 times faster inference (256 ms vs. 461 ms) and lower FLOPs (153.52 G vs. 224.54 G) due to its two-subnetwork design. However, its PSNR is 0.24 dB lower than ours, and it relies on a large number of feature map channels, resulting in a model size of 354.71 MB, which is about five times larger than that of our FSCNet (67.18 MB). We note that FSCNet’s four-stage subnetwork design, while providing higher restoration accuracy, incurs longer inference time compared with simpler two-stage architectures, highlighting a trade-off between restoration quality and computational efficiency.

When compared with MIMO-UNet [16], FSCNet also demonstrates a strong balance between performance and efficiency. MIMO-UNet exhibits lower computational complexity, yet FSCNet delivers clearly superior results with 0.57 dB higher PSNR. This advantage is further supported by the ablation results in Table 1, where our simplified variant, FSCNet-R4, achieves comparable performance to MIMO-UNet (32.48 dB PSNR and 0.958 SSIM vs. 32.44 dB and 0.957) while featuring a smaller model size (40.73 MB vs. 64.59 MB) and fewer FLOPs (130.05 G vs. 150.11 G). These results confirm that our architectural design achieves equivalent performance at lower computational cost, validating the efficiency of our optimization strategy.

Compared with earlier high-cost approaches such as SRNDeblur [8] (536.93 G FLOPs) and Gao et al. [10] (471.36 G FLOPs), FSCNet achieves 2.81 dB and 2.05 dB higher PSNR, respectively, while requiring only 41.8% and 47.6% of their FLOPs. Notably, DMPHN [12] reports the lowest FLOPs (128.80 G) but the slowest inference speed (765 ms) due to its patch-based processing pipeline. Since standard FLOPs estimation excludes the overhead of patch splitting and stitching, its theoretical efficiency does not align with actual runtime. In contrast, FSCNet adopts an invariant-scale multi-stage design, where all stages operate at the same spatial resolution as the input. This eliminates redundant multi-scale and patch-level feature alignment operations, enabling higher restoration quality while maintaining moderate complexity.

In addition to the quantitative evaluations in terms of PSNR and SSIM on the GoPro dataset, we further assess the perceptual quality of the restored images using a deep feature-based metric. While PSNR and SSIM effectively measure pixel-level reconstruction fidelity, they do not fully reflect perceptual quality. To complement these metrics, we additionally evaluate perceptual similarity using the Learned Perceptual Image Patch Similarity (LPIPS) [39] metric for key comparative methods on the GoPro test set. LPIPS assesses the deep feature-based similarity between restored images and their sharp ground truths, where lower scores indicate more natural and perceptually consistent reconstructions. As summarized in

Table 5. LPIPS comparison of key methods on GoPro test set.

Metric	DMPHN [12]	MIMO-UNet [16]	HINet [17]	FSCNet (Ours)
LPIPS	0.082	0.062	0.060	0.058

, our FSCNet achieves the lowest LPIPS score (0.058) among the compared methods. These results demonstrate that FSCNet achieves superior pixel-level accuracy (as verified by PSNR and SSIM) while producing restorations that are perceptually more consistent with the ground truth.

After confirming the pixel-level and perceptual advantages of FSCNet on the GoPro dataset, we further assess the robustness and generalization ability of FSCNet across multiple datasets with diverse blur patterns. In particular, we extend the quantitative evaluations to three additional benchmarks, HIDE [9], REDS [36], and RealBlur [37], which differ substantially in content, blur characteristics, and acquisition conditions, thereby offering a more comprehensive test of model generalization.

Table 6. Quantitative results on the HIDE [9], REDS [36], and RealBlur [37].

Models	HIDE		REDS		RealBlur-R		RealBlur-J		Weighted Avg
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
SRNDeblur [8]	28.36	0.902	26.84	0.873	35.27	0.937	28.48	0.861	28.69	0.889
Gao et al. [10]	29.11	0.913	26.89	0.873	35.39	0.938	28.39	0.859	28.94	0.892
DMPHN [12]	29.10	0.918	26.15	0.851	35.48	0.947	27.80	0.847	28.55	0.883
Liu et al. [11]	29.48	0.920	26.73	0.858	35.40	0.934	28.31	0.854	28.97	0.886
MIMO-UNet [16]	29.99	0.930	26.43	0.859	35.54	0.947	27.64	0.837	28.91	0.889
HINet [17]	30.33	0.932	26.87	0.867	35.75	0.950	28.17	0.849	29.30	0.895
FSCNet (Ours)	30.64	0.937	27.00	0.873	35.87	0.953	28.67	0.872	29.53	0.903

summarizes the quantitative evaluations of FSCNet and other competing methods across all four test subsets (HIDE, REDS, RealBlur-R, and RealBlur-J). FSCNet consistently achieves the highest PSNR: on HIDE, it reaches 30.64 dB and outperforms the second-ranked HINet [17] by 0.31 dB; on REDS, it leads with 27.00 dB, which is 0.13 dB higher than HINet; on RealBlur-R and RealBlur-J subsets, it also surpasses HINet by 0.12 dB (35.87 vs. 35.75 dB) and 0.50 dB (28.67 vs. 28.17 dB), respectively.

In addition to per-dataset results, we report the average PSNR and SSIM across all datasets to provide an overall measure of generalization. To ensure objectivity (accounting for varying sample sizes across subsets: HIDE: 2025 images, REDS: 3000 images, RealBlur-R/J: 980 images each), these averages are computed as image count-weighted averages (i.e., Weighted Avg in Table 6). FSCNet achieves the highest overall performance with a weighted average of 29.53 dB PSNR and 0.903 SSIM, further confirming its strong robustness under diverse blur conditions. In particular, although MIMO-UNet [16] demonstrates a lower computational complexity, its cross-dataset performance is less stable, and its weighted average PSNR and SSIM fail to maintain the advantage observed on GoPro. This indicates that FSCNet’s architecture offers not only a better performance–efficiency balance, but also superior generalization capability across varying blur domains.

4.3.2. Qualitative Evaluations

The qualitative evaluations on the GoPro [7] dataset are shown in Figure 6. The first column shows the blurred input images (with red boxes) and magnified blurred patches of the red-boxed regions, highlighting local blur details. The rest columns present the deblurred results of these magnified regions by SOTA methods [10,11,12,16,17] and FSCNet. We observe that FSCNet obtains the sharpest images while most of the other methods fail to restore the heavily blurry regions, e.g., the cars in motion and the car-plate numbers.

We further conduct visual comparisons between our FSCNet and comparative methods [10,11,12,16,17] on three datasets: HIDE [9], REDS [36], and RealBlur [37], with results shown in Figure 7. The first column presents blurred input images with red boxes, and the second column shows magnified blurred patches of these boxed regions. Columns 3–8 display deblurring results of these regions: Columns 3–7 correspond to comparative methods, and Column 8 to our FSCNet. These results demonstrate that our deblurred images retain more fine details than comparative methods. Specifically, FSCNet produces the sharpest outputs, whereas most other methods fail to restore severely blurred regions, such as pillar edges in the first row and window textures in the last row. Similarly, our method yields the most accurate restorations of billboard letters, ship railings, and red lights, with the fewest visual artifacts among all compared methods.

5. Conclusions

In this paper, we propose a novel fully-cascaded spatial-aware convolutional network (FSCNet) for motion deblurring. The proposed architecture is composed of simple yet efficient sub-networks that process blurry images with an invariant input scale, thus eliminating the need for multi-scale or patch-based processing and feature alignment between sub-networks. The fully-cascaded design connects all sub-networks rather than only adjacent ones, ensuring more comprehensive feature refinement and information flow. Furthermore, the spatial attention block (SAB) with the proposed channel-weighted spatial attention (CWSA) effectively enhances spatial feature extraction and detail restoration.

Extensive experiments on multiple benchmarks demonstrate the superiority of FSCNet over existing state-of-the-art methods. This advantage primarily stems from its core designs, including the multi-stage architecture with the invariant-scale input that reduces redundant computation and the lightweight FCFF and SAB modules that strengthen feature fusion. On the GoPro dataset, FSCNet achieves 33.01 dB PSNR and 0.962 SSIM, surpassing HINet by 0.24 dB and 0.003, while maintaining a model size of only 67.18 MB, approximately one-fifth of HINet’s parameters. It also achieves the lowest LPIPS value (0.058) among the compared methods, indicating that FSCNet produces restorations that are perceptually closer to the ground-truth sharp images. Across diverse datasets, including HIDE, REDS, and RealBlur, FSCNet consistently achieves the highest average PSNR (29.53 dB) and SSIM (0.903), confirming its strong generalization capability. Overall, FSCNet provides a well-balanced solution between restoration quality and computational efficiency, demonstrating consistent advantages in both quantitative accuracy and perceptual fidelity.