Uncertainty-Aware QoS Forecasting with BR-LSTM for Esports Networks

Abstract

Reliable forecasting of network QoS indicators such as latency, jitter, and packet loss is essential for managing real-time and risk-sensitive applications. This study addresses the challenge of uncertainty quantification in QoS prediction by proposing a Bayesian Regression-enhanced Long Short-Term Memory (BR-LSTM) framework. The method integrates Bayesian mean variance estimates into sequential LSTM learning to enable accurate point forecasts and well-calibrated confidence intervals. Experiments are conducted using a Mininet-based emulation platform that simulates dynamic esports network environments. The proposed model is benchmarked against ten probabilistic and deterministic baselines, including ARIMA, Gaussian Process Regression, Bayesian Neural Networks, and Monte Carlo Dropout LSTM. Results demonstrate that BR-LSTM achieves competitive accuracy while providing uncertainty intervals that improve decision confidence for Service-Level Agreement (SLA) management. The calibrated upper bound $(\mu +k\sigma )$  can be compared directly against SLA thresholds to issue early warnings and prioritize rerouting, pacing, or bitrate adjustments when the bound approaches or exceeds policy limits, while calibration controls false alarms and prevents unnecessary interventions. The findings highlight the potential of uncertainty-aware forecasting for intelligent information systems in latency-critical networks.

1. Introduction

Esports and cloud-gaming impose stringent end-to-end Quality of Service (QoS) requirements [1]. Millisecond-scale latency spikes, jitter bursts, and modest loss already disrupt responsiveness and perceived quality [2,3,4,5,6]. Operational QoS (RTT, throughput, access heterogeneity) varies over time and by path. Purely reactive control is therefore insufficient to maintain high-quality interactivity [7,8]. Operational reports further indicate that Quality of Experience (QoE) management is difficult to maintain with reactive mechanisms alone [9,10]. These observations motivate a predictive, risk-aware approach to QoS management for latency-critical interactive workloads.

Transport-layer design also shapes latency and loss. High-speed transports built on User Datagram Protocol (UDP), such as UDP-based Data Transfer (UDT), target high throughput with low delay in wide-area environments, whereas Reliable-UDP (RUDP) variants trade additional latency for stability [11,12]. Transport-layer choices involve latency–stability trade-offs. Transport configuration alone is therefore insufficient under rapidly fluctuating conditions, reinforcing the need for proactive prediction and control.

Recent studies have explored machine learning-based forecasting of QoS metrics, namely, latency, throughput, and loss, to trigger preemptive actions before degradation appears. Representative directions include Long Short-Term Memory (LSTM) sequence models for service-level or platform-level QoS forecasting [13], temporal transformer architectures that address non-stationarity and long-range dependencies [14], federated or hierarchical learning for distributed and privacy constrained settings [15], and Graph Neural Networks (GNNs) that encode topological and relational structure to remain robust under sparse or noisy observations [16]. Reputation-aware graph formulations further stabilize predictions in challenging regimes [17]. Taken together, these studies indicate that machine learning provides an effective basis for proactive QoS management under dynamic network conditions.

Despite recent progress, many studies still prioritize point prediction and offer limited guidance on predictive uncertainty and decision confidence. This is critical for latency-sensitive control loops such as preemptive switching, congestion pacing, and deadline-aware arbitration. Gaussian Processes (GP) provide probabilistic forecasts with posterior means and variances [18]. In deep learning, dropout is used as a Bayesian approximation, and uncertainty decomposition provides general mechanisms for estimating and interpreting predictive risk [19,20]. However, domain-tailored frameworks that jointly model temporal dependence and deliver calibrated risk bounds suitable for esports and cloud gaming operations remain comparatively scarce. This gap motivates the present study.

Compared with alternative uncertainty-aware temporal models, BR-LSTM injects per-step predictive summaries (μ, σ) at the input level and lets the sequence model propagate these uncertainty signals. Monte Carlo Dropout (MC-Dropout) LSTM represents epistemic uncertainty through weight stochasticity and typically requires multiple stochastic passes, while Gaussian Process Regression (GPR) encodes uncertainty in kernel posteriors with higher memory and scalability costs on multivariate sequences. By delivering calibrated μ + kσ upper bounds and propagating uncertainty through time, BR-LSTM provides decision-useful intervals under regime shifts while remaining lightweight for edge deployment.

Different game genres respond to network volatility in distinct ways. Massively Multiplayer Online Role Playing Games (MMORPGs), such as World of Warcraft and Black Desert, reduce real-time interaction to mitigate the effects of latency and jitter [7]. In contrast, real-time strategy and racing games rely on dead reckoning and action prediction to maintain consistency [8,21]. Mobile multiplayer games that operate over cellular networks further amplify latency variability because of wireless channel fluctuations [22]. This issue is exacerbated in cloud gaming environments by significant variations in Round Trip Time (RTT) [23,24]. In wireless-mesh backbone networks, LSTM-based routing has proven effective for QoS-aware path selection, outperforming classical protocols such as Ad hoc On-demand Distance Vector (AODV) by achieving higher packet delivery rates and throughput under dynamic conditions [25]. Moysen et al. [14] addressed this challenge by using location-independent User Equipment (UE) metrics, such as Reference Signal Received Power (RSRP) and Reference Signal Received Quality (RSRQ), to predict throughput in Long Term Evolution (LTE) heterogeneous networks (HetNets) without relying on Global Positioning System (GPS) data. This approach improves scalability and cost efficiency in mobile QoS prediction.

To address this gap, this work introduces a BR-LSTM framework. A front-end Bayesian Regression (BR) produces per-sample analytic means and variances that are then consumed by an LSTM to capture nonlinear temporal dependence. This design enables analytic variance propagation through the sequence and yields accurate point forecasts together with calibrated prediction intervals. Evaluation is conducted in a Mininet-based emulation environment under diverse network conditions. Comparative baselines include Support Vector Regression (SVR) [26], Random Forest (RF) [27], Multilayer Perceptron (MLP) [28,29], standard LSTM [13], Bayesian Neural Network (BNN) [30], MC-Dropout LSTM [19], GPR [18,31], and Quantile Regression (QR) [32], together with graph and distributed learning settings for completeness [17,33,34]. Metrics comprise Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and the Coefficient of Determination (R²), together with risk-centric indicators such as Prediction Interval Coverage Probability (PICP), Mean Prediction Interval Width (MPIW), and False Alarm Rate (FAR). To anchor the comparison with foundational time-series models that provide uncertainty natively, the study includes Autoregressive Integrated Moving Average (ARIMA) [35] and a linear state–space (Kalman) [36] baseline. Their point-estimation results are reported in

Table A1. Evaluation and risk analysis results.

Jitter
Metric	BNN	BR-LSTM	GPR	MC-Dropout LSTM	MLP	QR	RF	SVR	Standard LSTM	ARIMA	State–Space
MAE	4.61	6.62	3.33	6.80	3.92	8.12	3.05	4.18	6.71	3.85	3.24
RMSE	5.93	7.81	4.24	8.17	5.19	8.89	4.01	5.38	8.09	4.91	4.24
R2	0.43	0.03	0.71	−0.09	0.56	−0.28	0.74	0.53	−0.06	0.62	0.72
Latency
Metric	BNN	BR-LSTM	GPR	MC-Dropout LSTM	MLP	QR	RF	SVR	Standard LSTM	ARIMA	State–Space
MAE	28.70	32.49	25.58	33.77	35.94	100.68	30.63	28.41	33.21	31.67	24.99
RMSE	53.32	46.54	42.46	58.60	56.69	111.39	53.32	54.88	58.17	48.12	44.95
R2	0.16	0.01	0.17	−0.01	0.06	−2.64	0.16	0.12	0.01	0.08	0.20
Loss
Metric	BNN	BR-LSTM	GPR	MC-Dropout LSTM	MLP	QR	RF	SVR	Standard LSTM	ARIMA	State–Space
MAE	8.03	7.75	7.77	7.68	9.49	17.35	7.78	7.73	7.69	7.23	7.15
RMSE	9.90	9.86	9.87	9.43	12.16	19.33	9.53	9.47	9.41	8.92	8.93
R2	−0.11	0.00	0.00	−0.01	−0.68	−3.24	−0.03	−0.02	0.00	−0.01	−0.01

using the same split and metrics as the learning-based models. Unlike MC-Dropout LSTM, which approximates posterior uncertainty via stochastic masking, and unlike GPR, which models uncertainty through a kernel on raw signals, the proposed BR-LSTM first derives analytic per-sample means and variances with Bayesian Ridge and then propagates $({\mu }_t,{\sigma }_t)$ through a sequential LSTM. Injecting uncertainty at the input layer preserves the interpretability of $\mu$ and $\sigma$ and allows nonlinear temporal dependence to refine one-step-ahead risk bounds.

The main contributions of this study are summarized as follows:

• This study introduces a hybrid QoS forecasting model, BR-LSTM, which combines BR-derived uncertainty estimates with a sequential LSTM to enable calibrated, risk-aware prediction under dynamic network conditions.
• A comprehensive evaluation is performed against ten established baseline models, including ARIMA and a local level state–space model, within a unified Mininet-based simulation framework. The assessment covers point accuracy (MAE, RMSE, R²) and interval quality (PICP, MPIW, FAR).
• After calibration to target 95% PICP on a validation set, BR-LSTM attains near target coverage for latency and loss and improved coverage for jitter, while maintaining a small model footprint (0.07 MB) and low inference cost, which supports real-time edge deployment in esports networks. The calibrated upper bound aligns with SLA thresholds and provides an actionable trigger for early warnings with controlled false-alarm rates.

The remainder of this paper is organized as follows. Section 2 reviews related work on QoS forecasting and uncertainty-aware models and summarizes the nomenclature. Section 3 details the proposed BR-LSTM methodology, including the problem formulation, the BR front end, LSTM sequence modeling, and interval calibration. Section 4 describes the Mininet-based emulation and dataset generation with tc netem, the training and evaluation protocol, and the comparative results across MAE/RMSE/R², and risk metrics, including PICP, MPIW, FAR. Section 5 discusses the findings, emphasizing the coverage and sharpness trade-off, service level agreement (SLA) implications, and deployment considerations. Finally, Section 6 concludes the paper and outlines directions for future work.

2. Related Work

Interactive and cloud gaming are highly sensitive to end-to-end QoS fluctuations. Millisecond-scale impairments already degrade responsiveness and perceived quality. Field measurements show that access technology and mobility amplify temporal variability and path dependence. These effects make imperceptible latency difficult to sustain in mobile cloud gaming [37,38,39,40]. From an operational standpoint, reports from production ecosystems highlight the limits of purely reactive QoE and QoS controls during long-running sessions. Prior works link fine-grained QoS dynamics to perceptual outcomes and document frequent regime shifts under heterogeneous access and mobility. These findings motivate predictive, risk-aware control rather than post hoc mitigation.

This work builds on these findings by framing QoS forecasting as a calibrated risk estimation problem that outputs decision useful envelopes for latency-critical operations. One line of research focuses on time-series forecasting of QoS [29]. LSTM-based sequence models have been applied to forecast service level or platform level QoS attributes and have reported improvements over classical regressors when temporal dependence is strong [13,41].

Production pipelines that span telemetry to deployment show that performance forecasting can trigger preemptive traffic actions before degradation [23]. For real-time communications, packet-level modeling of concurrent Real-time Transport Protocol (RTP) flows has been used to obtain end-to-end QoS predictions that respect in-session constraints [42]. In edge-to-cloud scenarios, context-aware collaboration leverages auxiliary signals to mitigate geographic and uplink variability during QoS prediction [43]. In mobile settings, adding contextual signals likewise improves QoS predictability [44]. Complementary work in service ecosystems leverages multi-stage and multi-scale feature fusion or multi-modal integration to forecast QoS under diverse usage patterns [24,25]. Together, these studies indicate that learned temporal models are effective tools for forward-looking QoS management under dynamic conditions. Classical ARIMA and linear state–space models provide linear Gaussian baselines with native prediction intervals and serve as sanity checks. Both are included in the evaluation, as summarized in Table A1.

A second line of work exploits structural priors and distributed learning. GNN formulations encode topological and relational structures to improve robustness under sparse or noisy observations, and reputation-aware graph convolution has been used to enhance stability in challenging regimes [16,17]. Topology-aware recurrent designs, for example, the Topology-Aware QoS GRNN (TAQ-GRNN), integrate the network structure with gated recurrence to improve QoS prediction [45]. In systems that span multiple organizations or sites, federated and hierarchical learning supports privacy preserving and scalable QoS prediction [15]. Related efforts apply graph learning in cloud environments to anticipate SLA violations, showing that relational information can surface risk earlier than node-level predictors [46]. Under mobility and concept drift, distributed predictive schemes maintain accuracy with modest communication and energy overheads in automotive settings [47]. These results suggest that structural information and decentralized training are practical levers for robust QoS forecasting in the wild.

Despite these advances, much of the forecasting literature remains point estimate-centric and provides limited guidance on predictive uncertainty and the decision confidence required by latency-critical control loops. GP offers probabilistic forecasts with posterior means and variances but faces scalability challenges in large multivariate contexts [18]. Within deep learning, dropout is used as a Bayesian approximation, and uncertainty decomposition provides general mechanisms to estimate and interpret predictive risk, yet domain-tailored evaluations of calibrated intervals for esports and cloud gaming operations remain scarce [19,20]. This gap motivates models that jointly capture temporal dependence while yielding calibrated and decision-useful risk bounds, which is the focus of the present work.

3. Methodology

Although many models have been applied successfully to QoS prediction, most methods emphasize point estimation and overlook Uncertainty Quantification (UQ). This limitation is especially critical in dynamic and risk-sensitive applications such as esports and cloud gaming, where robust decision making depends not only on accurate predictions but also on reliable and well-calibrated confidence intervals. To address this gap, this paper presents a hybrid framework that integrates BR-LSTM networks. The proposed approach produces well-calibrated uncertainty intervals without sacrificing predictive accuracy.

This study focuses on three key QoS indicators in esports network environments: latency, jitter, and packet loss rate. To combine the time-series modeling strength of LSTMs with the uncertainty quantification capability of Bayesian methods, the BR-LSTM framework proceeds as follows. A BR stage first produces per-time step point estimates and uncertainty estimates for each QoS metric, denoted as ${\widehat{\mu }}_t$ and ${\widehat{\sigma }}_t$. These estimates are concatenated to form an enhanced feature vector that serves as input to the LSTM. The intuition is that providing both the per-step mean and variance supplies the LSTM with a baseline trend for each metric, upon which it can model nonlinear temporal dependence. Because the BR stage conditions only on the time index, it may miss abrupt traffic surges or routing changes. The LSTM is therefore trained to predict the next step mean and uncertainty, i.e., ${\widehat{\mu }}_{t+1}$ and ${\widehat{\sigma }}_{t+1}$, from these enriched input sequences [48]. The objective is to improve the accuracy of dynamic network modeling while simultaneously providing reliable uncertainty and risk quantification.

In the proposed framework, BR is first used to model the raw network features at each time step. With Gaussian priors, BR regularizes the parameters and infers their posterior distributions during training. This procedure yields two essential outputs for each QoS indicator, namely, the mean prediction and the associated prediction variance. These uncertainty measures capture potential fluctuations and anomalies in network behavior and serve as critical inputs for subsequent temporal modeling.

Next, the predicted means and variances for latency, jitter, and packet loss are concatenated to form a six-dimensional enhanced feature vector, which is then provided to the LSTM model. Using a sliding window of length L, the LSTM learns nonlinear temporal dependencies and long-term memory patterns among the QoS metrics and produces predictions for future time points. The final output comprises forecasts for all three QoS parameters, enabling forward-looking evaluation of esports network performance.

Placing BR before the LSTM provides real-time, input-level uncertainty estimates. This design enhances the interpretability and robustness of temporal modeling, especially in highly variable environments. Compared with feeding raw QoS data directly into an LSTM, the proposed architecture improves generalization and is well-suited for latency-sensitive and high-reliability applications, including esports platforms, streaming game servers, and cloud gaming infrastructures.

3.1. Problem Formulation

Let $y_t=[\mathrm{latenc}{\mathrm{y}}_t, \mathrm{jitte}{\mathrm{r}}_t, \mathrm{los}{\mathrm{s}}_t{]}^{\top }\in {\mathbb{R}}^3$ denote the QoS vector at time t. Given a sliding window $X_t=[y_{t-L+1},\dots ,y_t]$, the objective is to learn the one-step-ahead predictive distribution $p(y_{t+1}\mid X_t)\approx \mathcal{N}({\widehat{\mu }}_{t+1},\mathrm{diag}({\widehat{\sigma }}_{t+1}^2\left)\right)$, where ${\widehat{\mu }}_{t+1},{\widehat{\sigma }}_{t+1}\in {\mathbb{R}}^3$ are the per-metric mean and standard deviation for time t + 1 given history X_t, respectively.

For risk-aware control, the upper bound ${\widehat{\mu }}_{t+1}+k{\widehat{\sigma }}_{t+1}$ is compared with service-level thresholds. The scalar k is chosen on a validation split to target a PICP of approximately 0.95. The notation and the priors used in the Bayesian stage are summarized in

Table 1. BR-LSTM parameters.

Symbol	Description
L	Look-back window length
$\nu$	QoS metric index in {latency, jitter, loss}
$y_t\in {\mathbb{R}}^3$	QoS vector at time t
$y_t^{\left(\nu \right)}\in \mathbb{R}$	Scalar QoS for metric ν at time t
$X_t$	Past window
$x_t\in {\mathbb{R}}^d$	BR input (e.g., time index)
$X\in {\mathbb{R}}^{N\times d}$	BR design matrix
$y^{\left(\nu \right)}\in {\mathbb{R}}^N$	Targets for metric ν
$w^{\left(\nu \right)}\in {\mathbb{R}}^d$	Weights for metric ν
$\lambda$	$\mathrm{Prior} \mathrm{precision} \mathrm{of} w^{\left(\nu \right)}$
${\sigma }_n^2$	Observation noise variance
$\epsilon$	Observation noise
${\mu }_{w^{\left(\nu \right)}}$	$\mathrm{Posterior} \mathrm{mean} \mathrm{of} w^{\left(\nu \right)}$
${\sum }_{w^{\left(\nu \right)}}$	$\mathrm{Posterior} \mathrm{covariance} \mathrm{of} w^{\left(\nu \right)}$
$x^{*}$	New input for prediction
${\widehat{\mu }}^{*,\left(\nu \right)}$	BR predictive mean at x*
$({\widehat{\sigma }}^{*,\left(\nu \right)}{)}^2$	BR predictive variance at x*
${\widehat{\mu }}_t^{*,\left(\nu \right)}$	Time-indexed predictive mean at xt
${\widehat{\sigma }}_t^{*,\left(\nu \right)}$	Time-indexed predictive std. at xt
$z_t\in {\mathbb{R}}^6$	$[{\mu }_t^{*,\left(\mathrm{lat}\right)},{\sigma }_t^{*,\left(\mathrm{lat}\right)},{\mu }_t^{*,\left(\mathrm{jit}\right)},{\sigma }_t^{*,\left(\mathrm{jit}\right)},{\mu }_t^{*,\left(\mathrm{loss}\right)},{\sigma }_t^{*,\left(\mathrm{loss}\right)}]$
$Z_t$	Sequence input to LSTM
$\mathrm{LST}{\mathrm{M}}_{\theta }(\cdot )$	Sequence model
${\widehat{\mu }}_{t+1}\in {\mathbb{R}}^3$	Predicted mean QoS vector
${\widehat{\sigma }}_{t+1}\in {\mathbb{R}}^3$	Predicted standard deviation vector
k	Interval scaling factor
${\lambda }_{cov}$	Weight for coverage term
H	LSTM hidden size
N	Number of BR samples

.

3.2. BR-LSTM

The framework combines a per-timestep BR with a sequential LSTM module, allowing uncertainty information to propagate over time. For each metric $\nu \in \left\{\mathrm{latency},\mathrm{jitter},\mathrm{loss}\right\}$, a Bayesian linear model with a Gaussian prior is used as shown in (1).

$$y^{\left(\nu \right)}=X{w}^{\left(\nu \right)}+ϵ,ϵ\sim \mathcal{N}\left(0,{\sigma }_n^2\right),w^{\left(\nu \right)}\sim \mathcal{N}\left(0,{\lambda }^{-1}I\right)$$

(1)

Given observations $(X,y^{\left(\nu \right)})$ with $X\in {\mathbb{R}}^{N\times d}$ and $y^{\left(\nu \right)}\in {\mathbb{R}}^N$, where N is the number of BR training samples and d is the input dimension, the posterior over weights is Gaussian, with mean ${\mu }_{w^{\left(\nu \right)}}$ and covariance ${\sum }_{w^{\left(\nu \right)}}$. The predictive distribution for a new input $x^{*}$ is summarized in (2). All symbols used in (2)–(5) follow the notation summarized in Table 1.

$${\widehat{\mu }}^{*,\left(\nu \right)}=(x^{*}{)}^{\top }{\mu }_{w^{\left(\nu \right)}},({\widehat{\sigma }}^{*,\left(\nu \right)}{)}^2={\sigma }_n^2+(x^{*}{)}^{\top }{\sum }_{w^{\left(\nu \right)}}{x}^{*}$$

(2)

For each time step t (taking $x^{*}=x_t$), the time-indexed BR summaries that feed the LSTM are given in (3).

$${\widehat{\mu }}_t^{*,\left(\nu \right)}=(x_t{)}^{\top }{\mu }_{w^{\left(\nu \right)}},{\widehat{\sigma }}_t^{*,\left(\nu \right)}=\sqrt{{\sigma }_n^2+(x_t{)}^{\top }{\sum }_{w^{\left(\nu \right)}}{x}_t}$$

(3)

BR with a Gaussian likelihood and a zero-mean isotropic Gaussian prior on the weights is adopted. Conditioning on $\left(X,y\right)$ yields the posterior $\mathcal{N}\left({\mu }_{w^{\left(v\right)}},{\mathsf{\Sigma }}_{w^{\left(v\right)}}\right)$, with ${\mathsf{\Sigma }}_{w^{\left(v\right)}}=(\lambda I+{\sigma }_n^{-2}{X}^{\top }X{)}^{-1}$ and ${\mu }_{w^{\left(v\right)}}={\sigma }_n^{-2}{\mathsf{\Sigma }}_{w^{\left(v\right)}}{X}^{\top }{y}^{\left(v\right)}$. The predictive distribution at x* is $\mathcal{N}\left(\right(x^{*}{)}^{\top }{\mu }_{w^{\left(v\right)}},{\sigma }_n^2+\left(x^{*}{)}^{\top }{\mathsf{\Sigma }}_{w^{\left(v\right)}}{x}^{*}\right)$. These summaries define $\widehat{\mu }$ and $\widehat{\sigma }$ used in (2) and (3).

Stacking the three metrics forms a six-dimensional feature. $z_t=[{\mu }_t^{*,\left(\mathrm{lat}\right)},{\sigma }_t^{*,(\mathrm{lat})},{\mu }_t^{*,\left(\mathrm{jit}\right)},{\sigma }_t^{*,\left(\mathrm{jit}\right)},{\mu }_t^{*,\left(\mathrm{loss}\right)},{\sigma }_t^{*,\left(\mathrm{loss}\right)}{]}^{\top }\in {\mathbb{R}}^6$. The LSTM consumes $Z_t=[z_{t-L+1},\dots ,z_t]$ and outputs the next step mean and standard deviation as in (4).

$$\left[{\widehat{\mu }}_{t+1},{\widehat{\sigma }}_{t+1}\right]=\mathrm{LST}{\mathrm{M}}_{\theta }\left(Z_t\right),{\widehat{\mu }}_{t+1},{\widehat{\sigma }}_{t+1}\in {\mathbb{R}}^3$$

(4)

Under the Gaussian prior-likelihood setting of Bayesian Ridge, the predictive variance decomposes as $\mathrm{V}\mathrm{a}\mathrm{r}[y^{*}\mid x^{*}]={\sigma }_n^2+x^{*\mathrm{\top }}{\mathsf{\Sigma }}_w{x}^{*}$. The term ${\sigma }_n^2$ represents aleatoric noise, whereas $x^{*\mathrm{\top }}{\mathsf{\Sigma }}_w{x}^{*}$ captures epistemic uncertainty from the parameter posterior. The BR front end, therefore, supplies per-timestep $({\mu }_t,{\sigma }_t)$ signals that already contain both components. The sequence model consumes these inputs and maps them to $({\widehat{\mu }}_{t+1},{\widehat{\sigma }}_{t+1})$; the resulting ${\widehat{\sigma }}_{t+1}$ reflects propagated total predictive uncertainty rather than a separated decomposition. Interval calibration with a single factor k on a disjoint validation split corrects residual miscalibration before evaluation on the test split.

Let ${\widehat{\mu }}_{t+1}$ and ${\widehat{\sigma }}_{t+1}$ denote model outputs. The loss combines point accuracy and interval coverage as in (5). Here, k denotes the validation-calibrated interval scaling factor, and ${\lambda }_{cov}$ the coverage weight in the loss. Both are defined in Table 1.

$$\mathcal{L}=\mathrm{MAE}\left(\widehat{\mu },y\right)+{\lambda }_{cov}\left|\mathrm{PICP}\left(\widehat{\mu }\pm k\widehat{\sigma }\right)-0.95\right|$$

(5)

At inference, BR yields six scalars per step, and the LSTM produces $({\widehat{\mu }}_{t+1},{\widehat{\sigma }}_{t+1})\in {\mathbb{R}}^3\times {\mathbb{R}}^3$. The per-step cost is dominated by the LSTM forward pass O(LH + H²) with hidden size H; the BR stage is closed-form and lightweight. The overall footprint meets edge-deployment constraints with millisecond-level latency budgets.

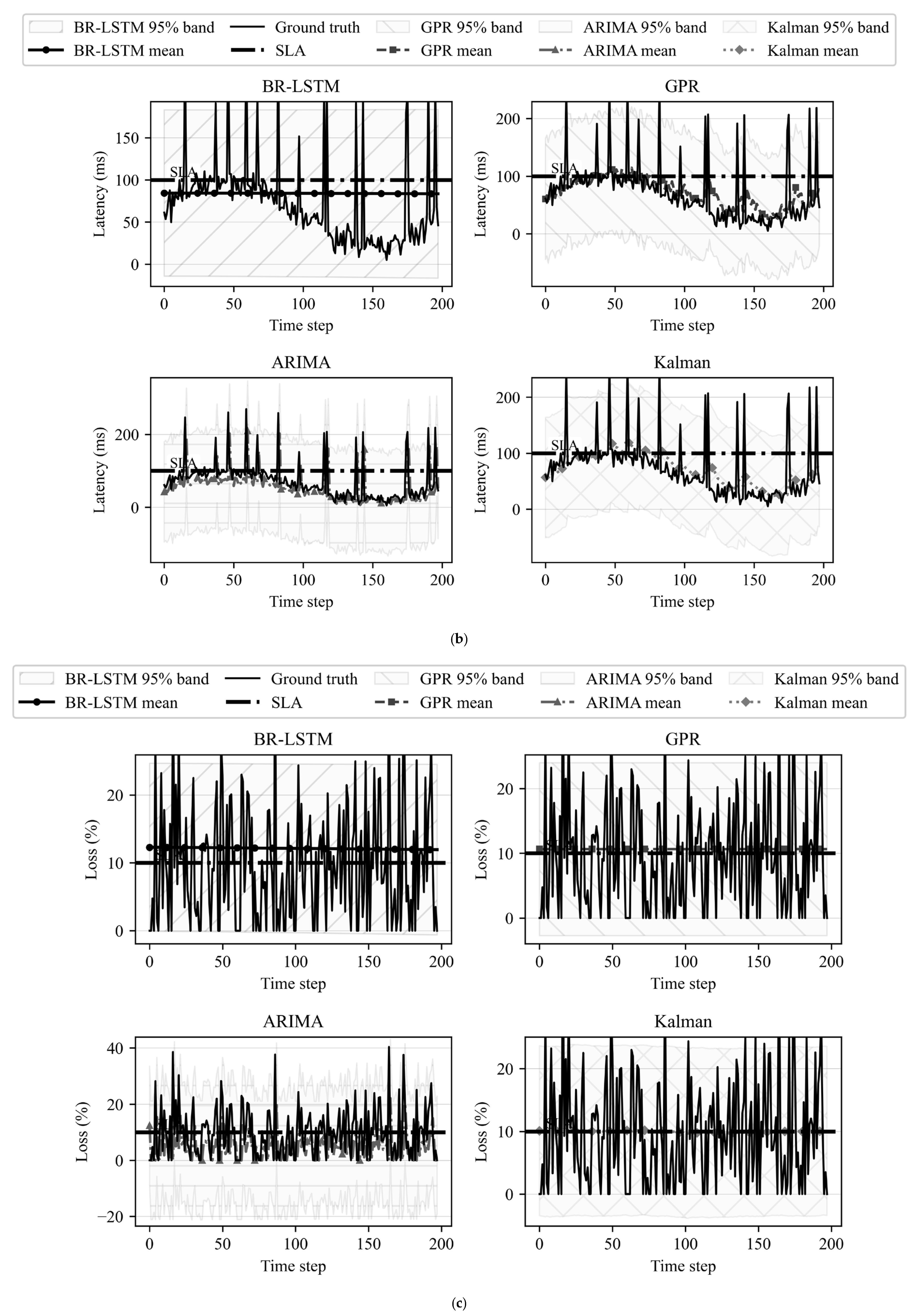
Unless noted otherwise, experiments use a one-layer LSTM (hidden size 64) with six input features and a look-back window $L=10$. Optimization uses Adam. The BR stage adopts Bayesian ridge (Gaussian) priors with default hyperparameters. All features are standardized, and the train/validation/test splits follow the evaluation protocol. Figures show one-step-ahead rolling forecasts on the held-out test split for latency, jitter, and packet loss. At time $t$, the model outputs a point estimate ${\widehat{y}}_t$ and an uncertainty interval $[{\widehat{y}}_t-k{\widehat{\sigma }}_t, {\widehat{y}}_t+k{\widehat{\sigma }}_t]$. The scale factor k is tuned once on the validation set to achieve 95% empirical coverage and is then fixed for testing. Using this global k avoids label leakage, preserves cross-model comparability, and yields intervals that combine model uncertainty with a fixed post hoc calibration. No dynamic adjustment of k is applied at test time, and the test split remains unseen during training and calibration. For service-level interpretation, horizontal lines mark the SLA thresholds for each metric. These plots complement the quantitative tables by indicating when the upper risk bound ${\widehat{y}}_t+k{\widehat{\sigma }}_t$ crosses the SLA, which directly relates to FAR. Reported metrics include PICP, MPIW, and FAR.

3.3. Baseline Models/Comparison Methods

To contextualize the performance of the proposed BR-LSTM model, ten representative baseline methods were re-implemented using identical training and validation splits, standard scaler normalization, and the same 1000-round dataset generated via Mininet simulation. Unless otherwise specified, all deterministic models were trained using the default settings provided by scikit-learn version 1.6.1. The complete hyperparameters and training settings for every baseline are summarized in

Table 2. Implementation details of models.

Category	Implementation Details
Standard LSTM	One stacked layer with hidden size 64; uses hyperbolic tangent and sigmoid activation gates; trained using the Adam optimizer [49] (learning rate = 1 × 10−3) for 30 epochs; outputs point forecasts only.
MC-Dropout LSTM	Same architecture as Standard LSTM, with dropout rate 0.30 applied after the recurrent layer; 20 stochastic forward passes at inference to estimate predictive mean and standard deviation (the prediction interval uses $\widehat{\mu }\pm 1.96\widehat{\sigma }$ (raw) or $\widehat{\mu }\pm k\widehat{\sigma }$ (calibrated, with k tuned on the validation set to target PICP = 95%), following Gal and Ghahramani [19]. For latency reporting, the single-pass measurement is used; per-sample wall time on CPU increases approximately linearly with the number of stochastic passes S.
BNN	Two fully connected layers (64 → 64 → 3) with dropout rate 0.20; trained for 100 epochs using Adam; 20 Monte Carlo samples used to derive predictive distributions.
QR	QR with quantile level τ = 0.95 and regularization α = 0.1; solved using the HiGHS optimizer as implemented in SciPy 1.15.2 (Python 3.12.3) to directly provide Q95 upper bounds.
GPR	Uses Radial Basis Function (RBF) and white noise kernels; default initialization of length scale; posterior variance used to estimate predictive uncertainty.
SVR	SVR with RBF kernel; parameters: C = 1.0 and epsilon = 0.1.
RF	RF with 100 trees; no depth limitation; Mean Squared Error (MSE) criterion used for node splitting.
MLP	One hidden layer with 100 Rectified Linear Unit (ReLU) neurons; trained using the Adam optimizer with a maximum of 500 iterations.
ARIMA	Seasonal-free ARIMA selected by auto_arima (AIC minimization); model orders re-estimated on the training split only; closed-form one-step forecast returns point prediction with 95% forecast interval from the analytic forecast error variance (no network epochs required).
Linear State–Space (Kalman)	Local-level Gaussian state–space model fitted via Durbin–Koopman EM; system and measurement noise variances learned by maximum likelihood on training data; recursive Kalman filter yields ${\widehat{\mu }}_{t+1}$ and ${\widehat{\sigma }}_{t+1}$; 95% interval reported as ${\widehat{\mu }}_{t+1}\pm 1.96{\widehat{\sigma }}_{t+1}$ (optionally recalibrated to $\widehat{\mu }\pm k\widehat{\sigma }$).

.

For each model, five evaluation metrics were computed on the standardized test set: MAE, RMSE, R², PICP, and MPIW. Predictions were then transformed back to physical units by reversing the normalization. For BR-based models and the MC-Dropout LSTM, the prediction interval is defined as $\widehat{\mu }\pm k\widehat{\sigma }$, with k chosen on the validation set to target 95% coverage. When comparing to SLA thresholds, the upper risk bound $\widehat{\mu }+k\widehat{\sigma }$ is reported. For QR, the model uses its τ quantile output directly as the upper risk bound.

Models without native uncertainty are evaluated only with point estimation metrics (Table A1). For models that produce predictive uncertainty, including BR-LSTM, BNN, MC-Dropout LSTM, GPR, ARIMA, and the state–space model, interval metrics are reported in

Table A2. Risk assessment using $\widehat{\mu }\pm 1.96\widehat{\sigma }$ and Q95 bounds. NA: not applicable (interval-based calibration metrics are not defined for the one-sided Q95 bound of QR).

Metric	SLA Threshold	Model	Risk Bound	k	Max	Mean	FAR_Raw(%)	FAR_Calibrated(%)	PICP_Raw(%)	PICP_Calibrated(%)	MPIW_Raw	MPIW_Calibrated
Jitter	50 ms	BNN	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	2.64	23.73	21.6	0	0	4.55	7.07	1.24	1.67
		BR-LSTM	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	3.17	31.63	31.25	0	47.98	55.56	82.83	23.19	37.51
		GPR	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	1.81	33.45	21.58	0	0	96.46	95.45	16.86	15.57
		MC-Dropout LSTM	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	2.84	22.83	21.72	0	0	2.53	5.56	0.77	1.11
		QR	Q95		34.55	34.55	0	NA	NA	NA	NA	NA
		ARIMA	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	2.1	41.65	20.89	0.51	0.51	95.96	97.47	20.24	21.68
		State–Space	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	1.91	34.98	21.44	0	0	95.45	94.95	16.7	16.27
Latency	100 ms	BNN	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	2.85	80.91	69.91	0	0	7.07	11.62	7.43	10.8
		BR-LSTM	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	2.24	84.36	84	85.35	85.35	92.93	93.43	173.4	198.17
		GPR	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	2.41	114.31	71.91	85.35	85.35	92.93	93.43	171.73	211.16
		MC-Dropout LSTM	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	2.87	75.68	70.53	0	0	3.54	6.06	4.01	5.88
		QR	Q95		191.77	191.77	85.86	NA	NA	NA	NA	NA
		ARIMA	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	2.48	209.71	55.2	85.35	85.35	88.89	93.43	215.57	272.77
		State–Space	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	2.48	118.87	70.64	85.35	85.35	92.93	93.94	168.69	213.44
Loss Rate	10%	BNN	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	3	12.48	9.92	35.35	39.9	4.04	7.07	1.13	1.73
		BR-LSTM	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	1.45	12.29	12.13	54.55	54.55	97.47	93.94	33.63	24.88
		GPR	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	1.45	10.65	10.65	54.55	54.55	97.47	93.43	36.09	26.7
		MC-Dropout LSTM	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	2.89	11.37	9.88	30.81	38.89	1.01	3.03	0.63	0.93
		QR	Q95		27.06	27.06	53.54	NA	NA	NA	NA	NA
		ARIMA	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	1.82	22.1	5.41	54.55	54.55	94.95	94.44	45.37	42.13
		State–space	$\widehat{\mu }\pm 1.96\widehat{\sigma }$	1.48	10.22	9.96	54.55	54.55	96.46	92.93	35.77	27.01

.

Table 3. Availability of risk indicators.

Category	Algorithms	Risk Indicator
Risk-Aware Models	BR-LSTM, BNN, MC-Dropout LSTM, GPR, Kalman (state–space), QR, ARIMA	$\mathrm{For} \mathrm{models} \mathrm{with} \widehat{\mu }$$, \widehat{\sigma }$$: \widehat{\mu }\pm k\widehat{\sigma }$ with k tuned to target about 95% PICP; for QR: qτ with τ = 0.95; for ARIMA or state–space: native 95% forecast interval, upper bound Unat
Deterministic Models	SVR, RF, MLP, Standard LSTM	Point prediction only

summarizes risk indicator availability, and

Table 4. Ranking of models by accuracy and risk detection.

Tier/Criterion	Model(s)	Representative Results	Risk-Bound Characteristics	Remarks
High Accuracy (non-probabilistic)	RF, MLP	Jitter R2 = 0.74 (RF) Jitter R2 = 0.56 (MLP)		Best point-forecast accuracy; no uncertainty estimates.
Balanced Accuracy + Calibrated Uncertainty	BR-LSTM	Latency MAE = 32.49 ms	Calibrated 95% prediction interval: - jitter upper bound = 31.63 ms (<50 ms SLA); - latency upper bound = 84.36 ms (<100 ms SLA); - loss upper bound = 12.29% (>10% SLA).	Good trade-off between accuracy and reliable risk bounds.
Conservative/Wide Upper Bound	QR (τ = 0.95)		Q95 bounds: - jitter 34.55 ms (<50 ms); - latency 191.77 ms (>100 ms); - loss 27.06% (>10%).	Percentile-based and wide; only jitter bound satisfies SLA. Suitable for worst-case provisioning; tends to over-reserve for latency and loss.
Conservative/Wide Upper Bound	ARIMA		Calibrated bounds typically wide; latency upper bound > 100 ms; jitter upper bound often <50 ms; loss upper bound >10%.	Conservative envelopes; coverage near nominal at the expense of width.
Well-calibrated and moderate width	State–space, GPR		Calibrated coverage close to nominal; jitter upper bound <50 ms; latency upper bound is higher than 100 ms; loss upper bound is near 10%; moderate width.	Balanced option with moderate width; provides tighter and more reliable jitter envelopes; useful as a complementary baseline.
Under-covered/Over-confident	MC-Dropout LSTM, BNN	Mean jitter PICP_cal = 5.56% (MC-Dropout LSTM); 7.07% (BNN)	Prediction intervals too narrow; severe under-coverage.	High point accuracy offset by unreliable risk estimates.
Moderate Accuracy (no uncertainty)	SVR	Latency R2 = 0.12; Jitter R2 = 0.53; Loss R2 = −0.02		Reasonable point forecasts but lacks uncertainty quantification.
Low Accuracy	Standard LSTM	Multiple metrics show negative R2 or high MAE/RMSE	Not applicable; deterministic model with no uncertainty estimates (no PICP, MPIW, FAR).	Moderate point forecasts but lacks uncertainty; unsuitable for risk-aware operation; baseline only.

provides the ranking.

This unified experimental protocol standardizes data preprocessing and training conditions, thereby ensuring that any performance differences can be attributed solely to the architectural characteristics of each model. As a result, any observed performance improvements in BR-LSTM can be attributed to its hybrid design and uncertainty-aware formulation, rather than to favorable hyperparameter configurations.

The study reports point metrics (MAE, RMSE, $R^2$) together with interval metrics (PICP, MPIW, FAR) relative to SLA thresholds. Because the held-out test series exhibit temporal dependence and occasional regime shifts, formal null-hypothesis tests on per-sample errors under i.i.d. assumptions may be anti-conservative. Accordingly, cross-model comparisons emphasize consistent effect directions and relative gaps across latency, jitter, and loss, while calibrated interval behavior is read alongside point accuracy. Serial-dependence-aware paired tests (e.g., moving-block bootstrap around paired error differences) are left to future work to quantify sampling uncertainty without assuming independence.

3.4. Computational Footprint and Relative Cost

A single forward pass is dominated by the LSTM term $O(LH+H^2)$, while the Bayesian Ridge front end remains closed form and lightweight. Under the reported configuration $(L=10,H=64)$, the overall footprint fits millisecond-level latency budgets on commodity CPUs used for edge dashboards.

The model uses a lightweight configuration $(L=10,H=64)$ to balance accuracy, stability, and edge deployability while avoiding overtuning that could bias cross-model comparisons. In this setting, L controls the receptive field of temporal dependencies, whereas H governs capacity and the $O\left(H^2\right)$ cost of the recurrent core. Under moderate changes to these settings, the claims in this study are framed around directional consistency and rank-order stability rather than exact point values. Interval behavior remains governed by the calibration procedure on the validation split, and the reported results, therefore, keep L and H fixed for fairness. Fuller ablations are left for future work.

To contextualize the models, a qualitative ranking by inference cost is provided in prose. Low-cost models include ARIMA and state space approaches with closed-form updates, RF with shallow depth, and a small MLP. Medium-cost models include SVR, whose inference depends on the number of support vectors, and the BR-LSTM variant with a single-layer LSTM. High-cost models include MC-Dropout LSTM, which requires multiple stochastic passes; BNNs, which rely on sampling; and GPR with large effective kernel sizes. This ranking reflects standard complexity terms and the reported architectural settings; no additional measurements are introduced.

4. Experiments

4.1. Experimental Settings

To rigorously evaluate the proposed BR-LSTM framework under realistic and dynamic network conditions representative of multiplayer esports environments, a customized multiplayer network emulation was developed by using Mininet. This emulation replicates competitive online gaming interactions and captures fluctuations in delay, jitter, and packet loss.

A star topology was employed, consisting of six player hosts (h1–h6) connected to a central game server (server1) via an OpenFlow-enabled switch (s1), as detailed in

Table 5. Simulation components.

Component	Quantity	Description
Player Hosts	6	Simulate individual esports players
Game Server	1	Central server for all players
Switch	1	Aggregates traffic between players and server

. Each player node communicates directly with the central server through the switch, using either TCP or UDP. Although the emulation supports both protocols, this study does not involve application-layer traffic generation. Instead, link conditions were configured directly using the tc netem utility to simulate network impairments. All links were instantiated using Mininet’s TCLink class, enabling fine-grained, dynamic control over key link-level parameters, including delay, jitter, and packet loss rate.

Network conditions were systematically varied in each simulation round to emulate realistic traffic dynamics and disturbances. Specifically, the link-level delay was modulated using a sinusoidal pattern to simulate cyclical network congestion.

The delay at round r was computed as follows: $D_r=30+20\times \mathrm{s}\mathrm{i}\mathrm{n}\left({\displaystyle \frac{2\pi r}{200}}\right)+noise,noise\sim U\left[-20,20\right]$, where 30 ms is the baseline delay, 20 ms is the modulation amplitude, 200 rounds define the period, and the additive noise is uniformly sampled from [−20,20] ms. Any delay value below 0 ms was clipped using Dr = max (Dr, 0 ms) to avoid non-physical negative delays. Jitter for each player was simulated as a sinusoidal signal with a mean of 20 ms, an amplitude of 10 ms, and a period of 100 rounds, superimposed with Gaussian noise ε~$𝒩$ (0, 5 ms). In addition, approximately 5% of rounds included jitter spikes ranging from 20 ms to 50 ms to emulate sporadic network turbulence. Packet loss was randomly injected in 20% of rounds, with the loss rate uniformly sampled between 10% and 80%.

To emulate severe degradation scenarios, every 30 rounds, one randomly selected player experienced either an additional 300 ms delay or elevated packet loss between 50% and 80%. Furthermore, in 10% of all rounds, extreme network anomalies were simulated by randomly assigning a player host either a complete disconnection (100% packet loss) or a delay spike of 500 ms.

Measurement metrics were derived directly from the network conditions configured at each simulation round. Crucially, the network QoS parameters were explicitly set and controlled for each player and the server via their respective virtual network interfaces (eth0), using the Linux Traffic Control (tc) utility and the netem (Network Emulator) queuing discipline.

It is important to note that this simulation focused exclusively on the controlled configuration and logging of QoS parameters. No application-layer traffic (e.g., generated by iperf) was transmitted between hosts, nor were active measurement tools (such as ping) used to estimate latency or packet loss. The primary objective was to generate a controlled dataset that reflects diverse and fluctuating network conditions, following predefined probabilistic rules, for the purpose of training and evaluating QoS prediction models. The dataset aims to compare methods and examine coverage-width behavior under diverse perturbations rather than to exhaustively capture all gameplay regimes. A lightweight configuration $(L=10,H=64)$ and conservative training settings reduce overfitting risk and help preserve fairness across baselines.

Average RTT was approximated as twice the mean one-way delay, under the assumption of symmetric paths typical in LAN-style esports environments. Jitter and packet loss rates were likewise derived directly from the configured tc parameters, thereby offering accurate and consistent ground truth values without the variability inherent in active measurement tools.

The 1000-round simulation yielded 1000 aggregated records, each summarizing latency, jitter, and packet loss across all six players. This dataset serves as the foundation for both training and rigorous evaluation of QoS forecasting models.

Table 6. Simulation results.

Feature	Mean	Std. Dev	Min	Q1	Median	Q3	Max
latency (ms)	70.2	49.56	1.38	35.14	64	89.56	299.46
jitter (ms)	21.69	7.84	5.96	15.02	21.8	27.86	47.25
loss rate (%)	10.34	9.12	0	1.84	9.47	16.37	48.57

presents descriptive statistics of the core QoS features, including average latency (ms), jitter (ms), and packet loss rate (%). The dataset spans a wide range of conditions, with latency between 1 and 299 ms, jitter between 6 and 47 ms, and packet loss rates between 0 and 49%. These variations are consistent with the stochastic and periodic configurations applied in the simulation and allow for comprehensive model evaluation under both stable and highly variable network scenarios.

This simulation framework offers a comprehensive and reproducible environment for evaluating the accuracy and risk estimation capabilities of various models under network dynamics that approximate real-time esports scenarios. The pseudocode presented in Figure 1 illustrates the unified pipeline used for training, validating, and comparing multiple predictive models for risk-aware QoS forecasting. This pipeline incorporates both conventional regression models and uncertainty-aware architectures, including BR-LSTM and BNN.

4.2. Experimental Details

This study focuses on predictive modeling and risk analysis of three key QoS indicators, namely, latency, jitter, and packet loss. The experimental dataset was generated with Mininet-based network simulations that emulate realistic and dynamic conditions typical of multiplayer online gaming environments. Bayesian ridge regression was first applied independently to each indicator to estimate the predictive mean $\widehat{\mu }$ and standard deviation $\widehat{\sigma }$, thereby introducing uncertainty information into the features. These statistics provide the inputs for subsequent modeling.

The BR-LSTM model accepts a six-dimensional input at each time step that contains the predicted means and standard deviations for latency, jitter, and packet loss. This format allows the model to represent both expected values and their associated uncertainties over time. Other baselines, including SVR, RF, MLP, QR, BNN, GPR, and standard LSTM variants, as well as ARIMA and a linear state–space Kalman model, were implemented using either the enhanced features or the original QoS metrics.

Feature representations were arranged in flattened or sequential form according to each model’s input requirements. A concise taxonomy grouped by learning paradigm and temporal capability is provided in

Table 7. Model classification by nature.

Category	Algorithms	Characteristics
Traditional ML	SVR, RF	Non-sequential; deterministic; no uncertainty estimates
Deterministic Neural Networks	MLP	Feed forward; high point accuracy; no risk bound
Sequential Deterministic	Standard LSTM	Captures temporal patterns; deterministic output
Bayesian Sequential	BR-LSTM, MC-Dropout LSTM	Sequence modeling with explicit uncertainty
Probabilistic Feed-forward	BNN	$\mathrm{Fully} \mathrm{Bayesian} \mathrm{weights}; \widehat{\mu }\pm k\widehat{\sigma }$ risk bounds
Kernel Probabilistic	GPR	Non-parametric; predictive; mean$\widehat{\mu }$ and $\widehat{\sigma }$
Quantile Regression	QR (qτ)	Directly predicts upper quantile; τ = 0.95
Classical Statistical	ARIMA	Linear autoregressive moving average with differencing; provides native 95% forecast interval
Sequential State–space	Local-level Kalman Filter	Linear Gaussian state–space with Bayesian recursive update; provides native 95% forecast interval

. The availability of probabilistic risk indicators for each algorithm, namely, $\widehat{\mu }\pm k\widehat{\sigma }$ or $q_{\tau }$ (τ = 0.95), is summarized in Table 3.

Sequential prediction used a sliding window of length ten to forecast the QoS state at time t + 1. To prevent data leakage, feature standardization parameters were fit on the training split only and then applied to the test data.

The dataset was partitioned into 80% training and 20% testing by random shuffling with a fixed seed to ensure statistical diversity and reproducibility. This partitioning and preprocessing protocol was applied consistently across all model training and evaluation procedures. Per-sample inference latency was measured on the CPU with a single thread and a batch size of one. Each model was warmed up and then timed over repeated runs to record the mean and the 95th percentile (p95) latency. The qualitative “Inference cost” labels in

Table 8. Computational cost comparison of models.

Model	Training Time (s)	Model Size (MB)	Latency (Mean) (ms)	Latency (p95) (ms)	Inference Cost (Single-Sample, CPU)
BNN	0.53	0.01	49.22	51.72	High
BR-LSTM	10.48	0.07	0.75	0.86	Low
GPR	0.24	14.96	4.46	5.20	Medium
MC-Dropout LSTM	11.26	0.07	0.51	0.77	Low
MLP	13.54	0.33	2.46	3.02	Medium
QR	24.8	0.01	2.23	3.22	Medium
RF	29.73	19.5	54.71	78.24	High
SVR	0.56	0.57	4.63	6.21	Medium
Standard LSTM	23.11	0.07	0.54	1.16	Low
ARIMA	0.88	3.03	15.77	18.46	High
Kalman	0.72	1.63	6.98	7.98	High

Notes: “Inference cost” labels follow the measured per-sample latency (Low ≤ 1 ms; 1–5 ms = Medium; >5 ms = High). MC-Dropout LSTM and BNN use S = 20 stochastic passes for predictive averaging in this study; Table 8 reports the single-pass latency, and executing S passes on CPU increases the per-sample wall time approximately S-fold.

are derived from these measurements using fixed thresholds: Low ≤ 1 ms; 1–5 ms = Medium; >5 ms = High. For stochastic predictors, the latency reflects the evaluated configuration. MC-Dropout LSTM and BNN use S = 20 stochastic passes for predictive averaging in this study (see Table 2). Table 8 reports the single-pass latency; executing S passes on the CPU increases the per-sample wall time approximately S-fold.

Model configurations and hyperparameters were selected based on preliminary experiments. Bayesian ridge regression used default values for the prior precision and the noise variance. The BR-LSTM model used an input size of six, 64 hidden units, a single hidden layer, a batch size of 16, and a learning rate of 0.001, and was trained for 30 epochs.

The same number of training epochs was applied to the standard LSTM (input size three) and to the MC-Dropout LSTM (input size three, dropout rate 0.3). The BNN accepted a flattened 30-dimensional input vector derived from a 10-step window of the three QoS features and was trained for one hundred epochs on the training split. GPR was configured with default kernel settings. The QR model targeted the ninety-fifth percentile and used a regularization parameter α = 0.1. The MLP consisted of a single hidden layer with one hundred neurons and ReLU activation, optimized with the Adam optimizer for five hundred iterations. The RF used one hundred trees with no maximum depth constraint. The SVR employed an RBF kernel with default regularization parameters.

Model performance was evaluated with standard regression metrics, including MAE, RMSE, and R². All scores were computed after applying the inverse standardization to restore the original units. In addition to point estimation, risk was assessed with Bayesian prediction intervals of the form $\widehat{\mu }\pm k\widehat{\sigma }$, where $\widehat{\mu }$ and $\widehat{\sigma }$ denote the predicted mean and standard deviation. The scaling factor k was tuned on the validation set to target approximately 95% coverage. For QR, risk evaluation used the 95th percentile prediction q_τ with τ = 0.95, which directly provides the upper bound of the QoS indicators.

For models that support uncertainty estimation, including BR-LSTM, MC-Dropout LSTM, BNN, and GPR, additional metrics PICP, MPIW, and FAR were reported. These metrics were computed relative to the SLA thresholds of 100 ms for latency, 50 ms for jitter, and 10% for packet loss. While MAE, RMSE, and R² assess point forecast accuracy, PICP captures the empirical coverage of the prediction intervals and MPIW measures their average width, reflecting sharpness. FAR quantifies the fraction of alarms that do not correspond to actual SLA violations. A reliable model should achieve high coverage with narrow intervals and a low FAR, thereby balancing calibration and informativeness.

In practice, the value of k is not fixed because the predictive uncertainty may deviate from a strict Gaussian distribution. Therefore, empirical calibration is performed by tuning k on the validation set. For a target of 95% coverage, we define the one-sided bounds as $L_i={\widehat{\mu }}_i-k{\widehat{\sigma }}_i$ and $U_i={\widehat{\mu }}_i+k{\widehat{\sigma }}_i$, with k $\in$ [1, 3] chosen to minimize |PICP−0.95|. The calibrated interval is then evaluated on the test set. The risk-centric indicators are defined in (6)–(8), where N is the number of test samples, $\mathcal{I}\left\{·\right\}$ is the indicator function, ϕ is the nominal miscoverage rate (for example, 0.05 for a 95% interval), and δ is the SLA upper bound for the corresponding QoS metric.

$$\mathrm{P}\mathrm{I}\mathrm{C}\mathrm{P}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N\mathcal{I}\left\{L_i\le y_i\le U_i\right\}$$

(6)

$$\mathrm{M}\mathrm{P}\mathrm{I}\mathrm{W}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N(U_i-L_i)$$

(7)

$$\mathrm{F}\mathrm{A}\mathrm{R}={\displaystyle \frac{{\sum }_{i=1}^N\mathcal{I}\{U_i>\delta ,y_i\le \delta \}}{max(1,{\sum }_{i=1}^{N}1\{U_i>\delta \left\}\right)}}\times 100$$

(8)

Calibration multiplies the interval half-width by the selected factor k, yielding calibrated interval width and alarm statistics (reported as MPIW_cal and FAR_cal). Each model is evaluated separately for each QoS metric to enable a detailed assessment of performance and risk. All experiments were conducted in a controlled Python environment to ensure reproducibility.

Unless stated otherwise, baseline implementations used the default parameters of the scikit learn library (version 1.6.1). This applies to Bayesian Ridge, SVR, RF Regressor, and GPR. For the MLP regressor, the maximum number of iterations was set to 500, with all other parameters kept at their default values. The QR model used a quantile level of 0.95, a regularization parameter α = 0.1, and the “highs” solver.

The MC-Dropout LSTM baseline was implemented in PyTorch (version 2.6.0 + cu124) with a hidden size of 64 and a dropout rate of 0.3. It was trained for 30 epochs using the Adam optimizer with a learning rate of 0.001 and a batch size of 16. The implementation used T = 20 stochastic forward passes; in a pilot study, $\widehat{\sigma }$ stabilized with less than 1% relative change beyond T = 20.

Although these configurations are common and reasonable, no systematic hyperparameter optimization was performed. Procedures such as cross-validated grid search or randomized search were not applied. Further tuning could potentially improve the performance of the baseline models.

MC-Dropout LSTM is reported as a single-pass measurement; if S stochastic passes are used to form a predictive average, the wall time on CPU scales approximately linearly with S. Bayesian neural networks similarly incur an S-dependent cost; when only a qualitative comparison is required, their inference is categorized as High under the stated thresholds.

4.3. Evaluation Results

Model performance was evaluated on three key QoS metrics, namely, latency, jitter, and packet loss rate. The evaluation employed standard regression metrics, including MAE, RMSE, and the coefficient of determination R². Beyond point prediction accuracy, the reliability of calibrated risk intervals in maintaining compliance with SLA thresholds was also examined. Out-of-sample R² on the test set was computed as $R^2=1-\sum (y-\widehat{y}{)}^2/\sum (y-{\overline{y}}_{\mathrm{test}}{)}^2$, where ${\overline{y}}_{\mathrm{test}}$ denotes the test-set mean. Negative values arise when the squared error of the model exceeds the variance of the test set around its mean. This can occur on nonstationary QoS traces with abrupt regime changes and indicates that the model underperforms a mean predictor on that segment.

The results are interpreted with an emphasis on directional consistency and relative gaps rather than formal p-values. Specifically, Table A1 (in the Appendix A) summarizes point errors (MAE, RMSE, R²), Table A2 (in the Appendix A) reports calibrated interval quality (PICP, MPIW, FAR), and the SLA-oriented visuals in Figure 2, Figure 3 and Figure 4 contextualize upper-bound interactions with policy thresholds. Read together, these materials support model ranking and trade-off interpretation across latency, jitter, and loss.

In addition to MAE and RMSE, this study reports R² as a scale-free complement. On highly nonstationary episodes with abrupt shifts, several models, including the proposed BR-LSTM, exhibit negative test set R². Such negative values are expected in nonstationary and regime-shifting network traces of the type used in this study. Nevertheless, MAE and RMSE show that these models consistently outperform naive or persistence baselines, indicating practical forecasting value, even under challenging conditions. This behavior follows directly from the out-of-sample definition: for those segments, the squared error exceeds the variance around the test set mean. It does not contradict the absolute error improvements observed in MAE and RMSE.

As summarized in Table 4, the overall ranking consolidates point accuracy (Table A1) and risk-aware interval behavior (Table A2). BR–LSTM yields a balanced trade-off between accuracy and calibrated risk bounds; RF/MLP lead in terms of pure point accuracy but lack uncertainty; QR provides conservative upper bounds; and MC-Dropout/BNN undercovers despite the narrow intervals.

On latency, the local level state–space model attains the lowest error (MAE 24.99 ms), followed by GPR (MAE 25.58 ms). Among neural baselines, BNN reaches 28.70 ms, whereas BR-LSTM and MC-Dropout LSTM achieve 32.49 ms and 33.77 ms, respectively. Explained variance is positive for state–space (R² = 0.20) and for GPR (R² = 0.17), while most other methods yield smaller values; QR remains an outlier with markedly larger error (MAE 100.68 ms, R² = −2.64). For jitter, RF provides the best point accuracy (MAE 3.05 ms, R² = 0.74), followed by state–space (MAE 3.24 ms, R² = 0.72) and GPR (MAE 3.33 ms, R² = 0.71). Neural models are competitive but not leading in this regime (for example, MLP MAE 3.92 ms, R² = 0.56; BNN MAE 4.61 ms, R² = 0.43; BR-LSTM MAE 6.62 ms, R² = 0.03). For packet loss, explained variance is generally limited; in MAE terms, state–space and ARIMA are strongest (7.15% and 7.23%), followed by standard LSTM (7.69%), MC-Dropout LSTM (7.68%), SVR (7.73%), and BR-LSTM (7.75%), with QR again worst (17.35%). Overall, deterministic accuracy favors state–space and GPR for latency and RF, state–space, and GPR for jitter, whereas state–space and ARIMA lead in packet loss MAE; the proposed BR-LSTM is competitive but not the top performer on MAE for this dataset.

Prediction interval quality was assessed using empirical coverage (PICP), mean interval width (MPIW), and FAR for both raw μ ± 1.96σ and calibrated μ ± kσ bands, with k tuned to target 95% coverage. For latency, calibrated intervals reach near nominal PICP across the uncertainty-aware baselines: state–space 93.94% (MPIW 213.44 ms), GPR 93.43% (211.16 ms), ARIMA 93.43% (272.77 ms), and BR-LSTM 93.43% (198.17 ms). BR-LSTM, therefore, attains competitive coverage with the narrowest calibrated bands among these models, whereas ARIMA requires substantially wider intervals to achieve similar coverage.

For jitter, calibration yields tight, near nominal bands for GPR (PICP 95.45%, MPIW 15.57 ms) and state–space (94.95%, 16.27 ms). ARIMA also attains high coverage (97.47%) but with wider intervals (21.68 ms). BR-LSTM improves with calibration but remains under-covered on jitter (82.83%) and relatively wide (37.51 ms).

For packet loss, calibrated BR-LSTM reaches PICP 93.94%, with the tightest intervals among the four uncertainty-aware baselines (MPIW: 24.88% points), while GPR (93.43%, 26.70) and state–space (92.93%, 27.01) are comparable. ARIMA maintains high coverage (94.44%) at the cost of very wide bands (42.13). In contrast, MC-Dropout and BNN produce extremely narrow intervals but severe under-coverage on latency (for example, PICP 6.06% and 11.62%), making them unsuitable for risk-aware operations without additional uncertainty mechanisms. These outcomes illustrate the classical coverage versus width trade-off: nominal coverage can be achieved with broader bands, whereas overly tight bands degrade reliability.

In comparing calibrated upper risk bounds with the service level thresholds of 50 ms for jitter, 100 ms for latency, and 10% for loss yields consistent patterns, for jitter, the calibrated upper bounds of BR-LSTM, GPR, state–space, and ARIMA all lie below the 50 ms threshold (approximately 31.63 to 41.65 ms); the QR q_τ is likewise below the threshold at 34.55 ms. For latency, BR-LSTM, at 84.36 ms, and MC-Dropout LSTM, at 75.68 ms, lie below 100 ms, whereas GPR, at 114.31 ms, state–space, at 118.87 ms, and ARIMA, at 209.71 ms, exceed the threshold, reflecting their wider calibrated bands. For packet loss, state–space at 10.22% and GPR at 10.65% sit near the 10% threshold, while BR-LSTM at 12.29%, MC-Dropout LSTM at 11.37%, ARIMA at 22.10%, and QR at 27.06% exceed it. Operationally, latency emerges as the primary risk driver. Models that maintain narrow yet calibrated envelopes during surge periods, such as BR-LSTM, provide clearer early warning signals, whereas very wide envelopes, such as ARIMA, are conservative but less actionable.

Taken together, Table 7 and Table A2 indicate that state–space and GPR lead in latency point accuracy; RF, state–space, and GPR lead in jitter accuracy; and state–space and ARIMA lead in packet loss MAE. After calibration, BR-LSTM provides competitive coverage with comparatively narrow bands for latency and loss, while GPR and state–space yield tight, near-nominal bands for jitter. ARIMA supplies a conservative envelope with high coverage but large widths. MC-Dropout and BNN exhibit severe under-coverage and would require stronger uncertainty modeling. These findings reconcile point accuracy with risk-aware behavior and can guide the choice of a forecaster depending on whether the priority is nominal tracking or SLA-oriented risk control.

5. Discussion

Across metrics, point accuracy and operational risk are only loosely coupled. Figure 4 shows that brief bursts can trigger SLA interactions even when global coverage is near nominal; conversely, very narrow bands can under-cover excursions despite favorable point errors. Together with Table A1 and Table A2, the plots show the trade-off between coverage and width. SLA monitoring should track the upper risk bound with its empirical coverage and low FAR; point errors alone are insufficient. Together with Table 4, these findings translate into an operational ranking that balances accuracy and actionable risk bounds for SLA-oriented decisions.

Given temporal dependence and regime shifts in the test traces, per-sample error tests that presume independence can misstate uncertainty. For this reason, this study refrains from reporting p-values and instead foregrounds effect directions and stable relative gaps across Table 7, Table A1 and Table A2 and Figure 2, Figure 3 and Figure 4, complemented by calibrated interval behavior against SLA thresholds. Because L mainly sets the temporal receptive field and H sets model capacity and computational cost, moderate adjustments primarily shift point errors without altering the directional conclusions emphasized in Table 7, Table A1 and Table A2 and Figure 2, Figure 3 and Figure 4. To preserve fairness across baselines, this study reports a fixed $(L=10,H=64)$ configuration and reserves exhaustive ablations for future work. Future work will incorporate paired testing (e.g., paired t-tests or Wilcoxon signed-rank) with serial-dependence-aware resampling (e.g., moving-block bootstrap) to produce confidence statements for model-to-model differences under realistic dependence.

Viewed through Figure 2 and Figure 3, BR-LSTM occupies a favorable operating point for latency assurance. After calibration, coverage is near the nominal target without uniformly wide intervals. For packet loss surveillance, among the well-calibrated baselines, it yields the tightest calibrated bands, which improves the precision of alarms during intermittent surges. For jitter, BR-LSTM is not leading; models with explicit stochastic smoothing, such as GPR and the state–space model, produce tighter yet reliable envelopes for small and frequent excursions. These patterns are consistent with the coverage and width frontier summarized in the evaluation.

Jitter is characterized by small and frequent excursions with a short correlation time. Kernel and state–space models encode local stochastic smoothing, which yields tighter and reliable jitter envelopes. In contrast, the BR-LSTM architecture increases variance where volatility emerges, such as burst onsets and regime transitions, which favors latency assurance and loss surveillance because these metrics exhibit trend-and-recovery dynamics with abrupt surges. This behavior explains why BR-LSTM is not the leading choice for jitter reliability yet attains competitive coverage with comparatively narrow calibrated bands for latency and loss. While tighter jitter control is required, context-conditioned or rolling calibration can further concentrate width on high-variance segments while preserving overall coverage.

Mechanistically, BR-LSTM couples a per-timestep BR, which supplies mean and variance cues, with a sequential LSTM that propagates these uncertainty signals through time. Calibration selects a single k on a validation split and then holds it fixed on the test split. The BR stage yields both epistemic and aleatoric components through the ${\sigma }_n^2+x^{\mathrm{\top }}{\mathsf{\Sigma }}_{w}x$ decomposition; the sequence model propagates these signals to produce ${\widehat{\sigma }}_{t+1}$, and the study calibrates the combined predictive band using the global k chosen on validation. The architecture tends to inflate variance where volatility emerges, such as burst onsets and regime transitions, rather than uniformly, which yields locally sharp yet adequately covered bands.

For jitter, GP and local level state–space models typically produce tight, well-calibrated envelopes, an advantage when small and frequent excursions dominate (see Figure 3 and Figure 4). Their memory footprint, however, is noticeably larger than compact neural baselines (Table 8). In contrast, BR-LSTM is burst-aware: it maintains calibration while avoiding excessive width during latency surges, which is preferable for SLA-centric alerting.

Classical ARIMA often attains coverage by broadening intervals. Figure 4 shows visibly wider bands, consistent with the larger MPIW required by classical baselines to meet coverage targets.

Dropout-based and weak Bayesian surrogates are overconfident. They produce narrow bands but under-cover across metrics (Figure 3), and Figure 4 shows that this under-coverage appears as missed excursions. Even when their apparent upper bounds are below the SLA in Figure 2, the intervals lack statistical reliability. BR-LSTM avoids this issue by combining calibrated coverage with operationally useful width.

Table 8 shows that BR-LSTM remains compact in memory (comparable to other lightweight neural baselines) while incurring moderate training time due to its two-stage procedure. GP and RF models are materially heavier in memory. Classical time-series models such as ARIMA and the local level state–space Kalman model exhibit minimal training time and moderate memory footprints, which makes them suitable as efficient statistical baselines. These costs are compatible with real-time dashboards and edge monitoring. Consequently, when the objective is to stay close to the latency SLA with calibrated guarantees, BR-LSTM is a sensible default, whereas for the tightest reliable jitter envelopes, GP and state–space components remain complementary.

In addition to training time and model size, Table 8 reports per-sample CPU inference latency (mean and p95). Under the stated thresholds, lightweight predictors fall into Low or Medium tiers and are thus compatible with tight edge budgets on CPU, whereas sampling- or kernel-based predictors generally occupy higher-latency tiers unless vectorized or parallelized. These measurements make the deployability implications explicit and clarify when accuracy gains warrant additional milliseconds on resource-constrained edge nodes.

A pragmatic selection rule is two-gated. The first gate enforces admissibility by calibration and accepts only models whose empirical coverage lies within a tight tolerance of the nominal target. The second gate prioritizes risk and, among the admissible models, selects the one that minimizes the upper risk bound relative to the metric-specific SLA.

Under this policy, BR-LSTM is typically preferred for latency and packet loss monitoring, whereas GP and state–space models are favored for jitter-specific refinement.

Beyond a global factor, dynamic or context-conditioned calibration can tighten intervals in stable regimes while preserving coverage during bursts. A time-varying scheme can recalibrate k on a rolling validation window to track gradual drift. A feature-conditioned scheme can assign $k\left(x\right)$ by context (e.g., mobility state or load bins) to approximate conditional coverage. Distribution-free conformal prediction provides another route by calibrating residuals on recent data, optionally with sliding windows or stratification by context. These options can reduce average interval width and align upper bounds with SLA thresholds more closely, subject to safeguards against small-sample instability and policies that prevent adaptation from using test outcomes. Empirical evaluation is left for future work. Second, exogenous drivers and regime-aware components, for example, state–space residuals or GP-style kernels layered on BR-LSTM, may reduce width at equal coverage, particularly for heavy-tailed loss bursts. These proposals are orthogonal to the reported results and are motivated directly by the coverage and sharpness trade-offs observed in Figure 2, Figure 3 and Figure 4.

Considering Figure 2, Figure 3 and Figure 4 and Table 8 jointly, BR-LSTM provides a balanced trade-off among calibrated uncertainty, burst-resilient risk control, and deployability. Classical ARIMA and Kalman state–space models are notable for computational efficiency and analytic uncertainty intervals; while they are generally less flexible for nonstationary or nonlinear dynamics than neural baselines, their low training cost and moderate memory usage make them practical for rapid prototyping and resource-constrained deployments.

After calibration, BR-LSTM achieves near-nominal coverage with the narrowest calibrated bands among uncertainty-aware baselines for latency and loss (Table A2), while GPR/state–space provides tighter and more reliable jitter envelopes (Table 4, Table A1 and Table A2). Extreme volatility or class imbalance in certain test traces can degrade interval coverage, especially for packet loss, which motivates future research on adaptive calibration and rare event detection.

Negative coefficients of determination arise on segments with pronounced nonstationarity or regime shifts where the squared error exceeds the variance around the test-set mean. In such cases, a constant baseline can outperform the fitted model locally. For decision making, point accuracy is therefore complemented with calibrated coverage (PICP), interval width (MPIW), false-alarm control (FAR), and SLA-oriented upper bounds $\mu +k\sigma$, which indicate whether alerts remain well-controlled under bursty conditions.

The Mininet dataset configures link-level QoS using tc netem without generating application-layer traffic, so feedback effects from real gaming workloads are not captured. This design isolates modeling effects under controlled, diverse conditions for fair method comparison, but external validity may be limited. Future work will incorporate traffic replay and semi-real testbeds and will evaluate the model on operational traces.

6. Conclusions

This study introduced a two-stage BR-LSTM framework for proactive QoS forecasting in dynamic esports networks. The model was evaluated against uncertainty-aware baselines (BNN, GPR, MC-Dropout LSTM, and QR) and classical time-series baselines (ARIMA and a local level state–space model). On point forecast accuracy (Table A1), BR-LSTM attains competitive errors across latency, jitter, and packet loss, for example, latency MAE 32.49 ms, jitter MAE 6.62 ms, and loss MAE 7.75%, while several baselines lead on specific metrics, such as state–space and GPR for latency and RF and state–space for jitter. These results position BR-LSTM as a strong neural alternative within the broader accuracy landscape.

With respect to risk-aware operation (Table A2), calibrated intervals of the form $\widehat{\mu }\pm k\widehat{\sigma }$ for BR-LSTM achieves near nominal coverage for latency and loss (PICP 93.43% and 93.94%, respectively) but sub-target coverage for jitter (82.83%). The corresponding upper risk bounds show that the latency envelope remains below the 100 ms SLA (84.36 ms) and the jitter envelope is comfortably below the 50 ms SLA (31.63 ms), whereas the packet loss bound remains above the 10% SLA (12.29%), reflecting the intrinsic difficulty of tail events in loss dynamics. These results highlight the persistent challenge of predicting packet loss under bursty and rare event conditions and motivate further work on tail risk modeling and adaptive calibration strategies. Taken together, the findings indicate a favorable coverage and sharpness trade-off for latency and a pragmatic envelope for loss, with jitter reliability being improvable through tighter local calibration.

From a deployment perspective, BR-LSTM maintains a compact footprint and a straightforward calibration workflow, which makes it suitable for real-time dashboards and edge scenarios. Evidence across Table 7 and Table A2 supports the following. For latency, BR-LSTM provides calibrated envelopes that remain under the SLA while preserving coverage. For jitter, GP and state–space models remain advantageous for the tightest reliable bands, with BR-LSTM competitive. For packet loss, all models encounter intermittent SLA interactions, which motivates loss-tail-aware enhancements. Classical ARIMA and Kalman models maintain extremely low training time and moderate memory, providing fast and interpretable benchmarks for practical monitoring systems, although with reduced flexibility for complex dynamics. The added per-sample latency in Table 8 indicates that models in the Low or Medium tiers meet sub-millisecond to few-millisecond CPU budgets on edge nodes without specialized accelerators, whereas higher-latency models remain appropriate when accuracy gains dominate and resources permit.

Calibrated upper bounds $\mu +k\sigma$ align naturally with SLA thresholds. Dashboards can surface early warnings when the upper bound approaches policy limits, while operators prioritize tickets or throttle nonessential traffic when risk persists across consecutive windows. For control loops, admissibility is first established by calibration; only models whose empirical PICP lies within a narrow tolerance of the nominal target are considered. Actions are then triggered when the upper bound exceeds metric-specific thresholds for latency, jitter, or loss. This workflow converts calibrated uncertainty into actionable signals for preemptive routing, pacing, or bitrate adaptation without relying on post hoc mitigation.

For network control, expose $\mu +k\sigma$ as a per-link risk score and incorporate it into a composite cost with latency, jitter, and packet loss. The controller selects routes that minimize this risk-weighted cost and triggers preemptive switching or pacing when the cost exceeds policy thresholds over consecutive windows.

Limitations and Future Work

While the proposed model demonstrates promising results, there are important limitations that remain, particularly in data realism and temporal calibration.

Data realism is a key challenge, as the current study relies on synthetic or controlled datasets. Real-world network congestion, unpredictable traffic, and heterogeneous access technologies are not fully captured. Incorporating live data and real-world traces will be a focus in improving robustness and generalization. Future work will evaluate rolling re-calibration, feature-conditioned (Mondrian) schemes, and distribution-free conformal prediction. The goal is to tighten intervals in stable regimes while preserving coverage during bursts, with safeguards against small-sample instability and leakage.