Classifying Protein-DNA/RNA Interactions Using Interpolation-Based Encoding and Highlighting Physicochemical Properties via Machine Learning
Abstract
1. Introduction
- Use of logarithmic labeling to highlight numerical values associated with the physicochemical properties of amino acids that predominate in protein–DNA/RNA interactions.
- Continuous representation of protein residues derived by interpolating discrete values relating to their physicochemical properties.
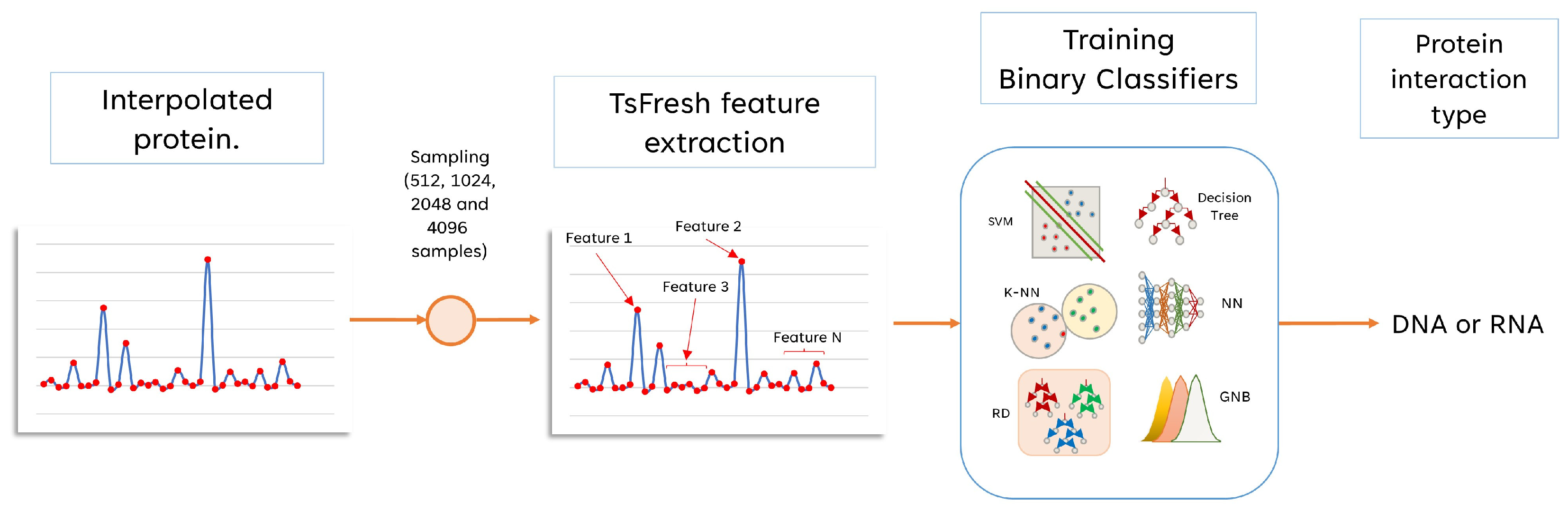
- Automatic feature extraction from continuous protein spectra using TSfresh (Time Series Feature extraction based on scalable hypothesis tests) Python package to feed and improve supervised binary classification (to infer protein interaction type).
- Comparison of the proposed approach based on continuous representation of protein sequences with k-mer counting, a method commonly used in bioinformatics.
2. Materials and Methods
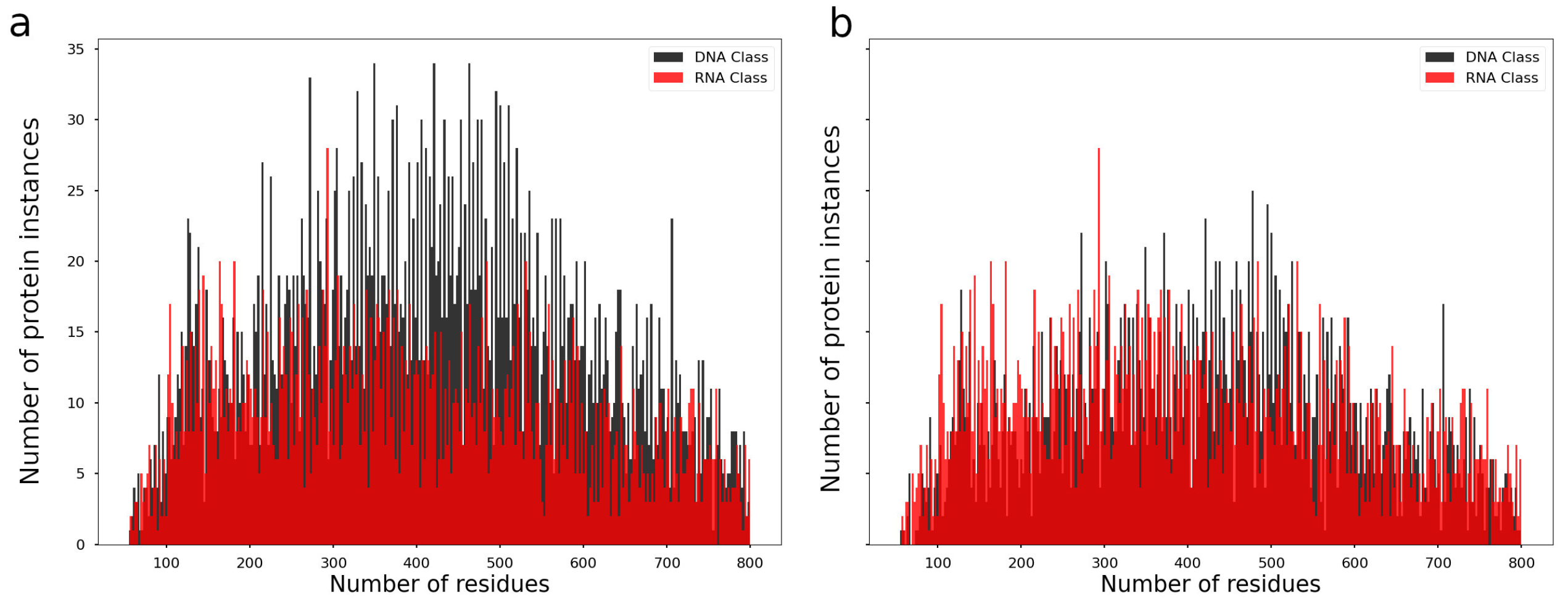
2.1. Protein Dataset
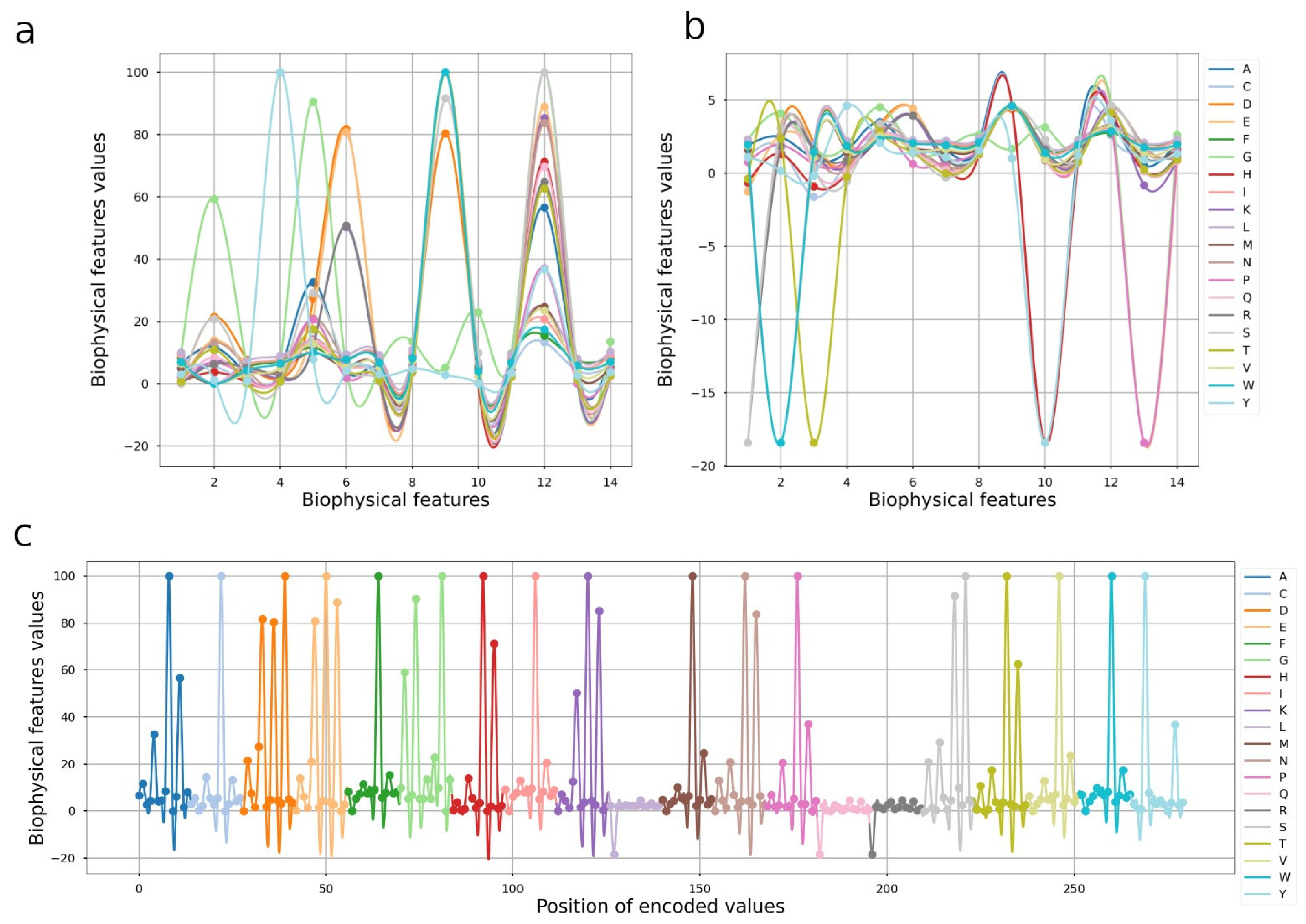
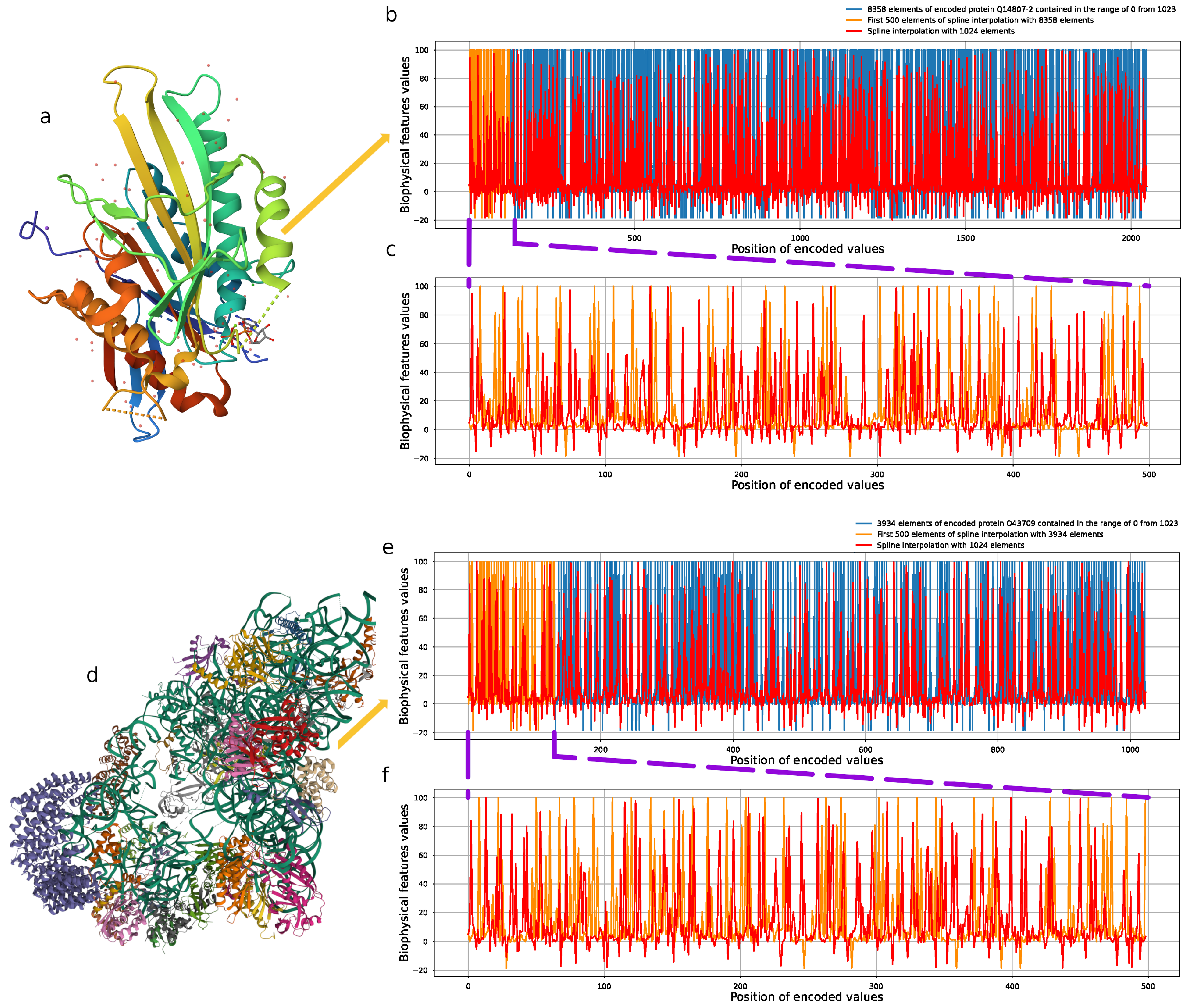
2.2. Proposed Encoding with Physicochemical Properties
2.3. Cubic B-Spline Interpolation
- a = 0
- b = Highest value in selected range.
- , , …, = M consecutive positions for encoded values.
2.4. Feature Extraction and Selection
2.5. Classifiers for Spline Interpolated Features
2.5.1. Decision Tree (DT)
2.5.2. Support Vector Machine (SVM)
2.5.3. K-Nearest Neighbors
2.5.4. Random Forest
2.5.5. Gaussian Naive Bayes
- is mean
- is standard deviation
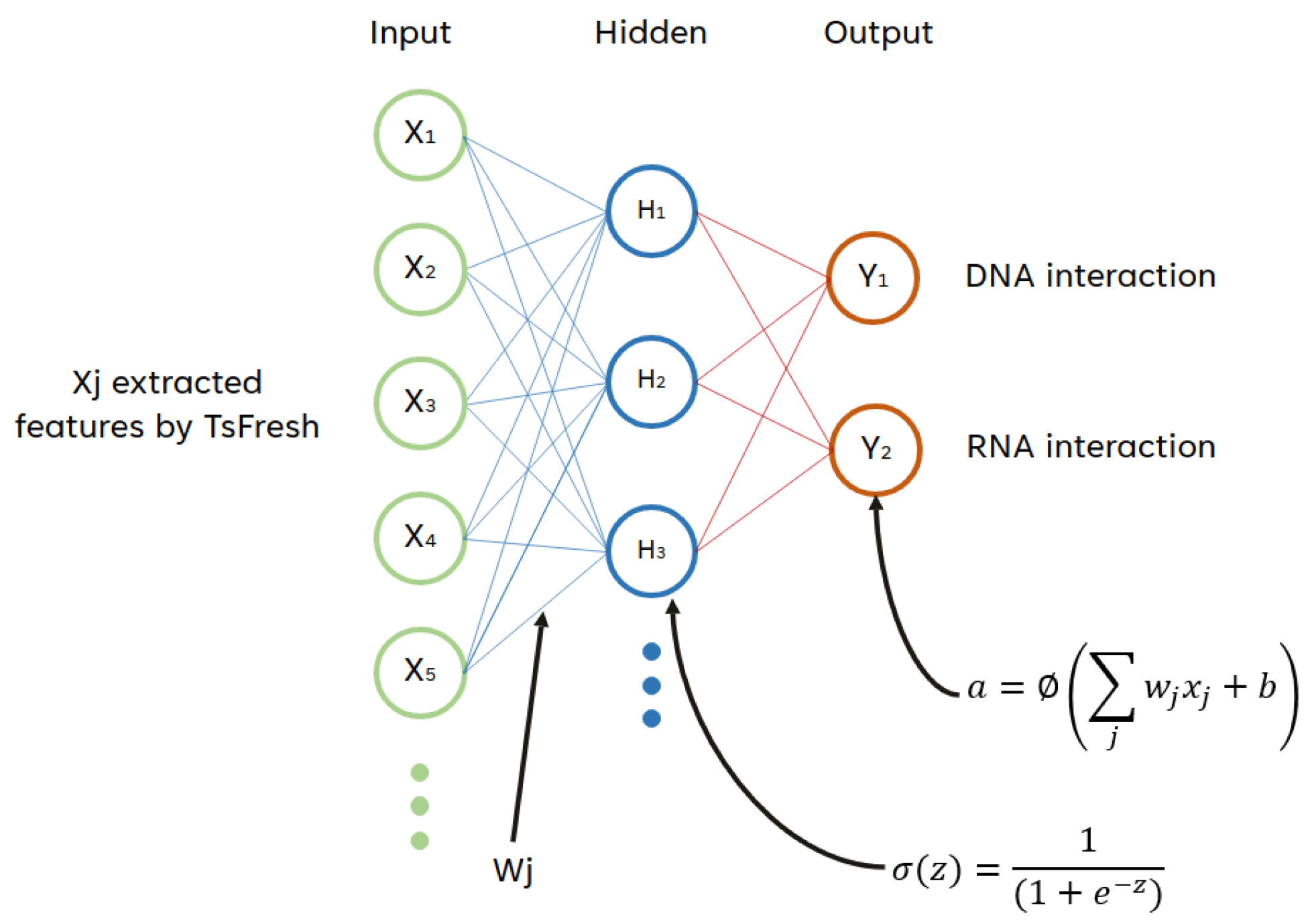
2.5.6. Multilayer Perceptron
2.6. Evaluation Metrics
3. Results
3.1. Dataset Balance Evaluation
3.2. Protein Encoding
3.3. Classifiers Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| DNA | Deoxyribonucleic Acid |
| RNA | Ribonucleic Acid |
| DL | Deep Learning |
| MLMs | Machine Learning Models |
| NLP | Natural Language Processing |
| LCA | Lowest Common Ancestor |
| PCPs | Physicochemical Properties |
| CNN | Convolutional Neural Network |
| MLP | Multilayer Perceptron |
| CNNs | Convolutional Neural Networks |
| LSTM | Long-Short Term Memory |
| GO | Gene Ontology |
| AAs | Amino Acids |
| DT | Decision Tree |
| SVM | Support Vector Machine |
| k-NN | K-Nearest Neighbor |
| RF | Random Forest |
| GNB | Gaussian Naive Bayes |
References
- Berg, J.M.; Tymoczko, J.L.; Stryer, L. Biochemistry, 5th ed.; W.H. Freeman: New York, NY, USA, 2002. [Google Scholar]
- Wang, P.; Fang, X.; Du, R.; Wang, J.; Liu, M.; Xu, P.; Li, S.; Zhang, K.; Ye, S.; You, Q.; et al. Principles of Amino-Acid-Nucleotide Interactions Revealed by Binding Affinities between Homogeneous Oligopeptides and Single-Stranded DNA Molecules. ChemBioChem 2022, 23, e202200048. [Google Scholar] [CrossRef]
- Sathyapriya, R.; Vishveshwara, S. Interaction of DNA with clusters of amino acids in proteins. Nucleic Acids Res. 2004, 32, 4109–4118. [Google Scholar] [CrossRef][Green Version]
- Solovyev, A.Y.; Tarnovskaya, S.I.; Chernova, I.A.; Shataeva, L.K.; Skorik, Y.A. The interaction of amino acids, peptides, and proteins with DNA. Int. J. Biol. Macromol. 2015, 78, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, M.M.; Khrapov, M.A.; Cox, J.C.; Yao, J.; Tong, L.; Ellington, A.D. AANT: The Amino Acid–Nucleotide Interaction Database. Nucleic Acids Res. 2004, 32, D174–D181. [Google Scholar] [CrossRef]
- Krüger, D.M.; Neubacher, S.; Grossmann, T.N. Protein–RNA interactions: Structural characteristics and hotspot amino acids. RNA 2018, 24, 1457–1465. [Google Scholar] [CrossRef]
- Gupta, R.; Srivastava, D.; Sahu, M.; Tiwari, S.; Ambasta, R.K.; Kumar, P. Artificial intelligence to deep learning: Machine intelligence approach for drug discovery. Mol. Divers 2021, 25, 1315–1360. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, W.; Xiao, W. DeepHE: Accurately predicting human essential genes based on deep learning. PLoS Comput. Biol. 2020, 16, e1008229. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Ma, R.; Wang, H. An improved deep learning method for predicting DNA-binding proteins based on contextual features in amino acid sequences. PLoS ONE 2019, 14, e0225317. [Google Scholar] [CrossRef]
- Ahmed, N.Y.; Alsanousi, W.A.; Hamid, E.M.; Elbashir, M.K.; Al-Aidarous, K.M.; Mohammed, M.; Musa, M.E.M. An Efficient Deep Learning Approach for DNA-Binding Proteins Classification from Primary Sequences. Int. J. Comput. Intell. Syst. 2024, 17, 88. [Google Scholar] [CrossRef]
- Zahiri, J.; Emamjomeh, A.; Bagheri, S.; Ivazeh, A.; Mahdevar, G.; Tehrani, H.S.; Mirzaie, M.; Fakheri, B.A.; Mohammad-Noori, M. Protein complex prediction: A survey. Genomics 2020, 112, 174–183. [Google Scholar] [CrossRef] [PubMed]
- Saigal, P.; Khanna, V. Multi-category news classification using Support Vector Machine based classifiers. SN Appl. Sci. 2020, 2, 458. [Google Scholar] [CrossRef]
- Peretz, O.; Koren, M.; Koren, O. Naive Bayes classifier-–An ensemble procedure for recall and precision enrichment. Eng. Appl. Artif. Intell. 2024, 136, 108972. [Google Scholar] [CrossRef]
- Xu, Z.; Li, P.; Wang, Y. Text Classifier Based on an Improved SVM Decision Tree. Phys. Procedia 2012, 33, 1986–1991. [Google Scholar] [CrossRef]
- Jiang, S.; Pang, G.; Wu, M.; Kuang, L. An improved K-nearest-neighbor algorithm for text categorization. Expert Syst. Appl. 2012, 39, 1503–1509. [Google Scholar] [CrossRef]
- Query Input and Database Selection—BlastTopics 0.1.1 Documentation. Available online: https://blast.ncbi.nlm.nih.gov/doc/blast-topics/ (accessed on 3 January 2025).
- Ofer, D.; Brandes, N.; Linial, M. The language of proteins: NLP, machine learning & protein sequences. Comput. Struct. Biotechnol. J. 2021, 19, 1750–1758. [Google Scholar] [CrossRef] [PubMed]
- ElAbd, H.; Bromberg, Y.; Hoarfrost, A.; Lenz, T.; Franke, A.; Wendorff, M. Amino acid encoding for deep learning applications. BMC Bioinform. 2020, 21, 235. [Google Scholar] [CrossRef]
- Koo, P.K.; Ploenzke, M. Deep learning for inferring transcription factor binding sites. Curr. Opin. Syst. Biol. 2020, 19, 16–23. [Google Scholar] [CrossRef]
- Manekar, S.C.; Sathe, S.R. A benchmark study of counting methods for high-throughput sequencing. GigaScience 2018, 7, giy125. [Google Scholar] [CrossRef]
- Hancock, J.T.; Asr, T.M.K. Survey on categorical data for neural networks. J. Big Data 2020, 7, 28. [Google Scholar] [CrossRef]
- Schaefer, M.H.; Lopes, T.J.S.; Mah, N.; Shoemaker, J.E.; Matsuoka, Y.; Fontaine, J.-F.; Louis-Jeune, C.; Eisfeld, A.J.; Neumann, G.; Perez-Iratxeta, C.; et al. Adding Protein Context to the Human Protein-Protein Interaction Network to Reveal Meaningful Interactions. PLoS Comput. Biol. 2013, 9, e1002860. [Google Scholar] [CrossRef] [PubMed]
- Mckenna, A.; Dubey, S. Machine learning based predictive model for the analysis of sequence activity relationships using protein function and protein descriptors. J. Biomed. Inform. 2022, 128, 104016. [Google Scholar] [CrossRef]
- Chen, K.-H.; Wang, T.-F.; Hu, Y.-J. Protein-protein interaction prediction using a hybrid feature representation and a stacked generalization scheme. BMC Bioinform. 2019, 20, 308. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.R.; Bridgland, A.; et al. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, Z.; Teng, Z.; Liu, X. PredAmyl-MLP: Prediction of Amyloid Proteins Using Multilayer Perceptron. Comput. Math. Methods Med. 2020, 2020, 8845133. [Google Scholar] [CrossRef]
- Das, S.; Chakrabarti, S. Classification and prediction of protein–protein interaction interface using machine learning algorithm. Sci. Rep. 2021, 11, 1761. [Google Scholar] [CrossRef]
- Arian, R.; Hariri, A.; Mehridehnavi, A.; Fassihi, A.; Ghasemi, F. Protein kinase inhibitors’ classification using K-Nearest neighbor algorithm. Comput. Biol. Chem. 2020, 86, 107269. [Google Scholar] [CrossRef]
- Peng, L.; Yuan, R.; Shen, L.; Gao, P.; Zhou, L. LPI-EnEDT: An ensemble framework with extra tree and decision tree classifiers for imbalanced lncRNA-protein interaction data classification. BioData Min. 2021, 14, 50. [Google Scholar] [CrossRef]
- Ao, C.; Zhou, W.; Gao, L.; Dong, B.; Yu, L. Prediction of antioxidant proteins using hybrid feature representation method and random forest. Genomics 2020, 112, 4666–4674. [Google Scholar] [CrossRef] [PubMed]
- Lou, W.; Wang, X.; Chen, F.; Chen, Y.; Jiang, B.; Zhang, H. Sequence Based Prediction of DNA-Binding Proteins Based on Hybrid Feature Selection Using Random Forest and Gaussian Naïve Bayes. PLoS ONE 2014, 9, e86703. [Google Scholar] [CrossRef] [PubMed]
- Arican, O.C.; Gumus, O. PredDRBP-MLP: Prediction of DNA-binding proteins and RNA-binding proteins by multilayer perceptron. Comput. Biol. Med. 2023, 164, 107317. [Google Scholar] [CrossRef]
- Ho, B.; Baryshnikova, A.; Brown, G.W. Unification of Protein Abundance Datasets Yields a Quantitative Saccharomyces cerevisiae Proteome. Cell Syst. 2018, 6, 192–205.e3. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Liu, Y.; Wang, S.; Wang, L. Effective prediction of short hydrogen bonds in proteins via machine learning method. Sci. Rep. 2022, 12, 469. [Google Scholar] [CrossRef]
- Yu, N.; Li, Z.; Yu, Z. Survey on encoding schemes for genomic data representation and feature learning—from signal processing to machine learning. Big Data Min. Anal. 2018, 1, 191–210. [Google Scholar] [CrossRef]
- Randhawa, G.S.; Hill, K.A.; Kari, L. ML-DSP: Machine Learning with Digital Signal Processing for ultrafast, accurate, and scalable genome classification at all taxonomic levels. BMC Genom. 2019, 20, 267. [Google Scholar] [CrossRef] [PubMed]
- Anastassiou, D. Genomic signal processing. IEEE Signal Process. Mag. 2001, 18, 8–20. [Google Scholar] [CrossRef]
- Wegman, E.J.; Wright, I.W. Splines in Statistics. J. Am. Stat. Assoc. 1983, 78, 351–365. [Google Scholar] [CrossRef]
- The UniProt Consortium. UniProt: The Universal Protein Knowledgebase in 2023. Nucleic Acids Res. 2023, 51, D523–D531. [Google Scholar] [CrossRef]
- SPARQL 1.1 Query Language. W3C Recommendation 21 March 2013. W3C; 2013. Available online: https://www.w3.org/TR/sparql11-query/ (accessed on 7 January 2025).
- Gene Ontology Consortium. Gene Ontology Resource [Internet]. Gene Ontology Consortium; c1999-2022. Available online: http://geneontology.org/ (accessed on 7 January 2025).
- Random. Python Software Foundation. 2022. Available online: https://docs.python.org/3/library/random.html (accessed on 7 January 2025).
- Perperoglou, A.; Sauerbrei, W.; Abrahamowicz, M.; Schmid, M. A review of spline function procedures in R. BMC Med. Res. Methodol. 2019, 19, 46. [Google Scholar] [CrossRef]
- Christ, M.; Braun, N.; Neuffer, J.; Kempa-Liehr, A.W. Time Series FeatuRe Extraction on basis of Scalable Hypothesis tests (TsFresh–A Python package). Neurocomputing 2018, 307, 72–77. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Decision Trees. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: Boston, MA, USA, 2005; pp. 165–192. [Google Scholar] [CrossRef]
- Chakraborty, A.; Mitra, S.; De, D.; Pal, A.J.; Ghaemi, F.; Ahmadian, A.; Ferrara, M. Determining Protein–Protein Interaction Using Support Vector Machine: A Review. IEEE Access 2021, 9, 12473–12490. [Google Scholar] [CrossRef]
- Taunk, K.; De, S.; Verma, S.; Swetapadma, A. A Brief Review of Nearest Neighbor Algorithm for Learning and Classification. In Proceedings of the 2019 International Conference on Intelligent Computing and Control Systems (ICCS), Madurai, India, 15–17 May 2019; pp. 1255–1260. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Zhang, J. New Machine Learning Algorithm: Random Forest. In Information Computing and Applications; Liu, B., Ma, M., Chang, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 246–252. [Google Scholar]
- Tayebi, Z.; Ali, S.; Murad, T.; Khan, I.; Patterson, M. PseAAsC2Vec protein encoding for TCR protein sequence classification. Comput. Biol. Med. 2024, 170, 107956. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, Global Edition; Pearson Education: London, UK, 2018. [Google Scholar]
- Gibbs, A.; Fitzpatrick, M.; Lilburn, M.; Easlea, H.; Francey, J.; Funston, R.; Diven, J.; Murray, S.; Mitchell, O.G.J.; Condon, A.; et al. A universal, high-performance ECG signal processing engine to reduce clinical burden. Ann. Noninvasive Electrocardiol. 2022, 27, e12993. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, M. A review of electroencephalogram signal processing methods for brain-controlled robots. Cogn. Robot. 2021, 1, 111–124. [Google Scholar] [CrossRef]
- Boshnakov, G. Introduction to Time Series Analysis and Forecasting, 2nd Edition, Wiley Series in Probability and Statistics, by Douglas C.Montgomery, Cheryl L.Jennings and MuratKulahci (eds). Published by John Wiley and Sons, Hoboken, NJ, USA, 2015. Total number of pag: 672 Hardcover: ISBN: 978-1-118-74511-3, ebook: ISBN: 978-1-118-74515-1, etext: ISBN: 978-1-118-74495-6. J. Time Ser. Anal. 2016, 37, 864. [Google Scholar] [CrossRef]


| AAs | H11 | H12 | H2 | NCI | P11 | P12 | P2 | SASA | V | F | A1 | E | T | A2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0.62 | 2.1 | −0.5 | 0.007 | 8.1 | 0 | 0.046 | 1.181 | 27.5 | −1.27 | 0.49 | 15 | −0.8 | 1.064 |
| C | 0.29 | 1.4 | −1.0 | −0.037 | 5.5 | 1.48 | 0.128 | 1.461 | 44.6 | −1.09 | 0.26 | 5 | 0.83 | 1.412 |
| D | −0.9 | 10 | 3 | −0.024 | 13 | 40.7 | 0.105 | 1.587 | 40 | 1.42 | 0.78 | 50 | 1.65 | 0.866 |
| E | −0.74 | 7.8 | 3 | 0.007 | 12.3 | 49.91 | 0.151 | 1.862 | 62 | 1.6 | 0.84 | 55 | −0.92 | 0.851 |
| F | 1.19 | −9.2 | −2.5 | 0.038 | 5.2 | 0.35 | 0.29 | 2.228 | 115.5 | −2.14 | 0.42 | 10 | 0.18 | 1.091 |
| G | 0.48 | 5.7 | 0 | 0.179 | 9 | 0 | 0 | 0.881 | 0 | 1.86 | 0.48 | 10 | −0.55 | 0.874 |
| H | −0.4 | 2.1 | −0.5 | −0.011 | 10.4 | 3.53 | 0.23 | 2.025 | 79 | −0.82 | 0.84 | 56 | 0.11 | 1.105 |
| I | 1.38 | −8.0 | −1.8 | 0.022 | 5.2 | 0.15 | 0.186 | 1.81 | 93.5 | −2.89 | 0.34 | 13 | −1.53 | 1.152 |
| K | −1.5 | 5.7 | 3 | 0.018 | 11.3 | 49.5 | 0.219 | 2.258 | 100 | 2.88 | 0.97 | 85 | −1.06 | 0.93 |
| L | 1.06 | −9.2 | −1.8 | 0.052 | 4.9 | 0.45 | 0.186 | 1.931 | 93.5 | −2.29 | 0.4 | 16 | −1.01 | 1.25 |
| M | 0.64 | −4.2 | −1.3 | 0.003 | 5.7 | 1.43 | 0.221 | 2.034 | 94.1 | −1.84 | 0.48 | 20 | −1.48 | 0.826 |
| N | −0.78 | 7 | 2 | 0.005 | 11.6 | 3.38 | 0.134 | 1.655 | 58.7 | 1.77 | 0.81 | 49 | 3 | 0.776 |
| P | 0.12 | 2.1 | 0 | 0.24 | 8 | 0 | 0.131 | 1.468 | 41.9 | 0.52 | 0.49 | 15 | −0.8 | 1.064 |
| Q | −0.85 | 6 | 0.2 | 0.049 | 10.5 | 3.53 | 0.18 | 1.932 | 80.7 | 1.18 | 0.84 | 56 | 0.11 | 1.015 |
| R | −2.53 | 4.2 | 3 | 0.044 | 10.5 | 52 | 0.291 | 2.56 | 105 | 2.79 | 0.95 | 67 | −1.15 | 0.873 |
| S | −0.18 | 6.5 | 0.3 | 0.005 | 9.2 | 1.67 | 0.062 | 1.298 | 29.3 | 3 | 0.65 | 32 | 1.34 | 1.012 |
| T | −0.05 | 5.2 | −0.4 | 0.003 | 8.6 | 1.66 | 0.108 | 1.525 | 51.3 | 1.18 | 0.7 | 32 | 0.27 | 0.909 |
| V | 1.08 | −3.7 | −1.5 | 0.057 | 5.9 | 0.13 | 0.14 | 1.645 | 71.5 | −1.75 | 0.36 | 14 | −0.83 | 1.383 |
| W | 0.81 | −10 | −3.4 | 0.038 | 5.4 | 2.1 | 0.409 | 2.663 | 145.5 | −3.78 | 0.51 | 17 | −0.97 | 0.893 |
| Y | 0.26 | −1.9 | −2.3 | 117.3 | 6.2 | 1.61 | 0.298 | 2.368 | 0.024 | −3.3 | 0.76 | 41 | −0.29 | 1.161 |
| Samples | Original Features | Relevant Features |
|---|---|---|
| 512 | 788 | 24 |
| 1024 | 788 | 152 |
| 2048 | 788 | 163 |
| 4096 | 788 | 178 |
| Samples | Algorithm | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|---|
| 512 | SVM | ||||
| k-NN | |||||
| DT | |||||
| RF | |||||
| GNB | |||||
| MLP | |||||
| 1024 | SVM | ||||
| k-NN | |||||
| DT | |||||
| RF | |||||
| GNB | |||||
| MLP | |||||
| 2048 | SVM | ||||
| k-NN | |||||
| DT | |||||
| RF | |||||
| GNB | |||||
| MLP | |||||
| 4096 | SVM | ||||
| k-NN | |||||
| DT | |||||
| RF | |||||
| GNB | |||||
| MLP |
| Samples | Algorithm | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|---|
| 512 | SVM | ||||
| k-NN | |||||
| DT | |||||
| RF | |||||
| GNB | |||||
| MLP | |||||
| 1024 | SVM | ||||
| k-NN | |||||
| DT | |||||
| RF | |||||
| GNB | |||||
| MLP | |||||
| 2048 | SVM | ||||
| k-NN | |||||
| DT | |||||
| RF | |||||
| GNB | |||||
| MLP | |||||
| 4096 | SVM | ||||
| k-NN | |||||
| DT | |||||
| RF | |||||
| GNB | |||||
| MLP |
| Dataset | Algorithm | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|---|
| Neural Based Methods | iDNA-Prot | - | - | ||
| Comp. tech. on PSSM | - | - | |||
| DPP-PseAAsC | - | - | |||
| iDNAProt-ES | - | - | |||
| CNN-BiLSTM | - | - | |||
| k-mer counting | SVM | ||||
| k-NN | |||||
| DT | |||||
| RF | |||||
| GNB | - - | - - | - - | - - | |
| MLP | |||||
| Our method | SVM | ||||
| k-NN | |||||
| DT | |||||
| RF | |||||
| GNB | |||||
| MLP |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabello-Lima, J.G.; Zapata-Morín, P.A.; Espinoza-Rodríguez, J.H. Classifying Protein-DNA/RNA Interactions Using Interpolation-Based Encoding and Highlighting Physicochemical Properties via Machine Learning. Information 2025, 16, 947. https://doi.org/10.3390/info16110947
Cabello-Lima JG, Zapata-Morín PA, Espinoza-Rodríguez JH. Classifying Protein-DNA/RNA Interactions Using Interpolation-Based Encoding and Highlighting Physicochemical Properties via Machine Learning. Information. 2025; 16(11):947. https://doi.org/10.3390/info16110947
Chicago/Turabian StyleCabello-Lima, Jesús Guadalupe, Patricio Adrián Zapata-Morín, and Juan Horacio Espinoza-Rodríguez. 2025. "Classifying Protein-DNA/RNA Interactions Using Interpolation-Based Encoding and Highlighting Physicochemical Properties via Machine Learning" Information 16, no. 11: 947. https://doi.org/10.3390/info16110947
APA StyleCabello-Lima, J. G., Zapata-Morín, P. A., & Espinoza-Rodríguez, J. H. (2025). Classifying Protein-DNA/RNA Interactions Using Interpolation-Based Encoding and Highlighting Physicochemical Properties via Machine Learning. Information, 16(11), 947. https://doi.org/10.3390/info16110947







