Abstract
Background and objectives: Evaluating Large Language Models (LLMs) presents two interrelated challenges: the general problem of assessing model performance across diverse tasks and the specific problem of using LLMs themselves as evaluators in pedagogical and educational contexts. Existing approaches often rely on single metrics or opaque preference-based methods, which fail to capture critical dimensions such as explanation quality, robustness, and argumentative diversity—attributes essential in instructional settings. This paper introduces PEARL, a novel framework conceived, operationalized, and evaluated in the present work using LLM-based scorers, designed to provide interpretable, reproducible, and pedagogically meaningful assessments across multiple performance dimensions. Methods: PEARL integrates three specialized rubrics—Technical, Argumentative, And Explanation-focused—covering aspects such as factual accuracy, clarity, completeness, originality, dialecticality, and explanatory usefulness. The framework defines seven complementary metrics: Rubric Win Count (RWC), Global Win Rate (GWR), Rubric Mean Advantage (RMA), Consistency Spread (CS), Win Confidence Score (WCS), Explanation Quality Index (EQI), and Dialectical Presence Rate (DPR). We evaluated PEARL by evaluating eight open-weight instruction-tuned LLMs across 51 prompts, with outputs scored independently by GPT-4 and LLaMA 3:instruct. This constitutes LLM-based evaluation, and observed alignment with the GPT-4 proxy is mixed across metrics. Results: Preference-based metrics (RMA, RWC, and GWR) show evidence of group separation, reported with bootstrap confidence intervals and interpreted as exploratory due to small samples, while robustness-oriented (CS and WCS) and reasoning-diversity (DPR) metrics capture complementary aspects of performance not reflected in global win rate. RMA and RWC exhibit statistically significant, FDR-controlled correlations with the GPT-4 proxy, and correlation mapping highlights the complementary and partially orthogonal nature of PEARL’s evaluation dimensions. Originality: PEARL is the first LLM evaluation framework to combine multi-rubric scoring, explanation-aware metrics, robustness analysis, and multi-LLM-evaluator analysis into a single, extensible system. Its multidimensional design supports both high-level benchmarking and targeted diagnostic assessment, offering a rigorous, transparent, and versatile methodology for researchers, developers, and educators working with LLMs in high-stakes and instructional contexts.
1. Introduction
Large Language Models (LLMs), such as GPT-4 [1], LLaMA 4 [2], Mistral/Mixtral [3,4], Claude 3 [5], and Gemini 2.5 [6], have emerged as fundamental tools in contemporary natural language processing (NLP), significantly advancing tasks including summarization, question answering, translation, classification, and dialog generation. These models vary in architectural design, scale, and licensing (proprietary vs. open-source), but collectively represent a transformative leap in AI capabilities and deployment. The transformer-based architectures underpinning these models have facilitated unprecedented capabilities like in-context learning, chain-of-thought reasoning, and multilingual comprehension, thus broadening their applicability to critical domains such as education, healthcare, scientific research, and law [7,8,9]. This study addresses both the general challenge of evaluating LLMs and the specific challenge of using LLMs themselves as evaluators, with particular emphasis on pedagogical and educational contexts.
Despite their extensive adoption, LLMs present notable evaluation challenges, particularly in open-ended or generative contexts where accuracy is nuanced, outputs are inherently diverse, and users require comprehensive explanations, not merely answers [10,11]. As reliance on LLMs for instructional purposes and decision support grows, evaluation methodologies must evolve to accurately assess essential attributes including interpretability, argumentative quality, robustness to input variations, and pedagogical utility—areas inadequately covered by traditional evaluation techniques [11,12,13].
An even more pronounced deficiency in existing metrics is the inadequate consideration of explanations provided by LLMs. Explanations are integral to tasks in educational and decision support contexts, where the rationale behind a response is as crucial as the response itself [14]. Neglecting the quality of justifications when evaluating LLMs leads to partial and potentially misleading assessments, underscoring the necessity for dedicated explanatory metrics [15].
Addressing these gaps, rubric-based evaluation (i.e., a structured assessment method in which evaluators use predefined criteria and performance levels to score responses) has gained traction in LLM assessment [16,17], offering structured criteria such as accuracy, clarity, completeness, and coherence. Although effectively applied in limited contexts, these methods have yet to be standardized and often do not separately evaluate explanations from responses, despite their strong pedagogic relevance in instructional and feedback-oriented contexts. Concurrently, research in explainable AI (XAI) highlights the need for evaluation frameworks that measure the clarity, accuracy, and utility of explanations in AI-generated outputs [18,19]. Similarly, efforts focused on alignment and safety, such as Reinforcement Learning from Human Feedback (RLHF), underline the importance of ethical and task-specific congruence, yet remain predominantly focused on upstream training rather than post hoc evaluation [20].
We develop and apply an evaluation approach that aligns with task rubrics, treats explanations as first-class evidence, and tests robustness to prompt variation.
The absence of such a framework limits both diagnostic utility and the educational relevance of current evaluation practices, reinforcing the need for a more structured and multidimensional approach.
To address these multifaceted challenges, we introduce PEARL, a rubric-driven, multi-metric evaluation framework for evaluating Large Language Models. PEARL emphasizes interpretable, reproducible, and pedagogically meaningful assessment. The framework is built upon rubric-based evaluation and incorporates formalized scoring procedures that allow for fine-grained and transparent analysis of model outputs. It captures not only factual accuracy but also explanation quality, argumentative quality, semantic robustness, and task-specific clarity. By addressing the limitations of token-level and pairwise methods, PEARL provides a unified structure suited for both diagnostic evaluation and educational feedback.
We evaluate model outputs along three complementary rubrics—technical quality, argumentative quality, and explanation quality—and use them consistently across all experiments.
We use seven interpretable metrics that cover comparative performance, explanation quality, reasoning diversity, robustness, and confidence; in the results we focus on what each metric reveals rather than restating specifications.
The main contributions of this work are as follows:
- (i)
- We identify key limitations in current LLM evaluation paradigms and synthesize requirements for interpretable, multidimensional assessment;
- (ii)
- We define the PEARL metric suite, including component rubrics and seven formalized metrics spanning accuracy, explanation, argumentation, and robustness;
- (iii)
- We validate the framework across four curated synthetic evaluation conditions using education-aligned prompt sets (rubric-matching, explanation tasks, dialectical sequences, and paraphrase consistency).
- (iv)
- We analyze alignment patterns relative to a model-based proxy (GPT-4), report Pearson r and Spearman ρ, and note mixed alignment across metrics, and show their advantage in producing pedagogically useful, reproducible, and model-agnostic feedback.
2. Background and Limitations of Existing Metrics
The evaluation of natural language generation systems has historically relied on a variety of metrics designed for specific tasks such as machine translation or summarization. However, the emergence of Large Language Models (LLMs) with open-ended generative capabilities necessitates a critical re-examination of these existing evaluation methodologies. In this section, we review the most widely used metric categories—token-level scores, pairwise comparisons, and rubric-based frameworks—and highlight their limitations in capturing the multifaceted nature of LLM outputs.
2.1. Token-Level Metrics: BLEU, ROUGE, and METEOR
Token-level metrics such as BLEU [21], ROUGE [22], and METEOR [23] have historically served as foundational tools for evaluating Natural Language Generation (NLG) systems. These metrics function by comparing the lexical overlap between the generated text and one or more reference texts, typically using n-gram matching or string similarity techniques. BLEU, for example, computes the precision of n-gram matches (up to 4 g), adjusted by a brevity penalty to avoid rewarding overly short outputs [21]. ROUGE focuses on recall and includes several variants, such as ROUGE-N and ROUGE-L, which are commonly used in summarization tasks [22]. METEOR adds several improvements over BLEU by incorporating synonym matching, stemming, and a harmonic mean of precision and recall [23].
Despite their utility in structured tasks like machine translation or headline generation, these metrics exhibit significant limitations when applied to outputs generated by large language models (LLMs) [24]. Modern LLMs such as GPT-4 or Claude 3 are capable of producing diverse, contextually appropriate, and semantically valid outputs that may diverge substantially from any reference phrasing [25]. Token-level metrics are generally insensitive to this diversity and often penalize semantically accurate but lexically distinct responses [26].
A fundamental limitation of BLEU, ROUGE, and METEOR lies in their inability to capture semantic equivalence [27]. These metrics operate primarily at the lexical level, relying on n-gram overlap between generated and reference texts. As a result, they often penalize meaning-preserving paraphrases that differ lexically from the reference, while sometimes rewarding outputs that are lexically similar but semantically incorrect [28]. This lexical bias undermines their reliability in evaluating factual accuracy, reasoning, and the overall quality of open-ended language generation tasks [29].
Furthermore, token-level metrics fail to capture higher-order linguistic properties such as syntactic structure, logical consistency, and discourse coherence. These dimensions are critical for evaluating outputs generated by large language models in educational, scientific, or decision support settings [30]. BLEU, in particular, has been shown to correlate poorly with human judgments in sentence-level evaluations and in tasks that involve long-form or explanatory text, which limits its reliability outside of structured translation scenarios [31].
In educational contexts, token-level metrics are inadequate. When large language models are used to generate or grade student responses, evaluation must consider the accuracy, clarity, and pedagogical usefulness of explanations—dimensions that BLEU and ROUGE entirely ignore [32]. Token overlap does not reflect human preferences in tasks involving creativity, justification, or multi-step reasoning, which makes these metrics fundamentally unfit for assessing instructional or open-ended outputs [33].
In summary, while token-level metrics offer speed and simplicity for baseline evaluations, they fail to capture key dimensions of large language model performance, including semantic accuracy, explanatory depth, and instructional relevance. Their continued dominance in evaluation pipelines risks obscuring model deficiencies and misrepresenting real-world capabilities, particularly in open-ended or pedagogically grounded applications.
2.2. Pairwise Comparison and Win-Rate Leaderboards
Pairwise evaluation has become a widely adopted strategy for comparing large language models, especially in public-facing leaderboards such as MT-Bench and Chatbot Arena [34]. In pairwise evaluation, two outputs generated by different models in response to the same prompt are presented side by side, and an evaluator, either a human annotator or a model such as GPT-4, selects the preferred response. Win rates are then aggregated across prompts to rank models based on their comparative performance. This method is appealing due to its simplicity, scalability, and compatibility with general-purpose prompting. It is also perceived as naturally aligned with human judgment and avoids the constraints of predefined reference answers or detailed annotation schemes [35].
Despite these practical advantages, pairwise evaluation introduces significant methodological limitations. Most importantly, it only generates a binary preference without revealing the underlying evaluation criteria [36]. Relevant dimensions such as factual accuracy, coherence, relevance, and explanation quality remain unassessed and difficult to interpret [37]. Consequently, win-rate scores offer minimal diagnostic insight and are inadequate for guiding model refinement, educational feedback, or detailed error analysis [38]. This opacity and lack of granularity significantly restricts the applicability of pairwise evaluation in research, educational, and safety-critical domains.
In addition, empirical studies have shown that pairwise preferences are influenced by systematic biases [38]. Evaluators, whether human or model-based, tend to favor responses that are longer, more confident in tone, or superficially fluent, even when these responses are less accurate or informative [39]. Such biases distort model comparisons by rewarding rhetorical style over substantive content. Pairwise evaluations are also vulnerable to position effects and prompt-specific artifacts, which further reduce their reliability [40]. Without structured rubrics or explicit scoring criteria, the results are difficult to reproduce and often lack consistency across different tasks or domains.
In conclusion, although pairwise evaluation has proven useful for large-scale benchmarking due to its simplicity and alignment with intuitive preference judgments, it remains fundamentally limited in scope and interpretability. Its reliance on binary outcomes, susceptibility to superficial biases, and inability to isolate specific quality dimensions constrain its applicability in contexts that demand analytical rigor and evaluative transparency. These constraints motivate the adoption of rubric-based methods capable of capturing the multifaceted nature of model performance.
2.3. Emergent Rubric-Based Evaluation
As the shortcomings of token-level metrics and pairwise evaluation methods have become increasingly evident, rubric-based scoring has emerged as a compelling alternative for assessing the diverse and context-dependent outputs of large language models [41]. Unlike evaluation techniques that reduce performance to scalar values or binary preferences, rubric-based approaches adopt a multi-dimensional perspective that reflects the compositional nature of language and reasoning [42]. By explicitly assessing aspects such as factual accuracy, clarity, completeness, and coherence, rubrics allow for more interpretable and diagnostic evaluation, particularly in open-ended tasks and instructional settings [18,43].
This evaluation paradigm has been particularly influential in instructional contexts, where the quality of a model’s reasoning process is as important as the final answer itself. In educational settings, rubrics are commonly used to evaluate student work by breaking down performance into well-defined components [44]. Similarly, in explainable AI and model assessment, rubric-based methods allow evaluators to distinguish between surface fluency and substantive content [45]. Studies have shown that rubric-based evaluations correlate better with human judgment than n-gram metrics or simple win-rate leaderboards, especially in tasks involving open-ended reasoning or multi-step justifications [46].
However, the growing use of rubric-based scoring has not yet been matched by consistent formalization or methodological rigor. Many existing implementations use ad hoc definitions of evaluation criteria, often without providing clear scoring instructions or structured aggregation procedures [47]. This lack of standardization limits comparability across studies and undermines the reproducibility of results. In many cases, rubrics are applied qualitatively and remain disconnected from quantitative analysis pipelines, making it difficult to integrate them into large-scale benchmarking or automated workflows [48].
A further limitation lies in the common tendency to evaluate responses holistically, without distinguishing between the quality of the answer and the quality of the explanation. This is particularly problematic in educational or decision support applications, where explanations are essential for transparency, learning, and trust [49]. Conflating the two dimensions obscures the model’s actual capabilities and restricts the usefulness of the feedback generated. Additionally, few rubric-based approaches consider other critical factors such as robustness to input variation or alignment with user intent and task requirements, which are increasingly important in real-world deployment scenarios [50].
These observations point to the need for a more principled, explanation-aware, and extensible approach to rubric-based evaluation. Such an approach should clearly separate answer content from explanatory reasoning, define scoring dimensions with formal precision, and support integration into both human and automated evaluation pipelines.
2.4. Absence of Explanation-Aware Metrics
A critical yet underexplored limitation of existing evaluation methodologies for large language models is the lack of metrics specifically designed to assess the quality of explanations. In the context of LLM outputs, explanations are defined as the parts of a response that articulate the underlying reasoning, justify the final answer, or provide intermediate steps and conceptual clarifications. These explanatory components are particularly important in tasks that go beyond binary accuracy—such as open-ended question answering, automated grading, and decision support—where users must understand not only what answer is given, but why.
We introduce the Explanation Quality Index (EQI), which evaluates the reasoning segment of a response as a first-class object. EQI scores clarity, factual accuracy, and task usefulness, enabling precise error analysis, pedagogically meaningful feedback, and the detection of misleading justifications that holistic scoring misses.
This lack of explanation-focused evaluation is also evident in generation-oriented approaches themselves. A well-known technique that illustrates this limitation is chain-of-thought prompting [51], which improves LLM reasoning by generating intermediate explanation steps. Although this technique elicits detailed justifications from models, it does not offer any formal method to assess their correctness, clarity, or usefulness. Most evaluations rely on solve rate (final-answer accuracy), without analyzing whether the reasoning path was valid or helpful. For example, models may arrive at the correct answer through flawed or coincidental logic or may produce thoughtful reasoning that leads to a partially incorrect outcome—scenarios that remain invisible under current metrics.
2.5. Alignment and Robustness: Poorly Captured
Two essential yet insufficiently evaluated dimensions in current large language model assessment are alignment and robustness. These aspects are critical for ensuring that models behave reliably, ethically, and predictably across diverse inputs and user expectations [52].
Alignment refers to the degree to which a language model follows task instructions while remaining consistent with human values, social expectations and ethical standards [53]. Although training techniques such as Reinforcement Learning from Human Feedback and Constitutional AI have been developed to guide model behavior, their effectiveness is often assessed through informal methods [54]. These include binary preference comparisons or manually curated prompt examples. Such approaches lack transparency, are difficult to reproduce, and offer limited insight into the reasons behind model decisions [55]. Moreover, they do not distinguish clearly between different types of alignment failures, such as deviations from factual accuracy, from ethical norms or from task requirements [53].
Robustness describes the model’s ability to maintain consistent and reliable behavior when the input is rephrased, reordered or perturbed [56]. This includes semantic-preserving variations such as paraphrasing or synonym substitution. In current benchmarks, robustness is rarely tested in a systematic or standardized way. Most evaluations rely on a single version of each prompt, assuming that the model’s output will remain unchanged if the meaning of the input stays the same [57]. However, recent studies have shown that models often respond inconsistently to inputs that are semantically equivalent [58]. This reveals fragility in the model’s reasoning process and coherence. Furthermore, current evaluations often conflate robustness with fluency, paying little attention to whether the core meaning and logic of the response remain intact [59].
These evaluation gaps have serious consequences. Without detailed and interpretable metrics for alignment and robustness, developers cannot receive precise feedback about how to improve model behavior [60]. Users, in turn, interact with systems that may behave inconsistently or unpredictably in similar situations. This lack of reliability undermines trust and limits the safe use of language models, especially in sensitive fields such as education, healthcare and legal analysis [61].
Future evaluation frameworks should incorporate dedicated metrics that assess both alignment and robustness explicitly. These metrics must capture not only whether an answer is acceptable, but also whether the model respects ethical norms, remains consistent when inputs are reformulated, and resists manipulation. Only through such detailed and principled evaluation can model behavior be effectively understood and improved.
3. The PEARL Metric Suite
The PEARL metric suite is structured into three main components: a set of design principles that guide the framework’s construction and applicability; a collection of specialized evaluation rubrics tailored to distinct aspects of LLM output, such as factual accuracy, explanatory quality, and argumentative quality; and a set of formalized metrics that quantify model behavior in a precise and interpretable manner. Together, these components enable consistent, reproducible, and pedagogically meaningful evaluation across diverse tasks and model types.
Figure 1 provides an overview of PEARL, showing how inputs produce model responses that are scored via three rubrics (Technical, Argumentative, and Explanation), how these rubric scores feed the seven metrics (RMA, RWC, GWR, CS, WCS, EQI, and DPR), and how the metrics support validation and analysis.
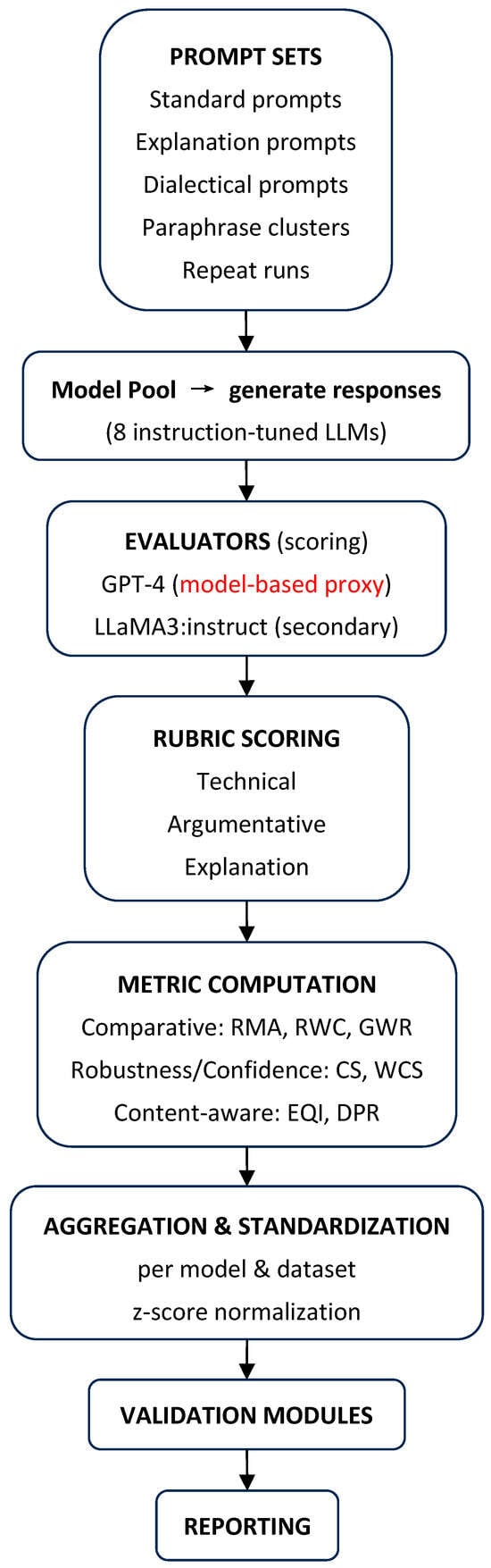
Figure 1.
PEARL framework overview. Inputs (prompt sets) generate model responses that are scored on three rubrics (Technical, Argumentative, Explanation). Rubric scores feed seven metrics: comparative (RMA, RWC, GWR), robustness/confidence (CS, WCS), and content-aware (EQI, DPR). Metrics support validation (agreement with a model-based proxy, stability, and discriminative power) and analysis (correlation/complementarity).
3.1. Design Principles
The PEARL framework is grounded in a set of foundational principles designed to address key limitations in existing evaluation methods for large language models. These principles emphasize interpretability, diagnostic precision, pedagogical value, and robustness, forming the conceptual backbone of the proposed rubrics and metrics.
A core principle of PEARL is the explicit separation between the answer and the explanation provided by a model. This distinction is particularly important in educational and reasoning-intensive contexts, where the accuracy of a conclusion and the quality of its underlying justification must be assessed independently. By evaluating answers and explanations as distinct components, PEARL enables more granular and transparent analysis of model behavior, including the identification of reasoning flaws that may otherwise be obscured by fluent or persuasive output.
Another essential principle is the use of structured rubrics to enhance interpretability. Rather than relying on aggregate scores or opaque preference judgments, PEARL introduces rubric-based evaluation criteria that reflect human-centered dimensions such as accuracy, clarity, completeness, and originality. These rubrics support both human and automated scoring and make evaluation results more explainable and reproducible.
The framework is also designed to align with pedagogical goals. Beyond ranking models, PEARL provides diagnostic feedback that can inform research on evaluation in educationally oriented tasks. The inclusion of explanation-focused assessment dimensions allows evaluators to measure the educational usefulness of model outputs, particularly in contexts like automated grading, formative assessment, or intelligent tutoring.
Finally, PEARL incorporates robustness and reproducibility as core design considerations. To ensure stability under prompt variations, the framework includes metrics that capture how consistent and reliable model outputs remain when the input is semantically preserved but phrased differently. This focus on robustness complements the interpretability and pedagogical principles by reinforcing the credibility and applicability of evaluation results across diverse usage scenarios.
Together, these principles position PEARL as a modular, extensible, and educationally grounded framework for evaluating the multifaceted outputs of large language models. Each of its three rubric-aligned dimensions (Technical, Argumentative, and Explanation) is aligned with a specific linguistic or pedagogical objective, further reinforcing the framework’s interpretability and instructional relevance. This multidimensional alignment is increasingly emphasized in recent work leveraging large language models for explainable, robust, and context-sensitive tasks [62].
3.2. Component Rubrics
The PEARL framework incorporates three distinct rubrics designed to assess different dimensions of large language model outputs. These rubrics are built to isolate specific evaluative goals, reflect human-centered criteria, and support granular, reproducible scoring. Each evaluation dimension is scored on a fixed scale from 1 to 10, enabling fine-grained comparisons and compatibility with all formalized metrics introduced in the PEARL suite.
The first is the Technical Rubric, developed for tasks where factual accuracy and procedural accuracy are essential. This rubric includes four dimensions. Accuracy measures whether the response accurately addresses the core content or task requirements. Clarity evaluates how effectively the response conveys its meaning, especially in terms of language precision and syntactic coherence. Completeness assesses whether all relevant parts of the answer are included, avoiding partial or fragmentary outputs. Finally, terminology focuses on the appropriate use of specialized or domain-specific vocabulary, ensuring that the model communicates with discipline-aligned precision. This rubric is particularly suited to technical or instructional contexts such as science, technology, engineering, and mathematics (STEM), education, medical question answering, or structured assessments.
The Argumentative Rubric is designed for open-ended, reasoning-intensive tasks where models are expected to construct a viewpoint, justify it, and engage with complexity. It also includes four dimensions. Clarity refers to the fluency and readability of the response, ensuring that arguments are expressed in a coherent and accessible way. Coherence assesses the logical flow of ideas and the consistency between claims and conclusions. Originality captures the degree of novelty or independent insight expressed in the response, rewarding models that avoid generic or templated phrasing. Dialectically measures the degree to which the response engages with opposing viewpoints or synthesizes contrasting perspectives. This dimension captures the model’s ability to reason beyond a single stance, reflecting skills essential for debate, critical thinking, and philosophical inquiry.
The third rubric focuses exclusively on the explanation generated by the language model, evaluating the part of the output that communicates how or why a certain answer was generated. It includes three core dimensions. Clarity reflects how clearly the reasoning process is articulated. Accuracy evaluates whether the explanation correctly describes the model’s logical steps, without introducing fallacies or hallucinations. Usefulness refers to the degree to which the explanation enhances user understanding, either by providing pedagogical value, revealing internal logic, or supporting trust in the response. This rubric is especially relevant for educational technologies, intelligent tutoring systems, and any scenario in which interpretability and learning support are essential.
The three rubrics in the PEARL framework are designed to function independently, enabling evaluators to adapt their application based on the specific demands of each task. For example, a concise factual question might be assessed using only the technical rubric, whereas an open-ended student essay in a philosophy course may require the combined use of all three rubrics. This modular approach ensures both flexibility and consistency across different evaluative scenarios, as reflected in the structure of the three rubrics and their corresponding dimensions summarized in Table 1.

Table 1.
Summary of the three rubrics used in the PEARL framework and their associated evaluation dimensions.
These rubrics draw inspiration from recent meta-analytic evidence showing that rubric use yields moderate positive effects on academic performance and small but meaningful effects on self-regulated learning and self-efficacy [63].
3.3. Formalized Evaluation Metrics
To operationalize the evaluation framework defined by the PEARL rubrics, we introduced a suite of seven formalized metrics designed to quantify large language model performance in a structured, interpretable, and multidimensional manner. These metrics address key limitations of existing evaluation methods by capturing not only overall preference or correctness, but also the quality of explanations, the presence of argument diversity, the stability of outputs under prompt variation, and the confidence of model comparisons. Each metric is designed to be modular and rubric-aware, enabling integration into both human-in-the-loop and automated scoring pipelines. Unlike traditional scalar scores or black-box preference judgments, the PEARL metrics support transparent benchmarking and pedagogically meaningful diagnostics that are essential for instructional and model refinement scenarios.
The seven PEARL metrics are grouped into four functional categories, each capturing a distinct dimension of model evaluation.
- (1)
- Comparative performance metrics include the Rubric Win Count (RWC), Global Win Rate (GWR), and Rubric Mean Advantage (RMA). These metrics measure the relative performance of different models by comparing their scores across individual rubric dimensions. This enables transparent comparison and ranking based on interpretable evaluation criteria.
- (2)
- The explanation-aware metric, Explanation Quality Index (EQI), evaluates the clarity, coherence, and pedagogical value of model-generated justifications.
- (3)
- The qualitative reasoning metric, Dialectical Presence Rate (DPR), measures the presence/frequency of dialectical reasoning elements across a structured sequence (opinion → counterargument → synthesis). Rather than progress, DPR reports a presence rate in [0,1] based on rubric-aligned scoring across the three stages.
- (4)
- Robustness and confidence metrics include the Consistency Spread (CS) and Win Confidence Score (WCS). These metrics assess model stability under prompt variation and the certainty of comparative outcomes.
This categorization reflects the multidimensional structure of PEARL and provides a coherent foundation for the metrics defined below.
Each PEARL metric targets a specific linguistic or pedagogical dimension. For instance, RMA quantifies score differences along aspects like completeness and clarity. EQI captures the clarity, fidelity, and pedagogical usefulness of model-generated explanations [64]. CS measures semantic stability across paraphrased prompts and captures robustness under linguistic variation [65]. Finally, DPR highlights the presence of dialectical reasoning and multi-perspective analysis in LLM-generated justifications [64].
3.3.1. Rubric Win Count (RWC)
The Rubric Win Count (RWC) is a comparative metric that quantifies the number of times a given model achieves higher rubric-level scores than another model across a collection of evaluation instances. Unlike overall preference scoring, which offers a holistic but opaque indication of superiority, RWC captures localized performance advantages within specific evaluation criteria, such as accuracy, clarity, or completeness. Since each per-dimension comparison contributes 0 or 1, with D rubric dimensions and ∣P∣ prompts it integer-valued and 0 ≤ RWC ≤ D⋅∣P∣.
The underlying mechanism assigns a “win” to a model whenever it receives a higher score than its comparator on a single rubric dimension for a given prompt. For example, in a scenario where two models are evaluated using a three-dimensional rubric, if one model outperforms the other on two of the three dimensions, it is credited with two wins for that instance. The RWC aggregates such occurrences across all prompts and rubric dimensions to compute a total count of dimension-level wins.
Formally, let
and
denote two models evaluated on a set of prompts
, using a rubric with
distinct dimensions. For each prompt
and dimension
, let
and
be the respective scores assigned to the two models. The RWC for model
over
is computed as follows:
where
is the indicator function that returns 1 if the condition is true and 0 otherwise.
A higher RWC score indicates that the model consistently achieves superior performance on individual rubric dimensions across multiple evaluation cases. This metric is particularly useful for diagnostic evaluation, as it reveals the frequency of targeted wins rather than relying on aggregate or subjective preference judgments.
3.3.2. Global Win Rate (GWR)
The Global Win Rate (GWR) is a normalized pairwise comparison metric that reflects the proportion of evaluation instances in which a model is preferred overall, based on rubric-level performance. Unlike the Rubric Win Count (RWC), which quantifies individual wins across rubric dimensions, GWR aggregates these outcomes into a single ratio indicating how frequently one model is globally preferred over another across the full set of prompts. Since each prompt contributes 0 (loss) or 1 (win)—and 1/2 for ties when applicable—GWR is the average over ∣P∣ prompts, hence 0 ≤ GWR ≤ 1.
For each evaluation instance, a model is assigned a win if it obtains a higher total rubric score than its comparator. The GWR is then computed as the number of such wins divided by the total number of evaluation instances. This metric yields a scalar value in the range [0, 1], where a score greater than 0.5 indicates that the model is more often preferred.
Formally, let
be the set of prompts and
the number of rubric dimensions. Let
, where
indexes the evaluation dimensions defined by the rubric. This represents the total rubric score of model
on prompt
. Then, the GWR of model
over
is defined as follows:
where
is the indicator function that returns 1 if the condition is true and 0 otherwise.
3.3.3. Rubric Mean Advantage (RMA)
The Rubric Mean Advantage (RMA) is a comparative metric that quantifies the average score margin by which one model outperforms another across all rubric dimensions and evaluation instances. Unlike RWC, which counts the number of rubric-level wins, and GWR, which measures the frequency of global preference, RMA captures the magnitude of model superiority by aggregating score differentials. Since each per-instance rubric total lies in [0, 10], the per-instance difference lies in [−10, 10]; RMA is the mean of these differences, hence −10 ≤ RMA ≤ 10 (centered at 0 when models are tied on average).
For each prompt and rubric dimension, the score difference between two models is computed. The RMA is then obtained as the mean of these differences across the full evaluation set, providing a signed value that reflects the overall advantage.
Formally, let
be the set of prompts and
the number of rubric dimensions. Let
denote the score of the model
on prompt
and dimension
, and let
, where
indexes the evaluation dimensions defined by the rubric. Then the RMA of model
over
is defined as follows:
A positive value indicates that
has, on average, higher rubric scores than
, while a negative value reflects the opposite. RMA is a signed quantity centered at 0; larger absolute values indicate larger average score margins across prompts and rubric dimensions.
3.3.4. Explanation Quality Index (EQI)
The Explanation Quality Index (EQI) is a scalar metric that quantifies the average quality of the explanations provided by a model, independently from the correctness of its answers. Unlike traditional metrics that evaluate responses holistically, EQI isolates the justification component of a response and measures its clarity, factual correctness, and pedagogical value. Since each explanation rubric dimension is scored on a 0–10 scale, EQI is their (possibly weighted) mean; therefore, 0 ≤ EQI ≤ 10.
This metric is grounded in the Explanation Rubric, which contains three dimensions:
- Clarity—the degree to which the explanation is easy to follow and well-articulated;
- Accuracy—whether the reasoning is logically sound and factually correct;
- Usefulness—the extent to which the explanation enhances user understanding or provides educational benefit.
Each dimension is scored on a fixed scale from 0 to 10, either by human evaluators or automated rubric-aligned models.
Let
be a model evaluated on a set of prompts
, and let
represent the rubric dimensions. For each prompt
and dimension
, let
denote the score assigned to model
. The EQI is defined as follows:
The resulting score lies in the range [1, 10] and reflects the model’s average explanation quality across all prompts and rubric dimensions. A high EQI indicates that the model consistently produces justifications that are not only correct, but also well-structured and instructive.
This metric is particularly useful in educational, formative assessment, and explainable AI (XAI) contexts, where understanding why an answer is given is as critical as the answer itself.
3.3.5. Dialectical Presence Rate (DPR)
The Dialectical Presence Rate (DPR) measures a model’s capacity for structured argumentative reasoning. It quantifies the presence of dialectical elements across the three sequential stages—opinion, counterargument, and synthesis—and yields a value in [0, 1] after normalization. With per-role totals on a 0–10 scale aggregated over the three roles, the normalization guarantees 0 ≤ DPR ≤ 1.
Each stage corresponds to a separate prompt and is evaluated using the Argumentative Rubric, which includes four dimensions: clarity, coherence, originality, and dialecticality. A higher rubric score reflects stronger reasoning and more effective engagement with complex or opposing perspectives.
For compactness, we denote the three roles as
(opinion),
(counterargument), and
(synthesis). Let
be a model evaluated on a set of structured prompts
, and let
be the total rubric score (0–10) aggregated over the four dimensions assigned to model
response at role
within prompt
.
The Dialectical Presence Rate is then defined as follows:
Here, Z is the normalization constant equal to the maximum attainable rubric total for one op–co–sy triplet. With three roles, each capped at 10 points, we have Z = 30. Therefore, DPR ∈ [0, 1], with higher values reflecting greater presence and integration of dialectical elements across the three stages.
DPR is particularly relevant in domains such as ethics, philosophy, law, or socio-political analysis, where responding to alternative perspectives and integrating them into a coherent synthesis is essential to argumentation quality and robustness.
3.3.6. Consistency Spread (CS)
The Consistency Spread (CS) is a robustness metric that quantifies the variation in a model’s outputs when exposed to semantically equivalent but syntactically different prompts. It measures how stable a model’s performance remains under prompt rephrasing, which is essential for ensuring reliable and reproducible behavior. CS is computed as the average absolute deviation of paraphrase rubric totals from their cluster mean; on a 0–10 rubric scale, 0 ≤ CS ≤ 5—the upper bound occurs when scores split between 0 and 10 (mean = 5, each deviation = 5).
Paraphrase clusters were manually authored and cross-checked by the author team to ensure semantic equivalence—preserving task intent, argumentative structure, and topical scope while varying only surface form. CS is reported both in aggregate and stratified by paraphrase type (lexical, syntactic, and discourse).
For each original prompt, multiple paraphrased versions
are constructed, each preserving the same semantic intent while varying surface form. Let
denote the set of original prompts (each associated with
paraphrases). For each paraphrased prompt, responses are scored using the same rubric as the original (e.g., Argumentative or Technical), ensuring consistent criteria across rephrasings. Score variation is then used to compute the Consistency Spread.
Let
denote the total rubric score assigned to model
for paraphrase
, and let
be the mean score across all
paraphrases associated with prompt
The overall Consistency Spread for model
is defined as follows:
The resulting value is non-negative, with lower values indicating more consistent behavior across paraphrases. A model with zero consistency spread would produce perfectly stable rubric scores regardless of prompt phrasing. CS complements accuracy-focused metrics by highlighting fragility or instability in model responses, especially in real-world usage where prompts are naturally varied.
3.3.7. Win Confidence Score (WCS)
The Win Confidence Score (WCS) quantifies the average normalized win-margin (|Δ_p|/Z), where |Δ_p| is the absolute per-prompt difference between the two models’ rubric totals and Z is the maximum attainable rubric total per prompt; higher values indicate more decisive separations, and the metric is symmetric with respect to the order of the two models. While win-based metrics like RWC or GWR indicate how often one model outperforms another, WCS measures how strongly the models differ in performance, regardless of which one wins. By construction, 0 ≤ WCS ≤ 1 because |Δ_p| ≤ Z for every prompt.
Let
and
be two models evaluated on a set of prompts
, using a rubric with
distinct dimensions, each scored on a fixed scale from 1 to 10. Let
index the rubric dimensions and let
denote the score assigned to model
for prompt
and dimension
.
For each prompt, we compute the total score difference between the two models:
The maximum possible difference per prompt is
, since each score ranges from 1 to 10 and the largest possible gap per dimension is
. To obtain a normalized measure of difference, we define the Win Confidence Score as follows:
The resulting value lies in the range [0, 1], where higher values indicate that the two models differ more significantly and consistently in their rubric scores across prompts. A value close to zero suggests marginal differences, while a high score implies strong, unambiguous performance gaps. Since WCS is based on absolute differences, it is symmetric and does not indicate which model is better—only how confidently they can be separated. This metric is especially useful when win rates are similar, but the strength of wins matters for model selection, benchmarking, or reporting statistically robust comparisons.
3.4. Linguistic and Pedagogical Dimensions Captured by PEARL
The PEARL metric suite extends beyond traditional benchmarking by embedding linguistic and pedagogical insights into model evaluation. Rather than treating model outputs as holistic artifacts, PEARL decomposes them into interpretable dimensions grounded in text linguistics, argumentation theory, and instructional science [66]. This multidimensionality enables PEARL to function not only as a performance assessment tool, but also as a diagnostic framework for analyzing structural strengths and weaknesses in generated responses.
While certain PEARL metrics—such as Rubric Win Count (RWC), Global Win Rate (GWR), and Win Confidence Score (WCS)—primarily reflect distributional or statistical patterns, they still relate indirectly to language. For instance, output variability reflected in WCS may correspond to prompt ambiguity, syntactic instability, or pragmatic under specification [67]. Similarly, shifts in RWC and GWR across prompts can often be traced to differences in surface complexity, lexical density, or rhetorical structure [68].
In contrast, four PEARL metrics—Rubric Mean Advantage (RMA), Explanation Quality Index (EQI), Dialectical Presence Rate (DPR), and Consistency Spread (CS)—are directly anchored in linguistic and educational theory. These metrics are designed to capture output features aligned with clarity, argument diversity, semantic reliability, and instructional value.
Rubric Mean Advantage (RMA) quantifies comparative performance along rubric dimensions such as clarity, completeness, and terminology. Clarity is associated with syntactic simplicity, lexical transparency, and organizational fluency. Completeness aligns with discourse macrostructures that require coverage of all obligatory rhetorical functions for a response to be pragmatically adequate [69]. Terminological precision relates to the accurate and context-appropriate use of domain-specific language, contributing to lexical cohesion and register control [70].
The Explanation Quality Index (EQI) focuses on the structural and pedagogical value of model-generated justifications. It incorporates both cohesion—achieved through explicit referential and connective ties—and coherence, understood as the inferential and conceptual integrity of the explanatory narrative [71]. In educational contexts, EQI aligns with instructional scaffolding: explanations should facilitate learning by breaking down complex reasoning into cognitively digestible steps [72]. Moreover, clarity, fidelity, and usefulness have emerged as core dimensions in recent evaluation frameworks for AI explanations [18].
Dialectical Presence Rate (DPR) measures the extent to which outputs incorporate counterarguments, alternative perspectives, or reflective concessions. This reflects the pragma-dialectical model of argumentation, where discourse aims to resolve differences through structured, reasoned dialog [73]. From a pedagogical standpoint, such dialectical engagement supports critical thinking and epistemic humility, central to dialogic pedagogy and argumentative writing [74].
Consistency Spread (CS) assesses semantic reliability across paraphrased or structurally varied inputs. From a linguistic standpoint, CS captures whether the model maintains stable meaning under surface-level variation. Recent research has shown that even subtle syntactic or lexical changes in prompts can lead to disproportionate variation in model responses [75]. Semantic consistency is therefore essential for ensuring interpretability, fairness, and reproducibility, particularly in educational or evaluative contexts where input variation is common [76].
The linguistic and pedagogical relevance of PEARL is made explicit through these metrics, each of which operationalizes a distinct theoretical construct. Rather than functioning as opaque performance scores, the metrics provide structured insight into model behavior across core textual dimensions. Table 2 provides an overview of these correspondences, mapping each PEARL metric to its associated linguistic and pedagogical properties.

Table 2.
Linguistic and pedagogical dimensions captured by each PEARL metric.
Taken together, these mappings highlight PEARL’s capacity to serve not merely as a benchmarking toolkit, but as a theoretically grounded diagnostic framework for evaluating language models in both research and educational settings.
3.5. Metric-Data Alignment and Task Requirements
To operationalize the PEARL metric suite, each evaluation must be grounded in a set of input prompts and response types tailored to the assumptions of each metric. While the rubric-based scoring protocol is uniform across tasks, the data requirements for computing each metric vary significantly. Some metrics operate over pairwise model comparisons, others require explanatory or dialectical content, and several depend on repeated runs to assess consistency and robustness.
We identify four core input structures that underpin PEARL evaluations:
- Standard prompts—general-purpose queries suitable for rubric scoring and model comparison.
- Explanation prompts—questions that explicitly request reasoning, justification, or pedagogical elaboration.
- Dialectical prompts—multi-turn tasks structured around dialectical reasoning (opinion, counterargument, synthesis).
- Repeat runs—multiple generations from the same model on the same prompt to test for consistency.
Each PEARL metric maps to one or more of these input types. Table 3 consolidates the input requirements, evaluation scenarios, and comparison modes for each metric, providing a single canonical reference.

Table 3.
Input requirements, evaluation scenarios, and comparison modes for each PEARL metric.
By aligning each metric with its corresponding data requirements, this framework ensures that PEARL can be applied with methodological precision and reproducibility. It supports both comprehensive evaluation across metrics and targeted analysis when only specific types of data are available.
4. Methodology for Metric Validation
To ensure the robustness, interpretability, and pedagogical validity of the PEARL metric suite, we implemented a multi-stage validation protocol. This methodology was designed to assess the sensitivity of each metric to controlled variations in response quality, its alignment with human judgment, and its applicability in realistic educational contexts. The evaluation process combined synthetic prompt sets and rubric-based LLM-based scoring. Together, these stages provide converging evidence for the reliability and diagnostic value of the proposed framework.
4.1. Validation Goals and Setup
The validation of the PEARL metric suite was designed to assess three core properties: sensitivity to rubric-aligned variation, alignment with expert-style rubric-based evaluations, and robustness across a range of educational prompts and input types.
To support this process, we constructed four distinct prompt sets, each corresponding to a particular type of evaluation scenario. Technical and argumentative prompts were designed to test factual accuracy, clarity, completeness, and terminology (used in RWC, GWR, RMA, and WCS). Explanation prompts elicited model-generated justifications for evaluating explanation quality (EQI). Dialectical tasks included opinion–counterargument–synthesis triplets to assess argumentative presence (DPR), while consistency was evaluated using stylistic paraphrase clusters designed to test intra-model stability (CS). Paraphrase clusters for CS were manually authored and cross-checked by the author team; semantic equivalence was confirmed via co-author review using a binary decision (equivalent or non-equivalent), and each variant was labeled by paraphrase type (lexical, syntactic, and discourse). Each prompt was designed to target specific rubric dimensions under controlled variation, enabling metric-level interpretation across diverse task formats.
Rubric-based annotations were carried out using a GPT-4 judge with a fixed prompt template and the study’s scoring rubrics [77,78]. A secondary scorer (LLaMA3) was also used for reliability checking. Annotators applied the rubrics independently to each model response, without access to gold answers or model identity. Scoring was performed separately for each dimension of the rubric associated with a given prompt type.
To ensure architectural and behavioral diversity, we evaluated eight open-weight large language models commonly used in academic and applied settings: Gemma 7B Instruct, Mistral 7B Instruct, Dolphin-Mistral, Zephyr 7B Beta, DeepSeek-R1 8B, LLaMA3 8B, OpenHermes, and Nous-Hermes 2. All models were tested using a common pool of prompts aligned with the PEARL rubrics and metric definitions, allowing for direct comparison across evaluation dimensions. This pool comprised 51 prompts in total, distributed across the four synthetic evaluation conditions used in this study: 15 paraphrase-consistency triplets for Consistency Spread (CS), 9 dialectical sequences (opinion → counterargument → synthesis) for Dialectical Presence Rate (DPR), 9 explanation tasks for Explanation Quality Index (EQI), and 18 rubric-matching comparisons for Rubric Win Count, Global Win Rate, Rubric Mean Advantage, and Win Confidence Score (RWC/GWR/RMA/WCS)—evenly split between technical and argumentative rubrics. All validation reported here is synthetic: The prompts were sourced from a mix of adapted public benchmarks and custom-designed items, with a focus on pedagogical and explanatory contexts.
The evaluation process relied on rubric-based scoring performed by large language models themselves. GPT-4 served as the primary evaluation agent across all metrics, selected for its strong alignment with human rubric-based judgment. To verify scoring consistency and assess inter-rater reliability, a secondary scorer—llama3:instruct—was employed in a subset of comparisons. Inter-scorer agreement was quantified with Cohen’s κ for categorical win labels (GWR, RWC) and with ICC(2,1) plus Lin’s concordance correlation coefficient (CCC) for continuous metrics (RMA, EQI, DPR, CS, and WCS).
The full list of evaluated models, along with their parameter sizes and evaluator roles, is presented in Table 4, which provides an overview of the model lineup and their function in the scoring pipeline.

Table 4.
Evaluated Language Models and Their Role in the Scoring Pipeline.
All models were run using their publicly released default configurations, including context window, token limit, temperature, and decoding strategy, exactly as provided by their developers at release time. The evaluation included only open-weight instruction-tuned models, acknowledging that their fine-tuning datasets and methods may vary, potentially influencing performance on certain prompts Generations were produced on a local Ollama server using engine default decoding and runtime settings. Engine defaults were temperature 0.8, top_p 0.9, top_k 40, seed 0, mirostat 0, num_predict −1, and num_ctx 2048. Generation provenance: Each prompt variant was generated once per model under these defaults and cached, and the same outputs were scored by both evaluators. No re-generation across runs was performed. Consequently, the reported metric values (RWC, GWR, RMA, WCS, EQI, DPR, and CS) were not affected by cross-run sampling variance.
The evaluation setup involved structured alignment between prompt type, rubric structure, and metric applicability. Metrics were only computed when the input format satisfied their structural constraints—such as the presence of parallel prompts for pairwise comparisons (RWC, GWR), grouped prompts for rubric-matching analysis (RMA), dialectical sequences for DPR, or semantically equivalent paraphrases for CS. Responses were generated by multiple large language models and evaluated in parallel across all scoring layers: human annotation, metric computation, and rubric dimension.
All metrics were computed within a unified implementation pipeline, using consistent data structures for prompts, responses, and rubric scores. Input processing, rubric interpretation, and scoring logic were standardized across all metrics, enabling reliable, model-agnostic comparisons between automatic outputs and human-aligned annotations.
Uncertainty was quantified using cluster-preserving paired bootstrap (B = 10,000) with 95% percentile confidence intervals. Given the small sample sizes (e.g., N = 8 models for some metrics), all hypothesis tests were treated as exploratory and are reported alongside effect sizes and confidence intervals rather than binary significance decisions. To address multiplicity, Benjamini–Hochberg false discovery rate control (q = 0.10) was applied within each family of related tests. We used the same bootstrap to compute 95% confidence intervals for the mean Δ (LLaMA3 − GPT-4) and for κ/ICC/CCC estimates.
4.2. Validation Scenarios
The PEARL metric suite was validated under distinct evaluation conditions, each designed to probe specific aspects of metric behavior. These conditions reflect different task structures, input formats, and rubric scopes associated with each metric. Rather than relying on random or generic prompts, each validation path was constructed to reflect a targeted diagnostic scenario. The following subsections describe the four evaluation conditions used in this study, grouped according to metric scope and input configuration.
4.2.1. Rubric-Matching Evaluation Conditions
This category includes metrics that assess the degree to which a model-generated response aligns with specific rubric dimensions, based on comparative or referential prompt configurations. RWC and GWR operate over pairs of responses to the same prompt, evaluating comparative completeness and rhetorical quality, respectively. RMA generalizes this comparison to groups of responses aligned with an underlying rubric pattern, while WCS extends the comparison across models, assessing confidence in verdict-level differences. The prompt sets used in these conditions were constructed to induce targeted variation in rubric dimensions while maintaining constant task intent, enabling the interpretation of metric outputs relative to known qualitative differences.
4.2.2. Explanation Quality Tasks
Explanation-based evaluation tasks were used to validate the EQI metric. Prompts in this category explicitly request a justification or explanation of a concept, process, or argument. The resulting responses are annotated along dimensions such as clarity, usefulness, and accuracy, and are expected to exhibit qualitative variation in explanatory quality across models. The evaluation setup tests whether EQI captures these differences in a way that aligns with expectations derived from the prompt design and rubric coverage.
4.2.3. Dialectical Reasoning Sequences
To evaluate the DPR metric, we employed prompt sequences that reflect structured dialectical sequence: an initial opinion, a counterargument, and a synthesis task. Each stage in the sequence was used to probe the model’s ability to integrate new reasoning, adjust claims, and produce higher-level synthesis. Model responses were evaluated for dialectical coherence and depth, and the DPR metric was applied across the sequence to measure the incidence and integration of dialectical elements in the scoring.
4.2.4. Stylistic Paraphrase Consistency
The CS metric was validated using clusters of prompts that express the same underlying idea in varied stylistic forms. These paraphrases differ in phrasing, structure, or rhetorical framing, but preserve the semantic intent of the task. The evaluation tests whether metric outputs remain consistent across these stylistic variants when applied to the same model. High CS scores indicate robustness to surface-level variation, while drops in consistency may reveal instability in how a model handles prompt form.
4.3. Metric-Rubric Alignment and Applicability
The PEARL metrics were designed to reflect specific rubric dimensions defined across technical, explanatory, and argumentative tasks. However, not all rubric criteria are amenable to automatic evaluation. Some dimensions—such as originality, nuance, or depth of insight—are highly context-dependent and remain beyond the scope of current automated approaches. The PEARL framework therefore focuses on a selected subset of rubric dimensions that exhibit structural regularities and can be operationalized through formal comparison logic.
Each metric applies to a specific type of input and encodes a particular evaluation function. For example, some metrics require pairs of responses to the same prompt (e.g., RWC and GWR), others rely on response groupings structured around rubric categories (e.g., RMA), and some operate over multi-model outputs (e.g., WCS). Other metrics are designed to assess individual responses, such as EQI for explanation quality or CS for stability under stylistic variation. DPR is unique in that it measures the presence and integration of dialectical elements across a predefined sequence (opinion, counterargument, synthesis).
To clarify this alignment between metrics, rubric scopes, and evaluation configurations, Table 3 consolidates the mapping of each metric to its required input structure and comparison mode; the evaluation scenario column encodes the rubric focus.
Each metric was applied only when the structure of the input and the scope of the rubric matched the formal conditions required for meaningful evaluation. For instance, RWC and GWR cannot be computed without parallel responses to the same prompt; RMA is valid only for grouped responses structured around rubric categories; and WCS requires paired rubric scores per prompt to compute normalized win-margin (|Δ|/Z). Similarly, DPR depends on temporally ordered inputs, EQI requires prompts eliciting explanatory reasoning, and CS relies on paraphrased prompt clusters that preserve semantic intent while altering surface form.
This strict alignment ensures that PEARL metrics are never applied beyond their diagnostic range. It also allows each score to retain interpretability in relation to the rubric dimension it targets, while preventing metric inflation or misuse in structurally incompatible evaluation contexts.
5. Results
This section reports the performance of the evaluated models according to the seven metrics defined in the PEARL framework. Quantitative outcomes are presented in tabular and graphical form, accompanied by an analysis of performance patterns, relative advantages, and potential trade-offs across evaluation dimensions.
5.1. Metric-Level Results
Results are presented for each metric in the order of the framework, with numerical values and concise interpretations. We use Δ = LLaMA3 − GPT-4. Positive values mean higher scores from LLaMA3, and negative values mean higher scores from GPT-4.
5.1.1. Rubric Win Count (RWC)
The Rubric Win Count (RWC) results are summarized in Table 5 and Figure 2. We report empirical results, highlighting evaluator-specific trends.

Table 5.
Evaluator agreement statistics for RWC by rubric.
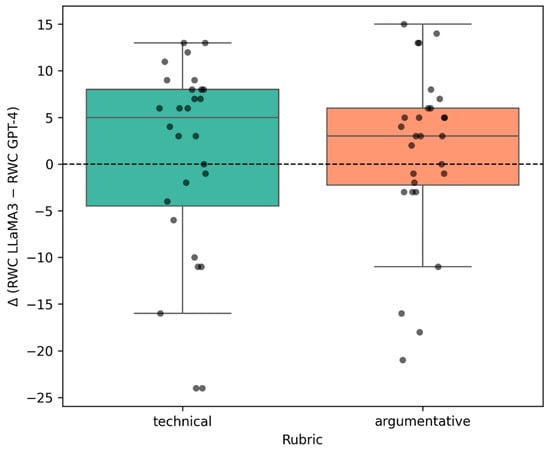
Figure 2.
Distribution of Δ by rubric type.
Table 5 reports the mean Δ, mean absolute difference (MAD), and the proportion of comparisons in which each evaluator assigned more wins, grouped by rubric. On average, Δ is slightly positive for both rubrics (0.86 for technical, 1.36 for argumentative), indicating a marginal tendency for LLaMA3:instruct to award more wins. Disagreements are more pronounced for technical prompts (MAD = 8.64) than for argumentative prompts (MAD = 7.00). In both rubrics, LLaMA3:instruct assigns more wins in 60.7% of comparisons, while GPT-4 does so in 35.7%. We also report inter-scorer agreement on per-dimension wins using Cohen κ, which is 0.00 with a 95% confidence interval from 0.00 to 0.00. The mean Δ LLaMA3 minus GPT-4 is 0.00 with a 95% confidence interval from −4.13 to 4.04 based on 56 units. Taken together, these estimates indicate no agreement beyond chance and no clear aggregate bias toward either evaluator at this level of aggregation.
The distribution of Δ values by rubric is illustrated in Figure 2. The technical rubric shows a wider interquartile range and more extreme outliers, consistent with the larger MAD in Table 5. Outliers in both rubrics correspond to model pairs where evaluator choice substantially altered the RWC outcome.
A detailed view of the largest disagreements is given in Table 6, which lists the ten comparisons with the highest |Δ| values. The most extreme differences (Δ = −24) occur in technical prompts for deepseek-r1:8b vs. gemma:7b-instruct and llama3:8b vs. mistral:7b-instruct, where GPT-4 assigns substantially more wins. Large negative gaps are also observed in argumentative prompts, such as llama3:8b vs. zephyr:7b-beta (Δ = −21) and llama3:8b vs. mistral:7b-instruct (Δ = −18). Conversely, notable positive differences, indicating more wins assigned by LLaMA3:instruct, include gemma:7b-instruct vs. nous-hermes2:latest (Δ = +15) and deepseek-r1:8b vs. (Δ = +14).

Table 6.
Top 10 largest evaluator disagreements for RWC.
RWC shows broad agreement between GPT-4 and LLaMA3. A few pairs display large |Δ| values that can change the pairwise winner.
5.1.2. Global Win Rate (GWR)
The Global Win Rate (GWR) results are summarized in Table 7 and Figure 3. We present empirical results and highlight evaluator divergences.

Table 7.
Evaluator agreement statistics for GWR by rubric.
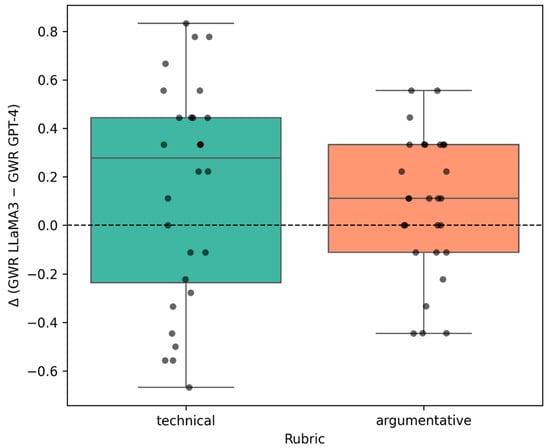
Figure 3.
Distribution of Δ by rubric type.
Table 7 summarizes the agreement between evaluators by rubric. Mean Δ is close to zero for both rubrics (+0.145 for technical, +0.083 for argumentative), indicating overall alignment in global preference patterns with a slight tendency for LLaMA3:instruct to report higher win ratios. Variability, as measured by the mean absolute difference (MAD), is higher for technical prompts (0.415) than for argumentative prompts (0.242). In line with this, LLaMA3:instruct assigns a higher GWR in 60.7% of technical comparisons and 57.1% of argumentative comparisons, while GPT-4 does so in 35.7% and 28.6% of cases, respectively. We also report inter-scorer agreement on per-prompt global winners using Cohen κ, which is 0.00 with a 95% confidence interval from 0.00 to 0.00. The mean Δ LLaMA3 minus GPT-4 is 0.00 with a 95% confidence interval from −0.16 to 0.17 based on 56 units. These estimates indicate no agreement beyond chance and no aggregate bias at the level of global win labels.
The distribution of Δ values is shown in Figure 3. Technical prompts exhibit a broader spread and more extreme outliers, consistent with the larger MAD in Table 7. Argumentative prompts display a tighter clustering around zero, suggesting closer alignment between evaluators in this rubric.
The most substantial disagreements are detailed in Table 8, which lists the top 10 comparisons with the largest |Δ| values. Extreme differences occur predominantly in technical prompts (8/10 cases), with Δ values reaching up to +0.833 for deepseek-r1:8b vs. nous-hermes2:latest (favoring LLaMA3:instruct) and down to −0.667 for dolphin-mistral:latest vs. gemma:7b-instruct (favoring GPT-4). Models such as gemma:7b-instruct (appearing in 5 pairs) and deepseek-r1:8b/nous-hermes2:latest (3 pairs each) occur frequently among these high-disagreement cases, indicating evaluator-dependent shifts in perceived global preference.

Table 8.
Top 10 largest evaluator disagreements for GWR.
The recurrence of identical Δ values in Table 8 is a direct consequence of the discrete resolution of the GWR metric. Given that GWR is defined as the proportion of prompt clusters won by a model within a rubric, the set of attainable scores is constrained by the number of clusters (e.g., for six clusters: 0.000, 0.167, 0.333, 0.500, 0.667, 0.833, 1.000). Consequently, Δ—computed as the difference between the GWR values assigned by LLaMA3:instruct and GPT-4—can only assume a limited set of discrete values, often repeating across comparisons. High-magnitude repetitions (e.g., ±0.833, ±0.667) correspond to cases of maximal evaluator divergence, in which one evaluator attributes nearly all available wins to a model, whereas the other attributes few or none. This reflects the sensitivity of GWR to evaluator choice under conditions of low sample cardinality per rubric.
GWR shows broad alignment between GPT-4 and LLaMA3. Some technical prompt pairs exhibit notable |Δ| outliers.
5.1.3. Rubric Mean Advantage (RMA)
The Rubric Mean Advantage (RMA) results are reported in Table 9 and Figure 4. We highlight effect sizes and evaluator-specific shifts.

Table 9.
Evaluator agreement statistics for RMA by rubric.
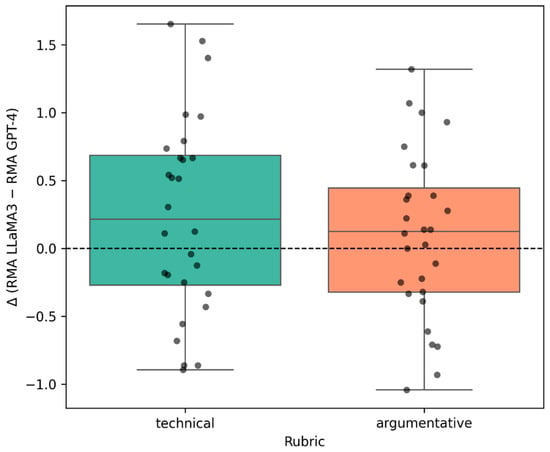
Figure 4.
Distribution of Δ by rubric type.
Table 9 summarizes the agreement statistics for RMA by rubric. Mean Δ values are slightly positive in both rubrics (+0.242 for technical, +0.097 for argumentative), indicating a mild tendency for LLaMA3:instruct to score closer to the rubric-defined answers. The magnitude of disagreement, measured by the mean absolute difference (MAD), is higher for technical prompts (0.628) than for argumentative prompts (0.500). In both rubrics, LLaMA3:instruct achieves higher RMA in 57.1% of comparisons, while GPT-4 does so in 42.9% of technical and 39.3% of argumentative comparisons. Inter-scorer agreement on RMA shows moderate absolute agreement. ICC(2,1) is 0.43 with a 95% confidence interval from 0.25 to 0.57 and Lin’s CCC is 0.42 with a 95% confidence interval from 0.25 to 0.56. The mean Δ LLaMA3 minus GPT-4 is 0.00 with a 95% confidence interval from −0.33 to 0.32 based on 56 paired units.
The distribution of Δ values is illustrated in Figure 4. Technical prompts may exhibit a wider spread if evaluators differ in interpreting technical correctness, whereas argumentative prompts are expected to yield closer agreement given the more qualitative nature of the criteria. Outliers in either rubric correspond to comparisons where evaluator choice substantially changes the measured alignment with the rubric.
The most substantial disagreements are detailed in Table 10, which lists the ten comparisons with the largest |Δ| values. Large positive Δ values—such as gemma:7b-instruct vs. nous-hermes2:latest (Δ = +1.652)—indicate cases where LLaMA3:instruct is markedly closer to the rubric-defined choice. Conversely, large negative Δ values—such as llama3:8b vs. openhermes:latest (Δ = −1.042)—indicate stronger rubric adherence by GPT-4.

Table 10.
Top 10 largest evaluator disagreements for RMA.
RMA shows broad alignment between GPT-4 and LLaMA3. High-|Δ| cases indicate evaluator-specific shifts in magnitude.
5.1.4. Explanation Quality Index (EQI)
The Explanation Quality Index (EQI) results are presented in Table 11 and Table 12. We describe evaluator differences and model-level patterns and note where the rankings diverge.

Table 11.
Evaluator agreement statistics for EQI (Δ = LLaMA3 − GPT-4).

Table 12.
Individual EQI scores by evaluator (Δ = LLaMA3 − GPT-4).
The analysis revealed a consistent upward bias from LLaMA3, with higher EQI scores than GPT-4 for all eight evaluated models. The average difference was +0.667 points on the 10-point rubric, with variability in the gap size across models (mean absolute deviation, MAD = 0.667). This bias was systematic, occurring in 100% of comparisons, and unlikely to be explained by chance (sign test, p ≈ 0.0078). Rank-order agreement between evaluators was low, with a Pearson correlation coefficient (r) of 0.135 for raw scores and Spearman’s ρ of 0.395 for rankings, indicating substantial divergence in model ordering. Bland–Altman analysis, which assesses agreement limits, showed that LLaMA3’s ratings ranged from approximately 0.85 points lower to 2.18 points higher than GPT-4’s, with the largest positive differences for Zephyr:7b-beta (+2.000) and Dolphin-Mistral (+1.666). These findings are summarized in Table 11. Inter-scorer agreement on EQI shows weak absolute agreement. ICC(2,1) is 0.03 with a 95% confidence interval from −0.14 to 0.34 and Lin’s CCC is 0.03 with a 95% confidence interval from −0.13 to 0.33. The mean Δ LLaMA3 minus GPT-4 is 0.67 with a 95% confidence interval from 0.20 to 1.21 based on 8 models, indicating negligible agreement and a small positive evaluator difference that favors LLaMA3 at the per-model level.
To provide a detailed view, Table 12 lists the individual EQI scores assigned by each evaluator, sorted by GPT-4’s ratings. This ordering maintains the reference-based ranking while allowing direct inspection of score differences. The table also shows the consistent positive bias of LLaMA3:instruct relative to GPT-4, with the largest gaps for zephyr:7b-beta (+2.000) and dolphin-mistral:latest (+1.666).
EQI analysis suggests that without proper calibration, secondary scorers such as LLaMA3:instruct may systematically inflate explanation quality ratings compared to a human-aligned reference, potentially altering model rankings and affecting the interpretability of evaluation outcomes in educational and benchmarking contexts.
5.1.5. Dialectical Presence Rate (DPR)
The Dialectical Presence Rate (DPR) results are presented in Table 13 and Table 14. We describe evaluator differences and their impact on model rankings.

Table 13.
Evaluator agreement statistics for DPR (Δ = LLaMA3 − GPT-4).

Table 14.
Individual DPR scores by evaluator (Δ = LLaMA3 − GPT-4).
The results indicate a consistent negative bias from LLaMA3, which scored all eight evaluated models lower than GPT-4. The average difference was −0.084, with a mean absolute deviation (MAD) of 0.084. This direction was consistent in 100% of comparisons, and the sign test suggests the pattern is unlikely to be due to chance (p ≈ 0.0078). Rank-order agreement between evaluators was weak to negative, with a Pearson correlation coefficient of −0.783 and Spearman’s ρ of −0.484, indicating that not only were the scores lower, but the relative ordering of models also differed substantially. These agreement statistics are summarized in Table 13. Inter-scorer agreement on DPR is near zero at the per-model level. ICC(2,1) is −0.02 with a 95% confidence interval from −0.05 to 0.00 and Lin’s CCC is −0.02 with a 95% confidence interval from −0.05 to 0.00. The mean Δ LLaMA3 minus GPT-4 is −0.08 with a 95% confidence interval from −0.10 to −0.07 based on 8 models, indicating a small negative evaluator difference that favors GPT-4.
To illustrate the extent of these differences, Table 14 presents the individual DPR scores for each model, sorted by GPT-4’s ratings and displayed side-by-side. The consistently negative Δ values indicate a downward bias from LLaMA3 across all models, with the largest absolute differences for deepseek-r1:8b (−0.108) and nous-hermes2:latest (−0.102).
DPR analysis suggests that without proper calibration, secondary scorers such as LLaMA3 may underestimate the presence of dialectical elements in model explanations, potentially affecting evaluations in contexts where balanced reasoning is a key performance indicator.
5.1.6. Consistency Spread (CS)
Consistency Spread (CS) results are presented in Table 15 and Table 16. We analyze stability under paraphrase variation and note where evaluator differences change model ordering.

Table 15.
Evaluator agreement statistics for CS (Δ = LLaMA3 − GPT-4).

Table 16.
Individual CS scores by evaluator (Δ = LLaMA3 − GPT-4).
The results show a systematic upward bias in CS reported by LLaMA3 for most models, suggesting a stronger perception of instability compared to GPT-4. The mean difference was +0.594, with a mean absolute difference (MAD) of 0.829. In 75.0% of cases, LLaMA3 reported higher CS values, and in 12.5% lower values; the sign test did not indicate a statistically significant departure at conventional thresholds (p ≈ 0.125). Rank-order agreement between evaluators was low and negative (Pearson r = −0.686, Spearman’s ρ = −0.565), suggesting consistent reversals in model ordering. These statistics are summarized in Table 15. Inter-scorer agreement on CS is weak and slightly negative. ICC(2,1) is −0.384 with a 95% confidence interval from −1.058 to 0.010, and Lin’s CCC is −0.344 at the per-model level with N equal to 8. The mean Δ LLaMA3 minus GPT-4 is 0.594 with a 95% confidence interval from 0.068 to 1.054, which indicates a small positive evaluator difference in favor of LLaMA3.
For greater detail, Table 16 lists the individual CS scores for each model, ordered ascending by GPT-4’s CS values and displayed side-by-side. Across models, LLaMA3 reports higher spread (lower consistency) than GPT-4, with large differences for llama3:8b (+1.472) and nous-hermes2:latest (+1.381), as well as a notable inversion for gemma:7b-instruct (−0.936), where LLaMA3 reported a lower CS than GPT-4.
CS analysis suggests that without calibration to a human-aligned reference, a secondary scorer such as LLaMA3 may overestimate instability under paraphrasing for a substantial proportion of models, potentially affecting conclusions about robustness and altering rankings in consistency-sensitive applications.
5.1.7. Win Confidence Score (WCS)
The Win Confidence Score (WCS) results are presented in Table 17 and Table 18. We describe the decisiveness of wins across models and how evaluator differences affect the margins.

Table 17.
Evaluator agreement statistics for WCS (Δ = LLaMA3 − GPT-4).

Table 18.
Individual WCSs by evaluator (Δ = LLaMA3 − GPT-4).
Across the eight evaluated models, the average difference was −0.020, with a mean absolute difference (MAD) of 0.021. LLaMA3 reported lower WCS values in 87.5% of cases and higher values in 12.5% of cases. The sign test does not suggest a statistically significant departure from chance (p ≈ 0.0703). Rank-order agreement between evaluators was weak and negative (Pearson r = −0.149, Spearman’s ρ = −0.071), indicating limited alignment in model ordering by win decisiveness. Table 17 summarizes these agreement statistics. Inter-scorer agreement on WCS is low to moderate at the paired-comparison level. ICC(2,1) is 0.22 with a 95% confidence interval from 0.00 to 0.42, and Lin’s CCC is 0.22 with a 95% confidence interval from 0.00 to 0.41 based on 56 pairs. The mean Δ LLaMA3 minus GPT-4 has a 95% confidence interval from −0.01 to 0.01, which indicates no aggregate evaluator bias on WCS.
The aggregated per-model WCSs are presented in Table 18, ordered by GPT-4’s ratings. The absolute differences remain small across all models. LLaMA3 consistently assigns slightly lower values, with the only exception being deepseek-r1:8b (+0.004), where its estimate marginally exceeds that of GPT-4.
WCS analysis indicates minimal bias between evaluators, but with a consistent small downward shift from LLaMA3. While these differences are unlikely to materially affect model rankings, they may slightly understate the decisiveness of wins when interpreted alongside directional metrics such as RWC and GWR.
5.2. Per-Metric Ablations
We assess robustness of the per-metric results along three dimensions: (i) response-length effects on EQI and WCS, and longer-response bias for pairwise metrics (GWR, RMA); (ii) sensitivity to rubric weighting by varying the technical vs. argumentative weights (wtech ∈ {0.25, 0.75}) relative to the equal-weights baseline (wtech = 0.5); and (iii) sensitivity to evaluator identity by comparing GPT-4- and LLaMA3-based rankings. Rows marked “trimmed” exclude the top quartile of absolute response-length differences.
Response-length effects are summarized in Table 19, which reports Pearson and Spearman correlations between EQI/WCS and mean response length under each scorer, together with the probability that the longer response wins (GWR) or yields a positive margin (RMA). For GWR and RMA, values above 0.5 indicate an advantage for longer responses; trimmed rows repeat the analysis after excluding the top quartile of absolute length differences.

Table 19.
Length-control ablations (EQI/WCS vs. response length; GWR/RMA longer-response effects; GPT-4 and LLaMA3 scorers).
Rubric-weighting sensitivity is reported in Table 20, which compares model rankings under wtech ∈ {0.25, 0.75} to the equal-weights baseline (wtech = 0.5) using Kendall’s τ and the maximum absolute rank change. Results are presented per metric and per evaluator to separate rubric effects from scorer effects.

Table 20.
Rubric-weighting sensitivity (Kendall τ vs. baseline wtech = 0.5; max |Δrank| across wtech∈{0.25, 0.75}; per metric and evaluator).
Evaluator-identity sensitivity is summarized in Table 21 as Kendall’s τ between GPT-4 and LLaMA3 based rankings for each metric, indicating the degree of agreement between scorers at the model-ranking level.

Table 21.
Evaluator-identity sensitivity (Kendall τ between GPT-4 and LLaMA3 rankings; per metric).
Overall, the ablations indicate that the principal findings and model rankings remain stable across response-length control, rubric-weight perturbations, and evaluator identity, with only modest residual sensitivity that does not alter the qualitative conclusions.
5.3. Cross-Metric Comparative Analysis
To capture a comprehensive picture of evaluator behavior, we aggregated the results for all seven evaluation metrics—RWC, GWR, RMA, EQI, DPR, CS, and WCS—using GPT-4 as the human-aligned reference and LLaMA3:instruct as the secondary scorer. For each metric, the score difference Δ was computed as LLaMA3 minus GPT-4, with positive values indicating higher scores from LLaMA3. Agreement between evaluators was quantified through Pearson and Spearman correlations, while the mean absolute difference (MAD) measured the average magnitude of disagreement. The sign test p-value assessed whether the observed directional differences were statistically significant.
A consolidated statistical overview of these comparisons is given in Table 22, which reports, for each metric, the average bias, the MAD, the proportion of models scored higher or lower by LLaMA3, the two correlation coefficients, and the sign test p-value. This table shows that LLaMA3 assigns higher scores than GPT-4 for most metrics, with RWC (+1.107) and EQI (+0.667) exhibiting the largest positive differences. CS (+0.594) and RMA (+0.169) also trend positively but to a lesser extent, while GWR shows only a minimal increase (+0.114). DPR (−0.084) and WCS (−0.020) are the only metrics where LLaMA3 tends to assign lower scores. The highest variability appears in RWC (MAD = 2.179), followed by CS (0.829) and EQI (0.667), indicating substantial per-model divergence, whereas WCS (0.021) and DPR (0.084) show very close numerical alignment.

Table 22.
Cross-metric agreement and bias statistics (Δ = LLaMA3 − GPT-4; per-model aggregation).
The correlation measures in the table reveal notable differences between metrics. RMA (Pearson = 0.550; Spearman = 0.643) and RWC (0.520; 0.527) achieve the highest concordance between evaluators despite the substantial bias in RWC. GWR shows weaker but positive agreement (0.350; 0.238), while EQI’s correlations are close to zero (0.135; 0.395). CS and DPR present strong negative correlations in both measures, indicating that the two evaluators tend to rank models in opposite order for these metrics. The sign test confirms statistically significant directional bias for EQI and DPR (p = 0.008 in both cases), showing that the bias is consistent across all models. For RMA, GWR, and WCS, the p-values (0.070) suggest weaker directional tendencies, while for RWC, the high p-value (0.289) indicates a lack of consistent direction despite the large mean difference.
The statistical findings are complemented by a visual synthesis in Figure 5, which presents four coordinated panels to capture the key dimensions of evaluator comparison. The first panel illustrates the mean differences, making the dominance of RWC and EQI immediately apparent, alongside the negative bias in DPR. The second panel depicts MAD values, clearly separating the high-variability metrics (RWC, CS, EQI) from the stable ones (WCS, DPR). The third panel displays Pearson correlations, highlighting the moderate positive alignment in RMA and RWC and the strong negative associations in CS and DPR. The fourth panel presents Spearman rank correlations, which follow similar patterns to the Pearson results and confirm the substantial drop in rank agreement for CS and DPR.
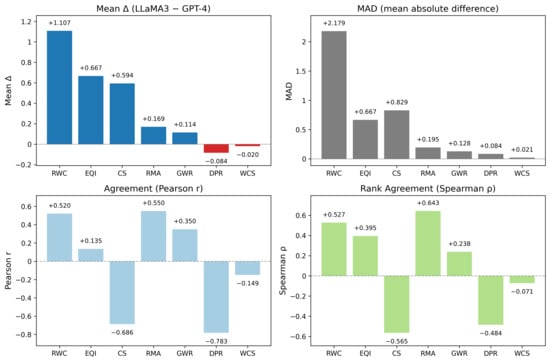
Figure 5.
Comparative summary across all metrics: Mean Δ, MAD, Pearson r, and Spearman ρ, computed via per-model aggregation from original comparison files.
Overall, the combined statistical and visual evidence demonstrates that bias magnitude, variability, and agreement can diverge sharply across metrics. Metrics such as RWC and EQI combine strong positive bias with moderate ordering agreement, whereas CS and DPR show smaller mean differences but low or negative agreement, indicating fundamental divergences in how the two evaluators assess and rank model quality. This highlights the importance of using multiple complementary metrics to obtain a robust picture of evaluator reliability.
5.4. Key Insights
Across all evaluation metrics, the comparison between LLaMA3 and the human-aligned GPT-4 reference reveals that bias is not uniform in direction or magnitude. Metrics such as RWC and EQI display the largest positive shifts, indicating that LLaMA3 tends to assign higher scores, while DPR and WCS show consistent, albeit smaller, negative differences. Notably, large bias does not always imply statistical consistency: RWC exhibits the greatest mean difference without a consistent directional pattern, whereas EQI and DPR present smaller absolute shifts but statistically significant bias according to the sign test.
The magnitude of score variability, as captured by the mean absolute difference, is highest for RWC, CS, and EQI, highlighting substantial per-model divergence. In contrast, WCS and DPR exhibit minimal variability, pointing to close numerical alignment between evaluators despite directional tendencies.
Agreement analyses show that substantial bias can coexist with stable model rankings. RMA and RWC achieve the highest Pearson and Spearman correlations, indicating moderate consistency in relative ordering even when absolute scores differ. Conversely, CS and DPR produce strong negative correlations in both measures, revealing that the two evaluators often rank models in opposite order for these metrics.
These findings emphasize that no single metric provides a complete picture of evaluator behavior. Reliable interpretation requires a multi-metric perspective that accounts for bias direction and magnitude, score variability, and both linear and rank-based agreement. The diversity of patterns observed here reinforces the need for complementary metrics to ensure robust and balanced evaluation.
6. Discussion
The PEARL metric suite has been developed to provide a structured and comprehensive approach to the evaluation of Large Language Models (LLMs). It integrates three rubric-aligned dimensions (Technical, Argumentative, and Explanation) within a unified rubric-based framework. In contrast to approaches that emphasize a single performance aspect or aggregate preference scores without transparency, PEARL applies distinct rubrics for answers and explanations, includes measures of stability under input variation, and accounts for argumentative reasoning. This structure enables the framework to capture both areas of convergence with human judgment and complementary aspects of model performance that may not be reflected in conventional metrics. The following subsections assess the validity of PEARL through four complementary perspectives: alignment with a model-based proxy evaluator, stability and robustness, discriminative power across performance levels, and coverage of multiple evaluation dimensions.
6.1. Alignment with a Model-Based Proxy (GPT-4)
Previous studies on the validation of evaluation metrics emphasize the importance of examining the extent to which metric scores correspond to human judgements [11,13,77,78]. Following this approach, the present analysis compares each PEARL metric with ratings provided by GPT-4, used here as a model-based proxy given reported alignment with expert rubric-based assessments [77,78]. For each metric, the Pearson correlation coefficient (r), measuring the strength of the linear relationship, and the Spearman rank correlation coefficient (ρ), capturing monotonic associations, were computed against GPT-4 reference scores within an LLM-based evaluation. The sample size (N) denotes the number of valid observations, while the associated p-values indicate the statistical significance of the correlations.
As shown in Table 23 and illustrated in Figure 6, the highest alignment with the model-based proxy was observed for RMA (N = 56, r = 0.535, ρ = 0.485, p < 0.001) and RWC (N = 56, r = 0.488, ρ = 0.404, p = 0.002). Both metrics are derived from rubric-level comparisons of model outputs and appear to capture dimensions such as factual accuracy, clarity, and completeness, which are also central to human rubric-based scoring. Their moderate positive associations with the model-based proxy are detailed in Table 23. The table reports Δ (LLaMA3—GPT-4) with 95% bootstrap CIs (B = 10,000) and Benjamini–Hochberg FDR decisions (q = 0.10), and all tests are interpreted as exploratory given N = 8 for CS/DPR/EQI.

Table 23.
Pearson and Spearman correlations between PEARL metrics and GPT-4 (model-based proxy) reference scores, with 95% CIs for Pearson r are computed via Fisher’s z. Δ and its 95% CI are estimated via paired bootstrap (B = 10,000). p-values are interpreted as exploratory; Benjamini–Hochberg FDR (q = 0.10) is applied across the Pearson tests in this table (✓ = rejected; – = not).
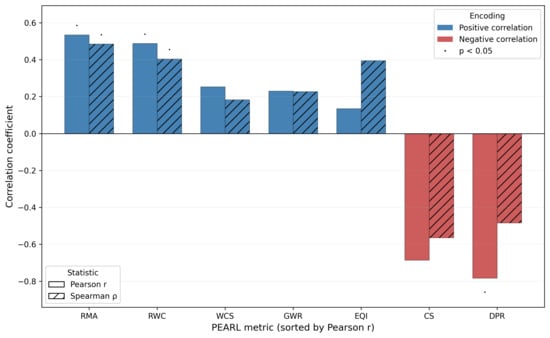
Figure 6.
Pearson (r, solid bars) and Spearman (ρ, hatched bars) correlations between PEARL metrics and GPT-4 reference scores. Bar colors indicate correlation sign; dots denote uncorrected p < 0.05 (exploratory).
GWR (N = 56, r = 0.230, ρ = 0.227) and WCS (N = 56, r = 0.254, ρ = 0.183) exhibit weaker but still positive associations. This pattern suggests that while global win rates and win confidence capture some aspects valued by the model-based proxy, they are less sensitive to fine-grained rubric dimensions and may be influenced by factors such as response length or style, which are not always directly aligned with rubric-defined quality.
Among the explanation- and robustness-oriented metrics, EQI (N = 8, r = 0.135, ρ = 0.395) shows modest alignment. This is expected: high-quality explanations—while pedagogically valuable—are not always prioritized in aggregate preference ratings that emphasize final answers over reasoning processes.
In contrast, CS (N = 8, r = −0.686, ρ = −0.565) and DPR (N = 8, r = −0.783, ρ = −0.484) present negative correlations with the model-based proxy. This need not indicate reduced metric quality; rather, it reflects that these measures target orthogonal properties. CS evaluates robustness to prompt variation, and DPR captures the inclusion and integration of alternative viewpoints—dimensions that are not necessarily rewarded in aggregate preference scores but are critical for reliability and argumentative depth. Negative correlations in this context indicate discriminant validity, confirming that PEARL includes metrics that assess distinct aspects of performance beyond those captured by conventional ranking-based evaluation.
To aid visual interpretation, Figure 6 presents the same data in graphical form, with solid bars for Pearson r and hatched bars for Spearman ρ. Blue indicates positive correlations, red indicates negative correlations, and dots denote uncorrected p < 0.05 (exploratory); FDR decisions (q = 0.10) are reported in Table 23.
Taken together, the correlation profile indicates convergent validity for metrics such as RMA and RWC—whose positive, statistically significant associations with the model-based proxy suggest alignment with rubric-level human judgment—while CS and DPR provide discriminant validity, capturing robustness and dialectical reasoning that are not directly reflected in global preference scores. The intermediate pattern for EQI is consistent with an explanation-focused construct that only partially overlaps with preference-oriented ratings. This distribution of results reflects PEARL’s intended multidimensional design: some metrics converge with model-based proxy assessments, whereas others offer complementary diagnostic value by quantifying aspects of model behavior not addressed by preference-based evaluation. Building on this distinction, the next subsection examines the stability dimension in greater depth, focusing on robustness under prompt variation and task reordering through the CS and WCS metrics.
6.2. Stability and Robustness of Metrics
The stability of evaluation metrics under semantically equivalent input variations is widely recognized as an important aspect of metric validity, particularly in contexts where reproducibility and reliability are required [49,53,56,59]. For transparency, we report CS both in aggregate and, when applicable, stratified by paraphrase type (lexical, syntactic, discourse), and we discuss sensitivity to paraphrase difficulty. Within the PEARL framework, robustness was assessed using two complementary measures: the Consistency Spread (CS), which quantifies variability in rubric scores across paraphrased prompts for the same task, and the Win Confidence Score (WCS), which reflects the decisiveness of comparative judgements between models. Lower CS values indicate greater stability, whereas higher WCS values indicate more decisive average win margins when a model is preferred.
As shown in Table 24, the mean CS across models is 0.294, with values ranging from 0.000 (highest stability) for deepseek-r1:8b and llama3:8b to 1.126 (lowest stability) for gemma:7b-instruct. Models such as dolphin-mistral:latest, nous-hermes2:latest, and openhermes:latest achieve intermediate stability (CS = 0.094), while zephyr:7b-beta and mistral:7b-instruct show higher variability (CS = 0.283 and 0.660, respectively). The average WCS is 0.079, with the most decisive comparative margins observed for llama3:8b (0.119) and the least decisive for zephyr:7b-beta (0.057).

Table 24.
Stability and robustness metrics per model. Lower CS indicates higher consistency across semantically equivalent prompts; WCS reports average win-margin decisiveness across matchups (GPT-4 evaluator).
These results suggest that certain models maintain consistent quality across semantically equivalent prompts, while others exhibit greater sensitivity to prompt variation. High stability, as observed for deepseek-r1:8b and llama3:8b, indicates robustness to lexical and structural perturbations, enhancing the interpretability and reproducibility of evaluation outcomes. Conversely, elevated CS values, such as that for gemma:7b-instruct, highlight possible fragility, where small changes in input formulation lead to noticeable differences in metric scores. WCS complements this picture by showing whether wins, when they occur, are marginal or decisive—information relevant for competitive benchmarking.
While PEARL comprises seven distinct metrics, CS and WCS are the only ones specifically designed to quantify stability and robustness. The remaining metrics address other dimensions—such as accuracy, explanation quality, and argumentative depth—and are therefore examined in separate subsections.
The relationship between CS and WCS for all evaluated models is visualized in Figure 7. The green-shaded area (top-left quadrant) represents the “ideal” region, combining low CS (high stability) with high WCS (decisiveness), while the red-shaded area (bottom-right quadrant) indicates “problematic” combinations of instability and low decisiveness. Models located in the ideal zone, such as llama3:8b, combine robustness with clear comparative advantages, whereas models in the problematic zone exhibit both variability under prompt changes and low win-margin confidence.
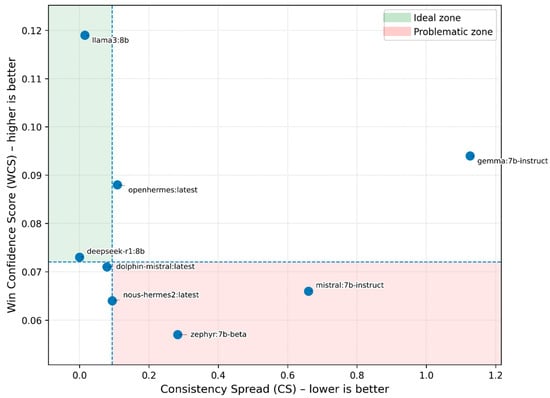
Figure 7.
Relationship between Consistency Spread (CS) and Win Confidence Score (WCS) for evaluated models. Lower CS indicates higher stability; higher WCS indicates greater decisiveness in comparative outcomes (GPT-4 evaluator).
In summary, the analysis of CS and WCS demonstrates that PEARL includes dedicated measures for assessing stability and robustness, providing complementary perspectives on consistency across prompt variations and the decisiveness of comparative outcomes. These metrics allow the framework to identify models that are both resilient to input perturbations and capable of producing clear, reproducible performance differences. By isolating stability as a distinct evaluation dimension, PEARL ensures that robustness is explicitly considered alongside other performance aspects, thereby enhancing the overall validity and reliability of the framework.
6.3. Discriminative Power Across Model Quality Levels
A core requirement for the validity of an evaluation metric is its capacity to consistently differentiate between models of demonstrably different quality [49,53,56,59]. Within the PEARL validation framework, this property complements the evidence on alignment with human-proxy judgements [11,13,77,78] by extending the analysis from correlational agreement to the ability to separate high and low-performing systems. Metrics with strong discriminative power are essential for guiding model selection, supporting benchmarking, and identifying performance improvements that are both statistically and practically meaningful.
The analysis was restricted to the intersection of models for which all seven PEARL metrics were available, ensuring direct comparability across measures. Two groups were defined from this common set: a high-performing group comprising llama3:8b, nous-hermes2:latest, and deepseek-r1:8b, and a low-performing group comprising openhermes:latest, dolphin-mistral:latest, and gemma:7b-instruct. Group membership was determined through a composite ranking of standardized scores from three rubric-based comparative metrics—RMA, RWC, and GWR—chosen for their strong association with model-based proxy preferences. This composite approach reduces reliance on a single metric and captures multiple facets of performance, including factual accuracy, clarity, and overall task success.
All metric scores were standardized using the z-score transformation to ensure comparability across different original scales. For each metric, we computed the mean score in the high and low groups, the difference Δ between group means, the standardized effect size (Cohen’s d), and two measures of statistical significance: p_Welch, the p-value from Welch’s t-test (a parametric test that does not assume equal variances between groups), and p_MW, the p-value from the Mann–Whitney U test (a non-parametric test based on rank distributions). Including both tests provides robustness, allowing us to confirm whether observed differences are consistent under different statistical assumptions.
All p-values are uncorrected and interpreted as exploratory due to small sample sizes; within-family multiplicity is controlled using Benjamini–Hochberg FDR (q = 0.10).
As shown in Table 25, RMA and GWR exhibit the strongest discriminative power, each with Δ ≈ 1.78 in z-score units, large effect sizes (d ≈ 2.49–2.65), and p_Welch ≈ 0.0479 (RMA) and ≈ 0.0539 (GWR); RWC shows a large but smaller separation (Δ ≈ 1.29; d ≈ 1.80; p_Welch ≈ 0.128). These rubric-based comparative metrics indicate directionally consistent separation; given the small N, we report these results as exploratory and foreground effect sizes (Δ, Cohen’s d) and uncertainty rather than dichotomous significance. WCS shows minimal separation, with Δ of 0.408 and d ≈ 0.35, indicating limited sensitivity to aggregate quality differences. EQI shows a small-to-moderate separation (Δ ≈ 0.934; d ≈ 1.07), con-sistent with its emphasis on explanation quality, a dimension valuable for interpretability but less tightly coupled with overall performance rankings. CS and DPR present positive Δ values, indicating higher scores in the high-performing group for these robustness and diversity-oriented measures. In this subset, both metrics are higher in the high-performing group; interpretation should consider metric normalization and task mix (CS higher = more variability; DPR higher = more perspective diversity).

Table 25.
Discriminative power across model quality levels for the intersection of models across metrics; scores normalized by metric. Effect sizes (Δ, Cohen’s d) are foregrounded; 95% bootstrap CIs (B = 10,000) are provided where applicable; p-values are interpreted as exploratory under small N, with BH-FDR (q = 0.10) applied within test families.
Taken together, these findings demonstrate that PEARL incorporates metrics capable of sharply distinguishing between performance tiers—most notably RMA, RWC, and GWR—while also including measures such as CS, DPR, and EQI that provide complementary insights into robustness, diversity, and explanation quality. This combination reflects the multidimensional design of PEARL and enables both reliable ranking and targeted diagnostic feedback across evaluation dimensions. The next section examines how these complementary strengths combine to provide comprehensive coverage of the evaluation space.
6.4. Complementarity and Coverage of Evaluation Dimensions
To investigate whether PEARL’s metrics capture overlapping or distinct aspects of model performance, we computed per-model scores from the model-based proxy evaluator (GPT-4) for the seven metrics (RMA, RWC, GWR, CS, WCS, EQI, DPR), considering only the set of models with complete data. Both Pearson and Spearman correlation coefficients were calculated to examine linear and rank-order relationships.
The complete model × metric matrix used for the analysis is shown in Table 26. Performance varies substantially across dimensions. For example, llama3:8b achieves top scores on preference-based metrics (GWR, RMA, RWC) but records a CS of 0.000, indicating that its outputs exhibit very high stability and low sensitivity to prompt variation. Conversely, gemma:7b-instruct obtains the highest CS (1.126) yet negative scores on RMA and RWC, suggesting that while its responses are stable, they may not align as well with comparative preference criteria. Deepseek-r1:8b and nous-hermes2:latest show balanced but moderate performance across most metrics, whereas zephyr:7b-beta records low scores on both preference and robustness metrics, indicating weaker overall capabilities.

Table 26.
Model × metric matrix for PEARL evaluation (per-model scores from the model-based proxy evaluator).
The Pearson correlations among these metrics are illustrated in Figure 8. The heatmap shows a tight clustering of RMA, RWC, and GWR, reflecting their shared focus on comparative preferences for accuracy and clarity. This grouping indicates that these metrics largely reinforce each other when ranking models. In contrast, CS and WCS are positioned further away from the preference cluster, with weak or negative correlations, suggesting that they measure robustness-related qualities that are not captured by head-to-head win rates. EQI occupies an intermediate position, showing moderate associations with preference metrics—its emphasis on explanation quality appears partly aligned but still distinct. DPR is located at the periphery, with negative or low correlations to most metrics, highlighting its unique focus on argumentative diversity.
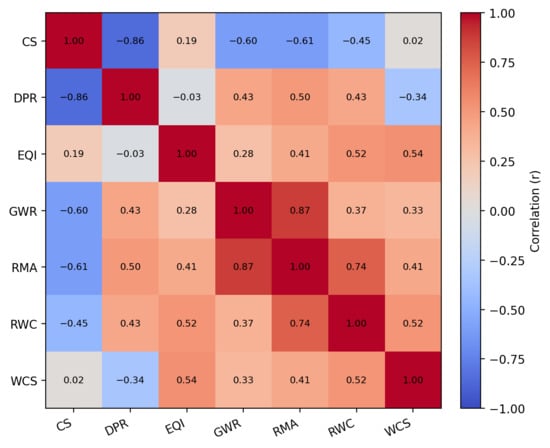
Figure 8.
Pearson correlation heatmap among PEARL metrics (per-model scores from the model-based proxy evaluator).
The Spearman rank-order correlations, shown in Figure 9, confirm the structure observed in the Pearson analysis. The same preference cluster emerges, while robustness, explanation quality, and diversity metrics remain relatively independent. Minor shifts in correlation strengths, particularly for EQI, point to non-linear relationships—some models maintain similar rankings for explanation quality despite differences in preference-based scores. This reinforces the idea that the metrics capture complementary rather than redundant dimensions of performance.
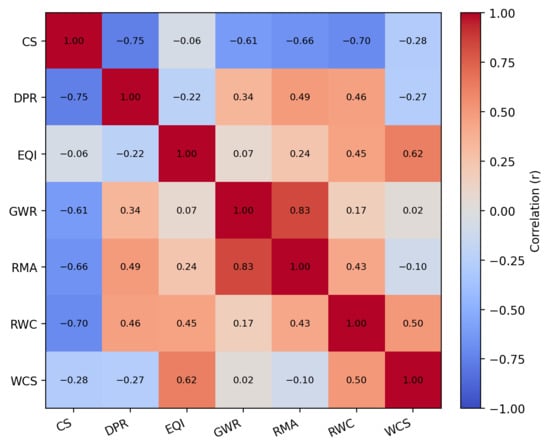
Figure 9.
Spearman correlation heatmap among PEARL metrics (per-model scores from the model-based proxy evaluator).
Overall, these results support a multidimensional view of model evaluation. Preference-based measures converge on identifying which models produce the most accurate and clear outputs in comparative settings, robustness metrics assess stability under variation, and content-focused metrics capture aspects of explanation quality and argumentative diversity. Together, they provide a richer and more nuanced assessment of model capabilities than any single metric could offer.
6.5. Limitations and Future Work
While the PEARL framework demonstrates strong potential for comprehensive evaluation of large language models, several limitations should be acknowledged to guide further development. Addressing these points will improve the robustness, generalizability, and practical value of the framework.
One limitation is the reliance on a single model-based proxy evaluator (GPT-4). Although GPT-4 aligns closely with expert human judgements, depending on a single reference introduces the risk of inheriting its inherent biases and blind spots. Future work should incorporate multiple independent evaluators, including domain experts, to diversify perspectives and strengthen metric validation.
Another limitation is the coverage of the evaluation dataset. The current benchmark focuses primarily on general-purpose reasoning and explanation tasks, which may not fully capture model behavior in specialized domains or multilingual contexts. Expanding the dataset to include domain-specific prompts (e.g., legal, medical, technical) and diverse languages will increase the applicability and external validity of the results.
The current implementation also assumes a static evaluation setting. Many commercial LLMs are updated regularly, which can alter their performance characteristics over time. Incorporating periodic re-evaluations will help track metric stability, detect performance drift, and ensure that rankings remain relevant in a dynamic landscape.
Finally, while PEARL covers seven complementary evaluation dimensions (RMA, RWC, GWR, CS, WCS, EQI, DPR), it does not explicitly measure attributes such as creativity, ethical reasoning, or adversarial robustness. Future iterations could integrate metrics targeting these aspects and explore meta-evaluation approaches to adapt metric weighting for specific application scenarios.
These extensions will enhance the robustness, fairness, and scope of PEARL, ensuring that it remains a reliable and adaptable tool for assessing LLM performance in an evolving AI ecosystem.
Given the small number of models for some metrics (N = 8), post hoc statistical power is limited and wide confidence intervals are expected; accordingly, all hypothesis tests are treated as exploratory and interpreted alongside effect sizes and confidence intervals rather than binary significance decisions.
7. Conclusions
This study introduced PEARL, a multi-metric evaluation framework designed to provide a comprehensive and fine-grained assessment of large language models (LLMs). The framework addresses the limitations of single-metric evaluations by integrating seven complementary metrics—RMA, RWC, GWR, CS, WCS, EQI, and DPR—each targeting distinct aspects of performance, including accuracy, clarity, stability, explanation quality, and argumentative diversity.
Empirical analysis demonstrated that PEARL’s preference-based metrics show mixed agreement patterns with a model-based proxy (GPT-4), with 95% CIs reported for all Pearson correlations, supporting their use for comparative model ranking. Stability-oriented measures (CS, WCS) captured robustness under prompt variation, while the diversity and explanation quality metrics (DPR, EQI) provided complementary diagnostic information not reflected in preference scores. The discriminative power analysis further indicated that the metrics could differentiate between models of varying quality in our dataset, and correlation analysis highlighted their complementarity in covering multiple evaluation dimensions.
Together, these findings suggested that PEARL was a useful tool for LLM evaluation, supporting both high-level benchmarking and targeted diagnostic analysis in our study. Unlike aggregate scoring approaches, PEARL’s multi-metric design helped practitioners identify specific strengths and weaknesses of models, informing deployment decisions in the application contexts we examined.
The educational implications follow from the rubric design and task coverage presented here. The present validation is synthetic, based on 51 prompts, eight open-weight models, and two model-based evaluators.
Future work will focus on broadening the scope and resilience of the framework by incorporating multiple evaluators, expanding task coverage to specialized and multilingual domains, and adding new metrics that capture creativity, ethical reasoning, and adversarial robustness. Additionally, we will conduct a human rating study with trained evaluators, quantify inter-rater reliability (Krippendorff’s α/ICC), and calibrate the LLM-based scorers to human anchors, reporting confidence intervals and effect sizes. These extensions will ensure that PEARL remains a reliable and adaptable resource for evaluating LLMs in a rapidly evolving technological landscape.
Author Contributions
Conceptualization, C.A., A.A.A., M.V.C. and E.P.; methodology, C.A. and M.V.C.; software, C.A., M.V.C. and A.A.A.; validation, C.A., A.A.A. and E.P.; data curation, A.C. and M.V.C.; writing—original draft preparation, C.A., A.A.A. and M.V.C.; writing—review and editing, A.A.A., E.P., C.N. and A.C.; visualization, M.V.C., C.N. and A.C.; supervision, C.A., M.V.C. and A.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The source code of the main modules is available at: https://github.com/anghelcata/pearl.git (accessed on 17 October 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- OpenAI. GPT-4 Technical Report. Available online: https://cdn.openai.com/papers/gpt-4.pdf (accessed on 30 July 2025).
- Meta. The Llama 4 Herd: The Beginning of a New Era of Natively Multimodal AI Innovation. Available online: https://ai.meta.com/blog/llama-4-multimodal-intelligence (accessed on 30 July 2025).
- Mistral.ai. Announcing Mistral 7B: A High-Performance Open-Weight Language Model. Available online: https://mistral.ai/news/announcing-mistral-7b (accessed on 30 July 2025).
- Mistral.ai. Mixtral of Experts 8x22B. Available online: https://mistral.ai/news/mixtral-8x22b (accessed on 30 July 2025).
- Anthropic. Claude 3 Model Family. Available online: https://www.anthropic.com/news/claude-3-family (accessed on 30 July 2025).
- Team, G.; Kavukcuoglu, K. Gemini 2.5: Our Most Intelligent AI Model. Available online: https://blog.google/technology/google-deepmind/gemini-model-thinking-updates-march-2025 (accessed on 30 July 2025).
- Iacobescu, P.; Marina, V.; Anghel, C.; Anghele, A.-D. Evaluating Binary Classifiers for Cardiovascular Disease Prediction: Enhancing Early Diagnostic Capabilities. J. Cardiovasc. Dev. Dis. 2024, 11, 396. [Google Scholar] [CrossRef]
- Susnea, I.; Pecheanu, E.; Cocu, A.; Istrate, A.; Anghel, C.; Iacobescu, P. Non-Intrusive Monitoring and Detection of Mobility Loss in Older Adults Using Binary Sensors. Sensors 2025, 25, 2755. [Google Scholar] [CrossRef] [PubMed]
- Anghele, A.-D.; Marina, V.; Dragomir, L.; Moscu, C.A.; Anghele, M.; Anghel, C. Predicting Deep Venous Thrombosis Using Artificial Intelligence: A Clinical Data Approach. Bioengineering 2024, 11, 1067. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Song, Y.; Iyyer, M.; Choi, E. A Critical Evaluation of Evaluations for Long-form Question Answering. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (ACL), Toronto, ON, Canada, 9–14 July 2023; pp. 3225–3245. [Google Scholar] [CrossRef]
- Hashemi, H.; Eisner, J.; Rosset, C.; Van Durme, B.; Kedzie, C. LLM-RUBRIC: A Multidimensional, Calibrated Approach to Automated Evaluation of Natural Language Texts. In Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics (ACL), Bangkok, Thailand, 11–16 August 2024; pp. 13806–13834. [Google Scholar] [CrossRef]
- Brimhall, B.L.; Neumann, J.M.; Moon, S.; Saluja, S.; Lee, N.J.; Hsu, W.; Fontaine, J.M. Current and future state of evaluation of large language models for clinical summarization tasks. npj Health Syst. 2025, 2, 6. [Google Scholar] [CrossRef]
- Joshi, B.; He, K.; Ramnath, S.; Sabouri, S.; Zhou, K.; Chattopadhyay, S.; Swayamdipta, S.; Ren, X. ELI-Why: Evaluating the Pedagogical Utility of Language Model Explanations. arXiv 2025, arXiv:2506.14200. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, H.; Yang, F.; Liu, N.; Deng, H.; Cai, H.; Wang, S.; Yin, D.; Du, M. Explainability for Large Language Models: A Survey. ACM Comput. Surv. 2023, 56, 20. [Google Scholar] [CrossRef]
- Zhou, J.; Gandomi, A.H.; Chen, F.; Holzinger, A. Evaluating the Quality of Machine Learning Explanations: A Survey on Methods and Metrics. Electronics 2021, 10, 593. [Google Scholar] [CrossRef]
- Gupta, R. Evaluating LLMs: Beyond Simple Metrics. In Proceedings of the INLG Workshop & ACL, Tokyo, Japan, 23–27 September 2024; Available online: https://medium.com/@ritesh.gupta.ai/evaluating-llms-beyond-simple-metrics-1e6babbed195 (accessed on 31 July 2025).
- Toloka.ai. LLM Evaluation Framework: Principles, Practices, and Tools. Available online: https://toloka.ai/blog/llm-evaluation-framework-principles-practices-and-tools (accessed on 31 July 2025).
- Lopes, P.; Silva, E.; Braga, C.; Oliveira, T.; Rosado, L. XAI Systems Evaluation: A Review of Human and Computer-Centred Methods. Appl. Sci. 2022, 12, 9423. [Google Scholar] [CrossRef]
- Meike, N.; Jan, T.; Shreyasi, P.; Elisa, N.; Michelle, P.; Yasmin, S.; Jörg, S.; van Keullen, M.; Christin, S. From Anecdotal Evidence to Quantitative Evaluation Methods: A Systematic Review on Evaluating Explainable AI. ACM Comput. Surv. 2023, 55, 295. [Google Scholar] [CrossRef]
- Stephen, C.; Xander, D.; Claudia, S.; Thomas Krendl, G.; Jérémy, S. Open Problems and Fundamental Limitations of Reinforcement Learning from Human Feedback. arXiv 2023, arXiv:2307.15217. [Google Scholar] [CrossRef]
- Kishore, P.; Salim, R.; Todd, W.; Wei-Jing, Z. BLEU: A Method for Automatic Evaluation of Machine Translation. In Proceedings of the 40th Annual Meeting of the Association for Computational Linguistics, Philadelphia, PA, USA, 6–12 July 2002; pp. 311–318. [Google Scholar] [CrossRef]
- Chin-Yew, L. ROUGE: A Package for Automatic Evaluation of Summaries. In Text Summarization Branches Out; Association for Computational Linguistics: Barcelona, Spain, 2004; pp. 74–81. Available online: https://aclanthology.org/W04-1013 (accessed on 31 July 2025).
- Banerjee, S.; Lavie, A. METEOR: An Automatic Metric for MT Evaluation with Improved Correlation with Human Judgments. In Proceedings of the ACL Workshop on Intrinsic and Extrinsic Evaluation Measures for MT and/or Summarization, Ann Arbor, MI, USA, 29 June 2005; pp. 65–72. Available online: https://aclanthology.org/W05-0909 (accessed on 31 July 2025).
- Blagec, K.; Dorffner, G.; Moradi, M.; Ott, S.; Samwald, M. A global analysis of metrics used for measuring performance in natural language processing. In Proceedings of the NLP Power! The First Workshop on Efficient Benchmarking in NLP, Dublin, Ireland, 26 May 2022; pp. 52–63. Available online: https://aclanthology.org/2022.nlppower-1.6/ (accessed on 31 July 2025).
- Shypula, A.; Li, S.; Zhang, B.; Padmakumar, V.; Yin, K.; Bastani, O. Evaluating the Diversity and Quality of LLM Generated Content. arXiv 2025, arXiv:2504.12522. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, Y.; Meng, F.; Zhou, J. Towards Multiple References Era—Addressing Data Leakage and Limited Reference Diversity in NLG Evaluation. In Proceedings of the Findings of the Association for Computational Linguistics: ACL 2024, Miami, FL, USA, 16 March 2024. [Google Scholar] [CrossRef]
- Sulem, E.; Abend, O.; Rappoport, A. BLEU is Not Suitable for the Evaluation of Sentence Splitting in Text Simplification. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP) 2018, Brussels, Belgium, 31 October–4 November 2018; pp. 738–744. [Google Scholar]
- Freitag, M.; Grangier, D.; Caswell, I. BLEU might be Guilty but References are not Innocent. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Online (Virtual), 16–20 November 2020; pp. 61–71. [Google Scholar] [CrossRef]
- Läubli, S.; Sennrich, R.; Volk, M. Has Machine Translation Achieved Human Parity? A Case for Document-Level Evaluation. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing (EMNLP), Brussels, Belgium, 31 October–4 November 2018; pp. 4791–4796. [Google Scholar] [CrossRef]
- Wiseman, S.; Shieber, S.; Rush, A. Challenges in Data-to-Document Generation. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing (EMNLP), Copenhagen, Denmark, 9–11 September 2017; pp. 2253–2263. [Google Scholar] [CrossRef]
- Reiter, E. A Structured Review of the Validity of BLEU in Evaluating NLG. Comput. Linguist. 2018, 44, 393–401. [Google Scholar] [CrossRef]
- Aggarwal, D.; Sil, P.; Raman, B.; Bhattacharyya, P. “I Understand Why I Got This Grade”: Automatic Short Answer Grading (ASAG) with Feedback. In Proceedings of the Artificial Intelligence in Education (AIED 2025), Palermo, Italy, 22–26 July 2025; pp. 304–318. [Google Scholar] [CrossRef]
- Su, Y.; Xu, J. An Empirical Study on Contrastive Search and Contrastive Decoding for Open-ended Text Generation. arXiv 2022, arXiv:2211.10797. [Google Scholar] [CrossRef]
- Zheng, L.; Chiang, W.L.; Sheng, Y.; Zhang, H. Chatbot Arena Leaderboard Week 8: Introducing MT-Bench and Vicuna-33B. Available online: https://lmsys.org/blog/2023-06-22-leaderboard (accessed on 31 July 2025).
- Wikipedia. LMArena. Available online: https://en.wikipedia.org/wiki/LMArena (accessed on 31 July 2025).
- Liusie, A.; Manakul, P.; Gales, M.J.F. LLM Comparative Assessment: Zero-shot NLG Evaluation through Pairwise Comparisons using Large Language Models. In Proceedings of the 18th Conference of the European Chapter of the Association for Computational Linguistics (EACL), St. Julians, Malta, 16 March 2024; pp. 139–151. [Google Scholar] [CrossRef]
- Li, Z.; Wang, C.; Ma, P.; Wu, D.; Wang, S.; Gao, C.; Liu, Y. Split and Merge: Aligning Position Biases in LLM-based Evaluators. In Proceedings of the 2024 Conference on Empirical Methods in Natural Language Processing (EMNLP), Miami, FL, USA, 12–16 November 2024; pp. 11084–11108. [Google Scholar] [CrossRef]
- Gao, M.; Liu, Y.; Hu, X.; Wan, X.; Bragg, J.; Cohan, A. Re-evaluating Automatic LLM System Ranking for Alignment with Human Preference. In Proceedings of the Findings of the Association for Computational Linguistics: NAACL 2025, Albuquerque, NM, USA, 29 April–4 May 2025; pp. 4605–4629. [Google Scholar] [CrossRef]
- Hu, Z.; Song, L.; Zhang, J.; Xiao, Z.; Wang, T.; Chen, Z.; Yuan, N.J.; Lian, J.; Ding, K.; Xiong, H. Explaining Length Bias in LLM-based Preference Evaluations. arXiv 2024, arXiv:2407.01085. [Google Scholar] [CrossRef]
- Shi, L.; Ma, C.; Liang, W.; Ma, W.; Vosoughi, S. Judging the Judges: A Systematic Investigation of Position Bias in Pairwise Comparative Assessments by LLMs. arXiv 2024, arXiv:2406.07791. [Google Scholar] [CrossRef]
- Barredo Arrieta, A.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R. Explainable Artificial Intelligence (XAI): Concepts, Taxonomies, Opportunities and Challenges toward Responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Emirtekin, E. Large Language Model-Powered Automated Assessment: A Systematic Review. Appl. Sci. 2025, 15, 5683. [Google Scholar] [CrossRef]
- Kim, S.; Oh, D. Evaluating Creativity: Can LLMs Be Good Evaluators in Creative Writing Tasks? Appl. Sci. 2025, 15, 2971. [Google Scholar] [CrossRef]
- Cisneros-González, J.; Gordo-Herrera, N.; Barcia-Santos, I.; Sánchez-Soriano, J. JorGPT: Instructor-Aided Grading of Programming Assignments with Large Language Models (LLMs). Future Internet 2025, 17, 265. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, W.; W, X.; Zhang, D. SedarEval: Automated Evaluation using Self-Adaptive Rubrics. In Proceedings of the Findings of the Association for Computational Linguistics: EMNLP 2024, Miami, FL, USA, 12–16 November 2024; pp. 16916–16930. [Google Scholar] [CrossRef]
- Kasai, J.; Sakaguchi, K.; Dunagan, L.; Morrison, J.; Le Bras, R.; Choi, Y.; Smith, N.A. Transparent Human Evaluation for Image Captioning. In Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics (NAACL), Seattle, WA, USA, 10–15 July 2022; pp. 3464–3478. [Google Scholar] [CrossRef]
- Martin, P.P.; Kranz, D.; Graulich, N. Revealing Rubric Relations: Investigating the Interdependence of a Research Informed and a Machine Learning Based Rubric in Assessing Student Reasoning in Chemistry. Int. J. Artif. Intell. Educ. 2024, 35, 1465–1503. [Google Scholar] [CrossRef]
- Sieker, J.; Junker, S.; Utescher, R.; Attari, N.; Wersing, H.; Buschmeier, H.; Zarrieß, S. The Illusion of Competence: Evaluating the Effect of Explanations on Users’ Mental Models of Visual Question Answering Systems. In Proceedings of the 2024 Conference on Empirical Methods in Natural Language Processing (EMNLP), Miami, FL, USA, 12–16 November 2024; pp. 19459–19475. [Google Scholar] [CrossRef]
- Chaudhary, M.; Gupta, H.; Bhat, S.; Varma, V. Towards Understanding the Robustness of LLM-based Evaluations under Perturbations. arXiv 2024, arXiv:2412.09269. [Google Scholar] [CrossRef]
- Leiter, C.; Lertvittayakumjorn, P.; Fomicheva, M.; Zhao, W.; Gao, Y.; Eger, S. Towards Explainable Evaluation Metrics for Machine Translation. J. Mach. Learn. Res. 2024, 25, 3686–3734. [Google Scholar]
- Wei, J.; Wang, X.; Schuurmans, D.; Bosma, M.; Ichter, B.; Xia, F.; Chi, E.H.; Le, Q.V.; Zhou, D. Chain-of-thought prompting elicits reasoning in large language models. In Proceedings of the 36th International Conference on Neural Information Processing Systems (NIPS’22), New Orleans, LA, USA, 28 November–9 December 2022; pp. 24824–24837. [Google Scholar]
- Ziegler, D.M.; Stiennon, N.; Wu, J.; Brown, T.B.; Radford, A.; Amodei, D.; Christiano, P.; Irving, G. Fine Tuning Language Models from Human Preferences. arXiv 2019, arXiv:1909.08593. [Google Scholar] [CrossRef]
- Zhu, K.; Wang, J.; Zhou, J.; Wang, Z.; Chen, H.; Wang, Y.; Yang, L.; Ye, W.; Gong, N.Z.; Zhang, Y.; et al. PromptRobust: Towards Evaluating the Robustness of Large Language Models on Adversarial Prompts. arXiv 2023, arXiv:2306.04528. [Google Scholar] [CrossRef]
- Li, Z.; Peng, B.; He, P.; Yan, X. Evaluating the Instruction Following Robustness of Large Language Models to Prompt Injection. In Proceedings of the 2024 Conference on Empirical Methods in Natural Language Processing (EMNLP), Miami, FL, USA, 12–16 November 2024; pp. 557–568. [Google Scholar] [CrossRef]
- Turner, E.; Soligo, A.; Taylor, M.; Rajamanoharan, S.; Nanda, N. Model Organisms for Emergent Misalignment. arXiv 2025, arXiv:2506.11613. [Google Scholar] [CrossRef]
- Moradi, M.; Samwald, M. Evaluating the Robustness of Neural Language Models to Input Perturbations. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing (EMNLP 2021, Long Papers), Online and Punta Cana, Dominican Republic, 7–11 November 2021; pp. 1558–1570. [Google Scholar] [CrossRef]
- Yang, J.; Chen, D.; Sun, Y.; Li, R.; Feng, Z.; Peng, W. Enhancing Semantic Consistency of Large Language Models through Model Editing: An Interpretability Oriented Approach. In Proceedings of the Findings of the Association for Computational Linguistics (ACL 2024), Bangkok, Thailand, 11–16 August 2024; pp. 3343–3353. [Google Scholar] [CrossRef]
- Elangovan, A.; Liu, L.; Xu, L.; Bodapati, S.B.; Roth, D. ConSiDERS-The-Human Evaluation Framework: Rethinking Human Evaluation for Generative Large Language Models. In Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics, Bangkok, Thailand, 11–16 August 2024; pp. 1137–1160. Available online: https://aclanthology.org/2024.acl-long.63/ (accessed on 31 July 2025).
- Ferdaus, M.M.; Abdelguerfi, M.; Ioup, E.; Niles, K.; Pathak, K.; Sloan, S. Towards Trustworthy AI: A Review of Ethical and Robust Large Language Models. arXiv 2024, arXiv:2407.13934. [Google Scholar] [CrossRef]
- Choudhury, A.; Chaudhry, Z. Large Language Models and User Trust: Consequence of Self-Referential Learning Loop and the Deskilling of Health Care Professionals. J. Med. Internet Res. 2024, 26, e56764. [Google Scholar] [CrossRef]
- Starke, G.; Gille, F.; Termine, A.; Aquino, Y.S.J.; Chavarriaga, R.; Ferrario, A.; Hastings, J.; Jongsma, K.; Kellmeyer, P.; Kulynych, B.; et al. Finding Consensus on Trust in AI in Health Care: Recommendations From a Panel of International Experts. J. Med. Internet Res. 2024, 27, e56306. [Google Scholar] [CrossRef]
- Zhen, H.; Shi, Y.; Huang, Y.; Yang, J.J.; Liu, N. Leveraging Large Language Models with Chain-of-Thought and Prompt Engineering for Traffic Crash Severity Analysis and Inference. Computers 2024, 13, 232. [Google Scholar] [CrossRef]
- Panadero, E.; Jonsson, A.; Pinedo, L.; Fernández-Castilla, B. Effects of Rubrics on Academic Performance, Self-Regulated Learning, and self-Efficacy: A Meta-analytic Review. Educ. Psychol. Rev. 2023, 35, 113. [Google Scholar] [CrossRef]
- Anghel, C.; Anghel, A.A.; Pecheanu, E.; Susnea, I.; Cocu, A.; Istrate, A. Multi-Model Dialectical Evaluation of LLM Reasoning Chains: A Structured Framework with Dual Scoring Agents. Informatics 2025, 12, 76. [Google Scholar] [CrossRef]
- Anghel, C.; Anghel, A.A.; Pecheanu, E.; Cocu, A.; Istrate, A. Diagnosing Bias and Instability in LLM Evaluation: A Scalable Pairwise Meta-Evaluator. Information 2025, 16, 652. [Google Scholar] [CrossRef]
- Melo, E.; Silva, I.; Costa, D.G.; Viegas, C.M.D.; Barros, T.M. On the Use of eXplainable Artificial Intelligence to Evaluate School Dropout. Educ. Sci. 2022, 12, 845. [Google Scholar] [CrossRef]
- Díaz, G.M. Supporting Reflective AI Use in Education: A Fuzzy-Explainable Model for Identifying Cognitive Risk Profiles. Educ. Sci. 2025, 15, 923. [Google Scholar] [CrossRef]
- Pan, Y.; Nehm, R.H. Large Language Model and Traditional Machine Learning Scoring of Evolutionary Explanations: Benefits and Drawbacks. Educ. Sci. 2025, 15, 676. [Google Scholar] [CrossRef]
- Dipper, L.; Marshall, J.; Boyle, M.; Hersh, D.; Botting, N.; Cruice, M. Creating a Theoretical Framework to Underpin Discourse Assessment and Intervention in Aphasia. Brain Sci. 2021, 11, 183. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Wu, X.; Wen, J.; Huang, C.; Luo, M.; Liu, L.; Zheng, Y. Evaluating Familiarity Ratings of Domain Concepts with Interpretable Machine Learning: A Comparative Study. Appl. Sci. 2023, 13, 2818. [Google Scholar] [CrossRef]
- Prentzas, J.; Binopoulou, A. Explainable Artificial Intelligence Approaches in Primary Education: A Review. Electronics 2025, 14, 2279. [Google Scholar] [CrossRef]
- Fernandes, P.; Treviso, M.V.; Pruthi, D.; Martins, A.F.T.; Neubig, G. Learning to Scaffold: Optimizing Model Explanations for Teaching. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS) 2022, New Orleans, LA, USA, 28 November–9 December 2022; Available online: https://papers.neurips.cc/paper_files/paper/2022/file/ea64883d500d31738cd39eb49a748fa4-Paper-Conference.pdf (accessed on 31 July 2025).
- Rizzo, L.; Verda, D.; Berretta, S.; Longo, L. A Novel Integration of Data-Driven Rule Generation and Computational Argumentation for Enhanced Explainable AI. Mach. Learn. Knowl. Extr. 2024, 6, 2049–2073. [Google Scholar] [CrossRef]
- Maine, F. Building the Foundations of Dialogic Pedagogy with Five- and Six-Year-Olds. Educ. Sci. 2025, 15, 251. [Google Scholar] [CrossRef]
- Leidinger, A.; van Rooij, R.; Shutova, E. The language of prompting: What linguistic properties make a prompt successful? arXiv 2023, arXiv:2311.01967. [Google Scholar] [CrossRef]
- Gozzi, M.; Di Maio, F. Comparative Analysis of Prompt Strategies for Large Language Models: Single-Task vs. Multitask Prompts. Electronics 2024, 13, 4712. [Google Scholar] [CrossRef]
- Hackl, V.; Krainz, A.; Bock, A. Is GPT-4 a Reliable Rater? Evaluating Consistency in GPT-4’s Text Ratings. Front. Educ. 2023, 8, 1272229. [Google Scholar] [CrossRef]
- Chen, Z.; Wan, T. Grading Explanations of Problem-Solving Process and Generating Feedback Using Large Language Models at Human-Level Accuracy. Phys. Rev. Phys. Educ. Res. 2025, 21, 010126. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).