Data-Driven Event-Triggering Control of Discrete Time-Delay Systems
Abstract
1. Introduction
2. Problem Formulation
2.1. Basic Assumptions for Data-Driven Control Method
2.2. Basic Assumptions and Forms of Event-Triggering Schemes
2.3. Discussion of Dynamic Event-Triggered Parameters
2.3.1. The Influence of
2.3.2. The Influence of
3. Data-Driven Analysis and Controller Design
3.1. Controller Synthesis for Known Time-Delay System
3.2. Controller Synthesis for Unknown Time-Delay System
| Algorithm 1 Controller Design Using Augmented Matrix |
|
| Algorithm 2 Controller Design Using Time-Delay Limit |
|
4. Examples and Simulations
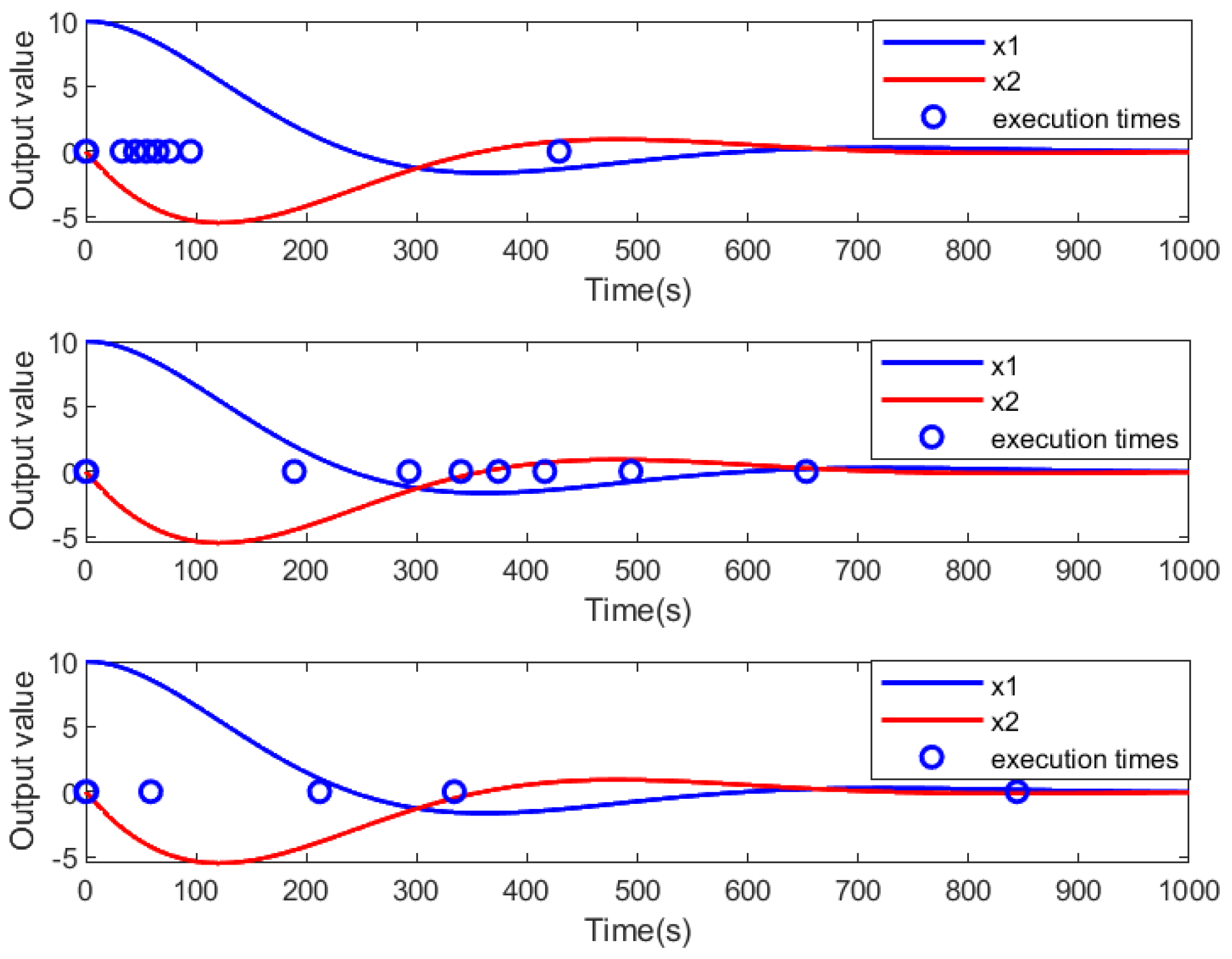
4.1. Numerical Verify for Results of Known Time-Delay System
4.2. Numerical Verify for Results of Unknown Time-Delay System
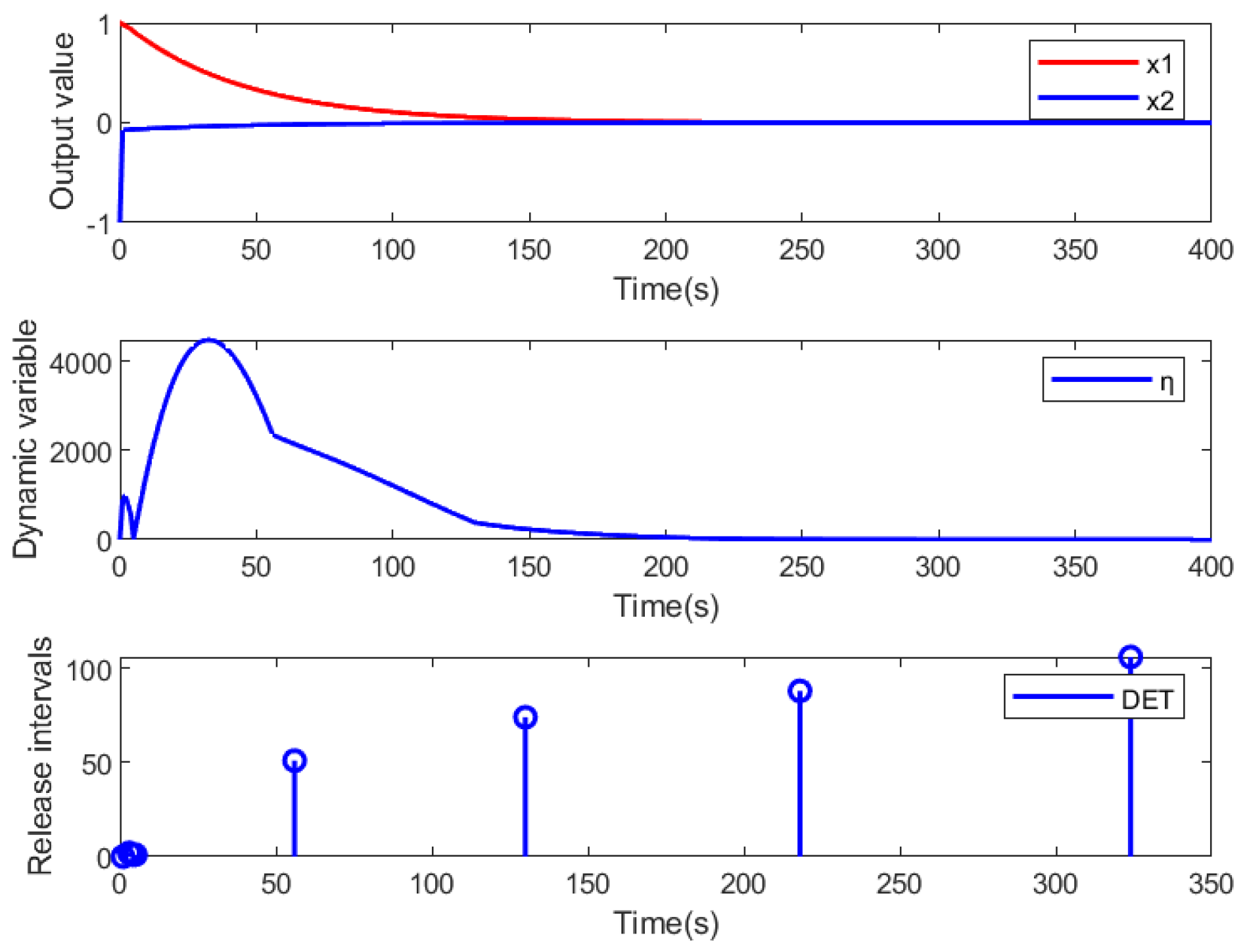
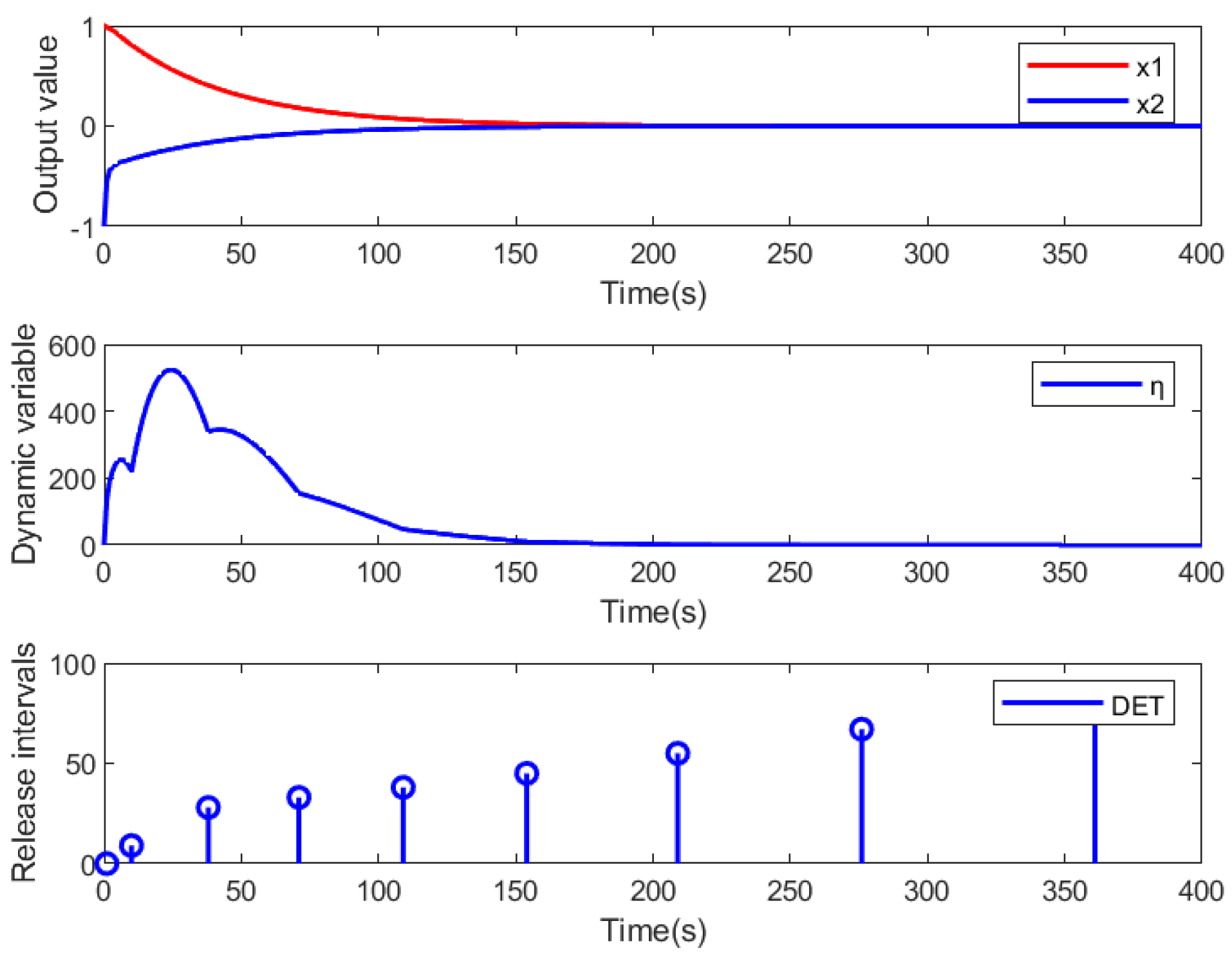
4.3. Dynamic Event-Triggering Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van Overschee, P.; De Moor, B. Subspace Identification for Linear Systems: Theory, Implementation, Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. Am. Soc. Mech. Eng. 1942, 64, 759–765. [Google Scholar] [CrossRef]
- Willems, J.C.; Rapisarda, P.; Markovsky, I.; De Moor, B.L. A note on persistency of excitation. Syst. Control Lett. 2005, 54, 325–329. [Google Scholar] [CrossRef]
- Markovsky, I.; Rapisarda, P. Data-driven simulation and control. Int. J. Control 2008, 81, 1946–1959. [Google Scholar] [CrossRef]
- Park, U.S.; Ikeda, M. Stability analysis and control design of lti discrete-time systems by the direct use of time series data. Automatica 2009, 45, 1265–1271. [Google Scholar] [CrossRef]
- Maupong, T.M.; Rapisarda, P. Data-driven control: A behavioral approach. Syst. Control Lett. 2017, 101, 37–43. [Google Scholar] [CrossRef]
- Safonov, M.G.; Tsao, T.-C. The unfalsified control concept: A direct path from experiment to controller. In Feedback Control, Nonlinear Systems, and Complexity; Springer: Berlin/Heidelberg, Germany, 1995; pp. 196–214. [Google Scholar]
- Hjalmarsson, H.; Gevers, M.; Gunnarsson, S.; Lequin, O. Iterative feedback tuning: Theory and applications. IEEE Control Syst. Mag. 1998, 18, 26–41. [Google Scholar]
- Shangtai, H.Z.J. Data-driven model-free adaptive control for a class of mimo nonlinear discrete-time systems. IEEE Trans. Neural Netw. 2011, 22, 2173–2188. [Google Scholar]
- Wu, A.-G.; Meng, Y. Data-driven adaptive optimal control for discrete-time linear time-invariant systems. Int. J. Syst. Sci. 2024, 55, 3069–3082. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G.; Lewis, F.L. Online actor–critic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica 2010, 46, 878–888. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, Z.-P. Computational adaptive optimal control for continuous-time linear systems with completely unknown dynamics. Automatica 2012, 48, 2699–2704. [Google Scholar] [CrossRef]
- Salvador, J.R.; de la Peña, D.M.; Alamo, T.; Bemporad, A. Data-based predictive control via direct weight optimization. IFAC-PapersOnLine 2018, 51, 356–361. [Google Scholar] [CrossRef]
- Li, Z.; Liu, K.; Wang, X.; Yuan, X.; Wang, Y. Efficient data-driven event-triggered predictive control for cyber-physical systems. J. Control Decis. 2024, 1–10. [Google Scholar] [CrossRef]
- Dai, T.; Sznaier, M. A moments based approach to designing mimo data driven controllers for switched systems. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 5652–5657. [Google Scholar]
- Tabuada, P. Event-triggered real-time scheduling of stabilizing control tasks. IEEE Trans. Autom. Control 2007, 52, 1680–1685. [Google Scholar] [CrossRef]
- Girard, A. Dynamic triggering mechanisms for event-triggered control. IEEE Trans. Autom. Control 2014, 60, 1992–1997. [Google Scholar] [CrossRef]
- Yi, X.; Liu, K.; Dimarogonas, D.V.; Johansson, K.H. Dynamic event-triggered and self-triggered control for multi-agent systems. IEEE Trans. Autom. Control 2018, 64, 3300–3307. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, H.; Liu, Y.; Tan, H. Dynamic event-triggered state estimation for discrete-time delayed switched neural networks with constrained bit rate. Syst. Sci. Control. Eng. 2024, 12, 2334304. [Google Scholar] [CrossRef]
- Li, Q.; Shen, B.; Wang, Z.; Huang, T.; Luo, J. Synchronization control for a class of discrete time-delay complex dynamical networks: A dynamic event-triggered approach. IEEE Trans. Cybern. 2018, 49, 1979–1986. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Yan, H.; Wang, Y.; Li, Z.; Wang, M. Fixed time cluster consensus for nonlinear multiagent systems by double dynamic event-triggered mechanisms. Int. J. Syst. Sci. 2024, 55, 3322–3336. [Google Scholar] [CrossRef]
- Wang, X.; Berberich, J.; Sun, J.; Wang, G.; Allgöwer, F.; Chen, J. Model-based and data-driven control of event-and self-triggered discrete-time linear systems. IEEE Trans. Cybern. 2023, 53, 6066–6079. [Google Scholar] [CrossRef] [PubMed]


| Symbol | Parameters |
|---|---|
| Time delay | |
| Threshold Parameter | |
| Decay Factor | |
| Weighting Parameter | |
| Augmented System Matrix | |
| Augmented Input Matrix | |
| and | Square Matrix |
| Pseudoinverse matrix of | |
| Pseudoinverse matrix of |
| Time Delay () | 2 | 5 | 10 | 15 | 20 |
|---|---|---|---|---|---|
| Theorem 1 | 0.30 s | 7.25 s | 110.95 s | 568.33 s | 1965.89 s |
| Theorem 2 (h = 50) | 0.06 s | 0.07 s | 0.07 s | 0.07 s | 0.07 s |
| Parametric | |||||
|---|---|---|---|---|---|
| = 0.97 | 13 | 9 | 11 | 12 | 12 |
| = 0.8 | 19 | 19 | 17 | 16 | 16 |
| = 0.6 | 19 | 19 | 18 | 18 | 18 |
| = 0.4 | 19 | 19 | 19 | 19 | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Y.; Li, Z.; Wang, Y. Data-Driven Event-Triggering Control of Discrete Time-Delay Systems. Information 2025, 16, 893. https://doi.org/10.3390/info16100893
Gong Y, Li Z, Wang Y. Data-Driven Event-Triggering Control of Discrete Time-Delay Systems. Information. 2025; 16(10):893. https://doi.org/10.3390/info16100893
Chicago/Turabian StyleGong, Yifan, Zhicheng Li, and Yang Wang. 2025. "Data-Driven Event-Triggering Control of Discrete Time-Delay Systems" Information 16, no. 10: 893. https://doi.org/10.3390/info16100893
APA StyleGong, Y., Li, Z., & Wang, Y. (2025). Data-Driven Event-Triggering Control of Discrete Time-Delay Systems. Information, 16(10), 893. https://doi.org/10.3390/info16100893





