Cross-Domain Residual Learning for Shared Representation Discovery

Abstract

In order to solve the problem of inconsistent data distribution in machine learning, domain adaptation based on feature representation methods extracts features from the source domain, and transfers them to the target domain for classification. The existing feature representation-based methods mainly solve the problem of inconsistent feature distribution between the source domain data and the target domain data, but only a few methods analyze the correlation of cross-domain features between the original space and shared latent space, which reduces the performance of domain adaptation. To this end, we propose a domain adaptation method with a residual module, the main ideas of which are as follows: (1) transfer the source domain data features to the target domain data through the shared latent space to achieve features sharing; (2) build a cross-domain residual learning model using the latent feature space as the residual connection of the original feature space, which improves the propagation efficiency of features; (3) use a regular feature space to sparse feature representation, which can improve the robustness of the model; and (4) give an optimization algorithm, and the experiments on the public visual datasets (Office31, Office-Caltech, Office-Home, PIE, MNIST-UPS, COIL20) results show that our method achieved 92.7% accuracy on Office-Caltech and 83.2% on PIE and achieved the highest recognition accuracy in three datasets, which verify the effectiveness of the method.

1. Introduction

In machine learning, it is necessary to have complete and sufficient training data for parameter tuning to achieve good performance. Therefore, the amount of data and the distribution of data features become an important factor. Traditional machine learning assumes that the training data and test data satisfy the condition of being independent and identically distributed. Under this assumption, most models work well. However, in practical applications, it is usually difficult to obtain a large amount of annotated data for a specific task, and data annotation is time-consuming and laborious, which leads to insufficient data in machine learning models. Moreover, there is a problem of inconsistent distribution of data between different data domains, which is called sample selection bias [1] or covariance displacement [2,3]. The above issues will reduce the robustness and reliability of traditional machine learning models, leading to a decrease in the performance of the model.

To avoid repetitive data annotation and improve the performance of the model, currently, domain adaptation (DA) methods that can achieve knowledge transfer between different domains, solving the problems of different data distributions and lack of train data in different domains effectively [4,5,6]. Domain adaptation can be mainly divided into instance-based methods, feature representation-based methods, and classifier-based methods. This paper focuses on the feature representation-based methods, which assumes that the relevant domain data has shared implicit features [7]. That is, the marginal distribution between data in different domains is matched [8]. Then, feature space information is used to align the domain data in the feature space in a mapping way to find the shared features between different domains. Therefore, a reliable machine learning model can be constructed using source domain data with sufficient labels [9]. By transferring source and target domain data features, common features between different domain data are utilized to expand the features of target domain data, reducing the strict constraint requirements of the model on data and improving the performance of the model [10].

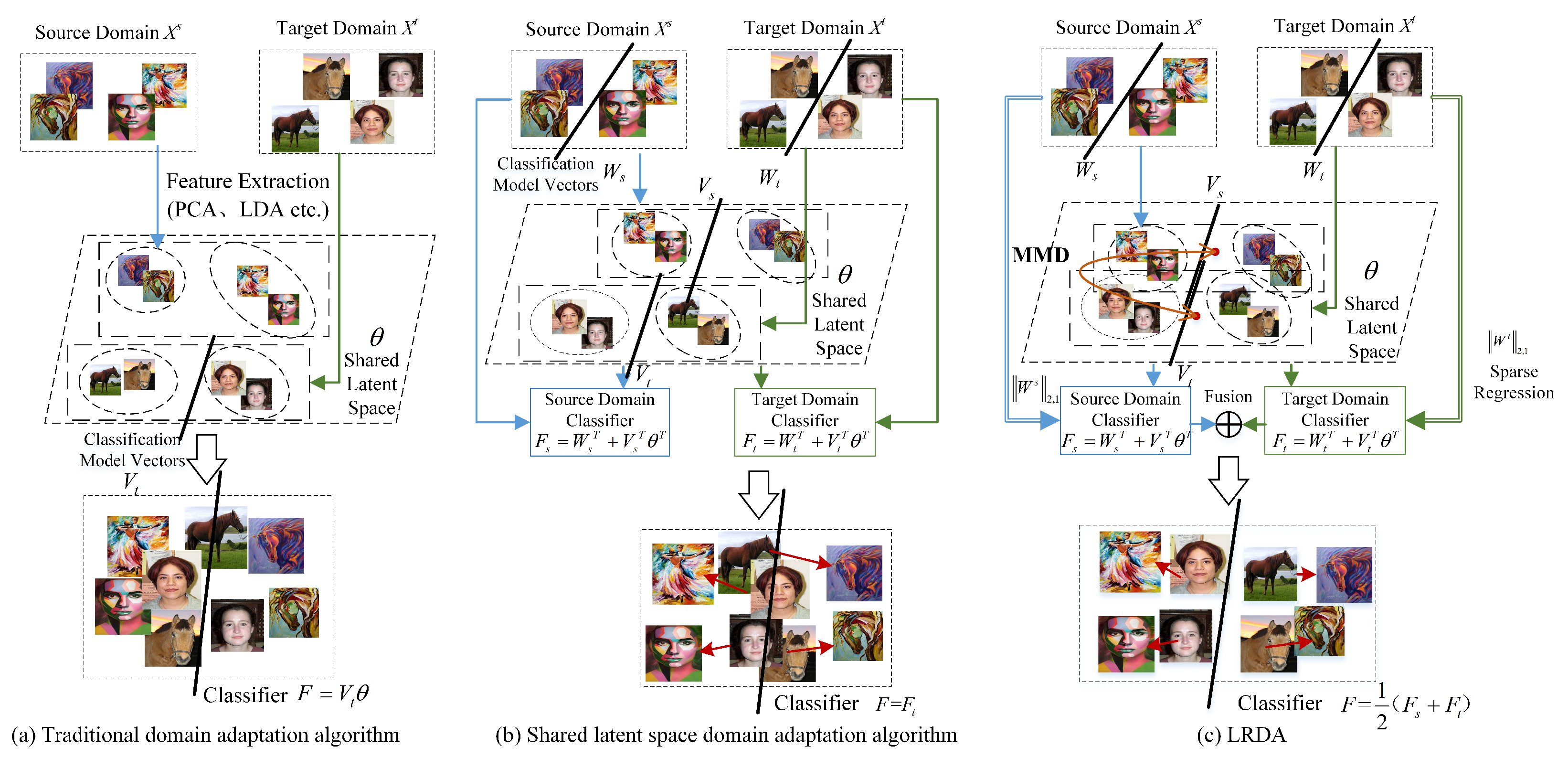
The initial domain adaptation methods based on feature representation use feature representation methods to transform source domain data and target domain data into latent space, and construct a classifier through the latent feature representation of the target domain. The principle of these methods is summarized in Figure 1a, which employs feature extraction to construct a feature invariant latent space and then design a classifier for the target domain [11]. Gheisari et al. [12] demonstrated that minimizing classification error while maximizing manifold consistency in a shared space led to improved classification accuracy on target domains compared to non-adaptive baselines. Zheng et al. [13] showed that finding a dimensionality reduction technique minimizing distribution distance in the latent space effectively enabled feature transfer, resulting in measurable performance gains. Blitzer et al. [14] established that modeling feature correlations across domains via structural correspondence learning identified pivot features crucial for cross-domain discrimination, enhancing adaptation robustness. Jiang et al. [15] extended this concept effectively to multi-view data, showing that incorporating latent space features across views significantly addressed the unique challenges posed by multi-perspective domain differences. Xu et al. [16] leveraged distributionally robust optimization for feature extraction under weak supervision, demonstrating enhanced robustness to distributional uncertainties and achieving competitive results.

Later methods incorporate the original space information, which can guide target domain classifier construction by combining it with latent space features. This joint information is then utilized to build the classifier [17,18], as shown in Figure 1b. Dong et al. [19] proved that embedding a shared low-dimensional latent space into an SVM (support vector machine) framework, constrained by source-target latent space alignment, substantially improved SVM performance in domain adaptation tasks compared to standard SVMs. Yao et al. [20] successfully expanded this concept to the more complex multi-source adaptation scenario, showing that constraining the predicted label matrix across sources further enhanced adaptation effectiveness and robustness. Zhang et al. [21] demonstrated that combining latent space features with target pseudo-labels effectively mined richer domain-invariant information, yielding state-of-the-art results on several benchmarks. However, the above methods do not consider the distribution of latent space features from the perspective of distribution consistency, and the differences in distribution will reduce the effectiveness of shared features, thereby reducing the performance of domain adaptation.

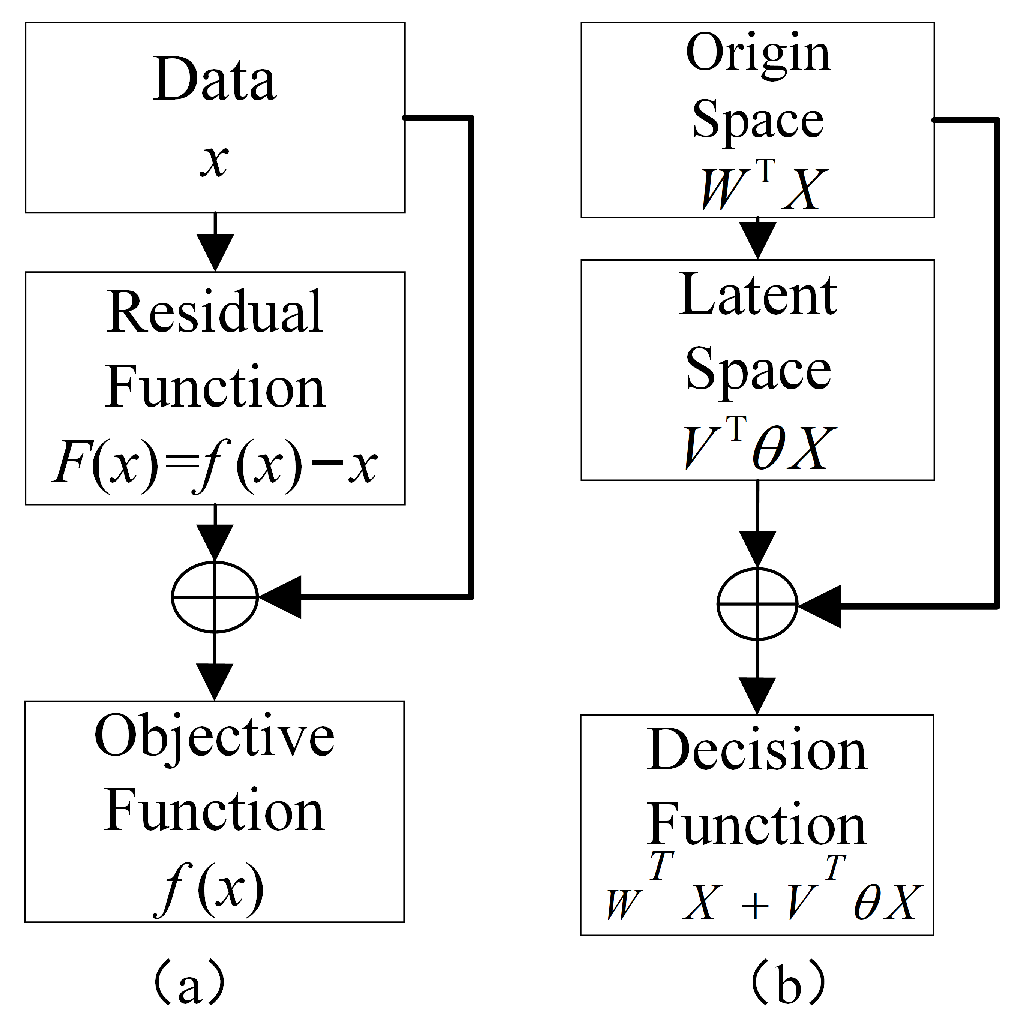
Inspired by Residual Network [22], we propose a shared latent space domain adaptation with residual model (LRDA) to make full use of the relationship between original feature and latent space feature in domains, and address the problem of mismatched distribution of latent space features in domain adaptation. Specifically, mapping the source and target domain data into a shared latent feature space, mining common features between source and target domains, to achieve the goal of fully utilizing the source domain data to enhance the feature expression of the target domain data. Subsequently, minimizing the distribution differences between the shared feature space of the source and target domain, ensuring latent space features have a more consistent feature distribution, and reducing model performance degradation caused by inconsistent feature distribution. Finally, by combining the original spatial features with the the latent space features in both source and target domain, a residual model is formed to reduce the difficulty of fitting the model and obtain a better classifier. Following the above description, the principle of LRDA is shown in Figure 1c.

The main contributions of this paper are:

1.

We introduce a shared latent space by source domain feature and target domain feature, constructing a latent space domain adaptation method. Measuring the differences in latent space feature distribution, further constraining the consistent distribution of shared feature spaces in the domain to align the feature distribution in the shared latent space.

2.

We build a residual model using the original feature space and latent feature space, optimizing residual function to reduce the difficulty of feature transfer and improve model performance.

3.

We adopt the $l_{2,1}$-norm for feature selection to sparsely represent the original feature, increasing the robustness of the model for outliers and noise naturally existing in dataset.

4.

Experiments verify that our method has better performance and can effectively recognize shallow and deep features, effectively improve the performance of cross-domain visual recognition tasks.

2. LRDA

2.1. Notation & Definition

We denote with small and capital letters respectively column vectors and matrices. We denote $X^s=\left[x_1^s,x_2^s,\dots ,x_{n_s}^s\right]\in {\mathbb{R}}^{d\times n_s}$ is the matrix of source domain data $x_i^s$, where d means d-dimension feature and $n_s$ is the number of source domain samples. We denote $Y^s=\left[y_1^s,y_2^s,\dots ,y_{n_s}^s\right]\in {\mathbb{R}}^{n_s\times c}$ is source domain label matrix, where $y_i^s={\{0,1\}}^{1\times c}$ is one-hot label for source domain data, and c is the number of categories. Source domain is denoted as $D_s=\left\{\left(x_i^s,y_i^s\right)\in X^s\times Y^s:i=1,2,\dots ,n_s\right\}$. In the same way, given $D_t=\left\{\left(x_j^t,y_j^t\right)\in X^t\times Y^t:j=1,2,\dots ,n_t\right\}$ as target domain, $X^t=\left[x_1^t,x_2^t,\dots ,x_{n_t}^t\right]\in {\mathbb{R}}^{d\times n_t}$ and $Y^t=\left[y_1^t,y_2^t,\dots ,y_{n_t}^t\right]\in {\mathbb{R}}^{n_t\times c}$ as target domain data matrix and target domain label matrix respectively. It is worth noting that the target domain data usually lacks complete label, but source and target domains share the same c-cardinality label set.

Assuming the distribution of the data is known, then the marginal probability distribution of the source domain data and the target domain data can be represented by $\mathcal{P}\left(X^s\right)$ and $\mathcal{Q}\left(X^t\right)$ respectively. The goal of domain adaptation is to design a robust model that can predict the labels of target domain data using samples from the source domain. As a matter of fact, $D_s$ and $D_t$ are neither identical nor uncorrelated, so their edge probability distributions are different. For domain adaptation problems, the source domain data and target domain data come from different domains. Therefore, it is assumed that $\mathcal{P}\left(X^s\right)\ne \mathcal{Q}\left(X^t\right)$. However, the distribution of category conditions for the source and target domain data is consistent, i.e., $\mathcal{P}\left(X^s\right|Y^s)=\mathcal{Q}\left(X^t\right|Y^t)$.

2.2. Formulation of LRDA

We design an objective function for latent space residual domain adaptation, which can simultaneously achieve the following goals: (1) finding a shared latent space to ensure that there are more common feature between the source domain data and the target domain data; (2) regularization the models of source domain and target domain to reduce the complexity of model structure; and (3) constraining in the latent space, the distribution of the source and target domains is consistent. Due to the lack of sufficient label in the target domain, we denote a label matrix $F=\left[f_1^t,f_2^t,\dots ,f_{n_t}^t\right]\in {\mathbb{R}}^{n_t\times c}$ corresponding to the target domain samples $X^t$. If the sample has a label, set $f_i^t=y_i^t$; otherwise $f_i^t$ is a pseudo label. Therefore, we can express our model using the following objective functions:

$$\begin{array}{cc}R\hfill & =\alpha \left(L\left(f_s\left(X^s\right),Y^s\right)+L\left(f_t\left(X^t\right),F\right)\right)\hfill \\ \hfill & +\beta \left({\Omega }_r\left(f_s\right)+{\Omega }_r\left(f_t\right)\right)\hfill \\ \hfill & +\gamma {\Omega }_d(X^s,X^t),\hfill \end{array}$$

(1)

where $f_s$ and $f_t$ are source and target domain classifiers, respectively. $L(·)$ comprises regression losses in the source and target domains. ${\Omega }_r$ is the regularization term of the source domain and the target domain to reduce the generalization error of model. ${\Omega }_d$ is used to align the distribution of data between the source and target domains. $\alpha$, $\beta$, $\gamma$ are regularization hyper parameter to adjust the weight.

Definition 1

(Residual model). Assuming data is x, the objective function of the residual model can be expressed as $f\left(x\right)=x+F\left(x\right)$, where $F\left(x\right)=f\left(x\right)-x$ is residual function. The structure of the residual model is shown in Figure 2a.

Ref. [22] proved that it is less difficult to optimize residuals $F\left(x\right)$ than optimization functions $f\left(x\right)$. Therefore, the objective function can be transformed into the following: let model $F\left(x\right)$ approximate the residual function $f\left(x\right)-x$ and use $x+F\left(x\right)$ to express the objective function.

Inspired by the residual model, we use the feature of the source and target domains to construct a shared latent feature space to constrain the classifier to integrate the common feature of the source and target domain. The latent feature space and the original feature space are constructed as a residual model, reducing the difficulty of fitting the model and improving the performance, as shown in Figure 2b. Specifically, the classifier of the shared feature space consists of two parts: the decision function of the original data and the decision function of the shared feature, which can be represented as follows:

$$\begin{array}{c}{f}_s\left(X^s\right)={W_s}^T{X}^s+V_s^T{\theta }^T{X}^s\hfill \\ f_t\left(X^t\right)={W_t}^T{X}^t+V_t^T{\theta }^T{X}^t,\hfill \end{array}$$

(2)

where $W_s$ and $W_t$ are the classification model vectors of the source domain and the target domain in the original space. $\theta \in {\mathbb{R}}^{r\times d}$ comprises shared latent spatial transformation matrices used to map the source domain and the target domain to the same feature space. r is the dimension of the shared feature space, $V_s$ and $V_t$ are the classification model vectors of $\theta X^s$ and $\mathit{\theta }{X}^t$, respectively. The source domain and target domain information are shared by $\mathit{\theta }$.

Then the regression loss of the residual model classifier is:

$$\begin{array}{c}\hfill L\left(f_s\left(X^s\right),Y^s\right)={∥{W_s}^T{X}^s+V_s^T{\mathit{\theta }}^T{X}^s-Y^s∥}^2\\ \hfill L\left(f_t\left(X^t\right),F\right)={∥{W_t}^T{X}^t+V_t^T{\mathit{\theta }}^T{X}^s-F∥}^2.\end{array}$$

(3)

In order to improve the robustness of the model, we conduct sparse regression on the feature extracted from the source domain and the target domain [23]. We use $l_{2,1}$-norms [24] to sparse the classification model vectors of the original space to obtain the function of ${\Omega }_r$:

$$\begin{array}{c}{\Omega }_r\left(f_s\right)={∥W_s∥}_{2,1}+{∥W_s+\mathit{\theta }{V}_s∥}^2\hfill \\ {\Omega }_r\left(f_t\right)={∥W_t∥}_{2,1}+{∥W_t+\mathit{\theta }{V}_t∥}^2.\hfill \end{array}$$

(4)

Due to the source and target domain commonly being $\mathcal{P}\left(X^s\right)\ne \mathcal{Q}\left(X^t\right)$, that is, inconsistent distribution between source and target domain. If simply applying a source domain classifier to target domain, it may lead to deterioration of model performance due to misaligned domain distribution. How to minimize the distribution gap between different domains is a key issue for DA. Therefore, we use the MMD (maximum mean discrepancy) [25] to calculate the average vector distance of data in the reproducing kernel Hilbert space, so as to measure the distribution difference between different domains. Therefore, minimizing Equation (5) can align the feature distribution differences in the shared space, and the transformed source and target domains have common latent space distribution feature:

$$\begin{array}{cc}\hfill {\Omega }_d(X^s,X^t)& ={∥{\displaystyle \frac{1}{n_s}}{\mathit{\theta }}^T{X}^s-{\displaystyle \frac{1}{n_t}}{\mathit{\theta }}^T{X}^t∥}^2\hfill \\ \hfill & =tr({\mathit{\theta }}^{T}XD{X}^T\mathit{\theta })\hfill \\ \hfill \mathrm{s}.\mathrm{t}.{\mathit{\theta }}^T\mathit{\theta }& =I_{r\times r},\hfill \end{array}$$

(5)

where $D_{i,j}=\left\{\begin{array}{c}\begin{array}{ccc}{\displaystyle \frac{1}{n_s^2}},& when& x_i,x_j\in X^s\end{array}\\ \begin{array}{ccc}{\displaystyle \frac{1}{n_t^2}},& when& x_i,x_j\in X^t\end{array}\\ {\displaystyle \frac{-1}{n_s{n}_t}},\hspace{1em}others\hfill \end{array}\right.$, $X=[X^s,X^t]$, r is the dimension of the shared hidden space according to matrix theory. By minimizing Equation (5), the feature in latent space has a similarly distribution, also ensuring both discriminant and domain invariance of the model.

2.3. Final Formulation

In summary, we propose a latent space domain adaptation with residual model. The algorithm schematic is shown in Figure 1c. Combining Equations (3)–(5), the objective function is as follows:

$$\begin{array}{cc}\hfill R_1=& arg\underset{W_s,W_t,V_s,V_t,F,\mathit{\theta }}{min}\hfill \\ \hfill +& \alpha \left({∥{X^s}^T{W}_s+X^{sT}{V}_s\mathit{\theta }-Y^s∥}^2\right.\hfill \\ \hfill +& \left.{∥{X^s}^T{W}_t+X^{sT}{V}_t\mathit{\theta }-F∥}^2\right)\hfill \\ \hfill +& \beta \left({∥W_s∥}_{2,1}+{∥W_t∥}_{2,1}\right.\hfill \\ \hfill +& \left.{∥W_s+\mathit{\theta }{V}_s∥}^2+{∥W_t+\mathit{\theta }{V}_t∥}^2\right)\hfill \\ \hfill +& \gamma tr({\mathit{\theta }}^{T}XD{X}^T\mathit{\theta }).\hfill \\ \hfill \mathrm{s}.\mathrm{t}.{\mathit{\theta }}^T\mathit{\theta }=& I_{r\times r}\hfill \\ \hfill F{F}^T=& I_{r\times r}\hfill \end{array}$$

(6)

The objective function is solved by minimize the $W_s$, $W_t$, $V_s$, $V_t$, F and $\mathit{\theta }$, and we apply these parameters to the decision functions $f_s\left(X^s\right)$ and $f_t\left(X^t\right)$. Thus we fuse decision functions linearly as final decision functions:

$$\begin{array}{c}\hfill m=\underset{m}{max}{\left(y_i^t=\phi f^s\left(x_i^t\right)+(1-\phi )f^t\left(x_i^t\right)\right)}_m.\end{array}$$

(7)

where $\phi \in \left[0,1\right]$ is hyper parameter to adjust the weight between source and the target domain classifiers. To simplify, we set $\phi =0.5$.

For the convenience of subsequent solutions, this paper converts Equation (6) to

$$\begin{array}{cc}\hfill R_2=& arg\underset{U_s,U_t,V_s,V_t,F,\mathit{\theta }}{min}\hfill \\ \hfill +& \alpha \left({∥{X^s}^T{U}_s-Y^s∥}^2+{∥{X^t}^T{U}_t-F∥}^2\right)\hfill \\ \hfill +& \beta \left({∥U_s∥}^2+{∥U_t∥}^2\right.\hfill \\ \hfill +& \left.{∥U_s-\mathit{\theta }{V}_s∥}_{2,1}+{∥U_t-\mathit{\theta }{V}_t∥}_{2,1}\right)\hfill \\ \hfill +& \gamma tr({\mathit{\theta }}^{T}XD{X}^T\mathit{\theta }),\hfill \end{array}$$

(8)

where $U_s=W_s+\mathit{\theta }{V}_s$, $U_t=W_t+\mathit{\theta }{V}_t$, are auxiliary variables for simplify the calculation.

3. Optimization Algorithm

To facilitate optimization, we refer to parameter alternation optimization methods in fuzzy clustering; we divide six variables into four groups, namely {$U_s$, $U_t$}, {$V_s$, $V_t$}, {F}, and {$\mathit{\theta }$}. We iteratively optimize these sets of parameters until the variables converge or the objective function is less than the threshold. Next, we optimize each part of the functions in Equation (8).

3.1. Optimization Procedure

3.1.1. Optimize $V_s$, $V_t$ by Fixing $U_s$, $U_t$, F and $\mathit{\theta }$

When $V_s={\mathit{\theta }}^T{U}_s$ and $V_t={\mathit{\theta }}^T{U}_t$, the objective function $R_2$ can obtain the minimum value regarding the variable $V_s$ and $V_s$.

Proof. 

Assuming that the variables $U_s$, $U_t$, F and $\mathit{\theta }$ are known, Equation (8) can be transformed into:

$$\begin{array}{c}\hfill R_3=arg\underset{V_s,V_t}{min}\beta \left.\left({∥U_s-\mathit{\theta }{V}_s∥}_{2,1}+{∥U_t-\mathit{\theta }{V}_t∥}_{2,1}\right.\right).\end{array}$$

(9)

Let:

$$\begin{array}{c}\hfill L_1=arg\underset{V_s}{min}\beta tr\left({\left(U_s-\mathit{\theta }{V}_s\right)}^T{M}_s\left(U_s-\mathit{\theta }{V}_s\right)\right),\\ \hfill L_2=arg\underset{V_t}{min}\beta tr\left({\left(U_t-\mathit{\theta }{V}_t\right)}^T{M}_t\left(U_t-\mathit{\theta }{V}_t\right)\right).\end{array}$$

(10)

In terms of the definition in Nie et al. [26], for matrix $A\in R^{n\times d}$, we can derive ${∥A∥}_{2,1}=2tr\left(A^{T}MA\right)$, where $M_{ii}={\displaystyle \frac{1}{2{∥A_{i,:}∥}_2}}$. By solving the derivative of Equation (10) w.r.t. $V_s$, $V_t$ and letting it equal to zero:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial L_1}{\partial V_s}}=0\Rightarrow V_s={\mathit{\theta }}^T{U}_s,\\ \hfill {\displaystyle \frac{\partial L_2}{\partial V_t}}=0\Rightarrow V_t={\mathit{\theta }}^T{U}_t.\end{array}$$

(11)

   □

3.1.2. Optimize $U_s$, $U_t$ by Fixing $V_s$, $V_t$, F and $\mathit{\theta }$

After obtaining the optimal value obtained from Section 3.1.1, when $U_s={A_s}^{-1}{B}_s$ and $U_t={A_t}^{-1}{B}_t$, the objective function $R_2$ can obtain the minimum value regarding the variable $U_s$ and $U_s$.

Proof. 

It is obvious that Equation (8) with fixed $V_s$, $V_t$, F and $\mathit{\theta }$ is equivalent to

$$\begin{array}{cc}\hfill R_4=& arg\underset{U_s,U_t}{min}\hfill \\ \hfill +& \alpha \left({∥{X^s}^T{U}_s-Y^s∥}^2+{∥{X^t}^T{U}_t-F∥}^2\right)\hfill \\ \hfill +& \beta \left({∥U_s∥}^2+{∥U_t∥}^2\right.\hfill \\ \hfill +& \left.{∥U_s-\mathit{\theta }{V}_s∥}_{2,1}+{∥U_t-\mathit{\theta }{V}_t∥}_{2,1}\right).\hfill \end{array}$$

(12)

Let

$$\begin{array}{cc}\hfill L_3=& arg\underset{U_s}{min}\alpha \left({∥{X^s}^T{U}_s-Y^s∥}^2\right)\hfill \\ \hfill +& \beta \left({∥U_s∥}^2+{∥U_s-\mathit{\theta }{V}_s∥}_{2,1}\right),\hfill \\ \hfill L_4=& arg\underset{U_t}{min}\alpha \left({∥{X^t}^T{U}_t-F∥}^2\right)\hfill \\ \hfill +& \beta \left({∥U_t∥}^2+{∥U_t-\mathit{\theta }{V}_t∥}_{2,1}\right).\hfill \end{array}$$

(13)

by solving the derivative of Equation (13) w.r.t. $V_s$, $V_t$ and letting it equal zero. We have

$$\begin{array}{c}\hfill U_s={A_s}^{-1}{B}_s,\\ \hfill U_t={A_t}^{-1}{B}_t.\end{array}$$

(14)

where $A_s=\alpha X^s{X^s}^T+\beta +\beta M_s$, $B_s=\alpha X^s{Y}^s+\beta M_s\mathit{\theta }{V}_s$, $A_t=\alpha X^t{X^t}^T+\beta +\beta M_t$ and $B_t=\alpha X^{t}F+\beta M_t\mathit{\theta }V$.    □

3.1.3. Optimize F by Fixing $U_s$, $U_t$, $V_s$, $V_t$ and $\mathit{\theta }$

After obtaining the optimal values from Section 3.1.1 and Section 3.1.2, the objective function $R_2$ can obtain the minimum value when $F={X^t}^T{U}_t$

Proof. 

Assuming known variables $U_s$, $U_t$, $V_s$, $V_t$ and $\mathit{\theta }$, then Equation (8) can be simplified to be:

$$\begin{array}{c}\hfill R_5=arg\underset{F}{min}\alpha \left({∥{X^t}^T{U}_t-F∥}^2\right).\end{array}$$

(15)

By setting the derivative of Equation (14) w.r.t. F as 0, the prediction labels F are obtained by $F={X^t}^T{U}_t$.    □

3.1.4. Optimize $\mathit{\theta }$ by Fixing $U_s$, $U_t$, $V_s$, $V_t$ and F

When the variable $U_s$, $U_t$, $V_s$, $V_t$ and F obtain the optimal solution obtained from Section 3.1.1, Section 3.1.2 and Section 3.1.3, the solution of $\mathit{\theta }$ can be transformed into a singular value decomposition (SVD) problem for the matrix O.

Proof. 

Then with fixed $U_s$, $U_t$ and F, we can get the optimal $\mathit{\theta }$ by solving

$$\begin{array}{cc}\hfill R_6=& arg\underset{V_s,V_t,\mathit{\theta }}{min}\hfill \\ \hfill & \beta \left({∥U_s-\mathit{\theta }{V}_s∥}_{2,1}+{∥U_t-\mathit{\theta }{V}_t∥}_{2,1}\right)\hfill \\ \hfill +& \gamma tr({\mathit{\theta }}^{T}XD{X}^T\mathit{\theta })\hfill \end{array}$$

(16)

To solve the minimum value of Equation (16), let $V_s={\mathit{\theta }}^T{U}_s$, $V_t={\mathit{\theta }}^T{U}_t$ and then Equation (16) can be rewritten as solving the generalized eigen-decomposition problem:

$$\begin{array}{cc}\hfill R_7=& arg\underset{\mathit{\theta }}{min}2\beta tr\left(-{\mathit{\theta }}^{T}U{U}^{T}N\mathit{\theta }-{\mathit{\theta }}^{T}NU{U}^T\mathit{\theta }\right)\hfill \\ \hfill +& \gamma tr({\mathit{\theta }}^{T}XD{X}^T\mathit{\theta })\hfill \\ \hfill =& arg\underset{\mathit{\theta }}{max}tr\left({\mathit{\theta }}^{T}O{O}^T\mathit{\theta }\right),\hfill \\ \hfill \mathrm{s}.\mathrm{t}.{\mathit{\theta }}^T\mathit{\theta }=& I_{r\times r}\hfill \end{array}$$

(17)

where $U=\left[U_s,U_t\right]$. Let $O{O}^T=2\beta U{U}^{T}N+2\beta NU{U}^T-\gamma XD{X}^T$. According to matrix theory, the solution of the above equation can be obtained by singular value decomposition of the matrix O. Let $O=E\Sigma G^T$, by descending the diagonal elements in the diagonal matrix $\Sigma$, the first r rows of $E^T$ are the optimal solutions for $\mathit{\theta }$.    □

3.2. Algorithm Description

According to the above optimization rules, the method adopts iterative learning strategy for parameter optimization to achieve parameter update and optimization. The algorithm description is shown in Algorithm 1.

Algorithm 1 Latent Space Domain Adaptation with Residual Model

Require: Source domain data and labels $X^s\times Y^s$, target source domain data and labels $X^t\times Y^t$, regularization hyper-parameter $\alpha$, $\beta$, $\gamma$, shared feature dimension r, the maximal iteration number N.   1: Set v = 0, set $U_s$, $U_t$, $V_s$, $V_t$, $\mathit{\theta }$ as uniform distribution matrix in $U[0,1]$, set threshold $\epsilon$ of objective function   2: while $v>N$ or $R_2<\epsilon$ do   3:    Compute $V_s={\mathit{\theta }}^T{U}_s$ and $V_t={\mathit{\theta }}^T{U}_t$   4:    Compute $A_s=\alpha X^s{X^s}^T+\beta +\beta M_s$ and $B_s=\alpha X^s{Y}^s+\beta M_s\mathit{\theta }{V}_s$   5:    Compute $A_t=\alpha X^t{X^t}^T+\beta +\beta M_t$ and $B_t=\alpha X^{t}F+\beta M_t\mathit{\theta }{V}_t$   6:    Compute $U=A^{-1}B$ and get $U_s$, $U_t$   7:    Compute $F={X^t}^T{U}_t$   8:   Compute $O{O}^T=2\beta U{U}^{T}N+2\beta NU{U}^T-\gamma XD{X}^T$, let $O=E\Sigma G^T$, by descending the diagonal elements in the diagonal matrix $\Sigma$, the first r rows of $E^T$ are the optimal solutions for $\mathit{\theta }$.   9:    Calculate the objective function $R_2$ according to Equation (8). 10:   Let $v=v+1$ 11: end while

4. Experiment and Analysis

In order to verify the effectiveness of LRDA, we experiment on 6 visual databases as benchmark domain databases, and compare with existing related methods.

4.1. Datasets

Table 1. Details of six domain adaptation datasets.

Database		Subset		Image Feature	Classes
Office31	Amazon	A	2817		31
	DSLR	D	498	AlexNet-FC7 (4096)
	Webcam	W	795
Office-Caltech	Amazon	A	958		10
	Caltech	C	1123	SURF (800)
	DSLR	D	157	DeCAF6 (4096)
	Webcam	W	295
Office-Home	Art	A	2421		65
	Clipart	Cl	4379	ResNet101-P5
	Product	Pr	4428	VGG-FC7
	Real-World	Rw	4357
PIE	C05	P1	3332		68
	C06	P2	1629
	C07	P3	1632	Pixel (1024)
	C08	P4	3329
	C09	P5	1632
MNIST-USPS	MNIST	M	2000	VGG-FC7	10
	USPS	U	1800
COIL20	COIL1	C1	720	VGG-FC7	20
	COIL2	C2	720

visually presents detailed information about the six datasets used in the experiment. Next, we will introduce each dataset.

1.

Office31 [27] contains images from Amazon (A), DSLR (D), and Webcam (W). There are 31 categories. Referring to [28], we use the characteristics of fine-tuning on AlexNet-FC7.

2.

Office-Caltech contains 10 categories of images between Caltech-256 (C) [29] and Office31, and each type contains more than 80 images. Among them, the number of images from sources C, A, W, and D are 1123, 958, 295, and 157. Office-Caltech provides SURF features and DeCAF features [30].

3.

Office-Home [31] includes the four following domains: art (sketching, painting, decoration, and other forms, A), clipart (collection of clipping images, Cl), products (object images without a background, Pr), and real-world (object images taken with ordinary cameras, RW). Each domain consists of 65 categories.

4.

PIE [32] involves the pose, illumination, and expressions of faces, including 68 people with 13 attitudes. Referring to [33], we select C05 (left), C07 (upward), C09 (down), C27 (front), and C29 (right).

5.

MNIST-UPS is composed of handwritten digital datasets MNIST [34] and UPS [35]. The experiments in this article are consistent with [35]; we select 2000 and 1800 images from MNIST and UPS, and the size of each image is 16 × 16.

6.

COIL20 [36] contains 20 objects, each rotating ${360}^{°}$ horizontally and capturing an image every $5^{°}$, obtaining 72 images per object. According to the direction of the shooting target, the database is divided into two subsets, namely COIL1 and COIL2. Specifically, COIL1 includes all images captured along the [0; 85] and [180; 265] directions, while COIL2 includes the remaining directions.

4.2. Benchmark Methods & Experimental Settings

The proposed algorithm can be applied to both shallow and deep models, and it is a universal optimization paradigm. Therefore, classic traditional algorithms and domain adaptation methods with good performance in recent years have been selected for comparison to verify the effectiveness of the algorithm. Specifically, we compare LRDA with shallow and deep unsupervised domain adaptation methods. The shallow methods are: SVM, GFK [37], JDA [33], DIP [38], CDDA [39], JGSA [30], SA [40], CORAL [28], ATI [41], DICE [42]. The deep methods are: DDC [43], DAN [44], DANN [45], DRCN [46], RTN [47], WDAN [48], JAN [49], ADDA [50], AutoDIAL [47], CAN [51], SFDA [9], GVB-GD [52], GSDA [53], SRDC [54], and DGA-DA [55]. In addition, we rerun public code of JGSA [30] and CORAL [28] and replicate the code of DGA-DA. The original experimental results of other methods were obtained from corresponding papers. We run the CORAL source code in LIBSVM and selected the optimal variant DICESVM method for its performance.

Parameter Setting: In the method of LRDA, there are three hyper parameters need to be set, which are used to balance the importance of residual classifiers, feature selection, and feature distribution alignment. Therefore, these three parameters have a crucial impact on the final performance of the algorithm. How to set is still an unresolved issue in machine learning. Referring to the work of Tao et al. [56], we use grid search strategy to solve this problem. Specifically, we adjust hyper parameters within the range of grids {${10}^{-6}$, ${10}^{-5}$,…, ${10}^5$, ${10}^6$} to find the parameter combination with the highest accuracy. The iteration limit was fixed at 100. At the same time, when the result of the objective function is less than the threshold $\epsilon =0.01$, the model training is completed and optimization is stopped. In order to achieve optimal results, all experimental algorithm parameters will be searched and adjusted.

Performance Evaluation: Due to target domain data without label, standard cross validation cannot be performed. To address this issue, we conduct p-fold cross validation on labeled source domain data, which trains using p-1 fold source domain data and target domain data, then calculates the average accuracy of all category data on 1-fold source domain data. The optimal parameters are obtained when the accuracy is highest. We repeated each experiment three times and calculated the average accuracy.

4.3. Results of Cross-Domain Recognition

In this section, we compare LRDA with other unsupervised adaptive peer methods. In the experimental results, the left side of → represents the source domain and the right side represents the target domain.

4.3.1. Results and on the Office31 Dataset

The comparison between LRDA and shallow domain adaptation method on the Office31 dataset is shown in

Table 2. Comparison of results with shallow DA methods on the Office31.

DATA	SVM	GFK	JDA	DIP	CDDA	JGSA	SA	CORAL	ATI	DICE	LRDA
A→D	57.8	58.2	66.5	56	64.1	67.5	59.4	60.4	70.3	68.5	67.8
A→W	56.9	59.4	68.8	51.9	65.2	62.3	57.7	57	68.7	72.5	74.5
D→A	47.2	45.9	56.3	44	55	55.6	47.2	47.6	55.3	58.1	59
D→W	95.8	95.6	97.7	95.3	97.2	98.1	95.1	96.2	95	97.2	98.4
W→A	45.5	43.8	53.5	42.3	53.8	52	46.5	46.3	56.9	60.3	60.8
W→D	98.6	98.6	99.6	98.8	99.8	99.8	99	99	98.7	100	98.9
Avg.	67.0	66.9	73.7	64.7	72.5	72.5	67.5	67.8	74.2	76.1	76.6

. LRDA can basically achieve the optimal recognition accuracy in subtasks. The results of deep domain adaptation methods are shown in

Table 3. Comparison of results with deep DA methods on the Office31.

DATA	DDC	DAN	DANN	DRCN	RTN	WDAN	JAN	ADDA	AutoDIAL	CAN	GVB-GD	GSDA	SRDC	SFDA	LRDA
A→D	64.4	67	72.3	66.8	71	64.5	71.8	72.4	73.6	74.6	75	74.8	75.8	76	74.4
A→W	61.8	68.5	73	68.7	73.3	66.8	74.9	75.1	75.5	79.3	74.8	75.7	75.7	74.2	76.8
D→A	52.1	54	53.4	56	50.5	53.8	58.3	58.8	58.1	60.1	53.4	53.5	56.7	56.6	58.7
D→W	95	96	96.4	96.4	96.8	95.9	96.6	97	96.6	97	98.7	99.1	99.2	98.5	99.1
W→A	52.2	53.1	51.2	54.9	51	52.7	55	57.3	59.4	58.7	53.7	54.9	57.1	55.5	58.8
W→D	98.5	99	99.2	99	99.6	98.7	99.5	99.6	99.5	97	100	100	100	99.8	99.5
Avg.	70.6	72.9	74.3	73.6	73.7	72.1	76	76.7	77.1	77.8	75.9	76.3	77.4	76.8	77.9

. It is worth noting that whether compared with shallow models or deep models, the recognition accuracies of LRDA in tasks A→D and W→D are slightly lower than comparison methods. The reason is LRDA needs a certain amount of target domain data to provide information for model decision-making, resulting in a greater preference for source domain data in the model. Overall, LRDA generally achieves good performance on both shallow and deep models, achieving 76.6% and 77.8% respectively, indicating its good applicability. In the comparison of deep models, LRDA does not have obvious advantages. However, deep models need a lot of extra training images and computing resource. This is not available in many practical applications and advanced computing platforms.

4.3.2. Results on the Office-Caltech Dataset

This section conducts cross-domain recognition experiments on Office-Caltech, with reference settings [8,9]. The results with SURF and DeCAF6 features are shown in

Table 4. Comparison of results on Office-Caltech with SURF feature.

DATA	GFK	JDA	DIP	OTGL	CDDA	JGSA	SA	CORAL	DICE	DGA-DA	LRDA
A→C	43.6	39.4	40	34.6	39.6	41.5	44.3	45.1	44.3	38.0	45.2
A→D	44.6	39.5	36.9	38.9	38.2	45.2	36.3	39.5	52.2	42.0	52.1
A→W	45.1	38.0	35.9	37	46.1	45.1	38.3	44.4	53.2	52.2	54.1
C→A	51.6	44.8	40.8	44.2	49.4	53.1	54.8	54.3	53.8	50.3	54.6
C→D	43.3	45.2	45.2	44.5	49.7	48.4	45.2	36.3	51.6	52.9	50.9
C→W	44.1	41.7	37.3	38.9	38.6	48.5	44.4	38.6	54.9	45.8	55.2
D→A	39.1	33.1	31.5	37.2	32.8	38.7	39.4	37.7	42.6	37.1	43.7
D→C	31.7	31.5	30.6	32.4	33.7	30.3	34.3	33.8	34.2	33.5	34.5
D→W	85.4	89.5	83.7	81.1	89.8	93.2	85.1	84.7	84.1	91.2	91.2
W→A	31.8	32.8	27.6	39.4	36.7	40.8	36.3	35.9	39.5	32.4	40.5
W→C	34.3	31.2	28.8	36.0	32	33.6	33.2	33.7	38.6	31.2	38.7
W→D	87.9	89.2	91.7	84.0	91.1	88.5	83.4	86.6	87.3	91.7	88.7
Avg.	48.5	46.3	44.2	45.7	48.1	50.6	47.9	47.6	53.0	49.8	54.1

and

Table 5. Comparison of results on Office-Caltech with DeCAF6 feature.

DATA	GFK	JDA	DIP	OTGL	CDDA	JGSA	DGA-DA	SA	CORAL	DICE	JDOT	ATI	RTN	LRDA
A→C	82.1	85	78.9	85.5	85.8	85	86.7	85	83.6	87.6	85.2	86.5	87.8	86.8
A→D	82.2	86.6	80.9	85	86.6	85.4	89.2	87.3	84.7	91.1	87.9	92.8	92.9	91.5
A→W	73.2	83.1	69.8	83.1	81.4	84.8	86.4	76.6	74.2	88.1	84.8	88.7	93.8	92.1
C→A	92.1	91	89.8	92.2	91.6	91.8	92.3	92.2	91.2	93.4	91.5	93.8	93.2	93.5
C→D	92.4	87.9	84.7	87.3	91.7	92.4	92.4	88.5	87.9	95.5	89.8	89.6	93.9	93.4
C→W	84.4	82.4	72.2	84.2	88.8	85.1	89.8	82	80.7	95.3	88.8	93.6	96.6	96.9
D→A	88.4	91	85.3	92.3	92.1	92.3	92.4	85.6	83.8	92.5	88.1	93.4	93.6	93.2
D→C	80.3	85.1	75.5	84.1	86.3	85.8	86.5	76.9	71.6	88.5	84.3	85.9	83.4	88.8
D→W	99	99.7	98.6	96.3	99	98.6	99	96.9	97.6	99	96.6	98.9	98.6	98.4
W→A	84.3	91.1	72.4	90.6	90.4	91.4	90.7	83.6	72.1	91.1	90.7	93.6	92.7	92.9
W→C	76.5	85.3	70.3	81.5	85.5	84.7	85.6	74.3	67.4	88	82.6	86.3	84.8	85.4
W→D	100	100	99.4	96.3	100	100	100	99.4	100	100	98.1	100	100	100
Avg.	86.2	89.1	81.5	88.2	89.9	89.8	90.9	85.7	82.9	92.5	89	91.9	92.6	92.7

. The LRDA achieves the highest recognition accuracy among 10 cross-domain recognition tasks with SURF features, only on C→D and W→D tasks are slightly lower than DICE and DGA-DA. In addition, LRDA achieves the highest average accuracy, demonstrating the effectiveness of the method. In experiments with DeCAF6 features, accuracy of LRDA is above 85% in all settings and achieves the best results in average accuracy particularly. Comparing with RTN based on the deep learning model AlexNet, LRDA achieves higher accuracy in all five experimental settings, with a higher accuracy of 5.4% in the D→C compared to RTN, resulting in significant performance improvement. This is due to the significant distribution differences between images of different concepts, it is difficult to align the fields. LRDA can further explore common features between different fields, thereby enhancing the ability of discriminators.

4.3.3. Results on the Office-Home Dataset

Table 6. Comparison of results with ResNet101-P5 features on the Office-Home.

DATA	GFK	JDA	DIP	CDDA	JGSA	DGA-DA	CNN	SA	CORAL	DICE	LRDA
Ar→Cl	35.8	40.5	35.5	40.8	40.8	40.8	36	36.7	36.3	42.6	42.5
Ar→Pr	54.4	58.9	54.3	57.7	58.2	57.7	53.7	54.7	54.1	61.1	60.9
Ar→Rw	65	67.5	64.9	66.3	67.5	66.3	64.6	65.3	65.3	68.3	68.6
Cl→Ar	39.2	40.8	39.5	41.3	40.8	41.3	39.2	39.9	39.2	43.3	43.1
Cl→Pr	48.4	51.9	48	51.7	52	51.7	48.9	48.3	47.9	54.3	54.7
Cl→Rw	51.8	55.2	51.9	53.9	54.6	53.9	51.7	51.4	51.5	57.1	57.5
Pr→Ar	42.3	45.1	41.9	46.1	45.3	46.1	41.2	41.4	41.5	48.3	48.4
Pr→Cl	32.5	33.3	32.1	35.4	33.5	35.4	32.9	33	32.7	35.9	35.5
Pr→Rw	64.1	67.2	63.7	66	66.4	66	63.2	64.4	64.1	69.2	68.8
Rw→Ar	58.1	58.8	58.2	59.1	58.5	59.1	57.9	57.8	57.7	60.2	59.3
Rw→Cl	39.5	44.2	39.2	45.3	43.8	45.3	39.5	40	39.5	46.2	46.0
Rw→Pr	69.6	72.4	69.6	71.6	72.4	71.6	68.9	69.5	69.3	73.5	72.7
Avg.	50.1	53	49.9	52.9	52.8	52.9	49.8	50.2	49.9	55	54.8

shows the cross-domain recognition results on Office-Home dataset with ResNet101-P5 features. We fine-tune the parameters on the ResNet101 and obtain the results by inputting the extracted fifth feature pooling layer into the unsupervised domain for adaptive learning. Notice that LRDA achieves the best recognition performance in five domain recognition tasks, with an average recognition accuracy rate 0.2% lower than DICE. We consider that DICE excludes the features of different types of data while incorporating the distribution of similar data.

Table 7. Comparison of results with VGG-F7 features on the Office-Home.

DATA	GSDA	GVB-GD	SRDC	SFDA	JAN	CDDA	JGSA	DICE	DAN	DANN	LRDA
Ar→Cl	61.3	57	52.3	59.7	45.9	42.6	41.9	43.5	43.6	45.6	44.4
Ar→Pr	76.1	74.7	76.3	79.5	61.2	62.3	63.1	64.2	57	59.3	64.2
Ar→Rw	79.4	79.8	81	82.4	68.9	69.2	70.1	70.5	67 9	70.1	70.6
Cl→Ar	65.4	64.6	69.5	69.7	50.4	46.3	46.5	46.7	45.8	47	46.1
Cl→Pr	73.3	74.1	76.2	78.6	59.7	52.9	54.1	54.6	56.5	58.5	56.9
Cl→Rw	74.3	74.6	78	79.2	61	57.8	59	59.4	60.4	60.9	59.5
Pr→Ar	65	65.2	68.7	66.1	45.8	50.5	50.4	51.8	44	46.1	50.7
Pr→Cl	53.2	55.1	53.8	57.2	43.4	43	42	43.9	43.6	43.7	44.1
Pr→Rw	80	81	81.7	82.6	70.3	69.6	70.5	71.8	67.7	68.5	69.8
Rw→Ar	72.2	74.6	76.3	73.9	63.9	63.1	62.3	64.1	63.1	63.2	63.7
Rw→Cl	60.6	59.7	57.1	60.8	52.4	47.9	46.2	48	51.5	51.8	52.4
Rw→Pr	83.1	84.3	85	85.5	76.8	73.8	73.1	74.3	74.3	76.8	74.7
Avg.	70.3	70.4	71.3	72.9	58.3	56.6	56.6	57.7	56.3	57.6	58.1

shows the cross-domain recognition results on Office-Home with VGG-F7 features. This experiment compares both shallow and deep models, and LRDA is the second-best performing method in terms of average accuracy, being only inferior to JAN. Counter-intuitively, LRDA achieves better result even than deep methods (e.g., DAN and DANN). In addition, the performance of GSDA, GVB-GD, SRDC, and SFDA methods is superior to that of LRDA methods in some tasks. The results indicate that above methods consider the differences between different categories of data or maintain the distribution structure of intra class data when extracting domain features, thereby improving the performance of the above methods. Nevertheless, LRDA still has good performance, especially achieving better performance than deep methods, indicating that shallow methods have advantages in domain adaptation tasks, reducing algorithm complexity and improving model efficiency while ensuring algorithm accuracy.

4.3.4. Results on the PIE Dataset

In the task of cross-domain facial recognition, this experiment uses two data preprocessing methods ($l_2$ normalization and z-score standardization) [42]. The experimental settings divide into two groups, and the recognition accuracies are shown in

Table 8. Recognition accuracies on the PIE Dataset with $l_2$ regularization.

DATA	DIP	OTGL	CDDA	JGSA	SA	CORAL	DGA-DA	GFK	JDA	CDDA	DICE	LRDA
P1→P2	29.9	59.4	76.3	62.2	32.8	31.8	76.4	42.2	76.1	77.5	85.1	83.6
P1→P3	32.8	58.7	72.3	60	34.5	31.9	72.5	53.7	74.1	77	86.9	86.4
P1→P4	36.7	0	92.1	80.6	43.5	41.8	92.1	69.8	92.8	90.3	95.2	95.9
P1→P5	12.7	48.4	60.7	45.1	22.5	19.9	60.8	43.9	70.8	67.8	71.8	72.7
P2→P1	25.8	61.9	77	68.2	27.7	26.6	77	43.2	79.8	77.3	76.8	77.1
P2→P3	53.4	64.4	77.5	64.9	37.3	35	77.5	54	80.2	81.1	79.1	78.6
P2→P4	50.1	0	87.1	77.6	58.5	59.7	87.1	69.1	90.4	88.5	93.5	93.6
P2→P5	29.5	52.7	64.3	52.3	27.1	25.9	63.6	42.6	68.3	70.4	72.3	71.6
P3→P1	22.7	57.9	80.8	62.9	29.1	25.1	80.8	51.6	78.3	81.2	80.1	80.7
P3→P2	36.3	64.7	72.2	60.3	37	36.5	72.2	52	81.2	82	77.7	80.4
P3→P4	45.8	0	84.7	71	54.8	54	84.7	72.1	92.3	91.7	95.1	94.8
Avg.	34.2	42.6	76.8	64.1	36.8	35.3	76.8	54.0	80.4	80.4	83.2	83.2

and

Table 9. Recognition accuracies on the PIE Dataset with z-score standardization.

DATA	DIP	OTGL	CDDA	JGSA	SA	CORAL	DGA-DA	GFK	JDA	CDDA	DICE	LRDA
P3→P5	20.2	52.8	64.3	51.2	30.5	26	64.5	50.9	70.5	79.9	78.1	78.6
P4→P1	31.4	0	93.6	84.4	52.4	48.3	93.4	72.6	95.1	89.7	96.8	96.1
P4→P2	67.5	0	93.2	83.5	70	69.7	93.2	75.8	94.7	94.8	96.6	95.7
P4→P3	76.8	0	92.2	80.8	72.7	72.7	92.2	80.9	92.4	92.1	94.5	94.0
P4→P5	36.5	0	74	65.9	48.6	48.5	74	61.1	80.8	85.1	90.4	89.8
P5→P1	14.2	45.7	68.1	53.5	34.5	32	67.7	45.3	64.1	67.3	79.4	78.8
P5→P2	29.3	51.3	65.1	57.5	30.9	30.4	65.4	38.9	74.2	74.5	71.4	72.2
P5→P3	31.7	52.6	70.5	54.3	31.9	32.6	71.6	47.7	75.3	79.3	82.7	82.3
P5→P4	26.3	0	79.7	62.3	45.1	44.5	79.7	59.3	81.7	80.3	89.5	88.9
Avg.	37.1	22.5	77.9	65.9	46.3	45.0	78.0	59.2	81.0	82.3	86.6	86.3

. In the experiment using the $l_2$ normalization (Table 8), we can clearly find that LRDA achieves the highest recognition accuracy in four tasks compared to shallow and deep methods. Moreover, LRDA has the highest average accuracy. In the experiment of z-score standardization, LRDA achieves recognition performance comparable to DICE and far superior to other recognition methods. Affected by the features in the background area in facial data, LRDA focuses on how to effectively convert features between the source and target domains, possibly aligning interference features in the background area. However, the recognition accuracy of LRDA on the PIE dataset is still comparable.

4.3.5. Results on the MNIST-USPS & COIL20 Dataset

In order to further demonstrate the advantages of the proposed method in cross-domain adaptation tasks of digital images,

Table 10. Recognition accuracies on the MNIST-USPS and COIL20 dataset.

DATA	GFK	SA	JDA	DIP	CDDA	ILS	JGSA	DGA-DA	CORAL	DICE	CPDM	LRDA
M→U	68.6	67.8	70.6	67.1	76.2	71.2	80.4	82.3	35.8	79.7	82.1	80.6
U→M	50.1	48.8	60	46.3	62.1	54.9	68.2	70.8	36.4	59.8	68.8	71.1
MU-Avg.	59.3	58.3	65.3	56.7	69.1	63	74.3	76.5	36.1	69.8	75.4	75.8
C1→C2	86.4	86.8	94.7	84.6	91.5	86.9	95.4	99.6	82.1	92.5	98.5	99.2
C2→C1	85	85	93.5	84	93.9	86.9	93.9	99.7	81.8	94.4	98.7	99.3
C1C2-Avg.	85.7	85.9	94.1	84.3	92.7	86.9	94.7	99.7	81.9	93.5	98.6	99.3

shows the cross-domain recognition performance on the MNIST-UPS dataset and COIL20. As can be seen from the first three rows, LRDA achieves the highest average accuracy, as well as U→M task. Nevertheless, the performance of LRDA is slightly lower than that of DGA-DA and DICE on the M→U task, possibly due to the significant differences between these two fields. In the M→U task, the feature distribution is difficult to close, and the feature projection methods of DGA-DA and DICE are more suitable for this type of data. The comparison results in last three rows of Table 9 indicate that the performance of LRDA is close to 100%, only slightly lower than DGA-DA, with a recognition accuracy reduction of approximately 0.5%. This is due to the exclusion of heterogeneous data by the DGA-DA method. Overall, LRDA is still significantly superior to other methods.

4.4. Convergence Analysis

In this section, we explore the convergence of the algorithm. LRDA adapts iterative learning strategy for parameter optimization to achieve parameter update optimization. Experiments use a computer with a memory of 64GB and an Intel i5-9600k CPU, use MATLAB (R2024a) as experimental platform. Figure 3 shows the convergence curve of LRDA. Three sets of experiments use Amazon (A), DSLR (D) and Webcam (W) as the source and target domains in Office31 dataset. The result shows that after 40–50 iterations of optimization, the algorithm achieves convergence in all three sets of experiments, indicating that the objective function of the model can be minimized through parameter iterative learning. It proves that the LRDA method has good convergence and can be optimized through parameter iteration.

4.5. Complexity Comparison

The domain adaptation method requires the extraction of features from two data domains, which lead to an increase in computation time.

Table 11. Computation time(s) of each domain adaptation method on Office31.

Task	JDA	DIP	SA	GFK	DICE	CDDA	CORAL	LRDA
A→D	71.2	65.1	74.7	77.6	126.3	116.6	64.2	114.8
D→W	45.5	54.4	59.6	723	71.33	96.4	48.4	92.8
W→A	147.1	220.3	135.5	234.7	240.9	319.1	238.2	225.9

compares the computational time of 8 domain adaptation methods on the Office13 dataset, with the experimental setup being the same as Section 4.4. The experimental result indicates that because of LRDA’s need for iterative optimization, its time cost is relatively high, which also occurs in DICE, CDDA, and CORAL. Because of its closed form, the computation time of GFK, DIP, and SA are relatively low. JDA needs feature decomposition of data; its computation time is increasing with the increase in data volume. However, according to the experiment in Section 4.3, although LRDA requires a longer computation time, its performance is higher than other methods.

5. Conclusions

In this study, we explore the mismatched distribution of latent space features and neglect the association between the original space and latent space. In response to these problems, we propose a latent space domain adaptation with residual model. LRDA reduces the difference in feature distribution in the shared latent space to enhance the feature expression. The objective function constructs the original feature space and the shared feature space as residual model to facilitate parameter optimization, improve model performance. The experiments compare LRDA with the-state-of-art shallow and deep domain adaptation algorithms on six open datasets, verify the proposed method is comparable.

From a broader perspective of cross-domain learning, this study provides a new solution to the multi-domain adaptive problem. Although the current model is mainly aimed at two domain adaptive scenarios, its residual modeling idea can be extended to multi-domain transfer learning, which is expected to realize knowledge transfer from multiple source domains to target domains by constructing hierarchical residual connections or designing multi spatial alignment mechanisms. In addition, in multi-modal data scenarios (such as vision text cross-modal learning), this method can provide the possibility of knowledge transfer between heterogeneous modes through mode-specific feature space decoupling and shared potential space modeling. It should be noted that due to the need to calculate the inter domain decision function, this method increases the time cost of the algorithm, and the balance between accuracy and time consumption is still a contradiction to be solved. In follow-up studies, we will further examine (1) how to batch train adaptive models in the field of large-scale data to reduce the time cost; (2) explore the automatic optimization scheme of super parameter settings (such as the meta learning strategy) to reduce the burden of grid search; and (3) expand the universality of the model in multi-domain migration and multi-modal scenarios, as well as promote cross-domain learning to more complex practical applications.