An Intelligent Algorithm for the Optimal Deployment of Water Network Monitoring Sensors Based on Automatic Labelling and Graph Neural Network
Abstract
1. Introduction
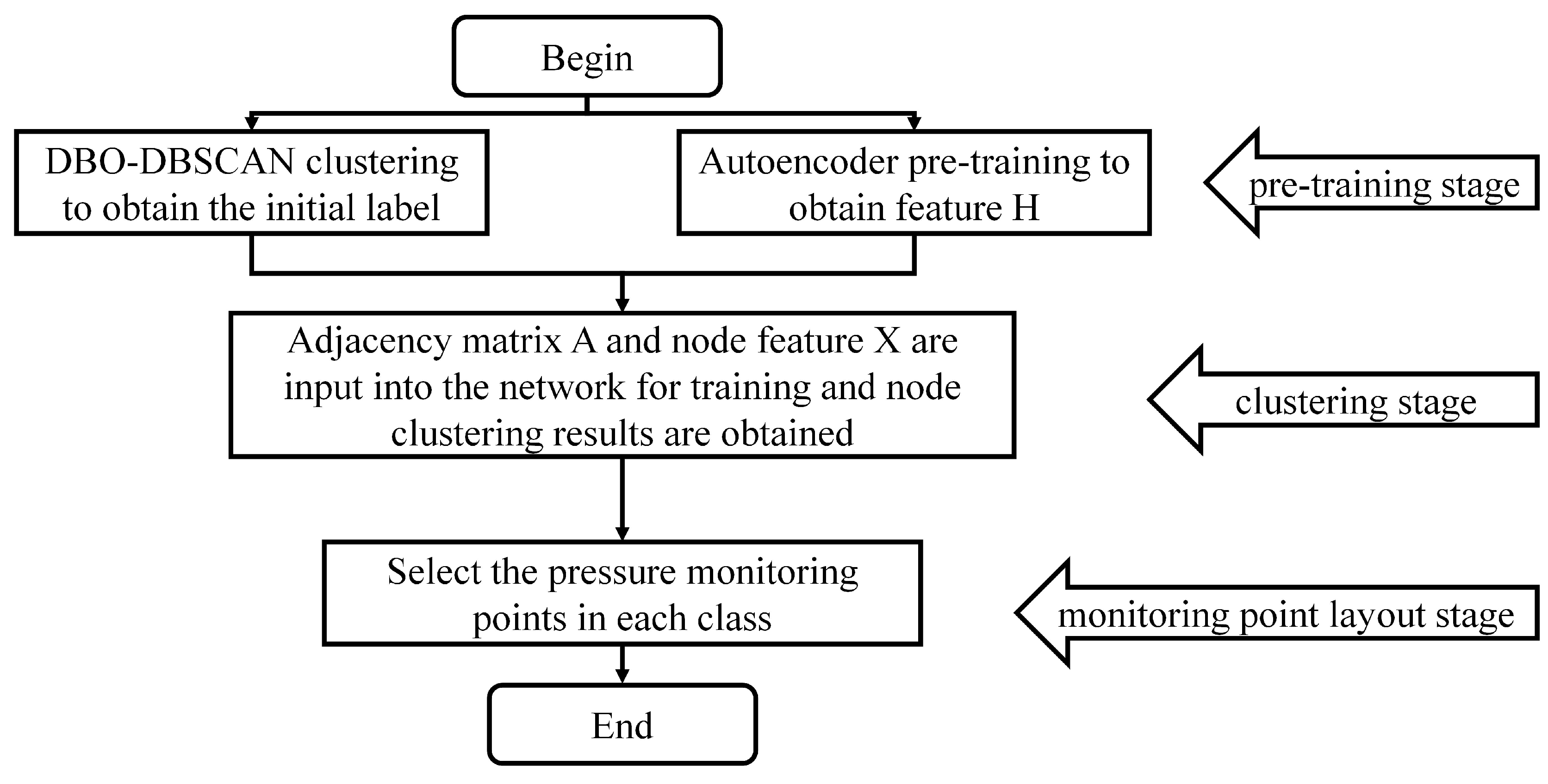
2. Methodology
2.1. Pre-Training
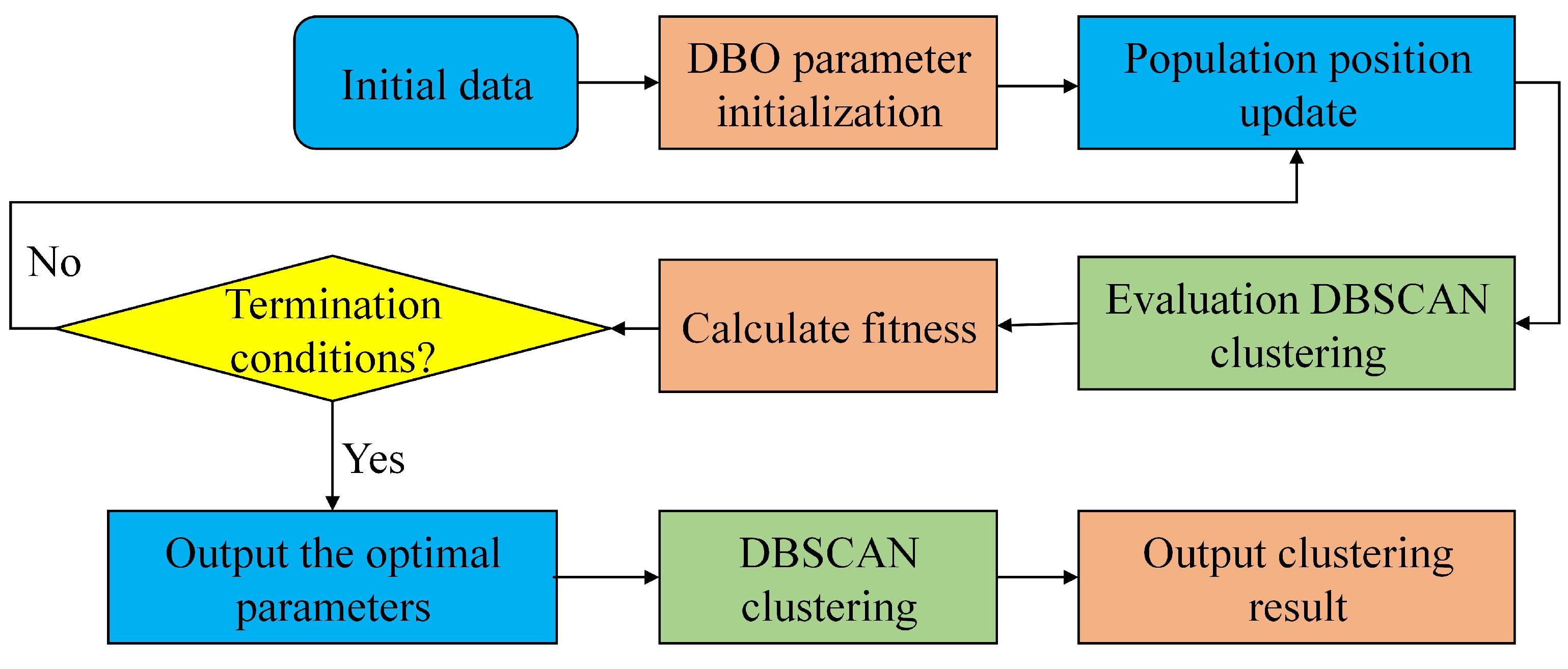
2.1.1. The Improved DBSCAN Algorithm
- Select any point X in the sample.
- Take this point as the center and EPS as the radius. If the number of sample points within the range is greater than or equal to MINPST, specify this point as the core point; otherwise, it is a non-core point.
- Start with adjacent samples at point X and repeat step 2 until all samples in this dataset are traversed. Finally, the clustering results, including core points, noise points, and non-core points, are obtained.
- Obtain the pressure P of the WDN under normal operating conditions.
- Change the node water requirements one by one to obtain the node water pressure of N nodes.
- Calculate the node pressure difference:
- Calculate the impact level of each node:where represents the influence degree of the node.
- Calculate the standard deviation of each node:where represents the standard deviation of nodes.
- Construct the node eigenmatrix of the i node, indicating that the data are connected; x and y denote the coordinates of the node.
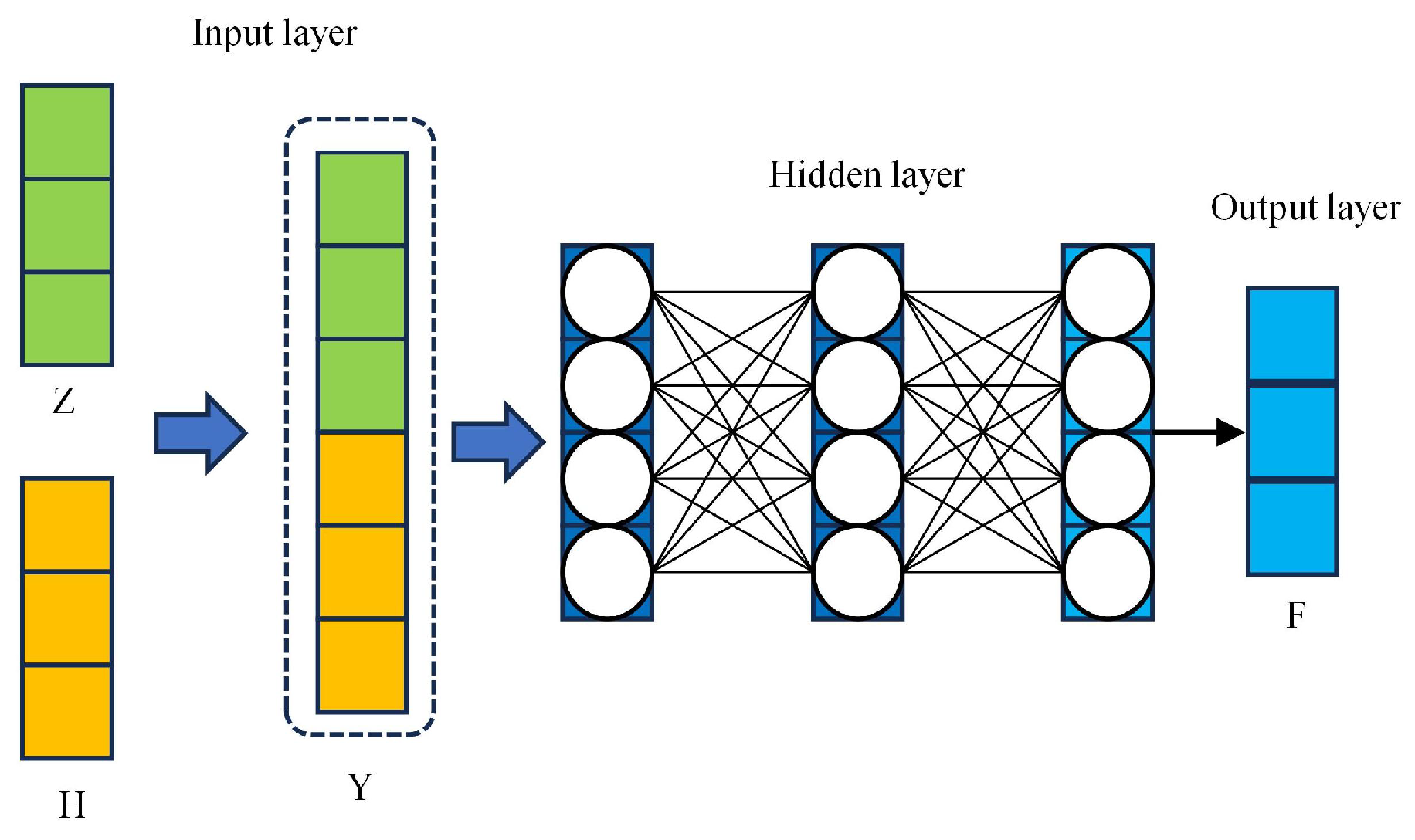
2.1.2. Auto-Encoder Module
2.2. Clustering
2.2.1. GCN Module
2.2.2. Self-Attention Module
2.2.3. Dual Self-Monitoring Module
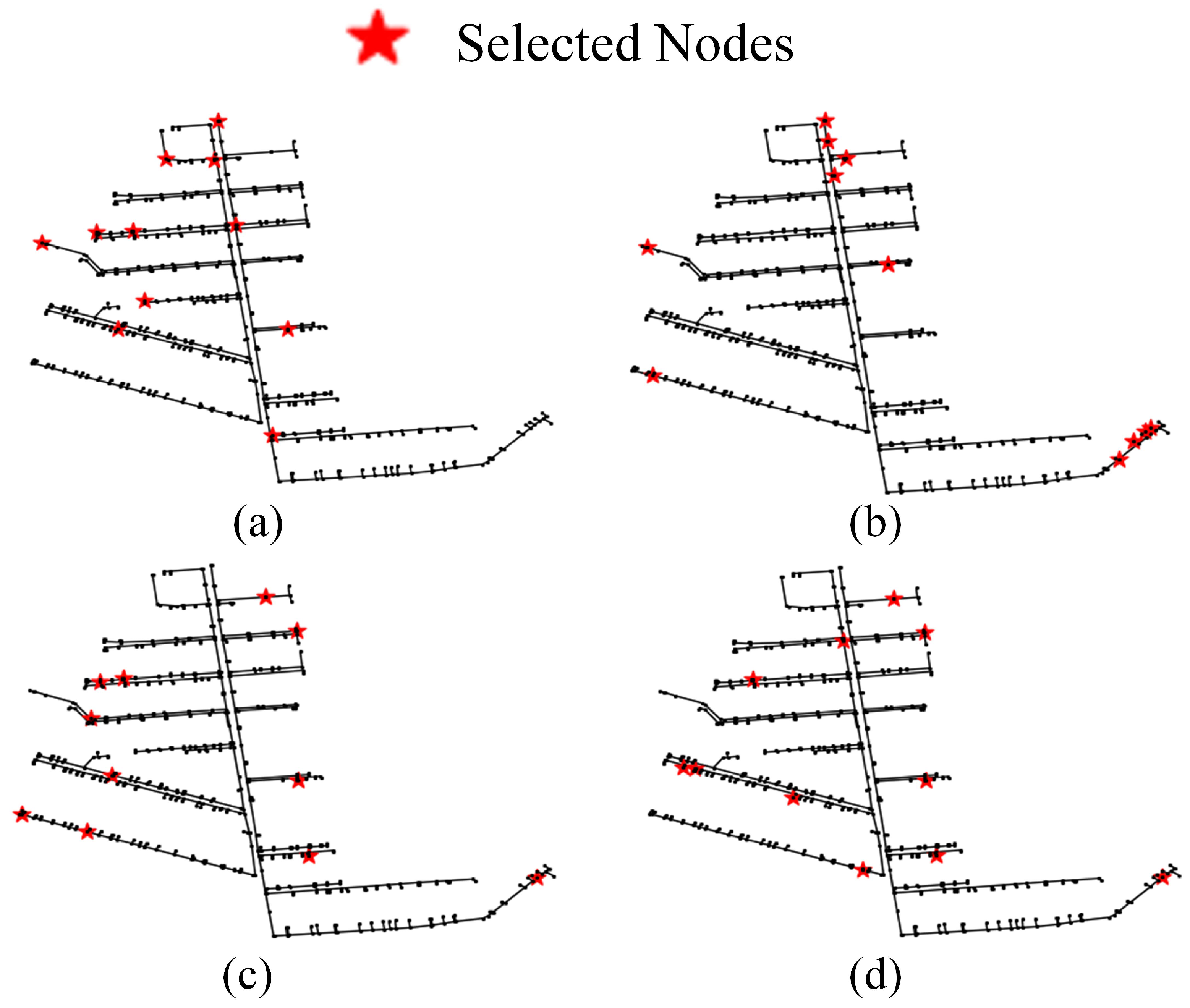
2.3. Placement of Monitoring Points
2.4. Leakage Identification
3. Results and Discussion
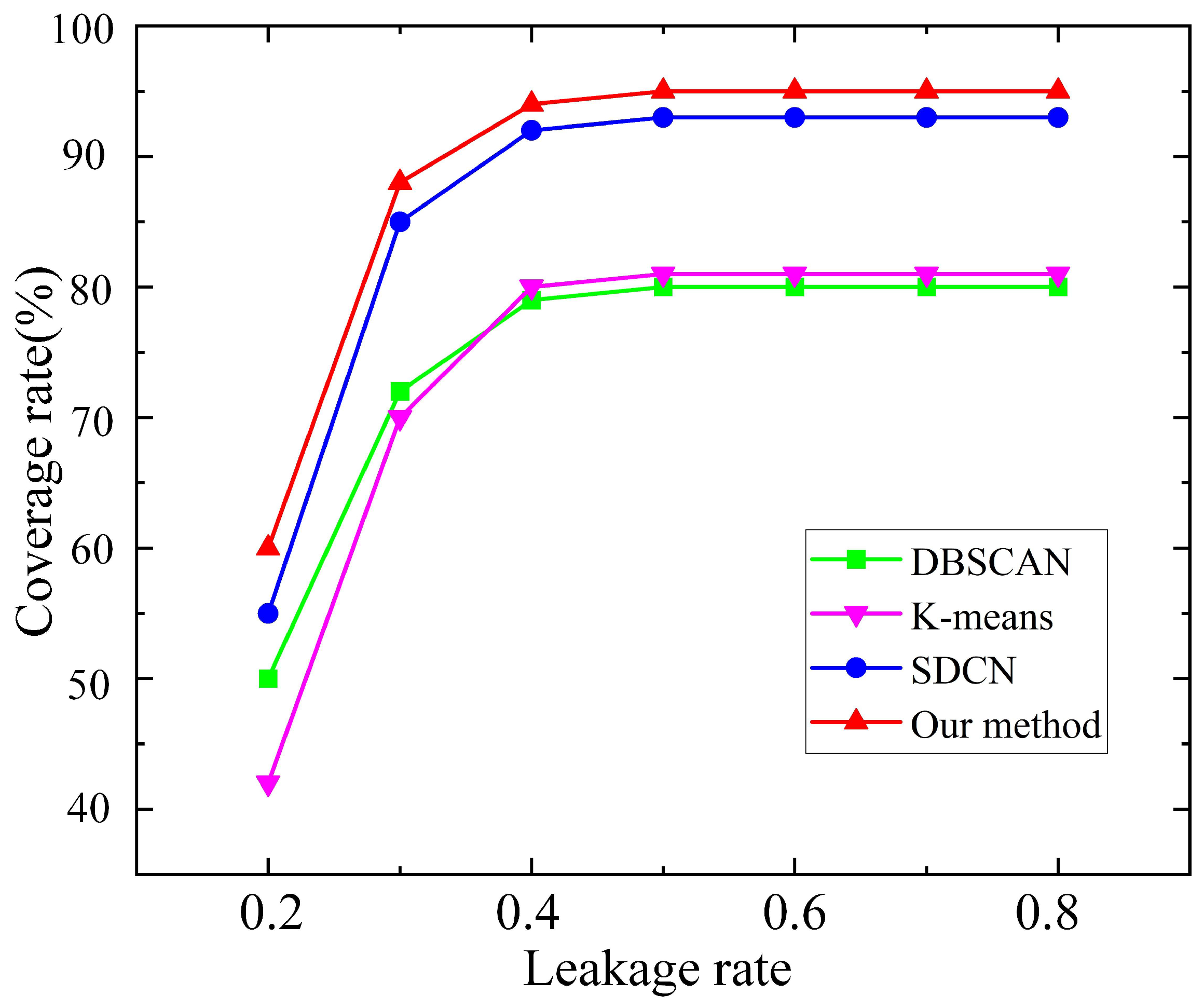
3.1. Evaluation Indicator
- Detection range of the monitoring point;
- Accuracy of leakage monitoring of WDN.
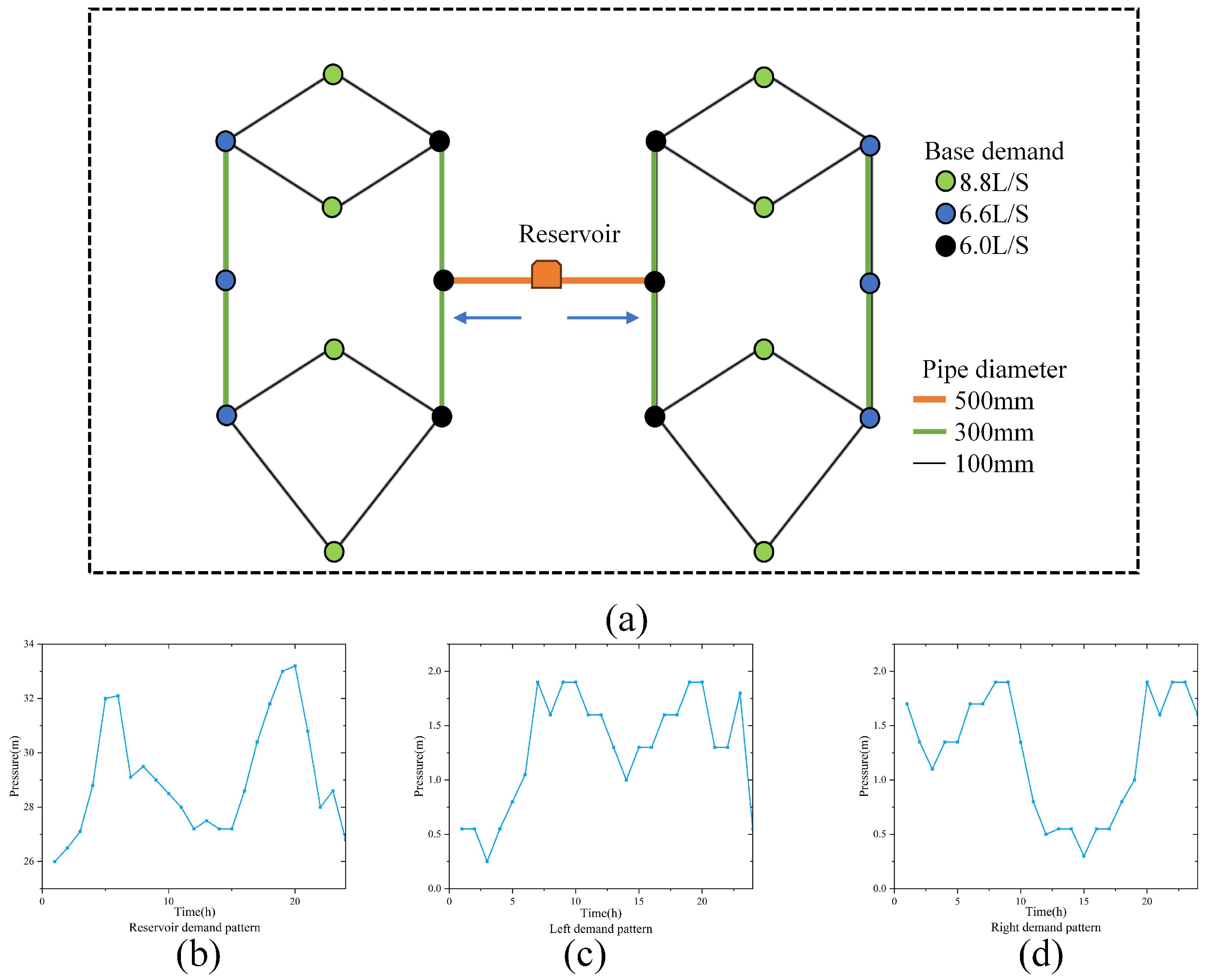
3.2. Case 1: Simple Net
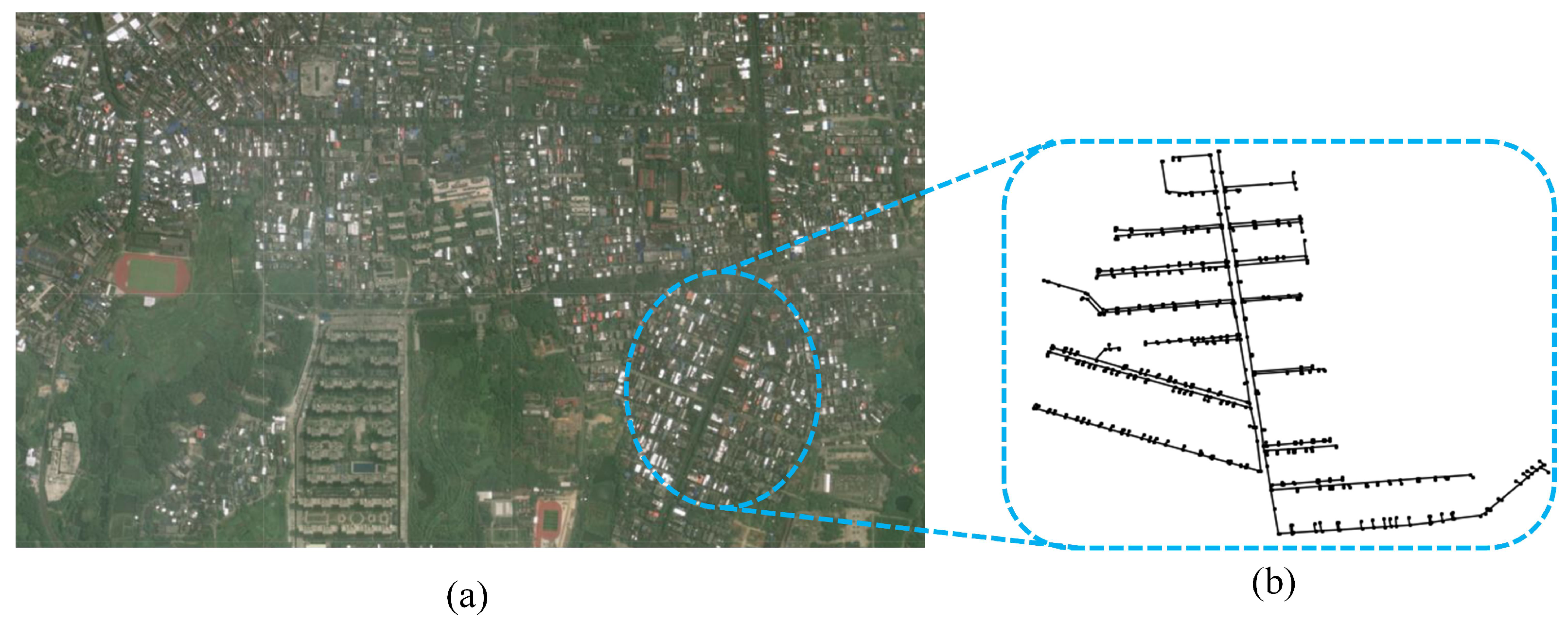
3.3. Case 2: Wanfudong Net
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WDNs | Water Distribution Networks |
| DBO | Dung Beetle Optimization algorithm |
| DBSCAN | Density-Based noise application Spatial Clustering |
| GCN | Graph Convolutional Networks |
| SDCN | Structural Deep Clustering Network |
| EGAE | Embedding Graph Auto-Encoder |
| EPANET | Environmental Protection Agency Network Analysis Tool |
| MINPST | minimum number of points |
| EPS | domain radius of the sampling points |
| S | Average silhouette coefficient of the cluster |
| The position of the i-th dung beetle at the t iteration | |
| X | The current local optimal position |
| Z | Data representation of the hidden layer |
| H | Data representation of auto-encoders |
| Y | The feature representation of the construction |
References
- Chan, T.K.; Chin, C.S.; Zhong, X. Review of current technologies and proposed intelligent methodologies for water distributed network leakage detection. IEEE Access 2018, 6, 78846–78867. [Google Scholar] [CrossRef]
- Wang, T.; Liu, S.; Qian, X.; Shimizu, T.; Dente, S.M.; Hashimoto, S.; Nakajima, J. Assessment of the municipal water cycle in China. Sci. Total Environ. 2017, 607, 761–770. [Google Scholar] [CrossRef]
- Fontanazza, C.M.; Notaro, V.; Puleo, V.; Freni, G. Multivariate statistical analysis for water demand modeling. Procedia Eng. 2014, 89, 901–908. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S. A review of data-driven approaches for burst detection in water distribution systems. Urban Water J. 2017, 14, 972–983. [Google Scholar] [CrossRef]
- Li, R.; Huang, H.; Xin, K.; Tao, T. A review of methods for burst/leakage detection and location in water distribution systems. Water Sci. Technol. Water Supply 2015, 15, 429–441. [Google Scholar] [CrossRef]
- Ferreira, B.; Antunes, A.; Carriço, N. Multi-objective optimization of pressure sensor location for burst detection and network calibration. Comput. Chem. Eng. 2022, 162, 107826. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Santonastaso, G.F.; Tzatchkov, V.G.; Alcocer-Yamanaka, V.H. Redundancy features of water distribution systems. Procedia Eng. 2017, 186, 412–419. [Google Scholar] [CrossRef]
- Wéber, R.; Hős, C. Efficient technique for pipe roughness calibration and sensor placement for water distribution systems. J. Water Resour. Plan. Manag. 2020, 146, 04019070. [Google Scholar] [CrossRef]
- Meier, R.W.; Barkdoll, B.D. Sampling design for network model calibration using genetic algorithms. J. Water Resour. Plan. Manag. 2000, 126, 245–250. [Google Scholar] [CrossRef]
- Zhou, X.; Tang, Z.; Xu, W.; Meng, F.; Chu, X.; Xin, K.; Fu, G. Deep learning identifies accurate burst locations in water distribution networks. Water Res. 2019, 166, 115058. [Google Scholar] [CrossRef]
- Wang, T.; Liu, Y. Optimization of pipe network pressure monitoring points based on hydraulic influence modification pressure monitoring point optimization. In Proceedings of the 2024 IEEE 6th International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 19–21 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 433–437. [Google Scholar]
- Cheng, W.; Chen, Y.; Xu, G. Optimizing sensor placement and quantity for pipe burst detection in a water distribution network. J. Water Resour. Plan. Manag. 2020, 146, 04020088. [Google Scholar] [CrossRef]
- Fei, J. Optimal arrangement of pressure monitoring points in water supply network based on intelligent optimization algorithm. In Hydraulic Structure and Hydrodynamics; Springer Nature: Singapore, 2024; pp. 451–461. [Google Scholar]
- Cheng, L.; Kun, D.; Tu, J.-P.; Dong, W.-X. Optimal placement of pressure sensors in water distribution system based on clustering analysis of pressure sensitive matrix. Procedia Eng. 2017, 186, 405–411. [Google Scholar] [CrossRef]
- Wang, F.; Bai, H.; Li, D.; Wang, J. Energy-Efficient Clustering Algorithm in Underwater Sensor Networks Based on Fuzzy C Means and Moth-Flame Optimization Method. IEEE Access 2020, 8, 97474–97484. [Google Scholar]
- Romero-Ben, L.; Cembrano, G.; Puig, V.; Blesa, J. Model-free sensor placement for water distribution networks using genetic algorithms and clustering. In Proceedings of the 10th IFAC Conference on Control Methodologies and Technology for Energy Efficiency (CMTEE), Toulouse, France, 11–13 November 2020; Volume 53, pp. 372–377. [Google Scholar]
- Wang, Y.; Tan, D.B.; Ye, S.; Hu, Z.K.; Yao, Z.L. Multi-criteria decision-making method for optimal sensor layout for leakage monitoring of water supply network. J. Changjiang River Sci. Res. Inst. 2024, 41, 178. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2017, arXiv:1609.02907. [Google Scholar] [CrossRef]
- Peng, S.; Cheng, J.; Wu, X.; Fang, X.; Wu, Q. Pressure sensor placement in water supply network based on graph neural network clustering method. Water 2022, 14, 150. [Google Scholar] [CrossRef]
- Li, J.; Zheng, W.; Wang, C.; Cheng, M. Optimal sensor placement for leak location in water distribution networks based on EGAE clustering algorithm. J. Clean. Prod. 2023, 426, 139175. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, X.; Li, J. Sensor placement for leak localization in water distribution networks based on graph convolutional network. IEEE Sens. J. 2022, 22, 21093–21100. [Google Scholar] [CrossRef]
- Zhou, X.; Wan, X.; Liu, S.; Su, K.; Wang, W.; Farmani, R. An all-purpose method for optimal pressure sensor placement in water distribution networks based on graph signal analysis. Water Res. 2024, 266, 122354. [Google Scholar] [CrossRef]
- Vittori, G.; Falkouskaya, Y.; Jimenez-Gutierrez, D.M.; Cattai, T.; Chatzigiannakis, I. Graph neural networks to model and optimize the operation of Water Distribution Networks: A review. J. Ind. Inf. Integr. 2025, 100880. [Google Scholar] [CrossRef]
- Bi, F.M.; Wang, W.K.; Chen, L. DBSCAN: Density-based spatial clustering of applications with noise. J. Nanjing Univ. 2012, 48, 491–498. [Google Scholar]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Michelucci, U. An introduction to autoencoders. arXiv 2022, arXiv:2201.03898. [Google Scholar] [CrossRef]
- He, X.; Wang, B.; Hu, Y.; Gao, J.; Sun, Y.; Yin, B. Parallelly adaptive graph convolutional clustering model. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 4451–4464. [Google Scholar] [CrossRef]
- Zhang, H.; Li, P.; Zhang, R.; Li, X. Embedding graph auto-encoder for graph clustering. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9352–9362. [Google Scholar] [CrossRef]
- Klise, K.A.; Hart, D.; Moriarty, D.M.; Bynum, M.L.; Murray, R.; Burkhardt, J.; Haxton, T. Water Network Tool for Resilience (WNTR) User Manual (No. SAND2017-8883R); Sandia National Laboratories: Albuquerque, NM, USA, 2017. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Berardi, L.; Laucelli, D.B.; Ripani, S.; Piazza, S.; Freni, G. Using water loss performance indicators to support regulation and planning in real water distribution systems. Digit. Water 2025, 3, 1–20. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]


| Method | Node Coverage Rates (%) |
|---|---|
| K-means | 83.3 |
| DBSCAN | 87.8 |
| SDCN | 94.4 |
| The proposed method | 94.4 |
| Method | Accuracy (%) |
|---|---|
| K-means | 90 |
| DBSCAN | 93 |
| SDCN | 99.07 |
| The proposed method | 99.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Wang, X.; Zhang, J.; Gao, X. An Intelligent Algorithm for the Optimal Deployment of Water Network Monitoring Sensors Based on Automatic Labelling and Graph Neural Network. Information 2025, 16, 837. https://doi.org/10.3390/info16100837
Shi G, Wang X, Zhang J, Gao X. An Intelligent Algorithm for the Optimal Deployment of Water Network Monitoring Sensors Based on Automatic Labelling and Graph Neural Network. Information. 2025; 16(10):837. https://doi.org/10.3390/info16100837
Chicago/Turabian StyleShi, Guoxin, Xianpeng Wang, Jingjing Zhang, and Xinlei Gao. 2025. "An Intelligent Algorithm for the Optimal Deployment of Water Network Monitoring Sensors Based on Automatic Labelling and Graph Neural Network" Information 16, no. 10: 837. https://doi.org/10.3390/info16100837
APA StyleShi, G., Wang, X., Zhang, J., & Gao, X. (2025). An Intelligent Algorithm for the Optimal Deployment of Water Network Monitoring Sensors Based on Automatic Labelling and Graph Neural Network. Information, 16(10), 837. https://doi.org/10.3390/info16100837







