Startup Survival Forecasting: A Multivariate AI Approach Based on Empirical Knowledge
Abstract
1. Introduction
2. Literature Review
3. Methodology
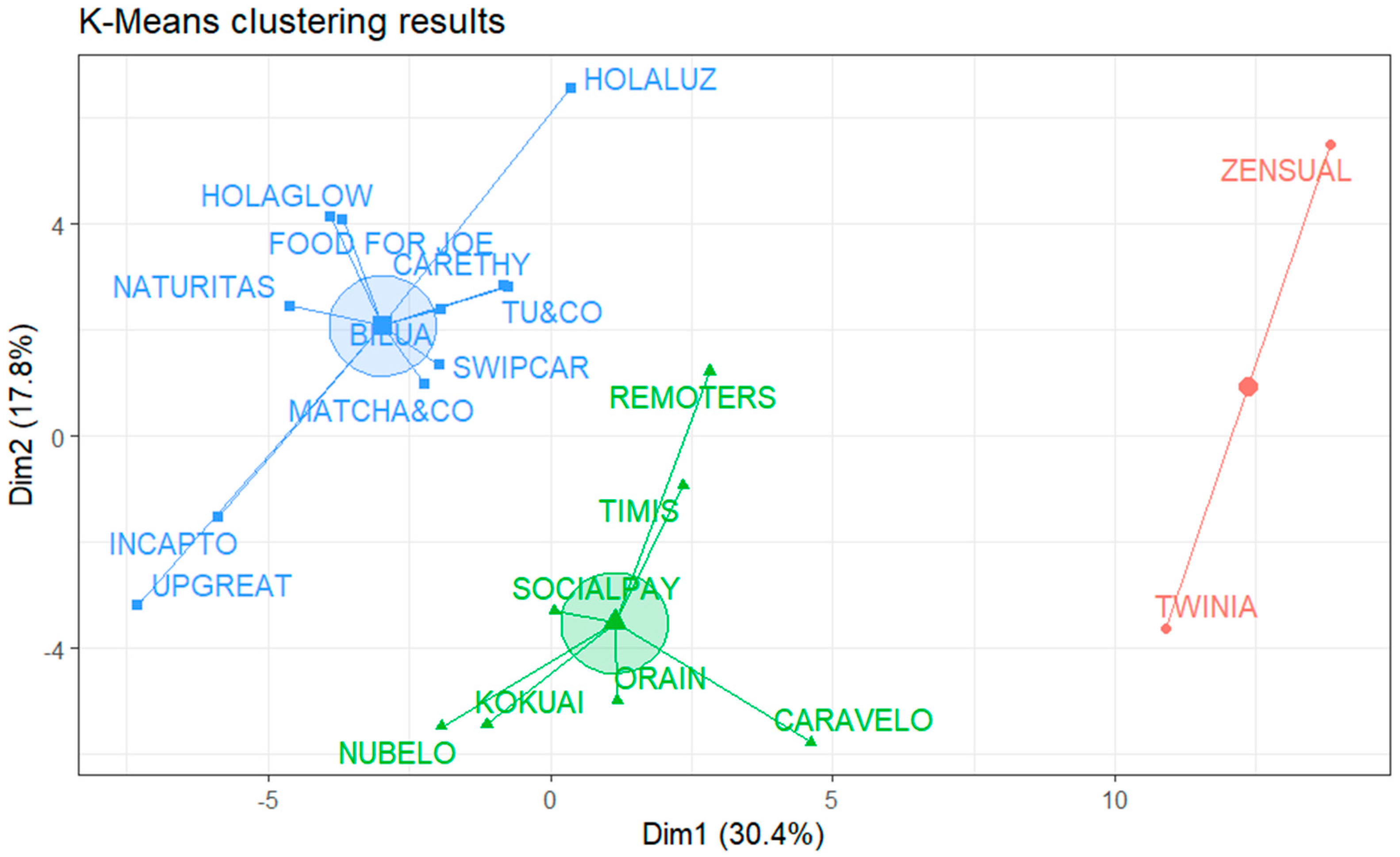
3.1. Experimental Data Acquisition
3.2. Mathematical Tools and Model Explanation
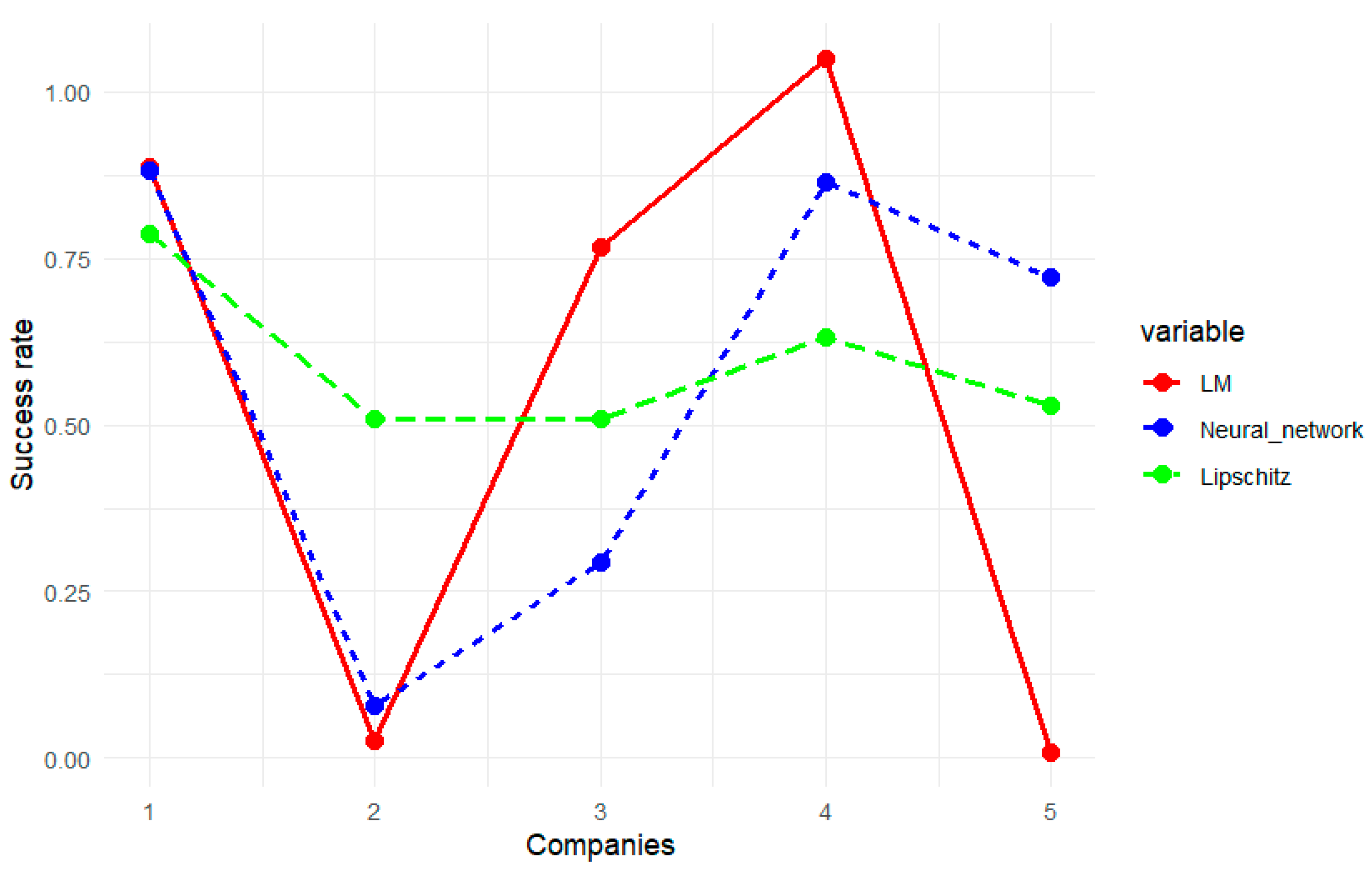
4. Results
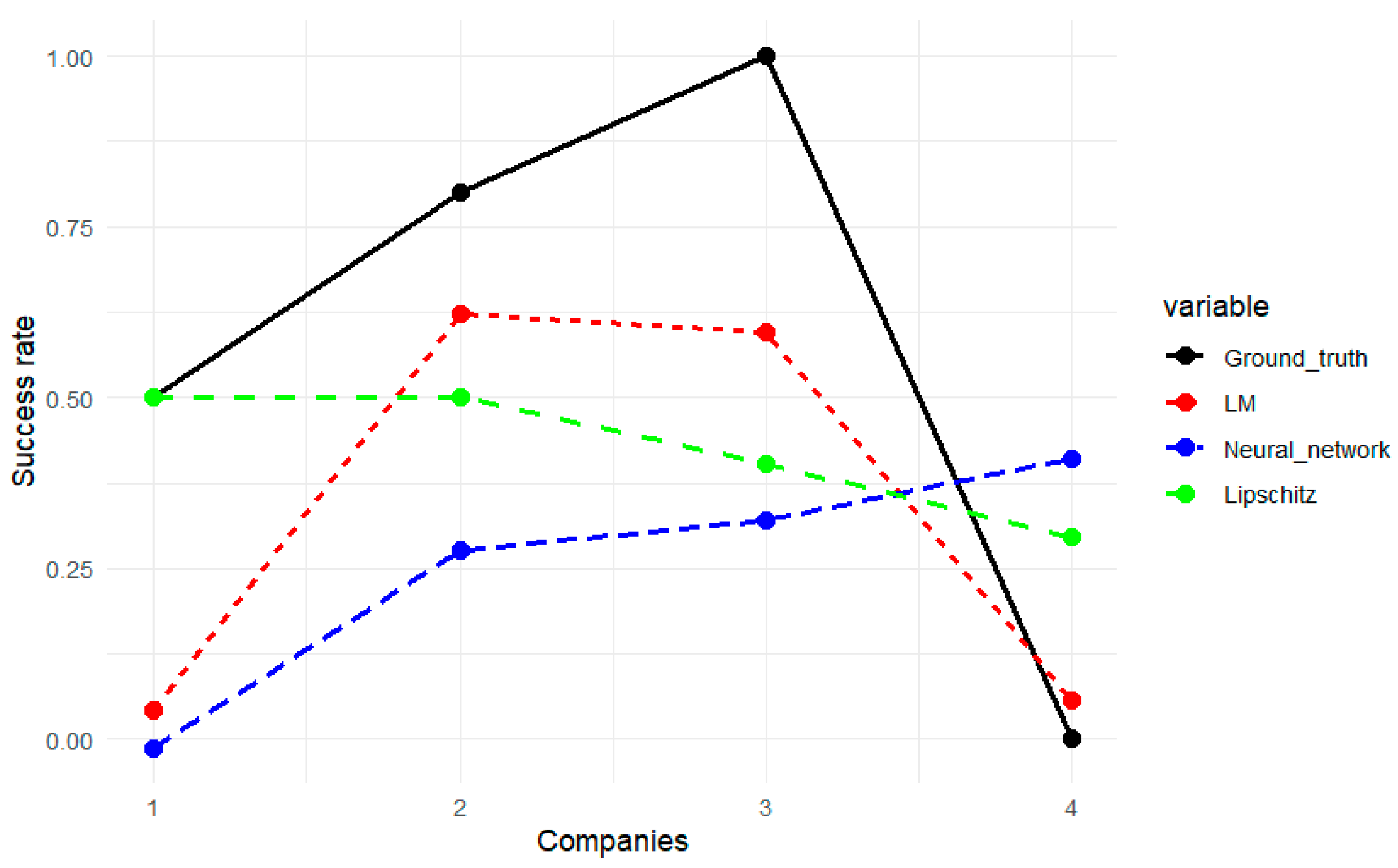
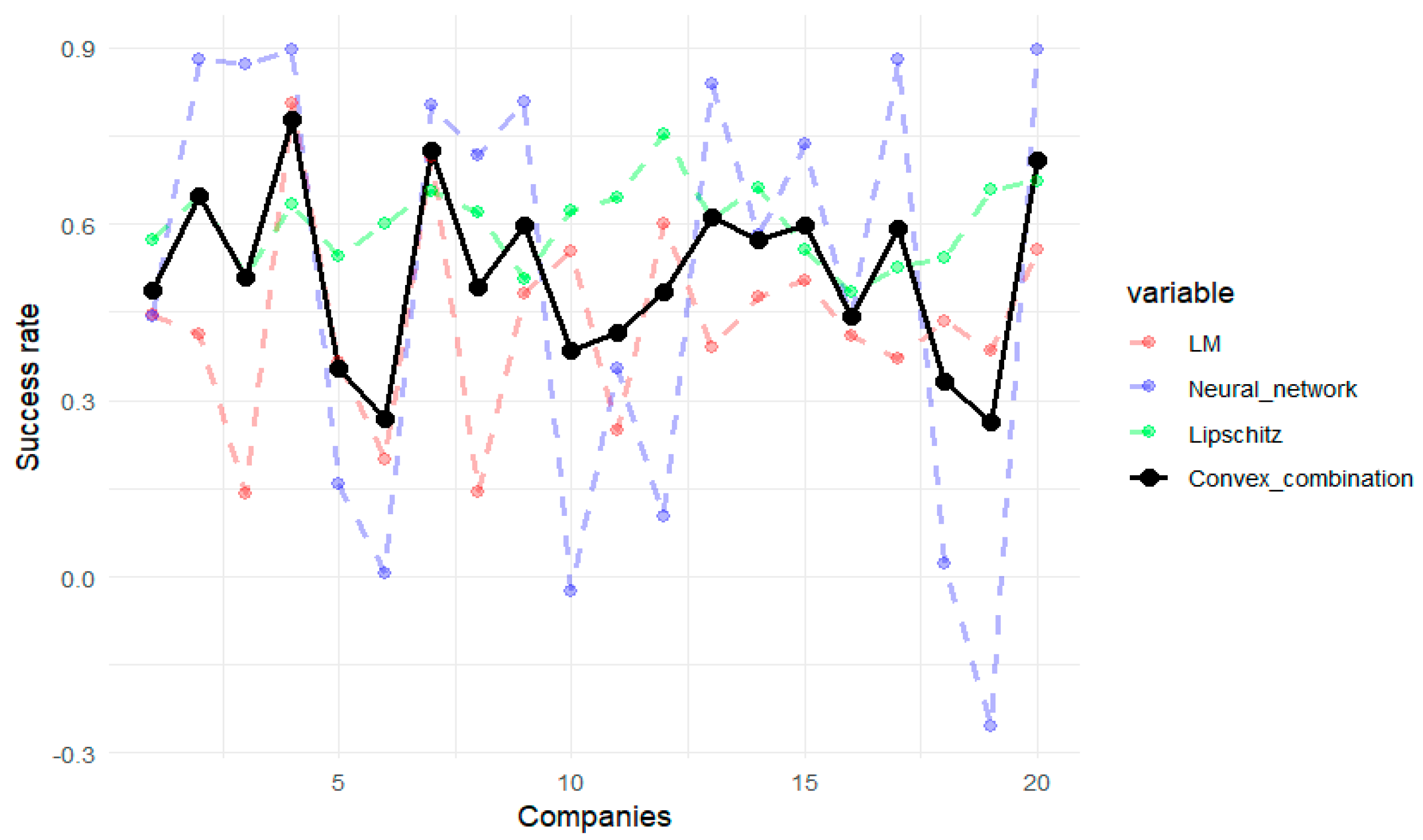
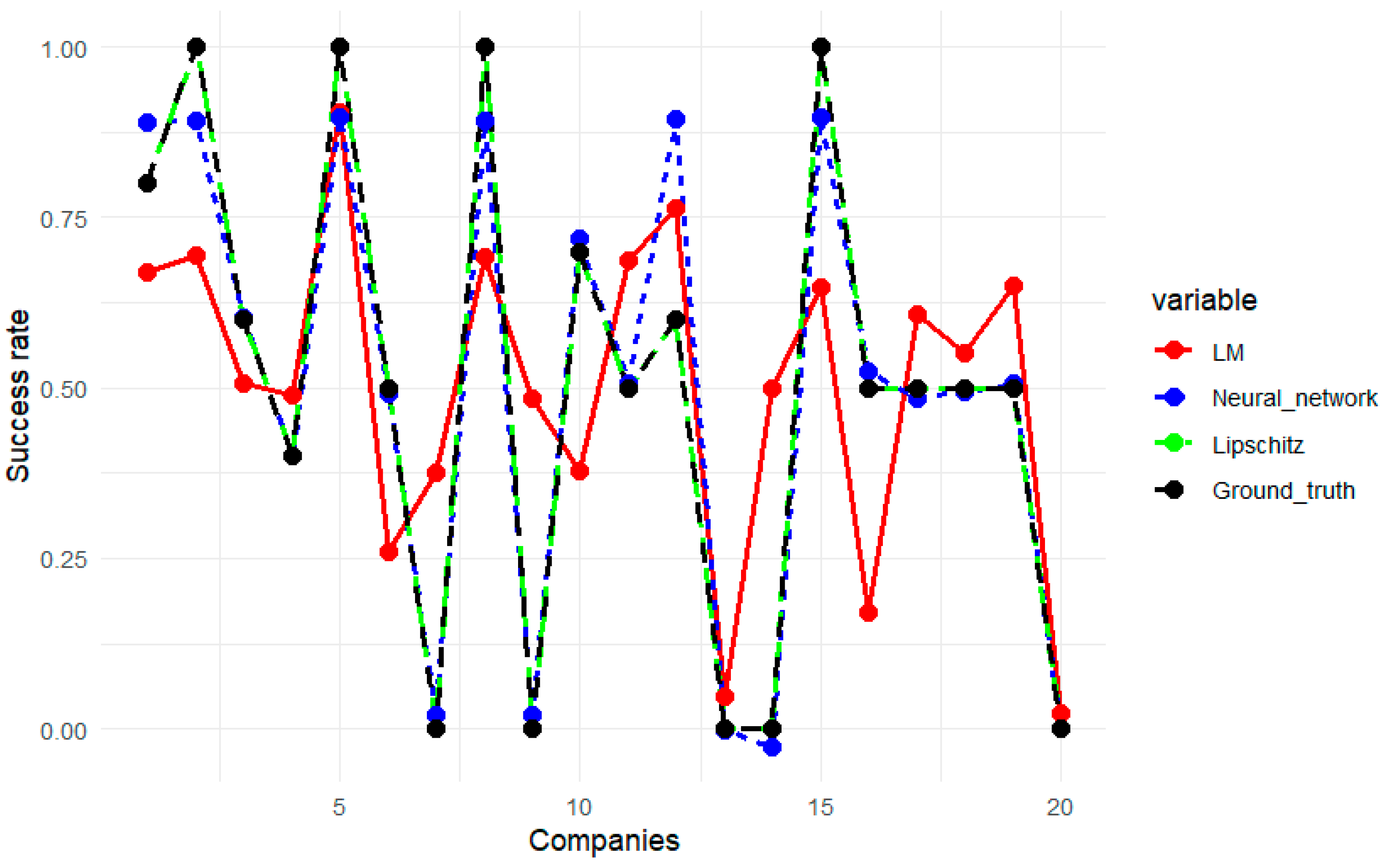
4.1. Overview of the Analytical Tool and Its Results
4.2. Team Dynamics (Block 1)
4.3. Market Conditions (Block 2)
4.4. Product and Service Differentiation (Block 3)
4.5. Financial Metrics (Block 4)
4.6. Strategic Vision and Timing (Block 5)
5. Discussion
5.1. Strengths of the Proposed Model
5.2. Theoretical Contributions
5.3. Empirical Contributions
5.4. Contributions to the Literature
5.5. Practical Implications
5.6. Limitations and Future Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Cantamessa, M.; Gatteschi, V.; Perboli, G.; Rosano, M. Startups’ roads to failure. Sustainability 2018, 10, 2346. [Google Scholar] [CrossRef]
- Cooper, R.G. Stage-gate systems: A new tool for managing new products. Bus. Horiz. 1990, 33, 44–54. [Google Scholar] [CrossRef]
- Wernerfelt, B. A resource-based view of the firm. Strateg. Manag. J. 1984, 5, 171–180. [Google Scholar] [CrossRef]
- Nambisan, S. Digital entrepreneurship: Toward a digital technology perspective of entrepreneurship. Entrep. Theory Pract. 2017, 41, 1029–1055. [Google Scholar] [CrossRef]
- Sun, X.; Abdullahi Usman, M. Drivers of platform ecosystem adoption: Does innovation capability translate these drivers into improved firm performance. Bus. Process Manag. J. 2025, 31, 118–145. [Google Scholar] [CrossRef]
- Chesbrough, H.W. Open Innovation: The New Imperative for Creating and Profiting from Technology; Harvard Business Press: Brighton, MA, USA, 2003. [Google Scholar]
- Granstrand, O.; Holgersson, M. Innovation ecosystems: A conceptual review and a new definition. Technovation 2020, 90, 102098. [Google Scholar] [CrossRef]
- Taleb, N.N. Antifragile: Things That Gain from Disorder; Random House: New York, NY, USA, 2012. [Google Scholar]
- Arnau, R.; Calabuig, J.M.; Erdogan, E.; Sánchez Pérez, E.A. Extension procedures for lattice Lipschitz operators on Euclidean spaces. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A-Mat. 2023, 117, 76. [Google Scholar] [CrossRef]
- Blom, T.; Mooij, J.M. Robustness of model predictions under extension. arXiv 2020, arXiv:2012.04723. [Google Scholar]
- Gassmann, O.; Frankenberger, K.; Csik, M. The Business Model Navigator: 55 Models That Will Revolutionise Your Business; Pearson: London, UK, 2014. [Google Scholar]
- Eisenmann, T.; Parker, G.; Van Alstyne, M. Strategies for two-sided markets. Harv. Bus. Rev. 2006, 84, 92–101. [Google Scholar]
- Fuertes-Callén, Y.; Cuellar-Fernández, B.; Serrano-Cinca, C. Predicting startup survival using first years financial statements. J. Small Bus. Manag. 2022, 60, 1314–1350. [Google Scholar] [CrossRef]
- Levie, J.; Lichtenstein, B.B. A terminal assessment of stages theory: Introducing a dynamic states approach to entrepreneurship. Entrep. Theory Pract. 2010, 34, 317–350. [Google Scholar] [CrossRef]
- Font-Cot, F.; Lara-Navarra, P.; Serradell-Lopez, E. Digital transformation policies to develop an effective startup ecosystem: The case of Barcelona. Transform. Gov. People Process Policy 2023, 17, 344–355. [Google Scholar] [CrossRef]
- Banerji, D.; Reimer, T. Startup founders and their LinkedIn connections: Are well-connected entrepreneurs more successful? Comput. Hum. Behav. 2019, 90, 46–52. [Google Scholar] [CrossRef]
- Brinckmann JA, N.; Kim, S.M. Why we plan: The impact of nascent entrepreneurs’ cognitive characteristics and human capital on business planning. Strateg. Entrep. J. 2015, 9, 153–166. [Google Scholar] [CrossRef]
- Davila, A.; Foster, G. Management control systems in early-stage startup companies. Account. Rev. 2007, 82, 907–937. [Google Scholar] [CrossRef]
- Porter, M.E. Competitive Strategy: Techniques for Analyzing Industries and Competitors; Free Press: Los Angeles, CA, USA, 1980. [Google Scholar]
- Altman, E.I. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. J. Financ. 1968, 23, 589–609. [Google Scholar] [CrossRef]
- Amat, O. Análisis de Estados Financieros; Gestión 2000: Barcelona, Spain, 1990. [Google Scholar]
- Erdoğan, E.; Ferrer-Sapena, A.; Jiménez-Fernández, E.; Sánchez-Pérez, E.A. Index spaces and standard indices in metric modelling. Nonlinear Anal. Model. Control 2022, 27, 803–822. [Google Scholar] [CrossRef]
- Ferrer-Sapena, A.; Erdogan, E.; Jiménez-Fernández, E.; Sánchez-Pérez, E.A.; Peset, F. Self-defined information indices: Application to the case of university rankings. Scientometrics 2020, 124, 2443–2456. [Google Scholar] [CrossRef]
- Di Franco, G.; Santurro, M. Machine learning, artificial neural networks and social research. Qual. Quant. 2021, 55, 1007–1025. [Google Scholar] [CrossRef]
- Dobson, A.J.; Barnett, A.G. An Introduction to Generalized Linear Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gangwani, D.; Zhu, X. Modeling and prediction of business success: A survey. Artif. Intell. Rev. 2024, 57, 44. [Google Scholar] [CrossRef]
- Blank, S.; Dorf, D. The Startup Owner’s Manual: The Step-by-Step Guide for Building a Great Company; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Kerr, W.R.; Nanda, R.; Rhodes-Kropf, M. Entrepreneurship as experimentation. J. Econ. Perspect. 2014, 28, 25–48. [Google Scholar] [CrossRef]
- Koumbarakis, P.; Volery, T. Predicting new venture gestation outcomes with machine learning methods. J. Small Bus. Manag. 2023, 61, 2227–2260. [Google Scholar] [CrossRef]
- Gujarathi, A.; Shukla, T.; Nirban, V. Probabilistic Prediction for a Start-Up Success Through Bayesian Networks-Based Machine Learning Approach. In Proceedings of the 2024 International Conference on Emerging Innovations and Advanced Computing (INNOCOMP), Sonipat, India, 25–26 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 513–518. [Google Scholar]
- Huang, K.; Zhou, Y.; Yu, X.; Su, X. Innovative entrepreneurial market trend prediction model based on deep learning: Case study and performance evaluation. Sci. Prog. 2024, 107, 00368504241272722. [Google Scholar] [CrossRef] [PubMed]
- Köseoğlu, S.D.; Patterson, A. Introduction to startup valuation: From idea to, I.P.O. In A Practical Guide for Startup Valuation: An Analytic Approach; Springer Nature: Cham, Switzerland, 2023; pp. 7–42. [Google Scholar]
- McCarthy, P.X.; Gong, X.; Stephany, F.; Braesemann, F.; Rizoiu, M.A.; Kern, M.L. The science of startups: The impact of founder personalities on company success. arXiv 2023, arXiv:2302.07968. [Google Scholar] [CrossRef]
- Thirupathi, A.N.; Alhanai, T.; Ghassemi, M.M. A machine learning approach to detect early signs of startup success. In Proceedings of the Second ACM International Conference on AI in Finance, Virtual Event, 3–5 November 2021; pp. 1–8. [Google Scholar]
- Dworak, D. Analysis of Founder Background as a Predictor for Start-Up Success in Achieving Successive Fundraising Rounds. Doctoral Thesis, University of Michigan, Ann Arbor, MI, USA, 2022. [Google Scholar]
- Risku, J. Improving the performance of early-stage software startups: Design and creativity viewpoints. arXiv 2021, arXiv:2108.00521. [Google Scholar]
- Polese, F.; Sirianni, C.A.; Guazzo, G.M. How Startups Attained Resilience During COVID-19 Pandemic Through Pivoting: A Case Study. In The International Research & Innovation Forum; Springer International Publishing: Cham, Switzerland, 2022; pp. 519–527. [Google Scholar]
- Zhang, J.; Yu, B.; Lu, C. Exploring the effects of innovation ecosystem models on innovative performances of startups: The contingent role of open innovation. Entrep. Res. J. 2021, 13, 1139–1168. [Google Scholar]
- Park, J.; Choi, S.; Feng, Y. Predicting startup success using two bias-free machine learning: Resolving data imbalance using generative adversarial networks. J. Big Data 2024, 11, 122. [Google Scholar] [CrossRef]
- Shi, Y.; Eremina, E.; Long, W. Machine learning models for early-stage investment decision making in startups. Manag. Decis. Econ. 2024, 45, 1259–1279. [Google Scholar] [CrossRef]
- Sevilla-Bernardo, J.; Sanchez-Robles, B.; Herrador-Alcaide, T.C. Success factors of startups in research literature within the entrepreneurial ecosystem. Adm. Sci. 2022, 12, 102. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Font-Cot, F.; Lara-Navarra, P.; Sánchez-Arnau, C.; Sánchez-Pérez, E.A. Startup Survival Forecasting: A Multivariate AI Approach Based on Empirical Knowledge. Information 2025, 16, 61. https://doi.org/10.3390/info16010061
Font-Cot F, Lara-Navarra P, Sánchez-Arnau C, Sánchez-Pérez EA. Startup Survival Forecasting: A Multivariate AI Approach Based on Empirical Knowledge. Information. 2025; 16(1):61. https://doi.org/10.3390/info16010061
Chicago/Turabian StyleFont-Cot, Francesc, Pablo Lara-Navarra, Claudia Sánchez-Arnau, and Enrique A. Sánchez-Pérez. 2025. "Startup Survival Forecasting: A Multivariate AI Approach Based on Empirical Knowledge" Information 16, no. 1: 61. https://doi.org/10.3390/info16010061
APA StyleFont-Cot, F., Lara-Navarra, P., Sánchez-Arnau, C., & Sánchez-Pérez, E. A. (2025). Startup Survival Forecasting: A Multivariate AI Approach Based on Empirical Knowledge. Information, 16(1), 61. https://doi.org/10.3390/info16010061





