Abstract
Accurately estimating the absolute distance and height of objects in open areas is quite challenging, especially when based solely on single images. In this paper, we tackle these issues and propose a new method that blends traditional computer vision techniques with advanced neural network-based solutions. Our approach combines object detection and segmentation, monocular depth estimation, and homography-based mapping to provide precise and efficient measurements of absolute height and distance. This solution is implemented on an edge device, allowing for real-time data processing using both visual and thermal data sources. Experimental tests on a height estimation dataset we created show an accuracy of 98.86%, confirming the effectiveness of our method.
1. Introduction
In many applications, it is necessary to measure the size of objects, as well as their distance and speed of movement relative to the observer. Depending on many geometric and physical factors of a given scene, various measurement methods can be used, e.g., sonars, lasers, etc. However, the images and measurements obtained using cameras can be much cheaper and more accessible; however, to measure the depth of the scene in general, we need a stereoscopic camera system, i.e., a two-camera system [1,2]. Nevertheless, modern deep learning methods enable both spatial and depth measurements using only single cameras, i.e., monocular images. Using a single, low-cost camera for these measurements is even more crucial in real-time edge systems [3], and we use this in the presented system.
Accurately estimating the spatial positions and parameters of objects, such as their location on a bird’s-eye view map, absolute distance, and height, is a crucial computer vision (CV) task with significant practical applications. In this paper, we present a new solution for estimating absolute distance and height by combining homography-based mapping algorithms with cutting-edge deep learning techniques. Our method leverages the advantages of both traditional and modern approaches to deliver highly accurate and efficient estimations under various conditions.
The proposed method integrates several crucial components to deliver a comprehensive solution for absolute height estimation. First, we capture video frames from both visual and thermography cameras and feed them into object detectors. For this purpose, we use the “You only look once” (YOLO) architectures, which are de facto state-of-the-art real-time object detectors [4]. Specifically, the YOLOv5 and YOLOv8 models are employed. They facilitate robust identification and localization of objects in a monocular view. On the other hand, for relative depth estimation, we use a transformer-based monocular depth estimation model called the dense prediction transformer (DPT) LeViT 224 [5,6]. This model learns to infer depth from a single image, allowing us to compute the relative distances among objects in the scene. Additionally, we apply homography-based mapping techniques to determine correspondences between points in different images or views. By leveraging homography projection, we can accurately map objects from the video frame plane to a bird’s-eye view 2D map, making it easier to estimate their distance from the camera. The final stage of our approach involves using polynomial regression to compute the absolute distance and height of objects.
The proposed solution is deployed on the AraBox edge device [7], as detailed in Section 3.1. This device, built on the Jetson Nano board, provides real-time data processing capabilities [3]. AraBox is tailored for work on anonymous data collection in order to operate in the Digital Out-of-Home (DOOH) advertising sector and fulfilling data privacy requirements. However, this technology is much more universal. AraBox devices can be used in many other business domains, such as waste reduction based on AI [8], production on industrial lines [9], healthcare for elderly care [10], and many more.
In our experiments, we showcase the effectiveness of our approach using an absolute height estimation dataset we prepared. The results indicate an accuracy of 98.86% in real-time performance, highlighting the practical aspect of our solution for various applications that demand precise absolute distance and height measurements.
This article is an extended version of our previous research work [11]. Compared to the previous version, we have modified several important system modules. Most importantly, in the path processing visible spectrum images, the already-mentioned novel YOLOv8 was employed for instance segmentation [12]. Then, the ArUco markers were added to facilitate system calibration [13]. Based on these, the homography-based mapping was improved. All these and further improvements are described in the following sections.
The structure of this paper is as follows: Section 2 offers an in-depth review of related works; these include such areas as object detection, homography-based mapping, monocular depth estimation, and absolute height estimation techniques. Section 3 provides a detailed description of our solution’s architecture, including the necessary configuration and calibration processes. Section 4 contains the experimental results that are divided into indoor and outdoor experiments, along with a description of the dataset used and the methodology employed. In the end, Section 5 presents conclusions on our findings and suggests potential areas for future enhancement.
2. Related Works
In this section, we review the existing research and progress in computer vision, emphasizing object detection, homography-based mapping, monocular depth estimation, and absolute height estimation techniques.
2.1. Object Detection
Object detection is a fundamental task in computer vision with numerous applications [14,15,16,17]. The most effective object detectors today are based on convolutional neural networks (CNNs). The initial breakthrough for CNN-based object detectors came with two-stage detectors like the region-based convolutional neural network (R-CNN), proposed by Girshick et al. [18], which demonstrated exceptional performance. This success led to further developments such as Fast R-CNN [19] and Faster R-CNN [20], which are improved two-stage detectors offering faster performance and higher accuracy. On the other hand, there are one-stage detectors. The best known examples of this approach is the original architecture called You Only Look Once (YOLO) [21], as well as Single-Shot Detector (SSD) [22]. These models are faster, and some of them can operate in real-time on edge devices, simultaneously having an accuracy comparable to two-stage detectors [23].
The prominent one-stage detection framework YOLO has evolved significantly over time. Its upgraded versions, namely YOLOv2 [24] and YOLOv3 [25], incorporated deeper convolutional backbones, residual skip connections, residual blocks, and upsampling techniques. These advancements have established YOLO as one of the fastest object detection methods while maintaining high accuracy. Bochkovskiy et al. introduced YOLOv4 [26], which further enhanced the training process by integrating techniques like CutMix for data augmentation, DropBlock for regularization, and architectural improvements such as the CSPDarknet53 backend network and path aggregation network with spatial attention blocks.
Afterwards, Jocher et al. introduced YOLOv5 [4], which revitalized the YOLO framework and enhanced its effectiveness. The YOLO-based architecture continues to lead as a cutting-edge object detector, with ongoing development and releases of subsequent versions under various monikers. Finally, the newest version of the YOLO family models—YOLOv8 [27]—was released. Created by the Ultralytics team, they implemented minor improvements in YOLOv5 architecture, changing the size and type of a few convolutional layers in the model’s backbone and bottleneck. They also improved model data augmentation techniques and prepared the model to also work in other tasks, such as instance segmentation, tracking, and pose estimation. These strides in object detection have notably enhanced the precision and swiftness of object detection across diverse applications.
2.2. Homography-Based Mapping
Homography-based mapping is a commonly employed method in computer vision for establishing correspondences between points in distinct images and ones seen under different points of view. It operates on the principle of homography, a projective transformation that transfers points from one plane to another. This technique finds extensive use across various applications, such as object tracking, panorama stitching, augmented reality, camera calibration, to name a few.
The studies conducted by Hartley and Zisserman [2], as well as Cyganek and Siebert [1], offer extensive insights into algorithms for homography computations. Furthermore, Szeliski’s research [28] explores methods for robust homography estimation under challenging conditions, such as outliers and noise. These investigations form the fundamental basis for our application of homography-based mapping in height estimation.
There are also novel approaches to homography estimation that are based on deep neural networks. For instance, DeTone et al. present the HomographyNet CNN for estimating the relative homography between pairs of images [29]. They report that in various scenarios, their network outperforms the traditional techniques. Similarly Nguyen et al. also propose a CNN for homography estimation [30]. They reported a faster inference speed compared to traditional algorithms. However, the application of such networks would require the preparation of new datasets.
2.3. Depth Estimation from Monocular Views
The goal of monocular depth estimation is to derive depth details from a single image. This poses challenges due to the inherent uncertainties of monocular vision. However, despite its limitations, a monocular approach to depth estimation holds significant importance across diverse fields, including an approximate 3D reconstruction, scene comprehension, autonomous navigation, and many more.
Over time, there has been notable advancements in techniques for monocular depth estimation. Initial methods emphasized hand-crafted features, a superpixel-based approach, and traditional computer vision algorithms [31,32,33]. However, with the progression of deep learning, convolutional neural networks have emerged as robust solutions for monocular depth estimation.
An important work in this domain is the pioneering research study by Eigen et al., where they introduced a CNN-driven method for predicting monocular depth [34]. This study laid the foundation for subsequent advancements in deep learning-based depth estimation. Another notable contribution is from Laina et al. [35], who devised a swifter and more efficient approach by training a fully convolutional residual network using ResNet-50 [36]. They replaced traditional fully connected layers with up-convolutional blocks and adapted the loss function accordingly, further pushing the boundaries of depth estimation techniques.
Following the rise of CNN-based approaches, numerous studies have emerged to address this domain. Several notable contributions stand out: Lee et al. [37] introduced a method centered on relative depth relationships within images. Ranftl et al. [38] developed a tool capable of blending multiple datasets during monocular depth estimation training, even when their annotations were incompatible, thus paving the way for future advancements in the field. Furthermore, Ranftl et al. [5] proposed an architecture for dense vision transformers in depth estimation, leveraging a transformer backbone to achieve more detailed and globally consistent predictions compared to traditional fully convolutional approaches. Finally, Graham et al. proposed the transformer-based monocular depth estimation model DPT LeViT 224 [6]. This is also the model we use in the presented system.
2.4. Absolute Height Estimation
Albeit less mainstream, compared to other tasks mentioned earlier, absolute height estimation presents an intriguing challenge in CV. To tackle this issue, several methodologies have emerged, utilizing techniques such as image depth estimation [39], convolutional neural networks [39,40,41], and convolutional–deconvolutional deep neural networks (CDNNs) [42].
An influential study in this field is the research study conducted by Yin et al. [39], who devised a four-stage estimator employing multiple CNN networks on a single-depth image. Their method demonstrated remarkable accuracy in height estimation, achieving up to 99.1%. It is noteworthy that their approach was tested under controlled laboratory conditions, focusing on subjects positioned around 2 m from the camera. Despite these controlled parameters, the results obtained were highly impressive.
Absolute height estimation remains a niche within the field of CV, with fewer studies conducted compared to more established tasks. Consequently, we consider it a compelling area warranting further research and development.
3. System Architecture
In this chapter, we introduce the primary contribution of our paper, which is the design of our system for estimating the absolute height and distance of objects. It is implemented on an edge device known as AraBox, created by MyLed [7]. The structure of our pipeline is depicted in Figure 1. The input signal comes from two branches: firstly from the visible spectrum and secondly from the thermal camera.
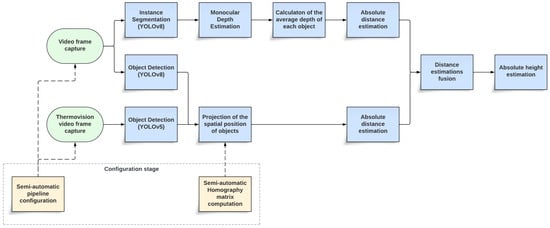
Figure 1.
Block diagram of our height estimation system.
In the first flow, we project the video signal onto a bird’s-eye view using homography-based mapping. This enables us to estimate the spatial position of objects, as well as their distance from the camera and height, based on initial configuration, polynomial regressions, and the height of bounding boxes estimated by YOLOv8. A similar process is applied to the thermal image signal, but with a different homography matrix.
The second flow is performed only on the video signal and utilizes YOLOv8 in instance segmentation mode [12]. It then uses the DPT LeViT 224 monocular depth estimation model [5,6]. This network estimates the relative depth of the image, and its output is combined with YOLOv8 masks to calculate the average depth value for each object. Using a polynomial regression model from the device configuration and the relative depths of the detected objects, we can estimate their absolute distance from the camera, as well as their absolute height, similar to the first flow. Finally, we average the results from all three flows to estimate the final height of the objects. More details on each of the pipeline steps are provided in the following subsections.
3.1. AraBox Device
AraBox, illustrated in Figure 2, is a device designed for completely anonymous data collection in the retail sector. It can be utilized in both brick-and-mortar stores and the outdoor advertising industry (especially in its digital format, known as DOOH). The core component of the device is an embedded system featuring a GPU, like the Jetson Nano, which handles the encryption and processing of data from connected cameras [3]. AraBox also includes a carrier board, power supply, fans, a special case, and two cameras: one with a regular vision (model ELP-USB500W05G-FD100) [43] and a thermal imaging camera (model SEEK Thermal MS202SP Micro Core) [44]. While AraBox has many use cases, we use it specifically for height estimation in our research.

Figure 2.
AraBox device—a version with normal and termovision cameras and a Jetson Nano board.
3.2. YOLOv5 and YOLOv8 Object Detectors
This part of our pipeline comprises a YOLOv8 model trained on visual images and a YOLOv5 model trained on a thermal dataset. Both datasets contain approximately 20,000 annotated photos captured in urban environments. The models’ outputs include the class of an object (such as human, car, or bus), its anchor location represented by two coordinates, and the height and width of the bounding box. YOLOv8 can also be used in instance segmentation mode, allowing us to obtain masks of the objects and use them for more detailed calculations of object depths, based on the monocular depth estimation models.
3.3. Homography-Based Mapping
The purpose of this step is to project the detected object’s location from a 3D image onto a 2D “map” presented from a bird’s-eye view, as illustrated in Figure 3. This projection allows us to estimate the object’s distance and height in subsequent steps. To accomplish this, we first have to perform a semi-automated calibration process, described in Section 3.7, and calculate the homography matrix for a given location. This matrix is then used to transform YOLOv5 and YOLOv8 detections onto a 2D plane. With the objects’ positions on this plane and the scale information saved during configuration, we can accurately estimate their distance from the camera and their height using polynomial regression.
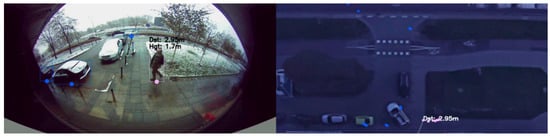
Figure 3.
An example of projecting the location of an object via homography-based mapping.
3.4. Monocular Depth Estimation
In this step, we employ the DPT Levit 224 [5,6] monocular depth estimation neural network. Given an input image, the network produces a map of relative depth estimates, where lower pixel values indicate objects that are farther from the camera. To increase the precision of our estimations, we first crop the image to exclude any visible sidewalls or casing fragments before feeding it into the neural network.
The DPT LeViT 224 model we utilize was trained using a publicly available tool designed for integrating various monocular depth estimation datasets [38]. By leveraging this pre-trained model, we can accurately estimate the relative depth of objects within the scene, even when they are partially obscured or have intricate geometries.
3.5. Absolute Distance Estimation of Objects
The estimation of object distance from the camera is conducted using two methods, depending on the outcomes of the preceding step. If distance estimation relies on the object’s spatial position derived from homography-based mapping, the process is straightforward. We simply multiply the object’s distance from the camera (in pixels) by the scaling factor specified in the device configuration—see Section 3.7.
Alternatively, when distance estimation utilizes monocular depth estimation, the procedure becomes more intricate. Here, we first compute the average depth value for each mask generated by YOLOv8. Subsequently, these values are substituted into a polynomial regression formula stored in the device’s configuration. This formula defines the relationship between depth values and distance at a specific location, facilitating a precise estimation of absolute distance. Detailed instructions on deriving the coefficients for these polynomials are provided in Section 3.7, which describes the configuration procedure.
3.6. Estimation of Absolute Height of Objects
Once the absolute distance of the object from the camera is determined, we proceed to estimate its height. This is achieved through polynomial regression, where we establish a relationship between the distance value and the actual height to pixel height ratio. Subsequently, we multiply this ratio by the object’s height in pixels obtained from the YOLOv5 and YOLOv8 detectors. This computation provides an accurate estimation of the object’s absolute height, which is the output of our pipeline.
3.7. Semi-Automatic Pipeline Configuration
As previously stated, a crucial aspect of our pipeline and essential for its proper functioning is the configuration and calibration tailored to each deployment location. Key parameters that require a configuration include homography matrices, coefficients for third-order polynomials used in distance and height regression, and the pixel-to-meter scale factor.
The first parameter to configure is the homography matrix. To simplify this process, we have implemented a semi-automated approach using ArUco markers [13]. These markers are synthetic square images featuring a distinct black border and an internal binary matrix that determines their unique identifier (ID). Figure 4 provides a visual representation of sample markers.

Figure 4.
Sample ArUco markers.
We developed a dedicated Python program for the calibration process. Its main task is to detect ArUco markers and their corresponding IDs at predefined locations relative to the camera, as illustrated in Figure 5. The program also measures the height of individuals holding markers in terms of pixels and stores them with locations in a dictionary (with markers’ IDs as keys). The sample detection made by the program is presented in Figure 6.
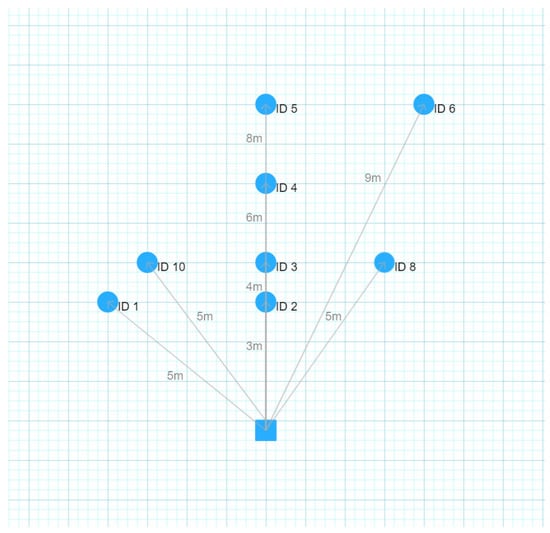
Figure 5.
The diagram illustrates the locations relative to the camera where a person should stand and hold an ArUco marker for program calibration. Each position corresponds to a distinct ArUco tag ID. These locations have been strategically chosen to ensure straightforward measurement. They are either aligned in a straight line in front of the camera or configured into triangles with sides of 3 m, 4 m, and 5 m, as well as another triangle with sides of 4 m, 8 m, and approximately 9 m.

Figure 6.
A sample photo taken by the program during a calibration process. In the photo, the program successfully detected the ArUco marker with ID 8 and detected the person holding it. The coordinates of the person’s bounding box for marker ID 8 were then saved by the program.
After finishing the measurements at each designated point, the program calculates the homography matrix and polynomial regression coefficients to determine the relationship between object pixel height and actual height relative to the distance from the camera. This way obtained regression curve is shown in Figure 7. For enhanced precision, the measurements can be repeated with a different individual, and the results can be averaged. These computed values should then be updated in the main program’s configuration file.
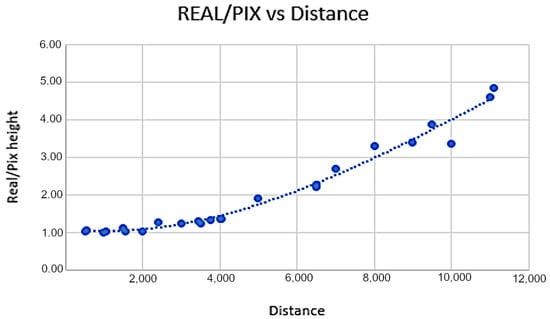
Figure 7.
Regression curve calculated in the calibration phase for mapping the height of objects in pixels to the height of objects in meters.
The final parameter essential for calibrating the device to a specific location is the scale that defines the real-world distance corresponding to one pixel on the 2D map. This scale can be precisely determined by measuring the distance between two reference points on Google Maps [45] and by comparing it to the pixel distance between those same points on our 2D map, as shown in Figure 8.

Figure 8.
An example of distance measurement for device calibration using Google Maps.
Once all parameters have been calibrated and configured, the device is prepared to accurately estimate the absolute height and distance of objects at the designated location. The complete calibration process usually takes about 15 min.
4. Experiments and Results
To verify the effectiveness of our method, we carried out an experiment using a small dataset consisting of videos of eleven individuals with known heights. The videos were recorded in two different locations—one in an outdoor setting and the other indoors. With this dataset, we evaluated the performance of our system following the methodology outlined in Section 4.2 and obtained an estimation accuracy of 98.86%.
The experiment was designed to evaluate the system’s accuracy in estimating the height of individuals under various environmental conditions and to validate the effectiveness of our method. In the following sections, we will discuss the details of the collected dataset, present our methodology, and provide the results obtained from our measurements.
4.1. Dataset
The dataset consists of 10 recordings, each featuring a different individual with a known height. These recordings were captured using the AraBox device (Section 3.1) and its cameras.
The dataset includes videos from two distinct locations: (i) indoors, specifically in an office space, with a total of three recordings, and (ii) outdoors—in a parking lot, with a total of seven recordings. The heights of the individuals ranged from 160 cm to 185 cm. Although the dataset is not large, we believe it offers enough variety to validate and confirm the effectiveness of our absolute height estimation method.
4.2. Validation Methodology
The following methodology was used to validate the performance of our method for estimating individuals’ absolute height. For each video in our dataset, our model performed height estimations on every frame where the YOLOv8 detection model identified a person. The estimated heights were recorded in a temporary table, and the measurements were averaged at the end of the video. For this purpose, Formula (1) was employed, where represents the averaged height measurement result, stands for the result from a single frame, and N is the number of frames in which the person was measured.
In the next step, these estimates were compared with the known actual heights of the individuals () to calculate percentage errors using Formula (2).
For a comprehensive evaluation, we stored all the results along with the results from each module of our system. These are shown in Table 1 and Table 2, respectively. These tables contain a consolidated record of the estimated heights, actual heights, and corresponding absolute errors for each video. Additionally, they include the estimated heights from each component of the pipeline, including homography-based mapping using the vision data (HBM vision), homography-based mapping using the thermal data (HBM thermo), monocular depth estimation (MDE), and the fusion module. On the other hand, results of the fusion module are calculated in accordance with the following formula:

Table 1.
Results of indoor experiment.

Table 2.
Results of outdoor experiments.
As evident, the fusion equation (Equation (3)) is not merely an arithmetic mean, given the predominant influence of the module reliant on monocular depth estimation. This preference stems from the homography-based mapping modules yielding comparable data, while the monocular depth estimation module contributes unique and supplementary information. Through this approach, we can systematically evaluate the precision and dependability of our height estimation technique across the complete dataset. The percentage errors calculated will enable us to evaluate the operational effectiveness of our system and pinpoint avenues for enhancement.
In the following sections, we will outline the specific outcomes derived from our assessment and examine the implications of these discoveries on the efficacy of our approach.
4.3. Results
The outcomes of our experiments are illustrated in three distinct tables. Table 1 presents the assessments conducted indoors for three individuals. Table 2 exhibits the assessments conducted in an outdoor setting for eight individuals. Lastly, Table 3 shows a consolidated summary of the results obtained across all experiments using a weighted average approach.

Table 3.
Summary of the results.
The achieved average accuracies in each experiment are as follows: 99.44% for Experiment 1 and 98.62% for Experiment 2, with an overall weighted average accuracy of 98.86%, respectively. These accuracy values represent the degree of agreement between the estimated heights and the actual heights of the individuals. A more detailed description of the experiments and their results is discussed below.
4.3.1. Experiment No. 1—Indoor Area
The first experiment was conducted indoors. That is, it was in an office space. We recorded the heights of three individuals ranging from 173 cm to 186 cm. On the other hand, the maximum distance from the camera in which they could walk was around 12 m. The system performed around 370 measurements for each person and then averaged them to obtain the final results, which are shown in Table 1. The average accuracy of the absolute height estimations in this experiment was 99.44%. The best-performing module was based on homography mapping, including a signal from the video camera with an error of only 0.90%. However, the worst-performing module was also homography-based mapping, but with a signal from the thermal camera. In this case, the percentage error equaled 4.29%. Figure 9 shows our method operating on data from the indoor experiment.

Figure 9.
Visualization of the key steps of our method in the indoor experiment.
4.3.2. Experiment No. 2—Outdoor Area
In the second experiment, we performed measurements in an open area, i.e., a small parking lot. Seven people with a height of 160 cm to 185 cm participated in this experiment. The maximum distance from the camera in which they could walk was around 20 m. For each participant, a varying number of measurements, ranging from 865 to 1968, were conducted and averaged. Figure 10 depicts exemplary images and measurements in the outdoor experiment. Table 2 shows the final results of this experiment. The average accuracy of the estimations in this case was 99.62%. Similar to the first experiment, the best-performing module was based on homography mapping, with a signal coming from the video camera with an error of only 1.94%. On the other hand, the worst-performing method was once again thermovision homography mapping, with an error equal to 4.39%.

Figure 10.
Visualization of the modules working in the outdoor experiment.
4.3.3. Summary of the Results
In summary, we attained a weighted average precision of 98.86%. Among the various modules utilized, the height estimation module using homography projection achieved the highest precision of 98.37%. Meanwhile, the monocular depth estimation module and the homography-based mapping utilizing thermal imaging achieved slightly lower precisions of 97.65% and 95.64%, respectively.
To explain these outcomes, let us observe that the reduced precision of the model operating on thermal imaging data can be linked to less precise detections by the YOLOv5 model on thermal images, which have a lower resolution than the ones from the visible spectrum. Also, the dataset used to train the YOLOv5 model for thermal images was smaller compared to the conventional dataset, potentially contributing to less robust results. It is worth noting that detections from the thermal-based model frequently exhibited a vertical axis overestimation of 10–15%, a phenomenon absent in standard data.
In relation to monocular depth estimation, specific difficulties arose from background conditions. For example, when a person crossed in front of a car, the model inferred that the person was nearer compared to when they were at an equivalent distance but without a car in the background. Despite this challenge, the outcomes of this experiment were deemed highly satisfactory, considering the complexity of the surroundings.
Experiment no. 2 yielded somewhat less robust findings attributed to the more intricate environment and increased maximum walking distance for individuals. Specifically, distances exceeding 15 m posed considerable challenges for the system in accurately determining both distances and consequently absolute heights.
Looking ahead, our objective is to broaden our dataset and conduct experiments in a greater variety of testing sites and involving a more diverse participant pool. This expansion aims to bolster and enhance our method. Moreover, we will concentrate on refining other facets of our approach, as elaborated in the subsequent section.
5. Conclusions and Future Works
In this paper, a method is presented for the precise determination of distance and height that integrates visual and thermal imaging data. This approach leverages cutting-edge technologies, such as object detection, segmentation, homography-based mapping, and monocular depth estimation, marking a substantial scientific advancement in real-world spatial positioning estimation.
Achieving an accuracy of 98.86%, our method shows encouraging outcomes, positioning it as viable option for deployment on edge devices. Nevertheless, we recognize opportunities for future refinements. Our focus will be placed on enhancing method accuracy and optimizing the setup and calibration procedures.
For future research, our key aim is to broaden our dataset by including more locations and a diverse participant pool. This expansion will offer valuable insights into how various modules of our height estimation approach perform under different environmental conditions. Assessing our method across a broader dataset will help pinpoint areas for enhancement and refine its overall effectiveness.
An additional enhancement to our proposed method will involve optimizing the setup and calibration procedures. Currently, it requires approximately 15 min for a skilled operator to configure the device for a new location. Our goal is to simplify and further automate this process, particularly focusing on automating the calculation of polynomial regression coefficients used in the distance and height estimation modules.
Furthermore, our future road map involves expanding our method with additional modules. These may encompass techniques such as monocular depth estimation using thermal imaging, a human pose estimation approach as detailed in Zheng et al. (2022) [46]. These enhancements are intended to augment the robustness and adaptability of our method in accurately estimating absolute distance and height.
Finally, the next improvement can consist of applying unsupervised deep homography. There are few examples of such methods. For example, DeTone et al. propose a deep convolutional neural network, called HomographyNet, for estimating the relative homography between pairs of images [29]. They report that in various scenarios, their network outperforms traditional techniques. On the other hand, Nguyen et al. also propose a deep CNN for homography estimation [30]. They reported faster inference speed compared to the traditional algorithms. However, this requires the collection of additional data.
In summary, our study demonstrates the feasibility of precise absolute distance and height estimation from a single viewpoint with a high degree of accuracy, which was achieved through a hybrid approach combining object detection and segmentation, homography-based mapping, and monocular depth estimation techniques. Additionally, we acknowledge the potential for future advancements and suggest avenues for further enhancements in this area.
Author Contributions
Conceptualization, B.C.; methodology, B.C.; software, J.G.-J. and M.K.; validation, B.C., S.G. and Ł.P.; resources, S.G.; data curation, M.K.; writing—original draft, J.G.-J. and B.C.; supervision, B.C.; project administration, Ł.P.; funding acquisition, Ł.P. All authors have read and agreed to the published version of the manuscript.
Funding
We are grateful for the financial support provided for this work by the National Centre for Research and Development, Poland, under grant no. POIR.01.01.01-00-1116/20.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Szymon Głogowski and Łukasz Przebinda were employed by the company MyLed. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Cyganek, B.; Siebert, J. An Introduction to 3D Computer Vision Techniques and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 459–474. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: New York, NY, USA, 2003. [Google Scholar]
- NVidia. Jetson Nano. 2024. Available online: https://developer.nvidia.com/embedded/jetson-nano (accessed on 5 June 2024).
- Jocher, G.; Chaurasia, A.; Stoken, A.; Borovec, J.; NanoCode012; Kwon, Y.; TaoXie; Fang, J.; imyhxy; Michael, K.; et al. Ultralytics/YOLOv5: V6.1—TensorRT, TensorFlow Edge TPU and OpenVINO Export and Inference. 2022. Available online: https://zenodo.org/records/6222936 (accessed on 27 June 2024).
- Ranftl, R.; Bochkovskiy, A.; Koltun, V. Vision Transformers for Dense Prediction. arXiv 2021, arXiv:2103.13413. [Google Scholar]
- Graham, B.; El-Nouby, A.; Touvron, H.; Stock, P.; Joulin, A.; Jégou, H.; Douze, M. LeViT: A Vision Transformer in ConvNet’s Clothing for Faster Inference. arXiv 2021, arXiv:2104.01136. [Google Scholar]
- MYLED sp. z o.o. 2021. Available online: https://myled.pl/ (accessed on 3 June 2024).
- Shahin, M.; Chen, F.F.; Bouzary, H.; Krishnaiyer, K. Integration of Lean practices and Industry 4.0 technologies: Smart manufacturing for next-generation enterprises. Int. J. Adv. Manuf. Technol. 2020, 107, 2927–2936. [Google Scholar] [CrossRef]
- Shahin, M.; Maghanaki, M.; Hosseinzadeh, A.; Chen, F.F. Improving operations through a lean AI paradigm: A view to an AI-aided lean manufacturing via versatile convolutional neural network. Int. J. Adv. Manuf. Technol. 2024, 133, 5343–5419. [Google Scholar] [CrossRef]
- Bekbolatova, M.; Mayer, J.; Ong, C.W.; Toma, M. Transformative Potential of AI in Healthcare: Definitions, Applications, and Navigating the Ethical Landscape and Public Perspectives. Healthcare 2024, 12, 125. [Google Scholar] [CrossRef]
- Gąsienica-Józkowy, J.; Cyganek, B.; Knapik, M.; Głogowski, S.; Przebinda, L. Estimation of absolute distance and height of people based on monocular view and deep neural networks for edge devices operating in the visible and thermal spectra. In Proceedings of the 18th Conference on Computer Science and Intelligence Systems (FedCSIS 2023), Warsaw, Poland, 17–20 September 2023; pp. 503–511. [Google Scholar] [CrossRef]
- Hafiz, A.M.; Bhat, G.M. A survey on instance segmentation: State of the art. Int. J. Multimed. Inf. Retr. 2020, 9, 171–189. [Google Scholar] [CrossRef]
- Garrido-Jurado, S.; Muñoz Salinas, R.; Madrid-Cuevas, F.; Marín-Jiménez, M. Automatic generation and detection of highly reliable fiducial markers under occlusion. Pattern Recogn. 2014, 47, 2280–2292. [Google Scholar] [CrossRef]
- Zaidi, S.S.A.; Ansari, M.S.; Aslam, A.; Kanwal, N.; Asghar, M.N.; Lee, B. A Survey of Modern Deep Learning based Object Detection Models. arXiv 2021, arXiv:2104.11892. [Google Scholar] [CrossRef]
- Gąsienica-Józkowy, J.; Knapik, M.; Cyganek, B. An ensemble deep learning method with optimized weights for drone-based water rescue and surveillance. Integr.-Comput.-Aided Eng. 2021, 28, 221–235. [Google Scholar] [CrossRef]
- Knapik, M.; Cyganek, B. Driver’s fatigue recognition based on yawn detection in thermal images. Neurocomputing 2019, 338, 274–292. [Google Scholar] [CrossRef]
- Cyganek, B.; Wozniak, M. Tensor-Based Shot Boundary Detection in Video Streams. New Gener. Comput. 2017, 35, 311–340. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. arXiv 2014, arXiv:1311.2524. [Google Scholar]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. arXiv 2016, arXiv:1506.01497. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. arXiv 2016, arXiv:1506.02640. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the Computer Vision—ECCV 2016; Springer International Publishing: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar] [CrossRef]
- Knapik, M.; Cyganek, B. Fast eyes detection in thermal images. Multimed. Tools Appl. 2021, 80, 3601–3621. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6517–6525. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Jocher, G.; Chaurasia, A.; Qiu, J. Ultralytics YOLOv8. 2023. Available online: https://github.com/ultralytics/ultralytics (accessed on 18 June 2023).
- Szeliski, R. Image Alignment and Stitching: A Tutorial. Found. Trends. Comput. Graph. Vis. 2006, 2, 1–104. [Google Scholar] [CrossRef]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Deep Image Homography Estimation. arXiv 2016, arXiv:1606.03798. [Google Scholar]
- Nguyen, T.; Chen, S.W.; Shivakumar, S.S.; Taylor, C.J.; Kumar, V. Unsupervised Deep Homography: A Fast and Robust Homography Estimation Model. arXiv 2018, arXiv:1709.03966. [Google Scholar] [CrossRef]
- Michels, J.; Saxena, A.; Ng, A.Y. High Speed Obstacle Avoidance Using Monocular Vision and Reinforcement Learning. In Proceedings of the 22nd International Conference on Machine Learning (ICML ’05), Bonn, Germany, 7–11 August 2005; ACM: New York, NY, USA, 2005; pp. 593–600. [Google Scholar] [CrossRef]
- Saxena, A.; Chung, S.; Ng, A. Learning depth from single monocular images. Adv. Neural Inf. Process. Syst. 2005, 18, 1161–1168. [Google Scholar]
- Hoiem, D.; Efros, A.A.; Hebert, M. Automatic photo pop-up. ACM Trans. Graph. 2005, 24, 577–584. [Google Scholar] [CrossRef]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth Map Prediction from a Single Image using a Multi-Scale Deep Network. arXiv 2014, arXiv:1406.2283. [Google Scholar]
- Laina, I.; Rupprecht, C.; Belagiannis, V.; Tombari, F.; Navab, N. Deeper Depth Prediction with Fully Convolutional Residual Networks. arXiv 2016, arXiv:1606.00373. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Lee, J.H.; Kim, C.S. Single-image depth estimation using relative depths. J. Vis. Commun. Image Represent. 2022, 84, 103459. [Google Scholar] [CrossRef]
- Ranftl, R.; Lasinger, K.; Hafner, D.; Schindler, K.; Koltun, V. Towards Robust Monocular Depth Estimation: Mixing Datasets for Zero-shot Cross-dataset Transfer. arXiv 2020, arXiv:1907.01341. [Google Scholar] [CrossRef]
- Yin, F.; Zhou, S. Accurate Estimation of Body Height From a Single Depth Image via a Four-Stage Developing Network. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 8264–8273. [Google Scholar] [CrossRef]
- Lee, D.S.; Kim, J.S.; Jeong, S.C.; Kwon, S.K. Human Height Estimation by Color Deep Learning and Depth 3D Conversion. Appl. Sci. 2020, 10, 5531. [Google Scholar] [CrossRef]
- Alphonse, P.; Sriharsha, K. Depth estimation from a single RGB image using target foreground and background scene variations. Comput. Electr. Eng. 2021, 94, 107349. [Google Scholar] [CrossRef]
- Mou, L.; Zhu, X.X. IM2HEIGHT: Height Estimation from Single Monocular Imagery via Fully Residual Convolutional-Deconvolutional Network. arXiv 2018, arXiv:1802.10249. [Google Scholar]
- ELP. Available online: http://www.elpcctv.com/fixed-focus-usb500w05g-series-c-46_81.html (accessed on 4 August 2024).
- Seek Thermal. Available online: https://www.thermal.com/micro-core.html (accessed on 4 August 2024).
- Google Maps. Available online: https://www.google.pl/maps (accessed on 24 April 2023).
- Zheng, C.; Wu, W.; Chen, C.; Yang, T.; Zhu, S.; Shen, J.; Kehtarnavaz, N.; Shah, M. Deep Learning-Based Human Pose Estimation: A Survey. arXiv 2022, arXiv:2012.13392. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).