Abstract
Reports produced by popular malware analysis services showed a disparity in samples available for different malware families. The unequal distribution between such classes can be attributed to several factors, such as technological advances and the application domain that seeks to infect a computer virus. Recent studies have demonstrated the effectiveness of deep learning (DL) algorithms when learning multi-class classification tasks using imbalanced datasets. This can be achieved by updating the learning function such that correct and incorrect predictions performed on the minority class are more rewarded or penalized, respectively. This procedure can be logically implemented by leveraging the deep reinforcement learning (DRL) paradigm through a proper formulation of the Markov decision process (MDP). This paper proposes SINNER, i.e., a DRL-based multi-class classifier that approaches the data imbalance problem at the algorithmic level by exploiting a redesigned reward function, which modifies the traditional MDP model used to learn this task. Based on the experimental results, the proposed formula appears to be successful. In addition, SINNER has been compared to several DL-based models that can handle class skew without relying on data-level techniques. Using three out of four datasets sourced from the existing literature, the proposed model achieved state-of-the-art classification performance.
1. Introduction
Despite the development of sophisticated defense and protection methods, malware remains the most relevant cyber threat, as it is the main cause of computer network infections [1]. In recent years, many mitigation techniques have been developed to contrast malware proliferation on the basis of malware analysis, which is generally divided into static and dynamic categories [2]. Static analysis consists of searching for malicious content using a set of well-known and engine-related rules during a scanning process. Several advances have been made in such a field, e.g., in the enhancement of yet another recursive acronym (YARA) rules to enable the detection of obfuscated malware [3,4]. Dynamic analysis allows the observation of the behavior of a malicious sample executed in a simulated and protected environment, i.e., a sandbox, which is typically used to run applications or open content without affecting the analysis platform [5]. The effectiveness of this technique is exploited to accurately examine uncertain samples representing a potential zero-day. The use of machine learning (ML) algorithms has been studied extensively to develop innovative detection methods for malware [6]. As a sub-field of ML, deep learning (DL) exhibited promising results in malware analysis tasks. In particular, multiple investigations have discussed the application of DL algorithms for the identification of malicious samples discovered by examining the sequence of application programming interfaces (APIs) labeled during its behavioral analysis [7,8,9]. In fact, these variables are commonly used by malware detection and classification techniques [10]. The results obtained emphasize the effectiveness of this paradigm in malware classification tasks, especially when different malware families must be classified, i.e., in multi-class classification problems [11,12,13]. However, data referred to different classes usually suffer from class imbalance because malicious samples are scarce for certain families, whereas they are plentiful for more widespread families [14,15,16]. Data imbalance represents a popular challenge in the cybersecurity domain [17]. Therefore, it is desirable to develop DL models capable of dealing with class skew, i.e., cost-sensitive approaches that do not require support methods such as data-level sampling algorithms, since the latter methods can alter the distribution of the original data, i.e., the representation of a real-world scenario [18]. In the domain of DL, deep reinforcement learning (DRL) has emerged as a promising area for inspecting the implementation of advanced cost-sensitive threat detection and protection approaches [19]. DRL takes advantage of DL models to approximate the functions involved in the complex reinforcement learning (RL) decision-making process. Recent studies on the application of DRL for cyber security tasks highlight the effectiveness of this technology in addressing the most relevant network intrusion problems [20,21,22]. Its popularity grows because of its flexibility in modeling problems addressed by accurately setting the so-called Markov decision process (MDP). In this regard, the MDP formulation proposed in [23] enables DRL to deal with imbalanced binary classification problems. Consequently, it is possible to develop a DRL classifier capable of tackling cyber threat detection tasks that suffer from class skew [24,25,26].
In our previous paper [27], the performance of several DRL-based classifiers capable of dealing with unbalanced data according to the MDP formulation presented in [28] was analyzed. As DRL agents, we examined the classic deep Q-network (DQN) model [29] and its double-Q-learning-based extension, i.e., the double deep Q-network (DDQN) [30]. Then, each was evaluated when equipped with state-of-the-art DRL techniques, namely, the dueling network design [31], the prioritized experience replay (PER) [32], and noisy networks (NoisyNets) for exploration [33]. As a result of this study, the dueling DQN appeared to be the most effective and robust model among a list of sixteen different DQN configurations. Encouraging results were also obtained from the use of DDQN networks and the PER technique. However, the algorithms evaluated appeared to be sensitive to a single minority class, thereby neglecting the problem of imbalance for any other minority classes in the training set. In addition, for very unbalanced datasets, the contribution to the majority classes must be less, but not very close to zero, to mitigate the risk of the vanishing gradients phenomenon. Both represent unwanted scenarios, and it is necessary to smooth out differences in absolute values returned by the cost function to balance and stabilize learning. In addition, a comparison with DL (cost-sensitive) solutions that represent current state-of-the-art models is required to validate the real effectiveness of DRL algorithms in this specific task. To satisfy these requirements, the contributions proposed in this paper, which significantly extends [27], can be summarized as follows:
- It presents SINNER, i.e., a DRL-based classifier, which leverages a reward function slightly modified compared to that proposed in [28].
- It provides an extended benchmark analysis that involves a state-of-the art DL-based malware family classifier that can deal with class skew at the algorithm level.
The remainder of this paper is organized as follows. Section 2 provides the background on malware analysis, outlines the underlying theory of the DRL field, and focuses on the main concepts used in this paper. The literature survey related to our study is discussed in Section 3. The formulation of the MDP tuple pertinent to this study is presented in Section 4, with a discussion of the reward-sensitive learning of the proposed classifier. Section 5 describes the experimental plan. The results are presented and discussed in Section 6. Finally, the main findings and potential future directions are outlined in Section 7.
2. Preliminaries
This section provides a theoretical framework that emphasizes two main aspects: (i) the characteristics of the variables involved in the problem faced according to the specific malware analysis type considered; (ii) the components of the proposed methodology.
2.1. Malware Analysis
Malware analysis is a fundamental aspect of computer system security. This type of process is implemented in various decision-making and application contexts and is typically categorized as static or dynamic according to the methods used in the procedural stages.
2.1.1. Static Analysis
Static analysis inspects the contents of an item without the need to execute it [34]. Note that such an object (e.g., a file or a network packet) has a structure that includes patterns that can be searched via a scanning process. The latter procedure can be performed to realize different functionalities, such as the extraction of some item’s structural characteristics or matching suspicious contents. For instance, in malware analysis, some static rules can be used by anti-virus (AV) engines to intercept well-known indicator of compromises (IoCs) contained in the target sample. For files running on Windows-like operating systems, these indicators can be represented by APIs imported into the portable executable (PE) header. A possible method to access these features relies on the use of the PE parser [35].
2.1.2. Dynamic Analysis
By employing a controlled environment, the execution of an object can be observed to analyze its behavior in the dynamic analysis of a sample [36]. This analysis is more thorough than the previous one, although it introduces a certain latency. Because the sample is examined during its execution, several types of information can be traced, such as (i) the network traffic generated, i.e., communication with systems from other computer networks; (ii) the operations performed on different file system items; (iii) all functions called upon by each executed process. With regard to the latter point, in the case of Windows-like operating systems, the sample can use some API functions to reach its desired goals. Typically, such an analysis is conducted using the so-called sandbox, such as Cuckoo (https://github.com/cuckoosandbox/cuckoo, accessed on 16 May 2024 (this engine has been actually replaced by CAPE: https://capev2.readthedocs.io/en/latest/, accessed on 16 May 2024)).
2.2. Deep Reinforcement Learning
RL has demonstrated effectiveness across various domains, including robotics, finance, healthcare, and gaming. For example, in robotics, RL algorithms are used for autonomous navigation and manipulation tasks [37,38]. In finance, RL is applied to algorithmic trading and portfolio management [39,40]. In healthcare, multiple clinical cases can be diagnosed [41]. These practical applications have increased interest in RL among researchers and practitioners and in the cybersecurity domain [42]. In the RL area, an agent learns a policy taking action on an environment through a trial-and-error strategy in discrete time steps [43]. During this training phase, the agent gains the ability to perform a desired task by opportunely setting the environment using the MDP tuple , where S and A represent the observation and action spaces, respectively; is the reward function yielding a scalar that the environment returns to assess the effectiveness of the action taken by the agent; is a probability function, determining given and ; is the discount factor () used to decide how much far-off rewards RL agents have to weight with respect to the immediate ones. Training usually involves many episodes (). Let be the j-th training episode. During this phase, the goal is to learn that can maximize the Q-function for each observation (or state) in S and for each action in A [44]. Tabular methods, such as Q-learning [45], a form of temporal difference (TD) learning, can be used to estimate the optimal action values. In some real-world applications, is very large depending on the problem faced, leading to the use of function approximation models to estimate . The rise of DL has significantly strengthened RL techniques. In fact, deep neural network (DNNs) have shown remarkable success in learning representations from raw data, enabling RL algorithms to handle high-dimensional sensory inputs like images and text. Therefore, DRL involves DNNs as estimators so that with the vector of the DNN weights.
2.2.1. Deep Q-Network
The DQN [29] represents a classical DRL algorithm that introduces two novel elements: (i) an experience replay (ER) memory that stores the experience tuples (), where determines whether is terminal; (ii) a target network () structured as the main network. This second DNN estimates the target value to be compared with in the calculation of the loss function , where:
Although the target network is equivalent to the main network, its parameter vector () is updated with the main network parameters () every steps. In contrast, the main network parameters are updated using a mini-batch (b) of tuples randomly sampled from according to a probability function. However, DQN suffers from overestimation because action selection and evaluation are not decoupled during the computation of the target value.
2.2.2. Double Deep Q-Network
The DDQN algorithm [30] primarily aims to reduce the overestimation problem encountered in DQN. Although the DDQN algorithm uses the same elements introduced in DQN, it overcomes over-optimistic value estimations by computing the target as follows:
Thus, the selection of action is independent of its evaluation. In particular, the main network selects the best action in the next state, whereas the target network estimates the value of this action [44]. Because the use of is unchanged, is updated by sampling a mini-batch of experience tuples from the ER used to minimize the loss function .
2.2.3. Dueling Network
In the taxonomy of the RL algorithms provided in [46], both DQN and DDQN belong to the off-policy group. Accordingly, these agents use the behavioral stochastic policy to explore and learn, whereas the target policy improves their ability to address the task. Recall that for this RL algorithm design type, the Q-function determines whether selecting an action is a good decision when the agent is in a given state. As a part of the domain of RL, the so-called value function, defined as , describes the quality of being in a particular state [44]. In addition, another function can be introduced, namely the advantage function as to determine the relative importance of each action. In [31], the authors argued that determining the value of each action choice was significant in some states and irrelevant in others. Therefore, they provided a novel DNN design, known as the dueling network, which separately computes the value and advantage functions to derive Q:
where the last hidden layer of the original DNN consists of two parallel sub-networks with vector parameters and , so that one outputs a scalar and the other outputs a vector of size, i.e., [31].
2.2.4. Prioritized Experience Replay
Using in both DQN and DDQN prevents the consumption of samples online and their subsequent discarding. Consequently, stored experiences can be used repeatedly to learn from. However, some experience tuples, also known as transitions, can result in a more effective learning process than others. In [32], the prioritization of these types of transitions is achieved by introducing the PER technique that exploits the TD error to assess the importance of a generic . For DQN, this can be expressed as . According to the suggestion of the authors, the priority can be assigned using the following two distinct strategies:
Specifically, the rank-based method uses to determine the rank; while is a small value that ensures the selection of samples with a non-zero probability. To correctly sample each transition, the priority calculated in Equation (4) is normalized by considering the maximum priority of any priority so far, determining the probability of being sampled:
where defines a trade-off between taking only transitions with high priority and random sampling (for , Equation (5) degenerates into uniform sampling). Finally, to ensure learning stability, importance sampling weights are used so that each transition assumes the following final importance score during sampling:
(typically set to 0.4 or 0.6) increases linearly over time to reach the unit value at the end of the learning. This hyper-parameter interacts with the prioritization exponent , since increasing both simultaneously intensifies prioritization while concurrently correcting importance sampling more strongly. Thus, Equation (6) is multiplied by , and the result is fed into the Q-learning update.
3. Related Work
This section reports a revision of related articles, i.e., (i) proposals that employed the same macro-paradigm and variables for malware classification; (ii) methodologies that approached the point problem, i.e., multi-class classification of malware using unbalanced datasets; (iii) algorithms and systems that applied the DRL paradigm in the malware analysis domain. Finally, the motivation for the proposed contribution derived from this revision is outlined.
3.1. Deep Learning for API-Based Malware Classification
The DL paradigm obtains encouraging results in malware detection based on features extracted during dynamic analysis, such as API system calls [47]. In [48], the API calls are initially preprocessed to remove subsequences when a single API call is repeated more than twice. The samples were then transformed using the one-hot encoding technique. Finally, the sequencing of API calls is modeled by using a DL algorithm consisting of two convolutional layers and one recurrent layer. In [49], the correlation between the APIs of a generic sequence was determined using word2vec. The obtained vectorized representation is used to train a convolutional neural network (CNN) for recognizing malicious samples. The ransomware detection problem based on API calls extracted during dynamic analysis using Cuckoo was tackled using a long short-term memory (LSTM) model in [50]. In [7], a bidirectional LSTM (BiLSTM) classifier is trained on a dataset consisting of preprocessed API sequences so that APIs consecutively occurring more than twice were removed. This DL classifier outperforms other DL algorithms, such as simple recurrent neural network (RNN), bidirectional gated recurrent unit (BiGRU), gated recurrent unit (GRU), and LSTM. In [51], the authors compared the performance of DL and shallow learning algorithms in terms of classification metrics and timing performance achieved on two different datasets composed of APIs invoked during behavioral analysis. This evaluation was extended to the multi-class malware classification problem with API calls in [52]. Specifically, three popular DL models such as BiLSTM, BiGRU, and deep neural network architecture for tabular data (TabNet) were analyzed and tested on two different state-of-the-art datasets composed of several API sequences, each labeled according to a proper malware family. In [14], the authors employed a pre-trained bidirectional encoder representations from transformers (BERT) base-uncased model to handle class imbalance in the task of classifying multiple categories of Android malware. The experimental phase leverages a dataset for which the dominant class is given by malware; thus, this dataset is under-sampled to obtain different imbalanced scenarios starting from which the robustness of the proposed approach was evaluated. In [53], a BiLSTM-based classification algorithm was implemented to extract the relationship information between APIs. Each of them is categorized according to the operation executed after a series of embedding and convolution operations to model the behavior of the software. In [54], four DL algorithms, i.e., multilayer perceptron (MLP), LSTM, GRU, and Transformer, are examined to classify eight malware categories according to the APIs employed during dynamic analysis. As a result of this analysis, the GRU model achieved better classification performance than the competitors. In [55], the authors leveraged a hybrid feature extraction method based on both CNNs and BiGRUs to differentiate malware and goodware given a sequence of API calls encoded using a natural language processing (NLP)-based approach. The authors of [56] propose an alternative method to improve classification accuracy through an algorithm based on the combination of two DL models, i.e., CNN and LSTM. This methodology leverages API calls and operating codes as a basis for the learning of the malware classification system. In [57], a methodology for malware classification using both malware and goodware PE files. Using a sandbox environment, it was possible to perform dynamic analysis and generate a dataset to filter irrelevant data, malware family classification, and API classification. The results showed a good ability to detect malicious activities, especially those related to file system APIs and registry manipulation. The so-called automated machine learning (AutoML) framework presented in [58] has been evaluated in [59] for malware detection. In particular, it has been employed to perform hyper-parameter tuning, i.e., research into the neural network architecture of multiple DL models that are trained using state-of-the-art malware-related datasets, such as EMBER and SOREL-20M. A well-fine-tuned CNN model was derived from this study that showed better performance than the existing online CNN malware classifiers. The authors of [60] introduce a transformer-based model that detects malware according to API sequences. The proposed methodology exploits a one-dimensional channel attention module to discover the correlation between each variable in the observed sequences. Malware categorization is realized using a reinforcement module that has the primary goal of counting the API frequency in order to analyze the sequences in detail. The results obtained in the experimental phase highlighted the accuracy of the model in distinguishing various malware families even in the presence of zero-day or adversary samples.
3.2. Imbalanced Multi-Class Malware Classification
In [61], class skew was approached at the data level using a random oversampler (ROS). As a classification framework, a multi-layer approach that leverages a combination of XGBoost and ExtraTree ensemble learning models is employed to classify nine malware categories. The ROS technique proved to be the best solution among the approaches compared in [11] to address class imbalance. In such an evaluation, the adjusted dataset was used to train a CNN model to classify several malware categories using three different datasets. In [62], the authors propose a combination of two DL algorithms, i.e., a CNN and an LSTM, for classifying malware images belonging to twenty-five different malware families. Furthermore, the proposed CNN-LSTM cost function is updated to realize a cost-sensitive approach capable of addressing class imbalance, thus driving learning in favor of minority classes. In [15], the problem of classifying nine different malware families in an imbalanced dataset is approached by deploying a self-attention mechanism. In [63], an augmented CNN-based malware classification is presented. Data augmentation is realized by leveraging additive noise techniques, such as Laplace, Gaussian, and Poisson noises. Given a specific noise ratio, increasing training samples in such a way addresses class imbalance and improves the performance of a CNN in classifying seven different malware families. In [12], the class skew is addressed using a random undersampler (RUS) strategy. The authors then evaluated the classification performance of a deep residual network (ResNet-18) by varying the last layer, i.e., classifying the extracted tensors using three traditional ML models instead of a softmax layer. In [16], the authors address the class skew of the training data using bootstrap sampling. The generated training sets are then used to fine-tune BERT and character architecture with no tokenization in neural encoders (CANINE) pre-trained models, producing a bagging-based ensemble model called random transformer forest (RTF), which showed impressive performance on three different unbalanced state-of-the-art datasets. The study proposed in [64] uses image conversion to tackle the problem of class identification of an unbalanced malware dataset. First, a malware sample is converted into a grayscale image and disassembled. Then, a variant of the residual network is used for classification. The model was trained following a decoupled learning strategy that adopts two different balancing methods for the learning step considered: (i) during the representation learning phase, the learner is trained following an instance-balanced sampling strategy, i.e., the selection probability of each training is the same; (ii) during the classifier learning phase, the model is fine-tuned by adopting a class-balanced sampling approach, so that the probability of sample selection is not dependent on the class density. To avoid re-balancing affecting the learning representations, the feature extractor remained fixed and only the classifier was optimized. The dataset used was that proposed by the Microsoft malware classification challenge. The results showed that the decoupled learning approach results in higher classification accuracy than the joint learning scheme. The study presented in [65] assesses the performance of multi-class classifiers for network intrusions using unbalanced data. Unlike previous studies that performed incorrect aggregation of classes (leading to a classification problem with a low number of classes) to tackle the imbalanced problem, in this study, class skew was adjusted relatively by merging the two aforementioned datasets. To interpret the obtained results, multiple explainable artificial intelligence (XAI) models were used, including local interpretable model-agnostic explanations (LIME) for evaluating single-instance models (resulting in unstable explanation) and shapley additive explanations (SHAP), which provides local and global evaluations. Among the compared classifiers, the classification and regression tree (CART) algorithm performed efficiently on a 28-class dataset. A further method to detect Android malware based on heterogeneous and unbalanced data was proposed in [66]. A model called IHODroid was proposed, specifically designed for unbalanced heterogeneous networks using a dataset covering various types of malware and benign applications. To address the unbalanced problem, the dataset was filled with data from generative adversarial networks. A generator of synthetic minority class nodes was then used together with a discriminator to discriminate the nodes generated by the generator. The results showed that the proposed IHODroid model achieves promising classification performance. In [67], the authors proposed an ensemble learning-based multi-class classifier, which involves some data-level pre-processing approaches to adjust the skewed class proportions of some network-anomaly datasets. Specifically, such data-level strategies implement a hybrid sampling plan that combines RUS and an adaptive synthetic sampling approach for imbalanced learning (ADASYN) until the actual majority(minority) class does not reach the average (ideal) number of samples per class, which is given by the total number of samples relative to the number of classes in the entire dataset. The noise is then removed using the Tomek links (T-link). On the basis of these results, the proposed classifier outperformed the competitors, alleviating the bias toward the majority class and weighting the performance of the minority class.
3.3. Deep Reinforcement Learning for Malware Analysis
The number of DRL-based applications has grown significantly in recent studies. In the cyber security domain, several DRL algorithms have been implemented to propose or improve network malware detection solutions [19]. In [68], a DQN-based approach is leveraged to select static features for malware detection purposes. In this scenario, the actions performed by the agent select a set of minimal features to improve the performance of traditional ML classifiers. Analogously, in [69], a DDQN agent is exploited for feature selection, showing a significant performance improvement in the task of Android malware detection when shallow learning algorithms are adopted as classifiers. In [70], a DRL agent is trained to stop the execution of a dynamically analyzed unknown sample to enhance the classification accuracy of the analysis. In [71], a DQN-based approach is used to evade malware detection techniques. In particular, the agent initially analyzes the sample to determine the sequence of actions that lead to malware metamorphosis, preserving its malicious objective while evading the target scanner. Using the policy learned by the agent, the escaped detector can be strengthened. The same objective is achieved in [72] by employing a modified version of an actor-critic agent to predict when behavior analysis should be suspended. In [73], an RL-based framework has been proposed to generate adversarial malware examples capable of evading state-of-the-art ML classifiers and antivirus engines. A similar approach is presented in [74], which uses a DQN agent to identify the set of actions that lead to the generation of new evasive malware samples. In [75], a DDQN agent is used to detect potentially different ransomware variants based on static features belonging to the PE header. In [76], the authors employ an actor-critic architecture with an experience replay agent to optimally schedule the use of classifiers in the ensemble learning model schema, converting a single-step classification problem into sequential decision-making addressed through DRL. In [77], the application of the well-known policy gradient-based proximal policy optimization (PPO) algorithm is considered for malware detection. The DRL-based agent was trained using dynamic features extracted from executable files. Several malware-related datasets were analyzed in order to provide a comprehensive evaluation. Compared with traditional methods, this method achieves competitive performance. In [78], the problem of detecting malware botnet in internet of things (IoT) contexts is tackled using a DDQN agent, which learns a policy according to the information provided (observation space) by a traffic handler that extracts network traffic features using damped incremental statistics methods combined with an attention reward mechanism. The overall framework demonstrated promising detection capability and computational effort.
3.4. Motivation
Based on the literature review discussed above, no previous study has addressed the problem of imbalanced multi-class classification of malware using API calls as features and DRL to implement a classifier. To the best of our knowledge, our paper [27] represents the first comprehensive comparison of DRL-based classifiers employed for the target problem. However, in [27] it was found that the adopted MDP may have problems due to the reward formulation, which affects learning stability and performance for individual classes. For this reason, this paper proposes a new reward formulation, which is discussed and analyzed in detail in the next section.
4. Methodology
This section defines the main components of the proposed methodology, describing (i) the environment setting, i.e., the design of the MDP [28] leveraged to address the imbalanced multi-class classification problem; (ii) the impact of the reward function on agent training; (iii) the proposed update of the reward function to address the drawback emerging in [27].
4.1. Environment Setting
To model the MDP according to the problem addressed, the formulation proposed in [28] has been exploited. This extends the imbalanced classification Markov decision process (ICMDP) presented in [23] to the multi-class scenario, so:
- Training data provide the observation space S; therefore, each training sample represents an observation for a specific timestep t. Note that , with m the number of samples within the training set and n the number of features.
- The action space A consists of all known labels for classes. Therefore, given K classes, , i.e., .
- The reward function represents the main component of the proposed cost-sensitive approach according to the following formula:where , refers to the true label of the observed , and represents the number of samples in the -th class. In this way, the agent can adjust the learning to be more sensitive to minority classes because the higher the , the lower the . Furthermore, in [28], the authors found that the use of the normalization factor improves the learning performance, having as the main effect the scaling of r so that it falls in .
- Finally, according to the definition of S, the states-transition probability is deterministic; thus, the agent advances from to , as determined by the order of the samples within S.
According to the MDP formulation provided, for each t, the agent analyzes a training sample and then predicts the class to which it belongs. The generic training episode ends () either when: (i) all samples within S have been classified; (ii) the agent performs a misclassification.
4.2. Reward-Sensitive Training Analysis
The learning of an optimal policy requires updating the neural network weights by optimizing the loss function introduced in Section 2.2.1. As a general rule, this is achieved using gradient descent algorithms, which also adjust the weights depending on the partial derivatives of the loss function, i.e.:
where, in the case of a DQN agent, the target value assumes the following two possible values using Equations (1) and (7) (deprived of for simplicity):
Substituting Equation (9) in Equation (8) and introducing an indicator function that returns 1 in the case of correct classification and 0 otherwise, the following formula is derived:
Each term in Equation (10) for class k is scaled by . This scaling ensures that the total influence of class k on the loss function gradient is compensated by the number of samples in the k-th class. This normalization makes the contribution of each sample from class k inversely proportional to its representation in the data set.
4.3. Modified Reward Function
A drawback that emerged in [27] was that the DRL-based classifier appeared to be sensitive to single classes with the lowest absolute number of samples. This can be attributed to the formulation of the reward function. In this regard, Table 1 shows the three different unbalanced scenarios (USs), i.e., the distribution of samples per malware family, used in the experiments presented in our previous study. Furthermore, for each pair of class–US, the corresponding is reported and calculated using Equation (7).

Taking into account US-2 and US-3, significant differences in values between classes can be observed. This value was the highest in the single minority class. This deviates considerably from the second and third minority class scores. Therefore, there is a need to reduce these deviations to realize a reward mechanism that can balance learning. Furthermore, for the same USs, the contribution of for the majority classes becomes negligible because it is very close to zero and exposed to the risk of vanishing gradients. Thus, it must be augmented while retaining a consistent (with respect to the problem faced) deviation from the reward values assumed for minority class predictions. To make the reward mechanism more stable and balanced and gradually adjust the magnitude of the reward contributions, we slightly update the reward function as follows:
The softmax applied to (+ for positive classification and − for misclassification) emphasizes larger values and gives less attention to values that were significantly smaller than the maximum value. Adding its complement to the starting value yields the desired smoothing of Equation (7) while preventing degeneration to higher magnitudes. In addition, in this manner, rewards for majority classes are closer to 1 rather than 0. For example, applying Equation (11) to US-3 leads to the following update: .
5. Experimental Setup
This section lists the materials and methods used in the experiments included in the evaluation phase. First, a description of the benchmarking approaches is provided. Then, the datasets, metrics, and test environment are discussed. Finally, the main settings of the proposed methodology are outlined.
5.1. Approaches Used for Benchmark
This section provides the list of approaches compared with SINNER. These were selected from the field of DL (shared with the proposed methodology), and they face the problem of class skew at the algorithmic level as follows:
- According to the literature review provided in Section 3, the following DL models are selected and combined with the cost-sensitive strategies proposed in [11,62], the working principle of which is shown in Table 2:
 Table 2. Cost-sensitive strategies used to drive the training phase of the compared DL models.
Table 2. Cost-sensitive strategies used to drive the training phase of the compared DL models.- -
- LSTM [79]: This popular model belongs to the class of RNNs. The structure of this network consists of three gates in its hidden layers: an input gate, an output gate, and a forget gate. These entities form the so-called memory cell, which traces the data flow, i.e., remembers or forgets information over time. In such a way, LSTMs can maintain long-term dependencies on sequential data. The LSTM used in our experiments has 100 units (size of hidden cells) connected to a final layer, which is a multi-class classification layer (K nodes, each having a softmax activation). Between these connections, there is a dropout layer to mitigate overfitting using a chance of of randomly discarding a neuron.
- -
- BiLSTM [80]: This differs from the aforementioned model regarding the adoption of a bidirectional layer, which enables the forwarding and backwarding of the input to two separate recurrent nets, both of which are connected to the same output layer (having the same properties of the LSTM last layer).
- -
- BiGRU [81]: This method uses a bidirectional approach to analyze sequences in both directions as the previous DL model described, involving as a main model the so-called GRU, which is an LSTM variant. In fact, the GRU has gating units (update and reset gates) that control the flow of information inside each unit without having separate memory cells. The update gate helps the model to determine how much of the past information (from previous time steps) must be passed to the future. In contrast, the reset gate is used by the model to determine how much of the past information is to be forgotten. In this case, the dropout rate is fixed so that a neuron can be discarded with a probability of 0.3.
- -
- TabNet [82]: This is a DL architecture specifically designed for tabular data. During each of the decision steps, such a model exploits a sequential attention mechanism to select features useful to perform a specific prediction, according to the aggregated information collected (the aggregation in dimension is realized by the attentive transformer component of the TabNet encoder). This property enhances the explainability of the model (because of the presence of a feature masking component, which is part of the TabNet decoder, i.e., the module delegated to reconstruct the features generated by the encoder). According to the suggestions provided by the authors of the original paper, , .
Lastly, all the above DL models optimize the loss function using the Adam optimization algorithm and sampling mini-batches of 128, 64, and 1024 training samples for LSTM, bidirectional models, and TabNet, respectively. A number of 50 epochs were considered for the first three models, whereas the last model was trained on 100 training epochs. - RTF [16]: This model consists of an ensemble of homogeneous (equivalent structure of base estimators) pre-trained transformer models. Each is fine-tuned to implement a sequence classification layer using a subset of training data obtained as a result of a stratified (to retain the class distribution coming from the original set) bootstrap sampling technique. Each i-th model, with , generates a probability employed in a majority voting schema, which leads to a traditional bagging method (exploiting the robustness of such an algorithmic procedure with respect to class skew). BERT and CANINE (including CANINE-C and CANINE-S variants) were evaluated as pre-trained models. The setting was the same as that proposed in the experimental evaluation of the original article (Table 7 in [16]).
5.2. Datasets Selected for This Study
The datasets selected for the experimental phase match those used by the authors of RTF, which achieved state-of-the-art performance for the problem at hand [16]. Specifically, four datasets have been used, which refer to statistical units (malware) generated by static and dynamic analysis processes, respectively. For each sample, the variables involved are the APIs with the meaning they take in relation to the type of analysis considered. These can be categorized and described as follows:
- APIs statically extracted from the PE structure of malware samples collected from two main providers, i.e., VirusShare (https://virusshare.com/, accessed on 16 May 2024) and VirusSample (https://www.virussamples.com/, accessed on 16 May 2024), which were labeled using the VirusTotal (https://www.virustotal.com/, accessed on 16 May 2024) engine [83]. These two datasets differ in the number of samples and malware families within each, but they share the feature space size as in [16].
- API sequences traced by dynamically analyzing each malware sample using the Cuckoo sandbox. These are collected in two different datasets, namely Catak [63] and Oliveira [84]. Note that while Catak represents the state-of-the-art in the category of multi-class malware classification problems using APIs, the Oliveira dataset was released as suitable for binary classification problems. Therefore, only the malware contained in the latter dataset were used and labeled, so they were assigned to the malware family indicated by the VirusTotal service. In this assignment process, statistical units without associated classes and malware families with fewer than 100 samples were discarded [16].
API series (in the case of static analysis datasets) and sequences (in the case of dynamic analysis datasets) are pre-processed according to the strategy adopted in [16]. In particular, we first extracted the sequences deprived of consecutive calls from the same API and then restricted the number of columns to 512 for Catak and 100 for the remaining. The distribution of samples for each malware category per dataset is shown in Figure 1. In addition, such a plot illustrates the prevalence of certain malware families compared to others. This property can be interpreted as the occurrence frequency of the given family (and samples within it) in the four datasets taken into account. This aspect is crucial to consider in order to observe that class skew is a real problem that can be attributed in part to the availability of samples for a given family. Finally, there are predominant categories for each individual dataset, and this emphasizes the problem of imbalance. As seen, to leave the distribution of samples unchanged in the resulting sets, the data were split into for training and for testing using a stratified holdout strategy.
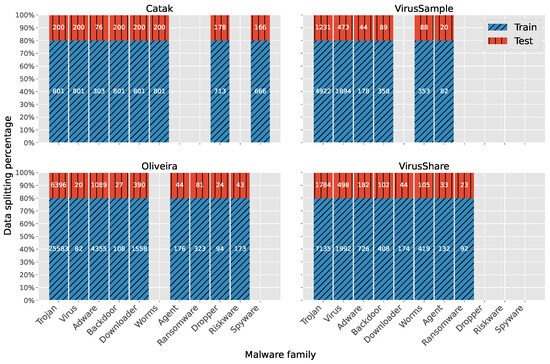
Figure 1.
No. of samples within each malware family per dataset divided using a stratified holdout.
5.3. Metrics
As part of the DL domain, it is essential to perform a training time analysis of all compared approaches because this metric represents the bottleneck of several DL-based classifiers employed in similar problems [85]. To further analyze the timing performance, the trend of the inference time (needed to predict all samples in the test set) is also monitored. Furthermore, depending on the problem tackled, a true positive (TP) represents a correct classification of samples associated with the positive class, whereas a false positive (FP) indicates a misclassification of samples belonging to the same class. Similarly, correct and incorrect classifications in the negative class are denoted with true negative (TN) and false negative (FN), respectively. This notation is valid considering a single class as the reference one at a time; hence, each computation must refer to a single class compared to the other for a multi-class classification problem involving K different classes [86]. According to [16], the following metrics are appropriate for the problem at hand:
- The F1 score, as the harmonic mean of precision (PREC) and true positive rate (TPR), defined as and , i.e., . Specifically, the macro-averaged metric was examined because it assumes that each class has the same impact regardless of its skew [86].
- The area under receiver operating characteristic curve (AUC) computed by identifying the surface below the graph that relates the false positive rate (FPR) to the TPR.
5.4. Setting of the Proposed Methodology
This section provides a description of the configurations of the DQNs evaluated in this study, which are shared with those used in [27]. In our previous paper, we adjusted the algorithmic configurations to maximize the F1 score using the Catak (100 columns) dataset and its undersampled versions. Deliberately, we did not alter the configuration of the RL and DL hyper-parameters to assess the performance actually achieved by SINNER on four different datasets (considering that in this paper the Catak consists of 512 columns). Because dataset-specific tuning was not performed, as was by RTF, we intentionally disadvantaged SINNER compared to the algorithm that achieved state-of-the-art performance for the target problem. For the RL part, we leveraged the following hyperparameter configuration: the discount rate was set to ; the update parameter period consisted of steps; the -greedy exploration policy was invoked to perform an action with a decay period of and . Instead, for the DL part, the main and target DNNs were implemented using two hidden layers, each with 512 nodes. The dueling layer consists of (i) a conv1D layer that has 64 filters and the kernel size set to 8; (ii) two fully connected streams such that one has a single neuron (to compute V), while the second comprises neurons (to compute ). The units of each DNN layer are activated by a rectified linear unit (RELU) function. The PER technique was implemented using the proportional variant. To support the scalability of the benchmark in the case of massive , a sum-tree data structure was used such that both updating and sampling operations require a complexity of . Using Equations (4)–(6), we set , , and . The is minimized using as the learning rate and considering tuples sampled (uniformly when PER was not activated) from the replay buffer (). Furthermore, training lasted , and the gradient descent strategy employed was the Adam optimizer. Figure 2 reports an example of the proposed methodology configuration, i.e., the dueling DDQN, supposing an observation space such that each state comprises 100 APIs.
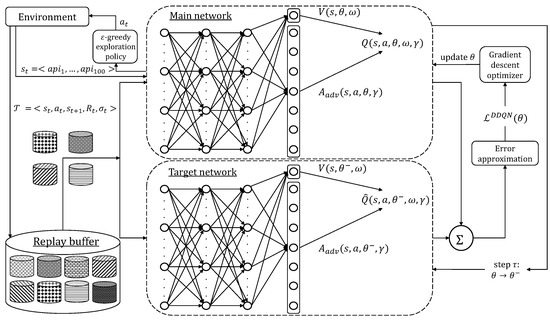
Figure 2.
Workflow of SINNER configured as a dueling DDQN with the ER not prioritized.
5.5. Hardware Settings and Implementation Details
The experiments were performed using the following hardware settings from our laboratory: AMD EPYC 7252 8-core processor 3.1 GHz CPU, two NVIDIA A30 24Gb GPUs (NVIDIA-SMI 535.171.04), and 64 Gb RAM (DDR43200 MHz). The benchmark algorithms were implemented in Python, using the latest versions of Numpy [87] and Pandas [88] libraries for data processing, and Tensorflow [89] as the framework for the DL model implementation. As indicated in [27], the proposed methodology extends the code provided by a public repository (https://github.com/Montherapy/Deep-reinforcement-learning-for-multi-class-imbalanced-classification, accessed on 19 April 2024). Lastly, the RTF follows its original implementation (https://github.com/Ferhat94/Random-Transformer-Forest, accessed on 21 May 2024).
6. Results and Discussion
This section presents and discusses the results obtained from the experimental evaluation. First, the effects derived from the redesigned reward function (Equation (11)) are outlined by analyzing the performance of the three top performers (i.e., the algorithms to which correspond the highest F1 score) on each dataset. These have been compared with the performance achieved by the same algorithm that takes advantage of the inverse reward formulation. Thus, if a top performer is obtained using Equation (11), its opposite will be given by the same algorithm trained using Equation (7), and vice versa. Following this study, we will analyze the performance of the best algorithm per dataset given different reward formulations. As a result of this process, the top four (one for each dataset) final algorithms represent the SINNER configuration to compare with the selected benchmark approaches.
6.1. Reward Influence Analysis
Figure 3 displays comparisons of the reward functions defined in Equations (7) and (11). In particular, the corresponding output of is evaluated for each malware family in a given dataset. It should be noted that the formulation of the reward function introduced in this paper (Equation (7) has been redesigned in Equation (11)) mitigates the difference in the magnitude of the reward values for classes that are not strictly outnumbered while remaining true to the traditional MDP model that emphasizes the single minority class. This trend can be observed from the distances between the scores of the two curves corresponding to the same malware family. Specifically, the distance between points corresponding to the absolute minority classes is smaller than all the others.
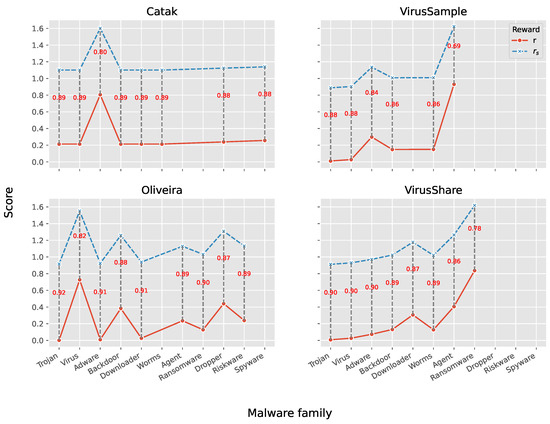
Figure 4 illustrates the pair of metric scores for the three top performers in correspondence with each dataset. The obtained results can be summarized as follows:
- The three algorithms that achieve the highest F1 score among all evaluated DRL configurations in the case of the Catak dataset are dueling DDQN, dueling DQN with PER and dueling DQN. This trio shares a key finding: the reward function used is Equation (11). With the same configuration, adopting Equation (7) results in a performance degradation that is more evident in the F1 score than in the AUC.
- Using the Oliveira dataset, among the top three performers, there are, once more, dueling DQN and dueling DDQN, followed by the dueling of DDQN with PER. As before, the best results are obtained using as the reward; in fact, it is remarkable that the three opposite algorithms achieve F1 scores that are half of those achieved by the algorithms using Equation (11). Similarly, using rather than r improves the AUC.
- Using the PER technique for the VirusSample dataset brings benefits that are reflected in the performance achieved by the dueling of DQN (which performs effectively also using the ER not prioritized) and DDQN algorithms, respectively. The dueling of DQN with PER, adopting for reward-sensitive training, reaches an F1 close to 80%, outperforming the same algorithm configuration trained using Equation (7) by . An improvement in F1 scores is also found for the remaining two algorithms using instead of r. In contrast, the opposite trend is shown by evaluating the AUC.
- The benefit achieved by introducing the revised reward formulation is confirmed for the VirusShare dataset, for which the top performers are given by the following three algorithms: dueling DDQN, dueling DQN, and dueling DDQN with PER.
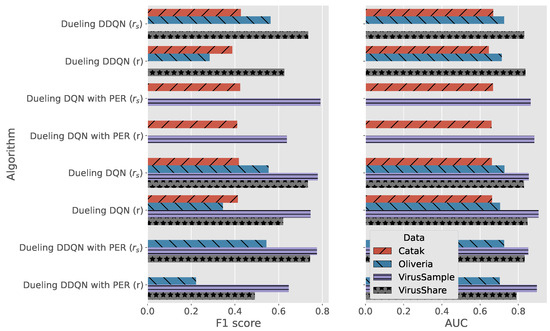
Figure 4.
F1 and AUC scores for the three top performers per dataset and their opposites.
Figure 5 shows an overall ranking that is favorable to algorithms that use as a reward function in place of r. Specifically, adopting leads to a better F1 score in 30 out of 31 cases (continuous curves exceed dashed curves), while the success rate decreases (but is still reasonable) to 58% for scenarios where a better AUC value is obtained.
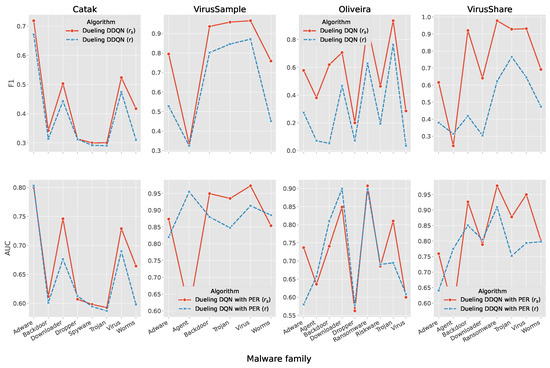
Figure 5.
F1 and AUC trends by malware class by the best algorithm per dataset and its opposite.
In correspondence with adware and ransomware, the dueling variants of DQN and DDQN achieve the maximum F1 per class, respectively. Moreover, the performance boost was also achieved in the remaining classes, as desired with the introduction of the new formula (Equation (11)).
Finally, Table 3 provides a summary of the algorithmic configurations, defined as the combination of DRL techniques that establish SINNER for each dataset to benchmark with selected algorithms from the related literature. It can be observed that SINNER employs dueling neural networks in each case.

Table 3.
SINNER best setting per dataset.
6.2. Performance Comparison
Table 4, Table 5, Table 6 and Table 7 provide a comparison of both timing (in seconds) and classification performance for all the algorithms evaluated in correspondence of the four different datasets. The results can be discussed as follows:

Table 4.
Classification metric scores achieved on the VirusShare dataset.

Table 5.
Classification metric scores achieved on the VirusSample dataset.

Table 6.
Classification metric scores achieved on the Catak dataset.

Table 7.
Classification metric scores achieved on the Oliveira dataset.
- Table 4 reveals that the cost-sensitive strategies proposed in [11] and [62] are uniquely beneficial to the BiLSTM model when using the VirusShare dataset. In fact, the remaining three DL algorithms do not produce satisfactory performance, with AUC values (∼0.5) indicating that the algorithms performed random classifications. However, the classification metric scores obtained by the BiLSTM algorithm do not reach the state-of-the-art performance achieved by the RTF algorithm. In addition, it appears to be extremely disadvantageous from the perspective of the required training time, which is the maximum in this list, regardless of the cost-sensitive strategy adopted. The proposed methodology outperforms all of the competitors in terms of F1 score and prediction time. Specifically, SINNER achieves a value of the F1 that is approximately 2% higher compared to the same obtained by RTF, requiring significantly less prediction time. On the other hand, RTF remains advantageous in terms of both the training period and the AUC value that it yields.
- In contrast to the previous case, Table 5 indicates that the results achieved by BiGRU are comparable to those obtained by the BiLSTM. In particular, the scores produced are comparable when adopting a specific cost-sensitive strategy; however, between the two alternatives, the one based on the use of the custom loss function proposed in [62] performs better in timing performance and F1 score. Furthermore, LSTM and TabNet combined with cost-sensitive strategies are also ineffective in this test. However, as mentioned previously, bidirectional classifiers do not achieve performance comparable to RTF, which is targeted by SINNER. In fact, the proposed methodology generated the closest F1 score to that achieved by RTF, with an inference time that is again shorter, although it is ten times longer in learning time and less in AUC.
- As shown in Table 6, SINNER appears to be underperforming when compared with bidirectional DL models combined with the pair of cost-sensitive strategies and RTF, which remains the state-of-the-art model on the Catak dataset with impressive F1 scores and AUC values. Therefore, it appears that SINNER has difficulty learning using an observation space with a large number of variables (n).
- According to Table 7, five top performers are identified using the Oliveira dataset, namely LSTM (that joins the top classifiers for the first time, indicating the presence of a temporal relationship between the variables in each statistical unit, which is a likely condition since the dataset is extracted from a dynamic analysis process); BiLSTM and BiGRU leveraging the strategy proposed in [62]; RTF, and SINNER. In particular, the five algorithms obtained F1 values between 0.561 and 0.569. While RTF remains the most advantageous in terms of AUC, SINNER stands out with respect to timing performance, requiring the second-lowest training time (LSTM is the top performer for this particular metric) and the lowest prediction time, which, as in all the cases discussed above, is approximately hundredths of seconds.
The main findings derived from such a discussion are summarized in Table 8.
7. Conclusions
Malware classification remains a key challenge in cybersecurity applications because it represents a feature required by various intrusion detection and prevention tools. When this task is approached using ML algorithms, it is critical to consider the skew of the training data to ensure that learning is not biased due to class imbalance, which is common in multi-class scenarios. This paper presented SINNER, that is, a DRL-based algorithm capable of classifying multiple malware categories, learning from data with skewed class proportions. The new reward design resulted in models with better performance than those using the classical formulation. These results offer promising scenarios for further performance improvement by identifying other reward formulations in a comprehensive ablation study. Based on the experimental results, SINNER consistently produced competitive F1 scores across different datasets and obtained the fastest prediction time. Therefore, it is a strong candidate for scenarios in which quick predictions are crucial. In addition, it generally requires less training time compared to some DL models. However, it falls behind RTF in AUC and sometimes in training time, suggesting that although SINNER is efficient, it can be improved to achieve the state-of-the-art performance demonstrated by RTF in certain datasets. In this regard, possible future directions of this study will regard the tuning of DNNs and ER hyper-parameters to further boost the classification metric scores. In addition, we will investigate feasible reductions in the size of the observation space to shorten the execution time required in the learning phase.
Author Contributions
Conceptualization, A.C. and A.M.; methodology, A.M.; software, A.M. and A.S.; validation, A.C., A.I. and A.M.; formal analysis, A.C., A.I. and A.M.; investigation, A.M.; resources, A.M. and A.S.; data curation, A.M. and A.S.; writing—original draft preparation, A.M. and A.S.; writing—review and editing, A.M.; visualization, A.M. and A.S.; supervision, A.C. and A.I. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Fondo Europeo di Sviluppo Regionale Puglia Programma Operativo Regionale (POR) Puglia 2014-2020-Axis I-Specific Objective 1a-Action 1.1 (Research and Development)-Project Title: CyberSecurity and Security Operation Center (SOC) Product Suite by BV TECH S.p.A., under Grant CUP/CIG B93G18000040007.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available in: Random-Transformer-Forest at https://github.com/Ferhat94/Random-Transformer-Forest/blob/main/datasets.zip (accessed on 21 May 2024) or reference number [16].
Conflicts of Interest
Authors were employed by the company BV TECH S.p.A. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
| ADASYN | Adaptive Synthetic Sampling Approach for Imbalanced Learning |
| AI | Artificial Intelligence |
| API | Application Programming Interface |
| AUC | Area Under Receiver Operating Characteristic Curve |
| AutoML | Automated Machine Learning |
| AV | Anti-Virus |
| BERT | Bidirectional Encoder Representations from Transformers |
| BiLSTM | Bidirectional Long Short-Term Memory |
| BiGRU | Bidirectional Gated Recurrent Unit |
| CANINE | Character Architecture with No Tokenization In Neural Encoders |
| CART | Classification and Regression Tree |
| CNN | Convolutional Neural Network |
| DL | Deep Learning |
| DNN | Deep Neural Network |
| DRL | Deep Reinforcement Learning |
| DQN | Deep Q-Network |
| DDQN | Double Deep Q-Network |
| ER | Experience Replay |
| FN | False Negative |
| FP | False Positive |
| FPR | False Positive Rate |
| GRU | Gated Recurrent Unit |
| ICMDP | Imbalanced Classification Markov Decision Process |
| IoC | Indicator of Compromise |
| IoT | Internet of Things |
| LIME | Local Interpretable Model-Agnostic Explanations |
| LSTM | Long Short-Term Memory |
| MDP | Markov Decision Process |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| NoisyNet | Noisy Network |
| NLP | Natural Language Processing |
| PE | Portable Executable |
| PER | Prioritized Experience Replay |
| PREC | Precision |
| PPO | Proximal Policy Optimization |
| RELU | Rectified Linear Unit |
| RL | Reinforcement Learning |
| RNN | Recurrent Neural Network |
| ROS | Random Oversampler |
| RTF | Random Transformer Forest |
| RUS | Random Undersampler |
| SHAP | Shapley Additive Explanations |
| TabNet | Deep Neural Network Architecture for Tabular Data |
| TD | Temporal Difference |
| T-link | Tomek Links |
| TN | True Negative |
| TP | True Positive |
| TPR | True Positive Rate |
| US | Unbalanced Scenario |
| XAI | Explainable Artificial Intelligence |
| YARA | Yet Another Recursive Acronym |
References
- Aboaoja, F.A.; Zainal, A.; Ghaleb, F.A.; Al-rimy, B.A.S.; Eisa, T.A.E.; Elnour, A.A.H. Malware detection issues, challenges, and future directions: A survey. Appl. Sci. 2022, 12, 8482. [Google Scholar] [CrossRef]
- Sibi Chakkaravarthy, S.; Sangeetha, D.; Vaidehi, V. A Survey on malware analysis and mitigation techniques. Comput. Sci. Rev. 2019, 32, 1–23. [Google Scholar] [CrossRef]
- Xu, L.; Qiao, M. Yara rule enhancement using Bert-based strings language model. In Proceedings of the 2022 5th International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Wuhan, China, 22–24 April 2022; pp. 221–224. [Google Scholar] [CrossRef]
- Coscia, A.; Dentamaro, V.; Galantucci, S.; Maci, A.; Pirlo, G. YAMME: A YAra-byte-signatures Metamorphic Mutation Engine. IEEE Trans. Inf. Forensics Secur. 2023, 18, 4530–4545. [Google Scholar] [CrossRef]
- Or-Meir, O.; Nissim, N.; Elovici, Y.; Rokach, L. Dynamic Malware Analysis in the Modern Era—A State of the Art Survey. ACM Comput. Surv. 2019, 52, 1–48. [Google Scholar] [CrossRef]
- Ucci, D.; Aniello, L.; Baldoni, R. Survey of machine learning techniques for malware analysis. Comput. Secur. 2019, 81, 123–147. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y. A Robust Malware Detection System Using Deep Learning on API Calls. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 1456–1460. [Google Scholar] [CrossRef]
- Vinayakumar, R.; Alazab, M.; Soman, K.P.; Poornachandran, P.; Venkatraman, S. Robust Intelligent Malware Detection Using Deep Learning. IEEE Access 2019, 7, 46717–46738. [Google Scholar] [CrossRef]
- Li, C.; Cheng, Z.; Zhu, H.; Wang, L.; Lv, Q.; Wang, Y.; Li, N.; Sun, D. DMalNet: Dynamic malware analysis based on API feature engineering and graph learning. Comput. Secur. 2022, 122, 102872. [Google Scholar] [CrossRef]
- Rabadi, D.; Teo, S.G. Advanced Windows Methods on Malware Detection and Classification. In Proceedings of the ACSAC ’20: 36th Annual Computer Security Applications Conference, Austin, TX, USA, 7–11 December 2020; pp. 54–68. [Google Scholar] [CrossRef]
- Alzammam, A.; Binsalleeh, H.; AsSadhan, B.; Kyriakopoulos, K.G.; Lambotharan, S. Comparative Analysis on Imbalanced Multi-class Classification for Malware Samples using CNN. In Proceedings of the 2019 International Conference on Advances in the Emerging Computing Technologies (AECT), Al Madinah Al Munawwarah, Saudi Arabia, 10 February 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Lu, Y.; Shetty, S. Multi-Class Malware Classification Using Deep Residual Network with Non-SoftMax Classifier. In Proceedings of the 2021 IEEE 22nd International Conference on Information Reuse and Integration for Data Science (IRI), Las Vegas, NV, USA, 10–12 August 2021; pp. 201–207. [Google Scholar] [CrossRef]
- Kumar, K.A.; Kumar, K.; Chiluka, N.L. Deep learning models for multi-class malware classification using Windows exe API calls. Int. J. Crit. Comput.-Based Syst. 2022, 10, 185–201. [Google Scholar] [CrossRef]
- Oak, R.; Du, M.; Yan, D.; Takawale, H.; Amit, I. Malware Detection on Highly Imbalanced Data through Sequence Modeling. In Proceedings of the 12th ACM Workshop on Artificial Intelligence and Security, Association for Computing Machinery, London, UK, 15 November 2019; pp. 37–48. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, S.; Xing, J.; Zhang, X.; Qi, Z.; Fu, G.; Qiang, Q.; Sun, H.; Zhang, J. Malware Classification on Imbalanced Data through Self-Attention. In Proceedings of the 2020 IEEE 19th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Guangzhou, China, 29 December 2020–1 January 2021; pp. 154–161. [Google Scholar] [CrossRef]
- Demirkıran, F.; Çayır, A.; Ünal, U.; Dağ, H. An ensemble of pre-trained transformer models for imbalanced multiclass malware classification. Comput. Secur. 2022, 121, 102846. [Google Scholar] [CrossRef]
- Wang, H.; Singhal, A.; Liu, P. Tackling imbalanced data in cybersecurity with transfer learning: A case with ROP payload detection. Cybersecurity 2023, 6, 2. [Google Scholar] [CrossRef]
- Naim, O.; Cohen, D.; Ben-Gal, I. Malicious website identification using design attribute learning. Int. J. Inf. Secur. 2023, 22, 1207–1217. [Google Scholar] [CrossRef]
- Sewak, M.; Sahay, S.K.; Rathore, H. Deep reinforcement learning in the advanced cybersecurity threat detection and protection. Inf. Syst. Front. 2023, 25, 589–611. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Reddi, V.J. Deep Reinforcement Learning for Cyber Security. IEEE Trans. Neural Networks Learn. Syst. 2021, 34, 3779–3795. [Google Scholar] [CrossRef] [PubMed]
- Kamal, H.; Gautam, S.; Mehrotra, D.; Sharif, M.S. Reinforcement Learning Model for Detecting Phishing Websites. In Cybersecurity and Artificial Intelligence: Transformational Strategies and Disruptive Innovation; Jahankhani, H., Bowen, G., Sharif, M.S., Hussien, O., Eds.; Springer: Berlin, Germany, 2024; pp. 309–326. [Google Scholar] [CrossRef]
- Shen, S.; Xie, L.; Zhang, Y.; Wu, G.; Zhang, H.; Yu, S. Joint Differential Game and Double Deep Q-Networks for Suppressing Malware Spread in Industrial Internet of Things. IEEE Trans. Inf. Forensics Secur. 2023, 18, 5302–5315. [Google Scholar] [CrossRef]
- Lin, E.; Chen, Q.; Qi, X. Deep Reinforcement Learning for Imbalanced Classification. Appl. Intell. 2020, 50, 2488–2502. [Google Scholar] [CrossRef]
- Yuan, F.; Tian, T.; Shang, Y.; Lu, Y.; Liu, Y.; Tan, J. Malicious Domain Detection on Imbalanced Data with Deep Reinforcement Learning. In Proceedings of the Neural Information Processing; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 464–476. [Google Scholar] [CrossRef]
- Maci, A.; Santorsola, A.; Coscia, A.; Iannacone, A. Unbalanced Web Phishing Classification through Deep Reinforcement Learning. Computers 2023, 12, 118. [Google Scholar] [CrossRef]
- Maci, A.; Tamma, N.; Coscia, A. Deep Reinforcement Learning-based Malicious URL Detection with Feature Selection. In Proceedings of the 2024 IEEE 3rd International Conference on AI in Cybersecurity (ICAIC), Houston, TX, USA, 7–9 February 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Maci., A.; Urbano., G.; Coscia., A. Deep Q-Networks for Imbalanced Multi-Class Malware Classification. In Proceedings of the 10th International Conference on Information Systems Security and Privacy—ICISSP, Roma, Italy, 26–28 February 2024; pp. 342–349. [Google Scholar] [CrossRef]
- Yang, J.; El-Bouri, R.; O’Donoghue, O.; Lachapelle, A.S.; Soltan, A.A.S.; Clifton, D.A. Deep Reinforcement Learning for Multi-class Imbalanced Training. arXiv 2022, arXiv:2205.12070. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Hasselt, H.V.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-Learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence; AAAI Press: Washington, DC, USA, 2016; Volume 30, pp. 2094–2100. [Google Scholar] [CrossRef]
- Wang, Z.; Schaul, T.; Hessel, M.; van Hasselt, H.; Lanctot, M.; de Freitas, N. Dueling Network Architectures for Deep Reinforcement Learning. In Proceedings of the 33rd International Conference on Machine Learning. PMLR, New York, NY, USA, 20–22 June 2016; Volume 48, pp. 1995–2003. [Google Scholar] [CrossRef]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. arXiv 2016, arXiv:1511.05952. [Google Scholar] [CrossRef]
- Fortunato, M.; Azar, M.G.; Piot, B.; Menick, J.; Osband, I.; Graves, A.; Mnih, V.; Munos, R.; Hassabis, D.; Pietquin, O.; et al. Noisy Networks for Exploration. arXiv 2019, arXiv:1706.10295. [Google Scholar] [CrossRef]
- Alkhateeb, E.; Ghorbani, A.; Habibi Lashkari, A. Identifying Malware Packers through Multilayer Feature Engineering in Static Analysis. Information 2024, 15, 102. [Google Scholar] [CrossRef]
- Gibert, D. PE Parser: A Python package for Portable Executable files processing. Softw. Impacts 2022, 13, 100365. [Google Scholar] [CrossRef]
- Yamany, B.; Elsayed, M.S.; Jurcut, A.D.; Abdelbaki, N.; Azer, M.A. A Holistic Approach to Ransomware Classification: Leveraging Static and Dynamic Analysis with Visualization. Information 2024, 15, 46. [Google Scholar] [CrossRef]
- Brescia, W.; Maci, A.; Mascolo, S.; De Cicco, L. Safe Reinforcement Learning for Autonomous Navigation of a Driveable Vertical Mast Lift. IFAC-PapersOnLine 2023, 56, 9068–9073. [Google Scholar] [CrossRef]
- Han, D.; Mulyana, B.; Stankovic, V.; Cheng, S. A Survey on Deep Reinforcement Learning Algorithms for Robotic Manipulation. Sensors 2023, 23, 3762. [Google Scholar] [CrossRef]
- Tran, M.; Pham-Hi, D.; Bui, M. Optimizing Automated Trading Systems with Deep Reinforcement Learning. Algorithms 2023, 16, 23. [Google Scholar] [CrossRef]
- Hu, Y.J.; Lin, S.J. Deep Reinforcement Learning for Optimizing Finance Portfolio Management. In Proceedings of the 2019 Amity International Conference on Artificial Intelligence (AICAI), Dubai, United Arab Emirates, 4–6 February 2019; pp. 14–20. [Google Scholar] [CrossRef]
- Yang, J.; El-Bouri, R.; O’Donoghue, O.; Lachapelle, A.S.; Soltan, A.A.S.; Eyre, D.W.; Lu, L.; Clifton, D.A. Deep reinforcement learning for multi-class imbalanced training: Applications in healthcare. Mach. Learn. 2023, 113, 2655–2674. [Google Scholar] [CrossRef]
- Chen, T.; Liu, J.; Xiang, Y.; Niu, W.; Tong, E.; Han, Z. Adversarial attack and defense in reinforcement learning-from AI security view. Cybersecurity 2019, 2, 11. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018; Available online: https://web.stanford.edu/class/psych209/Readings/SuttonBartoIPRLBook2ndEd.pdf (accessed on 18 January 2024).
- Wang, X.; Wang, S.; Liang, X.; Zhao, D.; Huang, J.; Xu, X.; Dai, B.; Miao, Q. Deep Reinforcement Learning: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5064–5078. [Google Scholar] [CrossRef] [PubMed]
- Jang, B.; Kim, M.; Harerimana, G.; Kim, J.W. Q-Learning Algorithms: A Comprehensive Classification and Applications. IEEE Access 2019, 7, 133653–133667. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, T. Taxonomy of Reinforcement Learning Algorithms. In Deep Reinforcement Learning: Fundamentals, Research and Applications; Dong, H., Ding, Z., Zhang, S., Eds.; Springer: Singapore, 2020; pp. 125–133. [Google Scholar] [CrossRef]
- Berman, D.S.; Buczak, A.L.; Chavis, J.S.; Corbett, C.L. A Survey of Deep Learning Methods for Cyber Security. Information 2019, 10, 122. [Google Scholar] [CrossRef]
- Kolosnjaji, B.; Zarras, A.; Webster, G.; Eckert, C. Deep Learning for Classification of Malware System Call Sequences. In Proceedings of the AI 2016: Advances in Artificial Intelligence; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 137–149. [Google Scholar] [CrossRef]
- Meng, X.; Shan, Z.; Liu, F.; Zhao, B.; Han, J.; Wang, H.; Wang, J. MCSMGS: Malware Classification Model Based on Deep Learning. In Proceedings of the 2017 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC), Nanjing, China, 12–14 October 2017; pp. 272–275. [Google Scholar] [CrossRef]
- Maniath, S.; Ashok, A.; Poornachandran, P.; Sujadevi, V.; A.U., P.S.; Jan, S. Deep learning LSTM based ransomware detection. In Proceedings of the 2017 Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 26–27 October 2017; pp. 442–446. [Google Scholar] [CrossRef]
- Cannarile, A.; Dentamaro, V.; Galantucci, S.; Iannacone, A.; Impedovo, D.; Pirlo, G. Comparing Deep Learning and Shallow Learning Techniques for API Calls Malware Prediction: A Study. Appl. Sci. 2022, 12, 1645. [Google Scholar] [CrossRef]
- Cannarile, A.; Carrera, F.; Galantucci, S.; Iannacone, A.; Pirlo, G. A Study on Malware Detection and Classification Using the Analysis of API Calls Sequences Through Shallow Learning and Recurrent Neural Networks. In Proceedings of the 6th Italian Conference on Cybersecurit (ITASEC22), CEUR Workshop Proceedings. Rome, Italy, 20–23 June 2022; Available online: https://ceur-ws.org/Vol-3260/paper9.pdf (accessed on 8 March 2024).
- Li, C.; Lv, Q.; Li, N.; Wang, Y.; Sun, D.; Qiao, Y. A novel deep framework for dynamic malware detection based on API sequence intrinsic features. Comput. Secur. 2022, 116, 102686. [Google Scholar] [CrossRef]
- Chanajitt, R.; Pfahringer, B.; Gomes, H.M.; Yogarajan, V. Multiclass Malware Classification Using Either Static Opcodes or Dynamic API Calls. In Proceedings of the AI 2022: Advances in Artificial Intelligence; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; Volume 13728, pp. 427–441. [Google Scholar] [CrossRef]
- Maniriho, P.; Mahmood, A.N.; Chowdhury, M.J.M. API-MalDetect: Automated malware detection framework for windows based on API calls and deep learning techniques. J. Netw. Comput. Appl. 2023, 218, 103704. [Google Scholar] [CrossRef]
- Bensaoud, A.; Kalita, J. CNN-LSTM and transfer learning models for malware classification based on opcodes and API calls. Knowl.-Based Syst. 2024, 290, 111543. [Google Scholar] [CrossRef]
- Syeda, D.Z.; Asghar, M.N. Dynamic Malware Classification and API Categorisation of Windows Portable Executable Files Using Machine Learning. Appl. Sci. 2024, 14, 1015. [Google Scholar] [CrossRef]
- He, X.; Zhao, K.; Chu, X. AutoML: A survey of the state-of-the-art. Knowl.-Based Syst. 2021, 212, 106622. [Google Scholar] [CrossRef]
- Brown, A.; Gupta, M.; Abdelsalam, M. Automated machine learning for deep learning based malware detection. Comput. Secur. 2024, 137, 103582. [Google Scholar] [CrossRef]
- Qian, L.; Cong, L. Channel Features and API Frequency-Based Transformer Model for Malware Identification. Sensors 2024, 24, 580. [Google Scholar] [CrossRef]
- Yunan, Z.; Huang, Q.; Ma, X.; Yang, Z.; Jiang, J. Using Multi-features and Ensemble Learning Method for Imbalanced Malware Classification. In Proceedings of the 2016 IEEE Trustcom/BigDataSE/ISPA, Tianjin, China, 23–26 August 2016; pp. 965–973. [Google Scholar] [CrossRef]
- Akarsh, S.; Simran, K.; Poornachandran, P.; Menon, V.K.; Soman, K. Deep Learning Framework and Visualization for Malware Classification. In Proceedings of the 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS), Coimbatore, India, 15–16 March 2019; pp. 1059–1063. [Google Scholar] [CrossRef]
- Catak, F.O.; Ahmed, J.; Sahinbas, K.; Khand, Z.H. Data augmentation based malware detection using convolutional neural networks. PeerJ Comput. Sci. 2021, 7, e346. [Google Scholar] [CrossRef]
- Liu, J.; Zhuge, C.; Wang, Q.; Guo, X.; Li, Z. Imbalance Malware Classification by Decoupling Representation and Classifier. In Proceedings of the Advances in Artificial Intelligence and Security; Sun, X., Zhang, X., Xia, Z., Bertino, E., Eds.; Springer: Cham, Switzerland, 2021; pp. 85–98. [Google Scholar] [CrossRef]
- Bacevicius, M.; Paulauskaite-Taraseviciene, A. Machine Learning Algorithms for Raw and Unbalanced Intrusion Detection Data in a Multi-Class Classification Problem. Appl. Sci. 2023, 13, 7328. [Google Scholar] [CrossRef]
- Li, T.; Luo, Y.; Wan, X.; Li, Q.; Liu, Q.; Wang, R.; Jia, C.; Xiao, Y. A malware detection model based on imbalanced heterogeneous graph embeddings. Expert Syst. Appl. 2024, 246, 123109. [Google Scholar] [CrossRef]
- Xue, L.; Zhu, T. Hybrid resampling and weighted majority voting for multi-class anomaly detection on imbalanced malware and network traffic data. Eng. Appl. Artif. Intell. 2024, 128, 107568. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Geng, J.; Kan, X. Feature Selection for Malware Detection Based on Reinforcement Learning. IEEE Access 2019, 7, 176177–176187. [Google Scholar] [CrossRef]
- Wu, Y.; Li, M.; Zeng, Q.; Yang, T.; Wang, J.; Fang, Z.; Cheng, L. DroidRL: Feature selection for android malware detection with reinforcement learning. Comput. Secur. 2023, 128, 103126. [Google Scholar] [CrossRef]
- Wang, Y.; Stokes, J.W.; Marinescu, M. Neural Malware Control with Deep Reinforcement Learning. In Proceedings of the MILCOM 2019 - 2019 IEEE Military Communications Conference (MILCOM), Norfolk, VA, USA, 12–14 November 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Li, B.; Wu, S.; Zhou, Y.; Huang, H. Evading Anti-Malware Engines with Deep Reinforcement Learning. IEEE Access 2019, 7, 48867–48879. [Google Scholar] [CrossRef]
- Wang, Y.; Stokes, J.; Marinescu, M. Actor Critic Deep Reinforcement Learning for Neural Malware Control. In Proceedings of the AAAI Conference on Artificial Intelligence. Association for the Advancement of Artificial Intelligence (AAAI), 2020, Hilton New York Midtown, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 1005–1012. [Google Scholar] [CrossRef]
- Song, W.; Li, X.; Afroz, S.; Garg, D.; Kuznetsov, D.; Yin, H. MAB-Malware: A Reinforcement Learning Framework for Blackbox Generation of Adversarial Malware. In Proceedings of the 2022 ACM on Asia Conference on Computer and Communications Security. Association for Computing Machinery, Nagasaki, Japan, 30 May–3 June 2022; pp. 990–1003. [Google Scholar] [CrossRef]
- Anderson, H.S.; Kharkar, A.; Filar, B.; Evans, D.; Roth, P. Learning to Evade Static PE Machine Learning Malware Models via Reinforcement Learning. arXiv 2018, arXiv:1801.08917. [Google Scholar] [CrossRef]
- Deng, X.; Cen, M.; Jiang, M.; Lu, M. Ransomware early detection using deep reinforcement learning on portable executable header. Cluster Computing 2023, 27, 1867–1881. [Google Scholar] [CrossRef]
- Birman, Y.; Hindi, S.; Katz, G.; Shabtai, A. Cost-effective ensemble models selection using deep reinforcement learning. Inf. Fusion 2022, 77, 133–148. [Google Scholar] [CrossRef]
- Atti, M.; Yogi, M.K. Application of Deep Reinforcement Learning (DRL) for Malware Detection. Int. J. Inf. Technol. Comput. Eng. (IJITC) 2024, 4, 23–35. [Google Scholar] [CrossRef]
- Al-Fawa’reh, M.; Abu-Khalaf, J.; Szewczyk, P.; Kang, J.J. MalBoT-DRL: Malware Botnet Detection Using Deep Reinforcement Learning in IoT Networks. IEEE Internet Things J. 2024, 11, 9610–9629. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM networks. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 4, pp. 2047–2052. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Arik, S.Ö.; Pfister, T. TabNet: Attentive Interpretable Tabular Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, 2021, Virtual conference, 2–9 February 2021; Volume 35, pp. 6679–6687. [Google Scholar] [CrossRef]
- Düzgün, B.; Cayir, A.; Demirkiran, F.; Kahya, C.; Gençaydın, B.; Dag, H. New Datasets for Dynamic Malware Classification. 2021. Available online: https://www.researchgate.net/publication/356664607_New_Datasets_for_Dynamic_Malware_Classification (accessed on 16 May 2024).
- De Oliveira, A.S.; Sassi, R.J. Behavioral Malware Detection Using Deep Graph Convolutional Neural Networks. TechRxiv 2019. [Google Scholar] [CrossRef]
- Do, N.Q.; Selamat, A.; Krejcar, O.; Herrera-Viedma, E.; Fujita, H. Deep Learning for Phishing Detection: Taxonomy, Current Challenges and Future Directions. IEEE Access 2022, 10, 36429–36463. [Google Scholar] [CrossRef]
- Grandini, M.; Bagli, E.; Visani, G. Metrics for Multi-Class Classification: An Overview. arXiv 2020, arXiv:2008.05756. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, Texas, USA, 28 June–3 July 2010; van der Walt, S., Millman, J., Eds.; pp. 56–61. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org (accessed on 5 February 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).