Optimizing the Deployment of an Aerial Base Station and the Phase-Shift of a Ground Reconfigurable Intelligent Surface for Wireless Communication Systems Using Deep Reinforcement Learning
Abstract
1. Introduction
2. Related Works
3. System Model and Problem Formulation
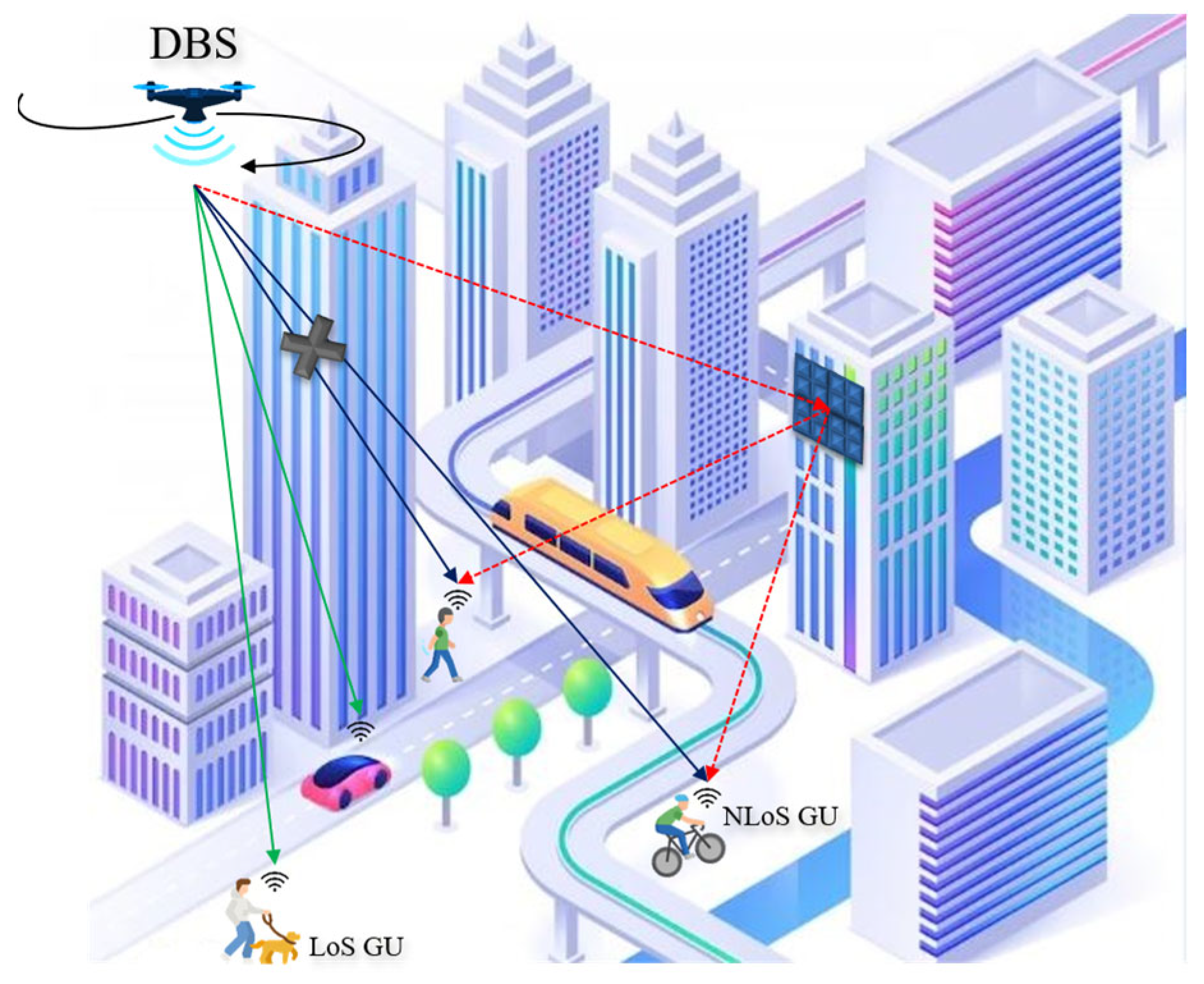
3.1. System Model
3.1.1. Channel Model
3.1.2. Phase-Shift Designs and Channel Rate
3.2. Problem Formulation
4. Stage of RIS-DWC Approach
4.1. General Reinforcement Learning Framework
4.2. DRL-Based RIS-DWC Mobility Control Strategy
| Algorithm 1: RIS-assisted DBS Trajectory and Phase Shift Design Strategy |
| Input: System action space, size of mini-batch, discount factor, number of timeslots, number of episodes, set of actions, learning rate β, exploration coefficient ∈. Output: The optimal DBS trajectory and the ground users’ coverage 1: Initialize main network with random weights θ; 2: Initialize target network with random weights = θ; 3: Initialize experience replay memory; /* Exploration Stage */ 4: For episode = 1 to E do 5: Set t =1, initialize the system to and update the DBS location; 6: While do 7: Obtain the state ; 8: The DBS select the action using the -greedy approach; with the probability ϵ, or select action by ; 9: Execute ; 10: Obtain the RIS phase-shifts based on Algorithm 2; 11: The DBS observes the next system state and receives the reward based on the Equation (13); 12: if DBS out of the target area, then cancel the action and apply accordingly; 13: end if 14: Store (, , , ) in the experience relay memory; /* Training Stage */ 15: Select a random mini-batch from the experience replay memory; 16: Calculate the target Q-value using (15); 17: The DRL agent updates the weights θ by minimizing the loss function using (16); 18: Update weights of the main network θ; 19: Update weights of the target network ; 20: t t+1; 21: end while 22: episode episode+1 23: end for |
| Algorithm 2: Algorithm for Phase-Shift optimization |
| Input: Number of the timeslots, number of episodes, set of actions, learning rate, size of mini-batch, state. Output: The optimal phase-shifts (0) = ; Initialize the maximum number of iterations Imax; Obtain the DBSs, ground users’ position, and the initial RIS phase-shifts; then, calculate the achievable rate (0); For i = 1, 2, …, Imax do For m = 1, 2, …, M do Fix the phase-shift of the m-th element, ∀m = m; Set when (i) is maximum; end for If (i) > then Find = (i); break; end if end for |
5. Performance Analysis
5.1. Implementation Details
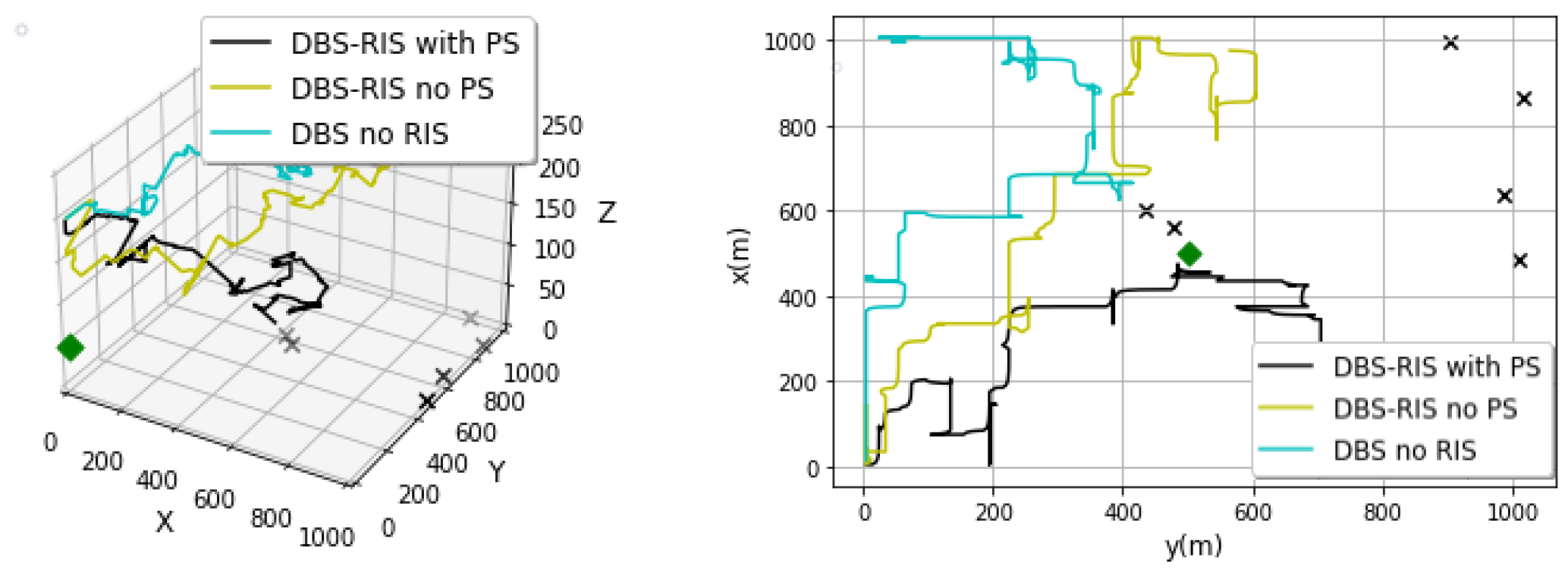
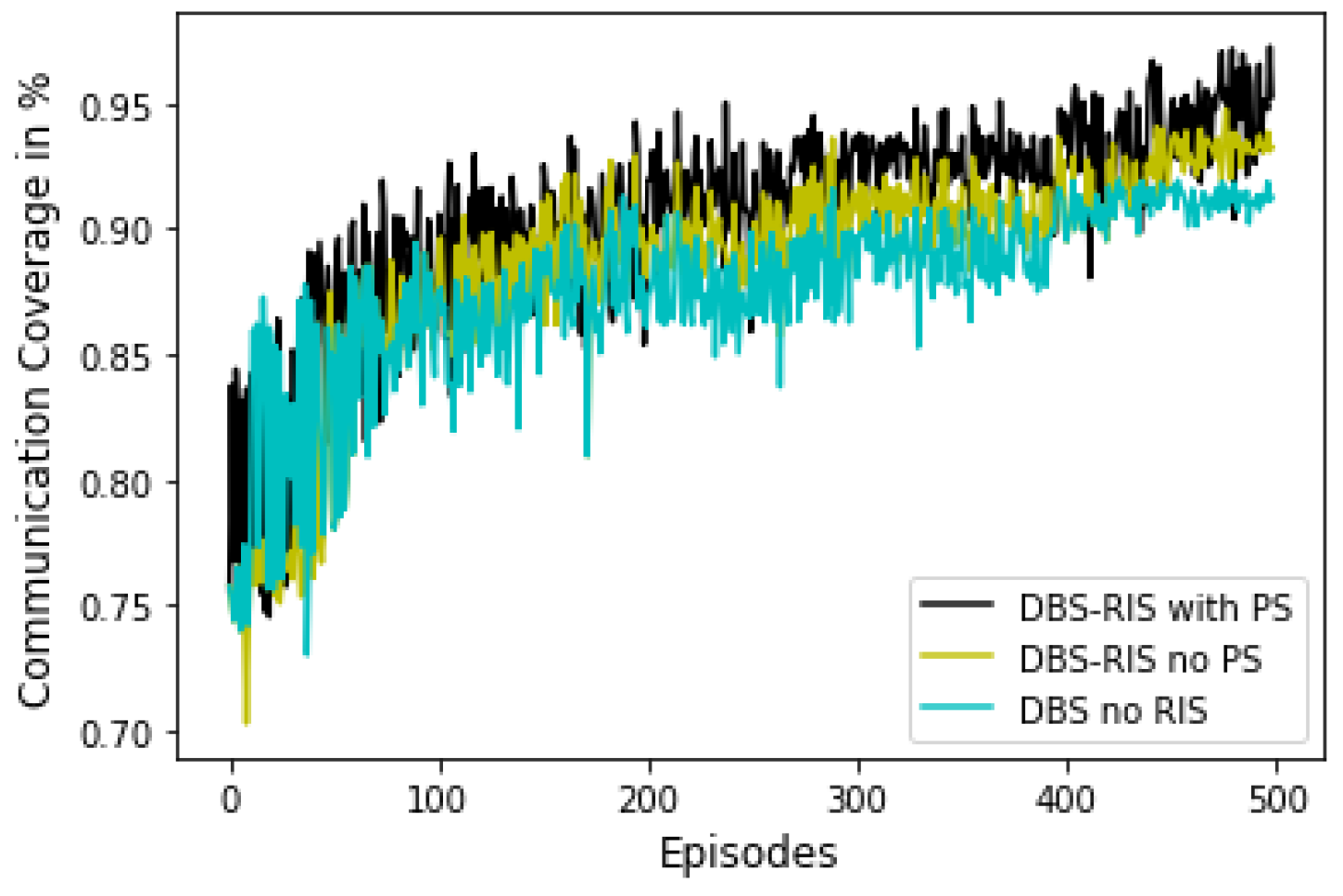
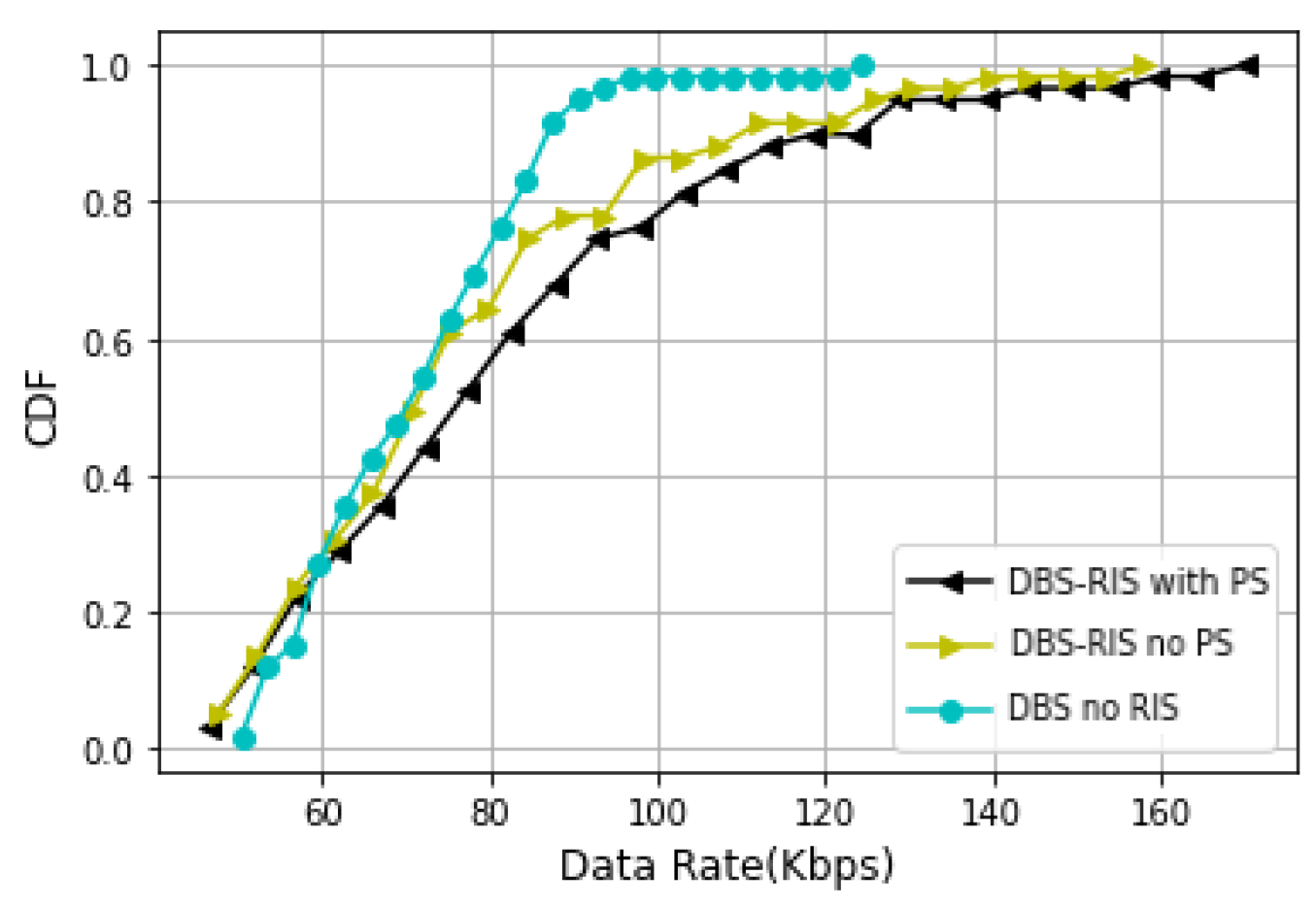
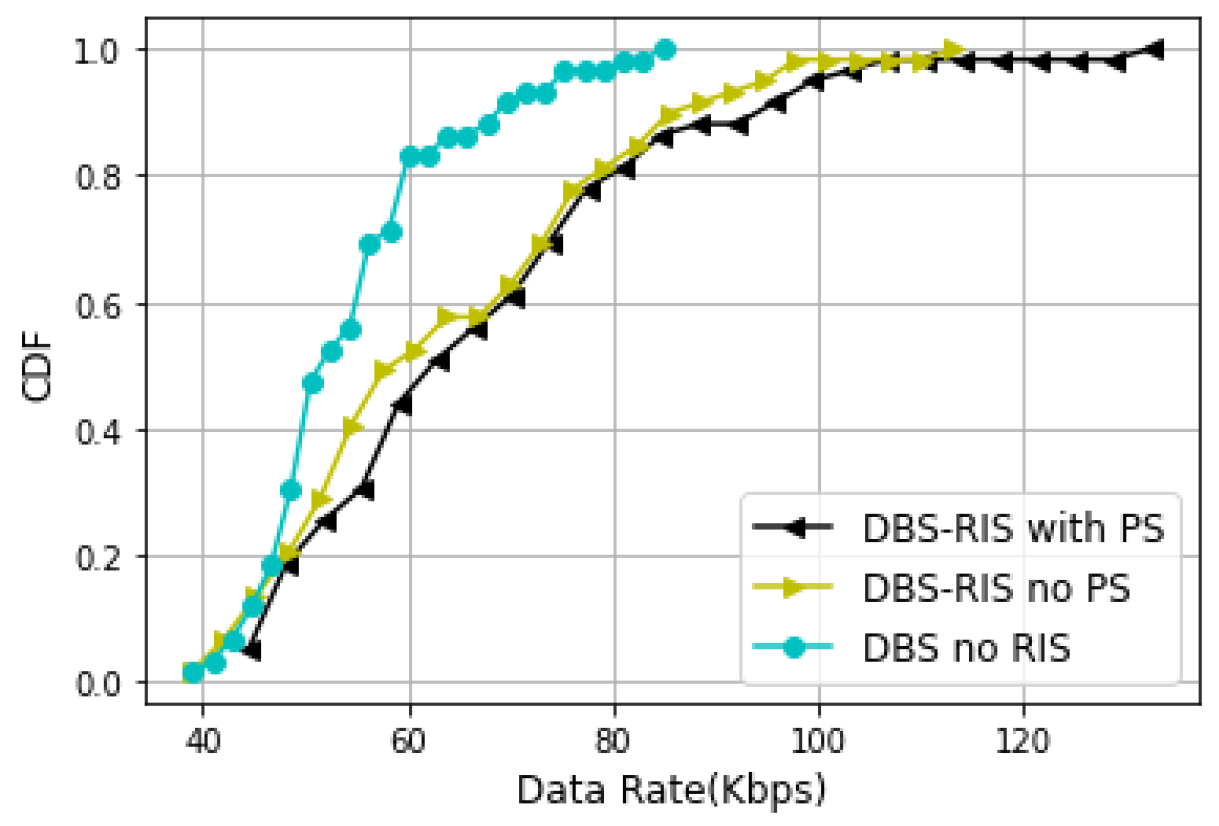
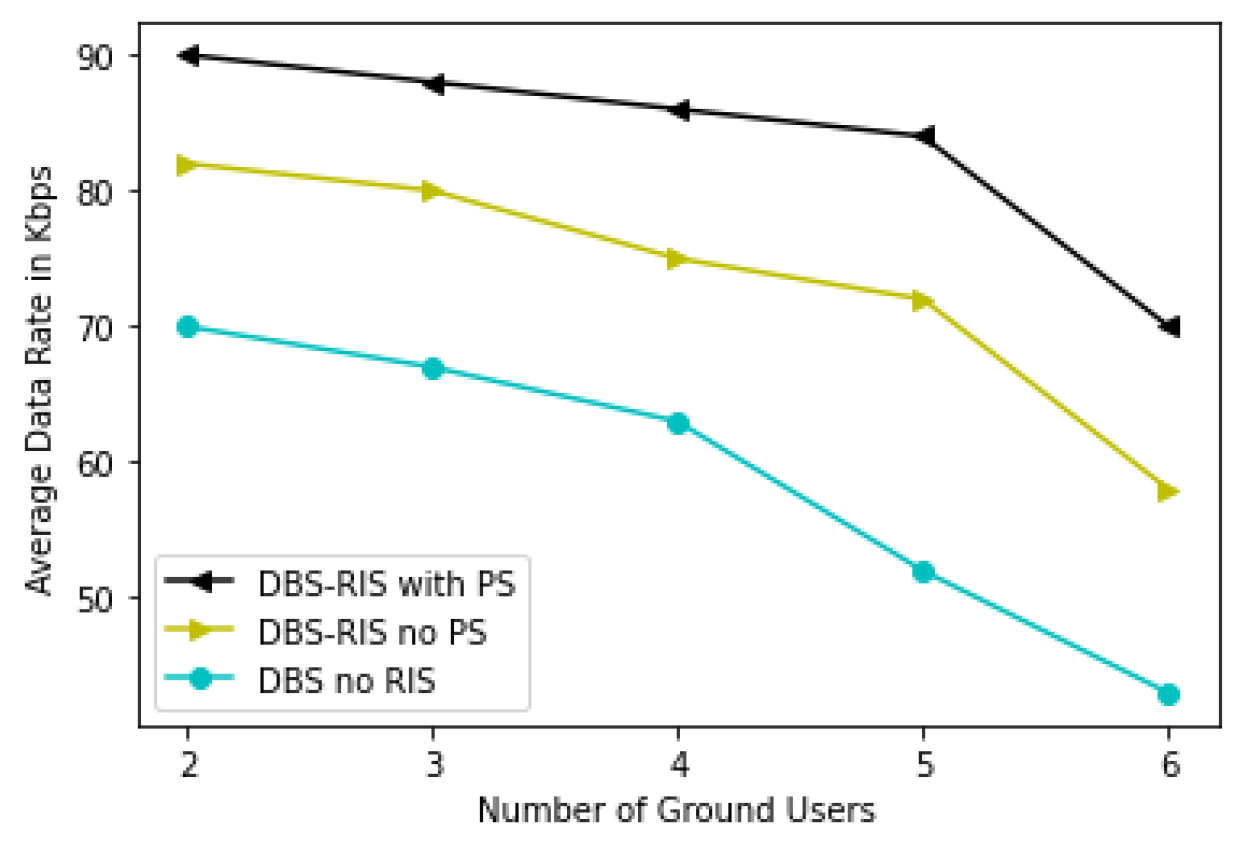
5.2. Results and Discussion
5.3. Computational Time and Complexity
6. Conclusions and Open Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khawaja, W.; Guvenc, I.; Matolak, D.W.; Fiebig, U.C.; Schneckenburger, N. A survey of air-to-ground propagation channel modeling for unmanned aerial vehicles. IEEE Commun. Surv. Tutor. 2019, 21, 2361–2391. [Google Scholar] [CrossRef]
- Cicek, C.T.; Gultekin, H.; Tavli, B.; Yanikomeroglu, H. UAV Base Station Location Optimization for Next Generation Wireless Networks: Overview and Future Research Directions. In Proceedings of the 2019 1st International Conference on Unmanned Vehicle Systems-Oman (UVS), Muscat, Oman, 5–7 February 2019; pp. 1–6. [Google Scholar]
- Di Renzo, M.; Zappone, A.; Debbah, M.; Alouini, M.S.; Yuen, C.; De Rosny, J.; Tretyakov, S. Smart radio environments empowered by reconfigurable intelligent surfaces: How it works state of research the road, ahead. IEEE J. Sel. Areas Commun. 2020, 38, 2450–2525. [Google Scholar] [CrossRef]
- Renzo, M.D.; Debbah, M.; Phan-Huy, D.T.; Zappone, A.; Alouini, M.S.; Yuen, C.; Sciancalepore, V.; Alexandropoulos, G.C.; Hoydis, J.; Gacanin, H.; et al. Smart radio environments empowered by reconfigurable AI metasurfaces: An idea whose time has come. Commun. Netw. 2019, 2019, 129. [Google Scholar]
- Xu, F.; Hussain, T.; Ahmed, M.; Ali, K.; Mirza, M.A.; Khan, W.U.; Ihsan, A.; Han, Z. The state of ai-empowered backscatter communications: A comprehensive survey. IEEE Internet Things J. 2023, 10, 21763–21786. [Google Scholar] [CrossRef]
- Jiao, H.; Liu, H.; Wang, Z. Reconfigurable Intelligent Surfaces aided Wireless Communication: Key Technologies and Challenges. In Proceedings of the 2022 International Wireless Communications and Mobile Computing (IWCMC), Dubrovnik, Croatia, 30 May–3 June 2022. [Google Scholar]
- Siddiqi, M.Z.; Mir, T. Reconfigurable intelligent surface-aided wireless communications: An overview. Intell. Converg. Netw. 2022, 3, 33–63. [Google Scholar] [CrossRef]
- Tesfaw, B.A.; Juang, R.T.; Tai, L.C.; Lin, H.P.; Tarekegn, G.B.; Nathanael, K.W. Deep Learning-Based Link Quality Estimation for RIS-Assisted UAV-Enabled Wireless Communications System. Sensors 2023, 23, 8041. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Duo, B.; Yuan, X.; Liang, Y.-C.; Di Renzo, M. Reconfigurable intelligent surface assisted UAV communication: Joint trajectory design and passive beamforming. IEEE Wirel. Commun. Lett. 2020, 9, 716–720. [Google Scholar] [CrossRef]
- Zhao, J.; Yu, L.; Cai, K.; Zhu, Y.; Han, Z. RIS-aided ground-aerial NOMA communications: A distributionally robust DRL approach. IEEE J. Sel. Areas Commun. 2022, 40, 1287–1301. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, J.; Feng, W.; Zhang, X.Y.; So, D.K.C.; Wong, K.-K.; Chambers, J.A. Throughput Maximization for RIS-assisted UAV-enabled WPCN. IEEE Accesss 2024, 12, 3352085. [Google Scholar] [CrossRef]
- Luong, N.C.; Hoang, D.T.; Gong, S.; Niyato, D.; Wang, P.; Liang, Y.C.; Kim, D.I. Applications of deep reinforcement learning in communications and networking: A survey. IEEE Commun. Surv. Tutor. 2019, 21, 3133–3174. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, Y.; Niyato, D.; Deng, R.; Wang, P.; Wang, L.C. Deep reinforcement learning for mobile 5G and beyond: Fundamentals, applications, and challenges. IEEE Veh. Technol. Mag. 2019, 14, 44–52. [Google Scholar] [CrossRef]
- Ji, P.; Jia, J.; Chen, J.; Guo, L.; Du, A.; Wang, X. Reinforcement learning based joint trajectory design and resource allocation for RIS-aided UAV multicast networks. Comput. Netw. 2023, 227, 109697. [Google Scholar] [CrossRef]
- Fan, X.; Liu, M.; Chen, Y.; Sun, S.; Li, Z.; Guo, X. Ris-assisted uav for fresh data collection in 3d urban environments: A deep reinforcement learning approach. IEEE Trans. Veh. Technol. 2022, 72, 632–647. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, M.; Zhou, H.; Wang, X.; Wang, N.; Long, K. Capacity maximization in RIS-UAV networks: A DDQN-based trajectory and phase shift optimization approach. IEEE Trans. Wirel. Commun. 2022, 22, 2583–2591. [Google Scholar] [CrossRef]
- Tarekegn, G.B.; Juang, R.T.; Lin, H.P.; Munaye, Y.Y.; Wang, L.C.; Bitew, M.A. Deep-Reinforcement-Learning-Based Drone Base Station Deployment for Wireless Communication Services. IEEE Internet Things J. 2022, 9, 21899–21915. [Google Scholar] [CrossRef]
- Ranjha, A.; Kaddoum, G. URLLC facilitated by mobile UAV relay and RIS: A joint design of passive beamforming, blocklength, and UAV positioning. IEEE Internet Things J. 2020, 8, 4618–4627. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP altitude for maximum coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Beamforming optimization for wireless network aided by intelligent reflecting surface with discrete phase shifts. IEEE Trans. Commun. 2019, 68, 1838–1851. [Google Scholar] [CrossRef]
- Wang, J.L.; Li, Y.R.; Adege, A.B.; Wang, L.C.; Jeng, S.S.; Chen, J.Y. Machine learning based rapid 3D channel modeling for UAV communication. In Proceedings of the 2019 16th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 11–14 January 2019; pp. 1–5. [Google Scholar]
- Tarekegn, G.B.; Juang, R.T.; Lin, H.P.; Munaye, Y.Y.; Wang, L.C.; Jeng, S.S. Channel Quality Estimation in 3D Drone Base Stations for Future Wireless Network. In Proceedings of the 2021 30th Wireless and Optical Communication Conference (WOCC), Taipei, Taiwan, 7–8 October 2021. [Google Scholar]
- Alzenad, M.; El-Keyi, A.; Yanikomeroglu, H. 3-D placement of an unmanned aerial vehicle base station for maximum coverage of users with different QoS requirements. IEEE Wirel. Commun. Lett. 2018, 7, 38–41. [Google Scholar] [CrossRef]
- Chen, Y.; Li, N.; Wang, C.; Xie, W.; Xv, J. A 3D placement of unmanned aerial vehicle base station based on multi-population genetic algorithm for maximizing users with different QoS requirements. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 967–972. [Google Scholar]
- Ma, D.; Ding, M.; Hassan, M. Enhancing cellular communications for UAVs via intelligent reflective surface. arXiv 2019, arXiv:1911.07631. [Google Scholar]
- Diamanti, M.; Charatsaris, P.; Tsiropoulou, E.E.; Papavassiliou, S. The prospect of reconfigurable intelligent surfaces in integrated access and backhaul networks. IEEE Trans. Green Commun. Netw. 2021, 6, 859–872. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 16, pp. 2094–2100. [Google Scholar]
- Deng, H.; Yin, S.; Deng, X.; Li, S. Value-based algorithms optimization with discounted multiple-step learning method in deep reinforcement learning. In Proceedings of the 2020 IEEE 22nd International Conference on High Performance Computing and Communications; IEEE 18th International Conference on Smart City; IEEE 6th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Yanuca Island, Fiji, 14–16 December 2020; pp. 979–984. [Google Scholar]
- Li, S.; Duo, B.; Di Renzo, M.; Tao, M.; Yuan, X. Robust secure UAV communications with the aid of reconfigurable intelligent surfaces. IEEE Trans. Wireless Commun. 2021, 20, 6402–6417. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Chen, Y. Machine learning empowered trajectory and passive beamforming design in UAV-RIS wireless networks. IEEE J. Sel. Areas Commun. 2021, 39, 2042–2055. [Google Scholar] [CrossRef]
- Mei, H.; Yang, K.; Liu, Q.; Wang, K. 3D-trajectory and phase-shift design for RIS-assisted UAV systems using deep reinforcement learning. IEEE Trans. Veh. Technol. 2022, 71, 3020–3029. [Google Scholar] [CrossRef]
- Li, Y.; Aghvami, A.H.; Dong, D. Path planning for cellular-connected UAV: A DRL solution with quantum-inspired experience replay. IEEE Trans. Wirel. Commun. 2022, 21, 7897–7912. [Google Scholar] [CrossRef]
- Li, Y.; Aghvami, A.H. Radio resource management for cellular-connected uav: A learning approach. IEEE Trans. Commun. 2023, 71, 2784–2800. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018; pp. 1–775. [Google Scholar]
- Mohi Ud Din, N.; Assad, A.; Ul Sabha, S.; Rasool, M. Optimizing deep reinforcement learning in data-scarce domains: A cross-domain evaluation of double DQN and dueling DQN. Int. J. Syst. Assur. Eng. Manag. 2024, 1–12. [Google Scholar] [CrossRef]
- Alharin, A.; Doan, T.N.; Sartipi, M. Reinforcement learning interpretation methods: A survey. IEEE Access 2020, 8, 171058–171077. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, T.; Liew, S.C. Deep-reinforcement learning multiple access for heterogeneous wireless networks. IEEE J. Sel. Areas Commun. 2019, 37, 1277–1290. [Google Scholar] [CrossRef]
- Abeywickrama, S.; Zhang, R.; Wu, Q.; Yuen, C. Intelligent reflecting surface: Practical phase shift model and beamforming optimization. IEEE Trans. Commun. 2020, 68, 5849–5863. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for Large-Scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]


| Notation | Detailed Definition |
|---|---|
| Location of the DBS | |
| Location of the ground users | |
| Location of the RIS | |
| Minimal and maximal altitudes of the DBS | |
| Minimal and maximal flying distances of the DBS | |
| Target area | |
| t | Phase-shift matrix of the RIS in timeslot t |
| Channel gain of user–DBS link | |
| Channel gain of DBS-RIS link | |
| Channel gain of RIS–ground user link | |
| Channel gain of ground user–RIS–DBS link | |
| Distance between the DBS and ground users | |
| Distance between the DBS and RIS | |
| Distance between the RIS and ground users | |
| Blockage probability | |
| Transmission power, noise power | |
| Path loss at the reference distance of 1 m | |
| Path loss exponent for RIS–user link | |
| Data rate of DBS–RIS–user link | |
| The coverage score |
| Parameters | Value |
|---|---|
| DBS transmit power | 5 mW |
| Bandwidth | 2 MHz |
| Noise power | −173 dBm |
| Path loss at 1 m α | −20 dB |
| Path loss β | 2.5 |
| Blocking parameters a, b [19] | 9.61, 0.16 |
| Carrier frequency fc | 2 Ghz |
| Number of RIS elements | 100 |
| Target area size | 1000 m × 1000 m |
| Episodes and time slots | 500, 2000 |
| Optimizer | Activation Function | Learning Rate | Minibatch Size | Discount Factor | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Adam | RMSProp | Sigmoid | ReLU | 0.001 | 0.0001 | 256 | 512 | 0.89 | 0.9 | |
| Coverage score | 0.942 | 0.955 | 0.942 | 0.955 | 0.942 | 0.955 | 0.942 | 0.955 | 0.942 | 0.955 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kabore, W.N.; Juang, R.-T.; Lin, H.-P.; Tesfaw, B.A.; Tarekegn, G.B. Optimizing the Deployment of an Aerial Base Station and the Phase-Shift of a Ground Reconfigurable Intelligent Surface for Wireless Communication Systems Using Deep Reinforcement Learning. Information 2024, 15, 386. https://doi.org/10.3390/info15070386
Kabore WN, Juang R-T, Lin H-P, Tesfaw BA, Tarekegn GB. Optimizing the Deployment of an Aerial Base Station and the Phase-Shift of a Ground Reconfigurable Intelligent Surface for Wireless Communication Systems Using Deep Reinforcement Learning. Information. 2024; 15(7):386. https://doi.org/10.3390/info15070386
Chicago/Turabian StyleKabore, Wendenda Nathanael, Rong-Terng Juang, Hsin-Piao Lin, Belayneh Abebe Tesfaw, and Getaneh Berie Tarekegn. 2024. "Optimizing the Deployment of an Aerial Base Station and the Phase-Shift of a Ground Reconfigurable Intelligent Surface for Wireless Communication Systems Using Deep Reinforcement Learning" Information 15, no. 7: 386. https://doi.org/10.3390/info15070386
APA StyleKabore, W. N., Juang, R.-T., Lin, H.-P., Tesfaw, B. A., & Tarekegn, G. B. (2024). Optimizing the Deployment of an Aerial Base Station and the Phase-Shift of a Ground Reconfigurable Intelligent Surface for Wireless Communication Systems Using Deep Reinforcement Learning. Information, 15(7), 386. https://doi.org/10.3390/info15070386









