A Survey of Computationally Efficient Graph Neural Networks for Reconfigurable Systems
Abstract
1. Introduction
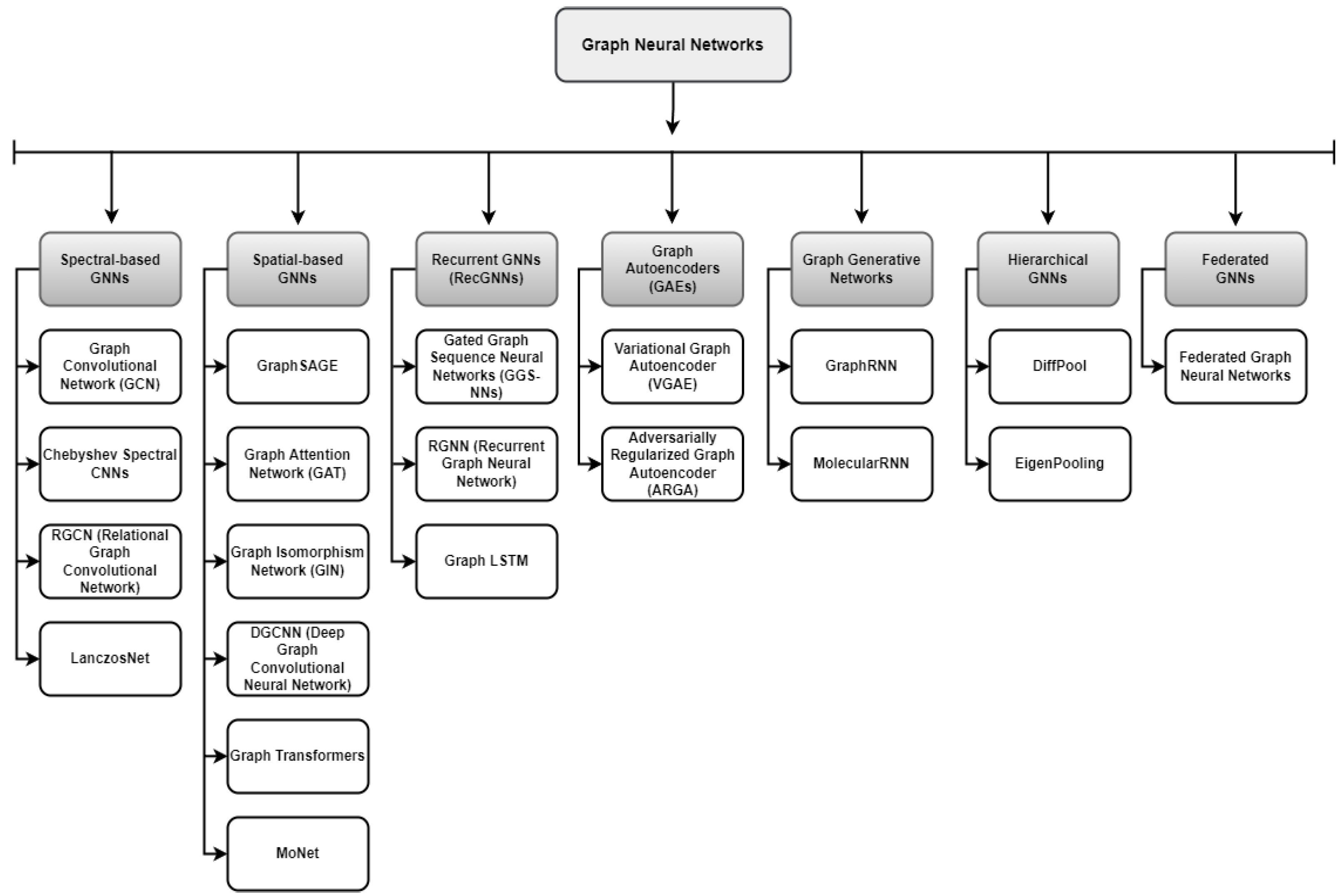
- GNN Basics and Theories: This paper presents the basic concepts of GNNs and their layers. Furthermore, it proposes a taxonomy of GNNs according to their variations.
- Quantization Methods and Lightweight Models: This survey includes reviews of quantization methods aimed at building lightweight GNN models for embedded systems or GPU- and CPU-based applications.
- FPGA-Based Hardware Accelerators: Our research describes in detail the work currently conducted on hardware-based accelerators (typically FPGAs) that can be used in current or future embedded device applications.
- Discussion and Future Research Directions: This study discusses study outcomes for future research based on the findings and provides insights about possible research gaps.
2. Background
| GNN Model | Description |
|---|---|
| GCN (graph convolutional network) [73] | For each node, a new feature vector is created by collecting information from neighboring nodes. |
| GIN (graph isomorphism network) [74] | For each node, an invariant feature vector is created with respect to its neighbors. |
| GAT (graph attention network) [75] | For each node, a new feature vector is created that considers the importance of neighboring nodes. |
| GraphSAGE [13] | A feature vector is generated for each node based on the different neighborhood levels. |
2.1. Graph Neural Networks
2.2. Graph Convolutional Networks
2.3. Graph Isomorphism Networks
2.4. Graph Attention Networks
2.5. GraphSAGE
2.6. Future Research Directions
3. Graph Neural Network Quantization
3.1. Quantization
3.1.1. Scalar Quantization
3.1.2. Vector Quantization
3.2. Quantization Approaches for GNNs
- Activation functions determine the output of each layer and provide a nonlinear transformation. It is necessary for the model to learn nonlinear relationships; therefore, activation functions are an essential component. Activations can be quantized to reduce computational costs.
- Feature matrix is a matrix that shows all the node features of graphs. Each row represents a node and the columns represent features. The feature matrix generates the largest input data of the GNN, and quantization significantly reduces the size and processing cost of these data.
- Weights are learnable parameters that refer to the connections between nodes or layers and can be optimized to improve the predictions of the model. Quantizing the weights reduces the memory requirements and computational costs of the model and facilitates the fitting of pre-trained models. They can often be quantized to lower the number of bits.
- Attention coefficients determine the degree of importance between nodes. These coefficients are calculated using the attention mechanism and allow the model to focus on specific nodes or edges. Quantization of this parameter in GNN models with attention coefficients is important for fully quantized efficient networks.
- Convolution matrix is a matrix used to combine the features of neighboring nodes and create new feature vectors. This matrix usually contains learnable weights and contains information specific to the graph structure. Quantization can reduce the memory and processing power required to store and compute this matrix.
- Weighted adjacency matrix represents the relationships between the nodes of a graph and the strength of these relationships. The weighted adjacency matrix is one of the basic building blocks of GNNs for information propagation. Quantization in models containing this matrix can reduce the computational cost.
| Publication | Year | Targetted Problem | Quantized Parameters | Datasets |
|---|---|---|---|---|
| Degree-Quant [36] | 2020 | Inefficient training/inference time | Weights, Activations | Cora, Citeseer, ZINC, MNIST, CIFAR10, Reddit-Binary |
| EXACT [87] | 2021 | High memory need for training | Activations | Reddit, Flicker, Yelp, obgn-arxiv, obgn-products |
| VQ-GNN [89] | 2021 | Challenges of sampling-based techniques | Convolution matrix, Node feature matrix | ogbn-arxiv, Reddit, PPI, ogbl-collab |
| SGQuant [90] | 2020 | High memory footprint for energy-limited devices | Feature matrix | Cora, Citeseer, Pubmed, Amazon—computers, Reddit |
| LPGNAS [91] | 2020 | Insufficient optimization research in the field | Weights, Activations | Cora, Citeseer, Pubmed, Amazon—computers and photos, Flicker, CoraFull, Yelp |
| Bahri et al. [92] | 2021 | Challenges in real-world applications due to model size and energy requirements | Weights, Feature matrix | obgn-products, obgn-protein |
| Wang et al. [93] | 2021 | Model inefficiency and scaling problems with inefficient real-valued parameters | Weights, Attention coefficients, Node embeddings | Cora, Citeseer, Pubmed, Facebook, wiki-vote, Brazil, USA |
| EPQuant [94] | 2022 | Limited availability on edge devices due to high requirements | Input embeddings, Weights, Learnable parameters | Cora, Citeseer, Pubmed, Reddit, Amazon2M |
| Bi-GCN [95] | 2021 | High memory requirements of GNNs | Weights, Node features | Cora, Pubmed, Flicker, Reddit |
| Dorefa-Graph [96] | 2024 | Cost-effective computing on embedded systems | Feature matrix, Weights, Adjacency matrix, Activations | Cora, Pubmed, Citeseer |
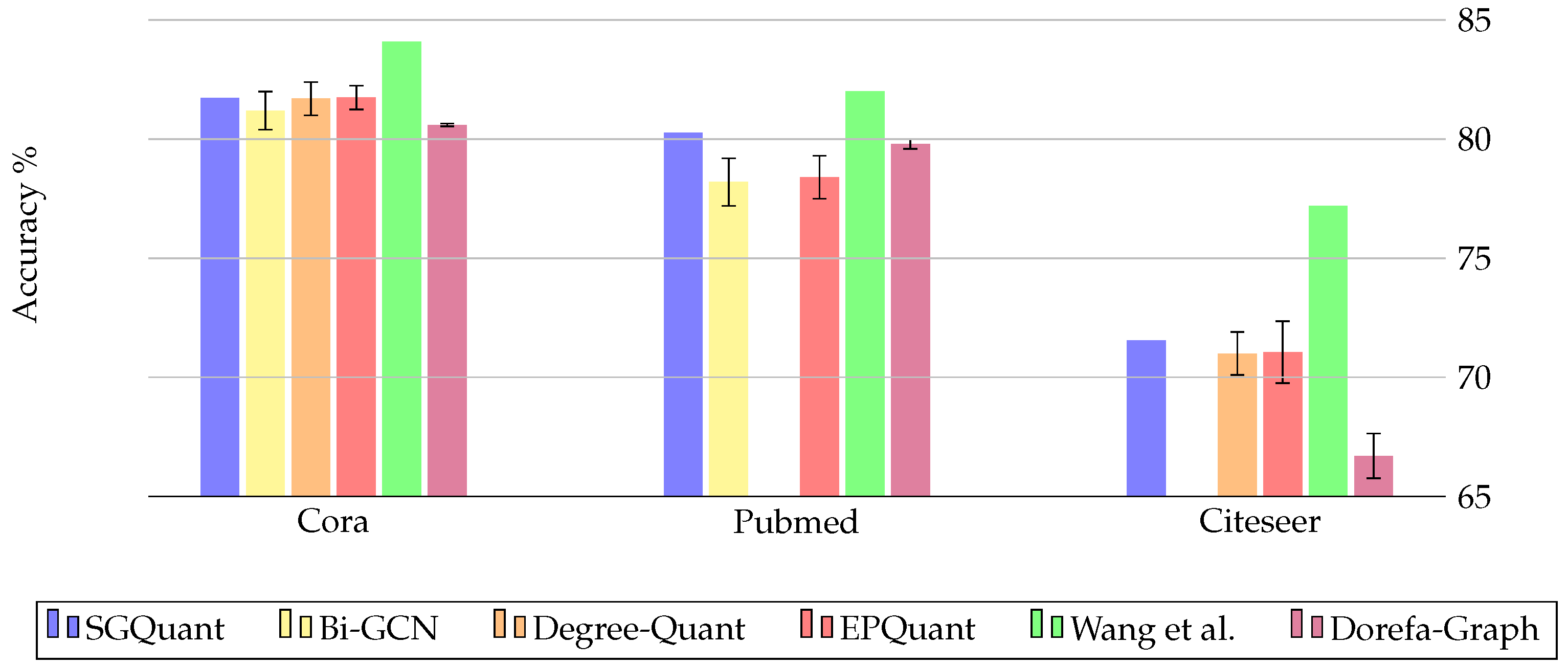
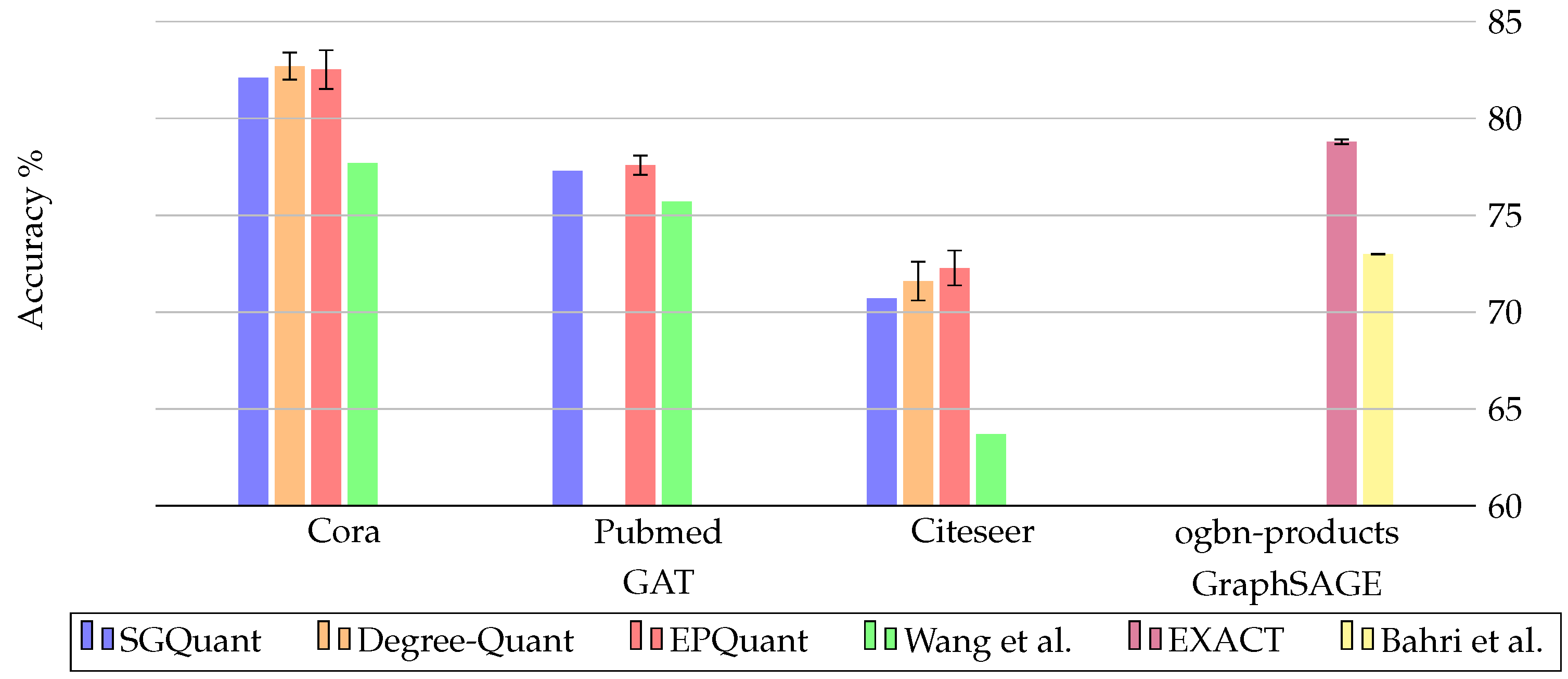
3.3. Future Research Directions
4. Graph Neural Network Acceleration
4.1. Hardware-Based Accelerator Approaches
4.2. FPGA-Based Accelerators Approaches
4.3. FPGA-Based Heterogeneous Approaches
4.4. Frameworks for FPGA-Based Accelerators
4.5. FPGA-Based Accelerator Approaches with Quantization
| Publication | Hardware | Resource Consumption | Quantized Parameters | Baselines |
|---|---|---|---|---|
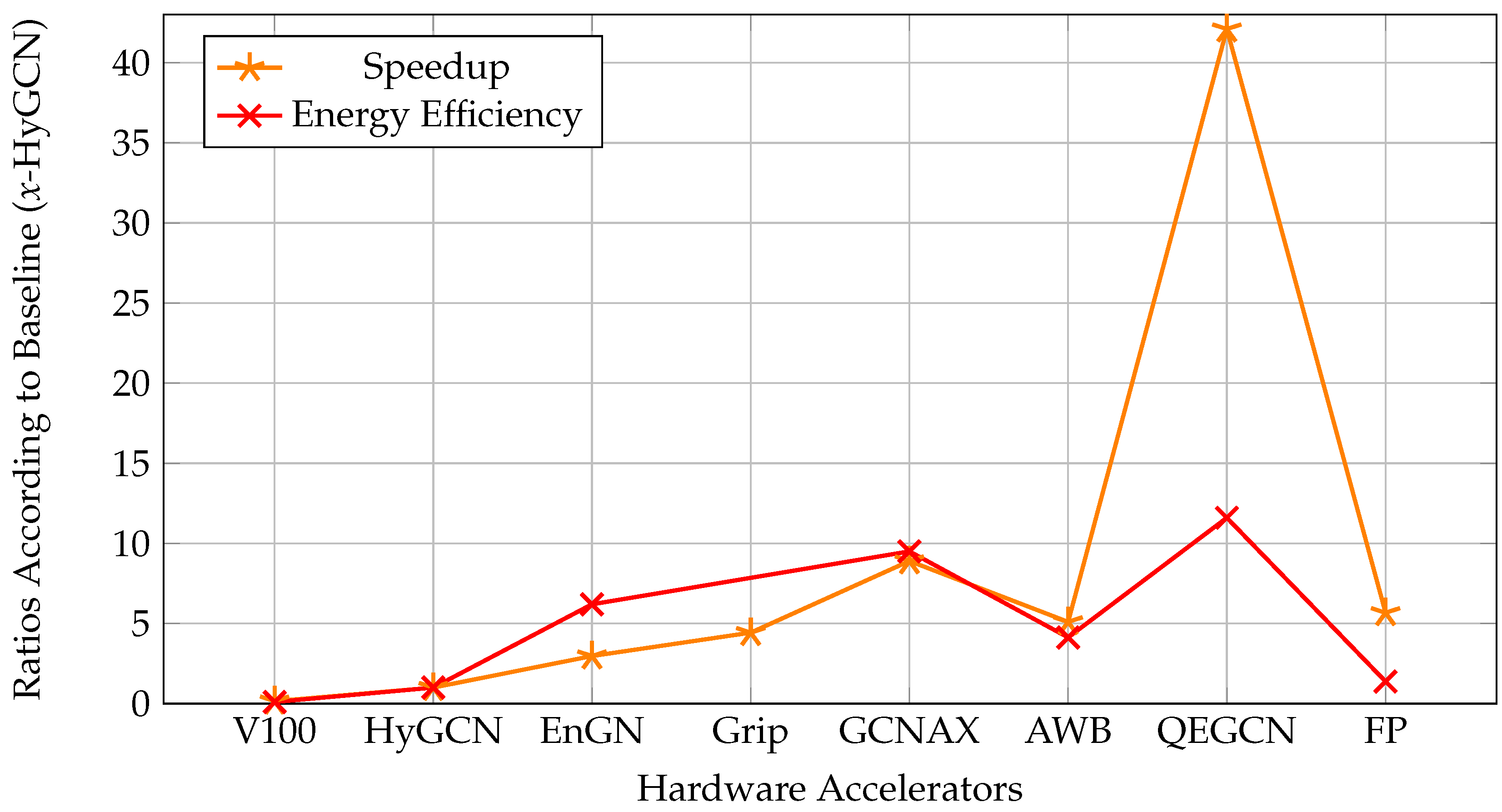
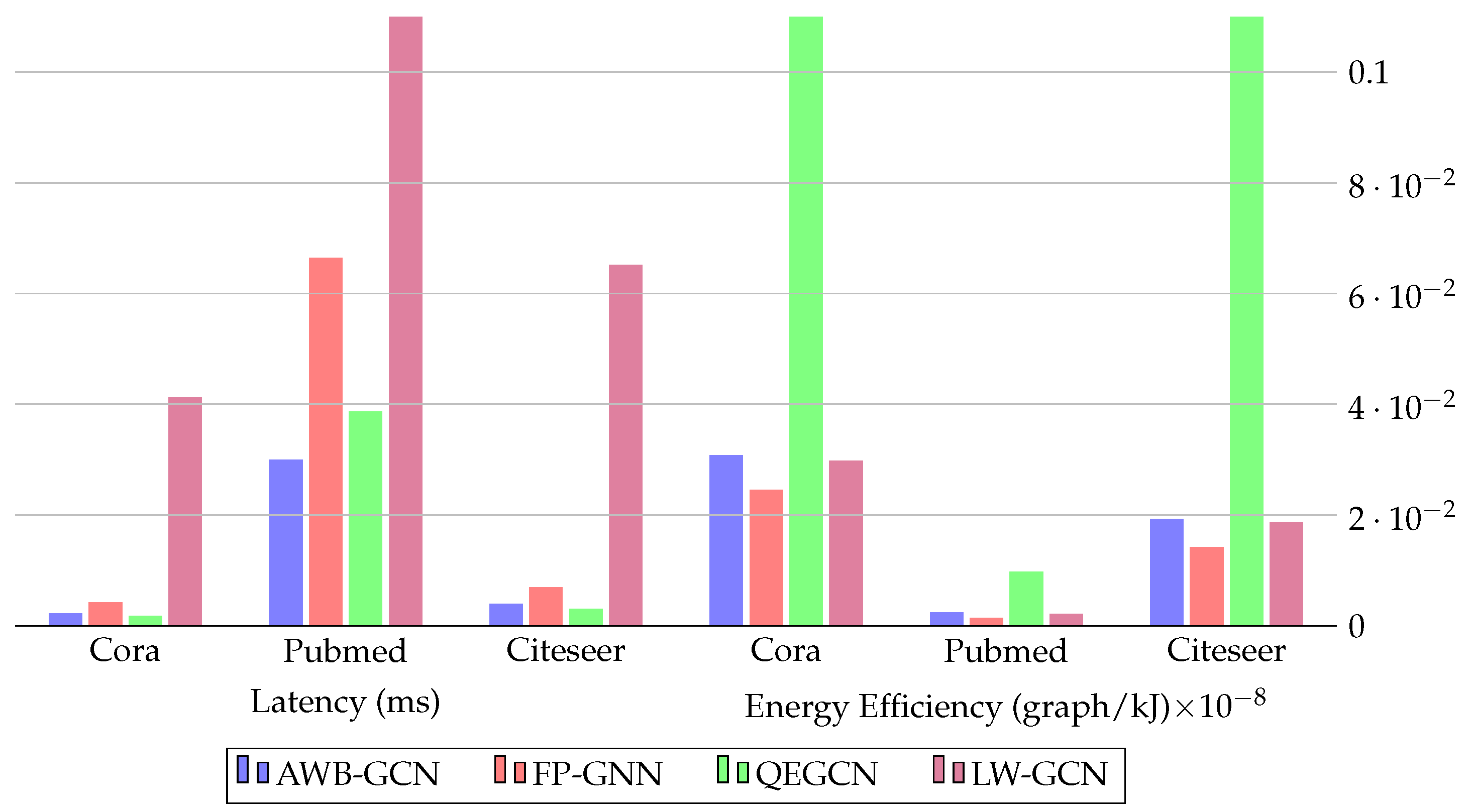
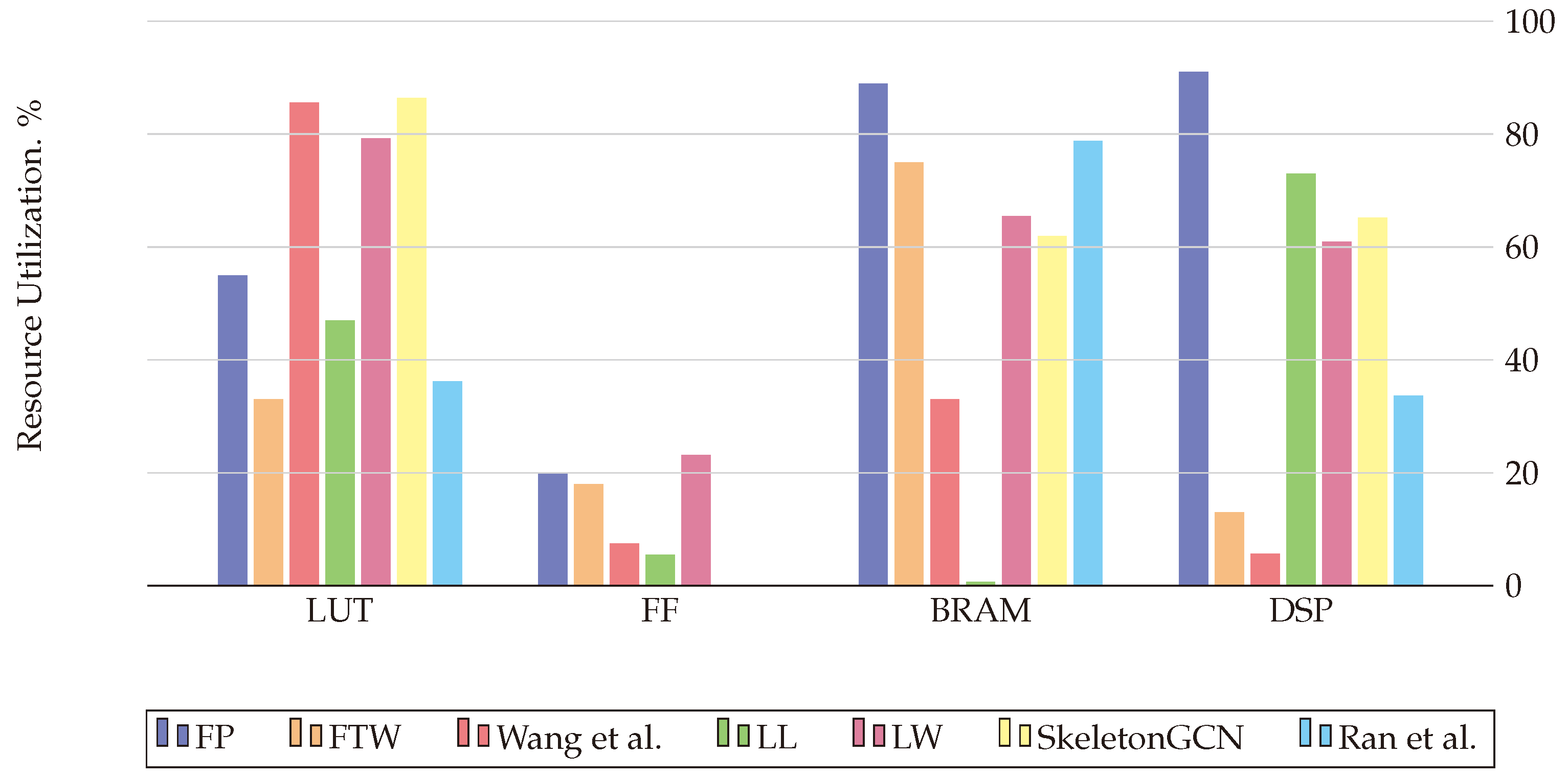
| FP-GNN [25] | VCU128 Freq: 225 MHz | LUT: 717,578 FF: 517,428 BRAM: 1792 DSP: 8192 | Features, weights 32-bit fixed point | PyG-CPU-GPU, HyGCN, GCNAX, AWB-GCN, I-GCN |
| LL-GNN [33] | Alveo U250 Freq: 200 MHz | LUT: 815,000 FF: 139,000 BRAM: 37 DSP: 8986 | Model parameters 12-bit fixed point | PyG-CPU-GPU |
| FPGAN [126] | Arria10 GX1150 Freq: 216 MHz | LUT: 250,570 FF: 338,490 BRAM: NI DSP: 148 | Features, weights fixed point | PyG-CPU-GPU |
| SkeletonGCN [127] | Alveo U200 Freq: 250 MHz | LUT: 1,021,386 FF: NI BRAM: 1338 DSP: 960 | Feature, adjacency matrices, trainable parameters 16-bit signed integer | PyG-CPU-GPU, GraphACT |
| QEGCN [128] | VCU128 Freq: 225 MHz | LUT: 21,935 FF: 9201 BRAM: 22 DSP: 0 | Features, weights 8-bit fixed point | PyG-CPU-GPU, DGL-CPU-GPU, HyGCN, EnGN, AWB-GCN, ACE-GCN |
| FTW-GAT [129] | VCU128 Freq: 225 MHz | LUT: 436,657 FF: 470,222 BRAM: 1502 DSP: 1216 | 8-bit int features3-bit int weights | PyG-CPU-GPU, FP-GNN |
| Wang et al. [130] | Alveo U200 Freq: 250 MHz | LUT: 101,000 FF: 11,700 BRAM: 1430 DSP: 392 | 1-bit integer features, weights 32-bit integer adjacency matrix | PyG-CPU-GPU, ASAP [114] |
| Ran et al. [131] | Alveo U200 Freq: 250 MHz | LUT: 427,438 FF: NI BRAM: 1702 DSP: 33.7 | Features, weights | PyG-CPU-GPU, HyGCN, ASAP [114], AWB-GCN, LW-GCN |
| Yuan et al. [132] | VCU128 Freq: 300 MHz | LUT: 3244 FF: 345 BRAM: 102.5 DSP: 64 | Features, weights 32-bit fixed point | PyG-CPU-GPU |
| LW-GCN [133] | Kintex-7 K325T Freq: 200 MHz | LUT: 161,529 FF: 94,369 BRAM: 291.5 DSP: 512 | Features, weights 16-bit signed fixed point | PyG-CPU-GPU, AWB-GCN |
4.6. FPGA-Based Accelerators for Embedded Applications
| Study | Target Device | Datasets | Fixed-Point Representation |
|---|---|---|---|
| gFADES [76] | Zynq Ultrascale+ XCZU28DR | Cora, Citeseer, Pubmed | - |
| LW-GCN [133] | Xilinx Kintex-7 | Cora, Citeseer, Pubmed | ✓ |
| Zhou et al. [134] | Xilinx ZCU104, Alveo U200 | Wikipedia, Reddit, GDELT | - |
| Hansson et al. [135] | Xilinx Zynq UltraScale+ | Cora, Citeseer, Pubmed | ✓ |
4.7. Future Research Directions
5. Discussion and Future Research Directions
5.1. Summary of Current Research
- Achieving a delicate balance between energy efficiency, training-output speed, and accuracy in unified approaches requires careful customization during the design phase according to the specific requirements of particular applications, highlighting the important role of future efforts in achieving this balance.
- Quantization methods employed during both the training and inference phases offer effective solutions to challenges such as computational complexity and memory demands in GNN models.
- Scalar quantization methods are prevalent in embedded systems due to their ease of implementation and the computational efficiency of integer arithmetic.
- Vector quantization provides higher compression ratios compared to scalar quantization by grouping multiple vectors together.
- Mixed precision approaches show the potential to maintain accuracy while reducing model size. However, different bit representations can introduce computational complexity from a hardware standpoint.
- Research shows that the accuracy achieved with 16-bit and 8-bit quantization values can be achieved with lower-bit numbers such as 4-bit and 2-bit.
- The current body of FPGA studies related to graph neural network (GNN) models is still insufficient to comprehensively address the complexities of embedded system applications.
- The adaptive nature of FPGA accelerators exhibits notable efficacy in accommodating diverse application requirements, demonstrating their potential for widespread adoption in various domains.
- While a significant portion of research efforts are focused on GNN inference, there is a critical need to accelerate the training phase.
- While the utilization of common datasets and network models provides an initial benchmark for researchers, the limited extension of studies to diverse application domains and the absence of the establishment of distinct baselines pose significant challenges requiring resolution.
5.2. Future Research Directions
- Combining vector and scalar quantization can offer the advantages of both integer arithmetic computational power and the high compression ratio of vector quantization, which is crucial for developing highly efficient low-dimensional models for hardware applications.
- For embedded system applications and accelerator studies, integer arithmetic provides high computational efficiency. Consequently, the development of fully quantized GNN models specifically designed for embedded system applications is crucial for efficient scalable future work.
- High accuracy levels can be achieved even at low bit levels with new quantization methods. In this context, the adoption of aggressive methods involving low-bit representations to integrate large GNN models into embedded device applications is expected to attract the attention of more researchers.
- The number of FPGA applications for embedded systems is quite insufficient compared to quantization studies, highlighting an important research gap in the FPGA field.
- There is a growing need to accelerate the training phase, especially for dynamic graph structures, and this is a research gap that requires further research.
- Although this work is focused on quantization and FPGA-based accelerators, additional techniques such as sampling, reordering, simplification, and knowledge distillation are currently being used with promising results. It is anticipated that interest in additional methods such as quantization and other approaches will grow in hardware-based applications.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric deep learning: Going beyond euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Gama, F.; Isufi, E.; Leus, G.; Ribeiro, A. Graphs, convolutions, and neural networks: From graph filters to graph neural networks. IEEE Signal Process. Mag. 2020, 37, 128–138. [Google Scholar] [CrossRef]
- Coutino, M.; Isufi, E.; Leus, G. Advances in distributed graph filtering. IEEE Trans. Signal Process. 2019, 67, 2320–2333. [Google Scholar] [CrossRef]
- Saad, L.B.; Beferull-Lozano, B. Quantization in graph convolutional neural networks. In Proceedings of the 29th IEEE European Signal Processing Conference (EUSIPCO), Dublin, Ireland, 23–27 August 2021; pp. 1855–1859. [Google Scholar]
- Zhu, R.; Zhao, K.; Yang, H.; Lin, W.; Zhou, C.; Ai, B.; Li, Y.; Zhou, J. Aligraph: A comprehensive graph neural network platform. arXiv 2019, arXiv:1902.08730. [Google Scholar] [CrossRef]
- Ju, X.; Farrell, S.; Calafiura, P.; Murnane, D.; Gray, L.; Klijnsma, T.; Pedro, K.; Cerati, G.; Kowalkowski, J.; Perdue, G.; et al. Graph neural networks for particle reconstruction in high energy physics detectors. arXiv 2020, arXiv:2003.11603. [Google Scholar]
- Ju, X.; Murnane, D.; Calafiura, P.; Choma, N.; Conlon, S.; Farrell, S.; Xu, Y.; Spiropulu, M.; Vlimant, J.R.; Aurisano, A.; et al. Performance of a geometric deep learning pipeline for HL-LHC particle tracking. Eur. Phys. J. C 2021, 81, 1–14. [Google Scholar] [CrossRef]
- Wu, L.; Chen, Y.; Shen, K.; Guo, X.; Gao, H.; Li, S.; Pei, J.; Long, B. Graph neural networks for natural language processing: A survey. Found. Trends® Mach. Learn. 2023, 16, 119–328. [Google Scholar] [CrossRef]
- Jiang, W.; Luo, J. Graph neural network for traffic forecasting: A survey. Expert Syst. Appl. 2022, 207, 117921. [Google Scholar] [CrossRef]
- Pope, J.; Liang, J.; Kumar, V.; Raimondo, F.; Sun, X.; McConville, R.; Pasquier, T.; Piechocki, R.; Oikonomou, G.; Luo, B.; et al. Resource-Interaction Graph: Efficient Graph Representation for Anomaly Detection. arXiv 2022, arXiv:2212.08525. [Google Scholar]
- Betkier, I.; Oszczypała, M.; Pobożniak, J.; Sobieski, S.; Betkier, P. PocketFinderGNN: A manufacturing feature recognition software based on Graph Neural Networks (GNNs) using PyTorch Geometric and NetworkX. SoftwareX 2023, 23, 101466. [Google Scholar] [CrossRef]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Huang, W.; Zhang, T.; Rong, Y.; Huang, J. Adaptive sampling towards fast graph representation learning. In Proceedings of the Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Wang, M.Y. Deep graph library: Towards efficient and scalable deep learning on graphs. In Proceedings of the ICLR Workshop on Representation Learning on Graphs and Manifolds, New Orleans, LA, USA, 6 May 2019. [Google Scholar]
- Lerer, A.; Wu, L.; Shen, J.; Lacroix, T.; Wehrstedt, L.; Bose, A.; Peysakhovich, A. Pytorch-biggraph: A large scale graph embedding system. Proc. Mach. Learn. Syst. 2019, 1, 120–131. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Networks Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, P.; Zhu, W. Deep learning on graphs: A survey. IEEE Trans. Knowl. Data Eng. 2020, 34, 249–270. [Google Scholar] [CrossRef]
- Geng, T.; Li, A.; Shi, R.; Wu, C.; Wang, T.; Li, Y.; Haghi, P.; Tumeo, A.; Che, S.; Reinhardt, S.; et al. AWB-GCN: A graph convolutional network accelerator with runtime workload rebalancing. In Proceedings of the 2020 53rd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Athens, Greece, 17–21 October 2020; pp. 922–936. [Google Scholar]
- Fey, M.; Lenssen, J.E. Fast graph representation learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar]
- Ferludin, O.; Eigenwillig, A.; Blais, M.; Zelle, D.; Pfeifer, J.; Sanchez-Gonzalez, A.; Li, S.; Abu-El-Haija, S.; Battaglia, P.; Bulut, N.; et al. TF-GNN: Graph neural networks in TensorFlow. arXiv 2022, arXiv:2207.03522. [Google Scholar]
- Yazdanbakhsh, A.; Park, J.; Sharma, H.; Lotfi-Kamran, P.; Esmaeilzadeh, H. Neural acceleration for GPU throughput processors. In Proceedings of the 48th International Symposium on Microarchitecture, Waikiki, HI, USA, 5–9 December 2015; pp. 482–493. [Google Scholar]
- Tian, T.; Zhao, L.; Wang, X.; Wu, Q.; Yuan, W.; Jin, X. FP-GNN: Adaptive FPGA accelerator for graph neural networks. Future Gener. Comput. Syst. 2022, 136, 294–310. [Google Scholar] [CrossRef]
- Nunez-Yanez, J.; Hosseinabady, M. Sparse and dense matrix multiplication hardware for heterogeneous multi-precision neural networks. Array 2021, 12, 100101. [Google Scholar] [CrossRef]
- Sit, M.; Kazami, R.; Amano, H. FPGA-based accelerator for losslessly quantized convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Field Programmable Technology (ICFPT), Melbourne, VIC, Australia, 11–13 December 2017; pp. 295–298. [Google Scholar]
- Zhang, B.; Kuppannagari, S.R.; Kannan, R.; Prasanna, V. Efficient neighbor-sampling-based gnn training on cpu-fpga heterogeneous platform. In Proceedings of the 2021 IEEE High Performance Extreme Computing Conference (HPEC), Virtual, 21–23 September 2021; pp. 1–7. [Google Scholar]
- Liang, S.; Wang, Y.; Liu, C.; He, L.; Huawei, L.; Xu, D.; Li, X. Engn: A high-throughput and energy-efficient accelerator for large graph neural networks. IEEE Trans. Comput. 2020, 70, 1511–1525. [Google Scholar] [CrossRef]
- Zhang, S.; Sohrabizadeh, A.; Wan, C.; Huang, Z.; Hu, Z.; Wang, Y.; Cong, J.; Sun, Y. A Survey on Graph Neural Network Acceleration: Algorithms, Systems, and Customized Hardware. arXiv 2023, arXiv:2306.14052. [Google Scholar]
- Zeng, H.; Prasanna, V. GraphACT: Accelerating GCN training on CPU-FPGA heterogeneous platforms. In Proceedings of the 2020 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Seaside, CA, USA, 23–25 February 2020; pp. 255–265. [Google Scholar]
- Kiningham, K.; Levis, P.; Ré, C. GReTA: Hardware optimized graph processing for GNNs. In Proceedings of the Workshop on Resource-Constrained Machine Learning (ReCoML 2020), Austin, TX, USA, 2–4 March 2020. [Google Scholar]
- Que, Z.; Loo, M.; Fan, H.; Blott, M.; Pierini, M.; Tapper, A.D.; Luk, W. LL-GNN: Low latency graph neural networks on FPGAs for particle detectors. arXiv 2022, arXiv:2209.14065. [Google Scholar]
- Zhao, L.; Wu, Q.; Wang, X.; Tian, T.; Wu, W.; Jin, X. HuGraph: Acceleration of GCN Training on Heterogeneous FPGA Clusters with Quantization. In Proceedings of the 2022 IEEE High Performance Extreme Computing Conference (HPEC), Virtual Conference, 19–23 September 2022; pp. 1–7. [Google Scholar]
- Gholami, A.; Kim, S.; Dong, Z.; Yao, Z.; Mahoney, M.W.; Keutzer, K. A survey of quantization methods for efficient neural network inference. In Low-Power Computer Vision; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022; pp. 291–326. [Google Scholar]
- Tailor, S.A.; Fernandez-Marques, J.; Lane, N.D. Degree-quant: Quantization-aware training for graph neural networks. arXiv 2020, arXiv:2008.05000. [Google Scholar]
- Goyal, P.; Ferrara, E. Graph embedding techniques, applications, and performance: A survey. Knowl.-Based Syst. 2018, 151, 78–94. [Google Scholar] [CrossRef]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: A comprehensive review. Comput. Soc. Netw. 2019, 6, 1–23. [Google Scholar] [CrossRef]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: Algorithms, applications and open challenges. In Proceedings of the Computational Data and Social Networks: 7th International Conference, CSoNet 2018, Shanghai, China, 18–20 December 2018; Proceedings 7. Springer: Berlin, Germany, 2018; pp. 79–91. [Google Scholar]
- Quan, P.; Shi, Y.; Lei, M.; Leng, J.; Zhang, T.; Niu, L. A brief review of receptive fields in graph convolutional networks. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence-Companion Volume, Thessaloniki, Greece, 14–17 October 2019; pp. 106–110. [Google Scholar]
- Asif, N.A.; Sarker, Y.; Chakrabortty, R.K.; Ryan, M.J.; Ahamed, M.H.; Saha, D.K.; Badal, F.R.; Das, S.K.; Ali, M.F.; Moyeen, S.I.; et al. Graph neural network: A comprehensive review on non-euclidean space. IEEE Access 2021, 9, 60588–60606. [Google Scholar] [CrossRef]
- Chami, I.; Abu-El-Haija, S.; Perozzi, B.; Ré, C.; Murphy, K. Machine learning on graphs: A model and comprehensive taxonomy. J. Mach. Learn. Res. 2022, 23, 3840–3903. [Google Scholar]
- Veličković, P. Everything is connected: Graph neural networks. Curr. Opin. Struct. Biol. 2023, 79, 102538. [Google Scholar] [CrossRef]
- Bhatti, U.A.; Tang, H.; Wu, G.; Marjan, S.; Hussain, A. Deep learning with graph convolutional networks: An overview and latest applications in computational intelligence. Int. J. Intell. Syst. 2023, 2023, 1–28. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, X.; Wei, M.; Li, Z. A comprehensive review of graph convolutional networks: Approaches and applications. Electron. Res. Arch. 2023, 31, 4185–4215. [Google Scholar] [CrossRef]
- Shabani, N.; Wu, J.; Beheshti, A.; Sheng, Q.Z.; Foo, J.; Haghighi, V.; Hanif, A.; Shahabikargar, M. A comprehensive survey on graph summarization with graph neural networks. IEEE Trans. Artif. Intell. 2024. [Google Scholar] [CrossRef]
- Ju, W.; Fang, Z.; Gu, Y.; Liu, Z.; Long, Q.; Qiao, Z.; Qin, Y.; Shen, J.; Sun, F.; Xiao, Z.; et al. A comprehensive survey on deep graph representation learning. Neural Netw. 2024, 173, 106207. [Google Scholar] [CrossRef]
- Liu, R.; Xing, P.; Deng, Z.; Li, A.; Guan, C.; Yu, H. Federated Graph Neural Networks: Overview, Techniques, and Challenges. IEEE Trans. Neural Netw. Learn. Syst. 2024. [Google Scholar] [CrossRef]
- Lopera, D.S.; Servadei, L.; Kiprit, G.N.; Hazra, S.; Wille, R.; Ecker, W. A survey of graph neural networks for electronic design automation. In Proceedings of the 2021 ACM/IEEE 3rd Workshop on Machine Learning for CAD (MLCAD), Raleigh, NC, USA, 30 August–3 September 2021; pp. 1–6. [Google Scholar]
- Liu, X.; Yan, M.; Deng, L.; Li, G.; Ye, X.; Fan, D. Sampling methods for efficient training of graph convolutional networks: A survey. IEEE/CAA J. Autom. Sin. 2021, 9, 205–234. [Google Scholar] [CrossRef]
- Varlamis, I.; Michail, D.; Glykou, F.; Tsantilas, P. A survey on the use of graph convolutional networks for combating fake news. Future Internet 2022, 14, 70. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Mao, Z.; Qin, Y.; Xiao, Z.; Feng, J.; Gu, Y.; Ju, W.; Luo, X.; Zhang, M. A survey on graph neural networks in intelligent transportation systems. arXiv 2024, arXiv:2401.00713. [Google Scholar]
- Lamb, L.C.; Garcez, A.; Gori, M.; Prates, M.; Avelar, P.; Vardi, M. Graph neural networks meet neural-symbolic computing: A survey and perspective. arXiv 2020, arXiv:2003.00330. [Google Scholar]
- Malekzadeh, M.; Hajibabaee, P.; Heidari, M.; Zad, S.; Uzuner, O.; Jones, J.H. Review of graph neural network in text classification. In Proceedings of the 2021 IEEE 12th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 1–4 December 2021. [Google Scholar]
- Ahmad, T.; Jin, L.; Zhang, X.; Lai, S.; Tang, G.; Lin, L. Graph convolutional neural network for human action recognition: A comprehensive survey. IEEE Trans. Artif. Intell. 2021, 2, 128–145. [Google Scholar] [CrossRef]
- Dong, G.; Tang, M.; Wang, Z.; Gao, J.; Guo, S.; Cai, L.; Gutierrez, R.; Campbel, B.; Barnes, L.E.; Boukhechba, M. Graph neural networks in IoT: A survey. ACM Trans. Sens. Netw. 2023, 19, 1–50. [Google Scholar] [CrossRef]
- Jia, M.; Gabrys, B.; Musial, K. A Network Science perspective of Graph Convolutional Networks: A survey. IEEE Access 2023. [Google Scholar] [CrossRef]
- Ren, H.; Lu, W.; Xiao, Y.; Chang, X.; Wang, X.; Dong, Z.; Fang, D. Graph convolutional networks in language and vision: A survey. Knowl.-Based Syst. 2022, 251, 109250. [Google Scholar] [CrossRef]
- Garg, R.; Qin, E.; Martínez, F.M.; Guirado, R.; Jain, A.; Abadal, S.; Abellán, J.L.; Acacio, M.E.; Alarcón, E.; Rajamanickam, S.; et al. A Taxonomy for Classification and Comparison of Dataflows for Gnn Accelerators; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2021. [Google Scholar]
- Li, S.; Tao, Y.; Tang, E.; Xie, T.; Chen, R. A survey of field programmable gate array (FPGA)-based graph convolutional neural network accelerators: Challenges and opportunities. PeerJ Comput. Sci. 2022, 8, e1166. [Google Scholar] [CrossRef]
- Liu, X.; Yan, M.; Deng, L.; Li, G.; Ye, X.; Fan, D.; Pan, S.; Xie, Y. Survey on graph neural network acceleration: An algorithmic perspective. arXiv 2022, arXiv:2202.04822. [Google Scholar]
- Abadal, S.; Jain, A.; Guirado, R.; López-Alonso, J.; Alarcón, E. Computing graph neural networks: A survey from algorithms to accelerators. ACM Comput. Surv. (CSUR) 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Liao, R.; Zhao, Z.; Urtasun, R.; Zemel, R.S. Lanczosnet: Multi-scale deep graph convolutional networks. arXiv 2019, arXiv:1901.01484. [Google Scholar]
- Dwivedi, V.P.; Bresson, X. A generalization of transformer networks to graphs. arXiv 2020, arXiv:2012.09699. [Google Scholar]
- Monti, F.; Boscaini, D.; Masci, J.; Rodola, E.; Svoboda, J.; Bronstein, M.M. Geometric deep learning on graphs and manifolds using mixture model cnns. arXiv 2016, arXiv:1611.08402. [Google Scholar]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated graph sequence neural networks. arXiv 2015, arXiv:1511.05493. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Pan, S.; Hu, R.; Long, G.; Jiang, J.; Yao, L.; Zhang, C. Adversarially regularized graph autoencoder for graph embedding. arXiv 2018, arXiv:1802.04407. [Google Scholar]
- You, J.; Ying, R.; Ren, X.; Hamilton, W.; Leskovec, J. Graphrnn: Generating realistic graphs with deep auto-regressive models. In Proceedings of the International Conference on Machine Learning. PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 5708–5717. [Google Scholar]
- Ying, Z.; You, J.; Morris, C.; Ren, X.; Hamilton, W.; Leskovec, J. Hierarchical graph representation learning with differentiable pooling. In Proceedings of the Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Ma, Y.; Wang, S.; Aggarwal, C.C.; Tang, J. Graph convolutional networks with eigenpooling. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 723–731. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Nunez-Yanez, J. Accelerating Graph Neural Networks in Pytorch with HLS and Deep Dataflows. In Proceedings of the International Symposium on Applied Reconfigurable Computing; Springer: Berlin, Germany, 2023; pp. 131–145. [Google Scholar]
- Chen, R.; Zhang, H.; Li, S.; Tang, E.; Yu, J.; Wang, K. Graph-OPU: A Highly Integrated FPGA-Based Overlay Processor for Graph Neural Networks. In Proceedings of the 2023 33rd IEEE International Conference on Field-Programmable Logic and Applications (FPL), Gothenburg, Sweden, 4–8 September 2023; pp. 228–234. [Google Scholar]
- Novkin, R.; Amrouch, H.; Klemme, F. Approximation-aware and quantization-aware training for graph neural networks. IEEE Trans. Comput. 2024, 73, 599–612. [Google Scholar] [CrossRef]
- Wan, B.; Zhao, J.; Wu, C. Adaptive Message Quantization and Parallelization for Distributed Full-graph GNN Training. In Proceedings of the Machine Learning and Systems, Miami Beach, FL, USA, 4–8 June 2023; Volume 5. [Google Scholar]
- Wu, Q.; Zhao, L.; Liang, H.; Wang, X.; Tao, L.; Tian, T.; Wang, T.; He, Z.; Wu, W.; Jin, X. GCINT: Dynamic Quantization Algorithm for Training Graph Convolution Neural Networks Using Only Integers. 2023. Available online: https://openreview.net/forum?id=cIFtriyX6on (accessed on 20 June 2024).
- Wang, Y.; Feng, B.; Ding, Y. QGTC: Accelerating quantized graph neural networks via GPU tensor core. In Proceedings of the 27th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Virtual, 2–6 April 2022; pp. 107–119. [Google Scholar]
- Ma, Y.; Gong, P.; Yi, J.; Yao, Z.; Li, C.; He, Y.; Yan, F. Bifeat: Supercharge gnn training via graph feature quantization. arXiv 2022, arXiv:2207.14696. [Google Scholar]
- Eliasof, M.; Bodner, B.J.; Treister, E. Haar wavelet feature compression for quantized graph convolutional networks. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 4542–4553. [Google Scholar] [CrossRef]
- Dai, Y.; Tang, X.; Zhang, Y. An efficient segmented quantization for graph neural networks. CCF Trans. High Perform. Comput. 2022, 4, 461–473. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, F.; Mo, Z.; Hu, Q.; Li, G.; Liu, Z.; Liang, X.; Cheng, J. A2Q: Aggregation-Aware Quantization for Graph Neural Networks. arXiv 2023, arXiv:2302.00193. [Google Scholar]
- Wang, S.; Eravci, B.; Guliyev, R.; Ferhatosmanoglu, H. Low-bit quantization for deep graph neural networks with smoothness-aware message propagation. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023; pp. 2626–2636. [Google Scholar]
- Liu, Z.; Zhou, K.; Yang, F.; Li, L.; Chen, R.; Hu, X. EXACT: Scalable graph neural networks training via extreme activation compression. In Proceedings of the International Conference on Learning Representations, Virtual Event, 3–7 May 2021. [Google Scholar]
- Eliassen, S.; Selvan, R. Activation Compression of Graph Neural Networks using Block-wise Quantization with Improved Variance Minimization. arXiv 2023, arXiv:2309.11856. [Google Scholar]
- Ding, M.; Kong, K.; Li, J.; Zhu, C.; Dickerson, J.; Huang, F.; Goldstein, T. VQ-GNN: A universal framework to scale up graph neural networks using vector quantization. Adv. Neural Inf. Process. Syst. 2021, 34, 6733–6746. [Google Scholar]
- Feng, B.; Wang, Y.; Li, X.; Yang, S.; Peng, X.; Ding, Y. Sgquant: Squeezing the last bit on graph neural networks with specialized quantization. In Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2020; pp. 1044–1052. [Google Scholar]
- Zhao, Y.; Wang, D.; Bates, D.; Mullins, R.; Jamnik, M.; Lio, P. Learned low precision graph neural networks. arXiv 2020, arXiv:2009.09232. [Google Scholar]
- Bahri, M.; Bahl, G.; Zafeiriou, S. Binary graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9492–9501. [Google Scholar]
- Wang, H.; Lian, D.; Zhang, Y.; Qin, L.; He, X.; Lin, Y.; Lin, X. Binarized graph neural network. World Wide Web 2021, 24, 825–848. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, Z.; Du, Z.; Li, S.; Zheng, H.; Xie, Y.; Tan, N. EPQuant: A Graph Neural Network compression approach based on product quantization. Neurocomputing 2022, 503, 49–61. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Yang, Z.; Yang, L.; Guo, Y. Bi-gcn: Binary graph convolutional network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1561–1570. [Google Scholar]
- Kose, H.T.; Nunez-Yanez, J.; Piechocki, R.; Pope, J. Fully Quantized Graph Convolutional Networks for Embedded Applications. In Proceedings of the 6th Workshop on Accelerated Machine Learning, Munich, Germany, 17 January 2024. [Google Scholar]
- Chen, Y.; Guo, Y.; Zeng, Z.; Zou, X.; Li, Y.; Chen, C. Topology-Aware Quantization Strategy via Personalized PageRank for Graph Neural Networks. In Proceedings of the 2022 IEEE Smartworld, Ubiquitous Intelligence & Computing, Scalable Computing & Communications Digital Twin, Privacy Computing, Metaverse, Autonomous & Trusted Vehicles (SmartWorld/UIC/ScalCom/DigitalTwin/PriComp/Meta), Haikou, China, 15–18 December 2022; pp. 961–968. [Google Scholar]
- Guo, Y.; Chen, Y.; Zou, X.; Yang, X.; Gu, Y. Algorithms and architecture support of degree-based quantization for graph neural networks. J. Syst. Archit. 2022, 129, 102578. [Google Scholar] [CrossRef]
- Xie, X.; Peng, H.; Hasan, A.; Huang, S.; Zhao, J.; Fang, H.; Zhang, W.; Geng, T.; Khan, O.; Ding, C. Accel-gcn: High-performance gpu accelerator design for graph convolution networks. In Proceedings of the 2023 IEEE/ACM International Conference on Computer Aided Design (ICCAD), San Francisco, CA, USA, 29 October–2 November 2023; pp. 1–9. [Google Scholar]
- Ma, L.; Yang, Z.; Miao, Y.; Xue, J.; Wu, M.; Zhou, L.; Dai, Y. {NeuGraph}: Parallel deep neural network computation on large graphs. In Proceedings of the 2019 USENIX Annual Technical Conference (USENIX ATC 19), Renton, WA, USA, 10–12 July 2019; pp. 443–458. [Google Scholar]
- Peng, H.; Xie, X.; Shivdikar, K.; Hasan, M.; Zhao, J.; Huang, S.; Khan, O.; Kaeli, D.; Ding, C. Maxk-gnn: Towards theoretical speed limits for accelerating graph neural networks training. arXiv 2023, arXiv:2312.08656. [Google Scholar]
- Yan, M.; Deng, L.; Hu, X.; Liang, L.; Feng, Y.; Ye, X.; Zhang, Z.; Fan, D.; Xie, Y. Hygcn: A gcn accelerator with hybrid architecture. In Proceedings of the 2020 IEEE International Symposium on High Performance Computer Architecture (HPCA), San Diego, CA, USA, 22–26 February 2020; pp. 15–29. [Google Scholar]
- Yin, L.; Wang, J.; Zheng, H. Exploring architecture, dataflow, and sparsity for gcn accelerators: A holistic framework. In Proceedings of the Great Lakes Symposium on VLSI 2023, Knoxville, TN, USA, 5–7 June 2023; pp. 489–495. [Google Scholar]
- Auten, A.; Tomei, M.; Kumar, R. Hardware acceleration of graph neural networks. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), Virtual Event, 20–24 July 2020; pp. 1–6. [Google Scholar]
- Chen, X.; Wang, Y.; Xie, X.; Hu, X.; Basak, A.; Liang, L.; Yan, M.; Deng, L.; Ding, Y.; Du, Z.; et al. Rubik: A hierarchical architecture for efficient graph neural network training. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 41, 936–949. [Google Scholar] [CrossRef]
- Li, J.; Louri, A.; Karanth, A.; Bunescu, R. GCNAX: A flexible and energy-efficient accelerator for graph convolutional neural networks. In Proceedings of the 2021 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Seoul, Republic of Korea, 27 February –3 March 2021; pp. 775–788. [Google Scholar]
- Li, J.; Zheng, H.; Wang, K.; Louri, A. SGCNAX: A scalable graph convolutional neural network accelerator with workload balancing. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 2834–2845. [Google Scholar] [CrossRef]
- Kiningham, K.; Levis, P.; Ré, C. GRIP: A graph neural network accelerator architecture. IEEE Trans. Comput. 2022, 72, 914–925. [Google Scholar] [CrossRef]
- Zhang, B.; Kannan, R.; Prasanna, V. BoostGCN: A framework for optimizing GCN inference on FPGA. In Proceedings of the 2021 IEEE 29th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Orlando, FL, USA, 9–12 May 2021; pp. 29–39. [Google Scholar]
- Zhang, C.; Geng, T.; Guo, A.; Tian, J.; Herbordt, M.; Li, A.; Tao, D. H-gcn: A graph convolutional network accelerator on versal acap architecture. In Proceedings of the 2022 32nd IEEE International Conference on Field-Programmable Logic and Applications (FPL), Belfast, UK, 29 August–2 September 2022; pp. 200–208. [Google Scholar]
- Romero Hung, J.; Li, C.; Wang, P.; Shao, C.; Guo, J.; Wang, J.; Shi, G. ACE-GCN: A Fast data-driven FPGA accelerator for GCN embedding. ACM Trans. Reconfigurable Technol. Syst. (TRETS) 2021, 14, 1–23. [Google Scholar] [CrossRef]
- Geng, T.; Wu, C.; Zhang, Y.; Tan, C.; Xie, C.; You, H.; Herbordt, M.; Lin, Y.; Li, A. I-GCN: A graph convolutional network accelerator with runtime locality enhancement through islandization. In Proceedings of the MICRO-54: 54th Annual IEEE/ACM International Symposium on Microarchitecture. Online Conference, 18–22 October 2021; pp. 1051–1063. [Google Scholar]
- Lin, Y.C.; Zhang, B.; Prasanna, V. Gcn inference acceleration using high-level synthesis. In Proceedings of the 2021 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 20–24 September 2021; pp. 1–6. [Google Scholar]
- Zhang, B.; Zeng, H.; Prasanna, V. Hardware acceleration of large scale gcn inference. In Proceedings of the 2020 IEEE 31st International Conference on Application-Specific Systems, Architectures and Processors (ASAP), Manchester, UK, 6-8 July 2020; pp. 61–68. [Google Scholar]
- Sohrabizadeh, A.; Chi, Y.; Cong, J. SPA-GCN: Efficient and Flexible GCN Accelerator with an Application for Graph Similarity Computation. arXiv 2021, arXiv:2111.05936. [Google Scholar]
- Gui, Y.; Wei, B.; Yuan, W.; Jin, X. Hardware Acceleration of Sampling Algorithms in Sample and Aggregate Graph Neural Networks. arXiv 2022, arXiv:2209.02916. [Google Scholar]
- Li, S.; Niu, D.; Wang, Y.; Han, W.; Zhang, Z.; Guan, T.; Guan, Y.; Liu, H.; Huang, L.; Du, Z.; et al. Hyperscale FPGA-as-a-service architecture for large-scale distributed graph neural network. In Proceedings of the 49th Annual International Symposium on Computer Architecture, New York, NY, USA, 18–22 June 2022; pp. 946–961. [Google Scholar]
- Chen, S.; Zheng, D.; Ding, C.; Huan, C.; Ji, Y.; Liu, H. TANGO: Re-Thinking quantization for graph neural network training on GPUs. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 11–17 November 2023; pp. 1–14. [Google Scholar]
- Zhang, B.; Zeng, H.; Prasanna, V. Low-latency mini-batch gnn inference on cpu-fpga heterogeneous platform. In Proceedings of the 2022 IEEE 29th IEEE International Conference on High Performance Computing, Data, and Analytics (HiPC), Bengaluru, India, 18–21 December 2022; pp. 11–21. [Google Scholar]
- Lin, Y.C.; Zhang, B.; Prasanna, V. Hp-gnn: Generating high throughput gnn training implementation on cpu-fpga heterogeneous platform. In Proceedings of the 2022 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Virtual Event, 27 February–1 March 2022; pp. 123–133. [Google Scholar]
- Sarkar, R.; Abi-Karam, S.; He, Y.; Sathidevi, L.; Hao, C. FlowGNN: A Dataflow Architecture for Real-Time Workload-Agnostic Graph Neural Network Inference. In Proceedings of the 2023 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Montreal, QC, Canada, 25 February–1 March 2023; pp. 1099–1112. [Google Scholar]
- Liang, S.; Liu, C.; Wang, Y.; Li, H.; Li, X. Deepburning-gl: An automated framework for generating graph neural network accelerators. In Proceedings of the 39th International Conference on Computer-Aided Design, Virtual, 2–5 November 2020; pp. 1–9. [Google Scholar]
- Chen, H.; Hao, C. Dgnn-booster: A generic fpga accelerator framework for dynamic graph neural network inference. In Proceedings of the 2023 IEEE 31st Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Marina Del Rey, CA, USA, 8–11 May 2023; pp. 195–201. [Google Scholar]
- Abi-Karam, S.; Hao, C. Gnnbuilder: An automated framework for generic graph neural network accelerator generation, simulation, and optimization. In Proceedings of the 2023 33rd IEEE International Conference on Field-Programmable Logic and Applications (FPL), Gothenburg, Sweden, 4–8 September 2023; pp. 212–218. [Google Scholar]
- Lu, Q.; Jiang, W.; Jiang, M.; Hu, J.; Shi, Y. Hardware/Software Co-Exploration for Graph Neural Architectures on FPGAs. In Proceedings of the 2022 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Nicosia, Cyprus, 4–6 July 2022; pp. 358–362. [Google Scholar]
- Yan, W.; Tong, W.; Zhi, X. FPGAN: An FPGA accelerator for graph attention networks with software and hardware co-optimization. IEEE Access 2020, 8, 171608–171620. [Google Scholar] [CrossRef]
- Wu, C.; Tao, Z.; Wang, K.; He, L. Skeletongcn: A simple yet effective accelerator for gcn training. In Proceedings of the 2022 IEEE 32nd International Conference on Field-Programmable Logic and Applications (FPL), Belfast, UK, 29 August–2 September 2022; pp. 445–451. [Google Scholar]
- Yuan, W.; Tian, T.; Wu, Q.; Jin, X. QEGCN: An FPGA-based accelerator for quantized GCNs with edge-level parallelism. J. Syst. Archit. 2022, 129, 102596. [Google Scholar] [CrossRef]
- He, Z.; Tian, T.; Wu, Q.; Jin, X. FTW-GAT: An FPGA-based accelerator for graph attention networks with ternary weights. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 4211–4215. [Google Scholar] [CrossRef]
- Wang, Z.; Que, Z.; Luk, W.; Fan, H. Customizable FPGA-based Accelerator for Binarized Graph Neural Networks. In Proceedings of the 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 27 May–1 June 2022; pp. 1968–1972. [Google Scholar]
- Ran, S.; Zhao, B.; Dai, X.; Cheng, C.; Zhang, Y. Software-hardware co-design for accelerating large-scale graph convolutional network inference on FPGA. Neurocomputing 2023, 532, 129–140. [Google Scholar] [CrossRef]
- Yuan, W.; Tian, T.; Liang, H.; Jin, X. A gather accelerator for GNNs on FPGA platform. In Proceedings of the 2021 IEEE 27th International Conference on Parallel and Distributed Systems (ICPADS), Beijing, China, 14–16 December 2021; pp. 74–81. [Google Scholar]
- Tao, Z.; Wu, C.; Liang, Y.; Wang, K.; He, L. LW-GCN: A lightweight FPGA-based graph convolutional network accelerator. ACM Trans. Reconfigurable Technol. Syst. 2022, 16, 1–19. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, B.; Kannan, R.; Prasanna, V.; Busart, C. Model-architecture co-design for high performance temporal gnn inference on fpga. In Proceedings of the 2022 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Lyon, France, 30 May–3 June 2022; pp. 1108–1117. [Google Scholar]
- Hansson, O.; Grailoo, M.; Gustafsson, O.; Nunez-Yanez, J. Deep Quantization of Graph Neural Networks with Run-Time Hardware-Aware Training. In Proceedings of the International Symposium on Applied Reconfigurable Computing; Springer: Berlin/Heidelberg, Germany, 2024; pp. 33–47. [Google Scholar]
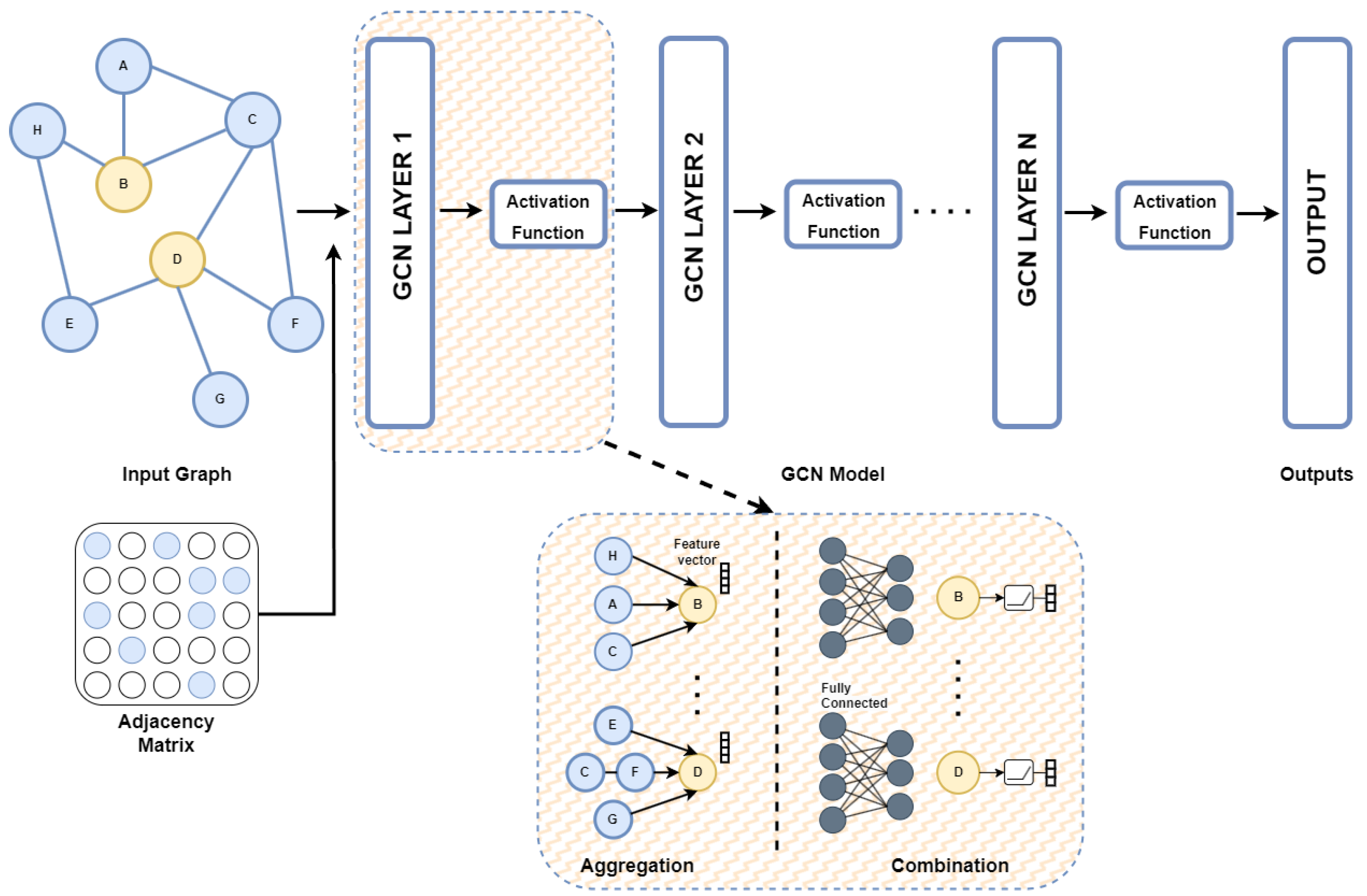


| Description | Notations | Description | Notations |
|---|---|---|---|
| Original graph | G | Feature matrix of l-th layer | |
| The set of graph vertices (nodes) | V | Trainable weight matrix for the l-th layer | |
| The set of graph edges | E | Diagonal degree matrix of A | |
| The feature of node v in layer l | Degree of node i | ||
| Number of node in graph G | N | Degree of node j | |
| Layer index | l | Sigmoid function | |
| Number of edges in graph G | M | Multi-layer perceptron | |
| Gather feature vector of node v in layer l | Learnable parameter | ||
| Adjacency matrix | A | Attention coefficients | |
| Normalized adjacency matrix | Transpose | T | |
| Concatenation | Linear transformation weight matrix | ||
| Maximum operation | Max-pooling operation | ||
| Graph neural network | Graph convolutional network | ||
| Field-Programmable Gate Array | Post-training quantization | ||
| Quantization aware training | Floating-point | ||
| Integer number | Lookup table | ||
| Flip flops | Digital signal processing element | ||
| Block RAM | High-level synthesis |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kose, H.T.; Nunez-Yanez, J.; Piechocki, R.; Pope, J. A Survey of Computationally Efficient Graph Neural Networks for Reconfigurable Systems. Information 2024, 15, 377. https://doi.org/10.3390/info15070377
Kose HT, Nunez-Yanez J, Piechocki R, Pope J. A Survey of Computationally Efficient Graph Neural Networks for Reconfigurable Systems. Information. 2024; 15(7):377. https://doi.org/10.3390/info15070377
Chicago/Turabian StyleKose, Habib Taha, Jose Nunez-Yanez, Robert Piechocki, and James Pope. 2024. "A Survey of Computationally Efficient Graph Neural Networks for Reconfigurable Systems" Information 15, no. 7: 377. https://doi.org/10.3390/info15070377
APA StyleKose, H. T., Nunez-Yanez, J., Piechocki, R., & Pope, J. (2024). A Survey of Computationally Efficient Graph Neural Networks for Reconfigurable Systems. Information, 15(7), 377. https://doi.org/10.3390/info15070377







