Enhancing Personalized Recommendations: A Study on the Efficacy of Multi-Task Learning and Feature Integration
Abstract
1. Introduction
- (1)
- How do different model architectures perform in terms of recommendation accuracy, as measured by RMSE and MAE?
- (2)
- What is the impact of incorporating diverse input feature sets, including user identifiers, item identifiers, and content attributes, on the predictive performance of recommendation models?
- (3)
- Can multi-task learning improve recommendation quality by jointly optimizing auxiliary tasks beyond rating prediction?
- (1)
- Systematically evaluating the impact of various feature combinations on model performance, providing empirical guidance for feature engineering pipelines in recommender systems.
- (2)
- Designing a novel multi-task deep learning architecture capable of jointly optimizing rating prediction and item preference classification objectives, effectively fusing heterogeneous feedback signals.
- (3)
- Conducting large-scale empirical evaluations on the MovieLens dataset and Book Recommendation dataset, demonstrating the effectiveness and superiority of the proposed multi-task learning approach in improving recommendation accuracy.
2. Related Work
3. Datasets
- genome-scores.csv: This file contains the relevance scores between movies and tags. Each row represents a movie tag and its associated relevance score, indicating the degree of relevance between the tag and the movie.
- genome-tags.csv: This file contains information about movie tags. Each row includes a tag ID and its corresponding tag content.
- movies.csv: This file contains basic information about movies. Each row corresponds to a movie, including the movie ID, title, and a list of genres it belongs to.
- ratings.csv: This file contains user rating records for movies. Each row represents a user’s rating for a particular movie, including the user ID, movie ID, rating value, and timestamp.
- tags.csv: This file contains tags added by users for movies. Each row records a tag added by a user for a specific movie, including the user ID, movie ID, tag content, and timestamp.
3.1. Data Cleaning
3.2. Label Encoding and Normalization
3.3. Data Analysis
3.3.1. Correlation Matrix and Heatmap
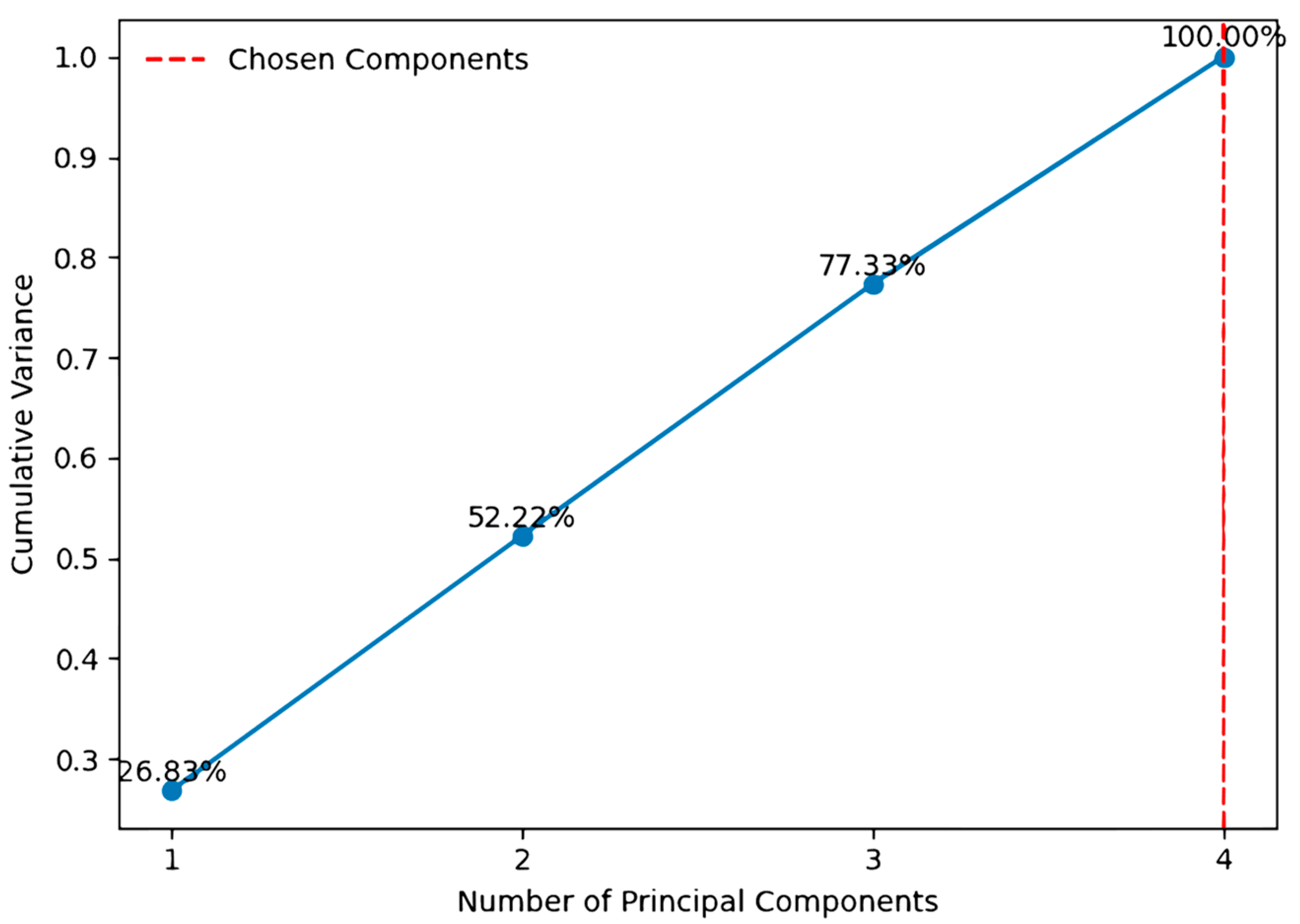
3.3.2. Principal Component Analysis
- (1)
- Data Centering
- (2)
- Covariance Matrix Computation
- (3)
- Eigendecomposition
- (4)
- Principal Component Selection
- (5)
- Dimensionality Reduction
- k is the number of retained principal components.
- is the ith eigenvalue, representing the variance of the ith principal component.
- n is the total number of principal components (the number of eigenvalues).
4. Modeling
5. Experiments
5.1. Dataset Introduction
5.2. Data Preprocessing
5.3. Model Design
| Algorithm 1 Multi-task Learning Model. |
| Inputs: : User ID : Movie ID : Tag ID : Genres : Rates Iteration times: 50 Outputs: RMSE & MAE Initialize parameters Θ, learning rate α 1: for t = 1…T do 2: Sample batch of (u, i, t, g, r) from training data # Compute embedding vectors 3: u_emb = ϕ_u(u; Θ_u) # User embedding 4: i_emb = ϕ_i(i; Θ_i) # Movie embedding 5: g_emb = ϕ_g(g; Θ_g) # Genre embedding 6: t_emb = ϕ_t(t; Θ_t) # Tag embedding # Concatenate embeddings 7: x = u_emb ⊕ i_emb ⊕ g_emb ⊕ t_emb # Pass through model 8: h = σ(W_1^Tx + b_1) # Dense layer with activation σ 9: p = σ(W_2^Th + b_2) # Likability prediction (0/1) 10: r_hat = W_3^Th + b_3 # Rating prediction # Compute losses 11: L_like = −∑ r∗log(p) + (1 − r)∗log(1 − p) # Binary cross-entropy 12: L_rating = ∑ (r − r_hat)^2 # Mean squared error 13: L = 0.8∗L_like + 0.2∗L_rating # Weighted loss # Compute gradients 14: ∇Θ = ∂L/∂Θ # Update parameters 15: Θ = Θ − α ∗ ∇Θ # Compute metrics on validation set 16: RMSE_val = sqrt(∑(r_val − r_hat_val)^2/N) 17: MAE_val = ∑|r_val − r_hat_val|/N End for |
Model Compilation and Evaluation Metrics
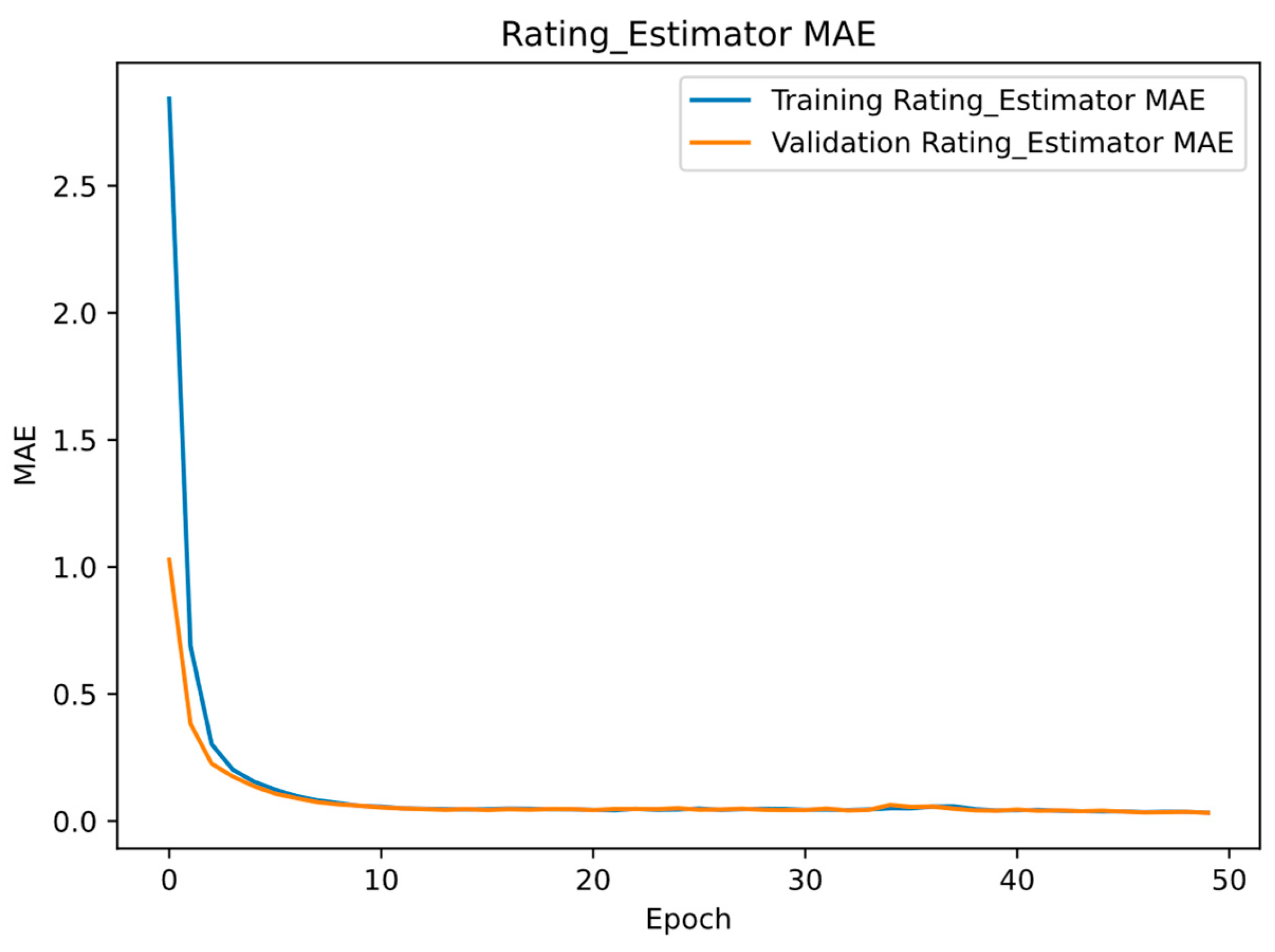
5.4. Training and Validation
6. Results and Discussion
6.1. Results of Using MovieLens Dataset
6.1.1. Loss Function Performance
6.1.2. RMSE
6.1.3. MAE
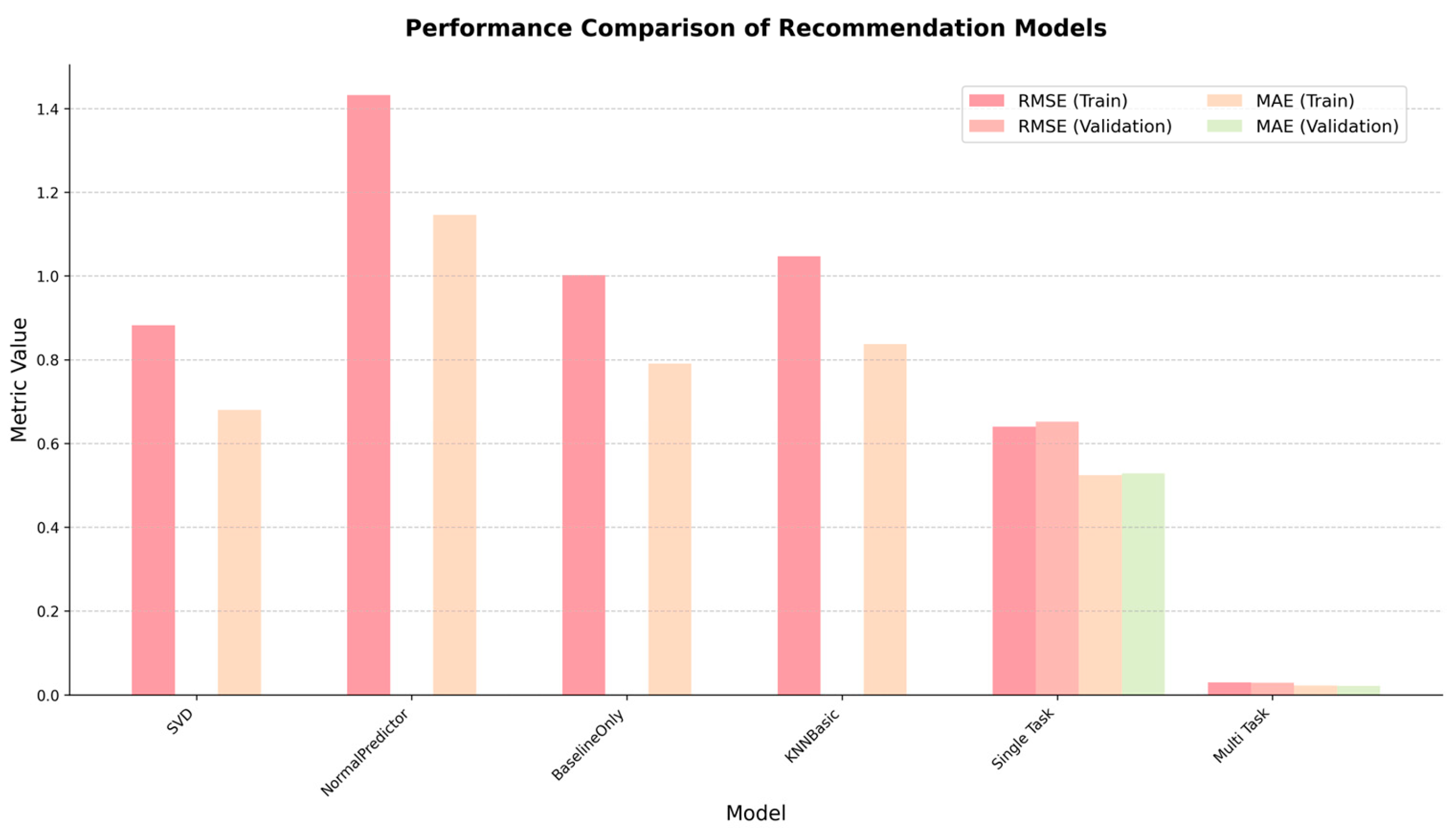
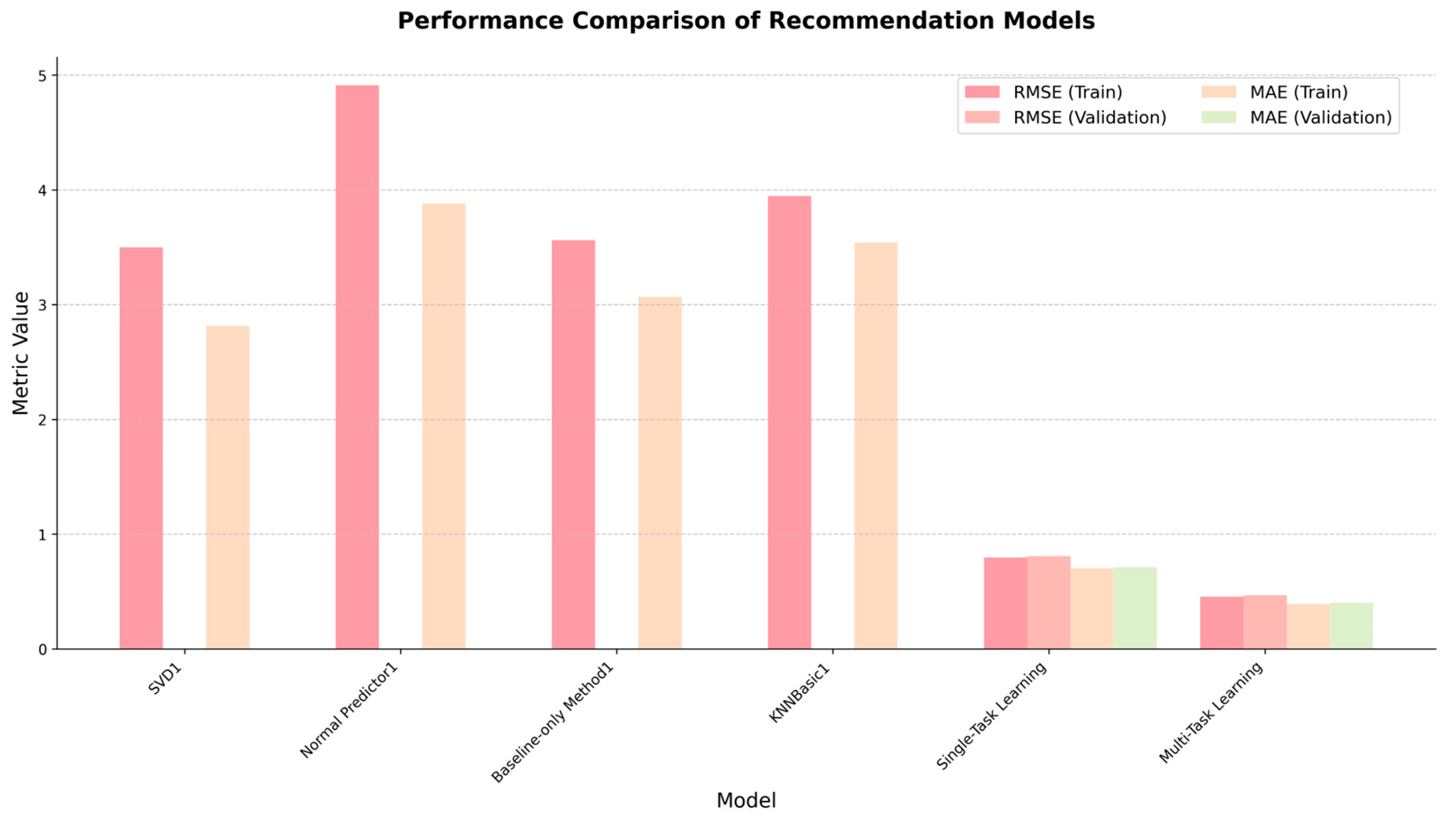
6.1.4. Comparison of Model Metrics for Different Approaches
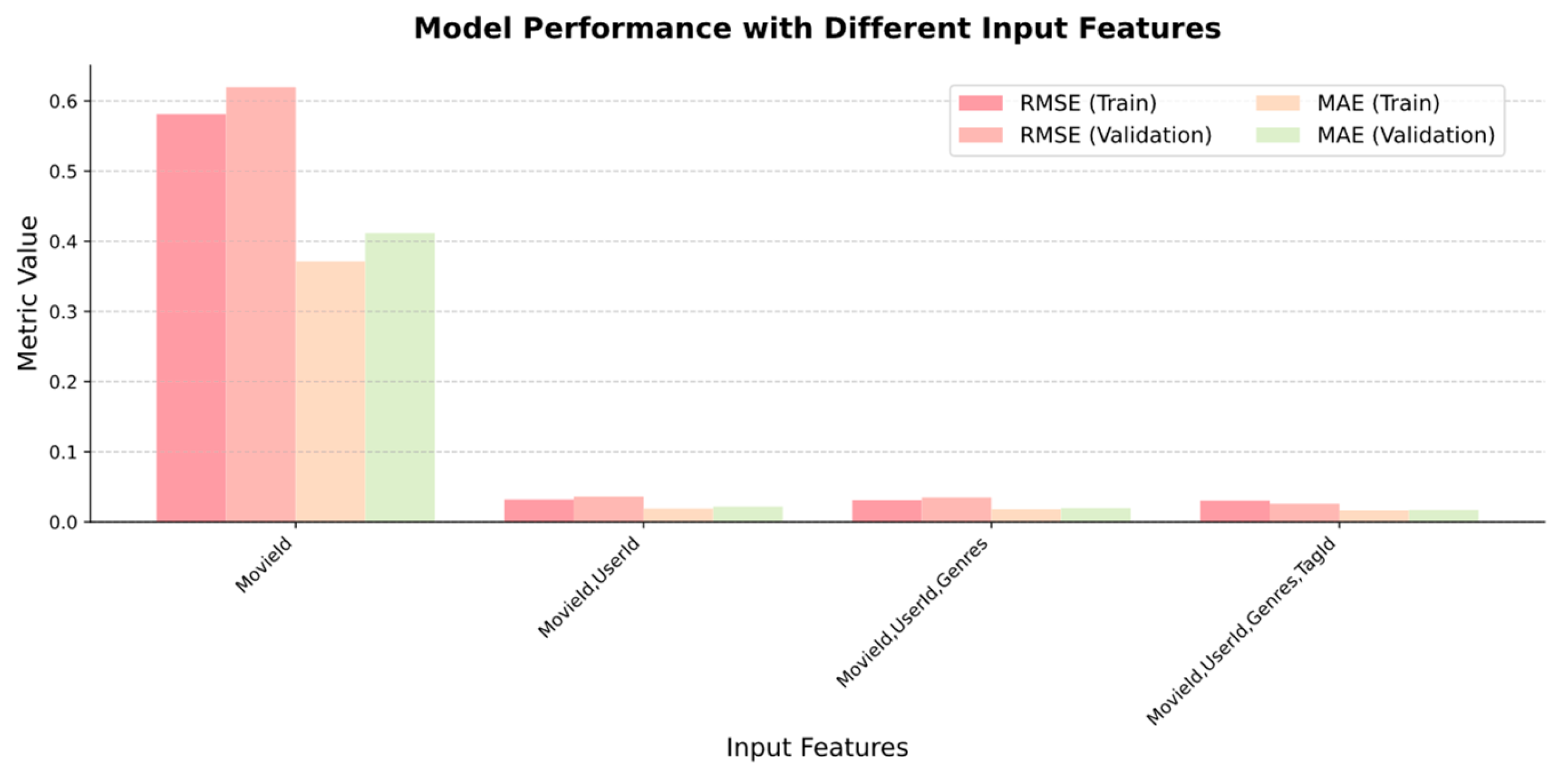
6.1.5. Comparison of Model Performance with Different Data Features
6.2. Results of Using Book Recommendation Dataset
6.2.1. Comparison of Model Metrics for Different Approaches
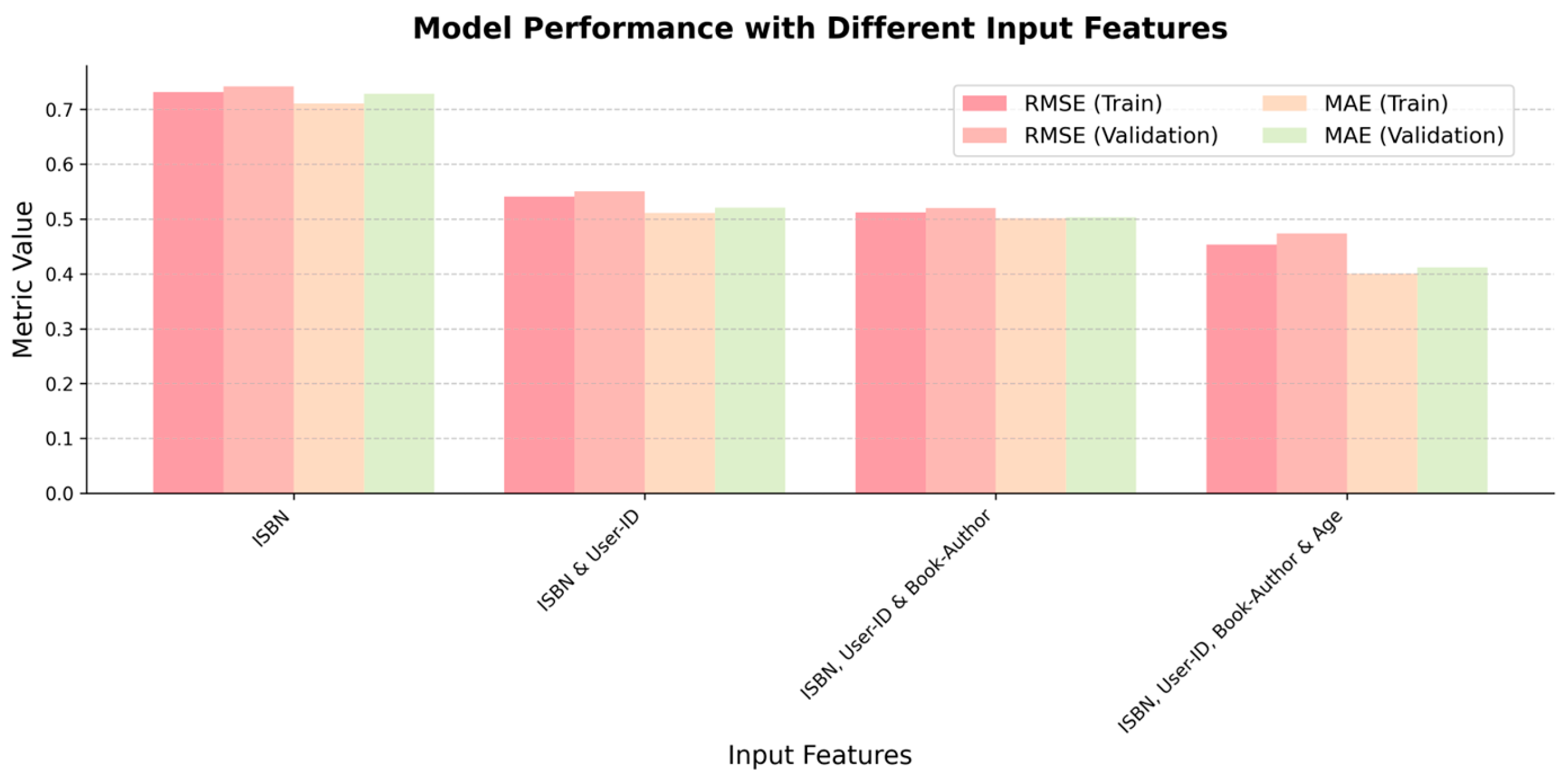
6.2.2. Comparison of Model Performance with Different Data Features
6.3. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Natarajan, S.; Vairavasundaram, S.; Natarajan, S.; Gandomi, A.H. Resolving Data Sparsity and Cold Start Problem in Collaborative Filtering Recommender System Using Linked Open Data. Expert Syst. Appl. 2020, 149, 113248. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Ren, Y. Employing Neighborhood Reduction for Alleviating Sparsity and Cold Start Problems in User-Based Collaborative Filtering. Inf. Retr. J. 2020, 23, 449–472. [Google Scholar] [CrossRef]
- Afoudi, Y.; Lazaar, M.; Al Achhab, M. Hybrid Recommendation System Combined Content-Based Filtering and Collaborative Prediction Using Artificial Neural Network. Simul. Model. Pract. Theory 2021, 113, 102375. [Google Scholar] [CrossRef]
- Widayanti, R.; Chakim, M.H.R.; Lukita, C.; Rahardja, U.; Lutfiani, N. Improving Recommender Systems Using Hybrid Techniques of Collaborative Filtering and Content-Based Filtering. J. Appl. Data Sci. 2023, 4, 289–302. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, D. A Survey of Recommender Systems with Multi-Objective Optimization. Neurocomputing 2021, 474, 141–153. [Google Scholar] [CrossRef]
- Zaizi, F.E.; Qassimi, S.; Rakrak, S. Multi-Objective Optimization with Recommender Systems: A Systematic Review. Inf. Syst. 2023, 117, 102233. [Google Scholar] [CrossRef]
- Njeri, N.R.; Ndung’u, R.N.; Mariga, W.G. Developing Hybrid-Based Recommender System with Naïve Bayes Optimization to Increase Prediction Efficiency. Int. J. Comput. Inf. Technol. 2021, 10, 96–103. [Google Scholar] [CrossRef]
- Fu, Z.; Niu, X.; Maher, M.L. Deep Learning Models for Serendipity Recommendations: A Survey and New Perspectives. ACM Comput. Surv. 2023, 56, 1–26. [Google Scholar] [CrossRef]
- Harper, F.M.; Konstan, J.A. The MovieLens Datasets: History and context. ACM Trans. Interact. Intell. Syst. 2015, 5, 1–19. [Google Scholar] [CrossRef]
- GroupLens. MovieLens 20M Dataset. Available online: https://www.kaggle.com/datasets/grouplens/movielens-20m-dataset (accessed on 15 May 2022).
- Ziegler, C.-N. Book Recommendation Dataset. Available online: https://www.kaggle.com/datasets/arashnic/book-recommendation-dataset (accessed on 16 May 2022).
- Eliyas, S.; Ranjana, P. Recommendation Systems: Content-Based Filtering vs Collaborative Filtering. In Proceedings of the 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Noida, India, 28–29 April 2022; pp. 1360–1365. [Google Scholar]
- Javed, U.; Shaukat, K.; Hameed, I.A.; Iqbal, F.; Mahboob Alam, T.; Luo, S. A Review of Content-Based and Context-Based Recommendation Systems. Int. J. Emerg. Technol. Learn. 2021, 16, 274. [Google Scholar] [CrossRef]
- Nallamala, S.H.; Bajjuri, U.R.; Anandarao, S.; Prasad, D.D.; Mishra, P. A Brief Analysis of Collaborative and Content Based Filtering Algorithms Used in Recommender Systems. IOP Conf. Ser. Mater. Sci. Eng. 2020, 981, 022008. [Google Scholar] [CrossRef]
- Wu, X. Comparison between Collaborative Filtering and Content-Based Filtering. Highlights Sci. Eng. Technol. 2022, 16, 480–489. [Google Scholar] [CrossRef]
- Zhou, Y.; Cao, Y.; Shang, Y.; Zhou, C.; Pan, S.; Zheng, L.; Li, Q. Explainable Hyperbolic Temporal Point Process for User-Item Interaction Sequence Generation. ACM Trans. Inf. Syst. 2023, 41, 1–26. [Google Scholar] [CrossRef]
- Alamdari, P.M.; Navimipour, N.J.; Hosseinzadeh, M.; Safaei, A.A.; Darwesh, A. A Systematic Study on the Recommender Systems in the E-Commerce. IEEE Access 2020, 8, 115694–115716. [Google Scholar] [CrossRef]
- Peng, S.; Siet, S.; Ilkhomjon, S.; Kim, D.-Y.; Park, D.-S. Integration of Deep Reinforcement Learning with Collaborative Filtering for Movie Recommendation Systems. Appl. Sci. 2024, 14, 1155. [Google Scholar] [CrossRef]
- Martins, G.B.; Papa, J.P.; Adeli, H. Deep Learning Techniques for Recommender Systems Based on Collaborative Filtering. Expert Syst. 2020, 37, e12647. [Google Scholar] [CrossRef]
- Fang, J.; Li, B.; Gao, M. Collaborative Filtering Recommendation Algorithm Based on Deep Neural Network Fusion. Int. J. Sens. Netw. 2020, 34, 71. [Google Scholar] [CrossRef]
- Aljunid, M.F.; Huchaiah, M.D. An Efficient Hybrid Recommendation Model Based on Collaborative Filtering Recommender Systems. CAAI Trans. Intell. Technol. 2021, 6, 480–492. [Google Scholar] [CrossRef]
- Feng, C.; Liang, J.; Song, P.; Wang, Z. A Fusion Collaborative Filtering Method for Sparse Data in Recommender Systems. Inf. Sci. 2020, 521, 365–379. [Google Scholar] [CrossRef]
- Huda, A.A.; Fajarudin, R.; Hadinegoro, A. Sistem Rekomendasi Content-Based Filtering Menggunakan TF-IDF Vector Similarity Untuk Rekomendasi Artikel Berita. Build. Inform. Technol. Sci. 2022, 4, 1679–1686. [Google Scholar] [CrossRef]
- Wakil, K.; Bakhtyar, R.; Ali, K.; Alaadin, K. Improving Web Movie Recommender System Based on Emotions. Int. J. Adv. Comput. Sci. Appl. 2015, 6, 218–226. [Google Scholar] [CrossRef][Green Version]
- Geetha, G.; Safa, M.; Fancy, C.; Saranya, D. A Hybrid Approach Using Collaborative Filtering and Content Based Filtering for Recommender System. J. Phys. Conf. Ser. 2018, 1000, 012101. [Google Scholar] [CrossRef]
- Ko, H.; Lee, S.; Park, Y.; Choi, A. A Survey of Recommendation Systems: Recommendation Models, Techniques, and Application Fields. Electronics 2022, 11, 141. [Google Scholar] [CrossRef]
- Li, H.; Han, D. A Novel Time-Aware Hybrid Recommendation Scheme Combining User Feedback and Collaborative Filtering. Mob. Inf. Syst. 2020, 2020, 8896694. [Google Scholar] [CrossRef]
- Nasser, A.M.; Bhagat, J.; Agrawal, A.; Devadas, T.J. Mean-Reversion Based Hybrid Movie Recommender System Using Collaborative and Content-Based Filtering Methods. Int. J. Stat. Appl. Math. 2023, 8, 121–137. [Google Scholar] [CrossRef]
- Saranya, K.G.; Sharma, A. A Critical Review on Location Based Hybrid Filtering Recommender Systems. J. Soft Comput. Paradig. 2023, 5, 1–10. [Google Scholar] [CrossRef]
- Ibrahim, M.A.; Bajwa, I.S.; Sarwar, N.; Hajjej, F.; Sakr, H.A. An Intelligent Hybrid Neural Collaborative Filtering Approach for True Recommendations. IEEE Access 2023, 11, 64831–64849. [Google Scholar] [CrossRef]
- Zhou, H.; Xiong, F.; Chen, H. A Comprehensive Survey of Recommender Systems Based on Deep Learning. Appl. Sci. 2023, 13, 11378. [Google Scholar] [CrossRef]
- Bobadilla, J.; Ortega, F.; Gutiérrez, A.; Alonso, S. Classification-Based Deep Neural Network Architecture for Collaborative Filtering Recommender Systems. Int. J. Interact. Multimed. Artif. Intell. 2020, 6, 68. [Google Scholar] [CrossRef]
- Yoon, J.H.; Jang, B. Evolution of Deep Learning-Based Sequential Recommender Systems: From Current Trends to New Perspectives. IEEE Access 2023, 11, 54265–54279. [Google Scholar] [CrossRef]
- Wu, L.; Xia, Y.; Min, S.; Xia, Z. Deep Attentive Interest Collaborative Filtering for Recommender Systems. IEEE Trans. Emerg. Top. Comput. 2023, 1, 1–15. [Google Scholar] [CrossRef]
- Chicaiza, J.; Valdiviezo-Diaz, P. A Comprehensive Survey of Knowledge Graph-Based Recommender Systems: Technologies, Development, and Contributions. Information 2021, 12, 232. [Google Scholar] [CrossRef]
- Sulikowski, P.; Kucznerowicz, M.; Bąk, I.; Romanowski, A.; Zdziebko, T. Online Store Aesthetics Impact Efficacy of Product Recommendations and Highlighting. Sensors 2022, 22, 9186. [Google Scholar] [CrossRef] [PubMed]
- Sulikowski, P. Evaluation of Varying Visual Intensity and Position of a Recommendation in a Recommending Interface Towards Reducing Habituation and Improving Sales. In Advances in E-Business Engineering for Ubiquitous Computing; ICEBE 2019; Lecture Notes on Data Engineering and Communications Technologies; Chao, K.M., Jiang, L., Hussain, O., Ma, S.P., Fei, X., Eds.; Springer: Cham, Switzerland, 2020; Volume 41. [Google Scholar] [CrossRef]
- Sulikowski, P.; Zdziebko, T.; Hussain, O.; Wilbik, A. Fuzzy Approach to Purchase Intent Modeling Based on User Tracking For E-commerce Recommenders. In Proceedings of the 2021 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Luxembourg, 11–14 July 2021; pp. 1–8. [Google Scholar]
- Gao, M.; Li, J.-Y.; Chen, C.-H.; Li, Y.; Zhang, J.; Zhan, Z.-H. Enhanced Multi-Task Learning and Knowledge Graph-Based Recommender System. IEEE Trans. Knowl. Data Eng. 2023, 35, 10281–10294. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, W.; Xu, W.; Lei, W.; Chua, T.-S.; Lam, W. A Unified Multi-Task Learning Framework for Multi-Goal Conversational Recommender Systems. ACM Trans. Inf. Syst. 2023, 41, 1–25. [Google Scholar] [CrossRef]
- Wan, X. Influence of Feature Scaling on Convergence of Gradient Iterative Algorithm. J. Phys. Conf. Ser. 2019, 1213, 032021. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, S.; Han, L.; Peng, Q. Hybrid matrix factorization for recommender systems in social networks. Neural Netw. World 2016, 26, 559–569. [Google Scholar] [CrossRef]
- Abdesselam, R. A Topological Approach of Principal Component Analysis. Int. J. Data Sci. Anal. 2021, 7, 20. [Google Scholar] [CrossRef]
- Atanu, E.Y. Analysis of Nigeria’s Crime Data: A Principal Component Approach Using Correlation Matrix. Int. J. Sci. Res. Publ. 2019, 9, p8503. [Google Scholar] [CrossRef]
- Salih Hasan, B.M.; Abdulazeez, A.M. A Review of Principal Component Analysis Algorithm for Dimensionality Reduction. J. Soft Comput. Data Min. 2021, 2, 20–30. [Google Scholar] [CrossRef]
- Yao, J.; Lopes, M. Rates of Bootstrap Approximation for Eigenvalues in High-Dimensional PCA. Stat. Sin. 2024, 33, 1461–1481. [Google Scholar] [CrossRef]
- Langworthy, B.; Cai, J.; Corty, R.W.; Kosorok, M.R.; Fine, J.P. Principal Components Analysis for Right Censored Data. Stat. Sin. 2023, 33, 1985–2016. [Google Scholar] [CrossRef]
- Sundararajan, R.R. Principal Component Analysis Using Frequency Components of Multivariate Time Series. Comput. Stat. Data Anal. 2021, 157, 107164. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal Component Analysis: A Review and Recent Developments. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Sahityabhilash, K.; Shyry, S.P. Impact of Loss Function Using M-LSTM Classifier for Sequence Data. Int. J. Psychosoc. Rehabil. 2020, 24, 3487–3494. [Google Scholar] [CrossRef]
- Dessain, J. Improving the Prediction of Asset Returns with Machine Learning by Using a Custom Loss Function. Adv. Artif. Intell. Mach. Learn. 2023, 3, 1640–1653. [Google Scholar] [CrossRef]
- Jun, H.; Kim, H.J. Loss Functions in Machine Learning for Seismic Random Noise Attenuation. Geophys. Prospect. 2023, 72, 978–995. [Google Scholar] [CrossRef]
- Hurtik, P.; Tomasiello, S.; Hula, J.; Hynar, D. Binary Cross-Entropy with Dynamical Clipping. Neural Comput. Appl. 2022, 34, 12029–12041. [Google Scholar] [CrossRef]
- Harwell, M. A Strategy for Using Bias and RMSE as Outcomes in Monte Carlo Studies in Statistics. J. Mod. Appl. Stat. Methods 2018, 17, 2726–2739. [Google Scholar] [CrossRef]
- Qi, J.; Du, J.; Siniscalchi, S.M.; Ma, X.; Lee, C.-H. On Mean Absolute Error for Deep Neural Network Based Vector-To-Vector Regression. IEEE Signal Process. Lett. 2020, 27, 1485–1489. [Google Scholar] [CrossRef]
- Colace, F.; Conte, D.; De Santo, M.; Lombardi, M.; Santaniello, D.; Valentino, C. A Content-Based Recommendation Approach Based on Singular Value Decomposition. Connect. Sci. 2022, 34, 2158–2176. [Google Scholar] [CrossRef]




| Genres | TagId | UserId | MovieId | |
|---|---|---|---|---|
| Genres | 1.000000 | −0.000478 | 0.013489 | −0.014273 |
| TagId | −0.000478 | 1.000000 | 0.000076 | 0.007608 |
| UserId | 0.013489 | 0.000076 | 1.000000 | −0.033311 |
| MovieId | −0.014273 | 0.007608 | −0.033311 | 1.000000 |
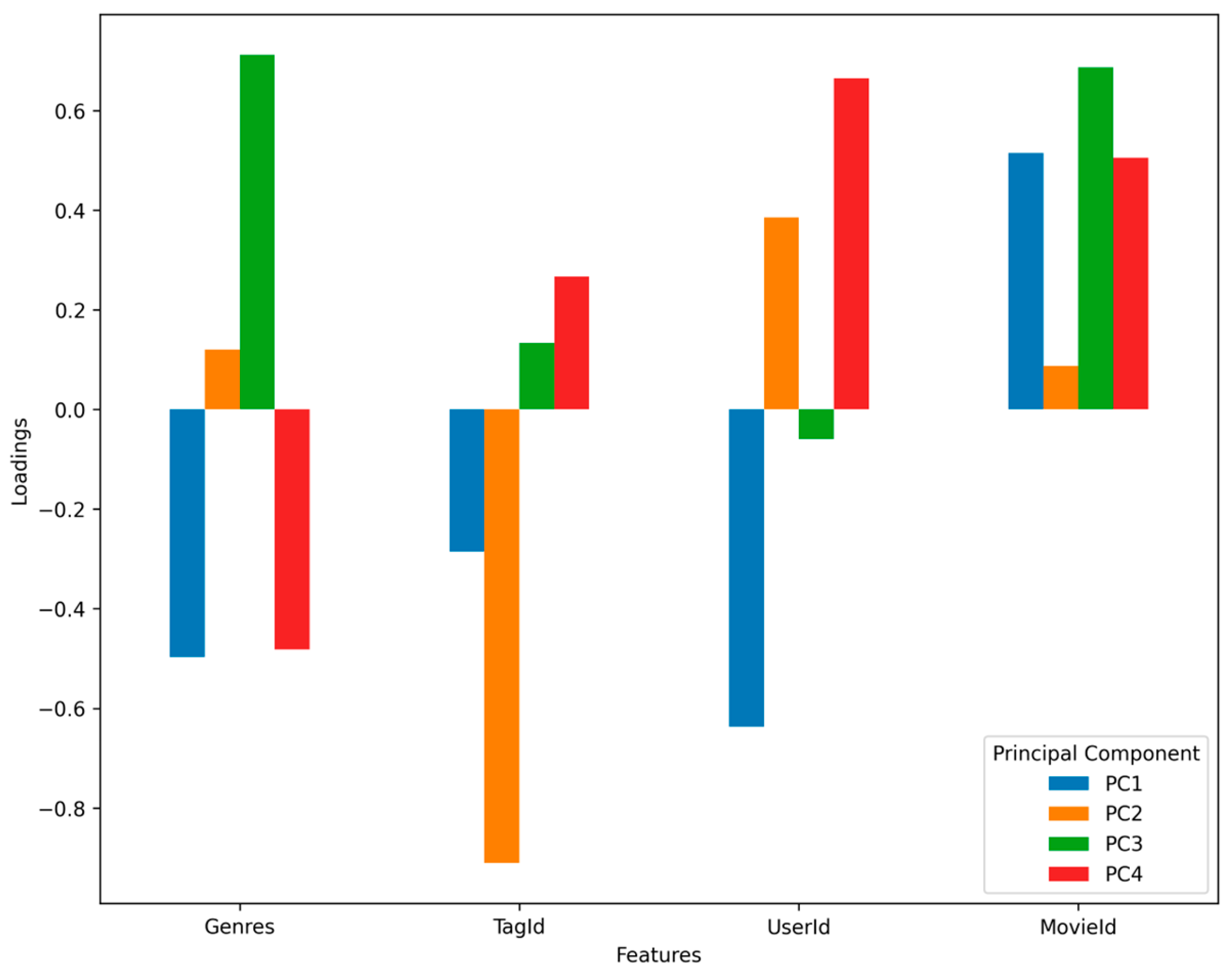
| Principal Component | Genres | TagId | UserId | MovieId |
|---|---|---|---|---|
| PC1 | −0.497154 | −0.285909 | −0.636770 | 0.515381 |
| PC2 | 0.119684 | −0.910569 | 0.385935 | 0.087145 |
| PC3 | 0.711801 | 0.133904 | −0.059909 | 0.686891 |
| PC4 | −0.481511 | 0.266814 | 0.664823 | 0.504944 |
| Metric Value | Data | SVD 1 | Normal Predictor 1 | Baseline-Only Method 1 | KNNBasic 1 | Single-Task Learning | Multi-Task Learning |
|---|---|---|---|---|---|---|---|
| RMSE | Training | 0.8822 | 1.4326 | 1.0021 | 1.0471 | 0.6397 | 0.0295 |
| Validation | 0.6517 | 0.0286 | |||||
| MAE | Training | 0.6794 | 1.1462 | 0.7902 | 0.8372 | 0.5244 | 0.0219 |
| Validation | 0.5279 | 0.0218 |
| Metric Value | Data | MovieId | MovieId and UserId | MovieId, UserId and Genres | MovieId, UserId, Genres and TagId |
|---|---|---|---|---|---|
| RMSE | Training | 0.5812 | 0.0320 | 0.0312 | 0.0305 |
| Validation | 0.6197 | 0.0362 | 0.0349 | 0.0259 | |
| MAE | Training | 0.3713 | 0.0191 | 0.0183 | 0.0164 |
| Validation | 0.4117 | 0.0218 | 0.0198 | 0.0171 |
| Metric Value | Data | SVD 1 | Normal Predictor 1 | Baseline-Only Method 1 | KNNBasic 1 | Single-Task Learning | Multi-Task Learning |
|---|---|---|---|---|---|---|---|
| RMSE | Training | 3.5 | 4.9108 | 3.5630 | 3.9458 | 0.7975 | 0.4563 |
| Validation | 0.8073 | 0.4676 | |||||
| MAE | Training | 2.8148 | 3.8818 | 3.0663 | 3.5405 | 0.7025 | 0.3911 |
| Validation | 0.7123 | 0.4015 |
| Metric Value | Data | ISBN | ISBN and User-ID | ISBN, User-ID and Book-Author | ISBN, User-ID, Book-Author and Age |
|---|---|---|---|---|---|
| RMSE | Training | 0.7312 | 0.5411 | 0.5121 | 0.4531 |
| Validation | 0.7423 | 0.5505 | 0.5202 | 0.4735 | |
| MAE | Training | 0.7105 | 0.5114 | 0.5015 | 0.4005 |
| Validation | 0.7281 | 0.5212 | 0.5032 | 0.4121 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Jin, E.; Zhang, H.; Chen, Y.; Yue, Y.; Dorado, D.B.; Hu, Z.; Xu, M. Enhancing Personalized Recommendations: A Study on the Efficacy of Multi-Task Learning and Feature Integration. Information 2024, 15, 312. https://doi.org/10.3390/info15060312
Wang Q, Jin E, Zhang H, Chen Y, Yue Y, Dorado DB, Hu Z, Xu M. Enhancing Personalized Recommendations: A Study on the Efficacy of Multi-Task Learning and Feature Integration. Information. 2024; 15(6):312. https://doi.org/10.3390/info15060312
Chicago/Turabian StyleWang, Qinyong, Enman Jin, Huizhong Zhang, Yumeng Chen, Yinggao Yue, Danilo B. Dorado, Zhongyi Hu, and Minghai Xu. 2024. "Enhancing Personalized Recommendations: A Study on the Efficacy of Multi-Task Learning and Feature Integration" Information 15, no. 6: 312. https://doi.org/10.3390/info15060312
APA StyleWang, Q., Jin, E., Zhang, H., Chen, Y., Yue, Y., Dorado, D. B., Hu, Z., & Xu, M. (2024). Enhancing Personalized Recommendations: A Study on the Efficacy of Multi-Task Learning and Feature Integration. Information, 15(6), 312. https://doi.org/10.3390/info15060312






