IUAutoTimeSVD++: A Hybrid Temporal Recommender System Integrating Item and User Features Using a Contractive Autoencoder †
Abstract
1. Introduction
- How can integrate user–item features within the timeSVD++ model to enhance the accuracy of rating predictions?
- How to compare the performance of the IUAutoTimeSVD++ model with the baseline models, assessing its superiority and effectiveness?
- How can we quantify the impact and significance of each component in our model to understand their individual contributions to improving recommendation predictions?
- What are the limitations of the proposed model to provide insights into its potential areas for improvement?
2. Related Work
2.1. MF Extensions
2.2. PMF Extensions
2.3. Contrastive Collaborative Filtering
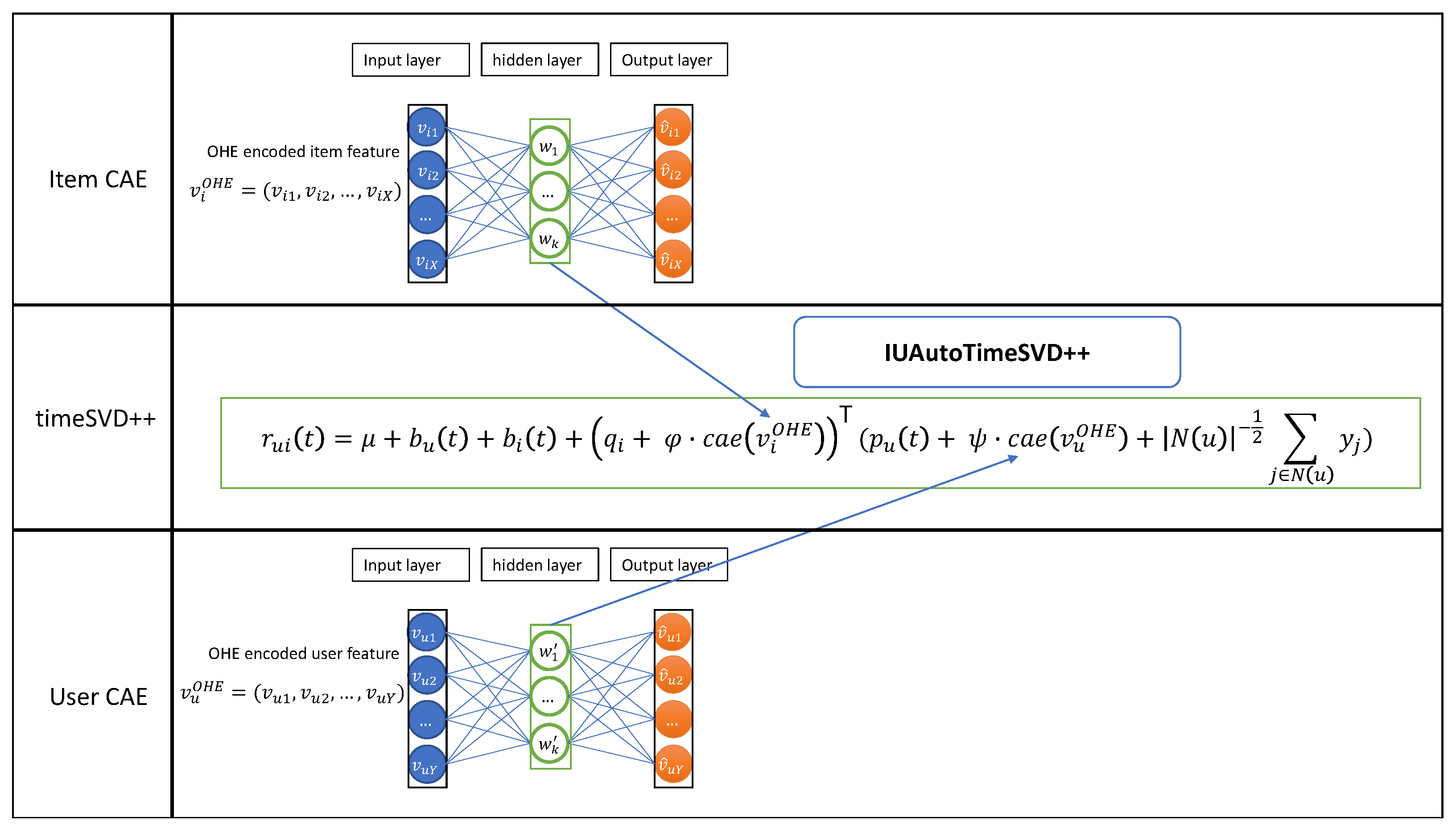
3. Our Model IUAutoTimeSVD++
3.1. Preliminary
3.2. Model Architecture
3.2.1. Temporal Latent Factors Model
Item Bias
Time Deviation
User Bias
User Latent Factors
3.2.2. Contractive Autoencoder
Encoder
Decoder
Objective Function
Regulation Term
3.3. IUAutoTimeSVD++ Methodology
3.3.1. One-Hot Encoding Representation
3.3.2. Features Extraction Using CAE
3.3.3. Rating Prediction Equation
3.3.4. Model Training and Optimization
4. Experimental Results
4.1. Datasets
4.2. Evaluation Metrics
4.3. Baseline Models
- MF: The basic variant of the matrix factorization model proposed in [14].
- PMF: A probabilistic variant of the matrix factorization proposed in [18].
- SVD++: An extension of the MF integrating the user implicit feedback proposed in [14].
- convMF: An extension of the PMF leveraging the textual content of the item and user reviews using CNN. [9].
- DBPMF: An extension of the PMF proposed in [19], leveraging item–user features using CNN.
- autoSVD++: A hybrid model proposed in [8] extending SVD++ through incorporating item features using CAE.
- SSAERec: A hybrid model proposed in [10] extending SVD++ and incorporating item features using stacked autoencoders.
- timeSVD++: The baseline temporal dynamic latent factors model proposed in [12].
4.4. Hyperparameter Analysis of Baseline Models and the Proposed Model
4.4.1. Categorization of Hyperparameters
4.4.2. Fine-Tuning Model Performance across Baseline and Proposed Model
Matrix Factorization (MF)
- Number of latent factors (k): This parameter controls the dimensionality of the latent factor space. It typically ranges from 10 to 100. Larger values may capture more complex interactions but increase computational cost and risk overfitting.
- Learning rate (): Determines the step size in the optimization process. Common values range from 0.001 to 0.1. Higher values can speed up convergence but may lead to instability.
- Regularization term (): Balances the model’s fit to the training data and its complexity. Values typically range from 0.01 to 0.1. Higher values penalize large parameter values, preventing overfitting.
- Number of epochs: The number of iterations for optimization. This parameter affects convergence and computational cost. The appropriate number of iterations can vary depending on factors such as the complexity of the dataset, the size of the model, and the optimization algorithm used.
SVD++
- Implicit feedback weight () Balances the influence of implicit feedback signals. It is crucial to tune this parameter to weigh implicit feedback appropriately.
Probabilistic Matrix Factorization (PMF)
- Variance of the Gaussian prior (): Controls the spread of the Gaussian distribution over latent factors. A smaller value imposes stronger regularization.
- Hyperparameters of the prior distribution: PMF often uses priors such as Gaussian or Laplace distributions. Tuning these hyperparameters influences the model’s robustness to overfitting.
ConvMF (Convolutional Matrix Factorization)
- Dimension: Similar to latent factor. It represents the size of latent dimension for users and items.
- : User regularization parameter.
- : Item regularization parameter.
- CNN hyperparameters: Includes hyper parameters used for training the CNN model to extract embedding representation of the word such as number of kernels per window size and the size of latent dimension for word vectors.
Deep Bias Probabilistic Matrix Factorization (DBPMF)
- Number of latent factors (K): Similar to MF and PMF, controls the dimensionality of latent factors.
- Hyperparameters of the dynamic model: DBPMF typically incorporates additional hyperparameters related to modeling temporal dynamics, such as transition matrices, state transition probabilities, and variance of state dynamics.
- Learning rate, regularization term, and variances: hyperparameters for optimizing the model and controlling the balance between fit to the data and model complexity.
AutoSVD++
- Hyperparameter for feature extraction: This parameter is used to normalize the vector features extracted using CAE and avoid the model overfitting. The paper [8] does not provide any additional information about CAE model training.
SSAERec
- Hyperparameter : This hyperparameter serves to normalize the Stacked Sparse Auto-Encoder (SSAE) utilized for extracting feature representations.
TimeSVD++
- : A regularization hyperparameter to control the time deviation term.
- : A hyperparameter used to control the time deviation. It depends on the dataset determined through cross validation.
- Number of Time Bins: The timeSVD++ splits the time dimension into multiple time bins to capture temporal dynamics. The number of time bins is a hyperparameter that determines the granularity of the temporal modeling.
IUAutoTimeSVD++
- Item CAE vector hyperparameter : Used to normalize the item vector features extracted using CAE and avoid the model overfitting. Based on experiments and validation, the values range from to .
- User CAE vector hyperparameter : Used to normalize the user vector features. Similar to , common values vary from to .
- CAE Hyperparameters: The CAE Hyperparameters used to train CAE to generate the user and item features are illustrated in the next subsection.
4.5. Hyperparameter Settings
4.5.1. CAE Training Hyperparameters
4.5.2. IUAutoTimeSVD++ Training Hyperparameters
4.6. Results
4.6.1. Numerical Results
4.6.2. Improvement Analysis
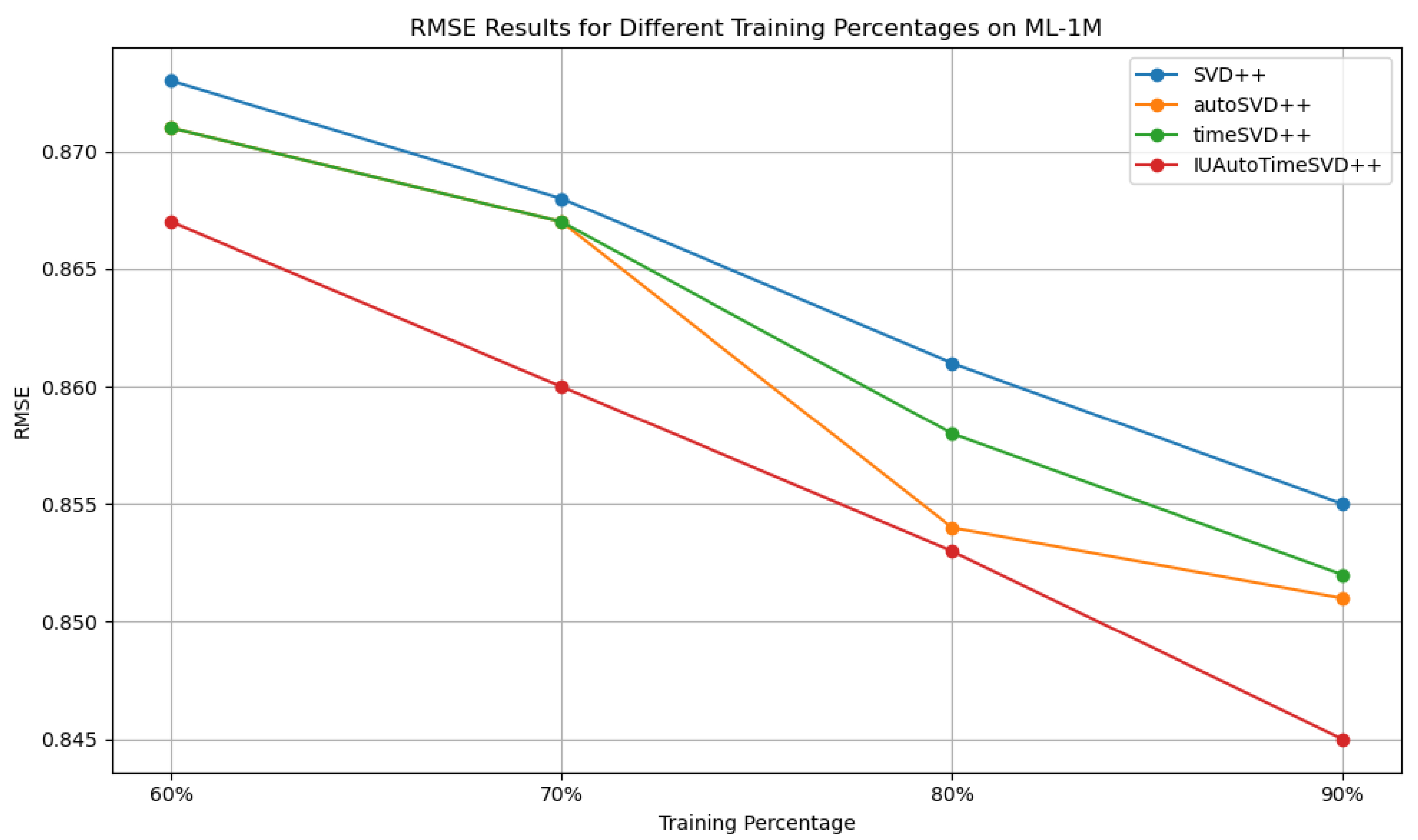
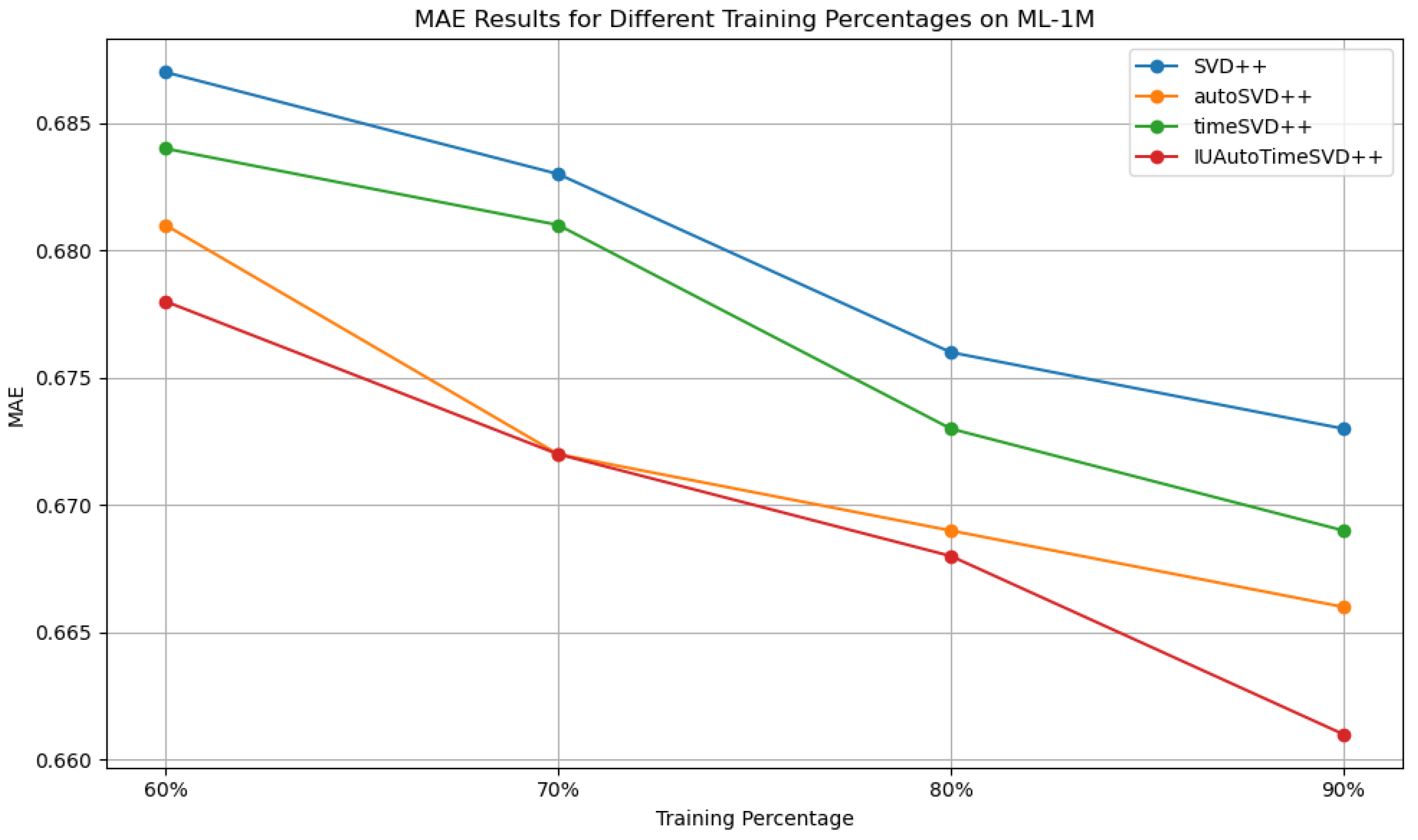
4.7. Effectiveness Study of Training Size Impact
Effectiveness Study Results Analysis
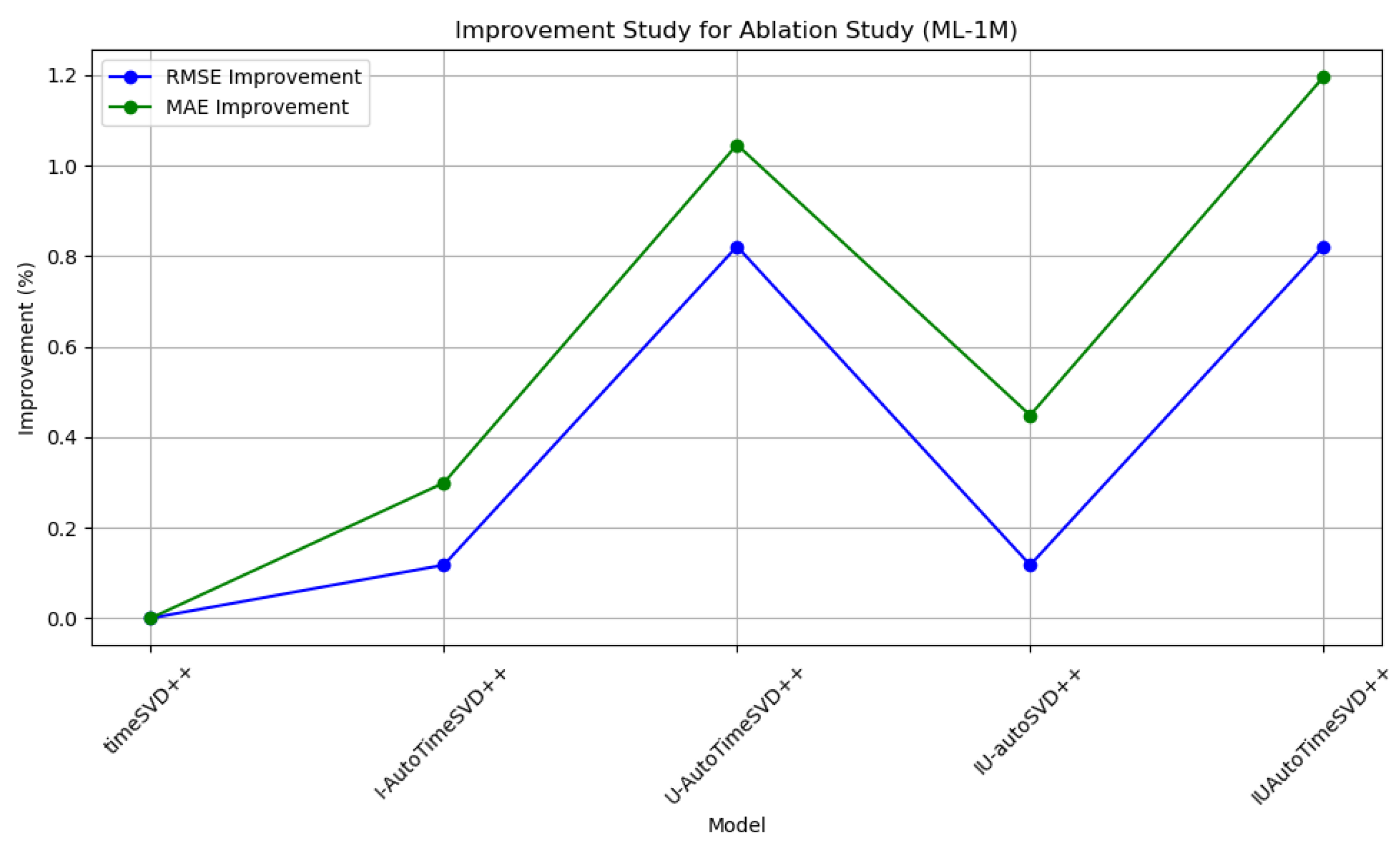
4.8. Ablation Study
4.8.1. Results
4.8.2. Improvement Ablation Study Analysis
4.9. Experimental Analysis on Sparse Synthetic Dataset: Subsampling MovieLens Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ricci, F.; Rokach, L.; Shapira, B. (Eds.) Recommender Systems Handbook, 2nd ed.; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Ekstrand, M.D.; Riedl, J.T.; Konstan, J.A. Collaborative Filtering Recommender Systems. Found. Trends Hum.-Comput. Interact. 2011, 4, 81–173. [Google Scholar] [CrossRef]
- Bell, R.M.; Koren, Y. Lessons from the Netflix Prize Challenge. SIGKDD Explor. Newsl. 2007, 9, 75–79. [Google Scholar] [CrossRef]
- Rendle, S.; Krichene, W.; Zhang, L.; Anderson, J. Neural Collaborative Filtering vs. Matrix Factorization Revisited. arXiv 2020, arXiv:2005.09683. [Google Scholar]
- Anelli, V.W.; Bellogín, A.; Di Noia, T.; Pomo, C. Reenvisioning Collaborative Filtering vs. Matrix Factorization. In Proceedings of the Fifteenth ACM Conference on Recommender Systems, Amsterdam, The Netherlands, 27 September–1 October 2021; pp. 521–529. [Google Scholar]
- Zhang, S.; Yao, L.; Sun, A.; Tay, Y. Deep Learning Based Recommender System: A Survey and New Perspectives. ACM Comput. Surv. 2019, 52, 1–38. [Google Scholar] [CrossRef]
- Mu, R. A Survey of Recommender Systems Based on Deep Learning. IEEE Access 2018, 6, 69009–69022. [Google Scholar] [CrossRef]
- Zhang, S.; Yao, L.; Xu, X. AutoSVD++: An Efficient Hybrid Collaborative Filtering Model via Contractive Auto-encoders. In Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval, Tokyo, Japan, 7–11 August 2017; pp. 957–960. [Google Scholar] [CrossRef]
- Kim, D.; Park, C.; Oh, J.; Lee, S.; Yu, H. Convolutional Matrix Factorization for Document Context-Aware Recommendation. In Proceedings of the 10th ACM Conference on Recommender Systems RecSys ’16, New York, NY, USA, 15–19 September 2016; pp. 233–240. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, C.; Chen, M.; Yuan, M. Integrating Stacked Sparse Auto-Encoder Into Matrix Factorization for Rating Prediction. IEEE Access 2021, 9, 17641–17648. [Google Scholar] [CrossRef]
- Azri, A.; Haddi, A.; Allali, H. autoTimeSVD++: A Temporal Hybrid Recommender System Based on Contractive Autoencoder and Matrix Factorization. In Proceedings of the Smart Applications and Data Analysis—4th International Conference, SADASC 2022, Marrakesh, Morocco, 22–24 September 2022; Hamlich, M., Bellatreche, L., Siadat, A., Ventura, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; Volume 1677, Communications in Computer and Information Science. pp. 93–103. [Google Scholar] [CrossRef]
- Koren, Y. Collaborative filtering with temporal dynamics. In Proceedings of the KDD09: The 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 447–456. [Google Scholar]
- Rifai, S.; Vincent, P.; Muller, X.; Glorot, X.; Bengio, Y. Contractive auto-encoders: Explicit invariance during feature extraction. In Proceedings of the 28th International Conference on International Conference on Machine Learning ICML’11, Madison, WI, USA, 28 June–2 July 2011; pp. 833–840. [Google Scholar]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix Factorization Techniques for Recommender Systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- He, R.; McAuley, J. VBPR: Visual Bayesian Personalized Ranking from Implicit Feedback. arXiv 2015, arXiv:1510.01784. [Google Scholar] [CrossRef]
- Abdollahi, B.; Nasraoui, O. Explainable Matrix Factorization for Collaborative Filtering. In Proceedings of the 25th International Conference Companion on World Wide Web WWW ’16 Companion, Geneva, Switzerland, 11–15 April 2016; pp. 5–6. [Google Scholar] [CrossRef]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T.S. Neural Collaborative Filtering. In Proceedings of the 26th International Conference on World Wide Web WWW ’17, Perth, Australia, 3–7 April 2017; pp. 173–182. [Google Scholar] [CrossRef]
- Mnih, A.; Salakhutdinov, R.R. Probabilistic Matrix Factorization. In Advances in Neural Information Processing Systems 20; Platt, J.C., Koller, D., Singer, Y., Roweis, S.T., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2008; pp. 1257–1264. [Google Scholar]
- Li, K.; Zhou, X.; Lin, F.; Zeng, W.; Alterovitz, G. Deep Probabilistic Matrix Factorization Framework for Online Collaborative Filtering. IEEE Access 2019, 7, 56117–56128. [Google Scholar] [CrossRef]
- Ren, X.; Xia, L.; Zhao, J.; Yin, D.; Huang, C. Disentangled contrastive collaborative filtering. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval, Taipei, Taiwan, 23–27 July 2023; pp. 1137–1146. [Google Scholar]
- Wang, Y.; Wang, X.; Huang, X.; Yu, Y.; Li, H.; Zhang, M.; Guo, Z.; Wu, W. Intent-aware Recommendation via Disentangled Graph Contrastive Learning. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, IJCAI-2023, Macao, 19–25 August 2023. [Google Scholar] [CrossRef]
- Bank, D.; Koenigstein, N.; Giryes, R. Autoencoders. arXiv 2021, arXiv:2003.05991. [Google Scholar]
- Harper, F.M.; Konstan, J.A. The movielens datasets: History and context. Acm Trans. Interact. Intell. Syst. 2015, 5, 1–19. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Recommender Systems: The Textbook, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gemulla, R.; Nijkamp, E.; Haas, P.J.; Sismanis, Y. Large-scale matrix factorization with distributed stochastic gradient descent. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 69–77. [Google Scholar] [CrossRef]


| Baseline Model | Extension | |||||||
|---|---|---|---|---|---|---|---|---|
| MF [14] | Model | Type | Technique | Year | Time factor | User features | Item features | Visual features |
| SVD++ [14] | Implicit feedback | Dot product | 2008 | |||||
| timeSVD++ [12] | Temporal | Dot product | 2009 | ✔ | ||||
| VBPR [15] | Visual | CNN | 2016 | ✔ | ||||
| EMF [16] | Explainability | Similarity | 2016 | |||||
| autoSVD++ [8] | Hybrid | Autoencoder | 2017 | ✔ | ||||
| NeuMF [17] | Embedding | MLP | 2017 | |||||
| SSAERec [10] | Hybrid | Autoencoder | 2021 | ✔ | ||||
| Baseline Model | Extension | |||||||
|---|---|---|---|---|---|---|---|---|
| PMF [18] | Model | Type | Technique | Year | Time factor | User features | Item features | Visual features |
| ConvMF [9] | Textual | CNN | 2016 | ✔ | ||||
| DBPMF [19] | Hybrid | CNN | 2019 | ✔ | ✔ | |||
| Notation | Description |
|---|---|
| The user’s set defined as | |
| The item’s set defined as | |
| n | The number of items where |
| m | The number of users where |
| OHE item features vector of size X | |
| OHE user features vector of size Y | |
| Interaction of rating matrix | |
| Low rank matrix representing items | |
| Low rank matrix representing users | |
| K | The latent factors space |
| k | The latent factors dimension |
| The rating value provided by a user u of an item i | |
| The rating value at the time t | |
| CAE | Contractive autoencoder |
| SVD | Single value decomposition |
| SGD | Stochastic gradient Descent |
| Parameter | Description |
|---|---|
| Time-based bin for mapping a day to its rank in a month | |
| Parameter for the drift concept | |
| Coefficient for the drift in user bias |
| Parameter | Definition |
|---|---|
| Bias term added to hidden layers for shifting output | |
| Additional bias term contributing to model flexibility | |
| Dimensionality of the latent space | |
| W | Weight matrix for transforming input data in the encoding process |
| Additional weight matrix, often associated with decoding in the autoencoder | |
| Regularization parameter controlling Jacobian regularization strength |
| Dataset | # Interactions | # Users | # Items | Sparsity (%) |
|---|---|---|---|---|
| MovieLens 100K | 100,000 | 943 | 1682 | 93.70 |
| MovieLens 1M | 1,000,209 | 6040 | 3952 | 95.53 |
| Element | Available Features |
|---|---|
| User | Age, gender, job |
| Item | Genre, Year of apparition |
| Parameter | Description | Value |
|---|---|---|
| I-CAE learning rate | (ML-100K), (ML-1M) | |
| U-CAE learning rate | (ML-100K), (ML-1M) | |
| k | Latent factors dimension | 10 |
| Learning rate | 0.005 | |
| Learning rate | 0.015 | |
| Learning rate | 0.015 | |
| Learning rate of user | 0.0004 | |
| Regularization | 0.005 | |
| Regularization | 0.007 | |
| Regularization | 0.001 | |
| Regularization of user | 0.00001 | |
| Control time deviation | 0.015 | |
| epochs | Number of iteration | 25 |
| Model | ML-100K RMSE | ML-1M RMSE |
|---|---|---|
| MF | 0.935 | 0.873 |
| PMF | 0.915 | 0.853 |
| SVD++ | 0.925 | 0.855 |
| timeSVD++ | 0.919 | 0.852 |
| convMF | 0.914 | 0.856 |
| DBPMF | 0.999 | 0.948 |
| autoSVD++ | 0.909 | 0.851 |
| SSAERec | 0.902 | 0.852 |
| IUAutoTimeSVD++ | 0.892 | 0.845 |
| Dataset | Training | Metrics | SVD++ | autoSVD++ | timeSVD++ | IUAutoTimeSVD++ |
|---|---|---|---|---|---|---|
| ML-100K | 90% | RMSE | 0.925 | 0.909 | 0.919 | 0.892 |
| MAE | 0.731 | 0.712 | 0.724 | 0.699 | ||
| 80% | RMSE | 0.943 | 0.925 | 0.929 | 0.912 | |
| MAE | 0.742 | 0.726 | 0.733 | 0.716 | ||
| 70% | RMSE | 0.935 | 0.920 | 0.939 | 0.915 | |
| MAE | 0.739 | 0.725 | 0.742 | 0.720 | ||
| 60% | RMSE | 0.944 | 0.938 | 0.941 | 0.936 | |
| MAE | 0.744 | 0.738 | 0.741 | 0.738 |
| Dataset | Training | Metrics | SVD++ | autoSVD++ | timeSVD++ | IUAutoTimeSVD++ |
|---|---|---|---|---|---|---|
| ML-1M | 90% | RMSE | 0.855 | 0.851 | 0.852 | 0.845 |
| MAE | 0.673 | 0.666 | 0.669 | 0.661 | ||
| 80% | RMSE | 0.861 | 0.854 | 0.858 | 0.853 | |
| MAE | 0.676 | 0.669 | 0.673 | 0.668 | ||
| 70% | RMSE | 0.868 | 0.859 | 0.867 | 0.860 | |
| MAE | 0.683 | 0.672 | 0.681 | 0.672 | ||
| 60% | RMSE | 0.873 | 0.871 | 0.871 | 0.867 | |
| MAE | 0.687 | 0.681 | 0.684 | 0.678 |
| Model | Time | Item Features | User Features |
|---|---|---|---|
| timeSVD++ | ✔ | ||
| I-AutoTimeSVD++ | ✔ | ✔ | |
| U-AutoTimeSVD++ | ✔ | ✔ | |
| IU-autoSVD++ | ✔ | ✔ | |
| IUAutoTimeSVD++ | ✔ | ✔ | ✔ |
| Model | RMSE | MAE |
|---|---|---|
| timeSVD++ | 0.919 | 0.724 |
| I-AutoTimeSVD++ | 0.896 | 0.704 |
| U-AutoTimeSVD++ | 0.896 | 0.704 |
| IU-autoSVD++ | 0.909 | 0.712 |
| IUAutoTimeSVD++ | 0.892 | 0.699 |
| Model | RMSE | MAE |
|---|---|---|
| timeSVD++ | 0.852 | 0.669 |
| I-AutoTimeSVD++ | 0.851 | 0.667 |
| U-AutoTimeSVD++ | 0.845 | 0.662 |
| IU-autoSVD++ | 0.851 | 0.666 |
| IUAutoTimeSVD++ | 0.845 | 0.661 |
| Dataset | # Interactions | # Users | # Items | Sparsity (%) |
|---|---|---|---|---|
| Synthetic MovieLens 100K | 30,000 | 943 | 1499 | 98.09 |
| Synthetic MovieLens 1M | 300,063 | 6040 | 3531 | 98.76 |
| Model | Synthetic ML-100K RMSE | Synthetic ML-1M RMSE |
|---|---|---|
| MF | 0.962 | 0.915 |
| SVD++ | 0.961 | 0.913 |
| timeSVD++ | 0.959 | 0.909 |
| autoSVD++ | 0.961 | 1.010 |
| IUAutoTimeSVD++ | 0.959 | 0.906 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azri, A.; Haddi, A.; Allali, H. IUAutoTimeSVD++: A Hybrid Temporal Recommender System Integrating Item and User Features Using a Contractive Autoencoder. Information 2024, 15, 204. https://doi.org/10.3390/info15040204
Azri A, Haddi A, Allali H. IUAutoTimeSVD++: A Hybrid Temporal Recommender System Integrating Item and User Features Using a Contractive Autoencoder. Information. 2024; 15(4):204. https://doi.org/10.3390/info15040204
Chicago/Turabian StyleAzri, Abdelghani, Adil Haddi, and Hakim Allali. 2024. "IUAutoTimeSVD++: A Hybrid Temporal Recommender System Integrating Item and User Features Using a Contractive Autoencoder" Information 15, no. 4: 204. https://doi.org/10.3390/info15040204
APA StyleAzri, A., Haddi, A., & Allali, H. (2024). IUAutoTimeSVD++: A Hybrid Temporal Recommender System Integrating Item and User Features Using a Contractive Autoencoder. Information, 15(4), 204. https://doi.org/10.3390/info15040204






