Bridging the Gap: Exploring Interpretability in Deep Learning Models for Brain Tumor Detection and Diagnosis from MRI Images
Abstract
1. Introduction
2. Literature on DL Models’ Explainability in Medical Imaging
3. Path-Oriented Methods and Transfer Learning Models
3.1. Path-Oriented Methods
3.1.1. Grad-CAM and Grad-CAM++
3.1.2. Integrated Gradient (IG)
3.1.3. Saliency Mapping
3.2. Transfer Learning Models
3.2.1. AlexNet
3.2.2. VGG16
3.2.3. VGG19
3.2.4. GoogLeNet
3.2.5. ResNet50
3.2.6. Inception V3
3.2.7. DenseNet121
3.2.8. Xception
3.2.9. EfficientNetB0
3.2.10. Vision Transformer (ViT)
3.3. Performance Evaluation
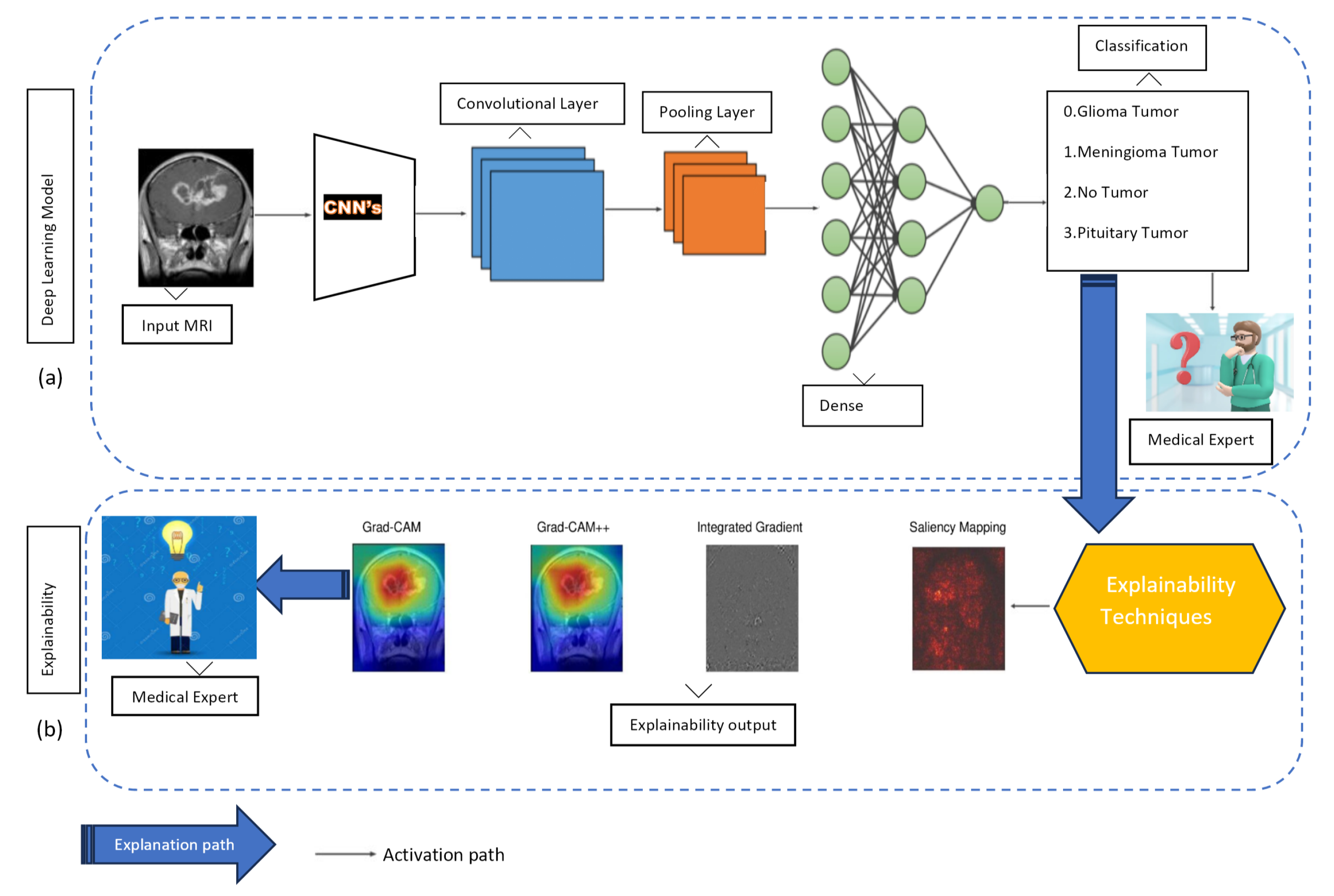
4. Method
5. Results and Discussion
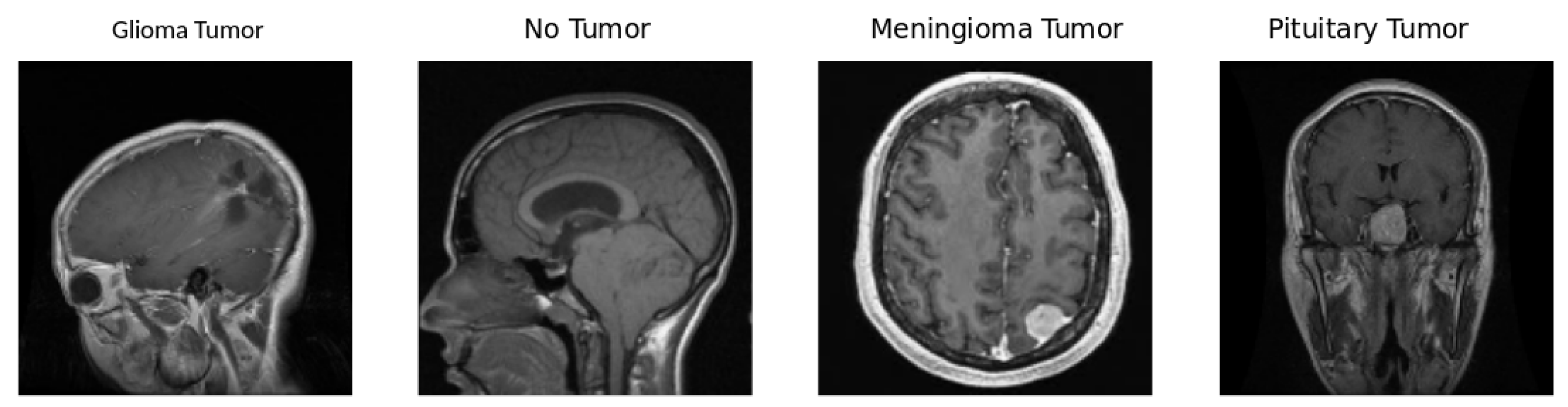
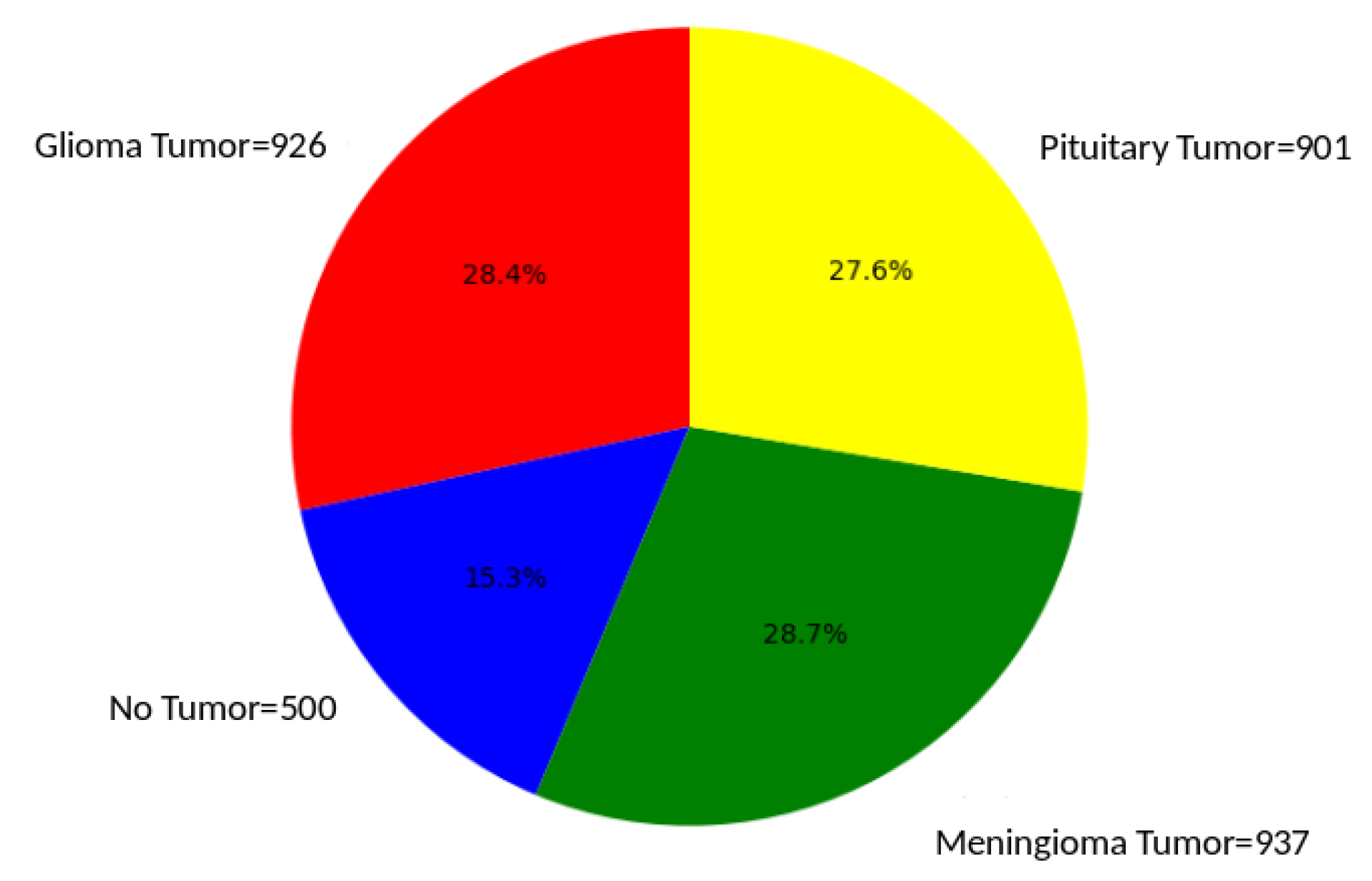
5.1. Dataset
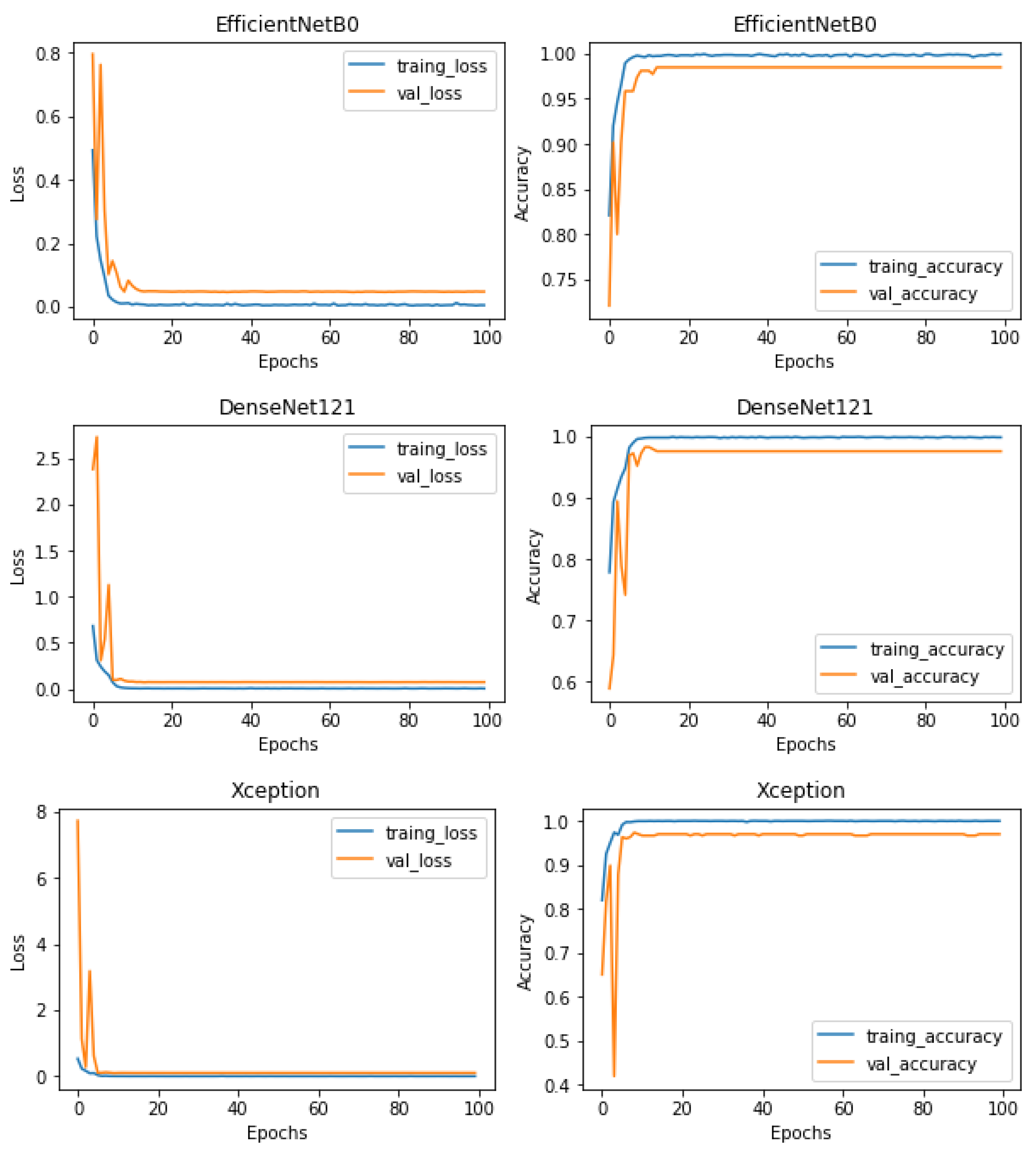
5.2. Training, Regularization, and Testing
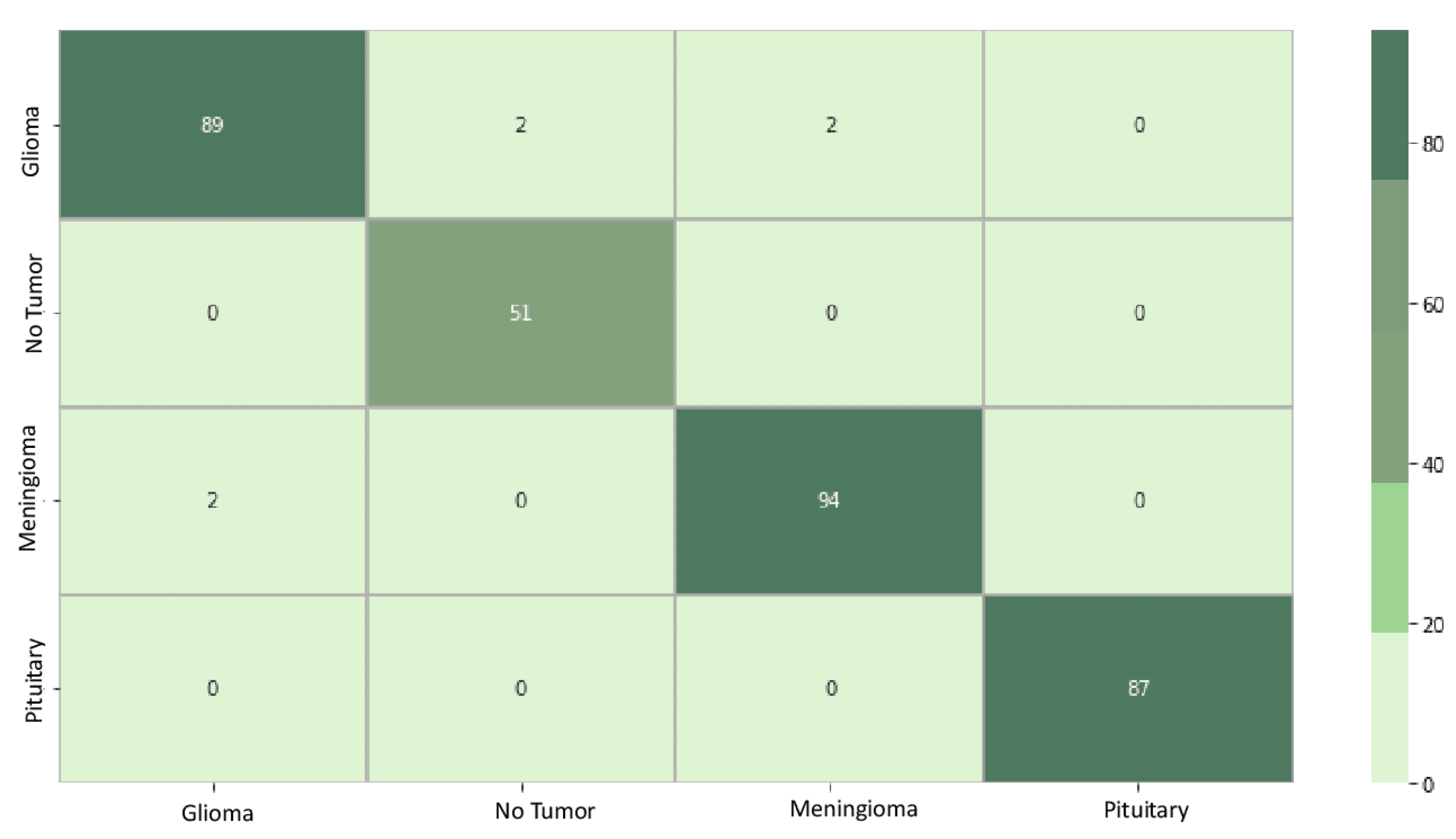
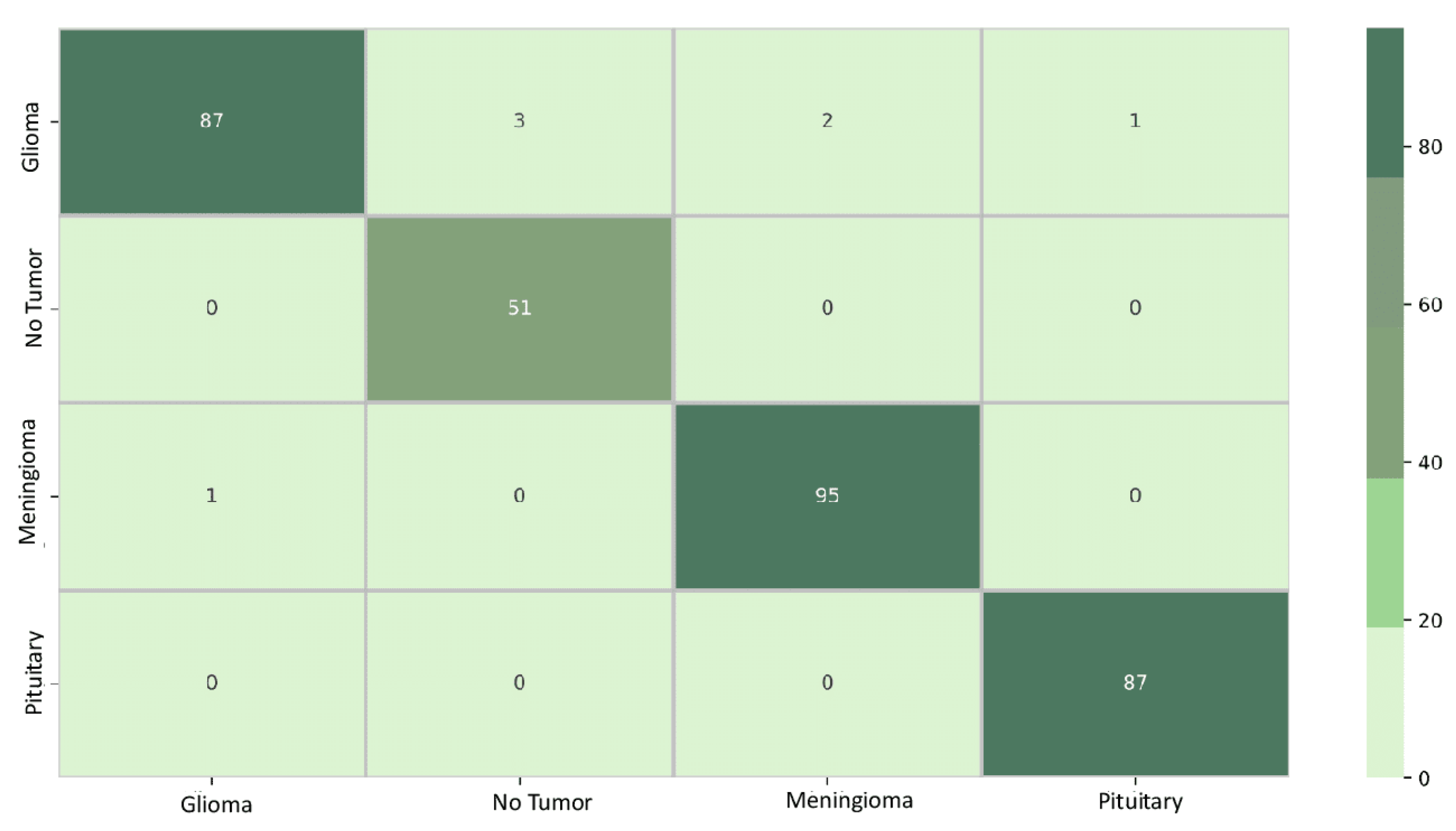
5.3. Classification Results
5.4. Interpretability Results
5.5. Discussion
- Model evaluation: The study comprehensively assesses various DL architectures, providing valuable insights into which models are most effective for brain tumor classification. This evaluation is crucial for guiding the selection of appropriate models in real-world medical imaging applications.
- Brain tumor diagnosis: Diagnosing a brain tumor is a challenging process that requires the correct and rapid examination of MRI scan images. The study’s findings directly contribute to enhancing the accuracy and reliability of DL models for identifying brain tumors, focusing on this specific medical area. This is critical for early diagnosis and treatment planning for patients.
- Model interpretability: The incorporation of explainability approaches, such as Grad-CAM, Grad-CAM++, IG, and Saliency Mapping, represents a significant scientific contribution. By using these methods, the study increases the interpretability of DL models, shedding light on the decision-making processes and providing valuable intuition into how these models arrive at their classifications, particularly in the context of brain tumor diagnosis.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Expansion |
| CNN | Convolutional Neural Network |
| CT | Computed Tomography |
| DL | Deep Learning |
| DeconvNET | Deconvolution NETwork |
| DeepLIFT | Deep Learning Important Features |
| F1 Score | Harmonic Precision–Recall Mean |
| Grad-CAM | Gradient-weighted Class Activation Mapping |
| GBP | Guided Back Propagation |
| LRP | Layerwise Relevance Propagation |
| MRI | Magnetic Resonance Imaging |
| ReLU | Rectified Linear Unit |
| SHAP | SHapley Additive exPlanation |
| TL | Transfer Learning |
| VGG | Visual Geometry Group |
| XAI | Explainable Artificial Intelligence |
References
- Bau, D.; Zhou, B.; Khosla, A.; Oliva, A.; Torralba, A. Network dissection: Quantifying interpretability of deep visual representations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6541–6549. [Google Scholar]
- Abiwinanda, N.; Hanif, M.; Hesaputra, S.T.; Handayani, A.; Mengko, T.R. Brain tumor classification using convolutional neural network. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering 2018, Prague, Czech Republic, 3–8 June 2018; Volume 1, pp. 183–189. [Google Scholar]
- Latif, G.; Butt, M.M.; Khan, A.H.; Butt, O.; Iskandar, D.A. Multiclass brain Glioma tumor classification using block-based 3D Wavelet features of MR images. In Proceedings of the 2017 4th International Conference on Electrical and Electronic Engineering (ICEEE), Ankara, Turkey, 8–10 April 2017; pp. 333–337. [Google Scholar]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- Brima, Y.; Atemkeng, M. Visual Interpretable and Explainable Deep Learning Models for Brain Tumor MRI and COVID-19 Chest X-ray Images. arXiv 2022, arXiv:2208.00953. [Google Scholar]
- Ebiele, J.; Ansah-Narh, T.; Djiokap, S.; Proven-Adzri, E.; Atemkeng, M. Conventional machine learning based on feature engineering for detecting pneumonia from chest X-rays. In Proceedings of the Conference of the South African Institute of Computer Scientists and Information Technologists 2020, Cape Town, South Africa, 14–16 September 2020; pp. 149–155. [Google Scholar]
- Brima, Y.; Atemkeng, M.; Tankio Djiokap, S.; Ebiele, J.; Tchakounté, F. Transfer learning for the detection and diagnosis of types of pneumonia including pneumonia induced by COVID-19 from chest X-ray images. Diagnostics 2021, 11, 1480. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-CAM++: Generalized gradient-based visual explanations for deep convolutional networks. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 839–847. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3319–3328. [Google Scholar]
- Zhang, Y.; Dong, Z.; Wu, L.; Wang, S.; Zhou, Z. Feature extraction of brain MRI by stationary wavelet transform. In Proceedings of the 2010 International Conference on Biomedical Engineering and Computer Science, Wuhan, China, 23–25 April 2010; pp. 1–4. [Google Scholar]
- Zeineldin, R.A.; Karar, M.E.; Elshaer, Z.; Coburger, J.; Wirtz, C.R.; Burgert, O.; Mathis-Ullrich, F. Explainability of deep neural networks for MRI analysis of brain tumors. Int. J. Comput. Assist. Radiol. Surg. 2022, 17, 1673–1683. [Google Scholar] [CrossRef]
- Philbrick, K.A.; Yoshida, K.; Inoue, D.; Akkus, Z.; Kline, T.L.; Weston, A.D.; Korfiatis, P.; Takahashi, N.; Erickson, B.J. What does deep learning see? Insights from a classifier trained to predict contrast enhancement phase from CT images. AJR Am. J. Roentgenol. 2018, 211, 1184–1193. [Google Scholar] [CrossRef] [PubMed]
- Martí-Juan, G.; Frías, M.; Garcia-Vidal, A.; Vidal-Jordana, A.; Alberich, M.; Calderon, W.; Piella, G.; Camara, O.; Montalban, X.; Sastre-Garriga, J.; et al. Detection of lesions in the optic nerve with magnetic resonance imaging using a 3D convolutional neural network. Neuroimage Clin. 2022, 36, 103187. [Google Scholar] [CrossRef] [PubMed]
- Zeiler, M.; Fergus, R. Visualizing and understanding convolutional networks. arXiv 2013, arXiv:1311.2901. [Google Scholar] [CrossRef]
- Chatterjee, S.; Das, A.; Mandal, C.; Mukhopadhyay, B.; Vipinraj, M.; Shukla, A.; Nagaraja Rao, R.; Sarasaen, C.; Speck, O.; Nürnberger, A. TorchEsegeta: Framework for interpretability and explainability of image-based deep learning models. Appl. Sci. 2022, 12, 1834. [Google Scholar] [CrossRef]
- Springenberg, J.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv 2014, arXiv:1412.6806. [Google Scholar] [CrossRef]
- Wood, D.A.; Kafiabadi, S.; Al Busaidi, A.; Guilhem, E.; Montvila, A.; Lynch, J.; Townend, M.; Agarwal, S.; Mazumder, A.; Barker, G.J. Deep learning models for triaging hospital head MRI examinations. Med. Image Anal. 2022, 78, 102391. [Google Scholar] [CrossRef]
- Saleem, H.; Shahid, A.R.; Raza, B. Visual interpretability in 3D brain tumor segmentation network. Comput. Biol. Med. 2021, 133, 104410. [Google Scholar] [CrossRef] [PubMed]
- Montavon, G.; Binder, A.; Lapuschkin, S.; Samek, W.; Müller, K.-R. Layer-wise relevance propagation: An overview In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Samek, W., Montavon, G., Vedaldi, A., Hansen, L., Müller, K.R., Eds.; Lecture notes in computer science; Springer: Cham, Switzerland, 2019; pp. 193–209. [Google Scholar]
- Golla, A.K.; Tönnes, C.; Russ, T.; Bauer, D.F.; Froelich, M.F.; Diehl, S.J.; Schoenberg, S.O.; Keese, M.; Schad, L.R.; Zöllner, F.G.; et al. Automated screening for abdominal aortic aneurysm in CT scans under clinical conditions using deep learning. Diagnostics 2021, 11, 2131. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Tong, L.; Zhu, Y.; Wang, M.D. COVID-19 automatic diagnosis with radiographic imaging: Explainable attention transfer deep neural networks. IEEE J. Biomed. Health Inform. 2021, 25, 2376–2387. [Google Scholar] [CrossRef] [PubMed]
- Karim, M.R.; Jiao, J.; Doehmen, T.; Cochez, M.; Beyan, O.; Rebholz-Schuhmann, D.; Decker, S. DeepKneeExplainer: Explainable knee osteoarthritis diagnosis from radiographs and magnetic resonance imaging. IEEE Access. 2021, 9, 39757–39780. [Google Scholar] [CrossRef]
- Lopatina, A.; Ropele, S.; Sibgatulin, R.; Reichenbach, J.R.; Güllmar, D. Investigation of deep-learning-driven identification of multiple sclerosis patients based on susceptibility-weighted images using relevance analysis. Front. Neurosci. 2020, 14, 609468. [Google Scholar] [CrossRef] [PubMed]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning important features through propagating activation differences. arXiv 2017, arXiv:1704.02685. [Google Scholar] [CrossRef]
- Gulum, M.A.; Trombley, C.M.; Kantardzic, M. A review of explainable deep learning cancer detection models in medical imaging. Appl. Sci. 2021, 11, 4573. [Google Scholar] [CrossRef]
- Singh, A.; Sengupta, S.; Lakshminarayanan, V. Explainable deep learning models in medical image analysis. J. Imaging 2020, 6, 52. [Google Scholar] [CrossRef]
- Wang, C.; Ma, J.; Shao, J.; Zhang, S.; Li, W. Predicting EGFR and PD-L1 status in NSCLC patients using multitask AI system based on CT images. Front. Immunol. 2022, 13, 813072. [Google Scholar] [CrossRef]
- Kumar, A.; Manikandan, R.; Kose, U.; Gupta, D.; Satapathy, S.C. Doctor’s dilemma: Evaluating an explainable subtractive spatial lightweight convolutional neural network for brain tumor diagnosis. ACM Trans. Multimed. Comput. Commun. Appl. 2021, 17, 1–26. [Google Scholar] [CrossRef]
- Uyulan, C.; Erguzel, T.T.; Turk, O.; Farhad, S.; Metin, B.; Tarhan, N. A class activation map-based interpretable transfer learning model for automated detection of ADHD from fMRI data. Clin. EEG Neurosci. 2022, 54, 151–159. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.J.; Hamm, C.A.; Savic, L.J.; Ferrante, M.; Schobert, I.; Schlachter, T.; Lin, M.; Weinreb, J.C.; Duncan, J.S.; Chapiro, J.; et al. Deep learning for liver tumor diagnosis part II: Convolutional neural network interpretation using radiologic imaging features. Eur. Radiol. 2019, 29, 3348–3357. [Google Scholar] [CrossRef] [PubMed]
- Akatsuka, J.; Yamamoto, Y.; Sekine, T.; Numata, Y.; Morikawa, H.; Tsutsumi, K.; Yanagi, M.; Endo, Y.; Takeda, H.; Hayashi, T. Illuminating clues of cancer buried in prostate MR image: Deep learning and expert approaches. Biomolecules 2019, 9, 673. [Google Scholar] [CrossRef] [PubMed]
- Fuhrman, J.D.; Gorre, N.; Hu, Q.; Li, H.; El Naqa, I.; Giger, M.L. A review of explainable and interpretable AI with applications in COVID-19 imaging. Med. Phys. 2022, 49, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Alshazly, H.; Linse, C.; Barth, E.; Martinetz, T. Explainable COVID-19 detection using chest CT scans and deep learning. Sensors 2021, 21, 455. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Xie, J.; Liu, R.; Hao, H.; Ma, Y.; Yan, K.; Liu, R.; Zheng, Y.; Zheng, J.; Liu, J.; et al. Automatic sequence-based network for lung diseases detection in chest CT. Front. Oncol. 2021, 11, 781798. [Google Scholar] [CrossRef] [PubMed]
- Lahsaini, I.; El Habib Daho, M.; Chikh, M.A. Deep transfer learning based classification model for COVID-19 using chest CT-scans. Pattern Recognit Lett. 2021, 152, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Garg, A.; Salehi, S.; Rocca, M.; Garner, R.; Duncan, D. Efficient and visualizable convolutional neural networks for COVID-19 classification using chest CT. Expert Syst. Appl. 2022, 195, 116540. [Google Scholar] [CrossRef]
- Ullah, F.; Moon, J.; Naeem, H.; Jabbar, S. Explainable artificial intelligence approach in combating real-time surveillance of COVID19 pandemic from CT scan and X-ray images using ensemble model. J. Supercomput. 2022, 78, 19246–19271. [Google Scholar] [CrossRef]
- Lu, S.Y.; Zhang, Z.; Zhang, Y.D.; Wang, S.H. CGENet: A deep graph model for COVID-19 detection based on chest CT. Biology 2022, 11, 33. [Google Scholar] [CrossRef]
- Jadhav, S.; Deng, G.; Zawin, M.; Kaufman, A.E. COVID-view: Diagnosis of COVID-19 using chest CT. IEEE Trans. Vis. Comput. Graph. 2022, 28, 227–237. [Google Scholar] [CrossRef] [PubMed]
- Nagaoka, T.; Kozuka, T.; Yamada, T.; Habe, H.; Nemoto, M.; Tada, M.; Abe, K.; Handa, H.; Yoshida, H.; Ishii, K.; et al. A deep learning system to diagnose COVID-19 pneumonia using masked lung CT images to avoid AI-generated COVID-19 diagnoses that include data outside the lungs. Adv. Biomed. Eng. 2022, 11, 76–86. [Google Scholar] [CrossRef]
- Suri, J.S.; Agarwal, S.; Chabert, G.L.; Carriero, A.; Paschè, A.; Danna, P.S.; Saba, L.; Mehmedović, A.; Faa, G.; Singh, I.M.; et al. COVLIAS 20-cXAI: Cloud-based explainable deep learning system for COVID-19 lesion localization in computed tomography scans. Diagnostics 2022, 12, 1482. [Google Scholar] [CrossRef] [PubMed]
- Pennisi, M.; Kavasidis, I.; Spampinato, C.; Schinina, V.; Palazzo, S.; Salanitri, F.P.; Bellitto, G.; Rundo, F.; Aldinucci, M.; Cristofaro, M.; et al. An explainable AI system for automated COVID-19 assessment and lesion categorization from CT-scans. Artif. Intell. Med. 2021, 118, 102114. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Liu, Z.; Maaten, L.V.D.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar] [CrossRef]
- Li, C.F.; Xu, Y.D.; Ding, X.H.; Zhao, J.J.; Du, R.Q.; Wu, L.Z.; Sun, W.P. MultiR-net: A novel joint learning network for COVID-19 segmentation and classification. Comput. Biol. Med. 2022, 144, 105340. [Google Scholar] [CrossRef] [PubMed]
- Williamson, B.J.; Khandwala, V.; Wang, D.; Maloney, T.; Sucharew, H.; Horn, P.; Haverbusch, M.; Alwell, K.; Gangatirkar, S.; Mahammedi, A.; et al. Automated grading of enlarged perivascular spaces in clinical imaging data of an acute stroke cohort using an interpretable, 3D deep learning framework. Sci. Rep. 2022, 12, 788. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.H.; Koo, H.W.; Lee, B.J.; Yoon, S.W.; Sohn, M.J. Cerebral hemorrhage detection and localization with medical imaging for cerebrovascular disease diagnosis and treatment using explainable deep learning. J. Korean Phys. Soc. 2021, 79, 321–327. [Google Scholar] [CrossRef]
- Singh, A.; Kwiecinski, J.; Miller, R.J.; Otaki, Y.; Kavanagh, P.B.; Van Kriekinge, S.D.; Parekh, T.; Gransar, H.; Pieszko, K.; Killekar, A.; et al. Deep learning for explainable estimation of mortality risk from myocardial positron emission tomography images. Circ. Cardiovasc. Imaging 2022, 15, e014526. [Google Scholar] [CrossRef]
- Jain, V.; Nankar, O.; Jerrish, D.J.; Gite, S.; Patil, S.; Kotecha, K. A novel AI-based system for detection and severity prediction of dementia using MRI. IEEE Access. 2021, 9, 154324–154346. [Google Scholar] [CrossRef]
- Hu, M.; Qian, X.; Liu, S.; Koh, A.J.; Sim, K.; Jiang, X.; Guan, C.; Zhou, J.H. Structural and diffusion MRI based schizophrenia classification using 2D pretrained and 3D naive convolutional neural networks. Schizophr. Res. 2022, 243, 330–341. [Google Scholar] [CrossRef]
- Zhang, X.; Han, L.; Zhu, W.; Sun, L.; Zhang, D. An explainable 3D residual self-attention deep neural network for joint atrophy localization and Alzheimer’s disease diagnosis using structural MRI. IEEE J. Biomed. Health Inform. 2021, 26, 5289–5297. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Proc. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9. [Google Scholar] [CrossRef]
- Mascarenhas, S.; Agarwal, M. A comparison between VGG16, VGG19 and ResNet50 architecture frameworks for Image Classification. In Proceedings of the 2021 International Conference on Disruptive Technologies for Multi-Disciplinary Research and Applications (CENTCON), Bengaluru, India, 19–21 November 2021; Volume 1, pp. 96–99. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 19–24 June 2016; pp. 1610–2357. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 19–24 June 2016; pp. 2818–2826. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Islam, M.N.; Hasan, M.; Hossain, M.K.; Alam, M.G.R.; Uddin, M.Z.; Soylu, A. Vision Transformer and explainable transfer learning models for auto detection of kidney cyst, stone and tumor from CT-radiography. Sci. Rep. 2022, 12, 11440. [Google Scholar] [CrossRef]
- Bhuvaji, S.; Kadam, A.; Bhumkar, P.; Dedge, S. Brain Tumor Classification (MRI) Kaggle Dataset. Available online: https://www.kaggle.com/datasets/sartajbhuvaji/brain-tumor-classification-mri/data (accessed on 20 July 2023).





| Hyperparameter | Setting |
|---|---|
| Batch size | 32 |
| Learning rate | |
| Epochs | 10 |
| Training and validation split | |
| Test split | |
| Optimizer | Adam |
| Input size | pixels |
| Loss function | Categorical cross-entropy |
| Model Name | Parameters | Training Accuracy | Loss |
|---|---|---|---|
| AlexNet | 61.9 M | 0.8763 | 0.3233 |
| DenseNet121 | 8.1 M | 0.9986 | 0.0057 |
| EfficientNetB0 | 5.3 M | 0.9991 | 0.0042 |
| GoogLeNet | 11.2 M | 0.9997 | 0.0027 |
| Inception V3 | 23.9 M | 0.9989 | 0.0084 |
| ResNet50 | 25.6 M | 0.9991 | 0.0044 |
| VGG16 | 138.4 M | 0.8698 | 0.4011 |
| VGG19 | 143.7 M | 0.8570 | 0.3953 |
| Vision Transformer | 86 M | 0.7484 | 0.5115 |
| Xception | 22.9 M | 1.0000 | 0.0021 |
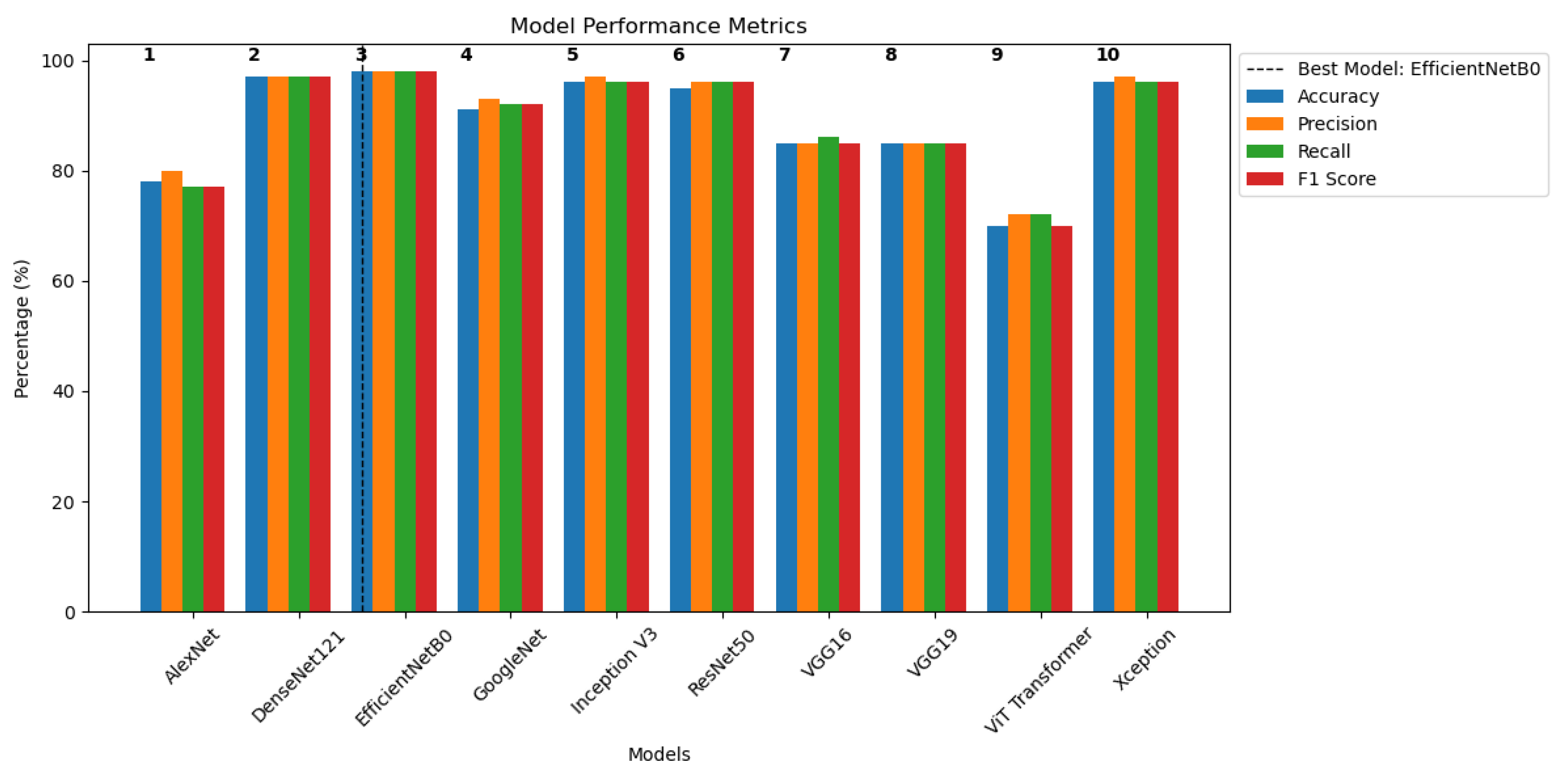
| Model Name | Accuracy % | Precision % | Recall % | F1 Score % |
|---|---|---|---|---|
| AlexNet | 78 | 80 | 77 | 77 |
| DenseNet121 | 97 | 97 | 97 | 97 |
| EfficientNetB0 | 98 | 98 | 98 | 98 |
| GoogLeNet | 91 | 93 | 92 | 92 |
| Inception V3 | 96 | 97 | 96 | 96 |
| ResNet50 | 95 | 96 | 96 | 96 |
| VGG16 | 85 | 85 | 86 | 85 |
| VGG19 | 85 | 85 | 85 | 85 |
| ViT Transformer | 70 | 72 | 72 | 70 |
| Xception | 96 | 97 | 96 | 96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nhlapho, W.; Atemkeng, M.; Brima, Y.; Ndogmo, J.-C. Bridging the Gap: Exploring Interpretability in Deep Learning Models for Brain Tumor Detection and Diagnosis from MRI Images. Information 2024, 15, 182. https://doi.org/10.3390/info15040182
Nhlapho W, Atemkeng M, Brima Y, Ndogmo J-C. Bridging the Gap: Exploring Interpretability in Deep Learning Models for Brain Tumor Detection and Diagnosis from MRI Images. Information. 2024; 15(4):182. https://doi.org/10.3390/info15040182
Chicago/Turabian StyleNhlapho, Wandile, Marcellin Atemkeng, Yusuf Brima, and Jean-Claude Ndogmo. 2024. "Bridging the Gap: Exploring Interpretability in Deep Learning Models for Brain Tumor Detection and Diagnosis from MRI Images" Information 15, no. 4: 182. https://doi.org/10.3390/info15040182
APA StyleNhlapho, W., Atemkeng, M., Brima, Y., & Ndogmo, J.-C. (2024). Bridging the Gap: Exploring Interpretability in Deep Learning Models for Brain Tumor Detection and Diagnosis from MRI Images. Information, 15(4), 182. https://doi.org/10.3390/info15040182






