A Method for Single-Phase Ground Fault Section Location in Distribution Networks Based on Improved Empirical Wavelet Transform and Graph Isomorphic Networks
Abstract
1. Introduction
2. Improved Empirical Wavelet Transformation and Signal Reconstruction
2.1. Empirical Wavelet Transformation
2.2. Weighted Permutation Entropy
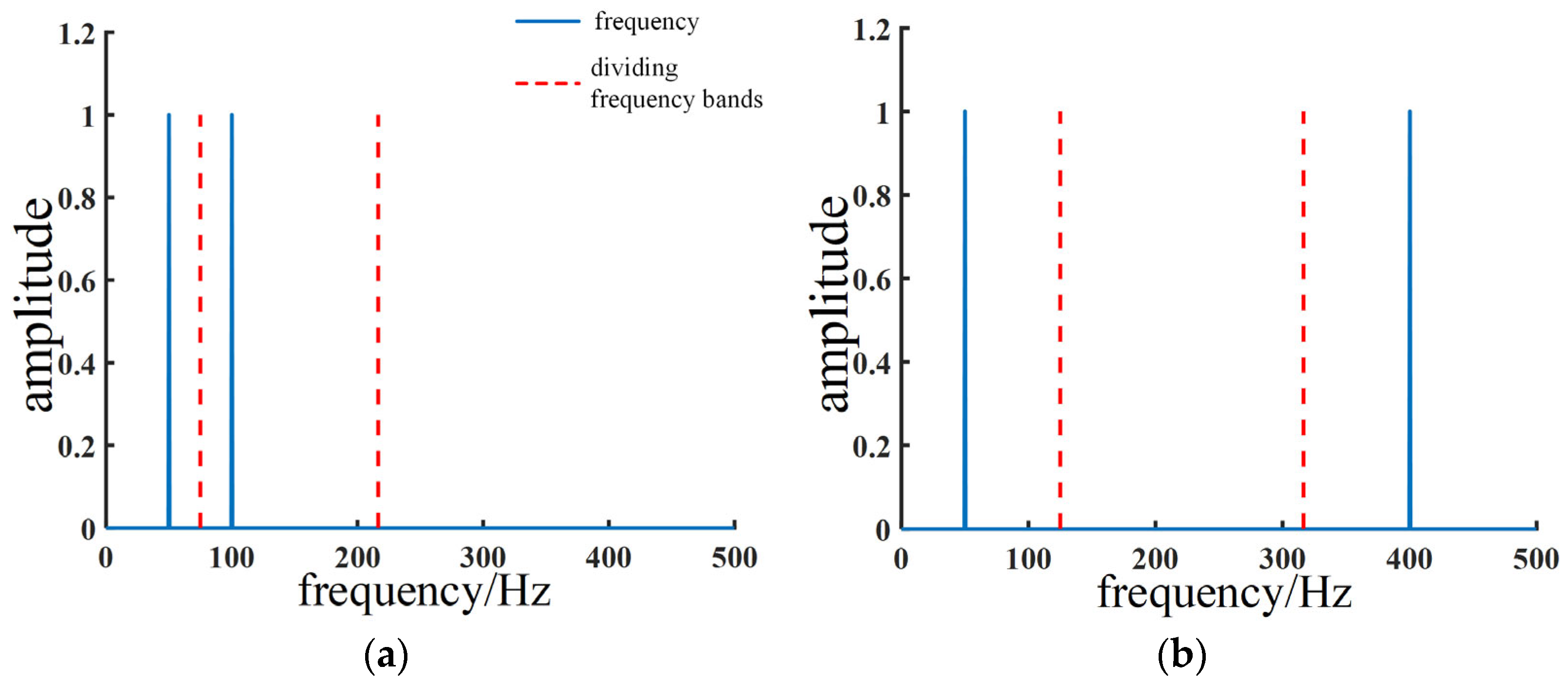
2.3. Improved Empirical Wavelet Transformation
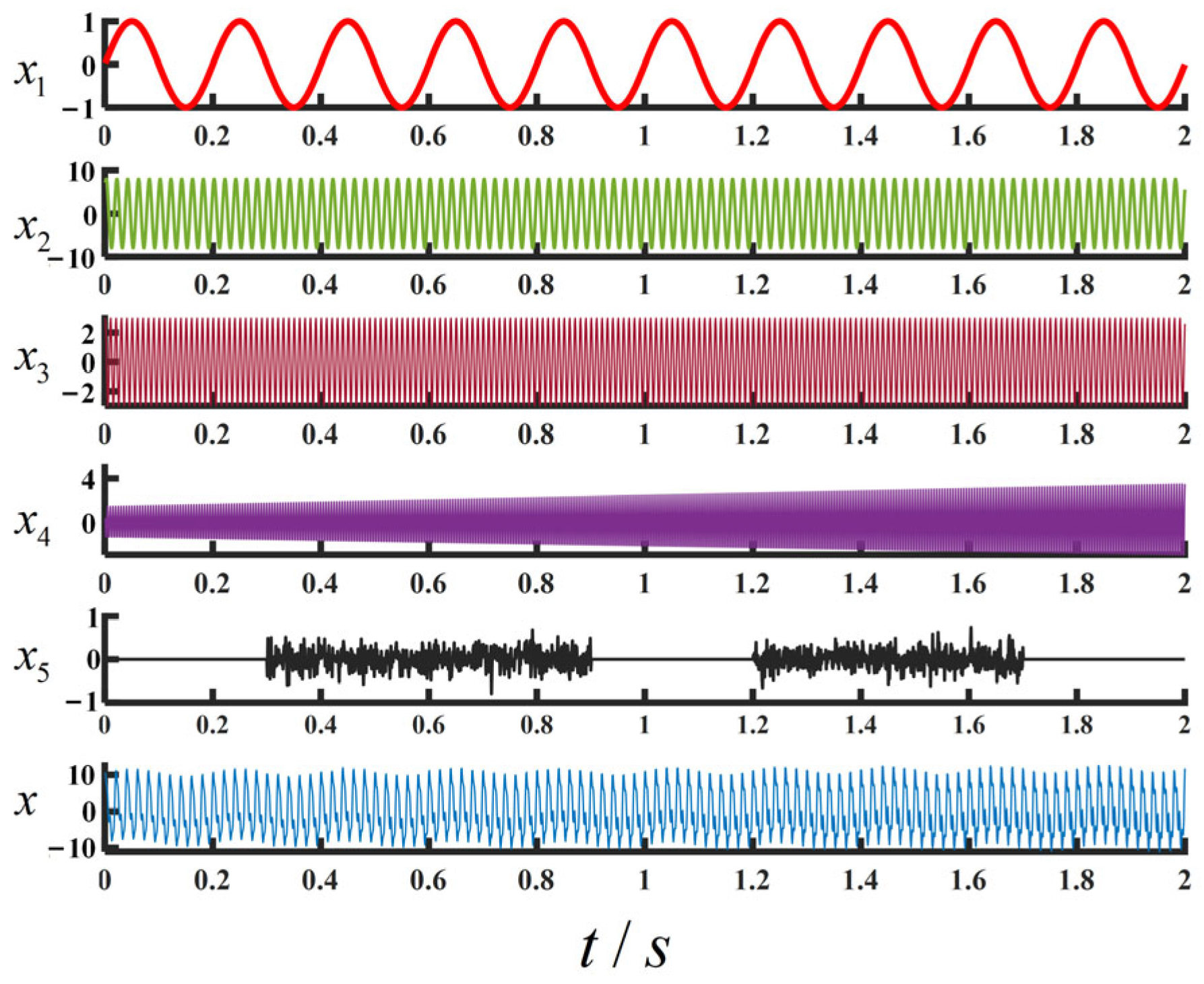
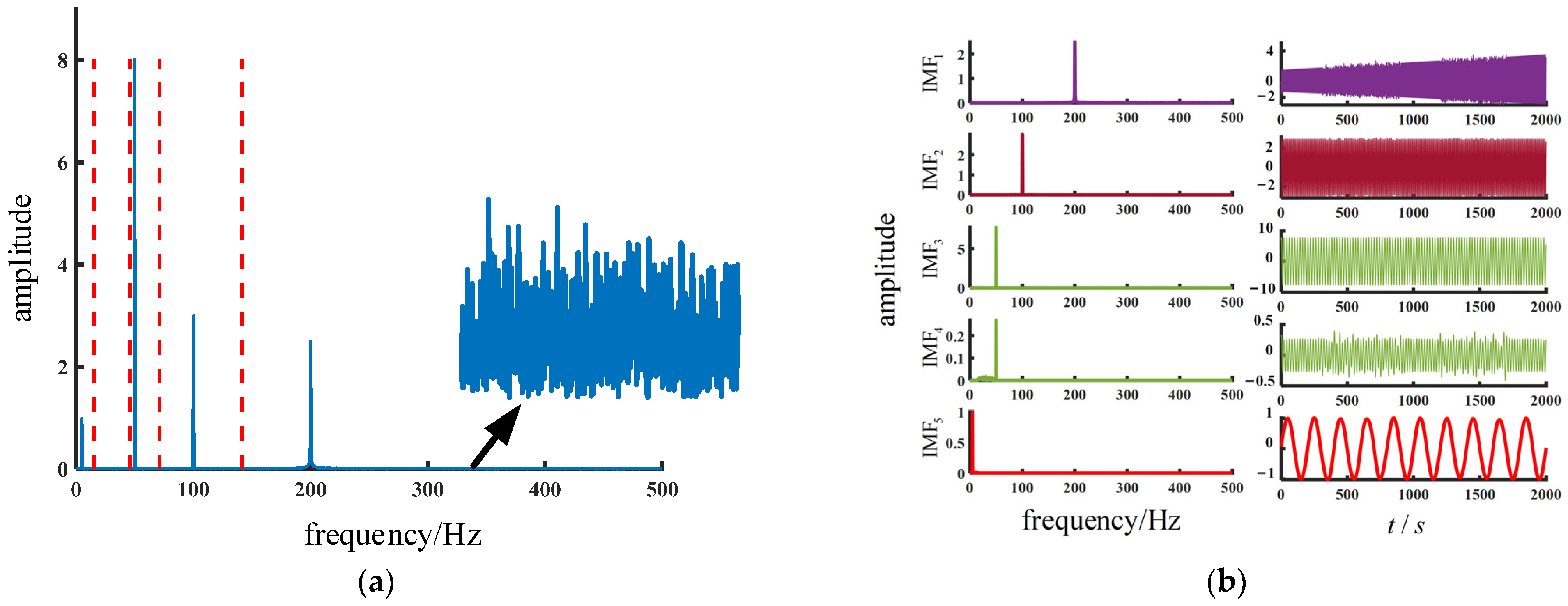
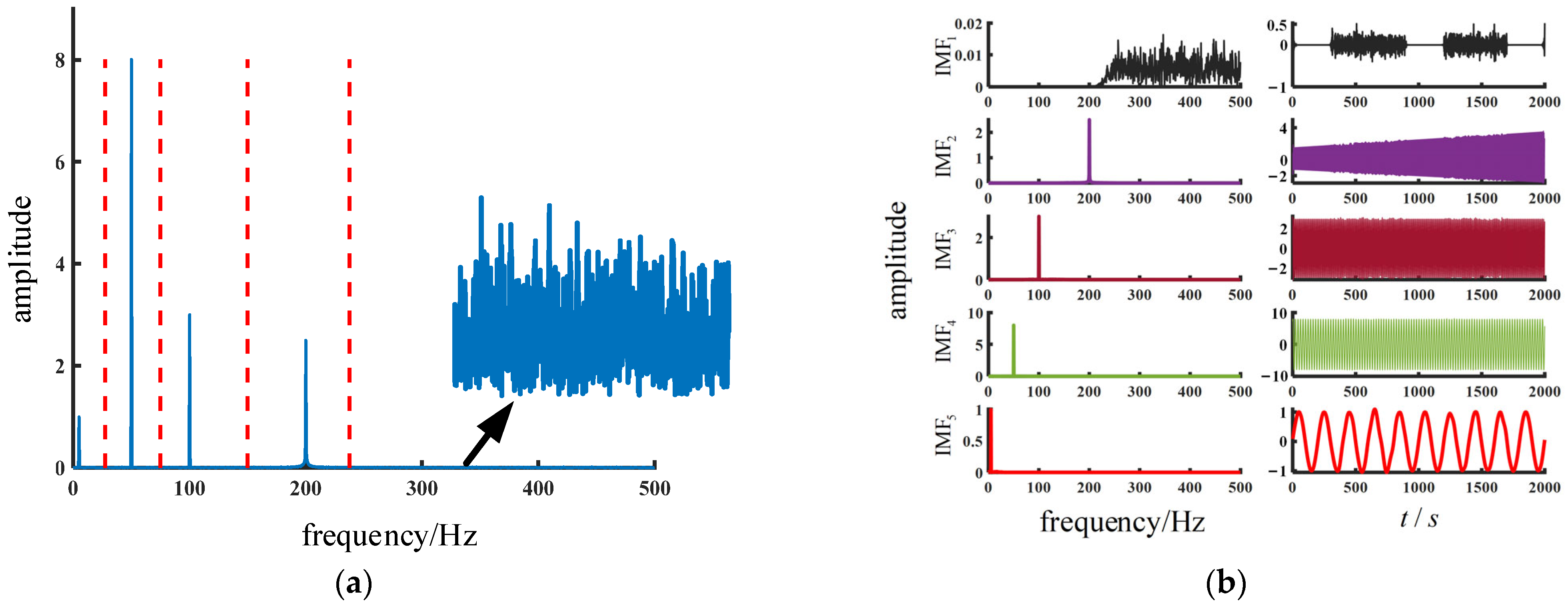
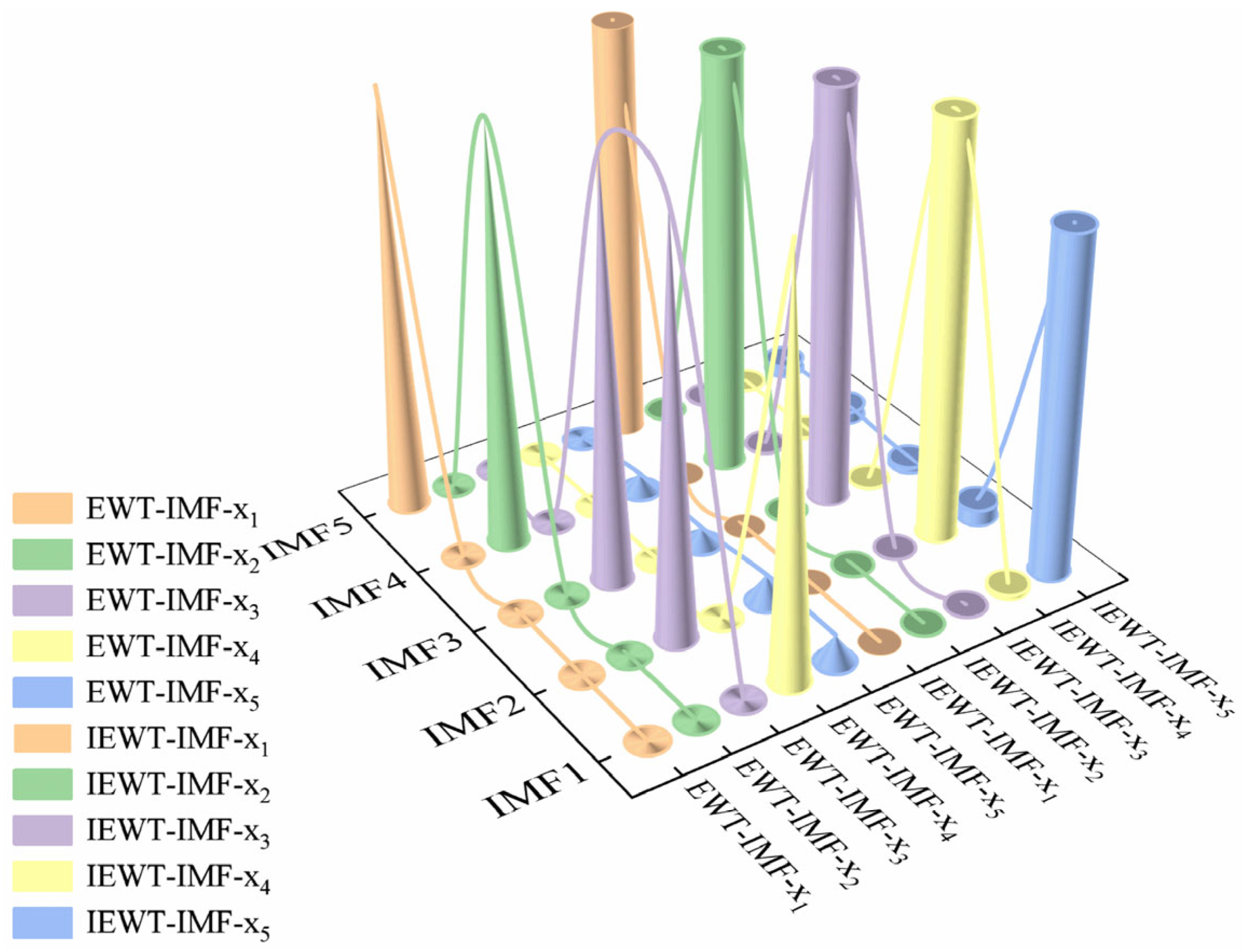
2.4. Decomposing and Reconstructing Simulated Signals Using EWT and Improved EWT
3. Graphical Neural Networks
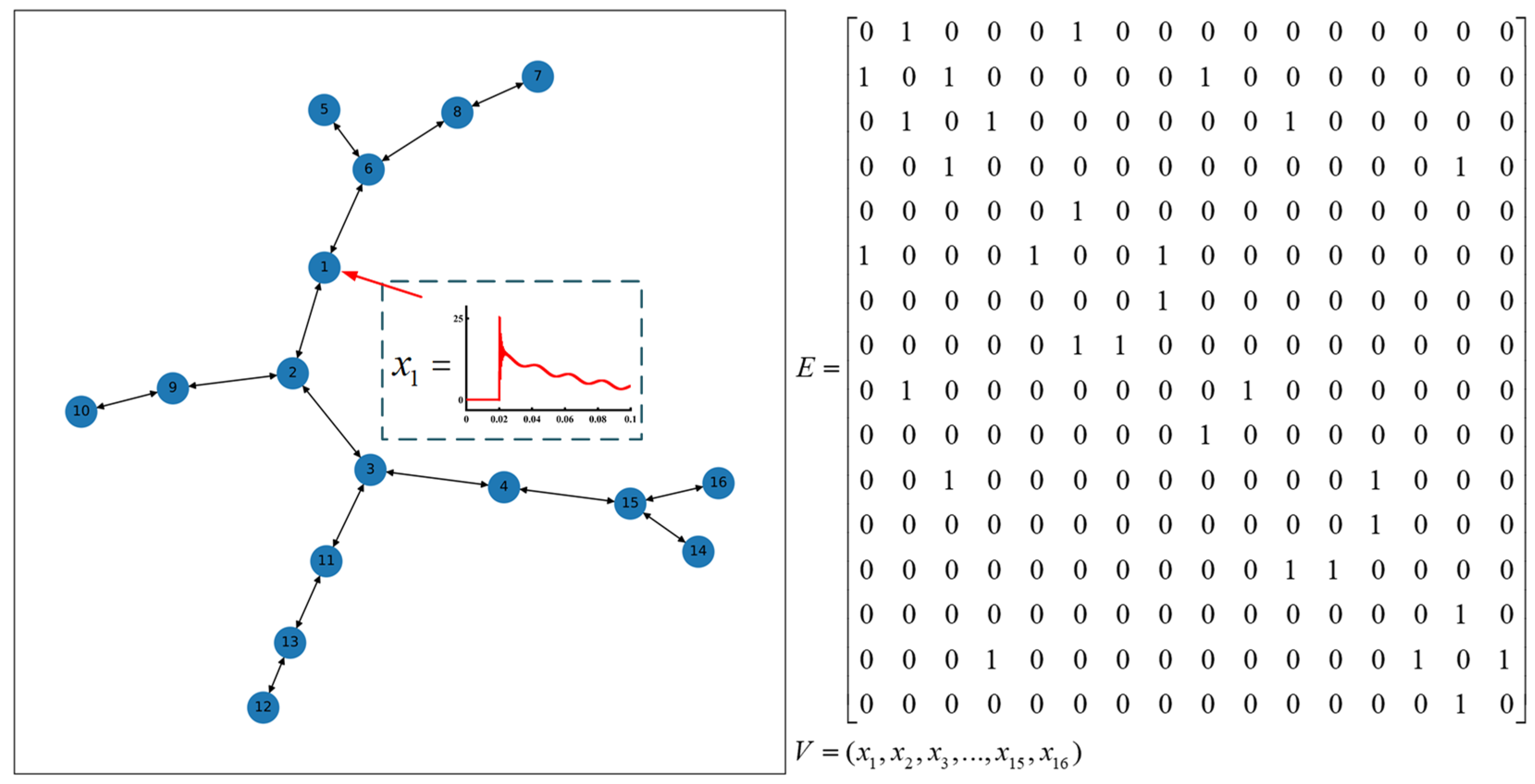
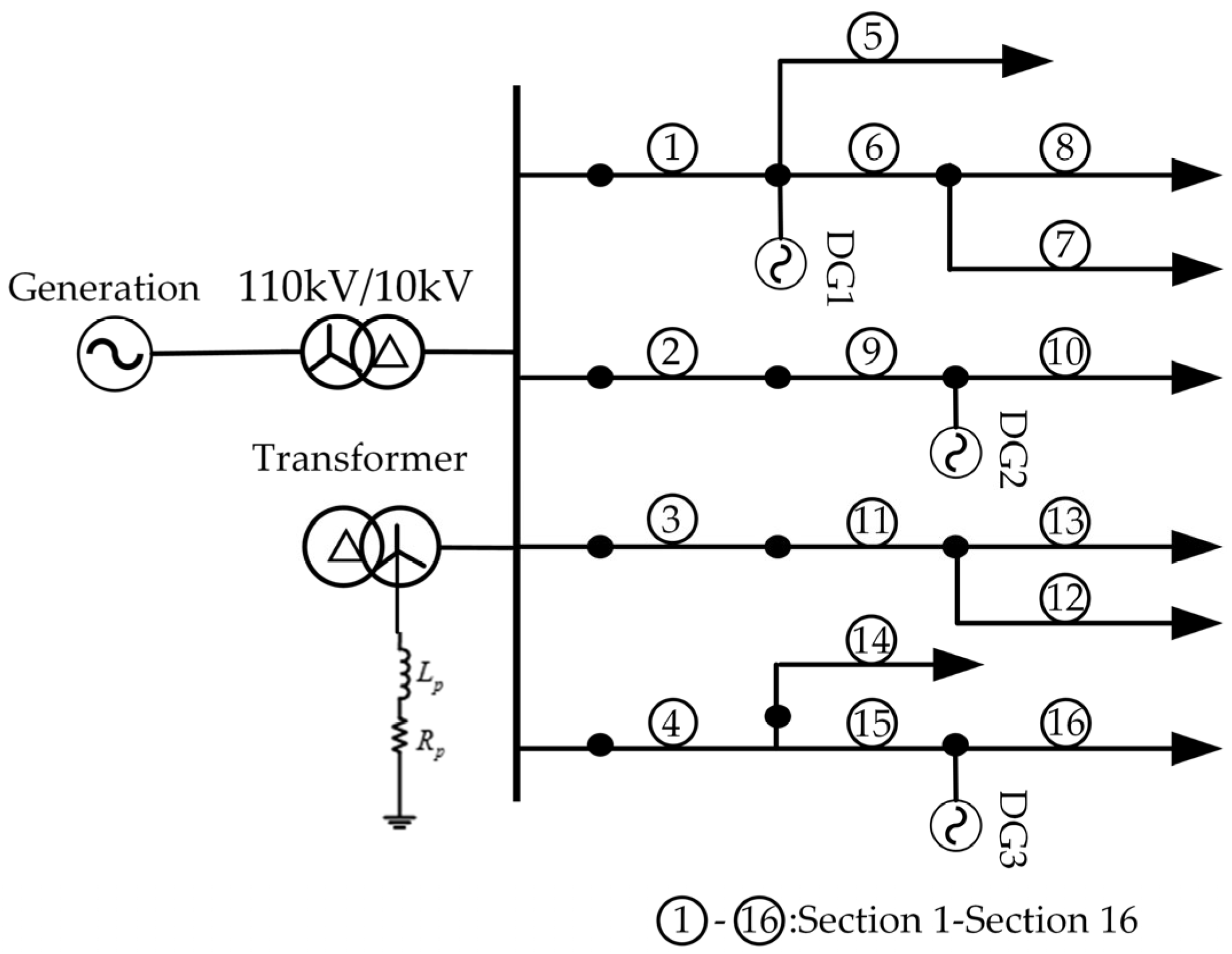
3.1. Diagrammatic Composition of the Distribution Network
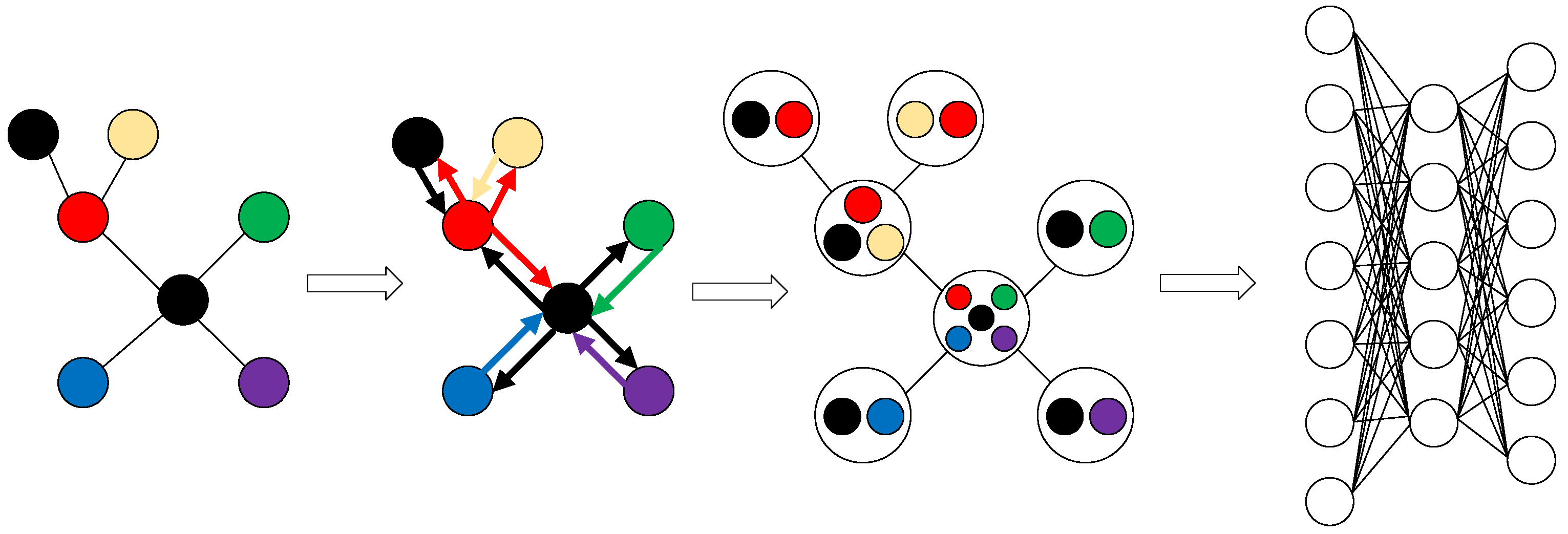
3.2. Graph Neural Network (GNN)
3.3. Graphical Isomorphic Network (GIN)
4. Experimental Verification and Analysis
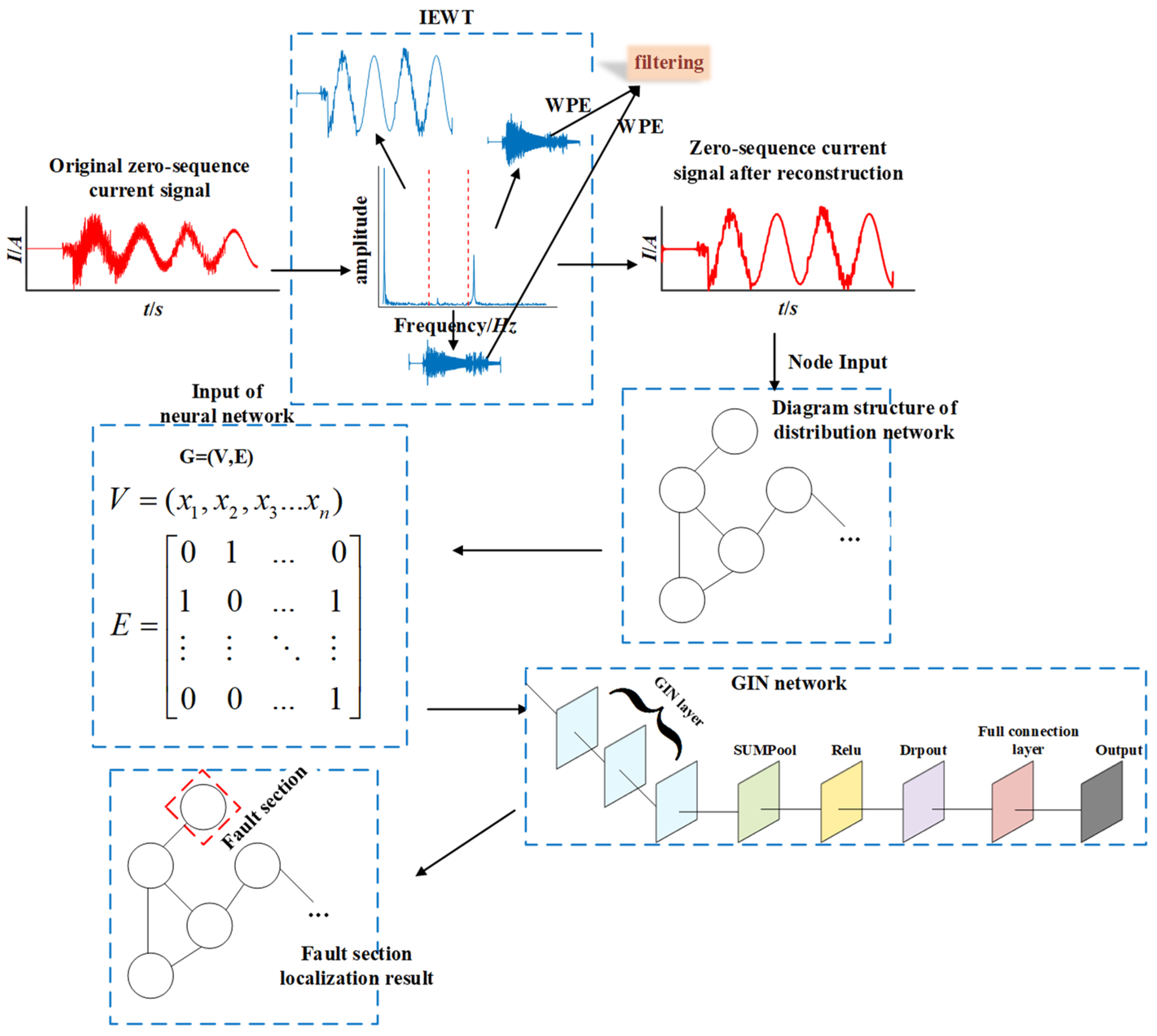
4.1. Fault Section Location Procedure
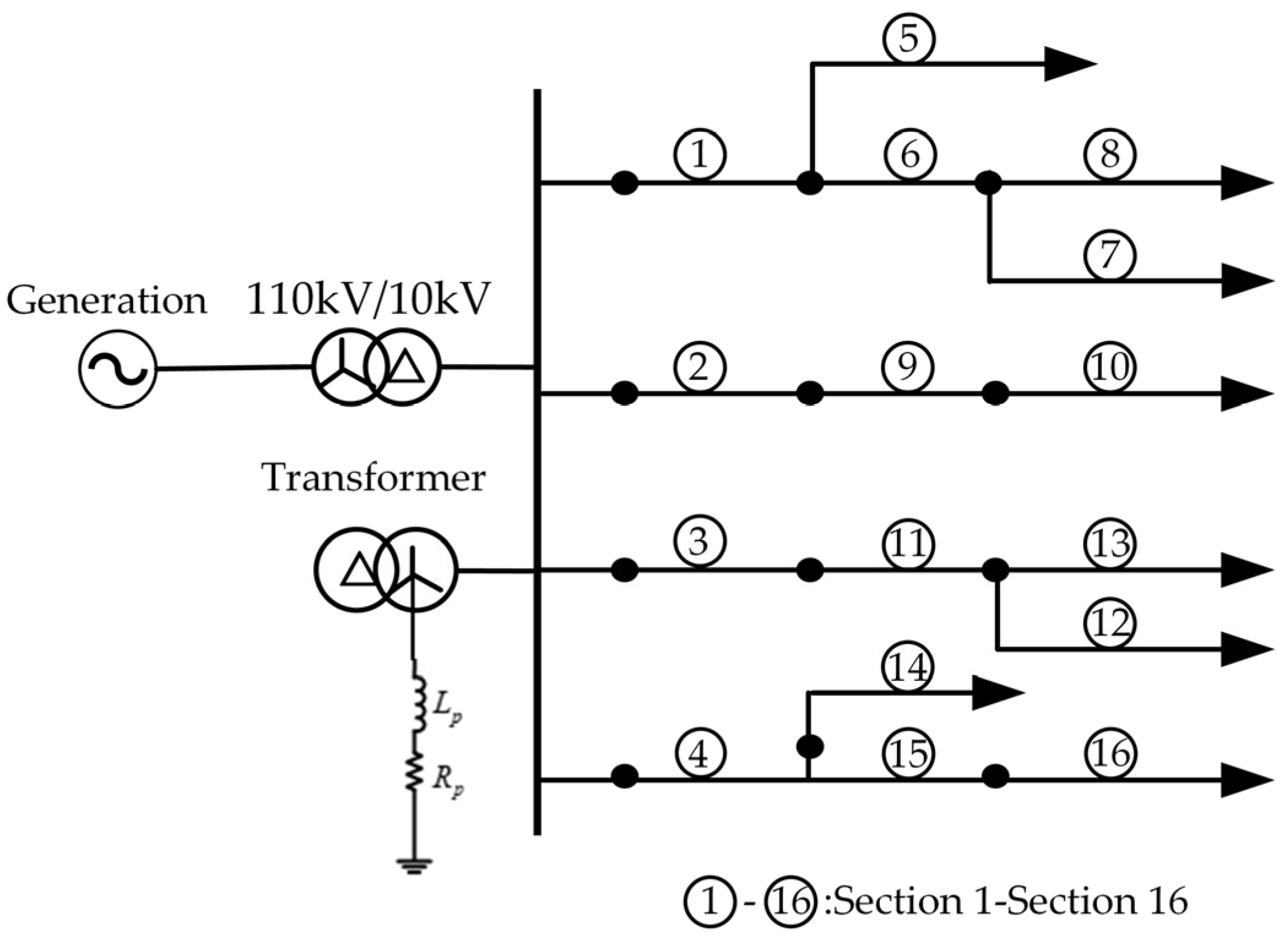
4.2. Simulation Environment
4.3. Data Acquisition and Neural Network Input
4.4. Verification and Analysis of Fault Section Localization Results
4.5. Comparative Verification
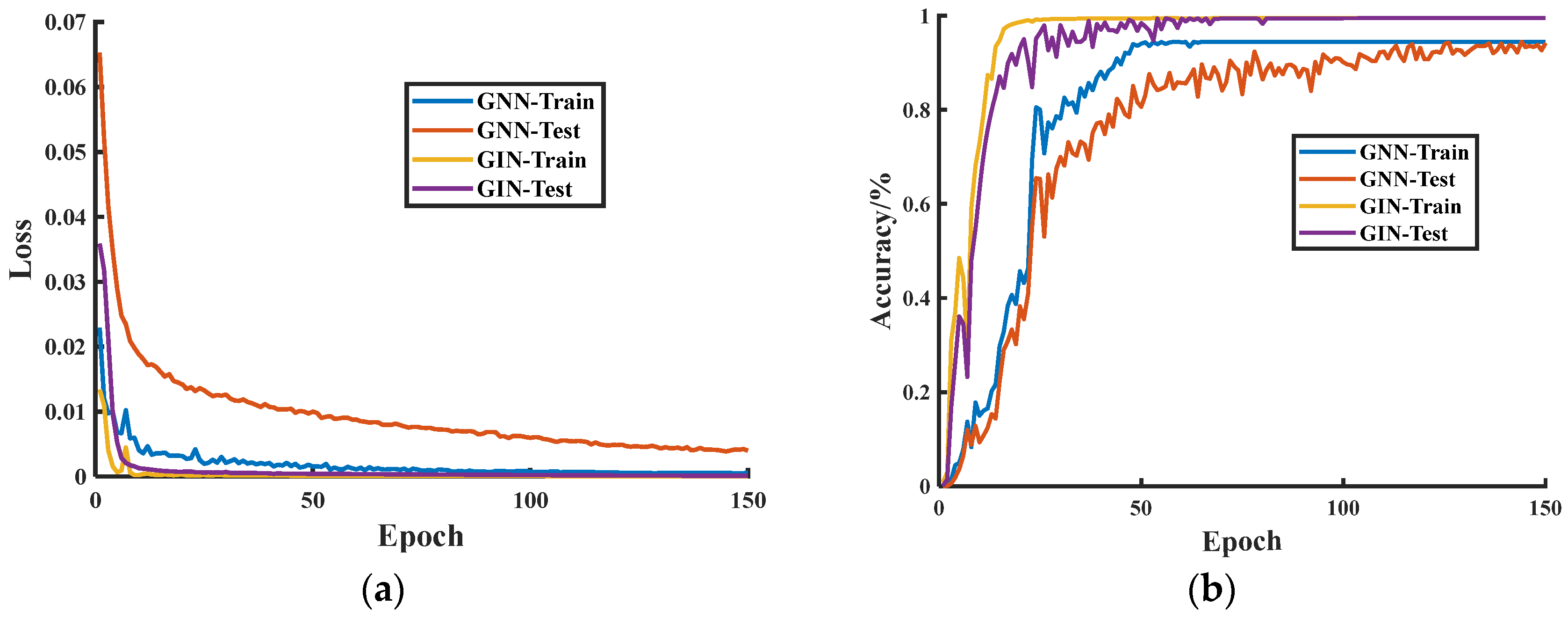
4.5.1. Comparative Validation of Different Neural Networks
4.5.2. Noise Immunity Verification
4.5.3. High-Resistance Grounding Comparative Validation
4.5.4. Validation of Distribution Networks with Distributed Energy Resources
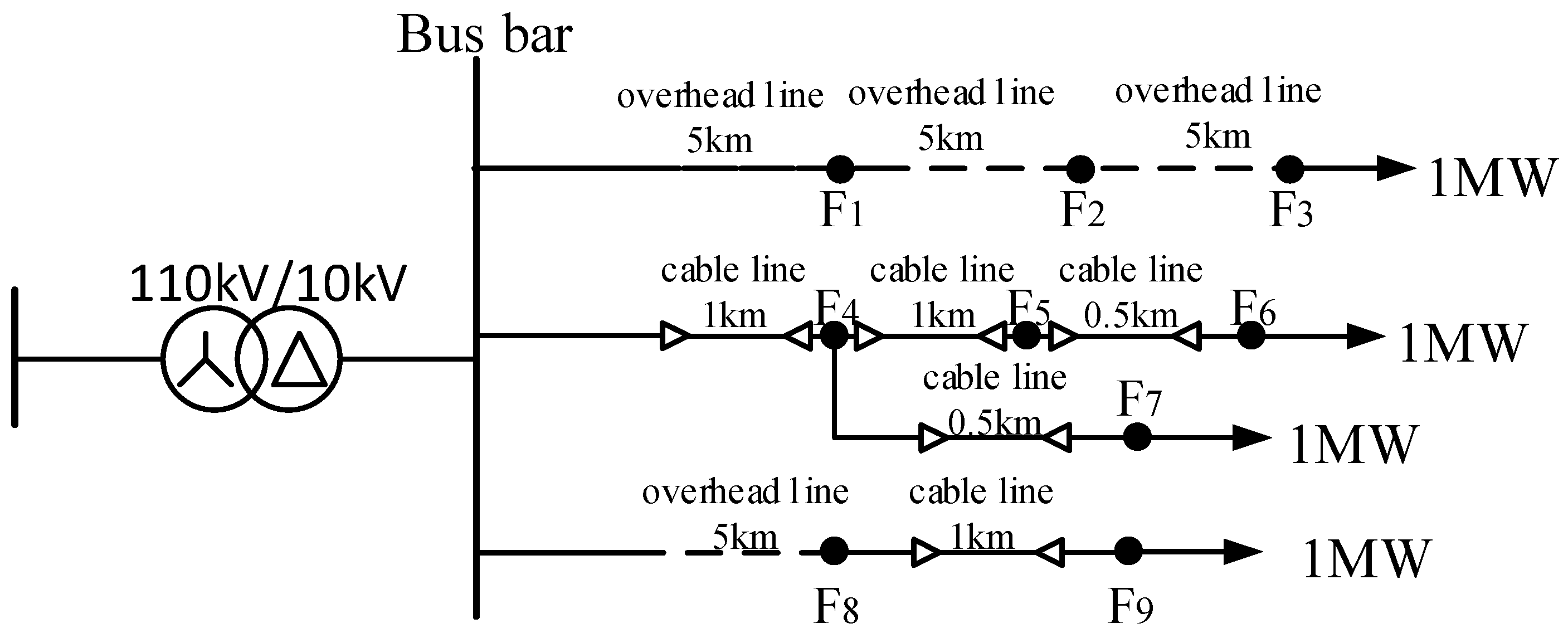
4.5.5. Dynamic Mold Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| EWT | empirical wavelet transform |
| IEWT | improved empirical wavelet transform |
| IMFs | intrinsic mode functions |
| PE | permutation entropy |
| WPE | weighted permutation entropy |
| GNN | graph neural network |
| GIN | graphical isomorphic network |
References
- Liang, J.; Jing, T.; Niu, H.; Wang, J. Two-terminal Fault Location Method of Distribution Network Based on Adaptive Convolution Neural Network. IEEE Access 2020, 8, 54035–54043. [Google Scholar] [CrossRef]
- Cheng, H.-J.; Meng, H.; Jiang, P.-J. Research on Fault Line Selection in Small-current Neutral Grounding Power System. In Proceedings of the 2013 IEEE International Conference on Vehicular Electronics and Safety, Dongguan, China, 28–30 July 2013; pp. 206–209. [Google Scholar] [CrossRef]
- Mirshekali, H.; Dashti, R.; Handrup, K.; Shaker, H.R. Real Fault Location in a Distribution Network Using Smart Feeder Meter Data. Energies 2021, 14, 3242. [Google Scholar] [CrossRef]
- Larik, N.A.; Li, M.S.; Wu, Q.H. Enhanced Fault Detection and Localization Strategy for High-Speed Protection in Medium-Voltage DC Distribution Networks Using Extended Kalman Filtering Algorithm. IEEE Access 2024, 12, 30329–30344. [Google Scholar] [CrossRef]
- Hamza, W.; Ali, B.S.B.; Abdul, W.; Hani, A.; Khalid, M.K. Fault Identification, Classification, and Localization in Microgrids Using Superimposed Components and Wigner Distribution Function. Front. Energy Res. 2024, 12, 1379475. [Google Scholar] [CrossRef]
- Kumar, A.; Bhalja, B.R.; Kumbhar, G.B. Novel Technique for Location Identification and Estimation of Extent of Turn-to-Turn Fault in Transformer Winding. IEEE T. Ind. Electron. 2023, 70, 7382–7392. [Google Scholar] [CrossRef]
- Xu, S.; Ouyang, J.; Chen, J.; Xiong, X. A Section Location Method of Single-Phase Short-Circuit Faults for Distribution Networks Containing Distributed Generators Based on Fusion Fault Confidence of Short-Circuit Current Vectors. Electronics 2024, 13, 1741. [Google Scholar] [CrossRef]
- Jiang, Z.; Zeng, X.; Liu, F.; Yu, K.; Bi, L.; Wang, Y. Active Fault-Locating Scheme for Hybrid Distribution Line Based on Mutation of Aerial-Mode Injected Pulse. Energies 2024, 17, 2248. [Google Scholar] [CrossRef]
- Sun, G.; Ma, W.; Wei, S.; Cai, D.; Wang, W.; Xu, C.; Zhang, K.; Wang, Y. A Fault Location Method for Medium Voltage Distribution Network Based on Ground Fault Transfer Device. Electronics 2023, 12, 4790. [Google Scholar] [CrossRef]
- Rezapour, H.; Jamali, S.; Bahmanyar, A. Review on Artificial Intelligence-Based Fault Location Methods in Power Distribution Networks. Energies 2023, 16, 4636. [Google Scholar] [CrossRef]
- Lin, W.-C.; Huang, W.-T.; Yao, K.-C.; Chen, H.-T.; Ma, C.-C. Fault Location and Restoration of Microgrids via Particle Swarm Optimization. Appl. Sci. 2021, 11, 7036. [Google Scholar] [CrossRef]
- Shafiullah, M.; Abido, M.A.; Abdel-Fattah, T. Distribution Grids Fault Location Employing ST based Optimized Machine Learning Approach. Energies 2018, 11, 2328. [Google Scholar] [CrossRef]
- Bukhari, S.B.A.; Kim, C.-H.; Mehmood, K.K.; Haider, R.; Saeed Uz Zaman, M. Convolutional Neural Network Based Intelligent Protection Strategy for Microgrids. IET Gener. Transm. Distrib. 2020, 14, 1177–1185. [Google Scholar] [CrossRef]
- Gao, J.; Guo, M.; Lin, S.; Chen, D. Advancing High Impedance Fault Localization Via Adaptive Transient Process Calibration and Multiscale Correlation Analysis in Active Distribution Networks. Measurement 2024, 229, 114431. [Google Scholar] [CrossRef]
- Kim, M.-S.; An, J.-G.; Oh, Y.-S.; Lim, S.-I.; Kwak, D.-H.; Song, J.-U. A Method for Fault Section Identification of Distribution Networks Based on Validation of Fault Indicators Using Artificial Neural Network. Energies 2023, 16, 5397. [Google Scholar] [CrossRef]
- Mirshekali, H.; Dashti, R.; Keshavarz, A.; Shaker, H.R. Machine Learning-Based Fault Location for Smart Distribution Networks Equipped with Micro-PMU. Sensors 2022, 22, 945. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; He, J.; Zhang, Y.; Zhang, D. Distribution Network Fault Location Method Based on Graph Attention Network. Power Grid Technol. 2021, 45, 2113–2121. [Google Scholar] [CrossRef]
- Gilles, J. Empirical Wavelet Transform. IEEE Trans. Signal Proces. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Feng, X.; Chen, Z.; Li, J.; Cai, J.; Liang, J. Electromagnetic Time Kurtosis for Time-Reversal Source Reconstruction with Band-Limited Signals. In Proceedings of the 2022 IEEE/MTT-S International Microwave Symposium—IMS 2022, Denver, CO, USA, 19–24 June 2022; pp. 12–15. [Google Scholar]
- Wang, X.; Gao, J.; Song, G.; Cheng, Q.; Wei, X.; Wei, Y. Faulty Line Selection Method for Distribution Network Based on Variable Scale Bistable System. J. Sens. 2016, 2016, 7436841. [Google Scholar] [CrossRef]
- Wang, Z.; Qiao, P.; Shi, B. Nonpenetrating Damage Identification Using Hybrid Lamb Wave Modes from Hilbert-Huang Spectrum in Thin-walled Structures. Shock Vib. 2017, 2017, 5164594. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, T.; Meng, R.; Liu, Q. Generalized Composite Multiscale Permutation Entropy and PCA Based Fault Diagnosis of Rolling Bearings. J. Vib. Shock 2018, 37, 61–66. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]






| Signal | Permutation Entropy | Weighted Permutation Entropy |
|---|---|---|
| White noise | 0.9712 | 0.9590 |
| Gaussian white noise | 0.9682 | 0.9622 |
| High-frequency sinusoidal signal | 0.4338 | 0.3828 |
| Fundamental frequency sinusoidal signal | 0.1102 | 0.1054 |
| AM signal | 0.3926 | 0.2458 |
| FM signal | 0.2452 | 0.1722 |
| AM/FM signa | 0.4311 | 0.2992 |
| Intermittent signal | 0.5270 | 0.9229 |
| Circuit Type | Resistance (Ω·km−1) | Inductance (mH·km−1) | Grounding Capacitance (μF·km−1) | |||
|---|---|---|---|---|---|---|
| Positive Phase | Zero Phase | Positive Phase | Zero Phase | Positive Phase | Zero Phase | |
| Overhead line | 0.178 | 0.25 | 1.21 | 5.54 | 0.015 | 0.012 |
| Cable line | 0.27 | 2.7 | 0.255 | 1.02 | 0.339 | 0.28 |
| Fault Section | Number of Samples | Accuracy/% | ||
|---|---|---|---|---|
| Method 1 | Method 2 | Method in This Paper | ||
| 1 | 120 | 90.14 | 94.18 | 99.89 |
| 2 | 120 | 91.72 | 94.89 | 99.96 |
| 3 | 120 | 90.99 | 94.70 | 99.94 |
| 4 | 120 | 90.15 | 95.19 | 99.87 |
| 5 | 120 | 90.46 | 95.89 | 99.95 |
| 6 | 120 | 90.15 | 94.89 | 99.94 |
| 7 | 120 | 90.46 | 94.89 | 99.89 |
| 8 | 120 | 90.37 | 94.60 | 99.98 |
| 9 | 120 | 90.87 | 95.30 | 99.90 |
| 10 | 120 | 91.15 | 95.56 | 99.95 |
| 11 | 120 | 90.53 | 95.89 | 99.96 |
| 12 | 120 | 90.10 | 95.18 | 99.92 |
| 13 | 120 | 91.97 | 95.41 | 99.86 |
| 14 | 120 | 91.34 | 95.56 | 99.95 |
| 15 | 120 | 91.22 | 95.28 | 99.97 |
| 16 | 120 | 91.90 | 95.65 | 99.88 |
| Signal-to-Noise Ratio/dB | Fault Section | Fault Type | Fault Location Result | ||
|---|---|---|---|---|---|
| Paper [10] | Paper [13] | This Paper | |||
| 35 | 3 | AG | 11 | 3 | 3 |
| 7 | BG | 7 | 7 | 7 | |
| 10 | CG | 10 | 10 | 10 | |
| 11 | AG | 12 | 11 | 11 | |
| 14 | BG | 14 | 14 | 14 | |
| 16 | CG | 16 | 16 | 16 | |
| 30 | 1 | AG | 1 | 1 | 1 |
| 6 | BG | 1 | 1 | 6 | |
| 7 | CG | 7 | 7 | 7 | |
| 9 | AG | 2 | 9 | 9 | |
| 11 | BG | 11 | 11 | 11 | |
| 15 | CG | 4 | 14 | 15 | |
| 25 | 2 | AG | 3 | 2 | 2 |
| 5 | BG | 5 | 5 | 5 | |
| 8 | CG | 1 | 7 | 8 | |
| 11 | AG | 11 | 11 | 11 | |
| 13 | BG | 3 | 13 | 13 | |
| 15 | CG | 15 | 15 | 15 | |
| 20 | 2 | AG | 9 | 1 | 2 |
| 5 | BG | 1 | 1 | 5 | |
| 7 | CG | 8 | 7 | 7 | |
| 12 | AG | 12 | 12 | 12 | |
| 13 | BG | 13 | 13 | 13 | |
| 16 | CG | 14 | 15 | 16 | |
| Grounding Resistance/Ω | Fault Section | Fault Type | Fault Location Result | ||
|---|---|---|---|---|---|
| Reference [1] | Reference [2] | This Paper | |||
| 1000 | 6 | AG | 5 | 6 | 6 |
| 7 | BG | 7 | 7 | 7 | |
| 10 | CG | 9 | 10 | 10 | |
| 13 | AG | 11 | 11 | 13 | |
| 14 | BG | 16 | 4 | 14 | |
| 15 | CG | 15 | 15 | 15 | |
| 1500 | 1 | AG | 2 | 1 | 1 |
| 5 | BG | 1 | 1 | 5 | |
| 6 | CG | 6 | 5 | 6 | |
| 7 | AG | 7 | 7 | 7 | |
| 13 | BG | 3 | 11 | 13 | |
| 16 | CG | 4 | 14 | 16 | |
| Fault Section | Number of Samples | Accuracy/% | ||
|---|---|---|---|---|
| Reference [1] | Reference [2] | This Paper | ||
| 1 | 120 | 90.42 | 93.18 | 99.89 |
| 2 | 120 | 88.74 | 92.77 | 99.84 |
| 3 | 120 | 88.73 | 93.12 | 99.78 |
| 4 | 120 | 90.95 | 93.56 | 99.83 |
| 5 | 120 | 89.15 | 93.59 | 99.8 |
| 6 | 120 | 88.66 | 93.76 | 99.8 |
| 7 | 120 | 88.66 | 92.55 | 99.87 |
| 8 | 120 | 90.67 | 92.47 | 99.87 |
| 9 | 120 | 89.48 | 93.13 | 99.8 |
| 10 | 120 | 89.26 | 93.09 | 99.87 |
| 11 | 120 | 89.86 | 93.34 | 99.81 |
| 12 | 120 | 90.26 | 93.36 | 99.82 |
| 13 | 120 | 89.09 | 92.05 | 99.82 |
| 14 | 120 | 89.09 | 93.65 | 99.79 |
| 15 | 120 | 88.30 | 92.53 | 99.87 |
| 16 | 120 | 88.06 | 93.32 | 99.87 |
| Fault Type | Fault Point | Transition Resistance | Fault Close Angle | Fault Location Result |
|---|---|---|---|---|
| AG | F1 | 0 W | 0° | F1 |
| BG | F2 | 500 W | 30° | F2 |
| CG | F3 | 1000 W | 60° | F3 |
| AG | F4 | 400 W | 60° | F4 |
| BG | F5 | 800 W | 120° | F5 |
| CG | F6 | 200 W | 30° | F6 |
| BG | F7 | 500 W | 150° | F7 |
| AG | F8 | 0 W | 0° | F8 |
| CG | F9 | 400 W | 60° | F9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Feng, L.; Hou, S.; Ren, G.; Wang, W. A Method for Single-Phase Ground Fault Section Location in Distribution Networks Based on Improved Empirical Wavelet Transform and Graph Isomorphic Networks. Information 2024, 15, 650. https://doi.org/10.3390/info15100650
Wang C, Feng L, Hou S, Ren G, Wang W. A Method for Single-Phase Ground Fault Section Location in Distribution Networks Based on Improved Empirical Wavelet Transform and Graph Isomorphic Networks. Information. 2024; 15(10):650. https://doi.org/10.3390/info15100650
Chicago/Turabian StyleWang, Chen, Lijun Feng, Sizu Hou, Guohui Ren, and Wenyao Wang. 2024. "A Method for Single-Phase Ground Fault Section Location in Distribution Networks Based on Improved Empirical Wavelet Transform and Graph Isomorphic Networks" Information 15, no. 10: 650. https://doi.org/10.3390/info15100650
APA StyleWang, C., Feng, L., Hou, S., Ren, G., & Wang, W. (2024). A Method for Single-Phase Ground Fault Section Location in Distribution Networks Based on Improved Empirical Wavelet Transform and Graph Isomorphic Networks. Information, 15(10), 650. https://doi.org/10.3390/info15100650





