Abstract
In modern industrial applications, production quality, system performance, process reliability, and safety have received considerable attention. This article proposes a dynamic event-triggered attack estimator for Markovian jump stochastic systems susceptible to actuator deception attacks. Utilizing the developed estimator, the presented attack-tolerant control strategy can tolerate the effects of such attacks and ensure the mean-square convergence of the overall closed-loop system. A dynamic event-triggered mechanism is implemented on the sensor side to optimize communication efficiency. To address the potential threat of deception attacks, a plug-and-play (PnP) secure monitoring and control architecture is introduced. This architecture facilitates the seamless integration of the designed attack-tolerant controller with the nominal feedback controller, thereby enhancing system security without requiring significant modifications to the existing control structure. The practicality and effectiveness of the proposed approaches are demonstrated through experimental results on a switched boost converter circuit.
1. Introduction
As Industry 4.0 progresses, wireless communication networks are increasingly supplanting wired transmissions in modern industrial systems, driven by their cost-effectiveness and superior remote transmission capabilities [1]. However, this shift towards networked communication renders these systems susceptible to a variety of cyber threats, including deception attacks, denial-of-service (DoS) attacks, and replay attacks [2,3,4]. In the field of complex system modeling, Markovian jump systems have emerged as a dominant paradigm over the past few decades. These systems are distinguished by their ability to capture abrupt structural and parametric changes, governed by underlying Markov chains [5]. Markovian jump systems have proven particularly effective in representing a diverse array of real-world applications, such as electrical power systems operating under fluctuating conditions, economic systems responding to policy shifts, and spacecraft systems influenced by variable environmental factors [6,7,8].
Deception attacks, also known as false data injection attacks, are widely recognized as the most destructive form of cyber threats [9]. These kinds of attacks compromise the integrity of control and measurement signals by injecting false data into the communication channels between sensors and actuators, which can rapidly unstabilize closed-loop systems. The detection and tolerance of such attacks are crucial in minimizing damage to critical infrastructure. Recent research has yielded significant advances in the field of deception attack detection and accommodation through various approaches. A comprehensive data-driven framework for secure data transmission and trustworthiness assessment against deception attack was proposed in [10], with subsequent work in [11] expanding this approach to detect data integrity issues, including both DoS and replay attacks. Parallel to these data-driven methods, the importance of model-based techniques for attack estimation and accommodation has gained recognition [9,12,13,14]. For instance, Ref. [12] introduced a descriptor switched sliding mode observer against deception attacks in continuous-time cyber-physical systems, focusing on attack mode identification and system state reconstruction. Similarly, Ref. [13] developed a secure attack estimator for discrete-time stochastic systems subject to random deception attacks, where an event-triggered transmission mechanism is employed to optimize the trade-off between attack estimation accuracy and energy efficiency.
Although the aforementioned studies have yielded promising results in addressing various attack scenarios, they exhibit limitations when confronted with the specific challenges posed by actuator deception attacks in Markovian jump systems. The complexities inherent in estimating attacks and implementing attack-tolerant control for this kind of system remain inadequately addressed. This gap in current research serves as a primary motivation for our present study, which aims to develop more comprehensive and robust solutions for Markovian jump systems against a variety of attacks.
It is important to highlight that in the domain of wireless communication technology, sensors are frequently powered by batteries with finite energy reserves [15,16]. In order to optimize the conservation of both battery energy and communication resources, the transmission of measurement signals to remote estimator is necessarily constrained. As a result, the transmission of signals deviates from continuous or periodic patterns. When consecutive data packets exhibit minimal variation, these signals can be categorized as redundant sampling data. In such instances, the updating or transmission of these signals becomes unnecessary, further optimizing resource utilization. This approach not only extends the operational lifespan of battery-powered sensors, but also enhances the overall efficiency of the wireless communication system in industrial applications.
The event-triggered transmission scheme has gained prominence due to its capacity to reduce transmission frequency by transmitting data only when a specific event condition is met. However, traditional approaches often employ static threshold parameters in event conditions, which cannot adequately reflect the dynamic nature of the system, leading to potential conservatism. To address this limitation, Ref. [17] first introduced a dynamic event-triggered transmission scheme that incorporates an internal dynamic variable. This innovative approach formulates the dynamic equation of the internal variable using a first-order filter, effectively making the internal variable a filtered representation of the event conditions found in traditional static event-triggered schemes. This design allows for dynamic threshold adjustment based on real-time system information.
In recent years, there has been growing interest among researchers in developing event conditions with adaptive threshold parameters for control and estimation in response to various system dynamics [18,19,20,21]. For example, a state estimator was proposed in [19] for discrete-time singularly perturbed systems with distributed time delays and dynamic event-triggered communication, ensuring exponentially mean-square ultimate boundedness of the estimation error. A subsequent study in [20] expanded this approach to an controller using a dynamic event-triggered mechanism to regulate data-packet transmissions. Following a similar concept of the dynamic event-triggered mechanism, Ref. [21] formulated a distributed adaptive event-triggered filter for sector-bounded nonlinear systems over a switching network. Nevertheless, to the best of our knowledge, the dynamic event-triggered mechanism has not yet been adequately explored for attack monitoring despite its clear engineering significance. Thus, a second motivation of this paper is to develop an efficient dynamic event-triggered transmission scheme for attack monitoring and reconstruction in Markovian jump systems.
The concept of plug-and-play (PnP) first appeared in the computer field. When a new external module is added to a computer, the system resources can be automatically configured without manually reconfiguring the total setup. PnP technology has been a focus area recently with the advantages of flexibility and reliability [22,23], which has also been extended to a wide range of applications [24,25]. However, many existing PnP methods modify the original control system without considering its structure. In many devices, the original monitoring and control systems are immutable. Therefore, the proposed attack monitoring and attack-tolerant control strategy in this study are implemented by a PnP monitoring and control architecture without changing the original system framework, and it can be designed and plugged into the original system independently.
Based on the preceding discussion, it becomes evident that there is a practical demand for a comprehensive study addressing dynamic event-triggered secure monitoring and attack-tolerant control for Markovian jump systems within a PnP framework, specifically targeting deception attacks of actuators. However, despite its clear relevance to engineering practice, this secure monitoring and control problem presents considerable theoretical challenges, primarily due to the three key factors.
- (1)
- Markovian jump systems pose significant challenges for attack monitoring and control due to their stochastic nature and abrupt structural changes. The primary challenge can be divided into two parts: first, designing an event-triggered estimator capable of simultaneously reconstructing system states and estimating attack signals; and second, developing an attack-tolerant controller to ensure the stability of Markovian jump systems across different operational modes, even in the presence of deception attacks.
- (2)
- Designing a dynamic event-triggered transmission mechanism with the corresponding attack estimator involves optimizing resource utilization by transmitting data only when necessary, while ensuring accurate attack estimation. A significant challenge arises from the inherent nature of event-triggered transmission, which can directly impact the real-time capabilities of attack monitoring. Unlike time-driven data transmission, event-triggered schemes may introduce delays or missed detections, potentially compromising the ability of the attack detector to respond promptly to attacks.
- (3)
- The third challenge focuses on constructing a PnP monitoring and control framework that can be integrated seamlessly into existing Markovian jump systems without modifying their original control structure. This involves designing PnP modules for attack detection and attack-tolerant control that can be independently developed and easily incorporated. The challenge lies in ensuring that the integration can not disrupt the existing nominal controller while enhancing the security of system.
This work investigates the problem of dynamic event-triggered attack estimation and attack-tolerant control for a class of Markovian jump systems. Considering actuator deception attacks, a plug-and-play secure monitoring and control architecture is implemented. The following contributions of this study are summarized as follows:
- (1)
- A new attack reconstruction method is proposed to estimate both the system state and deception attacks. Based on this estimator, an attack-tolerant controller is designed to stabilize the considered Markovian jump systems subject to actuator attacks. Sufficient conditions for the mean-square boundedness of both estimation errors and the closed-loop system dynamics are presented and rigorously proved.
- (2)
- A dynamic event-triggered transmission scheme is employed for communication between the sensor and remote estimator. This incorporates the event-triggered threshold parameter that is dynamically adjusted in order to achieve a balance between network load and the desired estimator accuracy. Furthermore, the proposed event-triggered attack monitoring strategy ensures the timely detection and alerting of deception attacks, significantly enhancing real-time monitoring capabilities.
- (3)
- A PnP secure monitoring and control architecture is presented in this work, which provides a reliable design approach for Markovian jump systems subject to potential deception attacks. The proposed PnP architecture is constructed to seamlessly integrate with existing control systems, enhancing system security without modifying or replacing the original control structure.
Nomenclature: In order to facilitate clarity and consistency within the context of this paper, the notations are employed as follows. represents the set of nonnegative integers. the notation is used to indicate an n-dimensional real vector space, while signifies a real matrix with n rows and m columns. Given a symmetric matrix , we denote positive (negative) definiteness by (). The symbols and are used to represent the smallest and largest eigenvalues of X, respectively. We employ to denote the identity matrix of dimension N, and 0 to represent a zero matrix of appropriate size. Unless otherwise specified, all matrices mentioned are assumed to have compatible dimensions. Additionally, symbolizes the Euclidean norm of a vector “·”. We apply to denote the expected value of Y, and to indicate the probability of Y occurring. For any real number , the notation is used to represent multiplied by itself. When dealing with a matrix , the superscripts “T” and “” are utilized to denote its transpose and inverse, respectively. In matrix representations, the symbol “*” is applied to indicate elements in diagonal positions that are transposes of their counterparts.
2. Model Description
In this paper, a class of discrete-time Markovian jump stochastic systems are considered as follows:
where the state has given initial value , the control input is , the measurement is , the noise signal is , which is assumed to be a zero-mean Gaussian white noise sequence with , and , , , , and are known time-varying matrices with appropriate dimensions. To model the impact of deception attacks targeting the actuator of system (1), an attack signal is introduced. This signal represents the influence of the attacker on the system’s actuator dynamics. The dynamic behavior of the attack signal is governed by the following form:
where is a known time-varying matrix, and the initial value of the attack signal is also determined, the term represents a zero-mean Gaussian white sequence with and is also independent of , and the bounds and are not arbitrarily chosen but are based on the analysis of real-world data relevant to the practical industrial system being modeled.
The variable is a limited model Markov chain in model space with transition probability matrix , described by:
where is the mode transition probability from i to j and . For the sake of convenience in presentation, we denote the following constant matrices with appropriate dimensions for each possible value of :
This research is concerned with the design of an estimator-based secure control strategy for a Markovian jump stochastic system (refer to Equation (1)). This system is susceptible to an additive deception attack directed at the actuator. To accurately reflect the evolving nature of the attack, we incorporate model (2), which effectively describes these dynamic changes. This model is well-established and commonly used in the relevant literature [13]. It is crucial to distinguish our secure control strategy from those in attack-tolerant control research. Our approach has two distinctive features. First, the introduced model incorporates the dynamics of the attack signal, as governed by model (2), in contrast to other works which assume constant attack signals. Second, we consider an unknown stochastic disturbance, a factor that is often neglected in other studies. Furthermore, it is important to highlight that model (2) encompasses constant attack signals as a special case, which occurs when matrix . This demonstrates the comprehensive nature of our model, which is capable of accommodating both dynamic and constant attack scenarios.
Remark 1.
Given the prevalence of Gaussian noise in a multitude of practical engineering applications and systems, the detection of attacks that exploit this inherent characteristic becomes a significantly more challenging problem. By strategically employing this existing noise, attackers can effectively mask their actions, thereby enhancing the stealth and potential success of their attempts. To realistically capture this dynamic and improve the effectiveness of the deception attack model, we model as a Gaussian distribution. This choice closely resembles the Gaussian noise that is inherent to engineering practice, allowing the attack signal to blend seamlessly into the system’s natural noise profile. This integration substantially increases the difficulty of distinguishing between system behavior and the influence of the attacker.
Before proceeding further, it is necessary to introduce the notion of stochastic stability.
Definition 1
(Definition 2, [26]). A discrete stochastic process is said to be exponentially mean-square ultimately bounded if there exists real scalars , , and , such that the following conditions hold:
where , , and .
3. Dynamic Event-Triggered Attack-Tolerant Control
This section presents a dynamic event-triggered sensor data transmission framework for an attack-tolerant control strategy in a class of discrete-time Markovian jump stochastic systems (1). The main results are presented in three sections. Section 3.1 describes a scheme for transmitting sensor data based on dynamic events, optimizing data transmission efficiency. Section 3.2 designs an estimator using the dynamic event-triggered framework. This estimator incorporates both state estimation and attack reconstruction. Section 3.3 implements an attack-tolerant control strategy using the designed estimator. The designed secure control strategy ensures that the system (1) maintains stability, resilience, and acceptable performance, thereby enhancing the system’s ability to withstand and recover from various deception attacks.
3.1. A Dynamic Event-Triggered Sensor Data Transmission Scheme
In practical applications, sensor data are often transmitted over digital networks such as wireless local-area networks and cellular data networks, which may have limited bandwidth due to design and implementation constraints. From a resource management perspective, transmitting measurements to remote estimators at every sampling interval is inefficient. Minor fluctuations between successive output samples typically do not require immediate updates to the remote estimator. Therefore, an efficient transmission scheme is necessary to reduce transmission frequency and optimize resource utilization.
This section proposes an output-dependent dynamic event-triggered sensor data transmission scheme, as illustrated in Figure 1. This scheme determines whether current sensor information needs to be transmitted to a remote estimator. The transmission times, denoted by are determined recursively based on the following event condition:
where represents the output estimation error at each time step, represents the communication error between the current measurement information and the last transmitted information, and denotes the state reconstruction of the remote estimator with initial value . The positive definite symmetric weighting matrices and are triggered parameters to be determined. Furthermore, is an internal dynamic variable in the following form:
with the given initial condition .
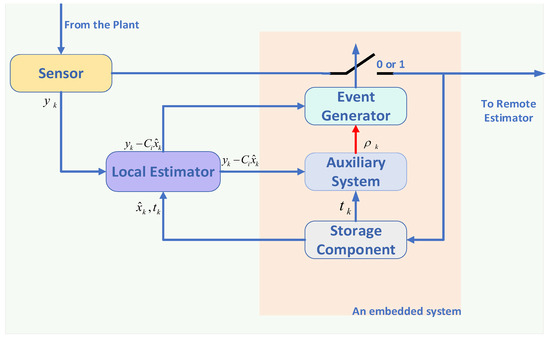
Figure 1.
Architecture of an embedded system with the dynamic event-triggered sensor data transmission scheme.
The structure of the proposed transmission scheme for remote estimation is depicted in Figure 1, where the auxiliary system is defined in (7). At each sampling instant, the measurement information and its time stamp k are collected into an embedded system. The event generator determines whether data packets should be transmitted over the communication network via event condition (6). It also checks the time stamps of newly arrived data packets and keeps the most recent ones unchanged until an update is necessary. The output estimation error is generated by the local estimator. The threshold of the proposed transmission scheme is stored by the storage component after data transmission.
Remark 2.
Compared to static event-triggered transmission schemes [27,28], the introduction of is a crucial component of the dynamic event-triggered transmission scheme (6). This incorporation is partially influenced by the internal-clock-based dynamic mechanism proposed in [17] for event-triggered control systems in the continuous-time domain. Unlike the mechanism in [17], which necessitated continuous monitoring of the system’s state, our scheme operates based on measurements at discrete time instants and utilizes local information to trigger data transmission. Consequently, the value of can be adjusted in real-time in response to the output estimation error.
The following two lemmas present crucial properties of the internal dynamic variable .
Lemma 1.
For the dynamic rule (7), with an initial condition , the inequality holds for all . Furthermore, the sequence demonstrates the property of monotonically increasing.
Proof.
Lemma 2.
Proof.
We will analyze two cases to prove the Inequality (9).
- Case 1: For , the event generator determines that measurement information should be transmitted over the communication network, and the corresponding communication error is zero (i.e., ). Lemma 1 guarantees that . Therefore, the following inequality holds:where the initial condition .
Remark 3.
The proposed dynamic event-triggered transmission scheme, analyzed through Equations (6) and (7), demonstrates the following characteristics. First, the scheme reduces the event-triggered threshold parameters, thereby enhancing the frequency of data transmission. This reduction results in a significant decrease in the estimation error when the current output estimation error or transmission error is substantial. Conversely, if the current remote estimator performs well or the current transmission data exhibits only minor fluctuations, the dynamic scheme will gradually cease to adjust the threshold parameters, thereby maintaining the current estimation performance. This adaptability enables the scheme to achieve a balance between efficient data transmission and maintaining acceptable estimation accuracy.
It is noteworthy that under specific conditions, the proposed dynamic event-triggered scheme can be simplified to existing transmission mechanisms. When the internal dynamic variable converges to a non-zero constant value , the scheme can be written as follows: . This equation corresponds to a static event-triggered scheme, an approach that has been well-studied and is discussed in references [28,29,30]. Additionally, if the gain matrices and are set to zero, Equation (6) reduces to the traditional time-driven transmission scenario, where data transmission occurs at pre-defined intervals. Hence, the proposed dynamic event-triggered scheme (6) offers greater flexibility in scheduling data transmission than either the static communication mechanism or the time-driven transmission scheme.
3.2. Attack Estimator
Under the above dynamic event condition (6), we are interested in designing the following attack estimator with the time period :
where the reconstructed system state, denoted by , and the reconstructed actuator deception attack, denoted by , are recursively calcuated through the estimation process. Matrices and represent estimator gains to be determined later. For notational simplicity, these also be denoted as and where . Furthermore, state estimation error and attack reconstruction error can be represented by and , respectively. Subtracting estimation form (12) from system (1) results in the state estimation error dynamics:
and the attack estimation error dynamics:
In what follows, we will rigorously prove that the state and attack estimation error associated with the estimator in Equation (12) exhibits a property of exponential mean-square boundedness using the Definition 1. This means that the mean squared value of the error tends exponentially to a certain bound over time. This mathematical result guarantees that the performance of the attack estimator improves over time and that the reconstructed attack eventually converges to the true attack with a high degree of accuracy.
Theorem 1.
Consider the discrete-time Markovian jump stochastic system described by Equation (1), incorporating the established dynamic event-triggered sensor data transmission scheme (6). Let the positive scalars , and the initial event-triggered threshold parameter be given. The error dynamics governed by Equations (13) and (14) are exponentially mean-square bounded if there exists a set of positive definite symmetric matrices , , weighting matrices , , and arbitrary matrices , that satisfy the following condition:
where for each system mode , , , , and . Moreover, the attack estimator gains can be calculated by and .
Proof.
The piecewise Lyapunov function is selected as follows:
where
and
Calculating the differences of the and along the trajectories of estimation error dynamics (12) and (13), and taking the mathematical expectation, we have:
In Equation (19):
and
where for , , , , and . According to the definitions of and , the extension can be obtained as follows:
Under the event condition (6), according to Lemma 2, we can derive the following inequality:
When the well-known Schur complement lemma is applied to Inequality (15), the result includes , . This allows us to derive the following inequality from Equation (24):
where , , , and denote the maximum and minimum eigenvalues of the matrix , respectively.
We now proceed to analyze the sufficient condition for the error dynamics (13) and (14) to achieve exponential stability in mean square, as indicated by the previously established inequalities. Recalling the definition of the piecewise Lyapunov function (16), we have:
where , , and , . It should be mentioned that when :
By continuity, we can find a constant such that the following inequality holds:
which can further imply that:
Clearly, Equation (30) yields:
Based on Definition 1, we can see that the dynamics of state and attack estimation errors converge to a region around zero with a certain bound. This means that the errors in estimating both the system state and potential attacks will eventually become and remain arbitrarily small. To quantify this specific bound, we introduce some notations:
Then, the ultimate upper bound is calculated as follows:
This completes the proof. □
Remark 4.
It is important to emphasize that this section proposes a dynamic event-triggered attack reconstruction framework. The proposed framework captures the practical scenario where sensor data transmission is triggered by events, as opposed to traditional time-triggered approaches. By considering the event-triggered nature of data transmission, we can analyze how it affects the performance of the attack estimator. Furthermore, the proposed framework incorporates the different bounds of the stochastic noise and . This flexibility allows for a more accurate analysis and potentially simplifies the design of the attack estimator algorithm.
3.3. Attack-Tolerant Controller
Extending the dynamic event-triggered attack estimator designed in Equation (12), the following part investigates the stability and performance of the overall Markovian jump stochastic system in terms of attack tolerance.
In order to achieve this goal, an attack-tolerant controller is introduced. This controller uses the estimated state and the estimated attack provided by the attack estimator to generate control inputs that reduce the effects of potential deception attacks. The structure of the attack-tolerant controller is presented as follows:
where is a set of controller gains to be designed. These gains determine how much weight the controller places on the estimated state and attack when calculating the control input. The design of these gains is critical to achieving effective attack-tolerant performance. To proceed, it is essential to consider the original Markovian jump stochastic system model (1) along with the attack-tolerant controller (34). By incorporating the controller action as a system input, we can establish the following closed-loop system dynamics:
where for each system mode i, the controller gain matrix is simplified as the .
The objective of Theorem 2 is to analyze the exponential mean-square boundedness of the dynamics of the closed-loop system represented by Equation (35). This theorem will serve as a pivotal component in the formal proof of the stability of the system under attack-tolerant control.
Theorem 2.
Assume that Theorem 1 holds. For each system mode i, a bound of stochastic noise , and a set of controller gains are provided. Furthermore, if there are a set of positive definite and symmetric matrices and a positive scalar , , satisfying the following constraint:
then the attack-tolerant controller designed in (34) can ensure that the state vectors of the overall system (35) are exponentially mean-square ultimately bounded.
Proof.
Consider the following Lyapunov-like functional candidate:
where incorporates information about the system’s estimation error. This term represents another Lyapunov function, (defined in Equation (16)), which relates to the estimation error dynamics governed by Equations (13) and (14). The notation is a series of positive definite and symmetric matrices for each system mode i, along with a scalar . Substituting Equations (16) and (35) into the difference of the Lyapunov-like functional candidate leads to:
where and . The definition of the system stochastic noise allows us to derive the following extension:
where , , and . Moreover, with the help of the constraint (36), Equation (39) can be further transformed into:
where , , , and . If , then it follows from Equation (40) that:
The following proof of Theorem 2 is omitted here due to its similarity to Theorem 1. However, the core concept involves utilizing the result from Definition 1. Theorem 1 guarantees that both the state and attack estimation errors converge to a region around zero with a certain bound . In essence, Theorem 2 builds on Theorem 1 by demonstrating that the attack-tolerant control strategy ensures the ultimate boundedness of the system state, thereby contributing to the overall stability of the closed-loop system. This completes the proof. □
We can now translate the Inequality (36) from Theorem 2 into a more formal mathematical expression. This will allow us to effectively obtain the gain parameters for the attack-tolerant control strategy.
Theorem 3.
Consider the discrete-time Markovian jump stochastic system described by Equation (1). For a specified positive scalar , the closed-loop system dynamics governed by Equation (35) are exponentially mean-square bounded if there exists a set of symmetric matrices and a group of arbitrary matrices (for each system mode i) that satisfy the following condition:
where , and . Furthermore, Controller gain matrices can, therefore, be determined by:
and other parameters are consistent with Theorem 2.
Proof.
To guarantee mean-square boundedness of the closed-loop system dynamics (35), the analysis of Theorem 2 indicates that gain matrices , , should be designed to make condition (36) holds. If , then the Inequality (36) is equivalent to:
where . If post- and premultiplying Equation (44) by , then it is obtained that:
where . Using the Schur complement lemma [31], we can demonstrate that Inequality (45) is mathematically equivalent to the previously established Inequality (36). The established equivalence allows us to conclude that the dynamics of the closed-loop system governed by Equation (35) is exponentially mean-square bounded. Furthermore, the determination of control gains for this attack-tolerant control strategy becomes straightforward. By solving Equation (45) for the controller gain matrices yields the following expression:
This completes the proof of Theorem 3. □
Supported by Theorems 2 and 3, the following corollary can be readily obtained for the design of the attack-tolerant control strategy without the stochastic noises and . In the absence of stochastic noises, the design process becomes significantly less complex, as the need to account for stochastic noise terms is eliminated. This enables a more streamlined approach to determining the attack-tolerant control gains.
Corollary 1.
Suppose that Theorems 2 and 3 hold. Let us consider a set of symmetric matrices , a group of arbitrary matrices , and a positive scalar . For each , if condition (36) holds, then the proposed attack-tolerant controller (34) can ensure that the overall closed-loop system (35) is exponentially mean-square stable. Moreover, the controller gain matrices can be computed as , .
Proof.
The proof of Corollary 1 parallels that of Theorem 2, and thus, it is omitted here for the sake of brevity and conciseness. □
Based on the theoretical results we have derived, a comprehensive algorithm is presented including the dynamic event-triggered remote attack estimation and secure control strategy, as outlined in Algorithm 1. This algorithm synthesizes the theoretical results into a practical framework designed to effectively counter various deception attacks while ensuring robust control performance. The integration of a dynamic event-triggered sensor data transmission scheme with attack reconstruction techniques constitutes the foundation of the secure strategy, which is designed to maintain system stability and operational reliability in the face of potential adversarial actions. This algorithmic approach not only utilizes our established theoretical foundations, but also provides a structured method for implementing and deploying resilient control systems capable of adapting to varying threat scenarios in real-time environments.
| Algorithm 1 Recursive algorithm of the attack estimation and attack-tolerant control |
Set the initial conditions: , , , and ;
|
As illustrated in Algorithm 1, a recursive approach is utilized for dynamic event-triggered attack estimation and attack-tolerant control. This approach starts by initializing estimates for the system state, attack, and internal event variables. At each time step, the algorithm executes a series of coordinated actions. First, an internal event variable is updated in order to reflect the current accuracy of the state and attack estimates. Following this update, the algorithm makes a critical decision based on the current conditions whether to acquire a new measurement from the sensor. This decision hinges on a comparison between the current output estimation error and the internal variable. If the condition is met, the algorithm prioritizes energy conservation by entering an “Energy-Saving Mode” (i.e., ). In this mode, the current measurement cannot be transmitted, and state and attack estimates are updated using the previously received measurement. Conversely, if , the algorithm switches to the “Robust Estimation Mode” (i.e., ) to guarantee precise state and attack reconstruction. Once the transmission mode is determined, the algorithm utilizes the available information to update the estimated system state and the estimated attack . Finally, the algorithm calculates a control input that considers both and . This secure control strategy can help the considered discrete-time Markovian jump stochastic system maintain stability and performance even when under different deception attacks. By dynamically adapting the data transmission based on the output estimation error, Algorithm 1 establishes a balance between achieving system performance and minimizing communication loads.
4. The Plug-and-Play Secure Monitoring and Control Architecture
Many existing system secure monitoring and/or control methodologies utilize “open-loop” design procedures, facilitating direct implementation as embedded modules [18,29]. However, practical systems often face challenges when dealing with pre-designed control systems. In such cases, reconfiguring controllers typically involves modifying or replacing the existing control structure, which proves impractical for numerous industrial applications, especially those where pre-designed control architectures are tightly encapsulated for safety reasons. This lack of flexibility can further restrict the implementation of security requirements.
To address this challenge, this section introduces a new PnP secure monitoring and control architecture. This framework offers an alternative solution by enabling the implementation of attack-tolerant control strategies in Algorithm 1 without requiring alterations to the existing feedback control system structure. It can be integrated seamlessly into the control loop, and can be independently plugged into the original system. Before exploring the details of the PnP secure monitoring and control structure, Section 4.1 will introduce the specific form of control strategy based on a dynamic event-triggered state estimator, which serves as the nominal feedback control approach.
4.1. Nominal Feedback Control
In this section, we focus on a discrete-time stochastic Markovian jump system without deception attacks described by Equation (1). To optimize communication efficiency and save network resources, a dynamic event-triggered mechanism (6) is implemented between the sensor and a remote estimator. This architecture facilitates the realization of a nominal feedback control loop, as illustrated in Figure 2. The core component of this control loop is an estimator-based feedback controller, characterized by the following form:
where the matrices and represent the estimator and controller gains, respectively, to be designed subsequently. For notational convenience, gain matrices can also be written as and for all i belonging to the set S. Paralleling the results calculated in Equation (13), the dynamics of the state estimation error can be derived as follows:
where . Additionally, the dynamics of the closed-loop system are determined as follows:
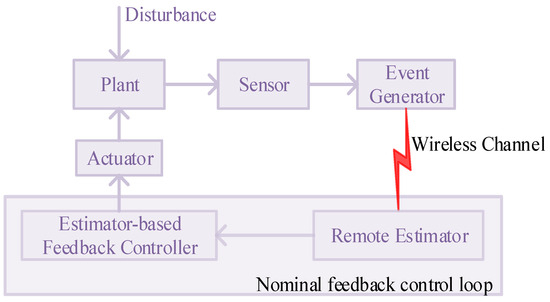
Figure 2.
The existing nominal control loop.
Subsequently, Theorem 4 provides the basis for further research.
Theorem 4.
Consider the discrete-time Markovian jump stochastic system without deception attacks , as shown in Equation (1), which integrates the previously introduced dynamic event-triggered sensor data transmission scheme (6), given positive scalars , β, and an initial event-triggered threshold parameter . Furthermore, if there exists a positive scalar , a set of positive definite symmetric matrices and , weighting matrices and , as well as arbitrary matrices and , such that, , the following conditions are satisfied:
where , , , , , and , then the presented estimator-based feedback controller (47) can realize that state estimation error (48) and the state vector of the closed-loop system (49) are exponentially mean-square bounded. For each system mode , the estimator gains and controller gains can be accordingly determined by and , respectively.
Proof.
Consider the following Lyapunov function:
where and are positive definite symmetric matrices for each system mode . The corresponding difference, , along the trajectories of state estimation error dynamics (48) and the closed-loop system dynamics (49) is given by:
where and for . By exploiting the property of the stochastic noise term of the system (1), we obtain the following expression:
where
and the parameter is a given positive scalar. Furthermore, Equation (54) can be provided according to event condition (23) as follows:
In Equation (56), the following notations are represented as:
Based on the constraints specified in Equations (50) and (51), it can be derived from Equation (58) that:
where an arbitrary scalar , , , , . By choosing , it follows from Equation (60) that:
The remaining proof for Theorem 4 is excluded due to its substantial similarity to the proof of Theorem 1. Both Theorems 1 and 4 are based on the principles outlined in Definition 1 and use analogous proof techniques to prove their results. Extending the principles established by Theorem 1, we can show that both the system state and the associated state estimation error asymptotically converge to a bounded neighborhood around the origin, characterized by the positive scalar . Consequently, the proposed estimator-based feedback controller, as defined by Equation (47), effectively guarantees the exponential mean-square stability of the closed-loop system governed by Equation (49). This completes the proof. □
Remark 5.
To ensure the exponential mean-square stability of the closed-loop system described by Equation (49), our previous analysis indicates that the controller gains , for all modes , should be designed to satisfy condition (51). To facilitate the design process and to transform the condition into a more tractable form, we apply a series of matrix manipulations. Specifically, when we post- and pre-multiply Equation (59) by the block diagonal matrix , the following expression is obtained:
where we introduce the notations and . To further simplify our design problem, we apply the Schur complement lemma [31], a powerful tool in matrix analysis and optimization. In addition, we introduce the notation , which represents a change of variables that linearizes the problem. Through these manipulations, we can show that Equation (62) is equivalent to the original stability condition (51).
4.2. Attack Monitoring Strategy
Prior to presenting an attack monitoring strategy, an attack indicative signal (i.e., residual) can be generated utilizing the output estimation error of the estimator (47) as follows:
Algorithm 2 describes an attack monitoring strategy involving a remote estimation system that relies on measurements from a battery-powered sensor. The system uses wireless communication to transmit data to a remote estimator. The decision to send current measurement data to the remote estimator is managed by an event-triggered data transmission scheme (6). When the event condition is met (i.e., ), the remote estimator receives the data; otherwise, if , the data are not sent. As illustrated in Figure 1, a local estimator calculates the residual online according to Equation (63). If the system is free of deception attacks (i.e., ), the expected value of the residual should approach zero. In contrast, if a deception attack occurs (i.e., ), the expected value of the residual will be significantly greater than zero.
| Algorithm 2 Event-triggered attack monitoring strategy |
| Step 1 Estimator design: A series of state estimators, as defined in Equation (47), are designed to provide estimates of the system state . Step 2 Residual calculation: Attack residuals, denoted as , are computed based on Equation (63). A small threshold, , is established to distinguish between normal and anomalous residual values. Step 3 Attack detection: If the calculated residual is below the threshold (), the system is considered to be in an attack-free mode and no attack alarm is generated. Step 4 Event-triggered data transmission: When the attack monitor enters an attack-free mode, an event-triggered mechanism (6) determines whether to transmit sensor measurements to the remote estimator. If the event condition is met (i.e., ), data are transmitted; otherwise, data transmission is prohibited to conserve energy. Step 5 Attack alarm: If the calculated residual exceeds or equals the threshold (i.e., ), a deception attack is declared, and an attack alarm is activated. To facilitate attack detection, sensor measurements are transmitted to the remote estimator, bypassing the event-triggered condition (6). |
Furthermore, if the residual value falls below the threshold , it indicates that the system is operating free of attacks. In this case, the event-triggered data transmission scheme (6) is employed to optimize power consumption. However, if exceeds or equals , it suggests that the system is suffering from a deception attack by a malicious adversary. In response, sensor data are manually transmitted to the remote estimator, bypassing the event-triggered mechanism. This approach can successfully address the problem of delayed detection of attacks. In particular, by manually sending sensor data to the remote estimator whenever the residual value exceeds a certain threshold, the system can immediately detect and respond to deception attacks. This immediate response helps overcome any delays that might occur if the data transmission relied solely on the event-triggered mechanism, which in some cases may not activate quickly enough. This strategy ensures that the system can detect and alert to attacks in a timely manner, improving the overall effectiveness of the monitoring process.
4.3. Plug-and-Play Operations
In our work, we propose a dynamic event-triggered sensor data transmission scheme (6) for secure monitoring and attack-tolerant control based on a PnP architecture, as illustrated in Figure 3. This architecture addresses the critical challenge of improving the cyber security of Markovian jump stochastic system (1) without compromising its stability. At the core of the architecture are both the secure monitoring module and the attack-tolerant control module, which operate in parallel with the real system, continuously assessing the state of the system without interfering with its primary operations. This parallel operation ensures real-time detection of deception attacks without introducing delays or computational overhead to the main control loop. The PnP nature of the architecture allows dynamic activation of attack-tolerant modules based on monitoring results, providing an adaptive and flexible security approach. This design preserves the existing nominal feedback control, ensuring closed-loop stability, while providing secure monitoring performance and attack tolerance through the PnP modules.
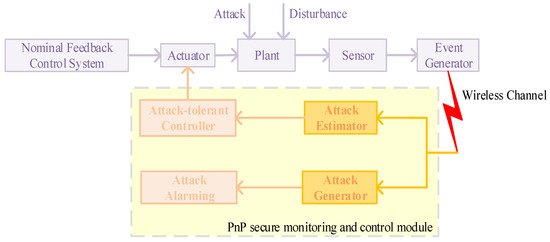
Figure 3.
Plug-and-play secure monitoring and control structure.
Specifically, two key components are embedded in the feedback control loop: an estimator-based attack indicator described by Equation (63) to detect deception attacks, and an attack-tolerant controller described by Equation (34) that employs the attack reconstruction technique of Equation (12) to maintain system performance even in the presence of detected deception attacks. This controller can utilize an online reconfiguration method to adjust system state behavior in real time based on the detected presence and nature of attacks. By maintaining the core control structure while adding these layers of security, our approach ensures that even if the security modules fail or are compromised, the system will continue to operate stably, albeit potentially vulnerable to attack. This architecture represents an advancement in balancing the need for enhanced security with the practical constraints of maintaining system stability and performance, and it provides a flexible method for improving the system’s resilience against deception attacks. The major advantages of the proposed PnP monitoring and control architecture are summarized as follows:
- (1)
- The secure monitoring and control are seamlessly integrated within a unified framework.
- (2)
- The residual-based monitoring module and the attack-tolerant controller exhibit the “plug-in” and “plug-out” ability, allowing for flexible system configuration. The design objectives for robustness and tolerance are separated: the robustness of the closed-loop can be improved through the design of , as detailed in Theorem 4, while the tolerance performance can be enhanced by designing the , as established in Theorem 2. Furthermore, the design of avoids the modification of the existing control system.
- (3)
- The architecture accommodates the integration of new sensors or actuators through straightforward reconfiguration of the “plug-in” components, preserving closed-loop stability.
The widespread adoption of data networking technologies in industrial control applications has transformed modern industrial systems. Advanced communication networks such as Ethernet, Profibus, Profinet, and CAN efficiently connect actuators, sensors, and controllers [32,33,34]. This connectivity enables seamless sharing of information across multiple control loops for a complete understanding of industrial systems. By fusing global information, the system can make intelligent decisions, enabling advanced, safe monitoring and control techniques. This networked architecture supports real-time data exchange throughout the system. As a result, it enables the implementation of secure monitoring and attack-tolerant control strategies that significantly improve the efficiency and adaptability of industrial operations.
Figure 4 illustrates the industrial operation of the proposed PnP monitoring and control architecture, which can utilize both wireless communication and a multi-core processor setup. The overall system consists of the controlled plant, followed by a Markovian jump process, an existing nominal control module, and a PnP coordinator, all connected via a wireless network. The PnP coordinator manages the “plug-in” modules, which include the residual-based secure monitoring module and the attack-tolerant controller, each equipped with its own configuration algorithms. These modules operate independently, but are managed by the PnP coordinator. This architecture enables flexible extensions to industrial control systems, providing secure monitoring and attack-tolerant control while maintaining system stability.
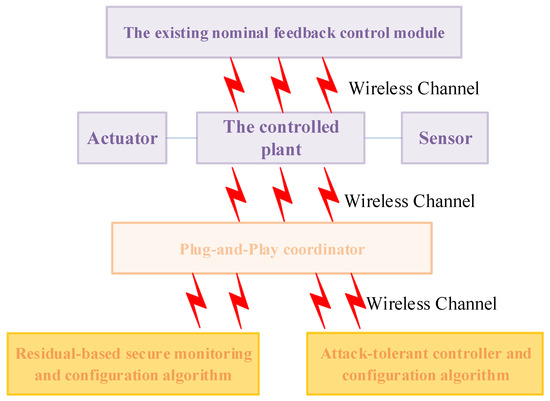
Figure 4.
Operations of the plug-and-play secure monitoring and control framework.
As illustrated in Figure 5, the proposed framework presents a comprehensive approach to secure monitoring and control, integrating these functions in a unified structure. At its core, the system features a residual-based monitoring module and an attack-tolerant controller module, both of which have been designed with the capacity for “plug-in” and “plug-out” capabilities. This design permits flexible system configuration and distinguishes between the objectives of robustness and tolerance. The robustness of the closed-loop system can be enhanced through the design of , as outlined in Theorem 4, while tolerance performance is improved by designing according to Theorem 2. It is noteworthy that the design of the augmented control system avoids modifying the existing control system, thus maintaining operational continuity. Moreover, the architectural design exhibits adaptability, enabling the integration of new sensors or actuators. This integration is achieved through a straightforward reconfiguration of the “plug-in” components, thereby ensuring that the closed-loop stability is preserved.
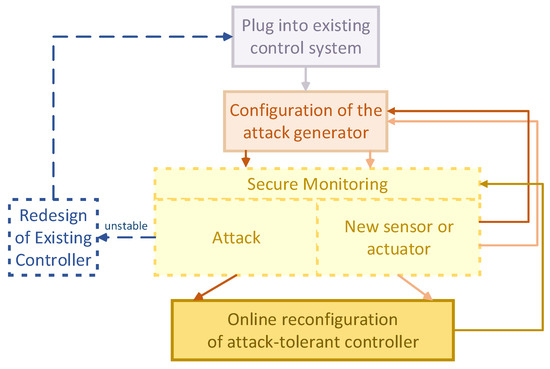
Figure 5.
A brief working principle of the PnP secure monitoring and control.
5. Case Study: PWM-Driven Boost Converter
In this section, a modified PWM (pulse-width modulation)-driven boost converter model borrowed from [7] is introduced as a practical background to illustrate the effectiveness of the effectiveness of the obtained theoretical results. In Figure 6, the PWM-driven boost converters considered are basic power electronic circuits that raise the output voltage above the input level. They operate by rapidly switching a semiconductor device, controlled by a PWM signal, to alternately store and transfer energy. These converters are widely used in renewable energy systems, electric vehicles, and portable electronics [7,35], where they play a critical role in efficient power management and voltage regulation. The detailed description of the PWM-driven boost converter is given in the following section.
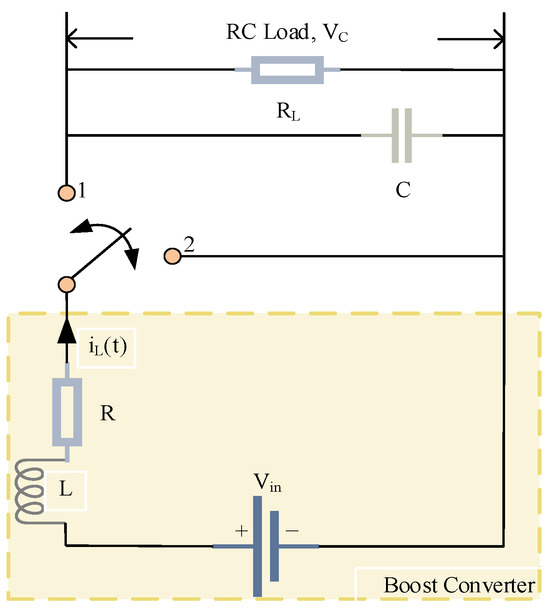
Figure 6.
A modified PWM-driven boost converter.
5.1. PWM-Driven Boost Converter: Description and Modeling
As depicted in Figure 6, the circuit components are denoted as follows: L represents the inductance, C symbolizes the capacitance, R denotes the inductor resistance, denotes the load resistance, and represents the source voltage. This converter, a fundamental circuit in power electronics, serves to regulate the source voltage, ensuring a stable output despite fluctuations in the input. In the boost converter, the switch can take two different modes.
It is interesting to note that the switch does not move in a predetermined sequence, but rather jumps from one position to another in a random manner. This seemingly chaotic behavior can be mathematically modeled as a Markov process with two finite states. A Markov process is particularly well-suited to this scenario because it can represent systems where the future state depends only on the current state, not on the sequence of events that preceded it. Utilizing the Kirchhoff voltage and current law, the differential equations for the boost converter are as follows:
- (1)
- Mode 1
- (2)
- Mode 2
Based on the results documented in study [7], we proceed to the following parameters:
- (1)
- Mode 1
- (2)
- Mode 2
The transition probability matrix are considered as:
with the initial mode . From the results of Theorems 1–4, the predetermined constants are chosen as follows: , , , and .
To facilitate our experiment, we parameterize the additional matrices in system (1) as shown below:
Furthermore, the two-mode Markov chain for the PWM-driven boost converter is visualized in Figure 7, which is established using the transition probability matrix specified in Equation (68).
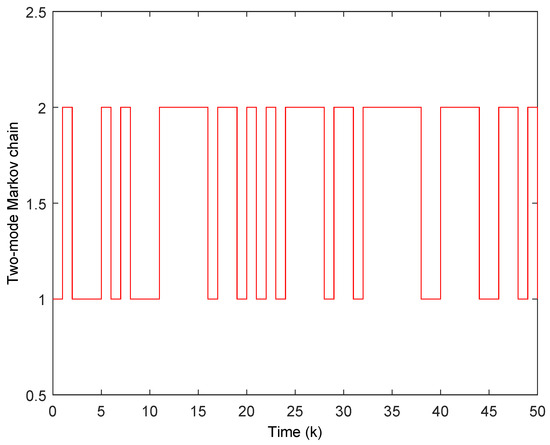
Figure 7.
Evolution of Markov chain .
5.2. PWM-Driven Boost Converter: Experimental Results and Analysis
Before evaluating the effectiveness of our proposed methods, we established the following three different attack scenarios.
- Case 1: A constant attack scenario
In this scenario, a persistent attack threat is simulated where the attacker introduces a fixed and unchanging signal to the considered system (1). This can represent a sustained attempt to manipulate a specific parameter on the actuator side, maintaining a consistent level of interference over time.
- Case 2: A time-varying attack scenariowhere we model a more dynamic threat environment. The attack parameters fluctuate over time and follow predetermined patterns. This scenario tests the ability of our algorithm to adapt to attacks and remain stable under changing attack conditions.
- Case 3: An incipient attack scenario
This case presents a scenario in which a malicious signal gradually increases in impact over time. Such a scenario can represent an attacker’s attempt to avoid detection by introducing subtle changes that accumulate to a significant impact, challenging early warning capabilities of our monitoring strategy.
To demonstrate the effectiveness of the proposed theoretical results in Algorithms 1 and 2, a series of experiments are conducted addressing three distinct attack cases: constant, time-varying, and incipient attacks. These experiments evaluate the performance of attack monitoring, attack reconstruction, and attack-tolerant control under each scenario.
5.2.1. Experiment I: Performance Evaluation of Attack Detection
Figure 8 demonstrates the timeliness and effectiveness of our attack monitoring strategy. The attack, which occurs at step 31, is immediately detected as the attack indicator signal rises sharply above the 0.12 threshold. This immediate detection exemplifies the algorithm’s responsiveness to abrupt, persistent attacks. The attack indicative signal persists at an elevated level throughout the remaining steps, illustrating the algorithm’s robust detection capability. The clear separation between “with attack” and “without attack” signals from step 31 onwards, coupled with the absence of false alarms before the attack, highlights the effectiveness of Algorithm 2.
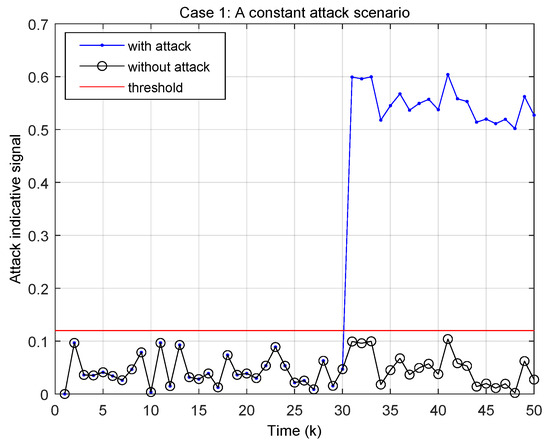
Figure 8.
Attack monitoring results for the constant attack (70).
In Figure 9, the algorithm again exhibits the performance of attack detection. At step 31, when the attack begins, the indicative signal immediately surges above the 0.16 threshold, showing precise and timely detection. Despite the subsequent fluctuations in attack intensity, the signal persistently remains above the threshold, demonstrating the algorithm’s capacity to maintain detection under time-varying attack conditions. The sharp contrast between pre- and post-attack signals highlights the algorithm’s effectiveness in identifying time-varying attack threats.
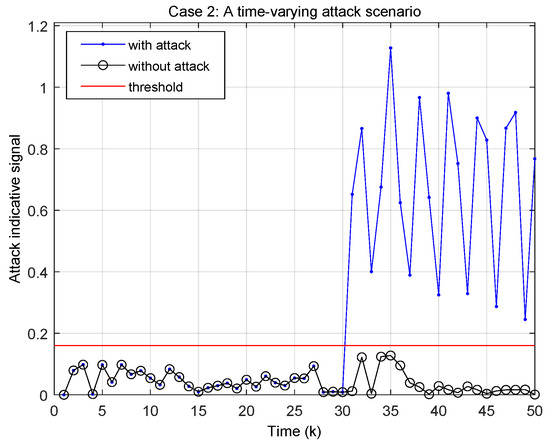
Figure 9.
Attack monitoring results for the time-varying attack (71).
The sensitivity of the algorithm is evaluated in Figure 10 through the analysis of the incipient attack (72). The attack initiates at step 31, and the algorithm detects this onset immediately, with the indicator signal beginning to rise at this exact step. The immediate response at step 31 demonstrates the algorithm’s sensitivity to even minor changes indicative of an incipient attack. The consistent rise of the indicator post-step 31 shows effective tracking of the gradually intensifying attack.
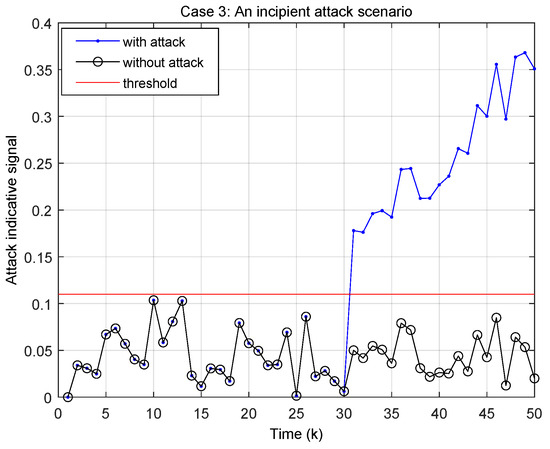
Figure 10.
Attack monitoring results for the incipient attack (72).
Across all three scenarios, The threshold selection for each scenario illustrates the algorithm’s capacity for different attack profiles while maintaining a high level of detection accuracy. Moreover, it is noteworthy that despite the implementation of a dynamic event-triggered transmission scheme, which could potentially introduce delays, the attack monitoring strategy consistently detects the attack at step 31 without any lag. This reveals the efficacy of the optimizations in Algorithm 2 in effectively mitigating any potential transmission-related detection delays.
5.2.2. Experiment II: Performance Assessment of Attack Reconstruction
Figure 11 presents a comparison of two methods for reconstructing a constant attack: a static event-triggered learning observer (SETLO), adapted from the existing excellent works [36,37], and the dynamic event-triggered attack estimator established in Equation (12). The proposed method demonstrates excellent performance in reconstructing the constant attack, closely tracking the actual attack signal. As evidenced by the magnified region, the proposed method demonstrates a slight advantage over SETLO in terms of accuracy. The event-triggered transmission behaviors of our method effectively minimize data transmission while maintaining robust reconstruction of the constant attack.
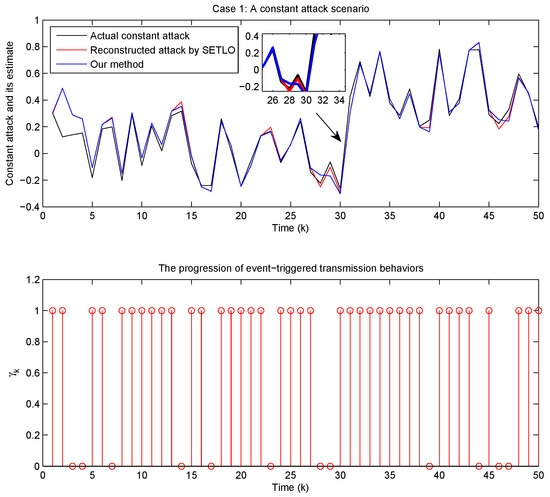
Figure 11.
Reconstruction of the constant attack (70).
Figure 12 illustrates the effectiveness of the proposed method in tracking the dynamic nature of the time-varying attack, which frequently coincides with the actual attack signal. The magnified area is provided to confirm the capacity of the proposed method to capture rapid changes in the attack signal. Moreover, it can be observed from Figure 12 that the attack estimator effectively minimizes data transmission while maintaining robust reconstruction of the time-varying attack by employing the designed dynamic event-triggered transmission scheme.
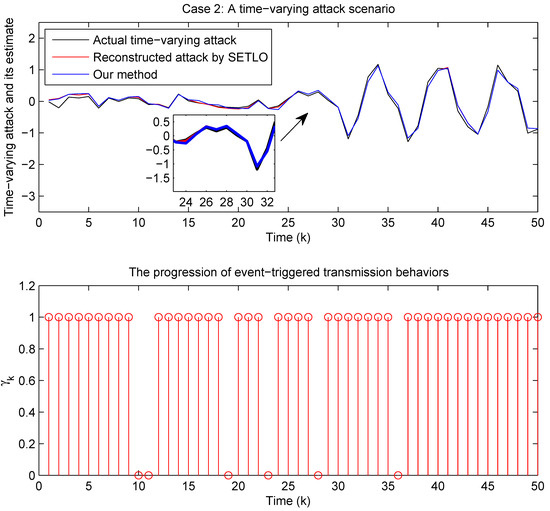
Figure 12.
Reconstruction of the time-varying attack (71).
For the incipient attack, the proposed method in Figure 13 demonstrates high sensitivity in reconstructing the gradually intensifying attack. The magnified zone shows that it can accurately capture the attack’s onset and subsequent growth. Additionally, the progression of event-triggered transmission behaviors can suggest that our attack estimator successfully reduces data transmission while ensuring a reliable reconstruction of the emerging attack.
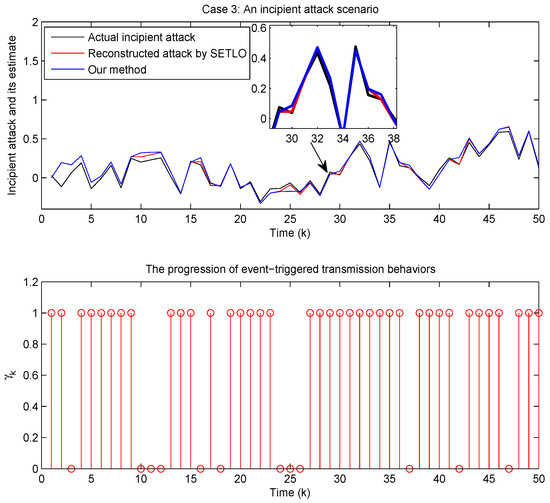
Figure 13.
Reconstruction of the incipient attack (72).
It is of particular interest to note that Figure 14 offers valuable insights into the transmission efficiency of the various methods under consideration. The proposed dynamic event-triggered transmission strategy displays superior efficiency for constant and incipient attack scenarios, requiring fewer transmissions compared to static event-triggered and time-driven methods. However, for the time-varying attack scenario, its transmission count is almost equivalent to that of the static event-driven method, likely due to the rapidly changing signal necessitating frequent updates.
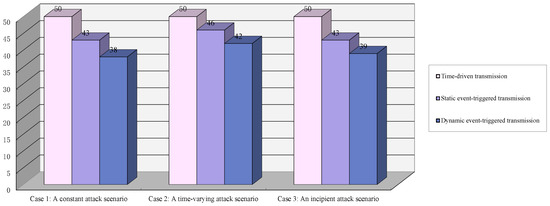
Figure 14.
Comparative results of transmission efficiency under various attack scenarios.
The proposed attack reconstruction method exhibits superior performance across various attack scenarios. The theoretical result combines accurate reconstruction with efficient event-triggered transmission, thereby outperforming SETLO in all cases. The ability of method to adapt its transmission behavior to different attack profiles makes it particularly suitable for real-world applications where attack characteristics may vary. The efficiency gains in transmission, especially for constant and incipient attacks, highlight the method’s potential for reducing communication load in attack-resilient control systems.
5.2.3. Experiment III: Performance Examination of Attack-Tolerant Control
Experiment III focuses on evaluating the effectiveness of the proposed attack-tolerant control strategy using the reconstructed attack information from Experiment II. The experiment examines the state response of system under three distinct attack scenarios. Figure 15, Figure 16 and Figure 17 illustrate the state responses for each attack case, respectively.
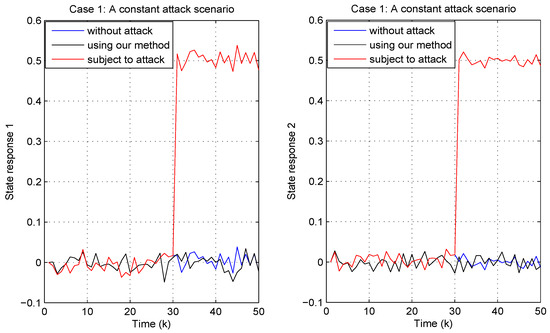
Figure 15.
Results of the attack-tolerant controller under the constant attack (70).
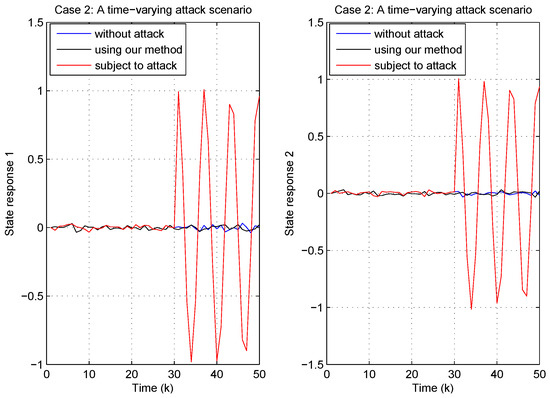
Figure 16.
Results of the attack-tolerant controller under the time-varying attack (71).
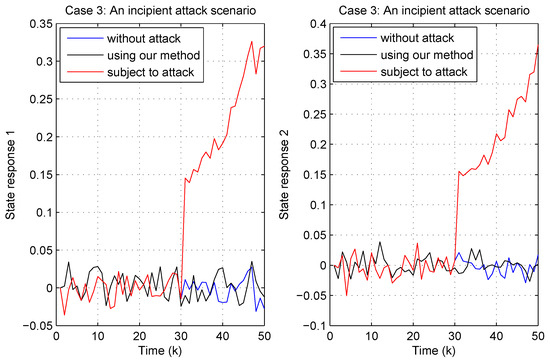
Figure 17.
Results of the attack-tolerant controller under the incipient attack (72).
In the scenario of the constant attack shown in Figure 15, both state responses examine the effectiveness of the proposed attack-tolerant controller. The state trajectories generated by the attack-tolerant controller exhibit a high degree of similarity to those generated in the absence of an attack, demonstrating consistent stability in the vicinity of the origin. In contrast, the system without the proposed controller demonstrates a notable divergence beginning at time step 31, with the state values rapidly increasing to approximately 0.5 and subsequently oscillating.
Figure 16 presents a more challenging case than the previous constant attack case. Here, the proposed method again shows remarkable performance. Despite the dynamic nature of the attack, the state responses with the attack-tolerant controller remain nearly indistinguishable from the no-attack case, exhibiting minimal variation close to zero. Conversely, when the attack-tolerant controller is not equipped, the system state response curves display significant oscillations in response to the time-varying attack, fluctuating between approximately −1 and 1. This indicates a substantial loss of control.
As depicted in Figure 17, the gradual nature of the incipient attack is evident. The proposed attack-tolerant controller effectively keeps the state responses close to the no-attack scenario. In the absence of the proposed attack-tolerant controller, the system state response curves exhibit a steadily increasing divergence in both states beginning from time step 31, ultimately reaching values of approximately 0.3 and 0.35 by the end of the simulation period.
This experiment highlights the crucial role of attack-tolerant control in maintaining system stability and performance amidst various attack scenarios. By ensuring that state responses remain closely aligned with the no-attack case across different attack scenarios, the proposed method demonstrates its adaptability and effectiveness in strengthening the resilience of control systems against potential threats.
In this section, three experiments evaluated attack detection, reconstruction, and tolerant control methods across constant, time-varying, and incipient attack scenarios. Experimental results showed effective and timely attack detection, accurate reconstruction with optimized transmission efficiency, and robust attack-tolerant control maintaining system stability. The proposed approach demonstrated effectiveness in enhancing the considered discrete-time Markovian jump stochastic system resilience against distinct attack cases, while reducing communication load through the dynamic event-triggered transmission scheme.
6. Conclusions and Future Work
This paper has proposed a PnP secure monitoring and control architecture for a class of Markovian jump stochastic systems vulnerable to deception attacks on the actuator side. We have constructed a dynamic event-triggered sensor data transmission scheme associated with an attack estimator to simultaneously reconstruct system states and actuator attacks. Utilizing real-time information on reconstructed attacks, a state-feedback-based controller has been designed to accommodate the effect of actuator attacks on system performance. The advantages of the proposed secure monitoring and attack-tolerant control strategy lie in the following three aspects:
- The introduced event-triggered attack monitoring strategy guarantees real-time attack detection and alarm, thereby enhancing monitoring capability.
- The proposed PnP architecture integrates with existing control systems without modifying or replacing the original control structure, extending its applicability in practical scenarios.
- The design problems of the attack estimator and attack-tolerant controller can be reformulated into linear matrix inequalities, which can be conveniently solved using mathematical software, thus reducing the complexity of the design process.
Finally, the applicability and reliability of our method have been verified by a switched boost converter circuit.
In future work, we intend to evaluate posterior probabilities as part of our results. This will involve developing novel algorithms that integrate posterior probability analysis for a class of Markovian jump stochastic systems. By combining these methods, we aim to create hybrid secure monitoring and attack-tolerant control strategies that are more robust and effective. We will also focus on secure monitoring and attack-tolerant control strategies for multi-point deception attacks. We will extend current attack models to encompass multiple attack scenarios, including replay attacks and denial-of-service attacks. Specifically, we plan to conduct in-depth research on analyzing the impact of multiple attacks on various cyber-physical systems, exploring the interactions and synergies between different attack types, analyzing the patterns of multi-point attacks in real cyber-physical systems.
Author Contributions
Conceptualization, Y.G.; Methodology, Y.L.; Validation, J.C.; Investigation, Y.L.; Data curation, Z.H.; Supervision, Y.W.; Funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Industry University Research Cooperation Project of Jiangsu Province under Grant BY20230752 and in part by the Wuxi Soft Science Research Program under Grant KX-24-A03.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jamwal, A.; Agrawal, R.; Sharma, M.; Giallanza, A. Industry 4.0 technologies for manufacturing sustainability: A systematic review and future research directions. Appl. Sci. 2021, 11, 5725. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S.; Dong, J.; Kaynak, O. A review on soft sensors for monitoring, control, and optimization of industrial processes. IEEE Sens. J. 2020, 21, 12868–12881. [Google Scholar] [CrossRef]
- Ghelani, D. Cyber security, cyber threats, implications and future perspectives: A Review. TechRxiv 2022. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S.; Kaynak, O. Data-driven monitoring and safety control of industrial cyber-physical systems: Basics and beyond. IEEE Access 2018, 6, 47374–47384. [Google Scholar] [CrossRef]
- Zhu, F.; Peng, L.; Yang, R. Event-triggered distributed filtering for Markov jump systems over sensor networks. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2021, 235, 1482–1493. [Google Scholar] [CrossRef]
- Shi, P.; Li, F. A survey on Markovian jump systems: Modeling and design. Int. J. Control Autom. Syst. 2015, 13, 1–16. [Google Scholar] [CrossRef]
- Wen, J.; Peng, L.; Nguang, S.K. Stochastic finite-time boundedness on switching dynamics Markovian jump linear systems with saturated and stochastic nonlinearities. Inf. Sci. 2016, 334, 65–82. [Google Scholar] [CrossRef]
- Wen, J.; Nguang, S.K.; Shi, P.; Nasiri, A. Robust H∞ Control of Discrete-Time Nonhomogenous Markovian Jump Systems via Multistep Lyapunov Function Approach. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 1439–1450. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, W.; Wu, Y. Event-Triggered Fault Estimation and Fault Tolerance for Cyber-Physical Systems with False Data Injection Attacks. Actuators 2023, 12, 197. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, S.; Yang, H.; Luo, H.; Chen, Z.; Yin, S.; Kaynak, O. Secure data transmission and trustworthiness judgement approaches against cyber-physical attacks in an integrated data-driven framework. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 7799–7809. [Google Scholar] [CrossRef]
- Wu, S.; Jiang, Y.; Luo, H.; Zhang, J.; Yin, S.; Kaynak, O. An integrated data-driven scheme for the defense of typical cyber-physical attacks. Reliab. Eng. Syst. Saf. 2022, 220, 108257. [Google Scholar] [CrossRef]
- Yang, H.; Yin, S.; Han, H.; Sun, H. Sparse actuator and sensor attacks reconstruction for linear cyber-physical systems with sliding mode observer. IEEE Trans. Ind. Inform. 2021, 18, 3873–3884. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, S.; Jin, Z.; Hu, Y. Secure state estimation for event-triggered cyber-physical systems against deception attacks. J. Frankl. Inst. 2022, 359, 11155–11185. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Q.G.; Feng, G.; Shi, Y.; Vasilakos, A.V. A survey on attack detection, estimation and control of industrial cyber–physical systems. ISA Trans. 2021, 116, 1–16. [Google Scholar] [CrossRef]
- Mazunga, F.; Nechibvute, A. Ultra-low power techniques in energy harvesting wireless sensor networks: Recent advances and issues. Sci. Afr. 2021, 11, e00720. [Google Scholar] [CrossRef]
- Sah, D.K.; Amgoth, T. Renewable energy harvesting schemes in wireless sensor networks: A survey. Inf. Fusion 2020, 63, 223–247. [Google Scholar] [CrossRef]
- Girard, A. Dynamic triggering mechanisms for event-triggered control. IEEE Trans. Autom. Control 2014, 60, 1992–1997. [Google Scholar] [CrossRef]
- Zhu, F.; Liu, X.; Peng, L. Adaptive consensus-based distributed H∞ filtering with switching topology subject to partial information on transition probabilities. Appl. Math. Comput. 2021, 411, 126534. [Google Scholar]
- Ma, L.; Wang, Z.; Cai, C.; Alsaadi, F.E. Dynamic Event-Triggered State Estimation for Discrete-Time Singularly Perturbed Systems with Distributed Time-Delays. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3258–3268. [Google Scholar] [CrossRef]
- Ma, L.; Wang, Z.; Cai, C.; Alsaadi, F.E. A dynamic event-triggered approach to H∞ control for discrete-time singularly perturbed systems with time-delays and sensor saturations. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6614–6625. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Yan, H.; Yang, F.; Zhou, X. Adaptive Event-Triggered Transmission Scheme and H∞ Filtering Co-Design Over a Filtering Network with Switching Topology. IEEE Trans. Cybern. 2019, 49, 4296–4307. [Google Scholar] [CrossRef] [PubMed]
- Huo, M.; Luo, H.; Wang, X.; Yang, Z.; Kaynak, O. Real-time implementation of plug-and-play process monitoring and control on an experimental three-tank system. IEEE Trans. Ind. Inform. 2020, 17, 6448–6456. [Google Scholar] [CrossRef]
- Wang, H.; Luo, H.; Jiang, Y.; Xu, X.; Li, X. A data-driven distributed control method for performance optimization of interconnected industrial processes. In Proceedings of the 2022 4th International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 24–27 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Wang, H.; Luo, H.; Ren, L.; Huo, M.; Jiang, Y.; Kaynak, O. Data-Driven Design of Distributed Monitoring and Optimization System for Manufacturing Systems. IEEE Trans. Ind. Inform. 2024, 20, 9455–9464. [Google Scholar] [CrossRef]
- Luo, H.; Yang, X.; Krueger, M.; Ding, S.X.; Peng, K. A plug-and-play monitoring and control architecture for disturbance compensation in rolling mills. IEEE/ASME Trans. Mechatron. 2016, 23, 200–210. [Google Scholar] [CrossRef]
- Tarn, T.J.; Rasis, Y. Observers for nonlinear stochastic systems. IEEE Trans. Autom. Control 1976, 21, 441–448. [Google Scholar] [CrossRef]
- Li, S.; Chen, Y.; Zhan, J. Event-triggered consensus control and fault estimation for time-delayed multi-agent systems with Markov switching topologies. Neurocomputing 2021, 460, 292–308. [Google Scholar] [CrossRef]
- Li, Y.; Peng, L. Event-triggered fault estimation for stochastic systems over multi-hop relay networks with randomly occurring sensor nonlinearities and packet dropouts. Sensors 2018, 18, 731. [Google Scholar] [CrossRef]
- Gao, Y.; Li, Y.; Peng, L. Event-triggered fault tolerant control for a class of state saturated systems subject to deception attacks. Trans. Inst. Meas. Control 2020, 42, 1935–1945. [Google Scholar] [CrossRef]
- Li, Y.; Li, P.; Chen, W. An energy-efficient data transmission scheme for remote state estimation and applications to a water-tank system. ISA Trans. 2017, 70, 494–501. [Google Scholar] [CrossRef]
- Ando, T. Generalized Schur complements. Linear Algebra Its Appl. 1979, 27, 173–186. [Google Scholar] [CrossRef]
- Vadi, S.; Bayindir, R.; Toplar, Y.; Colak, I. Induction motor control system with a Programmable Logic Controller (PLC) and Profibus communication for industrial plants—An experimental setup. ISA Trans. 2022, 122, 459–471. [Google Scholar] [CrossRef]
- Turcato, A.C.; Negri, L.H.B.L.; Dias, A.L.; Sestito, G.S.; Flauzino, R.A. A cloud-based method for detecting intrusions in profinet communication networks based on anomaly detection. J. Control Autom. Electr. Syst. 2021, 32, 1177–1188. [Google Scholar] [CrossRef]
- Fikriyadi, F.; Ritzkal, R.; Prakosa, B.A. Security Analysis of Wireless Local Area Network (WLAN) Network with the Penetration Testing Method. J. Mantik 2020, 4, 1658–1662. [Google Scholar]
- AlZawaideh, A.; Boiko, I. Analysis of a sliding mode DC–DC boost converter through LPRS of a nonlinear plant. IEEE Trans. Power Electron. 2020, 35, 12321–12331. [Google Scholar] [CrossRef]
- Chen, W.; Saif, M. An iterative learning observer for fault detection and accommodation in nonlinear time-delay systems. Int. J. Robust Nonlinear Control. IFAC-Affil. J. 2006, 16, 1–19. [Google Scholar] [CrossRef]
- Jia, Q.; Chen, W.; Zhang, Y.; Li, H. Fault reconstruction and fault-tolerant control via learning observers in Takagi–Sugeno fuzzy descriptor systems with time delays. IEEE Trans. Ind. Electron. 2015, 62, 3885–3895. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).