BACH: A Tool for Analyzing Blockchain Transactions Using Address Clustering Heuristics
Abstract
1. Introduction
2. Related Work
3. Heuristics Employed
- Multi-input address clustering: identifies groups of addresses by analyzing transactions for which multiple input addresses are used together, assuming they are controlled by the same entity.
- Change address clustering: identifies addresses that receive “change” from bitcoin transactions. When a transaction is made, if the input amount exceeds the output amount, the difference (change) is sent to a new address that is typically controlled by the sender.
- Coinbase address clustering: coinbase transactions, which are the first transactions in a block and reward miners, often direct outputs to specific addresses that are typically controlled by the same mining entity.
3.1. Multi-Input Address Clustering
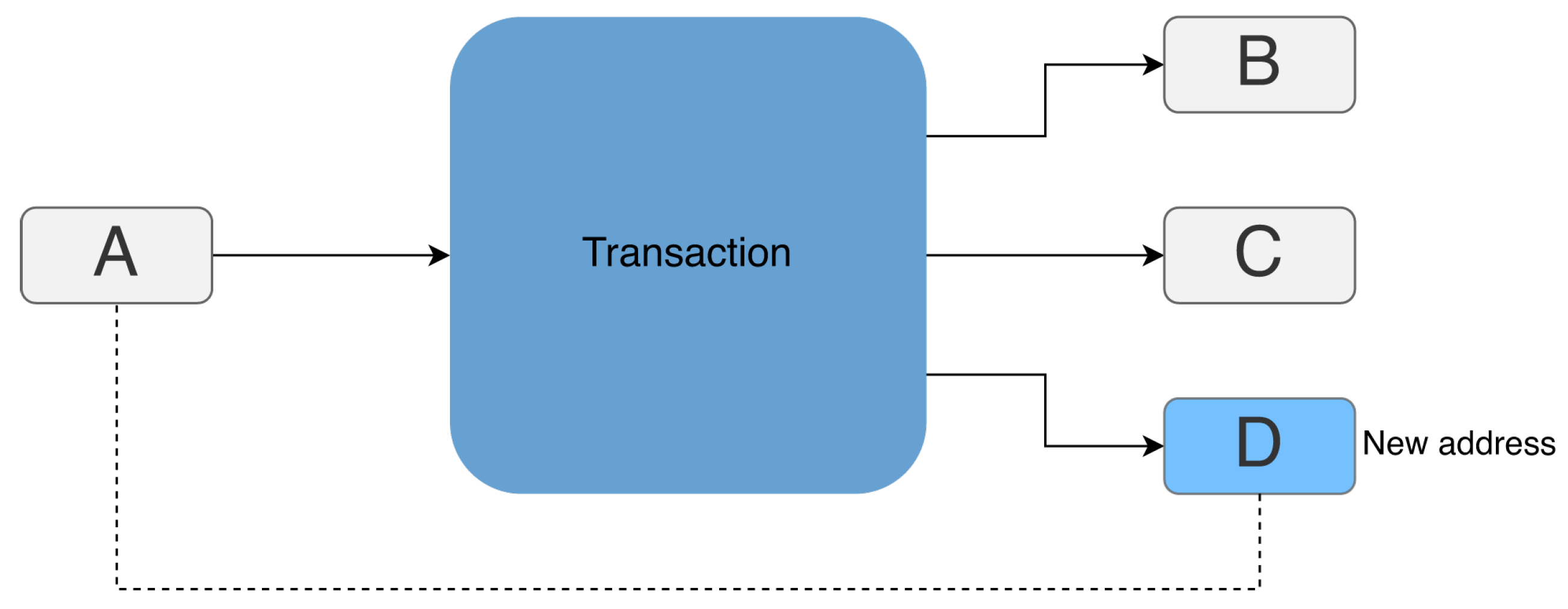
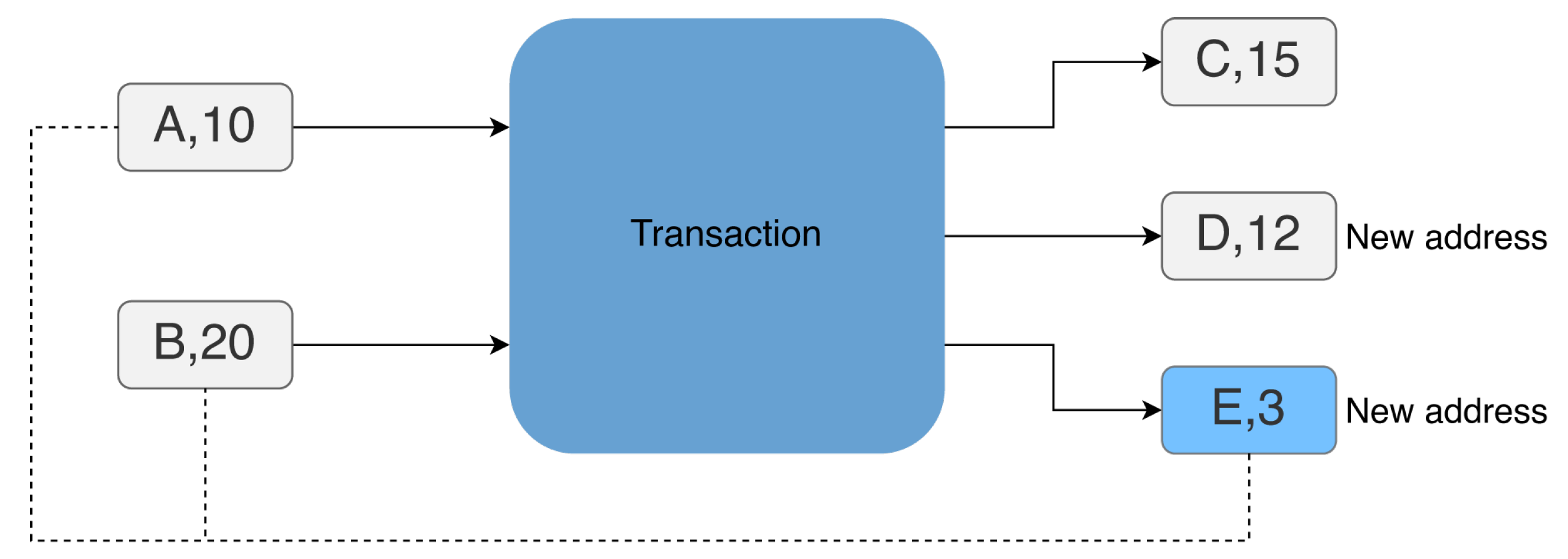
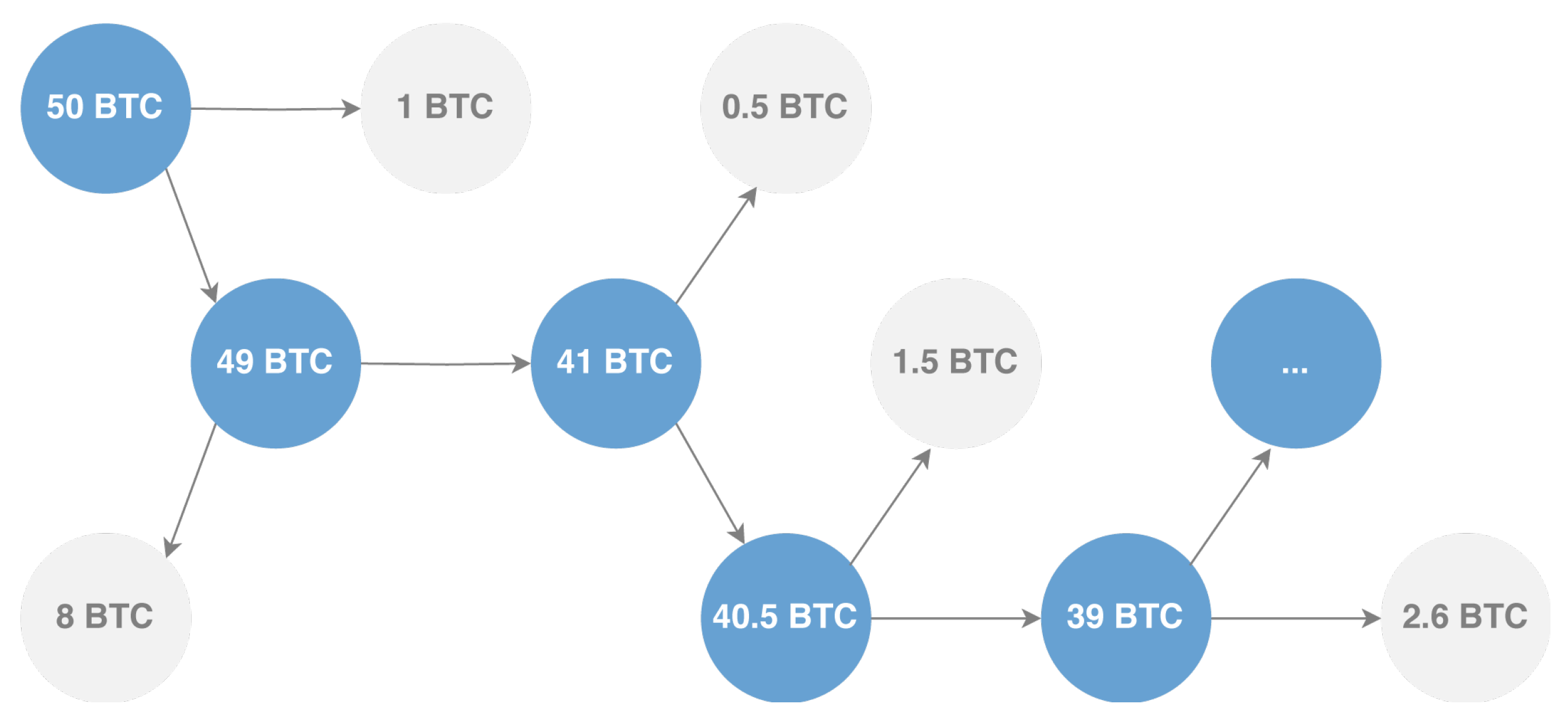
3.2. Change Address Clustering
- 1.
- t is not a coinbase transaction;
- 2.
- ;
- 3.
- ;
- 4.
- ;
- 5.
- ;
- 6.
- .
- Transaction t is not a Coinbase transaction. Miners create this special type of transaction as a reward for successfully mining a new block. This transaction is unique because it is the only way new bitcoins are introduced into circulation.
- There is at least one other output address of t that is different from a.
- For all output addresses of transaction t that are different from a, these addresses must already be recorded on the blockchain (belong to the set A of currently recorded addresses).
- This point is an alternative to the previous one and states that there is at least one output address of transaction t that is different from a and is not already recorded on the blockchain (does not belong to the set A).
- The amount sent to address a is less than the amounts sent to all other output addresses of transaction t.
- There is exactly one address a among the outputs of transaction t for which the amount sent is less than all the amounts of the inputs of transaction t.
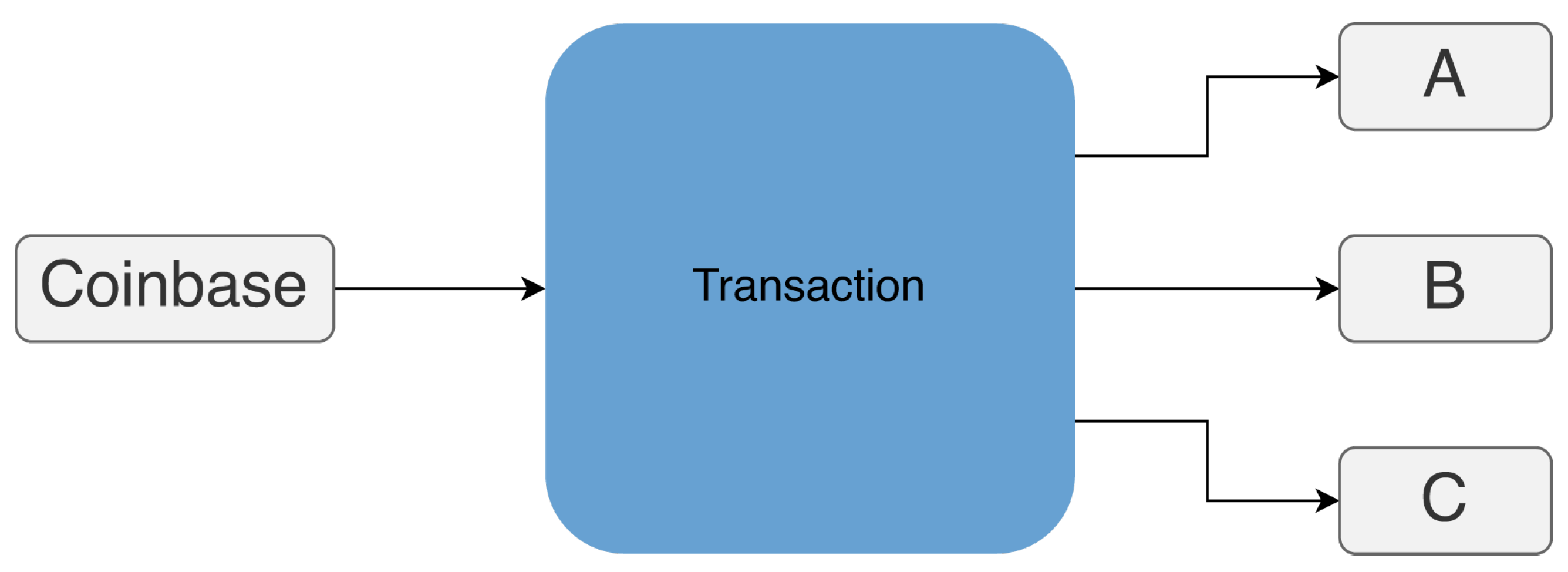
3.3. Coinbase Address Clustering
3.4. Accuracy and Limitations
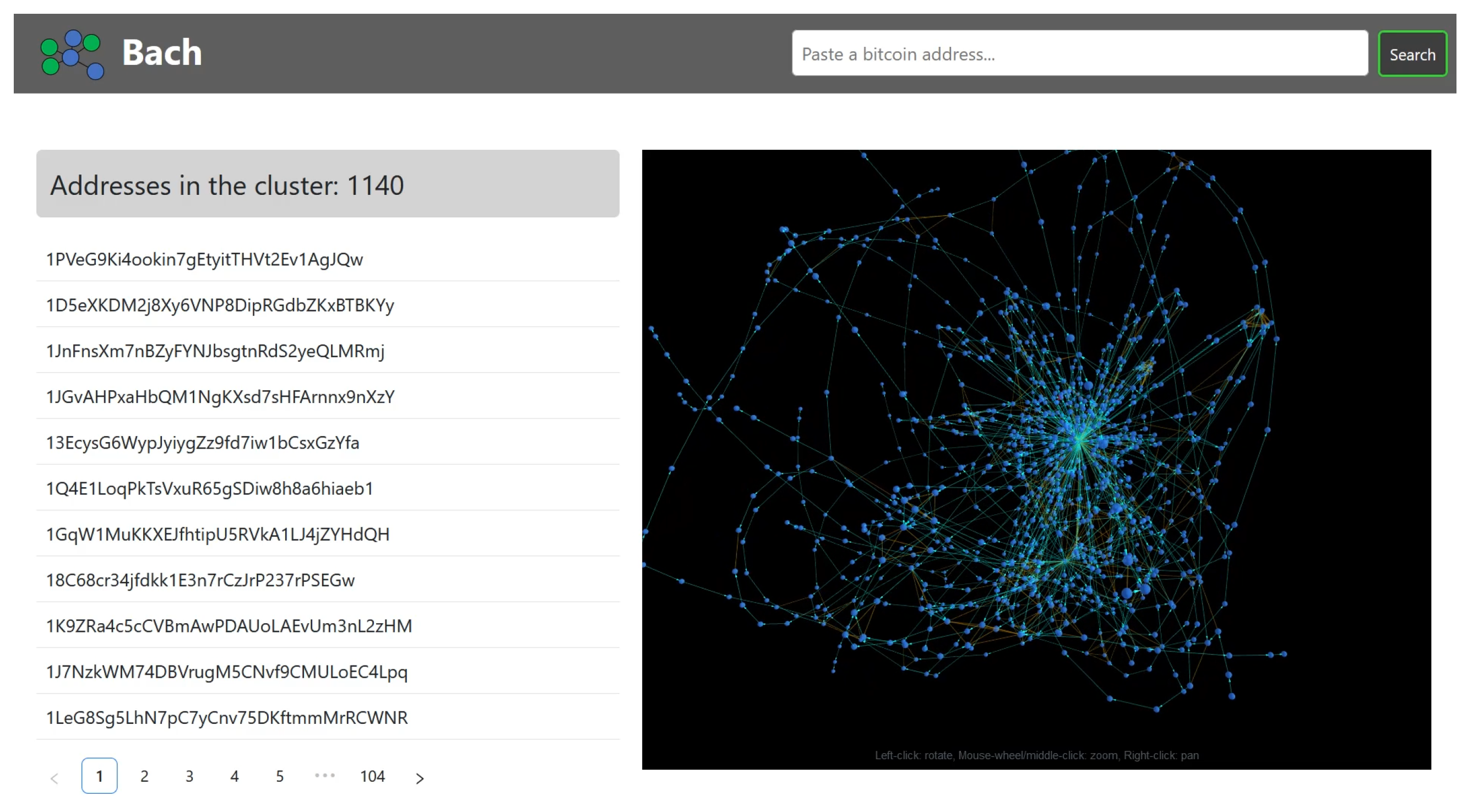
4. BACH
- The database containing the blockchain data;
- The server that provides this data through the database;
- The client that displays the results.
- The client application accepts input from the user and sends an HTTP request to the server;
- The server opens a connection with the database, performs the query, and receives the result;
- The server sends the result obtained to the client application that made the request;
- The client application displays the cluster data received from the server in a 3D graph. (https://github.com/semifredd0/Bach (accessed on 10 September 2024)).
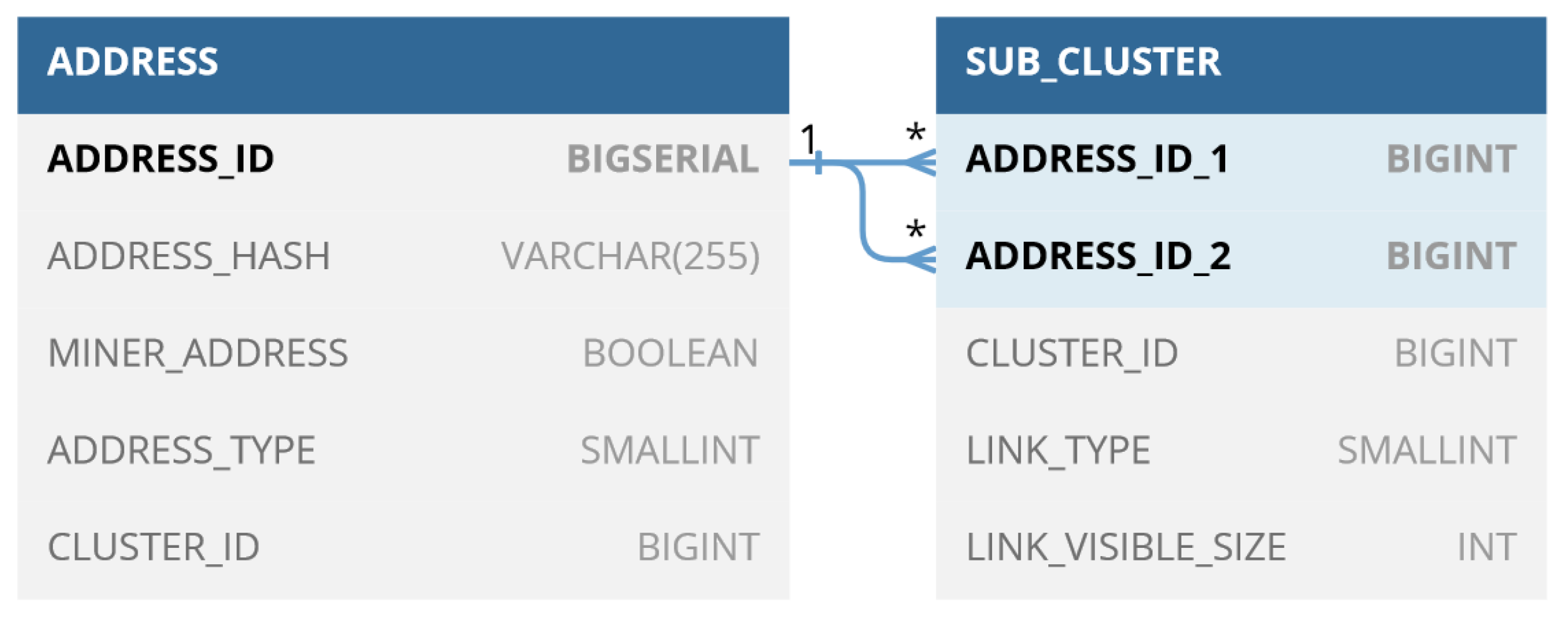
4.1. Database Construction
- create index hash_index on address(address_hash);
- create index subcluster_index on sub_cluster(address_id_1, address_id_2).
4.2. Server Architecture
- GET/{address}: returns all addresses belonging to the address cluster passed as parameter.
- GET/sub/{address}: returns all links between addresses belonging to the cluster of the address passed as a parameter.
- GET/info/{address}: returns all the links of the address passed as a parameter.
4.3. Web Application
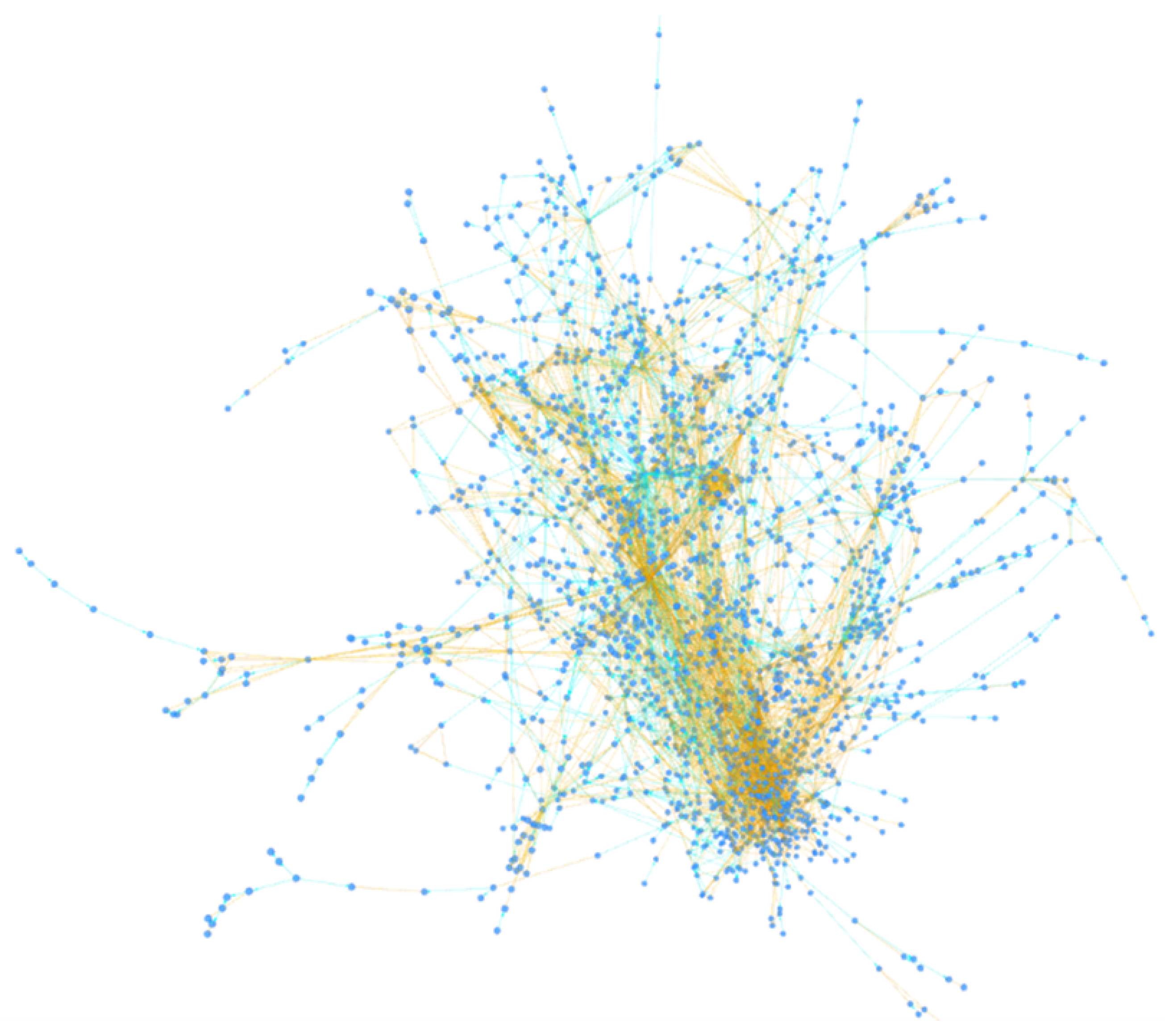
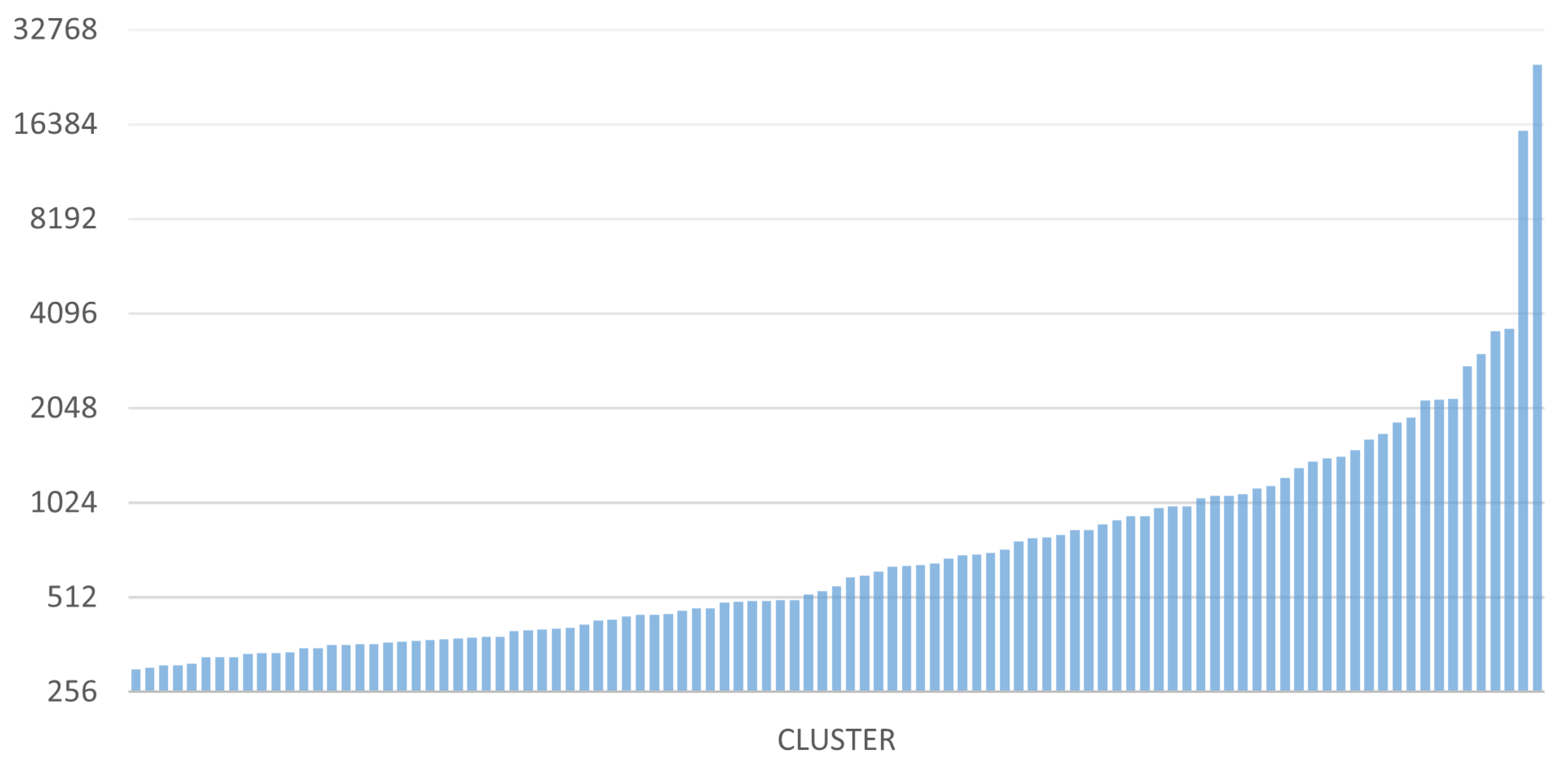
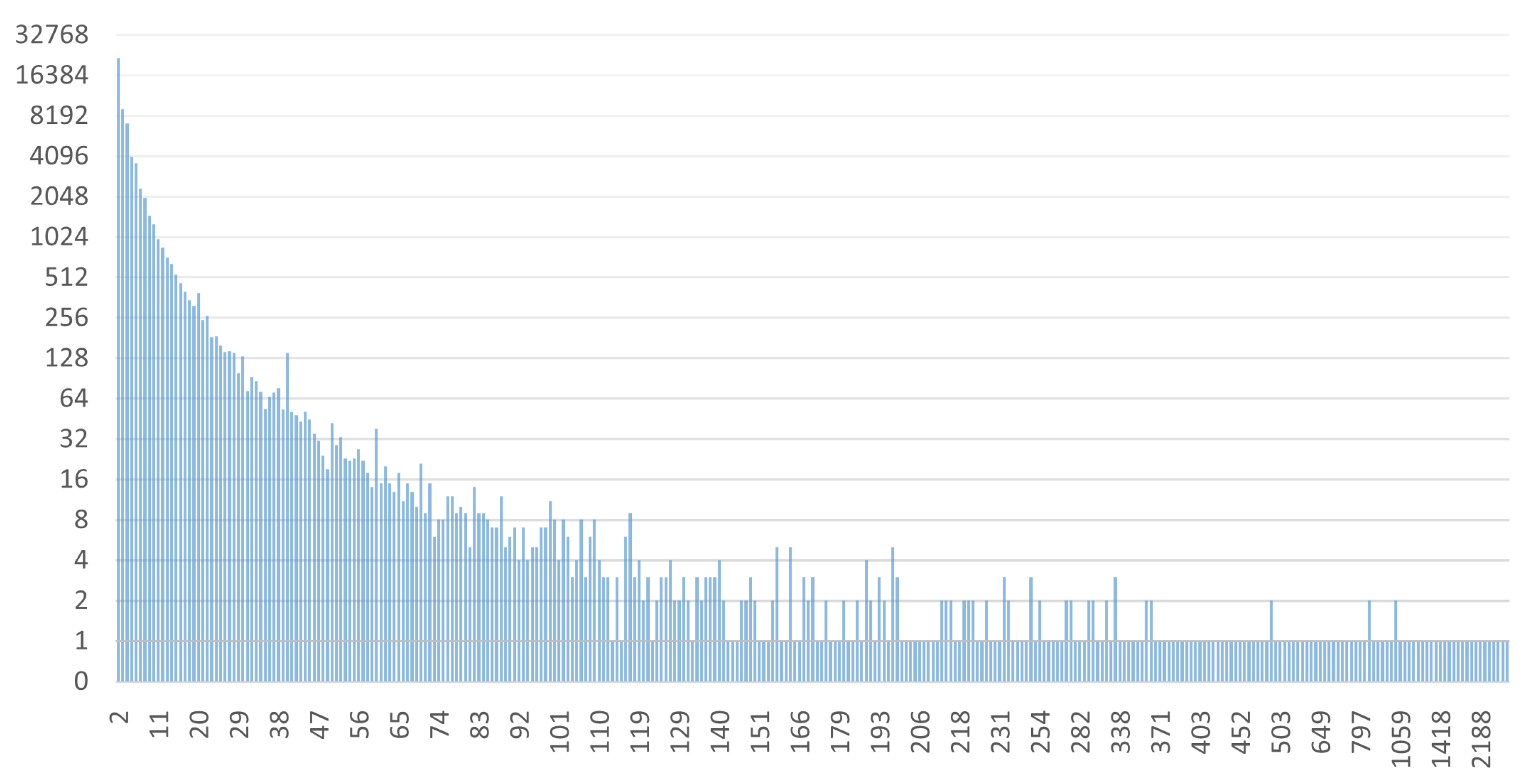
5. Experimentation
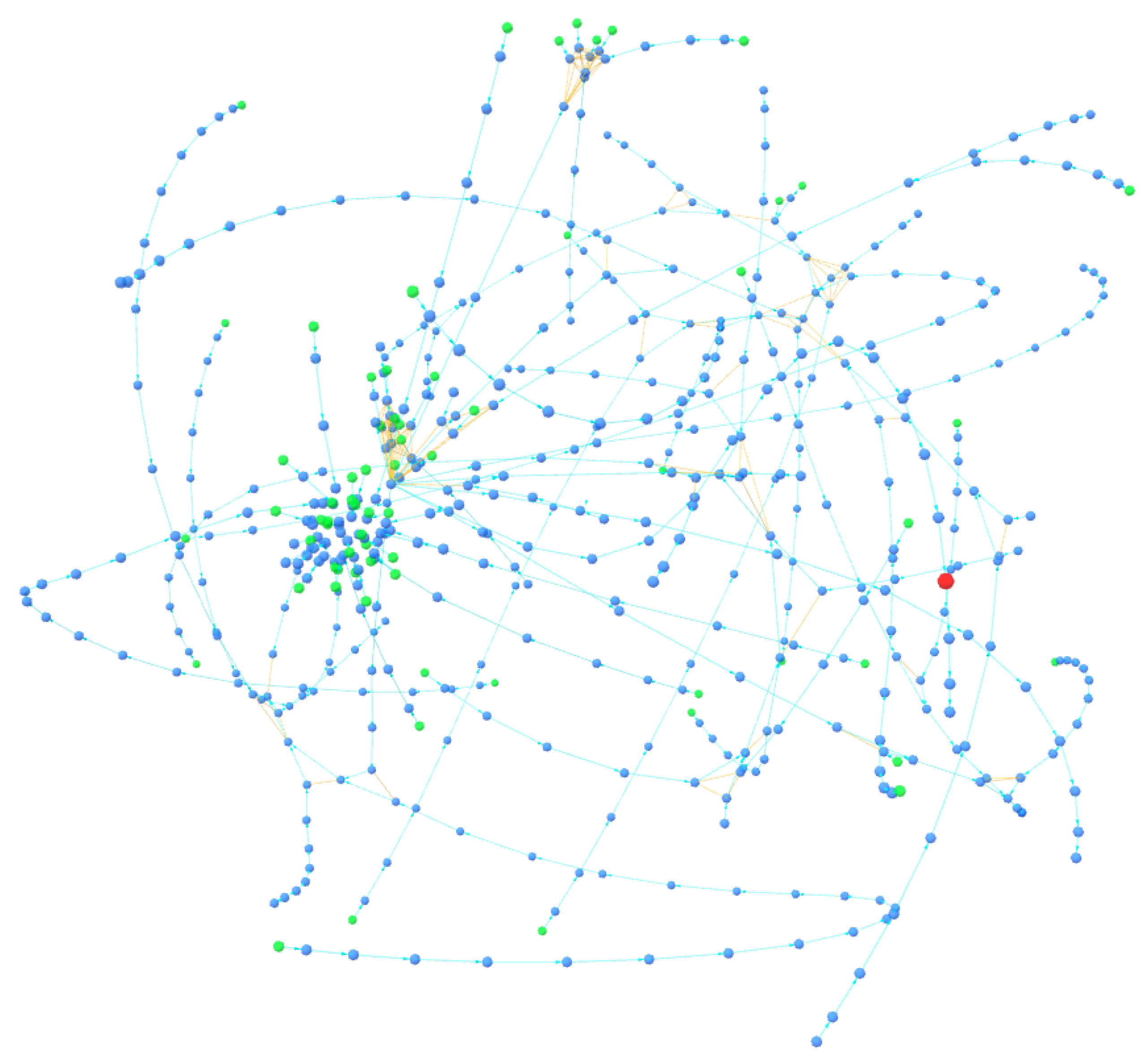
5.1. Detection of Peeling Chains
- Cluster A: 162G6uzHJpmxsM3EQFDLzEYCmx1hxnJtRR;
- Cluster B: 1Lgne9nu4ZzVyfqarr2Mdp8JmhsB3amvA8.
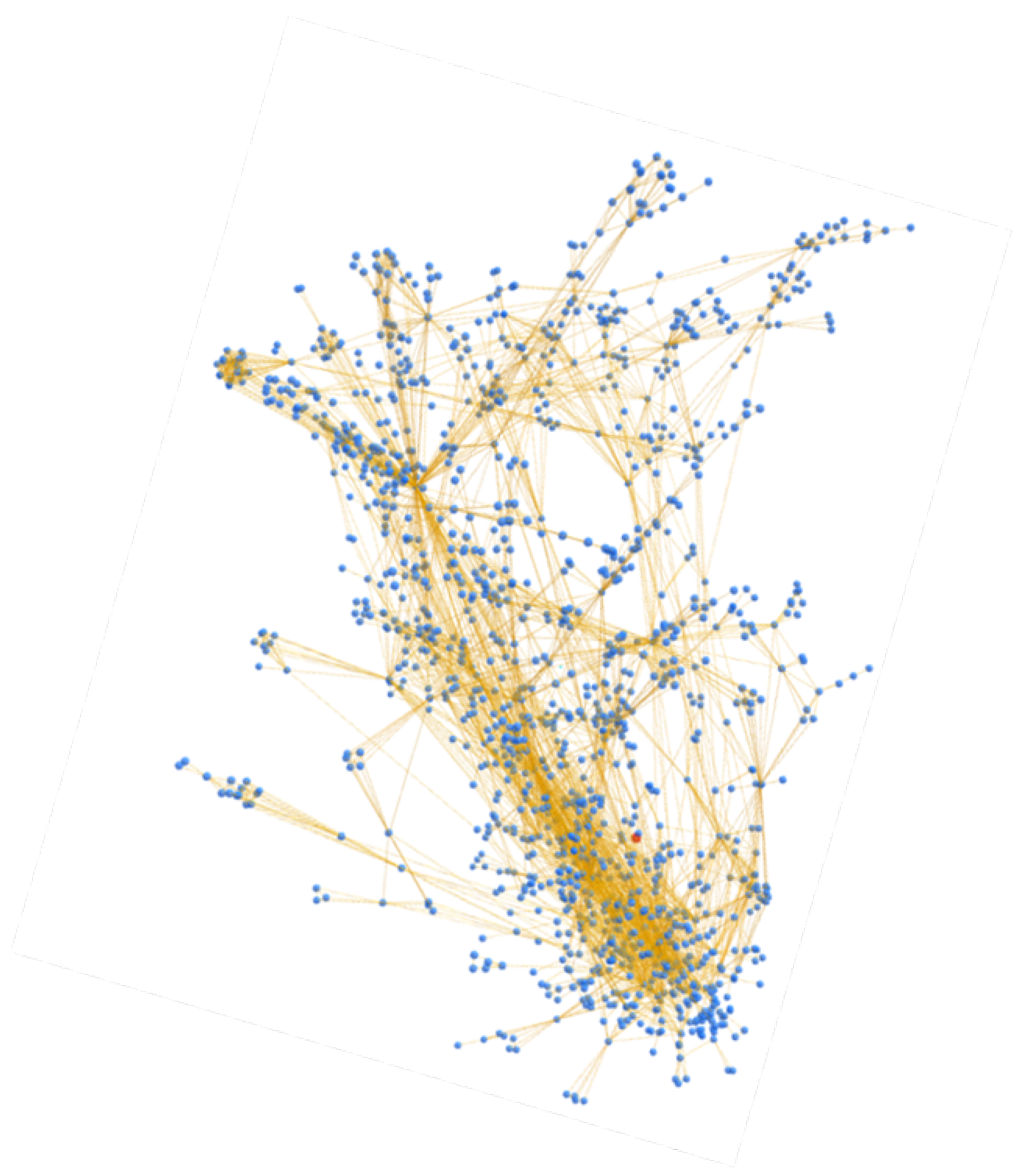
5.2. Comparison to WalletExplorer
- Uses only the multi-input clustering heuristic, thus not aggregating clusters that have a high probability of belonging to the same entity;
- Does not allow visualization of relationships between addresses in the same cluster but merely displays them all in the same table;
- Because of the previous point, it is impossible to visualize the cluster’s internal structure graphically since the relationships are not stored.
6. Conclusions
- Clustering algorithms can sometimes incorrectly link unrelated addresses or fail to link related addresses, leading to false positives and false negatives, respectively. This can result in misidentification and wrongful suspicion of innocent parties. BACH aims to minimize false positives through the use of heuristics and accurate thresholds, but since it is a heuristic approach, perfect results cannot be achieved.
- Criminals continuously evolve their methods to evade detection. Techniques such as using multiple wallets, coin mixing services, and privacy-centric cryptocurrencies can reduce the effectiveness of BACH.
- The sheer volume of bitcoin transactions can pose scalability challenges for BACH. Efficiently processing and analyzing large datasets requires significant computational resources.
- Researchers can update the algorithm by adding new clustering heuristics. These enhancements could improve the accuracy of address clustering and enable the identification of more complex transaction patterns.
- The integration of machine learning algorithms could be used to find common patterns within clusters and classify other similar entities that, despite following the same model, have not yet been classified. For example, the clusters of major bitcoin services (exchanges, mining pools, etc.) could be analyzed, and features could be extracted from the transactions. These large entities often execute a high volume of transactions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://www.ussc.gov/sites/default/files/pdf/training/annual-national-training-seminar/2018/Emerging_Tech_Bitcoin_Crypto.pdf (accessed on 10 September 2024).
- Raju, R.S.; Gurung, S.; Rai, P. An overview of 51% attack over Bitcoin network. In Contemporary Issues in Communication, Cloud and Big Data Analytics: Proceedings of CCB 2020; Springer: Berlin/Heidelberg, Germany, 2022; pp. 39–55. [Google Scholar]
- Kaminsky, D. Some Thoughts on Bitcoin. Available online: https://dankaminsky.com/2011/08/05/bo2k11/ (accessed on 25 June 2024).
- Irwin, A.S.; Turner, A.B. Illicit Bitcoin transactions: Challenges in getting to the who, what, when and where. J. Money Laund. Control 2018, 21, 297–313. [Google Scholar] [CrossRef]
- Meiklejohn, S.; Pomarole, M.; Jordan, G.; Levchenko, K.; McCoy, D.; Voelker, G.M.; Savage, S. A fistful of bitcoins: Characterizing payments among men with no names. In Proceedings of the 2013 Internet Measurement Conference, Barcelona, Spain, 23–25 October 2013; pp. 127–140. [Google Scholar]
- Shojaeinasab, A.; Motamed, A.P.; Bahrak, B. Mixing detection on bitcoin transactions using statistical patterns. IET Blockchain 2023, 3, 136–148. [Google Scholar] [CrossRef]
- Hong, Y.; Kwon, H.; Lee, J.; Hur, J. A practical de-mixing algorithm for bitcoin mixing services. In Proceedings of the 2nd ACM Workshop on Blockchains, Cryptocurrencies, and Contracts, Incheon, Republic of Korea, 4 June 2018; pp. 15–20. [Google Scholar]
- Wu, J.; Liu, J.; Chen, W.; Huang, H.; Zheng, Z.; Zhang, Y. Detecting mixing services via mining bitcoin transaction network with hybrid motifs. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 2237–2249. [Google Scholar] [CrossRef]
- De Balthasar, T.; Hernandez-Castro, J. An analysis of bitcoin laundry services. In Proceedings of the Secure IT Systems: 22nd Nordic Conference, NordSec 2017, Tartu, Estonia, 8–10 November 2017; Proceedings 22. Springer: Berlin/Heidelberg, Germany, 2017; pp. 297–312. [Google Scholar]
- Kokash, N. An Introduction to Heuristic Algorithms; Department of Informatics and Telecommunications: Trento, Italy, 2005; pp. 1–8. [Google Scholar]
- Kinkeldey, C.; Fekete, J.D.; Isenberg, P. Bitconduite: Visualizing and analyzing activity on the bitcoin network. In Proceedings of the EuroVis 2017—Eurographics Conference on Visualization, Posters Track, Barcelona, Spain, 12–16 June 2017; p. 3. [Google Scholar]
- Yue, X.; Shu, X.; Zhu, X.; Du, X.; Yu, Z.; Papadopoulos, D.; Liu, S. Bitextract: Interactive visualization for extracting bitcoin exchange intelligence. IEEE Trans. Vis. Comput. Graph. 2018, 25, 162–171. [Google Scholar] [CrossRef] [PubMed]
- Tovanich, N.; Heulot, N.; Fekete, J.D.; Isenberg, P. Visualization of blockchain data: A systematic review. IEEE Trans. Vis. Comput. Graph. 2019, 27, 3135–3152. [Google Scholar] [CrossRef] [PubMed]
- Androulaki, E.; Karame, G.O.; Roeschlin, M.; Scherer, T.; Capkun, S. Evaluating user privacy in bitcoin. In Proceedings of the Financial Cryptography and Data Security: 17th International Conference, FC 2013, Okinawa, Japan, 1–5 April 2013; Revised Selected Papers 17. Springer: Berlin/Heidelberg, Germany, 2013; pp. 34–51. [Google Scholar]
- Ermilov, D.; Panov, M.; Yanovich, Y. Automatic bitcoin address clustering. In Proceedings of the 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), Cancun, Mexico, 18–21 December 2017; pp. 461–466. [Google Scholar]
- Zhang, Y.; Wang, J.; Luo, J. Heuristic-based address clustering in bitcoin. IEEE Access 2020, 8, 210582–210591. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Shi, K.; Zhang, H. Improving Address Clustering in Bitcoin by Proposing Heuristics. IEEE Trans. Netw. Serv. Manag. 2022, 19, 3737–3749. [Google Scholar] [CrossRef]
- Zheng, B.; Zhu, L.; Shen, M.; Du, X.; Guizani, M. Identifying the vulnerabilities of bitcoin anonymous mechanism based on address clustering. Sci. China Inf. Sci. 2020, 63, 1–15. [Google Scholar] [CrossRef]
- Lewenberg, Y.; Bachrach, Y.; Sompolinsky, Y.; Zohar, A.; Rosenschein, J.S. Bitcoin mining pools: A cooperative game theoretic analysis. In Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems, Istanbul, Turkey, 4–8 May 2015; pp. 919–927. [Google Scholar]
- Reid, F.; Harrigan, M. An Analysis of Anonymity in the Bitcoin System. In Proceedings of the 2011 IEEE Third International Conference on Privacy, Security, Risk and Trust and 2011 IEEE Third International Conference on Social Computing, Boston, MA, USA, 9–11 October 2011; pp. 1318–1326. [Google Scholar] [CrossRef]
- Ron, D.; Shamir, A. Quantitative Analysis of the Full Bitcoin Transaction Graph. In Financial Cryptography and Data Security; Sadeghi, A.R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 6–24. [Google Scholar]
- Spagnuolo, M.; Maggi, F.; Zanero, S. BitIodine: Extracting Intelligence from the Bitcoin Network. In Financial Cryptography and Data Security; Christin, N., Safavi-Naini, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 457–468. [Google Scholar]
- Maxwell, G. Coinjoin: Bitcoin Privacy for the Real World. Available online: https://bitcointalk.org/?topic=279249 (accessed on 25 June 2024).
- Gong, Y.; Chow, K.P.; Ting, H.F.; Yiu, S.M. Analyzing the error rates of bitcoin clustering heuristics. In Proceedings of the IFIP International Conference on Digital Forensics, Virtual, 3–5 January 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 187–205. [Google Scholar]
- Chang, T.H.; Svetinovic, D. Improving bitcoin ownership identification using transaction patterns analysis. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 9–20. [Google Scholar] [CrossRef]
- Hercog, U.; Povše, A. Taint analysis of the Bitcoin network. arXiv 2019, arXiv:1907.01538. [Google Scholar]










| Indicators | WalletExplorer | BACH |
|---|---|---|
| Number of total clusters | 54,441 | 62,865 |
| Number of total relations | 3,597,427 | 4,315,813 |
| Size of the largest cluster | 10,084 | 25,377 |
| Database size | 4074 MB | 6454 MB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caringella, M.; Violante, F.; De Lucci, F.; Galantucci, S.; Costantini, M. BACH: A Tool for Analyzing Blockchain Transactions Using Address Clustering Heuristics. Information 2024, 15, 589. https://doi.org/10.3390/info15100589
Caringella M, Violante F, De Lucci F, Galantucci S, Costantini M. BACH: A Tool for Analyzing Blockchain Transactions Using Address Clustering Heuristics. Information. 2024; 15(10):589. https://doi.org/10.3390/info15100589
Chicago/Turabian StyleCaringella, Michele, Francesco Violante, Francesco De Lucci, Stefano Galantucci, and Matteo Costantini. 2024. "BACH: A Tool for Analyzing Blockchain Transactions Using Address Clustering Heuristics" Information 15, no. 10: 589. https://doi.org/10.3390/info15100589
APA StyleCaringella, M., Violante, F., De Lucci, F., Galantucci, S., & Costantini, M. (2024). BACH: A Tool for Analyzing Blockchain Transactions Using Address Clustering Heuristics. Information, 15(10), 589. https://doi.org/10.3390/info15100589







