Component Recognition and Coordinate Extraction in Two-Dimensional Paper Drawings Using SegFormer
Abstract
:1. Introduction
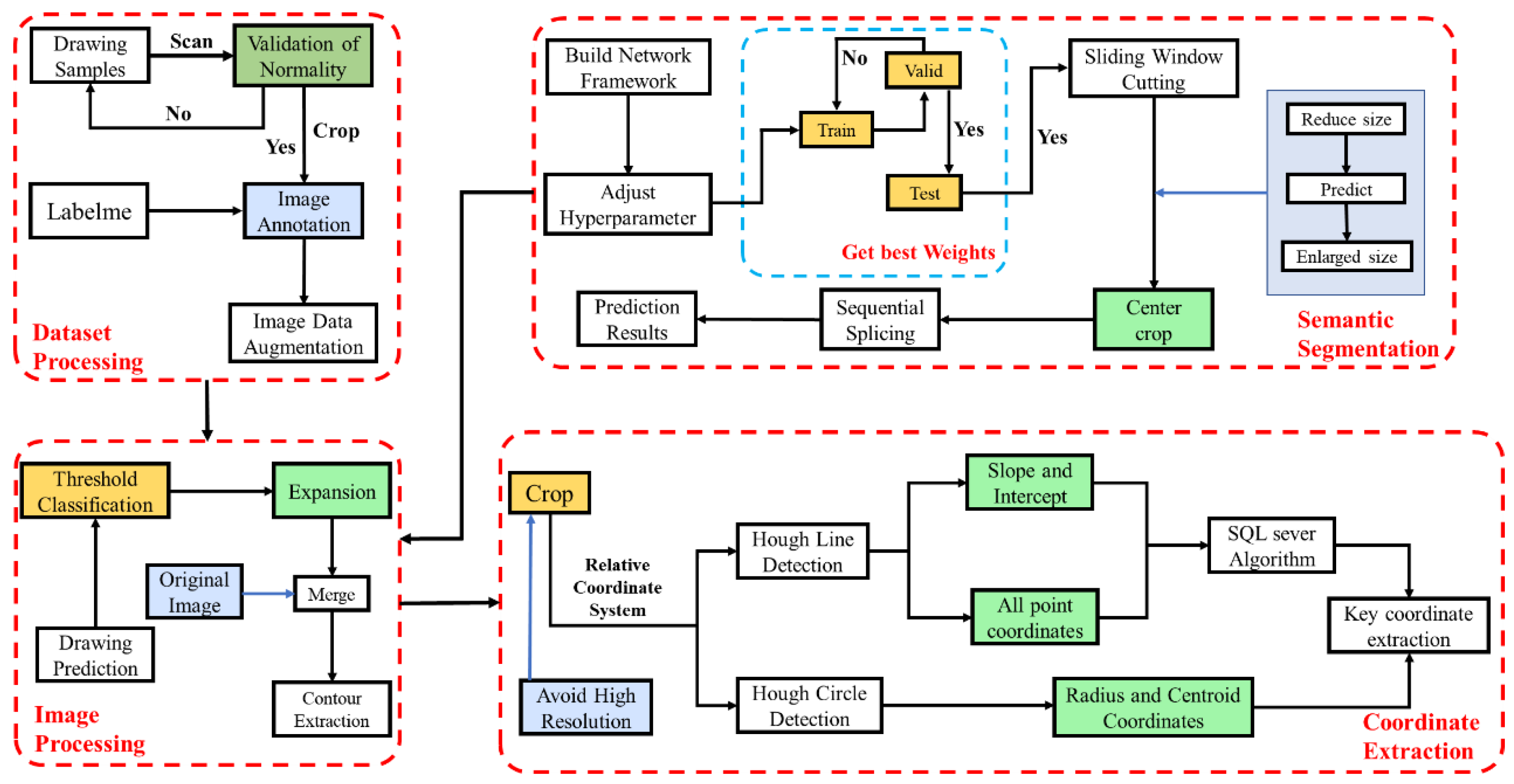
2. Methodology
2.1. SegFormer Network
2.2. Data Set
2.2.1. Image Noise Reduction Processing
2.2.2. Adaptive Augmentation for Image Data Set Optimization
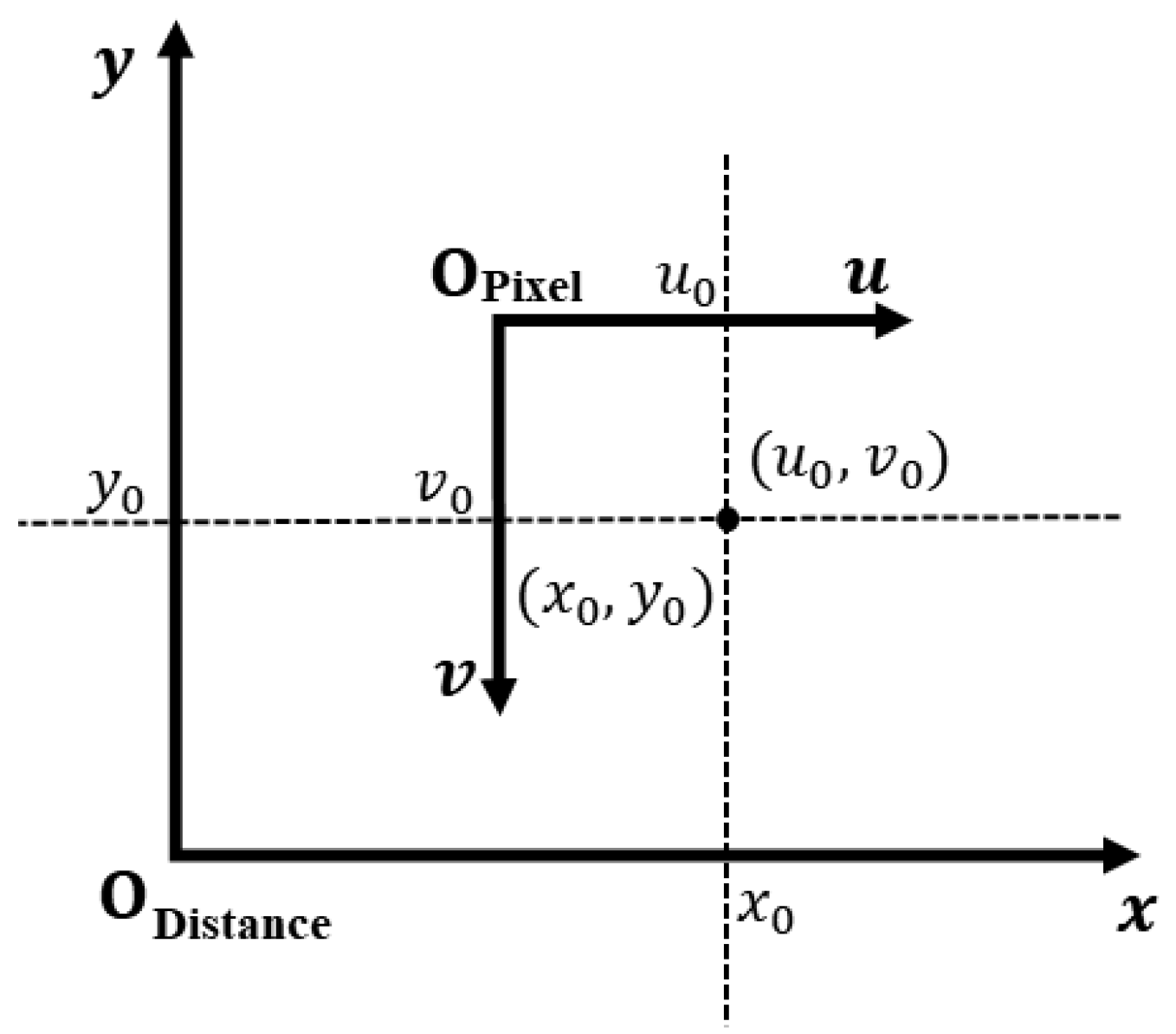
2.3. Coordinate System Processing
2.4. Image Processing
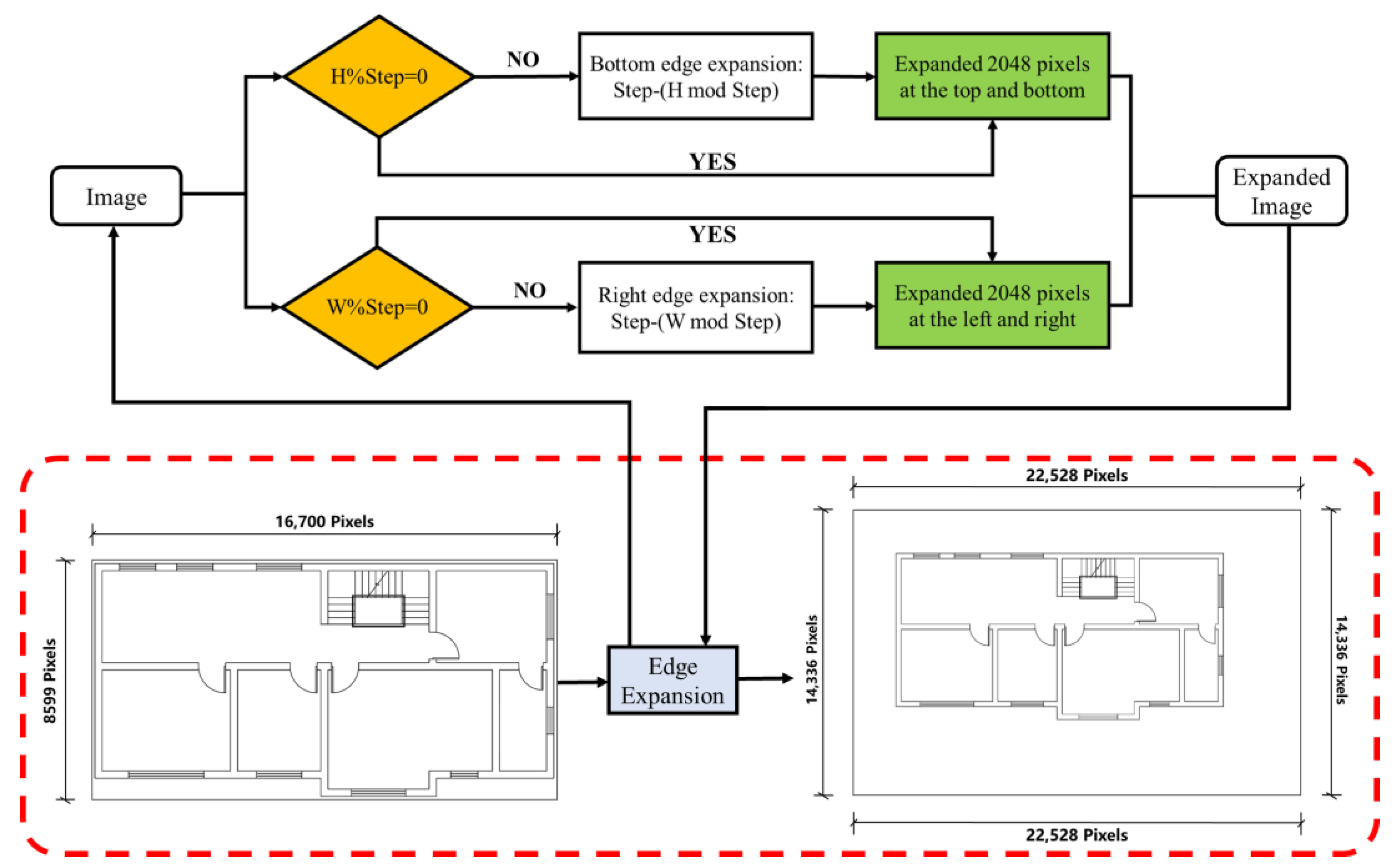
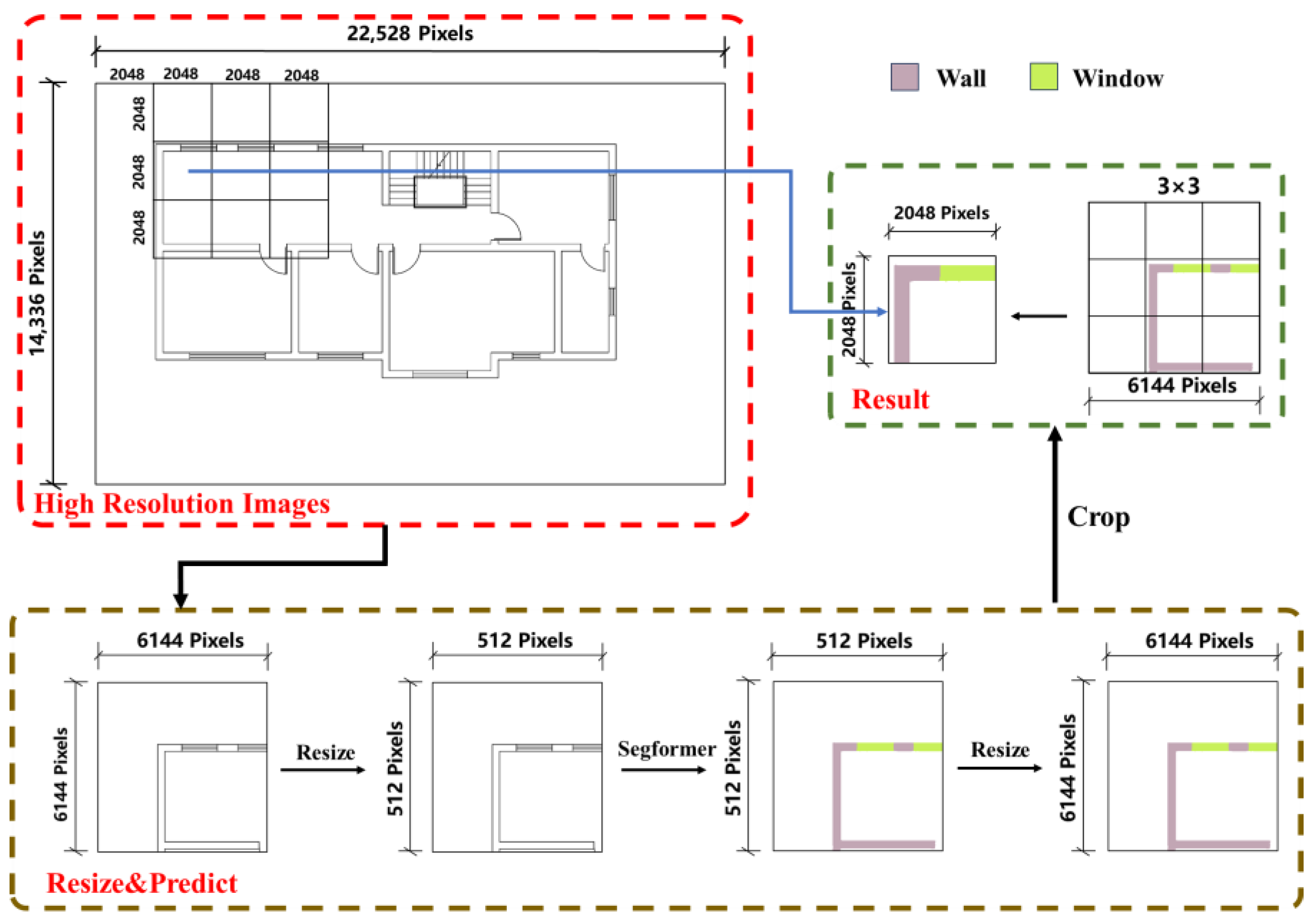
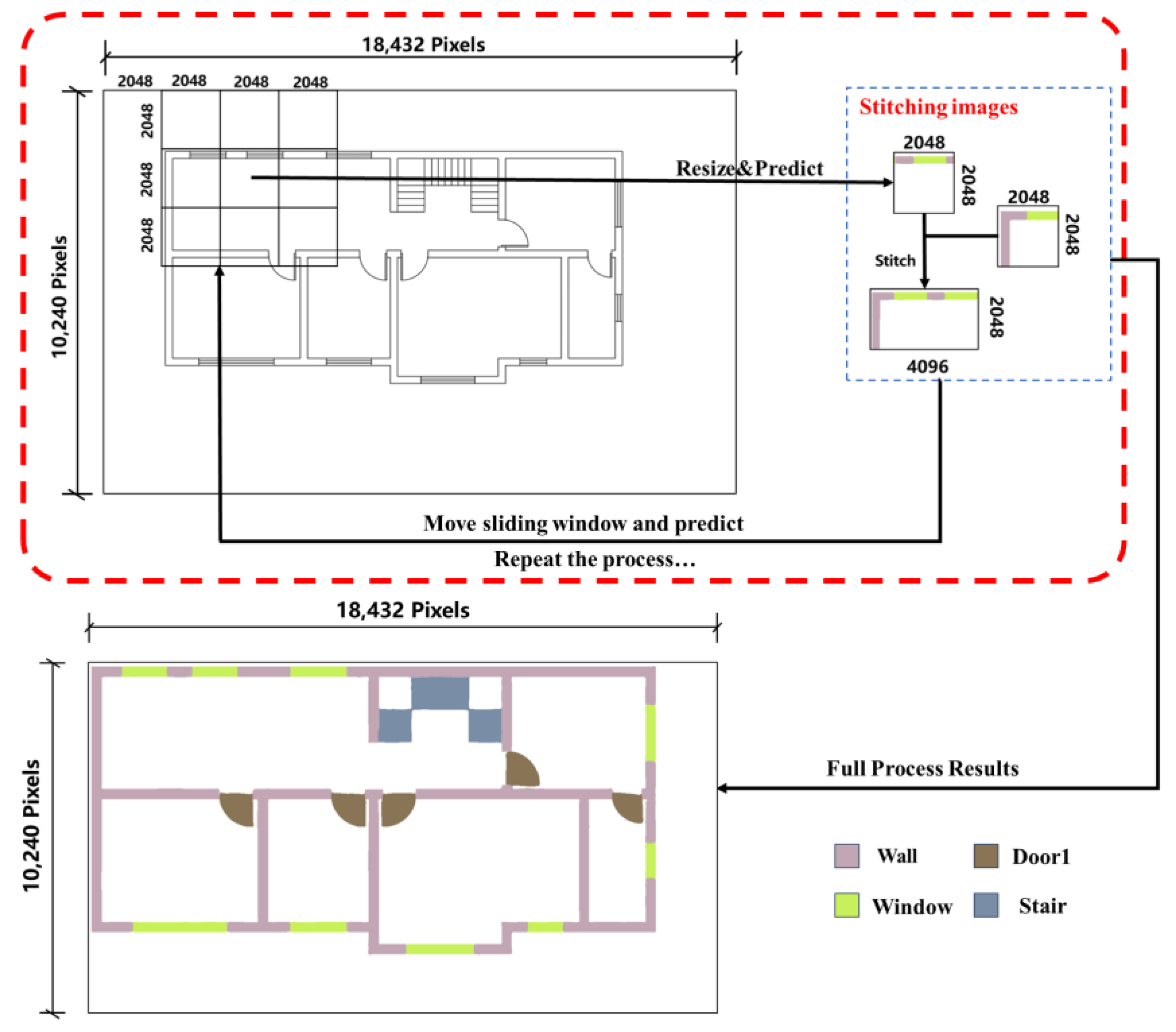
2.4.1. Semantic Segmentation Using the “Edge Expansion Sliding Window Cropping Method”
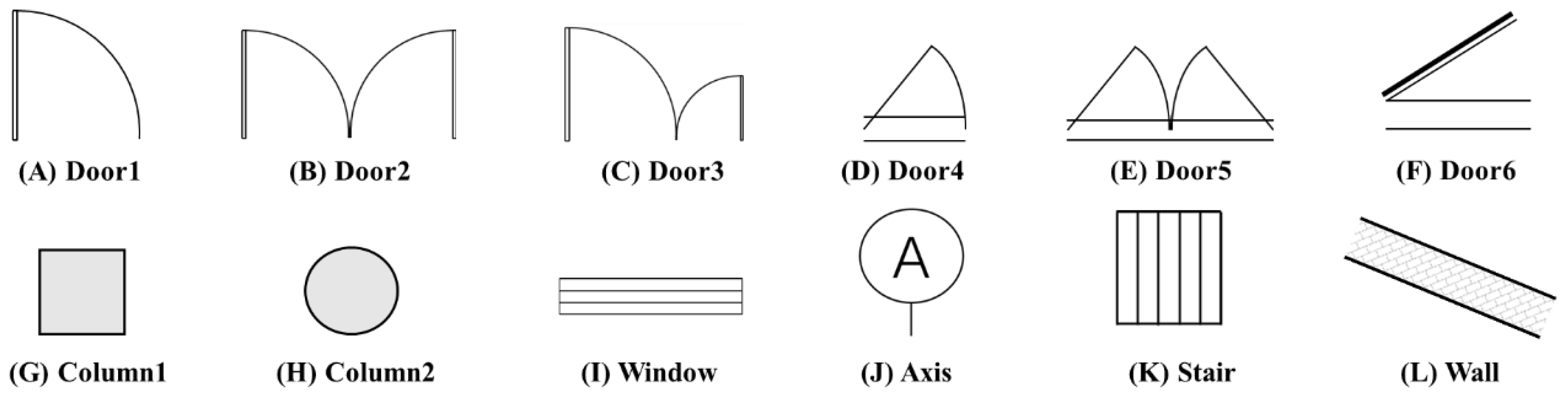
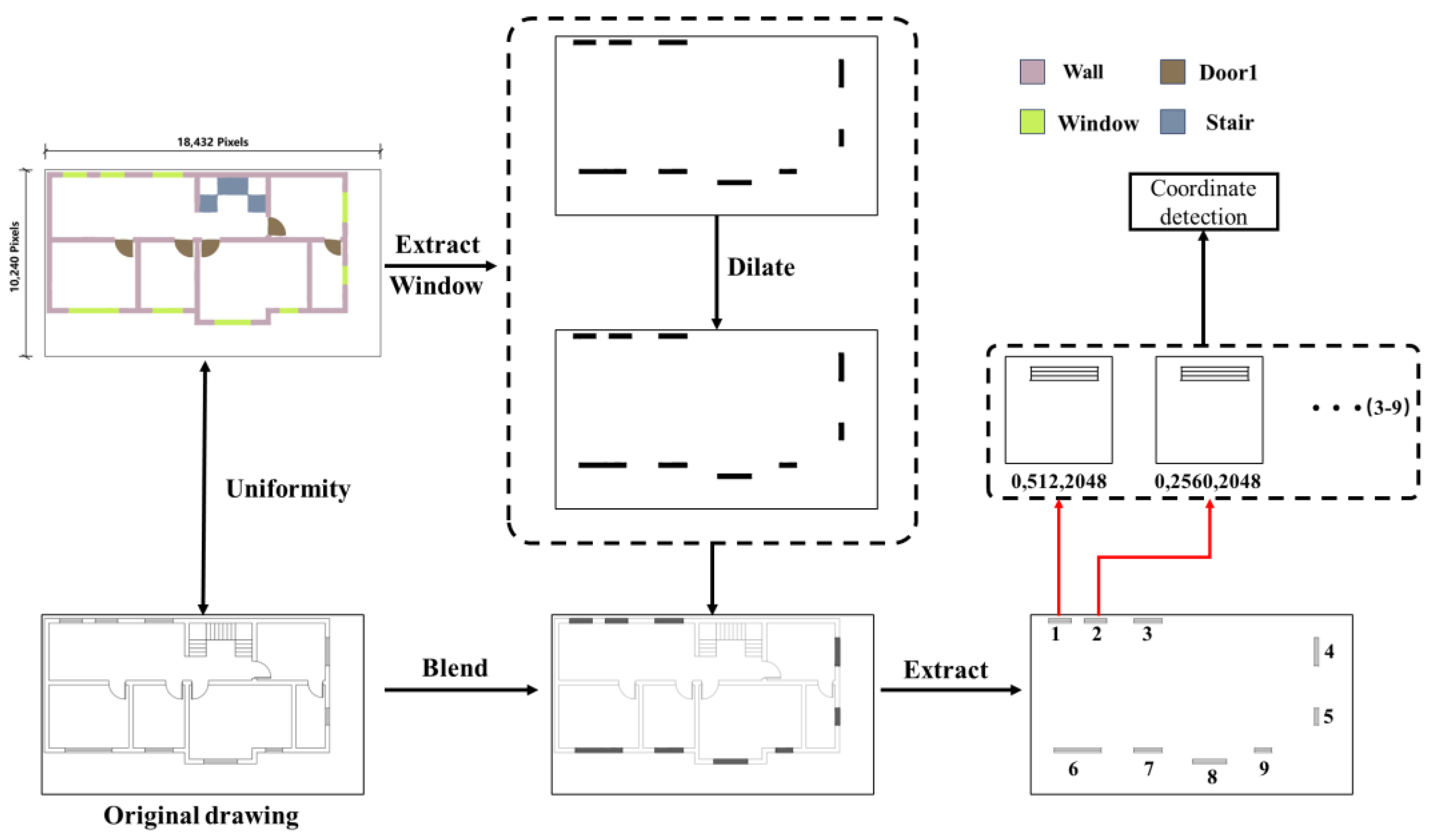
2.4.2. Classification and Contour Extraction Using Color Space
2.5. Hough Transform
2.5.1. Probabilistic Hough Line Detection
2.5.2. Hough Circle Detection
2.6. Querying and Outputting Coordinates Using SQL Server
3. Experiments
3.1. Experimental Environment
3.2. Characteristics and Partitioning of the Data Set
- Independent Single-Target (13%): Isolated entities such as columns and walls;
- Single-Target Intersecting (8%): Overlapping elements of a single category, e.g., intersecting beams;
- Double-Target Intersecting (51%): Common combinations like walls with doors or columns;
- Multi-Target Connected (28%): Complex intersections involving multiple component types, such as walls with doors and windows.
3.3. Characteristics and Partitioning of the Data Set
3.4. Hyperparameter Settings
3.5. Drawing Selection and Coordinate Detection
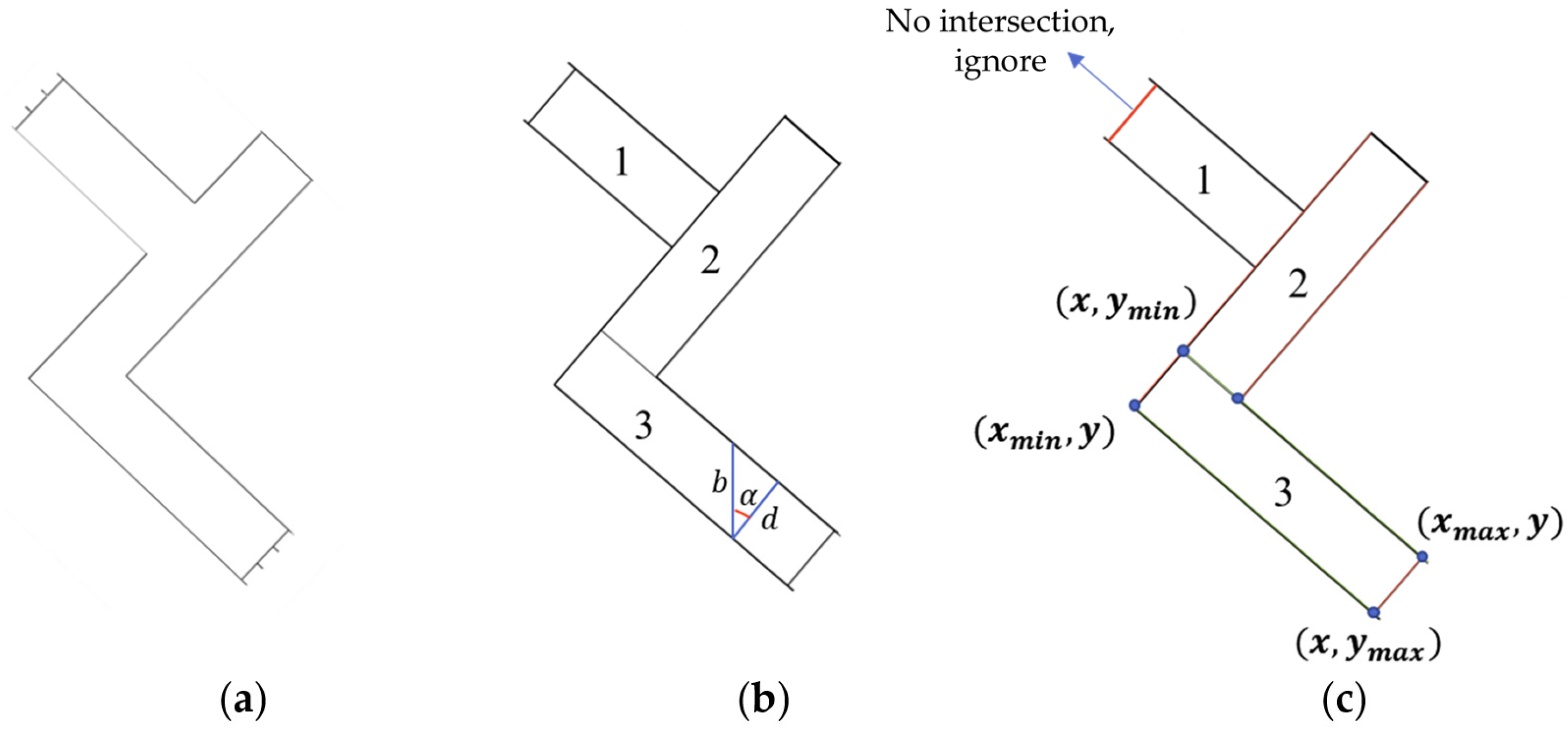
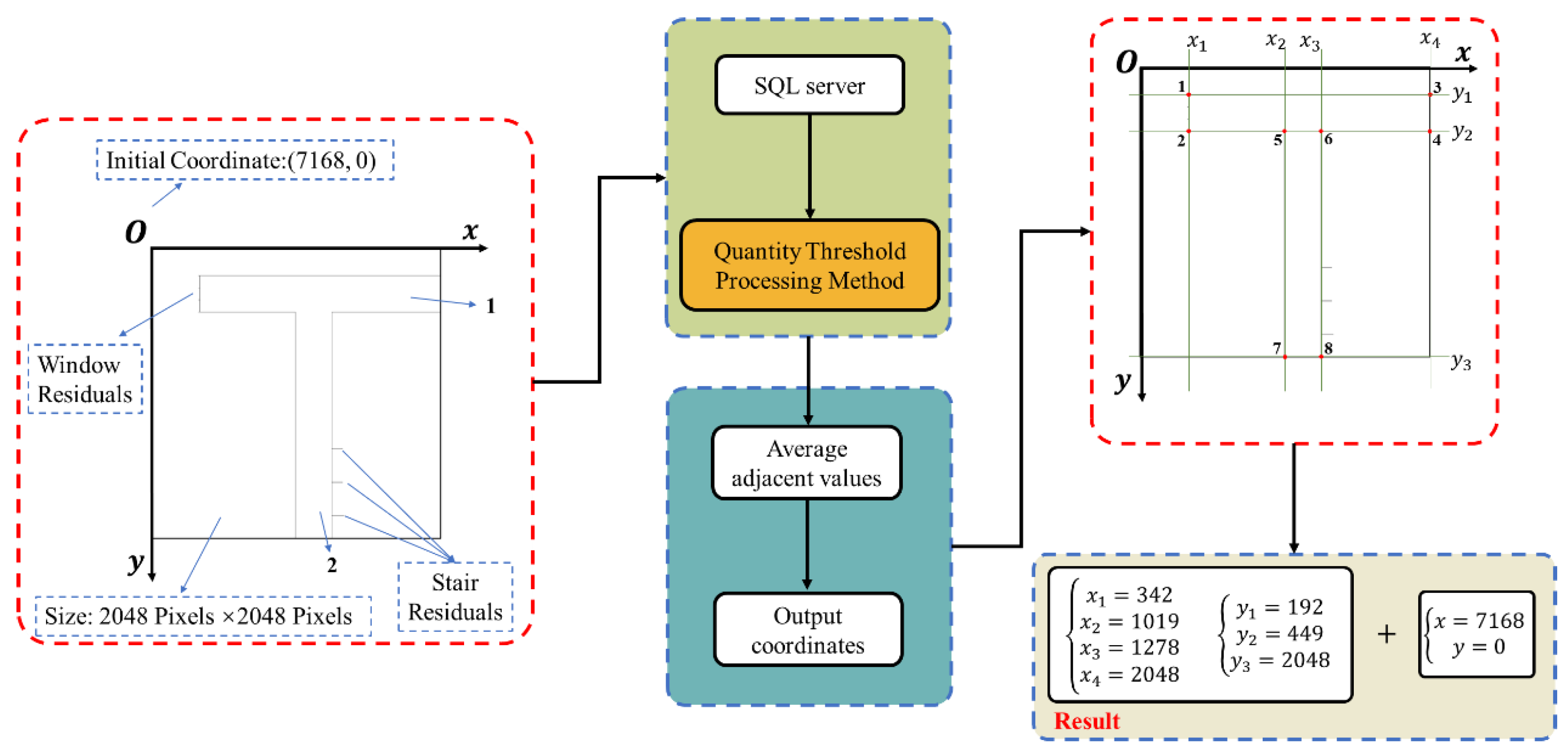
3.5.1. Components Composed of Line Segments with Zero or Infinite Slope
3.5.2. Components Composed of Line Segments with Constant Slope
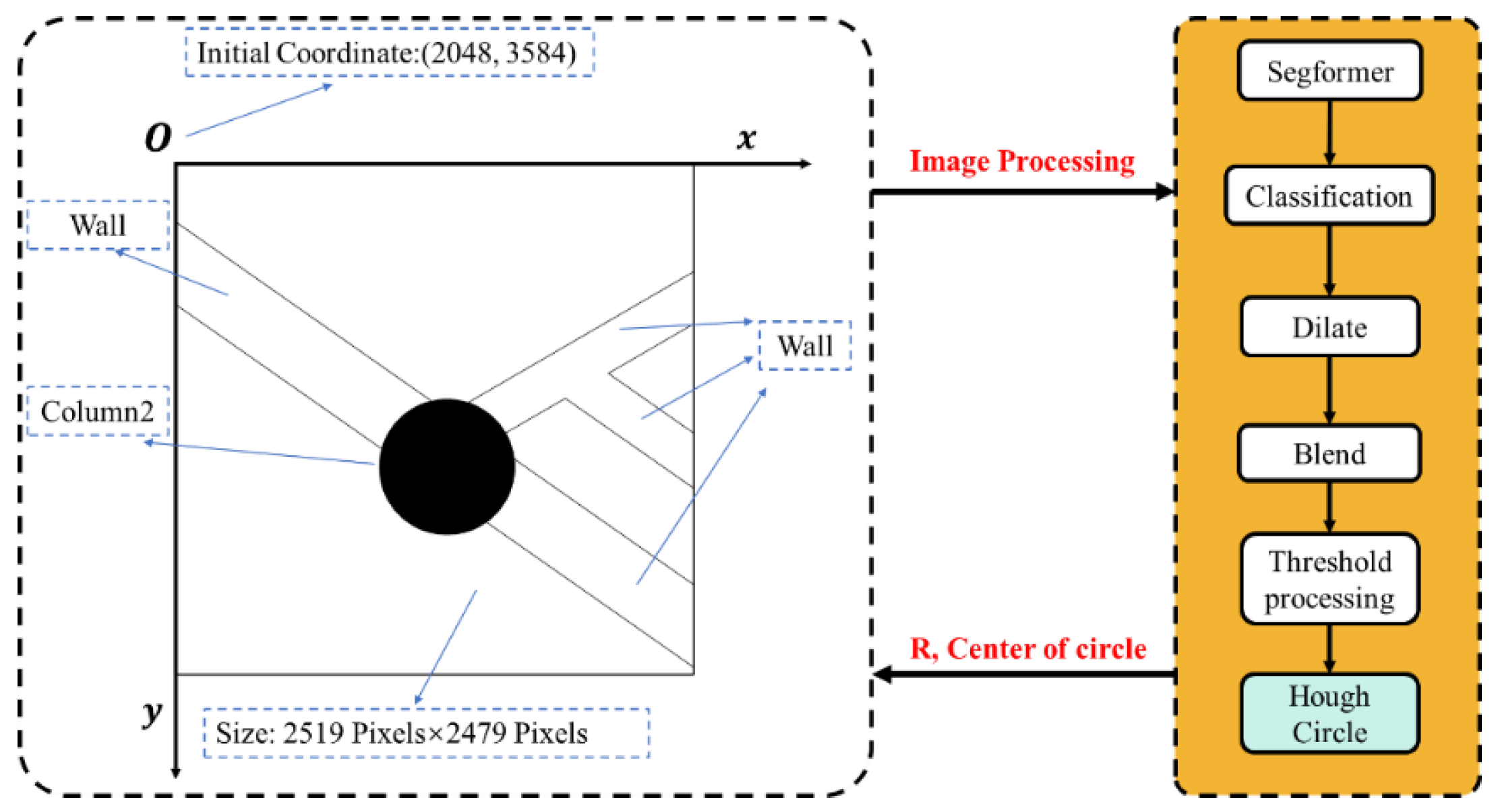
3.5.3. Circular Components
4. Results and Discussion
4.1. Performance Analysis of Deep Learning
4.1.1. Comparison of Deep Learning Models
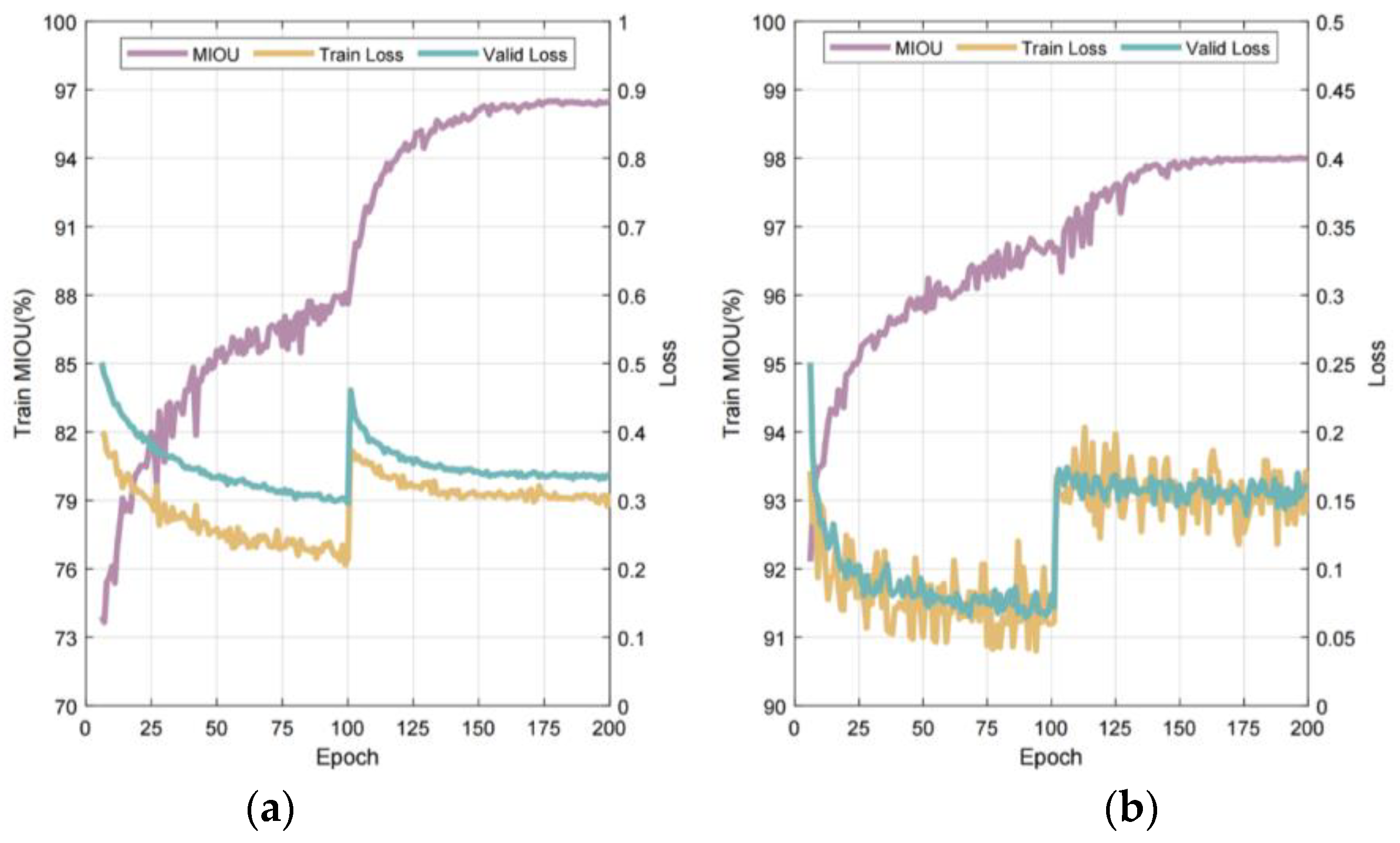
4.1.2. Training Monitoring Analysis with Established Hyperparameter Configuration
4.1.3. Training Monitoring Analysis with Established Hyperparameter Configuration
4.2. Conclusions and Analysis of Component Coordinate Detection
4.2.1. Detection of Component Coordinates with Segments Formed by Slopes of Zero or Infinity
4.2.2. Coordinate Detection of Components with Segments Formed by Constant Slopes
4.2.3. Detection of Component Coordinates with Segments Formed by Slopes of Zero or Infinity
4.3. Limitation
5. Conclusions
- The framework classifies components in two-dimensional blueprints using semantic data. Analyses include deep learning network selection, data set training, and error rates across categories. Notably, the ‘Edge Expansion Sliding Window Cropping Method’ was effective in high-resolution semantic segmentation, with the networks achieving IOU scores of 96.44% and 98.01%. Generally, prediction errors for component categories were below 0.5%, indicating standardized data sets and the precision and robustness of the models;
- By extracting semantic information, inflation and blending techniques effectively separate the target component’s contour in two-dimensional blueprints, minimizing irrelevant contour noise. Semantic segmentation’s classification properties refine coordinate detection on the processed blueprint, curtailing interference and errors;
- The integration of the “Quantity Threshold Processing Method” with SQL Server and algorithms such as the “Coordinate Local Extremum Method” and “Vertical Line Intersection Detection Method,” both incorporating the Hough Transform, yields improved coordinate detection accuracy. For line segment components, detection errors remain below 0.1%, and for circular components, within 0.15%, indicating exceptional performance.
- Employ higher-resolution blueprints to reduce coordinate detection errors by improving the pixel-to-dimension ratio;
- Enhance blueprint complexity and variety to broaden the study’s applicability;
- Refine coordinate detection techniques to address the identification of complex component contours;
- Leverage coordinate data to facilitate BIM model reconstruction and urban digitalization
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, B.; Liu, B.; Zhu, D.; Zhang, B.; Wang, Z.; Lei, K. Semiautomatic Structural BIM-Model Generation Methodology Using CAD Construction Drawings. J. Comput. Civ. Eng. 2020, 34, 04020006. [Google Scholar] [CrossRef]
- Volk, R.; Stengel, J.; Schultmann, F. Building Information Modeling (BIM) for existing buildings—Literature review and future needs. Autom. Constr. 2014, 38, 109–127. [Google Scholar] [CrossRef]
- Regassa Hunde, B. Debebe Woldeyohannes A. Future prospects of computer-aided design (CAD)—A review from the perspective of artificial intelligence (AI), extended reality, and 3D printing. Results Eng. 2022, 14, 100478. [Google Scholar] [CrossRef]
- Baduge, S.K.; Thilakarathna, S.; Perera, J.S.; Arashpour, M.; Sharafi, P.; Teodosio, B.; Shringi, A.; Mendis, P. Artificial intelligence and smart vision for building and construction 4.0: Machine and deep learning methods and applications. Autom. Constr. 2022, 141, 104440. [Google Scholar] [CrossRef]
- Wang, T.; Gan VJ, L. Automated joint 3D reconstruction and visual inspection for buildings using computer vision and transfer learning. Autom. Constr. 2023, 149, 104810. [Google Scholar] [CrossRef]
- Liu, F.; Wang, L. UNet-based model for crack detection integrating visual explanations. Constr. Build. Mater. 2022, 322, 126265. [Google Scholar] [CrossRef]
- Phan, D.T.; Ta, Q.B.; Huynh, T.C.; Vo, T.H.; Nguyen, C.H.; Park, S.; Choi, J.; Oh, J. A smart LED therapy device with an automatic facial acne vulgaris diagnosis based on deep learning and internet of things application. Comput. Biol. Med. 2021, 136, 104610. Available online: https://www.ncbi.nlm.nih.gov/pubmed/34274598 (accessed on 29 November 2023). [CrossRef]
- Phan, D.T.; Ta, Q.B.; Ly, C.D.; Nguyen, C.H.; Park, S.; Choi, J.; O Se, H.; Oh, J. Smart Low Level Laser Therapy System for Automatic Facial Dermatological Disorder Diagnosis. IEEE J. Biomed. Health Inform. 2023, 27, 1546–1557. Available online: https://www.ncbi.nlm.nih.gov/pubmed/37021858 (accessed on 24 November 2023). [CrossRef]
- Xia, Z.; Ma, K.; Cheng, S.; Blackburn, T.; Peng, Z.; Zhu, K.; Zhang, W.; Xiao, D.; Knowles, A.J.; Arcucci, R. Accurate identification and measurement of the precipitate area by two-stage deep neural networks in novel chromium-based alloys. Phys. Chem. Chem. Phys. 2023, 25, 15970–15987. Available online: https://www.ncbi.nlm.nih.gov/pubmed/37265373 (accessed on 26 November 2023). [CrossRef]
- Mo, Y.; Wu, Y.; Yang, X.; Liu, F.; Liao, Y. Review the state-of-the-art technologies of semantic segmentation based on deep learning. Neurocomputing 2022, 493, 626–646. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Darrell, Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the 2015 International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Vijay Badrinarayanan, R.C. Alex Kendall, Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A. Semantic image segmentation with deep convolutional nets and fully connected crfs. arXiv 2014, arXiv:1412.7062v4. [Google Scholar]
- Chen, L.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the 2018 European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 833–851. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and efficient design for semantic segmentation with transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar]
- Dang, L.M.; Wang, H.; Li, Y.; Nguyen, L.Q.; Nguyen, T.N.; Song, H.K.; Moon, H. Deep learning-based masonry crack segmentation and real-life crack length measurement. Constr. Build. Mater. 2022, 359, 129438. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, N.; Han, C.; Liang, D. Automated identification of fissure trace in mining roadway via deep learning. J. Rock Mech. Geotech. Eng. 2023, 15, 2039–2052. [Google Scholar] [CrossRef]
- Zhou, Q.; Situ, Z.; Teng, S.; Liu, H.; Chen, W.; Chen, G. Automatic sewer defect detection and severity quantification based on pixel-level semantic segmentation. Tunn. Undergr. Space Technol. 2022, 123, 104403. [Google Scholar] [CrossRef]
- Ji, A.; Xue, X.; Wang, Y.; Luo, X.; Xue, W. An integrated approach to automatic pixel-level crack detection and quantification of asphalt pavement. Autom. Constr. 2020, 114, 103176. [Google Scholar] [CrossRef]
- Ramani, V.; Zhang, L.; Kuang, K.S.C. Probabilistic assessment of time to cracking of concrete cover due to corrosion using semantic segmentation of imaging probe sensor data. Autom. Constr. 2021, 132, 103963. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Dang, L.M.; Lee, S.; Moon, H. Pixel-level tunnel crack segmentation using a weakly supervised annotation approach. Comput. Ind. 2021, 133, 103545. [Google Scholar] [CrossRef]
- Hao, Z.; Lu, C.; Li, Z. Highly accurate and automatic semantic segmentation of multiple cracks in engineered cementitious composites (ECC) under dual pre-modification deep-learning strategy. Cem. Concr. Res. 2023, 165, 107066. [Google Scholar] [CrossRef]
- Shim, J.-H.; Yu, H.; Kong, K.; Kang, S.-J. FeedFormer: Revisiting Transformer Decoder for Efficient Semantic Segmentation. Proc. AAAI Conf. Artif. Intell. 2023, 37, 2263–2271. [Google Scholar] [CrossRef]
- Meeran, S.; Pratt, M.J. Automated feature recognition from 2D drawings. Comput.-Aided Des. 1993, 25, 7–17. [Google Scholar] [CrossRef]
- Meeran, S.; Taib, J.M. A generic approach to recognising isolated, nested and interacting features from 2D drawings. Comput.-Aided Des. 1999, 31, 891–910. [Google Scholar] [CrossRef]
- Hwang, H.-J.; Han, S.; Kim, Y.-D. Recognition of design symbols from midship drawings. Ocean. Eng. 2005, 32, 1968–1981. [Google Scholar] [CrossRef]
- Huang, H.C.; Lo, S.M.; Zhi, G.S.; Yuen, R.K.K. Graph theory-based approach for automatic recognition of CAD data. Eng. Appl. Artif. Intell. 2008, 21, 1073–1079. [Google Scholar] [CrossRef]
- Yin, M.; Tang, L.; Zhou, T.; Wen, Y.; Xu, R.; Deng, W. Automatic layer classification method-based elevation recognition in architectural drawings for reconstruction of 3D BIM models. Autom. Constr. 2020, 113, 103082. [Google Scholar] [CrossRef]
- Neb, A.; Briki, I.; Schoenhof, R. Development of a neural network to recognize standards and features from 3D CAD models. Procedia CIRP 2020, 93, 1429–1434. [Google Scholar] [CrossRef]
- Manda, B.; Dhayarkar, S.; Mitheran, S.; Viekash, V.K.; Muthuganapathy, R. ‘CADSketchNet’—An Annotated Sketch dataset for 3D CAD Model Retrieval with Deep Neural Networks. Comput. Graph. 2021, 99, 100–113. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, X.; Lai, H. Reconstructing BIM from 2D structural drawings for existing buildings. Autom. Constr. 2021, 128, 103750. [Google Scholar] [CrossRef]
- Pan, Z.; Yu, Y.; Xiao, F.; Zhang, J. Recovering building information model from 2D drawings for mechanical, electrical and plumbing systems of ageing buildings. Autom. Constr. 2023, 152, 104914. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Z.; Wang, X. Validity of non-local mean filter and novel denoising method. Virtual Real. Intell. Hardw. 2023, 5, 338–350. [Google Scholar] [CrossRef]
- Zheng, J.; Song, W.; Wu, Y.; Liu, F. Image interpolation with adaptive k-nearest neighbours search and random non-linear regression. IET Image Process. 2020, 14, 1539–1548. [Google Scholar] [CrossRef]
- Wilson, G.R. Morphological operations on crack coded binary images. IEE Proc.—Vis. Image Signal Process. 1996, 143, 171. [Google Scholar] [CrossRef]
- Chutatape, O.; Guo, L. A modified Hough transform for line detection and its performance. Pattern Recognit. 1999, 32, 181–192. [Google Scholar] [CrossRef]
- Yao, Z.; Yi, W. Curvature aided Hough transform for circle detection. Expert Syst. Appl. 2016, 51, 26–33. [Google Scholar] [CrossRef]






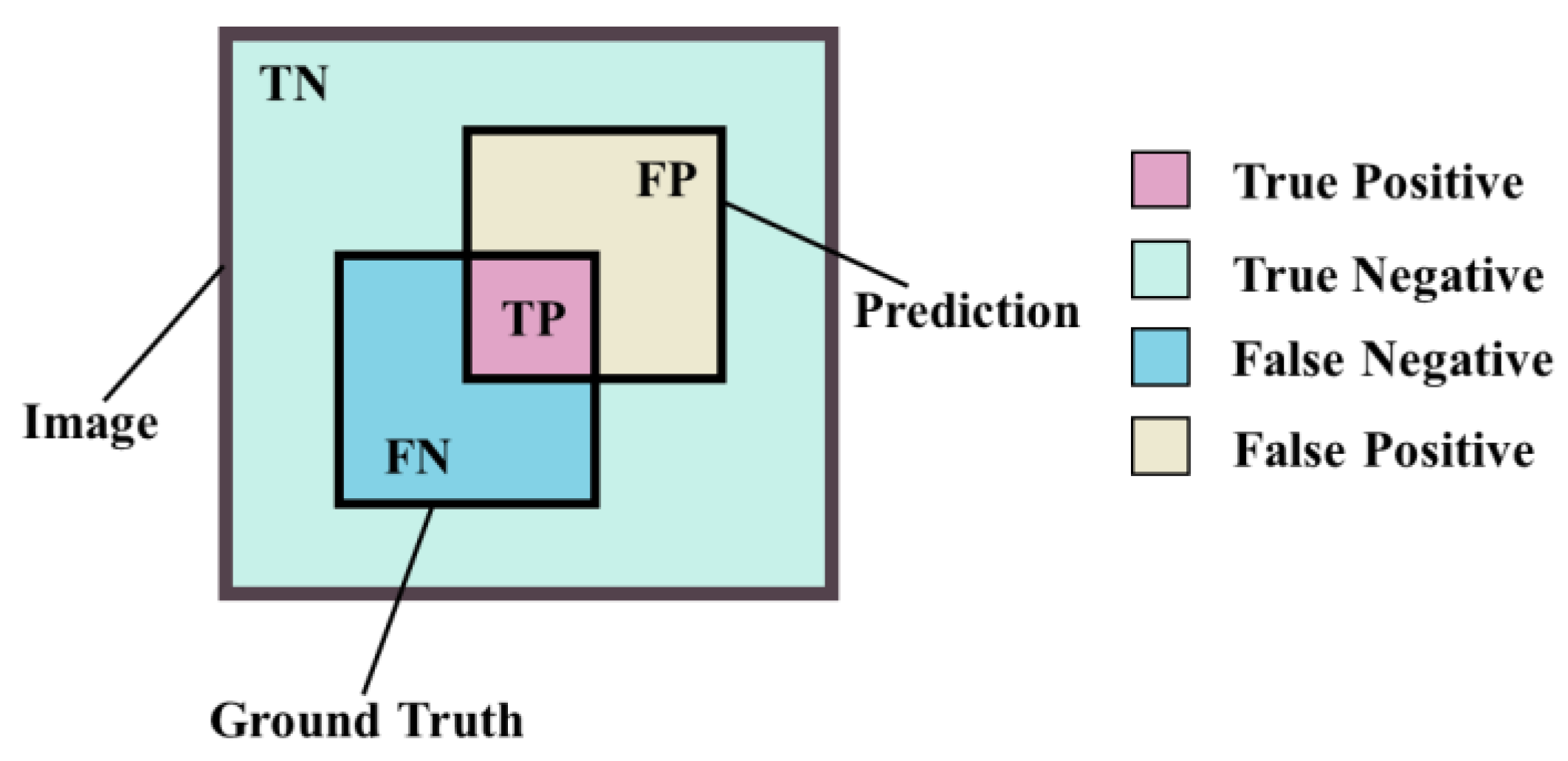
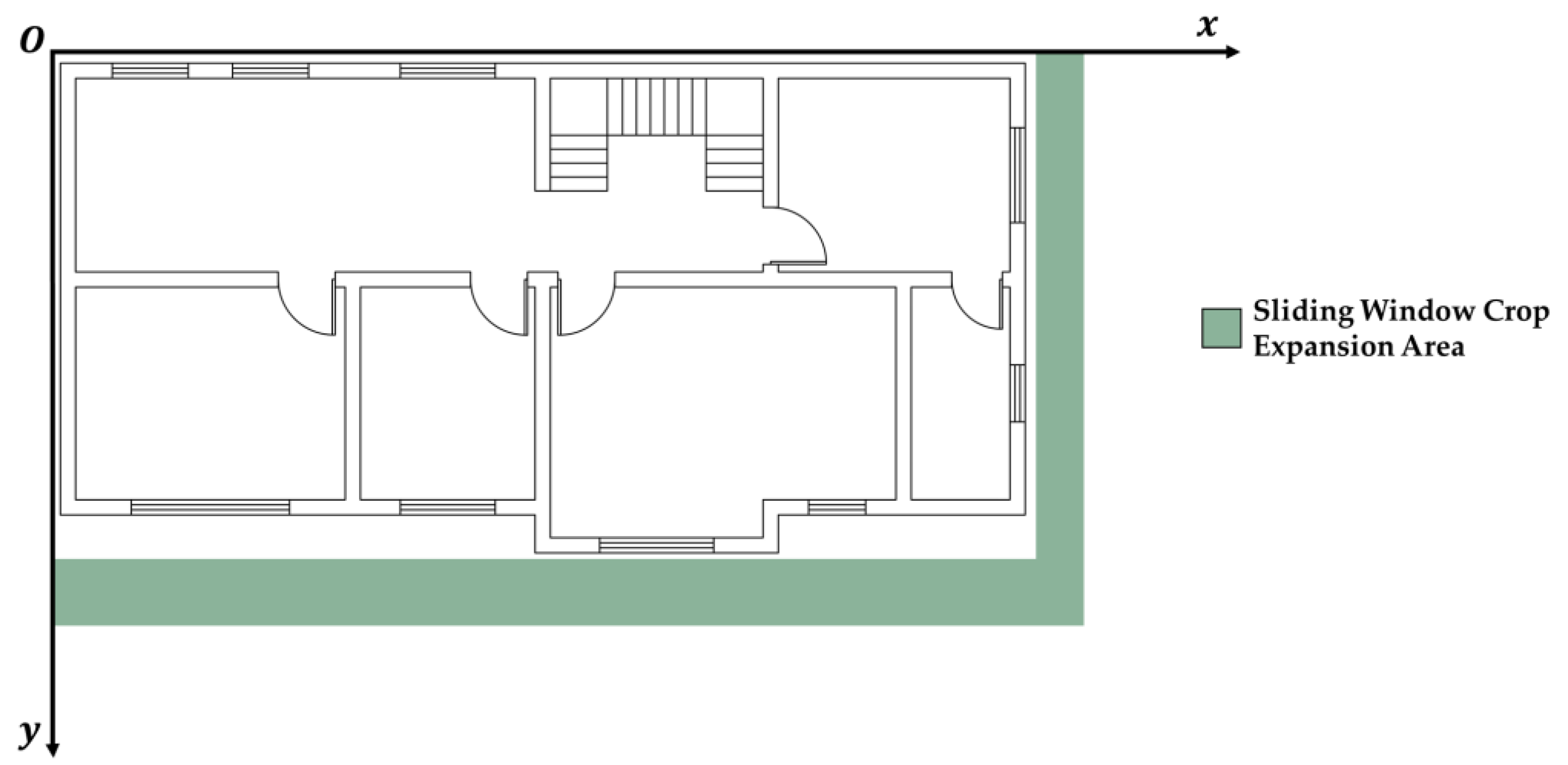
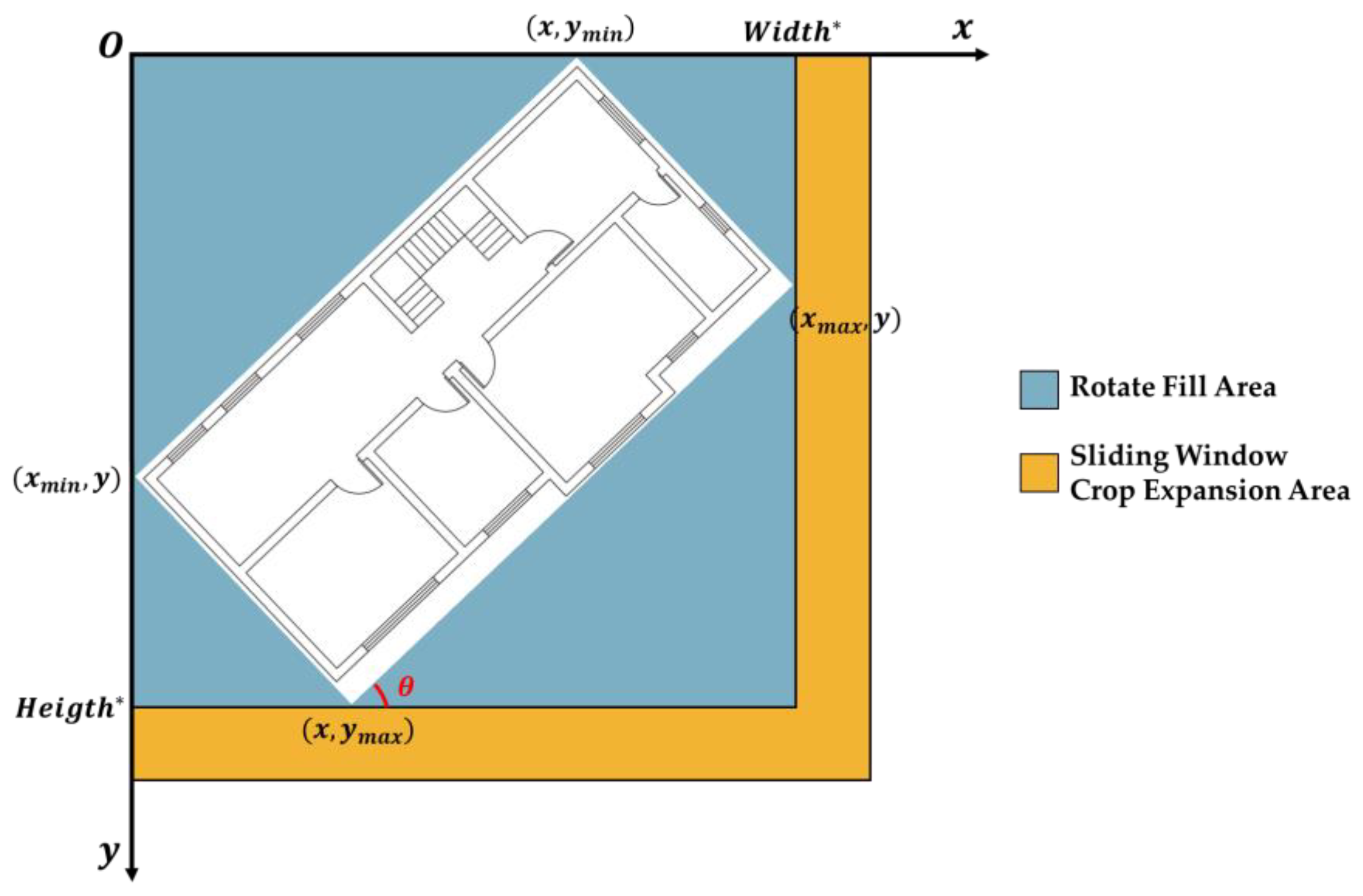
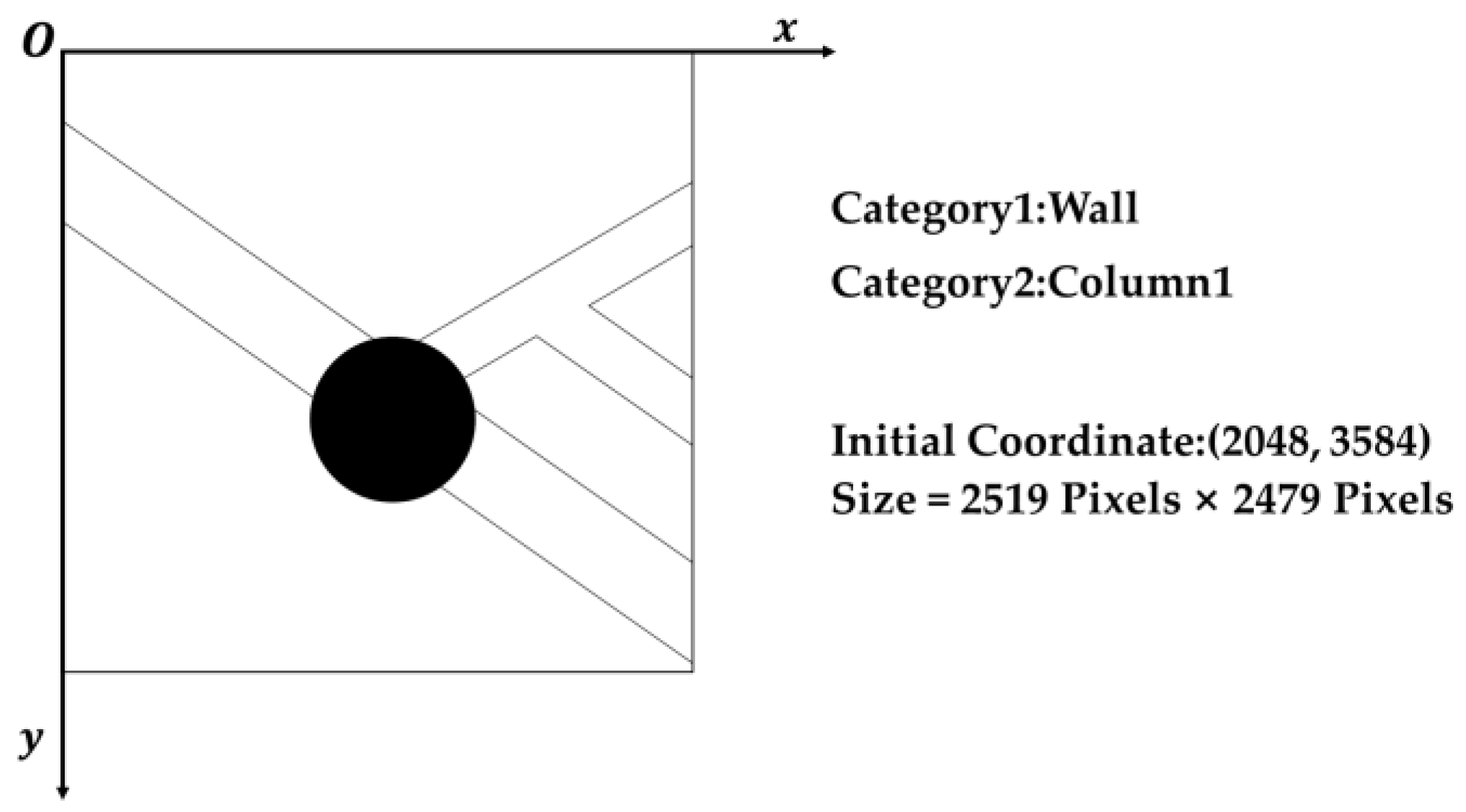


| Methods | Operation Execution |
|---|---|
| Rotation | Clockwise Angel = , , |
| Brightness | Enhancement factor = 1.2 |
| Sharpness | Enhancement factor = 2.3 |
| Chrominance | Enhancement factor = 1.2 |
| Contrast | Enhancement factor = 1.3 |
| Flip | Up and Down, Left and Right |
| Category | Key Coordinate Definition | Definition of Key Parameters |
|---|---|---|
| Door | Intersection Points between the Door and the Adjacent Walls | Width of Door |
| Rectangular Column | Center Point Coordinates of the Rectangular Column | Length and width of Rectangular Column |
| Cylindrical Column | Center Point Coordinates of the Cylindrical Column | Radius of the Cylindrical Column |
| Wall | Starting and Ending Points of the Wall | Length and width of Wall |
| Beam | Starting and Ending Points of the Beam | Length and width of Beam |
| Axis | Center Point Coordinates of the Axis Network Head | Connecting lines of the axial network on both sides |
| Window | Coordinates of the Four Corner Points of the Window | Width of Window |
| Parameter | Operation Execution |
|---|---|
| Init learning rate | (Min = |
| Batch size | 24 (freeze), 12 (unfreeze) |
| Optimizer | Adamw |
| Backbone | SegFormer-b2 |
| Learning rate decay type | cos |
| Weight decay | 0.01 |
| Loss | Cross-entropy loss |
| Epochs | 100 (freeze), 100 (unfreeze) |
| Model | Deeplabv3+ | U-Net | SegFormer | PSPNet | HRNet |
|---|---|---|---|---|---|
| Backbone | Xception | Resnet-50 | b2 | MobileNet | W-32 |
| Evaluation Metrics | Deeplabv3+ | U-Net | SegFormer | PSPNet | HRNet |
|---|---|---|---|---|---|
| MIoU (%) | 93.41 | 95.09 | 96.44 | 89.25 | 94.45 |
| PA (%) | 97.39 | 97.82 | 98.69 | 94.58 | 97.67 |
| Training Time | 20 h 35 min | 36 h 40 min | 42 h 17 min | 23 h 40 min | 25 h 54 min |
| Discipline | MIoU (%) | PA (%) | Categories | Data Volume (Sheet) |
|---|---|---|---|---|
| Architecture | 96.44 | 98.39 | 12 | 13,979 |
| Structure | 98.01 | 98.99 | 4 | 2619 |
| Class | BG | M | G | I | K |
|---|---|---|---|---|---|
| BG | 0.998 | 0.002 | 0 | 0 | 0 |
| M | 0.01 | 0.99 | 0 | 0 | 0 |
| G | 0.006 | 0.008 | 0.986 | 0 | 0 |
| I | 0.009 | 0.002 | 0 | 0.991 | 0 |
| K | 0.004 | 0 | 0 | 0 | 0.996 |
| Class | BG | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BG | 0.997 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 |
| A | 0.009 | 0.982 | 0.004 | 0 | 0.003 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 |
| B | 0.011 | 0 | 0.988 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 |
| C | 0.009 | 0 | 0 | 0.991 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| D | 0.009 | 0.001 | 0 | 0 | 0.982 | 0.006 | 0 | 0 | 0 | 0 | 0 | 0 | 0.002 |
| E | 0.012 | 0 | 0.006 | 0 | 0 | 0.981 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 |
| F | 0.007 | 0 | 0 | 0 | 0 | 0 | 0.991 | 0 | 0 | 0 | 0 | 0 | 0.002 |
| G | 0.006 | 0 | 0 | 0 | 0 | 0 | 0 | 0.993 | 0 | 0 | 0 | 0 | 0 |
| H | 0.015 | 0.001 | 0 | 0 | 0 | 0 | 0 | 0 | 0.982 | 0.001 | 0 | 0 | 0.001 |
| I | 0.012 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.002 | 0.983 | 0 | 0 | 0.003 |
| J | 0.009 | 0 | 0 | 0 | 0 | 0 | 0 | 0.004 | 0 | 0 | 0.987 | 0 | 0 |
| K | 0.006 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.994 | 0 |
| L | 0.019 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0 | 0.001 | 0.977 |
| Corner Point Index | Detected Pixel Coordinates | Detected Actual Coordinates | True Coordinates | Error in X Direction (‰) | Error in Y Direction (‰) |
|---|---|---|---|---|---|
| Wall (1) P1 | (7510, 192) | (6979.55, 9338.29) | (6982, 9336) | 0.351 | 0.245 |
| Wall (1) P2 | (7510, 449) | (6979.55, 9099.44) | (6982, 9096) | 0.351 | 0.345 |
| Wall (1) P3 | (9216, 192) | (8565.6, 9338.29) | (8567, 9336) | 0.163 | 0.245 |
| Wall (1) P4 | (9216, 449) | (8565.6, 9099.44) | (8567, 9096) | 0.163 | 0.345 |
| Wall (2) P5 | (8187, 449) | (7608.74, 9099.44) | (7611, 9096) | 0.297 | 0.378 |
| Wall (2) P6 | (8446, 449) | (7849.44, 9099.44) | (7851, 9096) | 0.199 | 0.378 |
| Wall (2) P7 | (8187, 2048) | (7608.74, 7613.38) | (7611, 7616) | 0.297 | 0.344 |
| Wall (2) P8 | (8446, 2048) | (7849.44, 7613.38) | (7851, 7616) | 0.199 | 0.344 |
| Corner Point Index | Detected Pixel Coordinates | Detected Actual Coordinates | True Coordinates | Error in X Direction (‰) | Error in Y Direction (‰) |
|---|---|---|---|---|---|
| Window P1 | (5445, 7858) | (5060.41, 11,539.03) | (5063, 11,545) | 0.512 | 0.517 |
| Window P4 | (5626, 8039) | (5228.62, 11,370.82) | (5231, 11,375) | 0.455 | 0.367 |
| Window P5 | (4306, 9000) | (4001.86, 10,477.70) | (4003, 10,485) | 0.285 | 0.696 |
| Window P8 | (4486, 9180) | (4169.14, 10,310.41) | (4171, 10,315) | 0.446 | 0.445 |
| Category | Detection COC | Detection R | Actual COC | Actual R | Error COC X(‰) | Error COC Y(‰) | Error R(‰) |
|---|---|---|---|---|---|---|---|
| Column2 | (3049.77, 4156.56) | 299.55 | (3053, 4160) | 300 | 1.06 | 0.827 | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, S.; Wang, D. Component Recognition and Coordinate Extraction in Two-Dimensional Paper Drawings Using SegFormer. Information 2024, 15, 17. https://doi.org/10.3390/info15010017
Gu S, Wang D. Component Recognition and Coordinate Extraction in Two-Dimensional Paper Drawings Using SegFormer. Information. 2024; 15(1):17. https://doi.org/10.3390/info15010017
Chicago/Turabian StyleGu, Shengkun, and Dejiang Wang. 2024. "Component Recognition and Coordinate Extraction in Two-Dimensional Paper Drawings Using SegFormer" Information 15, no. 1: 17. https://doi.org/10.3390/info15010017
APA StyleGu, S., & Wang, D. (2024). Component Recognition and Coordinate Extraction in Two-Dimensional Paper Drawings Using SegFormer. Information, 15(1), 17. https://doi.org/10.3390/info15010017






