Abstract
In this study, we propose a novel Temporal Development Generative Adversarial Network (TD-GAN) for the generation and analysis of videos, with a particular focus on biological and medical applications. Inspired by Progressive Growing GAN (PG-GAN) and Temporal GAN (T-GAN), our approach employs multiple discriminators to analyze generated videos at different resolutions and approaches. A new Temporal Discriminator (TD) that evaluates the developmental coherence of video content is introduced, ensuring that the generated image sequences follow a realistic order of stages. The proposed TD-GAN is evaluated on three datasets: Mold, Yeast, and Embryo, each with unique characteristics. Multiple evaluation metrics are used to comprehensively assess the generated videos, including the Fréchet Inception Distance (FID), Frechet Video Distance (FVD), class accuracy, order accuracy, and Mean Squared Error (MSE). Results indicate that TD-GAN significantly improves FVD scores, demonstrating its effectiveness in generating more coherent videos. It achieves competitive FID scores, particularly when selecting the appropriate number of classes for each dataset and resolution. Additionally, TD-GAN enhances class accuracy, order accuracy, and reduces MSE compared to the default model, demonstrating its ability to generate more realistic and coherent video sequences. Furthermore, our analysis of stage distribution in the generated videos shows that TD-GAN produces videos that closely match the real datasets, offering promising potential for generating and analyzing videos in different domains, including biology and medicine.
1. Introduction
Generative Adversarial Networks (GAN) [1] are prominent unsupervised architectures for generating synthetic data. Multiple versions aimed at creating diverse datasets have emerged [2]. GANs excel at generating images, and more recently, they have been employed to generate synthetic videos that capture moving objects. However, only focusing on the generation of videos emphasizing motion is not always optimal, particularly in fields such as medicine, where the goal of videos is focused on illustrating the temporal growth of a stationary object instead of its motion. This study presents a new approach for the generation of videos focusing on biological development. This type of data finds wide practical use in medicine, particularly in the areas of control, prediction, data expansion, and frame interpolation.
Generating temporal sequences of images that accurately capture the biological development of their content, be it medical images or photographs of natural elements, comes with several challenges. The first challenge is to ensure that each image is as realistic as possible, respecting the morphology and spatial coherence of the elements present in a real image. Furthermore, the group of images must display temporal coherence, meaning that there should be consistency related to changes in position, scale, or content between one image and its adjacent images that would occur in a real video. Unlike models that concentrate on generating motion-centered videos, in biological development videos, the content must transition consistently through specific stages. This means that transitioning between a significantly advanced or earlier stage is not feasible, thus creating the need to adapt the model to produce this particular type of data.
Previous research has focused on acquiring high-resolution videos with excellent image quality, creating videos from a text prompt, and achieving smooth motion. However, no model has been specifically developed to address the biological development aspect of video content.
In this study, we tackle this issue by introducing a new discriminator that evaluates the quality of the produced video by comparing its distribution with the actual dataset. During training, every frame of the fabricated video created with the GAN architecture is categorized and linked to a class present within the authentic dataset. A range of statistical measures are then used to evaluate this class vector in accordance with the general progression of classes in the training dataset, as well as the coherence of the class development for the duration of the video.
The sequences of images produced by the proposed model have various applications. The most frequent use is data augmentation for training other machine learning models that perform classification, prediction, and detection tasks [3,4]. This objective is particularly valuable in this field of study because acquiring such data is often highly costly both in terms of time and materials [5]. The time required for cell or microorganism growth can range from days to weeks, while disease or cancer control scenarios, such as melanoma growth on the skin, can take months or even years. The difficulty of gathering data highlights the necessity of techniques such as the one proposed. This technique enables reliable data augmentation, addresses issues such as class imbalance, and mitigates the lack of specific case studies. Moreover, obtaining new cases can aid in training expert personnel, allowing them to analyze a broader range of scenarios, including normal and abnormal development cases. Currently, to the best of our knowledge, there are no other models that focus specifically on the correct development of the stages depicted in the videos.
To conduct the experiments, the following methodology was employed. We tested the proposed model using three different datasets: one focused on embryonic development (Embryo), another depicting the growth of mold microorganisms on fruit over time (Mold), and finally, one showcasing the growth of a single-celled organism, yeast (Yeast). Using these three datasets provides diversity and allows for working in both grayscale (Embryo and Yeast) and color (Mold). To evaluate the proposed model against the original default model, widely used metrics in the literature were employed. These metrics include Fréchet Inception Distance (FID), Fréchet Video Distance (FVD), class accuracy, order accuracy, and Mean Squared Error (MSE), which assess both image quality and the coherence of the represented stages. Additionally, experiments were performed with varying numbers of classes in the unlabeled datasets to investigate the impact of this hyperparameter on the generation of synthetic image sequences.
The results support the viability of the proposed model. Regarding image quality, the proposed model achieves FID results that are very similar to the default model since this measure considers images separately, not as videos. However, there is an improvement in FVD for all datasets, a measure specialized in video evaluation. The proposed model also achieves lower MSE and class accuracy, indicating that fewer stages are in incorrect positions. Furthermore, the proposed TD-GAN model enhances class order accuracy by reducing the occurrence of stages that are not reflected in the training data. Through a thorough analysis of stage distributions, it is evident that the TD-GAN model generates videos that more accurately depict developmental stages compared to the default model.
The remainder of this article is organized as follows. Section 2 reviews the state of the art in video generation techniques. Section 3 introduces the proposed model in this work and the statistical measures used for coherence analysis. Section 4 and Section 5 describe the experiments conducted, the datasets used, and the results obtained. Finally, in Section 6 and Section 7, the results of the proposed model are analyzed, and the article is concluded.
2. Related Work
2.1. Image Generation
GAN models are widely used in the biomedical literature to generate images that aid in improved clinical analysis [2,6]. Li et al. [3] employed a GAN to produce high-resolution images depicting retinal vessel details and leaky structures during multiple critical phases. Zhao et al. [7] employed a GAN to generate computed tomography (CT) images from magnetic resonance (MR) imaging. CT images are crucial for target delineation and dose calculation during radiation therapy, as MR lacks the electron density information necessary for dose calculation. Li et al. [8] employed image generation through a new GAN called Diff-CoGAN for medical image segmentation of the hippocampus and spleen. Their proposal involved using two generators and one discriminator to work in a semi-supervised manner. In their approach, they introduced the intersection of two predicted maps and managed to outperform other semi-supervised GAN-based methods.
In biomedicine, the primary application of GANs is creating artificial instances to expand training datasets. There are multiple examples in the literature that prove how fake images are beneficial for classification algorithms that need a significant amount of images for training when real data are not easy available [9,10,11,12]. One example is the work of Mulé et al. [4], whih showed that generative models are effective in constructing images of uncommon medical cases. In their research, the authors produced a substantial amount of fake images depicting macrotrabecular-massive hepatocellular carcinoma from a restricted number of cases. Despite the good results achieved by these generative models, if the data exhibit class imbalance, it can lead to a very low level of variability in the generated dataset. This situation is quite common in biological and biomedical data collections due to the difficulty of obtaining such data. Therefore, Kuo et al. [13] proposed the introduction of a new block based on variational autoencoders into the classical GAN architecture. The model they proposed can generate more realistic synthetic datasets, achieving greater variability and better representation of underrepresented classes. Freitas et al. [5] used a cGAN model for data augmentation to improve bladder tumor segmentation in white-light cystoscopy videos. The authors reported an improvement of over 12% by including synthetic images in the training dataset.
2.2. Video Generation
Unlike static image GANs, the management of video GANs requires specific considerations because of the inherent intricacy of video data. Videos consist of multiple individual images combined with the temporal dimension, which calls for specialized methods [14]. The analysis of sequential data through deep learning has gained significant attention in the recent literature. This approach is particularly useful for tasks such as time series forecasting and estimating future values in time series [15]. Videos are commonly used in tasks such as audiovisual speech recognition, where GANs can be employed in a multimodal manner. An example of this type of work is presented by He et al. [16], who used images and sound to align audio points with video frames where a person is speaking. The authors claimed that the results are promising, but there is still considerable potential for development given the novelty of this area.
Similar to other machine learning models, GAN architectures can be classified as conditional and unconditional. Conditional models rely on the use of an initial signal to guide their output, which is typically text, audio, or an initial image [17,18,19]. On the opposite side, unconditional models create synthetic videos without any prior input, which makes the task more challenging. Nevertheless, these models serve as the basis for the previously mentioned conditional models. Among the most notable models are T-GAN [20,21], MoCoGAN [22], DVD-GAN [23], and GAN [24].
In recent years, many works have focused on video generation using images of generalist topics, such as sports, urban scenes, people, cloud movement, or even fireworks [21,25,26,27,28]. The aim of these works is to capture the movement of the objects appearing in the video, not their development over time. Segal et al. [29] leveraged this capability to produce artificial human skeleton motions by integrating a set of predetermined choreographies. These artificially generated videos were then used to expand the dataset and conduct control tasks. GANs excel in generating rare events. Mohamadipanah et al. [30] suggested using a GAN (Generative Adversarial Network) architecture to generate synthetic images of extensive bleeding videos that can aid in minimally invasive lobectomy procedures. This approach helps address the shortage of current data in this area. Similarly, as Issa et al. [31] affirmed, GANs can be used to increase the number of frames in videos. The authors proposed to use a GAN to preform super-resolution, denoising, and distortion correction on the fast-scanning acquisition of laser scanning microscopy videos, achieving an improvement up to 20x the speed of their standard high-resolution counterparts. The authors also claimed that this model generalizes to unseen data and requires only a few images for training. Furthermore, the model can be fine-tuned to work with different biological examples, increasing its utility in other fields. Similarly, Dashtbani et al. [32] proposed the use of a VAE-GAN model to generate new frames in videos of cerebral CT perfusion. This approach aimed to reduce the data acquisition time, which subsequently reduces the cumulative radiation dose and the risk of patient head motion. Through this implementation, the authors achieved a simultaneous reduction in examination time and radiation dose of 65% and 54.5%, respectively. Guo and Nahm [33] highlighted the need to generate realistic bronchoscopic videos for the development and evaluation of depth estimation methods as part of research on a vision-based bronchoscopic navigation system. In their work, they used a Spatial GAN model to generate realistic textures in videos, which are difficult to obtain due to limited accessibility.
In prior research, we explored the production of videos showing the progress of in vitro fertilized embryos [34], a field in which AI can be extremely useful and where work is continually being carried out to introduce new techniques [35]. It was noted that the produced synthetic videos could occasionally display inconsistencies in the sequence of developmental stages depicted in their frames. Consequently, we propose a GAN-based model approach, called Temporal Development GAN (TD-GAN), for the generation of videos that more accurately depict reality.
3. Materials and Methods
In this section, we first provide a description of the traditional GAN design and the advanced architecture upon which the proposed model is based. Following that, the methods involved in fake video generation are explained. Finally, we delve into the module where fake image sequences are analyzed to assist the model in generating biologically more accurate videos, along with the statistical measures employed in this process.
3.1. Generative Adversarial Networks
A model based on Generative Adversarial Networks (GANs) [1] that employs unsupervised training relies on the use of two interconnected yet opposing models: a Generator (G) and a Discriminator (D). This setup entails that G aims to generate images as realistically as possible, while D endeavors to distinguish whether the images it receives are fake or real. Both models are trained alternately to progressively learn how to generate more realistic images and differentiate between real and fake images, respectively. A GAN’s optimal end is that the distribution of real data () equals the distribution of generated images ().
A GAN’s training process can be represented in a formal manner, as shown in Equation (1). The first addend computes the probability of D predicting that real images (x) are authentic, while the second addend estimates the probability of D predicting that the generated images from G giving a noise z are not real.
3.2. Multiscale Image Generation
Despite the promising results obtained by the basic GAN model proposed by Goodfellow et al. [1], the generation of high-resolution photorealistic images requires the use of more complex models. One of the approaches that achieves superior results while also reducing computational cost is Progressive Growing GAN (PG-GAN), introduced by Karras et al. [36]. PG-GAN gradually increases the size of both the Generator and the Discriminator during training, starting with low-resolution images and progressing to high-resolution images. In this way, the models first learn the distribution of large-scale structures. Subsequently, the transition to larger sizes enables them to capture finer details.
Based on PG-GAN, it is clear that using images with reduced sizes allows the model to learn how to generate images with a realistic general structure while sacrificing fine details. This enables the model to grasp the distribution of large color blocks and shapes. As the size increases, the level of detail also escalates, allowing the model to learn how to generate more specific and distinguishing elements and incorporate them into the general blocks it had previously learned. Therefore, the model can generate much more realistic images by analyzing various resolutions of the same image than if it were to rely solely on a high-resolution version.
3.3. Image Classification
The Discriminator model (D) in GANs is essentially a binary classifier with one class for real cases and another for fake ones. There are various classification models available depending on the type of data being used, but in the context of images, one of the most widely used models is the Residual Network (ResNet) proposed by He et al. [37]. The ResNet model introduces the use of shortcuts that connect layers from earlier positions to subsequent layers to prevent information loss and, as a result, achieve better performance. When applied to image processing, ResNet employs convolutional operations to process the input and determine its class.
ResNet has been successfully applied in many image classification tasks, particularly in the 2D domain. However, it is not well-suited for video classification due to the additional dimensionality introduced by the temporal aspect. In response to this challenge, Hara et al. [38] proposed the use of 3D convolutions to process data in the height, width, and depth dimensions. Nevertheless, 3D convolutions are computationally heavier than their 2D counterparts, and this computational cost increases exponentially as the images become larger or as the number of images in the sequence grows.
3.4. Temporal Data Analysis
In the field of temporal data, the most renowned model is Long Short-Term Memory (LSTM) [39], often applied to text data. LSTM is a type of recurrent neural network (RNN) that maintains the state of information across its iterations. This model incorporates various gates to control the flow of information between instances of the network, enabling it to forget or retain the previous states and regulate how far information propagates through its output gate in those iterations.
The analysis of temporal data using generative models enables various tasks, such as classification, simulation, data augmentation, and generation of missing data [40]. Shi et al. [41] proposed the use of an LSTM block for the analysis of sequences of images and introduced Convolutional LSTM (CLSTM). Instead of working with discrete values, the authors suggested replacing the internal multiplication operations with convolutional operations, thus obtaining output matrices from the CLSTM block of the same size as the input matrices. In the field of biomedicine, the analysis of time sequences is of great interest. Currently, GANs have already demonstrated their viability in tasks such as prediction and diagnosis using textual data [42] and signal data (such as blood pressure and electrocardiograms) [43,44]. For this reason, this study proposes to exploit this capability to apply such models in the generation of image sequences that accurately represent biological development, respecting the order and nature of the stages.
3.5. Temporal Development GAN (TD-GAN)
As previously noted, video generation primarily captures object motion within images. Nonetheless, the analysis of the development of elements over time in biology and medicine focuses on the changes that stationary elements undergo rather than on their motion, which can be erratic due to imaging equipment alterations. In videos within these domains, the observed object progresses through distinct and already-known stages in a particular sequence. It is crucial to adhere to this order as any deviation may indicate developmental irregularities. However, the pace of transition between states does not necessarily remain constant. The exhaustiveness required to create such videos presents a formidable challenge for generative models.
To address this topic, this study suggests a novel model called Temporal Development GAN (TD-GAN) that incorporates a new discriminator block that analyzes the development of videos generated by the discriminator to acquire a better understanding of video coherence from a developmental viewpoint. The proposed model in this study is based on the architecture introduced by Saito et al. known as Temporal GAN (T-GAN) [21]. Inspired by the PG-GAN model, the authors proposed using multiple discriminators to assess cases of varying sizes and numbers of frames. They then aggregated the outputs from these discriminators to calculate a single loss, resulting in an overall discriminator score. This study suggests introducing a new discriminator that not only evaluates the quality of the video but also assesses its coherence in terms of the developmental stages of its content.
As shown in Figure 1, the model takes as input a noise vector z, which is processed through a fully connected network before passing through a CLSTM module known as the Temporal Generator. This process yields an array of noise matrices from a single noise input, with a number of matrices equal to the number of frames in the output video. Subsequently, the Image Generator processes each to generate an image that contributes to the future video.
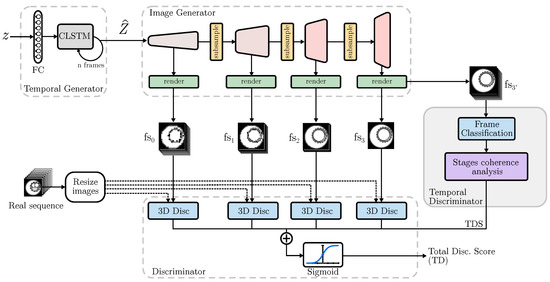
Figure 1.
Proposed TD-GAN architecture. Each fake sequence is processed by a 3D Discriminator at different sizes. The undergoes a stage coherence analysis to assess its similarity tp real data.
As the model progresses, subsampling blocks decrease the number of channels composing the video, thus reducing computational load. Consequently, each block responsible for rendering the images obtains increasingly detailed fake image sequences (). Thus, represents a video that contains all frames but at a lower image resolution. On the other hand, corresponds to a high-resolution video that has fewer frames. Real and fake videos are evaluated by several discriminators that use 3D convolutions to process the entire video and determine their authenticity. Furthermore, this study proposes a novel Temporal Discriminator that accepts a video sequence with frames of equal dimensions to the previous discriminator processing the fake sequence , but with a number of frames equal to the real videos.
Each sub-discriminator analyzes the fake and real samples from various perspectives. The ones examining smaller images evaluate the coherence between diverse frames and large image blocks, prioritizing general consistency over fine details. In contrast, those dealing with larger image sizes but fewer frames focus on producing realistic images with a greater level of detail. Meanwhile, the role of the proposed Temporal Discriminator (TD) is to guarantee that the stages depicted in the video accurately reflect the sequence observed in actual scenarios.
3.6. Temporal Discriminator
The proposed TD-GAN introduces a novel discriminator block that categorizes each frame individually and obtains a score related to the stages displayed in each image. This is achieved by comparing the distribution of developmental stages with those from the real dataset. The process is depicted in Figure 2.
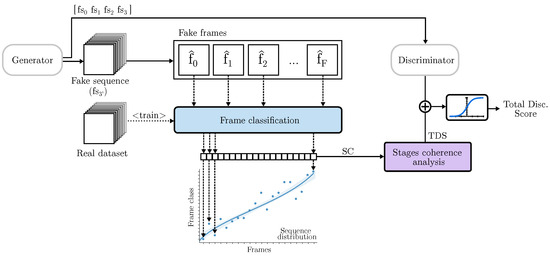
Figure 2.
Temporal Discriminator: Each frame of the fake sequence is classified to one of the stages of the real data. Its coherence is analyzed using statistical methods to assess how close the stages sequence is to real cases.
The initial step involves generating a complete video with an image resolution equal to the highest resolution used by the discriminators. To differentiate them, the sequence used by the TD is denoted as , while the one used by the final classical discriminator is named , with D representing the total number of 3D discriminators. TD employs a image classifier to categorize each frame of the video. This classifier is pre-trained using the real dataset. In cases where the dataset already has its own classification, that information is used. However, if the dataset lacks prior classification, a fictitious division is employed. This involves assuming that in a video with F frames, frame corresponds to class 0, frame to class 1, and frame to class F. This classification can be modified by grouping frames to reduce the number of classes. This topic is further discussed in Section 4.
After classifying all the frames, the resulting distribution of classes is compared to the distributions of real videos, producing a coherence measure. This is achieved through the use of the ANCOVA statistical measure (Analysis of Covariance). As described by Rutherford [45], ANCOVA assesses experimental manipulations on a dependent variable objectively and accurately. It is a statistical method used for evaluating the effect of frame position on the predicted class depending on its belonging class. A single-factor, single-covariate ANCOVA can be formally described as Equation (2), where j represents an observation of a class c and is the interception point over the y axis of the regression coefficient of the covariate variable Z influenced by the general covariate mean .
Lastly, stands for the associated unobserved error for the jth member in the c class, taking a value between 0 and the population (N) variance obtained by Equation (3).
Therefore, ANCOVA may be formally estimated for a class as the adjusted mean of all its observations as:
ANCOVA can be used to make comparisons between groups using an F-test, as shown in Equation (5) [45].
This is performed by first comparing the score obtained from different groups as addressed in Equation (6). In our case, the groups are real and fake, and we divided them by the degrees of freedom for the observations. Subsequently, they were divided by the variance of the difference between the adjusted means, which was further divided by the degrees of freedom for the error, as illustrated in Equation (7).
The similarity measure is obtained by comparing the real video set used for training the generative model and the classifier with the generated fake data. The closer these sets are, the more closely the fake videos resemble the real ones, thereby indicating the effectiveness of the Generator model.
The primary aim of generative video models is to produce videos that closely resemble reality. Consequently, it is of significant interest to assess the quality of each video individually, in addition to determining the status of the fake set. To conduct this evaluation, we suggest employing three criteria: one centered on how closely a video resembles real-life situations, another focused on the development of the stages included in the video, and a final measure that combines both approaches to yield a more precise, comprehensive appraisal of a video. To better analyze these cases, we used the Spearman correlation coefficient, hereafter referred to as Spearman, to check the coherence of the stages.
According to Xiao et al. [46], Spearman is a special case of the Pearson correlation coefficient, which uses monotonic relationships between two variables instead of linear relationships. It analyzes how well the data fit a monotonic function, that is, a function that is always increasing or decreasing. Spearman can be formally written as Equation (8), where N is the total number of samples and is the difference between each pair of observations ordered by its position [46].
Spearman takes into account the slope of the regression while providing a measure of the dispersion of the points examined. As a result, it outputs a measure value between −1 and 1, where 0 means that there is no slope and the observations are highly dispersed, while values close to −1 or 1 indicate very little dispersion and a good fit to a monotonic function. Finally, negative values are obtained from functions with an overall negative slope, while positive values are produced from those with a positive slope. Spearman can lead to situations where a video with high dispersion and slope gets a similar score as a video with low dispersion and slope.
Since this is a frame-by-frame analysis of the videos, it is important to note that a large dispersion means that there are very large jumps between frames, creating an unrealistic development. For this purpose, we used the Standard Error (SE) of a regression slope (Equation (9)) so that those videos whose points fit well on their regression line would obtain a better score than those whose points were too far apart. Consequently, the calculation of the DAS score was
Finally, we used a combination of the DAS and ANCOVA measures to obtain the final assessment of the video known as the Temporal Discriminator Score (TDS), taking into account both its “developmental realism” and its similarity to the training dataset. Its formal representation is shown in (10).
The proposed model consists of several 3D discriminators and a Temporal Discriminator. The 3D discriminators take a fake video sequence () and provide a judgment about its belonging to the real dataset, i.e., whether the video is real or fake. As mentioned before, the sizes of these discriminators are different, allowing them to analyze videos from different perspectives. Following the explanation of the base model [21], each real video (x) is subjected to a subsampling layer () to match the real videos size to that of the discriminator. The Equation (11) represents the score calculation for a real case.
When it comes to classifying fake cases, subsampling is not necessary because the outputs of the Generator are already of the appropriate size. The computation for a generated fake sequence () from an initial noise (z) by a Discriminator is formally represented in Equation (12).
In the architecture used, part of the discriminator is formed by several 3D sub-discriminators. To calculate the total score, the individual scores are summed and passed through a sigmoid function (), as seen in Equation (13).
The previous equation is extended by the Temporal Discriminator, which analyzes the stages represented in the video. This can be expressed by rewriting the equation as (14). By using both measures, we simultaneously evaluated realism from a development perspective and looked for adaptations to the real dataset. This measure was summed to the scores gathered from the other discriminators, thereby integrating it into the loss to communicate the quality of the created videos to the model. As a summary, in a more formal way, the total discriminator score () consists of the sum of the sub-discriminators processed by a sigmoid function () and the TDS of the proposed Temporal Discriminator. Let be the last sub-discriminator that takes the sample and let be the proposed Temporal Discriminator that takes the sample .
Finally, building on all the above components, the training process of TD-GAN with a real dataset , a total loss for the discriminators , and considering false cases generated from initial noise () can be formally represented as shown in Equation (15).
4. Experiments
4.1. Datasets
This section includes an analysis of the development video datasets used in the experiments.
4.1.1. Embryo Dataset
Embryo Development is a public time-lapse dataset created by Gomez et al. [47] of the culture of embryos that have undergone IVF. It consists of 704 videos in different focal planes for a total of 2.4 million images with a resolution of 500 × 500. The collection includes expert annotations for each stage of the embryo: polar body appearance, pronuclei appearance and disappearance, blastomere division from the 2-cell stage to the 9 (and more) cell stage, compaction, blastocyst formation, and expansion and hatching. The number of images for the five predominant stages ranges from 30K to almost 60K images, while for the other 11 classes, only three reach 20K; the rest hover around 10K. Each video captures the embryo’s development through different stages, but not all videos cover 100% of these stages. Approximately 160 videos have fewer than 10 stages, while 280 videos have 11, 12, or 15 stages in equal parts, and around 260 have between 13 and 14 stages.
Out of the total number of videos, 499 depict morphologically viable embryos that were selected for transfer. The remaining videos show embryos that were discarded due to poor development. These discarded embryos were used to study various abnormal embryonic features, such as abnormal morphology, fertilization issues, pro-nuclei count, necrosis, fragmentation, developmental delay, etc. Additionally, these videos were also used to study problems encountered during image acquisition, such as sharpness, focus, and brightness.
The embryo can be visualized more effectively by adjusting the focal plane of the microscope, as it is a three-dimensional object. There are seven focal planes available for the same videos, including F-0, F-45, F-30, F-15, F15, F30, and F45. Due to technical limitations, only one focal plane was used for training, and 20 evenly spaced frames were extracted from each video (some with more than 500 frames).
4.1.2. Mold Dataset
The second dataset is a custom collection of mold development videos [48]. It shows the development over time of Golden Delicious apples cut side by side, which we will refer to as Mold. A photograph was taken every 12 h for 10 days, yielding 20 images for each. In total, the development of 144 apple halves was captured for a total of 2880 images. Images were taken using a Nikon D5300 and an AF-P 18–55 mm lens every 12 h for 10 days. The apples were stored in groups of 6 in different containers, resulting in original images of 2992 × 2000 pixels at 300 ppp. Subsequently, the photography with a group of apples was automatically split to obtain individual images of 997 × 1000 resolution. When selecting the videos, those with problems, such as a lack of focus or lighting, were excluded. Each frame was accompanied by the exact position of the apple in the image, thus forming a bounding box composed of 4 dimensions: xPos, yPos, width, and height. The xPos and yPos values indicate where the center of the bounding box is with respect to point (0,0) in the top left-hand corner. They are calculated by dividing the position of point and by the width and height of the original image respectively.
The main objective of the dataset is to analyze the evolution over time of different types of mold that appear and grow day by day, as well as the evolution of browning and changes in color and shapes that appear on the surface. In contrast to the Embryo dataset, this type of data lacks a predefined division of stages, which complicates its development analysis. The images typically contain a moisture-absorbing cardboard background, a healthy surface, seeds in the central area, and various stages of mold development, including the initial stage with brown coloring, the subsequent stage with white–blue coloring, and new black mold. The videos demonstrate the rapid spread of blue mold across the entire surface, while black mold grows at a slower rate. This analysis can aid in the identification of various types of molds, its earlier detection, and prediction of its growth in future studies.
4.1.3. Yeast Dataset
The third dataset was created by Goldschmidt et al. [49]. It shows videos of Colonies of S. cerevisiae (Yeast) developing over time. Also known as Baker’s yeast, S. cerevisiae is a model organism that can grow at the scale of cell colonies, showing a diverse range of morphologies. Historically, beer brewers and bakers have distinguished between different strains of S. cerevisiae based on the visual identification of their morphology, but this is a difficult process that is extremely difficult to perform at a large scale.
Images were acquired at a median rate of one image every 23 min over the course of 3 days. They contained a total of 5500 videos that were selected as a representative ensemble of experimental data. These colonies represented 196 unique strains of the species. The videos depict the growth of yeast, including changes in size and the emergence of tubular structures on its surface. The morphology of these structures varies depending on the strain. These data can aid in the early and automatic classification of different species.
This dataset adds complexity to the video generation process, as the texture to be generated within each image is very complex and the model must maintain coherence between different frames. Additionally, unlike the other datasets, this one shows the constant growth of yeast that causes the initial and final images to be very different. In the cases of Embryo and Mold, the final and initial images are morphologically similar but show different stages.
4.2. Hyperparameters
The Temporal Discriminator employs different numbers of classes (or stages) depending on the dataset being evaluated. The Embryo dataset uses the original classification of 16 classes and adds an extra “empty” class for instances where frames are empty, indicating that the embryo has been removed. Accordingly, this results in a total of 17 classes. The first frames should show the initial phases (tPB2, tPNa and tPNf), while the intermediate images show the phases of cell proliferation (from t2 to t9+) and, at the end, the stages of blastulation (tM, tSB, tB, tEB and tHB) and the removal of the embryo for implantation (empty). When the dataset is unclassified, such as in the Mold and Yeast datasets, the automatic assignment of a class occurs. Due to the large number of possible combinations, an analysis of the accuracy of the ResNet18 model was conducted, taking into account different types of grouping, as depicted in Figure 3. These groupings range from each frame being a distinct class to groups of 2, 4, and 5 frames, resulting in a total of 4, 5, 10, and 20 classes.
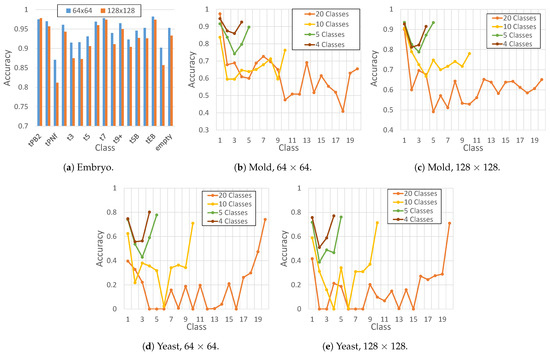
Figure 3.
Classification accuracy of ResNet18 for each dataset (Embryo, Mold, and yeast). The tested image sizes used in this experiments are 64 × 64 and 128 × 128. Lastly, the number of classes of the Embryo dataset was predefined as 17 (from tPB2 to empty); the tested number of clases for the Mold and Yeast datasets were 4, 5, 10, and 20. This way, different groupings were tested, where each group contained the same number of frames.
As depicted in Figure 3, the ResNet18 model achieves high accuracy for all classes, with the lowest accuracy of 0.81 for tPNf at 128 × 128 size and the highest accuracy of 0.98 for tEB at 64 × 64 size. For datasets that were not originally classified, accuracy increases as the number of classes decreases, with similar results obtained for 4 and 5 classes. Given this situation, in the experiments, a maximum of 20 classes and a minimum of 5 classes were used to facilitate a comparison between them. The choice of 5 classes was based on the fact that it offers the highest accuracy while sacrificing the fewest numbers of stages.
The experiments were conducted using image sizes of 64 × 64 and 128 × 128. We used the Adam optimizer with a learning rate of 1.0 × 10, decayed linearly to 0 over 300K iterations. We also employed 1 = 0.0 and 2 = 0.9 in the Adam optimizer [21]. The local batch size of each GPU was selected so it filled the GPU memory of an NVIDIA RTX3080ti (12 Gb). The number of dimensions of z was set to 256, and the number of channels was 1 (gray scale) for the Embryo and Yeast dataset and 3 (RGB) for Mold dataset. The source code and weights of the model can be found in the GitHub repository (https://github.com/pedrocelard/TempDev-GAN, accessed on 9 December 2023).
4.3. Evaluation Metrics
The most widely used evaluation metrics in the literature are the Inception Score (IS) [50], Fréchet Inception Distance (FID) [51], Fréchet Video Distance (FVD) [52], Structural Similarity (SSIM) [53], Peak Signal-to-Noise Ratio (PSNR) [54], and Mean Squared Error (MSE) [24]. Not all of them are suitable for the specific needs of certain studies, especially when it comes to unsupervised models where no ground truth is available to compare the images or the fake video with.
4.3.1. FID and FVD
As Unterthiner et al. [52] state, learning generative models of video is a much harder task than synthesizing static images, as the model must capture the temporal dynamics of a scene in addition to the visual presentation of objects. The authors propose the FVD to address the lack of available metrics to measure the performance of generative video models. FVD uses a pre-trained model to extract the features and measure the distance between the distribution of the real videos and the distribution of the fake videos, assuming that the smaller the distance between these distributions, the more similar the fake videos are to the real ones. Another common evaluation measure when working with generative models is the FID. It works similarly to the FVD but instead of working on the entire video, it uses the individual frames extracted from the video collection to calculate the distance between the true and false distributions.
4.3.2. Stage Accuracy
In addition to analyzing the distribution of images and videos with FID and FVD, this study examined the stages present in each frame of the videos, referred to as the stage accuracy. The accuracy of the classes in each frame was calculated with various degrees of freedom by assuming a linear correlation between frames and stages. This means that initial frames have early stages, while later frames have later stages. Due to differing development speeds, different classes may be present in different frames, meaning that intermediate frames have varying degrees of progression or delay depending on their position in the video. To account for this, three degrees of freedom () were used (0, 1, and 2). This means that if the desired class for frame f is , the degree of freedom allows for the accurate assignment of the class .
4.3.3. Stage Order Accuracy
Subsequently, the stage order was analyzed, assuming that, in normal development, stages should consistently ascend. Thus, it was expected that objects in the video progress gradually through each of the stages without significant leaps. To accomplish this, we employed the degrees of freedom and determined the correct order by ensuring that class was greater than or equal to class but did not exceed the imposed degrees of freedom (1, 2, or 3). Therefore, a correct frame can be of class or .
4.3.4. Mean Squared Error
Finally, the Mean Squared Error (MSE) was employed by comparing the class distribution with the mean class distribution of real videos. This statistical measure provides an indicative metric of the difference between these two distributions. An MSE close to 0 indicates minimal difference, while a higher MSE suggests significantly different distributions, thus indicating videos that do not closely resemble reality.
4.3.5. Unsuitable Metrics
Alternatively, IS is a viable metric in the case of generating generic themed images that are recognizable by the Inception network. This measure uses an Inception network pre-trained with the ImageNet dataset to obtain a value, but unlike FID and FVD, it does not use the real dataset for comparison. Although widespread, this measure is not useful if the generated images are not recognizable by the network, nor does it provide a measure of the quality or congruence of the videos. This situation is also true for the other measurements: SSIM, which is evaluated based on three aspects, namely the luminance, contrast, and structure of the original and generated images; MSE, which measures the sum of the square of the distance between the original and generated frames; and PSNR, which is the ratio between the maximum signal intensity and MSE. These metrics require a ground truth or, in other words, a real image to compare the output of the generative network to since the output should be as close to the ground truth as possible [14].
Furthermore, this study focuses on unsupervised models applied to biological images that do not resemble any ImageNet classes. Additionally, there is no ground truth to perform direct comparisons with, making the use of IS, MSE, PSNR, and SSIM metrics completely infeasible.
5. Results
This section provides an analysis of the data obtained from the experimental procedures, examining the numerical results, measurements, and statistical findings derived from our study.
5.1. Qualitative Analysis
In this section, the quality of the fake images produced by the proposed TD-GAN model is visually analyzed. To accomplish this, Figure 4 exhibits two fake sequences generated by the proposed model for each dataset with a size of 128 × 128. Each sequence includes ten frames extracted from the twenty that comprise each video.
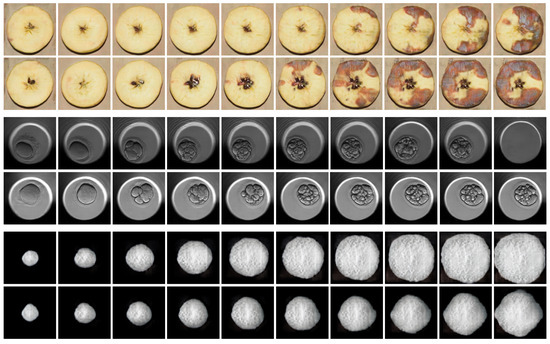
Figure 4.
Fake samples produced by TD-GAN using a 128 × 128 image size. The 2 top lines are fake videos of the Mold dataset. The 2 middle sequences represent the development of an embryo. Lastly, the 2 bottom sequences belong to the Yeast dataset, showing the growth of a single-cell cerevisae fungus.
The two top rows illustrate the progression of mold growth on apples as time passes. This dataset is unique due to its capacity for displaying images with three layers that capture colors. The mold grows gradually and evenly, while the overall shape of the apple remains constant. However, there are some irregularities in the seeds at the center, which should remain stable. This scenario emphasizes a work in progress requirement of these models, which is to differentiate between dynamic and stationary components over time. Despite this, the representation of mold development is excellent, which is the goal of the dataset.
The two central sequences display the progression of fertilized embryos. It can be observed how the initial frames exhibit an undivided body, while the blastomere divides into several cells in the intermediate frames. Eventually, compaction and the removal of the embryo for implantation take place. This extraction is reliant on human expertise; thus, the frame where this event happens may vary in the actual dataset.
Finally, the growth of the two yeast fungi is displayed in the lower two sequences. The growth is constant and provides a clear definition and strong contrast with the background. As the fungus grows, it produces a striated texture that is challenging to capture with perfect clarity due to its intricate details and small size. Nevertheless, the shadow and color variations on the body of the fungus, alongside its external shape, exhibit excellent spatial consistency within each image and among neighboring frames.
5.2. Distribution Distances
As mentioned above, the FID and FVD metrics use an Inception model to compare the distribution of generated data to that of real data. The main difference between these metrics is how they handle the data: FID evaluates individual frames within sequences, losing the concept of a video, while FVD treats sequences as a single entity. Consequently, FID provides a measure of image similarity, while FVD provides a measure of video similarity. A higher distance value indicates a significant difference between the distributions, so a lower value indicates better generation of fake instances.
Despite the widespread use of the FID and FVD metrics in the literature, it is not possible to make a direct comparison with other video generation studies. One of the main reasons is the novelty in the application of the proposed model, as it focuses on the analysis of biological development rather than the generation of videos with motion. A significant difference in motion datasets is the complete absence of stages, thus lacking any studiable development for drawing conclusions. This leads to the second reason: the measures are not interchangeable between different datasets because the distribution distances depend entirely on the specific data used.
Table 1 shows the results obtained for the Mold and Yeast datasets using the baseline model (Default) and the proposed model with 5 (TD-GAN 5) and 20 classes (TD-GAN 20). The baseline model is the unmodified T-GAN version 2 [21]. The hyperparameters used and the training and inference process are the same as those of the proposed model, ensuring a fair and equitable comparison.

Table 1.
FID and FVD results for Mold and Yeast datasets.
Next, in Table 2, the results obtained with the Embryo dataset are presented. This dataset was originally classified by experts with a total of 17 classes, which is the number of classes used in the proposed model.

Table 2.
FID and FVD results for Embryo dataset.
TD-GAN improves FID results in the Mold and Yeast datasets, with a slight decrease below the default model in the Mold dataset at size 128. Using 20 classes leads to a better FID, but the 5-class model outperforms the 20-class model by 1.2 with an image size of 64. The proposed model, however, does not improve the FID of the default (80.2) in the Embryo dataset. Instead, it achieves a comparable score of 86.5 with a size of 64. It is noteworthy that the FID calculates image results independently, disregarding any sequence or video progress.
Taking this into account, the FVD does analyze the sequence and allows us to obtain a better assessment of the model. The implementation of the TD-GAN model leads to a significant FVD improvement. Overall, the proposed TD-GAN model achieves a higher score without any biased evaluation. For the Mold dataset, the proposed model consistently achieves improvements ranging from 9.6% to 21.35%. For the Yeast dataset, the improvement reaches 35% and 41.7% for an image size of 128 and 7.8% and 15% for an image size of 64. This improvement is largely due to the high level of detail in the texture of S. cerevisae, which is lost when using a smaller image size. Finally, in the Embryo dataset, the results show an improvement of 3.4% for images of size 64 and 8.4% for images of size 128.
It is noteworthy that using 20 classes produces better results when generating 64 × 64 images, while 5 classes result in better image generation at a size of 128 × 128.
5.3. Class Accuracy
Class accuracy measures the precision with which the model generates images of a given stage throughout the frames of the video. In this way, we want to verify that the model can generate stages in their corresponding sections of the video, i.e., initial stages at the beginning of the video and final stages toward the end. Table 3 shows the results for the mold and yeast datasets, while Table 4 shows the results for the embryo dataset. In both cases, experiments are performed with three different degrees of freedom (0, 1, and 2), thus establishing a range of accuracy for different stages in each image.

Table 3.
Class accuracy for Mold and Yeast datasets.

Table 4.
Class accuracy for Embryo dataset.
The accuracy with which each image represents the most predominant class in the real dataset is improved when using the proposed TD-GAN. This improvement is observed in all the degrees of freedom used, obtaining better or very similar results to the standard model. Regarding the number of classes, the Mold dataset benefits from the use of 5 classes, improving the accuracy of the default model in all degrees of freedom, while 20 classes are a better option for the Yeast dataset. However, the improvement over the default model remains significant in both cases. In the case of the Embryo dataset, the improvement is also observed in all degrees of freedom, even increasing from 0.27 to 0.35 when generating 64 × 64 images.
When there are 0 or 1 degrees of freedom, the results are similar across different models. However, when the degrees of freedom increase to 2, the improvement becomes more noticeable. In the case of the default model, many stages are far from their ideal position, so increasing the degrees of freedom does not offer a significant improvement unless it is a disproportionate freedom. However, in many cases, the proposed model brings the generated stages closer to their realistic position, even if it cannot generate them entirely in the median position of the real dataset distribution.
5.4. Order Accuracy
The Order Accuracy metric assesses the progressive change of stages as observed in the real dataset, ensuring that a stage does not occur before a naturally preceding one or that the transition between stages is not too large. This is achieved by applying different degrees of freedom (1, 2, and 3), which refer to the difference that can exist between the stages of adjacent frames. Table 5 and Table 6 present the results obtained in the experiments.

Table 5.
Order accuracy for Mold and Yeast datasets.

Table 6.
Order accuracy for Embryo dataset.
Order accuracy aims to measure the coherence of stages across the video. In the case of the Mold and Yeast datasets, the proposed model achieves better results. The most significant improvement is observed when using 20 classes in the Yeast dataset, with a difference of 0.13 at a size of 64. For the Embryo dataset, the best results are also obtained with a degree of freedom of 3, but a significant improvement in the order of stages is observed with a degree of freedom of 1 when working with a size of 64. The score increases from 0.47 with the default model to 0.53 with the proposed model.
The Yeast dataset benefits the most from the proposed model in terms of the order of its stages. Its order accuracy increases from 0.78 to 0.91 with a size of 64. This improvement is due to the fact that the original model represents movement well, but it does not follow a correct pattern adjusted to the stages. The proposed model regulates and controls this pattern, generating sequences of stages that are more realistic.
5.5. Mean Squared Error
The Mean Squared Error (MSE) is the last statistical measure analyzed. To obtain these results, the mean distribution of the real cases was compared to the distribution of the fake cases. A high MSE indicates a significant difference between real and fake cases, suggesting that the generated cases are less similar to reality. Conversely, a low MSE indicates minimal differences between the distributions, meaning that the stages represented are similar to real cases. The MSE values for the various experiments conducted are presented in Table 7 and Table 8.

Table 7.
Mean Squared Error for Mold and Yeast datasets.

Table 8.
Mean Squared Error for Embryo dataset.
Again, the proposed model outperforms the default model. In this case, the best number of classes to be used depends on the dataset and the size used. For the Mold dataset, the best result is obtained with TD-GAN 5 at a size of 64, while at a size of 128, TD-GAN 20 excels. Conversely, for the Yeast dataset, the use of 20 classes benefits images with a size of 64, while 5 classes improves the results for images with a size of 128. Finally, with the Embryo dataset, the proposed model achieves a significant improvement over the default model in both sizes, going from 34.9 to 15.65 for 64 × 64 and from 8.1 to 6.15 for 128 × 128.
5.6. Stage Distribution Comparison
Finally, an analysis of the distribution of stages across the frames of the sequence was performed. Figure 5, Figure 6 and Figure 7 show representative plots of the stages in each frame. In all of them, the x-axis represents each frame of the video, and the y-axis represents the classes present in the real dataset. Simultaneously, the colors of the boxes relate to the stages of the video, grouping frames in sets of four: blue for early stages, reds and yellows for intermediate stages, and finally green.
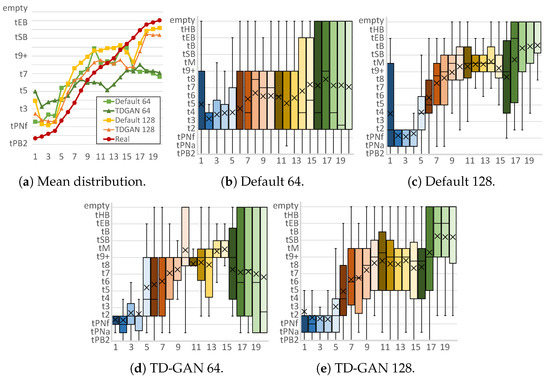
Figure 5.
Stage distributions per frame of fake embryo sequences. Horizontal axis represents each frame of the fake video, while the vertical axis shows the classification result (stage) for each frame. Each subfigure caption shows the model (default or proposed TD-GAN) and the image size used (64 or 128). Colors of the boxes relate to the stages of the video, grouping frames in sets of four: blue for early stages, reds and yellows for intermediate stages, and finally green.
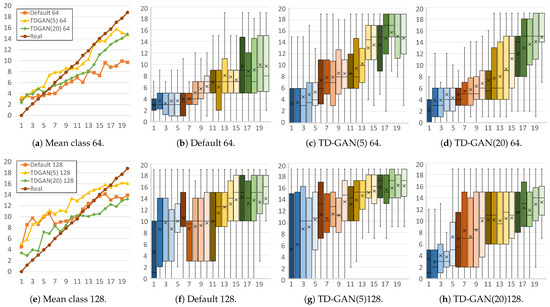
Figure 6.
Stage distributions per frame of fake mold sequences. The horizontal axis represents each frame of the fake video, while the vertical axis shows the classification result (stage) for each frame. Each subfigure caption shows the model (default or proposed TD-GAN), the number of classes (5 or 20), and the image size used (64 or 128). Colors of the boxes relate to the stages of the video, grouping frames in sets of four: blue for early stages, reds and yellows for intermediate stages, and finally green.
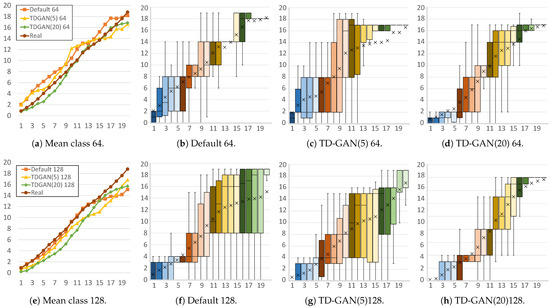
Figure 7.
Stage distributions per frame of fake yeast sequences. Horizontal axis represents each frame of the fake video, while the vertical axis shows the classification result (stage) for each frame. Each subfigure caption shows the model (default or proposed TD-GAN), the number of classes (5 or 20), and the image size used (64 or 128). Colors of the boxes relate to the stages of the video, grouping frames in sets of four: blue for early stages, reds and yellows for intermediate stages, and finally green.
First, Figure 5 analyzes the results obtained with the Embryo dataset. Figure 5a shows the mean class of all generated cases for each image. At a size of 64 × 64, the distribution of the default model shows that the classes in the final frames belong to earlier stages than those in the intermediate frames, an unrealistic situation since it is clear that the real class distribution is always increasing. With the proposed model, the distribution follows a more horizontal pattern but manages to stabilize the order of the stages. At a size of 128 × 128, both distributions follow a growing pattern that covers almost all stages. With the proposed model, a distribution is obtained that is more similar to the real dataset, especially in the case of the initial and intermediate images.
Analyzing Figure 5b,d, it can be seen that both models generate a large number of incorrect stages in the final frames of the video, thus obtaining a lower mean distribution. This situation changes when a larger image size is used, allowing the models to better discriminate the class represented in the image. The default model (Figure 5c) generates a large number of intermediate classes in the first frame that do not correspond to reality, and in the intermediate frames, the vast majority are classified as t9+, tsB, and tB. These stages occur when the number of cells in the embryo is very high and their fusion begins to form poorly defined structures. In contrast, with the proposed model (Figure 5e), the intermediate images have a higher number of stages with a reduced number of cells, which is more similar to reality. In addition, TD-GAN with a size of 128 eliminates the significant appearance of false stages in the early frames.
Next, Figure 6 shows the distribution of videos from the Mold dataset. With a size of 64 × 64 (Figure 6a), the TD-GAN model with 5 and 20 classes is closest to the real distribution. Furthermore, in Figure 6d, it can be seen how the use of 20 classes helps to achieve better accuracy in the first and last frames. This number of classes produces a smoother, more evenly increasing mean distribution with fewer differences between frames.
In the case of images with a size of 128, the use of 5 classes (Figure 6g) does not manage to improve the number of advanced stages in the early frames of the video, a situation that also occurs with the default model (Figure 6f), although it is able to offer a smoother distribution in the intermediate cases. Conversely, the TD-GAN model with 20 classes is able to produce fewer late stages in the early frames. In the last part of the video, the TD-GAN 5 model adapts better to reality than the model with 20 classes and the default model, a situation caused by the variability in real cases in this area due to cases of less pronounced development. These cases make the use of 5 classes better at locating the cases in this part of the sequences, while the use of 20 classes hinders the ability of the classifier to accurately predict the class being processed.
Finally, Figure 7 shows the distributions of the yeast dataset. For both sizes, the mean distributions are very similar, giving good results even with the default model. However, in the case of 64 × 64 images, as shown in Figure 7b–d, the default model generates a large number of incorrect stages in the first part of the video. Using 20 classes with TD-GAN improves this situation by achieving a growing distribution in which the first frames contains only initial stages.
On the other hand, with a size of 128, the default model (Figure 7e) has more difficulty generating the final frames, significantly increasing the number of different stages that appear in these areas. Again, the 20-class model (Figure 7h) can fine-tune the generation of these sequences and better refine the stages in each frame.
6. Discussion
After analyzing the results, it is clear that the proposed model enhances the production of synthetic sequences that closely match the actual developmental patterns seen in real-life cases.
Regarding FID and FVD, using fewer classes produces superior outcomes when handling smaller image sizes. This is due to the lower resolution of images, making it more challenging to create accurate representations of the visual differences between stages. Using 20 classes benefits from a higher image resolution, which generates finer details, enabling the subsequent classifier to detect and discriminate stages more precisely. Specifically, the proposed TD-GAN improves the distribution of videos as a single object (FVD). In the case of yeast, the stages are not only determined by the texture of the object or elements in the image but also by the size of the yeast cell itself, which is indicative of its developmental stage. This situation facilitates the study of the stages and allows the proposed model to achieve much better improvements compared to other datasets. As seen before, it achieves an improvement of about 42%. However, on the Embryo dataset, FID shows a slight decrease in performance. The Mold and Yeast datasets exhibit less defined classes compared to the Embryo dataset, where the transition between stages is more abrupt. Therefore, the model generates images with less variation between a frame and its neighbors. This type of intermediate frame with a class that is not specific to one stage or another is not annotated in the real dataset.
This effect is more pronounced for class accuracy. At low degrees of freedom, the difference in accuracy is very small, but as degrees of freedom are increased, the improvement becomes more significant. This is because the distributions of the stages are not always exact in reality. A stage may appear earlier or later depending on the evolution speed of the object present in the video, but it always respects the initial, intermediate, and final zones of the video, which may span several frames. Considering this stage development, the Order Accuracy measure shows how the stage arrangement also improves with the proposed model. The stages in real datasets are always increasing, so an object cannot go back in time. Similarly, a sudden jump of many stages is also considered an unrealistic evolution since variations in the speed of biological evolution have their limits. The growth of the object under study is a crucial element in determining its stage in the Yeast dataset. The default model can represent this change since it is designed for sequences of movement. However, it fails to do so in the correct order, and there are cases where smaller objects are seen after larger ones. The proposed model analyzes growth from a developmental perspective rather than just movement. Therefore, during training, irregular growth is penalized, resulting in an improved outcome. In the other two datasets, the change in size is almost imperceptible, as it is more of a change in texture, which makes it more difficult to distinguish between stages.
The average distribution of the real cases is used to compare them with the fake cases, thus obtaining a Mean Squared Error (MSE) for the fake sequences. The proposed model achieves a lower error than the standard model. In these cases, the use of a different number of classes affects the results for datasets that are not previously classified. Therefore, it is necessary to adapt the model to the dataset and the target size. Despite the usefulness of MSE, using only the mean classification hides relevant information, so a more in-depth analysis of the distributions was performed.
In the case of the Embryo dataset, the proposed model achieves a more smoothly increasing distribution, reducing the appearance of wrong stages in the initial and final images. The model proposed in this study effectively reduces the number of incorrect stages generated, resulting in a stage distribution that is closer to the mean of the training dataset. The model, which has a size of 64, significantly decreases the variation of stages classified at each position in the frame, except for the final stages. This is mainly due to the complexity of generating images that belong to the later stages. The high level of detail required in the images to discern small details allows for better classification of the stages in the case of images with a size of 128. It is believed that larger images in the Embryo dataset will make it easier to classify the stage of frames, resulting in better outcomes.
Similarly, for the Mold dataset, the intermediate frames show a variety of stages corresponding to the general stages of the video while achieving smoother overall development. The proposed model achieves a distribution closer to real cases in the initial and intermediate frames but diverges in the final frames. This is likely due to the high diversity in mold development. The initial and intermediate stages are similar in all training cases, but the final stages differ significantly among the different videos. This dataset could be improved by preprocessing the videos to adjust the positioning of the stages in the frames. For example, establishing stages based on the affected surface or the appearance of specific molds could be beneficial. Further data analysis could also enhance this case in future work.
Finally, the proposed model achieves more accurate frame generation in the initial and final stages with the Yeast dataset, especially when using 20 classes. The proposed model reduces the dispersion of classified stages across video frames, particularly in the initial and final frames. In this dataset, the difference between sizes 64 and 128 is subtle because the primary determinant of the stage is the size of the object, with texture playing a secondary role. Yeast size can be visualized similarly in both cases. However, the use of 5 or 20 classes has a greater impact than in the other datasets. When using 20 classes with yeast, a more tightly distributed pattern to a certain stage is observed in each frame, whereas using 5 classes increases the dispersion of stages within each position. This is primarily caused by the uniform growth of yeast in a controlled environment, which allows the model to discern the expected size of the object more precisely in certain positions of the video. In this scenario, a higher number of classes proves beneficial compared to a lower number.
7. Conclusions
In conclusion, this paper presents TD-GAN (Temporal Development Generative Adversarial Network), a novel approach aimed at improving the generation of synthetic sequences of images and particularly focused on biological development stages. TD-GAN introduces innovative components, such as a Temporal Discriminator (TD) and various metrics, to assess the quality and coherence of generated sequences.
Several experiments were conducted to evaluate TD-GAN’s performance across different datasets, image sizes (64 × 64 and 128 × 128), and class settings (5 and 20 classes). The FID and FVD metrics showed that the choice of the number of classes and image size significantly impacts the performance of the model. Smaller image sizes and fewer classes were more suitable for FID, whereas larger image sizes and more classes were beneficial for FVD. TD-GAN demonstrated improvements in class accuracy, ensuring that frames within a sequence correspond more closely to the real development stages. The degree of freedom in class assignment played a crucial role in enhancing class accuracy. The proposed model contributed to better order accuracy by generating sequences with more realistic and coherent developmental progressions. The gradual transition between stages is smoother, aligning with the expected biological development. Finally, the Mean Squared Error (MSE) analysis revealed that TD-GAN generally outperformed the default model, with smoother and more accurate stage progressions. It offered improved results across datasets, particularly in reducing the appearance of incorrect stages in the initial and final frames.
The deployment of the proposed TD-GAN model for video generation in the biomedical field holds significant potential. The model has the ability to generate realistic, time-dependent representations of biological processes, such as embryonic development or microbial growth, which can provide invaluable resources for training and enhancing medical professionals’ expertise. Furthermore, GAN-generated synthetic data can enhance the development of more resilient machine learning models, promoting advancements in predictive analytics and diagnostic tools. The use of such highly realistic fabricated data, which are not subject to data protection regulations like real data, could aid policymakers in supporting research initiatives that utilize GANs for video generation in the biomedical sector. This could foster collaborations between academic institutions, healthcare providers, and technology companies. This collaborative approach may expedite advancements in comprehending intricate biological phenomena, ultimately resulting in enhanced patient care and improved medical education.
TD-GAN presents a promising advancement in sequence generation, particularly in the context of biological development stages. It addresses challenges related to class accuracy, order accuracy, and overall stage coherence. While further fine-tuning and dataset-specific adjustments may be required, TD-GAN’s contributions to generating more realistic and coherent sequences hold significant potential in various applications, including computer vision and biological image analysis.
In future research, expanding the number of frames in the generated videos and increasing their image size holds promise for achieving even better results. More frames would make it easier to generate images representing intermediate classes that do not quite match previously established classes. Similarly, larger image sizes would allow for the generation of finer details, contributing to improved results.
In addition, the proposed discriminative block is not limited to the expansion of the default model. It can be included in the workflow of other models as well. This versatility extends its potential utility beyond sequence generation, offering advantages in classification tasks and synthetic sequence generation in various scenarios. As research continues, further improvements to TD-GAN and its application in diverse domains are likely, pushing the boundaries of what is achievable in synthetic sequence generation and paving the way for advanced computer vision and biological image analysis techniques.
Author Contributions
Conceptualization, P.C. and A.S.V.; methodology, P.C.; software, P.C. and J.M.S.-F.; validation, A.S.V.; formal analysis, J.M.S.-F.; investigation, P.C.; resources, E.L.I.; data curation, A.S.V.; writing—original draft preparation, P.C.; writing—review and editing, E.L.I. and L.B.; visualization, J.M.S.-F.; supervision, L.B.; project administration, E.L.I. and L.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from Gomez et al. [47], available at https://doi.org/10.5281/zenodo.6390798 (accessed on 21 December 2023), Goldschmidt et al. [49], available at https://doi.org/10.6084/m9.figshare.c.5526474 (accessed on 21 December 2023), and Celard et al. [48], available at https://doi.org/10.5281/zenodo.7778821 (accessed on 21 December 2023).
Acknowledgments
This work has been partially supported by the Conselleria de Cultura, Educación e Universidade (Xunta de Galicia) under the scope of funding ED431C 2022/03-GRC Competitive Reference Group and by the Ministerio de Ciencia e Innovación under the State Programmes for Knowledge Generation and Scientific and Technological Strengthening of the R&D&i System (PID2020-113673RB-I00). Pedro Celard is supported by a predoctoral fellowship from the Xunta de Galicia (ED481A 2021/286).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FID | Fréchet Inception Distance |
| FVD | Fréchet Video Distance |
| MSE | Mean Squared Error |
| PSNR | Peak Signal-to-Noise Ratio |
| SSIM | Structural Similarity |
| GAN | Generative Adversarial Network |
| LSTM | Long Short-Term Memory |
| CLSTM | Convolutional Long Short-Term Memory |
| G | Generator |
| D | Discriminator |
| TDS | Temporal Discriminator Score |
| TD-GAN | Temporal Development Generative Adversarial Network |
References
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Celard, P.; Iglesias, E.L.; Sorribes-Fdez, J.M.; Romero, R.; Vieira, A.S.; Borrajo, L. A survey on deep learning applied to medical images: From simple artificial neural networks to generative models. Neural Comput. Appl. 2023, 35, 2291–2323. [Google Scholar] [CrossRef]
- Li, P.; He, Y.; Wang, P.; Wang, J.; Shi, G.; Chen, Y. Synthesizing multi-frame high-resolution fluorescein angiography images from retinal fundus images using generative adversarial networks. BioMed. Eng. OnLine 2023, 22, 16. [Google Scholar] [CrossRef]
- Mulé, S.; Lawrance, L.; Belkouchi, Y.; Vilgrain, V.; Lewin, M.; Trillaud, H.; Hoeffel, C.; Laurent, V.; Ammari, S.; Morand, E.; et al. Generative adversarial networks (GAN)-based data augmentation of rare liver cancers: The SFR 2021 Artificial Intelligence Data Challenge. Diagn. Interv. Imaging 2023, 104, 43–48. [Google Scholar] [CrossRef]
- Freitas, N.R.; Vieira, P.M.; Tinoco, C.; Anacleto, S.; Oliveira, J.F.; Vaz, A.I.F.; Laguna, M.P.; Lima, E.; Lima, C.S. Multiple mask and boundary scoring R-CNN with cGAN data augmentation for bladder tumor segmentation in WLC videos. Artif. Intell. Med. 2024, 147, 102723. [Google Scholar] [CrossRef]
- Zhao, J.; Hou, X.; Pan, M.; Zhang, H. Attention-based generative adversarial network in medical imaging: A narrative review. Comput. Biol. Med. 2022, 149, 105948. [Google Scholar] [CrossRef]
- Zhao, B.; Cheng, T.; Zhang, X.; Wang, J.; Zhu, H.; Zhao, R.; Li, D.; Zhang, Z.; Yu, G. CT synthesis from MR in the pelvic area using Residual Transformer Conditional GAN. Comput. Med. Imaging Graph. 2023, 103, 102150. [Google Scholar] [CrossRef]
- Li, G.; Jamil, N.; Hamzah, R. An Improved Co-Training and Generative Adversarial Network (Diff-CoGAN) for Semi-Supervised Medical Image Segmentation. Information 2023, 14, 190. [Google Scholar] [CrossRef]
- Chai, L.; Wang, Z.; Chen, J.; Zhang, G.; Alsaadi, F.E.; Alsaadi, F.E.; Liu, Q. Synthetic augmentation for semantic segmentation of class imbalanced biomedical images: A data pair generative adversarial network approach. Comput. Biol. Med. 2022, 150, 105985. [Google Scholar] [CrossRef]
- Pavlou, E.; Kourkoumelis, N. Deep adversarial data augmentation for biomedical spectroscopy: Application to modelling Raman spectra of bone. Chemom. Intell. Lab. Syst. 2022, 228, 104634. [Google Scholar] [CrossRef]
- Ding, C.; Xiao, R.; Do, D.H.; Lee, D.S.; Lee, R.J.; Kalantarian, S.; Hu, X. Log-Spectral Matching GAN: PPG-Based Atrial Fibrillation Detection can be Enhanced by GAN-Based Data Augmentation With Integration of Spectral Loss. IEEE J. Biomed. Health Inform. 2023, 27, 1331–1341. [Google Scholar] [CrossRef]
- Biswas, A.; Bhattacharya, P.; Maity, S.P.; Banik, R. Data Augmentation for Improved Brain Tumor Segmentation. IETE J. Res. 2023, 69, 2772–2782. [Google Scholar] [CrossRef]
- Kuo, N.I.H.; Garcia, F.; Sönnerborg, A.; Böhm, M.; Kaiser, R.; Zazzi, M.; Polizzotto, M.; Jorm, L.; Barbieri, S. Generating synthetic clinical data that capture class imbalanced distributions with generative adversarial networks: Example using antiretroviral therapy for HIV. J. Biomed. Inform. 2023, 144, 104436. [Google Scholar] [CrossRef]
- Aldausari, N.; Sowmya, A.; Marcus, N.; Mohammadi, G. Video Generative Adversarial Networks: A Review. ACM Comput. Surv. 2022, 55, 30. [Google Scholar] [CrossRef]
- Casolaro, A.; Capone, V.; Iannuzzo, G.; Camastra, F. Deep Learning for Time Series Forecasting: Advances and Open Problems. Information 2023, 14, 598. [Google Scholar] [CrossRef]
- He, Y.; Seng, K.P.; Ang, L.M. Generative Adversarial Networks (GANs) for Audio-Visual Speech Recognition in Artificial Intelligence IoT. Information 2023, 14, 575. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Y.; Liu, Z.; Luo, P.; Wang, X. Talking Face Generation by Adversarially Disentangled Audio-Visual Representation. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, AAAI’19/IAAI’19/EAAI’19, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar] [CrossRef]
- Vougioukas, K.; Petridis, S.; Pantic, M. End-to-End Speech-Driven Realistic Facial Animation with Temporal GANs. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Long Beach, CA, USA, 15–20 June 2019; pp. 37–40. [Google Scholar]
- Mittal, G.; Wang, B. Animating Face using Disentangled Audio Representations. In Proceedings of the 2020 IEEE Winter Conference on Applications of Computer Vision (WACV), Snowmass Village, CO, USA, 1–5 March 2020; pp. 3279–3287. [Google Scholar] [CrossRef]
- Saito, M.; Matsumoto, E.; Saito, S. Temporal Generative Adversarial Nets with Singular Value Clipping. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2849–2858. [Google Scholar] [CrossRef]
- Saito, M.; Saito, S.; Koyama, M.; Kobayashi, S. Train Sparsely, Generate Densely: Memory-Efficient Unsupervised Training of High-Resolution Temporal GAN. Int. J. Comput. Vis. 2020, 128, 2586–2606. [Google Scholar] [CrossRef]
- Tulyakov, S.; Liu, M.Y.; Yang, X.; Kautz, J. MoCoGAN: Decomposing Motion and Content for Video Generation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1526–1535. [Google Scholar] [CrossRef]
- Clark, A.; Donahue, J.; Simonyan, K. Efficient Video Generation on Complex Datasets. arXiv 2019, arXiv:1907.06571. [Google Scholar]
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at Signal Fidelity Measures. IEEE Signal Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Kahembwe, E.; Ramamoorthy, S. Lower dimensional kernels for video discriminators. Neural Netw. 2020, 132, 506–520. [Google Scholar] [CrossRef]
- Sasithradevi, A.; Roomi, S.M.M.; Sivaranjani, R. Generative adversarial network for video analytics. In Generative Adversarial Networks for Image-to-Image Translation; Solanki, A., Nayyar, A., Naved, M., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 329–345. [Google Scholar] [CrossRef]
- Ho, J.; Salimans, T.; Gritsenko, A.; Chan, W.; Norouzi, M.; Fleet, D.J. Video Diffusion Models. arXiv 2022, arXiv:2204.03458. [Google Scholar] [CrossRef]
- Ge, S.; Hayes, T.; Yang, H.; Yin, X.; Pang, G.; Jacobs, D.; Huang, J.B.; Parikh, D. Long Video Generation with Time-Agnostic VQGAN and Time-Sensitive Transformer. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer: Cham, Switzerland, 2022; pp. 102–118. [Google Scholar]
- Segal, Y.; Hadar, O.; Lhotska, L. Assessing Human Mobility by Constructing a Skeletal Database and Augmenting it Using a Generative Adversarial Network (GAN) Simulator. Stud. Health Technol. Inform. 2022, 299, 97–103. [Google Scholar] [CrossRef]
- Mohamadipanah, H.; Kearse, L.; Wise, B.; Backhus, L.; Pugh, C. Generating Rare Surgical Events Using CycleGAN: Addressing Lack of Data for Artificial Intelligence Event Recognition. J. Surg. Res. 2023, 283, 594–605. [Google Scholar] [CrossRef]
- Issa, T.B.; Vinegoni, C.; Shaw, A.; Feruglio, P.F.; Weissleder, R.; Uminsky, D. Video-rate acquisition fluorescence microscopy via generative adversarial networks. In Proceedings of the 2020 IEEE 20th International Conference on Bioinformatics and Bioengineering (BIBE), Cincinnati, OH, USA, 26–28 October 2020; pp. 569–576. [Google Scholar] [CrossRef]
- Moghari, M.D.; Sanaat, A.; Young, N.; Moore, K.; Zaidi, H.; Evans, A.; Fulton, R.R.; Kyme, A.Z. Reduction of scan duration and radiation dose in cerebral CT perfusion imaging of acute stroke using a recurrent neural network. Phys. Med. Biol. 2023, 68, 165005. [Google Scholar] [CrossRef]
- Guo, L.; Nahm, W. Texture synthesis for generating realistic-looking bronchoscopic videos. Int. J. Comput. Assist. Radiol. Surg. 2023, 18, 2287–2293. [Google Scholar] [CrossRef]
- Celard, P.; Seara Vieira, A.; Sorribes-Fdez, J.M.; Romero, R.; Lorenzo Iglesias, E.; Borrajo Diz, L. Study on Synthetic Video Generation of Embryo Development. In Proceedings of the Hybrid Artificial Intelligent Systems, Salamanca, Spain, 5–7 September 2023; Springer: Cham, Switzerland, 2023; pp. 623–634. [Google Scholar]
- Miloski, B. Opportunities for artificial intelligence in healthcare and in vitro fertilization. Fertil. Steril. 2023, 120, 3–7. [Google Scholar] [CrossRef]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive Growing of GANs for Improved Quality, Stability, and Variation. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018—Conference Track Proceedings, Vancouver, BC, Canada, 30 April–3 May 2018; p. 149806. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Hara, K.; Kataoka, H.; Satoh, Y. Can Spatiotemporal 3D CNNs Retrace the History of 2D CNNs and ImageNet? In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 6546–6555. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zaballa, O.; Pérez, A.; Gómez Inhiesto, E.; Acaiturri Ayesta, T.; Lozano, J.A. Learning the progression patterns of treatments using a probabilistic generative model. J. Biomed. Inform. 2023, 137, 104271. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. In Advances in Neural Information Processing Systems; Cortes, C., Lawrence, N., Lee, D., Sugiyama, M., Garnett, R., Eds.; Neural Information Processing Systems Foundation, Inc. (NeurIPS): Montréal, QC, Canada, 2015; Volume 28. [Google Scholar]
- Festag, S.; Denzler, J.; Spreckelsen, C. Generative adversarial networks for biomedical time series forecasting and imputation. J. Biomed. Inform. 2022, 129, 104058. [Google Scholar] [CrossRef]
- Festag, S.; Spreckelsen, C. Medical multivariate time series imputation and forecasting based on a recurrent conditional Wasserstein GAN and attention. J. Biomed. Inform. 2023, 139, 104320. [Google Scholar] [CrossRef]
- Qu, Z.; Shi, W.; Tiwari, P. Quantum conditional generative adversarial network based on patch method for abnormal electrocardiogram generation. Comput. Biol. Med. 2023, 166, 107549. [Google Scholar] [CrossRef] [PubMed]
- Rutherford, A. ANOVA and ANCOVA: A GLM Approach; John Wiley & Sons: Staffordshire, UK, 2011. [Google Scholar]
- Xiao, C.; Ye, J.; Esteves, R.M.; Rong, C. Using Spearman’s correlation coefficients for exploratory data analysis on big dataset. Concurr. Comput. Pract. Exp. 2016, 28, 3866–3878. [Google Scholar] [CrossRef]
- Gomez, T.; Feyeux, M.; Boulant, J.; Normand, N.; David, L.; Paul-Gilloteaux, P.; Fréour, T.; Mouchère, H. A time-lapse embryo dataset for morphokinetic parameter prediction. Data Brief 2022, 42, 108258. [Google Scholar] [CrossRef] [PubMed]
- Celard, P.; Seara Vieira, A.; Iglesias, E.L.; Borrajo, L. GoldenDOT: Biological Development Time-Lapse Video Dataset. Iscience 2023, 23. [Google Scholar] [CrossRef]
- Goldschmidt, A.; Kunert-Graf, J.; Scott, A.C.; Tan, Z.; Dudley, A.M.; Kutz, J.N. Quantifying yeast colony morphologies with feature engineering from time-lapse photography. Sci. Data 2022, 9, 216. [Google Scholar] [CrossRef] [PubMed]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X.; Chen, X. Improved Techniques for Training GANs. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Red Hook, NY, USA, 4–9 December 2017; pp. 6629–6640. [Google Scholar]
- Unterthiner, T.; van Steenkiste, S.; Kurach, K.; Marinier, R.; Michalski, M.; Gelly, S. Towards Accurate Generative Models of Video: A New Metric & Challenges. arXiv 2018, arXiv:1812.01717. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Huynh-Thu, Q.; Ghanbari, M. The accuracy of PSNR in predicting video quality for different video scenes and frame rates. Telecommun. Syst. 2012, 49, 35–48. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).