Multi-Sensor Fusion Target Tracking Based on Maximum Mixture Correntropy in Non-Gaussian Noise Environments with Doppler Measurements
Abstract
1. Introduction
2. Background
2.1. Maximum Correntropy Criterion
2.2. Doppler Measurement Equation
3. Robust Fusion Filter Based on Maximum Mixture Correntropy
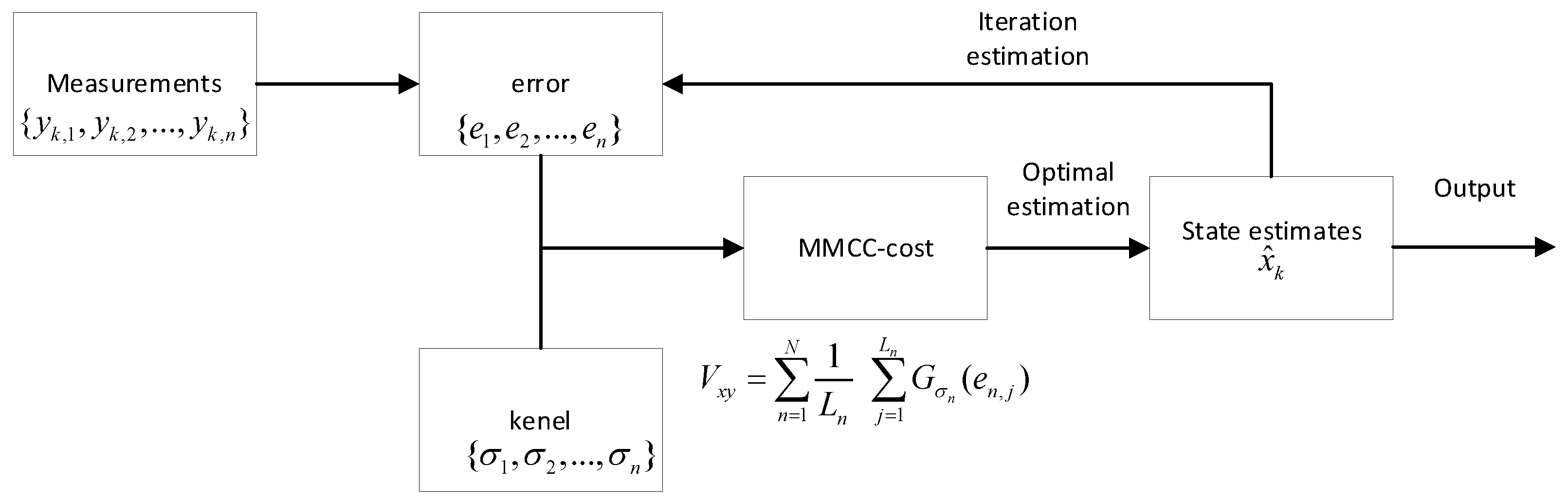
3.1. Mixture Correntropy Cost Function
3.2. Robust Fusion Information Filter Based on Maximum Correntropy Criterion
3.3. Analysis of the Algorithm Convergence
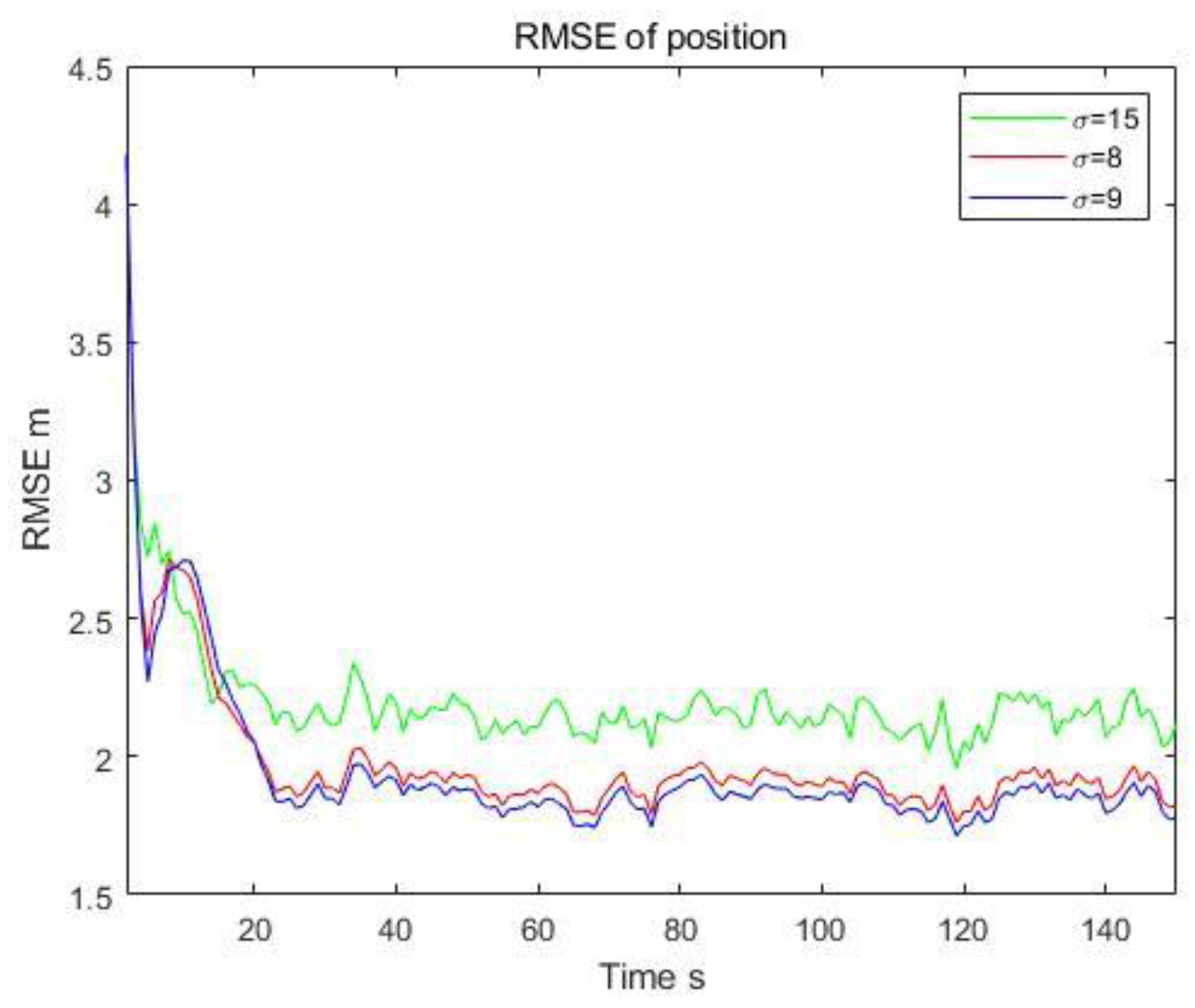
3.4. Discussion of the Kernel Selection
4. Simulation
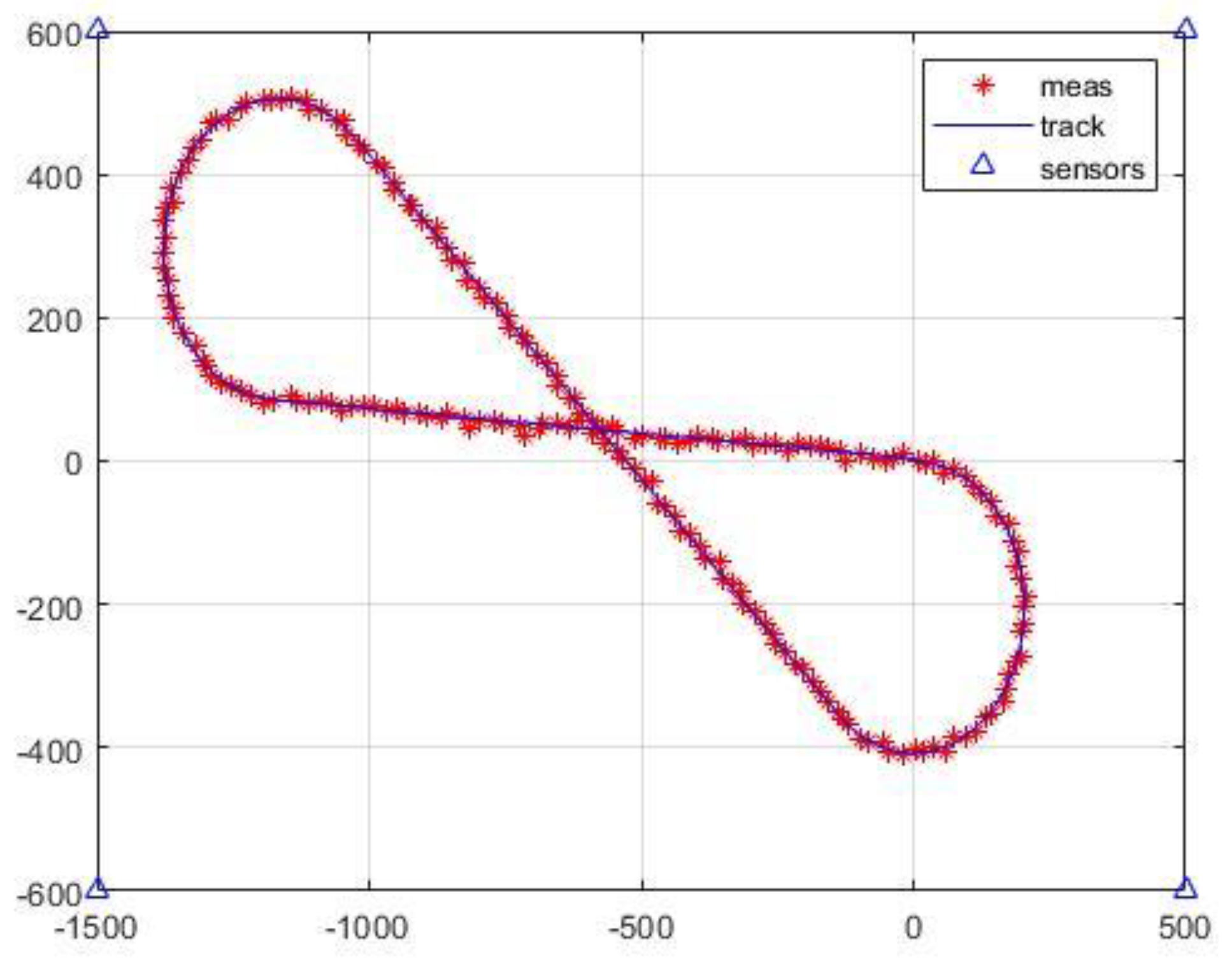
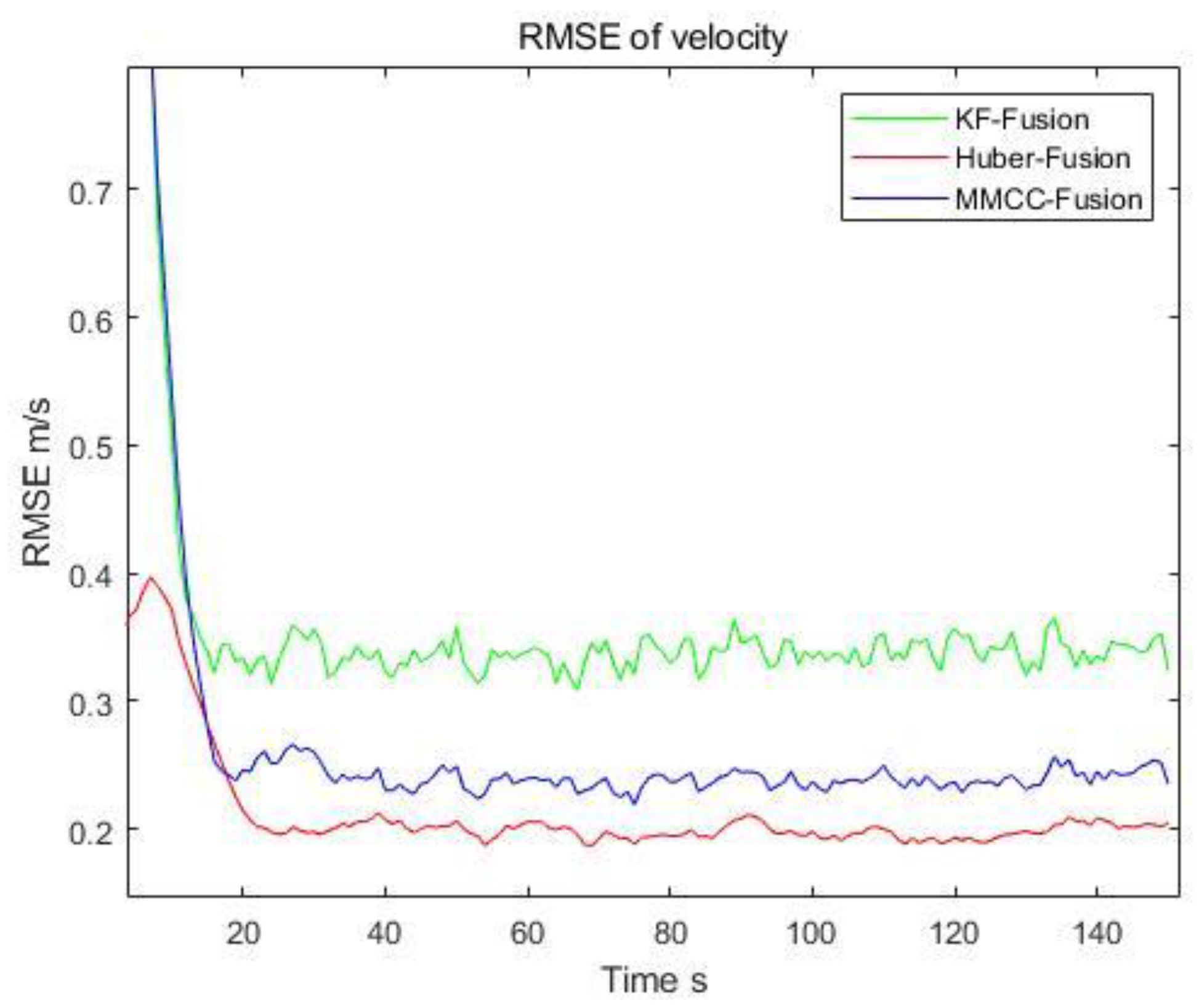
4.1. Numerical Example
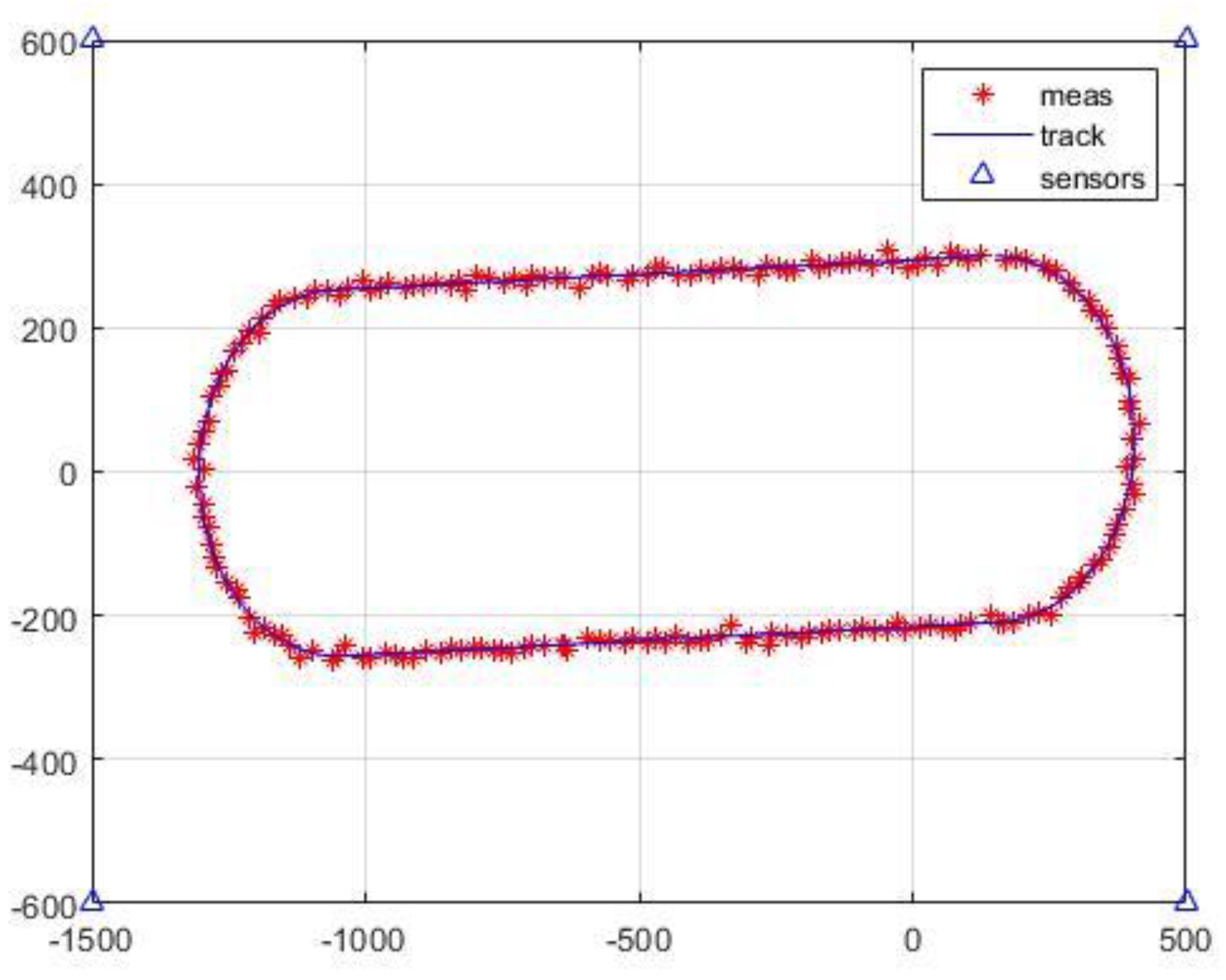
4.2. Autonomous Driving Data Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Wu, W.; Jiang, J.; Liu, W.; Feng, X.; Gao, L.; Qin, X. Augmented state gm-phd filter with registration errors for multi-target tracking by doppler radars. Signal Process. 2016, 120, 117–128. [Google Scholar] [CrossRef]
- Zheng, J. Structure and Performance Analysis of Signal Acquisition and Doppler Tracking in LEO Augmented GNSS Receiver. Sensors 2021, 21, 525. [Google Scholar] [CrossRef] [PubMed]
- Ristic, B.; Farina, A. Joint detection and tracking using multi-static doppler-shift measurements. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2012, Kyoto, Japan, 25–30 March 2012; pp. 3881–3884. [Google Scholar]
- Ristic, B.; Farina, A. Target tracking via multi-static Doppler shifts. IET Radar Sonar Navig. 2013, 7, 508–516. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Cantoni, A. The Cardinality Balanced Multi-target Multi-Bernoulli Filter and Its Implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar]
- Karlgaard, C.D. Nonlinear Regression Huber-Kalman Filtering and Fixed-Interval Smoothing. J. Guid. Control Dyn. 2014, 38, 322–330. [Google Scholar] [CrossRef]
- Karlgaard, C.; Schaub, H. Huber-based divided difference filtering. J. Guid. Control Dyn. 2007, 30, 885–891. [Google Scholar] [CrossRef]
- Graham, M.C.; How, J.P.; Gustafson, D.E. Robust state estimation with sparse outliers. J. Guid. Control Dyn. 2015, 38, 1229–1240. [Google Scholar] [CrossRef]
- Principe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer: New York, NY, USA, 2010. [Google Scholar]
- Liu, W.; Pokharel, P.P.; Principe, J.C. Correntropy: Properties, and applications in non-Gaussian signal processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- Chen, B.; Liu, X.; Zhao, H. Maximum correntropy Kalman filter. Automatic 2017, 76, 70–77. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, W.; Sun, S.; Li, L. Robust Information Filter Based on Maximum Correntropy Criterion. J. Guid. Control Dyn. 2016, 39, 1126–1131. [Google Scholar] [CrossRef]
- Chen, B.; Principe, J.C. Maximum correntropy estimation is a smoothed MAP estimation. IEEE Signal Process. Lett. 2012, 19, 491–494. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Zhao, H. Convergence of a Fixed-Point Algorithm under Maximum Correntropy Criterion. IEEE Signal Process. Lett. 2015, 22, 1723–1727. [Google Scholar] [CrossRef]
- Wang, G.Q.; Gao, Z.X.; Zhang, Y.G.; Ma, B. Adaptive maximum correntropy Gaussian filter based on variational Bayes. Sensors 2018, 18, 1960. [Google Scholar] [CrossRef] [PubMed]
- Gan, Q.; Harris, C.J. Comparison of two measurement fusion methods for Kalman-filter-based multisensor data fusion. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 273–279. [Google Scholar] [CrossRef]
- Wang, G.; Li, N.; Zhang, Y. Maximum correntropy unscented Kalman and information filters for non-Gaussian measurement noise. J. Frankl. Inst. 2017, 354, 8659–8677. [Google Scholar] [CrossRef]
- Udacity’s Self-Driving Car Simulator, Udacity, Mountain View, CA, USA. 2017. Available online: https://github.com/udacity/self-drivingcar-sim (accessed on 2 August 2023).


| Algorithm | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
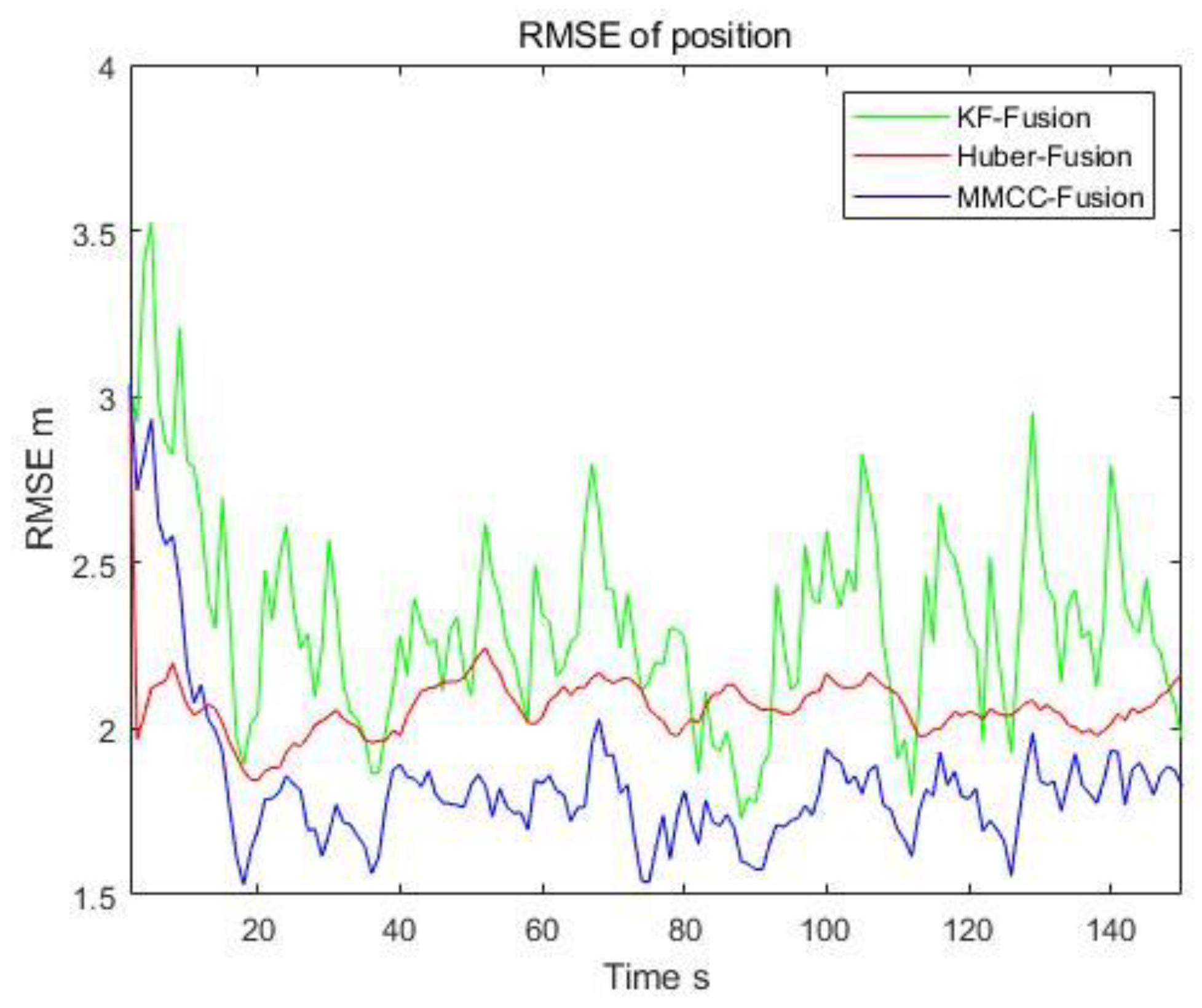
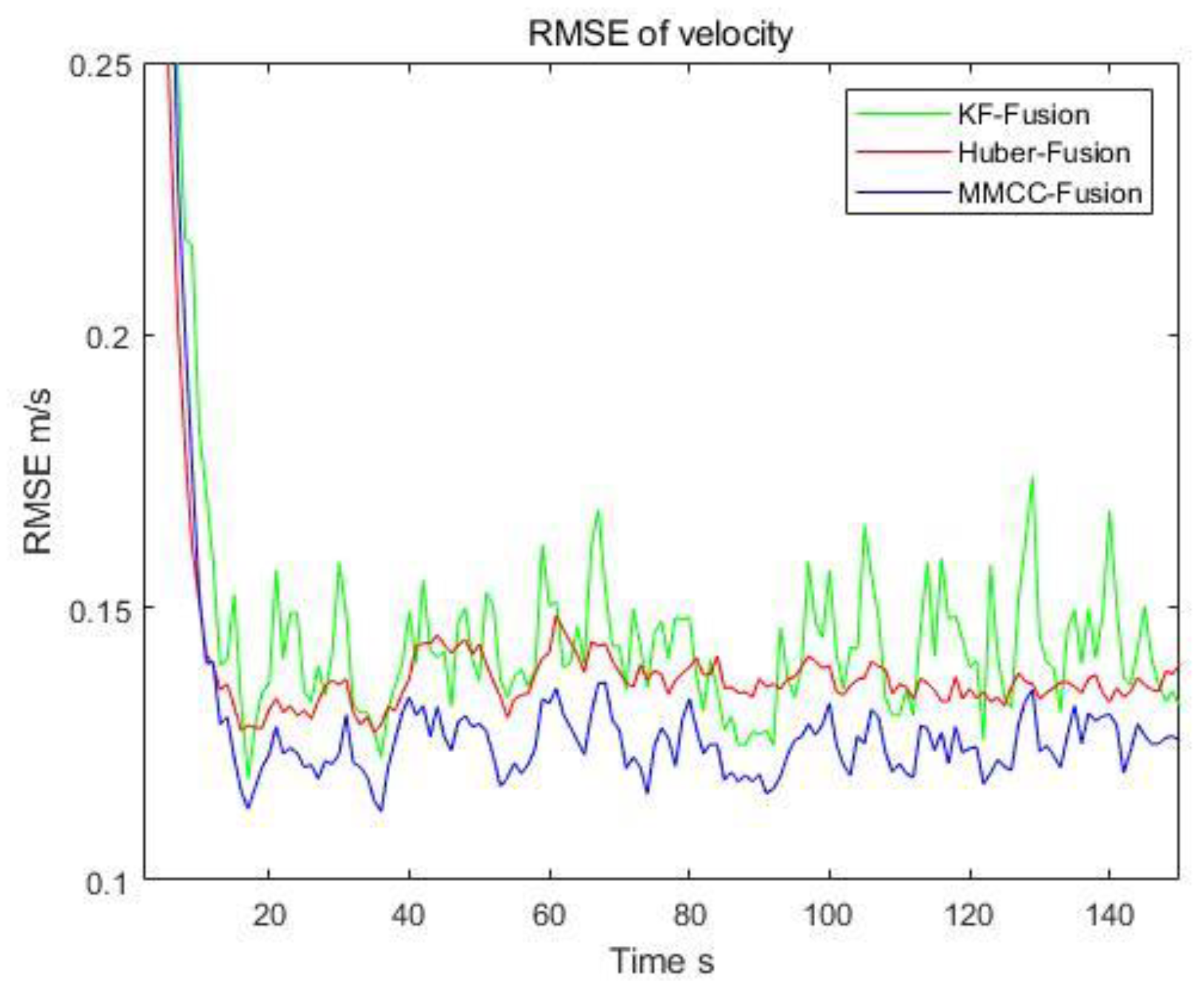
| KF-Fusion | 1.413 | 2.510 | 1.918 | 2.404 |
| Huber-Fusion | 2.165 | 2.050 | 1.907 | 2.226 |
| MMCC-Fusion | 1.555 | 1.753 | 1.725 | 1.890 |
| Algorithm | Kernel Widths | Iteration Num | ||
|---|---|---|---|---|
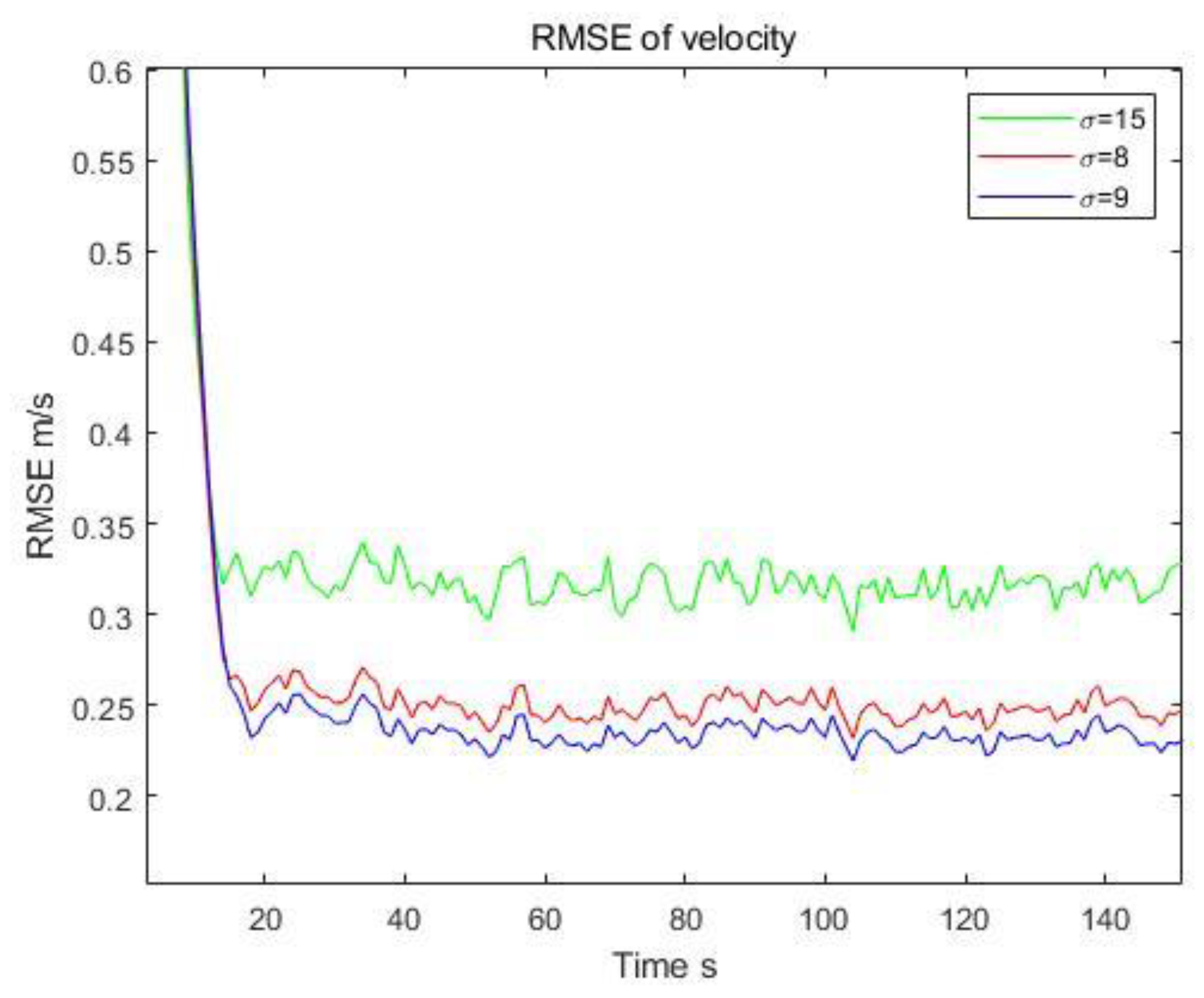
| MMCC-Fusion-IF | ) | 1.895 | 0.249 | 3.85 |
| ) | 1.840 | 0.234 | 2.98 | |
| ) | 2.164 | 0.306 | 2.36 | |
| KF-Fusion | 2.179 | 0.312 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, C.; Li, M.; Li, S. Multi-Sensor Fusion Target Tracking Based on Maximum Mixture Correntropy in Non-Gaussian Noise Environments with Doppler Measurements. Information 2023, 14, 461. https://doi.org/10.3390/info14080461
Yi C, Li M, Li S. Multi-Sensor Fusion Target Tracking Based on Maximum Mixture Correntropy in Non-Gaussian Noise Environments with Doppler Measurements. Information. 2023; 14(8):461. https://doi.org/10.3390/info14080461
Chicago/Turabian StyleYi, Changyu, Minzhe Li, and Shuyi Li. 2023. "Multi-Sensor Fusion Target Tracking Based on Maximum Mixture Correntropy in Non-Gaussian Noise Environments with Doppler Measurements" Information 14, no. 8: 461. https://doi.org/10.3390/info14080461
APA StyleYi, C., Li, M., & Li, S. (2023). Multi-Sensor Fusion Target Tracking Based on Maximum Mixture Correntropy in Non-Gaussian Noise Environments with Doppler Measurements. Information, 14(8), 461. https://doi.org/10.3390/info14080461






