2. Research Studies on World Economic Network
The study of the world economic network is based on the complex networks theory as developed in the last 23 years [
6].
In 1992, D. Smith and D. White, using financial data from 1965 to 1980 about imports for more than 100 countries, showed that the world economic network is structured in layers (core–periphery) consisting of groups of countries of decreasing order of influence. They found out that there is a tendency in the world economy to expand the core and reduce the number of peripheral countries [
7].
M.A. Serrano and M. Boguna in 2003 created a complex directed network using import–export data for the 40 most marketable products among countries for the year 2000 and presented the first empirical characterization of the world-trading web, calculating some typical properties that characterize complex networks such as distribution of grades, clustering coefficient, etc. Their calculations showed that the world trade network cannot be described as a classical random network because it displays the typical properties of a scale-free network with a small-world property and is highly clustered [
8].
In 2005, D. Garlaschelli and M.I. Loffredo studied the topological properties of the world trade web (WTW), which are closely related to the gross domestic product (GDP) of world countries from 1950 to 1996 and took into consideration the directional nature of the international trade routes and the time dependence of the parameters describing the topology WTW [
9].
Bhattacharya et al. in 2008 investigated the ranges of different quantities relevant to the world economic network (WEN), expanding their data from 1948 to 2000 and assuming that WEN is an undirected network with the commercial flows among countries as its edge weights. They noticed that WEN remained unchanged over a span of 53 years, implying robustness or universality. Among other things, they also showed that a big part of the world trade is controlled by a small club of rich countries that is shrinking as time goes by [
10].
Moving on, Fagiolo et al. showed in 2009 that for the years 1981–2000, apart from the structure of core–periphery, weak trade bonds characterize most countries, and rich countries have stronger trade bonds and are more tightly organized in groups. They also noticed that the world trade web (WTW) is statistically more clustered than if it were random, and all the properties of the network are remarkably stable through the years and not dependent on the weighting procedure [
11].
Globalization, which has occurred in the last decades, creates changes not only in terms of economics but also to the structural properties of socio-economic networks towards greater complexity. The increase in rank and connectivity of common economic networks causes greater uncertainty and instability dangers. D. Hossu et al. in 2009 applied network measurements to the world trade data and proposed some effective means of managing the complexity of the world economic network based on efficient models [
12].
The economic crisis of 2008 in the USA and its dissemination around the world led the greatest part of the researchers’ attempts to search for the countries that influence the global economy the most, that, is the countries that dominate exports. Towards this direction, the investigation of Reyes et al. in 2011 using data of transboundary bank loans for 184 countries for the years 1978–2009 showed that connectivity tends to decrease during and after systemic crises of national debt, using measurements of centrality, connectivity, and grouping. The world economic crisis of 2008–2009 is referred to as an unusually big disruption in the transboundary bank network [
13].
However, since the economic crisis of 2008 and onwards, other cases of countries with smaller GDPs and fewer exports were studied as well as how and how much the topology of the world macroeconomic network influences the spread of economic crises. In 2011, Lee et al. noted that the role of an individual country in the dissemination of crises does not only depend on its gross macroeconomic ability but also on its regional and world connectivity profile in the framework of the world economic network. The researchers expressed the opinion that the grouping of weaker countries on a peripheral scale may deteriorate the expansion of crises significantly, but on the other hand, this global network structure shows greater tolerance to extreme crises as compared to a more “globalized” random network [
14].
Furthermore, in a study by L. De Benedictis et al. in 2013, an economic dataset for 178 countries from 1995 to 2010 was used, and the topology and properties of the world trade network were investigated. Their study concerned the weighted and unweighted version of the world network and at the same time offered visualized network models for various commercial products [
15].
In a study published recently in 2022, D.G. Demiral and M.I. Yenilmez searched for the effects of the COVID-19 pandemic on global trade, by building networks with the 50 largest exporting countries. Degree, closeness, and betweenness centralities were calculated, and they found the existence of four or five clusters around countries with strong economies [
16].
The scope of this study is to analyze the global economy as a complex system of interdependent factors by employing complex network methods. It focuses on economic data from all countries worldwide, treating each country as a node and its exports as links. The analysis primarily revolves around identifying shifts in countries’ positions within the network and understanding the potential causes behind these changes through a geopolitical lens.
The motivation of our work is to extend the results of previous investigations in the following directions: (1) include the period 2008–2019, (2) characterize more precisely the world trade network by including additional indices (clustering coefficient, average path length, eccentricity, betweenness centrality, modularity, and number of communities), and (3) highlight geopolitical implications. More specifically, we address the following research questions:
- Q1.
How does the importance of countries in the global economy manifest in terms of network properties?
- Q2.
How do collaborations between countries and global geopolitical stability appear as network properties? Can we identify groups of countries with “stronger” links among them?
- Q3.
Can changes in the global economy be manifested and observed as changes in network properties? In particular, how does the trend towards globalization in the global economy manifest in terms of network metrics?
- Q4.
What are the geopolitical implications of the answers to questions Q1–Q3?
The methodology to address the above questions Q1–Q4 is as follows:
We employ complex network analysis tools for the study of geopolitical stability, particularly in the context of the global trading system using data on international trade;
We evaluate selected local and global network indicators of connectivity as well as average values, and we indicate the meaning of these values in the context of financial data;
We identify countries with weak and strong bonds, the related power dynamics, and the resulting geopolitical tensions that emerged in subsequent years.
6. Research Questions
The research questions Q1–Q4 (
Section 2) are answered as follows:
Q1. Network characterization of the importance of countries in the global economy.
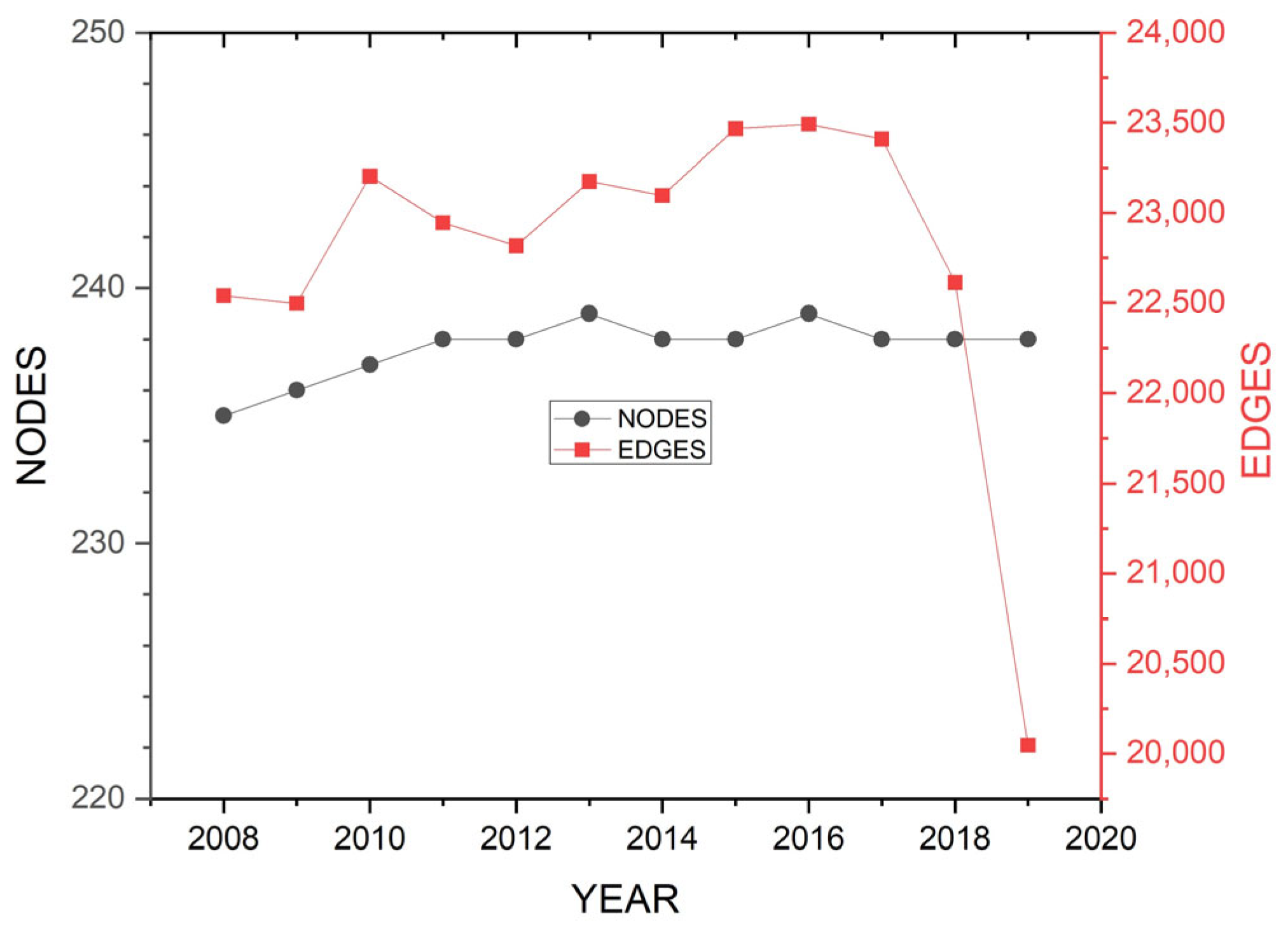
The world distribution of products is carried out in 239 destinations, which comprise the nodes of the network (
Section 3). Their total number varied very little (<1%) from 2008 to 2019. These nodes interconnected with a total sum of edges, which exceeds 23,000 most of the time. A fully interconnected network with the same number of nodes (Ν = 239) would normally have 56,882 edges. The diameter and the eccentricity (
Section 3.5) of the network take value three (
Table 5), indicating small trade pathways, i.e., high interconnectedness.
The USA, the U.K., France, the Netherlands, China, and Germany function as mediators indirectly connecting every country in the planet to any other country (
Section 3.7,
Table 8 and
Section 3.5,
Table 5). China appeared as a mediator later.
Q2. Collaborations between countries and global geopolitical stability as network properties and groups of countries with “strong” links.
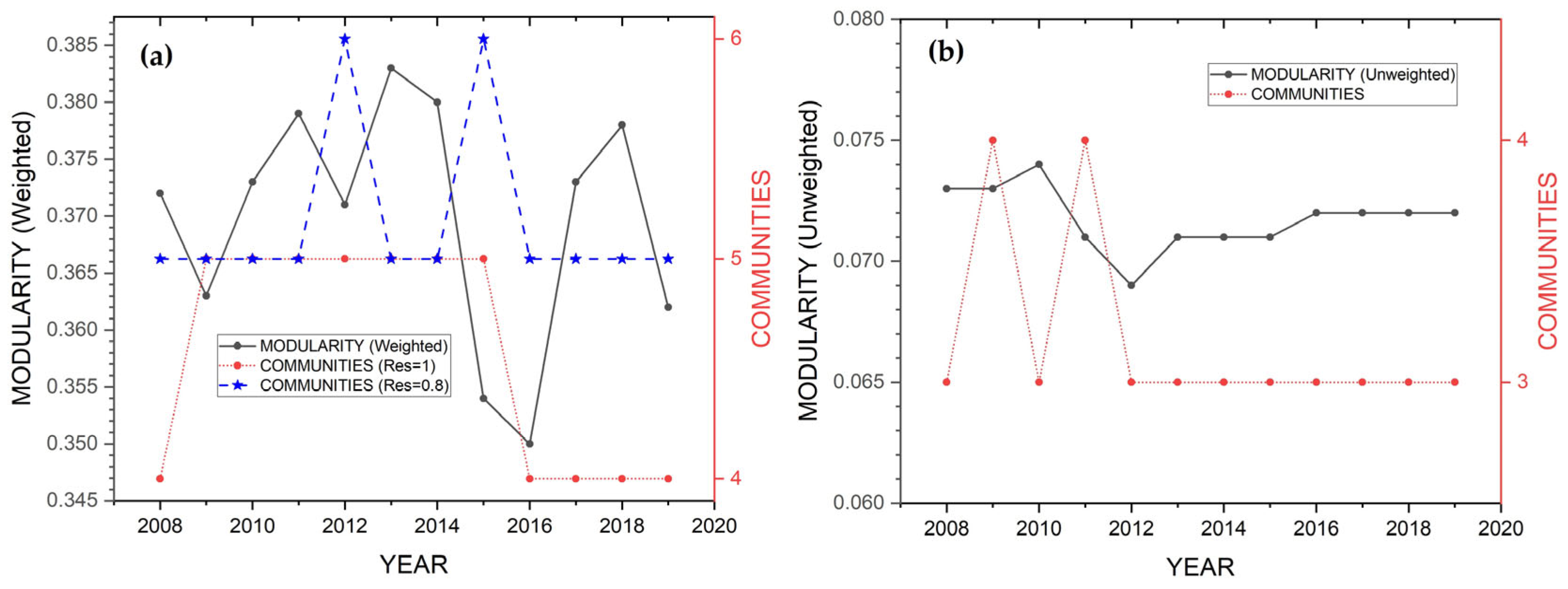
The search for groups of countries involved in the world trade with the modularity method (
Section 3.4) shows three main groups with more than 40 member countries each and with constant presence for the specific time period and three minor communities with a small number of member countries and sporadic appearance (
Figure 8 and
Figure 11). The three main groups are responsible for the distribution of the largest part of products on a global scale in such a way that the most remote destinations are three steps away from each other.
The modularity analysis of the unweighted WTN graph puts the key players (the USA, China, and Germany) in the same group as it takes into account the presence of links instead of the size of exports. In contrast, the weighted WTN analysis takes into account the size of transactions and is closer to the real state of the world trade (
Figure 9 and
Figure 10). Comparing the two different methods of network analysis, with and without weights, we observed big differences that we did not expect since we did not find anything similar anywhere in the literature. These differences were found in the number of groups that appear and in the countries from which they are composed.
The number of member countries in every group seems more dependent on basic economic indicators such as the currency rate, the GDP, and the exports of the leader country in this particular group. It is important to note that, for the period 2008–2019, the aggregate exports of key players was about 30% of the total world exports, and they had similar levels of exports.
Q3: Changes in the global economy as changes in network properties.
Density (
Section 3.1) appeared with remarkable stability until 2018 (
Figure 3, black line), indicating that the world economic network is robust (
Table 2). Observing in
Figure 3 with the red line the slow increase in the average clustering coefficient (
Section 3.3), we conclude that there is a tendency to create connections between partner countries. The small decrease (
Figure 13) in the average path length (
Section 3.5) means that the distances/steps between the network nodes are slowly decreasing, indicating progressive interconnectedness that is converging towards greater globalization of the economy. In this process, the USA, the U.K., and France gradually lose their leadership, while the Netherlands and Spain remain more or less stable (
Table 6,
Table 8 and
Table 10).
In contrast to the closeness, betweenness changes faster and more intensely (
Table 7 and
Table 9) since various politics can influence the route of goods and the intermediate stations. One example is the duties or restrictions that are imposed by countries on imports (2014–2016, the USA—taxes on all products coming from China) or on exports (2014–2015, Russia—embargo of products due to the occupation of Crimea).
All countries have very high eigenvector centrality (
Table 10), indicating that they act as strong regulators in the international trade. Moreover, as the annual average eigenvector centrality remains more or less constant for the whole period, there are no significant changes in the regulation of the international trade.
One of the objectives of this research was to seek whether the specific analysis can capture emerging economies during the researched period. As previous studies show, using unweighted centrality measures, the increasing importance of regional trade and of some emergent countries becomes evident. Instead, with weighted centrality measures, a more traditional core–periphery picture is confirmed [
15].
Q4: Geopolitical implications of the network analysis of the WTN from 2008 to 2019.
For the geopolitical implications of the network analysis of the WTN from 2008 to 2019, two key trends are observed:
- (i)
The trend towards increasing globalization of the world economy: This follows from the observed stability of average degree (
Section 5.1,
Table 2, and
Figure 4), the slowly increasing density (
Section 5.1,
Table 2, and
Figure 3), the increase in average clustering coefficient (
Section 5.1,
Table 2, and
Figure 3), and the decrease in the average path length (
Section 5.3,
Table 5, and
Figure 13);
- (ii)
The stability and economic independence of the group of EU countries (
Section 5.2 and
Figure 8);
The sporadic appearance of other groups with strong economic powers (India/South Africa, and Russia;
Section 5.2 and
Figure 8 and
Figure 11).
These trends have also been confirmed by other researchers using different methods of analysis [
31,
32,
33,
34,
35].
The stable economic model of a superpower (USA) is moving into a reconstruction phase, a state in which economic instability can occur [
33]. Global economic instability is very likely to have far-reaching consequences and potentially contribute to the outbreak of wars [
36,
37]. In the case of instability in global trading, uncertainty is increasing, the risk of investment is increasing, and war is very likely to break out [
38]. Critical reasons that contribute to the conflicts between countries or nations are the following:
Trade wars and protectionism: In early 2018, the USA government applied and expanded tariffs on Chinese goods in response to Beijing’s unfair practices, and China has retaliated, raising tariffs on U.S. exports [
39,
40]. It is obvious that in international geopolitics, countries raise economic borders to protect their domestic industries, which is equivalent with economic war, creating tension between nations, which is likely to trigger real war [
41,
42];
Emergence of economic alliances and blocks: In this case, due to economic instability and uncertainty, some countries may seek to form alliances and blocks in order to protect their economic interests and gain new leverage in global affairs. These blocks may cause rivalries that increase the likelihood of conflicts between opposing alliances [
43,
44];
Economic sanctions are a source of economic instability, serving as a tool of foreign policy. When countries impose severe economic sanctions, tensions increase, and military responses or escalations are provoked [
45].
A typical example of a trade war that causes geopolitical instability is the case mentioned above between the USA and China. The fact that both countries have taken measures during the researched period, affecting global trade and all the other countries, emerged within the present research (
Section 5.2 and
Figure 8).
In
Table 12, we present the calculations of our research in comparison with the previous works on the same topic as mentioned in
Section 2.
The results in the present work are very close to other works presented in
Table 12. The addition of more countries/nodes to our research and of course the changes in global economic data in the following years and up to 2008 cause some small differences, especially in the average path length and clustering coefficient indicators. We also confirmed that globalization is progressing, and the trade system has become a self-organized complex system that must be considered from now on as a whole [
8]. In addition, our research highlights the grouping of closely cooperating countries, and the only research related to a later period than ours found a similar structure in the WTN, with four or five communities and the same dominant countries [
16].
The theoretical contribution of our work is the demonstration that network theory can identify the roles of countries in the WTN as well as the emerging groups of countries using the appropriate network indices (
Section 3). Researchers may select the appropriate indices in order to obtain quantitative assessments addressing questions of interest. The results can be computed if we know the exports between countries.
Practical implications of our work include the following:
Stability of average degree (Conclusions, Q1);
Slowly increasing density (Conclusions, Q3);
Decreasing average path length (Conclusions, Q3).
The increasing clustering coefficient (Conclusions, Q3);
The positive value of modularity, indicating the presence of communities (Conclusions, Q2);
The number of communities (Conclusions, Q2);
The remarkable qualitative similarity of the evolution of world GDP (
Figure 5), with the average weighted degree (
Figure 4, red line);
The number of member countries in the group of USA and the number of member countries in the group of China evolve in opposite ways (
Figure 8a);
The results 1–7 confirm quantitively known assessments, while 8, 9, and 10 are novelties.
The limitation of our methodology is that we considered the global value of exports from one country to another. In order to have more accurate geopolitical implications, we intend to explore different kinds of exports and their geopolitical significance.
7. Conclusions and Future Work
This study encompasses a comprehensive analysis of the global economy using complex network methods, with a focus on identifying changes in countries’ positions within the world trade network and interpreting these changes through geopolitical terms. As evidenced by research analysis, its contributions lie in providing novel insights into the long-term trends, detailed explanations about the natural grouping of countries, and the interplay between trade dynamics and geopolitical stability, all of which enhance our understanding of the complex global economic landscape.
Based on the current study’s findings, the aim of future research is to supplement the dataset with data from 2019–2022 as well as the use of more sophisticated tools in order to enhance the understanding of the global economy using more complex network methods and geopolitical interpretations. Here are some future directions:
Long-term impact analysis: With access to data from 2019–2022, we can analyze the long-term impact of major events such as BREXIT, the COVID-19 pandemic, the different policies in the USA, and the war in Ukraine on the global economy. By tracking changes in countries’ positions within the world trade network before, during, and after these events, it is possible to identify any lasting effects and trends.
Geopolitical risk assessment: Utilizing more complex network methods, we can develop models to assess geopolitical risks in the global economy. By considering changes in countries’ centrality, connectivity, and trade dependencies in the world trade network, it may be possible to identify regions or countries that are more vulnerable to geopolitical shocks and economic disruptions.
Network resilience analysis: We can investigate the resilience of the world trade network in the face of various shocks and events. By applying entropy-based indicators and weighted centralities, the study can assess how the network adapts and reorganizes itself in response to geopolitical and economic changes, providing valuable insights into its stability and vulnerability.
Trade policy implications: The study can be extended to explore the implications of trade policies on the global economy. By analyzing the network dynamics and changes in countries’ trade positions, we can gain a deeper understanding of the impact of trade agreements, tariffs, and other policies on international trade patterns and economic growth.
Sector-specific analysis: Focusing on specific economic sectors can provide a more granular understanding of the world trade network. We can investigate how geopolitical events and policies impact particular industries and how their positions in the network evolve over time. This can shed light on the sector-specific vulnerabilities and opportunities in the global economy and supply chain.
Comparison with previous economic crises: To gain a broader perspective, we can compare the findings from the 2019–2022 period with previous economic crises, such as the 2008 financial crisis or other major historical events. This comparative analysis can highlight common patterns and differences, providing valuable lessons for policymakers and economists.
Predictive modeling: Using the enriched dataset and sophisticated tools, we can develop predictive models for the global economy’s future trends. By incorporating historical data on geopolitical events and their impacts, these models can help forecast potential scenarios and inform decision making.
Network visualization and interactive tools: Creating interactive visualizations of the world trade network can enhance the accessibility and understanding of the research findings for policymakers, economists, and the public. These tools can be made available in the research community to engage a broader audience and facilitate further exploration of the data.
By pursuing these future research directions, this study can contribute significantly to the field of global economics, geopolitics, and complex network analysis. It can also serve as a valuable resource for policymakers and stakeholders seeking to navigate the complexities of the global economy in an ever-changing world.
Author Contributions
Conceptualization, G.D.P., L.M., K.D. and I.A.; methodology, G.D.P., L.M., K.D. and I.A.; software, G.D.P.; validation, G.D.P., L.M., K.D. and I.A.; formal analysis, G.D.P., L.M., K.D. and I.A.; investigation, G.D.P. and L.M.; resources, G.D.P.; data curation, G.D.P.; writing—original draft preparation, G.D.P.; writing—review and editing, G.D.P., L.M., K.D. and I.A.; visualization, G.D.P., L.M., K.D. and I.A.; supervision, L.M., K.D. and I.A.; project administration, G.D.P., L.M., K.D. and I.A.; funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thurner, S.; Hanel, R.A.; Klimek, P. Introduction to the Theory of Complex Systems; Oxford University Press: Oxford, UK; New York, NY, USA, 2018. [Google Scholar]
- Albert, R.; Barabasi, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Newman, M.E.J. Networks: An Introduction; Oxford University Press: Oxford, UK; New York, NY, USA, 2010. [Google Scholar]
- Xinbo, W. Understanding the Geopolitical Implications of the Global Financial Crisis. Wash. Q. 2010, 33, 155–163. [Google Scholar] [CrossRef]
- Desai, R. Geopolitical economy: After US hegemony, globalization and empire. In The Future of World Capitalism; Pluto Press: London, UK; New York, NY, USA, 2013. [Google Scholar]
- Newman, M.E.J. Networks, 2nd ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 2018. [Google Scholar]
- Smith, D.A.; White, D.R. Structure and Dynamics of the Global Economy: Network Analysis of International Trade 1965–1980. Soc. Forces 1992, 70, 857. [Google Scholar] [CrossRef]
- Serrano, M.Á.; Boguñá, M. Topology of the world trade web. Phys. Rev. E 2003, 68, 015101. [Google Scholar] [CrossRef] [PubMed]
- Garlaschelli, D.; Loffredo, M.I. Structure and evolution of the world trade network. Phys. Stat. Mech. Its Appl. 2005, 355, 138–144. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Mukherjee, G.; Saramäki, J.; Kaski, K.; Manna, S.S. The International Trade Network: Weighted network analysis and modelling. J. Stat. Mech. Theory Exp. 2008, 2008, P02002. [Google Scholar] [CrossRef]
- Fagiolo, G.; Reyes, J.; Schiavo, S. The evolution of the world trade web: A weighted-network analysis. J. Evol. Econ. 2010, 20, 479–514. [Google Scholar] [CrossRef]
- Hossu, D.; Humaila, H.; Mocanu, S.; Saru, D. Complex networks to model the economic globalization process. IFAC Proc. Vol. 2009, 42, 62–64. [Google Scholar] [CrossRef]
- Reyes, J.A.; Minoiu, C. A Network Analysis of Global Banking: 1978–2009. IMF Work. Pap. 2011, 11, 1. [Google Scholar] [CrossRef]
- Lee, K.-M.; Yang, J.-S.; Kim, G.; Lee, J.; Goh, K.-I.; Kim, I. Impact of the Topology of Global Macroeconomic Network on the Spreading of Economic Crises. PLoS ONE 2011, 6, e18443. [Google Scholar] [CrossRef] [PubMed]
- De Benedictis, L.; Nenci, S.; Santoni, G.; Tajoli, L.; Vicarelli, C. Network Analysis of World Trade Using the BACI-CEPII Dataset. SSRN Electron. J. 2014, 14, 287–343. [Google Scholar] [CrossRef]
- Gönçer-Demiral, D.; İnce-Yenilmez, M. Network analysis of international export pattern. Soc. Netw. Anal. Min. 2022, 12, 156. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Pósfai, M. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory; in Graduate Texts in Mathematics; Springer: London, UK, 2008; Volume 244. [Google Scholar] [CrossRef]
- Knuth, D.E. Two Notes on Notation. Am. Math. Mon. 1992, 99, 403. [Google Scholar] [CrossRef]
- Gephi—The Open Graph Viz Platform. Available online: https://gephi.org/ (accessed on 17 January 2023).
- Tsiotas, D. Modeling of Interregional Transportation Systems Using Complex Network Analysis and Statistical Mechanics; University of Thessaly, School of Engineering, Department of Planning and Regional Development: Volos, Greece, 2016. [Google Scholar] [CrossRef]
- Spyropoulos, A.Z.; Bratsas, C.; Makris, G.C.; Ioannidis, E.; Tsiantos, V.; Antoniou, I. Entropy and Network Centralities as Intelligent Tools for the Investigation of Terrorist Organizations. Entropy 2021, 23, 1334. [Google Scholar] [CrossRef] [PubMed]
- Brandes, U.; Fleischer, D. Centrality Measures Based on Current Flow. In STACS 2005; Diekert, V., Durand, B., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3404, pp. 533–544. [Google Scholar] [CrossRef]
- World Integrated Trade Solution (WITS). Data on Export, Import, Tariff, NTM. Available online: https://wits.worldbank.org/Default.aspx?lang=en (accessed on 13 January 2023).
- DataBank. World Development Indicators. Available online: https://databank.worldbank.org/source/world-development-indicators (accessed on 14 January 2023).
- Blondel, V.D.; Guillaume, J.-L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Snidal, D. The Limits of Hegemonic Stability Theory. Int. Organ. 1985, 39, 579–614. [Google Scholar] [CrossRef]
- Radulescu, I.G.; Panait, M.; Voica, C. BRICS Countries Challenge to the World Economy New Trends. Procedia Econ. Financ. 2014, 8, 605–613. [Google Scholar] [CrossRef]
- Martin, S.; Brown, W.M.; Klavans, R.; Boyack, K.W. OpenOrd: An open-source toolbox for large graph layout. In Proceedings of the IS&T/SPIE Electronic Imaging, San Francisco, CA, USA, 27 January 2011; SPIE: Geneva, Switzerland, 2011; p. 786806. [Google Scholar] [CrossRef]
- Muzaffar, M.; Yaseen, Z.; Rahim, N. Changing Dynamics of Global Politics: Transition from Unipolar to Multipolar World. Lib. Arts Soc. Sci. Int. J. LASSIJ 2017, 1, 49–61. [Google Scholar] [CrossRef]
- Diesen, G. Europe as the Western Peninsula of Greater Eurasia. J. Eurasian Stud. 2021, 12, 19–27. [Google Scholar] [CrossRef]
- Diesen, G. The Disorderly Transition to a Multipolar World. New Perspect. 2019, 27, 125–129. [Google Scholar] [CrossRef]
- Brooks, S.G.; Wohlforth, W.C. The Rise and Fall of the Great Powers in the Twenty-first Century: China’s Rise and the Fate of America’s Global Position. Int. Secur. 2016, 40, 7–53. [Google Scholar] [CrossRef]
- Boxill, I.; Ideaz Institute. Ideaz Journal Vol. 10–12. Available online: https://www.academia.edu/31511006/Ideaz_Journal_vol_10_12 (accessed on 18 May 2023).
- Fukuyama, F. The End of History and the Last Man; 1st Free Press Trade; Free Press: New York, NY, USA, 2006. [Google Scholar]
- Greenspan, A. The Age of Turbulence: Adventures in a New World with a New Chapter on the Current Credit Crisis; Penguin Books: London, UK, 2008. [Google Scholar]
- Copeland, D. Economic Interdependence and War: A Theory of Trade Expectations. Int. Secur. 1996, 20, 5–41. [Google Scholar] [CrossRef]
- Kanapathy, E.S.I. America Is Showering China with New Restrictions. Foreign Policy 15/2/2022. Available online: https://foreignpolicy.com/2022/02/15/us-china-economic-financial-decoupling-controls-restrictions-sanctions/ (accessed on 18 May 2023).
- Brookings. The US-China Economic Relationship: A Comprehensive Approach. Available online: https://www.brookings.edu/articles/the-us-china-economic-relationship-a-comprehensive-approach/ (accessed on 18 May 2023).
- Subramanian, A. Eclipse: Living in the Shadow of China’s Economic Dominance; Peterson Institute for International Economics: Washington, DC, USA, 2011. [Google Scholar]
- Evenett, S.J.; Baldwin, R.E. The Collapse of Global Trade, Murky Protectionism, and the Crisis: Recommendations for the G20; Centre for Economic Policy Research: London, UK, 2009. [Google Scholar]
- Mansfield, E.D.; Milner, H.V. Votes, Vetoes, and the Political Economy of International Trade Agreements; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Ravenhill, J. The Political Economy of Asia-Pacific Trade Agreements; Oxford University Press: Oxford, UK, 2014. [Google Scholar] [CrossRef]
- Hufbauer, G.C.; Jung, E. Economic sanctions in the twenty-first century. In Research Handbook on Economic Sanctions; Van Bergeijk, P.A.G., Ed.; Edward Elgar Publishing: Northampton, MA, USA, 2021. [Google Scholar] [CrossRef]
Figure 1.
The number of countries lacking export data during 2008–2018.
Figure 2.
The number of nodes (black line) and the number of edges (red line).
Figure 3.
The variation of network density shown with the black line and the average clustering coefficient for the period 2008–2019 with the red line.
Figure 4.
The average degree of nodes without weights (black line) and with weights (red line).
Figure 5.
The variation of GDP in USD in the years 2008–2019. The local minimums are present in the same periods with the minimums in the average weighted degree indicator. Data source: World Development Indicators—The World Bank [
25].
Figure 6.
The (out) flow index for ten important countries.
Figure 7.
Fluctuation of modularity from 2008–2019 (black line, (
a)). The red and blue lines show the differences in the number of communities present, modifying the algorithm (case 1–case 2,
Table 2). The unweighted modularity is presented in (
b) for comparison.
Figure 8.
(
a) The modularity analysis in the first scenario produces three main communities and two minor ones. (
b) The exchange rate indicator USD–CNY. Data source: World Integrated Trade Solution—The World Bank [
24].
Figure 9.
The community structure of the WTN for the year 2008 involves four communities with the key players of the USA, China, Germany, and S. Arabia/UAE (a). The community structure for the corresponding unweighted graph involves three communities with mixed key players (b).
Figure 10.
(a) The community structure of the WTN for the year 2019 involves four communities with the key players of the USA, China, Germany, and S. Arabia/UAE (a). The community structure for the corresponding unweighted graph involves three communities with mixed key players (b).
Figure 11.
(a) The changes in the number of member countries in the three main communities (Germany, the USA, and China) are greater due to the appearance of minor communities (b) with more member countries (Saudi Arabia/HAE, South Africa/India, and Russia).
Figure 12.
(a) Fluctuations in the stable group of Germany appear whenever Russia’s group occasionally appears. (b) The negative interrelation and competition between China–India/South Africa.
Figure 13.
The decrease in the average path length.
Figure 14.
The fluctuations in closeness centrality for 10 important countries in the world trade with highest values.
Figure 15.
The fluctuations in betweenness centrality for 10 important countries in the world economy with highest values.
Figure 16.
The fluctuations in eigenvector centrality for 10 important countries in the world economy with highest values.
Table 1.
The countries with missing export data during 2008–2018.
| Anguilla | 2008 | Micronesia, Fed. Sts. | 2013 | Lesotho | 2017 | Iran, Islamic Rep. | 2018 |
| Grenada | 2008 | Venezuela | 2013 | Mali | 2017 | Lebanon | 2018 |
| Netherlands Antilles | 2008 | Iraq | 2014 | Nepal | 2017 | Libya | 2018 |
| Djibouti | 2009 | Montserrat | 2014 | Panama | 2017 | Maldives | 2018 |
| Faroe Islands | 2009 | Tonga | 2014 | Sri Lanka | 2017 | Montenegro | 2018 |
| Gabon | 2009 | Bangladesh | 2015 | St. Kitts and Nevis | 2017 | Mozambique | 2018 |
| Mayotte | 2009 | French Polynesia | 2015 | Albania | 2018 | Niger | 2018 |
| Syrian Arab Republic | 2010 | New Caledonia | 2015 | Andorra | 2018 | Oman | 2018 |
| Cook Islands | 2011 | Trinidad and Tobago | 2015 | Angola | 2018 | Palau | 2018 |
| Vanuatu | 2011 | Guinea | 2016 | Bahamas, The | 2018 | Sierra Leone | 2018 |
| Bhutan | 2012 | Kiribati | 2016 | Bahrain | 2018 | Solomon Islands | 2018 |
| Dominica | 2012 | Algeria | 2017 | Central African Republic | 2018 | Sudan | 2018 |
| Papua New Guinea | 2012 | Cameroon | 2017 | Dominican Republic | 2018 | Tanzania | 2018 |
| Turks and Caicos Islands | 2012 | Cote d’Ivoire | 2017 | Ethiopia | 2018 | Uganda | 2018 |
| | | East Timor | 2017 | Greenland | 2018 | Ukraine | 2018 |
Table 2.
Results of measurements of topological analysis of networks for 12 years. Nodes with no link in some years do not appear.
| Year | Nodes | Edges | Density | Avg Degree | Avg Weighted Degree | Avg Clustering Coefficient | Modularity (Weighted) | No. of Communities | Modularity (Unweighted Graph) | No. of Communities |
|---|
| Case 1 | Case 2 |
|---|
| 2008 | 235 | 22,540 | 0.410 | 95.915 | 66,543,933 | 0.737 | 0.372 | 4 | 5 | 0.073 | 3 |
| 2009 | 236 | 22,497 | 0.406 | 95.326 | 51,379,623 | 0.733 | 0.363 | 5 | 5 | 0.073 | 4 |
| 2010 | 237 | 23,204 | 0.415 | 97.907 | 63,215,973 | 0.739 | 0.373 | 5 | 5 | 0.074 | 3 |
| 2011 | 238 | 22,946 | 0.407 | 96.412 | 75,004,671 | 0.741 | 0.379 | 5 | 5 | 0.071 | 4 |
| 2012 | 238 | 22,818 | 0.405 | 95.874 | 75,145,707 | 0.738 | 0.371 | 5 | 6 | 0.069 | 3 |
| 2013 | 239 | 23,176 | 0.407 | 96.971 | 77,928,476 | 0.746 | 0.383 | 5 | 5 | 0.071 | 3 |
| 2014 | 238 | 23,098 | 0.409 | 97.050 | 78,185,259 | 0.746 | 0.380 | 5 | 5 | 0.071 | 3 |
| 2015 | 238 | 23,466 | 0.416 | 98.597 | 68,164,456 | 0.751 | 0.354 | 5 | 6 | 0.071 | 3 |
| 2016 | 239 | 23,492 | 0.413 | 98.293 | 65,917,133 | 0.751 | 0.350 | 4 | 5 | 0.072 | 3 |
| 2017 | 238 | 23,409 | 0.415 | 98.357 | 73,012,586 | 0.753 | 0.373 | 4 | 5 | 0.072 | 3 |
| 2018 | 238 | 22,613 | 0.401 | 95.013 | 80,075,605 | 0.750 | 0.378 | 4 | 5 | 0.072 | 3 |
| 2019 | 238 | 20,045 | 0.355 | 84.223 | 76,664,339 | 0.743 | 0.362 | 4 | 5 | 0.072 | 3 |
Table 3.
The communities and the number of their member countries based on modularity analysis (criterion 1, resolution = 1, GEPHI [
20]).
| Year | Germany | China | USA | S. Arabia/UAE | S. Africa/India | Africa 2 | SUM |
|---|
| 2008 | 76 | 86 | 54 | 19 | | | 235 |
| 2009 | 78 | 84 | 57 | 13 | | 4 | 236 |
| 2010 | 74 | 65 | 63 | 14 | 21 | | 237 |
| 2011 | 86 | 62 | 59 | 17 | 14 | | 238 |
| 2012 | 73 | 55 | 38 | 17 | 55 | | 238 |
| 2013 | 82 | 67 | 56 | 15 | 19 | | 239 |
| 2014 | 77 | 68 | 65 | 14 | 14 | | 238 |
| 2015 | 75 | 64 | 66 | 14 | 19 | | 238 |
| 2016 | 76 | 82 | 40 | 41 | | | 239 |
| 2017 | 73 | 52 | 50 | 63 | | | 238 |
| 2018 | 77 | 87 | 50 | 24 | | | 238 |
| 2019 | 77 | 98 | 46 | 17 | | | 238 |
| AVG | 77 | 73 | 54 | 22 | 24 | 4 | 238 |
Table 4.
The numerical distribution of countries in different communities in the second scenario about modularity (criterion 2, resolution = 0.8, GEPHI [
20]).
| Year | Germany | China | USA | S. Arabia/UAE | S. Africa/India | Russia | UK | SUM |
|---|
| 2008 | 64 | 51 | 40 | 14 | 66 | | | 235 |
| 2009 | 83 | 42 | 41 | 14 | 56 | | | 236 |
| 2010 | 70 | 83 | 49 | 13 | 22 | | | 237 |
| 2011 | 67 | 51 | 44 | 10 | 66 | | | 238 |
| 2012 | 50 | 46 | 34 | 19 | 51 | 38 | | 238 |
| 2013 | 70 | 106 | 40 | 15 | | | 8 | 239 |
| 2014 | 52 | 108 | 42 | 2 | | 34 | | 238 |
| 2015 | 55 | 75 | 35 | 11 | 10 | 52 | | 238 |
| 2016 | 62 | 55 | 65 | 32 | 25 | | | 239 |
| 2017 | 75 | 47 | 38 | 17 | 61 | | | 238 |
| 2018 | 72 | 61 | 57 | 30 | 18 | | | 238 |
| 2019 | 72 | 74 | 52 | 27 | 13 | | | 238 |
| AVG | 66 | 67 | 45 | 17 | 39 | 41 | 8 | 238 |
Table 5.
Geometrical analysis. The third column presents the minimum and the maximum values of out eccentricity observed during each year.
| Year | Diameter | Out Eccentricity
of Nodes (Min–Max) | Average Path Length |
|---|
| 2008 | 3 | 2–3 | 1.437 |
| 2009 | 3 | 2–3 | 1.442 |
| 2010 | 3 | 2–3 | 1.430 |
| 2011 | 3 | 2–3 | 1.428 |
| 2012 | 3 | 2–3 | 1.434 |
| 2013 | 3 | 2–3 | 1.417 |
| 2014 | 3 | 2–3 | 1.420 |
| 2015 | 3 | 2–3 | 1.407 |
| 2016 | 3 | 2–3 | 1.403 |
| 2017 | 3 | 2–3 | 1.390 |
| 2018 | 3 | 2–3 | 1.359 |
| 2019 | 3 | 2–3 | 1.360 |
Table 6.
Annual closeness centrality of the 18 countries with highest values. The five countries with highest centrality are indicated in light red.
| Country/Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | AVG |
|---|
| Germany | 0.98734 | 0.98326 | 0.97119 | 0.94800 | 0.95565 | 0.97143 | 0.97131 | 0.97131 | 0.97942 | 0.97131 | 0.97131 | 0.97934 | 0.97174 |
| U.K. | 0.97908 | 0.97510 | 0.97119 | 0.96342 | 0.94800 | 0.96748 | 0.97131 | 0.97531 | 0.96748 | 0.97531 | 0.97531 | 0.96342 | 0.96937 |
| France | 0.97500 | 0.96312 | 0.95935 | 0.94800 | 0.93676 | 0.96748 | 0.96342 | 0.96342 | 0.96356 | 0.97131 | 0.95951 | 0.95565 | 0.96055 |
| Netherlands | 0.97500 | 0.95918 | 0.96327 | 0.96342 | 0.96735 | 0.98755 | 0.97531 | 0.98340 | 0.98755 | 0.97934 | 0.98750 | 0.98750 | 0.97636 |
| Belgium | 0.97500 | 0.97107 | 0.95161 | 0.95565 | 0.96342 | 0.97541 | 0.97131 | 0.95951 | 0.95582 | 0.97131 | 0.97131 | 0.96735 | 0.96573 |
| Switzerland | 0.96694 | 0.94758 | 0.94779 | 0.94800 | 0.95181 | 0.95968 | 0.95565 | 0.95181 | 0.94071 | 0.95951 | 0.96735 | 0.94048 | 0.95311 |
| United States | 0.95902 | 0.95529 | 0.94779 | 0.95181 | 0.95565 | 0.94821 | 0.95181 | 0.94800 | 0.94821 | 0.94800 | 0.94800 | 0.94422 | 0.95050 |
| Spain | 0.95902 | 0.92885 | 0.94779 | 0.94048 | 0.93676 | 0.95582 | 0.94800 | 0.95565 | 0.96748 | 0.96342 | 0.94422 | 0.95951 | 0.95058 |
| Denmark | 0.95510 | 0.94758 | 0.95161 | 0.92578 | 0.92218 | 0.95582 | 0.94422 | 0.94800 | 0.94444 | 0.94048 | 0.94422 | 0.94048 | 0.94333 |
| Malaysia | 0.95510 | 0.94758 | 0.95161 | 0.94422 | 0.95565 | 0.94821 | 0.93307 | 0.95181 | 0.91892 | 0.92941 | 0.94048 | 0.91861 | 0.94122 |
| Italy | 0.95122 | 0.94758 | 0.95161 | 0.95565 | 0.94422 | 0.97143 | 0.95565 | 0.95951 | 0.95968 | 0.97131 | 0.95565 | 0.97934 | 0.95857 |
| India | 0.95122 | 0.94758 | 0.94779 | 0.93307 | 0.93676 | 0.93333 | 0.93676 | 0.93307 | 0.92607 | 0.92941 | 0.94048 | 0.95565 | 0.93927 |
| Other Asia, nes | 0.95122 | 0.95142 | 0.94400 | 0.94422 | 0.94048 | 0.92248 | 0.92218 | 0.90805 | 0.91539 | 0.91506 | 0.93676 | 0.91861 | 0.93082 |
| Sweden | 0.94737 | 0.95529 | 0.94400 | 0.94800 | 0.91861 | 0.94444 | 0.94800 | 0.94048 | 0.97541 | 0.95951 | 0.96342 | 0.94800 | 0.94938 |
| Korea, Rep. | 0.93976 | 0.95529 | 0.94400 | 0.95181 | 0.95181 | 0.94821 | 0.94048 | 0.93307 | 0.93333 | 0.94422 | 0.94422 | 0.93676 | 0.94358 |
| Canada | 0.93600 | 0.93626 | 0.92549 | 0.91506 | 0.92218 | 0.91188 | 0.94048 | 0.92218 | 0.92969 | 0.94048 | 0.92941 | 0.92941 | 0.92821 |
| Australia | 0.93600 | 0.92157 | 0.91829 | 0.90458 | 0.90805 | 0.89811 | 0.90458 | 0.90458 | 0.89811 | 0.90458 | 0.90805 | 0.90114 | 0.90897 |
| Thailand | 0.93227 | 0.95529 | 0.93281 | 0.93307 | 0.94422 | 0.94071 | 0.96342 | 0.96342 | 0.95200 | 0.95565 | 0.96735 | 0.95565 | 0.94965 |
| AVG | 0.95731 | 0.95272 | 0.94840 | 0.94301 | 0.94220 | 0.95043 | 0.94983 | 0.94848 | 0.94796 | 0.95165 | 0.95303 | 0.94895 | |
Table 7.
Annual relative increase in closeness centrality for 18 selected countries. Each column gives the relative increase with respect to the previous year. Negative values indicate decrease.
| Country/Year | 2008 (Cc) | 2009 (%) | 2010 (%) | 2011 (%) | 2012 (%) | 2013 (%) | 2014 (%) | 2015 (%) | 2016 (%) | 2017 (%) | 2018 (%) | 2019 (%) |
|---|
| Germany | 0.98734 | −0.4 | −1.2 | −2.4 | 0.8 | 1.7 | 0.0 | 0.0 | 0.8 | −0.8 | 0.0 | 0.8 |
| U.K. | 0.97908 | −0.4 | −0.4 | −0.8 | −1.6 | 2.1 | 0.4 | 0.4 | −0.8 | 0.8 | 0.0 | −1.2 |
| France | 0.97500 | −1.2 | −0.4 | −1.2 | −1.2 | 3.3 | −0.4 | 0.0 | 0.0 | 0.8 | −1.2 | −0.4 |
| Netherlands | 0.97500 | −1.6 | 0.4 | 0.0 | 0.4 | 2.1 | −1.2 | 0.8 | 0.4 | −0.8 | 0.8 | 0.0 |
| Belgium | 0.97500 | −0.4 | −2.0 | 0.4 | 0.8 | 1.2 | −0.4 | −1.2 | −0.4 | 1.6 | 0.0 | −0.4 |
| Switzerland | 0.96694 | −2.0 | 0.0 | 0.0 | 0.4 | 0.8 | −0.4 | −0.4 | −1.2 | 2.0 | 0.8 | −2.8 |
| United States | 0.95902 | −0.4 | −0.8 | 0.4 | 0.4 | −0.8 | 0.4 | −0.4 | 0.0 | 0.0 | 0.0 | −0.4 |
| Spain | 0.95902 | −3.1 | 2.0 | −0.8 | −0.4 | 2.0 | −0.8 | 0.8 | 1.2 | −0.4 | −2.0 | 1.6 |
| Denmark | 0.95510 | −0.8 | 0.4 | −2.7 | −0.4 | 3.6 | −1.2 | 0.4 | −0.4 | −0.4 | 0.4 | −0.4 |
| Malaysia | 0.95510 | −0.8 | 0.4 | −0.8 | 1.2 | −0.8 | −1.6 | 2.0 | −3.5 | 1.1 | 1.2 | −2.3 |
| Italy | 0.95122 | −0.4 | 0.4 | 0.4 | −1.2 | 2.9 | −1.6 | 0.4 | 0.0 | 1.2 | −1.6 | 2.5 |
| India | 0.95122 | −0.4 | 0.0 | −1.6 | 0.4 | −0.4 | 0.4 | −0.4 | −0.8 | 0.4 | 1.2 | 1.6 |
| Other Asia, nes | 0.95122 | 0.0 | −0.8 | 0.0 | −0.4 | −1.9 | 0.0 | −1.5 | 0.8 | 0.0 | 2.4 | −1.9 |
| Sweden | 0.94737 | 0.8 | −1.2 | 0.4 | −3.1 | 2.8 | 0.4 | −0.8 | 3.7 | −1.6 | 0.4 | −1.6 |
| Korea, Rep. | 0.93976 | 1.7 | −1.2 | 0.8 | 0.0 | −0.4 | −0.8 | −0.8 | 0.0 | 1.2 | 0.0 | −0.8 |
| Canada | 0.93600 | 0.0 | −1.1 | −1.1 | 0.8 | −1.1 | 3.1 | −1.9 | 0.8 | 1.2 | −1.2 | 0.0 |
| Australia | 0.93600 | −1.5 | −0.4 | −1.5 | 0.4 | −1.1 | 0.7 | 0.0 | −0.7 | 0.7 | 0.4 | −0.8 |
| Thailand | 0.93227 | 2.5 | −2.4 | 0.0 | 1.2 | −0.4 | 2.4 | 0.0 | −1.2 | 0.4 | 1.2 | −1.2 |
Table 8.
Annual betweenness centrality of the 18 countries with highest values. The five countries with highest centrality are indicated in light red.
| Country/Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | AVG |
|---|
| United States | 0.01580 | 0.01565 | 0.01233 | 0.01639 | 0.01580 | 0.01227 | 0.00876 | 0.00861 | 0.00795 | 0.00856 | 0.00793 | 0.00583 | 0.01132 |
| U.K. | 0.01028 | 0.00934 | 0.00918 | 0.00827 | 0.00773 | 0.00840 | 0.00924 | 0.00841 | 0.00630 | 0.00689 | 0.00684 | 0.00541 | 0.00802 |
| France | 0.00957 | 0.00882 | 0.00773 | 0.00658 | 0.00709 | 0.00814 | 0.00887 | 0.00675 | 0.00818 | 0.00636 | 0.00578 | 0.00534 | 0.00743 |
| Germany | 0.00918 | 0.00995 | 0.00819 | 0.00790 | 0.00908 | 0.00868 | 0.00858 | 0.00794 | 0.00855 | 0.00683 | 0.00662 | 0.00521 | 0.00806 |
| Netherlands | 0.00824 | 0.00828 | 0.00804 | 0.00759 | 0.00799 | 0.00941 | 0.00770 | 0.00898 | 0.00817 | 0.00873 | 0.00890 | 0.00707 | 0.00826 |
| Belgium | 0.00756 | 0.00839 | 0.00612 | 0.00629 | 0.00665 | 0.00724 | 0.00740 | 0.00628 | 0.00599 | 0.00572 | 0.00596 | 0.00503 | 0.00655 |
| Canada | 0.00719 | 0.00831 | 0.00675 | 0.00598 | 0.00670 | 0.00476 | 0.00608 | 0.00659 | 0.00610 | 0.00588 | 0.00512 | 0.00512 | 0.00622 |
| Australia | 0.00716 | 0.00661 | 0.00620 | 0.00611 | 0.00579 | 0.00461 | 0.00602 | 0.00514 | 0.00453 | 0.00494 | 0.00446 | 0.00446 | 0.00550 |
| China | 0.00691 | 0.00706 | 0.00602 | 0.00650 | 0.00834 | 0.00586 | 0.00663 | 0.00623 | 0.00548 | 0.00534 | 0.00510 | 0.00483 | 0.00619 |
| Switzerland | 0.00690 | 0.00629 | 0.00673 | 0.00656 | 0.00763 | 0.00637 | 0.00575 | 0.00611 | 0.00639 | 0.00603 | 0.00555 | 0.00555 | 0.00632 |
| Japan | 0.00679 | 0.00786 | 0.00723 | 0.00554 | 0.00540 | 0.00488 | 0.00515 | 0.00522 | 0.00554 | 0.00467 | 0.00448 | 0.00448 | 0.00560 |
| Italy | 0.00669 | 0.00730 | 0.00674 | 0.00737 | 0.00695 | 0.00795 | 0.00667 | 0.00667 | 0.00650 | 0.00648 | 0.00604 | 0.00516 | 0.00671 |
| Other Asia, nes | 0.00654 | 0.00695 | 0.00686 | 0.00656 | 0.00631 | 0.00520 | 0.00511 | 0.00507 | 0.00496 | 0.00417 | 0.00505 | 0.00505 | 0.00565 |
| Spain | 0.00637 | 0.00536 | 0.00707 | 0.00582 | 0.00549 | 0.00606 | 0.00612 | 0.00638 | 0.00580 | 0.00556 | 0.00531 | 0.00516 | 0.00588 |
| Denmark | 0.00619 | 0.00572 | 0.00583 | 0.00499 | 0.00488 | 0.00593 | 0.00509 | 0.00509 | 0.00472 | 0.00482 | 0.00473 | 0.00320 | 0.00510 |
| India | 0.00589 | 0.00673 | 0.00686 | 0.00647 | 0.00726 | 0.00665 | 0.00620 | 0.00531 | 0.00464 | 0.00433 | 0.00498 | 0.00498 | 0.00586 |
| Korea, Rep. | 0.00547 | 0.00596 | 0.00644 | 0.00630 | 0.00682 | 0.00567 | 0.00632 | 0.00520 | 0.00609 | 0.00492 | 0.00537 | 0.00537 | 0.00583 |
| South Africa | 0.00506 | 0.00474 | 0.00593 | 0.00557 | 0.00458 | 0.00460 | 0.00514 | 0.00410 | 0.00381 | 0.00468 | 0.00413 | 0.00409 | 0.00470 |
| AVG | 0.00765 | 0.00774 | 0.00724 | 0.00704 | 0.00725 | 0.00682 | 0.00671 | 0.00634 | 0.00609 | 0.00583 | 0.00569 | 0.00507 | |
Table 9.
Annual relative increase in betweenness centrality for 18 selected countries. Each column gives the relative increase with respect to the previous year. Negative values indicate decrease.
| Country/Year | 2008 (Cb) | 2009 (%) | 2010 (%) | 2011 (%) | 2012 (%) | 2013 (%) | 2014 (%) | 2015 (%) | 2016 (%) | 2017 (%) | 2018 (%) | 2019 (%) |
|---|
| United States | 0.01580 | −0.9 | −21.2 | 32.9 | −3.6 | −22.3 | −28.6 | −1.7 | −7.6 | 7.7 | −7.4 | −26.4 |
| U.K. | 0.01028 | −9.2 | −1.7 | −9.9 | −6.6 | 8.7 | 10.0 | −9.0 | −25.1 | 9.3 | −0.7 | −21.0 |
| France | 0.00957 | −7.9 | −12.3 | −14.9 | 7.7 | 14.9 | 8.9 | −23.9 | 21.2 | −22.2 | −9.2 | −7.5 |
| Germany | 0.00918 | 8.4 | −17.7 | −3.5 | 15.0 | −4.4 | −1.2 | −7.5 | 7.6 | −20.1 | −3.0 | −21.3 |
| Netherlands | 0.00824 | 0.6 | −2.9 | −5.6 | 5.3 | 17.7 | −18.1 | 16.6 | −9.1 | 6.8 | 2.0 | −20.6 |
| Belgium | 0.00756 | 11.1 | −27.1 | 2.8 | 5.6 | 9.0 | 2.2 | −15.1 | −4.6 | −4.6 | 4.3 | −15.5 |
| Canada | 0.00719 | 15.5 | −18.7 | −11.4 | 12.1 | −28.9 | 27.7 | 8.4 | −7.5 | −3.6 | −13.0 | 0.0 |
| Australia | 0.00716 | −7.6 | −6.2 | −1.3 | −5.3 | −20.4 | 30.5 | −14.5 | −11.9 | 9.0 | −9.8 | 0.0 |
| China | 0.00691 | 2.1 | −14.7 | 8.0 | 28.3 | −29.8 | 13.1 | −6.0 | −12.0 | −2.5 | −4.5 | −5.3 |
| Switzerland | 0.00690 | −8.9 | 6.9 | −2.4 | 16.2 | −16.5 | −9.7 | 6.1 | 4.7 | −5.6 | −7.9 | 0.0 |
| Japan | 0.00679 | 15.7 | −8.0 | −23.3 | −2.6 | −9.6 | 5.5 | 1.4 | 6.0 | −15.7 | −4.1 | 0.0 |
| Italy | 0.00669 | 9.1 | −7.7 | 9.3 | −5.7 | 14.3 | −16.0 | −0.1 | −2.5 | −0.2 | −6.8 | −14.6 |
| Other Asia, nes | 0.00654 | 6.3 | −1.4 | −4.4 | −3.8 | −17.5 | −1.8 | −0.7 | −2.1 | −16.0 | 21.1 | 0.0 |
| Spain | 0.00637 | −15.8 | 31.9 | −17.6 | −5.7 | 10.4 | 0.9 | 4.3 | −9.1 | −4.1 | −4.6 | −2.9 |
| Denmark | 0.00619 | −7.7 | 1.9 | −14.3 | −2.2 | 21.4 | −14.1 | −0.1 | −7.2 | 2.0 | −1.9 | −32.3 |
| India | 0.00589 | 14.3 | 2.1 | −5.8 | 12.2 | −8.4 | −6.8 | −14.3 | −12.6 | −6.7 | 14.9 | 0.0 |
| Korea, Rep. | 0.00547 | 8.9 | 8.0 | −2.2 | 8.4 | −16.9 | 11.3 | −17.7 | 17.2 | −19.3 | 9.1 | 0.0 |
| South Africa | 0.00506 | −6.4 | 25.2 | −6.0 | −17.8 | 0.5 | 11.7 | −20.2 | −7.2 | 22.9 | −11.7 | −1.1 |
Table 10.
Annual eigenvector centrality of the 18 countries with highest values. The five countries with highest centrality are indicated in light red.
| Country/Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | AVG |
|---|
| United States | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 0.99689 | 1.00000 | 0.99523 | 0.99766 | 0.99593 | 0.99756 | 0.99861 |
| France | 0.99065 | 0.98588 | 0.99233 | 0.98269 | 0.98311 | 0.98738 | 1.00000 | 0.98754 | 1.00000 | 0.98804 | 0.99525 | 0.99171 | 0.99038 |
| U.K. | 0.98867 | 0.98247 | 0.99977 | 0.98497 | 0.98815 | 0.98954 | 0.99284 | 0.98423 | 0.97178 | 0.99022 | 0.99313 | 0.98769 | 0.98779 |
| Germany | 0.98372 | 0.99137 | 0.98467 | 0.98716 | 0.98948 | 0.98944 | 0.99393 | 0.98746 | 0.98990 | 0.99545 | 0.99525 | 0.98771 | 0.98963 |
| China | 0.97913 | 0.98325 | 0.98631 | 0.97124 | 0.98760 | 0.98671 | 0.99757 | 0.99642 | 0.99388 | 1.00000 | 0.99300 | 1.00000 | 0.98959 |
| Netherlands | 0.97710 | 0.97825 | 0.99176 | 0.98863 | 0.98356 | 0.99045 | 0.98639 | 0.99731 | 0.98350 | 0.99838 | 1.00000 | 0.99756 | 0.98941 |
| Japan | 0.97188 | 0.98379 | 0.98415 | 0.97432 | 0.95287 | 0.97048 | 0.95951 | 0.97470 | 0.97691 | 0.97082 | 0.98344 | 0.97133 | 0.97285 |
| Italy | 0.96358 | 0.97594 | 0.97718 | 0.98110 | 0.97343 | 0.98715 | 0.97746 | 0.98481 | 0.98490 | 0.98988 | 0.99525 | 0.98098 | 0.98097 |
| Canada | 0.96182 | 0.97980 | 0.98402 | 0.97325 | 0.96914 | 0.96002 | 0.97054 | 0.98026 | 0.96934 | 0.97533 | 0.98158 | 0.98582 | 0.97424 |
| Belgium | 0.96145 | 0.97186 | 0.95526 | 0.96102 | 0.95938 | 0.97286 | 0.96965 | 0.96628 | 0.97066 | 0.97360 | 0.97328 | 0.97990 | 0.96793 |
| Switzerland | 0.95578 | 0.93797 | 0.96029 | 0.96407 | 0.96904 | 0.95782 | 0.95564 | 0.96381 | 0.97106 | 0.97592 | 0.98030 | 0.96956 | 0.96344 |
| Spain | 0.95557 | 0.94906 | 0.98379 | 0.96885 | 0.95099 | 0.97379 | 0.96505 | 0.97752 | 0.96680 | 0.97311 | 0.99075 | 0.98390 | 0.96993 |
| Denmark | 0.94690 | 0.91480 | 0.92710 | 0.93289 | 0.91588 | 0.93845 | 0.92406 | 0.94516 | 0.94567 | 0.96555 | 0.95429 | 0.94891 | 0.93830 |
| United Arab Emirates | 0.94073 | 0.92599 | 0.96254 | 0.95449 | 0.94931 | 0.96337 | 0.94988 | 0.95981 | 0.96291 | 0.96371 | 0.97796 | 0.96356 | 0.95619 |
| India | 0.93815 | 0.95717 | 0.96292 | 0.97335 | 0.96991 | 0.96875 | 0.96421 | 0.97485 | 0.96882 | 0.97517 | 0.98790 | 0.97869 | 0.96832 |
| Australia | 0.93635 | 0.92057 | 0.93253 | 0.95625 | 0.93962 | 0.93073 | 0.96150 | 0.96115 | 0.96177 | 0.96544 | 0.96930 | 0.95825 | 0.94945 |
| Hong Kong, China | 0.93496 | 0.93749 | 0.97350 | 0.96831 | 0.96517 | 0.94851 | 0.96726 | 0.97478 | 0.97145 | 0.97487 | 0.98515 | 0.95801 | 0.96329 |
| Sweden | 0.91578 | 0.93044 | 0.93968 | 0.94862 | 0.92454 | 0.93127 | 0.94115 | 0.95053 | 0.93260 | 0.94051 | 0.95040 | 0.91965 | 0.93543 |
| AVG | 0.96123 | 0.96145 | 0.97210 | 0.97062 | 0.96506 | 0.96926 | 0.97075 | 0.97592 | 0.97318 | 0.97854 | 0.98345 | 0.97560 | |
Table 11.
Annual relative increase in eigenvector centrality for 18 selected countries. Each column gives the relative increase with respect to the previous year. Negative values indicate decrease.
| Country/Year | 2008 (CE) | 2009 (%) | 2010 (%) | 2011 (%) | 2012 (%) | 2013 (%) | 2014 (%) | 2015 (%) | 2016 (%) | 2017 (%) | 2018 (%) | 2019 (%) |
|---|
| United States | 1.00000 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | −0.3 | 0.3 | −0.5 | 0.2 | −0.2 | 0.2 |
| France | 0.99065 | −0.5 | 0.7 | −1.0 | 0.0 | 0.4 | 1.3 | −1.2 | 1.3 | −1.2 | 0.7 | −0.4 |
| U. K. | 0.98867 | −0.6 | 1.8 | −1.5 | 0.3 | 0.1 | 0.3 | −0.9 | −1.3 | 1.9 | 0.3 | −0.5 |
| Germany | 0.98372 | 0.8 | −0.7 | 0.3 | 0.2 | 0.0 | 0.5 | −0.7 | 0.2 | 0.6 | 0.0 | −0.8 |
| China | 0.97913 | 0.4 | 0.3 | −1.5 | 1.7 | −0.1 | 1.1 | −0.1 | −0.3 | 0.6 | −0.7 | 0.7 |
| Netherlands | 0.97710 | 0.1 | 1.4 | −0.3 | −0.5 | 0.7 | −0.4 | 1.1 | −1.4 | 1.5 | 0.2 | −0.2 |
| Japan | 0.97188 | 1.2 | 0.0 | −1.0 | −2.2 | 1.8 | −1.1 | 1.6 | 0.2 | −0.6 | 1.3 | −1.2 |
| Italy | 0.96358 | 1.3 | 0.1 | 0.4 | −0.8 | 1.4 | −1.0 | 0.8 | 0.0 | 0.5 | 0.5 | −1.4 |
| Canada | 0.96182 | 1.9 | 0.4 | −1.1 | −0.4 | −0.9 | 1.1 | 1.0 | −1.1 | 0.6 | 0.6 | 0.4 |
| Belgium | 0.96145 | 1.1 | −1.7 | 0.6 | −0.2 | 1.4 | −0.3 | −0.3 | 0.5 | 0.3 | 0.0 | 0.7 |
| Switzerland | 0.95578 | −1.9 | 2.4 | 0.4 | 0.5 | −1.2 | −0.2 | 0.9 | 0.8 | 0.5 | 0.4 | −1.1 |
| Spain | 0.95557 | −0.7 | 3.7 | −1.5 | −1.8 | 2.4 | −0.9 | 1.3 | −1.1 | 0.7 | 1.8 | −0.7 |
| Denmark | 0.94690 | −3.4 | 1.3 | 0.6 | −1.8 | 2.5 | −1.5 | 2.3 | 0.1 | 2.1 | −1.2 | −0.6 |
| United Arab Emirates | 0.94073 | −1.6 | 3.9 | −0.8 | −0.5 | 1.5 | −1.4 | 1.0 | 0.3 | 0.1 | 1.5 | −1.5 |
| India | 0.93815 | 2.0 | 0.6 | 1.1 | −0.4 | −0.1 | −0.5 | 1.1 | −0.6 | 0.7 | 1.3 | −0.9 |
| Australia | 0.93635 | −1.7 | 1.3 | 2.5 | −1.7 | −0.9 | 3.3 | 0.0 | 0.1 | 0.4 | 0.4 | −1.1 |
| Hong Kong, China | 0.93496 | 0.3 | 3.8 | −0.5 | −0.3 | −1.7 | 2.0 | 0.8 | −0.3 | 0.4 | 1.1 | −2.8 |
| Sweden | 0.91578 | 1.6 | 1.0 | 1.0 | −2.5 | 0.7 | 1.1 | 1.0 | −1.9 | 0.8 | 1.1 | −3.2 |
Table 12.
Comparison of our calculations with previous research on the world trade network.
| | Topology of the WTW [8] | The ITN [10] | The Evolution of the WTW [11] | Network Analysis of WT [15] | Network Analysis of IEP [16] | This Paper |
|---|
| Years/period | 2000 | 1948–2000 | 1981–2000 | 1995–2010 | 2019–2020 | 2008–2019 |
| Nodes | 179 | 76–187 | 159 | 178 | 50 | 238 |
| Avg degree | 43 | | | | | 97 |
| Links/edges | | 1494–10,252 | | 22,000 | | 20,045–23,492 |
| Density | | 0.524–0.590 | 0.55–0.65 | 0.53–0.7 | | 0.355–0.416 |
| Avg path length | 1.8 | | | | | 1.359–1.442 |
| Clust. coeff. | 0.65 | | 0.82 | | | 0.733–0.753 |
| Modularity | | | | | | 0.350–0.383 |
| Communities | | | | | 4–5 | 4–5 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).