D0L-System Inference from a Single Sequence with a Genetic Algorithm
Abstract
:1. Introduction
- A new line detection algorithm,
- Extending the current capabilities of inference algorithms for D0L-systems from a single sequence from two to at least three rules,
- Improving the execution speed of heuristic algorithms for systems with one or two rules and reducing the number of assumptions that need to be made about the grammars being inferred.
2. Materials and Methods
2.1. L-Systems
2.2. Grammatical Inference
2.3. Genetic Algorithms
2.4. Related Works
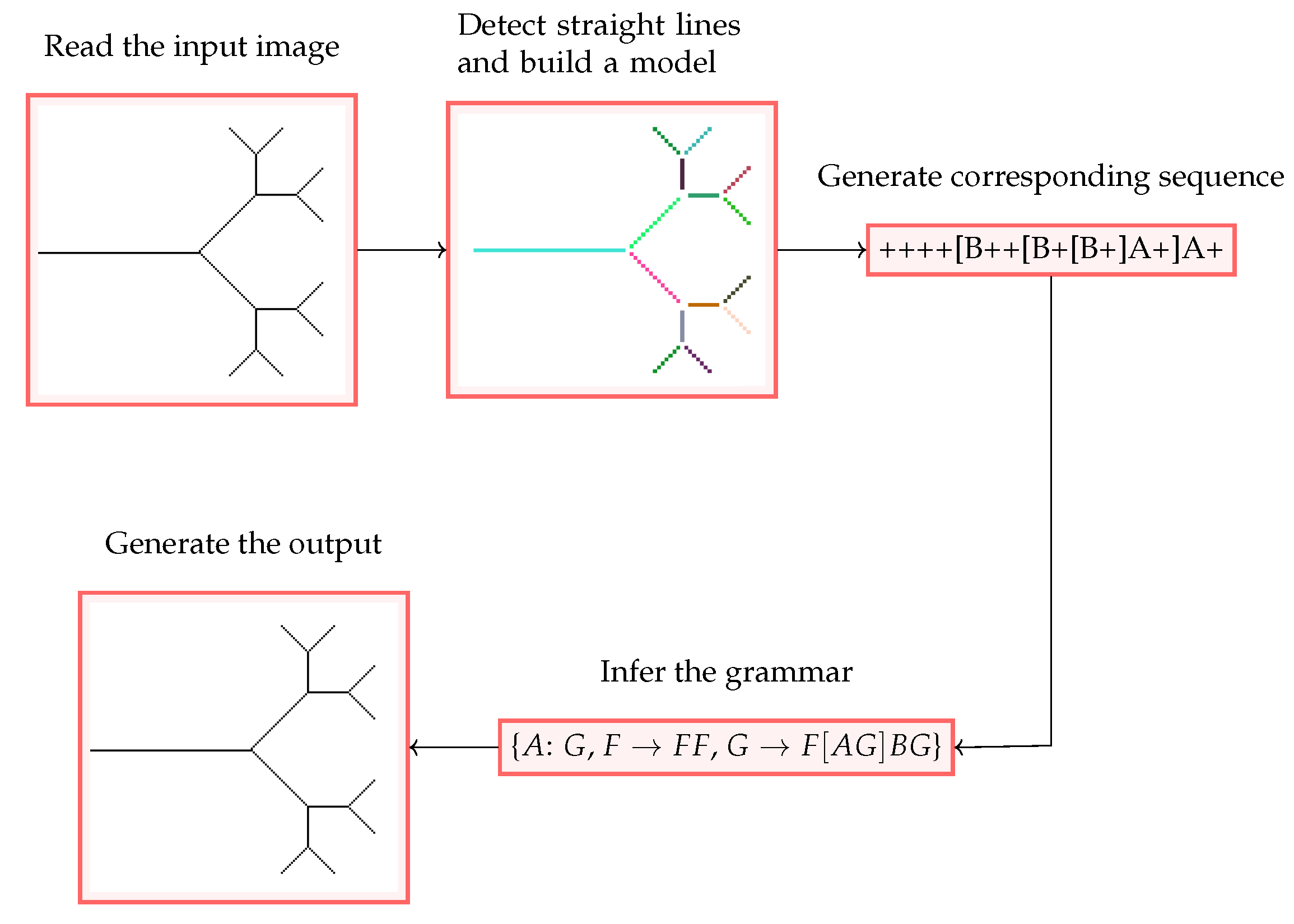
2.5. Inferring Grammar from a Single Input Image
2.6. Image Parsing
2.6.1. Straight Line Detection
2.6.2. Model Building
2.6.3. Sequence Generation
2.7. Grammar Inference
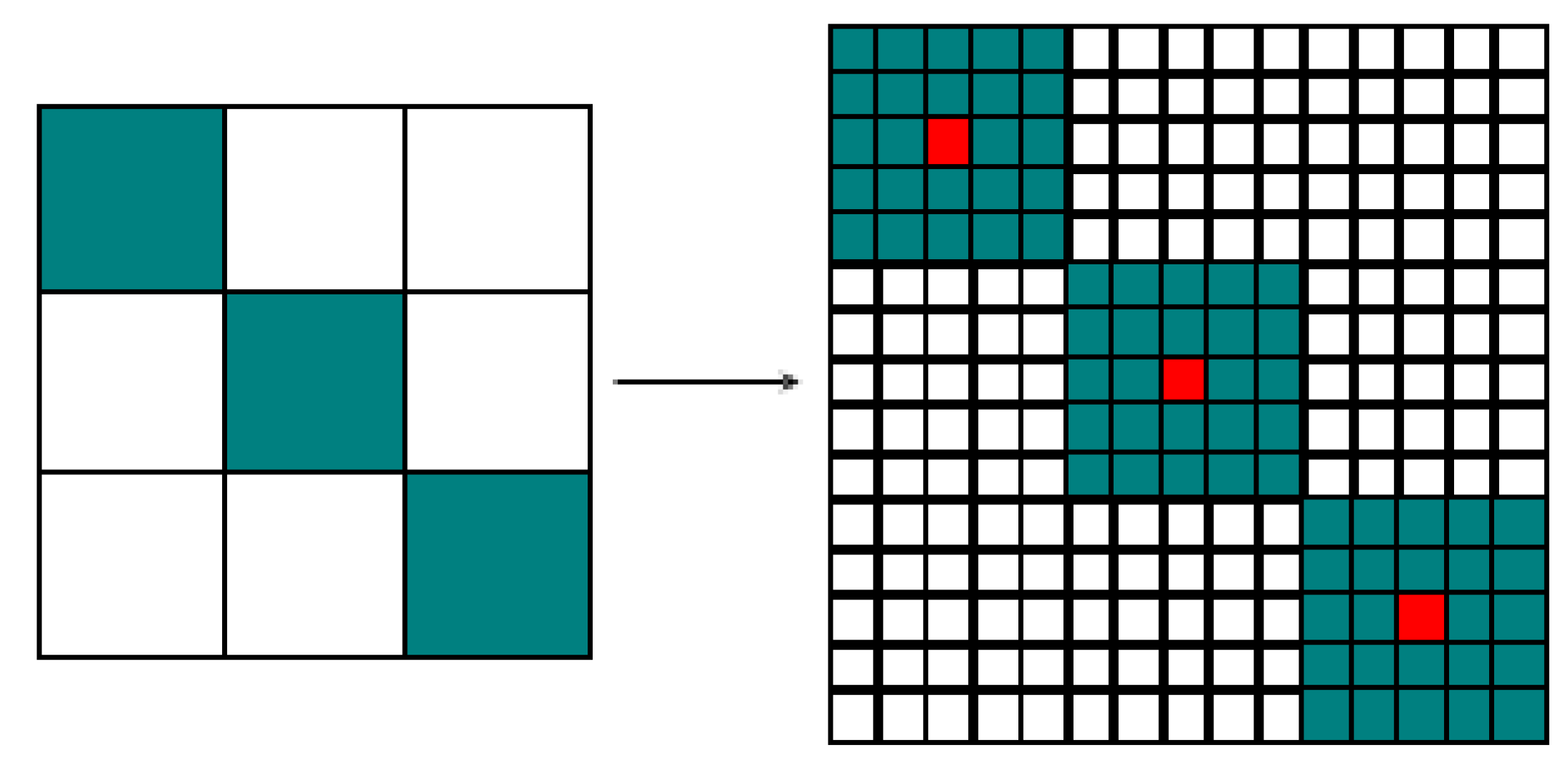
2.7.1. Calculating Sequence Length at the nth Iteration of System
| Algorithm 1: L-system inference |
 |
2.7.2. System Independence from Terminal Symbols
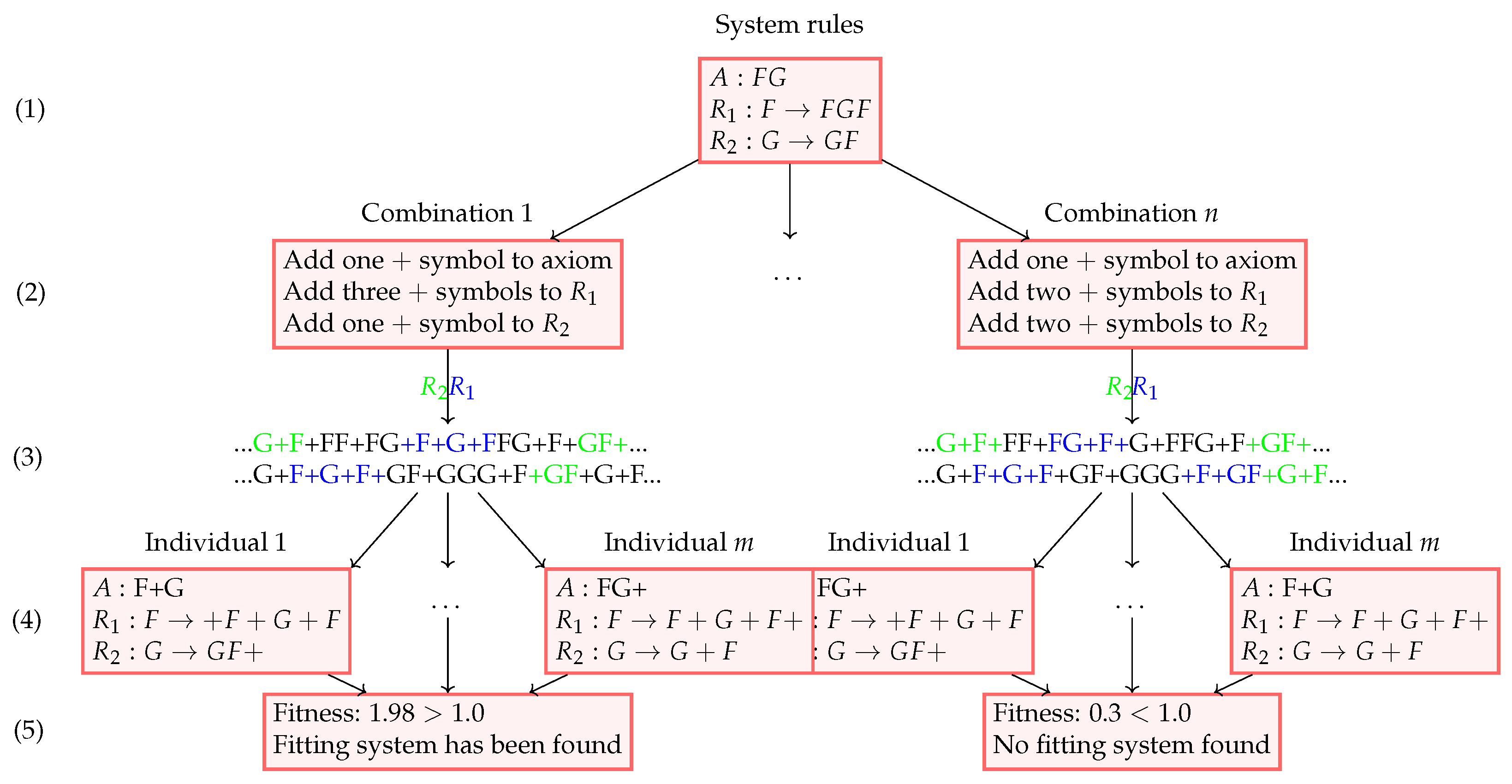
2.7.3. Genetic Algorithm
Initial Population Generation
Genetic Operators
Fitness Function
| Algorithm 2: Fitness function |
 |
3. Results
3.1. Grammar Inference
3.2. More Complex Systems
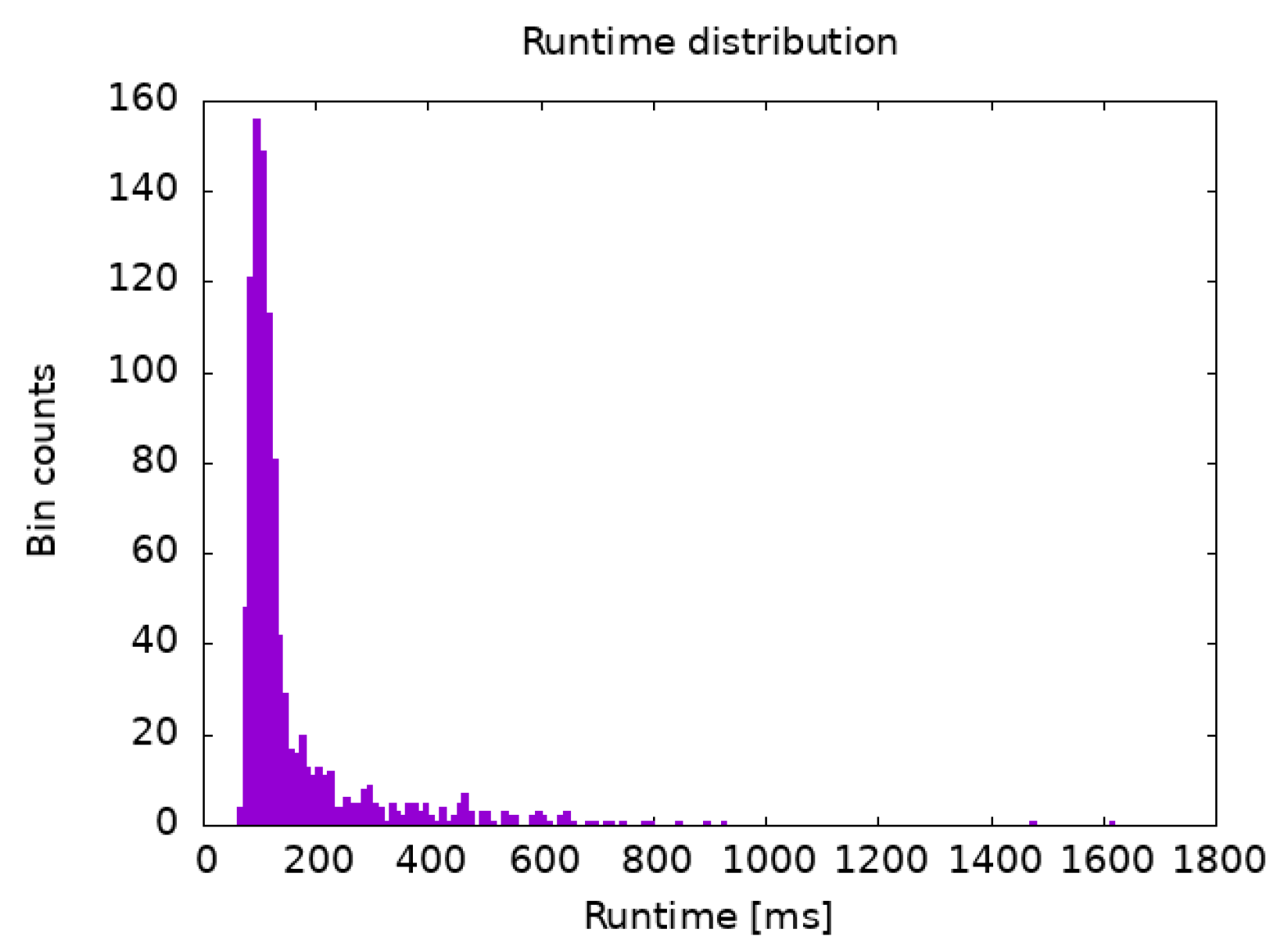
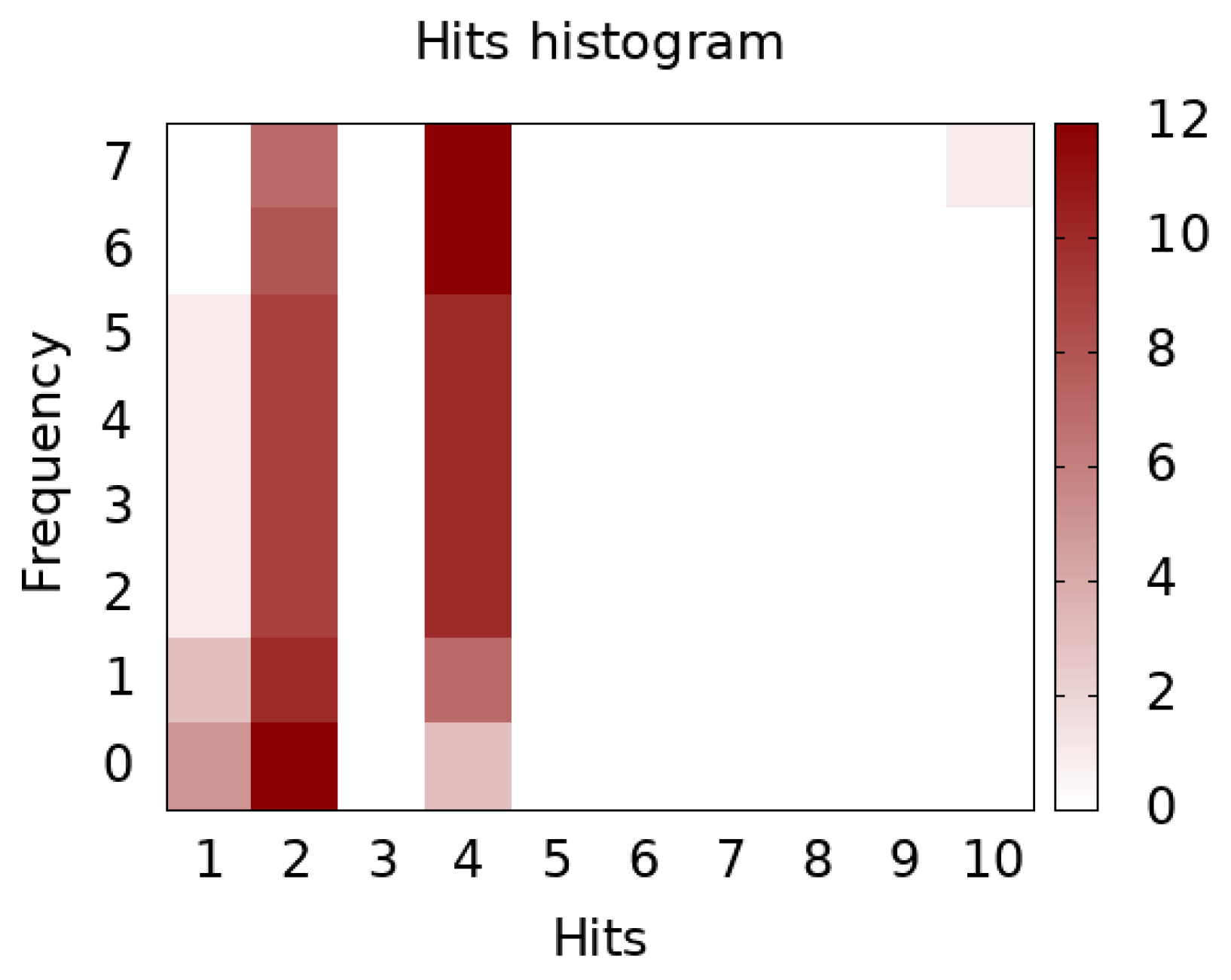
3.3. Runtime Distribution
3.4. Koch Island
3.5. Genetic Programming Using BNF Grammar
3.6. Crossover between Individuals with Different Rule Counts
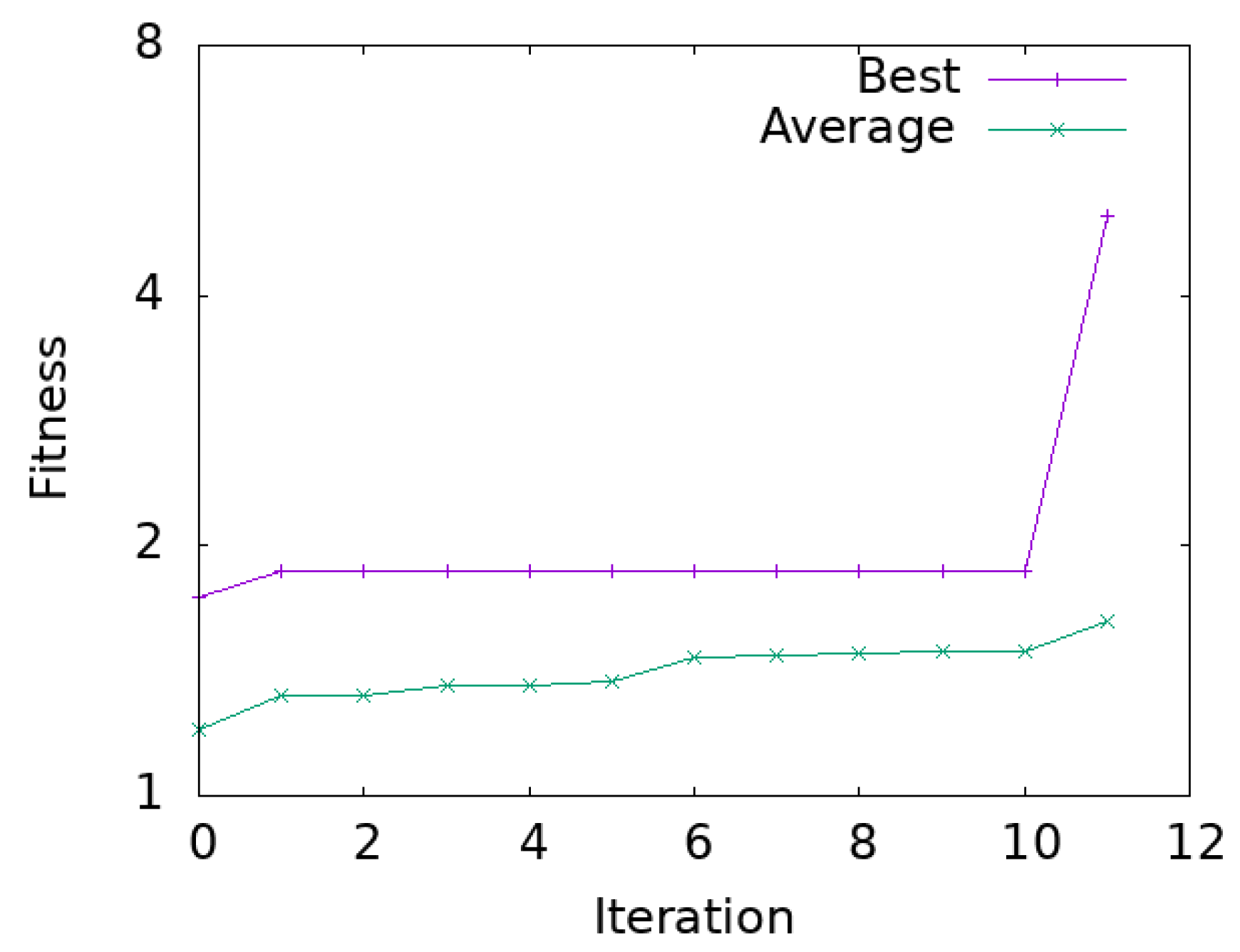
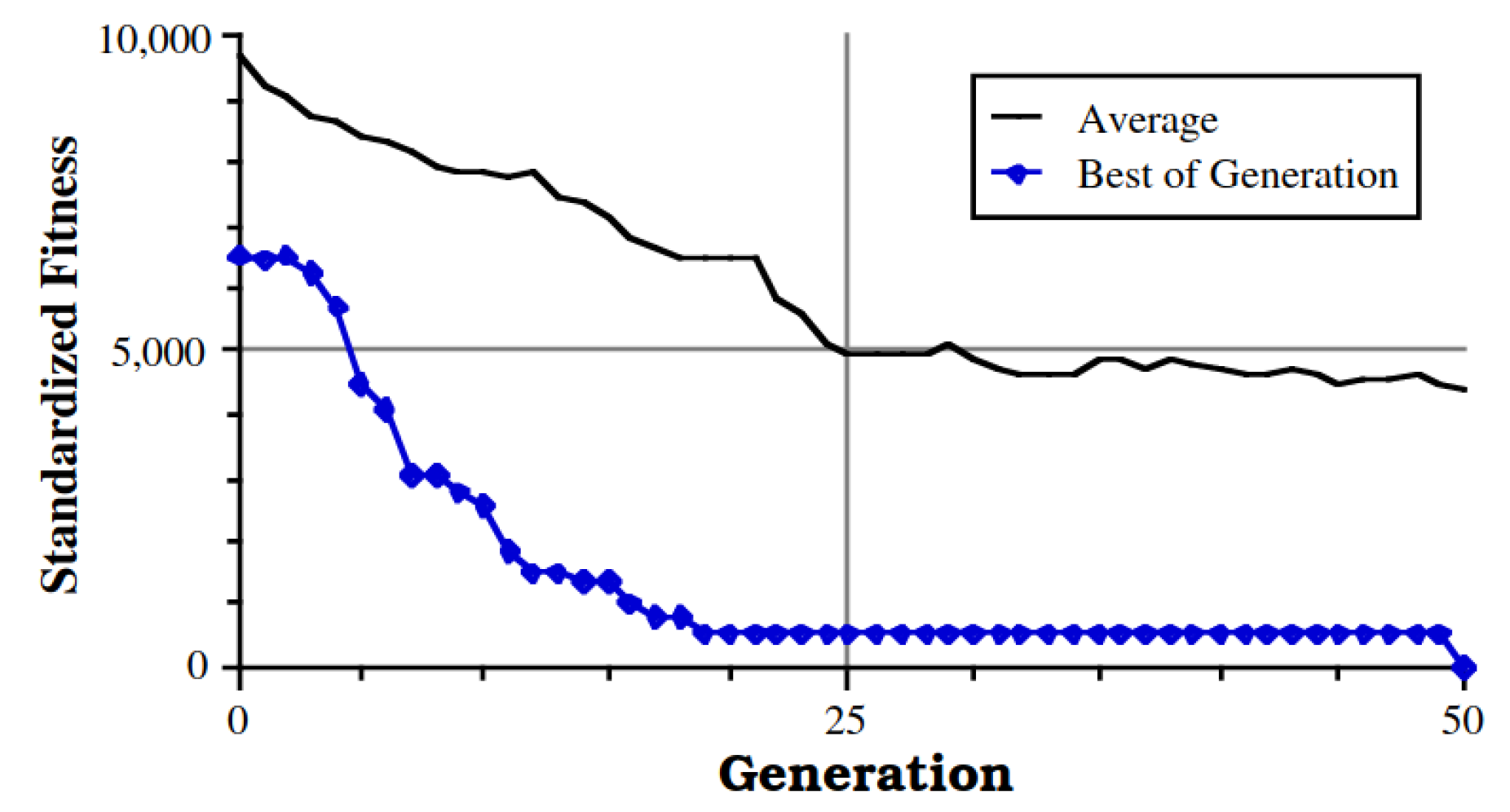
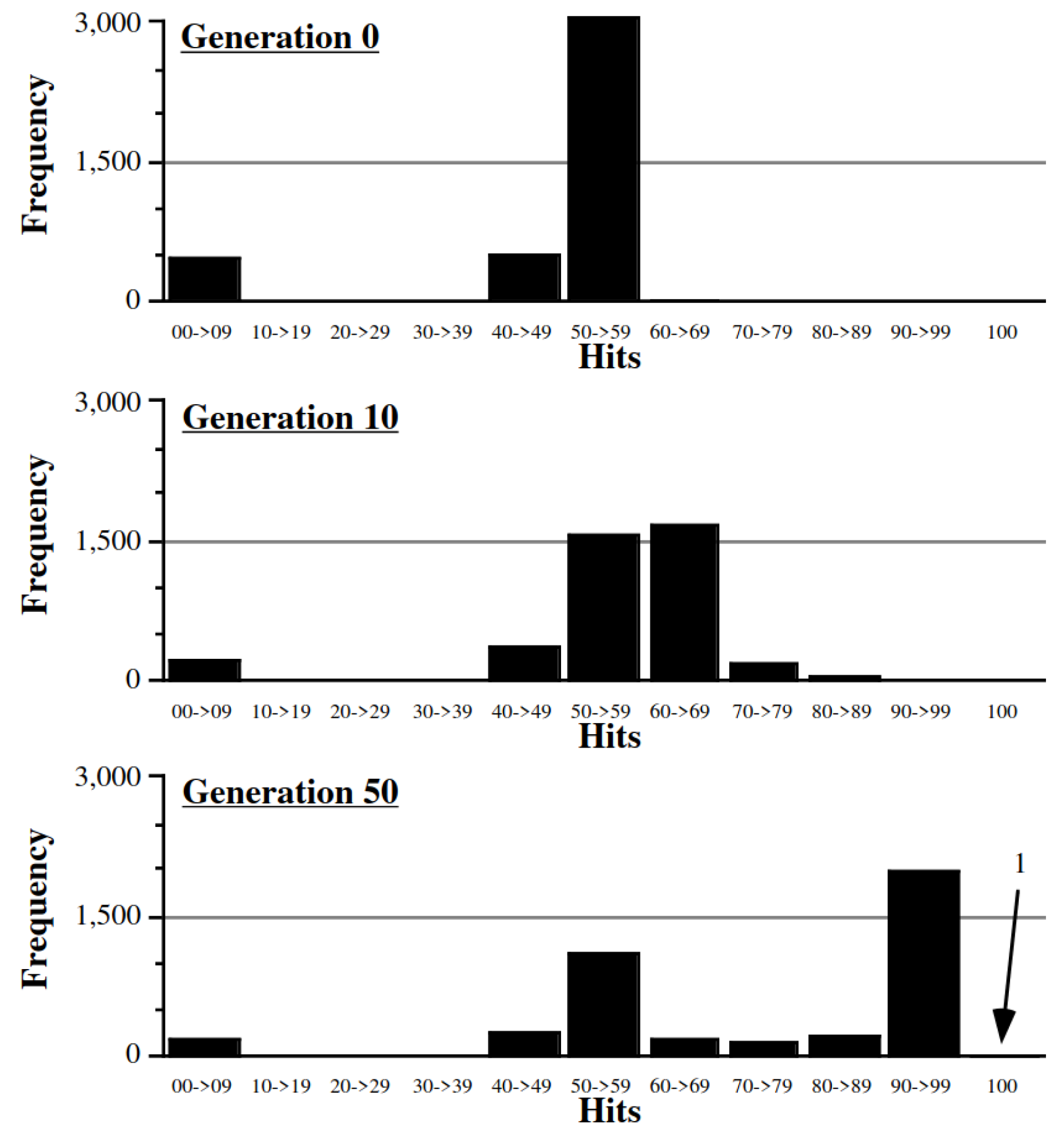
3.7. Comparison with Generational GA Approach
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Komosinski, M.; Adamatzky, A. Artificial Life Models in Software; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Langton, C. Artificial Life: Proceedings of an Interdisciplinary Workshop on the Synthesis and Simulation of Living Systems; Routledge: Oxfordshire, UK, 2019. [Google Scholar]
- Rozenberg, G.; Salomaa, A. The Mathematical Theory of L Systems; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Parish, Y.I.; Müller, P. Procedural modeling of cities. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 12–17 August 2001; pp. 301–308. [Google Scholar]
- Manousakis, S. Non-standard Sound Synthesis with L-systems. Leonardo Music J. 2009, 19, 85–94. [Google Scholar] [CrossRef]
- Prusinkiewicz, P. Graphical applications of L-systems. In Proceedings of the Graphics Interface, Vancouver, BC, Canada, 26–30 May 1986; Volume 86, pp. 247–253. [Google Scholar]
- De la Higuera, C. Grammatical Inference: Learning Automata and Grammars; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Whitley, D. An overview of evolutionary algorithms: Practical issues and common pitfalls. Inf. Softw. Technol. 2001, 43, 817–831. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Metaheuristic algorithms: A comprehensive review. In Computational Intelligence for Multimedia Big Data on the Cloud with Engineering Applications; Academic Press: Cambridge, MA, USA, 2018; pp. 185–231. [Google Scholar]
- Santos, E.; Coelho, R.C. Obtaining l-systems rules from strings. In Proceedings of the 2009 3rd Southern Conference on Computational Modeling, Rio Grande, Brazil, 23–25 November 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 143–149. [Google Scholar]
- Nakano, R.; Yamada, N. Number theory-based induction of deterministic context-free L-system grammar. In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, Valencia, Spain, 25–28 October 2010; SCITEPRESS: Setúbal, Portugal, 2010; Volume 2, pp. 194–199. [Google Scholar]
- Koza, J.R. Discovery of rewrite rules in Lindenmayer systems and state transition rules in cellular automata via genetic programming. In Proceedings of the Symposium on Pattern Formation (SPF-93), Claremont, CA, USA, 13 February 1993; Citeseer: Princeton, NJ, USA, 1993; pp. 1–19. [Google Scholar]
- Eszes, T.; Botzheim, J. Applying Genetic Programming for the Inverse Lindenmayer Problem. In Proceedings of the 2021 IEEE 21st International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 18–20 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 000043–000048. [Google Scholar]
- Runqiang, B.; Chen, P.; Burrage, K.; Hanan, J.; Room, P.; Belward, J. Derivation of L-system models from measurements of biological branching structures using genetic algorithms. In Developments in Applied Artificial Intelligence: 15th International Conference on Industrial and Engineering Applications of Artificial Intelligence and Expert Systems IEA/AIE 2002, Cairns, Australia, 17–20 June 2002; Springer: Cham, Switzerland, 2002; pp. 514–524. [Google Scholar]
- Beaumont, D.; Stepney, S. Grammatical Evolution of L-systems. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 2446–2453. [Google Scholar]
- Bernard, J.; McQuillan, I. New techniques for inferring L-systems using genetic algorithm. In Proceedings of the Bioinspired Optimization Methods and Their Applications: 8th International Conference, BIOMA 2018, Paris, France, 16–18 May 2018; Springer: Cham, Switzerland, 2018; pp. 13–25. [Google Scholar]
- Bernard, J.; McQuillan, I. A fast and reliable hybrid approach for inferring L-systems. In Proceedings of the ALIFE 2018: The 2018 Conference on Artificial Life, Tokyo, Japan, 23–27 July 2018; MIT Press: Cambridge, MA, USA, 2018; pp. 444–451. [Google Scholar]
- Bernard, J.; McQuillan, I. Techniques for inferring context-free Lindenmayer systems with genetic algorithm. Swarm Evol. Comput. 2021, 64, 100893. [Google Scholar] [CrossRef]
- McQuillan, I.; Bernard, J.; Prusinkiewicz, P. Algorithms for inferring context-sensitive L-systems. In Proceedings of the Unconventional Computation and Natural Computation: 17th International Conference, UCNC 2018, Fontainebleau, France, 25–29 June 2018; Springer: Cham, Switzerland, 2018; pp. 117–130. [Google Scholar]
- Bernard, J.; McQuillan, I. Inferring stochastic L-systems using a hybrid greedy algorithm. In Proceedings of the 2018 IEEE 30th International Conference on Tools with Artificial Intelligence (ICTAI), Volos, Greece, 5–7 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 600–607. [Google Scholar]
- Bernard, J.; McQuillan, I. Stochastic L-system inference from multiple string sequence inputs. Soft Comput. 2022, 27, 6783–6798. [Google Scholar] [CrossRef]
- Bernard, J.; McQuillan, I. Inferring Temporal Parametric L-systems Using Cartesian Genetic Programming. In Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 580–588. [Google Scholar]
- Lee, S.; Hyeon, D.; Park, G.; Baek, I.-j.; Kim, S.W.; Seo, S.W. Directional-DBSCAN: Parking-slot detection using a clustering method in around-view monitoring system. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 349–354. [Google Scholar]
- Prusinkiewicz, P.; Hanan, J. Lindenmayer Systems, Fractals, and Plants; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 79. [Google Scholar]
- Purnomo, K.D.; Sari, N.P.W.; Ubaidillah, F.; Agustin, I.H. The construction of the Koch curve (n, c) using L-system. In AIP Conference Proceedings; AIP Publishing LLC: Woodbury, NY, USA, 2019; Volume 2202, p. 020108. [Google Scholar]
- Guo, J.; Jiang, H.; Benes, B.; Deussen, O.; Zhang, X.; Lischinski, D.; Huang, H. Inverse procedural modeling of branching structures by inferring L-systems. ACM Trans. Graph. (TOG) 2020, 39, 1–13. [Google Scholar] [CrossRef]
- Syswerda, G. A study of reproduction in generational and steady-state genetic algorithms. In Foundations of Genetic Algorithms; Elsevier: Amsterdam, The Netherlands, 1991; Volume 1, pp. 94–101. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łabędzki, M.; Unold, O. D0L-System Inference from a Single Sequence with a Genetic Algorithm. Information 2023, 14, 343. https://doi.org/10.3390/info14060343
Łabędzki M, Unold O. D0L-System Inference from a Single Sequence with a Genetic Algorithm. Information. 2023; 14(6):343. https://doi.org/10.3390/info14060343
Chicago/Turabian StyleŁabędzki, Mateusz, and Olgierd Unold. 2023. "D0L-System Inference from a Single Sequence with a Genetic Algorithm" Information 14, no. 6: 343. https://doi.org/10.3390/info14060343
APA StyleŁabędzki, M., & Unold, O. (2023). D0L-System Inference from a Single Sequence with a Genetic Algorithm. Information, 14(6), 343. https://doi.org/10.3390/info14060343







