Abstract
This article is devoted to the study of the entropic orderliness of road safety systems of various dimensionalities. The author’s methodology for quantitative assessment of the quality of the road safety systems is based on the use of information entropy analysis, the essence of which is to assess the significance (or “weights”) of various information-technological stages of the road traffic accident rate formation process. The main emphasis in this paper is on the philosophical interpretation of the results of entropic evaluation of the orderliness of urban road safety systems. The article aimed to philosophically understand the reasons for the diversity in the results of assessing the entropy of road safety (RS) in Russian cities. Within the framework of this goal, the results of the analysis of the state of the issue, ideological approaches and methods for assessing the relative entropy of urban road safety systems were presented. The study was based on analyzing statistics that characterize the processes of the formation of road traffic accidents in Russian cities classified into three groups based on population size. The experimental results obtained were explained from the point of view of human psychology. Rather, results were explained from the perspective of human psychology. The final results of the study once again illustrated the objectivity of Hegel’s dialectical laws and, perhaps, once again shattered illusions about the possibility of achieving high levels of road safety in cities by building rigid systems to regulate the actions of traffic participants. In the author’s opinion, the results of the presented philosophical analysis will be useful to managers specializing in the management of complex systems (not only transport but also other fields) to comprehend the contradictions of the complex nature of humans and the paradoxes of their behavior when their freedom of action is restricted through external control.
1. Introduction
1.1. General Provisions
Safety is a fundamental social need. Creating conditions for the growth and prosperity of the state is the purpose of ensuring safety. Saving the population is the basic link to solving this state problem. The issues of ensuring road safety take an important place in the framework of the policy of saving the population. Damage from road traffic accidents in different countries can reach 1–3% of the gross domestic product [1,2,3,4]. Reducing this damage is an important state problem. Finding its best solution requires a scientific and philosophical foundation and technologies based on this foundation.
The road traffic accident rate formation is a probabilistic process, and it is not surprising that it was from these standpoints that its study began. In 1949, for the first time, R. Smeed [5] presented ideas on the use of a probabilistic approach to the analysis of the specifics of the road traffic accident rate. Today, specific indicators for assessing the road traffic accident rate proposed by R. Smeed (Human Risk HR, Transportation Risk TR) are used for comparative studies of Road Safety (RS) in all countries of the world [1,2,3,6]. However, the possibilities of such a comparative analysis are seriously limited. Thus, the HR and TR indicators do not characterize the structure of the road traffic accident rate or the specific features of the accident rate formation process. However, it is precisely the decomposition of the whole into parts and the proportional assessment of the significance of the parts as a whole that is the philosophical meaning of analysis.
This article attempts to structure the road traffic accident rate in Russian cities as a phenomenon into its constituent parts and evaluate the contribution of these parts to the overall final result. To do this, we need to consider the road traffic accident rate as a process or a chain of links between cause and effect.
The tool for evaluating the specifics of process structuring is information entropy analysis. It enables us to evaluate the structural organization of any system as a consequence of the specific nature of its process functioning. Of course, any system is always complex, consisting of many subsystems connected by system relations. The processes of functioning in complex systems are practically impossible to study qualitatively in detail. The way out of this situation is to simplify systems by combining many subsystems into higher-level systems. So, having seriously simplified the considered system of RS, we can consider it a targeted implementation of the solution of the following four management tasks:
- Minimizing of the number of road traffic accidents (RTA) and their consequences;
- Minimizing of the number of RTA victims;
- Minimizing of the number of RTA deaths;
- Minimizing of the socio-economic damage caused by road traffic accidents rate.
The essence of management as a professional activity is to transfer the controlled system from its actual state to the desired or target state [7]. The efficiency of management depends on two factors, i.e., correct goals and effective tools for solving problems to achieve the goals. So, the ultimate goal of road safety management is to minimize the socio-economic damage from accidents [1,2,3,6]. Achieving the final goal is associated with achieving intermediate goals. Using information entropy analysis enables us to evaluate the contribution of particular tasks to achieving the final goal and redistribute managerial efforts (for example, optimize resource allocation) [8].
1.2. An Overview of the Field Significance, Purpose and Objectives of the Study, Important Contributions
Road safety, along with efficiency, is one of the key generalizing categories of the quality of urban transport systems. A search of publications on the topic “Road safety research article” performed in the Researchgate.net database showed access to 94,441 publications. Even a cursory glance at some of these publications suggests an extremely wide range of approaches to the study of road safety issues.
Classifying these approaches is a separate task and is not the purpose of this article. It is worth noting, however, that studies related to the assessment of the probabilistic uncertainty of the contribution of influencing factors to road safety are a fairly significant part of chronologically recent studies.
Within this study, the semantic load, the main ideas and the methodology for quantifying the entropy of road safety (on the example of Russian cities) are considered. The research results are analyzed from the standpoint of structural analysis, in particular the assessment of the contribution of various links in the causal mechanism to the final road traffic accident rate.
The finding that technological differences in traffic management have an important impact on safety is not new. What is new is the idea that attempts to protect road users by increasing the complexity of traffic light cycles are ineffective and can lead to the paradoxical effects of an increased road traffic accident rate. The results of the author’s research allow us to conclude that the behavior of road users and their readiness to respond to the occurrence of dangerous situations depend primarily on their attentiveness. The attempt to protect road users through the technology of separation of traffic in space and minimization of conflicts, on the contrary, relaxes them and reduces their vigilance and concern for the safety of their actions. This is a good example of the real-life manifestation of the dialectical law of the unity and struggle of opposites.
1.3. Outline of the Article
The article is organized in eight sections, as follows: Section 2 presents the results of the analysis of previously performed works directly or indirectly related to the topic of the article. Section 3 presents a method for quantifying the Relative entropy Hn RS of urban road safety systems as the most important indicator of system orderliness. Section 4 provides information on the sources of data on road traffic accidents in Russian cities and the principles for classifying urban road safety systems into groups. Section 5 and Section 6 are key to this article. Section 5 presents the results of the study of the information entropy specifics of the road traffic accident rate in a Russian city and an explanation of these results. Section 6 focuses on a specific comparative example of the semantic interpretation of various results of evaluating the Relative entropy Hn-3 RS. Section 7 discusses the issues of the philosophical aspects of the information entropy analysis of the road traffic accident rate in Russian cities and the interpretation of the meaning of the Relative entropy indicator Hn RS of urban road safety systems. The article ends with general conclusions and methodological recommendations on the use of information entropy analysis in RS management at the municipal level (Section 8). The Appendix A of the article also present the results of calculations of the Relative entropy Hn RS of urban road safety systems (for 92 cities in Russia) and the necessary information to illustrate the specifics of the road traffic accident rate in Russian cities.
1.4. Study’s Limitations
The main problem with studies based on the analysis of official statistics is the lack of reliability of the data used. To one degree or another, all countries have this problem. As indicated in [9], in most IRTAD member countries, 100% of deaths in road accidents are recorded, with the exception of the Netherlands (≈94% of deaths are recorded), Spain (≈97% of deaths are recorded) and Switzerland (≈98% of deaths are recorded) [9]. As for data on injuries received in road accidents, the statistics is less accurate. Even cases of severe injuries are not always recorded. For example, in the US, ≈5% of serious injuries are not accounted for; in other IRTAD member countries, the share of such unrecorded cases can reach 20–30% [9].
In Russia, the level of underreporting of road deaths (due to errors in the classification of causes) usually reaches 5–6% [10], and that of road injuries can reach 20% [11]. However, these errors are systematic in nature and are typical for all regions and cities in Russia. For the purposes of comparative studies (regarding regions and cities of one country), the significance of this kind of error is small.
2. Analysis of Previous Works
Attempts to classify and determine the place of the science of the causes, effects and patterns of the functioning of the motor transport complex often lead to methodological issues. The science of the causes and effects of road traffic accidents belongs simultaneously to the socio-technical (to a lesser extent) and socio-economic (to a greater extent) sciences. Thus, according to R. Elvik [12], the science of road traffic accident rate patterns belongs to the class of social sciences. The main known criticism of the traditional paradigm of social sciences is its weak methodology in comparison with the natural sciences [13]. This manifests itself in the impossibility of using the experimental method for scientific purposes in the field of social sciences [14]. Perhaps this is the main explanation for the rather frequent use of entropy approaches to cognition when it is impossible to conduct an active experiment [15].
It is believed that the work “The entropy law and the economic process” by N. Georgescu-Roegen [16,17] became the impetus for using the entropy approach in socio-economic research. Over the following 50 years, this scientific field has developed rapidly. Today, six main areas for using the entropy approach in socio-economic research have been identified [18]. Table 1 presents prominent representatives of each of these areas.

Table 1.
Areas of using the entropy approach in socio-economic sciences.
Entropy approaches are also used for solving problems of optimizing transport systems [47,48,49,50,51,52,53,54,55]. S.K. Mazumder et al. [47], H. Zhou et al. [48], S. Yu et al. [49], O. Bazaluk et al. [50], A.I. Petrov [51,52], E. Bernton et al. [53], M. Nutz [54], and M. Liero et al. [55] present options for optimizing the functioning of transport systems based on applying entropy.
The main result of the analysis is establishing the possibilities in using entropy characteristics in assessing the quality of system management.
The issues of the quality of system management are closely related to the ideas of tektology, or “general organizational science”, developed by A.A. Bogdanov [56]. It was his works that were the fundamental principle of synergetics—a science that explains the formation and self-organization of structures in open systems that are far from thermodynamic equilibrium [57].
Here, several definitions of system orderliness should be given (in general and in relation to the subject of research).
Orderliness is a property of complex systems associated with the quality of the system structure and the orderliness of the behavior of system elements.
Transport systems, like any other, are characterized by the presence of a structure (composition of elements, a certain number of connections between them, a proportional relationship between the number and size of system elements).
Structural orderliness is a system property that identifies the degree of probabilistic certainty of one or another of its states.
Systems with a high level of orderliness are characterized by purposeful behavior and high efficiency in terms of achieving their goals. Systems with a low level of orderliness, on the contrary, are characterized by signs of a lack of goal setting, chaotic functioning and low efficiency in terms of achieving the goals.
A road safety system is a subsystem of the transport system, which, in turn, is also “large” and “complex” in relation to lower order systems. Road safety systems, to some extent, manifest the property of system orderliness.
The orderliness of road safety systems is a system property that characterizes the degree of freedom of behavior of system elements and is realized in the form of practical implementation of the action of a set of rules and prohibitions that structure the system and limit the freedom of its changes.
Entropy H and its derivatives—relative entropy Hn and entropy coefficient Kh—are the characteristics or quantitative indicators of the system orderliness. The orderliness of road safety systems can be quantitatively measured by entropy H and its derivatives (Hn and Kh) [51,52].
3. Method of Quantitative Assessment of the Relative Entropy Hn RS, the Most Important Indicator of the Orderliness of Urban Road Safety Systems
3.1. Main Idea of the Method
Figure 1 shows the causal chain of formation of the road traffic accident rate.
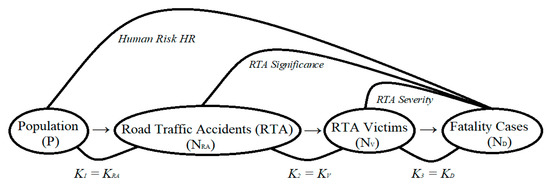
Figure 1.
Simplified causal chain of the road traffic accident rate and the road safety management process.
Of course, in reality, each block of the chain is complex (i.e., a system with many intra-system connections). However, as part of assessing the specifics of process structuring, these blocks must be enlarged as much as possible.
Moreover, without accurate information about the parameters of the functioning of one or another link in the causal chain, we can further simplify the process under study. Figure 1 shows the simplest version of the causal chain of accident rate formation, consisting of only four blocks and connected by only three intra-system relations. These are the relations between the population and the number of road accidents (estimated by HR): between the number of road accidents and the number of victims in road accidents (estimated by the RTA Significance indicator); between the number of victims and the number of deaths in these accidents (estimated by RTA Severity).
Particular tasks of road safety management are minimizing both HR, RTA Significance, RTA Severity and information transfer coefficients Ki (Figure 1) between the blocks of the causal chain “Population P—Road Traffic Accidents NRA—RTA Victims NV—Fatality Cases ND” (1):
where Xi+1 is the value of the characteristic of the subsequent block of the causal chain of the process under study; Xi is the value of the characteristic of the previous block of the causal chain. Table 2 elaborates on this approach.
Ki = Xi+1/Xi,

Table 2.
Information transfer coefficients Ki.
Accordingly, K1 or KRA determines the probability of participation of an average city resident in an accident; K2 or KV characterizes the magnitude of the accident, i.e., the average number of victims per road accident; K3 or KD characterizes the severity of the accident, i.e., the proportion of those killed in road accidents.
Information transfer coefficients Ki ultimately determine the weight significance of each link in the causal chain and influence the formation of entropy characteristics of the system under study. In the case of relative weight equivalence of the contribution of all three links of the process to the final result, the entropy of the process H (or a measure of the uncertainty of the event—in particular, the death of a person in an accident) is maximized. If the significance of different parts of the process is not the same, the entropy H decreases. The process of functioning of such a system is the result of managerial influence and violence against the controlled system. A decrease in the system entropy H is the result of such managerial influence. Thus, the value of the system entropy H is a quantitative measure of the quality of the road safety system management.
So, in order to identify the quality of the road safety management in Russian cities, we need to quantify the structural-informational entropy of the process under study. To do this, we use the classical approaches of C. Shannon [58,59].
3.2. Method of Quantitative Assessment of the Relative Entropy Hn RS of Road Safety Systems
The author previously presented the method for quantifying the relative entropy of road safety systems Hn RS in various versions [51,52,60].
The method includes the following set of actions.
Stage 1.
Structuring the road safety system and describing the final result of its functioning in the form of a causal chain, where each subsequent stage of the process is generated as an effect of previously completed stages.
The causal chain of the process of formation of the road traffic accident rate in cities is described as follows (Figure 2).
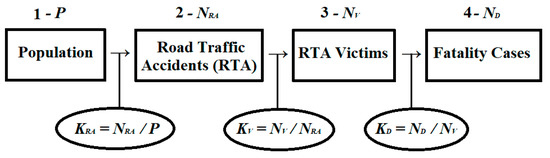
Figure 2.
Three-link causal mechanism of the road traffic accident rate formation.
Stage 2.
Determining the numerical values of coefficients Ki information transfer over the channel under study.
The transfer coefficient of the i-link is (2) the ratio of the values of its output characteristic (Aout) to the value of the input characteristic (Ain):
Ki = Aout/Ain,
In particular, we need to determine the values of the coefficients Ki (3):
Identifying the values of the coefficients Ki of information transfer over the channel makes it possible to set priorities in the field of road safety management by identifying the so-called “weak” links in the causal mechanism of the road traffic accident rate formation.
Stage 3.
Determining the so-called positive or positive contribution Q relative to the weight of the corresponding link of the transformation process under study in the causal chain of information transfer “Population P—Road Traffic Accidents NRA—RTA Victims NV—Fatality Cases ND”.
The physical meaning of the positive contribution Q of various elements of the chain “Population P—Road Traffic Accidents NRA—RTA Victims NV—Fatality Cases ND” to the final result of the road traffic accident rate is a measure of the volume of information or the derivative of the entropy of the process under study.
For the three-link method of determining entropy (H-3), this can be done by (4):
Because ln(Xi > 1) takes a negative value, we need to get rid of this effect. To do this, the calculation of QV uses the calculation of ln in relation to the direct value (KV), while the calculation of QRA, QD uses the calculation of ln in relation to the reciprocal values (1/KRA); (1/KD).
Stage 4.
Determining the numerical values of weight coefficients
to assess the positive contribution Q of various elements of the chain “Population P—Road Traffic Accidents NRA—RTA Victims NV—Fatality Cases ND”.
For this, we use the algorithm (5):
Having calculated the values of the positive weight of various links in the causal chain allows solving the main task of entropy analysis—assessing the degree of influence of various blocks (links) of the information transfer chain in the formation of the final result—the state of the road safety system.
Stage 5.
Determining the logarithmic values of the “weight” of the positive of various links in the causal chain and their product with the “weights” of the positive
.
Since the classical Shannon’s formula uses logarithmic values of the “weights”, we must first calculate the natural logarithms of the corresponding “weights” of the positive links of the chain, and then the results of multiplying the logarithms of the corresponding “weights” by the values of the “weights”.
Stage 6.
Directly calculating the entropy of the process of ensuring road safety according to the classical formula of C.E. Shannon (6):
where
- n—the number of links in the causal chain of the road traffic accident rate formation;
- —positive weight coefficients of chain links that meet the normalization condition .
Stage 7.
Calculating the Relative entropy Hn of the process of ensuring road safety in Russian cities can be carried out by the formula (7):
where
- n—the number of links in the causal chain of the road traffic accident rate formation;
- n = 3 for the case of estimating the entropy of urban road safety management systems.
The theoretical range of values of Hn-3 = [0; 1]. Further, it will be shown that the actual (2021) range of values for the entire population (n = 92) of the studied road safety systems of Russian cities Hn-3 RS 2021 = [0.490; 0.709].
4. Data
According to the results of the All-Russian population census [61], there were 1118 cities in Russia in 2020. This paper presents the results of assessing the Relative entropy Hn-3 RS 2021 of urban road safety systems in Russian cities of three categories (Table 3).

Table 3.
General characteristics of the cities of the Russian Federation studied to assess the level of road safety orderliness (assessment characteristic—Hn-3 RS 2021).
The choice of such dissimilar sets of cities for comparative studies was determined by the following considerations:
- The compared groups of cities are not neighbors within the classification (there is a 3–10-fold difference in population).
- The style, organization and quality of life of citizens in such cities are radically different.
- The structural complexity of the management systems of the most important subsystems of the urban economy in such cities also varies significantly.
Data on the numerical values of indicators—elements of the causal chain “Population P—Road Traffic Accidents NRA—RTA Victims NV—Fatality Cases ND”—were obtained from the official website of the State Inspectorate for Road Traffic Safety of the Russian Federation [62].
5. Results of the Study of Information Entropy Specifics of the Road Traffic Accident Rate in Russia’s Cities
5.1. Quantification of the Relative Entropy Hn-3 RS of Urban Road Safety Systems
This section presents the results of assessing the entropy orderliness of road safety systems in Russian cities of three categories. Table A1, Table A2 and Table A3 present summary tables of data with numerical values of the Relative entropy Hn-3 RS of urban road safety systems.
For category A cities (4 cities in total), the range of values of Hn-3 RS = [0.596; 0.650].
For category B cities (23 cities in total), the range of values of Hn-3 RS = [0.581; 0.709].
For category C cities (65 cities in total), the range of values of Hn-3 RS = [0.490; 0.707].
Table 4 and Table 5 show the distribution frequency of Hn-3 RS values of road safety systems of cities in categories B and C by ranges of values.

Table 4.
Distribution of urban road safety systems in large (Population = 500…1000 thous. people) cities of Russia (2021) by ranges of values of the Relative entropy Hn-3 RS.

Table 5.
Distribution of urban road safety systems in small (Population = 50…100 thous. people) cities of Russia (2021) by ranges of values of the Relative entropy Hn-3 RS.
It is clear that small towns are characterized by a shift in the values of the Relative entropy Hn-3 RS to the left relative to Hn-3 RS of large cities.
5.2. Specifics of the Processes of the Road Traffic Accident Rate Formation in Urban Road Safety Systems with Different Levels of the Relative Entropy Hn-3 RS
Table 6 presents data based on which we can identify the specifics of the mechanism for the formation of relatively high or, conversely, relatively low values of the Relative Entropy Hn-3 RS.

Table 6.
Comparative values of the Relative entropy Hn-3 RS (2021) for the road safety systems of two cities of the Russian Federation of the same category and the explanation of this difference based on the values of Ki.
Note that there are certain ratios Ki leader/Ki outsider between the corresponding Ki values for leading cities and outsider cities for each category (Table 7).

Table 7.
Specifics of the variety of road traffic accident rate for cities of the same category, determined by the ratio Ki leader/Ki outsider.
So, the variety of numerical values of Hn-3 RS for cities in the same category is determined by the specifics of the processes of formation of the road traffic accident rate (varieties of Ki combinations). In different Russian cities, road traffic accident rates have their own characteristic features. The presented argument is valid for the road safety systems of Russian cities in all three categories.
5.3. Structural Interpretation of the Assessment Results of the Relative Entropy Hn-3 RS
The interpretation of the data in Table 6 and Table 7 allows us to present the following speculative picture. In cities where the Relative entropy of road safety systems Hn-3 RS is high (Hn-3 RS ≥ 0.70), the probability of an accident is very high (high values of K1), but the chance of dying is relatively low (low values of K3). Conversely, in cities where the Relative entropy of road safety systems Hn-3 RS is relatively low (Hn-3 RS ≤ 0.60), the probability of an accident is lower (low values of K1), but the chance of dying is higher (high values of K3). These two essentially opposite dispositions are exacerbated by the nature of the specific number (per 1 average accident) of victims. Hn-3 RS is slightly higher at high K2 levels.
The meaning of this interpretation is the structural differentiation of the significance, from the standpoint of death in an accident, of the probabilities of various stages of the process of road traffic accident rate formation.
A high probability of an accident increases the value of the Relative entropy Hn-3 RS of road safety systems. A high probability of death in an accident reduces the value of Hn-3 RS. How do we interpret this conclusion at an understandable level?
6. Specific Comparative Example of the Semantic Interpretation of Various Results of Assessing the Relative Entropy Hn-3 RS
The author was lucky to live and work in a city (Tyumen) whose road safety system is characterized by the highest value of Hn-3 RS among comparable Russian cities in terms of population (Hn-3 RS 2021 = 0.709). On the other hand, the author knows quite well the situation in the field of traffic management and safety in another Russian city—Novosibirsk.
The Relative entropy of the road safety system of this city is low (Hn-3 RS 2021 = 0.596). The expertise of the author allows conducting a comparative assessment of two essentially dissimilar strategies for ensuring road safety that are selected and implemented by the municipal authorities of these cities.
Table 8 presents data necessary for semantic interpretation.

Table 8.
Data characterizing the structural specifics of road traffic accident rates in the compared cities (2021).
The first thing you immediately pay attention to is a significantly higher number of accidents and victims of accidents in Tyumen, a city two times smaller in population than Novosibirsk. So, we note that a higher probability of the formation of an accident is typical for Tyumen. This probability is three times higher than in Novosibirsk (K1 Tyumen/K1 Novosibirsk = 0.00178/0.00060 = 2.97).
The second thing is that the severity of road accidents or the proportion of deaths to the number of victims in road accidents in Tyumen is almost three times lower than in Novosibirsk (K3 Tyumen/K3 Novosibirsk = 0.0252/0.0706 = 0.36). This means that with a significantly lower number of accidents than in Tyumen, the death rate of participants in these accidents in Novosibirsk is much higher.
The question arises: what are the reasons for this specificity? The answers will be presented a little later, but now we will note that the structure of the road traffic accident rate in Novosibirsk and Tyumen is fundamentally different. The Relative entropy Hn-3 RS determines the degree of uncertainty of the probability of death of citizens in an accident. A comparison of the values of the Relative entropy Hn-3 RS of urban road safety systems characterizes the traffic situation in Novosibirsk as more certain than in Tyumen, from the standpoint of the probability of death in an accident. Therefore, we must remember that the probability of death of people in an accident is not the only sign characterizing the state of the road safety system. The aspect of the semantic ambiguity of the characteristics of the state of the road safety system will be considered in Section 6 of this paper.
And now we compare the specific (per 1000 people; per 1 km2 of the city area) indicators of the road traffic accident rate in Novosibirsk and Tyumen (Table 9).

Table 9.
Data characterizing the spatial and geographical specifics of road traffic accident rates in the compared cities (2021).
Specific spatial characteristics of the road traffic accident rate (per 1000 people; per km2) are much lower in Novosibirsk than in Tyumen. The only exception is the number of deaths in road accidents/km2. It is this aspect that determines the greater certainty of the probability of death in an accident in Novosibirsk compared to Tyumen.
6.1. Specifics of Traffic Management on the Roads of Cities with High (Tyumen) and Low (Novosibirsk) Levels of the Relative Entropy Hn-3 RS
Highlighting the characteristic distinctive features of traffic management systems in the compared cities, it is necessary to note the following three most important observations:
- According to Russian Traffic rules [63], the permitted speed in cities is 60 km/h; the non-penalized threshold for exceeding this limit is 20 km/h. The actual speed of most vehicles in Russian cities under favorable conditions (summer, dry road surface, no traffic jams) is 75–80 km/h. On city roads of the first and second categories (for example, on the belt road around Tyumen), traffic is allowed at a speed of 90 km/h; the actual speed reaches 105–110 km/h. This is a fairly high speed for vehicles, which does not fully ensure road safety.
- In Tyumen, 96% of all traffic light units in the city are characterized by the obligatory dedicated pedestrian phase in the traffic light cycle. In Novosibirsk, no more than 25% of the city’s traffic lights have a dedicated pedestrian phase. This clear visual difference between the traffic management systems in the two compared cities is the main impression for the observer.
- A distinctive feature of traffic management in Tyumen is not only a dedicated pedestrian phase in the traffic light cycle but also more complex multi-phase cycles of traffic light regulation in general. The purpose of such a management decision is to differentiate vehicle and pedestrian flows in time and to minimize the number of conflict points at intersections. In Novosibirsk, traffic managers pay much less attention to the differentiation of traffic flows over time.
6.2. Specifics of the Behavior of Road Users on the Roads of Cities with High (Tyumen) and Low (Novosibirsk) Levels of the Relative Entropy Hn-3 RS
The fundamental difference in the behavioral reactions of road users in Tyumen and Novosibirsk can be characterized as follows.
- Tyumen drivers and pedestrians are generally characterized by relatively greater carelessness and a lower level of concentration. This is facilitated by the common and expected absence of conflict at the intersections of the city’s road network [63]. Car and pedestrian flows are separated in time by using multi-phase traffic control schemes. In Novosibirsk, the situation is reversed: drivers and pedestrians are alert constantly. The reason for this is the presence of conflict points at intersections [64,65,66,67,68,69]. As a result, there is less likelihood of dangerous traffic situations due to the greater attention of road users to the general situation.
- At the same time, we can state the fact of a greater intensity of drivers’ operator actions in Tyumen and traffic on the stretches of the city’s road network at relatively higher speeds than in Novosibirsk. Analyzing this observation, the author came to the conclusion that Tyumen drivers try to use the high dynamics (intense acceleration, high speed) as a compensation for the loss of time during numerous and rather long downtimes while waiting for a permitting traffic signal at regulated intersections [70,71]. In Novosibirsk, these actions of drivers are expressed to a lesser extent than in Tyumen. The reason is the lesser loss of time for Novosibirsk traffic participants while waiting for the permitting traffic signal.
- The specifics of urban demographics, in particular the median age of the population, have a certain influence on the behavior of road users. In Novosibirsk, the median age of the population is 38.9 years; in Tyumen—35.8 years [72]. The level of acceptable risk homeostasis [73,74] in Tyumen is higher than in Novosibirsk. The reason is the peculiarities of age demographics.
The above considerations are easily consistent with the concept of the common space of H. Monderman [65,66,67,68]. Applying his ideas in relation to the comparison of traffic management practices in Tyumen and Novosibirsk, we can draw two important conclusions:
- An attempt to complicate the traffic management system in order to increase road safety reduces the severity of accidents, but increases the probability of their occurrence (more on this in Section 6.1);
- The first conclusion leads to the second conclusion about changing the structure of the accident rate, but not eliminating or reducing it when trying to complicate the road safety management system.
6.3. Specifics of the Localization of Places and the Probability of an Accident on the Roads of Cities with a High and Low Level of the Relative Entropy Hn-3 RS
An analysis of the localization of places where accidents are concentrated is also necessary to understand the specifics of the road traffic accident rate in the compared cities.
According to the terminology of the Russian regulatory document on the registration of road accidents [75], the place of concentration of road accidents (accident cluster) in the city is considered to be a section of the road not exceeding 200 m in length or an intersection where five or more accidents with victims or three or more accidents of one type (for example, collision with a pedestrian) occurred.
Figure 3 shows a heat map of the places of concentration of road accidents with victims (either dead or injured) in the two compared cities.
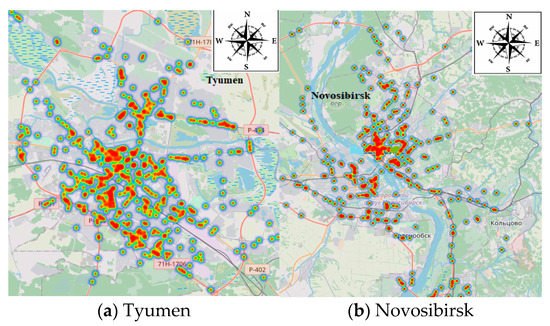
Figure 3.
Localization of places of accidents with victims [62].
Figure 4 shows a heat map of places of fatal accidents in the two compared cities (places of mass death of people in road accidents are marked).
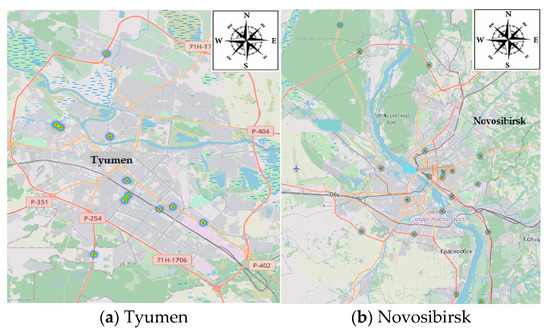
Figure 4.
Localization of places of fatal road accidents [62].
An analysis of the localization of places of deaths in road accidents shows that they happened on such sections of the urban road network where either a high-speed limit (80 and 90 km/h) was initially allowed or there are conditions (free-flow traffic) for violating the requirements of the current speed limit in Russian cities (60 km/h).
There is a certain specific nature to the types of accidents determined by the traffic management system. On road sections with continuous traffic, car collisions are very frequent; at intersections, pedestrians are more likely to be hit.
Figure 5 shows an example of the localization of a place of frequent collisions with pedestrians (Tyumen; city center; intersection of M. Toreza St. and A. Gerzena St.).
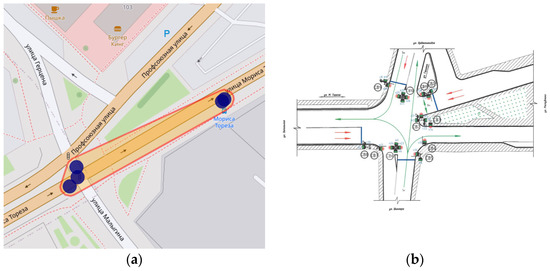
Figure 5.
Relationship between the complexity of managing traffic at the intersection and the unwillingness of pedestrians to wait for the permitting traffic light signal. (a) Location of 5 pedestrian collisions during 2021 [62]. (b) Scheme of one of the 7 phases of the traffic light cycle at the intersection.
The example in Figure 5 is characterized by the fact that there is a certain connection between the scheme of traffic light regulation and the behavior of pedestrians. The total duration of the 7-phase traffic light control cycle during the morning rush hour (7:30–9:00) on weekdays is 176 seconds. Such a long cycle and waiting for permission to cross the carriageway result in a fairly frequent violation of traffic light instructions by pedestrians. Experimental observations have shown that at least 10–12% of pedestrians cross the carriageway at a given location of the Tyumen road network (Tyumen; city center; the intersection of M. Toreza St. and Gerzena St.) without waiting for the permitting traffic light and violating the requirements of the Traffic Rules. This is explained by the fact that several iterations of pedestrians waiting to be allowed to move are required. Not all of them are disciplined. The unpreparedness of drivers for pedestrians to enter the carriageway and the high speed of movement lead to cars colliding with pedestrians. The estimated frequency of such collisions (knockdowns) is relatively low—only about 5 cases per ≈ 102,200 traffic light cycles/year. The probability of pedestrian collisions Pp. collision on a given road section Pp. collision = 0.000049 = 4.9 ∙ 10−5 cases/traffic light cycle. For other intersections of the road network of the city, similar probabilities vary in the range of Pp. collision = 9 ∙ 10−6 … Pp.collision = 5.6∙ 10−5 cases/traffic light cycle. Similar calculations for Novosibirsk show a relatively lower probability of collision with pedestrians (Pp. collision = 4 ∙ 10−6 … Pp. collision = 1.6 ∙ 10−5 cases/traffic light cycle) at regulated intersections. This is another example of the negative impact of a reduced sense of danger among road users on the final level of road safety when implementing the task of reducing traffic conflicts.
6.4. Specifics of the Rolling Stock Used by the Population of Cities with High (Tyumen) and Low (Novosibirsk) Levels of the Relative Entropy Hn-3 RS
Another interesting point that deserves attention is the specifics of the rolling stock of the population of the compared cities. Table 10 presents comparative data characterizing the specifics (by three features) of the rolling stock used in the compared cities.

Table 10.
Data characterizing the specifics of the car fleet in the compared cities (as of March, 2023) [62].
It is clear that in the two cities compared, the vehicle fleets are very different. A more modern car fleet in Tyumen implies a higher level of active and passive safety. Even more significant is that the use of right-hand drive cars in right-hand traffic sharply limits visibility when driving. Obviously, this also has a certain effect on traffic conditions. A consequence of the specifics of the car fleet in the compared cities is a higher level of passive safety of motorists in Tyumen. At the physical level, this is expressed in a relatively lower level of severity of the consequences of an accident in Tyumen (K3 Tyumen = KD Tyumen = 0.0252) than in Novosibirsk (K3 Novosibirsk = KD Novosibirsk = 0.0706).
7. Discussion of the Results
7.1. Models of Statistical Relation of Information Transfer Coefficients Ki with the Relative Entropy Hn-3 RS of Urban Road Safety Systems
Section 6 presents the mechanisms for the formation of system orderliness in relation to road safety on the example of a qualitative comparison of two urban road safety systems (with high and low levels of the Relative entropy Hn-3 RS). However, we need to generalize these conclusions for a larger number of system objects, in particular, for all 92 cities of the Russian Federation participating in the study.
Table A4 provides data to build models Hn-3 RS = f(Ki) for all 92 cities.
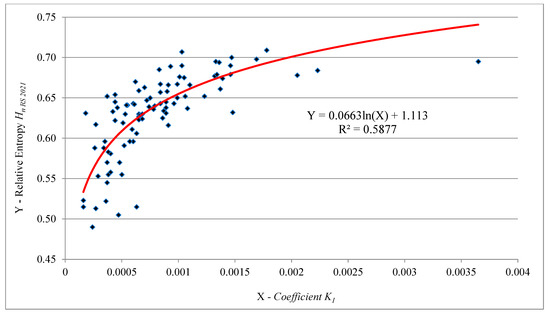
Figure 6.
Model Hn-3 RS = f(K1) for the studied road safety systems (2021)—92 cities of the Russian Federation.
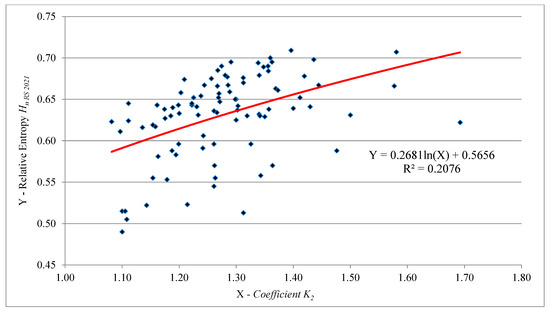
Figure 7.
Model Hn-3 RS = f(K2) for the studied road safety systems (2021)—92 cities of the Russian Federation.
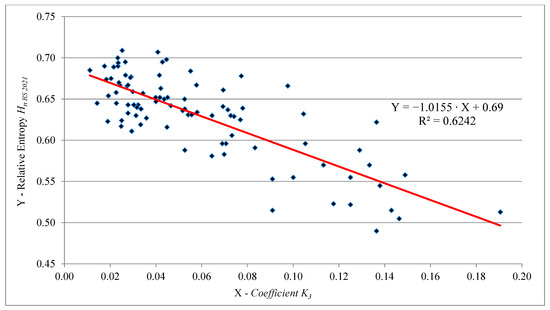
Figure 8.
Model Hn-3 RS = f(K3) for the studied road safety systems (2021)—92 cities of the Russian Federation.
At low levels of the relative entropy Hn RS of urban road safety systems, the probability of an accident decreases (Figure 6). However, at the same time, the severity of the consequences of road accidents is growing (Figure 8). The influence of the specific number of victims in road accidents is weakly expressed (Figure 7).
Let us try to explain the results.
Any accident is the result of the loss of control over the car by the driver in a specific traffic situation. This often happens when the stopping distance Sstopping way of a car (8) in braking mode exceeds the distance Sdistance between this car and the local place of potential road accident at the moment of danger formation.
where
- T—total time T = (T1 + T2 + 0.5∙T3) required to ensure efficient braking with the maximum possible deceleration, s;
- T1—reaction time of the driver to the danger, s;
- T2—brake actuation time, s;
- T3—time to reach maximum car deceleration, s;
- Vv—original speed of the car, m/s;
- j—deceleration of the car in full braking mode (breaking slip).
Entropy H, as a characteristic of the state of the motor transport system (Man—Car—Road—Environment), affects the reaction time of the driver and pedestrian to the danger. A standard value of T1 = 0.6–0.8 seconds (for different conditions). Under conditions of high entropy, T1 increases to 1.0–1.2 seconds, i.e., 1.5 times. As a result, the total time required to achieve full braking mode T = (T1 + T2 + 0.5∙T3) under conditions of high entropy of T increases by 40%. The stopping distance of the car Sstopping way in full braking mode is increased two-fold (Table 11).

Table 11.
Changing the braking mode parameters of the car with a high and low level of the entropy Hn RS of road safety systems.
So, the high probability of an accident in a city characterized by a high level of the Relative entropy Hn RS (Table 8) is explained, first of all, by the peculiarities of the speed limit and the reduced level of attention of road users due to their unreasonable belief in the absence of road interference when using a multiphase traffic light control system. A natural consequence of this is the high values of the stopping way S stopping way in a full braking mode.
Let us consider the phenomenon of relatively low severity of road accidents in urban systems with a high level of the Relative entropy Hn RS. There are supposedly two mechanisms at work here. Firstly, there is a phenomenon of active reduction of the potential energy of the vehicle in full braking mode. By the time the energy passes from the potential to the kinetic state, its level decreases to levels that are more or less safe for life. The loss of potential energy of the car occurs due to the release of heat in the brake mechanisms.
For a higher-quality fleet of cars (Table 10) in Tyumen, these processes obviously proceed in a safer mode.
Secondly, in Tyumen, the first aid system is better organized than in Novosibirsk. The paper [76] shows that Tyumen is one of the best cities in Russia in terms of the organization of emergency medical care. Novosibirsk occupies a relatively low place in this rating.
These considerations can be extended to other cities [77] and their transport systems.
Models in Figure 6 and Figure 8 generally confirm the explanations presented in Section 7.1 for the extreme cases of Hn-3 RS (Tyumen and Novosibirsk).
7.2. Logarithmic Law in the Description of the Ranking Distribution of Road Safety Systems in Russian Cities in Terms of Human Risk HR, RTA Severity and Hn RS
Sometimes, for debatable reasoning, it is useful to render experimental data from one scale to another. This procedure has become widespread because it works reliably under weak assumptions about the initial data. In this case, the results of the transformation of data on the values of HR2021, RTA Severity2021 and Hn-3 RS 2021 are presented on the ranking scale. Figure 9 and Figure 10 show ranking models HR2021 = f(Rank) and RTA Severity2021 = f(Rank).
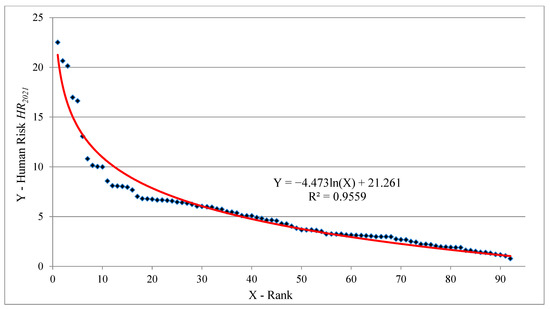
Figure 9.
Ranking model HR2021 = f(Rank) for the studied road safety systems (2021)—92 cities of the Russian Federation.
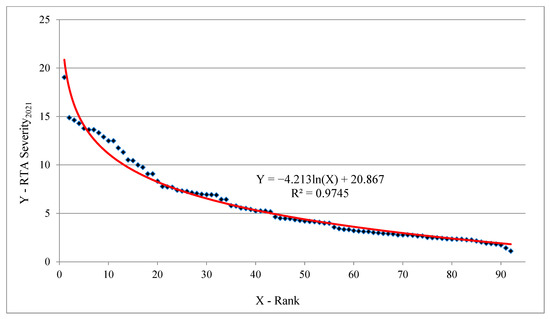
Figure 10.
Ranking model RTA Severity2021 = f(Rank) for the studied road safety systems (2021)—92 cities of the Russian Federation.
Taking into account that these ranking models obey the logarithmic law well, we can draw two conclusions:
- -
- About the fundamentally different states of road safety systems in Russian cities (obviously, corresponding to different road safety paradigms [78]);
- -
- About the incorrectness of applying the same type of road safety management methods in cities characterized by such different levels of the two important indicators (HR, RTA Severity).
Hence the fallacy of spreading a uniform strategy and standard regulatory approaches to road safety management in all cities in Russia. Different cities of Russia require the use of different tools in the field of road safety. This will result in the use of different traffic control policies in different cities in the same country. Of course, this can cause a lot of discussion about the possibility of implementing this proposal in one country. However, the best practices of other countries (for example, the USA) argue for such a possibility. Figure 11 presents the ranking models from Figure 9 and Figure 10 in a linearized form. Figure 12 presents a ranking distribution model, Hn RS 2021 = f(Rank).
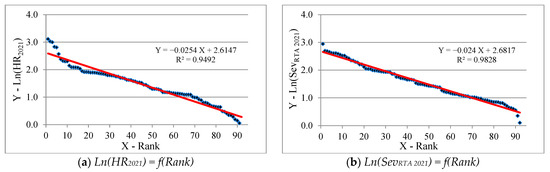
Figure 11.
Linearized form of the ranking models Ln(HR2021) = f(Rank) and Ln(Sev RTA 2021) = f(Rank) for the studied road safety systems (2021)—92 cities of the Russian Federation.
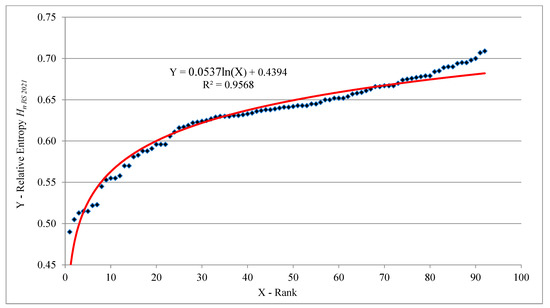
Figure 12.
Ranking model Hn RS 2021 = f(Rank) for the studied road safety systems (2021)—92 cities of the Russian Federation.
The model Hn RS 2021 = f(Rank) also obeys the logarithmic law well, which confirms the conclusion about the serious heterogeneity of the road safety systems of Russian cities—in this case, in terms of their system orderliness. This fact also confirms the idea that different (unequal) approaches to road safety should be applied in different cities of one large country.
7.3. Philosophical and Semantic Aspects of Information Entropy Analysis of the Road Traffic Accident Rate
The materials of this study allow us to talk about another example of confirming the laws of dialectics of G.W.F. Hegel [79].
The dialectical law of the unity and struggle of opposites [79] manifests itself in a very unexpected form. As the case of Russian cities shows, attempts to complicate the system of traffic management in order to decrease the road traffic accident rate do not lead to unambiguously positive results. Improving one parameter of the state of the road safety system results in the deterioration of its other parameter. For example, complex multi-phase traffic control systems (model city—Tyumen) not only do not reduce but, on the contrary, increase the likelihood of an accident. The introduction of multi-phase traffic signal control systems in Tyumen, according to the initiators of this measure, was supposed to reduce the number of road conflicts and, as a result, minimize the number of accidents. In reality, the opposite effect was achieved—the number of accidents increased [62]. This was due to a change in the structure of the process of accident rate formation as a result of the reaction of the controlled system to the control action. It turns out that as the conflict between traffic flows decreases, the level of specific probability of an accident increases. The reason for this is a decrease in the attentiveness of road users due to their confidence in the absence of a possible danger, their choice of more dangerous forms of transport behavior, and a general increase in systemic risk homeostasis [72,73]. On the other hand, as the probability of an accident increases, its severity decreases.
The dialectical law of the transition of quantity into quality [79] is illustrated by logarithmic models of the connection between various aspects of the functioning of road safety systems and the final level of their orderliness. Examples of this thesis are the models Hn-3 RS = f(K1) and Hn RS 2021 = f(Rank) presented, respectively, in Figure 6 and Figure 12.
In this context, the dialectical law of negation of the negation [79] must be interpreted in two ways. First, attempts to complicate the traffic control system sooner or later lead to the need to simplify it. Second, this argument cannot be abstracted for all cases. Obviously, we need to differentiate various road transport locations and choose the most optimal operating conditions for them. This allows us to conclude that there is an optimal state for urban road safety systems. Finding this state is evidently not easy. Therefore, it is more correct to talk about the rational state of urban road safety systems (Hn optimum RS city), which provides an acceptable balance between the various elements of the process described by the information transfer coefficients Ki between the blocks of the causal chain “Population P—Road Traffic Accidents NRA—RTA Victims NV—Fatality Cases ND”.
Information entropy analysis of the processes of formation of the urban road traffic accident rate cannot replace the usual methods for identifying the actual level of road safety, which have already become traditional. However, identifying the Relative entropy Hn RS city allows us to draw important conclusions about the level of orderliness of urban road safety systems that cannot be obtained in the traditional way.
For clarity, there is an example in Table 12 and Table 13. Two Russian cities (population of about 67.5 thousand people) located in different geographical (climatic) zones are characterized by different levels of the road traffic accident rate (HR2021, RTA Severity2021) but the same level of the Relative entropy Hn RS city (0.631–0.632). Let us analyze the causes and meaning of this.

Table 12.
Comparison of two diverse examples of Russian cities with the same population, but with different efficiency of road safety systems.

Table 13.
Comparison of specific aspects of the road traffic accident rate formation in two different Russian cities.
Previously (Section 7.1; Figure 6, Figure 7 and Figure 8), it was found that the patterns represented by the models Hn-3 RS = f(Ki) are formed very differently (Figure 13) in relation to different links in the causal chain.
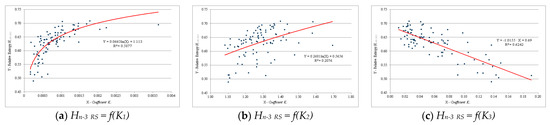
Figure 13.
Variety of models of the statistical link Hn-3 RS = f(Ki).
Comparing the values of the corresponding coefficients K1 = KRA; K2 = KV; K3 = KD for road safety systems of the Russian cities of Feodosia and Minusinsk, note the following:
- -
- The probability of becoming a participant in a road accident in Feodosia is higher than in Minusinsk;
- -
- The specific number of victims in road accidents in Feodosia is higher than in Minusinsk.
Given these two links in the causal chain, the Relative entropy Hn-3 RS of the road safety system in Feodosia should be higher than in Minusinsk. However, the third link in the causal chain changes everything. It is the probability of death in a road accident that sharply reduces the final value of Hn-3 RS in Feodosia. The resulting values of the Relative entropy Hn-3 RS of road safety systems in the two compared cities are almost the same (Hn-3 RS = 0.631–0.632).
HR2021 and RTA Severity2021 in Feodosia are much higher than in Minusinsk. From the standpoint of quantitative analysis (HR2021; RTA Severity2021), the road safety systems in the compared cities are very different. From the standpoint of qualitative analysis (Hn-3 RS), they are almost the same. What does this mean for road safety specialists? Hn-3 RS determines the degree of probabilistic certainty of a person’s death in an accident. In Feodosia, the road safety situation is much worse (high HR2021; RTA Severity2021) than that of the model situation (Minusinsk plays the role). The main conclusion of comparing the two cities in terms of assessing the quality of road safety systems is that system capabilities are identical, but the levels of the actual accident rate are different. This means that Feodosia is characterized by large systemic reserves for increasing road safety. Utilizing them in practice will bring the HR and RTA Severity indicators to the level of Minusinsk.
7.4. Comparing the Obtained Results with Other Studies
An important part of any study is comparing the findings with those of other scientists. So, it is necessary to refer to the results of research [80,81,82,83,84,85,86,87].
The study [80] attempted to evaluate traffic safety based on the concept of intrinsic safety. G. Tingting et al. [80] conclude that «ranking influencing factors on road safety are: the human’s alertness > road and the environment’s completeness > vehicle’s technical > human’s self-consciousness > natural conditions > vehicle’s maintenance». At the same time, they refer not only to their research but also to articles Z. Rui and Y. Zhenhong [81], Z. Wei and L. Xiaojing [82], Q. Chen and C. Xiaofang [83], L. Honghong and W. Ni. [84]. Similar and even more modern results can be found in the works of M. Damjanović et al. [85], Ž. Stević et al. [86] and M. Li et al. [87].
The contribution of [85] is reflected in the development of an integrated multiphase model for the analysis of traffic safety in Montenegro. The paper [86] analyzes the risk assessment for the movement of buses on the road sections, which are included as potential alternatives. The article [87] proposes a new method of urban rail accident risk analysis based on complex networks that studies the location and cause of risks separately and adds mechanical connection, signal connection and electrical connection among risk points on the basis of traditional causal factors. The ideas presented in [80,81,82,83,84,85,86,87] are in good agreement with the conclusions presented in this article.
7.5. Prospects for Further Research
Contemplating the possibilities of further development of this area of research, the author considers the possible transformation of the results presented in this article and in [51,52] into a unified theory of spatiotemporal dialectics of road safety processes. Of course, the most serious place in this theory should be taken by the results of future studies of the relationship between the complexity of traffic control systems (within the research area of Complexity) and the psycho-physiological reactions of road users and their choice of certain behavior programs. Ultimately, it is one of the areas of study of cognitive management of complex organizational and technical systems [88,89,90,91]. Conceptually, these studies go beyond the study of the impact of the principles and methods of traffic management on road traffic accidents. A possible symbiosis of the science of road safety based on the use of information-entropy analysis and cognitive methods for managing human behavior is potentially very promising.
8. Conclusions
The example given in Section 7.3 illustrates the meaning of the Orderliness of road safety systems and its main characteristic—Relative entropy Hn-3 RS.
Of course, the use of classic indicators—HR2021, RTA Significance, and RTA Severity—for road safety assessment continues to be relevant since they make it possible to quantify it. The proposed practical indicator of the Orderliness of urban road safety systems—Relative entropy Hn-3 RS—plays the role of a qualitative indicator (in relation to the assessment of systemic quality). Hn-3 RS allows us to quantify the RS quality. Analysis of the value of the coefficients Ki = KRA, KV and KD of the causal chain of accident formation allows us to detail the meaning of the conclusion about the accident rate level in the city and to understand the essence of the “Road Safety” concept in relation to a particular city.
The article gives a very indicative comparison of two urban traffic management systems—in Novosibirsk and Tyumen. The lower value of Hn-3 RS in Novosibirsk, compared to Tyumen, well illustrates the benefits of putting into practice the ideas of H. Monderman [65,66,67,68] and the concept of his authorship—the common space concept. Despite the fact that the common space concept is still actively criticized [64], one must clearly understand the reasons for this criticism. Thus, the analysis of criticisms by S. Moody and S. Melia [64] shows that the common space cannot be safe in the case of complex, multi-lane intersections with heavy traffic. This concept works perfectly for small towns with light traffic. With regard to the road network of large cities, it can be used only for the peripheral areas of the city or for the central areas of the city, but in areas with a serious restriction on the speed of traffic (30 km/h or 20 miles/h).
Another important conclusion drawn from the results of this study is that the constant complication of urban traffic management systems is futile. As shown by Russian statistics, this ultimately leads to an increased frequency of accidents, which is the opposite of the goal of improving the road safety situation. This is explained by the total decrease in the attentiveness and responsibility of road users when creating conditions for their conflict-free movement. The case of Tyumen, as a city with the highest Hn-3 RS value among all Russian cities, shows that managerial attempts to completely eliminate conflict among road users do not result in a decrease in road traffic accidents but change their structure (the probability of accidents increases while the severity of their consequences decreases).
This study should contribute to deepening knowledge about the essence of the phenomenon of “Road safety”, about the nature of causal relationships between the complexity of traffic management systems and the result of their use, as well as about the dialectics of changing human behavior in traffic situations when changing the principles of traffic regulation.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The author would like to thank Victor I. Kolesov for his friendly support and professional communication. The author would like to thank the anonymous referees for their very useful suggestions.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A

Table A1.
Information about the road traffic accident rate [61] and the Relative entropy Hn-3 RS of urban road safety systems in largest (Population = 1500…13000 thous. people) Russian cities (2021).
Table A1.
Information about the road traffic accident rate [61] and the Relative entropy Hn-3 RS of urban road safety systems in largest (Population = 1500…13000 thous. people) Russian cities (2021).
| NoNo | City | City Population, People | Road Traffic Accidents (RTA), Unit | RTA Victims, People | RTA Fatality Cases, Ptople | Human Risk HR, Deaths in RTA/ 100 Thous. People | RTA Severity, % | Hn-3 RS |
|---|---|---|---|---|---|---|---|---|
| 1 | Moscow | 13,010,112 | 8516 | 10,008 | 358 | 2.75 | 3.58 | 0.627 |
| 2 | St. Petersburg | 5,601,911 | 5006 | 5878 | 197 | 3.52 | 3.35 | 0.638 |
| 3 | Novosibirsk | 1,633,595 | 980 | 1175 | 83 | 5.08 | 7.06 | 0.596 |
| 4 | Ekaterinburg | 1,544,376 | 1164 | 1513 | 66 | 4.27 | 4.36 | 0.650 |

Table A2.
Information about the road traffic accident rate [61] and the Relative entropy Hn-3 RS of urban road safety systems in large (Population = 500…1000 thous. people) Russian cities (2021).
Table A2.
Information about the road traffic accident rate [61] and the Relative entropy Hn-3 RS of urban road safety systems in large (Population = 500…1000 thous. people) Russian cities (2021).
| NoNo | City | City Population, People | Road Traffic Accidents (RTA), Unit | RTA Victims, People | RTA Fatality Cases, Ptople | Human Risk HR, Deaths in RTA/ 100 Thous. People | RTA Severity, % | Hn-3 RS |
|---|---|---|---|---|---|---|---|---|
| 1 | Krasnodar | 948,827 | 939 | 1219 | 64 | 6.75 | 5.25 | 0.650 |
| 2 | Saratov | 830,155 | 1103 | 1503 | 40 | 4.82 | 2.66 | 0.695 |
| 3 | Tyumen | 816,800 | 1452 | 2027 | 51 | 6.24 | 2.52 | 0.709 |
| 4 | Togliatti | 693,072 | 633 | 802 | 22 | 3.17 | 2.74 | 0.666 |
| 5 | Izhevsk | 646,468 | 544 | 652 | 21 | 3.25 | 3.22 | 0.643 |
| 6 | Barnaul | 631,127 | 830 | 1066 | 31 | 4.91 | 2.91 | 0.677 |
| 7 | Ulyanovsk | 625,462 | 634 | 832 | 24 | 3.84 | 2.88 | 0.676 |
| 8 | Irkutsk | 617,315 | 861 | 1041 | 19 | 3.08 | 1.83 | 0.674 |
| 9 | Khabarovsk | 610,305 | 647 | 821 | 37 | 6.06 | 4.51 | 0.652 |
| 10 | Makhachkala | 604,266 | 333 | 476 | 33 | 5.46 | 6.93 | 0.641 |
| 11 | Yaroslavl | 601,403 | 598 | 744 | 18 | 2.99 | 2.42 | 0.667 |
| 12 | Vladivostok | 600,871 | 737 | 903 | 36 | 5.99 | 3.99 | 0.652 |
| 13 | Orenburg | 572,819 | 482 | 612 | 21 | 3.67 | 3.43 | 0.657 |
| 14 | Tomsk | 568,508 | 227 | 264 | 17 | 2.99 | 6.44 | 0.581 |
| 15 | Kemerovo | 552,546 | 568 | 770 | 18 | 3.26 | 2.34 | 0.690 |
| 16 | Novokuznetsk | 544,583 | 382 | 523 | 22 | 4.04 | 4.21 | 0.663 |
| 17 | Ryazan | 534,801 | 730 | 977 | 23 | 4.30 | 2.35 | 0.694 |
| 18 | Naberezhnye Chelny | 532,074 | 478 | 575 | 13 | 2.44 | 2.26 | 0.658 |
| 19 | Astrakhan | 524,371 | 702 | 899 | 24 | 4.58 | 2.67 | 0.679 |
| 20 | Kirov | 521,091 | 762 | 971 | 17 | 3.26 | 1.75 | 0.690 |
| 21 | Penza | 516,450 | 759 | 1032 | 24 | 4.65 | 2.33 | 0.700 |
| 22 | Sevastopol | 509,992 | There is no reliable data | |||||
| 23 | Balashikha | 507,307 | 139 | 161 | 4 | 0.79 | 2.48 | 0.617 |
| 24 | Lipetsk | 503,213 | 436 | 552 | 32 | 6.36 | 5.80 | 0.634 |

Table A3.
Information about the road traffic accident rate [61] and the Relative entropy Hn-3 RS of urban road safety systems in small (Population = 50…100 thous. people) Russian cities (2021).
Table A3.
Information about the road traffic accident rate [61] and the Relative entropy Hn-3 RS of urban road safety systems in small (Population = 50…100 thous. people) Russian cities (2021).
| NoNo | City | City Population, People | Road Traffic Accidents (RTA), Unit | RTA Victims, People | RTA Fatality Cases, Ptople | Human Risk HR, Deaths in RTA/ 100 Thous. People | RTA Severity, % | Hn-3 RS |
|---|---|---|---|---|---|---|---|---|
| 1 | Novokuibyshevsk | 99,469 | 38 | 48 | 6 | 6.03 | 12.50 | 0.555 |
| 2 | Tobolsk | 98,772 | 144 | 193 | 8 | 8.10 | 4.15 | 0.679 |
| 3 | Votkinsk | 96,861 | 52 | 64 | 2 | 2.06 | 3.13 | 0.641 |
| 4 | Sarov | 96,479 | 93 | 108 | 3 | 3.11 | 2.78 | 0.643 |
| 5 | Mezhdurechensk | 96,088 | 28 | 33 | 3 | 3.12 | 9.09 | 0.553 |
| 6 | Serov | 95,141 | 36 | 43 | 3 | 3.15 | 6.98 | 0.583 |
| 7 | Sarapul | 94,554 | 42 | 52 | 1 | 1.06 | 1.92 | 0.654 |
| 8 | Anapa | 94,340 | 344 | 444 | 19 | 20.14 | 4.28 | 0.695 |
| 9 | Leninsk-Kuznetsky | 93,288 | 80 | 104 | 8 | 8.58 | 7.69 | 0.625 |
| 10 | Ukhta | 92,479 | 156 | 224 | 10 | 10.81 | 4.46 | 0.698 |
| 11 | Glazov | 91,921 | 34 | 48 | 2 | 2.18 | 4.17 | 0.652 |
| 12 | Magadan | 91,797 | 126 | 173 | 12 | 13.07 | 6.94 | 0.661 |
| 13 | Michurinsk | 89,876 | 54 | 66 | 2 | 2.23 | 3.03 | 0.643 |
| 14 | Lobnya | 89,522 | 14 | 17 | 2 | 2.23 | 11.76 | 0.523 |
| 15 | Kansk | 88,362 | 42 | 53 | 6 | 6.79 | 11.32 | 0.570 |
| 16 | Kamensk-Shakhtinsky | 87,113 | 35 | 47 | 7 | 8.04 | 14.89 | 0.558 |
| 17 | Buzuluk | 86,042 | 71 | 90 | 1 | 1.16 | 1.11 | 0.685 |
| 18 | Kiselevsk | 85,339 | 72 | 104 | 6 | 7.03 | 5.77 | 0.667 |
| 19 | Ivanteevka | 82,779 | 20 | 22 | 3 | 3.62 | 13.64 | 0.490 |
| 20 | Novotroitsk | 82,463 | 36 | 44 | 1 | 1.21 | 2.27 | 0.645 |
| 21 | Zheleznogorsk | 81,619 | 59 | 75 | 3 | 3.68 | 4.00 | 0.647 |
| 22 | Kuznetsk | 79,800 | 86 | 112 | 8 | 10.03 | 7.14 | 0.637 |
| 23 | Ust-Ilimsk | 79,746 | 52 | 67 | 2 | 2.51 | 2.99 | 0.659 |
| 24 | Yalta | 78,171 | 174 | 236 | 13 | 16.63 | 5.51 | 0.684 |
| 25 | Ozersk | 78,128 | 37 | 41 | 6 | 7.68 | 14.63 | 0.505 |
| 26 | Gelendzhik | 75,504 | 155 | 220 | 17 | 22.52 | 7.73 | 0.678 |
| 27 | Chernogorsk | 75,348 | 43 | 57 | 6 | 7.96 | 10.53 | 0.596 |
| 28 | Usolye-Sibirskoe | 75,062 | 49 | 53 | 1 | 1.33 | 1.89 | 0.623 |
| 29 | Novoaltaysk | 74,586 | 78 | 98 | 2 | 2.68 | 2.04 | 0.675 |
| 30 | Shadrinsk | 74,400 | 69 | 93 | 2 | 2.69 | 2.15 | 0.689 |
| 31 | Verkhnyaya Pyshma | 74,262 | 55 | 77 | 6 | 8.08 | 7.79 | 0.639 |
| 32 | Troitsk | 72,723 | 47 | 62 | 4 | 5.50 | 6.45 | 0.630 |
| 33 | Chapaevsk | 70,944 | 30 | 36 | 1 | 1.41 | 2.78 | 0.633 |
| 34 | Belovo | 70,611 | 78 | 123 | 12 | 16.99 | 9.76 | 0.666 |
| 35 | Birobidzhan | 70,433 | 63 | 70 | 1 | 1.42 | 1.43 | 0.645 |
| 36 | Feodosia | 67,750 | 100 | 134 | 14 | 20.66 | 10.45 | 0.632 |
| 37 | Minusinsk | 67,234 | 60 | 74 | 4 | 5.95 | 5.41 | 0.631 |
| 38 | Sosnovy Bor | 67,054 | 53 | 63 | 2 | 2.98 | 3.17 | 0.640 |
| 39 | Anzhero-Sudzhensk | 66,933 | 56 | 72 | 2 | 2.99 | 2.78 | 0.667 |
| 40 | Buynaksk | 66,422 | 12 | 18 | 1 | 1.51 | 5.56 | 0.631 |
| 41 | Zarechny | 65,493 | 23 | 29 | 2 | 3.05 | 6.90 | 0.596 |
| 42 | Gorno-Altaysk | 64,504 | 59 | 67 | 3 | 4.65 | 4.48 | 0.616 |
| 43 | Gukovo | 62,658 | 10 | 11 | 1 | 1.60 | 9.09 | 0.515 |
| 44 | Asbest | 62,285 | 21 | 31 | 4 | 6.42 | 12.90 | 0.588 |
| 45 | Zelenogorsk | 61,821 | 23 | 29 | 4 | 6.47 | 13.79 | 0.545 |
| 46 | Donskoy | 61,477 | 28 | 38 | 2 | 3.25 | 5.26 | 0.638 |
| 47 | Izberbash | 61,296 | 16 | 19 | 1 | 1.63 | 5.26 | 0.588 |
| 48 | Revda | 60,761 | 40 | 54 | 4 | 6.58 | 7.41 | 0.629 |
| 49 | Berezovsky | 60,334 | 62 | 98 | 4 | 6.63 | 4.08 | 0.707 |
| 50 | Sibai | 60,017 | 38 | 42 | 6 | 10.00 | 14.29 | 0.515 |
| 51 | Polevskoy | 60,012 | 41 | 55 | 4 | 6.67 | 7.27 | 0.630 |
| 52 | Lytkarino | 59,937 | 16 | 21 | 4 | 6.67 | 19.05 | 0.513 |
| 53 | Kumertau | 59,129 | 26 | 44 | 6 | 10.15 | 13.64 | 0.622 |
| 54 | Fryazino | 58,938 | 21 | 24 | 3 | 5.09 | 12.50 | 0.522 |
| 55 | Prokhladny | 58,747 | 22 | 30 | 4 | 6.81 | 13.33 | 0.570 |
| 56 | Nyagan | 58,733 | 46 | 58 | 3 | 5.11 | 5.17 | 0.636 |
| 57 | Krasnoturinsk | 55,910 | 29 | 36 | 3 | 5.37 | 8.33 | 0.591 |
| 58 | Severomorsk | 54,473 | 33 | 43 | 2 | 3.67 | 4.65 | 0.642 |
| 59 | Volzhsk | 52,703 | 36 | 40 | 1 | 1.90 | 2.50 | 0.624 |
| 60 | Vorkuta | 52,292 | 33 | 41 | 3 | 5.74 | 7.32 | 0.606 |
| 61 | Goose-Crystal | 51,998 | 32 | 42 | 1 | 1.92 | 2.38 | 0.670 |
| 62 | Snezhinsk | 51,921 | 26 | 30 | 3 | 5.78 | 10.00 | 0.555 |
| 63 | Arsenyev | 52,723 | 31 | 34 | 1 | 1.90 | 2.94 | 0.611 |
| 64 | Salekhard | 51,186 | 26 | 30 | 1 | 1.95 | 3.33 | 0.619 |
| 65 | Kotelniki | 50,723 | 27 | 32 | 1 | 1.97 | 3.13 | 0.630 |

Table A4.
The data on the values of entropy HRS and relative entropy Hn RS of road safety provision systems in the Russian cities (2021) and their corresponding values of information transformation coefficients Ki.
Table A4.
The data on the values of entropy HRS and relative entropy Hn RS of road safety provision systems in the Russian cities (2021) and their corresponding values of information transformation coefficients Ki.
| NoNo | Cities | Values (2021) | ||||
|---|---|---|---|---|---|---|
| HRS | Hn RS | K1 = KRA | K2 = KV | K3 = KD | ||
| Largest cities (1500 thous. people < Population < 13,000 thous. people) | ||||||
| 1 | Moscow | 0.689 | 0.627 | 0.00065 | 1.1752 | 0.0358 |
| 2 | St. Petersburg | 0.700 | 0.638 | 0.00089 | 1.1742 | 0.0335 |
| 3 | Novosibirsk | 0.655 | 0.596 | 0.00060 | 1.1990 | 0.0706 |
| 4 | Ekaterinburg | 0.715 | 0.650 | 0.00075 | 1.2998 | 0.0436 |
| Large cities (500 thous. people < Population < 1000 thous. people) | ||||||
| 1 | Krasnodar | 0.714 | 0.650 | 0.00099 | 1.2982 | 0.0525 |
| 2 | Saratov | 0.763 | 0.695 | 0.00133 | 1.3626 | 0.0266 |
| 3 | Tyumen | 0.779 | 0.709 | 0.00178 | 1.3960 | 0.0252 |
| 4 | Togliatti | 0.732 | 0.666 | 0.00091 | 1.2670 | 0.0274 |
| 5 | Izhevsk | 0.707 | 0.643 | 0.00084 | 1.1985 | 0.0322 |
| 6 | Barnaul | 0.744 | 0.677 | 0.00132 | 1.2843 | 0.0291 |
| 7 | Ulyanovsk | 0.743 | 0.676 | 0.00101 | 1.3123 | 0.0288 |
| 8 | Irkutsk | 0.740 | 0.674 | 0.00139 | 1.2091 | 0.0183 |
| 9 | Khabarovsk | 0.717 | 0.652 | 0.00106 | 1.2689 | 0.0451 |
| 10 | Makhachkala | 0.704 | 0.641 | 0.00055 | 1.4294 | 0.0693 |
| 11 | Yaroslavl | 0.733 | 0.667 | 0.00099 | 1.2441 | 0.0242 |
| 12 | Vladivostok | 0.716 | 0.652 | 0.00123 | 1.2252 | 0.0399 |
| 13 | Orenburg | 0.722 | 0.657 | 0.00084 | 1.2697 | 0.0343 |
| 14 | Tomsk | 0.639 | 0.581 | 0.00040 | 1.1630 | 0.0644 |
| 15 | Kemerovo | 0.758 | 0.690 | 0.00103 | 1.3556 | 0.0234 |
| 16 | Novokuznetsk | 0.728 | 0.663 | 0.00070 | 1.3691 | 0.0421 |
| 17 | Ryazan | 0.762 | 0.694 | 0.00136 | 1.3384 | 0.0235 |
| 18 | Naberezhnye Chelny | 0.722 | 0.658 | 0.00090 | 1.2029 | 0.0226 |
| 19 | Astrakhan | 0.746 | 0.679 | 0.00134 | 1.2806 | 0.0267 |
| 20 | Kirov | 0.758 | 0.690 | 0.00146 | 1.2743 | 0.0175 |
| 21 | Penza | 0.769 | 0.700 | 0.00147 | 1.3597 | 0.0233 |
| 22 | Sevastopol | 0.678 | 0.617 | 0.00027 | 1.1583 | 0.0248 |
| 23 | Balashikha | 0.697 | 0.634 | 0.00087 | 1.2661 | 0.0580 |
| Small cities (50 thous. people < Population < 100 thous. people) | ||||||
| 1 | Novokuibyshevsk | 0.610 | 0.555 | 0.00038 | 1.2632 | 0.1250 |
| 2 | Tobolsk | 0.746 | 0.679 | 0.00146 | 1.3403 | 0.0415 |
| 3 | Votkinsk | 0.704 | 0.641 | 0.00054 | 1.2308 | 0.0313 |
| 4 | Sarov | 0.706 | 0.643 | 0.00096 | 1.1613 | 0.0278 |
| 5 | Mezhdurechensk | 0.607 | 0.553 | 0.00029 | 1.1786 | 0.0909 |
| 6 | Serov | 0.640 | 0.583 | 0.00038 | 1.1944 | 0.0698 |
| 7 | Sarapul | 0.719 | 0.654 | 0.00044 | 1.2381 | 0.0192 |
| 8 | Anapa | 0.763 | 0.695 | 0.00365 | 1.2907 | 0.0428 |
| 9 | Leninsk-Kuznetsky | 0.687 | 0.625 | 0.00086 | 1.3000 | 0.0769 |
| 10 | Ukhta | 0.767 | 0.698 | 0.00169 | 1.4359 | 0.0446 |
| 11 | Glazov | 0.717 | 0.652 | 0.00037 | 1.4118 | 0.0417 |
| 12 | Magadan | 0.726 | 0.661 | 0.00137 | 1.3730 | 0.0694 |
| 13 | Michurinsk | 0.706 | 0.643 | 0.00060 | 1.2222 | 0.0303 |
| 14 | Lobnya | 0.575 | 0.523 | 0.00016 | 1.2143 | 0.1176 |
| 15 | Kansk | 0.627 | 0.570 | 0.00048 | 1.2619 | 0.1132 |
| 16 | Kamensk-Shakhtinsky | 0.613 | 0.558 | 0.00040 | 1.3429 | 0.1489 |
| 17 | Buzuluk | 0.753 | 0.685 | 0.00083 | 1.2676 | 0.0111 |
| 18 | Kiselevsk | 0.732 | 0.667 | 0.00084 | 1.4444 | 0.0577 |
| 19 | Ivanteevka | 0.538 | 0.490 | 0.00024 | 1.1000 | 0.1364 |
| 20 | Novotroitsk | 0.709 | 0.645 | 0.00044 | 1.2222 | 0.0227 |
| 21 | Zheleznogorsk | 0.711 | 0.647 | 0.00072 | 1.2712 | 0.0400 |
| 22 | Kuznetsk | 0.700 | 0.637 | 0.00108 | 1.3023 | 0.0714 |
| 23 | Ust-Ilimsk | 0.724 | 0.659 | 0.00065 | 1.2885 | 0.0299 |
| 24 | Yalta | 0.752 | 0.684 | 0.00223 | 1.3563 | 0.0551 |
| 25 | Ozersk | 0.555 | 0.505 | 0.00047 | 1.1081 | 0.1463 |
| 26 | Gelendzhik | 0.744 | 0.678 | 0.00205 | 1.4194 | 0.0773 |
| 27 | Chernogorsk | 0.654 | 0.596 | 0.00057 | 1.3256 | 0.1053 |
| 28 | Usolye-Sibirskoe | 0.685 | 0.623 | 0.00065 | 1.0816 | 0.0189 |
| 29 | Novoaltaysk | 0.742 | 0.675 | 0.00105 | 1.2564 | 0.0204 |
| 30 | Shadrinsk | 0.756 | 0.689 | 0.00093 | 1.3478 | 0.0215 |
| 31 | Verkhnyaya Pyshma | 0.702 | 0.639 | 0.00074 | 1.4000 | 0.0779 |
| 32 | Troitsk | 0.693 | 0.630 | 0.00065 | 1.3191 | 0.0645 |
| 33 | Chapaevsk | 0.695 | 0.633 | 0.00042 | 1.2000 | 0.0278 |
| 34 | Belovo | 0.732 | 0.666 | 0.00110 | 1.5769 | 0.0976 |
| 35 | Birobidzhan | 0.709 | 0.645 | 0.00089 | 1.1111 | 0.0143 |
| 36 | Feodosia | 0.694 | 0.632 | 0.00148 | 1.3400 | 0.1045 |
| 37 | Minusinsk | 0.693 | 0.631 | 0.00089 | 1.2333 | 0.0541 |
| 38 | Sosnovy Bor | 0.703 | 0.640 | 0.00079 | 1.1887 | 0.0317 |
| 39 | Anzhero-Sudzhensk | 0.733 | 0.667 | 0.00084 | 1.2857 | 0.0278 |
| 40 | Buynaksk | 0.693 | 0.631 | 0.00018 | 1.5000 | 0.0556 |
| 41 | Zarechny | 0.655 | 0.596 | 0.00035 | 1.2609 | 0.0690 |
| 42 | Gorno-Altaysk | 0.676 | 0.616 | 0.00091 | 1.1356 | 0.0448 |
| 43 | Gukovo | 0.565 | 0.515 | 0.00016 | 1.1000 | 0.0909 |
| 44 | Asbest | 0.646 | 0.588 | 0.00034 | 1.4762 | 0.1290 |
| 45 | Zelenogorsk | 0.599 | 0.545 | 0.00037 | 1.2609 | 0.1379 |
| 46 | Donskoy | 0.701 | 0.638 | 0.00046 | 1.3571 | 0.0526 |
| 47 | Izberbash | 0.646 | 0.588 | 0.00026 | 1.1875 | 0.0526 |
| 48 | Revda | 0.691 | 0.629 | 0.00066 | 1.3500 | 0.0741 |
| 49 | Berezovsky | 0.776 | 0.707 | 0.00103 | 1.5806 | 0.0408 |
| 50 | Sibai | 0.566 | 0.515 | 0.00063 | 1.1053 | 0.1429 |
| 51 | Polevskoy | 0.692 | 0.630 | 0.00068 | 1.3415 | 0.0727 |
| 52 | Lytkarino | 0.563 | 0.513 | 0.00027 | 1.3125 | 0.1905 |
| 53 | Kumertau | 0.684 | 0.622 | 0.00044 | 1.6923 | 0.1364 |
| 54 | Fryazino | 0.574 | 0.522 | 0.00036 | 1.1429 | 0.1250 |
| 55 | Prokhladny | 0.626 | 0.570 | 0.00037 | 1.3636 | 0.1333 |
| 56 | Nyagan | 0.698 | 0.636 | 0.00078 | 1.2609 | 0.0517 |
| 57 | Krasnoturinsk | 0.650 | 0.591 | 0.00052 | 1.2414 | 0.0833 |
| 58 | Severomorsk | 0.705 | 0.642 | 0.00061 | 1.3030 | 0.0465 |
| 59 | Volzhsk | 0.686 | 0.624 | 0.00068 | 1.1111 | 0.0250 |
| 60 | Vorkuta | 0.666 | 0.606 | 0.00063 | 1.2424 | 0.0732 |
| 61 | Goose-Crystal | 0.736 | 0.670 | 0.00062 | 1.3125 | 0.0238 |
| 62 | Snezhinsk | 0.609 | 0.555 | 0.00050 | 1.1538 | 0.1000 |
| 63 | Arsenyev | 0.671 | 0.611 | 0.00059 | 1.0968 | 0.0294 |
| 64 | Salekhard | 0.680 | 0.619 | 0.00051 | 1.1538 | 0.0333 |
| 65 | Kotelniki | 0.692 | 0.630 | 0.00053 | 1.1852 | 0.0313 |
References
- Blincoe, L.J.; Miller, T.R.; Zaloshnja, E.; Lawrence, B.A. The Economic and Societal Impact of Motor Vehicle Crashes, 2010 (Revised); Report No. DOT HS 812 013; National Highway Traffic Safety Administration: Washington, DC, USA, 2015. Available online: https://crashstats.nhtsa.dot.gov/Api/Public/ViewPublication/812013 (accessed on 8 February 2023).
- Blincoe, L.; Miller, T.; Wang, J.-S.; Swedler, D.; Coughlin, T.; Lawrence, B.; Guo, F.; Klauer, S.; Dingus, T. The Economic and Societal Impact of Motor Vehicle Crashes, 2019 (Revised); Report No. DOT HS 813 403; National Highway Traffic Safety Administration: Washington, DC, USA, 2023; Available online: https://www.researchgate.net/publication/367460305_The_Economic_and_Societal_Impact_of_Motor_Vehicle_Crashes_2019_Revised/link/63eea3fb2958d64a5cd5f9d0/download (accessed on 8 February 2023).
- IRTAD Road Safety Annual Report 2022; OECD Publishing: Paris, France, 2022. Available online: https://www.itf-oecd.org/sites/default/files/docs/irtad-road-safety-annual-report-2022.pdf (accessed on 8 February 2023).
- Petrov, A.I.; Kolesov, V.I. Road traffic accident rate in Russia: Main socio-economic factors of its formation and spatio-temporal features. Econ. Soc. Chang. Facts Trends Forecast. 2021, 14, 199–220. [Google Scholar] [CrossRef]
- Smeed, R.J. Some Statistical Aspects of Road Safety Research. J. R. Stat. Soc. Ser. A 1949, 112, 1–34. [Google Scholar] [CrossRef]
- Global Status Report on Road Safety 2018. World Health Organization, Geneva, 2018. Available online: https://www.who.int/publications/i/item/9789241565684 (accessed on 11 February 2023).
- Doyle, P. Marketing Management and Strategy; Prentice Hall Europe: London, UK; New York, NY, USA, 1998; p. 465. [Google Scholar]
- Provost, F.; Fawcett, T. Data Science for Business; O’Reilly Media, Inc.: Beijing, China; Cambridge, UK; Tokyo, Japan, 2013; p. 409. Available online: https://www.booksfree.org/wp-content/uploads/2022/06/Data-Science-for-Business-by-Foster-Provost-and-Tom-Fawcett-pdf-free-download-booksfree.org_.pdf (accessed on 13 February 2023).
- Derriks, H.M.; Mak, P.M. Underreporting of Road Traffic Casualties: IRTAD Special Report. 2007, p. 39. Available online: https://www.itf-oecd.org/sites/default/files/docs/repndl2007.pdf (accessed on 15 February 2023).
- Pyankova, A.I.; Fattakhov, T.A.; Kozlov, V.A. The association between beverage-specific alcohol consumption and mortality among road users in Russia, 1965–2019. Accid. Anal. Prev. 2022, 178, 106859. [Google Scholar] [CrossRef] [PubMed]
- Fattahov, T.A.; Piankova, A.I. The Years of Life Lost as a Result of Road Traffic Accidents in Russia in 2000–2012. Probl. Sotsialnoi Gig Zdravookhranenniia Istor. Med. 2018, 26, 271–275. [Google Scholar] [CrossRef]
- Elvik, R. Which is the more important for road safety—Road design or driver behavioural adaptation? Traffic Saf. Res. 2022, 2, 000009. [Google Scholar] [CrossRef]
- Halkos, G.; Kitsos, C. Uncertainty in environmental economics: The problem of entropy and model choice. Econ. Anal. Policy 2018, 60, 127–140. [Google Scholar] [CrossRef]
- Webster, M.; Sell, J. Why Do Experiments? In Laboratory Experiments in the Social Sciences; Academic Press: Cambridge, MA, USA, 2014; Chapter 1; pp. 5–21. [Google Scholar] [CrossRef]
- Serra, D. The Experimental method in economics: Old issues and new challenges. Rev. Philos. Économique 2012, 1, 3–19. [Google Scholar] [CrossRef]
- Georgescu-Roegen, N. The Entropy Law and the Economic Process; Harvard University Press: Cambridge, MA, USA, 1971; p. 457. [Google Scholar] [CrossRef]
- Georgescu-Roegen, N. The Entropy Law and the Economic Process in Retrospect. East. Econ. J. 1986, 12, 3–25. [Google Scholar]
- Islamutdinov, V.F.; Kurikov, V.M. On the application of the entropy approach in economic research. Sib. Financ. Sch. 2022, 2, 168–178. (In Russian) [Google Scholar] [CrossRef]
- Avery, J.S. CADMUS. A papers series of the South-East European Division of the World Academy of Art and Science (SEED-WAAS). Entropy Econ. 2012, 1, 166–179. [Google Scholar]
- Halkos, G.; Kitsos, C. Relative risk and innovation activities: The case of Greece. Innov. Manag. Policy Pract. 2012, 14, 156–159. [Google Scholar] [CrossRef]
- Devine, S. An Economy Viewed as a Far–from–Equilibrium System from the Perspective of Algorithmic Information Theory. Entropy 2018, 20, 228. [Google Scholar] [CrossRef] [PubMed]
- Bailey, K.D. Social Entropy Theory; SUNY Press: Albany, NY, USA, 1990; Available online: https://books.google.ru/books?hl=ru&lr=&id=gSX-tdH0Z0kC&oi=fnd&pg=PR13&ots=xzeA4KCxe8&sig=DCEhhYxoprF8eOHiViiW0AdHsSw&redir_esc=y#v=onepage&q&f=false (accessed on 27 February 2023).
- Mayer, A.L.; Donovan, R.P.; Pawlowski, C.W. Information and entropy theory for the sustainability of coupled human and natural systems. Ecol. Soc. 2014, 19, 11. [Google Scholar] [CrossRef]
- Tolstykh, T.; Shmeleva, N.; Vertakova, Y.; Plotnikov, V. The Entropy Model for Sustainability Assessment in Industrial Ecosystems. Inventions 2020, 5, 54. [Google Scholar] [CrossRef]
- Saslow, W.M. An economic analogy to thermodynamics. Am. J. Phys. 1999, 67, 1239–1247. [Google Scholar] [CrossRef]
- Vozna, L.Y. The Notion of Entropy in Economic Analysis: The Classical Examples and New Perspectives. J. Heterodox Econ. 2016, 3, 1–16. [Google Scholar] [CrossRef]
- Antoniou, I.; Ivanov, V.V.; Kryanev, A.V.; Matokhin, V.V.; Shapovalov, M.V. On the efficient resources distribution in economics based on entropy. Phys. A Stat. Mech. Its Appl. 2004, 336, 549–562. [Google Scholar] [CrossRef]
- Zheng, F.; Song, Q. Entropy Maximization Based Capability Allocation of Clothing Production Enterprises in Sharing Economy. IFAC-PapersOnLine 2019, 52, 211–216. [Google Scholar] [CrossRef]
- Prigogine, I. The rediscovery of value and the opening of economics. Chapter 2. In The Evolutionary Foundation of Economics; Cambridge University Press: Cambridge, UK, 2005; pp. 61–69. [Google Scholar]
- Ho, M.W. What is (Schrödinger’s) Negentropy? Mod. Trends Bio Kinet. 1994, 3, 50–61. Available online: https://www.researchgate.net/publication/255612623_What_is_Schrodinger's_Negentropy (accessed on 2 March 2023).
- Jaynes, E.T. How Should We Use Entropy in Economics? (Some Half-Baked Ideas in Need of Criticism); St. John’s College: Cambridge, UK, 1991. Available online: https://bayes.wustl.edu/etj/articles/entropy.in.economics.pdf (accessed on 2 March 2023).
- Raine, A.; Foster, J.; Potts, J. The New Entropy Law and the Economic Process. Ecol. Complex. 2006, 3, 354–360. Available online: https://www.researchgate.net/publication/223632694_The_new_entropy_law_and_the_economic_process (accessed on 2 March 2023). [CrossRef]
- Chen, J. An Entropy Theory of Value. SSRN Electron. J. 2002, 1–22. [Google Scholar] [CrossRef]
- Yang, J. Information theoretic approaches in economics. J. Econ. Surv. 2018, 32, 940–960. [Google Scholar] [CrossRef]
- Rodríguez, R.A.; Cáceres-Hernández, J.J. Information, entropy, value, and price formation: An econophysical perspective. Phys. A: Stat. Mech. Its Appl. 2018, 512, 74–85. [Google Scholar] [CrossRef]
- Anttila, J.; Annila, A. Natural Game. Phys. Lett. A 2011, 375, 3755–3761. Available online: https://arxiv.org/abs/1103.1656v1 (accessed on 3 March 2023). [CrossRef]
- Caticha, A.; Golan, A. An entropic framework for modeling economies. Phys. A Stat. Mech. Its Appl. 2014, 408, 149–163. [Google Scholar] [CrossRef]
- Cabrales, A.; Gossner, O.; Serrano, R. Entropy and the value of information for investors. Am. Econ. Rev. 2013, 103, 360–377. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, H.; Wang, Z.; Zhang, J. Test the principle of maximum entropy in constant sum 2 × 2 game: Evidence in experimental economics. Phys. Lett. A 2012, 376, 1318–1322. [Google Scholar] [CrossRef]
- Smith, J. Maximum Entropy and Information Theory Approaches to Economics; The Boeing Company: Arlington, VA, USA, 2018; p. 22. Available online: https://doi.org/10.2139/ssrn.3094757 (accessed on 5 March 2023).
- Foley, D.K. Information Theory and Behavior; Department of Economics, The New School for Social Research: New York, NY, USA, 2017; p. 21. Available online: https://www.researchgate.net/publication/322024633_Information_theory_and_behavior (accessed on 6 March 2023). [CrossRef]
- Scharfenaker, E.; Foley, D.K. A Maximum Entropy Solution to Quantal Response Equilibria in Economic Models. 2016, p. 27. Available online: https://www.researchgate.net/publication/312153408_A_Maximum_Entropy_Solution_to_Quantal_Response_Equilibria_in_Economic_Models (accessed on 6 March 2023). [CrossRef]
- Judge, G. Entropy maximization as a basis for information recovery in dynamic economic behavioral systems. Econometrics 2015, 3, 91–100. [Google Scholar] [CrossRef]
- Judge, G. Micro-Macro Connected Stochastic Dynamic Economic Behavior Systems. Econometrics 2018, 6, 46. [Google Scholar] [CrossRef]
- Duan, Y.; Mu, H.; Li, N.; Li, L.; Xue, Z. Research on comprehensive evaluation of low carbon economy development level based on AHP-Entropy method: A case study of Dalian. Energy Procedia 2016, 104, 468–474. [Google Scholar] [CrossRef]
- Jakimowicz, A. The Role of Entropy in the Development of Economics. Entropy 2020, 22, 452. [Google Scholar] [CrossRef]
- Mazumder, S.K.; Das, N.C. Maximum Entropy and Utility in a Transportation System. Yugosl. J. Oper. Res. 1999, 9, 27–34. Available online: http://elib.mi.sanu.ac.rs/files/journals/yjor/17/yujorn17p27-34.pdf (accessed on 9 March 2023).
- Zhou, H.; Bouyekhf, R.; Moudni, A.E.L. Concept of Transportation Entropy and Its Application in Traffic Signal Control. IFAC Proc. Vol. 2013, 46, 37–42. [Google Scholar] [CrossRef]
- Yu, S.; Liu, Y.; Liang, X. Evolution of Regional Transport Structure Information Entropy and Its Dynamic Analysis. J. Transp. Syst. Eng. Inf. Technol. 2011, 11, 91–96. [Google Scholar] [CrossRef]
- Bazaluk, O.; Kotenko, S.; Nitsenko, V. Entropy as an Objective Function of Optimization Multimodal Transportations. Entropy 2021, 23, 946. [Google Scholar] [CrossRef] [PubMed]
- Petrov, A.I. Entropy Method of Road Safety Management: Case Study of the Russian Federation. Entropy 2022, 24, 177. [Google Scholar] [CrossRef]
- Petrov, A.I. Information and Entropy Aspects of the Specifics of Regional Road Traffic Accident Rate in Russia. Information 2023, 14, 138. [Google Scholar] [CrossRef]
- Bernton, E.; Ghosal, P.; Nutz, M. Entropic Optimal Transport: Geometry and Large Deviations. Duke Math. J. 2022, 171, 3363–3400. Available online: https://arxiv.org/pdf/2102.04397.pdf (accessed on 11 March 2023). [CrossRef]
- Nutz, M. Introduction to Entropic Optimal Transport. 2022. Available online: https://www.math.columbia.edu/~mnutz/docs/EOT_lecture_notes.pdf (accessed on 12 March 2023).
- Liero, M.; Mielke, A.; Savare, G. Optimal Entropy-Transport Problems and a New Hellinger-Kantorovich Distance between Positive Measures. 2016. Available online: https://arxiv.org/pdf/1508.07941.pdf (accessed on 13 March 2023).
- Bogdanov, A.A. Tectology. Universal Organizational Science; Academic Project: Moscow, Russia, 2020; p. 712. Available online: https://royallib.com/book/bogdanov_aleksandr/tektologiya_vseobshchaya_organizatsionnaya_nauka.html?ysclid=lf5k6g3cj6149182741 (accessed on 15 March 2023). (In Russian)
- Haken, H. Synergetics: An Introduction: Nonequilibrium Phase Transitions and Self-Organization in Physics, Chemistry, and Biology; Springer: Berlin, Germany; New York, NY, USA, 1978; p. 355. [Google Scholar]
- Shannon, C.E. Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication Theory of Secrecy Systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Kolesov, V.; Petrov, A. Cybernetic Modeling in Tasks of Traffic Safety Management. Transp. Res. Procedia 2017, 20, 305–310. [Google Scholar] [CrossRef]
- Official Website of the Federal State Statistics Service of the Russian Federation. Available online: https://rosstat.gov.ru/vpn_popul (accessed on 16 March 2023).
- The Official Website of the State Traffic Inspectorate of the Russian Federation. Indicators of the State of Road Safety. Available online: http://stat.gibdd.ru/ (accessed on 1 March 2023).
- Traffic Regulations 2023. Official Text with Illustrations; Piter: Moscow, Russia, 2023; p. 96. [Google Scholar]
- Moody, S.; Melia, S. Shared space—Research, policy and problems. Proc. Inst. Civ. Eng. Transp. 2014, 167, 384–392 . [Google Scholar] [CrossRef]
- Monderman, H. An exploration of a more fundamental view on traffic structure. In Proceedings of the Third International Conference on Safety and Environment in the 21st Century: Lessons from the Past, Shaping the Future, Tel Aviv, Israel, 7–10 November 1994; pp. 390–396. [Google Scholar]
- Monderman, H.; Clarke, E.; Baillie, B.H. Shared space—The alternative approach to calming traffic. Traffic Eng. Control. 2006, 47, 290–292. [Google Scholar]
- Methorst, R.; Gerlach, J.; Boenke, D.; Leven, J. Shared Space: Safe or Dangerous? A Contribution to Objectification of a Popular Design Philosophy. 2007. Available online: https://wwbpa.org/wp-content/uploads/2010/12/SharedSpace-Safe-or-Dangerous-Walk21.pdf (accessed on 19 March 2023).
- Monderman, H.; Clarke, E. What’s next for shared space? We look at the UK experience. Traffic Eng. Control. 2008, 49, 205–207. [Google Scholar]
- Li, Y.; Cheng, H.; Zeng, Z.; Liu, H.; Sester, M. Autonomous Vehicles Drive into Shared Spaces: eHMI Design Concept Focusing on Vulnerable Road Users. Available online: https://arxiv.org/pdf/2104.06916v1.pdf (accessed on 20 March 2023).
- Bucchi, A.; Sangiorgi, C.; Vignali, V. Traffic Psychology and Driver Behavior. Procedia Soc. Behav. Sci. 2012, 53, 973–980. [Google Scholar] [CrossRef]
- Zhang, X.; Chang, R.; Sui, X.; Li, Y. Influences of Emotion on Driving Decisions at Different Risk Levels: An Eye Movement Study. Front. Psychol. 2022, 13, 788712. [Google Scholar] [CrossRef]
- Russian Demographic Data Sheet. 2019. Available online: http://populationrussia.ru/data/RussianDemographicDataSheet2019_web.pdf (accessed on 21 March 2023).
- Wilde, G.J.S. The Theory of Risk Homeostasis: Implications for Safety and Health. Risk Anal. 1982, 2, 209–225. [Google Scholar] [CrossRef]
- Wilde, G.J.S.; Target Risk 3. Risk Homeostasis in Everyday Life (Electronic Copy). 2014, p. 235. Available online: https://safetyrisk.net/wp-content/uploads/2016/09/Target-Risk-3-Free-Download.pdf (accessed on 21 March 2023).
- ODM 218.6.015-2015 Recommendations on Accounting and Analysis of Road Accidents on the Highways of the Russian Federation. Available online: https://docs.cntd.ru/document/1200120721?ysclid=lek8tio876301734531 (accessed on 22 March 2023).
- Bagnenko, S.F.; Miroshnichenko, A.G.; Alimov, R.R.; Shlyafer, S.I. Assessment of emergency medical care delivered in different conditions in the Russian Federation. Anesteziol. Reanimatol. 2021, 2, 124–130. [Google Scholar] [CrossRef]
- Russian Healthcare System Overview. Available online: file:///C:/Users/Artur/Downloads/f68e677a2e9b501660f093c5c11b62a3.pdf (accessed on 29 March 2023).
- Blinkin, M.Y.; Reshetova, E.M. Road Safety: The History of the Issue, International Experience, Basic Institutions; Publishing House of the Higher School of Economics: Moscow, Russia, 2013; 240p. (In Russian) [Google Scholar]
- Hegel, G.W.F. Lectures on the Philosophy of World History; Oxford University Press: Oxford, UK, 1975; p. 252. [Google Scholar]
- Tingting, G.; Wuhong, W.; Zhongyi, X. Intrinsic Safety Evaluation for Urban Road Traffic Based on Information Entropy and Triangular Fuzzy Number. MATEC Web Conf. 2016, 81, 681020. [Google Scholar] [CrossRef]
- Rui, Z.; Zhenhong, Y. Research on fuzzy comprehensive evaluation system of tailings based on entropy technology. J. Sci. Technol. 2011, 7, 107–111. [Google Scholar]
- Wei, Z.; Xiaojing, L. A comprehensive evaluation method based on information entropy. Sci. Technol. Eng. 2010, 10, 5839–5843. [Google Scholar]
- Qin, C.; Chen, X.; Yang, Y.; Gui, W. Research on safety Three-level evaluation of tailings reservoir based on FAHP-IE method. Control. Eng. China 2014, 21, 995–1000. [Google Scholar]
- Liu, H.H.; Wang, N.; Xie, J.C.; Jiang, R.G. Fuzzy assessment of city ecosystem health based on entropy weight method. Eng. J. Wuhan Univ. 2014, 47, 755–759. [Google Scholar]
- Damjanović, M.; Stević, Ž.; Stanimirović, D.; Tanackov, I.; Marinković, D. Impact of the number of vehicles on traffic safety: Multiphase modeling. Facta Univ. Ser. Mech. Eng. 2022, 20, 177–197. [Google Scholar] [CrossRef]
- Stević, Ž.; Subotić, M.; Softić, E.; Božić, B. Multi-Criteria Decision-Making Model for Evaluating Safety of Road Sections. J. Intell. Manag. Decis. 2022, 1, 78–87. [Google Scholar] [CrossRef]
- Li, M.; Zhou, X.Y.; Liu, J.X.; Ma, W.K.; Li, X.W. Topological Modeling and Analysis of Urban Rail Transit Safety Risk Relationship. J. Intell. Manag. Decis. 2022, 1, 108–117. [Google Scholar] [CrossRef]
- Tsvetkov, V.Y. Complexity Index. Eur. J. Technol. Des. 2013, 1, 64–69. [Google Scholar]
- Tsvetkov, V.Y. Information Constructions. Eur. J. Technol. Des. 2014, 5, 147–152. [Google Scholar]
- Tsvetkov, V.Y. Cognitive information models. Life Sci. J. 2014, 11, 468–471. [Google Scholar]
- Hung, S.Y. Expert versus novice use of the executive support systems: An empirical study. Inf. Manag. 2003, 40, 177–189. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).