Quadrilateral Mesh Generation Method Based on Convolutional Neural Network
Abstract
1. Introduction
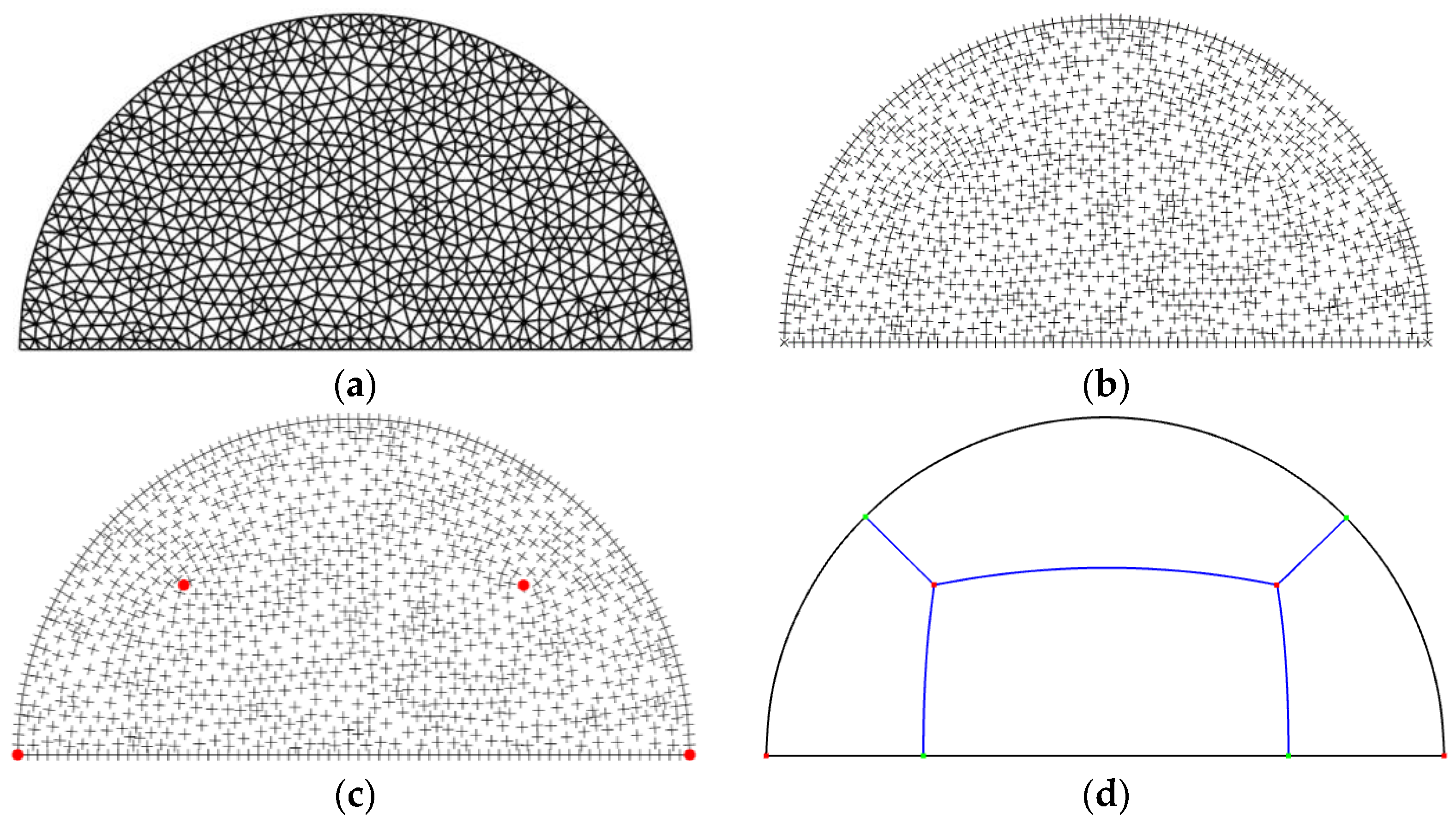
2. Model Data for Domain Decomposition
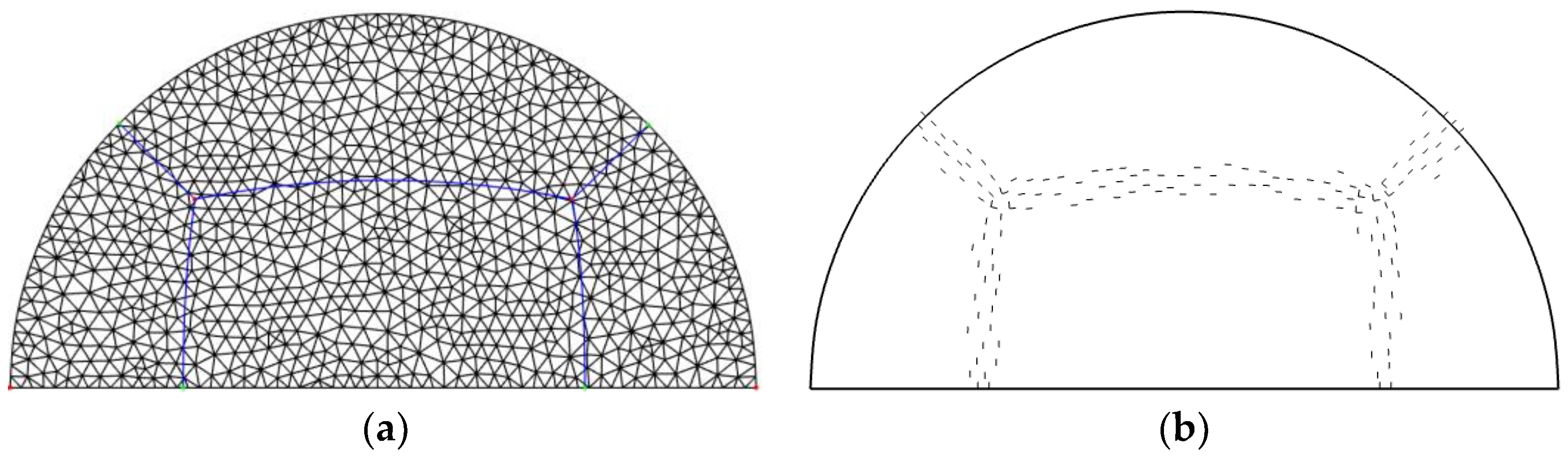
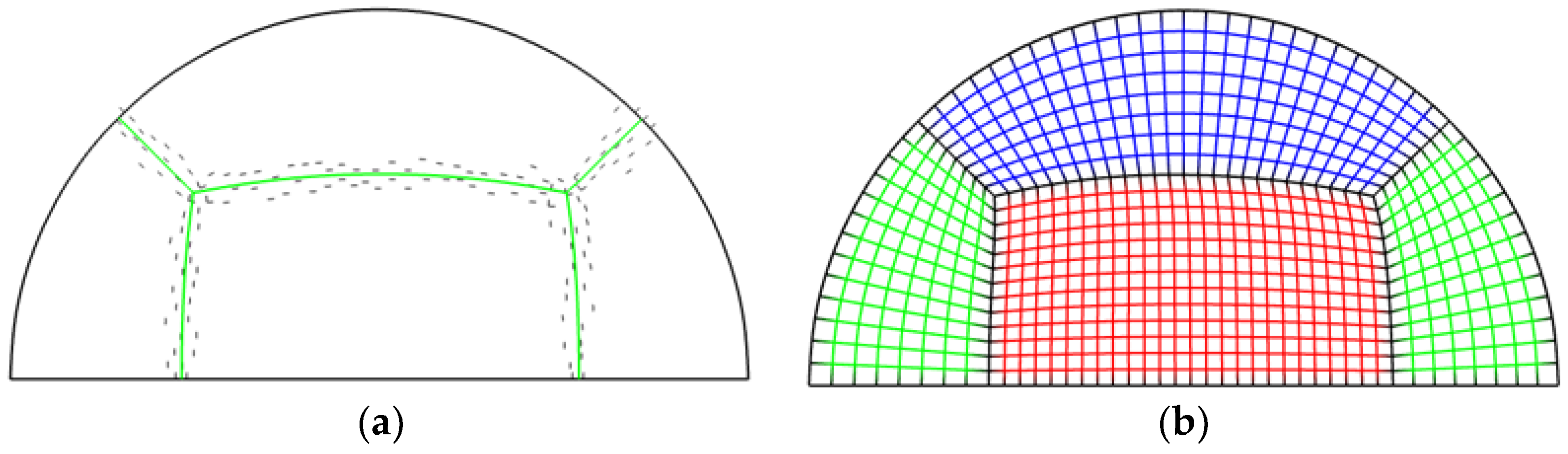
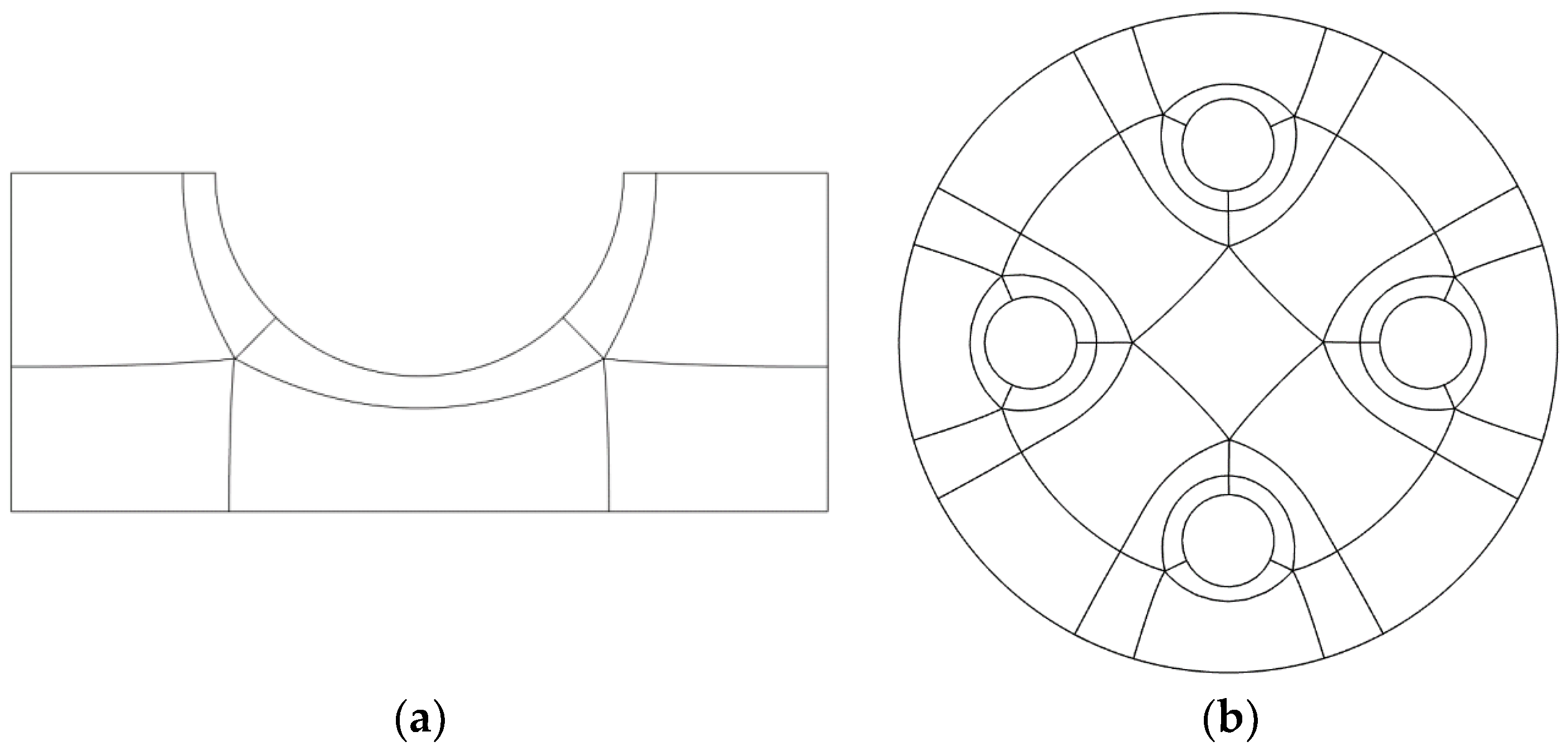
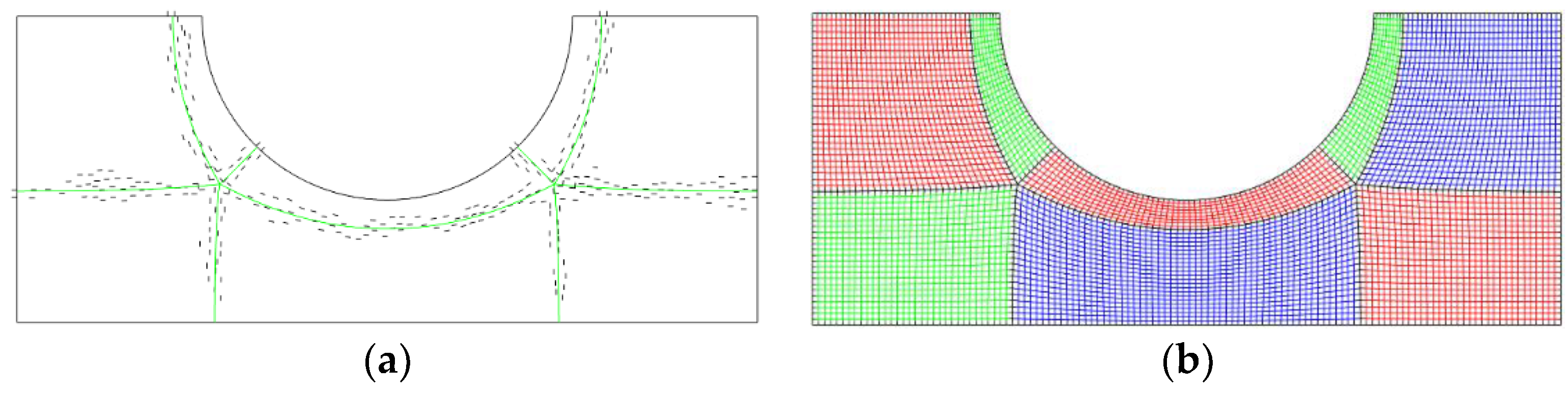
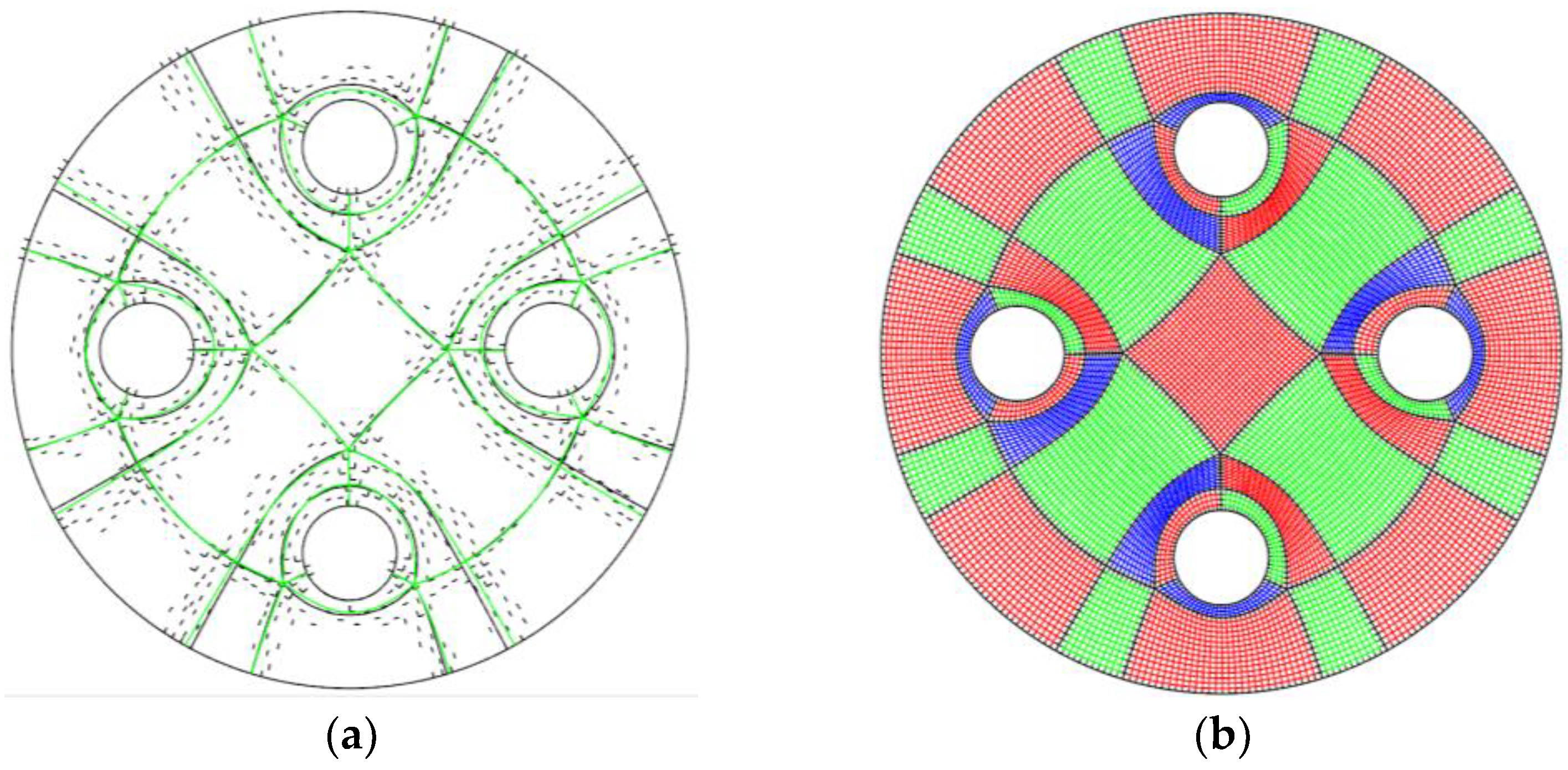
2.1. Domain Decomposition Based on the Frame Field
2.2. Training Data
3. Neural Network Model and Its Training
3.1. Neural Network Model
3.2. Loss Function and Training
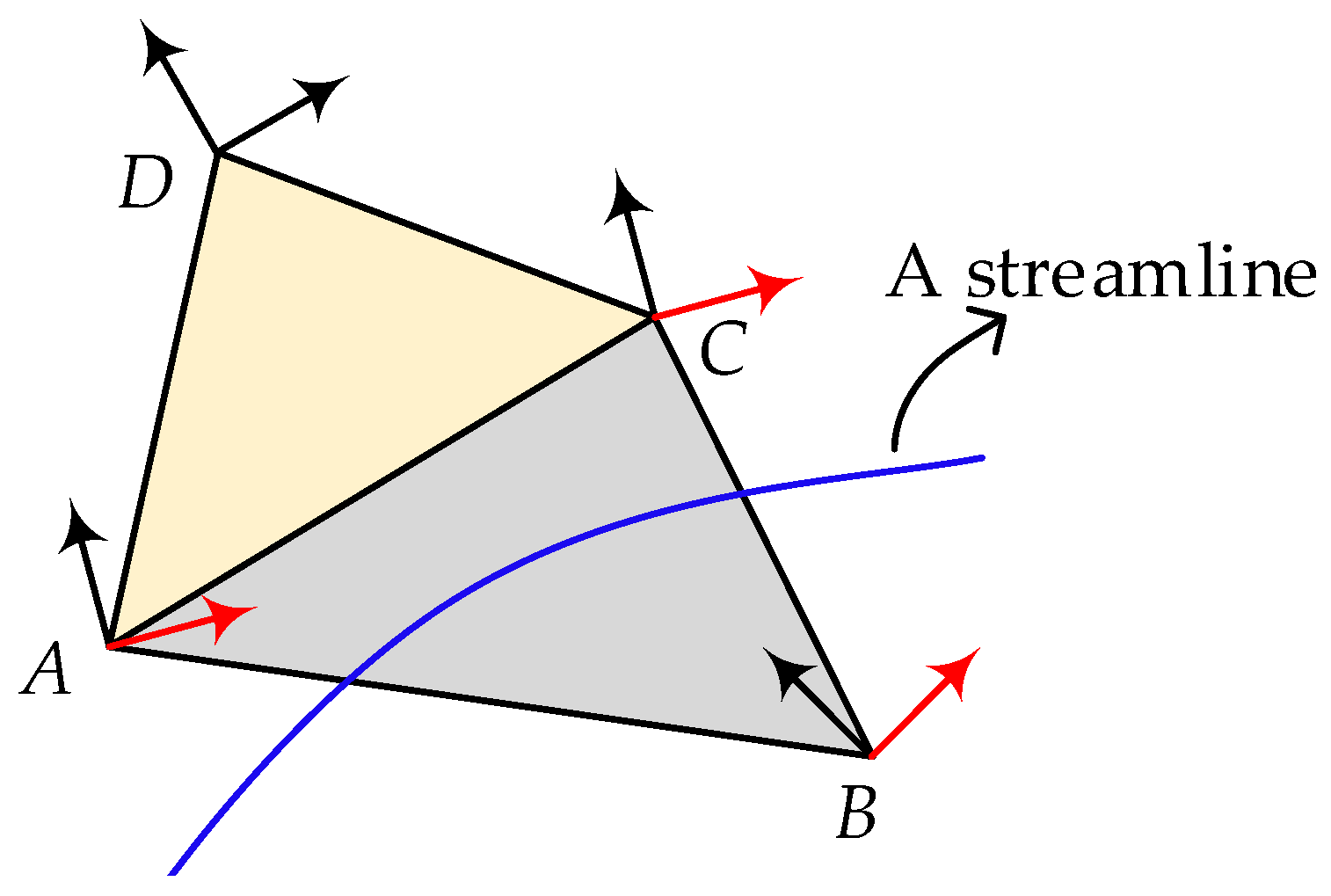
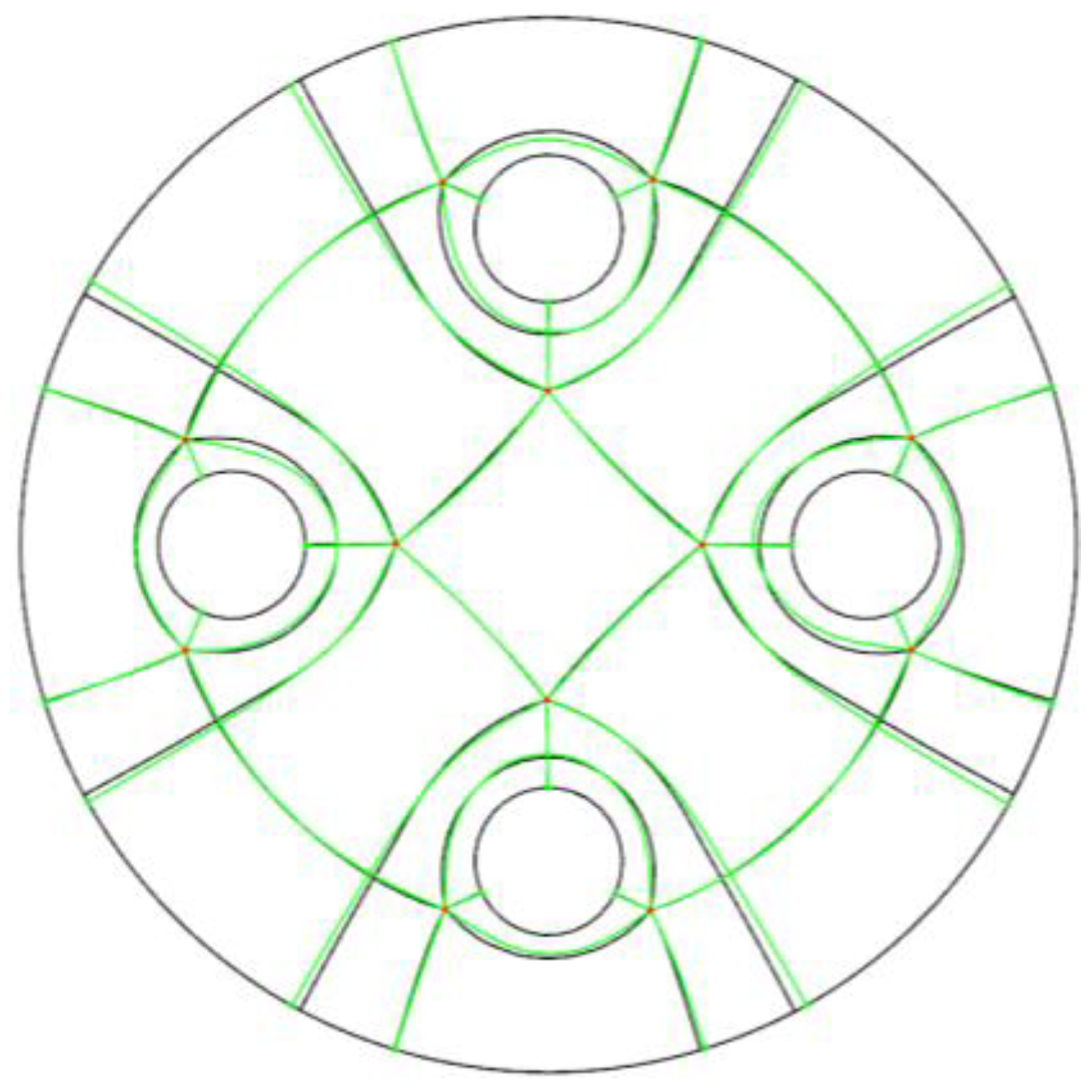
4. Streamline Extraction and Quad Mesh Generation
- (1)
- Take the singular point and its extension direction as the initial current node (denoted as ) and the initial current extension direction (denoted as ), and add into the streamline , becoming a node of the streamline ;
- (2)
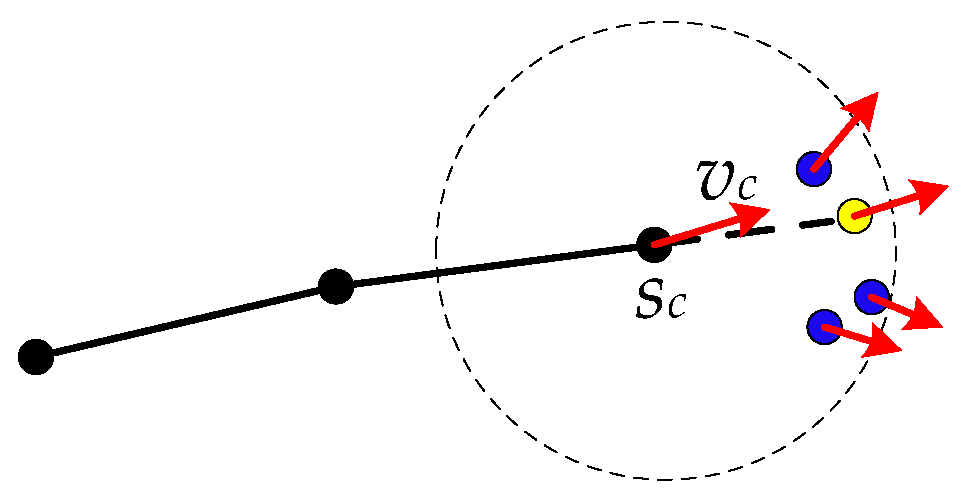
- Among the nodes with frame components marked with label 1, find m neighboring nodes of the current node , denoted as , and their frame components, denoted as . Let a be the closest node to , whose corresponding has the smallest angle with vector (then, is regarded as the next node of the streamline), and add it into . Figure 8 presents the schematic for choosing the next node of the streamline; the nodes in blue in the circle centered at the current node are candidate neighboring nodes, and the node in yellow is the node that satisfies the above conditions, and therefore, it is chosen as the next node of the streamline;
- (3)
- Update the value of to be , and the value of to be ;
- (4)
- If is a singular node or a boundary node, the entire streamline is extracted; otherwise, go to step 2.
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baker, T.J. Mesh generation: Art or science? Prog. Aerosp. Sci. 2005, 41, 29–63. [Google Scholar] [CrossRef]
- Bommes, D.; Lévy, B.; Pietroni, N.; Puppo, E.; Silva, C.; Tarini, M.; Zorin, D. Quad-mesh generation and processing: A survey. Comput. Graph. Forum 2013, 32, 51–76. [Google Scholar] [CrossRef]
- Bunin, G. A continuum theory for unstructured mesh generation in two dimensions. J. Comput. Aided Geom. Des. 2008, 25, 14–40. [Google Scholar] [CrossRef]
- Sun, L.; Armstrong, C.G.; Robinson, T.T.; Papadimitrakis, D. Quadrilateral multiblock decomposition via auxiliary subdivision. J. Comput. Des. Eng. 2021, 8, 871–893. [Google Scholar] [CrossRef]
- Zheng, Z.; Gao, S.; Shen, C. A progressive algorithm for block decomposition of solid models. Eng. Comput. 2022, 38, 4349–4366. [Google Scholar] [CrossRef]
- Fang, X.; Bao, H.; Tong, Y.; Desbrun, M.; Huang, J. Quadrangulation through morse-parameterization hybridization. ACM Trans. Graph. (TOG) 2018, 37, 1–15. [Google Scholar] [CrossRef]
- Fogg, H.J.; Armstrong, C.G.; Robinson, T.T. Automatic generation of multiblock decompositions of surfaces. J. Numer. Methods Eng. 2015, 101, 965–991. [Google Scholar] [CrossRef]
- Kowalski, N.; Ledoux, F.; Frey, P. Automatic domain partitioning for quadrilateral meshing with line constraints. J. Eng. Comput. 2015, 31, 1–17. [Google Scholar] [CrossRef]
- Jezdimirovic, J.; Chemin, A.; Remacle, J.F. Mul-ti-block decomposition and meshing of 2D domain using Ginzburg–Landau PDE. In Proceedings of the 28th International Meshing Roundtable, Buffalo, NY, USA, 14–17 October 2019. [Google Scholar]
- Xiao, Z.; He, S.; Xu, G.; Chen, J.; Wu, Q. A boundary element-based automatic domain partitioning approach for semi-structured quad mesh generation. Eng. Anal. Bound. Elem. 2020, 113, 133–144. [Google Scholar] [CrossRef]
- Li, N.; Shen, Q.; Song, R.; Chi, Y.; Xu, H. MEduKG: A Deep-Learning-Based Approach for Multi-Modal Educational Knowledge Graph Construction. Information 2022, 13, 91. [Google Scholar] [CrossRef]
- Hayat, A.; Morgado-Dias, F.; Bhuyan, B.P.; Tomar, R. Human Activity Recognition for Elderly People Using Machine and, Deep Learning Approaches. Information 2022, 13, 275. [Google Scholar] [CrossRef]
- Heidari, A.; Jamali MA, J.; Navimipour, N.J.; Akbarpour, S. A QoS-Aware Technique for Computation Offloading in IoT-Edge Platforms Using a Convolutional Neural Network and Markov Decision Process. IT Prof. 2023, 25, 24–39. [Google Scholar] [CrossRef]
- Heidari, A.; Navimipour, N.J.; Jamali MA, J.; Akbarpour, S. A green, secure, and deep intelligent method for dynamic IoT-edge-cloud offloading scenarios. Sustain. Comput. Inform. Syst. 2023, 38, 100859. [Google Scholar] [CrossRef]
- Bhatt, J.; Hashmi, K.A.; Afzal, M.Z.; Stricker, D. A survey of graphical page object detection with deep neural networks. Appl. Sci. 2021, 11, 5344. [Google Scholar] [CrossRef]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Riegler, G.; Ulusoy, A.O.; Geiger, A. Octnet: Learning deep 3d representations at high resolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; p. 3577. [Google Scholar]
- Wang, P.S.; Liu, Y.; Guo, Y.X.; Sun, C.Y.; Tong, X. O-cnn: Octree-based convolutional neural networks for 3d shape analysis. ACM Trans. Graph. 2017, 36, 72. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
- Feng, Y.; Feng, Y.; You, H.; Zhao, X.; Gao, Y. Meshnet: Mesh neural network for 3d shape representation. Proc. AAAI Conf. Artif. Intell. 2019, 33, 8279–8286. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Yao, S.; Yan, B.; Chen, B.; Zeng, Y. An ANN-based element extraction method for automatic mesh generation. Expert Syst. Appl. 2005, 29, 193–206. [Google Scholar] [CrossRef]
- Wang, N.; Lu, P.; Chang, X.; Zhang, L. Preliminary investigation on unstructured mesh generation technique based on advancing front method and machine learning methods. Chin. J. Theor. Appl. Mech. 2021, 53, 740–751. [Google Scholar]
- Wang, N.; Lu, P.; Chang, X.; Zhang, L.; Deng, X. Unstructured mesh size control method based on artificial neural network. Chin. J. Theor. Appl. Mech. 2021, 53, 2682–2691. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- E. Bernhardsson Annoy at GitHub. Available online: https://github.com/spotify/annoy (accessed on 30 September 2020).



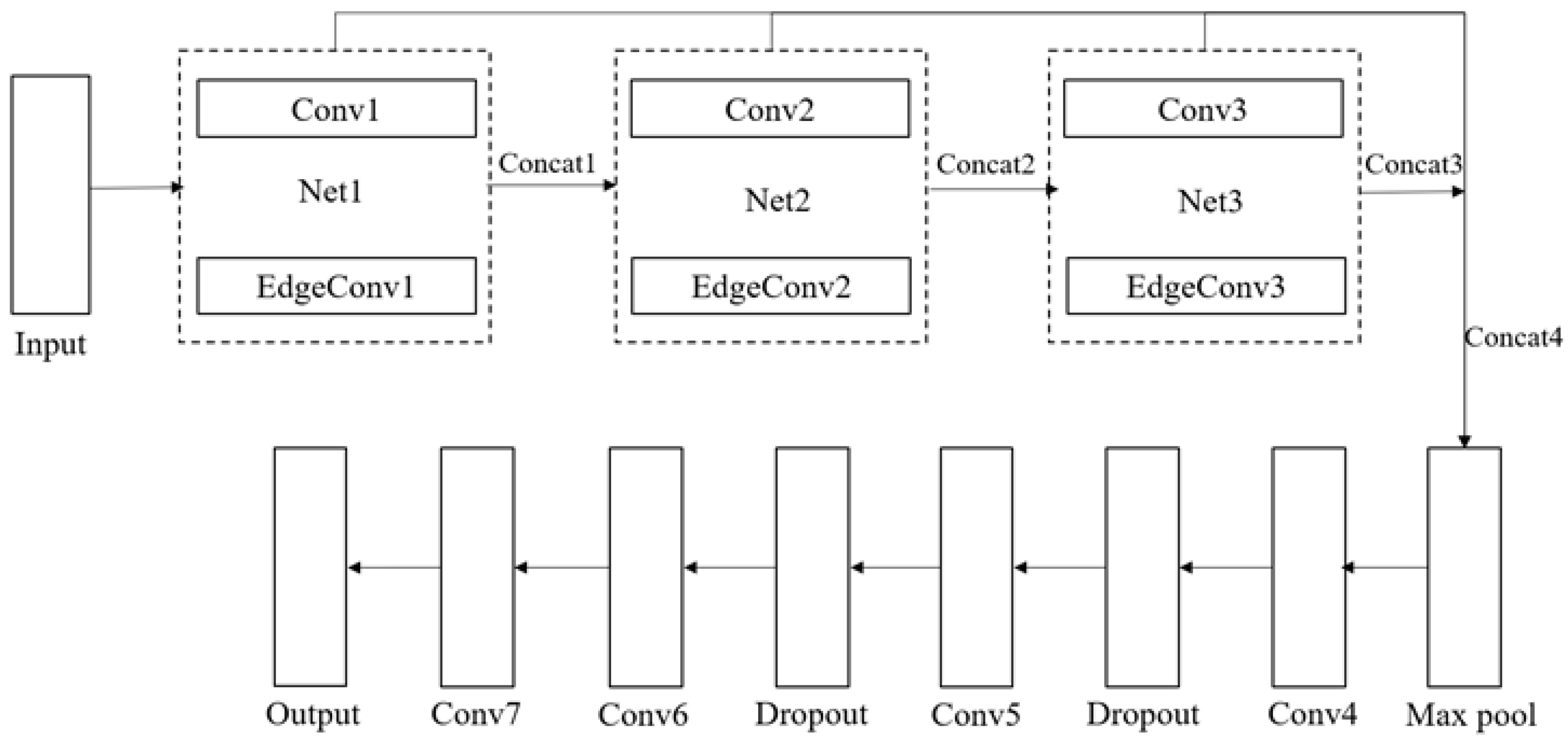


| Layers | Input | Channels | Kernel | Stride | Padding | Output |
|---|---|---|---|---|---|---|
| Conv1 | [4,2048,4,1] | 16 | [1,1,1,16] | [1,1,1,1] | VALID | [4,2048,4,16] |
| Edge Conv1 | [4,2048,10,4] | 16 | [1,1,1,16] | [1,1,1,1] | VALID | [4,2048,10,16] |
| Concat1 | [4,2048,16,16] | -- | -- | -- | -- | -- |
| Conv2 | [4,2048,16,1] | 32 | [1,1,1,32] | [1,1,1,1] | VALID | [4,2048,16,32] |
| Edge Conv2 | [4,2048,10,16] | 32 | [1,1,1,32] | [1,1,1,1] | VALID | [4,2048,10,32] |
| Concat2 | [4,2048,36,32] | -- | -- | -- | -- | -- |
| Conv3 | [4,2048,32,1] | 64 | [1,1,1,64] | [1,1,1,1] | VALID | [4,2048,32,64] |
| Edge Conv3 | [4,2048,10,32] | 64 | [1,1,1,64] | [1,1,1,1] | VALID | [4,2048,10,32] |
| Concat3 | [4,2048,42,64] | -- | -- | -- | -- | -- |
| Concat4 | [4,2048,1,112] | -- | -- | -- | -- | -- |
| Max pool | [4,2048,1,112] | -- | [1,2048,1,1] | -- | -- | [4,1,1,512] |
| Expand | [4,1,1,512] | -- | -- | -- | -- | [4,2048,1,512] |
| Conv4 | [4,2048,1,512] | 256 | [1,1,512,256] | [1,1,1,1] | VALID | [4,2048,1,256] |
| Droupout | [4,2048,1,256] | -- | -- | -- | -- | -- |
| Conv5 | [4,2048,1,256] | 256 | [1,1,256,256] | [1,1,1,1] | VALID | [4,2048,1,256] |
| Droupout | [4,2048,1,512] | -- | -- | -- | -- | -- |
| Conv6 | [4,2048,1,256] | 128 | [1,1,512,128] | [1,1,1,1] | VALID | [4,2048,1,128] |
| Conv7 | [4,2048,1,128] | 2 | [1,1,128,2] | [1,1,1,1] | VALID | [4,2048,1,2] |
| Squeeze | [4,2048,1,2] | -- | -- | -- | -- | -- |
| Topology Name | Data Size | IoU | Accuracy |
|---|---|---|---|
| The concave topology | 2000 | 0.852 | 0.981 |
| The four-hole topology | 2000 | 0.821 | 0.965 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Cai, X.; Zhao, Q.; Xiao, Z.; Xu, G. Quadrilateral Mesh Generation Method Based on Convolutional Neural Network. Information 2023, 14, 273. https://doi.org/10.3390/info14050273
Zhou Y, Cai X, Zhao Q, Xiao Z, Xu G. Quadrilateral Mesh Generation Method Based on Convolutional Neural Network. Information. 2023; 14(5):273. https://doi.org/10.3390/info14050273
Chicago/Turabian StyleZhou, Yuxiang, Xiang Cai, Qingfeng Zhao, Zhoufang Xiao, and Gang Xu. 2023. "Quadrilateral Mesh Generation Method Based on Convolutional Neural Network" Information 14, no. 5: 273. https://doi.org/10.3390/info14050273
APA StyleZhou, Y., Cai, X., Zhao, Q., Xiao, Z., & Xu, G. (2023). Quadrilateral Mesh Generation Method Based on Convolutional Neural Network. Information, 14(5), 273. https://doi.org/10.3390/info14050273





