1. Introduction
Based on data from the U.S. Fire Administration, the number of fire-related deaths has been on an upward trend, with an average of 3500 people losing their lives to fires each year. A survey by the European Fire Safety Alliance found that 37% of fire safety experts believe that collective housing, such as apartments, should receive greater attention. The timely and reliable identification of fires within buildings has great practical significance. People need to spend most of their time in indoor environments such as bedrooms, offices, and living rooms. Once a fire occurs, it can pose a very serious threat to life. In addition, with the increasingly complex building structures, higher floors, and more diverse types and materials of items within buildings, the danger posed by fires has also increased.
Fires can be classified into two types: flame and smoldering. Flame is a common manifestation of fires and refers to visible flames that produce bright light and heat, as well as a large amount of smoke. The combustion energy of flame comes from the combustible materials themselves, such as wood, paper, and liquid fuels. The combustion process of open flame is usually obvious and easily detected. Smoldering fires, on the other hand, refer to the situation where combustion occurs without significant increases in temperature or visible flames. This type of fire often occurs in poorly ventilated environments, where the combustible materials contain high moisture content, such as damp cotton and other materials, or in areas with high humidity. Smoldering fires are difficult to detect but can also generate toxic gases and particles, posing a high level of danger. Therefore, in fire safety, it is necessary to improve the accuracy and timeliness of fire alarms for both types of fires.
Fire detection is mainly based on sensitive devices that collect images, aerosols, smoke and other fire-related information and respond with corresponding measurements [
1]. In the field of image processing, the main features detected are the visual changes associated with a fire, such as color, brightness, shape, and spectral characteristics. For private places such as residential bedrooms, sensors are commonly used to collect environmental data for detection, which is more practical and cost-effective. Traditional warning methods often use smoke alarms. However, smoke alarms may be affected by specific fire situations and external environmental interferences. This can lead to false alarms, missed alarms, and other issues. False alarms waste the resources of fire departments and reduce the comfort of residents. Therefore, it is necessary to develop an accurate fire alarm system.
One alarm method currently known is to install both photoelectric smoke sensors and ionization smoke detectors. Ionization smoke detectors are sensitive to rapidly burning fires and primarily detect smoke particles, so they are not suitable for installation in locations where smoke is regularly produced. On the other hand, photoelectric sensors trigger alarms when smoke particles obstruct light propagation, making them more suitable for detecting smoldering fires. Inspired by this fire alarm method, the current mainstream approach to fire detection is to use information fusion methods that can be widely applied to various environments. Information fusion can be achieved through methods such as weighted averages, least squares estimation, fuzzy theory, clustering analysis, neural networks, and expert systems. This paper focuses on using artificial intelligence methods to achieve fire alarm systems. Okayama [
2] first proposed a fire recognition system that introduced a three-layer neural network that uses temperature, smoke, and gas sensor data to identify fires and highlighted the advantages of using neural networks in this field, which can reflect complex input–output combinations even in the absence of relevant experiential knowledge of input–output causality. Chen and Fu [
3] established a fire alarm system based on a Bayesian network (BN) model, which demonstrated the feasibility and effectiveness of a BN-based fire alarm system using powerful graphical knowledge representation and effective handling of uncertain results. Their research confirmed the feasibility and effectiveness of using input from CO, CO
2, temperature, and smoke sensors to analyze different fire probabilities in alarm systems. Nakıp and Güzeliş [
4] designed a multi-sensor system consisting of gas, temperature and humidity, heat, and smoke sensors using a Raspberry Pi 3-based sensor information acquisition circuit. He also developed a neural network fire prediction system based on trend extraction, which demonstrated the advantages of trend prediction over a normal multilayer perceptron (MLP) model. Wu et al. [
5] proposed a neural network that also introduced trend extraction, which was improved based on the Kendall-τ trend extraction formula [
6] and achieved fire detection based on temperature, smoke, and CO sensor information. The trend-based multi-sensor fire alarm algorithm takes into account changes in sensor data as the fire develops, but the trend calculation method is relatively fixed, making it difficult to adapt to different fire situations, and data preprocessing methods, such as averaging filtering, still need to be incorporated, leading to some resource waste.
To address existing issues, we propose a multi-sensor fire alarm model from the perspective of time series analysis based on a neural network. In this paper, we select three characteristic parameters, namely carbon monoxide, temperature, and smoke concentration. Unlike previous methods that require a large amount of data preprocessing to remove sensor noise, we first analyze the trend extraction methods of time series and analyze the advantages of the second-order exponential smoothing method in processing sensor data. Then, we establish a neural network algorithm model, introducing a recurrent neural network (RNN) structure to fit the second-order exponential smoothing formula for indoor fire data. To demonstrate the superiority of the proposed algorithm, we select multiple evaluation metrics and compare them with the metrics of existing algorithms. Finally, we apply our proposed model to fire data collected from another real-world residential setting and analyze the alarm time. The results show that our algorithm can effectively identify fire incidents within a reasonable time frame, demonstrating significant advantages over traditional alarm systems.
3. Dataset and Training Method
The dataset used in this study is derived from the home fire experiments conducted by the National Institute of Standards and Technology (NIST) in the United States [
13]. The experiments involved burning various materials indoors and collecting sensor data at different stages of the fire, including before ignition, early stages, full development, and extinguishment. The performance of several commercially available smoke alarms was also tested. According to statistics, the most frequent types of indoor fires are smoldering upholstered furniture in the living room, flaming upholstered furniture in the living room, smoldering mattresses in the bedroom, and flaming mattresses in the bedroom. Therefore, the dataset selected for this study includes SDC02, SDC05, SDC06, SDC07, SDC08, and SDC11, with a sampling rate of 5 s. These experiments covered the above types of fires and were all conducted in an 85-square-meter manufactured home with a layout similar to most residential buildings.
Table 2 provides specific information on the selected training datasets.
In the research field of multi-sensor home fire recognition algorithms, selecting appropriate sensor parameters is crucial for improving the sensitivity and anti-interference of fire detection. Experimental studies conducted by the Department of Fire Protection Engineering at the University of Maryland indicate that a combination of temperature rise, CO, and smoke sensors is one of the best choices [
14]. Moreover, from the perspective of practical feasibility and cost, there are already examples of fire alarm devices that incorporate these three sensors in the market, such as the smart alarm from Kidde, a manufacturer of fire and safety products. Therefore, this study selects temperature, smoke density, and CO as the fire characteristic parameters collected by sensors. Temperature rise is a fundamental manifestation of combustion, while smoke is generated by all combustible materials during combustion, and its concentration varies depending on the burning material and oxygen content. Compared with smoke, CO is generated earlier, ranging from several tens of minutes to a few hours after the start of the fire. Under normal conditions, the concentration of CO in the air is low, making it a unique marker of fire. Unlike H
2O, O
2, and CO
2, which are not easily affected by the environment and human activities, even in the kitchen environment during cooking, the CO concentration is generally below 20 ppm. CO is suitable for early fire detection and is less likely to produce false alarms.
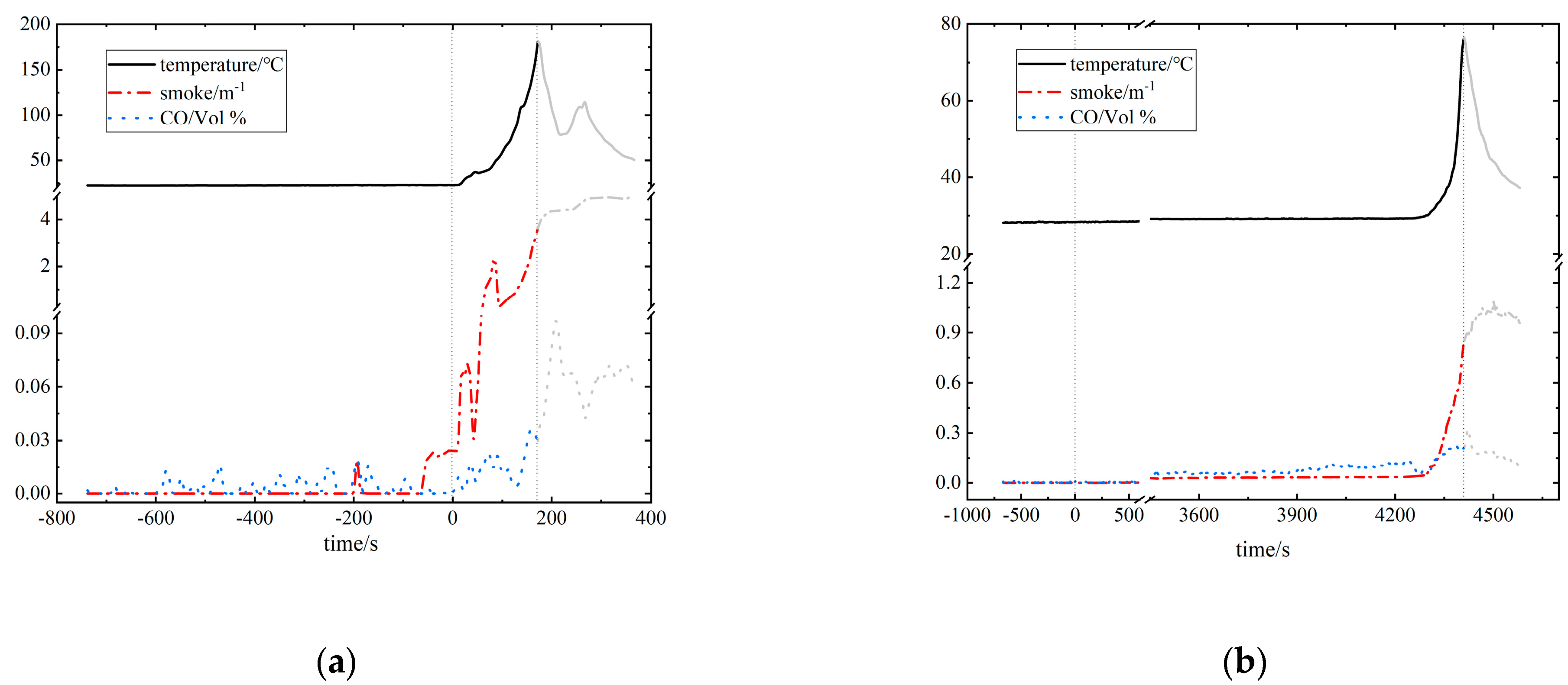
Taking the example of a mattress burning with flame in the bedroom and a chair smoldering in the living room, the sensor data of the three parameters are shown in
Figure 6. Before the fire, the values of all parameters in the environment were relatively stable. After ignition at time 0, the sensor data started to fluctuate. As the fire spread to various objects in the house and was affected by ventilation and other environmental factors, the fire intensity gradually decreased, and the sensor data gradually returned to normal. The smoldering fire developed much more slowly than the open flame, and the CO parameter showed the first fluctuations, confirming our decision to include CO as the fire characteristic parameter. Our goal in this study is to develop an algorithm that can accurately identify the occurrence of fire in emergencies. Therefore, we only need to use the data information before the peak of the fire development, as data indicated before the gray curve in
Figure 6.
The original sensor time series data were preprocessed by forming a new dataset consisting of tuples with three time points. As the sensor data had different dimensions, it was normalized to values between 0 and 1 for use during neural network training. The dataset was then split into training, validation, and testing sets in the ratios of 0.7, 0.15, and 0.15, respectively. The proposed algorithm flow and related parameters are shown in
Figure 7.
The algorithm is trained using the backpropagation method and the Adam optimizer, which combines momentum and adaptive learning rate methods to help the neural network converge quickly. The gradient of each parameter is calculated according to the loss function, and the gradient descent optimization algorithm is used in backpropagation to update the parameters and minimize the loss value. The loss function of the neural network is used to measure the difference between the neural network output and the target output. In this paper, the data label indicates whether a fire has occurred, and the binary cross-entropy loss function can effectively measure the match between the classification probability and the true label. The calculation method of binary cross-entropy is shown in Formula (12), where M is the number of training sets,
is the label of training data m,
is the training data m, and
is the neural network model with weight
.
4. Assessment Method
This study mainly compared several algorithms that consider the development trend of fires, including the algorithm that introduces the development trend of fires from existing literature in
Section 3 and the algorithm proposed in this paper that introduces the second-order exponential smoothing method. The following algorithms were selected for comparison.
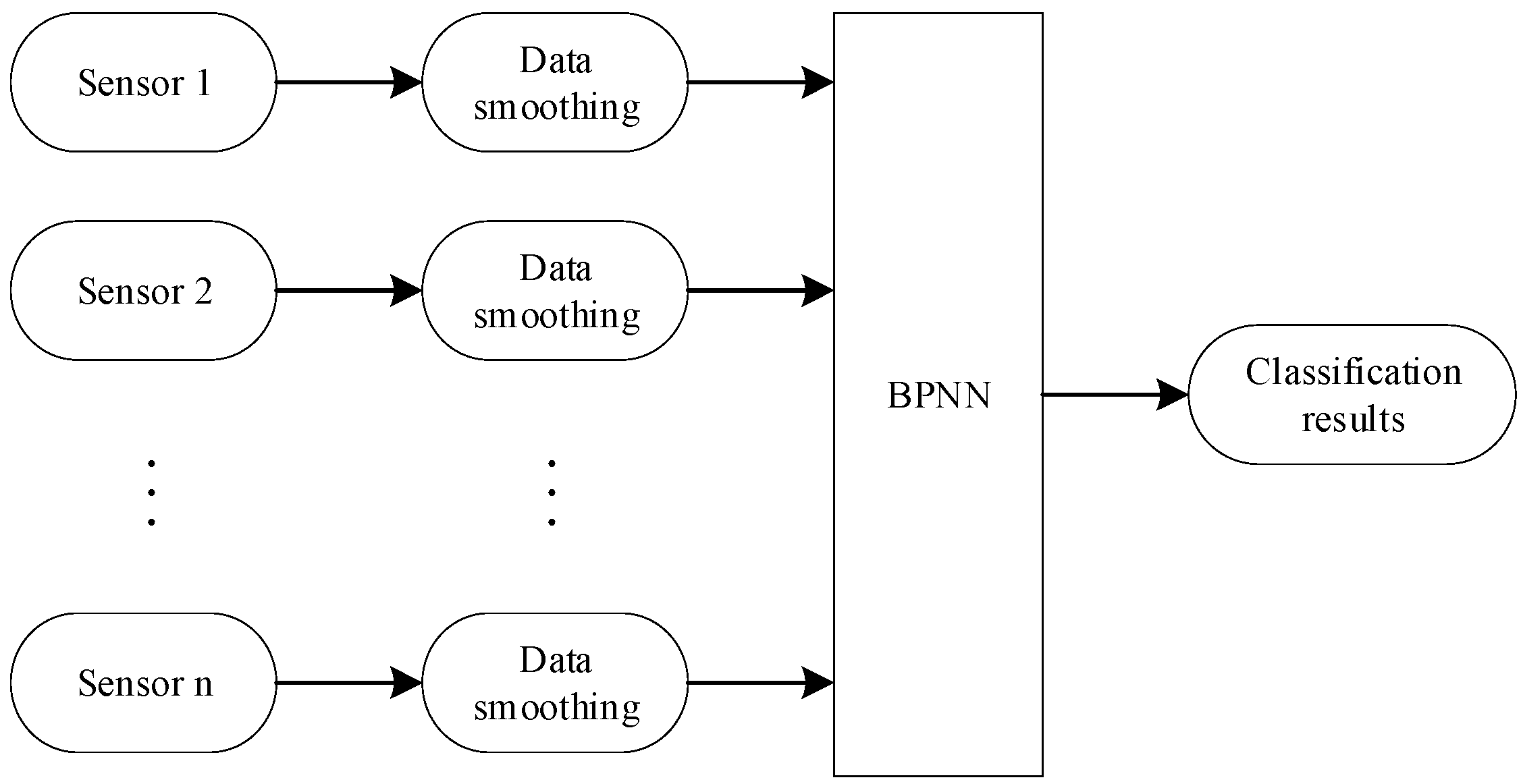
The first algorithm compared in this paper is a neural network, as shown in
Figure 1, where the sensor data are only processed with a simple average filter (BPNN).
The second algorithm compared in this paper is the one proposed in reference [
4] (TPNN).
The third algorithm compared in this paper is the “Improved kendall-τ NN” proposed in reference [
5], which extracts the fire development trend using an improved Kendall-τ formula from sensor data.
A neural network directly incorporating the second-order exponential smoothing formula, where the smoothing parameters α and β are set to empirical values (α = 0.5, β = 0.5) and fitted using the TRF and Dogbox methods (ES-formula NN).
A neural network model with an RNN structure fitted to the second-order exponential smoothing formula proposed in this paper (ES-RNN).
Classification in fire detection is a binary model where a positive label is assigned to the result when a fire is detected, and a negative label is assigned when there is no fire. Therefore, the neural network classification results can be divided into the following situations:
True positive (TP) refers to the samples that are correctly predicted as positive labels.
False negative (FN) refers to the samples that are incorrectly predicted as negative labels.
True negative (TN) refers to the samples that are correctly predicted as negative labels.
False positive (FP) refers to the samples that are incorrectly predicted as positive labels.
To evaluate the performance of the algorithm models and determine whether they are suitable for indoor fire detection, we have selected the following evaluation metrics based on specific data to support the rationality of the algorithms.
Accuracy is a metric that measures the proportion of correctly classified samples in the total number of samples. It is defined as shown in Equation (13).
Precision measures the proportion of true positive cases among all positive cases identified by the model. It is calculated as shown in Equation (14). Compared to accuracy, precision focuses more on positive samples, that is, examining whether there are any misclassifications when judging the results as fire incidents.
Recall represents the ability of an algorithm to identify positive cases. The formula is shown as (15). In this paper, positive cases refer to fire incidents, and recall represents the ability to identify fire incidents.
The F1 score, with a range of values between 0 and 1, is the harmonic mean of precision and recall. It provides a more comprehensive evaluation than precision and recall alone when either of them is not sufficient to fully capture the model’s performance [
15]. In this paper, we also use the F1 score to evaluate the model’s ability to identify fire incidents, with fire incidents being considered positive. The formula is shown in Equation (16):
The receiver operating characteristic (ROC) curve is plotted based on two metrics: true positive rate and false positive rate, as shown in Formulas (17) and (18):
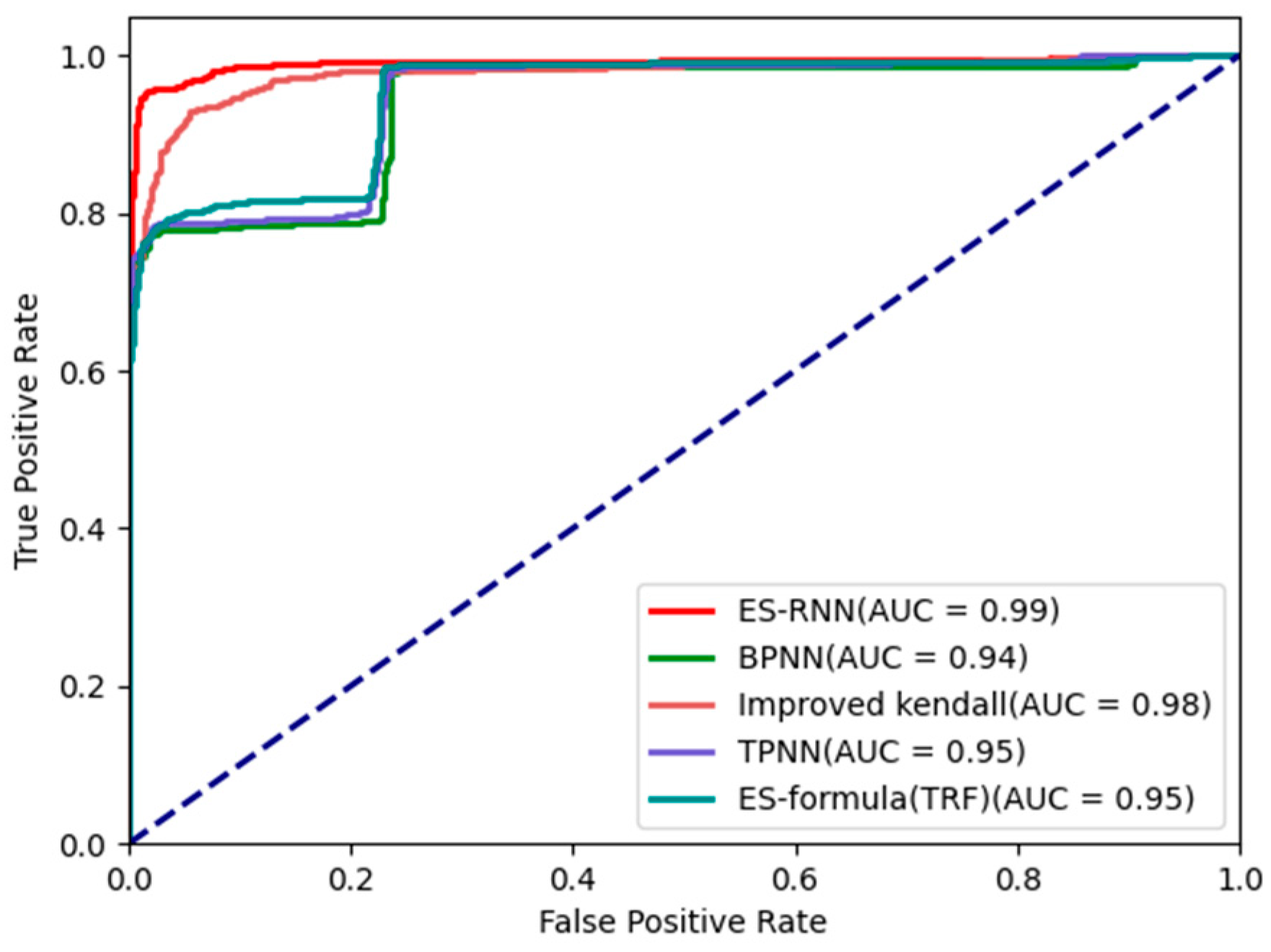
Neither TPR nor FPR is affected by class imbalance. The FPR represents the degree of false reporting of fires, while the TPR represents the coverage ratio of the classification results as having fires. Therefore, the lower the FPR and the higher the TPR, the better the performance of the model. Area under ROC curve (AUC) is a comprehensive measure of the overall performance of the model corresponding to the classification threshold traversed. The area below the diagonal line represents random classification. The steeper the ROC curve and the larger the AUC, the better the model performance.
The Matthews Correlation Coefficient (MCC) calculates the Pearson product–moment correlation coefficient between the actual and predicted values using a contingency table and is not affected by imbalanced datasets [
16]. The MCC calculation is shown in Equation (19):
The MCC ranges from −1 to +1, where a perfect classifier has an MCC of 1, an MCC of 0 corresponds to random classification, and a completely inverted binary classification results in an MCC of −1 [
17].
Author Contributions
Conceptualization, L.A., L.C. and X.H.; investigation, L.A.; methodology L.A.; validation, L.A.; data curation, L.A.; writing—original draft preparation, L.A.; writing—review and editing, L.A., L.C. and X.H.; supervision, L.C.; funding acquisition, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Chinese Academy of Sciences Network Security and Informatization Project (CAS-WX2021SF-0113).
Data Availability Statement
Acknowledgments
The first author, L.A., hereby acknowledges the Institute of Microelectronics of the Chinese Academy of Sciences (IMECAS) and the EDA Center.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yancheng, C.; Liheng, W. Design and Implementation of Fire Monitoring and Warning User Terminal System. In Proceedings of the 2022 International Conference on Artificial Intelligence and Computer Information Technology (AICIT), Yichang, China, 16–18 September 2022; pp. 1–5. [Google Scholar]
- Okayama, Y. A primitive study of a fire detection method controlled by artificial neural net. Fire Saf. J. 1991, 17, 535–553. [Google Scholar] [CrossRef]
- Chen, J.; Fu, J.Q. Fire Alarm System Based on Multi-Sensor Bayes Network. In Proceedings of the 2012 International Workshop on Information and Electronics Engineering, Harbin, China, 10–11 March 2012; pp. 2551–2555. [Google Scholar]
- Nakıp, M.; Güzeliş, C. Multi-Sensor Fire Detector based on Trend Predictive Neural Network. In Proceedings of the 2019 11th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2019; pp. 600–604. [Google Scholar]
- Wu, L.; Chen, L.; Hao, X. Multi-Sensor Data Fusion Algorithm for Indoor Fire Early Warning Based on BP Neural Network. Information 2021, 12, 59. [Google Scholar] [CrossRef]
- Wu, L.B.; Yuan, H. Fire Detection and Control Engineering; University of Science and Technology of China Press: Hefei, China, 2013. [Google Scholar]
- Hamed, K. Exact distribution of the Mann–Kendall trend test statistic for persistent data. J. Hydrol. 2009, 365, 86–94. [Google Scholar] [CrossRef]
- Brown, R.G.; Meyer, R.F.; D’Esopo, D.A. The Fundamental Theorem of Exponential Smoothing. Oper. Res. 1961, 9, 673–687. [Google Scholar] [CrossRef]
- Li, G.; Cai, Z.; Kang, X.; Wu, Z.; Wang, Y. ESPSA: A prediction-based algorithm for streaming time series segmentation. Expert Syst. Appl. 2014, 41, 6098–6105. [Google Scholar] [CrossRef]
- Gardner, E.S., Jr. Exponential smoothing: The state of the art. J. Forecast. 1985, 4, 1–28. [Google Scholar] [CrossRef]
- Wu, L.F.; Liu, S.F.; Yang, Y.J. Grey double exponential smoothing model and its application on pig price forecasting in China. Appl. Soft Comput. 2016, 39, 117–123. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, X.; Liu, R.; Zhang, H.B. Research on Network Security Trend Prediction Based on Exponential Smoothing Algorithm. In Proceedings of the 2020 IEEE 11th International Conference on Software Engineering and Service Science (Icsess 2020), Beijing, China, 16–18 October 2020; pp. 507–510. [Google Scholar]
- Bukowski, R.W.; Peacock, R.D.; Averill, J.D.; Cleary, T.G.; Bryner, T.G.; Walton, W.D.; Reneke, P.A.; Kuligowski, E.D. Performance of Home Smoke Alarms: Analysis of the Response of Several Available Technologies in Residential Fire Settings; Technical Note (NIST TN); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2006; p. 1455. [Google Scholar]
- Cestari, L.A.; Worrell, C.; Milke, J.A. Advanced fire detection algorithms using data from the home smoke detector project. Fire Saf. J. 2005, 40, 1–28. [Google Scholar] [CrossRef]
- Parker, C. An Analysis of Performance Measures for Binary Classifiers. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining, Vancouver, BC, Canada, 11–14 December 2011; pp. 517–526. [Google Scholar]
- Powers, D. Evaluation: From Precision, Recall and F-Factor to ROC, Informedness, Markedness & Correlation. Mach. Learn. Technol. 2008, 2, 2229–3981. [Google Scholar]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
The structure of information fusion fire warning system.
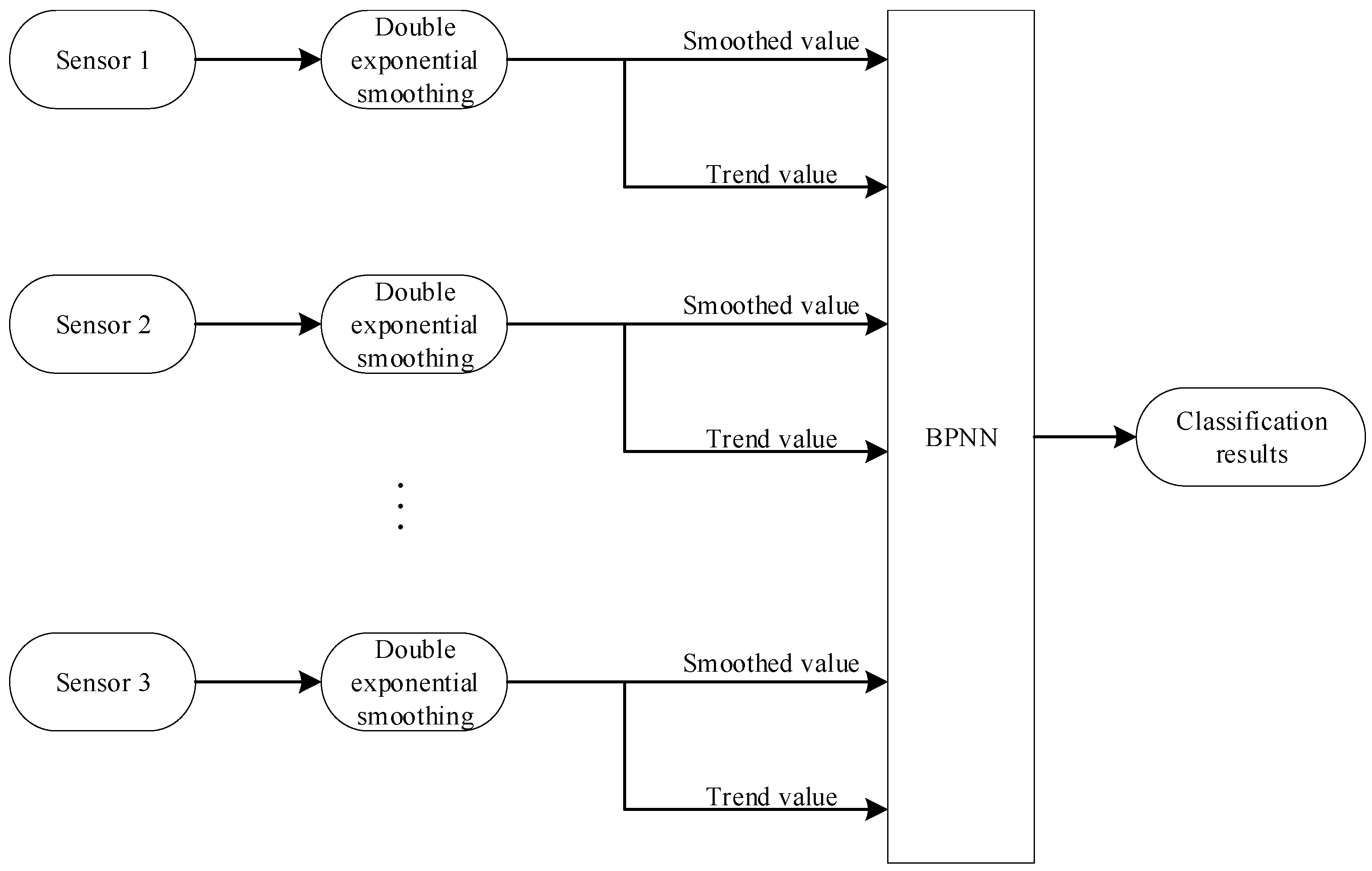
Figure 2.
The structure of information fusion fire warning system with trend extraction.
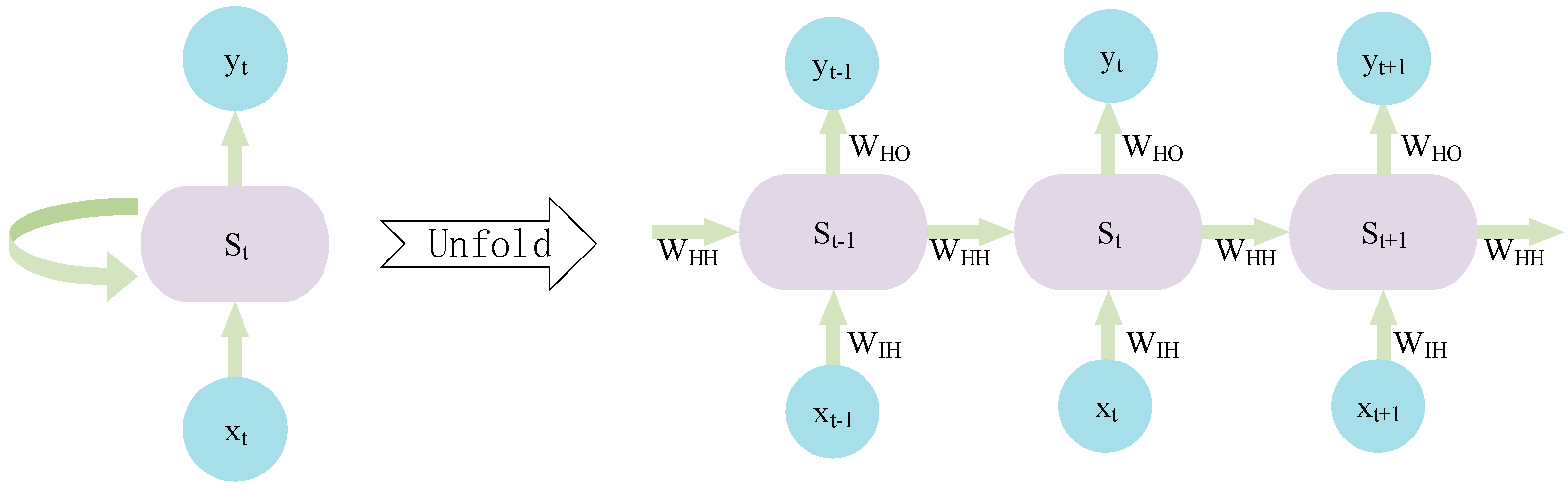
Figure 3.
Single−layer RNN model architecture.
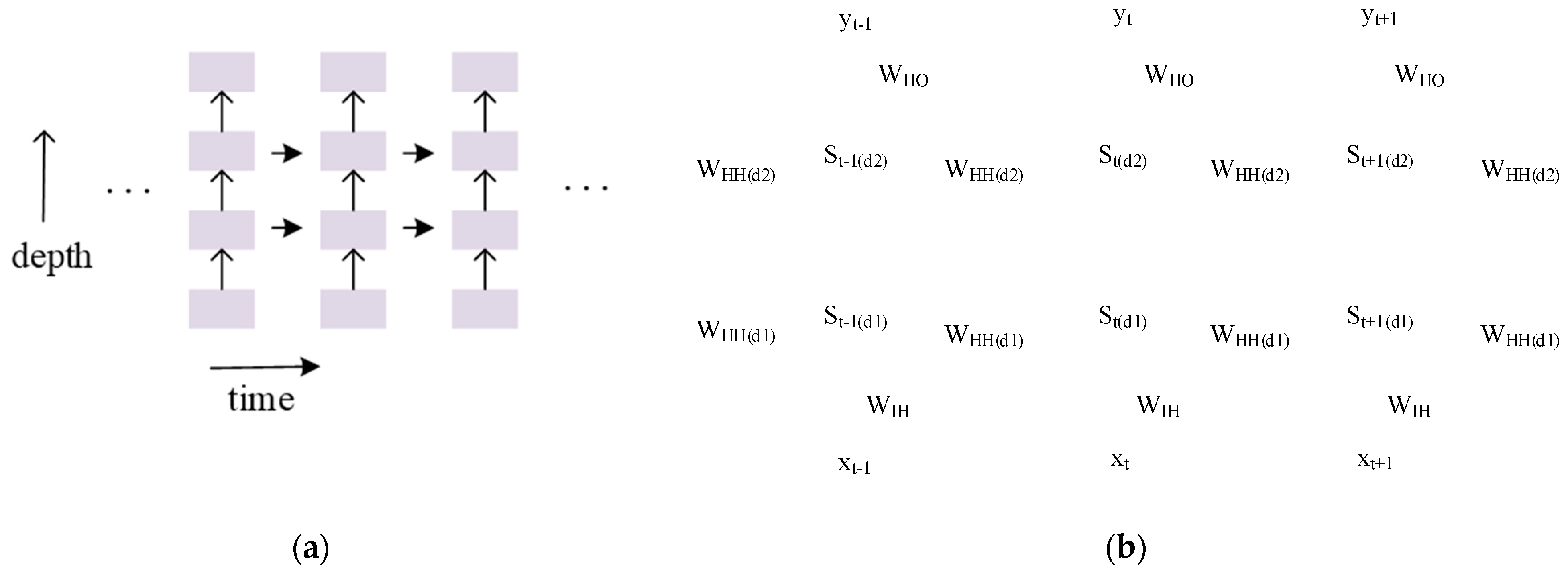
Figure 4.
(a) The structure of multi−layer RNN model; (b) two−layer RNN structure used for fitting in second−order exponential smoothing.
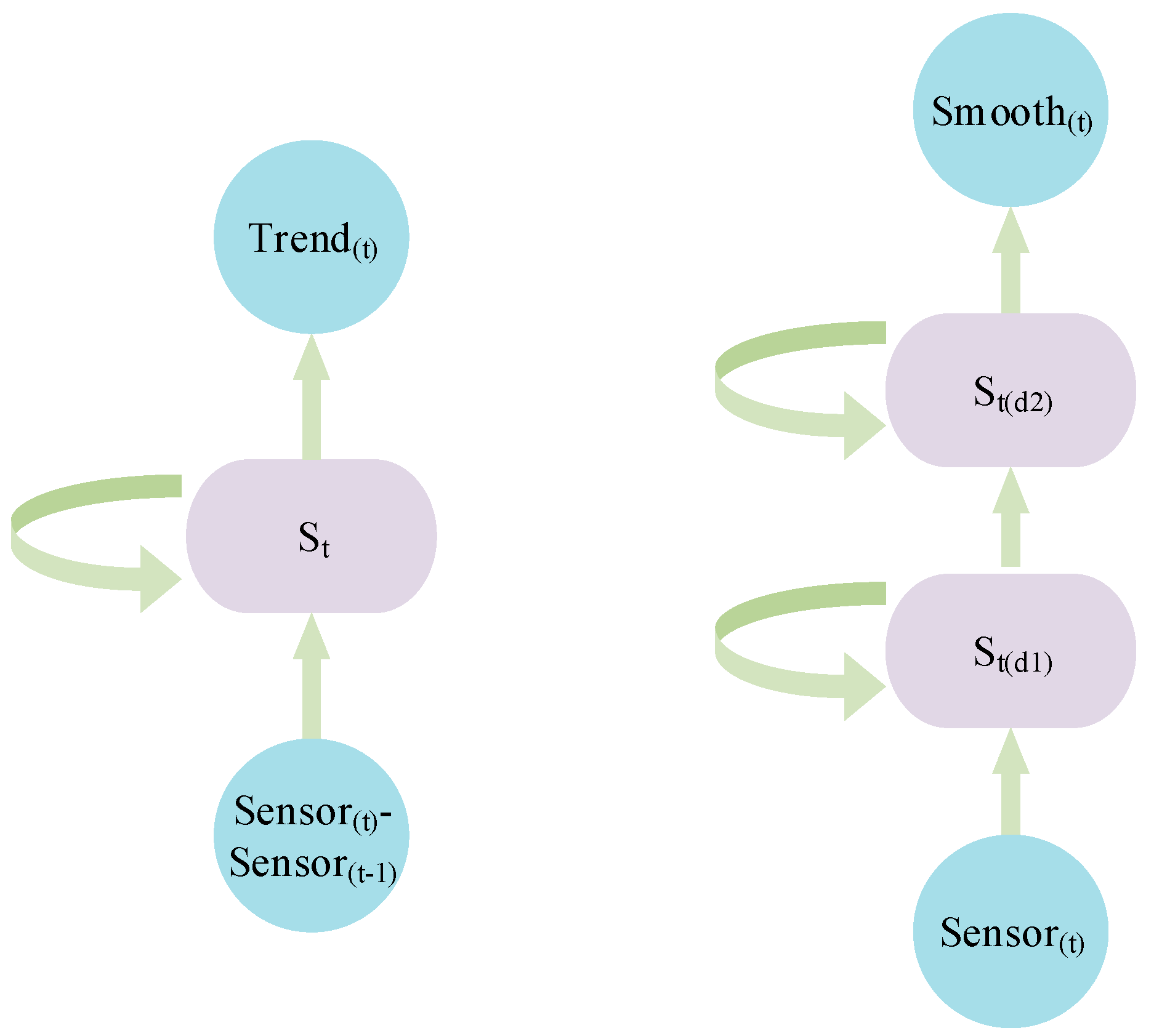
Figure 5.
The structure of RNN fitting second−order exponential smoothing.
Figure 6.
Example of how sensor data changes during a fire including (a) the sensor data of flaming mattress in bedroom; (b) the sensor data of smoldering chair in living room.
Figure 7.
Flowchart of ES−RNN algorithm.
Figure 8.
Comparison of ROC/AUC results among different algorithms.
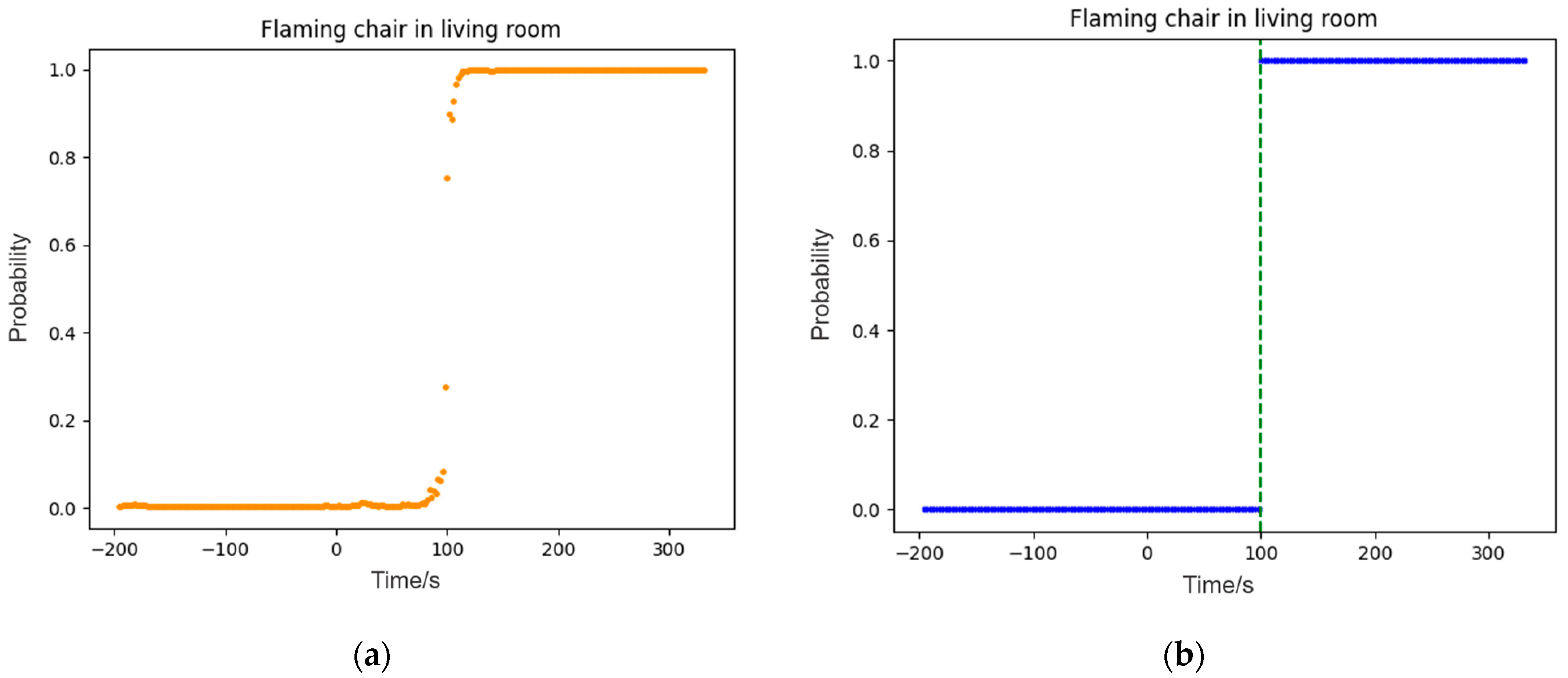
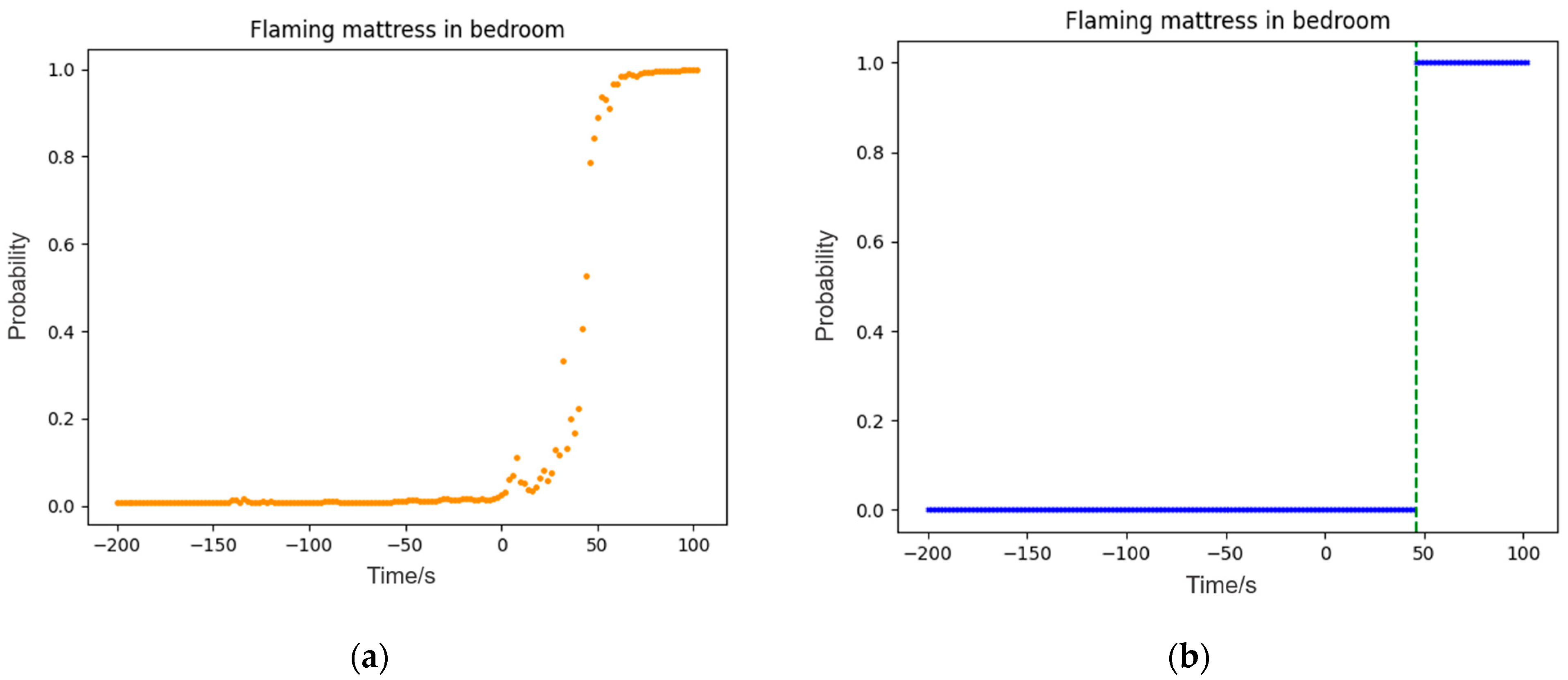
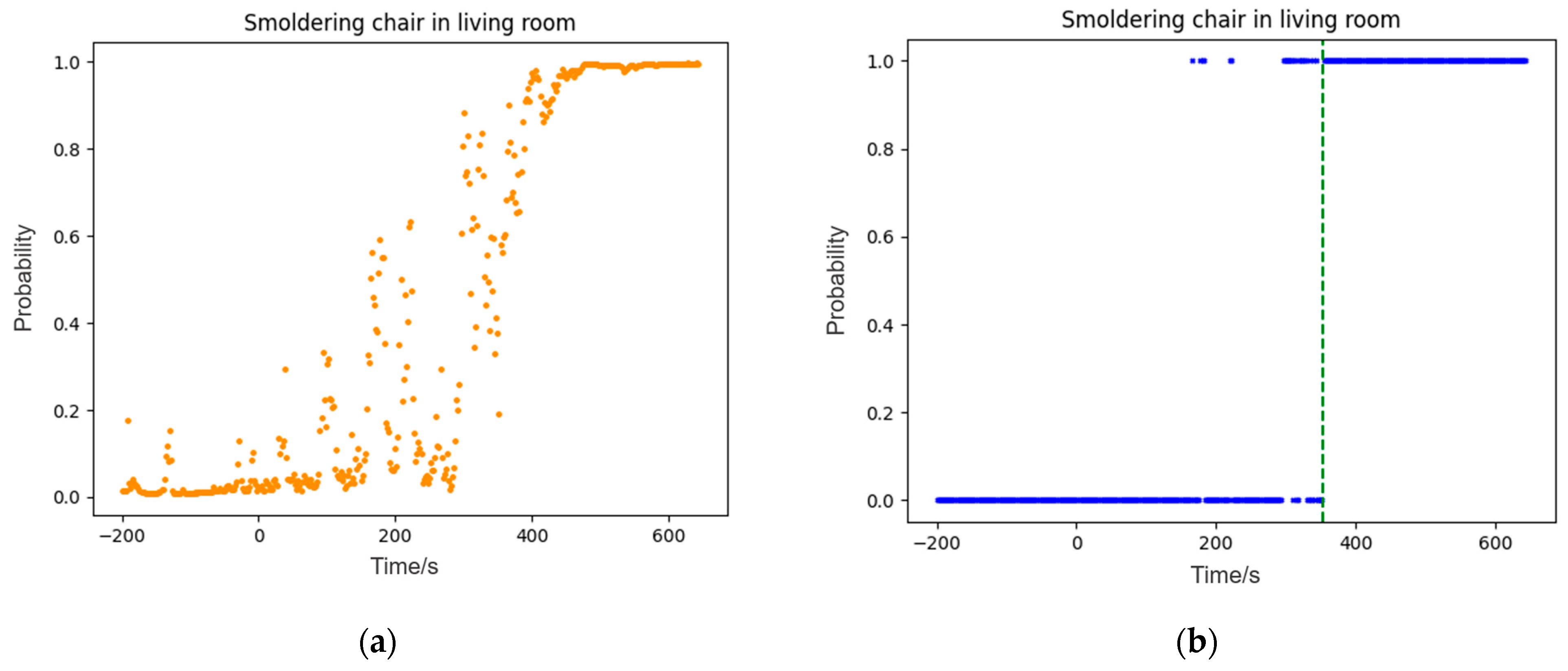
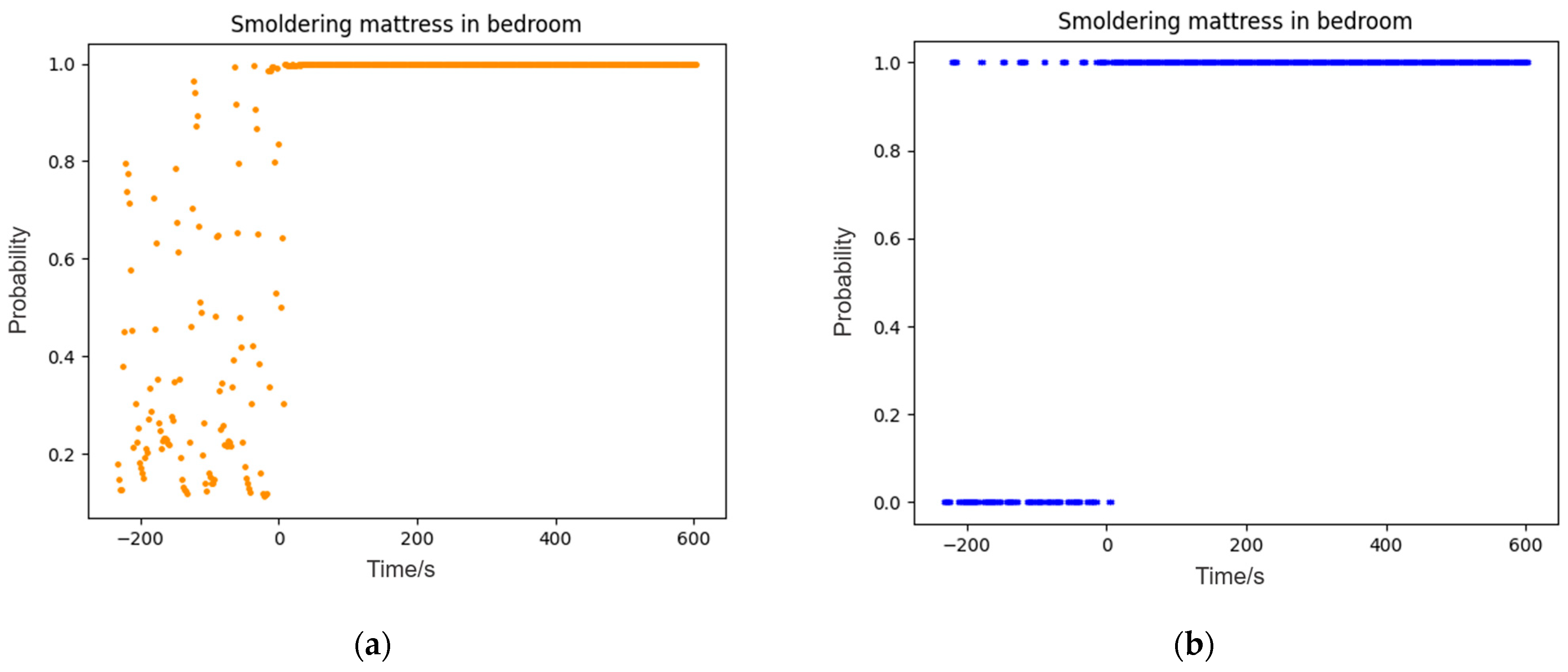
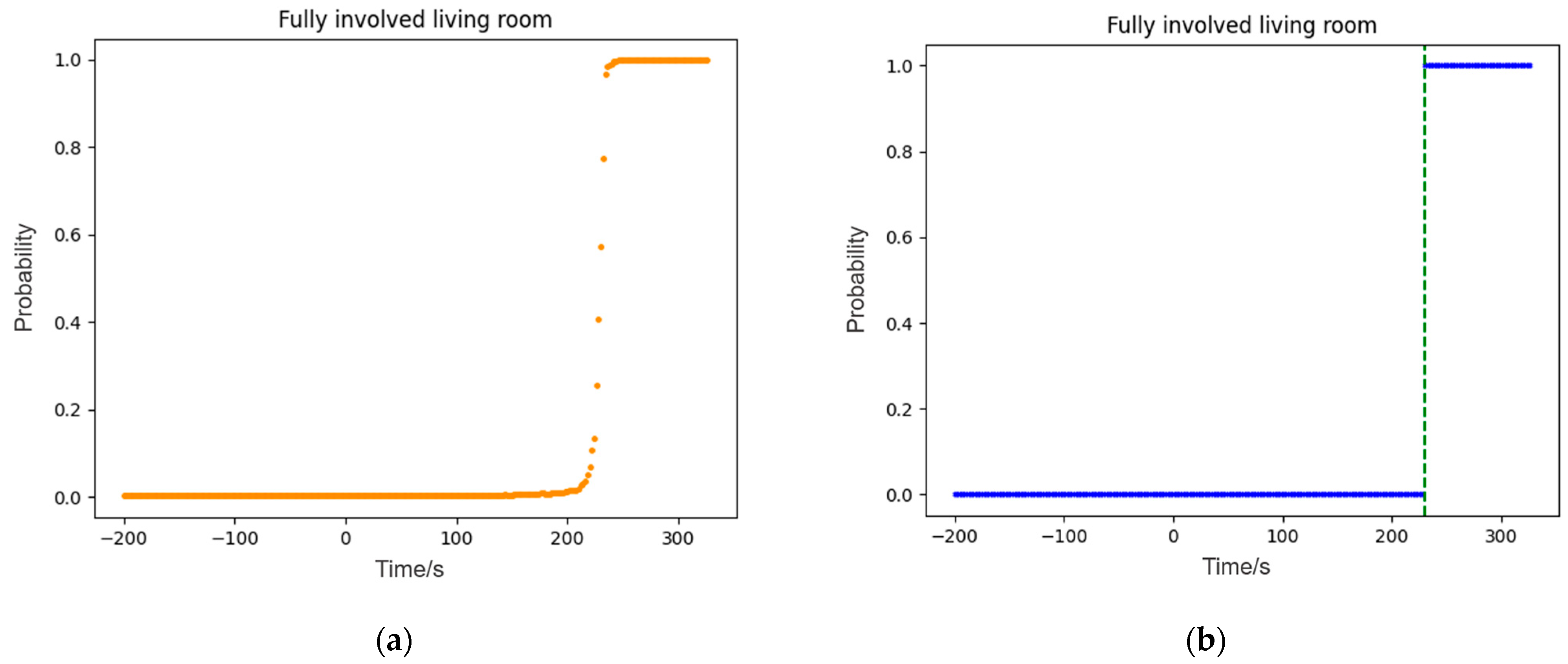
Figure 9.
(a) Model output of experiment I; (b) results of alarm time in experiment I.
Figure 10.
(a) Model output of experiment II; (b) results of alarm time in experiment II.
Figure 11.
(a) Model output of experiment III; (b) results of alarm time in experiment III.
Figure 12.
(a) Model output of experiment IV; (b) results of alarm time in experiment IV.
Figure 13.
(a) Model output of experiment V; (b) results of alarm time in experiment V.
Figure 14.
(a) Model output of experiment VI; (b) results of alarm time in experiment VI.
Figure 15.
(a) Model output of experiment VII; (b) results of alarm time in experiment VII.
Figure 16.
(a) Model output of experiment VIII; (b) results of alarm time in experiment VIII.
Table 1.
Exponential smoothing parameters fitted using TRF and Dogbox methods.
| Sensor | Temperature | Smoke | CO |
|---|
| Parameter | α | β | α | β | α | β |
|---|
| TRF | 0.20 | 0.26 | 0.99 | 0.99 | 0.99 | 0.18 |
| Dogbox | 0.06 | 0 | 0.99 | 1 | 0.99 | 0.18 |
Table 2.
The NIST dataset selected for training.
| Dataset | Location of the Fire | Ignition Source | Type of Fire | Amount of Data |
|---|
| SDC02 | Living Room | Chair | Flame | 313 |
| SDC05 | Bedroom | Mattress | Flame | 196 |
| SDC06 | Bedroom | Mattress | Smoldering | 1220 |
| SDC07 | Bedroom | Mattress | Flame | 170 |
| SDC08 | Bedroom | Mattress | Smoldering | 1928 |
| SDC11 | Living Room | Chair | Smoldering | 3543 |
| Total | 7370 |
Table 3.
Comparison of performance metrics among different algorithms.
| | Accuracy | Precision | Recall | F1-
Score | FPR | MCC | AUC |
|---|
| ES-RNN | 0.98 | 0.96 | 0.98 | 0.97 | 0.03 | 0.95 | 0.99 |
| BPNN | 0.90 | 0.96 | 0.77 | 0.86 | 0.02 | 0.79 | 0.94 |
| TPNN | 0.90 | 0.96 | 0.78 | 0.86 | 0.02 | 0.79 | 0.95 |
| NN | 0.94 | 0.92 | 0.93 | 0.92 | 0.06 | 0.87 | 0.98 |
| 0.89 | 0.93 | 0.79 | 0.86 | 0.04 | 0.78 | 0.91 |
ES-formula NN
(TRF Fitting) | 0.93 | 0.88 | 0.97 | 0.92 | 0.09 | 0.87 | 0.95 |
ES-formula NN
(Dogbox Fitting) | 0.92 | 0.86 | 0.97 | 0.91 | 0.11 | 0.84 | 0.95 |
Table 4.
Comparison results of alarm time between traditional sensors and ES-RNN model.
| Num | Type of Fire | Alarm Time of Smoke Alarms (Photoelectric and Ionization) [s] | Alarm Time of
CO Alarms [s] | Alarm Time of
the Proposed Model [s] |
|---|
| I | Flaming Chair in Living Room | 116–176 | 202–282 | 96 |
| II | Flaming Chair in Living Room | 126–238 | 254–302 | 100 |
| III | Flaming Mattress in Bedroom | 32–108 | 154–214 | 46 |
| IV | Flaming Mattress in Bedroom
(Burn Room Door Closed) | 160–454 | 264–2044 | 180 |
| V | Smoldering Chair in Living Room | 1162–4902 | 744–4896 | 353 |
| VI | Smoldering Chair in Living Room
(Air Conditioning on Second Floor) | 1156–4252 | 2030–4248 | 3541 |
| VII | Smoldering Mattress in Bedroom | Alarm not Reached | Alarm not Reached | Not Sure |
| VIII | Fully involved living room | 76–232 | - | 230 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).