A Deep Learning Model for Ship Trajectory Prediction Using Automatic Identification System (AIS) Data
Abstract
1. Introduction
2. Methodology
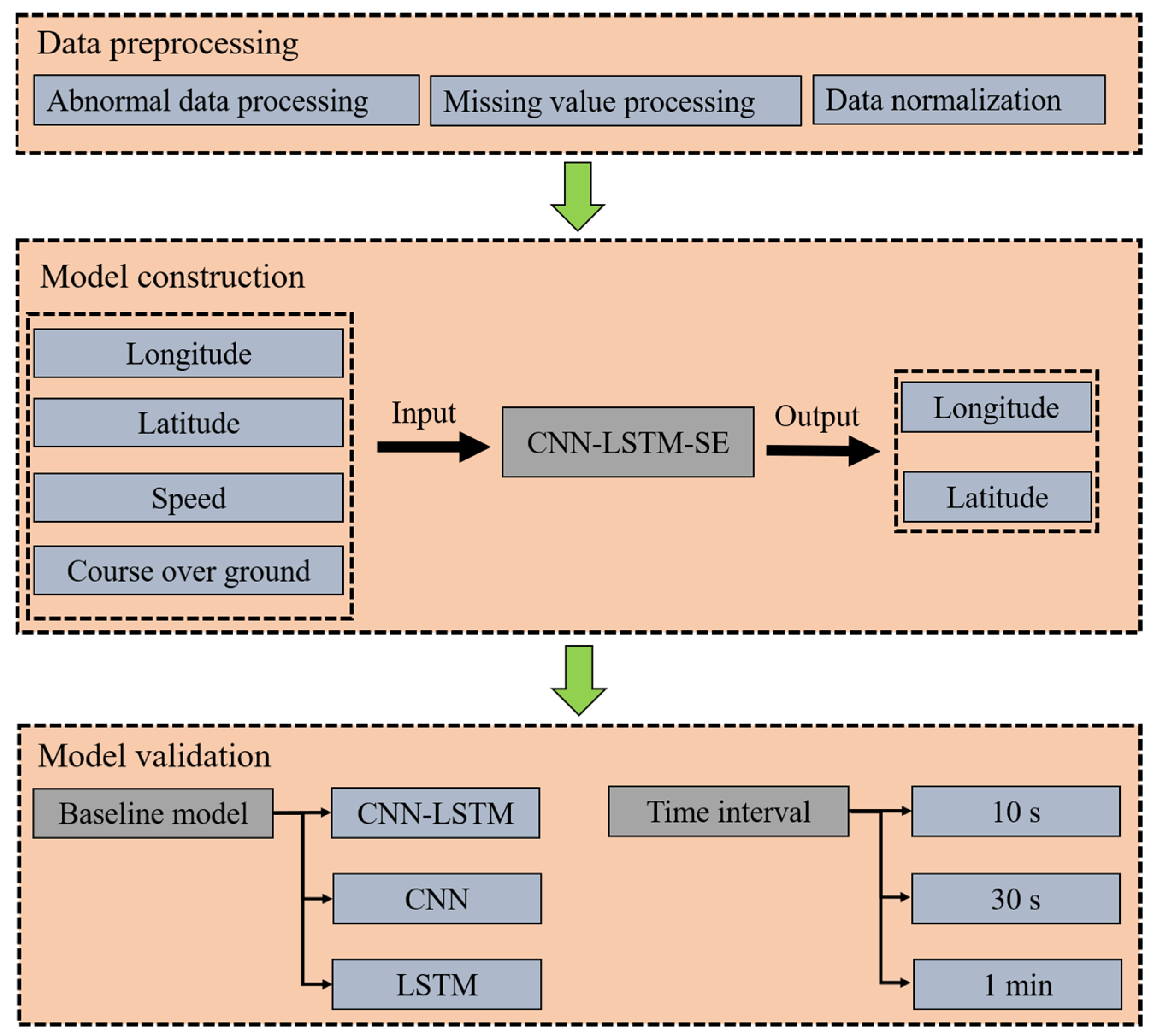
2.1. Research Framework
2.2. Data Preprocessing
2.3. Ship Trajectory Prediction Based on CNN-LSTM-SE
2.3.1. Convolutional Neural Network (CNN)
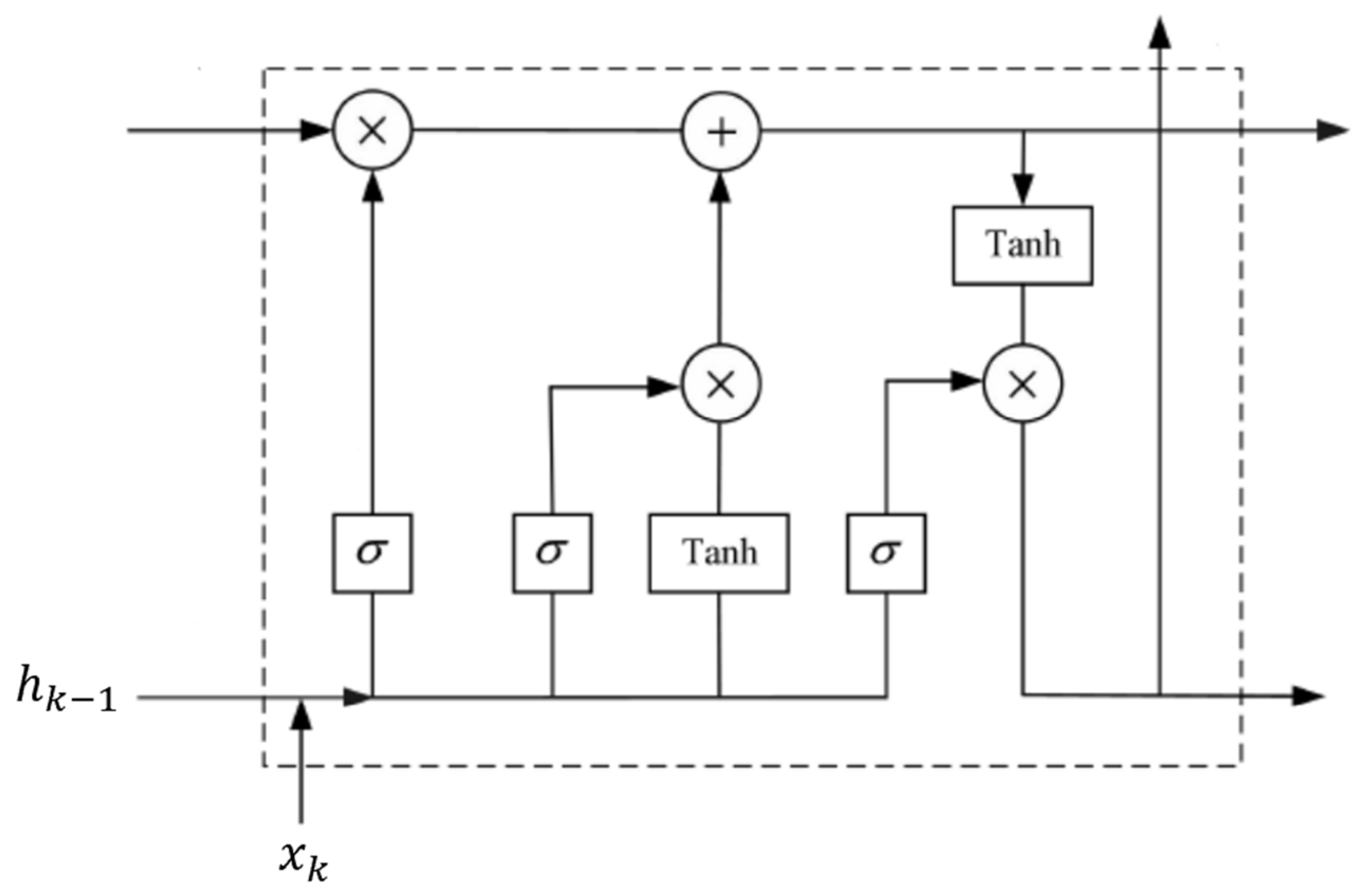
2.3.2. Long Short-Term Memory (LSTM)
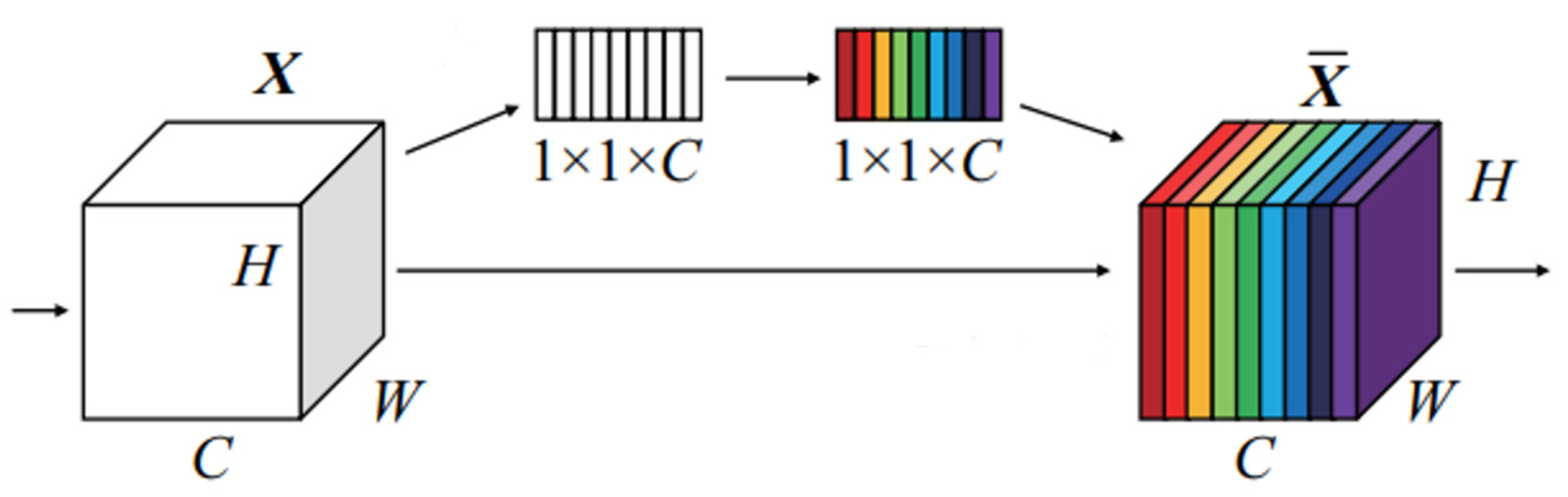
2.3.3. Squeeze-and-Excitation Network (SE)
2.3.4. CNN-LSTM-SE Model
2.4. Evaluation Index
3. Experiments
3.1. Experimental Setup
3.2. Experimental Data
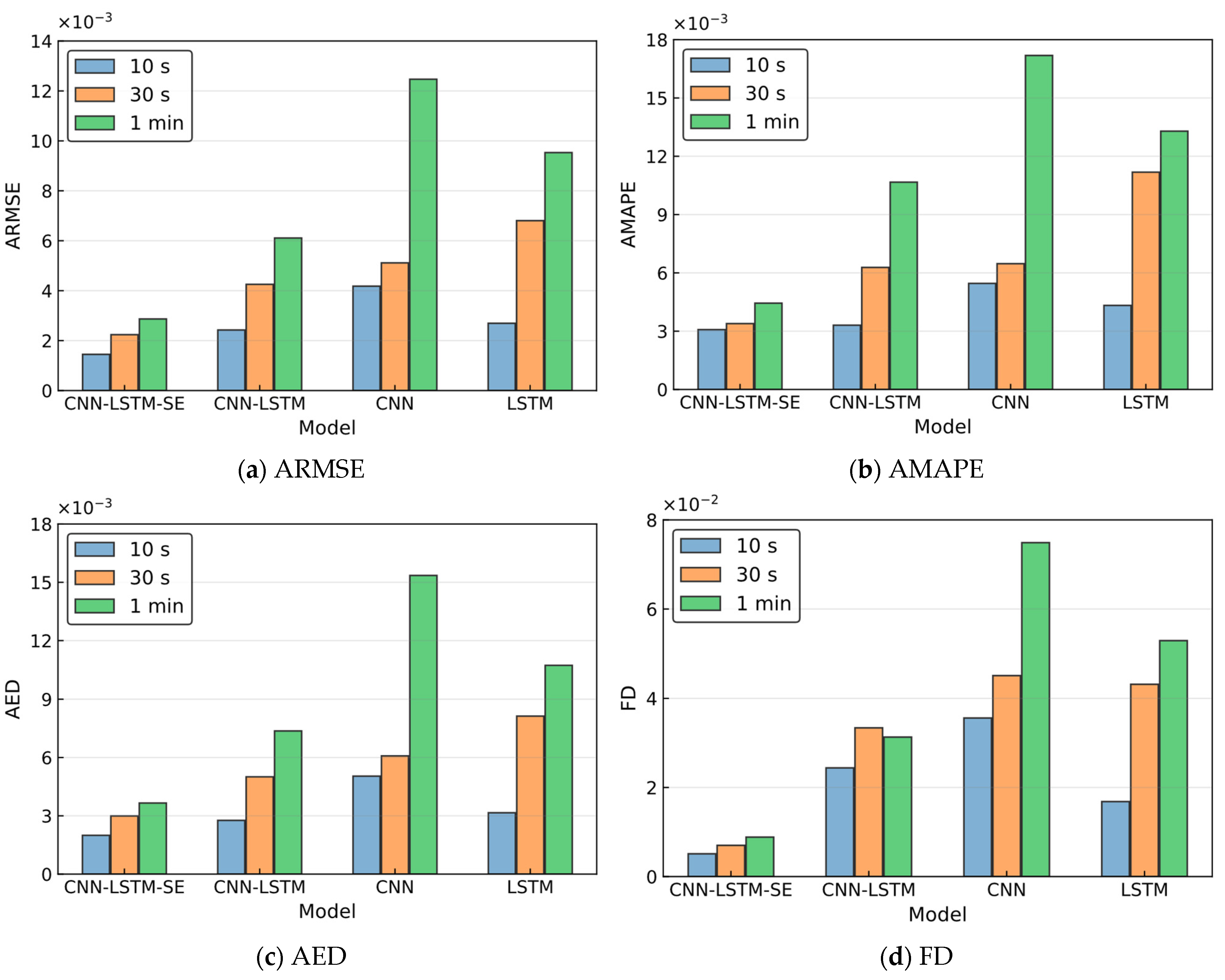
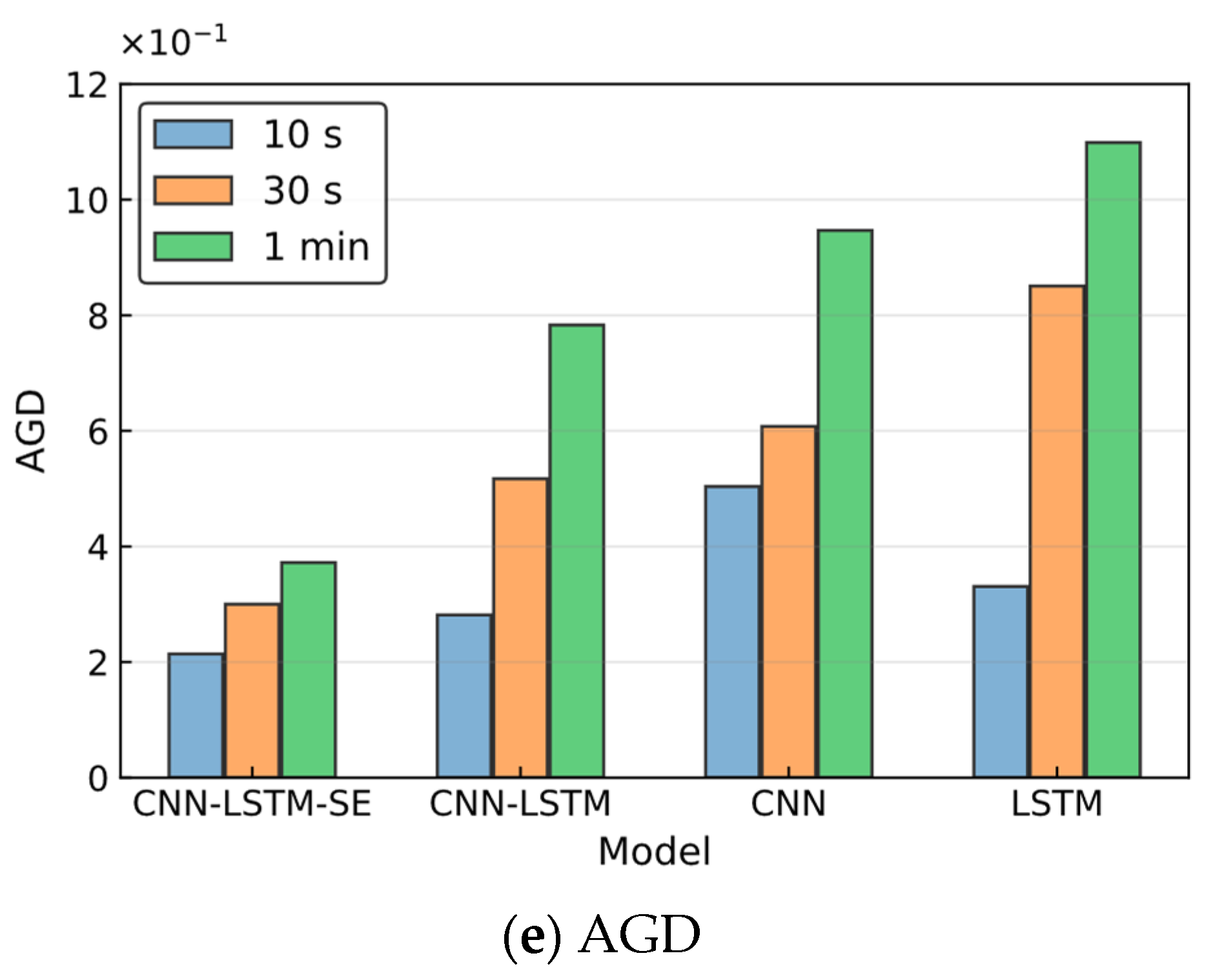
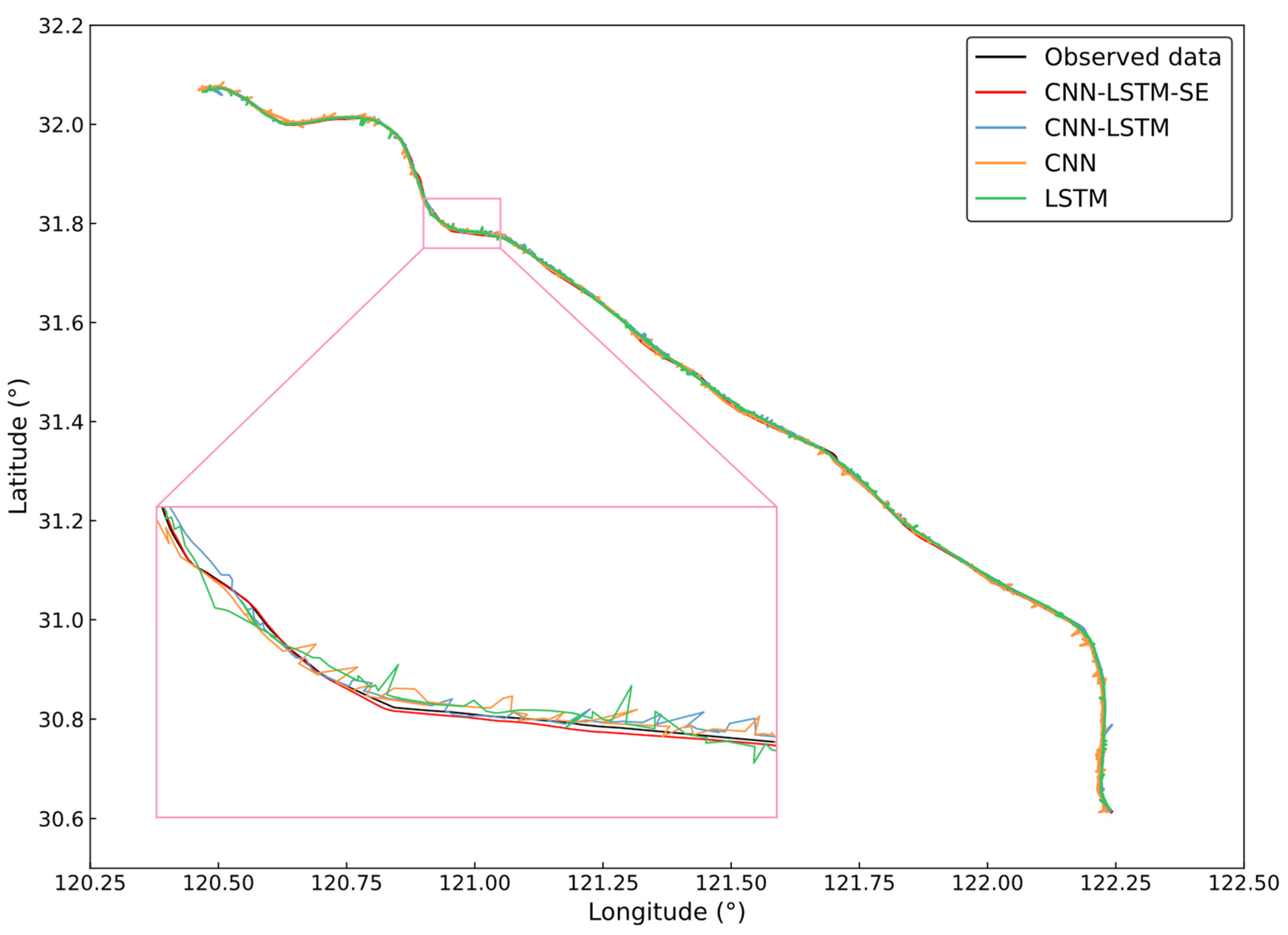
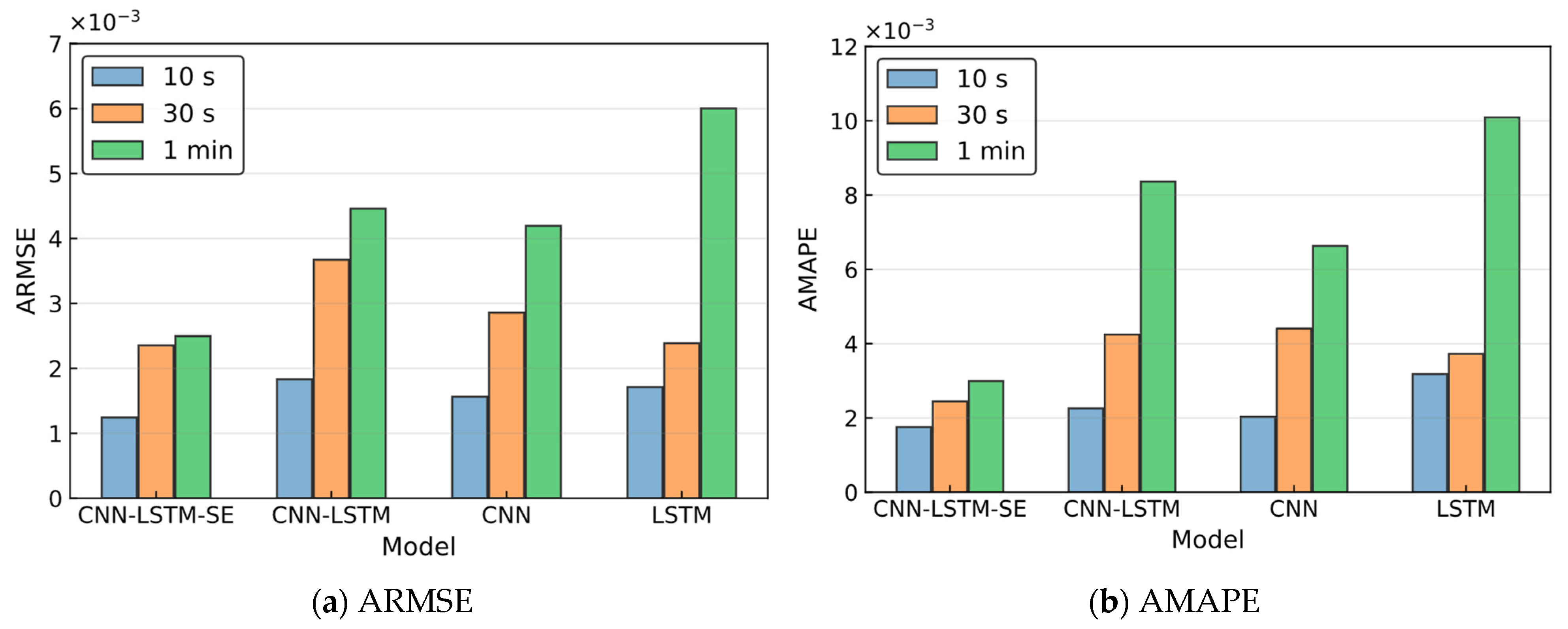
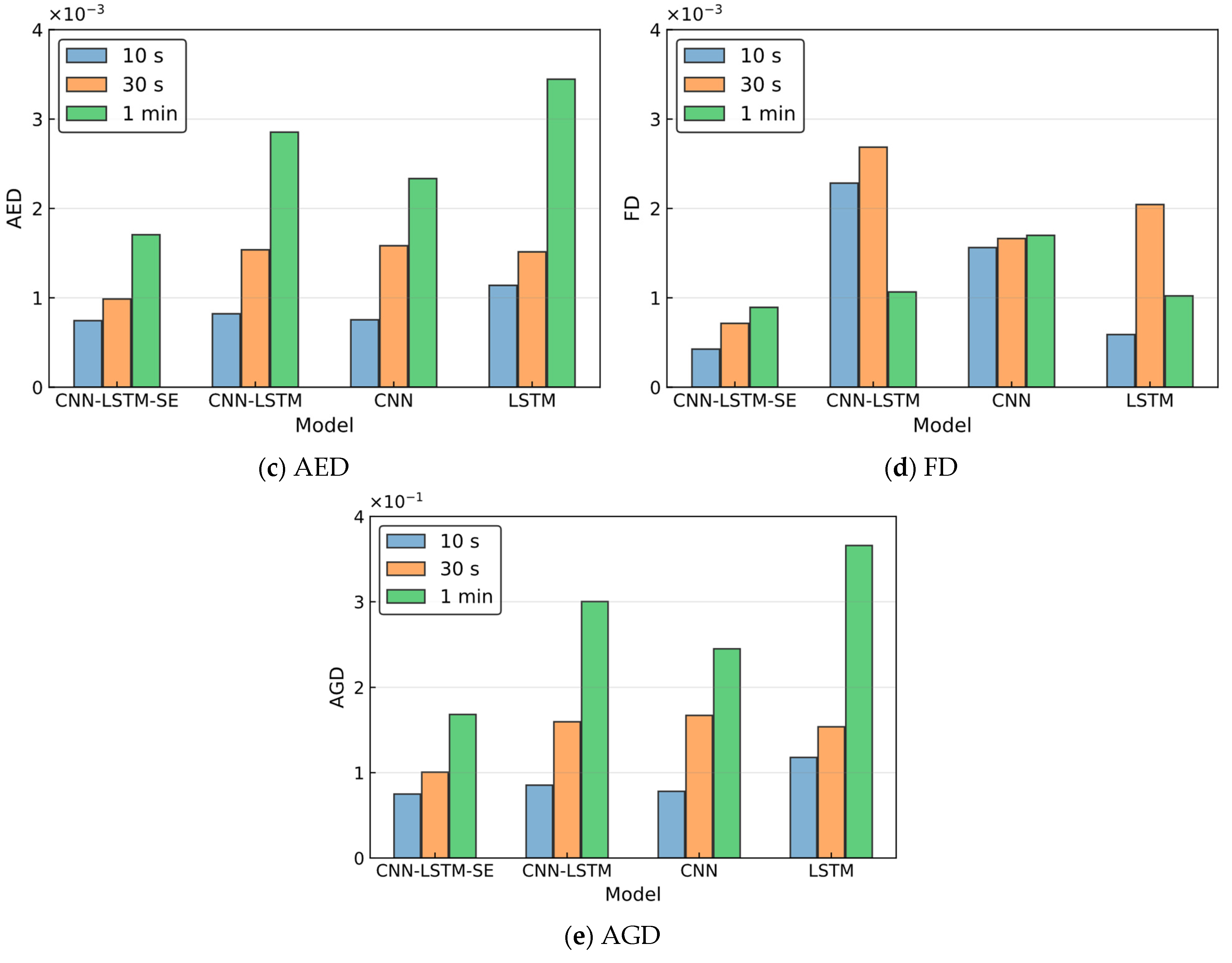
3.3. Results
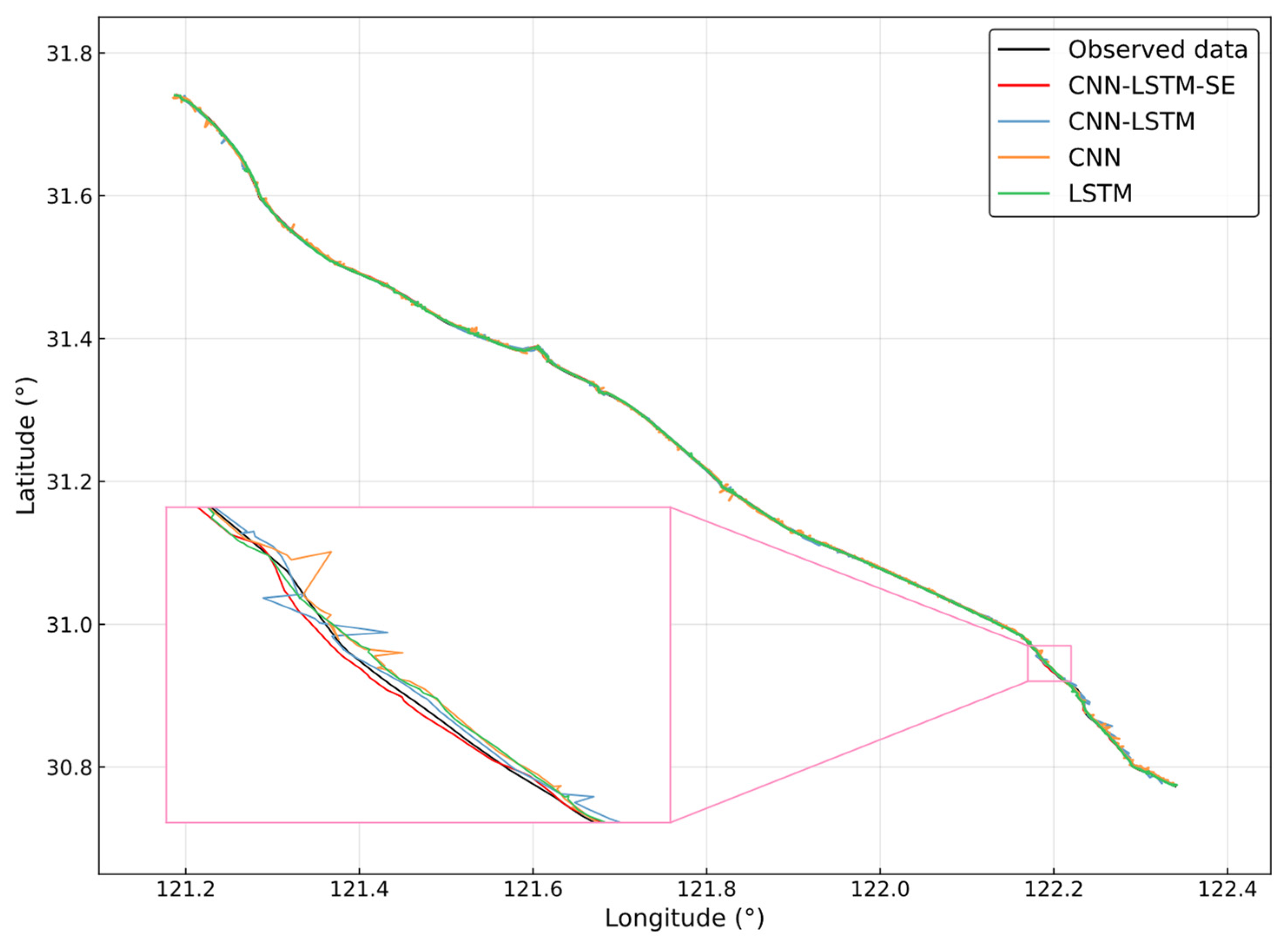
3.3.1. Analysis of Ship-1 Trajectory Prediction Results
3.3.2. Analysis of Ship-2 Trajectory Prediction Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, D.; Ma, W.; Hao, S.; Jin, S.; Qu, F. Ship’s Response to Low-Sulfur Regulations: From the Perspective of Route, Speed and Refueling Strategy. Comput. Ind. Eng. 2021, 155, 107140. [Google Scholar] [CrossRef]
- Benz, L.; Münch, C.; Hartmann, E. Development of a Search and Rescue Framework for Maritime Freight Shipping in the Arctic. Transp. Res. A Policy Pract. 2021, 152, 54–69. [Google Scholar] [CrossRef]
- Zhou, Y.; Daamen, W.; Vellinga, T.; Hoogendoorn, S. Review of Maritime Traffic Models from Vessel Behavior Modeling Perspective. Transp. Res. Part C Emerg. Technol. 2019, 105, 323–345. [Google Scholar] [CrossRef]
- Guo, S.; Mou, J.; Chen, L.; Chen, P. An Anomaly Detection Method for AIS Trajectory Based on Kinematic Interpolation. J. Mar. Sci. Eng. 2021, 9, 609. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Y.; Li, B.; Qi, Z. Ship Abnormal Behavior Detection Method Based on Optimized GRU Network. J. Mar. Sci. Eng. 2022, 10, 249. [Google Scholar] [CrossRef]
- Chen, K.; Zhu, Y.; Yan, K.; Cai, Y.; Ren, Z.; Gao, D. The Ship Track Prediction Method Based on Long Short-term Memory Network. Ship Ocean Eng. 2019, 48, 121–125. [Google Scholar] [CrossRef]
- Gao, M.; Shi, G.-Y. Ship-Handling Behavior Pattern Recognition Using Ais Sub-Trajectory Clustering Analysis Based on the T-Sne and Spectral Clustering Algorithms. Ocean Eng. 2020, 205, 106919. [Google Scholar] [CrossRef]
- Murray, B.; Perera, L.P. Ship behavior prediction via trajectory extraction-based clustering for maritime situation awareness. J. Ocean Eng. Sci. 2022, 7, 1–13. [Google Scholar] [CrossRef]
- Rodger, M.; Guida, R. Classification-Aided SAR and AIS Data Fusion for Space-Based Maritime Surveillance. Remote Sens. 2021, 13, 104. [Google Scholar] [CrossRef]
- Murray, B.; Perera, L.P. A Dual Linear Autoencoder Approach for Vessel Trajectory Prediction Using Historical Ais Data. Ocean Eng. 2020, 209, 107478. [Google Scholar] [CrossRef]
- Gao, D.; Zhu, Y.; Zhang, J.; He, Y.; Yan, K.; Yan, B. A Novel MP-LSTM Method for Ship Trajectory Prediction Based on Ais Data. Ocean Eng. 2021, 228, 108956. [Google Scholar] [CrossRef]
- Feng, H.; Cao, G.; Xu, H.; Ge, S. IS-STGCNN: An Improved Social spatial-temporal graph convolutional neural network for ship trajectory prediction. Ocean Eng. 2022, 266, 112960. [Google Scholar] [CrossRef]
- Liu, R.W.; Liang, M.; Nie, J.; Lim, W.Y.B.; Zhang, Y.; Guizani, M. Deep Learning-Powered Vessel Trajectory Prediction for Improving Smart Traffic Services in Maritime Internet of Things. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3080–3094. [Google Scholar] [CrossRef]
- Chen, X.; Wei, C.; Zhou, G.; Wu, H.; Wang, Z.; Biancardo, S.A. Automatic Identification System (AIS) Data Supported Ship Trajectory Prediction and Analysis via a Deep Learning Model. J. Mar. Sci. Eng. 2022, 10, 1314. [Google Scholar] [CrossRef]
- Qian, L.; Zheng, Y.; Li, L.; Ma, Y.; Zhou, C.; Zhang, D. A New Method of Inland Water Ship Trajectory Prediction Based on Long Short-Term Memory Network Optimized by Genetic Algorithm. Appl. Sci. 2022, 12, 4073. [Google Scholar] [CrossRef]
- Liu, J.; Shi, G.; Zhu, K. Vessel Trajectory Prediction Model Based on AIS Sensor Data and Adaptive Chaos Differential Evolution Support Vector Regression (ACDE-SVR). Appl. Sci. 2019, 9, 2983. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.; Niu, J.; Wu, Q.M.J.; Li, G. Track Prediction for HF Radar Vessels Submerged in Strong Clutter Based on MSCNN Fusion with GRU-AM and AR Model. Remote Sens. 2021, 13, 2164. [Google Scholar] [CrossRef]
- Volkova, T.A.; Balykina, Y.E.; Bespalov, A. Predicting Ship Trajectory Based on Neural Networks Using AIS Data. J. Mar. Sci. Eng. 2021, 9, 254. [Google Scholar] [CrossRef]
- Park, J.; Jeong, J.; Park, Y. Ship Trajectory Prediction Based on Bi-LSTM Using Spectral-Clustered AIS Data. J. Mar. Sci. Eng. 2021, 9, 1037. [Google Scholar] [CrossRef]
- Suo, Y.; Chen, W.; Claramunt, C.; Yang, S. A Ship Trajectory Prediction Framework Based on a Recurrent Neural Network. Sensors 2020, 20, 5133. [Google Scholar] [CrossRef]
- Bao, K.; Bi, J.; Gao, M.; Sun, Y.; Zhang, X.; Zhang, W. An Improved Ship Trajectory Prediction Based on AIS Data Using MHA-BiGRU. J. Mar. Sci. Eng. 2022, 10, 804. [Google Scholar] [CrossRef]
- Sørensen, K.A.; Heiselberg, P.; Heiselberg, H. Probabilistic Maritime Trajectory Prediction in Complex Scenarios Using Deep Learning. Sensors 2022, 22, 2058. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Lu, J.; Chen, X.; Yan, Z.; Yan, Y.; Sun, Y. High-fidelity data supported ship trajectory prediction via an ensemble machine learning framework. Phys. A 2022, 586, 126470. [Google Scholar] [CrossRef]
- Gao, D.; Zhu, Y.; Soares, C.G. Uncertainty modelling and dynamic risk assessment for long-sequence AIS trajectory based on multivariate Gaussian Process. Reliab. Eng. Syst. Safe 2023, 230, 108963. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, L.; Qian, L.; Cheng, B.; Hou, W.; Zhuang, Y. Sine-SSA-BP Ship Trajectory Prediction Based on Chaotic Mapping Improved Sparrow Search Algorithm. Sensors 2023, 23, 704. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, S.; Feng, D. A New Method for Short-Term Traffic Flow Prediction Based on Multi-Segments Features. In Proceedings of the 2020 12th International Conference on Machine Learning and Computing, Shenzhen, China, 15–17 February 2020; ACM: New York, NY, USA, 2020; pp. 34–38. [Google Scholar] [CrossRef]
- Zhao, T.; Wu, X. Pyramid Feature Attention Network for Saliency Detection. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3080–3089. [Google Scholar] [CrossRef]
- Wang, K.; Ma, C.; Qiao, Y.; Lu, X.; Hao, W.; Dong, S. A Hybrid Deep Learning Model with 1dcnn-Lstm-Attention Networks for Short-Term Traffic Flow Prediction. Phys. A Stat. Mech. Appl. 2021, 583, 126293. [Google Scholar] [CrossRef]
- Hu, Y.K.; Xia, W.; Hu, X.X.; Sun, H.Q.; Wang, Y.H. Prediction of Ship Track Based on Recurrent Neural Network. Sys. Eng. Elect. Technol. 2020, 42, 871–877. [Google Scholar] [CrossRef]
- Capobianco, S.; Millefiori, L.M.; Forti, N.; Braca, P.; Willett, P. Deep Learning Methods for Vessel Trajectory Prediction Based on Recurrent Neural Networks. IEEE Trans. Aero. Elec. Sys. 2021, 57, 4329–4346. [Google Scholar] [CrossRef]
- Tengesdal, T.; Johansen, T.A.; Brekke, E.F. Ship Collision Avoidance Utilizing the Cross-Entropy Method for Collision Risk Assessment. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11148–11161. [Google Scholar] [CrossRef]
- Liu, Z.; Zhuang, Y.; Jia, P.; Wu, C. A Novel Underwater Image Enhancement and Improved Underwater Biological Detection Pipeline. arXiv 2022. [Google Scholar] [CrossRef]
- Wu, S.; Chen, X.; Shi, C.; Shi, C.; Fu, J.; Wang, S. Ship detention prediction via feature selection scheme and support vector machine (SVM). Marit. Policy Manag. 2022, 49, 140–153. [Google Scholar] [CrossRef]
- Zhao, J.; Yan, Z.; Chen, X.; Han, B.; Wu, S.; Ke, R. k-GCN-LSTM: A k-hop Graph Convolutional Network and Long–Short-Term Memory for ship speed prediction. Phys. A 2022, 606, 128107. [Google Scholar] [CrossRef]
- Cornia, M.; Baraldi, L.; Serra, G.; Cucchiara, R. Predicting Human Eye Fixations via an LSTM-Based Saliency Attentive Model. IEEE Trans. Image Process. 2018, 27, 5142–5154. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Yu, C.-H.; Lin, Y.-T.; Su, H.-L.; Kan, K.-W.; Liu, F.-C.; Chen, C.-T.; Lin, Y.-T.; Hsu, H.-F.; Lin, Y.-H. The Potential Application of Spring Sargassum glaucescens Extracts in the Moisture-Retention of Keratinocytes and Dermal Fibroblast Regeneration after UVA-Irradiation. Cosmetics 2019, 6, 17. [Google Scholar] [CrossRef]
- Ran, X.; Shan, Z.; Fang, Y.; Lin, C. An LSTM-Based Method with Attention Mechanism for Travel Time Prediction. Sensors 2019, 19, 861. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 7132–7141. [Google Scholar]
- Peng, Y.; Xiang, W. Short-Term Traffic Volume Prediction Using GA-BP Based on Wavelet Denoising and Phase Space Reconstruction. Phys. A 2020, 549, 123913. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Li, T.; Guo, J.; Huang, W.; Wei, Y.; Cao, J. An Interpretable Model for Short Term Traffic Flow Prediction. Math. Comput. Simul. 2020, 171, 264–278. [Google Scholar] [CrossRef]
- Mazzarella, F.; Vespe, M.; Alessandrini, A.; Tarchi, D.; Aulicino, G.; Vollero, A. A novel anomaly detection approach to identify intentional AIS on-off switching. Expert Syst. Appl. 2017, 78, 110–123. [Google Scholar] [CrossRef]
- Wang, S.; He, Z. A Prediction Model of Vessel Trajectory Based on Generative Adversarial Network. J. Navig. 2021, 74, 1161–1171. [Google Scholar] [CrossRef]

| Model | Time Interval | Parameter Name | Optimal Parameters |
|---|---|---|---|
| CNN-LSTM-SE | 10 s | Kernel size | 2 |
| Stride | 2 | ||
| LSTM node | 300 | ||
| Linear layer node | 100 | ||
| Output layer node | 2 | ||
| 30 s | Kernel size | 2 | |
| Stride | 1 | ||
| LSTM node | 300 | ||
| Linear layer node | 100 | ||
| Output layer node | 2 | ||
| 1 min | Kernel size | 2 | |
| Stride | 1 | ||
| LSTM node | 150 | ||
| Linear layer node | 50 | ||
| Output layer node | 2 |
| Time Interval | Model | ARMSE | AMAPE | AED | FD | AGD |
|---|---|---|---|---|---|---|
| 10 s | CNN-LSTM-SE | 0.0014 | 0.0031 | 0.0020 | 0.0051 | 0.2141 |
| CNN-LSTM | 0.0024 | 0.0033 | 0.0028 | 0.0244 | 0.2816 | |
| CNN | 0.0042 | 0.0055 | 0.0050 | 0.0356 | 0.5037 | |
| LSTM | 0.0027 | 0.0043 | 0.0032 | 0.0168 | 0.3308 | |
| 30 s | CNN-LSTM-SE | 0.0022 | 0.0034 | 0.0030 | 0.0070 | 0.3001 |
| CNN-LSTM | 0.0043 | 0.0063 | 0.0050 | 0.0334 | 0.5171 | |
| CNN | 0.0051 | 0.0065 | 0.0061 | 0.0451 | 0.6077 | |
| LSTM | 0.0068 | 0.0112 | 0.0081 | 0.0432 | 0.8504 | |
| 1 min | CNN-LSTM-SE | 0.0029 | 0.0044 | 0.0037 | 0.0089 | 0.3721 |
| CNN-LSTM | 0.0061 | 0.0107 | 0.0074 | 0.0313 | 0.7831 | |
| CNN | 0.0125 | 0.0172 | 0.0154 | 0.0749 | 0.9467 | |
| LSTM | 0.0095 | 0.0133 | 0.0107 | 0.0529 | 1.0987 |
| Time Interval | Model | ARMSE | AMAPE | AED | FD | AGD |
|---|---|---|---|---|---|---|
| 10 s | CNN-LSTM-SE | 0.0012 | 0.0018 | 0.0007 | 0.0043 | 0.0750 |
| CNN-LSTM | 0.0018 | 0.0023 | 0.0008 | 0.0228 | 0.0854 | |
| CNN | 0.0016 | 0.0020 | 0.0008 | 0.0156 | 0.0781 | |
| LSTM | 0.0017 | 0.0032 | 0.0011 | 0.0059 | 0.1179 | |
| 30 s | CNN-LSTM-SE | 0.0024 | 0.0024 | 0.0010 | 0.0071 | 0.1006 |
| CNN-LSTM | 0.0037 | 0.0042 | 0.0015 | 0.0269 | 0.1597 | |
| CNN | 0.0029 | 0.0044 | 0.0016 | 0.0166 | 0.1671 | |
| LSTM | 0.0024 | 0.0037 | 0.0015 | 0.0204 | 0.1538 | |
| 1 min | CNN-LSTM-SE | 0.0025 | 0.0030 | 0.0017 | 0.0089 | 0.1682 |
| CNN-LSTM | 0.0045 | 0.0084 | 0.0029 | 0.0107 | 0.3002 | |
| CNN | 0.0042 | 0.0066 | 0.0023 | 0.0170 | 0.2448 | |
| LSTM | 0.0060 | 0.0101 | 0.0034 | 0.0102 | 0.3659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xiao, Y. A Deep Learning Model for Ship Trajectory Prediction Using Automatic Identification System (AIS) Data. Information 2023, 14, 212. https://doi.org/10.3390/info14040212
Wang X, Xiao Y. A Deep Learning Model for Ship Trajectory Prediction Using Automatic Identification System (AIS) Data. Information. 2023; 14(4):212. https://doi.org/10.3390/info14040212
Chicago/Turabian StyleWang, Xinyu, and Yingjie Xiao. 2023. "A Deep Learning Model for Ship Trajectory Prediction Using Automatic Identification System (AIS) Data" Information 14, no. 4: 212. https://doi.org/10.3390/info14040212
APA StyleWang, X., & Xiao, Y. (2023). A Deep Learning Model for Ship Trajectory Prediction Using Automatic Identification System (AIS) Data. Information, 14(4), 212. https://doi.org/10.3390/info14040212





