Abstract
Various software engineering paradigms and real-time projects have proved that software testing is the most critical and highly important phase in the SDLC. In general, software testing takes approximately 40–60% of the total effort and time involved in project development. Generating test cases is the most important process in software testing. There are many techniques involved in the automatic generation of these test cases which aim to find a smaller group of cases that could allow for an adequacy level to be achieved which will hence reduce the effort and cost involved in software testing. In the structural testing of a product, the auto-generation of test cases that are path focused in an efficient manner is a challenging process. These are often considered optimization problems and hence search-based methods such as genetic algorithm (GA) and swarm optimizations have been proposed to handle this issue. The significance of the study is to address the optimization problem of automatic test case generation in search-based software engineering. The proposed methodology aims to close the gap of genetic algorithms acquiring local minimum due to poor diversity. Here, dynamic adjustment of cross-over and mutation rate is achieved by calculating the individual measure of similarity and fitness and searching for the more global optimum. The proposed method is applied and experimented on a benchmark of five industrial projects. The results of the experiments have confirmed the efficiency of generating test cases that have optimum path coverage.
1. Introduction
Software systems have been expanded in many sections of our life such as transportation, health, and media. Software reliability is very important and software testing is a way for verifying the right to work of a software system. Software testing is the most expensive process and also time-consuming in the entire SDLC. The users accept a software product only after the same has undergone all levels of testing [1,2,3]. The effectiveness of software testing is mainly the verification and validation of the product and is dependent on the maximum errors found and rectified before the release of a product. This activity in turn is dependent on the test case’s quality. Test case generation is an important thing to be completed in a testing life cycle. As a measure to cut down costs, many methods have been attempted for automating the process of test case generation which has produced good results in dynamic testing. Automatic software testing is a widely studied area in search-based software engineering (SBSE). Search-based methods have been the focus of research in automating the process of test case generations for achieving control flow over the structure. Automated test data generation is a persistent problem in achieving adequate control flow dependencies in a program [4]. An important goal of auto-test generation includes the creation of multi-level test data which would ensure a robust product with quality through proper checking of code paths [5]. One of the key tasks in testing is the generation of data for testing which satisfies a given adequate criteria and the best example is white box testing [6]. In search-based techniques, the coordination between the parameter setting and the performance of optimization is complicated and has less understanding [7]. With certain coverage conditions given, the challenge of test case generation lies in searching for a dataset that leads to maximum coverage when it is given as input to the program under testing. Although automated testing gives more efficiency in the SD, there are more complicated problems associated with it. There is no generalization of the testing scripts across multiple applications and can easily create many challenges for the application [8]. Many model-based testing has been developed where the test cases are handwritten by humans and only the execution has been automated in the entire process. Further, the auto-test script generation is found to be capable of identifying defects based on the paths, and often the assertions are coded explicitly over the script.
As a consequence, the present approaches do not provide a complete automatic test case generation and there is a substantial manual process needed. Metaheuristic algorithms such as genetic algorithms are more used in the optimization problems of software engineering. These use a global searching phenomenon and are easily applicable to many optimization issues. The generation of software test cases is also an optimization problem where the objective is that the effort should be in a minimum order and the number of errors identified should be maximum [9]. The difficulty in identifying the controlled path has a consequence of stagnation during experiments. This stagnation in turn causes a delay in the overall process. Hence, additional data have to be made used for generating auto test cases and hence increases the data cost [10]. The search-based techniques are found to have an issue in achieving global optimum [11]. This manuscript proposes an adaptive genetic algorithm for the auto test case generation where the population is diverse. The aim of the study is to bring in a technical contribution to address the issue of path generation in structural program testing. The work proposes an adaptive genetic algorithm for automatic test case generation that maintains population diversity. The significant contribution of the study is that the proposed method addresses the issue of cross-over and mutation by dynamically adjusting them based on the variations among individual and fitness value similarities. This enhances the search exploration to achieve more global optimum. The proposed methodology addresses structural path testing, and future research is aimed to extend the model for non-structural path testing. A dynamic adjustment on the cross-over and mutation rate is completed in line with the variations in the similarity of individuals and the fitness functions that increase the searching options of obtaining the global optimum.
The rest of the manuscript is structured as: Section 2 gives the gist of the related works carried out on the genetic algorithm-based methods for automatic test case generation. Section 3 describes the problem considered and Section 4 deals with the proposed methodology in detail. Section 5 elaborates on the experimental analysis and results discussion. Section 6 gives the conclusion with future research directions.
2. Related Works
A range of methods have been proposed in the literature for addressing the issue of auto-test case generations and the most effective method was found to be the use of metaheuristic algorithms [12,13,14]. When this technique is applied for the automatic generation of test cases, the information on the feedback that concerns the tested program is used for determining whether the data included for the test meets the requirements. The mechanism of feedback gradually makes adjustments to the test data till the requirements are met. These methods have led to substantial research growth in the recent past. A FU_B method [15,16] was proposed where the software cases are generated based on an annealing GA that is simulated. A technique for an optimized test case generation by making use of the tabula and clustering methods was introduced in [17,18,19]. Among many of the methods proposed, genetic algorithms are widely adopted. The process of auto-test case generation was looked at as an NP problem [20]. The primary focus here was to make a choice on the appropriate test cases in an automated manner. In order for the test cases to be generated, there are many algorithms proposed based on the inspiration from nature [21,22]. These algorithms help in generating appropriate test cases. The automatic test cases were generated using the GA and analysis of mutation was performed in [23,24,25,26].
The US-RDG [27,28] was proposed where the focus was on the grey box testing. The proposed method combines the session information of the user and obtains a request dependence graph(RDG) of the application being tested. Genetic algorithms are then used for the auto-generation of test cases. The proposed method was simulated, and the results prove that it has better impacts than the conventional session-based testing approaches. The coverage of the path and the rate at which the faults were detected were high within a small suite of test beds. An EGA (evolutionary genetic algorithm) [29] was proposed which made use of the simulated and annealing-motivated approach for the auto-generation of test cases is introduced. The fitness function of the target is brought by the instrumentation of the program with the aid of the branch distance method and GA is used for the generation of test cases. Experiments were conducted and comparisons with other state-of-the-art methods are carried out in terms of the total count of generations that were needed for reaching the target and the time consumed for generating the test cases.
A novel method using GA and mutation optimization was proposed in [30]. The proposed method intends to generate test cases automatically by the combination of random search and conscious refinement. All of the test cases are generated in a random manner initially and then the set of required cases is filtered using the GA. In order to measure the sufficiency of the number of test cases to be generated, the scores were assigned to mutation based on the analysis. The experiment was carried out in a C program module and the results obtained achieved 100% coverage in both branches and boundaries. An evolutionary structure-based GA was proposed in [31,32] for test case generation such that there is a high level of coverage in code is completed by a minimum number of test cases.
In the literature, it has been seen that many parameters are involved in determining the performance of a genetic algorithm which include cross-over and mutation. These parameters are vital for determining how the search space is exploited. Improper parameterization stops the algorithm to discover solutions of high quality as these parameters have a large influence on performance. An unfortunate fact here is in general, the algorithms are configured by the practitioner who is not likely to be an expert in search-based solutions. The major gap in the literature is that only very few studies have been carried out to address the issue of genetic algorithms falling in local optimum due to less diversity. This hinders the performance of automatic test case generation which uses genetic algorithms.
Problem Definition
In the modern era of software engineering, many research works have acknowledged the effective performance of genetic algorithms in test case generation. The performance of GAs in most of the cases directly depends on the parameters which include cross-over rate PC and mutation rate Pm [33,34]. These parameters decide how the given space of search is exploited and when the parameters are defined poorly, solution discovery becomes more complicated as the parameter values are directly responsible for the performance of an algorithm [35,36]. Practically, the choice of an algorithm is left to the practitioner who often does not have expertise in search-based methods. In addition, the GA’s population might come to local optimum owing to the substantial decline in the diversity in a later part which stops the auto-test case generations using genetic methods. In order to overcome this issue, this work introduces an adaptive genetic algorithm that can adjust the rate of cross-over and mutation in a dynamic manner in the course of optimization through the effective maintenance of a diverse population.
3. Proposed Methodology
The proposed framework takes the genetic algorithm as a base. These are widely used metaheuristic algorithms in search-based software engineering (SBSE) [37]. The core issue in these cases is how the collaborative performance of the GA is ensured in the process of testing. The proposed framework is shown in Figure 1.
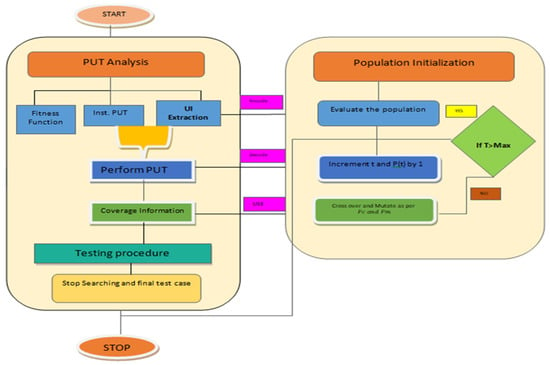
Figure 1.
Proposed AGA framework.
The proposed framework as seen in the figure is seen from two perspectives. The first is in terms of PUT (program under test) analysis and the second is in terms of population initialization. The following section explains the proposed framework.
3.1. PUT Analysis
The PUT analysis compartment in the proposed method has different components which are summarized here.
3.1.1. Fitness Function
Path-oriented methods are largely used in automatic test case generation as it is cost-effective. Here, the model converts the global objectives into small local objectives which can traverse through one target path across multiple branches of the program. As it is an optimization problem, the design of the fitness function is required which is completed by this block.
3.1.2. Instrument PUT
In order for the proposed model to understand what is being completed in a program, the instrumentation block collects the coverage of data without affecting the underlying logic of the program. The instrumentation is performed here using the beta version of the real-time application.
3.1.3. UI Extraction
This block is used to exhibit possible test cases of the program under test. The results from UI extraction are the success and failure scenarios of the GUI test. In the proposed method, UI extraction is performed for all the programs under tests taken from different industries.
Perform PUT: The outcomes of instrumentation and UI extraction are modeled and fed as input to the actual performer, i.e., using the parser.
3.1.4. Coverage
The individual paths that are decoded then enter as input to the drive and collect back the appropriate information on coverage. The test cases that are generated then realize when the coverage is complete for a scenario and in that GA component, it records the complete information on the coverage of individual path testing nodes. For example, if a particular path is set as a target, the optimal solution will be obtained at the end of the program.
The working explanation for the block B of the architecture proposed is explained in the following Section 3.3.
In general, from the testing perspective, the process has a couple of important components, a parser, and a test driver. The former is responsible for performing analysis on the lexical and syntax of the code for the adaptive function. The proposed method addresses both of them. The latter is used to input the parameters to the application that is under testing. From the GA’s perspective, feedback is used based on the value of fitness for guiding the update of a population which focuses on genetic operations such asselection, mutations, and cross-over for decoding the formal into original parameters. It enables us to learn about the superiority of solution vectors with the help of the driver. The following section provides more information.
The fundamental flow of the algorithm is as shown: The following actions are to be performed at the initial level based on the program to be tested in terms of statistical analysis.
- The information from the interface is to be extracted.
- The instrumentation formulation corresponds to the structural components of the program with pre-determined test adequacy condition C.
- Formulation of the fitness function as per condition C.
The parameters chosen as the input are then to be coded inside the unique vector genes. In parallel, the population denoted by which is the generation inside the population P, is then initialized in association with the cross-over rate denoted by and the rate of mutation given as and time is initialized as 0. Then, the individuals thatare decoded are entered as the input parameter for driving the program under tests and for collecting the concerned information of the coverage. The value of fitness for every individual is then calculated for obtaining the P(t) by making use of the input parameters that are associated with the information on the coverage. Last, the P(t) is modified by making use of pre-defined operators such as selection, mutation, and cross-over till the point of termination is satisfied. In the framework proposed, the stopping criteria are set based on acouple of situations that are expected in general.
- When the evolution reaches a maximum, i.e., MAXGEN.
- When the test case generated realizes the throughout coverage on the target that covers all the elements.
From the testing point of view, the proposed process has a couple of important components namely the parser which is static, and the test driver.The former takes up the responsibility of program analysis based on the semantics and lexically. This is performedto design the instrument and the adaptive fitness function. The latter is mainly supposed to do the job of entering the parameters inside the application that is subjected to test and collect all the information on the coverage and thereafter calculate the fitness. Fromthe GA point of view, feedback is used as per the fitness for guiding the updated population. The formal description of the parameters is decoded into actual ones by keeping the focus on general operators of GA such as the selection, cross-over, and mutation. The test drivers hencehelp in learning the superiority of the solution’s vector.
3.2. Computing Fitness Function
The path-focused techniques are largely adopted in testing the program structures as these are proven cost-effective [38]. These methods require the execution of a given path based on the control flow. The test data generator module in the proposed method helps in breaking down the global minimum into different partial minimums that consist of dealing with a single target path with numerous branches in a program. The problem of generating test cases with genetic methods can be considered a problem of optimization [39] where the test data generation has to cover the complete path and designing the fitness function is very important to solve the same. In order to cover separate branches. The fitness function is formulated as a function which takes up a target “t” as a path with an input “x” where x takes the values as in represented as vectors belonging to the input of the function, which is under test with the domain Dmn of the inputs xn denoting the set of all possible values which xn is capable of holding.
As a fact, the fitness function computation gets involved with couple of components called the and the [40]. The level of approach is made used for the assessment of the path followed by the given in put in line with the targeted branch for calculating the control dependencies which are not executed through the path. Figure 2 shows the control graph generated of the program under study. Consider that ith individual of xi over the and the path of the target is denoted by P(TARGET).
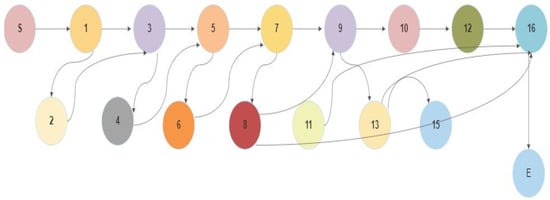
Figure 2.
Control flow graph of the proposed model. Numbers denote the node numbers, Source (S) and End node (E).
The level of approach for calculating the fitness function is given in the Equation (1).
In the above equation, denotes the count of the nodes that are untraversed in the path in line to the target P(TARGET) and the modulus function gives the numerical value of the count of nodes for the structural path which is set as target when the given input is for executing the program to be tested. For instance, suppose that P(TARGET) = “S →1,2,3,4,5,6,8,16→E” and 1,2,3,4,5,7,9,10,11,12,13,14,15,16→E, then the level of approach can be computed as in Equation (2).
As far as the is considered for the calculation of fitness, the Korel and Tray’s method [41] are used. Consider a scenario where the teat case execution gets diverged from the branch, which is set as the target, the expresses as how far the input satisfies the predicate’s constraint set at which the test case flow went “wrong”. In other words, it defines as how close the given input was climbing down to the next level of approach. Some of the basic functions are shown in Table 1. Here, Q represents a positive integer in such a way that an objective function is always returning a value that is smaller than 0 if at all the predicate computation is false. The maximum is not pre-determined and hence the conventional approach for normalization is not applicable. Instead, a normalized as in the Equation (3) is used.

Table 1.
BDF for branch predicates.
The fitness can be computed as in Equation (4) for the complete program under testing and are calculated by the and by applying normalization as per Table 1.
Table 1 describes some of the branch distant functions. Here, the K represent the positive integer in a way that the objective function shall return a non-zero value when the predicate is not true. As the maximum distance of the branch is not usually known, the normalization cannot be applied in a standard way and hence it is completed through Equation (2).
The fitness function is then assigned for each of the chromosome on the path “”. Here, denotes the total branch count in the path which is set as the target. gives the weight on each branch and is the constant which takes the value of 0.01 in the proposed experiment. In general, the difficulty lies in reaching every individual and varies among different branches which need the weights to be initialized differently on them. As a thumb rule, the degree of nesting (Dn) is greater. The difficulty in arriving at the branch is also great. For this, the weights of the branches need to be increased. The degree of nesting of a particular branch Dbchi can be calculated using the statistical analysis of the program.
The fitness function is then assigned to every chromosome, i.e., the individual input (x) of the path which is taken as the target. Here, S denotes the total count of the branches in the target and W denotes the branch weight. The level of difficulty in reaching the individual varies between branches. Hence, the weights are to be set differently. Normally, the larger degree of nesting of a branch tends to a greater degree of difficulty to reach the branch which results in a condition to increase the weight. The degree of nesting is calculated through static program analysis. The maximum degree of nesting is denoted as ndMAX and the minimum as ndMIN. The nesting weight is then calculated using Equation (4).
Figure 2 depicts the sample control flow graph of a program that classifies the four times of a triangle.
Initial Parameter Setting
The parameter configuration is completed in various methods in software engineering either by fine-tuning before the optimization or dynamically adjusting during the run time. The latter method is adopted here as it has more effect than fine-tuning as the adaptive theory does not have a predefined schedule and also does not extend those solutions. The proposed method used the population diversity method for designing the AGA operators by dynamic adjustments. In order to address the issue of pre-mature convergence, the Hamming method is used to define the parameters.
3.3. Adjustment of the Parameters
There exists two different ways in which the parameters can be adjusted in the software engineering paradigm. The first is to tune the parameter values ahead of optimization and the second is by adjusting the parameters dynamically during the run time. Runtime adjustments are called controlled parameter settings and are more effective than the former as the schedule is not predefined in the case of adaptive control and here, the size of the solution is not extended [41]. In the proposed model, first, a divertive metric for the population is introduced and the same is used for the design of adaptive GA operations for the dynamical adjustment of parameters.
3.3.1. Diverse Metric of Population
The important issue in most metaheuristic algorithms is premature convergence. Various studies have shown that there is an intact relation between premature convergence and the lack of sufficient diversity in the population. A reasonable description of population diversity is seen as a critical problem for most search-based algorithms. The Hamming distance is one of the common ways to define the same, but it does not take on individual fitness-related information into consideration [42]. A diverse metric for the population is introduced in this paper which deals with both issues.
3.3.2. GA Parameter Design
Genetic-oriented operators are often essential for acquiring the second generation in a given set of populations and are very crucial in the evolutionary incremental iterations. The conventional GA that has constant values for crossover and mutation rates faces the search stop hindrance phenomenon in a later part owing to the lack of proper diversity over the entire population.
The conventional operators such as selection, crossover, and mutation are dynamically adjusted for improvement in the efficiency of the algorithm. Selection operators are used for the determination of chromosomes which are to be used as the parent in the offspring creation which again populates the consequent generation. The choice of methods includes the probability-based techniques and the roulette method, which are the best to use in generic GAs. However, these suffer from drawbacks such as maintaining a constant level of pressure inside the search space which is required to select the best individual. In the initial iterations, the variance of the fitness is found to be usually of a high order. As the most-fit individuals will have a higher probability of being granted greater opportunities to become a parent owing to the high pressure in the search space. This again will lead to the issue of premature convergence and also as in the later part of the generations as when the fitness between the individuals seems similar, the variance of fitness also will become low which leads to stagnation in the searching process.
The linear method of ranking for all individuals is the method that is proposed to handle the issue. The individuals here are ranked based on fitness and a temporary fitness value is assigned based on the rank, instead of using the fitness value directly. A ranking methodology with a given value Y where 1 < Y2, allows a certain value to Y for the best individual (1.0) for the intermediate individual. The worst will be assigned the value of 2-Z. The proposed framework uses a linear method of ranking for the selection operator where the Y is assigned a value of 1.8. The entire operation is then regulated using the probability function of the crossover PC. The rate of crossover is defined as the guarantee of the population being diverged. If this has a large value, the better individual’s gene that has a high fitness value will be destroyed easily. On the other hand, if it is too small, the search process will be slowed down. It is assumed that the parent is denoted by xi and xj and owing to the selection, crossover, and mutation parameters the PC can be obtained through Equation (6).
In order to avoid PC becoming greater than 1, the degree in which the population is to be diverged (DPD) must be normalized. Although there are many ways to normalize, NORMALIZEDPD = where is a constant and is the method which is adopted in the proposed method. The PC calculation brings out the fact that when the DPD is kept low, the rate of crossover is to be increased and in parallel, the diversity in the population is also improved. When the “f” is lower than the , it prevents premature convergence. The PC is set to 1 for avoiding over-optimization of the parameters in a given solution space.
The primary purpose of the mutation is for increasing the local searching capability of the genetic algorithms and to maintain population diversity. The same is achieved by the bit flipping of the binary set of strings at a certain probability PM. On the one side, it is very difficult for producing fresh individuals and the diversity of the population cannot be assured if the rate of mutation is very small. On the other, it may also cause notable damage to the genes leading to the degradation of search methods. Hence, an adaptive probability for the mutation is used here based on the DPD. The same is obtained through Equation (7).
Here, the PM is set to a smaller value and the rate of mutation shall be changed in an adaptive manner for maintaining the diverse population inline with the diversity of individual’s while
4. Implementation
For the sake of descriptive convenience, the proposed method is abbreviated as AGA and the pseudo-code of the same is depicted in Figure 3. The population is made to evolve as per the AGA criteria till an optimum solution is arrived at. The stopping criteria of the proposed method are as follows:

Figure 3.
Algorithm for test case generation.
- The information on the coverage is recorded on individual traversal of test paths. When a specific path is completely covered, the optimum solution is found, and the search is stopped.
- As some of the test paths may be difficult for covering or left uncovered, the search stops after reaching a given number of iterations.
5. Results and Discussion
This section deals with the experimental analysis of the proposed AGA model when applied for the automatic test case generation for path coverage on a benchmark and on five industrial project codes. In order to prove the effectiveness of the proposed AGA, conventional methods such as GA, IGA, and random search methods are taken for comparison. A basic system configuration was used. The experiments were conducted to test the efficiency of the proposed AGA. The efficiency is mapped in terms of the mean execution (ME) for a given range of input and different sizes of POP, the execution time, the maximum number of evaluations completed for complete traversal, and the average execution time. The success rate is defined and calculated for the proposed method and compared with that of other methods. It is seen that the proposed method outperforms the other methods and also seen that the proposed method shows consistency in terms of success rate even when the range is increased while other methods degrade in performance as the range of POP is increased. Table 1 and Table 2 depicts the same.

Table 2.
Comparative analysis of performance metrics.
Criteria for Evaluation and Parameter Adjustments
The criteria for termination are when at least a single datum is found for traversing the path under test or if the number of total iterations in the evolution has reached the current value. Some of the criteria for evaluations for testing the effectiveness are as under:
EVAL: It is the total evaluations for an individual on every method.
T: It is the search time taken for generating the test data for every method.
SR: It is the rate of success, and it is defined as the success percentage in the generation of test data for traversing the path to the total count of experiments carried out.
To ensure a very small difference in the sampling of individuals, the proposed method adopts a similar population size and the same initial level of population. The conventional parameters such as the individual code are handled by binary codes, the selection operator will be handled by the linear ranking method, and the single point mutation handles the rate of mutation. The crossover and mutation rates are assigned the initial values of 0.1 and 0.9, respectively. In the proposed method, the parameter for weightage η is used for the calculation of the degree of diversity in population—DPS is set to 0.5 for making it convenient to compare with other methods.
- The AGA proposed in this paper have success in generation of datum for traversing the path under target with few evaluations on each input. For instance, when the range of input is (250), the evaluation mean is 6012.5 which is about 12.4 times smaller than that of the IGA and 29.2times lower than that of the GA. This is the same when compared to that of the random approach, where the mean (E) is 115,248.6 which is 32.5 times more than the proposed AGA as shown in Table 3. The same is represented in Figure 4.
 Table 3. Comparison of AGA and random approach.
Table 3. Comparison of AGA and random approach.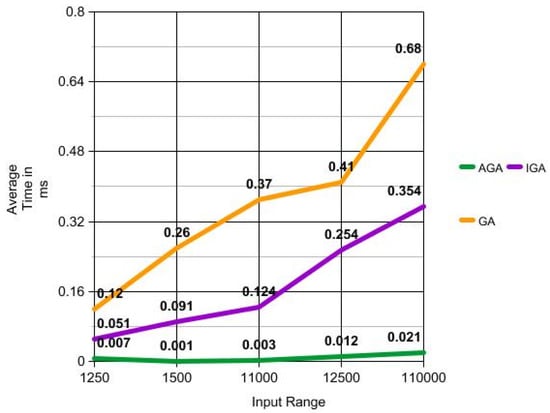 Figure 4. Comparison of execution time.
Figure 4. Comparison of execution time. - As far as the searching time is considered, the average T(s) in the case of AGA is 0.0007 whereas, in the case of IGA and GA, these are 0.051 and 0.12, respectively, for the input range [1250]. By this, we can come to the conclusion that the other methods take more time to execute than the proposed AGA. It is also seen that the random method has less time complexity than IGA and GA and it is due to the fact that it does not include the time taken for the computation of fitness value and the same is given in Figure 5.
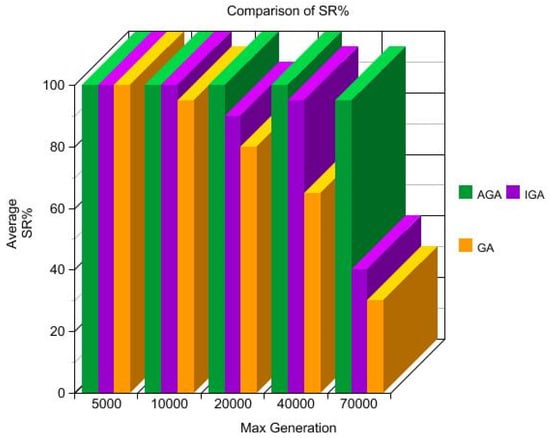 Figure 5. Comparison of success rate.
Figure 5. Comparison of success rate. - Although the evaluation process of the proposed AGA is similar to that of other genetic approaches such as IGA and GA, the total count of the evaluation has substantially reduced because of the adaptive method of adjusting the parameters which makes the time required for searching to be minimal. This proves the efficiency of the proposed method in optimization.
- The success rate was found to be 100% when the range of input was kept small. However, as the range of input reached 11,000, the SR in the case of IGA and GA is reduced to 90% and 80%, respectively. The case is still worse when the range of input reaches 110,000, where the proposed AGA has still 90% SR, but for the other methods, it comes down drastically to 40% and 30%, respectively. Figure 6 and Figure 7 represent the same.
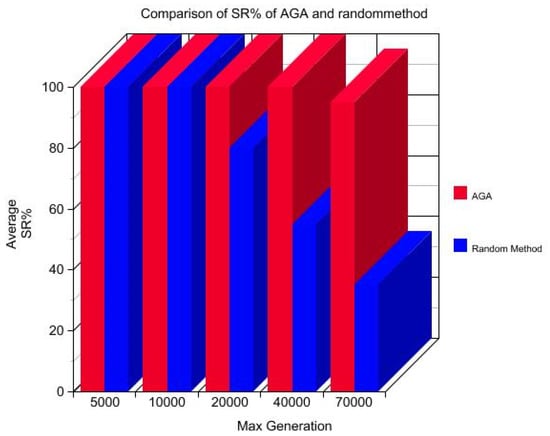 Figure 6. Comparison of success rate of AGA and random method.
Figure 6. Comparison of success rate of AGA and random method.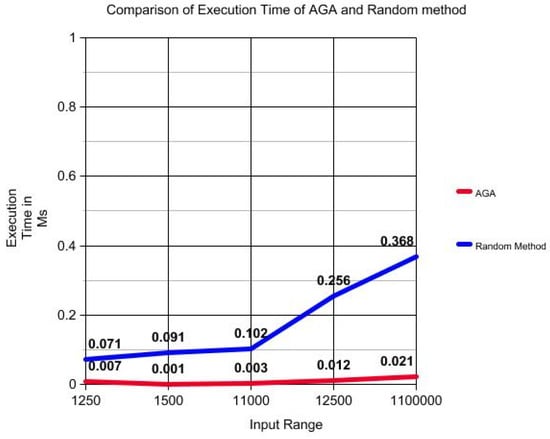 Figure 7. Comparison of execution time of AGA and random method.
Figure 7. Comparison of execution time of AGA and random method.
Figure 8 and Figure 9 depict the comparison of mean evaluation and standard deviation of the same. It is seen that the proposed method has performed better. For further verification of the efficiency of the proposed method, there were fiveindustrial programs chosen [25]. The traversing path is selected randomly for each of the programs. The setting of the parameters is shown in Table 4. LOC denotes the line of code. It is arranged that in this set of experiments, each of the methods runs 100 times. The statistical results are tabulated in Table 5.
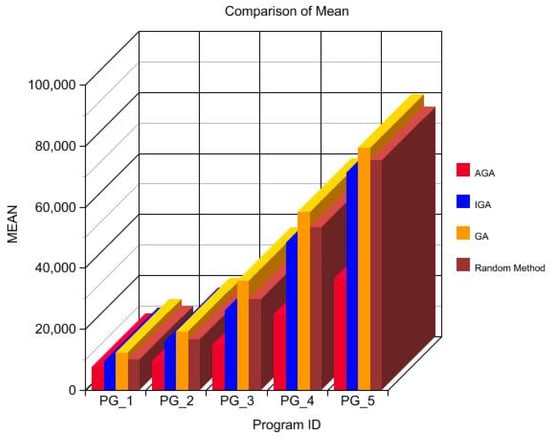
Figure 8.
Comparison of mean evaluation.
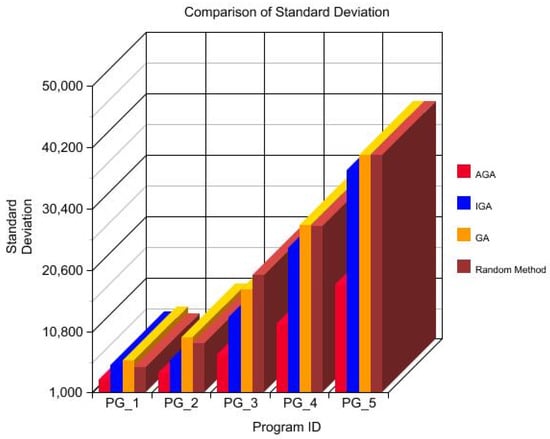
Figure 9.
Comparison of standard deviation.

Table 4.
Parameter setting for the industrial trial programs.

Table 5.
Mean search time and success rate comparison of industrial programs.
- The proposed method proves effective once again in terms of the mean (E) for the generation of path-focused data than the other methods (IGA and GA and also the random method) for the five programs considered. Table 5 and Figure 8 and Figure 9 describe the same. As is seen in Figure 8, the effectiveness of the proposed AGA is more obvious as the scale of the input is increased.
- As the standard deviation is considered on the five industrial programs, the PG-1 has an SD of 3012.4 which is 21.2% lesser than the 5412.5 of IGA and 25.8% lesser than that of the 6214.8 in case of GA and 23.4% lesser than the 5064.2 of that of the random method. This indicates that the performance and the stability of the proposed AGA are more than the other methods taken for comparative study. The same is depicted in Figure 10 and Figure 11.
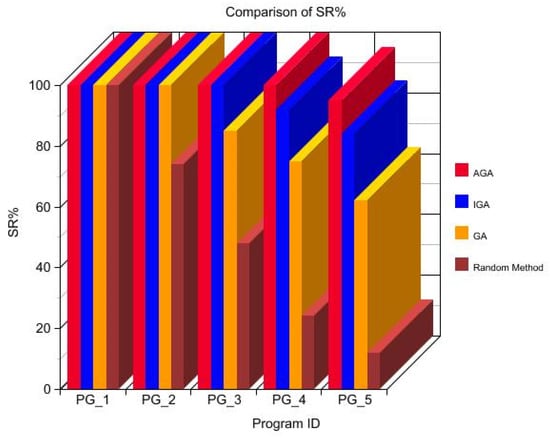 Figure 10. Comparison of success rate in industrial program data.
Figure 10. Comparison of success rate in industrial program data.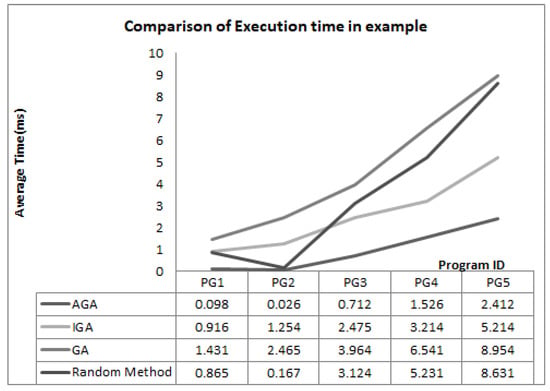 Figure 11. Comparison of execution time in industrial programs in terms of the T(s) on the 5 industrial programs considered, the proposed method doesnot bag the best in all the programs considered. As it is seen that the PG_3 has some deviations. However, it is evident that the average T(s) is minimum as far as when the proposed method is implemented in the industrial programs. It is also evident from Table 6 that the SR is maintained as 100% in case of AGA till the input reaches a large LOC of 8500 whereas, in case of other methods under study, there is a constant decrease in the SR% as the LOC is increased and it reaches 84%, 62%, and 12% as far as the IGA, GA, and random are compared with. The graphical representation is given in Figure 10 and Figure 11, respectively.
Figure 11. Comparison of execution time in industrial programs in terms of the T(s) on the 5 industrial programs considered, the proposed method doesnot bag the best in all the programs considered. As it is seen that the PG_3 has some deviations. However, it is evident that the average T(s) is minimum as far as when the proposed method is implemented in the industrial programs. It is also evident from Table 6 that the SR is maintained as 100% in case of AGA till the input reaches a large LOC of 8500 whereas, in case of other methods under study, there is a constant decrease in the SR% as the LOC is increased and it reaches 84%, 62%, and 12% as far as the IGA, GA, and random are compared with. The graphical representation is given in Figure 10 and Figure 11, respectively.
6. Conclusions
This paper presents a model for generating automatic test cases based on the adaptive learning of a genetic algorithm (AGA). The proposed method is intended to increase the efficiency by effective maintenance of the diversity of the population under study by introducing dynamic adjustment of crossover and mutation parameters. The experiments prove that the proposed AGA is more efficient than the other variations such as IGA and GA and alsorandom-based methods when used for path-focused testing. The future directions are planned on the efficient design of adaptive operators and to design methodology for identifying the best fitness automatically when the defect identification is considered. Further enhancements are also planned in enhancing the proposed method of non-structural testing.
Author Contributions
Conceptualization, M.R. and K.L.; Methodology R.S.; Software, M.R.; Validation, L.E.S.; Formal analysis, K.L.; Investigation, L.E.S.; Writing—original draft, M.R. and K.L.; Writing—review & editing, K.L. and R.S.; Project administration, K.L.; Funding acquisition, K.L. and L.E.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| SDLC | Software development life cycle |
| GA | Genetic algorithm |
| SOSE | Search based software engineering |
| FU_B | Fuzzy union bias |
| NP | Non-deterministic polynomial |
| US-RDG | Unsupervised request dependence graph |
| EGA | Evolutionary genetic algorithm |
| BDF | Branch distance functions |
| BOOL | Boolean |
| EVAL | Evaluation |
| AGA | Adaptive genetic algorithm |
| IGA | Improved genetic algorithm |
| LOC | Lines of code |
References
- Prasanna, M.; Sivanandam, S.N.; Venkatesan, R.; Sundarrajan, R. A Survey on Automatic Test Case Generation. Acad. Open Internet J. 2015, 15. Available online: http://www.acadjournal.com/ (accessed on 12 November 2022).
- Mcminn, P. Search-based software test data generation: A survey. Softw. Test. Verif. Reliab. 2004, 14, 105–156. [Google Scholar] [CrossRef]
- Ribeiro, J.C.B.; Zenharela, M.A.; Vega, F.F.D. Adaptive Evolutionary Testing: An Adaptive Approach to Search-Based Test Case Generation for Object-Oriented Software. Stud. Comput. Intell. 2010, 284, 185–197. [Google Scholar]
- Varshney, S.; Mehrotra, M. Search based software test data generation for structural testing: A perspective. ACM SIGSOFT Softw. Eng. Notes 2013, 38, 1–6. [Google Scholar] [CrossRef]
- Fu, B. Automated Software Test Data Generation Based on Simulated Annealing Genetic Algorithms. Comput. Eng. Appl. 2005, 41, 82–84. [Google Scholar]
- Eiben, A.E.; Smit, S.K. Parameter tuning for configuring and analyzing evolutionary algorithms. Swarm Evol. Comput. 2011, 1, 19–31. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive Differential Evolution with Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Wu, N.; Song, F.; Li, X. Study of a Quantum Framework for Search Based Software Engineering. Int. J. Theor. Phys. 2013, 52, 2181–2186. [Google Scholar] [CrossRef]
- Korel, B. Dynamic method for software test data generation. Softw. Test. Verif. Reliab. 1992, 2, 203–213. [Google Scholar] [CrossRef]
- Do, H.; Elbaum, S.; Rothermel, G. Supporting Controlled Experimentation with Testing Techniques: An Infrastructure and its Potential Impact. Empir. Softw. Eng. 2005, 10, 405–435. [Google Scholar] [CrossRef]
- Fraser, G. Gamification of software testing. In Proceedings of the 12th International Workshop on Automation of Software Testing (AST’17), Buenos Aires, Argentina, 20–21 May 2017; IEEE Press: Buenos Aires, Argentina, 2017; pp. 2–7. [Google Scholar] [CrossRef]
- de Jesus, G.M.; Ferrari, F.C.; Porto, D.D.P.; Fabbri, S.C.P.F. Gamification in Software Testing: A Characterization Study. In Proceedings of the III Brazilian Symposium on Systematic and Automated Software Testing (SAST’18), Sao Carlos, Brazil, 17–21 September 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 39–48. [Google Scholar] [CrossRef]
- Abdulwareth, A.J.; Al-Shargabi, A.A. Toward a Multi-Criteria Framework for Selecting Software Testing Tools. IEEE Access 2021, 9, 158872–158891. [Google Scholar] [CrossRef]
- Bohme, M.; Paul, S. A Probabilistic Analysis of the Efficiency of Automated Software Testing. IEEE Trans. Softw. Eng. 2016, 42, 345–360. [Google Scholar] [CrossRef]
- Peng, Z.; Chen, T.-H.; Yang, J. Revisiting Test Impact Analysis in Continuous Testing from the Perspective of Code Dependencies. IEEE Trans. Softw. Eng. 2022, 48, 1979–1993. [Google Scholar] [CrossRef]
- Stadler, C.; Montanari, F.; Baron, W.; Sippl, C.; Djanatliev, A. A Credibility Assessment Approach for Scenario-Based Virtual Testing of Automated Driving Functions. IEEE Open J. Intell. Transp. Syst. 2022, 3, 45–60. [Google Scholar] [CrossRef]
- Xu, D.; Xu, W.; Kent, M.; Thomas, L.; Wang, L. An Automated Test Generation Technique for Software Quality Assurance. IEEE Trans. Reliab. 2015, 64, 247–268. [Google Scholar] [CrossRef]
- Oliveira, C.; Aleti, A.; Grunske, L.; Smith-Miles, K. Mapping the Effectiveness of Automated Test Suite Generation Techniques. IEEE Trans. Reliab. 2018, 67, 771–785. [Google Scholar] [CrossRef]
- Matinnejad, R.; Nejati, S.; Briand, L.C.; Bruckmann, T. Test Generation and Test Prioritization for Simulink Models with Dynamic Behavior. IEEE Trans. Softw. Eng. 2019, 45, 919–944. [Google Scholar] [CrossRef]
- Shahbazi, A.; Miller, J. Black-Box String Test Case Generation through a Multi-Objective Optimization. IEEE Trans. Softw. Eng. 2016, 42, 361–378. [Google Scholar] [CrossRef]
- Durelli, V.H.S.; Durelli, R.S.; Borges, S.S.; Endo, A.T.; Eler, M.M.; Dias, D.R.C.; Guimaraes, M.P. Machine Learning Applied to Software Testing: A Systematic Mapping Study. IEEE Trans. Reliab. 2019, 68, 1189–1212. [Google Scholar] [CrossRef]
- Kan, H.-X.; Wang, G.-Q.; Wang, Z.-D.; Ding, S. A method of minimum reusability estimation for automated software testing. J. Shanghai Jiaotong Univ. (Sci.) 2013, 18, 360–365. [Google Scholar] [CrossRef]
- Durán, A.; Benavides, D.; Segura, S.; Trinidad, P.; Ruiz-Cortés, A. FLAME: A formal framework for the automated analysis of software product lines validated by automated specification testing. Softw. Syst. Model. 2017, 16, 1049–1082. [Google Scholar] [CrossRef]
- Denisov, E.Y.; Voloboy, A.G.; Biryukov, E.D.; Kopylov, M.S.; Kalugina, I.A. Automated Software Testing Technologies for Realistic Computer Graphics. Program. Comput. Softw. 2021, 47, 76–87. [Google Scholar] [CrossRef]
- Gupta, M.; Fu, J.; Bastani, F.B.; Khan, L.R.; Yen, I.-L. Rapid goal-oriented automated software testing using MEA-graph planning. Softw. Qual. J. 2007, 15, 241–263. [Google Scholar] [CrossRef]
- Zhao, Z.-L.; Huang, D.; Ma, X.-X. TOAST: Automated Testing of Object Transformers in Dynamic Software Updates. J. Comput. Sci. Technol. 2022, 37, 50–66. [Google Scholar] [CrossRef]
- Suryasarman, V.M.; Biswas, S.; Sahu, A. RSBST: An Accelerated Automated Software-Based Self-Test Synthesis for Processor Testing. J. Electron. Test. 2019, 35, 695–714. [Google Scholar] [CrossRef]
- Godboley, S.; Panda, S.; Dutta, A.; Mohapatra, D.P. An Automated Analysis of the Branch Coverage and Energy Consumption Using Concolic Testing. Arab. J. Sci. Eng. 2017, 42, 619–637. [Google Scholar] [CrossRef]
- Tsai, B.; Stobart, S.; Parrington, N.; Mitchell, I. Automated class testing using threaded multi-way trees to represent the behaviour of state machines. Ann. Softw. Eng. 1999, 8, 203–221. [Google Scholar] [CrossRef]
- Khari, M.; Kumar, P.; Burgos, D.; Crespo, R.G. Optimized test suites for automated testing using different optimization techniques. Soft Comput. 2018, 22, 8341–8352. [Google Scholar] [CrossRef]
- Tramontana, P.; Amalfitano, D.; Amatucci, N.; Fasolino, A.R. Automated functional testing of mobile applications: A systematic mapping study. Softw. Qual. J. 2019, 27, 149–201. [Google Scholar] [CrossRef]
- Qi, X.-F.; Wang, Z.-Y.; Mao, J.-Q.; Wang, P. Automated Testing of Web Applications Using Combinatorial Strategies. J. Comput. Sci. Technol. 2017, 32, 199–210. [Google Scholar] [CrossRef]
- Hofer, F.; Russo, B. IEC 61131-3 Software Testing: A Portable Solution for Native Applications. IEEE Trans. Ind. Inform. 2019, 16, 3942–3951. [Google Scholar] [CrossRef]
- Bures, M.; Frajtak, K.; Ahmed, B.S. Tapir: Automation Support of Exploratory Testing Using Model Reconstruction of the System Under Test. IEEE Trans. Reliab. 2018, 67, 557–580. [Google Scholar] [CrossRef]
- Harrison, N.B. Teaching software testing from two viewpoints. J. Comput. Sci. Coll. 2010, 26, 55–62. [Google Scholar]
- Whitmire, D.; Alvin, C. A case study in software testing: Verification of a face identification algorithm for planar graphs. J. Comput. Sci. Coll. 2019, 35, 173–184. [Google Scholar]
- Manikumar, T.; Kumar, A.J.S.; Maruthamuthu, R. Automated test data generation for branch testing using incremental genetic algorithm. Sādhanā 2016, 41, 959–976. [Google Scholar] [CrossRef]
- Rubtsov, Y.F. Development of automated systems of scientific research for control and testing of electrical machinery. Russ. Electr. Eng. 2012, 83, 596–598. [Google Scholar] [CrossRef]
- Guo, X.; Okamura, H.; Dohi, T. Automated Software Test Data Generation with Generative Adversarial Networks. IEEE Access 2022, 10, 20690–20700. [Google Scholar] [CrossRef]
- de Matos, E.C.B.; Sousa, T.C. From formal requirements to automated web testing and prototyping. Innov. Syst. Softw. Eng. 2010, 6, 163–169. [Google Scholar] [CrossRef]
- Banerjee, D.; Yu, K.; Aggarwal, G. Image Rectification Software Test Automation Using a Robotic ARM. IEEE Access 2018, 6, 34075–34085. [Google Scholar] [CrossRef]
- Mirza, A.M.; Khan, M.N.A.; Wagan, R.A.; Laghari, M.B.; Ashraf, M.; Akram, M.; Bilal, M. ContextDrive: Towards a Functional Scenario-Based Testing Framework for Context-Aware Applications. IEEE Access 2021, 9, 80478–80490. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).