A Lattice-Based Certificateless Traceable Ring Signature Scheme

Abstract

A ring signature (RS) scheme enables a group member to sign messages on behalf of its group without revealing the definite signer identify, but this also leads to the abuse of anonymity by malicious signers, which can be prevented by traceable ring signatures (TRS). Up until that point, traceable ring signatures have been secure based on the difficult problem of number-theoretic (discrete logarithms or RSA), but since the advent of quantum computers, traditional traceable ring signatures may no longer be secure. Thus Feng proposed a lattice based TRS, which are resistant to attacks by quantum computers. However, that works did not tackle the certificate management problem. To close this gap, a quantum-resistant certificateless TRS scheme was proposed in the study. To the best of our knowledge, this is the first lattice based certificateless TRS. In detail, a specific TRS scheme was combined with the lattice-based certificateless signature technology to solve the certificate management problem while avoid key escrow problem. Additionally, a better zero-knowledge protocol is used to improve the computational efficiency of the scheme, and by reducing the soundness error of the zero-knowledge protocol, the number of runs of the zero-knowledge protocol is reduced, so that the communication overhead of the scheme is reduced. Under random oracle model, the proposed scheme satisfies tag-linkability, anonymity, exculpability and is secure based on the SIS problem and the DLWE problem. In conclusion, the proposed scheme is more practical and promising in e-voting.

1. Introduction

With the popularity of the Internet, a variety of intelligent applications have come into being, and the security of data and privacy is an important prerequisite in the information age. RS provides users with unconditional anonymity and does not require a ring administrator for their services. However, in e-voting [1,2], e-cash [3], blockchain [4], Vehicular Ad-Hoc Network (VANET) [5] and some application scenarios [6] that do not require full anonymity, unconditional anonymity allows some malicious users to sign the same event without restriction and without revealing their identity information, which poses certain security risks. For example, in e-voting and e-cash, users can sign multiple times for the same event without being detected, so both e-voting and e-cash require the protection of user anonymity while providing non-reusability, especially in e-cash, where non-reusability prevents double-spending attacks. This is where TRS comes in to meet these needs. The TRS is a balance between the strong traceability of group signatures and the strong anonymity of RS. When a malicious user irresponsibly signs multiple times in the same event, the traceability of the TRS can detect and find the malicious user, and when the user signs honestly, the anonymity remains. Thus, in applications where full anonymity is not required, TRS is more useful.

TRS operates primarily within the framework of PKI [7]. In this case, each user’s public-private key pair is generated by themselves, and in order to let others know that the user has a correspondence with their published public key, a trusted third-party authority needs to be brought in to issue a digital certificate proving the correspondence, which we generally refer to as a CA. As generating and verifying certificates require a certain amount of storage space and computational overhead, the management of certificates requires huge overhead as the number of users increases, which is often referred to as the CMP.

To solve CMP described above and to ease the administrative burden, Shamir et al. [8] designed an identity-based cryptography scheme in 1984. Its aim to optimize public key management by removing public key certificates. Instead of generating a public key, the user simply selects the identity information associated with it himself as the public key, for instance, name, email, etc. The user then simply sends his identity information to KGC and KGC generates private key to the user by identity information. As all of the private keys are produced by the KGC, there is a certain security risk if the KGC is malicious.

To solve KEP, Al-Riyami and Paterson et al. [9] designed a CLPKC scheme in 2003. Under the certificate-free framework, the user’s private key is divided into two components, one component is the private key generated by KGC, the other component is a random value of the user’s own choice, so KGC cannot get all the keys. Through such a design, CLPKC solves the KEP while removing the public key certificate.

But past CLTRS have been based on number-theoretic assumptions. Facing quantum computers, cryptographic schemes relied on traditional number theory may be able to be broken efficiently, and applications [10] designed around the security of traditional cryptographic schemes can become insecure. In 1994, the Shor algorithm proposed by Shor et al. [11] can break the widely used RSA encryption algorithm, so cryptographic schemes based on the RSA hard assumption may become less secure. Not only that, there are some quantum algorithms that can crack other difficult problems in number theory, the traditional cryptographic schemes may present security risks, so cryptographic schemes based on number theory will face great challenges. To address the security concerns posed by quantum computers, post-quantum cryptographic schemes and applications based on post-quantum cryptographic schemes have emerged successively, these include isogeny-based cryptographic scheme [12], the supersingular isogeny key encapsulation protocol [13], the variant of SABER and Falcon [14], the signature scheme CRYSTALS-Dilithium [15], lattice cryptography also being one of post-quantum cryptographic schemes. In 1996, Ajtai et al. [16] pioneered to prove that the difficulty of lattice-hard problems is equivalent in the average case to the worst case, which makes lattice-based cryptosystem have a theoretical basis for providing security proofs. In addition, lattice ciphers can build complex applications. Therefore, this paper aims to design a certificate-less traceable ring signatures on lattice, which is important for application background such as VAENT and e-voting.

1.1. Related Works

RS is first proposed by Rivest et al. [17] in 2001, it differs from group signatures in that it can be formed spontaneously, thus eliminating the need for group administrators. Subsequently, research on RS has grown and various RS schemes [18,19,20,21,22,23] have been proposed. Although RS provides anonymity to the users in the ring, they also facilitate malicious users, who can sign an event without restriction without revealing their identity. In some scenarios (e.g., electronic voting), we don’t want that to happen. Figure 1 is the signature process of the RS.

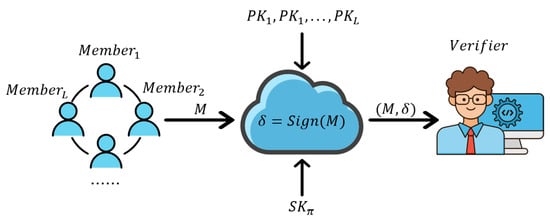
Figure 1. Ring Signature.

To limit the degree of anonymity of RS, Liu et al. [24] in 2004 constructed a LRS, it can link two signatures which signed by the same member. LRS limits the abuse of anonymity to a certain extent. Various improvements to LRS schemes [3,25,26,27,28,29,30] have subsequently been proposed. Although LRS can limit anonymity to some extent, honest users still have no way of knowing exactly which user is maliciously signing in multiple times.

In order to trace the identity of the malicious user, TRS emerged. This concept was first proposed by Fujisaki et al. [31] in 2007, where each user can only sign at most once under the same tag, and when a user signs two different messages, they are tracked by the tracking algorithm and their identity is revealed. Thus, TRS can make honest members anonymous while tracking malicious members, making TRS useful in many applications. Various improvements to TRS schemes [4,6,32,33,34,35,36] have also been proposed. Of these, ref. [32] improves the scheme of [31] by reducing the signature size and communication overhead. The relationship between the signature and ring sizes is linear in [31], while the signature size in [32] is square-root related to the ring size. [33] proposed an identity-based TRS, so that TRS does not have to bear huge certificate management overhead. Ref. [34] extends the number of times users can sign on the same label in TRS, allowing users to sign for K times. Only when the number of signatures exceeds K times, the user is traced. Ref. [6] constructs a TRS based on certificate-less, which eliminates the overhead of CMP of [31] and solves the KEP of [32], and it is proved security under the SM. Ref. [35] improves the security model on the basis of [6]. Compared with [6], ref. [35] does not use bilinear pairing, so the computation cost is reduced. Ref. [36] proposes an identity-based TRS whose signature size is constant. The TRS constructed by [4] supports multi-user authorization.

RS, LRS and TRS relied on number theory have made a lot of achievements. With the maturation of quantum computers, cryptography schemes that rely on number theory may have security risks. Therefore, it is of great significance to construct cryptographic schemes that can resist quantum computer attacks. Hard problems with lattices is able to achieve worst-case to average-case reductions, and many cryptographic primitives can be constructed using lattices. Therefore, lattice-based cryptographic schemes have become the focus of many researchers.

In 2010, Brakerski et al. [37] designed a generic construction for RS and instantiated the generic construction, proposing the first lattice-based RS. Two years later, Tian et al. [38] and Lyubashevsky et al. [39] each came up with a lattice-based RS, where Lyubashevsky’s scheme does not use algorithm to get trapdoors, but draws directly from inside the normal distribution, so it will run more efficiently. Libert et al. [40] designed a RS with a Merkle tree based accumulator and a Stern-like protocol in 2016, its signature size has been reduced to a logarithmic relationship with the ring size from the original linear relationship. After two years, Wang et al. [41] improves on [39] by designing a RS scheme without trapdoors, and the scheme is more secure and efficient. In 2019, Lu et al. [42] proposes a practical RS called Raptor, which suitable for small-scale rings.

Melchor et al. [43] designed a LRS from lattice, which based on [39] by combining the Fiat-Shamir model. Based on the core idea of [40], Yang et al. [44] designed a LRS on lattice in 2017. Torres et al. [45] and Baum et al. [46] both constructed a one-time LRS from lattice in 2018, respectively, and their schemes can be regarded as a migration of discrete logarithm based LRS [24] on lattice. Lu et al. [42] provided a new idea to design one-time LRS in 2019. In 2021, Le et al. [47] constructed two identity-based LRS, one constructed on standard lattice and the other on ideal lattice. Hu et al. [48] constructs a lattice-based LRS by designing a new lattice basis extending algorithm in 2022. Ye et al. [49] designed an LRS based on the NTRU lattice to optimize the signature size and improve the efficiency of the signature algorithm.

In 2020, Feng et al. [50] constructs a general framework for TRS and designs the first lattice-based TRS by instantiating this framework on standard lattices.

In summary, there are fewer lattice-based TRS schemes, and the existing lattice-based TRS have CMP, which may be hindered in application to practical scenarios.

1.2. Our Contributions

In this paper, in order to effectively remove the burden of certificate management in [50] and prevent KEP, we designed an efficient CLTRS on lattice.

• The security of most TRS schemes relies on difficult assumptions in number theory, and the security of these schemes may become insecure for quantum computers, so we designed a lattice-based CLTRS. In our scheme, we treat the member’s identity information as the member’s public key, thus effectively solving the CMP in [50]. Meanwhile, we divide the member’s private key into two parts, one produced by KGC and one chosen by member, and by doing so, our scheme also does not have the KEP like in [29,36,47].
• Based on SIS, DLWE hard assumptions, uniqueness of function F and multi-input correlation intractability of hash family, our scheme is proved to be security and it is satisfies the tag-linkability, type I anonymity, type II anonymity, type I exculpability and type II exculpability under the ROM. Furthermore, compared to [51,52], although the signature size of our scheme is larger, our member secret key is smaller and also achieves public traceability, which the identity will no longer be anonymous if the member maliciously signs twice under the same label.
• Our scheme combines the efficient zero-knowledge protocol proposed by [53], and to argue the relation that our scheme wants to prove, we make modifications based on [53] to construct the privacy-preserving primitives suitable for our scheme. The Stern protocol used in [50] has a soundness error of 2/3 for single run protocol, while the efficient zero-knowledge protocol used in our scheme has a soundness error of 1/poly for single run protocol. To obtain negligible soundness error, our scheme repeats the zero-knowledge protocol fewer times than [50]. Thus, compared to the scheme in the [50], the size of the zero-knowledge proof generated by our scheme will be smaller for the same parameters. When computing the root node of the Merkle tree, [50] retains only one auxiliary node at each level, therefore, for the verification of the path from leaf node to root node, the parent node of leaf node needs to be calculated by the leaf node and its sibling nodes first, and then the parent node of the upper layer can be calculated by the sibling nodes of the layer where the parent node and the parent node reside, and so on, and finally the root node can be obtained. This verification process is a serial calculation process. In this paper, two auxiliary nodes are reserved in each layer of the tree. Therefore, when calculating the root node, the process of calculating the left and right child nodes of each layer to obtain the parent node can be calculated in parallel, and there is no need to calculate step by step from the lowest leaf node. Therefore, the verification process of our scheme is more efficient.

2. Certificate-Less Traceable Ring Signature

2.1. Definition

An CLTRS consists of eight efficient algorithms as follows:

$(pp,msk)\leftarrow \mathbf{CLTRS}.\mathbf{Setup}\left(1^{\lambda }\right)$: Input the security parameter $1^{\lambda }$, and outputs a public system parameter pp and a master secret key msk.

$s_i\leftarrow$ExtractPartialPrivateKey$(pp,i{d}_i,msk)$: Input pp, an identity $i{d}_i\in {\{0,1\}}^{\ast }$ of user $U_i$ for $i\in \left[L\right]$, and msk, then generate a partial private key $s_i$ with respect to $i{d}_i$.

$v_i\leftarrow$SetSecretValue$(pp,i{d}_i)$: Input pp, $i{d}_i\in {\{0,1\}}^{\ast }$ of user $U_i$ for $i\in \left[L\right]$, then returns a secret value $v_i$ to the user $U_i$.

$s{k}_i\leftarrow$SetPrivateKey$(pp,s_i,v_i)$: Input pp, $s_i$ and $v_i$, then returns a secret key $s{k}_i$ corresponding to the user $U_i$.

$y_i\leftarrow$SetPublicKey$(pp,s{k}_i)$: Input pp and $s{k}_i=(s_i,v_i)$, then returns a public key $y_i$ corresponding to the user $U_i$.

$\delta \leftarrow \mathbf{CLTRS}.\mathbf{Sign}(pp,I,R,M,id,s{k}_{id})$: Input pp, an issue I, a ring R, a message M, an identity id and $s{k}_{id}$, outputs a ring signature $\delta$.

$b\leftarrow \mathbf{CLTRS}.\mathbf{Verify}(pp,I,R,M,\delta )$: Input pp, an issue I, a ring R, a message M and a ring signature $\delta$, return $b=1$ if accepting the signature or $b=0$ for rejecting it.

$\eta \leftarrow \mathbf{CLTRS}.\mathbf{Trace}(pp,I,R,M,\delta ,M^{\prime },{\delta }^{\prime })$: Input $pp$, an issue I, a ring R, and two valid tuples $(M,\delta )$ and $(M^{\prime },{\delta }^{\prime })$, outputs $\eta \in \{accept,linked,id\}$.

Definition 1

(Completeness). An $CLTRS$ scheme satisfies complete, if for $(pp,msk)\leftarrow \mathbf{CLTRS}.\mathbf{Setup}\left(1^{\lambda }\right)$, $s_i\leftarrow \mathbf{ExtractPartialPrivateKey}(pp,i{d}_i,msk)$, $v_i\leftarrow \mathbf{SetSecretValue}(pp,i{d}_i)$, $s{k}_i\leftarrow \mathbf{SetPrivateKey}$ $(pp,s_i,v_i)$, $y_i\leftarrow \mathbf{SetPublicKey}$$(pp,s{k}_i)$, $\delta \leftarrow \mathbf{CLTRS}.\mathbf{Sign}(pp,I,R,M,id,s{k}_{id})$, there is $1\leftarrow \mathbf{CLTRS}.\mathbf{Verify}(pp$, $I,R,M,\delta )$ holds. That is,

$$\mathrm{Pr}\left[\begin{array}{cc}0\leftarrow \mathbf{CLTRS}.\mathbf{Verify}(pp,I,R,M,\delta ):\hfill & \\ (pp,msk)\leftarrow \mathbf{CLTRS}.\mathbf{Setup}\left(1^{\lambda }\right),\hfill & \\ s_i\leftarrow \mathbf{ExtractPartialPrivateKey}(pp,i{d}_i,msk),\hfill & \\ v_i\leftarrow \mathbf{SetSecretValue}(pp,i{d}_i),\hfill & \\ s{k}_i\leftarrow \mathbf{SetPrivateKey}(pp,s_i,v_i),\hfill & \\ y_i\leftarrow \mathbf{SetPublicKey}(pp,s{k}_i),\hfill & \\ \delta \leftarrow \mathbf{CLTRS}.\mathbf{Sign}(pp,I,R,M,id,s{k}_{id}).\hfill \end{array}\right]\le negl\left(n\right).$$

Definition 2

(Public Traceability). An $CLTRS$ scheme satisfies publicly traceable, if for $(pp,msk)\leftarrow \mathbf{CLTRS}.\mathbf{Setup}\left(1^{\lambda }\right)$, $s_i\leftarrow \mathbf{ExtractPartialPrivateKey}(pp,i{d}_i$, $msk)$, $v_i\leftarrow \mathbf{SetSecretValue}(pp,i{d}_i)$, $s{k}_i\leftarrow \mathbf{SetPrivateKey}(pp,s_i,v_i)$, $y_i\leftarrow \mathbf{SetPublicKey}(pp,s{k}_i)$, $\delta \leftarrow \mathbf{CLTRS}.\mathbf{Sign}(pp,I,R,M,id,s{k}_{id})$ and ${\delta }^{\prime }\leftarrow \mathbf{CLTRS}.\mathbf{Sign}$ $(pp,I,R,M^{\prime },i{d}^{\prime },s{k}_{i{d}^{\prime }})$, there is overwhelming probability that

$$\mathbf{CLTRS}.\mathbf{Trace}(pp,I,R,M,\delta ,M^{\prime },{\delta }^{\prime })=\left\{\begin{array}{cccc}accept\hfill & \hfill ,& if\hfill & \hfill id\ne i{d}^{\prime },\\ linked\hfill & \hfill ,& elseif\hfill & \hfill M=M^{\prime },\\ id\hfill & \hfill ,& otherwise\hfill & \hfill M\ne M^{\prime },\end{array}\right.$$

holds.

2.2. Security Models

In the framework of the certificateless, two categories of adversaries exist. The first type of adversary ${\mathcal{A}}_I$ is an external adversary, which can replace the user’s public key but cannot access the system master secret key; the second type of adversary ${\mathcal{A}}_{II}$ is an internal adversary, which can control the KGC and direct the generation of the system secret key but cannot replace the target user’s public key.

A secure CLTRS scheme should satisfy tag-linkability, type I anonymity, type II anonymity, type I exculpability and type II exculpability. The following are definitions of these security properties.

Definition 3

(Tag-Linkability). Tag-Linkability means that under the same label, for any PPT adversary $\mathcal{A}$, even if it has L ring member secret keys, it cannot generate $L+1$ valid signatures satisfying that any two signatures are generated by different secret keys. Since an adversary $\mathcal{A}$ in tag linkability can know all of the user’s secret keys, there is no need to consider distinguishing the type of adversary in this security model. We define the probability of $\mathcal{A}$ winning the following games as the $\mathcal{A}$’s advantage.

1. 

Setup. Execute $\mathbf{CLTRS}.\mathbf{Setup}\left(1^{\lambda }\right)$ algorithm, the challenger $\mathcal{C}$ obtains $pp$ and $msk$, and then sends $pp$ to $\mathcal{A}$ but $msk$ is saved itself.

2. 

$\mathbf{Query}$. $\mathcal{A}$ conducts the following queries:

• $CreateUserQuery(pp,i{d}_i)$. When the adversary $\mathcal{A}$ submits a user $i{d}_i$, $\mathcal{C}$ checks it in $lis{t}_{CU}(i{d}_i,s_i,v_i,s{k}_i,y_i)$, if $i{d}_i$ is exists, then returns $(p{k}_i,s{k}_i)$; otherwise, $\mathcal{C}$ runs algorithms $ExtractPartialPrivateKey,SetSecretValue$, $SetPrivateKey,SetPublicKey$ to generate $s_i$, $v_i$, $s{k}_i$ and $y_i$, then returns $y_i$ to adversary $\mathcal{A}$ and adds tuple $(i{d}_i,s_i,v_i,s{k}_i,y_i)$ to $lis{t}_{CU}$.
• $PartialPrivateKeyQuery(pp,i{d}_i)$. When the adversary $\mathcal{A}$ submits a user $i{d}_i$, $\mathcal{C}$ checks $i{d}_i$ in the $lis{t}_{CU}$ and returns $s_i$ to $\mathcal{A}$.
• $ReplacePublicKeyQuery(pp,i{d}_i,y_i^{\prime })$. When the adversary $\mathcal{A}$ submits the user $i{d}_i$ and $y_i$, $\mathcal{C}$ substitutes $y_i$ for $y_i^{\prime }$.
• $SignQuery(pp,i{d}_i,I,R,M)$. When the adversary $\mathcal{A}$ submits the user $i{d}_i$, issue I, ring R and message M, $\mathcal{C}$ return $\delta \leftarrow CLTRS.Sign(pp,s{k}_i,$$I,R,M)$ to $\mathcal{A}$.

3. 

$\mathbf{Forgery}$. $\mathcal{A}$ forgeries $L+1$ tuples $(I,R,M_h,{\delta }_h)$ with $h\in \{1,\cdots ,L+1\}$. $\mathcal{A}$ wins if

(a) 

$1\leftarrow \mathbf{CLTRS}.\mathbf{Verify}(pp,I,R,M_h,{\delta }_h)$ for $\forall h\in \{1,\cdots ,L+1\}$;

(b) 

$accept\leftarrow \mathbf{CLTRS}.\mathbf{Trace}(pp,I,R,M_k,{\delta }_k,M_h,{\delta }_h)$ for all $k,h\in \{1,\cdots ,L+1\}$ with $k\ne h$.

(c) 

$\mathcal{A}$ has at most L ring member $sk$, and the pk of these ring members are all in tag Γ.

The probability of $\mathcal{A}$ winning the game holds in relation to $\mathcal{A}$’s advantage as follows

$$Ad{v}_{\mathcal{A}}^{TaL}=\mathrm{Pr}\left[\mathcal{A}wins\right].$$

Anonymity means that given any valid signature, it is hard for anyone to realize the identity of the signer. There is a need to distinguish between ${\mathcal{A}}_I$ and ${\mathcal{A}}_{II}$ in the security model of anonymity, so a secure CLTRS, needs to satisfy both type I $Anonymity$ and type II $Anonymity$.

Definition 4

(Type I Anonymity). If a CLTRS is type I Anonymity, the advantage of ${\mathcal{A}}_I$ to win the following games is negligible.

1. 

$\mathbf{Setup}$. Execute $CLTRS.Setup\left(1^{\lambda }\right)$ algorithm, the challenger $\mathcal{C}$ obtains $pp$ and $msk$, and saves $msk$ secretly, ${\mathcal{A}}_I$ obtains pp from $\mathcal{C}$.

2. 

$\mathbf{Query}\mathbf{1}$. ${\mathcal{A}}_I$ conducts the following four kinds of queries:

• $CreateUserQuery(pp,i{d}_i)$. When the adversary ${\mathcal{A}}_I$ submits a user $i{d}_i$, $\mathcal{C}$ checks it in $lis{t}_{CU}(i{d}_i,s_i,v_i,s{k}_i,y_i)$, if $i{d}_i$ is exists, then returns $y_i$; otherwise, $\mathcal{C}$ runs algorithms $ExtractPartialPrivateKey,SetSecretValue$, $SetPrivateKey,SetPublicKey$ to generate $s_i$, $v_i$, $s{k}_i$ and $y_i$, then returns $y_i$ to adversary ${\mathcal{A}}_I$ and adds tuple $(i{d}_i,s_i,v_i,s{k}_i,y_i)$ to $lis{t}_{CU}$.
• $PartialPrivateKeyQuery(pp,i{d}_i)$. When the adversary ${\mathcal{A}}_I$ submits a user $i{d}_i$, $\mathcal{C}$ checks $i{d}_i$ in the $lis{t}_{CU}$ and returns $s_i$ to ${\mathcal{A}}_I$.
• $ReplacePublicKeyQuery(pp,i{d}_i,y_i^{\prime })$. When the adversary ${\mathcal{A}}_I$ submits the user $i{d}_i$ and $y_i$, $\mathcal{C}$ substitutes $y_i$ for $y_i^{\prime }$.
• $SignQuery(pp,i{d}_i,I,R,M)$. When the adversary ${\mathcal{A}}_I$ submits the user $i{d}_i$, issue I, ring R and message M, $\mathcal{C}$ return $\delta \leftarrow CLTRS.Sign(pp,s{k}_i,I$, $R,M)$ to ${\mathcal{A}}_I$.

3. 

$\mathbf{Challenge}$. ${\mathcal{A}}_I$ refers two tuples $(M^{\ast },I^{\ast },R^{\ast },i{d}_0)$ and $(M^{\ast },I^{\ast },R^{\ast },i{d}_1)$ to $\mathcal{C}$, where $i{d}_0,i{d}_1\in R^{\ast }$ such that $PPKQ(pp,i{d}_0),PPKQ(pp,i{d}_1),SQ(pp,i{d}_0,I^{\ast }$, $R^{\ast },·)$ and $SQ(pp,i{d}_1,I^{\ast },R^{\ast },·)$ have not been referred to $\mathbf{Query}\mathbf{1}$. $\mathcal{C}$ chooses randomly $b\stackrel{\$}{\leftarrow }\{0,1\}$, returns $\delta \leftarrow$$\mathbf{CLTRS}.\mathbf{Sign}(pp,s{k}_b,I^{\ast },R^{\ast },M)$ to ${\mathcal{A}}_I$.

4. 

$\mathbf{Query}\mathbf{2}$. Similarly to $\mathbf{Query}\mathbf{1}$, in addition to ${\mathcal{A}}_I$ does not have access to $PPKQ(pp,i{d}_0),PPKQ(pp,i{d}_1),SQ(pp,i{d}_0,I^{\ast },R^{\ast },·)$ and $SQ(pp,i{d}_1,I^{\ast },R^{\ast },·)$.

5. 

$\mathbf{Guess}$. ${\mathcal{A}}_I$ outputs a guess b’ for b. $\mathcal{A}$ wins if b’ = b.

The probability of ${\mathcal{A}}_I$ winning the game holds in relation to ${\mathcal{A}}_I$’s advantage as follows

$$Ad{v}_{{\mathcal{A}}_I}^{anon}=|\mathrm{Pr}[b^{\prime }=b]-1/2|.$$

Definition 5

(Type II Anonymity). If a CLTRS is type II Anonymity, the advantage of ${\mathcal{A}}_{II}$ winning the following game is negligible.

1. 

$\mathbf{Setup}$. Execute $CLTRS.Setup\left(1^{\lambda }\right)$ algorithm, the challenger $\mathcal{C}$ obtains $pp$ and $msk$, and then sends them to ${\mathcal{A}}_{II}$.

2. 

$\mathbf{Query}\mathbf{1}$. ${\mathcal{A}}_{II}$ conducts the following four kinds of queries:

• $CreateUserQuery(pp,i{d}_i)$. The same as $CUQ$ of type I Anonymity.
• $PartialPrivateKeyQuery(pp,i{d}_i)$. The same as $RPKQ$ of type I Anonymity.
• $ReplacePublicKeyQuery(pp,i{d}_i,y_i^{\prime })$. The same as $SQ$ of type I Anonymity.
• $SignQuery(pp,i{d}_i,I,R,M)$. When the adversary ${\mathcal{A}}_{II}$ submits the user $i{d}_i$, issue I, ring R and message M, $\mathcal{C}$ return $\delta \leftarrow CLTRS.Sign(pp,s{k}_i,I$, $R,M)$ to ${\mathcal{A}}_{II}$.

3. 

$\mathbf{Challenge}$. ${\mathcal{A}}_{II}$ refers two tuples $(M^{\ast },I^{\ast },R^{\ast },i{d}_0)$ and $(M^{\ast },I^{\ast },R^{\ast },i{d}_1)$ to $\mathcal{C}$, where $i{d}_0,i{d}_1\in R^{\ast }$ such that $RPKQ(pp,i{d}_0),RPKQ(pp,i{d}_1),SQ(pp,i{d}_0,I^{\ast }$, $R^{\ast },·)$ and

$SQ(pp,i{d}_1,I^{\ast },R^{\ast },·)$ have not been referred to $\mathbf{Query}\mathbf{1}$. $\mathcal{C}$ chooses randomly $b\stackrel{\$}{\leftarrow }\{0,1\}$, returns $\delta \leftarrow$$\mathbf{CLTRS}.\mathbf{Sign}(pp,s{k}_b,I^{\ast },R^{\ast },M)$ to ${\mathcal{A}}_{II}$.

4. 

$\mathbf{Query}\mathbf{2}$. Similarly to $\mathbf{Query}\mathbf{1}$, in addition to ${\mathcal{A}}_{II}$ does not have access to $RPKQ(pp,i{d}_0),RPKQ(pp,i{d}_1),SQ(pp,i{d}_0,I^{\ast },R^{\ast },·)$ and $SQ(pp,i{d}_1,I^{\ast },R^{\ast },·)$.

5. 

$\mathbf{Guess}$. ${\mathcal{A}}_{II}$ outputs a guess b’ for b. $\mathcal{A}$ wins if b’ = b.

The probability of ${\mathcal{A}}_{II}$ winning the game holds in relation to ${\mathcal{A}}_{II}$’s advantage as follows

$$Ad{v}_{{\mathcal{A}}_{II}}^{anon}=|\mathrm{Pr}[b^{\prime }=b]-1/2|.$$

Exculpability implies that anonymity is lost only if the identical ring member signs different messages under the identical label. There is a need to distinguish between ${\mathcal{A}}_I$ and ${\mathcal{A}}_{II}$ in the security model of exculpability, so a secure CLTRS, needs to satisfy both type I $exculpability$ and type II $exculpability$.

Definition 6

(Type I Exculpability). If a CLTRS is type I exculpability, the advantage of ${\mathcal{A}}_I$ winning the following game is negligible.

1. 

$\mathbf{Setup}$. Execute $CLTRS.Setup\left(1^{\lambda }\right)$ algorithm, the challenger $\mathcal{C}$ obtains $pp$ and $msk$, and saves $msk$ secretly, ${\mathcal{A}}_I$ obtains pp from $\mathcal{C}$.

2. 

$\mathbf{Query}$. ${\mathcal{A}}_I$ conducts the following four kinds of queries:

• $CreateUserQuery(pp,i{d}_i)$. When the adversary ${\mathcal{A}}_I$ submits a user $i{d}_i$, $\mathcal{C}$ generates $s_i$, $v_i$, $s{k}_i$ and $y_i$, returns $(p{k}_i,s{k}_i)$ to adversary ${\mathcal{A}}_I$, and then adds tuple $(i{d}_i,s_i,v_i,s{k}_i,y_i)$ to $lis{t}_{CU}$.
• $PartialPrivateKeyQuery(pp,i{d}_i)$. When the adversary ${\mathcal{A}}_I$ submits a user $i{d}_i$, $\mathcal{C}$ checks $i{d}_i$ in the $lis{t}_{CU}$ and returns $s_i$ to ${\mathcal{A}}_I$.
• $ReplacePublicKeyQuery(pp,i{d}_i,y_i^{\prime })$. When the adversary ${\mathcal{A}}_I$ submits the user $i{d}_i$ and the public key $y_i$, $\mathcal{C}$ substitutes $y_i$ for $y_i^{\prime }$.
• $SignQuery(pp,i{d}_i,I,R,M)$. When the adversary ${\mathcal{A}}_I$ submits the user $i{d}_i$, issue I, ring R and message M, $\mathcal{C}$ return $\delta \leftarrow CLTRS.Sign(pp,s{k}_i,I$, $R,M)$ to ${\mathcal{A}}_I$.

3. 

$\mathbf{Forgery}$. ${\mathcal{A}}_I$ forgeries two tuples $(I^{\ast },R^{\ast },\overline{M},\overline{\delta })$ and $(I^{\ast },R^{\ast },M^{\prime },{\delta }^{\prime })$. It wins if

(a) 

$1\leftarrow \mathbf{CLTRS}.\mathbf{Verify}(pp,I^{\ast },R^{\ast },\overline{M},\overline{\delta })$;

(b) 

$1\leftarrow \mathbf{CLTRS}.\mathbf{Verify}(pp,I^{\ast },R^{\ast },M^{\prime },{\delta }^{\prime })$;

(c) 

${\mathcal{A}}_I$ has not been queried about $PPKQ(pp,i{d}^{\ast })$ and $CUQ(pp,i{d}^{\ast })$ where $i{d}^{\ast }\in R^{\ast }$;

(d) 

${\mathcal{A}}_I$ has made at most one of $SQ(pp,i{d}^{\ast },I^{\ast },R^{\ast },\overline{M})$ and $SQ(pp,i{d}^{\ast },I^{\ast },R^{\ast }$, $M^{\prime })$;

(e) 

$p{k}^{\ast }\leftarrow \mathbf{CLTRS}.\mathbf{Trace}(pp,I^{\ast },R^{\ast },\overline{M},\overline{\delta },M^{\prime },{\delta }^{\prime })$.

The probability of ${\mathcal{A}}_I$ winning the game holds in relation to ${\mathcal{A}}_I$’s advantage as follows

$$Ad{v}_{{\mathcal{A}}_I}^{Excul}=\mathrm{Pr}\left[{\mathcal{A}}_{I}wins\right].$$

Definition 7

(Type II Exculpability). If a CLTRS is type II exculpability, the advantage of ${\mathcal{A}}_{II}$ winning the following game is negligible.

1. 

$\mathbf{Setup}$. Execute $CLTRS.Setup\left(1^{\lambda }\right)$ algorithm, the challenger $\mathcal{C}$ obtains $pp$ and $msk$, and sends them to ${\mathcal{A}}_{II}$.

2. 

$\mathbf{Query}$. ${\mathcal{A}}_{II}$ conducts the following four kinds of queries:

• $CreateUserQuery(pp,i{d}_i)$. The same as $CUQ$ of type I exculpability.
• $PartialPrivateKeyQuery(pp,i{d}_i)$. The same as $PPKQ$ of type I exculpability.
• $ReplacePublicKeyQuery(pp,i{d}_i,y_i^{\prime })$. The same as $RPKQ$ of type I exculpability.
• $SignQuery(pp,i{d}_i,I,R,M)$. The same as $SQ$ of type I exculpability.

3. 

$\mathbf{Forgery}$. ${\mathcal{A}}_{II}$ forgeries two tuples $(I^{\ast },R^{\ast },\overline{M},\overline{\delta })$ and $(I^{\ast },R^{\ast },M^{\prime },{\delta }^{\prime })$. It wins if

(a) 

$1\leftarrow \mathbf{CLTRS}.\mathbf{Verify}(pp,I^{\ast },R^{\ast },\overline{M},\overline{\delta })$;

(b) 

$1\leftarrow \mathbf{CLTRS}.\mathbf{Verify}(pp,I^{\ast },R^{\ast },M^{\prime },{\delta }^{\prime })$;

(c) 

${\mathcal{A}}_{II}$ has not been queried about $RPKQ(pp,i{d}^{\ast })$ and $CUQ(pp,i{d}^{\ast })$ where $i{d}^{\ast }\in R^{\ast }$;

(d) 

${\mathcal{A}}_{II}$ has made at most one of $SQ(pp,i{d}^{\ast },I^{\ast },R^{\ast },\overline{M})$ and $SQ(pp,i{d}^{\ast },I^{\ast },R^{\ast }$, $M^{\prime })$;

(e) 

$p{k}^{\ast }\leftarrow \mathbf{CLTRS}.\mathbf{Trace}(pp,I^{\ast },R^{\ast },\overline{M},\overline{\delta },M^{\prime },{\delta }^{\prime })$.

The probability of ${\mathcal{A}}_{II}$ winning the game holds in relation to ${\mathcal{A}}_{II}$’s advantage as follows

$$Ad{v}_{{\mathcal{A}}_{II}}^{Excul}=\mathrm{Pr}\left[{\mathcal{A}}_{II}wins\right].$$

As proved in [31], if a TRS implements both tag-linkability and exculpability, then it also implements unforgeability. This also holds for CLTRS.

3. Preliminaries

3.1. Hardness Assumptions

Definition 8

(Short Integer Solution Problem [16]). Let n,m,q ∈ $\mathbb{N}$, and a real number $\beta \in \mathbb{R}$, the SIS problem is: For an arbitrary random matrix $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$, searching a non-zero vector $\mathbf{s}\in {\mathbb{Z}}^m$, such that $\mathbf{A}·\mathbf{s}=0modq$ and ${∥\mathbf{s}∥}_{\infty }\le \beta$.

Definition 9

(Decisional Learning With Errors Problem [54]). Let n, q $\ge 2$, $\mathbf{u}\in {\mathbb{Z}}_q^n$. Given k instances, DLWE problem is to identify whether the k instances are drawn from a random distribution over ${\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$ or from distribution ${\mathbf{A}}_{\mathbf{u},\beta }$, where ${\mathbf{A}}_{\mathbf{u},\beta }$ over ${\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$ is achieved by picking a vector in $\mathbf{x}\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^n$ and a positive real number in $t\stackrel{\$}{\leftarrow }\odot$, and then returning $(\mathbf{x},\mathrm{y}=\mathbf{x}·\mathbf{u}+t)$.

Definition 10

(Decisional Learning With Rounding Problem [55]). Given k instances, DLWR problem is to identify whether the k instances are drawn from a random distribution over ${\mathbb{Z}}_q^n\times {\mathbb{Z}}_p$ or from distribution ${\mathbf{A}}_{\beta }$, where ${\mathbf{A}}_{\beta }$ over ${\mathbb{Z}}_q^n\times {\mathbb{Z}}_p$ is achieved by picking a vector in $\mathbf{x}\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^n$ and picking a integer in $\beta \stackrel{\$}{\leftarrow }{\mathbb{Z}}_p$, and then returning $(\mathbf{x},\mathrm{b}={\lfloor {\mathbf{x}}^T·\mathbf{fi}\rceil }_p)$. For any ${\mathbf{x}}^{\prime }\in {\mathbb{Z}}_q^m$, we denote ${\lfloor {\mathbf{x}}^{\prime }\rceil }_p$ as $\lfloor (p/q){\mathbf{x}}^{\prime }\rceil modp$.

3.2. Trapdoor Mechanism

Definition 11

(G-trapdoor [56]). Let $\widehat{m},q,n,k\in \mathbb{N}$ and $\mathbf{A}\in {\mathbb{Z}}_q^{\widehat{m}\times n},\mathbf{G}\in {\mathbb{Z}}_q^{\widehat{m}\times \widehat{m}k}$ be matrices with $n\ge \widehat{m}k$. Define $\mathbf{H}\in {\mathbb{Z}}_q^{\widehat{m}\times \widehat{m}}$ as an invertible matrix. The matrix $\mathbf{A}$ and its corresponding G-trapdoor $\mathbf{R}$ satisfy the following constraints: $\mathbf{A}\left[\begin{array}{c}\mathbf{R}\\ {\mathbf{I}}_{\widehat{m}k}\end{array}\right]=\mathbf{HG}modq$.

We define $\mathbf{G}={\mathbf{I}}_n⨂{\mathbf{g}}^t\in {\mathbb{Z}}_q^{\widehat{m}\times \widehat{m}k}$, where $k=\lceil {log}_{2}q\rceil$, ${\mathbf{g}}^t=(1,2,\cdots ,2^{k-1})\in {\mathbb{Z}}^{\widehat{m}\times \widehat{m}},$ ${\mathbf{I}}_{\widehat{m}}\in {\mathbb{Z}}^{\widehat{m}\times \widehat{m}}$ and ⨂ denotes the tensor product. In the following, let $q\ge 2$, $\overline{m}\ge 1$, and $n=\overline{m}+\widehat{m}k$.

• (GenTrap Algorithm [56]): Given a uniformly random matrix $\overline{\mathbf{A}}\in {\mathbb{Z}}_q^{\widehat{m}\times \overline{m}}$ and an invertible matrix $\mathbf{H}\in {\mathbb{Z}}_q^{\widehat{m}\times \widehat{m}}$, the PPT algorithm outputs a random matrix $\mathbf{A}=\left[\overline{A}|\mathbf{HG}-\overline{\mathbf{A}}\mathbf{R}\right]$ and a G-trapdoor $\mathbf{R}\sim D_{\sigma }^{\overline{m}\times \widehat{m}k}$ (the ∼ indicates that the distribution of G-trapdoor $\mathbf{R}$ obeys the Gaussian distribution $D_{\sigma }^{\overline{m}\times \widehat{m}k}$). Also, $s_1\left(\mathbf{R}\right)\le \sigma ·\frac{1}{\sqrt{2\pi }}·(\sqrt{\overline{m}}+\sqrt{\widehat{m}k})$.
• (SampleD Algorithm [56]): Given a G-trapdoor $\mathbf{R}\in {\mathbb{Z}}_{\sigma }^{\overline{m}\times \widehat{m}k}$ for $\mathbf{A}\in {\mathbb{Z}}_q^{\widehat{m}\times (\overline{m}+\widehat{m}k)}$, an invertible matrix $\mathbf{H}\in {\mathbb{Z}}^{\widehat{m}\times \widehat{m}}$, a uniform vector $\mathbf{u}\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^{\widehat{m}}$ and Gaussian parameter $\sigma \ge \sqrt{7{\left(s_1\left(\mathbf{R}\right)\right)}^2+1}·\omega \left(\sqrt{log\widehat{m}}\right)$, the PPT algorithm outputs a vector $\mathbf{e}\in {\mathbb{Z}}^{\overline{m}+\widehat{m}k}$ sampled from a distribution that is statistically close to $D_{{\mathsf{\Lambda }}_{\mathbf{u}}^{\perp }\left(\mathbf{A}\right),\sigma }$.

For simplicity we set $\mathbf{H}$ to the unit matrix ${\mathbf{I}}_n$ and omit it.

3.3. Pseudorandom Function Family

Let $n,p,q,m\in \mathbb{N}$ which are polynomial in security parameter $\lambda$ and $H:{\{0,1\}}^{\ast }\to {\mathbb{Z}}_q^{m\times n}$. The specific description of the PRF is as follows:

• KeyGen. The key generation algorithm randomly chooses a vector $\mathbf{u}\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^n$ and outputs the vector $\mathbf{u}$.
• Eval. Given a string $\mathsf{\Gamma }$ of any length, the evaluation algorithm returns $F^H(\mathbf{u},\mathsf{\Gamma })={\lfloor H\left(\mathsf{\Gamma }\right)·\mathbf{u}\rceil }_p$.

Definition 12

(PRF in the QROM [50]). For any quantum PPT adversary $\mathcal{A}$, if $F^H:\mathcal{S}\times \mathcal{U}\to \mathcal{T}$ satisfies pseudorandomness under QROM, then the following conclusion is satisfied.

$$\begin{gathered} \left|\mathrm{Pr}\left[{\mathcal{A}}^{F^H(s,·),H(·)}\left(1^n\right)=1:s\leftarrow \mathcal{S}\right]-\mathrm{Pr}\left[{\mathcal{A}}^{\mathsf{\Theta }(·),H(·)}\left(1^n\right)=1:\mathsf{\Theta }\leftarrow \mathcal{F}[\mathcal{U}:\mathcal{T}]\right]\right| \\ \le negl\left(n\right), \end{gathered}$$

where H is a QROM and $\mathcal{F}[\mathcal{U}:\mathcal{T}]$ indicates any functions from $\mathcal{S}$ to $\mathcal{T}$.

Lemma 1

([50]). Let $n,m,q,p\in {\mathbb{N}}^{+}$, ${\mathcal{B}}_{\chi }$ be a U-bounded error distribution s.t. $m>(n+1)logq$, $q\ge p·\sqrt{m}·U·n^{\omega \left(1\right)}$. Under the LWE difficulty assumption, $F^H$ has pseudorandomness in the QROM.

In our scheme, we need F to have the following two properties.

• $\mathbf{Uniqueness}$ For a string of arbitrary length $x\leftarrow \chi$, the following probabilities conditions are satisfied:
  $$\mathrm{Pr}[\exists {\mathbf{s}}_1,{\mathbf{s}}_2\in \mathcal{S},{\mathbf{s}}_1\ne {\mathbf{s}}_2\wedge F_{{\mathbf{s}}_1}\left(x\right)=F_{{\mathbf{s}}_2}\left(x\right)]\le negl\left(\lambda \right).$$
• $\mathbf{Intersection}-\mathbf{Free}\mathbf{Range}$ For any two distinct vectors ${\mathbf{y}}_1,{\mathbf{y}}_2\in Y$ and any polynomial $N(·)$, the following probabilities conditions are satisfied:
  $$\mathrm{Pr}[\exists k_1,k_2,h_1,h_2\le N\left(\lambda \right),k_1{\mathbf{y}}_1+h_1{\mathbf{z}}_1=k_2{\mathbf{y}}_2+h_2{\mathbf{z}}_2:{\mathbf{z}}_1,{\mathbf{z}}_2\leftarrow Y]\le negl\left(\lambda \right),$$

  where Y is composed of vectors with rational numbers as elements.

Lemma 2

(Uniqueness [44]). If $m\ge n·(logq+1)/(logp-1)$, then $F^H$ is a secure function with uniqueness.

Definition 13

(Sparse Relation [57]). A relation ensemble $Q=\{Q_{\mu }\subset {({\{0,1\}}^{y(\mu )})}^{k(\mu )}$$\times {({\{0,1\}}^{x(\mu )})}^{k(\mu )}\}$ is sparse, if for any $(x_1,\cdots ,x_k)$ the following conclusion is satisfied:

$$\mathrm{Pr}\left[(y_1,\cdots ,y_k)\leftarrow {\left({\{0,1\}}^{y\left(\mu \right)}\right)}^{k\left(\mu \right)}:(x_1,\cdots ,x_k,y_1,\cdots ,y_k)\in Q_{\mu }\right]\le negl\left(\mu \right)$$

Definition 14

(Multi-input correlation intractability [50]). Given a relation ensemble $Q=\{Q_{\mu }\subset {({\{0,1\}}^{y(\mu )})}^{k(\mu )}\times {({\{0,1\}}^{x(\mu )})}^{k(\mu )}\}$, we say that hash famliy $\mathcal{H}$ = (HK,H) satisfies correlation intractable if any efficient adversary has the following relation holds:

$$\begin{gathered} \mathrm{Pr}[hk\leftarrow HK\left(1^{\mu }\right);(x_1,\cdots ,x_k)\leftarrow \mathcal{A}\left(hk\right):(x_1,\cdots ,x_k,H_{hk}\left(x_1\right),\cdots ,H_{hk}\left(x_k\right))\in Q_{\mu }]\in \\ negl\left(\mu \right) \end{gathered}$$

Lemma 3

([50]). If $F:S\times B\to T$ is a unique PRF with an intersection free range, it holds that

$$\mathrm{Pr}[a\leftarrow \mathcal{X}:R_{a}isnotsparse]\le negl\left(\lambda \right).$$

3.4. Lattice-Based Accumulator

The accumulator presented in [53] will be used to construct our scheme. Let $\lambda$ represent the security parameter and $n=poly\left(\lambda \right),q=poly\left(\lambda \right)$. Let $L=2^{\ell },k=\lceil logq\rceil$, $m=nk$ where $\ell \in {\mathbb{N}}^{+}$. The specific algorithm is shown below:

• $\mathbf{A}.\mathbf{Setup}$. Sample a random matrix $\mathbf{B}=\left({\mathbf{B}}_1\right|{\mathbf{B}}_2)\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^{n\times 2m}$ and returns the value of the public parameter $para=\mathbf{B}$.
• $\mathbf{A}.\mathbf{Acc}$. The algorithm sets ${\mathbf{t}}_{\ell ,i}={\mathbf{c}}_i$ when given $\mathcal{R}={\left\{{\mathbf{c}}_i\right\}}_{i\in [0,L-1]}\in {\left({\{0,1\}}^m\right)}^L$. Next for $j\in [0,\ell -1]$ and $i\in [0,2^j-1]$, it defines ${\mathbf{t}}_{j,i}=bin({\mathbf{B}}_1·{\mathbf{t}}_{j+1,2i}+{\mathbf{B}}_2·{\mathbf{t}}_{j+1,2i+1})$. Lastly, the accumulated value ${\mathbf{t}}_{0,0}$ is returned.
• $\mathbf{A}.\mathbf{Witness}$. The algorithm generates ${\mathbf{t}}_{j,i}$ just like the accumulate algorithm when given $\mathcal{R}={\left\{{\mathbf{c}}_i\right\}}_{i\in [0,L-1]}\in {\left({\{0,1\}}^m\right)}^L$ and an element $\mathbf{c}={\mathbf{c}}_{i^{\ast }}$. Finally, $(bin(i^{\ast }),{\{{\mathbf{t}}_{j,f\left(j\right)}\}}_{j\in [1,\ell ]},{\{{\mathbf{t}}_{j,g\left(j\right)}\}}_{j\in [1,\ell ]})$ is returned, where $f\left(j\right)=\lfloor i^{\ast }/\left(2^{\ell -j}\right)\rfloor$ and $g\left(j\right)=4\lfloor \frac{i^{\ast }}{2^{\ell -(j-1)}}\rfloor -\lfloor \frac{i^{\ast }}{\left(2^{\ell -j}\right)}\rfloor +1$.
• $\mathbf{A}.\mathbf{Verify}$. Given an accumulated value $\mathbf{t}$, an element $\mathbf{c}$ and a witness $(\iota ,{\{{\mathbf{h}}_j\}}_{j\in [1,\ell ]}$, ${\{{\mathbf{k}}_j\}}_{j\in [1,\ell ]})$, the algorithm returns 1 if
  $$\left\{\begin{array}{c}bin({\mathbf{B}}_{1+\iota \left[1\right]}·{\mathbf{h}}_1+{\mathbf{B}}_{2-\iota \left[1\right]}·{\mathbf{k}}_1)=\mathbf{t},\hfill \\ \forall j\in [2,\ell ],bin({\mathbf{B}}_{1+\iota \left[j\right]}·{\mathbf{h}}_j+{\mathbf{B}}_{2-\iota \left[j\right]}·{\mathbf{k}}_j)={\mathbf{h}}_{j-1}.\hfill \end{array}\right.$$

4. Our Certificate-Less Traceable Ring Signature Scheme

4.1. Construction

In our scheme, the ring R denotes the set of user’s identity information and user’s public key, $L=2^{\ell }$ is the capacity of ring R, and a label $\mathsf{\Gamma }$ is the contains both ring R and issue I. $\mathcal{R}$ denotes the set of leaf node that participates in the accumulator operation.

• $\mathbf{Setup}$($1^{\lambda }$)
  • Choose lattice parameter $n=\mathcal{O}\left(\lambda \right)$, Gaussian parameter ${\sigma }_1,{\sigma }_2$, a U-bound distribution $B_{\mathcal{X}}$, integer $q\ge 2$ and prime p satisfies $q\ge p·U·n^{w\left(1\right)}$, $\widehat{N}=w(log\lambda )$, $\overline{m}>1$, $k=\lceil logq\rceil$, $n:=\overline{m}+\widehat{m}k\ge \mathcal{O}(\widehat{m}logq)$, $m>(n+1)·(logq)$, $m\ge n(logq+1)/(logp-1)$, $m^{\prime }=m·\lceil logp\rceil$, $m^{″}=n·\lceil logq\rceil$.
  • Set $params=(\widehat{m},n,m,m^{\prime },m^{″},p,q,t)$, choose hash functions $H_1:{\{0,1\}}^{\ast }\to {\mathbb{Z}}_q^{m\times 2n}$, $H_2:{\{0,1\}}^{\ast }\to {\mathbb{Z}}_p^m$ and $H_3:{\{0,1\}}^{\ast }\to {\mathbb{Z}}_q^{\widehat{m}}$.
  • Choose random matrices ${\mathbf{A}}_0\leftarrow {\mathbb{Z}}_q^{m\times n}$, ${\mathbf{D}}_1,{\mathbf{D}}_2\leftarrow {\mathbb{Z}}_q^{n\times m^{\prime }}$, $\mathbf{B}=\left[{\mathbf{B}}_1\right|{\mathbf{B}}_2]\leftarrow {\mathbb{Z}}_q^{n\times m^{″}}$.
  • Randomly select a matrix ${\mathbf{A}}^{\prime }\in {\mathbb{Z}}_q^{\widehat{m}\times \overline{m}}$, then running $Gentrap$ to obtain $(\mathbf{A},{\mathbf{T}}_{\mathbf{A}})$, and set $mpk=\mathbf{A}\in {\mathbb{Z}}_q^{\widehat{m}\times n}$ and $msk={\mathbf{T}}_{\mathbf{A}}\sim D_{{\sigma }_1}^n$.
    Output $pp=(params,H_1,H_2,H_3,\mathbf{A},{\mathbf{A}}_0,\mathbf{B},{\mathbf{D}}_1,{\mathbf{D}}_2)$.
• $\mathbf{ExtractPartialPrivateKey}$($pp,msk,i{d}_i$)
  For an arbitrary identity $i{d}_i\in {\{0,1\}}^{\ast }$, define the associated vector ${\mathbf{a}}_{i{d}_i}$ as
  $${\mathbf{a}}_{i{d}_i}=H_3\left(i{d}_i\right)\in {\mathbb{Z}}_q^{\widehat{m}},$$

  run $SampleD(\mathbf{A},{\mathbf{T}}_{\mathbf{A}},{\mathbf{a}}_{i{d}_i},{\sigma }_2)$ to get ${\mathbf{s}}_i\in {\mathbb{Z}}_q^n$, where ${\sigma }_2\ge \sqrt{7{(s_1({\tilde{T}}_A))}^2+1}$, $\mathbf{A}·{\mathbf{s}}_i={\mathbf{a}}_{i{d}_i}modq$, and ${\mathbf{s}}_i$ is statistically close to $D_{{\mathsf{\Lambda }}^{\mathbf{u}}\left(\mathbf{A}\right),{\sigma }_2}$. Output ${\mathbf{s}}_i$.
• $\mathbf{SetSecretValue}$($pp,i{d}_i$)
  The signer selects a random vector $\mathbf{k}\in D_{{\mathbb{Z}}^n,{\sigma }_2}$, satisfying $\parallel \mathbf{k}\parallel \le {\sigma }_2·\sqrt{n}$ and set his secret value ${\mathbf{v}}_i=\mathbf{k}$.
• $\mathbf{SetPrivateKey}$($pp,{\mathbf{s}}_i,{\mathbf{v}}_i$)
  On input the public parameters $pp$, signer’s partial ptivate key ${\mathbf{s}}_i={\mathbf{s}}_{i{d}_i}$ and secret value ${\mathbf{v}}_i=\mathbf{k}$, this algorithm sets full priavte key $s{k}_i=({\mathbf{s}}_i,{\mathbf{v}}_i)$.
• $\mathbf{SetPublicKey}$($pp,s{k}_i$)
  On input the public parameters $pp$ and user’s full priavte key $s{k}_i$, the user computes ${\mathbf{y}}_i={\lfloor {\mathbf{A}}_0·{\mathbf{v}}_i\rceil }_p\in {\mathbb{Z}}_p^m$ and returns his public key ${\mathbf{y}}_i$.
• $\mathbf{Sign}$($pp,s{k}_{\pi },I,R,M$)
  Prase $pp=(params,H_1,H_2,H_3,\mathbf{A},{\mathbf{A}}_0,\mathbf{B},{\mathbf{D}}_1,{\mathbf{D}}_2)$, $\mathsf{\Gamma }=\{R={(r_i=(i{d}_i,{\mathbf{y}}_i))}_{[L]},I\},s{k}_{\pi }=({\mathbf{s}}_{\pi },{\mathbf{v}}_{\pi })$.
  • Compute ${\mathbf{A}}_{\mathsf{\Gamma }}=\left({\mathbf{A}}_{{\mathsf{\Gamma }}_1}\right|{\mathbf{A}}_{{\mathsf{\Gamma }}_2})=H_1\left(\mathsf{\Gamma }\right)\in {\mathbb{Z}}_q^{m\times 2n}$.
  • Compute ${\mathbf{b}}_{\pi }={\lfloor {\mathbf{A}}_{{\mathsf{\Gamma }}_1}·{\mathbf{s}}_{\pi }+{\mathbf{A}}_{{\mathsf{\Gamma }}_2}·{\mathbf{v}}_{\pi }\rceil }_p$, and ${\mathbf{b}}_0=H_2(\mathsf{\Gamma },M)\in {\mathbb{Z}}_p^m$.
  • Compute $\alpha =\frac{{\mathbf{b}}_{\pi }-{\mathbf{b}}_0}{\pi }modp$, and ${\mathbf{b}}_i={\mathbf{b}}_0+\alpha ·i$ for all $i\ne \pi$.
  • Compute ${\mathbf{c}}_j=bin({\mathbf{D}}_1·bin\left(H_2\left(r_j\right)\right)+{\mathbf{D}}_2·bin\left({\mathbf{b}}_j\right))$ for $j\in \left[L\right]$, and define $\mathcal{R}=\{{({\mathbf{c}}_j)}_{[L]}\}$.
  • Compute $\mathbf{t}=A.Acc(\mathbf{B},\mathcal{R})$ and $w_A=A.Witness(\mathbf{B},\mathcal{R},\mathbf{t},{\mathbf{c}}_{\pi })$ where $w_A=(\mathbf{wit},{\{{\mathbf{h}}_j\}}_{j\in [1,\ell ]},{\{{\mathbf{k}}_j\}}_{j\in [1,\ell ]})$.
  • Define $\chi =(\mathbf{A},{\mathbf{A}}_0,{\mathbf{A}}_{\mathsf{\Gamma }},{\mathbf{D}}_1,{\mathbf{D}}_2,\mathbf{B},\mathbf{t})$ as the statement, and define $W=({\mathbf{sk}}_{\pi }=({\mathbf{s}}_{\pi },{\mathbf{v}}_{\pi }),r_{\pi },{\mathbf{b}}_{\pi },{\mathbf{c}}_{\pi },w_A)$ as the witness. Run $Proof(\chi ,W)$ of NIZKAoK to obtain a proof:
    $$\begin{array}{c}\mathsf{\Pi }=SPK\{(\mathbf{A},{\mathbf{A}}_0,{\mathbf{A}}_{\mathsf{\Gamma }},{\mathbf{D}}_1,{\mathbf{D}}_2,\mathbf{B},\mathbf{t}),({\mathbf{sk}}_{\pi },r_{\pi },{\mathbf{b}}_{\pi },{\mathbf{c}}_{\pi },w_A):\\ \mathbf{A}·{\mathbf{s}}_{\pi }={\mathbf{a}}_{i{d}_{\pi }}\wedge {\mathbf{y}}_{\pi }={\lfloor {\mathbf{A}}_0·{\mathbf{v}}_{\pi }\rceil }_p\wedge {\mathbf{b}}_{\pi }={\lfloor {\mathbf{A}}_{{\mathsf{\Gamma }}_1}·{\mathbf{s}}_{\pi }+{\mathbf{A}}_{{\mathsf{\Gamma }}_2}·{\mathbf{v}}_{\pi }\rceil }_p\\ \wedge {\mathbf{c}}_{\pi }=bin({\mathbf{D}}_1·bin\left(H_2\left(r_{\pi }\right)\right)+{\mathbf{D}}_2·bin\left({\mathbf{b}}_{\pi }\right))\\ \wedge A.Verif{y}_{\mathbf{B}}(\mathbf{t},{\mathbf{c}}_{\pi },(\mathbf{wit},{\{{\mathbf{h}}_j\}}_{j\in [1,\ell ]},{\{{\mathbf{k}}_j\}}_{j\in [1,\ell ]}))\}[M].\end{array}$$
  • Output the signature $\delta =(\alpha ,\mathsf{\Pi })$.
• $\mathbf{Verify}$($pp,I,R,\delta ,M$)
  Prase $pp=(params,H_1,H_2,H_3,\mathbf{A},{\mathbf{A}}_0,\mathbf{B},{\mathbf{D}}_1,{\mathbf{D}}_2)$, $\mathsf{\Gamma }=\{R={(r_i=(i{d}_i,{\mathbf{y}}_i))}_{[L]},I\}$, $\delta =(\alpha ,\mathsf{\Pi })$.
  • Let ${\mathbf{A}}_{\mathsf{\Gamma }}=\left({\mathbf{A}}_{{\mathsf{\Gamma }}_1}\right|{\mathbf{A}}_{{\mathsf{\Gamma }}_2})=H_1\left(\mathsf{\Gamma }\right)$ and ${\mathbf{b}}_0=H_2(\mathsf{\Gamma },M)$.
  • For all $i\in \left[L\right]$, we caculate ${\mathbf{b}}_i={\mathbf{b}}_0+\alpha ·i$.
  • Caculate ${\mathbf{c}}_j=bin({\mathbf{D}}_1·bin\left(H_2\left(r_j\right)\right)+{\mathbf{D}}_2·bin\left({\mathbf{b}}_j\right))$ for $j\in \left[L\right]$, let $\mathcal{R}=\{{\left({\mathbf{c}}_j\right)}_{\left[L\right]}\}$.
  • Caculate $\mathbf{t}=A.Acc(\mathbf{B},\mathcal{R})$.
  • Define $\chi =(\mathbf{A},{\mathbf{A}}_0,{\mathbf{A}}_{\mathsf{\Gamma }},{\mathbf{D}}_1,{\mathbf{D}}_2,\mathbf{B},\mathbf{t})$ as statement, and run $v\leftarrow Verify(X,\mathsf{\Pi })$ of NIZKAoK.
  • Output 1 if $v=1$. Otherwise, output 0.
• $\mathbf{Trace}$($pp,\mathsf{\Gamma },M,\delta ,M^{\prime },{\delta }^{\prime }$)
  Prase $pp=(params,H_1,H_2,H_3,\mathbf{A},{\mathbf{A}}_0,\mathbf{B},{\mathbf{D}}_1,{\mathbf{D}}_2)$, $\mathsf{\Gamma }=\{R={(r_i=(i{d}_i,{\mathbf{y}}_i))}_{\left[L\right]},I\}$, $\delta =(\alpha ,\mathsf{\Pi })$, ${\delta }^{\prime }=({\alpha }^{\prime },{\mathsf{\Pi }}^{\prime })$.
  • Let ${\mathbf{b}}_0=H_2(\mathsf{\Gamma },M)$, then calculate ${\mathbf{b}}_i={\mathbf{b}}_0+\alpha ·i$ for all $i\in \left[L\right]$.
  • Let ${\mathbf{b}}_0^{\prime }=H_2(\mathsf{\Gamma },M^{\prime })$, then calculate ${\mathbf{b}}_i^{\prime }={\mathbf{b}}_0^{\prime }+{\alpha }^{\prime }·i$ for all $i\in \left[L\right]$.
  • If for all $i\in \left[L\right]$ there is $b_i=b_i^{\prime }$, return linked.
  • If only one index $i\in \left[L\right]$ satisfies $b_i=b_i^{\prime }$, return $i{d}_i$.
  • otherwise, return accept.

4.2. Correctness

• $\mathbf{Completeness}$. In our scheme, $\alpha$ is generated by subtracting two integer vectors and then dividing by $\pi$, where $\pi \in [1,L]$ is an integer since p is a large prime number and is much larger than L, so $\pi$ is relatively prime to the prime p, then $\alpha$ is always an integer vector. The verifier can always restore the sequence $t_i$ based on $\alpha$, label $\mathsf{\Gamma }$, and message M. Because of the $\mathit{completeness}$ of the NIZKAoK protocol, for honestly generated signatures, the verifier always outputs $1\leftarrow \mathbf{CLTRS}.\mathbf{Verify}(pp,\mathsf{\Gamma },\delta ,M)$.
• $\mathbf{Public}\mathbf{Traceability}$. According to the definition of public traceability, there are three cases.
  • When $M=M^{\prime }$ and $\pi ={\pi }^{\prime }$, it means that the signer signs the same message twice, so we can get ${\mathbf{b}}_0={\mathbf{b}}_0^{\prime }$ and ${\mathbf{b}}_{\pi }={\mathbf{b}}_{{\pi }^{\prime }}^{\prime }$, then $\alpha =\frac{{\mathbf{b}}_{\pi }-{\mathbf{b}}_0}{\pi }=\frac{{\mathbf{b}}_{{\pi }^{\prime }}-{\mathbf{b}}_0^{\prime }}{{\pi }^{\prime }}={\alpha }^{\prime }$ can be easily computed. According to the equation ${\mathbf{b}}_i={\mathbf{b}}_0+\alpha ·i$, we know that ${\mathbf{b}}_i={\mathbf{b}}_i^{\prime }$ for all $i\in [1,L]$. Thereby, $\mathbf{CLTRS}.\mathbf{Trace}$ algorithm will output $“linked”$.
  • When $M\ne M^{\prime }$ and $\pi ={\pi }^{\prime }$, it means that the signer signs different messages. In this case we can get ${\mathbf{b}}_0\ne {\mathbf{b}}_0^{\prime }$ but ${\mathbf{b}}_{\pi }={\mathbf{b}}_{{\pi }^{\prime }}^{\prime }$. According to the equation ${\mathbf{b}}_i={\mathbf{b}}_0+\alpha ·i$, we observe that ${\mathbf{b}}_i={\mathbf{b}}_i^{\prime }$ when i is the position of the signer in the ring. So $\mathbf{CLTRS}.\mathbf{Trace}$ algorithm will output $p{k}_i$.
  • When $\pi \ne {\pi }^{\prime }$, it means that different signers sign messages. As shown in [50], the $\mathbf{CLTRS}.\mathbf{Trace}$ algorithm will output accept with overwhelming probability.

5. The Underlying Zero-Knowledge Argument System

In this section, we will introduce efficient zero-knowledge protocols presented in [53], which will be used to construct our scheme. Similar to the Stern protocol, the efficient zero-knowledge protocol can represent most lattice-based relations. Different from the Stern protocol, the efficient zero-knowledge protocol adds an additional set $\mathcal{M}$ to express the linear equation, which is used to express the quadratic constraint of the witness; and it has the same standard soundness as the Stern protocol, but the soundness error is only the inversion of a polynomial.

The efficient ZKAoK protocol proves relation $\mathfrak{R}$ as follow:

$$\begin{array}{c}\mathfrak{R}=\{(\mathbf{A},\mathbf{e},\mathcal{M}),(\mathbf{s})\in ({\mathbb{Z}}_q^{m\times n}\times {\mathbb{Z}}_q^m\times {({[1,n]}^3)}^l)\times ({\mathbb{Z}}_q^n):\\ \mathbf{A}·\mathbf{s}=\mathbf{e}\wedge \forall (m,l,r)\in \mathcal{M},\mathbf{s}[m]=\mathbf{s}[l]·\mathbf{s}[r]\}\end{array}$$

where the set $\mathcal{M}$ is used to express the quadratic constraint of the witness x.

The specific construction corresponding to the relation $\mathfrak{R}$ is given in the [53] and interested readers can go to learn more.

We will use the above efficient ZKAoK to build our CLTRS scheme. In our protocol, the prover $\mathcal{P}$ sends the public statement $X=(\mathbf{A},{\mathbf{A}}_0,{\mathbf{A}}_{\mathsf{\Gamma }},{\mathbf{D}}_1,{\mathbf{D}}_2,\mathbf{B},\mathbf{t})$ and the proof $\mathsf{\Pi }$ to the verifier $\mathcal{V}$, and $\mathcal{V}$ believes that secret witness $W=({\mathbf{sk}}_{\pi },r_{\pi },{\mathbf{b}}_{\pi },{\mathbf{c}}_{\pi },{\mathbf{w}}_A=(\mathbf{wit},{\{{\mathbf{h}}_j\}}_{j\in [1,l]},{\{{\mathbf{k}}_j\}}_{j\in [1,l]}))$ possessed by $\mathcal{P}$ satisfies the following relationship after verifying $\mathsf{\Pi }$.

$$\begin{array}{ccc}\hfill {\mathfrak{R}}_{CLTRS}& =& \{(\mathbf{A},{\mathbf{A}}_0,{\mathbf{A}}_{\mathsf{\Gamma }},{\mathbf{D}}_1,{\mathbf{D}}_2,\mathbf{B},\mathbf{t})\in \hfill \\ & & {\mathbb{Z}}_q^{\widehat{m}\times n}\times {\mathbb{Z}}_q^{m\times n}\times {\mathbb{Z}}_q^{m\times n}\times {\mathbb{Z}}_q^{n\times m^{\prime }}\times {\mathbb{Z}}_q^{n\times m^{\prime }}\times {\mathbb{Z}}_q^{n\times 2m^{″}}\times {\mathbb{Z}}_q^n;\hfill \\ & & ({\mathbf{sk}}_{\pi }=({\mathbf{s}}_{\pi },{\mathbf{v}}_{\pi }),r_{\pi }=(i{d}_{\pi },{\mathbf{y}}_{\pi }),{\mathbf{b}}_{\pi },{\mathbf{c}}_{\pi },{\mathbf{w}}_A=(\mathbf{wit},{\{{\mathbf{h}}_j\}}_{j\in [1,l]},{\{{\mathbf{k}}_j\}}_{j\in [1,l]}))\hfill \\ & & \in {\mathbb{Z}}_q^{2n}\times {(0,1)}^{\ell }\times {\mathbb{Z}}_p^m\times {\mathbb{Z}}_p^m\times {\{0,1\}}^{m^{″}}\times ({(0,1)}^l\times {\{{(0,1)}^{m^{″}}\}}^l\times {\{{(0,1)}^{m^{″}}\}}^l):\hfill \end{array}$$

$$\begin{array}{ccc}& & H_3\left(i{d}_{\pi }\right)={\mathbf{a}}_{i{d}_{\pi }}=\mathbf{A}·{\mathbf{s}}_{\pi }modq\hfill \end{array}$$

(1)

$$\begin{array}{ccc}& & \wedge {\mathbf{b}}_{\pi }={\lfloor {\mathbf{A}}_{\mathsf{\Gamma }}·{\mathbf{sk}}_{\pi }\rceil }_p={\lfloor {\mathbf{A}}_{{\mathsf{\Gamma }}_1}·{\mathbf{s}}_{\pi }+{\mathbf{A}}_{{\mathsf{\Gamma }}_2}·{\mathbf{v}}_{\pi }\rceil }_p\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& & \wedge {\mathbf{y}}_{\pi }={\lfloor {\mathbf{A}}_0·{\mathbf{v}}_{\pi }\rceil }_p\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& & \wedge {\mathbf{c}}_{\pi }=bin({\mathbf{D}}_1·bin\left(H_2\left(r_{\pi }\right)\right)+{\mathbf{D}}_2·bin\left({\mathbf{b}}_{\pi }\right))\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& & \wedge A.Verif{y}_{\mathbf{B}}(\mathbf{t},{\mathbf{c}}_{\pi },(\mathbf{wit},{\{{\mathbf{h}}_j\}}_{j\in [1,l]},{\{{\mathbf{k}}_j\}}_{j\in [1,l]}))\}\hfill \end{array}$$

(5)

Next, we show how the five equations in relation ${\mathfrak{R}}_{CLTRS}$ can be reduced to some instance in relation $\mathfrak{R}$. Among them, we are able to directly apply the transformation of Section 4.4 in [53] to reduce the Equation (5) to the relation $\mathfrak{R}$, so the following focuses on the reduction of the other four equations.

5.1. ZKAoK of Linear Equation with Short Solution

For the first equation ${\mathbf{a}}_{i{d}_{\pi }}=\mathbf{A}·{\mathbf{s}}_{\pi }modq$, we need to hide the ${\mathbf{s}}_{\pi }$ and ${\mathbf{a}}_{i{d}_{\pi }}$, so the Equation (1) can be transformed to the following form:

$$\mathbf{A}·{\mathbf{s}}_{\pi }-{\mathbf{a}}_{i{d}_{\pi }}=\mathbf{0}modq.$$

(6)

By observing the Equation (6) we let ${\overline{\mathbf{A}}}_1=\left(\mathbf{A}\right|-{\mathbf{I}}_{\widehat{m}}),{\overline{\mathbf{x}}}_1={\left(\begin{array}{cc}{\mathbf{s}}_{\pi }^T& {\mathbf{a}}_{i{d}_{\pi }}^T\end{array}\right)}^T$ and ${\overline{\mathbf{y}}}_1=\mathbf{0}$. Therefore, to prove that Equation (1) holds, it is equivalent convert to prove that following equation holds:

$${\overline{\mathbf{A}}}_1·{\overline{\mathbf{x}}}_1={\overline{\mathbf{y}}}_{1}modq.$$

(7)

For the fourth equation ${\mathbf{c}}_{\pi }=bin({\mathbf{D}}_1·bin\left(H_2\left(r_{i{d}_{\pi }}\right)\right)+{\mathbf{D}}_2·bin\left({\mathbf{b}}_{\pi }\right))$, we need to hide the ${\mathbf{c}}_{\pi },r_{i{d}_{\pi }}$ and ${\mathbf{b}}_{\pi }$. Let ${\mathbf{d}}_1=bin\left(H_2\left(r_{i{d}_{\pi }}\right)\right)$ and ${\mathbf{d}}_2=bin\left({\mathbf{b}}_{\pi }\right)$. The Equation (4) can be transformed to the following form:

$${\mathbf{D}}_1·{\mathbf{d}}_1+{\mathbf{D}}_2·{\mathbf{d}}_2-{\mathbf{H}}_n·{\mathbf{c}}_{\pi }=\mathbf{0}modq.$$

(8)

By observing the Equation (8) we set the new witness ${\overline{\mathbf{x}}}_2={\left(\begin{array}{ccc}{\mathbf{d}}_1^T& {\mathbf{d}}_2^T& {\mathbf{c}}_{\pi }^T\end{array}\right)}^T$, set ${\overline{\mathbf{A}}}_2=({\mathbf{D}}_1|{\mathbf{D}}_2|-{\mathbf{H}}_n)$ and ${\overline{\mathbf{y}}}_2=\mathbf{0}$ where ${\mathbf{H}}_n={\mathbf{I}}_n⨂\left(\begin{array}{cccc}1& 2& \cdots & 2^{k_q-1}\end{array}\right),k_q=\lceil logq\rceil$. To prove that Equation (8) holds, it is equivalent to prove the following equation holds:

$${\overline{\mathbf{A}}}_2·{\overline{\mathbf{x}}}_2={\overline{\mathbf{y}}}_{2}modq.$$

(9)

Then we need to do a binary decomposition of the witness ${\overline{\mathbf{x}}}_1$. We let ${\overline{\mathbf{x}}}_b=bin\left({\overline{\mathbf{x}}}_1\right)$ and ${\overline{\mathbf{A}}}_b={\overline{\mathbf{A}}}_1·{\mathbf{H}}_{n+\widehat{m}}$, where bin is a binary decomposition function and ${\mathbf{H}}_{n+\widehat{m}}={\mathbf{I}}_{n+\widehat{m}}⨂\left(\begin{array}{cccc}1& 2& \cdots & 2^{k_q-1}\end{array}\right)$. Then we combine Equation (7) and Equation (9) as below:

$${\mathbf{A}}_{com}=\left(\begin{array}{cc}{\overline{\mathbf{A}}}_b& \mathbf{0}\\ \mathbf{0}& {\overline{\mathbf{A}}}_2\end{array}\right),{\mathbf{x}}_{com}={\left(\begin{array}{cc}{\overline{\mathbf{x}}}_b^T& {\overline{\mathbf{x}}}_2^T\end{array}\right)}^T,{\mathbf{y}}_{com}={\left(\begin{array}{cc}{\overline{\mathbf{y}}}_1^T& {\overline{\mathbf{y}}}_2^T\end{array}\right)}^T.$$

At last we set $\mathcal{M}={\left\{(i,i,i)\right\}}_{i\in [1,(2\widehat{m}+2n)k_q+2m{k}_p]}$,$k_p=\lceil logp\rceil$.

In doing so, we reduce the relation ${\mathfrak{R}}_{(1)}=\{(\mathbf{A}),({\mathbf{s}}_{\pi },{\mathbf{a}}_{i{d}_{\pi }})\in ({\mathbb{Z}}_q^{\widehat{m}\times n}\times ({\mathbb{Z}}_q^n\times {\mathbb{Z}}_q^{\widehat{m}}))\}$ and ${\mathfrak{R}}_{(3)}=\{({\mathbf{D}}_1,{\mathbf{D}}_2),(bin(H_2(r_{i{d}_{\pi }})),bin({\mathbf{b}}_{\pi }),{\mathbf{c}}_{\pi })\in ({\mathbb{Z}}_q^{n\times m^{\prime }}\times {\mathbb{Z}}_q^{n\times m^{\prime }}\times ({\{0,1\}}^{m{k}_p}\times {\{0,1\}}^{m{k}_p}\times {\{0,1\}}^{n{k}_q}))\}$ to $\mathfrak{R}$, both the witness and $\mathcal{M}$ are size of $(\widehat{m}+2n)k_q+2m{k}_p$.

5.2. ZKAoK of PRF Preimage

For the second Equation (2) ${\mathbf{b}}_{\pi }={\lfloor {\mathbf{A}}_{\mathsf{\Gamma }}·{\mathbf{sk}}_{\pi }\rceil }_p$, we also need to hide the ${\mathbf{sk}}_{\pi }$ and ${\mathbf{b}}_{\pi }$. Specifically, let $m,n$ be positive integers, p be a prime number and q is an integer with $q>p\ge 2$. We can express Equation (2) as the following relation:

$${\mathfrak{R}}_{(2)}=\{({\mathbf{A}}_{\mathsf{\Gamma }}),({\mathbf{sk}}_{\pi },{\mathbf{b}}_{\pi })\in ({\mathbb{Z}}_q^{m\times n})\times ({\mathbb{Z}}_q^{2n}\times {\mathbb{Z}}_p^m):{\mathbf{b}}_{\pi }={\lfloor {\mathbf{A}}_{\mathsf{\Gamma }}·{\mathbf{sk}}_{\pi }\rceil }_p\}$$

We demonstrate the above relation ${\mathfrak{R}}_{\left(2\right)}$ by reducing it to an instance of the relation $\mathfrak{R}$ through suitable transformations. We convert the ${\mathbf{b}}_{\pi }={\lfloor {\mathbf{A}}_{\mathsf{\Gamma }}·{\mathbf{sk}}_{\pi }\rceil }_{p}modq$ to the following form:

$$\left\{\begin{array}{c}{\mathbf{A}}_{\mathsf{\Gamma }}·{\mathbf{sk}}_{\pi }={\mathbf{b}}_{\pi }^{\prime }modq,\hfill \\ \lfloor \frac{p}{q}·{\mathbf{b}}_{\pi }^{\prime }\rceil ={\mathbf{b}}_{\pi }modp.\hfill \end{array}\right.$$

As shown in [44,58], the second equation $\lfloor \frac{p}{q}·{\mathbf{b}}_{\pi }^{\prime }\rceil ={\mathbf{b}}_{\pi }modp$ holds iff each element of the vector $\frac{q}{p}{\mathbf{b}}_{\pi }-{\mathbf{b}}_{\pi }^{\prime }$ is in $[0,\frac{q}{p})$, and thus above equation can be transformed in the following:

$$\left\{\begin{array}{c}{\mathbf{A}}_{\mathsf{\Gamma }}·{\mathbf{sk}}_{\pi }={\mathbf{b}}_{\pi }^{\prime }modq,\hfill \\ {\mathbf{e}}^{\prime }=\frac{q}{p}{\mathbf{b}}_{\pi }-{\mathbf{b}}_{\pi }^{\prime }modq.\hfill \end{array}\right.$$

Then we can transform it into a linear equation with short solution. Next, we will describe how the process of reduction is carried out. In the following, we will omit all $modq$ operations for simplicity.

First, we will draw on the separation technique mentioned in [59] to convert ${\mathbf{e}}^{\prime }$ to a binary vector ${\mathbf{e}}_b^{\prime }$. Setting $\zeta =\frac{q}{p}-1$, $k=\lceil log\zeta \rceil$. The size of ${\mathbf{e}}_b^{\prime }$ is $k·m$.

Let $\mathbf{g}=(\lfloor \frac{\zeta +1}{2}\rfloor \parallel \cdots \parallel \lfloor \frac{\zeta +2^{i-1}}{2^i}\rfloor \parallel \cdots \parallel \lfloor \frac{\zeta +2^{k-1}}{2^k}\rfloor \parallel )$, $\mathbf{G}={\mathbf{I}}_m⨂\mathbf{g}$, which satisfies $\mathbf{G}·{\mathbf{e}}_b^{\prime }={\mathbf{e}}^{\prime }$.

Then, let ${\mathbf{sk}}_{\pi }^{\ast }=bin({\mathbf{sk}}_{\pi })$, ${\mathbf{b}}_{\pi }^{\prime \ast }=bin({\mathbf{b}}_{\pi }^{\prime })$, ${\mathbf{b}}_{\pi }^{\ast }=bin(\frac{q}{p}{\mathbf{b}}_{\pi })$, ${\mathbf{H}}_m={\mathbf{I}}_m⨂$

$\left(\begin{array}{ccccc}1& 2& 4& \cdots & 2^{k_q-1}\end{array}\right)$, ${\mathbf{H}}_n={\mathbf{I}}_n⨂\left(\begin{array}{ccccc}1& 2& 4& \cdots & 2^{k_q-1}\end{array}\right)$, where $k_q=\lceil logq\rceil$. We set

$${\mathbf{A}}_{\mathbf{1}}^{\prime }=\left(\begin{array}{cccc}{\mathbf{A}}_{\mathsf{\Gamma }}·{\mathbf{H}}_n& -{\mathbf{H}}_m& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathbf{H}}_m& \mathbf{G}& -{\mathbf{H}}_m\end{array}\right),$$

$${\mathbf{x}}_{\mathbf{1}}^{\prime }={\left(\begin{array}{cccc}{\mathbf{sk}}_{\pi }^{\ast T}& {\mathbf{b}}_{\pi }^{{}^{\prime }\ast T}& {\mathbf{e}}^{\prime }{T}_b& {\mathbf{b}}_{\pi }^{\ast T}\end{array}\right)}^T,{\mathbf{u}}_{\mathbf{1}}^{\prime }={\left(\begin{array}{cc}\mathbf{0}& \mathbf{0}\end{array}\right)}^T.$$

For the third Equation (3) ${\mathbf{y}}_{\pi }={\lfloor {\mathbf{A}}_0·{\mathbf{v}}_{\pi }\rceil }_p$, its structural form is similar to that of Equation (2). Referring to the transformation of Equation (2) above, we can obtain

$$\left\{\begin{array}{c}{\mathbf{A}}_0·{\mathbf{v}}_{\pi }={\mathbf{y}}_{\pi }^{\prime }modq,\hfill \\ {\mathbf{e}}^{″}=\frac{q}{p}{\mathbf{y}}_{\pi }-{\mathbf{y}}_{\pi }^{\prime }modq.\hfill \end{array}\right.$$

Then, let ${\mathbf{v}}_{\pi }^{\ast }=bin\left({\mathbf{v}}_{\pi }\right),{\mathbf{y}}_{\pi }^{\prime \ast }=bin\left({\mathbf{y}}_{\pi }^{\prime }\right),{\mathbf{y}}_{\pi }^{\ast }=bin\left(\frac{q}{p}{\mathbf{y}}_{\pi }\right),{\mathbf{H}}_m={\mathbf{I}}_m⨂$

$\left(\begin{array}{ccccc}1& 2& 4& \cdots & 2^{k_q-1}\end{array}\right)$, ${\mathbf{H}}_n={\mathbf{I}}_n⨂\left(\begin{array}{ccccc}1& 2& 4& \cdots & 2^{k_q-1}\end{array}\right)$, where $k_q=\lceil logq\rceil$. We set

$${\mathbf{A}}_{\mathbf{2}}^{\prime }=\left(\begin{array}{cccc}{\mathbf{A}}_0·{\mathbf{H}}_n& -{\mathbf{H}}_m& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathbf{H}}_m& \mathbf{G}& -{\mathbf{H}}_m\end{array}\right),$$

$${\mathbf{x}}_{\mathbf{2}}^{\prime }={\left(\begin{array}{cccc}{\mathbf{v}}_{\pi }^{\ast T}& {\mathbf{y}}_{\pi }^{{}^{\prime }\ast T}& {\mathbf{e}}^{″}{T}_b& {\mathbf{y}}_{\pi }^{\ast T}\end{array}\right)}^T,{\mathbf{u}}_{\mathbf{2}}^{\prime }={\left(\begin{array}{cc}\mathbf{0}& \mathbf{0}\end{array}\right)}^T$$

Then we combine Equation (2) and Equation (3) as below:

$${\mathbf{A}}_{com}^{\prime }=\left(\begin{array}{cc}{\mathbf{A}}_1^{\prime }& \mathbf{0}\\ \mathbf{0}& {\mathbf{A}}_2^{\prime }\end{array}\right),{\mathbf{x}}_{com}^{\prime }={\left(\begin{array}{cc}{\mathbf{x}}_1^{{}^{\prime }T}& {\mathbf{x}}_2^{{}^{\prime }T}\end{array}\right)}^T,{\mathbf{u}}_{com}^{\prime }={\left(\begin{array}{cc}{\mathbf{u}}_1^{{}^{\prime }T}& {\mathbf{u}}_2^{{}^{\prime }T}\end{array}\right)}^T.$$

At last we set $\mathcal{M}={\left\{(i,i,i)\right\}}_{i\in [1,(3n+2m)k_q+2mk+2m{k}_p]}$.

By doing so, we reduce the relation ${\mathfrak{R}}_{\left(2\right)}=\{\left({\mathbf{A}}_{\mathsf{\Gamma }}\right),({\mathbf{sk}}_{\pi },{\mathbf{b}}_{\pi })\in \left({\mathbb{Z}}_q^{m\times 2n}\right)\times \left({\mathbb{Z}}_q^{2n}\right)\times \left({\mathbb{Z}}_p^m\right):{\mathbf{b}}_{\pi }={\lfloor {\mathbf{A}}_{\mathsf{\Gamma }}·{\mathbf{sk}}_{\pi }\rceil }_p\}$ and ${\mathfrak{R}}_{\left(3\right)}=\{\left({\mathbf{A}}_0\right),({\mathbf{v}}_{\pi },{\mathbf{y}}_{\pi })\in \left({\mathbb{Z}}_q^{m\times n}\right)\times \left({\mathbb{Z}}_q^n\right)\times \left({\mathbb{Z}}_p^m\right):{\mathbf{y}}_{\pi }={\lfloor {\mathbf{A}}_0·{\mathbf{v}}_{\pi }\rceil }_p\}$ to $\mathfrak{R}$, both the witness and $\mathcal{M}$ are size of $(2n+2m)k_q+2mk+2m{k}_p$.

6. Security Analysis

First of all, the output result is accepted when the two tuples $(I,R,M,\delta )$ and $(I,R,M^{\prime },{\delta }^{\prime })$ are used as input to the $\mathbf{CLTRS}.\mathbf{Trace}$ algorithm, which indicates that there is no index number s.t. ${\mathbf{b}}_i={\mathbf{b}}_i^{\prime }$, where ${\left({\mathbf{b}}_i\right)}_{\left[L\right]}$ and ${\left({\mathbf{b}}_i^{\prime }\right)}_{\left[L\right]}$ are computed from $(I,R,M,\delta )$ and $(I,R,M^{\prime },{\delta }^{\prime })$ respectively. Along this line of thinking, if we can show that the probability that other cases lead to an output result that is not accepted is negligible or impossible, then the proof of tag-linkability is complete. Other cases include the following two possibilities: (1) when there exist two or more indexes $i_k$ satisfying ${\mathbf{b}}_{i_k}={\mathbf{b}}_{i_k}^{\prime }$ for $k=0,1$, then it is shown that ${\mathbf{b}}_j={\mathbf{b}}_j^{\prime }$ for all $j\in \left[L\right]$, because two different lines have two points of intersection, it follows that the two lines must coincide, as a result, $\mathbf{CLTRS}.\mathbf{Trace}$ algorithm will output $linked$. (2) when only one index exists that satisfies ${\mathbf{b}}_i={\mathbf{b}}_i^{\prime }$, this means that the same signer has signed different messages, so $\mathbf{CLTRS}.\mathbf{Trace}$ algorithm will output $p{k}_i$, which indicates that the user’s identity will be exposed. Therefore, we have the following conclusions.

Theorem 1

(Tag-linkability). Under the ROM, if the SIS assumption holds, the underlying NIZKAoK is proof of knowledge and F has uniqueness, then the CLTRS scheme is tag-linkable.

Proof. 

According to the definition of the traceable algorithm, we can easily know that when the return result obtained from two tuples $(I,R,M,\delta )$ and $(I,R,M^{\prime },{\delta }^{\prime })$ as input is accepted, it means that there is no exist ${\mathbf{b}}_j={\mathbf{b}}_j^{\prime }$ where $j\in \left[L\right]$. And for $L+1$ valid signatures, the result obtained for any two of them as input to the tracing algorithm is accepted, it indicates that there exist $L+1$ different ${\mathbf{b}}_{j,\pi }$, where $j\in [L+1]$. Since the generation of ${\mathbf{b}}_{j,\pi }$ corresponds uniquely to $s{k}_j$ and $s{k}_j$ corresponds uniquely to $p{k}_j$, so ${\mathbf{b}}_{j,\pi }$ corresponds uniquely to the public key $p{k}_j$, which indicates the existence of $L+1$ different public keys, while there are at most L different public keys in the ring, hence the contradiction, so the adversary cannot break the tag-linkability. If $\mathcal{A}$ can break the tag-linkability, then $\mathcal{C}$ can construct the following algorithm to break the SIS hard problem. The simulation works as follows:

• SIS instance. The challenger $\mathcal{C}$ receives an SIS instance $\mathbf{F}\leftarrow {\mathbb{Z}}_q^{\widehat{m}\times n}$, $\mathcal{C}$ needs to look for a non-zero vector $\mathbf{s}\in {\mathbb{Z}}_q^n$ satisfying $\mathbf{F}·\mathbf{s}=\mathbf{0}modq$, which $\parallel \mathbf{s}\parallel \le \beta$ and $\beta ={\sigma }_2·\sqrt{n}$.

• $\mathbf{Setup}$: Given the system parameter $1^{\lambda }$, instead of running the real zero-knowledge, $\mathcal{C}$ invokes simulator ${\mathcal{S}}_{sim}$ to generate the public parameters, the remaining parameters are generated unchanged except that $mpk$ is replaced with $\mathbf{F}$, then sends $pp$ to $\mathcal{A}$ and $msk$ is kept itself.
• $\mathbf{Query}$. $\mathcal{C}$ initializes initially empty lists $lis{t}_{H_1}$, $lis{t}_{H_2}$, $lis{t}_{H_3}$, $lis{t}_{CU}$, $lis{t}_{SQ}$ and keeps the consistency of answers to adversaries by maintaining these tables,

  (a)

  H${}_1$Query. When $\mathcal{A}$ submits a label ${\mathsf{\Gamma }}_i$ to this oracle, $\mathcal{C}$ first checks if ${\mathsf{\Gamma }}_i$ in the $lis{t}_{H_1}$, if it exists, returns the corresponding ${\mathbf{A}}_{{\mathsf{\Gamma }}_i}$. Otherwise, $\mathcal{C}$ picks a random matrix ${\mathbf{A}}_{{\mathsf{\Gamma }}_i}\leftarrow {\mathbb{Z}}_q^{m\times 2n}$, and returns it to $\mathcal{A}$.

  (b)

  H${}_2$Query. When $\mathcal{A}$ submits a tuple $({\mathsf{\Gamma }}_i,M_i)$, $\mathcal{C}$ first checks if the tuple in the $lis{t}_{H_2}$, if it exists, returns the corresponding ${\mathbf{b}}_{i,0}$. Otherwise, $\mathcal{C}$ picks a random vector ${\mathbf{b}}_{i,0}\leftarrow {\mathbb{Z}}_p^m$, and returns it to ${\mathcal{A}}_I$.

  (c)

  H${}_3$Query. When $\mathcal{A}$ submits an $i{d}_i$ to this oracle, $\mathcal{C}$ first checks if $i{d}_i$ in the $lis{t}_{H_3}$, if it exists, returns the corresponding ${\mathbf{a}}_{i{d}_i}$. Otherwise, $\mathcal{C}$ randomly selects a ${\mathbf{s}}_i\leftarrow {\mathbb{Z}}_p^n$ where ${\mathbf{s}}_i$ is statistically close to $D_{{\mathsf{\Lambda }}^{\mathbf{u}}\left(\mathbf{A}\right),{\sigma }_2}$, computes ${\mathbf{a}}_{i{d}_i}=\mathbf{F}·{\mathbf{s}}_{i}modq$, and returns it to $\mathcal{A}$.

  (d)

  $\mathbf{CreateUserQuery}$. When $\mathcal{A}$ submits an $i{d}_i$, $\mathcal{C}$ first checks if $i{d}_i$ in the $lis{t}_{CU}$, if it exists, returns the corresponding key pairs $(p{k}_i,s{k}_i)$. Otherwise, $\mathcal{C}$ calls the $\mathbf{PartialPrivateKeyQuery}$ with $i{d}_i$ to obtain ${\mathbf{s}}_i$, and then runs $SetSecretValue$, $SetPrivateKey$, $SetPublicKey$ algorithm to generate ${\mathbf{v}}_i$, $s{k}_i$ and ${\mathbf{y}}_i$, returns $(p{k}_i,s{k}_i)$ to adversary $\mathcal{A}$, then adds tuple $(i{d}_i,{\mathbf{s}}_i,{\mathbf{v}}_i,s{k}_i,{\mathbf{y}}_i)$ to $lis{t}_{CU}$.

  (e)

  $\mathbf{PartialPrivateKeyQuery}$. When $\mathcal{A}$ submits an $i{d}_i$, $\mathcal{C}$ first checks if ${\mathbf{a}}_{i{d}_i}$ in the $lis{t}_{H_3}$, if it exists, returns the corresponding partial private key ${\mathbf{s}}_i$. Otherwise, $\mathcal{C}$ runs $H_3$ to generate ${\mathbf{s}}_i$ and returns it to $\mathcal{A}$.

  (f)

  $\mathbf{ReplacePublicKeyQuery}$. When $\mathcal{A}$ submits an $i{d}_i$ and a ${\mathbf{y}}_i^{\prime }$ to this oracle, $\mathcal{C}$ substitutes $y_i$ for $y_i^{\prime }$.

  (g)

  $\mathbf{SignQuery}$. When the adversary $\mathcal{A}$ submits the user $i{d}_i$, issue I, ring R and message M, $\mathcal{C}$ return $\delta \leftarrow CLTRS.Sign(pp,s{k}_i,I,R,M)$ to $\mathcal{A}$.

• $\mathbf{Forgery}$. We assume that the signature ${\delta }_i$ contains the sequence $({\mathbf{b}}_{i,1},\cdots$, ${\mathbf{b}}_{i,L+1})$. This assumption is well-founded because we can simply recover the sequence from the tuple $(I,R,M_i,{\delta }_i)$. The probability that $\mathcal{A}$ forges $L+1$ valid signatures ${\delta }_i=({\alpha }_i,{\mathsf{\Pi }}_i)$ on $L+1$ tuples $(I,R,M_i)$ while the trace algorithm takes any two signatures as input and obtains an output that is both accept is non-negligible, where $i\in [L+1].$ That means

  (a)

  $CLTRS.Verify(pp,I,R,{\delta }_i,M_i)=1,\forall i\in [L+1]$,

  (b)

  $CLTRS.Trace(pp,I,R,M_h,{\delta }_h,M_k,{\delta }_k)=accept,\forall h,k\in [L+1],s.t.,h\ne k$.

• $\mathbf{Analysis}$. During the initialization phase, although we do not run the real ZKAoK protocol but invoke a simulator ${\mathcal{S}}_{sim}$ for the ZKAoK protocol, the adversary $\mathcal{A}$ cannot detect our substitution due to the zero-knowledge property. According to the proof of knowledge property, the extractor $\mathcal{E}$ capable of extracting the witness from each $(M_i,{\delta }_i=({\alpha }_i,{\mathsf{\Pi }}_i))$, where witness $w=({\pi }_i,s{k}_{{\pi }_i})$, since condition (ii) holds and the unique of the function F, so there is no $s{k}_{{\pi }_k}=s{k}_{{\pi }_h}$ where $k,h\in [L+1]$. For each secret key $s{k}_{{\pi }_i}=({\mathbf{s}}_{{\pi }_i},{\mathbf{v}}_{{\pi }_i})$ we have the following relationship holding:
  $$H_3\left(i{d}_i\right)=\mathbf{F}·{\mathbf{s}}_{{\pi }_i}\wedge {\mathbf{y}}_i={\lfloor {\mathbf{A}}_0·{\mathbf{v}}_{{\pi }_i}\rceil }_p.$$
  There are only L public keys in R. Then it means that there exists one pk matching two different sk. For the equation $H_3\left(i{d}_i\right)=\mathbf{F}·{\mathbf{s}}_{{\pi }_i}$, if there exists another ${\mathbf{s}}^{\ast }$ satisfying $H_3\left(i{d}_i\right)=\mathbf{F}·{\mathbf{s}}^{\ast }$, then it can get $\mathbf{F}·({\mathbf{s}}_{{\pi }_i}-{\mathbf{s}}^{\ast })=\mathbf{0}modq$, and $({\mathbf{s}}_{{\pi }_i}-{\mathbf{s}}^{\ast })$ is a resolution to the SIS problem, therefore, the probability of this happening is negligible. For the equation ${\mathbf{y}}_i={\lfloor {\mathbf{A}}_0·{\mathbf{v}}_{{\pi }_i}\rceil }_p$, if there exists another $v^{\ast }$ satisfying ${\mathbf{y}}_i={\lfloor {\mathbf{A}}_0·{\mathbf{v}}^{\ast }\rceil }_p$, then it breaks Uniqueness of F, the probability of this happening is also negligible. In summary, the probability of the adversary $\mathcal{A}$ being able to forge a successful forgery is negligible. Therefore, our scheme is satisfies tag-linkability.

□

Theorem 2

(Type I Anonymity). The CLTRS scheme is type I anonymous security under the ROM, if the DLWE assumption holds and the underlying NIZKAoK is zero-knowledge.

Proof. 

In the proof of anonymity, we are proving it by means of game hopping, which achieves indistinguishability between games by changing some negligible setting between every two games in order to be undetectable to the adversary. That is, the probability that arbitrary PPT adversary ${\mathcal{A}}_I$ can distinguish the difference between every two games is negligible. We define the advantage of ${\mathcal{A}}_I$ in Game i by $Ad{v}_{{\mathcal{A}}_I,Gamei}^{Ano{n}_I}\left(1^{\lambda }\right)$.

• Game 0: It is type I anonymous game which $b=0$. $\mathcal{C}$ operates algorithm $CLTRS.Setup$ in the Setup phase, saves $msk$ secretly, ${\mathcal{A}}_I$ obtains $pp$ from $\mathcal{C}$.
• Game 1: The game and Game 0 are identical, besides when ${\mathcal{A}}_I$ submits a $PPKQ\left(i{d}_i\right)$ to $H_3$, the challenger chooses randomly ${\mathbf{a}}_{i{d}_i}\leftarrow {\mathbb{Z}}_p^{\widehat{m}}$ and set $H_3\left(i{d}_i\right)={\mathbf{a}}_{i{d}_i}$, then $\mathcal{C}$ keeps a $lis{t}_{H_3}(i{d}_i,{\mathbf{a}}_{i{d}_i})$ to respond consistently. In ROM, ${\mathcal{A}}_I$ is unable to discern the difference between Game 1 and Game 0. Therefore, we obtain
  $$Ad{v}_{{\mathcal{A}}_I,Game1}^{Ano{n}_I}\left(1^{\lambda }\right)\approx Ad{v}_{{\mathcal{A}}_I,Game0}^{Ano{n}_I}\left(1^{\lambda }\right).$$
• Game 2: The game and Game 1 are identical, besides $\mathcal{C}$ uses simulator $\mathcal{S}$ replace the real NIZK proof system. $\mathcal{C}$ uses $\mathcal{S}$ to obtain $pp$ instead of using the real NIZK. By doing so, the challenger is able to generate valid proofs properly without the use of $s{k}_b$. When ${\mathcal{A}}_I$ submits the challenge message $M^{\ast }$ during the challenge phase, $\mathcal{C}$ invokes $\mathcal{S}$ to generate the valid simulation proof ${\mathsf{\Pi }}^{\ast }$ instead of running the real NIZK to generate ${\mathsf{\Pi }}_{real}$. Based on the zero-knowledge property, we have
  $$Ad{v}_{{\mathcal{A}}_I,Game2}^{Ano{n}_I}\left(1^{\lambda }\right)\approx Ad{v}_{{\mathcal{A}}_I,Game1}^{Ano{n}_I}\left(1^{\lambda }\right).$$
• Game 3: The game and Game 2 are identical, besides when it is necessary to run the $F_{s{k}_b}$, $\mathcal{C}$ first finds whether a corresponding tuple $({\mathsf{\Gamma }}_i,M_i,{\mathbf{b}}_{i,\pi })$ exists for the $lis{t}_{F_{s{k}_b}}$ and, if so, returns the corresponding ${\mathbf{b}}_{i,\pi }$. Otherwise, $\mathcal{C}$ takes a stochastic vector ${\mathbf{b}}_{i,r}$, sends it to ${\mathcal{A}}_I$, and adds the vector ${\mathbf{b}}_{i,r}$ to the $lis{t}_F$. So $\mathcal{C}$ can simulate $F_{s{k}_b}$ by keeping $lis{t}_F$. For any vector $\mathbf{b}={\lfloor {\mathbf{A}}_{{\mathsf{\Gamma }}_1}·\mathbf{s}+{\mathbf{A}}_{{\mathsf{\Gamma }}_2}·\mathbf{v}\rceil }_p$, We can convert it to $\frac{q}{p}·\mathbf{b}-{\mathbf{A}}_{{\mathsf{\Gamma }}_2}·\mathbf{v}={\mathbf{A}}_{{\mathsf{\Gamma }}_1}·\mathbf{s}+\mathbf{e}modq$ where $\mathbf{e}\in [0,\frac{q}{p})$, if adversary ${\mathcal{A}}_I$ can distinguish between $\frac{q}{p}·\mathbf{b}-{\mathbf{A}}_{{\mathsf{\Gamma }}_2}·\mathbf{v}$ and $\frac{q}{p}·{\mathbf{b}}_{i,r}-{\mathbf{A}}_{{\mathsf{\Gamma }}_2}·\mathbf{v}$ without knowing secret key $\mathbf{s}$ and error $\mathbf{e}$, $\mathcal{C}$ may utilize the adversary to crack DLWE problem. Due to the difficulty of the DLWE problem, the probability of ${\mathcal{A}}_I$ to distinguish between $\mathbf{b}$ and ${\mathbf{b}}_{i,r}$ is negligible. Thus, we have
  $$({\mathbf{A}}_{\mathsf{\Gamma }},\mathsf{\Gamma },\mathbf{v},\mathbf{b}:\mathbf{b}\leftarrow F_{s{k}_b}\left(\mathsf{\Gamma }\right))\approx ({\mathbf{A}}_{\mathsf{\Gamma }},\mathsf{\Gamma },\mathbf{v},\mathbf{b}:\mathbf{b}\leftarrow {\mathbb{Z}}_p^m).$$

  And thus
  $$Ad{v}_{{\mathcal{A}}_I,Game3}^{Ano{n}_I}\left(1^{\lambda }\right)\approx Ad{v}_{{\mathcal{A}}_I,Game2}^{Ano{n}_I}\left(1^{\lambda }\right).$$
  Obviously, in Game 3, the generation of signatures $\alpha$ is essentially replaced by random numbers, meaning that the generation of $\alpha$ is already independent of $s{k}_b$. By the same token, when Game 0 is selected with b of 1, the change between each two games is the same as the change from Game 0 to Game 3 above, so when $b=1$, Game 0 is also indistinguishable from Game 3, and since whether $b=0$ or $b=1$, the final Game 3 obtained is identical, it can be easily obtained that when $b=0$ is selected and when $b=1$ is selected, it is indistinguishable for the adversary is indistinguishable for the adversary ${\mathcal{A}}_I$. Thus we have
  $$Ad{v}_{{\mathcal{A}}_I,Game0,b=0}^{Ano{n}_I}\left(1^{\lambda }\right)\approx Ad{v}_{{\mathcal{A}}_I,Game0,b=1}^{Ano{n}_I}\left(1^{\lambda }\right).$$

  So our scheme satisfies type I anonymity.

□

Theorem 3

(Type II Anonymity). The CLTRS scheme is type II anonymous security under the ROM, if the DLWE assupmtion holds and the underlying NIZKAoK is zero-knowledge.

Proof. 

The idea of the proving of Theorem 3 is similar to that of Theorem 2, except that in the proving of Theorem 3 it is the second type of adversary ${\mathcal{A}}_{II}$ that has to be faced. However, the goal is still to make it difficult for ${\mathcal{A}}_{II}$ to identify the difference between each of the two games. That is, the probability that arbitrary PPT ${\mathcal{A}}_{II}$ can distinguish the difference between every two games is negligible. We define the advantage of ${\mathcal{A}}_{II}$ in Game i by $Ad{v}_{A_{II},Gamei}^{Ano{n}_{II}}\left(\lambda \right)$.

• Game 0: It is type II anonymous game which $b=0$. $\mathcal{C}$ operates algorithm $CLTRS.Setup$ in the Setup phase, then sends $pp$ and $msk$ to ${\mathcal{A}}_{II}$.
• Game 1: The game and Game 0 are identical, besides $\mathcal{C}$ use simulator $\mathcal{S}$ replace the real NIZK proof system. $\mathcal{C}$ calls simulator $\mathcal{S}$ to produce the public parameters instead of using the real NIZK. By doing so, the challenger is able to generate valid proofs properly without the use of $s{k}_b$. When ${\mathcal{A}}_{II}$ submits the challenge message $M^{\ast }$ during the challenge phase, $\mathcal{C}$ invokes simulator $\mathcal{S}$ to generate a valid simulation proof ${\mathsf{\Pi }}^{\ast }$ instead of running the real NIZK to generate ${\mathsf{\Pi }}_{real}$. Based on the zero-knowledge property, we have
  $$Ad{v}_{{\mathcal{A}}_{II},Game1}^{Ano{n}_{II}}\left(1^{\lambda }\right)\approx Ad{v}_{{\mathcal{A}}_{II},Game0}^{Ano{n}_{II}}\left(1^{\lambda }\right).$$
• Game 2: The game and Game 1 are identical, besides when it is necessary to run the $F_{s{k}_b}$, $\mathcal{C}$ first finds whether a corresponding tuple $({\mathsf{\Gamma }}_i,M_i,{\mathbf{b}}_{i,\pi })$ exists for the $lis{t}_{F_{s{k}_b}}$ and, if so, returns the corresponding ${\mathbf{b}}_{i,\pi }$. Otherwise, $\mathcal{C}$ takes a stochastic vector ${\mathbf{b}}_{i,r}$, sends it to ${\mathcal{A}}_{II}$, and adds the vector ${\mathbf{b}}_{i,r}$ to the $lis{t}_F$. So $\mathcal{C}$ can simulate $F_{s{k}_b}$ by keeping $lis{t}_F$. For any vector $\mathbf{b}={\lfloor {\mathbf{A}}_{{\mathsf{\Gamma }}_1}·\mathbf{s}+{\mathbf{A}}_{{\mathsf{\Gamma }}_2}·\mathbf{v}\rceil }_p$, We can convert it to $\frac{q}{p}·\mathbf{b}-{\mathbf{A}}_{{\mathsf{\Gamma }}_1}·\mathbf{s}={\mathbf{A}}_{{\mathsf{\Gamma }}_2}·\mathbf{v}+\mathbf{e}modq$ where $\mathbf{e}\in [0,\frac{q}{p})$, if adversary ${\mathcal{A}}_{II}$ can distinguish between $\frac{q}{p}·\mathbf{b}-{\mathbf{A}}_{{\mathsf{\Gamma }}_1}·\mathbf{s}$ and $\frac{q}{p}·{\mathbf{b}}_{i,r}-{\mathbf{A}}_{{\mathsf{\Gamma }}_1}·\mathbf{s}$ without knowing secret key $\mathbf{s}$ and error $\mathbf{e}$, $\mathcal{C}$ may utilize the adversary to crack DLWE problem. Due to the difficulty of the DLWE problem, the probability of an adversary ${\mathcal{A}}_{II}$ being able to distinguish between $\mathbf{b}$ and ${\mathbf{b}}_{i,r}$ is negligible. Thus, we have
  $$({\mathbf{A}}_{\mathsf{\Gamma }},\mathsf{\Gamma },\mathbf{v},\mathbf{b}:\mathbf{b}\leftarrow F_{s{k}_b}\left(\mathsf{\Gamma }\right))\approx ({\mathbf{A}}_{\mathsf{\Gamma }},\mathsf{\Gamma },\mathbf{v},\mathbf{b}:\mathbf{b}\leftarrow {\mathbb{Z}}_p^m).$$

  And thus
  $$Ad{v}_{{\mathcal{A}}_{II},Game2}^{Ano{n}_{II}}\left(1^{\lambda }\right)\approx Ad{v}_{{\mathcal{A}}_{II},Game1}^{Ano{n}_{II}}\left(1^{\lambda }\right).$$

  The same principle as the type I anonymity, we change $b=0$ of Game 0 to $b=1$ and then to Game 2, the adversary still cannot identify the distinction between Game 0 and Game 2 at $b=1$, so we can get a real anonymous game where the adversary cannot distinguish whether the value of b is selected as 0 or 1. Thus, we have
  $$Ad{v}_{{\mathcal{A}}_{II},Game0,b=0}^{Anon}\left(1^{\lambda }\right)\approx Ad{v}_{{\mathcal{A}}_{II},Game0,b=1}^{Ano{n}_{II}}\left(1^{\lambda }\right).$$

  So our scheme satisfies type II anonymity.

□

Theorem 4

(Type I Exculpability). If hash family H is multi-input correlation intractable, NIZKAoK is proof of knowledge, and the function $F^H$ is unique with an intersection-free range, the CLTRS is type I exculpable under the ROM.

Proof. 

Assume that there has a PPT adversary ${\mathcal{A}}_I$ with access to ROM, it inquiries the random oracles $H_1,H_2,H_3$ up to $q_{h_1},q_{h_2},q_{h_3}$ times and makes a maximum of $q_s$ signing queries, if it can break the exculpability with non-negligible probability $ϵ$, then we may construct adversaries ${\mathcal{C}}_I$ and ${\mathcal{C}}_{II}$ to break uniqueness of F and multi-input correlation intractable of H with probability $\frac{ϵ}{2q_{h_1}·q_s}$ and $\frac{ϵ}{2}$, respectively.

• Adversary${\mathcal{C}}_I$. Given a challenge matrix ${\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_1}\in {\mathbb{Z}}_q^{m\times n}$ which is random, it is an instance of function uniqueness. The adversary ${\mathcal{C}}_I$ need to look for a non-zero vector $\tilde{\mathbf{s}}\in {\mathbb{Z}}_q^n$ and a vector ${\tilde{\mathbf{e}}}_s\in {(-\frac{q}{p},\frac{q}{p})}^m$ satisfying ${\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_1}·\tilde{\mathbf{s}}={\tilde{\mathbf{e}}}_{s}modq$, adversary ${\mathcal{C}}_I$ constructs the following game to attack the uniqueness of the function.

1.1

$\mathbf{Setup}$. Given the system parameter $1^{\lambda }$, instead of running the real zero-knowledge protocol, $\mathcal{C}$ calls simulator ${\mathcal{S}}_{sim}$ to produce the public parameters, and remaining parameters are generated unchanged, then sends $pp$ to ${\mathcal{A}}_I$ and $msk$ is kept itself.

1.2

$\mathbf{Queries}$. ${\mathcal{C}}_I$ initializes initially empty lists $lis{t}_{H_1}$, $lis{t}_{H_2}$, $lis{t}_{H_3}$, $lis{t}_{CU}$, $lis{t}_{SQ}$ and keeps the consistency of answers to adversaries by maintaining these tables. We assume that adversary ${\mathcal{A}}_I$ must have done the following queries before forging: ${\mathcal{A}}_I$ will submit a query with label ${\mathsf{\Gamma }}^{\ast }=(I^{\ast },R^{\ast })$ to $H_1$ for the $i^{\ast }$-th time where $i^{\ast }\in [1,q_{h_1}]$ and submit a query with tuple $(i{d}^{\ast },{\mathsf{\Gamma }}^{\ast }=(I^{\ast },R^{\ast }),M^{\ast })$ to $SQ$ for the $j^{\ast }$-th time where $j^{\ast }\in [1,q_s]$ and $i{d}^{\ast }\in R^{\ast }$.

(a)

H${}_1$Query. For the $i\in [1,q_h]$ times of asking, if $i=i^{\ast }$, ${\mathcal{A}}_I$ will submit the label ${\mathsf{\Gamma }}^{\ast }$, ${\mathcal{C}}_I$ picks a random matrix ${\mathbf{A}}_{{\mathsf{\Gamma }}_2^{\ast }}\leftarrow {\mathbb{Z}}_q^{m\times n}$, and then sets ${\mathbf{A}}_{{\mathsf{\Gamma }}^{\ast }}=\left({\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_1}\right|{\mathbf{A}}_{{\mathsf{\Gamma }}_2^{\ast }})$, at last returns it to ${\mathcal{A}}_I$; otherwise if $i\ne i^{\ast }$, ${\mathcal{A}}_I$ will submit the label ${\mathsf{\Gamma }}_i$, ${\mathcal{C}}_I$ picks a random matrix ${\mathbf{A}}_{{\mathsf{\Gamma }}_i}\leftarrow {\mathbb{Z}}_q^{m\times 2n}$ and outputs it to ${\mathcal{A}}_I$.

(b)

H${}_2$Query. When ${\mathcal{A}}_I$ submits a tuple $({\mathsf{\Gamma }}_i,M_i)$, ${\mathcal{C}}_I$ first checks if the tuple in the $lis{t}_{H_2}$, if it exists, returns the corresponding ${\mathbf{b}}_{i,0}$. Otherwise, ${\mathcal{C}}_I$ picks a random vector ${\mathbf{b}}_{i,0}\leftarrow {\mathbb{Z}}_p^m$, and returns it to ${\mathcal{A}}_I$.

(c)

H${}_3$Query. When ${\mathcal{A}}_I$ submits an $i{d}_i$, ${\mathcal{C}}_I$ first checks if $i{d}_i$ in the $lis{t}_{H_3}$, if it exists, returns the corresponding ${\mathbf{a}}_{i{d}_i}$. Otherwise, ${\mathcal{C}}_I$ randomly selects a vector ${\mathbf{s}}_i\leftarrow {\mathbb{Z}}_p^n$ where ${\mathbf{s}}_i\in D_{{\mathsf{\Lambda }}^{\mathbf{u}}\left(\mathbf{A}\right),{\sigma }_2}$ satisfying $\parallel {\mathbf{s}}_i\parallel \le {\sigma }_2\sqrt{n}$, computes ${\mathbf{a}}_{i{d}_i}=\mathbf{A}·{\mathbf{s}}_i$, and returns it to ${\mathcal{A}}_I$.

(d)

$\mathbf{CreateUserQuery}$. When ${\mathcal{A}}_I$ submits an $i{d}_i$, ${\mathcal{C}}_I$ first checks if $i{d}_i$ in the $lis{t}_{CU}$, if it exists, returns the corresponding key pairs $(p{k}_i,s{k}_i)$. Otherwise, ${\mathcal{C}}_I$ calls the $\mathbf{PartialPrivateKeyQuery}$ with $i{d}_i$ to obtain ${\mathbf{s}}_i$, and then runs $SetSecretValue$, $SetPrivateKey$, $SetPublicKey$ algorithm to generate ${\mathbf{v}}_i$, $s{k}_i$ and ${\mathbf{y}}_i$, returns $(p{k}_i,s{k}_i)$ to adversary ${\mathcal{A}}_I$, then adds tuple $(i{d}_i,{\mathbf{s}}_i,{\mathbf{v}}_i,s{k}_i,{\mathbf{y}}_i)$ to $lis{t}_{CU}$.

(e)

$\mathbf{PartialPrivateKeyQuery}$. When ${\mathcal{A}}_I$ submits an $i{d}_i$, ${\mathcal{C}}_I$ first checks if ${\mathbf{a}}_{i{d}_i}$ in the $lis{t}_{H_3}$, if it exists, returns the corresponding ${\mathbf{s}}_i$. Otherwise, ${\mathcal{C}}_I$ runs $H_3$ to generate ${\mathbf{s}}_i$ and outputs it to ${\mathcal{A}}_I$.

(f)

$\mathbf{ReplacePublicKeyQuery}$. When ${\mathcal{A}}_I$ submits an $i{d}_i$ and a ${\mathbf{y}}_i^{\prime }$, $\mathcal{C}$ substitutes $y_i$ for $y_i^{\prime }$.

(g)

$\mathbf{SignQuery}$. For the $j\in [1,q_s]$ times of asking, if $j=j^{\ast }$, ${\mathcal{A}}_I$ will submit a tuple $(i{d}^{\ast },{\mathsf{\Gamma }}^{\ast },M^{\ast })$, instead of running $F_{s{k}_{i{d}^{\ast }}}$, ${\mathcal{C}}_I$ computes ${\mathbf{b}}_{j^{\ast },{\pi }^{\ast }}={\lfloor {\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_1}·{\mathbf{s}}_{{\pi }^{\ast }}+{\mathbf{A}}_{{\mathsf{\Gamma }}_2^{\ast }}·{\mathbf{v}}_{{\pi }^{\ast }}\rceil }_p$, and invokes simulator ${\mathcal{S}}_{sim}$ to generate the proof, the remaining steps remain unchanged, returns the generated signature ${\delta }^{\ast }$ to ${\mathcal{A}}_I$. Otherwise if $j\ne j^{\ast }$, ${\mathcal{A}}_I$ will submit a tuple $(i{d}_j,{\mathsf{\Gamma }}_j,M_j)$, ${\mathcal{C}}_I$ runs $F_{s{k}_j}$ to compute ${\mathbf{b}}_{j,\pi }$, the remaining steps remain unchanged, returns the generated signature ${\delta }_j$ to ${\mathcal{A}}_I$.

1.3

$\mathbf{Forgery}$. Assume ${\mathcal{A}}_I$ outputs two tuples $(I^{\ast },R^{\ast },\overline{M},\overline{\delta })$ and $(I^{\ast },R^{\ast },M^{\prime },{\delta }^{\prime })$ s.t.

(a)

$\mathbf{CLTRS}.\mathbf{Verify}(pp,I^{\ast },R^{\ast },\overline{M},\overline{\delta })=1$;

(b)

$\mathbf{CLTRS}.\mathbf{Verify}(pp,I^{\ast },R^{\ast },M^{\prime },{\delta }^{\prime })=1$;

(c)

${\mathcal{A}}_I$ has not been queried about $PPKQ(pp,i{d}^{\ast })$ and $CUQ(pp,i{d}^{\ast })$ where $i{d}^{\ast }\in R^{\ast }$;

(d)

${\mathcal{A}}_I$ has made at most one of $SQ(pp,i{d}^{\ast },I^{\ast },R^{\ast },\overline{M})$ and $SQ(pp,i{d}^{\ast },I^{\ast },R^{\ast }$, $M^{\prime })$;

(e)

$\mathbf{CLTRS}.\mathbf{Trace}(pp,I^{\ast },R^{\ast },\overline{M},\overline{\delta },M^{\prime },{\delta }^{\prime })=p{k}^{\ast }$.

Suppose ${\pi }^{\ast }$ is the location of $p{k}^{\ast }$ in $R^{\ast }$.

1.4

$\mathbf{Analysis}$. Here, we assume that one of the two signatures output by the adversary is the challenge signature of the previous query, which indicates a situation where the user honestly generates a signature and the adversary ${\mathcal{A}}_I$ forges another valid signature to trap the honest user. We supposes that $\overline{\delta }$ is the challenge signature ${\delta }^{\ast }$. According to proof of knowledge, the extractor $\mathcal{E}$ capable of extracting witnesses $w=({\mathbf{s}}_{{\pi }^{\prime }},{\mathbf{v}}_{{\pi }^{\ast }})$ of ${\delta }^{\prime }$, since condition (iii) holds, according to the $CLTRS.Trace$ algorithm, there is one and only one vector at the identical position in the sequence of ${\mathbf{b}}_i^{\ast }$ and ${\mathbf{b}}_i^{\prime }$ is equal, which means ${\lfloor {\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_1}·{\mathbf{s}}_{{\pi }^{\ast }}+{\mathbf{A}}_{{\mathsf{\Gamma }}_2^{\ast }}·{\mathbf{v}}_{{\pi }^{\ast }}\rceil }_p={\lfloor {\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_1}·{\mathbf{s}}_{{\pi }^{\prime }}+{\mathbf{A}}_{{\mathsf{\Gamma }}_2^{\ast }}·{\mathbf{v}}_{{\pi }^{\ast }}\rceil }_p$, then we can obtain ${\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_1}·({\mathbf{s}}_{{\pi }^{\ast }}-{\mathbf{s}}_{{\pi }^{\prime }})={\tilde{\mathbf{e}}}_{s}modq$. This means that for a random matrix ${\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_1}$, we find the nonzero vector $\tilde{\mathbf{s}}=({\mathbf{s}}_{{\pi }^{\ast }}-{\mathbf{s}}_{{\pi }^{\prime }})$ and the vector ${\tilde{\mathbf{e}}}_s\in {(-\frac{q}{p},\frac{q}{p})}^m$ satisfying ${\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_1}·\tilde{\mathbf{s}}={\tilde{\mathbf{e}}}_s$. So we have broken through the unique of function F with non-negligible probability $\frac{ϵ}{2q_{h_1}·q_s}$. Therefore, it is infeasible that the adversary ${\mathcal{A}}_I$ will succeed in attacking in this case.

• Adversary${\mathcal{C}}_{II}$. Adversary ${\mathcal{C}}_{II}$ will construct the following game. If ${\mathcal{A}}_I$ is capable of winning type I exculpability game by a probability of $ϵ$, then ${\mathcal{C}}_{II}$ uses adversary ${\mathcal{A}}_I$ to break multi-input correlation intractability of H with probability $\frac{ϵ}{2}$.

2.1

$\mathbf{Setup}$. Same as 1.1 Setup.

2.2

$\mathbf{Queries}$. ${\mathcal{C}}_{II}$ initializes initially empty lists $lis{t}_{H_1}$, $lis{t}_{H_2}$, $lis{t}_{H_3}$, $lis{t}_{CU}$, $lis{t}_{SQ}$ and keeps consistency of answers to adversaries by maintaining these tables.

(a)

H${}_1$Query. When ${\mathcal{A}}_I$ submits a label ${\mathsf{\Gamma }}_i$ to this oracle, ${\mathcal{C}}_{II}$ first checks if ${\mathsf{\Gamma }}_i$ in the $lis{t}_{H_1}$, if it exists, returns the corresponding ${\mathbf{A}}_{{\mathsf{\Gamma }}_i}$. Otherwise, ${\mathcal{C}}_{II}$ picks a random matrix ${\mathbf{A}}_{{\mathsf{\Gamma }}_i}\leftarrow {\mathbb{Z}}_q^{m\times 2n}$, and returns it to ${\mathcal{A}}_I$.

(b)

H${}_2$Query. Same as 1.2 H${}_2$Query.

(c)

H${}_3$Query. Same as 1.2 H${}_3$Query.

(d)

$\mathbf{CreateUserQuery}$. Same as 1.2 CreateUserQuery.

(e)

$\mathbf{PartialPrivateKeyQuery}$. Same as 1.2 PartialPrivateKeyQuery.

(f)

$\mathbf{ReplacePublicKeyQuery}$. Same as 1.2 ReplacePublicKeyQuery.

(g)

$\mathbf{SignQuery}$. When ${\mathcal{A}}_I$ submits a tuple $(i{d}_i,I,R,M)$ to this oracle, ${\mathcal{C}}_{II}$ first checks if tuple $(i{d}_i,I,R,M)$ in the $lis{t}_{SQ}$, if it exists, returns the corresponding signature $\delta =(\alpha ,\mathsf{\Pi })$. Otherwise, ${\mathcal{C}}_{II}$ runs $CLTRS.Sign$ to generate signature $\delta =(\alpha ,\mathsf{\Pi })$ and returns it to ${\mathcal{A}}_I$, then adds the tuple $(i{d}_i,I,R,M,\alpha ,\mathsf{\Pi })$ to $lis{t}_{SQ}$.

2.3

$\mathbf{Forgery}$. Same as 1.3 Forgery.

2.4

$\mathbf{Analysis}$. In this case, neither tuple $(I^{\ast },R^{\ast },\overline{M})$ nor tuple $(I^{\ast },R^{\ast },M^{\prime })$ has been made $SQ(pp,·,·,·,i{d}^{\ast })$. That is, the user did not perform a signature, but the adversary ${\mathcal{A}}_I$ forged two valid signatures to trap the user. Since condition (v) holds, according to the definition of $CLTRS.Trace$ algorithm, the sequence ${\overline{\mathbf{b}}}_i$ and value of index ${\pi }^{\ast }$ in the sequence ${\mathbf{b}}_i^{\prime }$ are equal which means

$$H_2({\mathsf{\Gamma }}^{\ast },\overline{M})+{\pi }^{\ast }\overline{\alpha }=H_2({\mathsf{\Gamma }}^{\ast },M^{\prime })+{\pi }^{\ast }{\alpha }^{\prime },$$

Same as case 1, according to proof of knowledge, there exists an extractor $\mathcal{E}$ capable of extracting witnesses $w=(\overline{\pi },s{k}_{\overline{\pi }})$ and $w^{\prime }=({\pi }^{\prime },s{k}_{{\pi }^{\prime }})$ from $\overline{\mathsf{\Pi }}$ and ${\mathsf{\Pi }}^{\prime }$ respectively,

$$F_{s{k}_{\overline{\pi }}}\left({\mathsf{\Gamma }}^{\ast }\right)=H_2({\mathsf{\Gamma }}^{\ast },\overline{M})+{\pi }^{\ast }\overline{\alpha }, \mathrm{and} F_{s{k}_{{\pi }^{\prime }}}\left({\mathsf{\Gamma }}^{\ast }\right)=H_2({\mathsf{\Gamma }}^{\ast },M^{\prime })+{\pi }^{\ast }{\alpha }^{\prime },$$

Then, it holds that

$$H_{hk}({\mathsf{\Gamma }}^{\ast },\overline{M})+{\pi }^{\ast }\frac{F_{s{k}_{\overline{\pi }}}\left({\mathsf{\Gamma }}^{\ast }\right)-H_{hk}({\mathsf{\Gamma }}^{\ast },\overline{M})}{\overline{\pi }}=H_{hk}({\mathsf{\Gamma }}^{\ast },M^{\prime })+{\pi }^{\ast }\frac{F_{s{k}_{{\pi }^{\prime }}}\left({\mathsf{\Gamma }}^{\ast }\right)-H_{hk}({\mathsf{\Gamma }}^{\ast },M^{\prime })}{{\pi }^{\prime }},$$

Here we also consider two situations, the first situation is when $\overline{\pi }={\pi }^{\prime }$, but in this case, $\overline{\pi }={\pi }^{\prime }$ means that there is a dishonest user who signs two different messages, so the output is targeted to that dishonest user. Another situation is when $\overline{\pi }\ne {\pi }^{\prime }$, we can get

$$\overline{\pi }{\pi }^{\prime }·{\overline{\mathbf{b}}}_0+{\pi }^{\ast }{\pi }^{\prime }({\overline{\mathbf{b}}}_{\overline{\pi }}-{\overline{\mathbf{b}}}_0)=\overline{\pi }{\pi }^{\prime }·{\mathbf{b}}_0^{\prime }+{\pi }^{\ast }\overline{\pi }({\mathbf{b}}_{{\pi }^{\prime }}^{\prime }-{\mathbf{b}}_0^{\prime }),$$

it means that $(({\mathsf{\Gamma }}^{\ast },\overline{M}),({\mathsf{\Gamma }}^{\ast },M^{\prime }),H_2({\mathsf{\Gamma }}^{\ast },\overline{M})$, $H_2({\mathsf{\Gamma }}^{\ast },M^{\prime }))\in R_a$. As shown in [50], $R_a$ is a sparse relation. Thus, if ${\mathcal{A}}_I$ wins the type I exculpability game with non-negligible probability $ϵ$, then ${\mathcal{C}}_{II}$ can break the multi-input correlation intractability of $H_2$ with non-negligible probability $\frac{ϵ}{2}$. It contradicts the multi-input correlation intractability of $H_2$.

To sum up, the adversary ${\mathcal{A}}_I$ cannot make a successful attack to exculpability, so our scheme satisfies the type I exculpability. □

Theorem 5

(Type II Exculpability). If hash family H is multi-input correlation intractable, NIZKAoK is proof of knowledge, and the function F is unique with an intersection-free range, the CLTRS is type II exculpable under the ROM.

Proof. 

The proving of this theorem is analogous to the way of proving Theorem 4. ${\mathcal{A}}_{II}$ inquiries the random oracles $H_1,H_2,H_3$ up to $q_{h_1},q_{h_2},q_{h_3}$ times and makes a maximum of $q_s$ signing queries, if it can break the exculpability with non-negligible probability $ϵ$, we may construct adversaries ${\mathcal{D}}_I$ and ${\mathcal{D}}_{II}$ to break uniqueness of F and multi-input correlation intractable of H with probability $\frac{ϵ}{2q_{h_1}·q_s}$ and $\frac{ϵ}{2}$, respectively.

• Adversary${\mathcal{D}}_I$. Given a challenge matrix ${\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_2}\in {\mathbb{Z}}_q^{m\times n}$ which is random, it is an instance of function uniqueness. The adversary ${\mathcal{D}}_I$ need to look for a non-zero vector $\tilde{\mathbf{v}}\in {\mathbb{Z}}_q^n$ and a vector ${\tilde{\mathbf{e}}}_v\in {(-\frac{q}{p},\frac{q}{p})}^m$ satisfying ${\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_2}·\tilde{\mathbf{v}}={\tilde{\mathbf{e}}}_{v}modq$, adversary ${\mathcal{D}}_I$ constructs the following game to attack the uniqueness of the function.

3.1

Setup. Similar to 1.1 Setup, except that $msk$ does not require confidentiality but is sent to the adversary ${\mathcal{A}}_{II}$ along with the public parameter $pp$.

3.2

$\mathbf{Queries}$. ${\mathcal{D}}_I$ initializes initially empty lists $lis{t}_{H_1}$, $lis{t}_{H_2}$, $lis{t}_{H_3}$, $lis{t}_{CU}$, $lis{t}_{PPK}$, $lis{t}_{SQ}$ and keeps consistency of answers to adversaries by maintaining these tables. We assume that adversary ${\mathcal{A}}_{II}$ must have done the following queries before forging: ${\mathcal{A}}_{II}$ will submit a query with label ${\mathsf{\Gamma }}^{\ast }=(I^{\ast },R^{\ast })$ to $H_1$ for the $i^{\ast }$-th time where $i^{\ast }\in [1,q_{h_1}]$ and submit a query with tuple $(i{d}^{\ast },{\mathsf{\Gamma }}^{\ast }=(I^{\ast },R^{\ast }),M^{\ast })$ to $SQ$ for the $j^{\ast }$-th time where $j^{\ast }\in [1,q_s]$ and $i{d}^{\ast }\in R^{\ast }$.

(a)

$H_1$ Query. For the $i\in [1,q_h]$ times of asking, if $i=i^{\ast }$, ${\mathcal{A}}_{II}$ will submit the label ${\mathsf{\Gamma }}^{\ast }$, ${\mathcal{D}}_I$ picks a random matrix ${\mathbf{A}}_{{\mathsf{\Gamma }}_1^{\ast }}\leftarrow {\mathbb{Z}}_q^{m\times n}$ and sets ${\mathbf{A}}_{{\mathsf{\Gamma }}^{\ast }}=({\mathbf{A}}_{{\mathsf{\Gamma }}_1^{\ast }}|{\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_2})$, at last returns it to ${\mathcal{A}}_{II}$; otherwise if $i\ne i^{\ast }$, ${\mathcal{A}}_{II}$ will submit the label ${\mathsf{\Gamma }}_i$, ${\mathcal{D}}_I$ picks a random matrix ${\mathbf{A}}_{{\mathsf{\Gamma }}_i}\leftarrow {\mathbb{Z}}_q^{m\times 2n}$ and returns it to ${\mathcal{A}}_{II}$.

(b)

$H_2$ Query. Same as 1.2 $H_2$ Query.

(c)

$H_3$ Query. When ${\mathcal{A}}_{II}$ submits an $i{d}_i$, ${\mathcal{D}}_I$ randomly selects a vector ${\mathbf{a}}_{i{d}_i}\leftarrow {\mathbb{Z}}_q^{\widehat{m}}$ and sets $H_3\left(i{d}_i\right)={\mathbf{a}}_{i{d}_i}$, then returns ${\mathbf{a}}_{i{d}_i}$ to ${\mathcal{A}}_{II}$.

(d)

CreateUserQuery. When ${\mathcal{A}}_{II}$ submits an $i{d}_i$, ${\mathcal{D}}_I$ first checks if $i{d}_i$ in the $lis{t}_{CU}$, if it exists, returns the corresponding key pairs $(p{k}_i,s{k}_i)$. Otherwise, ${\mathcal{D}}_I$ calls $SampleD(A,T_A,{\mathbf{a}}_{i{d}_i},{\sigma }_2)$ to obtain ${\mathbf{s}}_i$ when $i{d}_i$ exists in $lis{t}_{H_3}$, if $i{d}_i$ exists in $lis{t}_{H_3}$, ${\mathcal{D}}_I$ calls $ExtractPartialPrivateKey$ algorithm to obtain ${\mathbf{s}}_i$, and then runs $SetSecretValue$, $SetPrivateKey$, $SetPublicKey$ algorithm to generate ${\mathbf{v}}_i$, $s{k}_i$ and ${\mathbf{y}}_i$, sends $(p{k}_i,s{k}_i)$ to adversary ${\mathcal{A}}_{II}$, then adds tuple $(i{d}_i,{\mathbf{s}}_i,{\mathbf{v}}_i,s{k}_i,{\mathbf{y}}_i)$ to $lis{t}_{CU}$.

(e)

ParticalPrivateKeyQuery. When ${\mathcal{A}}_{II}$ submits an $i{d}_i$, ${\mathcal{D}}_I$ first checks if the $i{d}_i$ exists in $lis{t}_{CU}$, if it exists, returns the corresponding ${\mathbf{s}}_i$; otherwise ${\mathcal{D}}_I$ checks if the $i{d}_i$ exists in $lis{t}_{PPK}$, if it exists, returns the corresponding ${\mathbf{s}}_i$; otherwise ${\mathcal{D}}_I$ checks if the $i{d}_i$ exists in $lis{t}_{H_3}$, if it exists, runs $SampleD(A,T_A,{\mathbf{a}}_{i{d}_i},{\sigma }_2)$ to get ${\mathbf{s}}_i$ and returns it to ${\mathcal{A}}_{II}$; otherwise, ${\mathcal{D}}_I$ runs $H_3\left(i{d}_i\right)$ to get ${\mathbf{a}}_{i{d}_i}$, and returns ${\mathbf{s}}_i\leftarrow SampleD(A,T_A,{\mathbf{a}}_{i{d}_i},{\sigma }_2)$ to ${\mathcal{A}}_{II}$.

(f)

ReplacePublicKeyQuery. When ${\mathcal{A}}_{II}$ submits an $i{d}_i$ and a ${\mathbf{y}}_i^{\prime }$, ${\mathcal{D}}_I$ replaces the user’s public key ${\mathbf{y}}_i$ with ${\mathbf{y}}_i^{\prime }$.

(g)

SignQuery. For the $j\in [1,q_s]$ times of asking, if $j=j^{\ast }$, ${\mathcal{A}}_{II}$ will submit a tuple $(i{d}^{\ast },{\mathsf{\Gamma }}^{\ast },M^{\ast })$, instead of running $F_{s{k}_{i{d}^{\ast }}}$, ${\mathcal{D}}_I$ computes ${\mathbf{b}}_{j^{\ast },{\pi }^{\ast }}={\lfloor {\mathbf{A}}_{{\mathsf{\Gamma }}_1^{\ast }}·{\mathbf{s}}_{{\pi }^{\ast }}+{\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_2^{\ast }}·{\mathbf{v}}_{{\pi }^{\ast }}\rceil }_p$, and invokes simulator ${\mathcal{S}}_{sim}$ to generate the proof, the remaining steps remain unchanged, returns the generated signature ${\delta }^{\ast }$ to ${\mathcal{A}}_{II}$. Otherwise if $j\ne j^{\ast }$, ${\mathcal{A}}_{II}$ will submit a tuple $(i{d}_j,{\mathsf{\Gamma }}_j,M_j)$, ${\mathcal{D}}_I$ runs $F_{s{k}_j}$ to compute ${\mathbf{b}}_{j,\pi }$, the remaining steps remain unchanged, returns the generated signature ${\delta }_j$ to ${\mathcal{A}}_{II}$.

3.3

$\mathbf{Forgery}$. Assume ${\mathcal{A}}_{II}$ outputs two tuples $(I^{\ast },R^{\ast },\overline{M},\overline{\delta })$ and $(I^{\ast },R^{\ast },M^{\prime },{\delta }^{\prime })$ s.t.

(a)

$\mathbf{CLTRS}.\mathbf{Verify}(pp,I^{\ast },R^{\ast },\overline{M},\overline{\delta })=1$;

(b)

$\mathbf{CLTRS}.\mathbf{Verify}(pp,I^{\ast },R^{\ast },M^{\prime },{\delta }^{\prime })=1$;

(c)

${\mathcal{A}}_{II}$ has not been queried about $RPKQ(pp,i{d}^{\ast })$ and $CUQ(pp,i{d}^{\ast })$ where $i{d}^{\ast }\in R^{\ast }$;

(d)

${\mathcal{A}}_{II}$ has made at most one of $SQ(pp,i{d}^{\ast },I^{\ast },R^{\ast },\overline{M})$ and $SQ(pp,i{d}^{\ast },I^{\ast },R^{\ast },M^{\prime })$;

(e)

$\mathbf{CLTRS}.\mathbf{Trace}(pp,I^{\ast },R^{\ast },\overline{M},\overline{\delta },M^{\prime },{\delta }^{\prime })=p{k}^{\ast }$.

Suppose ${\pi }^{\ast }$ is the location of $p{k}^{\ast }$ in $R^{\ast }$.

3.4

$\mathbf{Analysis}$. Here, we assume that one of the two signatures output by the adversary is the challenge signature of the previous query, which indicates a situation where the user honestly generates a signature and the adversary ${\mathcal{A}}_{II}$ forges another valid signature to trap the honest user. We supposes that $\overline{\delta }$ is the challenge signature ${\delta }^{\ast }$. According to proof of knowledge, the extractor $\mathcal{E}$ capable of extracting witnesses $w=({\mathbf{s}}_{{\pi }^{\ast }},{\mathbf{v}}_{{\pi }^{\prime }})$ of ${\delta }^{\prime }$, since condition (iii) holds, according to the $CLTRS.Trace$ algorithm, there is one and only one vector at the identical position in the sequence of ${\mathbf{b}}_i^{\ast }$ and ${\mathbf{b}}_i^{\prime }$ is equal, which means ${\lfloor {\mathbf{A}}_{{\mathsf{\Gamma }}_1^{\ast }}·{\mathbf{s}}_{{\pi }^{\ast }}+{\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_2}·{\mathbf{v}}_{{\pi }^{\ast }}\rceil }_p={\lfloor {\mathbf{A}}_{{\mathsf{\Gamma }}_1}·{\mathbf{s}}_{{\pi }^{\ast }}+{\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_2}·{\mathbf{v}}_{{\pi }^{\prime }}\rceil }_p$, then we can obtain ${\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_2}·({\mathbf{v}}_{{\pi }^{\ast }}-{\mathbf{v}}_{{\pi }^{\prime }})={\tilde{\mathbf{e}}}_{v}modq$. This means that for a random matrix ${\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_2}$, we find the nonzero vector $\tilde{\mathbf{v}}=({\mathbf{v}}_{{\pi }^{\ast }}-{\mathbf{v}}_{{\pi }^{\prime }})$ and the vector ${\tilde{\mathbf{e}}}_v\in {(-\frac{q}{p},\frac{q}{p})}^m$ satisfying ${\tilde{\mathbf{A}}}_{{\mathsf{\Gamma }}_2}·\tilde{\mathbf{v}}={\tilde{\mathbf{e}}}_v$. So we have broken through the unique of function F with non-negligible probability $\frac{ϵ}{2q_{h_1}·q_s}$. Therefore, it is infeasible that the adversary ${\mathcal{A}}_{II}$ will succeed in attacking in this case.

• Adversary${\mathcal{D}}_{II}$. Adversary ${\mathcal{D}}_{II}$ will construct the following game. If adversary ${\mathcal{A}}_{II}$ can break the type II exculpability game with probability $ϵ$, then ${\mathcal{D}}_{II}$ uses adversary ${\mathcal{A}}_{II}$ to break the multi-input correlation intractability of the hash function H with probability $\frac{ϵ}{2}$.

4.1

$\mathbf{Setup}$. Same as 3.1 Setup.

4.2

$\mathbf{Queries}$. ${\mathcal{D}}_{II}$ initializes initially empty lists $lis{t}_{H_1}$, $lis{t}_{H_2}$, $lis{t}_{H_3}$, $lis{t}_{CU}$, $lis{t}_{PPK}$$lis{t}_{SQ}$ and keeps consistency of answers to adversaries by maintaining these tables.

(a)

H${}_1$Query. Same as 2.2 H${}_1$Query.

(b)

H${}_2$Query. Same as 1.2 H${}_2$Query.

(c)

H${}_3$Query. Same as 3.2 H${}_3$Query.

(d)

$\mathbf{CreateUserQuery}$. Same as 3.2 CreateUserQuery.

(e)

$\mathbf{PartialPrivateKeyQuery}$. Same as 3.2 PartialPrivateKeyQuery.

(f)

$\mathbf{ReplacePublicKeyQuery}$. Same as 3.2 ReplacePublicKeyQuery.

(g)

$\mathbf{SignQuery}$. Same as 2.2 SignQuery.

4.3

$\mathbf{Forgery}$. Same as 3.3 Forgery.

4.4

$\mathbf{Analysis}$. In this case, neither tuple $(I^{\ast },R^{\ast },\overline{M})$ nor tuple $(I^{\ast },R^{\ast },M^{\prime })$ has been made $SQ(pp,·,·,·,i{d}^{\ast })$. Similar to the Analysis in 4.4, we can obtain the following equation as well

$$\overline{\pi }{\pi }^{\prime }·{\overline{\mathbf{b}}}_0+{\pi }^{\ast }{\pi }^{\prime }({\overline{\mathbf{b}}}_{\overline{\pi }}-{\overline{\mathbf{b}}}_0)=\overline{\pi }{\pi }^{\prime }·{\mathbf{b}}_0^{\prime }+{\pi }^{\ast }\overline{\pi }({\mathbf{b}}_{{\pi }^{\prime }}^{\prime }-{\mathbf{b}}_0^{\prime }),$$

it means that $(({\mathsf{\Gamma }}^{\ast },\overline{M}),({\mathsf{\Gamma }}^{\ast },M^{\prime }),H_2({\mathsf{\Gamma }}^{\ast },\overline{M})$, $H_2({\mathsf{\Gamma }}^{\ast },M^{\prime }))\in R_a$. As shown in [50], $R_a$ is a sparse relation. Thus, if ${\mathcal{A}}_{II}$ break the type II exculpability game with non-negligible probability $ϵ$, then ${\mathcal{D}}_{II}$ may break the multi-input correlation intractability of $H_2$ with non-negligible probability $\frac{ϵ}{2}$. It contradicts the multi-input correlation intractability of $H_2$.

To sum up, the adversary ${\mathcal{A}}_{II}$ cannot make a successful attack to exculpability, so our scheme satisfies the type II exculpability.

□

In summary, our scheme satisfies type I exculpability for ${\mathcal{A}}_I$ and type II exculpability for ${\mathcal{A}}_{II}$. Therefore, our scheme satisfies exculpability.

7. Efficiency

In the aspect of efficiency, we concentrate on the signature length of the scheme. Looking at the form of the signature it is easy to see that it is made up of two components $\alpha$ and $\mathsf{\Pi }$, one being the parameters used by the tracing algorithm and the other being the proof $\mathsf{\Pi }$ generated by the NIZK protocol, as the NIZK proof protocol is obtained by the interactive ZK protocol employing the Fiat-Shamir transformation. That’s why it is also known as SPK. The scale of the signature $\delta$ of our scheme depends mainly on the scale of ZK proof $\mathsf{\Pi }$, so the scale of the signature $\delta$ can be estimated by analysing the size of ZK proof $\mathsf{\Pi }$. As shown in [53], the $\mathsf{\Pi }$ producted by efficient ZKAoK in Section 4 consists of two parts, a commitment and N tuples. So, we can obtain

$$\parallel \mathsf{\Pi }\parallel =(log(2p+1)+\kappa +(3l_1+2l_2+2n+2\ell )·logq)·N+(l_1+n)·logq,$$

where n is the witness size and ℓ is the size of $\mathcal{M}$.

The proved statement contains five equations. Every relational equation can be transformed into an example of the relation $\mathfrak{R}$. The primitive to be argued by Equations (1) and (4) is linear equation with short solution; therefore, Equations (1) and (4) can be integrated together and then reduced to the relation $\mathfrak{R}$. According to the conclusion in the section above, we can know that the size of witness and M are both $(\widehat{m}+2n)k_q+2m{k}_p$; while the primitive to be argued by Equations (2) and (3) is PRF preimage, we can know that the size of witness and M both are $(2n+2m)k_q+2mk+2m{k}_p$. The last relation ${\mathfrak{R}}_{\left(5\right)}$ argues knowledge of a member in the accumulator. Just like analysis in [53], the length of witness is $2\ell +4l_1\ell +2l_2\ell$ and the size of $\mathcal{M}$ is $\ell +2l_1\ell +2l_2\ell$. We combining above five relations to get the size of the witness is

$$\mathfrak{W}=(3n+\widehat{m}+2m)k_q+2mk+2m{k}_p+2\ell +4n\ell +2n{k}_q\ell ,$$

and the size of $\mathcal{M}$ is

$$\mathfrak{M}=(3n+\widehat{m}+2m)k_q+2mk+2m{k}_p+\ell +4n\ell +2n{k}_q\ell ,$$

(the repeated part such as ${\mathbf{a}}_{i{d}_i},{\mathbf{s}}_i,{\mathbf{b}}_i,{\mathbf{c}}_i$, we only need to counted only once).

We set $\widehat{p},\widehat{\kappa },\widehat{l_1},\widehat{l_2},\widehat{N}$ be parameters used in NIZK protocol. So we have

$$\parallel \mathsf{\Pi }\parallel =(log(2\widehat{p}+1)+\widehat{\kappa }+(3\widehat{l_1}+2\widehat{l_2})·k+2\mathfrak{W}+2\mathfrak{M})·\widehat{N}+(\widehat{l_1}+\mathfrak{W})·k$$

bits.

Compared with [51], $msk$ and $sk$ of our scheme is shorter, and although the signature scale is larger compared to [51], our scheme implements linkability and public traceability. Compared with [52], our scheme has smaller $sk$ and the scheme in [52] does not implement linkability and traceability;

Compared with [50], in the case of the same public key and secret key, the communication cost of our scheme is relatively small, the size of signature of [50] is $t·\mathcal{O}(n{log}^{3}q+log\mathcal{L}·nlogq)$, and the signature of our scheme is $\widehat{N}·\mathcal{O}(n{log}^{2}q+log\mathcal{L}·nlogq)$ under the same parameter setting. $\widehat{N}$ and t, respectively, are the number of protocols that need to be performed to achieve negligible soundness error. Since the zero-knowledge single-execution protocol used by our scheme has a smaller soundness error, less time is required to reach a negligible soundness error, and thus the resulting signature size is smaller. The detailed comparison is shown in Table 1 and Table 2 below.

Table 1. Theoretical estimation of key sizes and signature sizes of lattice-based ring signature.

Scheme	PK Size	MSK Size	SK Size	Signature Size
CLR [51]	$\mathcal{O}\left(n^2{log}^{2}q\right)$	$\mathcal{O}\left(n^2{log}^{3}q\right)$	$\mathcal{O}\left(n^2{log}^{3}q\right)$	$\mathcal{O}(\mathcal{L}·n{log}^{2}q)$
CLR [52]	$\mathcal{O}(n^2{log}^{2}q+\mathcal{L}·n^{2}logq)$	$\mathcal{O}(nlogq)$	$\mathcal{O}(n^2{log}^{3}q+\mathcal{L}·n^2{log}^{2}q)$	$\mathcal{O}\left(n^2{log}^{2}q\right)$
TRS [50]	$\mathcal{O}\left(n{log}^{3}q\right)$	-	$\mathcal{O}\left(n{log}^{2}q\right)$	$t·\mathcal{O}(n{log}^{4}q+log\mathcal{L}·n{log}^{2}q)$
Ours	$\mathcal{O}\left(n{log}^{3}q\right)$	$\mathcal{O}(nlogq)$	$\mathcal{O}\left(n{log}^{2}q\right)$	$\widehat{N}·\mathcal{O}(n{log}^{3}q+log\mathcal{L}·n{log}^{2}q)$

Table 2. Functional comparison of lattice-based ring signature.

Scheme	Quantum Resistant	Anonymity	Unforgeability	Linkability	Traceability	Certificateless
CLR [51]	✓	✓	✓	×	×	✓
CLR [52]	✓	✓	✓	×	×	✓
TRS [50]	✓	✓	✓	✓	✓	×
Ours	✓	✓	✓	✓	✓	✓

−$\left|ID\right|$ denotes the length of the ID, $\mathcal{L}$ represents the size of the ring, $PK$, $MSK$, $SK$ denote public key, master secret key, secret key respectively.

8. Conclusions

In this paper, we constructed a CLTRS scheme on lattice, and it satisfies tag-linkability, anonymity, and exculpability under the ROM. We used a more efficient ZK protocol to replace the Stern-like protocol, the soundness error of the single-execution protocol is reduced from 2/3 to 1/poly, thus reducing the communication cost. And our scheme not only eliminates the burden of certificate management, but also eliminates the problem of key escrow. In the future work, we can consider using ideal lattices or modular lattices to replace standard lattices, and construct the scheme under standard model. It is also worth studying to replace zero-knowledge proof by attribute-based signature scheme so as to avoid the use of zero-knowledge proof.