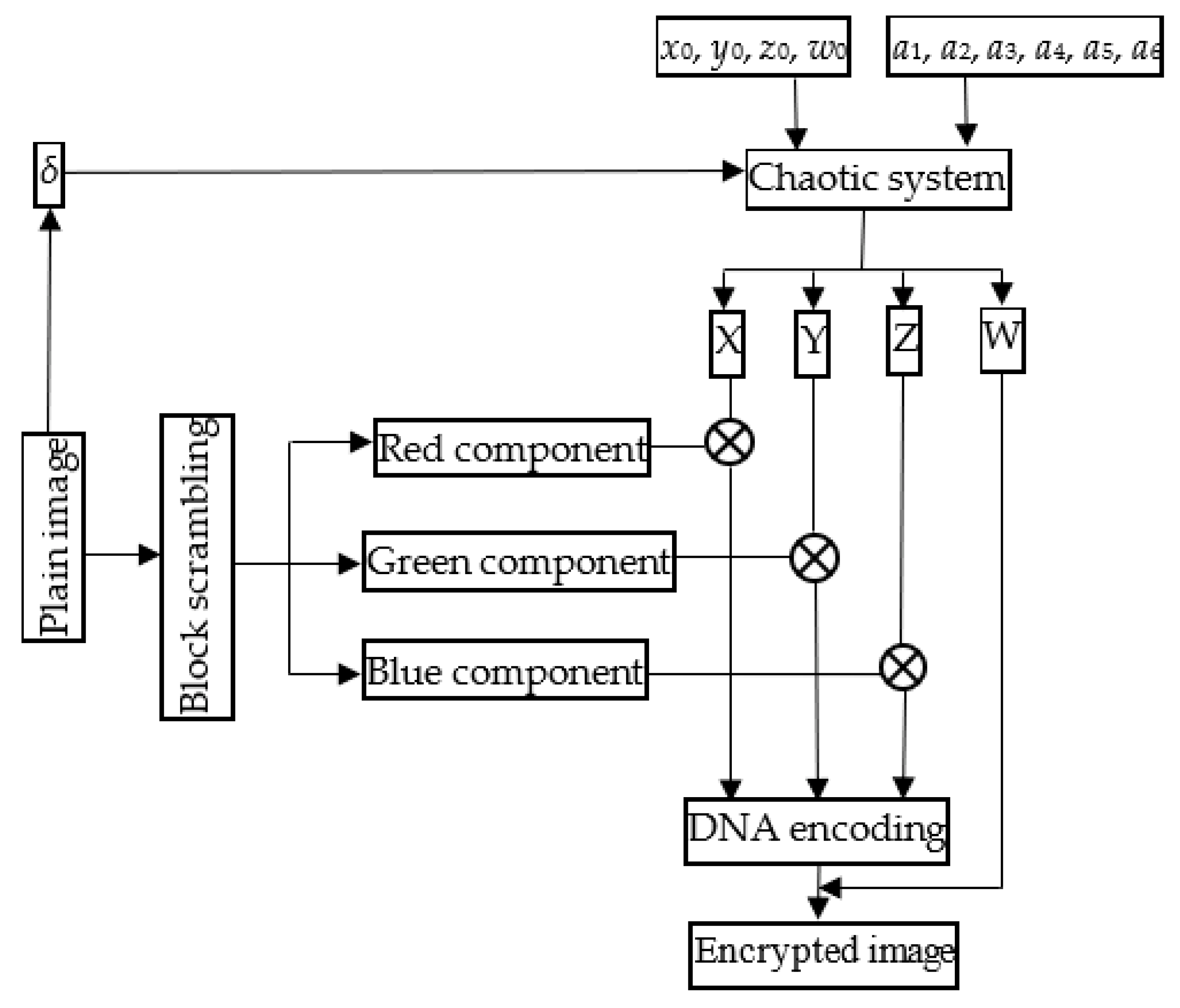
3. Structure of the Algorithm
The flowchart of the designed image encryption algorithm is illustrated in
Figure 5, and the main steps of the encryption algorithm are described in detail here.
Step 1. The number of transmitted images is judged. If multiple images are transmitted at the same time, we combine images to improve encryption efficiency. If only one image is transmitted, the encryption operation can be directly performed. That is to say, the plain image is a single image, or a combined image composed of several images.
Step 2. An interrupt parameter is generated based on plain image with a size of L = M × N by calculation formula:
. Parameters and initial state vector are (x0 + δ, y0 + δ, z0 + δ, w0 + δ) and (a1 + δ, a2 + δ, a3 + δ, a4 + δ, a5 + δ, a6 + δ), respectively.
Step 3. The plain image is divided into several sub-blocks: , the size of every block is V × V, thus the total number of sub-blocks is L/v2. In this paper, the Zigzag transform is used to scramble the 8 × 8 sub-block images.
Step 4. In the proposed encryption scheme, as part of the secret key, parameter δ is combined with another part of the secret key to generate the initial input of the novel four-dimensional chaotic system. Based on the two parts of the secret key, the novel four-dimensional chaos generates four chaotic sequences: X = φ(x), Y = φ(y), Z = φ(z), and W = φ(w). The function φ is defined as .
Step 5. The Red, Green, and Blue components of the scrambled image are labeled with , and they are subjected to the XOR operation with sequences X, Y, and Z and to generate sequences and , respectively. The main calculation formulas are and .
Step 6. Using rule 2 in
Table 2, the processed fourth chaotic sequence is subjected to the DNA encoding and XOR operations with
.
In the designed symmetric algorithm, decryption and encryption are reciprocal operations.
Author Contributions
Conceptualization, software, formal analysis, resources, supervision, J.Z.; methodology, investigation, data curation, writing—review and editing, S.W.; funding acquisition, validation, visualization, L.Z.; writing—original draft preparation, J.Z., S.W. and L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 11226337, 11501525), the Science and Technology Foundation of Henan Province of China (Grant No. 222102210250), the Research on Teaching Reform of Henan Polytechnic (Grant No. 2021J058), the Scientific Research of Henan Polytechnic (Grant No. 2022ZK49), the Basic Research Projects of Key Scientific Research Projects Plan in Henan Higher Education Institutions (20zx003), Henan Natural Science Foundation (222300420579), and the Teaching Reform and Practice Program of Vocational Education in Henan Province (Grant No. [2023] 03049).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baptista, M.S. Cryptography with chaos. Phys. Lett. A 1998, 240, 50–54. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurcat. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Xu, Q.; Sun, K.; He, S.; Zhu, C. An effective image encryption algorithm based on compressive sensing and 2D-SLIM. Opt. Lasers Eng. 2020, 134, 106178. [Google Scholar] [CrossRef]
- Hu, G.; Xiao, D.; Zhang, Y.; Xiang, T. An efficient chaotic image cipher with dynamic lookup table driven bit-level permutation strategy. Nonlinear Dynam. 2017, 87, 1359–1375. [Google Scholar] [CrossRef]
- Ye, G.D.; Wong, K.W. An image encryption scheme based on time-delay and hyperchaotic system. Nonlinear Dynam. 2012, 71, 259–267. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.; Zhang, Y. A novel chaotic block image encryption algorithm based on dynamic random growth technique. Opt. Lasers Eng. 2015, 66, 10–18. [Google Scholar] [CrossRef]
- Riyahi, M.; Kuchaki Rafsanjani, M.; Motevalli, R. A novel image encryption scheme based on multi-directional diffusion technique and integrated chaotic map. Neural Comput. Appl. 2021, 33, 14311–14326. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Lai, Q. 2D hyperchaotic system based on Schaffer function for image encryption. Expert Syst. Appl. 2003, 213, 119076. [Google Scholar] [CrossRef]
- Chen, G.; Mao, Y.; Chui, C. A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solitons Fract. 2004, 21, 749–761. [Google Scholar] [CrossRef]
- Hanis, S.; Amutha, R. Double image compression and encryption scheme using logistic mapped convolution and cellular automata. Multimed. Tools Appl. 2018, 77, 6897–6912. [Google Scholar] [CrossRef]
- Belazi, A.; El-Latif, A.A.A.; Belghith, S. A novel image encryption scheme based on substitution-permutation network and chaos. Signal Process. 2016, 128, 155–170. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Toktas, F.; Alenezi, F. 2D eπ-map for image encryption. Inf. Sci. 2022, 589, 770–789. [Google Scholar] [CrossRef]
- Lai, Q.; Hu, G.; Erkan, U.; Toktas, A. A novel pixel-split image encryption scheme based on 2D Salomon map. Expert Syst. Appl. 2003, 213, 118845. [Google Scholar] [CrossRef]
- Farah, M.A.B.; Farah, A.; Farah, T. An image encryption scheme based on a new hybrid chaotic map and optimized substitution box. Nonlinear Dynam. 2020, 99, 3041–3064. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Bao, X. A novel chaotic image encryption scheme using DNA sequence operations. Opt. Lasers Eng. 2015, 73, 53–61. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Yang, K. An image encryption algorithm based on the memristive hyperchaotic system, cellular automata and DNA sequence operations. Signal Process. Image Commun. 2017, 52, 6–19. [Google Scholar]
- Li, Z.; Peng, C.; Tan, W. A novel chaos-based image encryption scheme by using randomly DNA encode and plaintext related permutation. Appl. Sci. 2020, 10, 7469. [Google Scholar] [CrossRef]
- Nematzadeh, H.; Enayatifar, R.; Yadollahi, M. Binary search tree image encryption with DNA. Optik 2020, 202, 163505. [Google Scholar] [CrossRef]
- Dong, W.; Li, Q.; Tang, Y.; Zeng, M.H.R. A robust and multi chaotic DNA image encryption with pixel-value pseudorandom substitution scheme. Opt. Commun. 2021, 15, 127211. [Google Scholar] [CrossRef]
- Yildirim, M. Optical color image encryption scheme with a novel DNA encoding algorithm based on a chaotic circuit. Chaos Solitons Fract. 2022, 155, 111631. [Google Scholar] [CrossRef]
- Li, C.; Lin, D.; Lü, J. Cryptanalyzing an image-scrambling encryption algorithm of pixel bits. IEEE Multimed. 2017, 24, 64–71. [Google Scholar] [CrossRef]
- Chen, L.; Chen, J.; Ma, L.; Wang, S. Cryptanalysis of a chaotic image cipher based on plaintext-related permutation and lookup table. Nonlinear Dynam. 2020, 100, 3959–3978. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, J.; Chen, D. Cryptanalysis of an Image Encryption Algorithm Based on a 2D Hyperchaotic Map. Entropy 2022, 24, 1551. [Google Scholar] [CrossRef] [PubMed]
- Erkan, U.; Toktas, A.; Enginoğlu, S.; Akbacak, E.; Thanh, N.H.D. An image encryption scheme based on chaotic logarithmic map and key generation using deep CNN. Multimed. Tools Appl. 2022, 81, 7365–7391. [Google Scholar] [CrossRef]
- Özkaynak, F. Brief review on application of nonlinear dynamics in image encryption. Nonlinear Dynam. 2018, 92, 305–313. [Google Scholar] [CrossRef]
- Pareschi, F.; Rovatti, R.; Setti, G. On statistical tests for randomness included in the NIST SP800-22 test suite and based on the binomial distribution. IEEE Trans. Inf. Foren. Secur. 2012, 7, 491–505. [Google Scholar] [CrossRef]
- Gao, H.; Wang, X. Chaotic image encryption algorithm based on Zigzag transform with bidirectional crossover from random position. IEEE Access 2021, 9, 105627–105640. [Google Scholar] [CrossRef]
- Ying, J.; He, F.; Wang, H. Color image encryption based on the combination of Zigzag scanning laser speckle and chaos. Laser Mag. 2018, 39, 85–88. [Google Scholar]
- Guesmi, R.; Farah, M.A.B.; Kachouri, A.; Samet, M. A novel chaos-based image encryption using DNA sequence operation and secure hash algorithm SHA-2. Nonlinear Dyn. 2016, 83, 1123–1136. [Google Scholar] [CrossRef]
- Hosy, K.M.; Kamal, S.T.; Darwish, M.M. A color image encryption technique using block scrambling and chaos. Multimed. Tools Appl. 2022, 81, 505–525. [Google Scholar] [CrossRef]
- Chen, L.; Yin, H.; Yuan, L.; Machado, A.T.; Wu, R.; Alam, Z. Double color image encryption based on fractional order discrete improved Henon map and Rubik’s cube transform. Signal Process. Image Commun. 2021, 97, 116363. [Google Scholar]
- Wang, Y.; Chen, L.; Yu, K.; Lu, T. Image encryption algorithm based on lattice hash function and privacy protection. Multimed. Tools Appl. 2022, 81, 18251–18277. [Google Scholar] [CrossRef]
- Ge, F.; Qin, Z.; Chen, Y. Integrated time-fractional diffusion processes for fractional-order chaos-based image encryption. Sensors 2021, 21, 6838. [Google Scholar] [CrossRef]
- Wu, J.; Liao, X.; Yang, B. Image encryption using 2D Henon sine map and DNA approach. Signal Process. 2018, 153, 11–23. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Inf. Sci. 2013, 222, 323–342. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.; Again, S. NPCR and UACI randomness tests for image encryption. Cyber J. 2011, 1, 31–38. [Google Scholar]
- Hua, Z.; Zhou, Y. Image encryption using 2D logistic-adjusted-sine map. Inf. Sci. 2016, 339, 237–253. [Google Scholar] [CrossRef]
- Liao, X.; Lai, S.; Zhou, Q. A novel image encryption algorithm based on self-adaptive wave transmission. Signal Process. 2010, 90, 2714–2722. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.; Li, P.; Wang, X.-Y. A new color image encryption scheme based on 2DNLCML system and genetic operation. Opt. Lasers Eng. 2020, 128, 106040. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Ma, C.; Cao, Y. Dynamic analysis of an improper fractional-order laser chaotic system and its image encryption application. Opt. Lasers Eng. 2020, 129, 106031. [Google Scholar] [CrossRef]
- Hu, G.; Li, B. Coupling chaotic system based on unit transform and its applications in image encryption technique. Signal Process. 2018, 178, 107790. [Google Scholar] [CrossRef]
- Rehman, A.U.; Liao, X.; Ashraf, R.; Ullah, S.; Wang, H. A color image encryption technique using exclusive-OR with DNA complementary rules based on chaos theory and SHA-2. Optik 2018, 159, 348–367. [Google Scholar] [CrossRef]
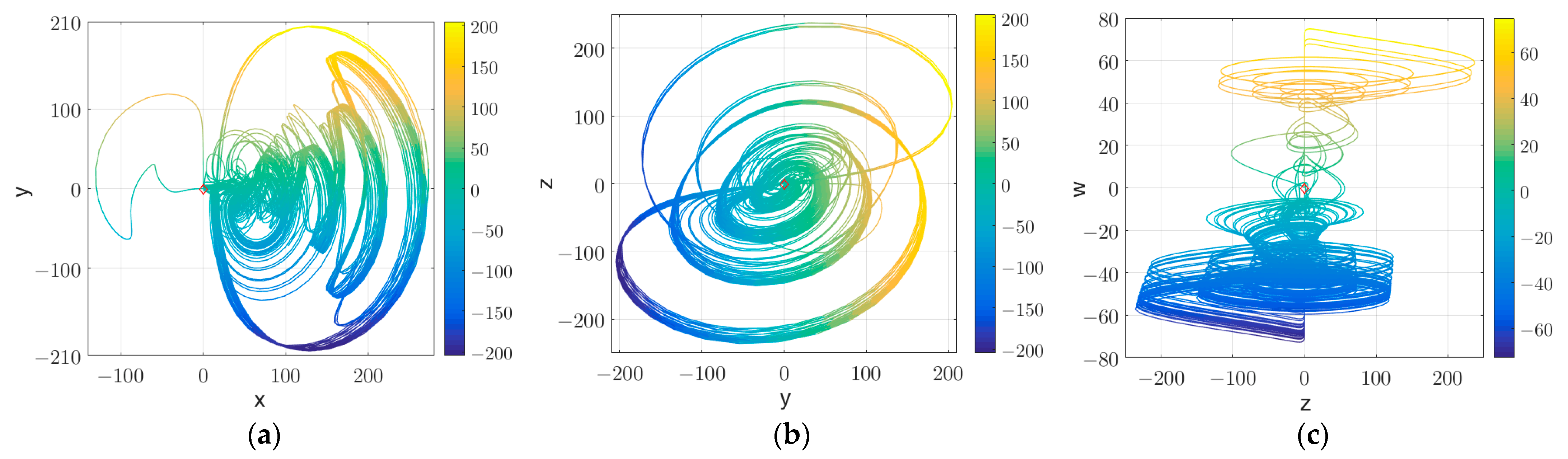
Figure 1.
The chaotic behavior of system (1): (a) x–y plane; (b) y–z plane; (c) z–w plane; (d) x–y–z plane, (e) w–x–y plane.
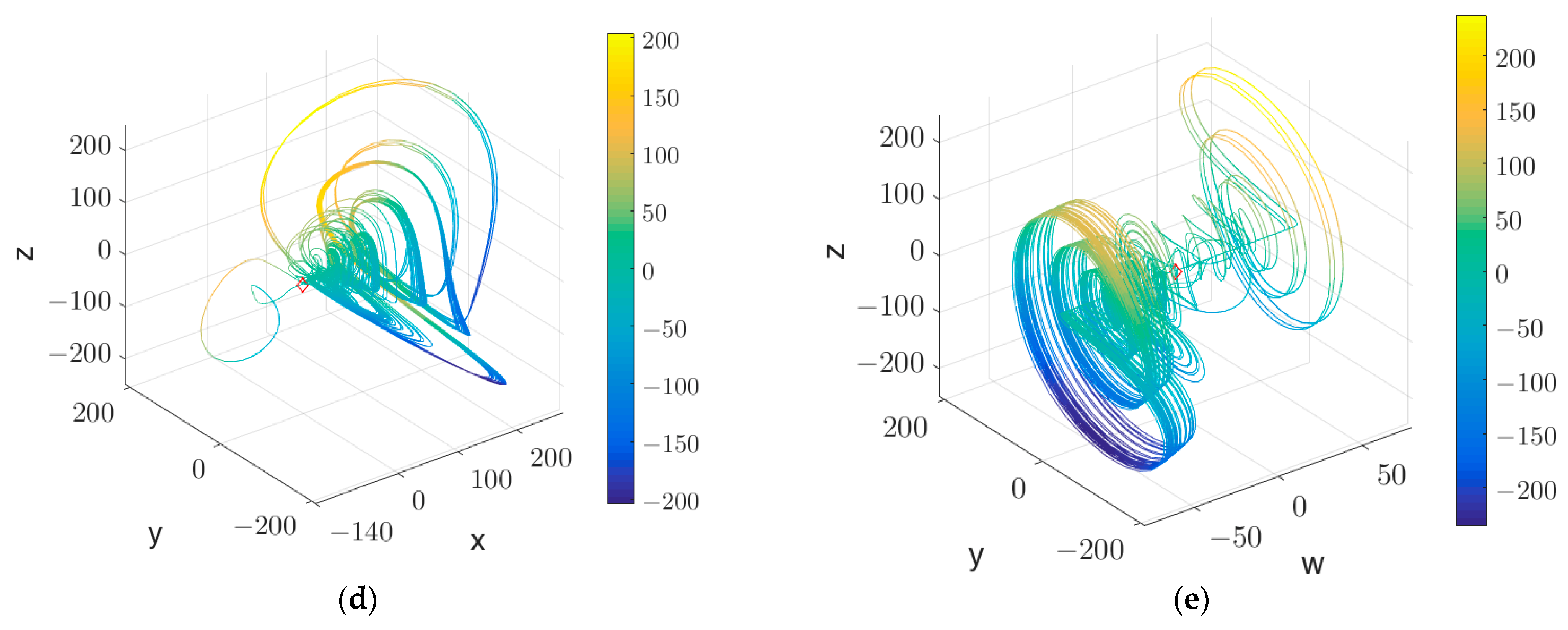
Figure 2.
Nonlinear dynamical characters of the variable y: (a) time sequence; (b) p-s plane; (c) Lyapunov exponents; (d) Lyapunov dimensions of system (1).
Figure 3.
Self-correlation comparison results of random sequences generated before and after sequence transformation: (a) primitive chaos sequence; (b) improved chaos sequence.
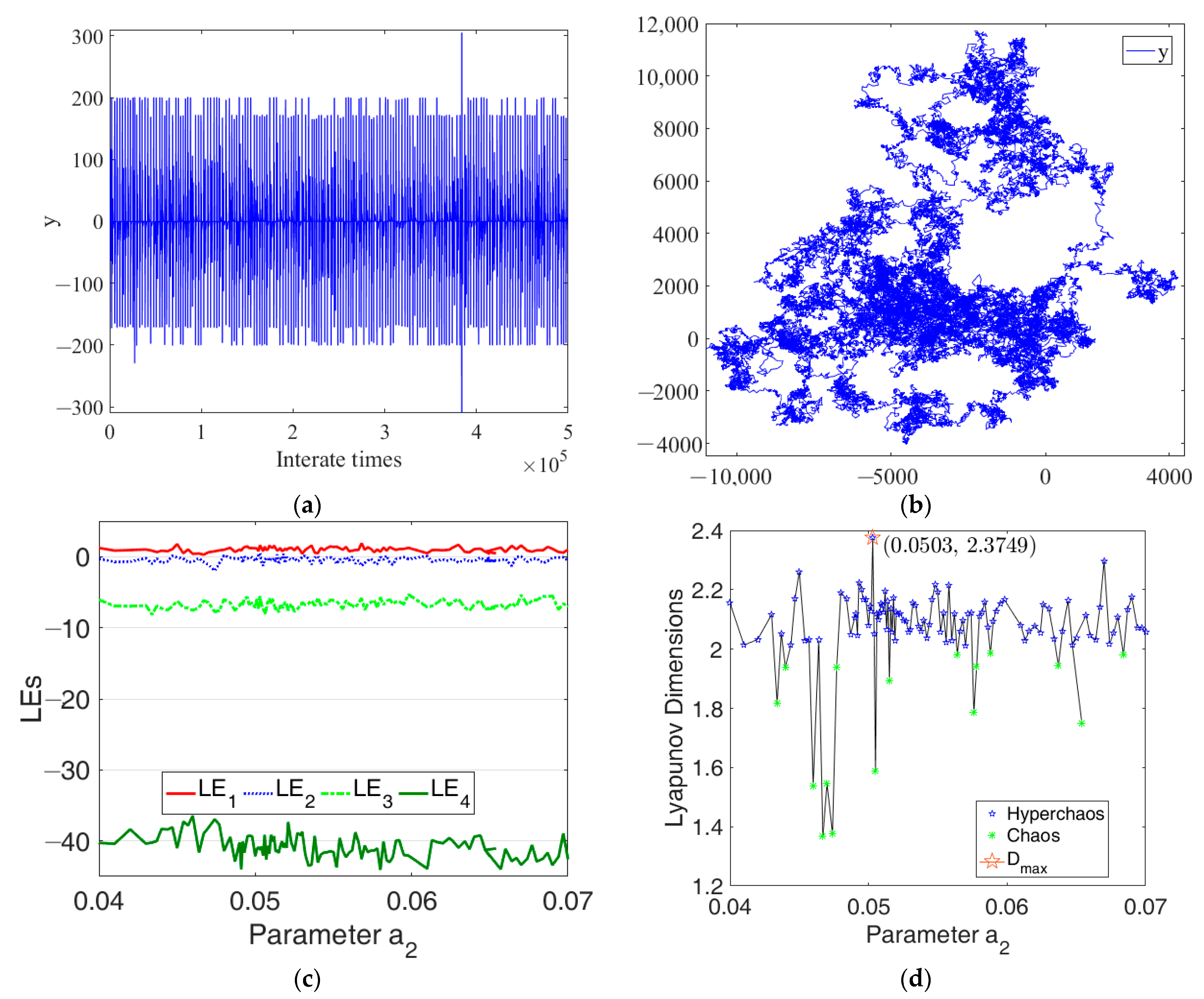
Figure 4.
Zigzag scanning process. For a 5 × 5 matrix: (a) Zigzag transformation diagram; (b) the transformed matrix. For 8 × 8 block Lena color image: (c) plain image; (d) process of Zigzag transform; (e) scrambled Lena image.
Figure 5.
The flowchart of the cryptosystem.
Figure 6.
Encryption results for gray image: (a) Earth image; (b) histogram of (a); (c) encrypted Clock image; (d) histogram of (c); (e) Oakland image; (f) histogram of (e); (g) encrypted Pentagon image; (h) histogram of (g).
Figure 7.
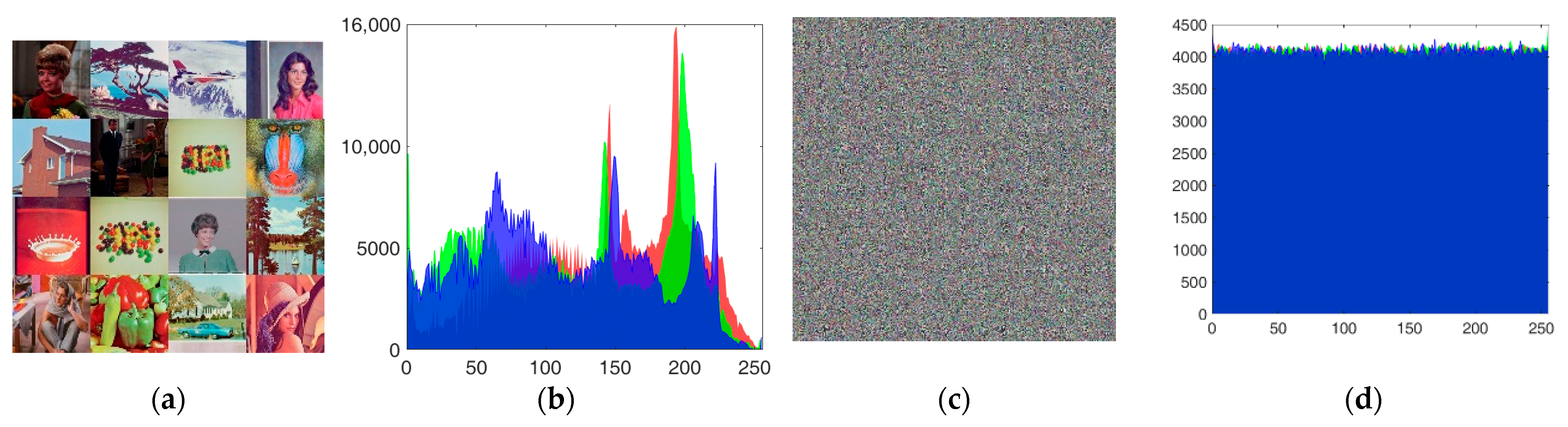
Encryption results for Combined image: (a) Combined image; (b) histogram of (a); (c) encrypted Combined image; (d) histogram of encrypted Combined image.
Figure 8.
Encryption results for gray image: (a) Clock image; (b) Histogram of (a); (c) Encrypted Clock image; (d) histogram of (c); (e) Pentagon image; (f) histogram of (e); (g) encrypted Pentagon image; (h) histogram of (g).
Figure 9.
Correlation analysis in horizontal, vertical, Diagonal and Counter-Diagonal directions: (a1)–(d1) and (a2)–(d2) are the correlations of the Red channel, Green channel, and Blue channel of the Earth color image and the encrypted Earth image, respectively. (a3)–(d3) and (a4)–(d4) are the correlations of the Red channel, Green channel, and Blue channel of the Clock gray image and the encrypted Clock image, respectively.
Figure 10.
Partial non-overlapping image blocks of Clock image.
Figure 11.
State space plots for different initial conditionals.
Figure 12.
Key sensitivity analyses (a) encrypted image; (b) decrypted image with x0(1) = 0.02; (c) decrypted image with x0(1) = 0.02 + 10−14.
Figure 13.
Decryption results of encrypted Combined image after cropping attacks: (a) 1/16 degree of cropping; (b) 1/4 degree of cropping; (c) 1/2 degree of cropping; (d) 3/4 degree of cropping; (e–h) decrypted images of (a–d).
Figure 14.
Decrypted Combined image after salt and pepper noise attacks: (a) with a noise strength of 0.01; (b) with a noise strength of 0.05; (c) with a noise strength of 0.1; (d–f) Decrypted images of (a–c).
Table 1.
Test Result of FIPS 140-2 Random Properties of chaotic sequence y.
| Test Value | Monobit Test | Poker Test | Runs Test | Long Run Test |
|---|
| Run Length |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|
| Bit 0 | 9988 | 25.6832 | 2628 | 1232 | 600 | 310 | 161 | 152 | 0 |
| Bit 1 | 10,012 | 2575 | 1317 | 512 | 321 | 142 | 156 | 0 |
| Theory Value | 9925~10,725 | 2.16~46.17 | 2315~2685 | 1114~1386 | 527~723 | 240~384 | 103~209 | 103~209 | 0 |
| Result | Pass | Pass | Pass | Pass | Pass | Pass | Pass | Pass | Pass |
Table 2.
DNA coding rules.
| Rule | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 00 | A | A | T | T | G | G | C | C |
| 11 | T | T | A | A | C | C | G | G |
| 01 | C | G | C | G | T | A | T | A |
| 10 | G | C | G | C | A | T | A | T |
Table 3.
DNA base addition, subtraction, and XOR operation.
| Base | Addition/Subtraction | XOR |
|---|
| A | A/A | T/T | C/C | G/G | A | T | C | G |
| T | T/A | A/A | G/T | C/C | T | A | G | C |
| C | C/T | G/G | A/A | T/T | C | G | A | T |
| G | G/C | C/C | T/G | A/A | G | C | T | A |
Table 4.
Correlation coefficients of test images.
| Size | Image | | Plain Image | Encrypted Image |
|---|
| 1024 × 1024 | Earth | Red | 0.9498 | 0.9461 | 0.9336 | 0.9440 | −6.7918 × 10−4 | −2.3418 × 10−4 | −1.6835 × 10−4 | −6.0686 × 10−4 |
| Green | 0.9871 | 0.9859 | 0.9864 | 0.9476 | −6.1831 × 10−4 | 7.5871 × 10−4 | 1.9887 × 10−4 | 1.5069 × 10−6 |
| Blue | 0.9870 | 0.9859 | 0.9741 | 0.9863 | 9.2456 × 10−5 | −8.2715 × 10−5 | −3.4478 × 10−4 | −1.2586 × 10−5 |
| 1024 × 1024 | Oakland | Red | 0.9144 | 0.9067 | 0.8868 | 0.8959 | −3.0901 × 10−4 | 4.7237 × 10−4 | 5.7641 × 10−4 | −6.41116 × 10−4 |
| Green | 0.77241 | 0.7704 | 0.7253 | 0.7410 | 9.4721 × 10−4 | −6.8982 × 10−5 | −3.3608 × 10−4 | 7.6725 × 10−5 |
| Blue | 0.4309 | 0.4357 | 0.3876 | 0.4042 | −7.5263 × 10−4 | −2.8086 × 10−5 | 1.2194 × 10−4 | −2.1374 × 10−4 |
| 1024 × 1024 | Combined image | Red | 0.9723 | 0.9594 | 0.9442 | 0.9440 | 7.4802 × 10−4 | −2.3138 × 10−4 | 4.2696 × 10−5 | 5.1063 × 10−4 |
| Green | 0.9606 | 0.9522 | 0.9285 | 0.9220 | −5.6293 × 10−4 | 2.9770 × 10−4 | −1.0965 × 10−4 | 5.2233 × 10−4 |
| Blue | 0.9314 | 0.9196 | 0.8874 | 0.8859 | 4.6697 × 10−4 | −3.5340 × 10−5 | 0.0061 | 1.2482 × 10−5 |
| 256 × 256 | Gray Clock | | 0.9396 | 0.9672 | 0.9175 | 0.9266 | 8.0196 × 10−4 | 6.7981 × 10−4 | 2.7856 × 10−4 | 0.0033 |
| Ref. [14] | | | | | 0.022085 | 0.026092 | −0.003475 | |
| Ref. [15] | | | | | 0.0024 | −0.0246 | −0.0081 | |
| 1024 × 1024 | Pentagon | | 0.7793 | 0.8405 | 06456 | 0.8179 | −4.3352 × 10−5 | 2.5509 × 10−5 | −2.1782 × 10−4 | 3.0509 × 10−4 |
Table 5.
Correlation coefficients of encrypted Lena image in R, G, and B channels.
| Planes | Directions | Plain Images | Proposed | Ref. [30] | Ref. [31] | Ref. [32] | Ref. [33] | Ref. [34] |
|---|
| Red | Horizontal | 0.9475 | 0.000033 | 0.0064 | −0.0067 | −0.0217 | −0.00076 | 0.0035 |
| Vertical | 0.9727 | −0.000295 | 0.0160 | −0.0065 | 0.0654 | 0.01125 | −0.0014 |
| Diagonal | 0.9045 | −0.000085 | −0.0026 | 0.0006 | −0.0381 | −0.00255 | 0.0415 |
| Green | Horizontal | 0.9517 | −0.000574 | −0.0026 | −0.0050 | −0.0526 | −0.00478 | 0.0029 |
| Vertical | 0.9751 | −0.000513 | 0.0034 | 0.0003 | −0.0193 | −0.01236 | 0.0040 |
| Diagonal | 0.9159 | 0.000736 | 0.0125 | 0.7931 | 0.0364 | 0.00442 | 0.0031 |
| Blue | Horizontal | 0.9063 | 0.000390 | 0.0091 | −0.0071 | 0.0219 | 0.00622 | 0.0029 |
| Vertical | 0.9487 | 0.000301 | −0.0045 | 0.0020 | −0.4160 | 0.00950 | 0.0040 |
| Diagonal | 0.8545 | −0.000137 | −0.0090 | 0.0015 | −0.0567 | 0.00172 | 0.0031 |
Table 6.
Information entropy of plaintext and ciphertext images.
| Test Images | Earth | Oakland | Combined Images | Clock | Pentagon |
|---|
| Red | Green | Blue | Red | Green | Blue | Red | Green | Blue |
|---|
| Plain image | 6.5723 | 7.4511 | 6.7625 | 6.7458 | 6.0677 | 4.9460 | 7.7201 | 7.7389 | 7.7840 | 6.7056 | 6.7326 |
| Encrypted image | 7.9919 | 7.9916 | 7.9916 | 7.9921 | 7.9919 | 7.9918 | 7.9921 | 7.9872 | 7.9993 | 7.9985 | 7.9920 |
Table 7.
Test results of NPCR and UACI.
| Images | Earth | Combined Images | Clock |
|---|
| Red | Green | Blue | Red | Green | Blue | Proposed | Ref. [37] | Ref. [38] |
|---|
| Pixel value | 102 | 25 | 99 | 226 | 137 | 113 | 197 | | |
| New pixel value | 103 | 26 | 100 | 227 | 134 | 114 | 198 | | |
| NPCR (%) | 99.6176 | 99.6280 | 99.5977 | 99.6504 | 99.5873 | 99.6117 | 99.5935 | 99.5703 | 49.8280 |
| UACI (%) | 33.4502 | 33.4412 | 33.4755 | 33.4131 | 33.4910 | 33.4655 | 33.4789 | 33.4302 | 17.0621 |
Table 8.
PSNR and MSE for three channels of Combined image.
| Attack | MSE | PSNR (dB) |
|---|
| Red | Green | Blue | Mean | Red | Green | Blue | Mean |
|---|
| Cropping ratio | 1/16 | 6.1906 | 7.0087 | 6.5744 | 6.5912 | 38.9338 | 39.6744 | 39.9521 | 39.5201 |
| 1/4 | 32.7330 | 27.4837 | 25.5995 | 28.6054 | 32.9809 | 33.7400 | 34.0484 | 33.5897 |
| 1/2 | 65.6912 | 55.0312 | 51.5109 | 57.4111 | 29.9557 | 30.7247 | 31.0118 | 30.5641 |
| 3/4 | 98.2682 | 82.2418 | 77.1118 | 85.8739 | 28.2066 | 28.9798 | 23.1080 | 26.7648 |
| Pepper–salt noise densities | 0.01 | 2.0369 | 23.4718 | 2.6262 | 9.3783 | 45.0409 | 44.2005 | 43.9374 | 44.3929 |
| 0.05 | 10.1128 | 12.1453 | 12.7559 | 11.6713 | 38.0820 | 37.2867 | 37.0736 | 37.4807 |
| 0.1 | 19.6899 | 23.6605 | 25.0473 | 22.7992 | 35.1883 | 34.3905 | 34.1431 | 34.5739 |
Table 9.
Comparison with other algorithms for key space.
| Scheme | Proposed | Ref. [30] | Ref. [32] | Ref. [39] | Ref. [40] | Ref. [41] | Ref. [42] |
|---|
| key space | 10150 | 1035 | 2512 | 1056 | 2449 | 2312 | 1094 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).