Abstract
Cloud computing and relevant emerging technologies have presented ordinary methods for processing edge-produced data in a centralized manner. Presently, there is a tendency to offload processing tasks as close to the edge as possible to reduce the costs and network bandwidth used. In this direction, we find efforts that materialize this paradigm by introducing distributed deep learning methods and the so-called Federated Learning (FL). Such distributed architectures are valuable assets in terms of efficiently managing resources and eliciting predictions that can be used for proactive adaptation of distributed applications. In this work, we focus on deep learning local loss functions in multi-cloud environments. We introduce the MulticloudFL system that enhances the forecasting accuracy, in dynamic settings, by applying two new methods that enhance the prediction accuracy in applications and resources monitoring metrics. The proposed algorithm’s performance is evaluated via various experiments that confirm the quality and benefits of the MulticloudFL system, as it improves the prediction accuracy on time-series data while reducing the bandwidth requirements and privacy risks during the training process.
1. Introduction
In present times, there is massive data generation from a constantly and exponentially increasing number of edge devices, such as wearables, smartphones, smart cards, sensors, GPS-enabled devices, mobile phones, and other IoT devices. The IDC Data Age 2025 report on “The Digitization of the World: From Edge to Core” forecasts that the total data to be generated by the year 2025 is estimated to reach an astounding 175 zettabytes—a tenfold increase from 2016 levels. The edge-proximate Internet of Things (IoT) devices, alone, are expected to generate over 90 zettabytes of data. Such massive data volumes require adequately substantial data processing and interpretation capabilities [1,2]. Currently, there are nearly 7 billion connected IoT devices [3] and 3 billion smartphones around the world. These devices are equipped with increasingly advanced sensors, computing, and communication capabilities. New data-intensive applications, data services, and distributed workloads, increasingly dictate new architectures to sufficiently support proactive maintenance and management of these dynamic environments. Technical specifications are required to support highly available, data-intensive applications that can be provided through multi-cloud environments at remote sites. These specifications will target both current requirements and future innovations, ultimately driving the adoption of Edge Cloud Computing Architectures [4]. With the massive increase in the number of edge devices and the advancements in computation technology, the Federated Learning [5,6] techniques may cope with the challenges of this domain. But, in order to do so, these techniques need to be extended to utilize in a more efficient way the total computing power across the cloud computing continuum thus improving prediction analytics over distributed streamed data. The exploitation of various data sources hosted on edge devices increases the data availability and contributes to improved federated algorithms training, along with their respected prediction accuracy.
According to the usual deep learning process, data are gathered in one place for centralized processing. This includes detection, classification (i.e., in training and test data), and prediction of future events and values. An example can be considered with temperature sensors’ data, residing at the edge of the network and an application topology that is used to process them. In this case, deep learning may help in the prediction of future incidents relevant to temperature fluctuations or forecasting on edge and cloud resources metrics (such as CPU consumption). Such accurate predictions may indicate the need for proactive reconfigurations to maintain the desired quality of service (QoS). The centralized data processing approach generates a lot of issues that are related to limited bandwidth problems and unstable connection issues. Such issues may increase the delay in the deep learning process and deteriorate the final forecasting accuracy. Moreover, other resource constraints, in terms of huge storage capacity and extreme CPU consumption in a centralized server, constitute also a problem that may cause delays in the outcome of the learning process or even give corrupted results according to relevant works [3]. Moreover, the fact that in a centralized approach, all the sensitive and non-sensitive data are sent to a remote cloud server, imposes a full set of security concerns and private data leakages. This is due to the fact the produced data must leave their origin source node (i.e., edge devices) and be aggregated in an external centralized cloud node. During this raw data exchange process, many security risks are introduced such as man-in-the-middle attacks, distributed denial of service (DDoS) attacks, data, and deep learning model poisoning, adversarial threats, etc. [7].
Federated Learning (FL) and Edge Computing systems give a solution to the above problems since both FL and Edge Computing technology refer to a close-to-data-source framework that brings the data processing activity closer to the data source, integrating network, computing, storage, and other capabilities. In these cases, a distributed algorithm is used which provides near-end services such as predictions and prognosis results to end users [8,9]. FL enables incremental training of deep learning models with shared data from cloud and private edge nodes, without explicitly exchanging any private data [10]. It supports privacy and data security protection by design and, at the same time, it can reduce network load and achieve lower latency and power consumption [11]. Particularly, FL allows for local nodes to train several local models, by using local data and at the same time to propagate the locally trained hyper-parameters with a central model located on a centralized server. Thus, no exchange of raw or private data takes place among these nodes but only their model hyper-parameters can be exchanged. In this way, we may argue that FL brings the learning process closer to the data sources.
Despite the above-presented benefits of Federated Learning, there are still a few challenges and risks. As it is widely known, the identification of rare incidents or abnormal events and behavior patterns during a general deep learning process in cyber-security, safety-critical systems, and enemy activities is called anomaly detection [12]. Back-propagation is the essence of neural and deep neural network training. It is the practice of fine-tuning the weights of a learning network based on the error rates coming from loss functions obtained from the previous epoch in an iterative process. When data abnormalities and patterns do exist during these iterations, high values of loss functions are produced that may cause time delays and give deteriorated final weight parameters in the models. This fact may lead to prediction inaccuracies for future values or events for various measured metrics, i.e., CPU consumption in the virtual machines of a multi-cloud environment.
In this paper, a decentralized and operationally independent from one specific cloud provider (multi-cloud architecture) FL model is used for the prediction of time-related metric values. The introduced approach not only leverages the widely known benefits over a centralized data approach, such as lower network bandwidth use (resources constraints), lower latency, less data privacy issues, but it also adopts a client node selective approach. In this way, it increases the accuracy in the prediction of time-related metrics by elaborating both the detection and rejection of data abnormalities. Furthermore, it investigates, for each client node, the sufficient data size to develop a high-quality model. During the mentioned FL process, Deep Learning models are used, a fact that increases even more the total model accuracy. What is more, in this work an extended algorithm and experiment setup takes place with respect to the data distribution of various nodes in the FL cluster. In half of the nodes, data samples are distributed randomly per node and have uniform information. In other words, data are Identically and Independent Distributed (IID) meaning that there are no overall trends–the distribution does not fluctuate and all items in the sample are taken from the same probability distribution. Having IID data at the client side means that each mini-batch of data used for a client’s local update is statistically identical to a uniformly drawn sample from the entire training dataset, which is the union of all local datasets at the clients of the FL system. In practice, it is unrealistic to assume that the local data on each client node are always IID. Thus, in the remaining half of the nodes, all data have the same label representing the cases where nodes have non-uniform information. This happens because the entire dataset has samples with multiple different labels and belongs to the non-IID data scenario. As a result, we can argue that this work also innovates in the way the data distribution can take place in various nodes of an FL cluster (combination of iid and non-iid scenario) because the data distribution is unknown beforehand in most of the real scenarios.
Therefore, a selective FL model aggregation algorithm is used based on two conditions that should both be satisfied. Firstly, the data size condition ensures sufficient data volume in terms of training data. Often, the amount of local training data is different for each client node. Secondly, the local loss function value condition helps with anomaly detection in the data of each client node. If a high loss value exists on a client node, this proves the low quality of local (i.e., anomalous case) data that may give inaccurate local model parameters. In our approach, such client nodes should be excluded from the global model training process. This path is used since a given local training dataset is not representative of the population distribution. By using these two crucial conditions along with the fact that Deep Learning [13,14] non-convex optimization local loss functions [15] are being used in MulticloudFL, it ensures a higher total accuracy of the whole system in terms of metrics prediction values in a multi-cloud environment. The non-convex optimization loss functions applied at each client node have the same advantages as convex functions and at the same time benefit from the fact that optimization is achieved faster when searching for a local optimum rather than on a global optimum (convex functions), by using convex methods such as stochastic gradient descent [14,16] and mini-batching.
The rest of the paper is organized as follows. Section 2 discusses related work on Federated Learning mechanisms in Edge, cloud, and multi-cloud computing systems. In Section 3, we start by presenting the general flow of our MulticloudFL system (client participation adaptive federated learning system) for supporting forecasting in distributed de-centralized cloud environments. Moreover, the client selection adaptive federated learning algorithm along with the control algorithm are presented. The system architecture is presented in Section 4. In Section 5, an illustrative example is analyzed presenting experimental results of our work and comparisons with previous research works. Finally, the paper is summarized, and conclusions are presented in Section 6.
2. Related Work
In this section, we discuss some of the research performed concerning the FL mechanisms in Edge cloud and multi-cloud computing systems. Various parameters are examined in this section such as the synchronous or asynchronous communication used. Previous Federated Learning approaches use synchronous communication protocols in which the server distributes the central model to a selected portion of clients and aggregates model information by applying weighted averaging, after receiving all updates from these clients. This method is costly due to synchronization delay since the server needs to wait for all local updates before aggregating data. The consideration of lagging devices is inevitable, while network unreliability can cause problems in the federated learning process. On the other hand, the asynchronous communication methods on federated learning are presented as alternatives where the server can aggregate without waiting for any lagging client nodes. However, this method assumes a fixed magnitude of client data during the training process, which is not practical in real-life settings. The use of convex or non-convex deep learning local loss functions is examined in state-of-the-art presented works in this section since the convergence guarantee of adaptive aggregation schemes is considered only for convex local loss functions and a restricted family of non-convex problems. Finally, global aggregation methods, the client participation or selection option, and the prediction accuracy performed are examined in this section as well.
An asynchronous online federated learning framework is presented in the work [8] where some edge devices are connected to the central cloud server in an online way. This server aggregates the local device model parameters that were extracted by using convex and deep learning loss functions executed locally at each device. Good prediction performance is achieved (for the used datasets) but there are no aggregation decisions based on local data size, nor any client selection processes that improve the final prediction accuracy (as in our MulticloudFL approach). A similar asynchronous communication method is followed in the research work of [17], where the proposed approach has near-linear convergence to a global optimum, for strongly convex functions. Deep learning local loss functions are not used in this work [17]. Moreover, even though the whole system shows that it can converge quickly, it seems that it cannot handle data abnormalities or heterogeneous client data effectively.
Considering mobile edge computing networks, the work by [11] uses FL to accurately forecast the resource requests of the more popular application types in the network. By using synchronous communication among the mobile edge devices and cloud servers and by applying convex local loss functions, the proposed model achieves a high accuracy level for resource demand predictions. The aggregation at the global level is based on a weighted model according to the data size located in each mobile edge device. Nevertheless, no client participation decision takes place and thus no possible data abnormalities can be avoided or excluded. In another work [18], a traffic flow prediction system is proposed following an FL approach. In this case, an accurate and privacy-preserving traffic prediction model provides promising results in terms of improved forecasting higher over the advanced deep learning models. There is no compromise in the privacy and security of raw data for each end-user device. Nevertheless, no weighted global aggregation method is used, based on each client data size, nor client participation decisions with an adaptive global aggregation time window are used (as in MulticloudFL).
In comparison to the traditional distributed learning paradigms and FL processes with global aggregation, an innovative privacy-enriched FL method is proposed in [9]. In this work, a compressed communication method among nodes and a cloud parameter server is applied for security reasons, without a significant effect on the accuracy in comparison to non-compressed methods. Nevertheless, by not using Deep Learning local loss functions and without client participation decision, the expected and the pragmatic achieved accuracy results are not high enough. What is more, since the reliability in terms of data content used by local models may vary from client to client of an FL system, the work [19] proposes a selective model aggregation for online anomaly detection. Because several trained models can possibly contain characteristics of anomalous data, the unsatisfying local models can be excluded from FL, which is a fact that finally improves anomaly detection accuracy. Unfortunately, there is no condition for examining in each local node the efficient data size for the local training that would increase accuracy even more.
A synchronous way of communication between client and server in an FL system is examined in the work of [20] that exchanges Gradient Descent parameters and finally uses the global aggregation of these gradient parameters at each learning step on the aggregator server. No deep learning loss functions are used, and no client participation decision is an option in this method. The results show a significant communication reduction in comparison to ordinary FL systems but no significant improvement in prediction accuracy. Another work on abnormal client behavior is presented in the work [21] and concerns cases that may intentionally or unintentionally deviate from the ordinary federated model learning resulting in abnormal behaviors. In this work, a synchronous communication method is applied by using all types of loss functions such as convex, non-convex, and deep learning along with a global aggregation method based only on local loss function values.
An evaluation of some Federated Learning Aggregation Algorithms is examined in terms of application to Human Activity Recognition in the work by [22]. The aggregation algorithms that are used are FedAvg, FedPer, and FedMA. The experiment results show a moderate overall prediction accuracy for classification problems. No data abnormalities or other special issues on FL are examined in this work. Another approach for FL that takes into consideration cases of data heterogeneity can be found in the research [23]. More specifically, in this research, a FedPer, a base and personalization layer approach for federated training of deep feedforward neural networks is proposed which can combat the ill effects of statistical network heterogeneity. Nevertheless, data abnormalities issues that may appear in such environments and their possible resolution are not part of this work.
In the research work [24], new optimization algorithms of FL are proposed based on cloud edge computing to overcome the problem that is caused by the hardware restrictions of participating mobile devices since large computational resources are needed for using the algorithm of FedAvg. In the presented work, there is a separation of the process that concerns the completion of local updates both on the mobile devices and on the edge server, and on the process of global aggregation which is executed among edge servers and the central server. Nevertheless, no client participation method is used to tackle abnormalities in the personal data of clients and thus cannot improve the prediction accuracy further.
The client participation method applied in the presented FL Mobile Edge system [25] seems to mitigate resource constraint problems such as limited computational resources or poor wireless channel conditions. In that way, the new method allows the server to aggregate as many client updates as possible, accelerate performance improvement in Machine Learning models, and use Deep Learning local loss functions. Nevertheless, the client selection takes place in a random way which means that it does not significantly improve the prediction accuracy nor does it efficiently handle possible client data abnormalities.
In the work [26], an FL system is developed for handling intensive care heterogeneous data in a cloud-distributed environment. The algorithm LoAdaBoost, which increases the efficiency of the federated machine learning system in terms of prediction accuracy, is used but with a slow convergence. The ordinary resources constraint problem is not taken into consideration nor the client selection decisions in the distributed environment. On the other hand, concerning the work [27] there is an FL optimization system presented that resolves issues that have to do with heterogeneity in federated networks. The missing point in this approach is the consideration of data abnormalities in the clients, which negatively affect the forecasting accuracy.
Finally, elaborated work at [16] shows a gradient-descent-based FL system with an adaptive control algorithm that determines the best trade-off frequency between local update and global parameter aggregation to find the minimum global loss function. This significant work [16] constitutes the starting point for our MulticloudFL approach in this paper. The loss function in [16] corresponds to the specific resource parameters of the FL system. The results show good performance in terms of accuracy, but they do not take into consideration the deep learning local loss functions in the respective clients, nor do they consider revisions in client participation according to any data abnormalities. These two important dimensions are covered in our MulticloudFL approach, as extensions to [16] to further increase the prediction accuracy of various monitoring metrics, e.g., CPU consumption in VMs used for hosting multi-cloud data-intensive applications.
In contrast to the state-of-the-art presented, our work formally addresses both the issues of dynamically determining the global aggregation frequency within a given time resource budget and the improvement of prediction accuracy by excluding data abnormalities. This improvement takes place by using: (i) deep learning local loss function in each FL client while taking into consideration the data abnormalities in the local client data during global aggregation; and (ii) by considering adequate data volumes during the client participation process in the global aggregation procedure of MulticloudFL. Moreover, our work presents an innovative approach to the way the data distribution can take place in various nodes of the FL cluster (a combination of iid and non-iid scenarios). Finally, deep learning local loss function is used in each participating node that shows a very good convergence in comparison to other functions. A fundamental comparison of the above research works and their features is shown in Table 1.

Table 1.
Relevant research work comparison.
3. Research Methodology of Client Participation Adaptive Federated Learning System
3.1. General Flow
In our paper, we present a gradient descent algorithm adapted from [16] to solve the machine learning problem that refers to the minimization of the global loss function of a FL that involves multi-cloud and edge nodes:
where is the parameter vector of the global model when it reaches its minimum. F(w) is the global loss function of all the distributed client nodes (multi-cloud nodes or edge nodes) datasets:
where N defines the number of client nodes, denotes the size of the local client node dataset, and D the total size of the dataset of the entire edge and multi-cloud computing system, provided in the following listing:
Last, is the client node’s local loss function that captures the error of the client node’s model on its local training data. Thus, each client node i has its local model parameter where t = 0,1,2,… denotes the iteration index. At t = 0, the aggregator initializes the communication to clients and sends the initial model parameter w(0) along with the time step to all client nodes. In this way, the local parameters for all nodes i are initialized to the same value. More specifically, the initial global model weights w(0), before starting the learning process, are set to the value zero. After one or more local iterations, a global aggregation occurs on the aggregator server only if the time of execution is a multiple of the basic time step i.e., t = K where K = integer number.
For the timestamp t > 0, new values of the local model parameters are calculated based on the gradient descent update rule of the local loss function for each client node i. Every local update uses as the initial value for the current iteration the value that came from the previous iteration t-1, according to the following gradient descent rule:
where n is the learning rate. The global aggregation process gathers multiple client updates to further improve the FL model. We already defined that the system performs τ* steps of local updates at each client node between every two global aggregations. After the global aggregation, the local parameter at each node client i usually changes. For clarification, we use (t) to emphasize the parameter at node i after possible global aggregation. If no aggregation is performed at iteration t, we have (t) = . If aggregation has occurred at iteration t then ≠ and for that reason we set = , where the is the weighted average according to the data volume contribution from each client node:
Our work is related to the work [16] where a gradient-descent-based FL system with an adaptive control algorithm was introduced. Compared to [16], the current paper presents an innovative client selection method among the client nodes that participate in every global aggregation. Given the fact that local client nodes are likely to contain noisy or anomalous data and have potential risks of being attacked, we carefully select members that participate in the federated learning process. Otherwise, aggregating inaccurate or insecure local models’ parameters into the global model setup may inversely reduce the prediction accuracy. Moreover, a single client node may face insufficient training data to develop a high-quality model because of limited computation and energy resources. Thus, we should exclude it from the model aggregation to avoid its adverse impact on the global model.
The proposed selection method is based on an adaptive threshold coming from the value of local data sizes and on an appropriate loss function threshold value coming from the local loss values of client nodes. Both these adaptive thresholds are calculated from their mean values of the local data sizes and local losses, respectively, minus the standard deviation for each case. We are considering the mean values because we want the client participating nodes to be in an almost similar state regarding the losses of their models and the amount of data used for training. The standard deviation parameter is a commonly used deviation affordable in such cases of finding similar member conditions. After an analysis of the aggregator to find the optimum adaptive threshold for local data sizes and local loss function executed, two major conditions are considered:
- The data size of each node should be bigger than an adaptive threshold of data sizes as mentioned before, to be able to contribute effectively to the global aggregation process.
- The adequate small value of each local loss function for each client node should be below the already mentioned threshold. Otherwise, a large and above-the-threshold local loss value implies a high probability that the state of the chosen client is deviating from the normal client states. Consequently, the specific client should be excluded from the model parameters aggregation to avoid its adverse impact on the global model.
Because the above thresholds come from mean values of nodes participating in the FL cluster, the possibility of not satisfying both of the above conditions by any client is not considered feasible. At least one node of the FL cluster will participate in the global aggregation in each iteration loop.
In the current work, Deep Learning, i.e., Long short-term memory (LSTM) algorithm [28] local loss functions are used in the local iterations, as a new type of local loss function in comparison to previous work [16]. This decision further increases the prediction accuracy of our MulticloudFL. The local models converge to a local minimum. Our FL model is gradient-based as already stated and a novel convergence bound is achieved that incorporates non-independent and identically distributed (non i.i.d) data distributions among nodes and an arbitrary number of local updates between two global aggregations. Of course, we have to highlight that a parameter that influences the convergence rate is the step size, which is a hyperparameter that needs fine-tuning during the initial setup of our model in order to ensure convergence.
Moreover, a major operation of MulticloudFL is the fact that given a specific amount of resources’ constraints, i.e., the maximum available time in which the FL system should have completed the learning process, it should find the optimal values of and T = K* (as already defined) so that the global loss function of the FL system is minimized at the end (Equation (2)). For that purpose, a Control Algorithm is applied. The step time for each local update and the parameters of this Control Algorithm are optimized, first locally at each client node and finally after each global aggregation procedure. In general, as part of the whole FL process, the crucial point is the examination of whether the minimum value of the global loss function has been achieved. If not, then the new calculated model parameters and new step time are sent back to the client nodes, the local training on the nodes is re-initiated and the whole described learning process is repeated. It is true that the process of the multi-cloud synchronous federated learning may initially cause some delays as the number of participating nodes increases. Of course, the whole FL system is fully scalable in terms of nodes, and, in conjunction with the control algorithm, the time execution is optimized. Theoretically, no restrictions on the number of participating nodes should be met. In Figure 1, we provide a flow diagram that depicts the main steps of our MulticloudFL.
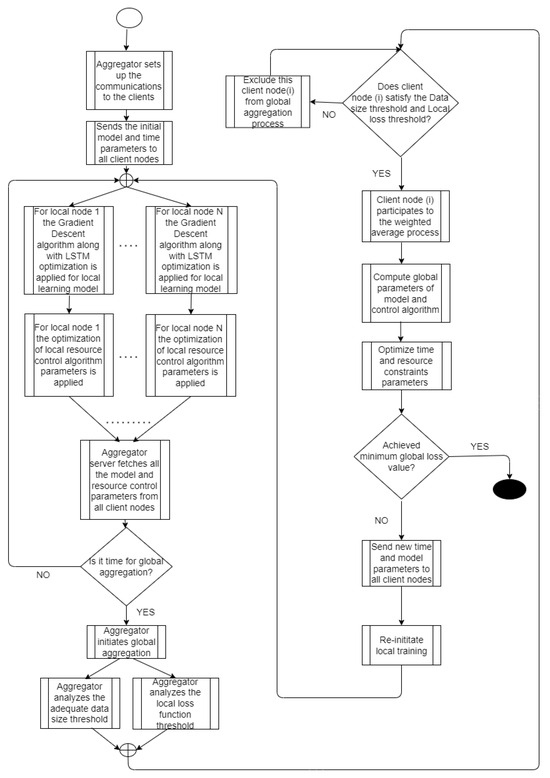
Figure 1.
General flow of the MulticloudFL system.
3.2. Client Selection Adaptive Federated Learning Algorithm
In the FL system that is presented in this paper, an innovative method is proposed that ensures an increase in the final prediction accuracy. The previous works [16,25] use a weighted average method during global aggregation of all the connected client nodes (meaning either multi-cloud nodes or edge nodes). The already existing research works, as it was discussed in Section 2, cannot provide an adequate solution for coping with the low quality of local client data (abnormalities) nor cope with cases of small local data volumes that cannot successfully train ML algorithms. With our new adaptive FL multi-cloud client selection method, both discussed drawbacks are avoided effectively.
Specifically, the first part of our selection algorithm, which runs on the aggregator server, incorporates the discovery process of the data residing in each client and the related final local loss values before global aggregation takes place. As soon as the discovery process is complete, an adaptive threshold is calculated after the analysis of gathered information, that considers the existence of extreme data abnormalities meaning data points that differ enormously from other observations. These extreme data abnormalities called outliers [29] may exist due to variability in the measurement or it may indicate an experimental error and not a violation of any anomalous condition. These can cause serious problems in statistical analysis and for that purpose, they should be avoided.
For these reasons, we define an adaptive threshold thr for the distributed dataset by excluding the outliers that may exist in local data or local loss values as follows:
where we use the standard deviation as the std function in the above equations. The dynamic selection process of Equations (6) and (7) is based mostly on experimental results. Assuming a Gaussian distribution for the data size and the loss, rejecting the lowest part below 1σ, is equivalent to accepting 5 out of 6 nodes. This is a tradeoff to ignore the outliers without having much underutilization. This approach represents a fail-safe mechanism to avoid the dilution of the performance of the total model with less trained nodes.
The second step of our client selection algorithm is the global aggregation on the server following a weighted-average process according to each client’s data size. In this process, only the clients whose data size satisfies the above data threshold and, at the same time, those whose local loss functions are smaller than the above-defined loss threshold, take part in the global aggregation. In this way, we ensure that data with adequate volume size contribute additively to the learning process without adding data with erroneous behavior that may lead to incorrect and inaccurate prediction results.
The described process is shown in the following Equation (8) and in the following Algorithm 1 where we describe the presented algorithm using pseudocode.
Therefore, in Equation (8), we assume that our FL system has N client nodes: 1, 2,…, N with local datasets for each of these nodes. denotes the data size of the local dataset for each client node i that should satisfy both of the two mentioned conditions for local data size and local loss value. Moreover, denotes the locally trained model parameters of client node i that will participate in the global aggregation giving, in the end, the weighted average of the w(t) global model parameter.
| Algorithm 1 Client Selection FL Algorithm |
| Client Selection FL Algorithm |
| Require: Local minibatch size B, number of client participants m per global aggregation, number of local iterations τ, learning rate n, N total number of client nodes Ensure: Global model w(t) |
[Participant i] receive w global model parameter for i participant from Server Local Training (i,w): Split local dataset Di to minibatches of size B minimum For each local epoch j from 1 to τ DO: For each b ε B DO: wi <-- w - n*ΔL(w;b) (n is the learning rate and ΔL is the gradient of local Loss on b.) end For end For send the wi model parameter to Server |
| [Server] Initialize w(0): For each iteration τ from 1 to Τ(=κ*τ) DO: Receive from Client Participants all wi local model parameters For each Client Participant (1,…,N) DO in parallel: wi(t+1) <-- LocalTraining (i,w(t)) end For Discover from all Client participants N: - Data Size Threshold T1 - Local Loss Threshold T2 Choose a subset of S of m participants from N when the 2 conditions are achieved: participant Data Size > T1 and Loss value <T2 For each participant i ε S (1,…,m): Calculate the Average Weighted Aggregation based on Data Size of each client (Equation (8)) end For end For send to Client Participants the new w global model parameter values |
3.3. Control Algorithm
In this subsection, the resources control algorithm for adaptive FL is presented, which describes the steps that are followed for recomputing the τ* (time window) after every global aggregation execution based on parameters from the last state of the system.
Specifically, the important point in our control algorithm is the optimum use of available computing resources within the scope of minimizing the prediction errors and thus the loss function during FL training. Consequently, for the distributed stochastic gradient descent [14] used in our case, the problem turns out to be the optimization of the values of Τ and τ and thus τ*. These optimized parameters manage to minimize the final global loss function of the system given the specific resource constraints. We define the equation that relates the Τ and τ as T = K*τ, which helps with the process of minimization of the local and global loss functions.
In general, we consider M different types of resources that may involve various cases such as time, communication bandwidth, heat energy, etc. For each m{1,2,…, Μ}, for each local update step, all nodes of the multi-cloud FL system consume units of type m resource and each global aggregation step consumes units of type m resource where both and > 0 (finite numbers). For the given parameters for Τ and τ the total consumed resource is given by the following equation:
For Equation (9), it is important to note that, during the FL process, each client node i first computes the local loss value and then sends the result to the server aggregator to compute the global loss function weighted aggregated value. Since each client node knows the K-th global model parameter values only after the K-th global aggregation (global model parameters are known to each node after global aggregation completes), the local loss function at the K-th round will be sent to the aggregator at the K + 1 time aggregation step and the aggregator then computes the K-th global loss function, which is sent back to all clients. In order to compute the last global loss function (T = K*τ) an additional local and global update is needed at the end and that is why the plus one addition: (T + 1) and (K + 1) parameters are used in Equation (9).
Saying that is the total resource consumption of type m, our control algorithm tries to find a minimum value of the global loss function to complete the Federated Learning process by ensuring the utilization of a maximum value of the total budget of type-m resource:
with the condition: (T + 1) + (K + 1)
In general terms, it is very difficult to use an analytical expression to relate τ and Κ and their effect on the Global Loss Function of the multi-cloud FL system. This difficulty can be recognized in the correlation point of the convergence property with gradient descent while at the same time, it is imperative to find the impact of the global aggregation frequency on the convergence property. and coefficients can also be time-varying. For that reason, we propose the mentioned iterative FL control algorithm.
According to the theoretical analysis and definitions presented in relevant work [16], the basic task of the control algorithm is the minimization of the following expression, which is derived from the Equation (10) and comes as the result of the substruction of a given global loss function F(w) from its minimum value (constant). With this approximation and by rearranging the inequality constraints of Equation (10) as follows, we can conclude the value of G(τ):
where and is the total resource consumption of type m. Moreover, n is the learning rate, φ is the Constant defined in the Lemma 2 control parameter in Algorithm 2, h(τ) is the function showing the gap difference between the model parameters obtained from distributed and centralized gradient descents, ρ is the Lipschitz parameter, and β is the Smoothness parameter. All these definitions are explained in the work of [16].
Based on the above expression, the minimization of G(τ) for the optimal value of τ (which represents the number of local update steps that are executed between two global aggregations) is defined as τ* and is given by the following expression:
and after the optimal definition of the above τ*, we can calculate the optimal total number of global aggregation steps K* as follows:
The expression of G(τ) has parameters that are related to the resources’ consumption parameters and other parameters ρ, β, and δ that are related to the loss function characteristics. This calculation takes place in real time during the FL process.
The values of are derived from the measurements of resource metric consumptions at the client nodes side and the aggregator side, respectively. For the time resources used in our work, the maximum computation time per local update at all nodes is considered Moreover, the aggregator refers to the total resource type m (i.e., time) consumption of each resource and compares the total resource consumption against the resource budget In other words, correspond to the actual time needed for each local update and for each global aggregation. If the consumed resources approach the budget limit of a specific type m resource (in our case m is time) then it stops the learning process of the algorithm and returns the final result.
The values of ρ, β, δ are estimated from the local and global losses and gradients computed locally at each client node and globally at the aggregator server, during the FL. For the efficiency of this calculation, each client node needs to have access to both its local model parameter and at the same time to the related global model parameters (same iteration at timestamp t) created at the aggregator, which can happen when global aggregation is completed at iteration t. Because global model parameters are known to each node after global aggregation completes, the calculated values ρ, β, δ are only available for re-calculating τ* starting from the second global aggregation step after initialization, which uses estimates from the previous global aggregation step. This is obvious in the description of the Control Algorithm in Algorithm 2.
Moreover, during the re-computation in the aggregation after each global aggregation step, we look for new values of τ* with the upper limitation of γ threshold times the current value of τ* and find τ* that minimizes, as already discussed before, G(τ) whereby γ > 0 is a fixed parameter. This γ threshold is configurable. The role of γ is to limit the search space and to prevent τ* from growing too rapidly and causing inaccuracies at the end [16]. Moreover, a maximum value of τ* is used because if τ* reaches too large values it is going to violate the total resource budget and deteriorate the operation of the system. The new estimated value τ* is sent back to each node after global aggregation along with the global model parameters just calculated. The description of the major points of the Control Algorithm is shown in Algorithm 2.
We note that the Algorithms presented in this paper differ from previous work [16] mainly on the selection method applied during the FL process and the Regressive Deep Learning method for minimization of the local loss function. Moreover, the Control Algorithm used takes into consideration the resource parameters only of the selected clients. To be more specific, the aggregator server after selecting the appropriate clients that participate in global aggregation, calculates the global values of ρ, β, δ as the mean value of only the selected clients. These new calculated values are those that contribute to the final re-estimation of τ* according to Equation (12). These innovative and newly introduced calculations are proved to give more accurate prediction results compared to work [16] as shown in the next sections.
| Algorithm 2 Resources Control Algorithm |
| Control Algorithm |
| Require: Resource budget R, control parameter φ, search range parameter γ, maximum τ value τmax Define: global model parameter vector w(t) local model parameter vector wi(t) local resource parameter ci local resource parameter bi ------------------------------------------------------------------------------------------------------- |
[ Server] Initialize τ* <-- 1 ; Initialize t <-- 0 ; Initialize s <-- 0 //s resource counter; Initialize w(0) as a constant; Initialize w(global) <--- w(0); REPEAT: send w(t) parameters and τ* to all client nodes; save iteration index of last transmission of w(t): t0<-t ; next global aggregation is after τ iterations : t <-- t + τ*; Receive wi(t), ci from each client node ; compute the weighted average with client selection of w(t) global model; Receive ρi, βi, Local Loss function, Anadelta of Local Loss fuction from each client selected node i; Estimate weighted average ρ based on Data Size of each client selected node i; Estimate weighted average β based on Data Size of each client selected node i; Compute Anadelta of loss function and from difference of Anadeltas of local and global loss functions estimate finally the weighted average δ ; [see ref [6]] Compute new value of τ* according to Equation (9) via linear search on integer values of τ within [1, min {γτ*;τmax}; Estimate resource consumptions cm, bm using cι received from all nodes ι and local parameters at the aggregator; sm <-- sm +cm * τ+bm; IF sm>Rm then decrease τ* to the maximum possible value such that the estimated resource consumption for remaining iterations is within Resource budget Rm. [Participant] Receive w(t) and new τ* from Server; Estimate local ρi,βi Estimate type-m (time) resource consumption cm,i for one local update at node i; Send all parameters wi(t) (updated) , ρi, βi, local loss function of wi(t) , anadelta of loss function of wi(t), to Server |
4. Architecture of the System
As stated in the Introduction section, in this paper we introduce a Federated Learning approach with decentralized client nodes (multi-cloud and edge) that is implemented as a client-server architecture. It uses multiple node clients hosted in various cloud providers with a remote aggregator server located in any of these cloud providers. The whole system performs both local processing tasks and remote coordination/execution tasks.
As shown in the flow chart of Section 3.1, in the MulticloudFL system the learning process includes local model update steps, where each client node (multi-cloud node or edge node) performs gradient descent to adapt the local model parameters. This is described in Equation (4) where n is the learning rate which is defined as the step size of the model parameter update. The definition of the learning rate value takes place at the configuration file of the system where the chosen value is a result of various experiments towards finding the optimum one. The training epoch represents a complete repetition of the parameter update that involves the complete training dataset at a certain time. It is important to note that the learning rate should be selected wisely so that it does not influence the learning process. The gradient descent algorithm is used to minimize training errors and to repetitively update the network hyper-parameters through every training epoch.
The learning rate has a huge impact on training neural networks and federated algorithms. It can speed up the training time, help navigate flat surfaces better, and overcome pitfalls of non-convex functions. Adaptive learning rates allow us to change the learning rates for the FL model parameters in response to gradient and momentum.
In our local client node model implementation, the optimization method of Adam has been used [30]. Adam, which denotes adaptive moment estimation, is the latest evolution of adaptive learning algorithms that integrate the ideas from AdaGrad, RMSProp, and momentum [31,32]. Just like AdaGrad and RMSProp, Adam provides an individual learning rate for each model parameter. It has been designed specifically for training deep neural networks, it is more memory efficient and needs less computational power than the other two algorithms. Adam uses the first moment (mean used in RMSProp optimizer) as well as the second moments of the gradients utilizing the exponential moving average of the squared gradient. In other words, the mechanism of Adam is used to calculate adaptive linear regression for each parameter in the model.
When the amount of training data is large, it is usually computationally prohibitive to compute the gradient descent of the loss function defined on the entire local client dataset. In cases such as our work, stochastic gradient descent is used [8,20], which elaborates the gradient computed on the loss function defined on a randomly sampled dataset of the whole local available training data, which is called a mini-batch. Every mini-batch can be considered an undersized collection of samples with no overlap between them. Each local iteration step (τ) corresponds to a step of gradient descent where the gradient is calculated on a mini-batch of local training data. The mini-batch changes for every step (τ) of local iteration, i.e., for each new local iteration, a new mini-batch of a given size is randomly selected from the local training data.
During the training of the local model on each node a method of lowering the risk of overfitting and speeding up the training process is applied, which is called dropout [33]. In the dropout technique, we randomly choose units and nullify their weights and outputs so that they do not influence the forward pass or the backpropagation during the training. By contrast, the full-scale network is utilized to perform prediction during the testing process.
According to the above, the local model updates, minimize the loss function defined according to the data content of the local dataset. The federated learning process also executes global aggregation steps after the model parameters are trained locally (in node clients) and then they are sent to an aggregator mode, located in a remote server in the cloud. The aggregator selects the “appropriate” client nodes to achieve the optimum prediction accuracy, by taking the weighted average of their model parameters according to their local data volume. After the completion of an aggregation process, the updated parameters are sent back to all the node clients belonging to the FL system.
Due to the adaptive resource nature of MulticloudFL, the frequency of global aggregation can be re-estimated during the learning process, and it can take values that minimize the global loss function of the whole system (see Equations (1) and (12)). In this way, the frequency of global aggregation performs efficient use of the available resources of the FL system without over-using or under-using the resources. In our case, the major resource dynamically adapted is the time parameter.
A high-level view of the system architecture is provided in Figure 2.
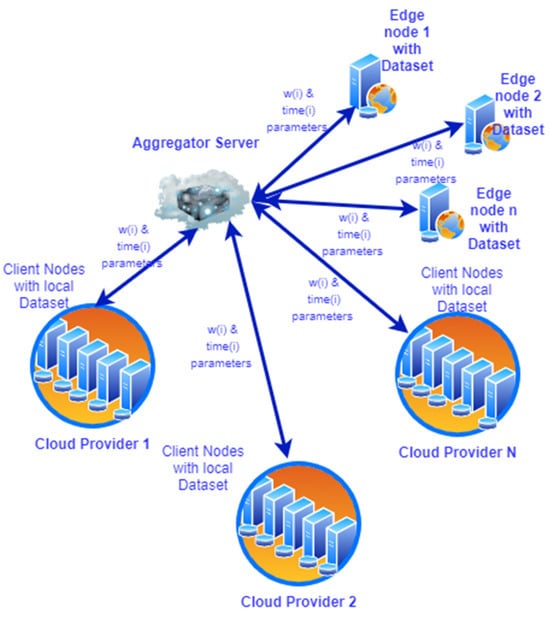
Figure 2.
MulticloudFL System Architecture.
Moreover, in Figure 3, we ground the general flow presented in Section 3.1, and discuss the technology used for each of the components of the system developed. In that figure, we present the new innovative elements and modules developed in comparison to the ones presented in work [16]. The two basic functionalities that MulticloudFL introduces and evolves are the deep learning use for local loss functions optimizations (i.e., LSTM algorithm), the Client parameters discovery module, and the Client selection method that ensures higher prediction accuracy.
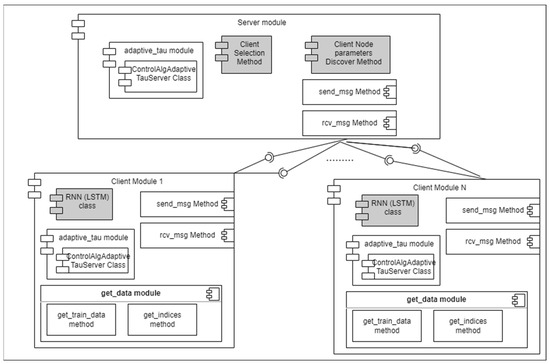
Figure 3.
Conceptual Code Architecture.
The model used is a deep recurrent neural network that elaborates supervised learning with labeled data. To be more specific, time series data that refer to CPU consumption over time are used as training and test/validation datasets. Thus, we have a case of regression problem. Our RNN model uses the long short-term memory approach (LSTM). LSTM network is one of the emerging methods for time series prediction and has been widely researched during the last few years. The suitability of LSTMs arises from the fact that they can learn the dependencies between the data points. LSTM models develop a function to learn from the previous historic points to predict future points. A hidden layer is included in our model and a dropout layer to avoid, as already mentioned, the phenomenon of overfitting. The initial values of global model weights before the learning process are set to the value of zero, as discussed previously. This is achieved by filling with zeros the array vector of global_grad_global_weight of class ControlAlgAdaptiveTauServer.
As can be seen in the described class diagram of Figure 3, our client-server basic schema architecture is given by the Server-Client modules. To be more specific, the server is the central module where the global aggregation process, the Client parameters discovery method, and the Client selection method run as part of the Client Selection Adaptive Federated Learning Algorithm (described in Section 3.1). Moreover, the adaptivetau module is used in the Server with the ControlAlgAdaptiveTauServer Class as part of the control algorithm process for the optimization of the resources (time) usage (τ value) by using the selected client nodes parameters and resources. Last, on the server side the two methods used for the communications with the client nodes (multi-cloud and edge nodes) are the send_msg and recv_msg methods.
On the Client nodes side, the core module that is used in each client is the Client module. With the help of this module local update steps are executed in each client of the FL until a local convergence is achieved by using the Gradient Descent algorithm and the Loss function of LSTM that is included in the RNN class. Moreover, the mentioned local learning process is executed based on the local data of each client by fetching the data for training, with the methods get_data() and get_train_data () from the local dataset storage. The get_indices() method is used for the Stochastic Gradient Descent data read. As in the Server side, the methods: send_msg and recv_msg are also used here to help for the communications and model parameters exchange among client nodes and aggregator server. Finally, the ControlAlgAdaptiveTauClient is used in each client as part of the control algorithm process (for the optimization of τ value).
It is important to mention that the various modules, classes, and methods are implemented by using python language version 3. The open-source libraries developed by Google of Tensorflow [34] are used in our FL system, focusing on the Keras technology [35]. A general overview of the Architecture with the newly developed modules emphasized with gray color is shown in the following Figure 3.
Regarding the deployment process of the model of the Federated System, we follow the following steps:
- Train and Build the final model where the final global loss function will be minimal according to Figure 1. The server.py module is located on the central server, which aggregates the various local trained weights and the client.py module, which is located on each of the nodes (local weights).
- After the training of the model, its parameters are saved with the model.save function of Tensorflow Keras library (https://www.tensorflow.org/guide/keras (accessed on 1 January 2021)) on the aggregator central server. In this way, the model is saved in a format that can be loaded in various server nodes where the inference data (real data) reside. The above command saves the trained model in the HDF5 file format [36], which includes both the model architecture and the learned weights.
- In order to deploy the Trained model to various nodes, we use the Tensorflow Serving and then the local inference on each node’s real data of the federated system can take place.
- After the deployment of the mentioned model, predictions based on real data (i.e., test/validation) take place.
The implementation of the described Architecture of our MulticloudFL system can be found for more detailed analysis on GitHub: https://github.com/vasilaros/Multicloud-Federated-Learning-FL.git (accesed on 1 September 2023).
5. Experimental Results
We note that the Client Participation Adaptive Federated Learning System (MulticloudFL), presented in this paper, has been tested and evaluated in several real-application scenarios. In this section, we present one of them as an illustrative example for highlighting the value of our approach. We refer to a Computational Fluid Dynamic Simulation application inspired by one of the Nebulous pilots introduced by the ICON company for the analysis of fluid models (https://www.iconcfd.com/ (accessed on 1 September 2023)) and fluid mobility-related data. This application produces valuable insights that refer to simulations that examine model design and the effectiveness of fluid dynamics. More specifically, the simulation application concerns a two-dimensional fluid case. Initially, the fluid is flowing from left to right, and a linear barrier diverts the fluid and creates vortices. The colors appearing in the application similar to the ICON case indicate the curl, or local rotational motion, of the fluid. By using the controls to adjust the flow speed and viscosity, the application draws different barriers, drags the fluid around, plots other quantities besides the curl, shows the force exerted by the fluid on the barriers, and measures the fluid’s density and velocity at any point. Computational Fluid Dynamic Application is focused on simulations requiring a variable number of resources. Specifically, we planned three categories of simulations: hi-fi (high fidelity), low-fi (low-fidelity), and a combination of them. The former low-fi or low-fidelity simulations which give pixel-moderate, required few CPU resources (Figure 4) because the low-fi simulation was used to build knowledge. The simulations in this category became the least real to the learner. These included static models and two-dimensional displays that gave a general (not in detail) view of reality. On the other hand, the hi-fi or high-fidelity simulations, which are typically represented by pixel-perfect, production-ready, interactive prototypes required high performance, especially concerning CPU (Figure 5). This is because the hi-fi simulation is about a test that mirrors or closely simulates a real-world situation in which test takers act based on the scenario and available information just as they would in real life. There is also a third simulation case as a combination of the two already mentioned which gave CPU polarized workload data (Figure 6).
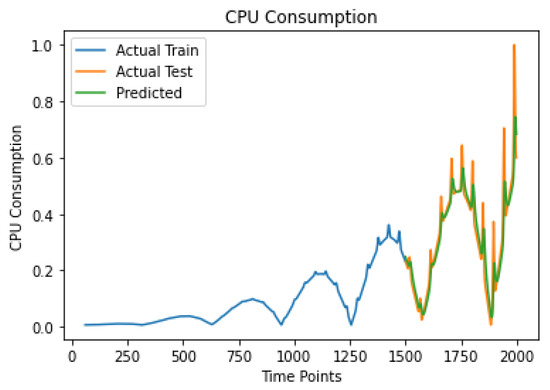
Figure 4.
CPU Increasing Load with Spikes prediction result.
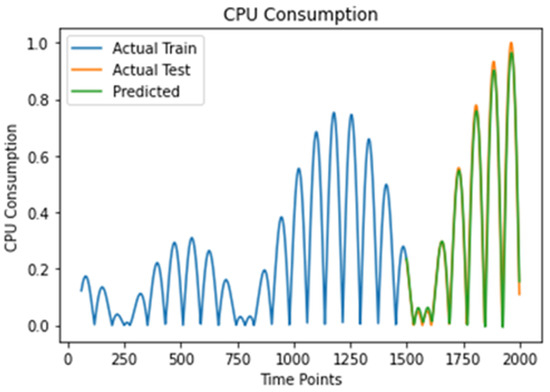
Figure 5.
CPU Periodically Increasing Load with Fluctuations prediction result.
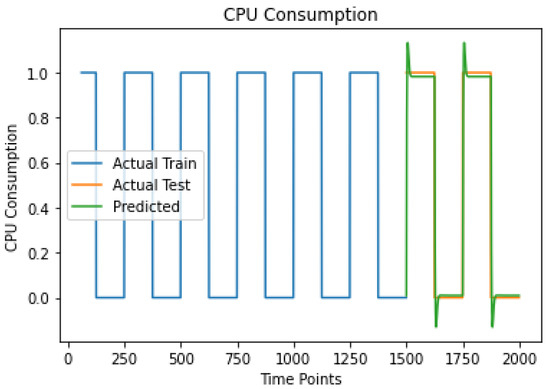
Figure 6.
CPU Polarized Workload prediction result.
The MulticloudFL System copes with the above challenge of dynamically diverse demand. It helps the Computational Fluid Dynamic Simulation application to obtain the resources proactively to minimize cost and optimize the cost-to-simulation-time ratio based on end-user constraints, depending on individual Service Level Agreements (SLAs) and the number and type of simulations requested. The computing resources are dynamically optimized on the fly based on the current load and projected simulation loads.
The initial deployment of this application consists of two main component instances (excluding the aggregator instance) and then the re-deployment of the application is examined on 3, 5, and 20 main component instances since the specific application does not need more nodes for efficient deployment.
To evaluate the performance of the proposed MulticloudFL, we used an experimental environment of three types of datasets over CPU consumption metrics by using 2 up to 20 client nodes coming as results of the three simulation cases of the distributed Fluid Dynamic Simulation application (Figure 4, Figure 5 and Figure 6). The CPU consumption for each node (virtual machine) refers to the total CPU core consumption per node of the system. Specific CPU workload accuracy prediction metrics were used for the evaluation of each simulation case. There is also the need to validate the stability of the total federated learning model. Thus, we cannot fit the model just to the training data and expect that would accurately work on real data it has never encountered before. There is a need for assurance that the federated model has appropriately received most of its patterns from the actual data, and it is not picking up too much on the noise, or in other words it is low on bias and variance. In our experiments, we have used an amount of local data of 2000 CPU consumption (%) time series points (consumption-time per second) measurements for each node. From that data, 75% of them are used for training the local gradient node model and 25% for the validation-test of the local node model. We used most of the data for training purposes because otherwise, we could risk losing important patterns and trends in the data set, which in turn could increase the bias-induced error. Moreover, each node used the gradient computed on the loss function, which was defined on a randomly sampled data subset (mini-batch) to approximate the real gradient. In other words, the stochastic gradient descent is used for each node of the federated system and thus the data used for local training in each iteration are different from node to node. Each local iteration step (epoch) corresponds to a step of gradient descent where the gradient is computed on a mini-batch of local training data. This mini-batch changes for every step (epoch) of local iteration randomly from the local training data.
The usage of test or validation data (inference process) is a very useful technique for assessing the effectiveness of the federated learning model, particularly in cases where we need to mitigate overfitting. These kinds of data represent the use of data that the model has never encountered before.
The environment was set up with the help of Docker Cloud technology in a virtual architecture [37]. The aggregator server and each client node were implemented by deploying a virtual machine with 4 cores VCPU, 8 GB RAM, and 30 GB Hard Disk Drives each time.
5.1. Experiment Measurement Setup
We used a multi-cloud and edge computing environment with varying nodes from 2 to 20 and heterogeneous datasets in terms of local data content and local data size. This means that each node uses for each local iteration a different subset of data (different mini-batch of data). The aggregator is located on a server separated from these nodes. For the specific conducted experiments, we used as resource type only the time parameter. Thus, M = 1. For the values used in our control algorithm, and correspond to the actual time used for each local update and global aggregation, respectively. We compare our experimental results with experimental results on a similar type of time regression dataset by using the Adaptive Federated Learning method already presented in the research work [16].
We use three different types of Datasets and the Stochastic Gradient Descent method for reading the data as a local solver (optimizer). The three datasets come from the measured CPU consumptions of the three simulation cases of the Computational Fluid Dynamic Simulation distributed application. These measurements come from one of the nodes of the distributed system for each case. The first simulation case gives the “CPU Increasing Load with Spikes” results, which are quite anomalous fluctuations of CPU workload with constantly increasing spikes (Figure 4). The related metric results are shown in Table 2 for further evaluation. The second simulation case presents the “CPU Periodically Increasing Load with Fluctuations prediction result”, which refers to very abrupt fluctuations of CPU workload (Figure 5) and its related metrics are given in Table 3. Finally, the last simulation case gives data for CPU workload, which is presented in Figure 6 “CPU Polarized Workload” and the related results metrics are given in Table 4. For the specific data type, CPU consumption refers to periodic CPU workload fluctuation between a minimum (0%) and a maximum value (100%).

Table 2.
CPU Increasing Load with Spikes—prediction accuracy metrics.

Table 3.
CPU Periodically Increasing load with fluctuations—prediction accuracy metrics.

Table 4.
CPU Polarized Workload—prediction accuracy metrics.
For all the datasets, the mini-batch sampling uses the same initial random data source at all nodes, which means that when the datasets at all nodes are of the same data type, the mini-batches at all nodes are also identical in size in the same iteration. The model that is used as a loss function in our SGD comes from the LSTM algorithm [28]. The data distribution to our clients (nodes) is random and with various data sizes and data contents for each of them.
The control parameters used in the configuration file of our multi-cloud edge FL system are as follows. We use search range parameter γ = 10, we set τmax = 100 (maximum τ value), the control parameter is set to φ = 0.01 for the LSTM algorithm [28] that is used in the loss function and the gradient descent step size is set to n = 0.1. This value of learning rate was found to be the optimum after many trial and error efforts giving that optimum performance. Moreover, the resource (i.e., time used) budget for our experiments is set to R = 15 s. The parameter for denoting that all data should be read by using stochastic gradient descent is also set to yes as already explained. The number of Data Points used in total in MulticloudFL is 2000 from where the various random mini-batches of data come from.
One major parameter in our setup is the data distribution in different nodes. Regarding the distribution settings, we followed a combined method of uniform and non-uniform data distribution cases. This means that data samples with the first half of the labels are distributed to the first half of the nodes where each node has uniform information. The other samples are distributed to the second half of the nodes with data that have the same label in each node. This represents the case where each node has non-uniform information because the entire dataset has samples with multiple different labels. To be more specific, each time that there are more labels than nodes, each node may have data with more than one label, but the number of labels at each node is no more than the total number of labels divided by the total number of nodes rounded to the next integer.
In our setup, we used specific hyperparameters for our model: a dense regression deep learning network with 50 neurons (one LSTM hidden layer), a time distributed Dense Layer, and a dropout layer (output) with a rate equal to 0.2. For the time-distributed Dense Layer, we process 60 time steps of the input sequence at a time. The learning rate as already stated came after many trials to be equal to 0.1, which is an optimum value giving a low global loss function and convergence of the algorithm. Moreover, an optimization with adaptive moment estimation is used.
5.2. Experiment Measurement Results and Analysis
In the experiments shown in this section, CPU consumption metrics are used from various client nodes to give an accurate prediction of future CPU consumption (workload). Therefore, after the training of the Total FL algorithm, there is a comparison between the Inference results (Predicted green lines in the figures) and the Real expected results (Actual Test orange lines). We adopt the Mean Absolute Error (MAE) [38], Mean Squared Error or Loss [39] (MSE), Root Mean Squared Error (RMSE) [40], Mean Absolute Percentage Error (MAPE) [41], and Symmetric Mean Absolute Percentage Error (SMAPE) [42] to give an overview of the accuracy achieved for each data type case (n = number of nodes, is the pragmatic value (orange lines in the following figures), is the predicted value (green lines)):
We examined three types of Datasets: one that contains CPU consumption patterns with increasing spikes, another dataset with periodic fluctuations of CPU consumption, and a third case where a polarized CPU consumption pattern is present. All the datasets refer to CPU consumption (workload) metrics gathered from each node of our Multicloud FL Computing system. For each of the Dataset types, we measured the accuracy by using the above equations giving a visualization graph. For each experiment conducted, we make a comparison with the case with no Client Selection in the Adaptive Federated Learning Algorithm and with non-Deep Learning local loss function (as dictated by [16]) and calculated the differences as already stated in previous Section 5.1.
Additionally, as described already in Section 3.3 for the Control Algorithm and regarding the time complexity and time management we can argue that, when we have an unlimited time budget, it is always optimal to set τ = 1 and perform global aggregation after every step of local update. However, when the time resource is limited, the training will be terminated after a finite number of iterations, thus the value of T is finite. Of course, the number of nodes that are excluded for the global aggregation influences the total execution time of the FL algorithm and is expected to reduce it. Comparisons of the current work of this paper with the respective time execution results of work [16] are presented later in this section.
The first type of Dataset gives us the following results by applying the Client Participation Adaptive Federated Learning System (MulticloudFL system) with Deep Learning Regressive (LSTM) local loss functions running at each node locally. We use 2–20 nodes and 1 aggregator server for CPU Increasing Load with Spikes. The specific dataset as explained before concerns low-phi Computational Fluid Dynamic Simulation:
In Table 5, the above-mentioned results of MulticloudFL show improved outcomes (decreased loss functions) against the metric results of [16] in which there is no Client Selection Adaptive Federated Learning Algorithm participation and there is no use of Deep Learning local loss function.

Table 5.
Comparison % metrics values for CPU Increasing with Load Spikes.
The second type of Dataset that we used for our experiments is the CPU Periodically Increasing Load with Fluctuations which provided the following results. The specific dataset concerns hi-fi Computational Fluid Dynamic Simulation Case:
In Table 6, the above-mentioned CPU consumption results of MulticloudFL present improved outcomes (decreased loss functions) against the metric results of [16] in which there is no Client Selection Adaptive Federated Learning Algorithm participation and no use of Deep Learning local loss function.

Table 6.
Comparison % metrics values for CPU Periodically Increasing load with fluctuations.
The third type of Dataset refers to CPU Polarized Workload, which comes from an application simulation case of a combination of the two already mentioned (hi-fi and low-fi) giving the following results:
In Table 7, the above-mentioned CPU consumption results of MulticloudFL present improved outcomes (decreased loss functions) against the metric results of [16].

Table 7.
Comparison % metrics values for CPU Polarized Workload.
Regarding the training time execution results, in order to evaluate the final model weights set, we compare the various time metrics among the two approaches (MulticloudFL and [16]). The number of nodes varies from 2 to 20 for each of the three different dataset types already described. We may see the following three graphs (Figure 7, Figure 8 and Figure 9 where time is given in minutes on the vertical axis (Y) and the number of FL Client nodes is given on the horizontal axis (X)):
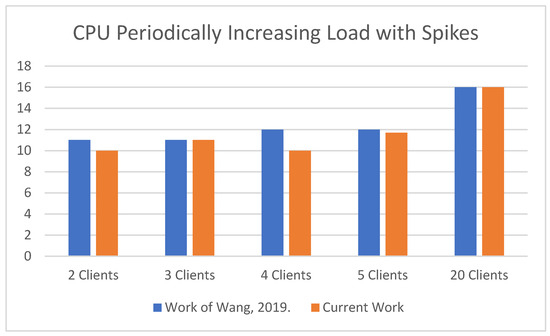
Figure 7.
CPU Periodically Increasing Load with Spikes in time executions results (current work and work of [16]).
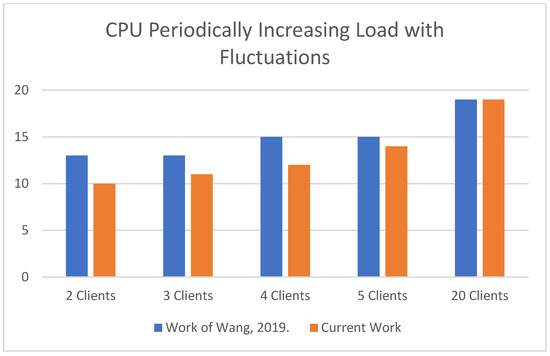
Figure 8.
CPU Periodically Increasing Load with Fluctuations in time execution results (current work and work of [16]).
Figure 9.
CPU Polarized Workload time executions results (current work and work of [16]).
5.3. Discussion
Concluding the results from all dataset types, it seems that Table 2, Table 3 and Table 4 present a better performance regarding the MAE metric values for MulticloudFL from 3% up to 20% compared to the MAE metric measured values of the adaptive federated learning system of the work [16]. The specific metric expresses the results of measuring the difference between two continuous time variables: the actual CPU consumption and its predicted value. We can see that the CPU-polarized workload gives better MAE values than those given for CPU-increasing load and CPU-increasing load with spikes because in CPU-polarized workload the predicted and actual values are extremely close to each other without any peculiar or outlier behavior of observed actual data. In other words, MAE gives less weight to outliers and performs better when they do not exist [43].
For MSE (loss definition) and RMSE metrics, there is also an improvement in the measured values as can be seen in Table 2, Table 3 and Table 4 for our current MulticloudFL system compared to the measured results of the Adaptive Federated system of work [16]. More specifically, the improvement varies from 1% up to almost 20% for all dataset types. This is an expected outcome since our client selection algorithm copes effectively with client data that cause high local loss values during the training process, such as the spikes do. These loss values are excluded during the total FL process. Therefore, specifically for the dataset of CPU Increasing load with spikes, better results have been observed than the other two dataset types. The same stands for RMSE, which is sensitive to extreme values as well. Following the same concept, MAPE is quite sensitive to outliers and peculiar data graphs and performs better in their absence [43,44,45]. We find from the results that all three workload datatypes provide improved results that vary from 1% to 38% in comparison to the measured results of the Adaptive Federated system of work [16] with CPU Polarized Workload dataset giving better MAPE results. This is due to the fact that it does not contain any outliers. Nevertheless, it is widely known from [43,45,46], that SMAPE is very sensitive and depends heavily on the level of time series and on the existence of extremely small actual values (close to zero). This is why we observe worse performance both for CPU Polarized Workload and CPU Increasing Load with Fluctuations for the SMAPE accuracy metric. The first datatype of CPU Increasing Load with Spikes does not include many CPU consumption values close to zero and performs better in terms of SMAPE.
Generally speaking, the results in the current work show an increase in the prediction accuracy in comparison to previously presented research works [9,16,18] as explained before. The use of Deep Learning local loss functions in combination with the selection methods presented in previous sections is an innovative approach that has not been used in previous works [19,21,25]. It is important to note that the convergence time seems to be also improved compared to work [16] since only the selected clients are taken into consideration in every global iteration. Finally, we should mention that the proposed methods for time regressive type of problems presented in this work are freshly introduced providing improved and accurate predictions. Thus, it is going a step further from the current SOTA, which usually offers prediction improvements performed for data classification problems [11,16,22]. Last but not least, our current work gives better time execution training time meaning better time resource efficiency of the total algorithm.
Nevertheless, despite the many advantages of the current work, we can detect some limitations, especially regarding the process of multi-cloud synchronous federated learning. One significant limitation is that the total FL model does not consider participants who can join halfway through the training process (i.e., training already in progress). Asynchronous communication is proposed to resolve that issue and improve the scalability and efficiency of the FL approach. Moreover, another limitation seems to be the convergence of the model based on the fine-tuning of its hyperparameters. This process depends on the experience of the engineer who designs the model that needs to take into account many trade-off tunings such as the convergence with the time execution.
6. Conclusions
Federated learning methods were originally proposed to enable clients to collaboratively train a machine learning model while ensuring privacy for each cloud client node. In this paper, we focus on the gradient-descent-based federated learning algorithm that includes both local updates using Deep Learning local loss functions and global aggregation techniques. After applying the global aggregation techniques, we exclude cloud node clients that may deteriorate the prediction accuracy and the performance of the system. A control algorithm is also used to achieve the optimal frequency between local updates and global aggregations to obtain a global minimum loss value under specific resource constraints. Using various types of experimental datasets, we presented an improvement from 3% up to 38%, in terms of prediction accuracy in comparison to related methods presented in previous works [16]. Both iid and non-iid dataset scenarios have been investigated on the mentioned experimental results.
Nevertheless, some limitations already mentioned in the previous section exist, and they relate to: (i) potential participant nodes that may join halfway through the learning process and (ii) potential scalability issues that may arise due to the synchronous way of communication among the participating clients. An asynchronous mode of communication may be examined in the future as a possible improvement of the current work.
In future work, we will also examine possible encryption methods that may apply to the trained local model parameters that are exchanged among cloud clients and the central cloud servers of the FL system to avoid man-in-the-middle attacks, data leakages, or other similar cyberattacks. Moreover, there could exist a trustworthy federation schema based on various concepts such as the trust scores of various nodes of the FL system in a safe network [46,47]. The importance of the above observations motivates the following open questions:
- How can we protect our FL system from malicious participants who may send incorrect or malicious model parameters to falsify the learning global aggregation process?
- Can we set up our MulticloudFL in a blockchain-trustworthy network?
- Can we consider, in the MulticloudFL client selection, process any trust score metrics as criteria for node selection in the global model aggregation process?
- How may security issues of edge devices or edge servers decrease the accuracy predictions of the FL multi-cloud system?
The above questions are challenges for future tasks that could elaborate and enhance the presented system.
Author Contributions
Initial idea and design of the paper V.-A.S., Y.V. and G.M.; First draft of paper V.-A.S.; Federated Learning Architecture Overview V.-A.S., Y.V. and G.M.; Related work analysis, V.-A.S., Y.V. and G.M.; Research methodology V.-A.S., Y.V. and G.M.; Algorithm Analysis and Design V.-A.S.; Implementation of Algorithm V.-A.S.; Experiment Results Analysis and Evaluation V.-A.S., Y.V. and G.M.; Final evaluation V.-A.S., Y.V. and G.M.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the EU’s Horizon research and innovation programme under grant agreement No. 101070516 NebulOuS project. The authors would like to thank the partners of the Nebulous project (https://www.nebulouscloud.eu/ (accessed on 7 December 2022) and especially ICON for the introduced pilot demonstrator that inspired our experimentation approach. This work reflects only the authors’ view, and the European Commission is not responsible for any use that may be made of the information it contains.
Data Availability Statement
Data can be found from the related cases described: https://nebulouscloud.eu/use-cases/ (accessed on 24 September 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alahakoon, D.; Nawaratne, R.; Xu, Y.; De Silva, D.; Sivarajah, U.; Gupta, B. Self-Building Artificial Intelligence and Machine Learning to Empower Big Data Analytics in Smart Cities. Inf. Syst. Front. 2020, 25, 221–240. [Google Scholar] [CrossRef]
- Wang, S.; Tuor, T.; Salonidis, T.; Leung, K.; Makaya, C.; He, T.; Chan, K. When edge meets learning: Adaptive control for resource-constrained distributed machine learning. In Proceedings of the IEEE INFOCOM 2018—IEEE Conference on Computer Communications, Honolulu, HI, USA, 16–19 April 2018; pp. 63–71. [Google Scholar] [CrossRef]
- Lim, W.Y.B.; Luong, N.C.; Hoang, D.T.; Jiao, Y.; Liang, Y.-C.; Yang, Q.; Niyato, D.; Miao, C. Federated Learning in Mobile Edge Networks: A Comprehensive Survey. IEEE J. Commun. Surv. Tutor. 2020, 22, 2031–2063. [Google Scholar] [CrossRef]
- Sittón-Candanedo, I.; Alonso, R.S.; Rodríguez-González, S.; Coria, J.A.G.; De La Prieta, F. Edge Computing Architectures in Industry 4.0: A General Survey and Comparison. In Proceedings of the SOCO 2019: 14th International Conference on Soft Compu-ting Models in Industrial and Environmental Applications, Seville, Spain, 1 May 2019; pp. 121–131. [Google Scholar] [CrossRef]
- Konecny, J.; McMahan, H.B.; Ramage, D.; Richtarik, P. Federated optimization: Distributed machine learning for on-device intelligence in Machine Learning. arXiv 2016, arXiv:1610.02527. [Google Scholar]
- Konecny, J.; McMahan, H.B.; Yu, F.X.; Richtarik, P.; Suresh, A.R.; Bacon, D. Federated learning: Strategies for improving communication efficiency in Machine Learning. arXiv 2016, arXiv:1610.05492. [Google Scholar]
- Bdtechtalks: The Security Threat of Adversarial Machine Learning Is Real. Available online: https://bdtechtalks.com/2020/10/26/adversarial-machine-learning-threat-matrix/ (accessed on 2 April 2020).
- Chen, Y.; Slawski, M.; Ning, Y.; Rangwala, H. Asynchronous Online Federated Learning for Edge Devices with Non-IID Data. arXiv 2020, arXiv:1911.02134. [Google Scholar]
- Lu, X.; Liao, Y.; Lio, P.; Hui, P. Privacy-Preserving Asynchronous Federated Learning Mechanism for Edge Network Computing. IEEE Access 2020, 8, 48970–48981. [Google Scholar] [CrossRef]
- Imakura, A.; Inaba, H.; Okada, Y.; Sakurai, T. Interpretable collaborative data analysis on distributed data. Expert Syst. Appl. 2021, 177, 114891. [Google Scholar] [CrossRef]
- Fantacci, R.; Picano, B. A Federated Learning Framework for Mobile Edge Computing Nodes. CAAI Trans. Intell. Technol. 2020, 5, 15–21. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, T.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 20–58. [Google Scholar] [CrossRef]
- Martin-Doñas, J.M.; Gomez, A.M.; Gonzalez, J.A.; Peinado, A.M. A Deep Learning Loss Function Based on the Perceptual Evaluation of the Speech Quality. IEEE Signal Process. Lett. 2018, 25, 1680–1684. [Google Scholar] [CrossRef]
- Toulis, P.; Airoldi, E. Asymptotic and finite-sample properties of estimators based on stochastic gradients. Ann. Stat. 2017, 45, 1694–1727. [Google Scholar] [CrossRef]
- Srivastava, Y.; MuraliShiv, V.; Dubey, R. A Performance Evaluation of Loss Functions for Deep Face Recognition. In Proceedings of the 7th National Conference on Computer Vision, Pattern Recognition, Image Processing, and Graphics, NCVPRIPG, Hubballi, India, 22–24 December 2019. [Google Scholar]
- Wang, S.; Tuor, T.; Salonidis, T.; Leung, K.; Makaya, C.; He, T.; Chan, K. Adaptive Federated Learning in Resource Constrained Edge Computing Systems. IEEE J. Sel. Areas Commun. 2019, 37, 1205–1221. [Google Scholar] [CrossRef]
- Xie, C.; Koyejo, O.; Gupta, I. Asynchronous Federated Optimization. In Proceedings of the OPT2020: 12th Annual Workshop on Optimization for Machine Learning, Online, 11–12 December 2020; pp. 1–11. [Google Scholar]
- Liu, Y.; Yu, J.J.Q.; Kang, J.; Niyato, D.; Zhang, S. Privacy-preserving traffic flow prediction: A federated learning approach. IEEE Internet Things 2020, 7, 7751–7763. [Google Scholar] [CrossRef]
- Qin, Y.; Matsutani, H.; Kondo, M. A Selective Model Aggregation Approach in Federated Learning for Online Anomaly Detection. In Proceedings of the 2020 International Conferences on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData) and IEEE Congress on Cybermatics (Cybermatics), Rhodes, Greece, 20 November 2020. [Google Scholar]
- Chen, T.; Giannakis, G.B.; Suny, T.; Yin, W. LAG: Lazily Aggregated Gradient for Communication Efficient Distributed Learning. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Li, S.; Cheng, Y.; Liu, Y.; Wang, W.; Chen, T. Abnormal Client Behavior Detection in Federated Learning. In Proceedings of the 2nd International Workshop on Federated Learning for Data Privacy and Confidentiality (NeurIPS 2019), Vancouver, BC, Canada, 13 December 2019; pp. 1–7. [Google Scholar]
- Ek, S.; Portet, F.; Lalanda, P.; Vega, G. Evaluation of Federated Learning Aggregation Algorithms with Application to Human Activity Recognition. In Proceedings of the UbiComp-ISWC ‘20: Adjunct Proceedings of the 2020 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2020 ACM International Symposium on Wearable Computers, Online, 12–17 September 2020; pp. 638–643. [Google Scholar]
- Arivazhagan, M.; Aggrarwal, V.; Singh, A.; Choudhary, S. Federated Learning with Personalization Layers. In Proceedings of the AISTATS 2020: The 23rd International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020. [Google Scholar]
- Ye, Y.; Li, S.; Liu, F.; Tang, Y.; Hu, W. EdgeFed: Optimized Federated Learning Based on Edge Computing. IEEE Access 2020, 8, 209191–209198. [Google Scholar] [CrossRef]
- Nishio, T.; Yonetani, R. Client Selection for Federated Learning with Heterogeneous Resources in Mobile Edge. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–7. [Google Scholar]
- Huang, L.; Yin, Y.; Fu, Z.; Zhang, S.; Deng, H.; Liu, D. LoAdaBoost: Loss-based AdaBoost federated machine learning with reduced computational complexity on IID and non-IID intensive care data. PLoS ONE 2020, 15, e0230706. [Google Scholar] [CrossRef]
- Li, Τ.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated Optimization in Heterogeneous Networks. In Proceedings of the 3rd MLSys Conference, Austin, TX, USA, 2–4 March 2020; pp. 1–22. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Hodge, V.; Austin, J. A Survey of Outlier Detection Methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Definition of AdaGrad Optimizer. Available online: https://optimization.cbe.cornell.edu/index.php?title=AdaGrad (accessed on 20 April 2020).
- Definition of RMSProp Optimizer. Available online: https://optimization.cbe.cornell.edu/index.php?title=RMSProp (accessed on 20 April 2020).
- Bengio, Y. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Definition and Description of Tensorflow Environments. Available online: https://www.tensorflow.org/ (accessed on 20 April 2020).
- Definition of Keras Library of Tensorflow. Available online: https://www.tensorflow.org/api_docs/python/tf/keras (accessed on 20 April 2020).
- Definition of HDF5 File Format. Available online: https://www.hdfgroup.org/solutions/hdf5/ (accessed on 20 April 2020).
- Definition and Description of Docker Environments. Available online: https://www.docker.com/ (accessed on 20 April 2020).
- DeGroot, M.H. Optimal Statistical Decisions; McGraw-Hill Book Co.: New York, NY, USA, 1970; p. 232. [Google Scholar]
- Mood, A.; Graybill, F.; Boes, D. Introduction to the Theory of Statistics; McGraw-Hill: New York, NY, USA, 1974; p. 229. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Sungil, K.; Heeyoung, K. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2006, 32, 669–679. [Google Scholar] [CrossRef]
- Tofallis, C. A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation. J. Oper. Res. Soc. 2015, 66, 1352–1362. [Google Scholar] [CrossRef]
- Armstrong, J.S.; Collopy, F. Error measures for generalizing about forecasting methods: Empirical comparisons. Int. J. Forecast. 1992, 8, 69–80. Available online: https://econpapers.repec.org/RePEc:eee:intfor:v:8:y:1992:i:1:p:69-80 (accessed on 9 February 2021). [CrossRef]
- Makridakis, S. Accuracy measures: Theoretical and practical concerns. Int. J. Forecast. 1993, 9, 527–529. [Google Scholar] [CrossRef]
- Goodwin, P.; Lawton, R. On the asymmetry of the symmetric MAPE. Int. J. Forecast. 1999, 15, 405–408. [Google Scholar] [CrossRef]
- Alkhabbas, F.; Alawadi, S.; Ayyad, M.; Spalazzese, R. ART4FL: An Agent-based Architectural Approach for Trustworthy Federated Learning in the IoT. In Proceedings of the 8th IEEE International Conference on Fog and Mobile Edge Computing, Washington, DC, USA, 26–28 June 2021; pp. 1–7. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning Research in Deep Learning; The MIT Press: London, UK, 2016; pp. 475–710. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).