Abstract
Multiple unmanned aerial vehicle (multi-UAV) systems have gained significant attention in applications, such as aerial surveillance and search and rescue missions. With the recent development of state-of-the-art multiagent reinforcement learning (MARL) algorithms, it is possible to train multi-UAV systems in collaborative and competitive environments. However, the inherent vulnerabilities of multiagent systems pose significant privacy and security risks when deploying general and conventional MARL algorithms. The presence of even a single Byzantine adversary within the system can severely degrade the learning performance of UAV agents. This work proposes a Byzantine-resilient MARL algorithm that leverages a combination of geometric median consensus and a robust state update model to mitigate, or even eliminate, the influence of Byzantine attacks. To validate its effectiveness and feasibility, the authors include a multi-UAV threat model, provide a guarantee of robustness, and investigate key attack parameters for multiple UAV navigation scenarios. Results from the experiments show that the average rewards during a Byzantine attack increased by up to 60% for the cooperative navigation scenario compared with conventional MARL techniques. The learning rewards generated by the baseline algorithms could not converge during training under these attacks, while the proposed method effectively converged to an optimal solution, proving its viability and correctness.
1. Introduction
Multi-UAV systems have emerged as an essential research field in the past decade and are increasingly being widely used in applications like target tracking, traffic monitoring, fire detection, crop monitoring, and search and rescue operations, which require team formation and coordination [1,2,3,4,5]. The advantages of multi-UAV systems are manifold, including but not limited to improved coverage, increased mission robustness, and enhanced data collection capabilities. Multi-UAV systems can accomplish complex tasks within complex environments, which are far beyond the capabilities of single-UAV solutions. Due to the unpredictability and dynamic nature of the mentioned tasks, a predefined solution may not always be guaranteed to perform well. Therefore, data-driven learning-based methods are extremely useful to generate an optimal and workable solution to these tasks. Multiagent reinforcement learning, which inherently learns from agent interactions and handles high-dimensional continuous state spaces, offers a promising approach to tackling complex decision-making problems. It enables UAVs to learn from interactions with the environment, receive feedback in the form of rewards or penalties, and improve their performance over time through trial and error.
Unfortunately, recent studies have exposed the vulnerability of UAVs to a range of attacks, compromising their integrity, security, and ultimately, the performance of multi-UAV systems [6,7,8,9,10]. In many multi-UAV applications, agent coordination is achieved through timely communication and data transfer, including information such as location coordinates, velocity, and direction. If any agent is compromised by a malicious attacker, it can transmit corrupted data to other agents within the team, influencing their actions and manipulating group behavior. A malicious agent can strategically disrupt the task execution of a multiagent system by relaying corrupted messages to unsuspecting agents within its network. Such cyberattacks against multiagent systems can result in significant financial losses, jeopardize critical missions, and damage an organization’s reputation. Therefore, it is crucial for agent-based systems in distributed networks to ensure a sufficient level of security for large-scale deployment. Previous research has addressed security vulnerabilities in multiagent systems, emphasizing membership authorization, authentication, access control, trust management, and protection against security threats [11,12]. In addition, there have been instances where intruders with malicious intent intercepted communication signals from drones and manipulated them to compromise the intended mission. To address these security concerns, Brust et al. [13] proposed a defense UAV system consisting of a swarm of good UAV agents that can detect a malicious UAV and subsequently escort it outside of the flight zone. However, a malicious UAV can often evade detection by pretending to be a good agent and subtly manipulating communication signals with minor biases. As such, a robust and comprehensive approach is necessary to make the multiagent system resilient to malicious agents, even when they remain undetected.
While current research primarily focuses on well-known threats to UAVs, such as GPS jamming, spoofing, deauthentication attacks, denial of service, and data interception attacks [14,15], the risks associated with Byzantine attacks on multi-UAV systems have not been fully investigated. With the increasing adoption of UAV teams for security and military applications, Byzantine attacks pose a significant threat. In a Byzantine attack, a dishonest agent masquerades as an honest agent and compromises the integrity of the multiagent system by disseminating inaccurate information. The classical Byzantine general’s problem, introduced by [16], emphasizes the need for a reliable system that can function even when some components fail. This problem inspired the development of Byzantine fault tolerance (BFT) systems, which protect distributed networks against such threats and enhance system resilience. The authors acknowledge that Byzantine attacks can severely impact the learning performance of agents in multi-UAV applications, as demonstrated by the simulated experiments. Therefore, it is imperative to address this vulnerability and promptly mitigate the risks associated with Byzantine attacks in multiagent reinforcement learning environments.
The proposed method seeks to protect multi-UAV systems from a potential Byzantine attack in a MARL environment and is based on the preliminary work published in [17]. Typical multi-UAV systems lack a consensus model that can tolerate even a single Byzantine failure. The cybersecurity risks involved with such systems inspired us to find a solution that can adequately handle a few malicious agents without compromising the safety and objective of the entire multiagent system. The authors propose a three-step approach based on a geometric median consensus model and a robust state update model based on perceived threat in the system to provide resiliency against corrupted data from Byzantine agents in the multiagent environment.
The key contributions in this work that underscore the distinctions from the previous work in [17] are summarized below:
- To ensure that the proposed method will perform reliably and consistently under all conditions, the current work provides a theoretical guarantee of robustness against Byzantine attacks during MARL training.
- The present work includes a Byzantine threat model from a multi-UAV system perspective to identify the associated risks. This is particularly relevant in decentralized and distributed multi-UAV systems, where the assumption of malicious or faulty agents is essential for ensuring their integrity.
- Additional studies and experiments are conducted to analyze the impact of key attack parameters on learning performance during a Byzantine attack. The present work also examines whether the proposed method can mitigate Byzantine attacks when attack parameters are varied.
The rest of the paper is organized as follows: In Section 2, the authors review prior work related to vulnerabilities in UAVs and Byzantine fault tolerance. In Section 3, the authors discuss some background on multiagent reinforcement learning and multi-UAV cooperative navigation. The authors then provide the problem definition in Section 4 and introduce the threat model considered in Section 5. The work proposes a Byzantine-resilient MARL model in Section 6, followed by Section 7, which details the implementation of this model in multi-UAV navigation scenarios. The results are discussed in Section 8, and finally, the findings and contribution of this paper are summarized in Section 9.
2. Literature Review
2.1. Secure Mechanisms in Multi-UAV Systems
As civilian drones continue to be integrated into the national airspace, the rising number of cyberattacks against against UAV networks is a cause for concern [18]. Recently, several authentication mechanisms have been proposed to address security vulnerability [19,20,21]. De Melo et al. [19] proposed UAVouch to identify malicious UAVs operating in a multi-UAV system. Their proposed method used a combination of public key authentication and location validation, and identified position falsification attacks during military surveillance with an accuracy of over . Walia et al. [20] proposed a mutual authentication technique to detect fake identities in a flying ad hoc network (FANET) due to Sybil attacks. Similarly, the authors in [21] proposed a lightweight authentication scheme (iTCALAS) to protect drones from traceability and stolen verifier attacks during surveillance operations.
Trust management mechanisms have been considered by some authors to detect malicious UAVs [22,23,24]. Keshavarz et al. [22] proposed a trust monitoring framework that can detect DDoS and GPS spoofing attacks by observing task completion, path deviation, and energy consumption characteristics of UAVs. Similarly, the authors in [24] proposed an algorithm based on linear regression to determine the trust value of nodes for detecting malicious nodes in FANETs. Both authentication and trust management are important security mechanisms, but they cannot protect protect multi-UAV systems from more complex attacks. For example, Byzantine attacks are performed by nodes that are fully trusted and that have already been authenticated and verified in the system. In such instances, authentication or trust mechanisms cannot be relied upon to provide the integrity of information.
2.2. Byzantine-Tolerant Machine Learning
Traditional distributed machine learning assumes the integrity of the training participants and the reliability of the data used for training, lacking the capability to handle adversarial behaviors. In recent years, a surge of research has emerged in this field that takes into account the presence of adversaries. Some of these studies have specifically focused on the tolerance of Byzantine failures, along with the associated complex issues [25]. Numerous Byzantine fault-tolerant (BFT) approaches in machine learning rely on filtering schemes that necessitate robust aggregation rules. Blanchard et al. [26] investigated the ability of a distributed stochastic gradient descent (SGD) learning model to withstand a Byzantine adversary. Their findings revealed that no linear combination of gradients can tolerate even a single Byzantine adversary during the learning process. As a result, they proposed the Krum aggregation rule, which satisfies the Byzantine resilience property for the distributed stochastic gradient descent method. However, it should be noted that their approach does not achieve linear time complexity, unlike aggregation rules employing the geometric median as a consensus. In a similar vein, Xie et al. [27] conducted a comparison of three median-based aggregation rules for distributed synchronized SGD models that exhibit Byzantine resilience under specific conditions. The notable advantage of these median-based aggregation rules over the previous method is the ability to aggregate without requiring precise knowledge of the number of Byzantine attackers present in the distributed system. Although these techniques make significant strides in addressing the challenges posed by adversaries, there is still room for advancements to enhance their scalability, efficiency, and adaptability in real-world scenarios.
2.3. Byzantine Fault Tolerance in Multi-UAV Systems
While Byzantine fault tolerance has received significant attention in distributed machine learning research, its application to mitigate Byzantine attacks in multi-UAV systems has been limited to only a few works [28,29,30,31,32,33]. Its practical implementation in real-world scenarios has been relatively unexplored in the literature. Some of recent studies propose the utilization of blockchain technologies to achieve consensus in the presence of malicious agents. Strobel et al. [28] exploited blockchain-based smart contracts to develop a consensus protocol that can prevent Byzantine and Sybil attacks on a swarm of robots. Although the idea of blockchain-based consensus protocols is exciting, the energy cost for the verification of blockchain transactions is very high. Therefore, this is not ideal for message transactions between UAVs that are limited in power supply and require a fast response time. Furthermore, scalability and storage requirements for blockchains in multi-UAV systems remain an issue because the addition of more agents into the multi-UAV system increases the size of the blockchain, and this can exhaust the limited memory storage in UAVs. Bing et al. [29] proposed a spectrum sensing method for UAVs based on isolating cognitive radio nodes that can mitigate the influence of Byzantine attacks. Although the proposed method can sufficiently resist Byzantine attacks, its effectiveness and application are just limited to deception attacks in cognitive radio networks. More recently, the authors in [31] provided proof of work for the implementation of Byzantine fault tolerance in UAV swarm exploration tasks using a BFT consensus mechanism. However, implementation was limited to cooperative tasks only with predefined Byzantine agents, and the performance of their approach in multiagent competitive environments or with an undetermined number of Byzantine agents is not known. A comparison of the related works is listed in Table 1 for reference. With the adversarial attacks and defenses constantly evolving with time, BFT in a multi-UAV system remains an active area of research.

Table 1.
Comparison of works related to secure mechanisms in multi-UAV systems.
3. Related Background
3.1. Multiagent Reinforcement Learning
In recent years, multiagent reinforcement learning (MARL) has emerged as a highly successful approach for addressing decision-making problems in machine learning [34,35]. In MARL, the agents with the environment can either collaborate with each other towards a common goal in a cooperative scenario, or compete against each other in a competitive scenario. Advancements such as the advantage actor critic model (A2C), deep deterministic policy gradient model (DDPG), and multiagent actor–critic model (MADDPG) have shown significant promise in tackling various decision-making challenges [36,37,38].
The framework of multiagent reinforcement learning can be characterized as a Markovian game between N agents operating in a configuration state space defined by . Each agent in the environment can choose an action from a set of actions based on a set of observations through a policy defined by a policy , where is the policy parameter for agent i in the environment. The state transition function is defined as and each agent gets a reward defined by the reward function on the transition to the next state. The aim of each agent is to maximize its expected return over time which is given by
where is the discount factor of the agent’s reward.
Using the policy gradient theorem, the gradient of the expected return can be written as
where is an action-value function. For each agent, the function outputs a Q-value based on the actions and observations of all the other agents.
The centralized action-value function () is then updated according to the policy gradient Equation (2). The action value function is learned by minimizing the regression loss function as given below:
where
3.2. Navigation Model for Multi-UAV Systems
A multi-UAV system can be mathematically represented using the fundamentals of graph theory. Let the information exchange within a multi-UAV system be represented by an undirected graph , where the vertices correspond to a team of dynamic UAVs and the edges correspond to the possibility of information transmission between two UAVs.
The adjacency matrix (A) tells us whether two UAVs in the multiagent system are adjacent enough to create a communication link between them.
The degree matrix (D) is used to represent the number of adjacent UAVs for a given UAV
where is the number of connected links for the agent .
The Laplacian matrix () is given by
The above Laplacian matrix associated with graph G is symmetric for undirected graphs and relates to useful properties of multiagent networks. In many multi-UAV systems, sensors on the UAV can only measure the relative position and velocity of adjacent UAVs with respect to itself. In such systems, agent i can only access information about the relative states of adjacent agents rather than the global states. The relative state of agent i can be written as
This relative information () along with the associated Laplacian of the graph () can then be used in a feedback control system for multiagent coordination between agents.
Assuming a team of n homogenous UAVs moving on a horizontal plane, the state vector can be represented as , where and are planar positional coordinates of agent i and is the angle of heading direction. The motion model is then given by
where is the linear velocity and is the angular velocity of the i-th robot and is the control input. The objective for centralized co-operative localization is to estimate the full state vector of the system, i.e.,
Although the motion model defined is for a 2-D planar movement, a similar approach can be used to extend the model for a 6-degree-of-freedom system like a multirotor quadcopter. To estimate the state vector using EKF, the motion Jacobian is given by
For the cooperative navigation problem, the agents in the multi-UAV system share their relative heading direction () and range distances (r) with all the adjacent agents for the state estimation .
The range distance () between agents i and j is given by
Furthermore, the relative bearing measurements or heading direction () equation is given by
4. Problem Definition
Let us consider a multiagent system of N agents with a state update model in a discrete time step, . Suppose each agent has a state observation model as
where is the measurement vector, is the observation matrix of agent j, is the state vector that needs to be estimated, and is the measurement noise. At each time step k, the current state of the multiagent system is approximated based on the information obtained from all the other agents in the environment. If denotes the estimated state of the multiagent system, should be to be as close to the true state as possible for an accurate state update model. By the definition of omniscience presented in [39], the estimated state asymptotically converges to the true state of the agents if the following condition holds:
Thus, given a set of adversaries b within a multiagent system with N agents, the problem definition is to find a resilient algorithm for a state update such that the condition given by Equation (15) holds. Generally, a minimizer function such as the least square formulation is used to estimate the state vector [40]
where is the collective state measurement and is the collective observation from N agents.
However, in the presence of a Byzantine attack, a malicious agent can modify his/her state measurement from its true value () to an altered value (). The attacker can then send the altered state measurement () instead to other unsuspecting agents, in which case, the above function (16) will not be minimized and state estimation will be far from accurate. Consequently, a more robust approach is needed to tolerate Byzantine adversaries in the multiagent system.
5. Threat Model
For the threat model, let the communication process within a multiagent system be represented by a communication graph . Each agent relies on the exchange of information from other agents through the set of links in to update the state of the multiagent system. The authors consider the possibility that there may be a set of dishonest nodes () that are acting as Byzantine adversaries. The authors also assume that these Byzantine adversaries can alter the information that they are sending to other nodes in by any arbitrary value to deceive the multiagent system.
Security threat and Byzantine agent: From a multi-UAV system perspective, the current work defines any threat that can hinder the learning capabilities of UAVs, leading to an inaccurate predictive model for a specific task, as a vulnerability within the system (Figure 1). In this work, the authors focus on resolving Byzantine attacks in the multi-UAV system. Specifically, a Byzantine attack in the multi-UAV system implies that one or more of the UAVs act arbitrarily and deviate from the prescribed protocols. If any UAV behaves in this manner, it is considered as a Byzantine agent, posing a security threat to the entire multiagent system.
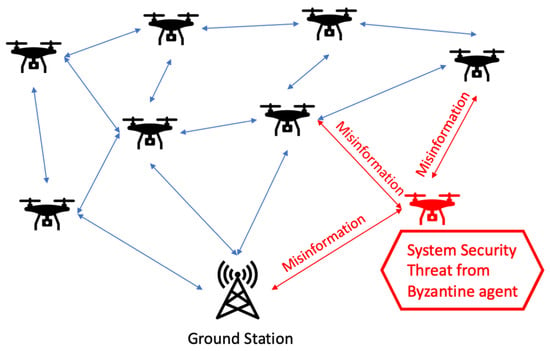
Figure 1.
Threat model for a multi-UAV system with Byzantine agents.
Within the multi-UAV system, the Byzantine agents will intentionally transmit corrupted or false state observations to other neighboring UAVs with the goal of hindering the learning performance of the agents. To ensure the system’s resilience against Byzantine attacks, it is relied on a consensus among the participating agents. It is assumed that the majority of the agents within the learning environment are inherently honest in their behavior.
Colluding adversaries: Most of the existing literature makes an explicit assumption that Byzantine adversaries act independently during malicious attacks, meaning that they do not collude with one another. However, in reality, Byzantine agents may choose to collaborate, increasing their chances of success in an attack. For instance, considering a scenario where b Byzantine agents send random state vectors for a consensus, achieving consensus in a specific direction becomes challenging due to their noncooperative strategies. However, when colluding adversaries work together, they can influence the consensus by sending multiple state vectors in the same direction.
For simplicity, this work assumes that attackers in the multiagent system act independently. This means that the Byzantine adversaries () do not collude with each other during an attack. Additionally, the authors assume a synchronous state update model here. Moreover, the authors in this work adopt an f-total adversarial model [41], which means that the multiagent graph () can tolerate a maximum of f-adversaries within ().
6. Methodology
The proposed method introduces a Byzantine-resilient integrity model (Figure 2) into the MARL framework to effectively defend against Byzantine attacks while still enabling the agents to learn an optimal behavior. This additional model serves the purpose of achieving consensus on the information shared among all agents. In the navigation experiments, this shared information encompasses the states of agents observed by each UAV within the multiagent environment. The model takes as input the agents’ state information, which may or may not be compromised, and produces a consensus for all the states. Importantly, this model guarantees that even if one or more agents disseminate corrupted information about agent states, the updated agent states in the MARL model remain unbiased unless more than half of the agents engage in malicious behavior.
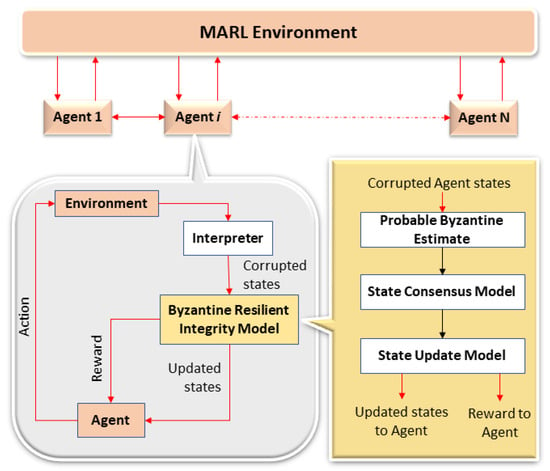
Figure 2.
Proposed model for Byzantine resilience in the MARL environment.
6.1. Proposed Method
In the presence Byzantine adversaries, a concise three-step approach is outlined below to address the MARL problem.
- Potential Byzantine estimate: Based on the average rewards and the instances of penalties accrued in each training episode, an estimation is made for the potential number of Byzantine agents present within the MARL environment.
- State consensus model: Each agent observes its neighboring agents and communicates their states with the other agents in the environment. A consensus on all agents’ states is then derived from these observations using a geometric median aggregation method. This consensus method ensures a resilient state estimate, maintaining its reliability as long as the proportion of malicious agents within the MARL environment remains below the breakdown point of .
- State update model: Finally, each agent adjusts the state consensus, depending on the potential presence of Byzantine agents in the environment. In the presence of a Byzantine threat, greater weight is attributed to an agent’s own direct observations, signifying a higher level of self-trust compared with observations from other agents. Conversely, when there is no suspicion of a Byzantine threat, both direct and indirect observations are equally trusted. This allocation of weightage to direct and indirect observations further enhances the robustness of the consensus model.
6.2. Byzantine-Resilient MARL Algorithm
As outlined above, the authors introduce an algorithm designed for robust multiagent learning in the presence of Byzantine agents. Algorithm 1 provides an elaborate representation of the steps involved.
| Algorithm 1 Byzantine-resilient multiagent reinforcement learning. |
|
Let us consider a multiagent navigation scenario in which N agents are being trained to navigate in the environment with the help of reinforcement learning. Agents can interact with peers and choose their action in this environment based on a policy that maximizes the agents’ total reward. However, prior to the policy gradient update, the user estimates the potential number of Byzantine agents based on observed rewards and penalties due to the agents’ actions (lines 10–13, Algorithm 1). This estimation, although approximate, operates under the assumption that remarkably low rewards and high penalties in the MARL environment are a consequence of the actions of Byzantine agents. This simplifies the removal of agents from the consensus model when their actions raise suspicions. If the user suspects agents out of N total agents to be Byzantine, the algorithm then proceeds to determine a consensus regarding observed states, using the geometric median convergence function among agents (line 15, Algorithm 1). Finally, the resilience of this algorithm is bolstered further by implementing the state update model as discussed in Section 6.1 to give us a robust state estimation even in the presence of adversaries.
6.3. Robustness Guarantee
To guarantee robustness against a Byzantine adversary during training, the agents in the MARL environment must be able to reach a consensus for observed states even in the presence of Byzantine observations. The agents use a geometric median consensus for agreement on observations from other agents in the environment. The geometric median is a robust estimator used in many aggregation methods. Let us consider a set of multidimensional vectors . Then its geometric median can be mathematically defined as
where denotes the Euclidean norm. For a noncollinear set of vectors , their geometric median is always unique.
The robustness property of the geometric median estimator has been stated in a few previous works [42,43] and can be validated through the following lemma from [42].
Lemma 1.
Suppose we consider a set of n points in a Hilbert space defined by and their geometric median is . For any and , if for , where
then a subset exists with such that .
The above lemma suggests that for a given set of points , if any arbitrary Byzantine point (z) is at a far distance from their geometric median , then that Byzantine point (z) is also at a far distance from a constant fraction of the given set of points. A complete proof for Lemma 1 can be found in [42] and included here for completeness.
Proof.
Let us denote . For the sake of argument, suppose that the converse is true. This means that . Let be the directional derivative at the point in the direction .
Since the point minimizes F over , . Additionally,
Now, if , then we have
If , then
which leads to a contradiction. Hence, the assumption cannot be true, and this concludes the proof. □
7. Experimental Scenarios
For demonstrating the effectiveness of Algorithm 1, two distinct navigation tasks are considered as illustrated in Figure 3. The two tasks are carried out in 2-D environments having continuous observations and discrete action spaces.
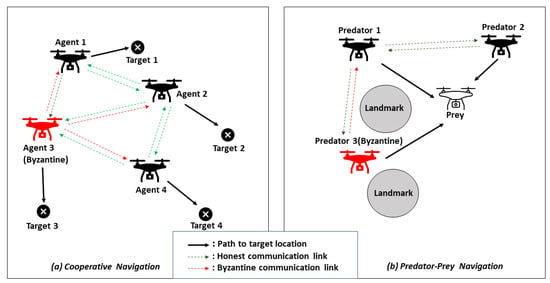
Figure 3.
Navigation scenarios with Byzantine agents.
- Cooperative navigation: In this task, each UAV collaborates with other agents to navigate toward a designated landmark, ensuring that all landmarks are covered. Agents receive collective rewards based on their proximity to any landmark (building) during each step. Penalties are incurred for collisions with other agents or landmarks. With sufficient training, the agents acquire the ability to reach their respective target landmarks by coordinating with one another.
- Predator–prey navigation: In this task, the MARL environment comprises a set of UAVs working in unison to capture an adversary with superior speed. Agents are rewarded for successfully intercepting the suspect (adversary) while facing penalties for collisions with one another. With sufficient training, agents learn to cooperate with other predator agents to navigate the environment and capture the prey agent.
The experiments with the proposed method use a 2-layered MLP (64 units, rectified linear unit activation) for the policy training, and the learning performance is compared with baseline methods [36,37,38]. Two kinds of attacks, namely, position bias and replacement in position [17], were considered during the evaluation.
Simulation Environment
The simulation environment used for these tasks are based on a set of communication-oriented environments adopted from the multiparticle environments (MPEs) [38]. It is dependent on OpenAI’s open-source Python library, Gym [44], for the implementation of reinforcement learning algorithms. Agents in the simulated environment are UAVs that have the ability to navigate, communicate, observe, and interact with each other. Targets are static locations that act as the goal position for an agent to reach, whereas landmarks are the static entities that the agents have to navigate around to reach their target. Each agent’s observation space consists of a vector consisting of the position and velocity of the agent, relative positions and velocities of other agents, relative positions of the landmarks, and received communications from cooperative agents. The action space is discrete, where agents are able to select any action to move left, right, up, or down with a specified velocity between 0.0 and 1.0 in any of the four directions. All the agents (benign and malicious) can transmit continuous values through various communication channels available in the environment.
The number of agents considered in simulation varied from a minimum of 3 to a maximum of 9 agents across all the scenarios. The agents were rewarded both globally and locally based on the task assigned. The ratio between the relative weights of the local and the global rewards was set to a value of . Initially, the agents were randomly placed at multiple locations across the map at the start of an episode. Each episode ran for a maximum number of steps for an agent specified by the maximum cycles parameter. The maximum cycles parameter was set to 25 for each episode. The simulation was run in a Python 3.8 environment using an Ubuntu 18.04 LTS operating system.
8. Results Analysis
The results of the MARL simulation experiments are presented below, wherein the learning performance of the proposed algorithm was analyzed during a Byzantine attack and compared against the baseline algorithms. Performance evaluation metrics for MARL depend on the specific objectives and characteristics of the multiagent system. The following performance metrics were used for the analysis of the results.
- Average reward: The average cumulative reward obtained by all agents over a set of episodes. It provides a measure of the overall performance of the agents.
- Individual agent reward: The reward achieved by each individual agent. This helps assess the contribution of each agent to the collective goal.
- Learning curve: Plots of cumulative reward over time or episodes, providing insights into how well agents learn and adapt.
8.1. Learning Performance
8.1.1. Cooperative Navigation
The first task examined a cooperative navigation scenario involving 9 agents and 9 landmarks. Three of the agents acted as Byzantine agents, transmitting corrupted positional data to their peers. In this attack, the relative positions of other agents and landmarks were compromised through the addition of a bias value drawn from a normal distribution (). To assess the learning performance in the training phase, the mean episode reward was calculated over 1000 iterations, and the average was plotted against the total no. of episodes trained. Figure 4a demonstrates the learning performance of the proposed algorithm. While the learning performance of the baselines (A2C, DDPG, and MADDPG) deteriorated over time due to the actions of Byzantine agents, the proposed algorithm achieved convergence to an optimal solution. The mean episode rewards in the proposed algorithm closely approximated those of a learning environment without any malicious agents. During the Byzantine attack, the average value of the reward for the proposed method taken over 5000 training episodes was −48, whereas the same for the baselines were −74 ([36]), −100 ([37]), and −121 ([38]). Thus, the proposed method showed an improvement of , , and over the algorithms in [36,37,38], respectively.
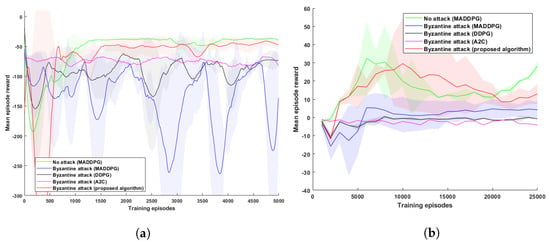
Figure 4.
MARL performance in multi-UAV navigation scenarios. (a) Cooperative navigation environment (no. of agents, ; no. of malicious agents, ; bias in corrupted data ()) (b). Predator–prey environment (3 predators, 1 prey, 1 malicious predator agent, bias in corrupted data ()).
It is noteworthy that the baseline algorithms, lacking resiliency mechanisms, struggled to maintain a consistently high reward and exhibited significant variance in performance between episodes. This was caused by false positional information from the malicious agent making benign agents choose actions that were detrimental to their cooperative strategies. This led to collisions between agents, resulting in them moving farther away from their expected target. On the other hand, the reward curve for the proposed algorithm with Byzantine resiliency followed close to the reward curve with no attack, suggesting that the effect of a Byzantine attack can be considerably mitigated.
8.1.2. Predator–Prey Navigation
The second task explored a predator–prey scenario featuring three predator agents and one prey. Among the predators, one agent was malicious and sending corrupted positional data to other agents. Just like the first scenario, the relative positions of other agents and landmarks were compromised through the addition of a bias value drawn from a normal distribution (). Figure 4b illustrates the learning performance of the proposed algorithm. Unlike the previous task, there is no clear convergence in this plot. Here, the predator agents and the prey learn from each other’s actions and adapt their learning policies continuously over time. Nonetheless, in the presence of Byzantine agents, the proposed algorithm outperformed the baselines with a higher episode reward. The average reward obtained by the agents for the proposed algorithm was 11, while that of [36,37,38] was −2, 1, and 3, respectively, during the predator–prey navigation training.
An interesting observation is the reduced variance in episode rewards compared with the cooperative navigation scenario. This can be attributed to the prey agent learning a suboptimal policy, leading it to move farther away from the predator agents. Consequently, it became challenging for the predators to catch up with the prey, resulting in relatively lower reward values.
8.2. Analysis of Key Attack Parameters
Further simulations were conducted to investigate the impact of various key components during a Byzantine attack. By systematically modifying specific parameters of an attack, this analysis aimed to assess their individual contributions to the overall performance of the proposed algorithm. The results of these studies provide insights into the significance of these components and help us understand their roles in achieving robustness against Byzantine attacks.
8.2.1. Number of Agents
Figure 5 shows a side-by-side learning comparison of the proposed algorithm with the baseline during the cooperative navigation scenario when the total number of agents was varied (). In each case, 40% of the total agents were malicious and sending corrupted data to other agents. During the Byzantine attack, the average reward obtained by the agents with the proposed algorithm (−6 for , −21 for , −33 for , −64 for ) was consistently higher than that of the baseline algorithm (−41 for , −62 for , −93 for , −122 for ). Since the simulations considered the same action space for all cases, the mean episode reward decreases as N increased due to more collisions in the action space. From the plot, it is evident that the proposed algorithm outperformed the baseline algorithm for all the four values of N considered.
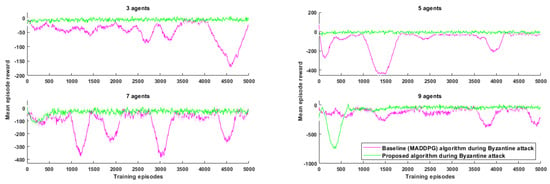
Figure 5.
Variation of total no. of agents: MARL performance in a cooperative navigation environment during an attack (40% malicious agents, bias in corrupted data ()).
8.2.2. Position Bias during Attack
The learning performance of the baseline algorithm degraded significantly during a position bias attack as the value of added bias was increased. A low positional bias () added by a malicious attacker may still cause the rewards to converge with degraded performance. On the other hand, the mean episode reward failed to converge entirely when a very high positional bias () was added by the attacker. With the baseline algorithm, the average reward obtained by the agents degraded from a value of −15 to values of −81, −93, −102, and −159 when the added position bias was increased gradually. However, it is clear from the plots in Figure 6 that the proposed algorithm was able to achieve convergence with a higher average reward value (−15) than the baseline for any added positional bias.
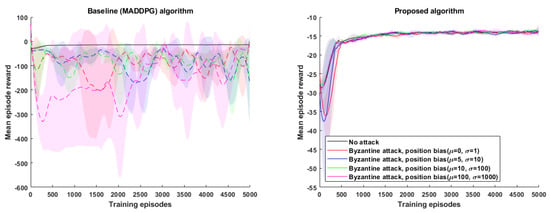
Figure 6.
Variation of position bias: MARL performance in a cooperative navigation environment (total no. of agents, ; malicious agents, ).
8.2.3. Number of Malicious Agents
In this experiment, the number of malicious attackers in the MARL environment was varied, and the performance of the proposed algorithm was evaluated during an attack scenario. The results, as depicted in Figure 7, showcase a side-by-side comparison with the baseline algorithm. Specifically, the simulation focused on a cooperative navigation scenario with agents and introduced a position replacement attack. The simulated attacks varied the percentage of malicious agents, examining cases where it was 20%, 40%, and 60% of the total number of agents, respectively. For the baseline algorithm, the average reward obtained by the agents degraded from a value of −17 without any malicious agent to values of −72, −85, and −59 with 20%, 40%, and 60% of the agents acting maliciously, respectively. However, with the exception of the case where 60% of the agents were malicious, the proposed algorithm consistently outperformed the baseline and demonstrated superior performance, with average rewards converging to an optimal value of −17. This outcome was anticipated since the proposed algorithm relies on a geometric median consensus model with a breakdown point of 0.5. This indicates that the algorithm achieves optimal convergence of mean episode rewards as long as fewer than 50% of the agents within the MARL environment are malicious.
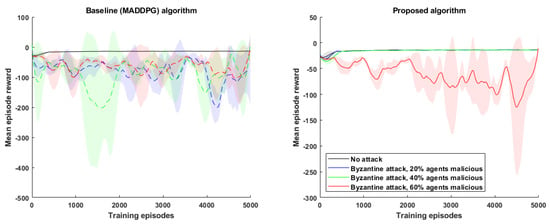
Figure 7.
Variation of the number of malicious agents: MARL performance in a cooperative navigation environment (total no. of agents, , bias in corrupted data ()).
9. Conclusions and Future Work
With the increasing integration of UAVs into multiagent systems for critical coordinated tasks, the vulnerability of UAVs to malicious threats, particularly Byzantine attacks, has become a significant concern. While multiagent reinforcement learning methods have been employed to tackle coordinated tasks, the presence of a Byzantine agent can severely disrupt the learning process. This paper proposed a resilient algorithm for multiagent reinforcement learning that effectively mitigates Byzantine attacks against the agents present in the environment. This resiliency is based on a geometric median consensus model that can sufficiently tolerate corrupted information from up to 50% of the total agents in the MARL environment. To demonstrate the practicality of the algorithm, the authors specifically focus on two multi-UAV use case scenarios based on cooperative navigation and predator–prey navigation, respectively. The results from the experiments illustrate how a Byzantine adversary can potentially result in the nonconvergence of agent rewards during the learning process. The learning rewards obtained by the agents during the simulated Byzantine attack show that the performance of the proposed algorithm surpassed the baseline MARL techniques by as much as 60% for the cooperative navigation scenario.
As cyber threats continue to evolve and attacks become more sophisticated, the current work can be extended in the future to handle complex scenarios and different types of attacks. For example, most of the Byzantine-resilient techniques assume that adversaries do not collude with each other during an attack. This is a very strong assumption to make because there is no such guarantee in real-world adversarial attacks. Colluding adversaries not only can degrade learning performance more severely, but also are very difficult to detect and identify in a multi-UAV system. In the future, addressing these challenges can further enhance the resiliency of multi-UAV systems against evolving cyber threats.
Author Contributions
Conceptualization, J.K.M.; Methodology, J.K.M.; Software, J.K.M.; Validation, X.C. and R.L.; Formal analysis, X.C. and J.K.M.; Data curation, J.K.M. and X.C.; Writing—original draft, J.K.M.; Writing—review & editing, X.C., R.L., Q.W. and J.K.M.; Visualization, X.C., R.L. and J.K.M.; Supervision, X.C.; Project administration, X.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wise, R.; Rysdyk, R. UAV coordination for autonomous target tracking. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6453. [Google Scholar]
- Elloumi, M.; Dhaou, R.; Escrig, B.; Idoudi, H.; Saidane, L.A. Monitoring road traffic with a UAV-based system. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Merino, L.; Caballero, F.; Martinez-de Dios, J.; Ollero, A. Cooperative fire detection using unmanned aerial vehicles. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 1884–1889. [Google Scholar]
- Cuaran, J.; Leon, J. Crop monitoring using unmanned aerial vehicles: A review. Agric. Rev. 2021, 42, 121–132. [Google Scholar] [CrossRef]
- Scherer, J.; Yahyanejad, S.; Hayat, S.; Yanmaz, E.; Andre, T.; Khan, A.; Vukadinovic, V.; Bettstetter, C.; Hellwagner, H.; Rinner, B. An autonomous multi-UAV system for search and rescue. In Proceedings of the First Workshop on Micro Aerial Vehicle Networks, Systems, and Applications for Civilian Use, Florence, Italy, 18 May 2015; pp. 33–38. [Google Scholar]
- Lin, J.; Dzeparoska, K.; Zhang, S.Q.; Leon-Garcia, A.; Papernot, N. On the Robustness of Cooperative Multi-Agent Reinforcement Learning. In Proceedings of the 2020 IEEE Security and Privacy Workshops (SPW), San Francisco, CA, USA, 21 May 2020; pp. 62–68. [Google Scholar] [CrossRef]
- Gleave, A.; Dennis, M.; Kant, N.; Wild, C.; Levine, S.; Russsell, S. Adversarial Policies: Attacking Deep Reinforcement Learning. arXiv 2020, arXiv:1905.10615. [Google Scholar]
- Rodday, N.M.; Schmidt, R.d.O.; Pras, A. Exploring security vulnerabilities of unmanned aerial vehicles. In Proceedings of the NOMS 2016–2016 IEEE/IFIP Network Operations and Management Symposium, Istanbul, Turkey, 25–29 April 2016; pp. 993–994. [Google Scholar]
- Lakew Yihunie, F.; Singh, A.K.; Bhatia, S. Assessing and exploiting security vulnerabilities of unmanned aerial vehicles. In Smart Systems and IoT: Innovations in Computing: Proceeding of SSIC 2019; Springer: Singapore, 2020; pp. 701–710. [Google Scholar]
- Dahiya, S.; Garg, M. Unmanned aerial vehicles: Vulnerability to cyber attacks. In Proceedings of the UASG 2019: Unmanned Aerial System in Geomatics 1; Springer: Cham, Switzerland, 2020; pp. 201–211. [Google Scholar]
- Cremonini, M.; Omicini, A.; Zambonelli, F. Multi-agent systems on the Internet: Extending the scope of coordination towards security and topology. In Proceedings of the European Workshop on Modelling Autonomous Agents in a Multi-Agent World, Valencia, Spain, 30 June–2 July 1999; pp. 77–88. [Google Scholar]
- Jung, Y.; Kim, M.; Masoumzadeh, A.; Joshi, J.B. A survey of security issue in multi-agent systems. Artif. Intell. Rev. 2012, 37, 239–260. [Google Scholar] [CrossRef]
- Brust, M.R.; Danoy, G.; Bouvry, P.; Gashi, D.; Pathak, H.; Gonçalves, M.P. Defending against intrusion of malicious uavs with networked uav defense swarms. In Proceedings of the 2017 IEEE 42nd Conference on Local Computer Networks Workshops (LCN Workshops), Singapore, 9 October 2017; pp. 103–111. [Google Scholar]
- Krishna, C.L.; Murphy, R.R. A review on cybersecurity vulnerabilities for unmanned aerial vehicles. In Proceedings of the 2017 IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR), Shanghai, China, 11–13 October 2017; pp. 194–199. [Google Scholar]
- Zhi, Y.; Fu, Z.; Sun, X.; Yu, J. Security and privacy issues of UAV: A survey. Mob. Netw. Appl. 2020, 25, 95–101. [Google Scholar] [CrossRef]
- Lamport, L.; Shostak, R.; Pease, M. The Byzantine Generals Problem. ACM Trans. Program. Lang. Syst. 1982, 4, 382–401. [Google Scholar] [CrossRef]
- Medhi, J.K.; Huang, C.; Liu, R.; Chen, X. Byzantine Resilient Reinforcement Learning for Multi-Agent UAV Systems. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 2472. [Google Scholar]
- Altawy, R.; Youssef, A.M. Security, privacy, and safety aspects of civilian drones: A survey. ACM Trans. Cyber-Phys. Syst. 2016, 1, 1–25. [Google Scholar] [CrossRef]
- De Melo, C.F.E.; e Silva, T.D.; Boeira, F.; Stocchero, J.M.; Vinel, A.; Asplund, M.; de Freitas, E.P. UAVouch: A secure identity and location validation scheme for UAV-networks. IEEE Access 2021, 9, 82930–82946. [Google Scholar] [CrossRef]
- Walia, E.; Bhatia, V.; Kaur, G. Detection of malicious nodes in flying ad-hoc networks (FANET). Int. J. Electron. Commun. Eng. 2018, 5, 6–12. [Google Scholar] [CrossRef]
- Ali, Z.; Chaudhry, S.A.; Ramzan, M.S.; Al-Turjman, F. Securing smart city surveillance: A lightweight authentication mechanism for unmanned vehicles. IEEE Access 2020, 8, 43711–43724. [Google Scholar] [CrossRef]
- Keshavarz, M.; Shamsoshoara, A.; Afghah, F.; Ashdown, J. A real-time framework for trust monitoring in a network of unmanned aerial vehicles. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 6–9 July 2020; pp. 677–682. [Google Scholar]
- Bai, J.; Zeng, Z.; Wang, T.; Zhang, S.; Xiong, N.N.; Liu, A. TANTO: An Effective Trust-Based Unmanned Aerial Vehicle Computing System for the Internet of Things. IEEE Internet Things J. 2022, 10, 5644–5661. [Google Scholar] [CrossRef]
- Tangade, S.; Kumaar, R.A.; Malavika, S.; Monisha, S.; Azam, F. Detection of Malicious Nodes in Flying Ad-hoc Network with Supervised Machine Learning. In Proceedings of the 2022 Third International Conference on Smart Technologies in Computing, Electrical and Electronics (ICSTCEE), Bengaluru, India, 16–17 December 2022; pp. 1–5. [Google Scholar]
- Bouhata, D.; Moumen, H. Byzantine Fault Tolerance in Distributed Machine Learning: A Survey. arXiv 2022, arXiv:2205.02572. [Google Scholar]
- Blanchard, P.; El Mhamdi, E.M.; Guerraoui, R.; Stainer, J. Machine learning with adversaries: Byzantine tolerant gradient descent. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Xie, C.; Koyejo, O.; Gupta, I. Generalized byzantine-tolerant sgd. arXiv 2018, arXiv:1802.10116. [Google Scholar]
- Strobel, V.; Castelló Ferrer, E.; Dorigo, M. Blockchain technology secures robot swarms: A comparison of consensus protocols and their resilience to byzantine robots. Front. Robot. AI 2020, 7, 54. [Google Scholar] [CrossRef] [PubMed]
- Bing, Y.; Wang, L.; Chen, Z. A Spectrum Sensing Method for UAV Swarms Under Byzantine Attack. In Proceedings of the International Conference on Autonomous Unmanned Systems, Changsha, China, 24–26 September 2021; pp. 1748–1758. [Google Scholar]
- Hacohen, S.; Medina, O.; Grinshpoun, T.; Shvalb, N. Improved GNSS localization and Byzantine detection in UAV swarms. Sensors 2020, 20, 7239. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Zhang, L.; Dong, Z. UAV Swarm Exploration With Byzantine Fault Tolerance. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 7150–7154. [Google Scholar]
- Kong, L.; Chen, B.; Hu, F. LAP-BFT: Lightweight Asynchronous Provable Byzantine Fault-Tolerant Consensus Mechanism for UAV Network. Drones 2022, 6, 187. [Google Scholar] [CrossRef]
- Hu, W.; Huo, X.; Zhang, Y. Research on UAV Swarm Technology Based on Practical Byzantine. In Proceedings of the 2022 5th International Conference on Machine Learning and Machine Intelligence, Xiamen, China, 23–25 September 2022; pp. 199–206. [Google Scholar]
- Busoniu, L.; Babuska, R.; De Schutter, B. A Comprehensive Survey of Multiagent Reinforcement Learning. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2008, 38, 156–172. [Google Scholar] [CrossRef]
- Terry, J.; Black, B.; Grammel, N.; Jayakumar, M.; Hari, A.; Sullivan, R.; Santos, L.S.; Dieffendahl, C.; Horsch, C.; Perez-Vicente, R.; et al. Pettingzoo: Gym for multi-agent reinforcement learning. Adv. Neural Inf. Process. Syst. 2021, 34, 15032–15043. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–June 24 2016; pp. 1928–1937. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning, Beijing, China, 22–24 June 2014; pp. 387–395. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Park, S.; Martins, N.C. Necessary and sufficient conditions for the stabilizability of a class of LTI distributed observers. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 7431–7436. [Google Scholar]
- Yang, Z.; Gang, A.; Bajwa, W.U. Adversary-resilient distributed and decentralized statistical inference and machine learning: An overview of recent advances under the Byzantine threat model. IEEE Signal Process. Mag. 2020, 37, 146–159. [Google Scholar] [CrossRef]
- Mitra, A.; Sundaram, S. Byzantine-resilient distributed observers for LTI systems. Automatica 2019, 108, 108487. [Google Scholar] [CrossRef]
- Minsker, S. Geometric median and robust estimation in Banach spaces. Bernoulli 2015, 21, 2308–2335. [Google Scholar] [CrossRef]
- Chen, Y.; Su, L.; Xu, J. Distributed statistical machine learning in adversarial settings: Byzantine gradient descent. Proc. ACM Meas. Anal. Comput. Syst. 2017, 1, 1–25. [Google Scholar] [CrossRef]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).