An Instance- and Label-Based Feature Selection Method in Classification Tasks

Abstract

Feature selection is crucial in classification tasks as it helps to extract relevant information while reducing redundancy. This paper presents a novel method that considers both instance and label correlation. By employing the least squares method, we calculate the linear relationship between each feature and the target variable, resulting in correlation coefficients. Features with high correlation coefficients are selected. Compared to traditional methods, our approach offers two advantages. Firstly, it effectively selects features highly correlated with the target variable from a large feature set, reducing data dimensionality and improving analysis and modeling efficiency. Secondly, our method considers label correlation between features, enhancing the accuracy of selected features and subsequent model performance. Experimental results on three datasets demonstrate the effectiveness of our method in selecting features with high correlation coefficients, leading to superior model performance. Notably, our approach achieves a minimum accuracy improvement of 3.2% for the advanced classifier, lightGBM, surpassing other feature selection methods. In summary, our proposed method, based on instance and label correlation, presents a suitable solution for classification problems.

1. Introduction

Classification is a fundamental task in machine learning, with diverse applications across various fields [1,2]. In this task, the inputs are typically represented as vectors. However, not all elements in a vector contain relevant or beneficial information for classification; some may even have a detrimental effect on the classification task. Therefore, the selection of informative elements within a sample is a topic of great interest among researchers [3,4,5,6].

By reducing feature dimensionality, feature selection significantly enhances model performance, reduces computational complexity, and improves the efficiency of data analysis and modeling processes [7]. On the other hand, manifold learning focuses on dimensionality reduction through manifolds. By assuming that data points are distributed along low-dimensional manifolds, manifold learning aims to decrease the dimensionality of the data while preserving local relationships [8]. This approach has proven particularly valuable in addressing high-dimensional nonlinear problems and attaining a clear representation of the data. Leveraging nonlinear mapping, manifold learning algorithms effectively map high-dimensional data to low-dimensional spaces, facilitating a more profound analysis of the underlying data structures [9].

Feature selection and manifold learning reduce data redundancy and maintain important features. Feature selection reduces dimensionality and removes irrelevant information during manifold learning. Manifold learning is able to analyze local structures and correlations in the lower feature space [10]. This integrated method improves data processing and modeling processes, improving following procedures.

In this paper, we propose a novel feature selection method that takes into account both instance correlation and label correlation. Our method involves using the least squares method [11] to calculate the linear relationship between each feature and the target variable. By fitting a linear model, we obtain weights for each feature. Features with higher weights or stronger correlations can be selected as the final subset. Regularization methods can further constrain feature selection and model complexity, finding an optimal subset with good generalization performance. In cases of sparsity, the $L_{2,1}$ norm is preferred for controlling non-zero coefficients due to its smoother nature and insensitivity to outliers. For exploring deep structural information of labels, introducing a separation variable captures label correlations and transforms the problem into a separable convex optimization problem. This approach preserves global and local structural information, improving performance. Consistency in label correlations is ensured by aligning the predicted label matrix with the ground truth label matrix and considering the similarity between adjacent instances. The objective function is optimized through the alternating direction multiplier method [12].

The main contributions are as follows:

• We introduce a novel unsupervised feature selection method that takes into account both instance correlation and label correlation, effectively mitigating the impact of noise in data.
• We improve performance by introducing a low-dimensional embedding vector to learn potential structural spatial information.
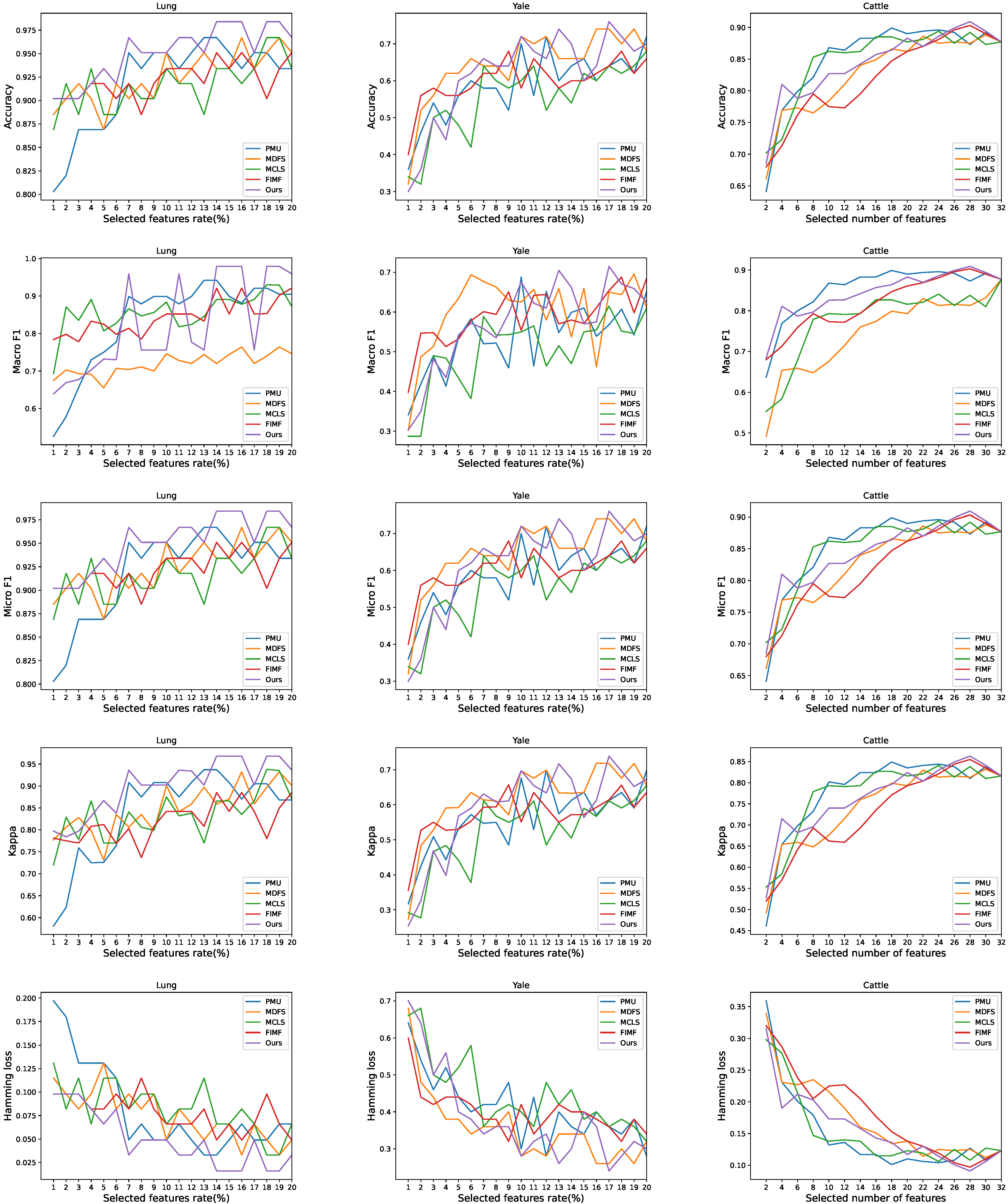
• Our method outperforms existing approaches like PMU, MDFS, MCLS, and FIMF, showing significant improvements in a series of experiments.

2. Related Work

Feature selection methods have a rich research history and can be broadly categorized into two approaches [3,4,7]. The first approach involves generating a new lower-dimensional vector by utilizing vector elements from existing samples. The second approach focuses on selecting specific elements from existing vectors to construct a new vector. These methods play a crucial role in reducing dimensionality and improving the efficiency of feature representation.

Principal component analysis [3,13] is a commonly used dimensionality reduction method that projects the original data onto a new coordinate system, retaining a minimal number of principal components to reduce the dimensionality while preserving important information from the original data. However, it also has some limitations. For example, it cannot consider class information, performs poorly on non-linearly distributed data, and is sensitive to outliers.

The newly generated vectors using the methods above may need to be more consistent with the original vectors. However, the chi-squared test can help to compensate for this deficiency. The chi-squared test [4,14] is used to select discrete features and target variables. Using the chi-squared statistic, it measures the correlation between the feature and the target variable. However, the test assumes independence between the feature and the target variable and may provide incorrect results if this assumption is not met. Additionally, small sample sizes may lead to unstable results.

In fact, each element in the feature vector of the sample is not completely independent, and they have correlation, which can be used to improve the effectiveness of feature selection. PMU [15] is a feature selection approach that leverages the mutual information between the selected features and the tag set. It can be applied to diverse classification problems. The experimental results validate the effectiveness of this method in improving classification performance. PMU proves to be a valuable and efficient tool for feature selection in classification problems. The feature subset $f^{+}$ is obtained by the following equation:

$$J=\tilde{I}(\{S,f^{+}\};L)-\tilde{I}(S;L),$$

(1)

where S denotes an input feature set, L denotes a label set, and $\tilde{I}(S;L)$ denotes the multivariate mutual information. FIMF [16] proposed a fast feature selection method based on information theory feature ranking to address the research gap in computationally efficient feature selection methods. The results indicate that the method significantly reduces the time required to generate feature subsets, particularly for large datasets, but its accuracy is limited. The objective function of FIMF is as follows:

$$J\left(f\right)={\tilde{V}}_2(f\times L_1^{{}^{\prime }})+\sum _{k=3}^{b+1}{(-1)}^k{\tilde{V}}_k(f\times Q_{k-1}^{{}^{\prime }}),$$

(2)

where f denotes a feature set; L denotes a label set; Q is a set of labels consisting of the highest-entropy labels.

$MCLS$ [17] uses manifold learning to transform the logical label space into a Euclidean label space and constrains the similarity between samples through corresponding numerical labels. The final selection criteria integrate both supervised information and the local properties of the data. The formula for computing the i-th feature is as follows:

$$MCL{S}_i=\frac{{\tilde{f}}_i^T\widehat{L}{\tilde{f}}_i}{{\tilde{f}}_i^T\widehat{D}{\tilde{f}}_i}·\frac{f_i^T{\widehat{L}}^M{f}_i}{f_i^T{\widehat{L}}^C{f}_i},$$

(3)

where $f_i$ denotes the i-th feature; L is a Laplacian matrix; D is a diagonal matrix. In order to reduce dimensionality and select relevant features, MDFS [18] proposed a manifold regularized embedded multi-label feature selection method. This method constructs a low-dimensional embedding that adapts to the label distribution, considers label correlations, and utilizes $L_{2,1}$ norm regularization for feature selection. The objective function of MDFS is as follows:

$$mi{n}_{F,W,b}Tr\left(F^{T}LF\right)+\left|\right|XW+1_n{b}^T-{F\left|\right|}_F^2+\alpha \left|\right|F-{Y\left|\right|}_F^2+\beta Tr\left(F{L}_0{F}^T\right)+{\gamma \left|\right|W\left|\right|}_{2,1},$$

(4)

where $\alpha ,\beta ,\gamma$ are hyperparameters. However, this method did not take into account the potential structural information contained in the label. This method has enlightening effects on our research.

3. Materials and Methods

In this section, we propose a novel unsupervised feature selection method. Subsequently, detailed explanations are provided on three components: notations, problem formulation, and optimization.

3.1. Notations

Considering the extensive derivation of formulas and symbol labeling in this paper,

Table 1. Explanation of professional terms.

No.	Definition	Description
1	$Tr\left(A\right)$	Trace of A
2	${\left|\right|A\left|\right|}_F$	F-norm of A
3	${\left|\right|A\left|\right|}_{2,1}$	2,1-norm of A
4	$A^T$	The transposition of A
5	$I_d$	D dimensional identity matrix
6	n	Number of samples
7	d	Number of features per sample
8	c	Number of categories
9	X	Feature vector
10	W	Weight matrix
11	V	Predicted label matrix
12	L	Laplacian matrix
13	Y	Ground truth label of dataset

is provided to present the symbols that may appear. It is assumed that A is an arbitrary matrix mentioned in the table.

3.2. Problem Formulation

In the process of feature selection, we use the least squares method to calculate the linear relationship between each feature and the target variable. By fitting a linear model, the weight of each feature can be obtained. Based on these weights, we can select features with high weight or correlation as the final feature subset, which can be used as the basis for feature selection. In addition, the least squares method is further extended through regularization methods to constrain feature selection and model complexity. This can help us to find the optimal subset of features with good generalization performance, improving the predictive ability and interpretability of the model. The basic formula is as follows:

$$mi{n}_{W,b}{\left|\right|XW+1_n{b}^T-Y\left|\right|}_F^2+{\alpha \left|\right|W\left|\right|}_p^2,$$

(5)

where p is the norm representation and W is a feature selection matrix, which is the key to solving the problem.

In feature selection, the $L_1$ norm is usually used to count the number of non-zero coefficients to encourage model selection to select sparse features. However, the $L_1$ norm is not ideal for selecting non-zero coefficients, as it tends to select some non-zero coefficients and compress other coefficients to zero without explicitly controlling the number of non-zero coefficients. In contrast, $L_{2,1}$ norm can better handle the sparsity of features. $L_{2,1}$ norm firstly calculates the sum of the $L_2$ norms of each feature vector, and then the $L_1$ norm is calculated for these results. The $L_{2,1}$ norm can better constrain the number of non-zero coefficients because it is smoother and insensitive to outliers. Since Y is a ground truth value label and a constant, and $1_n{b}^T$ is also a constant, they can be merged together. Therefore, the formula is simplified as follows:

$$mi{n}_{W,b}{\left|\right|XW-Y\left|\right|}_F^2+{\alpha \left|\right|W\left|\right|}_{2,1}^2.$$

(6)

The process of completing feature selection is that Y is approximate to $XW$, so $w^T{x}_i-w^T{x}_j$ is used to represent the distance, and $S_{ij}$ is used to describe the similarity between two vectors. Using this method can reduce the negative impact of noise in the original data and reduce the spatial dimension to reduce the computational cost. In this way, the instance association is increased and expressed by the following formula:

$$\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m\left|\right|w^T{x}_i-w^T{x}_j{\left|\right|}_2^2{S}_{ij}=Tr\left(W^T{X}^T(D-S)XW\right)=Tr\left(W^T{X}^{T}LXW\right)$$

(7)

where L is a Laplacian matrix, which can be obtained by multiplying the matrix of similarity S by the matrix of diagonals D, where $d_{ii}={\sum }_{j=0}^n{S}_i$. The detail is as follows:

$$S=\left\{\begin{array}{cc}{e}^{-0.5\frac{\left|\right|x_i-x_j{\left|\right|}_2^2}{{\sigma }^2}},\hfill & \mathrm{if}i\ne j;\hfill \\ 1,\hfill & \mathrm{if}i=j.\hfill \end{array}\right.$$

(8)

$$D={\left[\begin{array}{cccc}{d}_{11}& 0& \cdots & 0\\ 0& d_{22}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & d_{nn}\end{array}\right]}_{n\times n}$$

(9)

$$L=D-S$$

(10)

In order to explore the underlying structural information of the labels, we introduce a separate variable V for capturing label correlations. By incorporating the low-dimensional embedding V, the aforementioned problem is transformed into a separable convex optimization problem, which preserves both global and local structured information, thereby enhancing performance. To ensure consistent correlation of labels, the predicted label matrix V should match the ground truth label matrix Y, and the instances within matrix V should exhibit similarity when they are adjacent. Based on the aforementioned analysis, we have formulated an equation to describe the label correlation.

$$mi{n}_V\sum _{i=1}^n{E}_{ii}\sum _{j=1}^l{(V_{ij}-Y_{ij})}^2+\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{S}_{ij}\left|\right|v_i-v_j{\left|\right|}_2^2.$$

(11)

After conversion, it can be obtained that

$$mi{n}_{V}Tr[{(V-Y)}^{T}E(V-Y)]+Tr(V^{T}LV),$$

(12)

where E is a diagonal matrix with large numerical values for its elements. The two terms in this formula preserve global and local information, respectively. Given the correlation between matrix V and Y, it is crucial to enforce non-negativity of V in classification tasks to ensure its validity.

In summary, the ultimate objective function is formulated as:

$$\begin{array}{cc}\hfill & mi{n}_{W,V}\left|\right|XW-{V\left|\right|}_F^2+{\alpha \left|\right|W\left|\right|}_{2,1}^2+\beta Tr\left(W^T{X}^{T}LXW\right)+\hfill \\ \hfill & \gamma (Tr[{(V-Y)}^{T}E(V-Y)]+Tr(V^{T}LV)])s.t.V\ge 0,\hfill \end{array}$$

(13)

where $\alpha$, $\beta$, and $\gamma$ are hyperparameters. And then, we will optimize this objective function to obtain the solution to the problem.

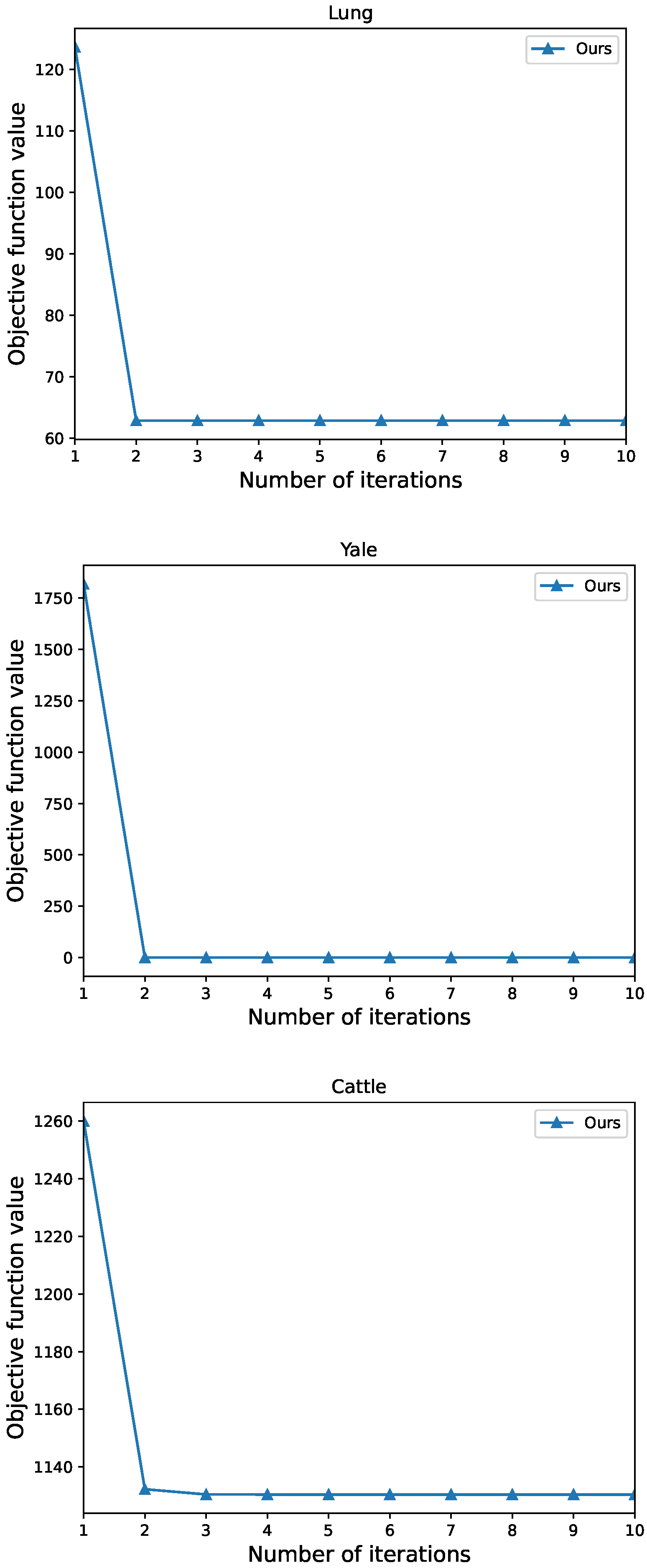
3.3. Optimization

We have designed an optimization algorithm for the designed objective function. The objective function can be transformed into:

$$\begin{array}{cc}\hfill & \Gamma =mi{n}_{W,V}Tr[{(XW-V)}^T(XW-V)]+\alpha Tr(W^{T}AW)+\beta Tr(W^T{X}^{T}LXW)+\hfill \\ \hfill & \gamma (Tr[{(V-Y)}^{T}E(V-Y)]+Tr(V^{T}LV)])s.t.V\ge 0,\hfill \end{array}$$

(14)

where A is a diagonal matrix with its elements defined as $\frac{1}{2}\left|\right|w^i{\left|\right|}_2$. Subsequently, we employ the alternating direction method of multipliers to solve the aforementioned problem.

3.3.1. Solve W as given V

By setting the partial derivative $\frac{\partial \Gamma }{\partial W}=0$, we can obtain

$$\begin{array}{cc}\hfill & \frac{\partial (Tr\left[{(XW-V)}^T(XW-V)\right]+\alpha Tr\left(W^{T}AW\right)+\beta Tr\left(W^T{X}^{T}LXW\right))}{\partial W}=0\hfill \\ \hfill & \Rightarrow X^{T}XW-X^{T}V+\alpha \mathrm{\Lambda }W+\beta X^{T}LXW=0\hfill \\ \hfill & \Rightarrow W={(X^{T}X+\alpha \mathrm{\Lambda }+\beta X^{T}LX)}^{-1}{X}^{T}V,\hfill \end{array}$$

(15)

$$\mathrm{\Lambda }={\left[\begin{array}{cc}\frac{1}{2\left|\right|w_1{\left|\right|}_2+\epsilon }& \\ & \frac{1}{2\left|\right|w_2{\left|\right|}_2+\epsilon }& \\ & & \ddots & \\ & & & \frac{1}{2\left|\right|w_d{\left|\right|}_2+\epsilon }\end{array}\right]}_{d\times d},$$

(16)

where $\epsilon$ represents a non-zero constant that serves the purpose of safeguarding the algorithm against potential crashes caused by a denominator equal to zero.

3.3.2. Solve V as given W

By setting the partial derivative $\frac{\partial \Gamma }{\partial V}=0$, we can obtain

$$\begin{array}{cc}\hfill & \frac{\partial (Tr\left[{(XW-V)}^T(XW-V)\right]+\gamma (Tr\left[{(V-Y)}^{T}E(V-Y)\right]+Tr\left(V^{T}LV\right)])}{\partial V}=0\hfill \\ \hfill & \Rightarrow XW+V+\gamma (LV+EV-EY)=0\hfill \\ \hfill & \Rightarrow V={[\gamma (L+E)+I]}^{-1}(\gamma EY+XW),\hfill \end{array}$$

(17)

Therefore, the solution to this issue is illustrated by Equations (15) and (17). To attain the ultimate solution, it is recommended to iterate through the aforementioned procedure until convergence. The iterative algorithm is outlined in Algorithm 1.

Algorithm 1: The iterative optimization.
	Input: The feature matrix $\mathbf{X}\in R^{n\times d}$, label matrix $\mathbf{Y}\in R^{n\times c}$, and hyperparameters $\alpha$, $\beta$, $\gamma$.
	Output: The first K features obtained by sorting the results of ${\left|\right|W\left|\right|}_2$.
1	Initialization: Randomly initialize $W_0\in R^{d\times c}$, $V_0\in R^{n\times c}$ and E, set $\epsilon$ = 0.01.
2	Calculate L, $\mathrm{\Lambda }$ using Equation (10), Equation (16), respectively.
3	while not converged do
4			Calculate $W\leftarrow iteration\_W(X,\mathrm{\Lambda },L,V,\alpha ,\beta )$, update W by Equation (15).
5			Calculate $V\leftarrow iteration\_V(X,L,E,Y,W,\gamma )$, update V by Equation (17).
6			Calculate $\mathrm{\Lambda }\leftarrow iteration\_lambda(W,\epsilon )$, update $\mathrm{\Lambda }$ by Equation (16).
7	end
8	Sort $\left|\right|W_i{\left|\right|}_2$ in descending order and filter out the top K features from the sorted list.

4. Results and Discussion

4.1. Datasets

To evaluate and validate this method, these publicly available datasets were carefully selected, including well-known image dataset Yale and biological dataset Lung. In addition, Cattle dataset (https://www.kaggle.com/datasets/twisdu/dairy-cow, accessed on 1 August 2023) is also used, which is specifically curated for the task of cattle pose estimation, with pose classification serving as its downstream objective. Through thorough analysis of the relative positions of key points, the dataset enables an accurate determination of the cattle’s pose, thereby achieving the ultimate goal of precise pose classification. The detailed information of these datasets is presented in

Table 2. The detailed information of these datasets.

Datasets	Number of Samples	Number of Features	Number of Categories
Lung	203	3312	5
Yale	165	1024	15
Cattle	1800	32	3

. All datasets are divided into training and testing sets in a 7:3 ratio.

4.2. Evaluation Metrics

In this paper, to thoroughly evaluate the performance of all methods, we employed the following five evaluation metrics for comprehensive evaluation: accuracy, macro-$F_1$, micro-$F_1$, kappa [19], and Hamming loss [20].

• Accuracy

  $$accuracy(y,\tilde{y})=\frac{1}{n}\sum _{i=0}^{n-1}F(y,\tilde{y}),F(y,\tilde{y})=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}y\ne \tilde{y};\hfill \\ 1,\hfill & \mathrm{if}y=\tilde{y}.\hfill \end{array}\right.$$

  (18)
• Macro-$F_1$ and Micro-$F_1$

  $$\begin{array}{cc}\hfill & F_1=\frac{2\times Precision\times Recall}{Precision+Recall}\hfill \\ \hfill & Precision=\frac{TP}{TP+FP}\hfill \\ \hfill & Recall=\frac{TP}{TP+FN}\hfill \end{array}$$

  (19)

  where $TP$ is the number of positive samples correctly identified. $FP$ is the number of negative samples for false positives. $FN$ is the number of missed positive samples. To obtain the macro-$F_1$ score, first calculate the $F_1$ value for each individual category, and then compute the average of all $F_1$ values across all categories. After, calculate the overall accuracy and recall rate. Then, compute the $F_1$ value to obtain the micro-$F_1$ score.
• Kappa

  $$K=\frac{(p_o-p_e)}{1-p_e},$$

  (20)

  where $p_o$ refers to the empirical probability of agreement on the label assigned to any sample, also known as the observed agreement ratio. On the other hand, $p_e$ represents the expected agreement between annotators when labels are assigned randomly. To estimate $p_e$, a per-annotator empirical prior over the class labels is employed.
• Hamming loss

  $$L_{Hamming}(y,\tilde{y})=\frac{1}{n\ast c}\sum _{i=1}^{n-1}\sum _{j=0}^{c-1}P(y,\tilde{y}),P(y,\tilde{y})=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{y}_{i,j}\ne \widetilde{y_{i,j}};\hfill \\ 1,\hfill & \mathrm{if}{y}_{i,j}=\widetilde{y_{i,j}}.\hfill \end{array}\right.$$

  (21)

where y is a ground truth label and $\tilde{y}$ is a predicted label.

Accuracy is a widely used performance evaluation metric for classification tasks. It represents the proportion of correctly classified samples among all the classified samples. The micro-$F_1$ score considers the overall count of true positives, false negatives, and false positives across all categories, while the macro-$F_1$ score considers the $F_1$ score for each individual category and calculates their unweighted average. It is important to note that the macro-$F_1$ score does not consider the potential imbalance between different categories. The kappa coefficient is a measure used to assess consistency in testing. In the context of classification problems, consistency refers to the alignment between the model’s predicted results and the actual classification outcomes. It is calculated based on the confusion matrix and ranges between −1 and 1, with values typically greater than 0. Hamming loss is a metric utilized to analyze misclassification on individual labels. A lower value of this metric indicates better performance, as it signifies fewer misclassifications. The aforementioned set of five metrics is employed for evaluating the performance of the method.

4.3. Experimental Setup

To ensure a fair and unbiased evaluation of all methods, a traversal search strategy is adopted to select the hyperparameters for each method within the range of [0.1, 0.2, …, 1.0]. Additionally, feature selection was performed based on the magnitude of the feature number values in the dataset. Specifically, due to the number of features in the Lung and Yale datasets, a percentage-based filtering approach is employed, ranging from 1% to 20% in steps of 1%. Alternatively, the Cattle dataset, with only 32 features, undergoes feature selection based on the number of key points, ranging from 2 to 32 in steps of 2, taking into account their actual significance.

For the purpose of conducting experiments, the LightGBM classification algorithm [21] is employed, which is a highly performant framework for gradient-enhanced decision trees, which has been optimized and improved based on the GBDT library xgboost [22]. It boasts faster training speeds and lower memory consumption compared to traditional GBDT algorithms [23,24], utilizes a histogram-based algorithm, and introduces mutually exclusive feature bundling to enhance model performance. It also incorporates the GOSS training strategy, which selectively retains samples with larger gradients to expedite the training process. Based on the aforementioned characteristics, a good performance is achieved.

Upon completing the above steps, each method will be executed 20 times. The mean and standard deviation are calculated for the indicators of 20 experiments, and the absence of variance indicates that the experimental results are the same without any difference. The mean values of the evaluation metrics will be recorded for further analysis.

4.4. Experiment Results

We conducted comparative experiments using the PMU, MDFS, MCLS, and FIMF methods. We also proposed distinct filtering strategies based on the number of features present in each dataset sample. The performance of each method on the dataset was evaluated using five metrics. As depicted in

Table 3. The comparative results of our method with PMU, MDFS, MCLS, and FIMF based on various evaluation metrics including accuracy, macro-F1, micro-F1, kappa, and Hamming loss is presented. LightGBM is presented, where the classification algorithm can be used directly without the need for any feature selection.

Lung
Methods	accuracy	macro-F1	micro-F1	kappa	Hamming loss
LightGBM	0.918	0.716	0.918	0.836	0.082
PMU	0.957 ± 0.021	0.909 ± 0.072	0.957 ± 0.021	0.912 ± 0.042	0.043 ± 0.021
MDFS	0.952 ± 0.021	0.901 ± 0.067	0.952 ± 0.021	0.902 ± 0.044	0.048 ± 0.021
MCLS	0.959 ± 0.030	0.892 ± 0.112	0.959 ± 0.030	0.915 ± 0.056	0.041 ± 0.030
FIMF	0.957 ± 0.025	0.919 ± 0.071	0.957 ± 0.025	0.919 ± 0.040	0.043 ± 0.025
Ours	0.984	0.979	0.984	0.968	0.016
Yale
Methods	accuracy	macro-F1	micro-F1	kappa	Hamming loss
LightGBM	0.660	0.607	0.660	0.636	0.340
PMU	0.662 ± 0.035	0.632 ± 0.026	0.662 ± 0.035	0.636 ± 0.037	0.338 ± 0.035
MDFS	0.716 ± 0.034	0.705 ± 0.035	0.716 ± 0.034	0.694 ± 0.035	0.284 ± 0.034
MCLS	0.586 ± 0.048	0.551 ± 0.047	0.586 ± 0.048	0.555 ± 0.052	0.414 ± 0.048
FIMF	0.672 ± 0.091	0.669 ± 0.070	0.672 ± 0.091	0.647 ± 0.097	0.328 ± 0.091
Ours	0.760	0.715	0.760	0.739	0.240
Cattle
Methods	accuracy	macro-F1	micro-F1	kappa	Hamming loss
LightGBM	0.877	0.877	0.877	0.816	0.123
PMU	0.899	0.899	0.899	0.849	0.101
MDFS	0.892	0.892	0.892	0.838	0.108
MCLS	0.894	0.894	0.894	0.841	0.106
FIMF	0.903	0.903	0.903	0.855	0.097
Ours	0.909	0.909	0.909	0.863	0.091

, our method outperforms all others in terms of every metrics, securing the first position.

To further illustrate the influence of retaining different feature ratios on the final classification results, we conducted multiple sets of experiments based on the settings outlined in Section 4.3. The results corresponding to varying numbers of features are displayed in the Figure 1. This allows for a comprehensive understanding of how different feature ratios affect the classification outcomes.

The horizontal axis of the figures is the number of features selected in the task. The vertical axis denotes the value of evaluation indicators. As the number of features increases, the accuracy of classification increases. While the curve is not monotonous, it is fluctuating. The Hamming loss is decreasing along with the increase in selected features.

According to the results, our method outperforms the other methods on all three datasets. On the Lung dataset, our method achieved an accuracy of 0.984, a macro-F1 score of 0.979, a micro-F1 score of 0.984, a kappa coefficient of 0.968, and a Hamming loss of 0.016. These results indicate that our method is highly accurate and effective in classifying lung data. Similarly, on the Yale dataset, our method achieved an accuracy of 0.760, a macro-F1 score of 0.715, a micro-F1 score of 0.760, a kappa coefficient of 0.739, and a Hamming loss of 0.240. This demonstrates the superior performance of our method compared to other approaches. Lastly, on the Cattle dataset, our method achieved an accuracy of 0.909, a macro-F1 score of 0.909, a micro-F1 score of 0.909, a kappa coefficient of 0.863, and a Hamming loss of 0.091. These results further validate the effectiveness of our method for accurately classifying cattle data.

The above experimental results indicate that our method can better capture global and local potential information between features, thereby filtering out features that are more important to the classification task and improving the accuracy of the final classification. In contrast, LightGBM, which does not involve feature selection, performed relatively well on the Lung and Cattle datasets but showed lower performance on the Yale dataset. The other methods also showed varying degrees of performance across the different datasets. Overall, our proposed method demonstrates superior performance in terms of accuracy, F1 scores, kappa coefficient, and Hamming loss on all three datasets. These results highlight the effectiveness of our method for classification tasks and its potential for practical applications.

4.5. Analysis

During the iteration process, note that the objective function value for the tth iteration is ${\Gamma }_t$, and the objective function value for the $t-1$th iteration is ${\Gamma }_{t-1}$. The iteration is terminated if either the absolute difference between ${\Gamma }_{t-1}$ and ${\Gamma }_t$ is less than 0.01 or if the iteration count exceeds 10.

Figure 2 illustrates the variation in the objective function value during the iteration of our method on each dataset. It is evident that the objective function value has converged significantly by the second epoch. This observation demonstrates the efficiency and fast convergence of our method.

4.6. Ablation Study

In order to better distinguish the effect of each part of the objective function, we divided the objective function into three basic parts, named the basic formula ($BASE$), instance correlation ($IC$), and label correlation ($LC$), and conducted ablation experiments on each dataset. The specific formulas for the three parts of goal division are as follows:

$$BASE=mi{n}_{W,b}{\left|\right|XW-Y\left|\right|}_F^2+{\alpha \left|\right|W\left|\right|}_{2,1}^2,$$

(22)

$$IC=mi{n}_{W,V}\left|\right|XW-{V\left|\right|}_F^2+{\alpha \left|\right|W\left|\right|}_{2,1}^2+\beta Tr\left(W^T{X}^{T}LXW\right),$$

(23)

$$\begin{array}{cc}\hfill & LC=mi{n}_{W,V}Tr\left[{(XW-V)}^T(XW-V)\right]+\alpha Tr\left(W^{T}AW\right)+\beta Tr\left(W^T{X}^{T}LXW\right)+\hfill \\ \hfill & \gamma (Tr\left[{(V-Y)}^{T}E(V-Y)\right]+Tr\left(V^{T}LV\right)]).\hfill \end{array}$$

(24)

We start with Equation (22) as the baseline and then incorporate the $IC$ module into the objective function, which considers the noise elimination of the original data. As shown in

Table 4. Our method conducts ablation experiments on various datasets, where $BASE$, $IC$, and $LC$ correspond to formulas Equation (22), Equation (23), and Equation (24), respectively.

Lung
Modules	accuracy	macro-F1	micro-F1	kappa	Hamming loss
$BASE$	0.934	0.764	0.934	0.871	0.066
$IC$	0.967	0.955	0.967	0.936	0.033
$LC$	0.984	0.979	0.984	0.968	0.016
Yale
Modules	accuracy	macro-F1	micro-F1	kappa	Hamming loss
$BASE$	0.640	0.616	0.640	0.614	0.360
$IC$	0.700	0.670	0.700	0.676	0.300
$LC$	0.760	0.715	0.760	0.739	0.240
Cattle
Methods	accuracy	macro-F1	micro-F1	kappa	hamming loss
$BASE$	0.885	0.885	0.885	0.827	0.115
$IC$	0.905	0.905	0.905	0.858	0.095
$LC$	0.909	0.909	0.909	0.863	0.091

, this leads to an improvement in classification accuracy. With the help of this module, all of the evaluation indicators witnessed progress of different sizes in the three datasets. The accuracy of classification was improved by 6% in the Yale dataset. Following the $IC$ module, the $LC$ module is added to the objective function, taking into account the distance between the low-dimensional embedded label V and the predicted label $WX$, as well as the ground truth value label and the internal elements of V. This incorporation of both global and local information during the process enhances the accuracy of the method. The $LC$ module helped the method to obtain improvements in all the indicators. It is notable that the Hamming loss was no more than half of what it was before in the lung dataset. The experiments show that the improvements in this paper are effective, bringing benefits to the classification task.

5. Conclusions

In this paper, we have introduced a novel unsupervised feature selection method that incorporates both instance correlation and label correlation. By considering instance correlation, we can mitigate the negative impact of noise in the datasets. Additionally, our approach utilizes a low-dimensional embedded vector to capture global and local information through label correlation. Experimental results have demonstrated that our method outperforms existing approaches such as PMU, MDFS, MCLS, and FIMF, thus validating the effectiveness of our improvements. Moving forward, our future work will explore the underlying relationship between global and local label information.