An Instance- and Label-Based Feature Selection Method in Classification Tasks
Abstract
:1. Introduction
- We introduce a novel unsupervised feature selection method that takes into account both instance correlation and label correlation, effectively mitigating the impact of noise in data.
- We improve performance by introducing a low-dimensional embedding vector to learn potential structural spatial information.
- Our method outperforms existing approaches like PMU, MDFS, MCLS, and FIMF, showing significant improvements in a series of experiments.
2. Related Work
3. Materials and Methods
3.1. Notations
3.2. Problem Formulation
3.3. Optimization
3.3.1. Solve W as given V
3.3.2. Solve V as given W
| Algorithm 1: The iterative optimization. | |||
| Input: The feature matrix , label matrix , and hyperparameters , , . | |||
| Output: The first K features obtained by sorting the results of . | |||
| 1 | Initialization: Randomly initialize , and E, set = 0.01. | ||
| 2 | Calculate L, using Equation (10), Equation (16), respectively. | ||
| 3 | while not converged do | ||
| 4 | Calculate , update W by Equation (15). | ||
| 5 | Calculate , update V by Equation (17). | ||
| 6 | Calculate , update by Equation (16). | ||
| 7 | end | ||
| 8 | Sort in descending order and filter out the top K features from the sorted list. | ||
4. Results and Discussion
4.1. Datasets
4.2. Evaluation Metrics
- Accuracy
- Macro- and Micro-where is the number of positive samples correctly identified. is the number of negative samples for false positives. is the number of missed positive samples. To obtain the macro- score, first calculate the value for each individual category, and then compute the average of all values across all categories. After, calculate the overall accuracy and recall rate. Then, compute the value to obtain the micro- score.
- Kappawhere refers to the empirical probability of agreement on the label assigned to any sample, also known as the observed agreement ratio. On the other hand, represents the expected agreement between annotators when labels are assigned randomly. To estimate , a per-annotator empirical prior over the class labels is employed.
- Hamming loss
4.3. Experimental Setup
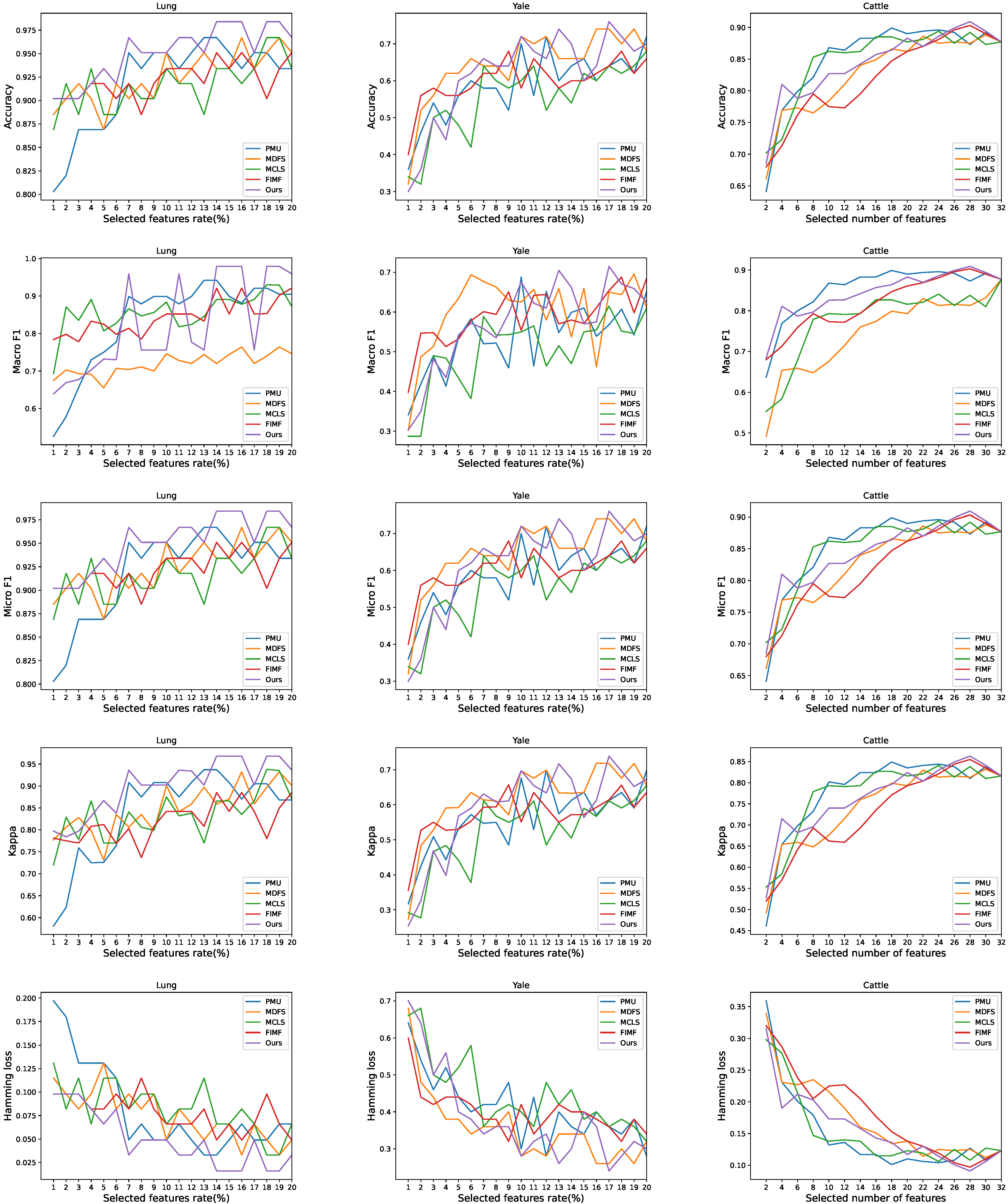
4.4. Experiment Results
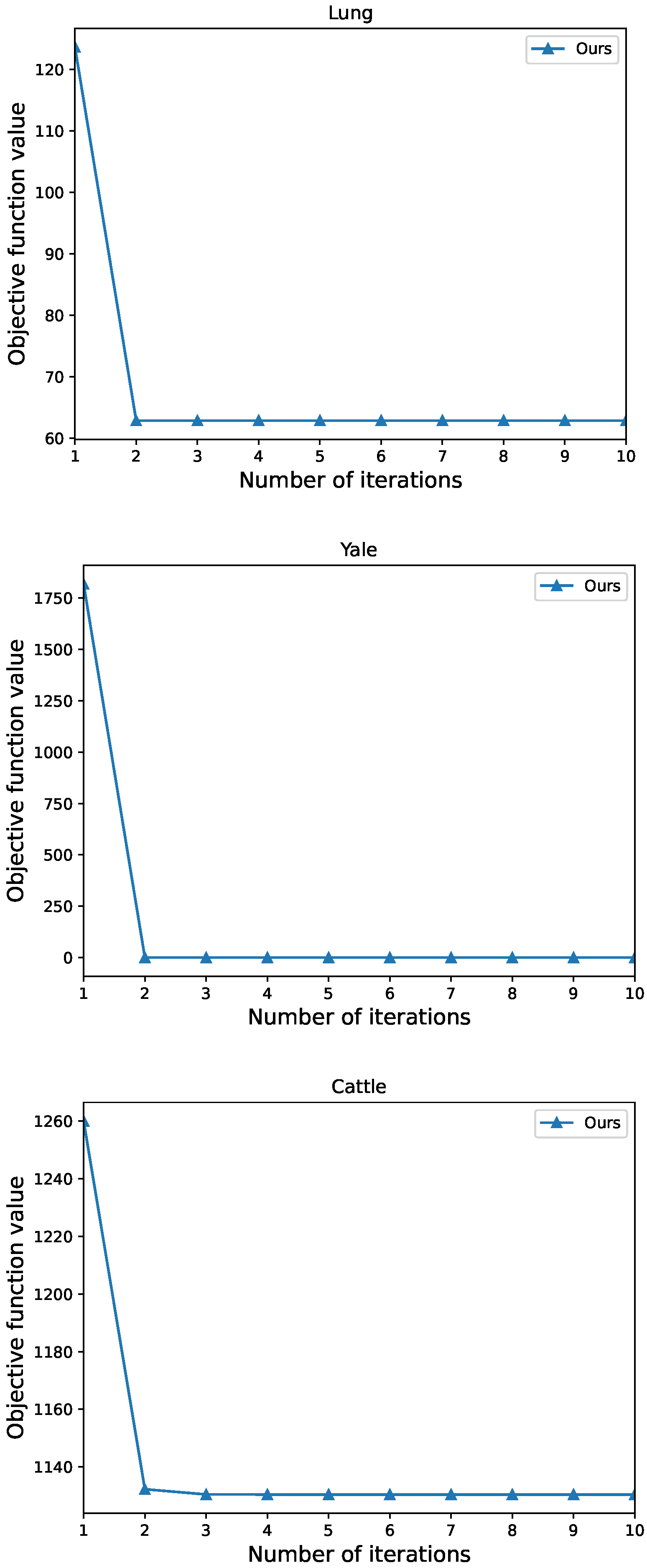
4.5. Analysis
4.6. Ablation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LightGBM | A highly efficient gradient boosting decision tree |
| PMU | Feature selection for multi-label classification using multivariate mutual information |
| MDFS | Manifold regularized discriminative feature selection for multi-label learning |
| MCLS | Manifold-based constraint Laplacian score for multi-label feature selection |
| FIMF | Fast multi-label feature selection based on information-theoretic feature ranking |
| GBDT | Gradient boost decision tree |
| xgboost | Extreme gradient boosting |
References
- Sidey-Gibbons, J.A.M.; Sidey-Gibbons, C.J. Machine learning in medicine: A practical introduction. BMC Med. Res. Methodol. 2019, 19, 64. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Botón, C.; Casillas-Pérez, D.; Casanova-Mateo, C.; Ghimire, S.; Cerro-Prada, E.; Gutierrez, P.; Deo, R.; Salcedo-Sanz, S. Machine learning regression and classification methods for fog events prediction. Atmos. Res. 2022, 272, 106157. [Google Scholar] [CrossRef]
- Shlens, J. A Tutorial on Principal Component Analysis. arXiv 2014, arXiv:1404.1100. [Google Scholar]
- Meesad, P.; Boonrawd, P.; Nuipian, V. A Chi-Square-Test for Word Importance Differentiation in Text Classification. In Proceedings of the International Conference on Information and Electronics Engineering, Bangkok, Thailand, 28–29 May 2011. [Google Scholar]
- Spencer, R.; Thabtah, F.; Abdelhamid, N.; Thompson, M. Exploring feature selection and classification methods for predicting heart disease. Digit. Health 2020, 6, 205520762091477. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xu, G.; Liang, L.; Jiang, K. Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis. Mech. Syst. Signal Process. 2015, 54–55, 259–276. [Google Scholar] [CrossRef]
- Kileel, J.; Moscovich, A.; Zelesko, N.; Singer, A. Manifold Learning with Arbitrary Norms. J. Fourier Anal. Appl. 2021, 27, 82. [Google Scholar] [CrossRef]
- Ni, Y.; Koniusz, P.; Hartley, R.; Nock, R. Manifold Learning Benefits GANs. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 11255–11264. [Google Scholar] [CrossRef]
- Tang, B.; Song, T.; Li, F.; Deng, L. Fault diagnosis for a wind turbine transmission system based on manifold learning and Shannon wavelet support vector machine. Renew. Energy 2014, 62, 1–9. [Google Scholar] [CrossRef]
- Tan, C.; Chen, S.; Geng, X.; Ji, G. A label distribution manifold learning algorithm. Pattern Recognit. 2023, 135, 109112. [Google Scholar] [CrossRef]
- Jiang, B.N. On the least-squares method. Comput. Methods Appl. Mech. Eng. 1998, 152, 239–257. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. In Foundations and Trends® in Machine Learning; Now Publishers: Hanover, ML, USA, 2011; Volume 3, pp. 1–122. [Google Scholar]
- Lever, J.; Krzywinski, M.; Altman, N. Principal component analysis. Nat. Methods 2017, 14, 641–642. [Google Scholar] [CrossRef]
- Sumaiya Thaseen, I.; Aswani Kumar, C. Intrusion detection model using fusion of chi-square feature selection and multi class SVM. J. King Saud Univ.—Comput. Inf. Sci. 2017, 29, 462–472. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.W. Feature selection for multi-label classification using multivariate mutual information. Pattern Recognit. Lett. 2013, 34, 349–357. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.W. Fast multi-label feature selection based on information-theoretic feature ranking. Pattern Recognit. 2015, 48, 2761–2771. [Google Scholar] [CrossRef]
- Huang, R.; Jiang, W.; Sun, G. Manifold-based constraint Laplacian score for multi-label feature selection. Pattern Recognit. Lett. 2018, 112, 346–352. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, Z.; Li, C.; Zhou, C.; Li, S. Manifold regularized discriminative feature selection for multi-label learning. Pattern Recognit. 2019, 95, 136–150. [Google Scholar] [CrossRef]
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Medica 2012, 22, 276–282. [Google Scholar] [CrossRef]
- Tsoumakas, G.; Vlahavas, I. Random k-Labelsets: An Ensemble Method for Multilabel Classification. In Machine Learning: ECML 2007; Kok, J.N., Koronacki, J., Mantaras, R.L.D., Matwin, S., Mladenič, D., Skowron, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4701, pp. 406–417. ISSN 0302-9743. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Appel, R.; Fuchs, T.; Dollár, P.; Perona, P. Quickly Boosting Decision Trees—Pruning Underachieving Features Early. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
| No. | Definition | Description |
|---|---|---|
| 1 | Trace of A | |
| 2 | F-norm of A | |
| 3 | 2,1-norm of A | |
| 4 | The transposition of A | |
| 5 | D dimensional identity matrix | |
| 6 | n | Number of samples |
| 7 | d | Number of features per sample |
| 8 | c | Number of categories |
| 9 | X | Feature vector |
| 10 | W | Weight matrix |
| 11 | V | Predicted label matrix |
| 12 | L | Laplacian matrix |
| 13 | Y | Ground truth label of dataset |
| Datasets | Number of Samples | Number of Features | Number of Categories |
|---|---|---|---|
| Lung | 203 | 3312 | 5 |
| Yale | 165 | 1024 | 15 |
| Cattle | 1800 | 32 | 3 |
| Lung | |||||
| Methods | accuracy | macro-F1 | micro-F1 | kappa | Hamming loss |
| LightGBM | 0.918 | 0.716 | 0.918 | 0.836 | 0.082 |
| PMU | 0.957 ± 0.021 | 0.909 ± 0.072 | 0.957 ± 0.021 | 0.912 ± 0.042 | 0.043 ± 0.021 |
| MDFS | 0.952 ± 0.021 | 0.901 ± 0.067 | 0.952 ± 0.021 | 0.902 ± 0.044 | 0.048 ± 0.021 |
| MCLS | 0.959 ± 0.030 | 0.892 ± 0.112 | 0.959 ± 0.030 | 0.915 ± 0.056 | 0.041 ± 0.030 |
| FIMF | 0.957 ± 0.025 | 0.919 ± 0.071 | 0.957 ± 0.025 | 0.919 ± 0.040 | 0.043 ± 0.025 |
| Ours | 0.984 | 0.979 | 0.984 | 0.968 | 0.016 |
| Yale | |||||
| Methods | accuracy | macro-F1 | micro-F1 | kappa | Hamming loss |
| LightGBM | 0.660 | 0.607 | 0.660 | 0.636 | 0.340 |
| PMU | 0.662 ± 0.035 | 0.632 ± 0.026 | 0.662 ± 0.035 | 0.636 ± 0.037 | 0.338 ± 0.035 |
| MDFS | 0.716 ± 0.034 | 0.705 ± 0.035 | 0.716 ± 0.034 | 0.694 ± 0.035 | 0.284 ± 0.034 |
| MCLS | 0.586 ± 0.048 | 0.551 ± 0.047 | 0.586 ± 0.048 | 0.555 ± 0.052 | 0.414 ± 0.048 |
| FIMF | 0.672 ± 0.091 | 0.669 ± 0.070 | 0.672 ± 0.091 | 0.647 ± 0.097 | 0.328 ± 0.091 |
| Ours | 0.760 | 0.715 | 0.760 | 0.739 | 0.240 |
| Cattle | |||||
| Methods | accuracy | macro-F1 | micro-F1 | kappa | Hamming loss |
| LightGBM | 0.877 | 0.877 | 0.877 | 0.816 | 0.123 |
| PMU | 0.899 | 0.899 | 0.899 | 0.849 | 0.101 |
| MDFS | 0.892 | 0.892 | 0.892 | 0.838 | 0.108 |
| MCLS | 0.894 | 0.894 | 0.894 | 0.841 | 0.106 |
| FIMF | 0.903 | 0.903 | 0.903 | 0.855 | 0.097 |
| Ours | 0.909 | 0.909 | 0.909 | 0.863 | 0.091 |
| Lung | |||||
| Modules | accuracy | macro-F1 | micro-F1 | kappa | Hamming loss |
| 0.934 | 0.764 | 0.934 | 0.871 | 0.066 | |
| 0.967 | 0.955 | 0.967 | 0.936 | 0.033 | |
| 0.984 | 0.979 | 0.984 | 0.968 | 0.016 | |
| Yale | |||||
| Modules | accuracy | macro-F1 | micro-F1 | kappa | Hamming loss |
| 0.640 | 0.616 | 0.640 | 0.614 | 0.360 | |
| 0.700 | 0.670 | 0.700 | 0.676 | 0.300 | |
| 0.760 | 0.715 | 0.760 | 0.739 | 0.240 | |
| Cattle | |||||
| Methods | accuracy | macro-F1 | micro-F1 | kappa | hamming loss |
| 0.885 | 0.885 | 0.885 | 0.827 | 0.115 | |
| 0.905 | 0.905 | 0.905 | 0.858 | 0.095 | |
| 0.909 | 0.909 | 0.909 | 0.863 | 0.091 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Q.; Liu, S.; Zhao, C.; Li, S. An Instance- and Label-Based Feature Selection Method in Classification Tasks. Information 2023, 14, 532. https://doi.org/10.3390/info14100532
Fan Q, Liu S, Zhao C, Li S. An Instance- and Label-Based Feature Selection Method in Classification Tasks. Information. 2023; 14(10):532. https://doi.org/10.3390/info14100532
Chicago/Turabian StyleFan, Qingcheng, Sicong Liu, Chunjiang Zhao, and Shuqin Li. 2023. "An Instance- and Label-Based Feature Selection Method in Classification Tasks" Information 14, no. 10: 532. https://doi.org/10.3390/info14100532
APA StyleFan, Q., Liu, S., Zhao, C., & Li, S. (2023). An Instance- and Label-Based Feature Selection Method in Classification Tasks. Information, 14(10), 532. https://doi.org/10.3390/info14100532





