Comparative Analysis of Deep Learning Architectures and Vision Transformers for Musical Key Estimation
Abstract
:1. Introduction
2. Related Work
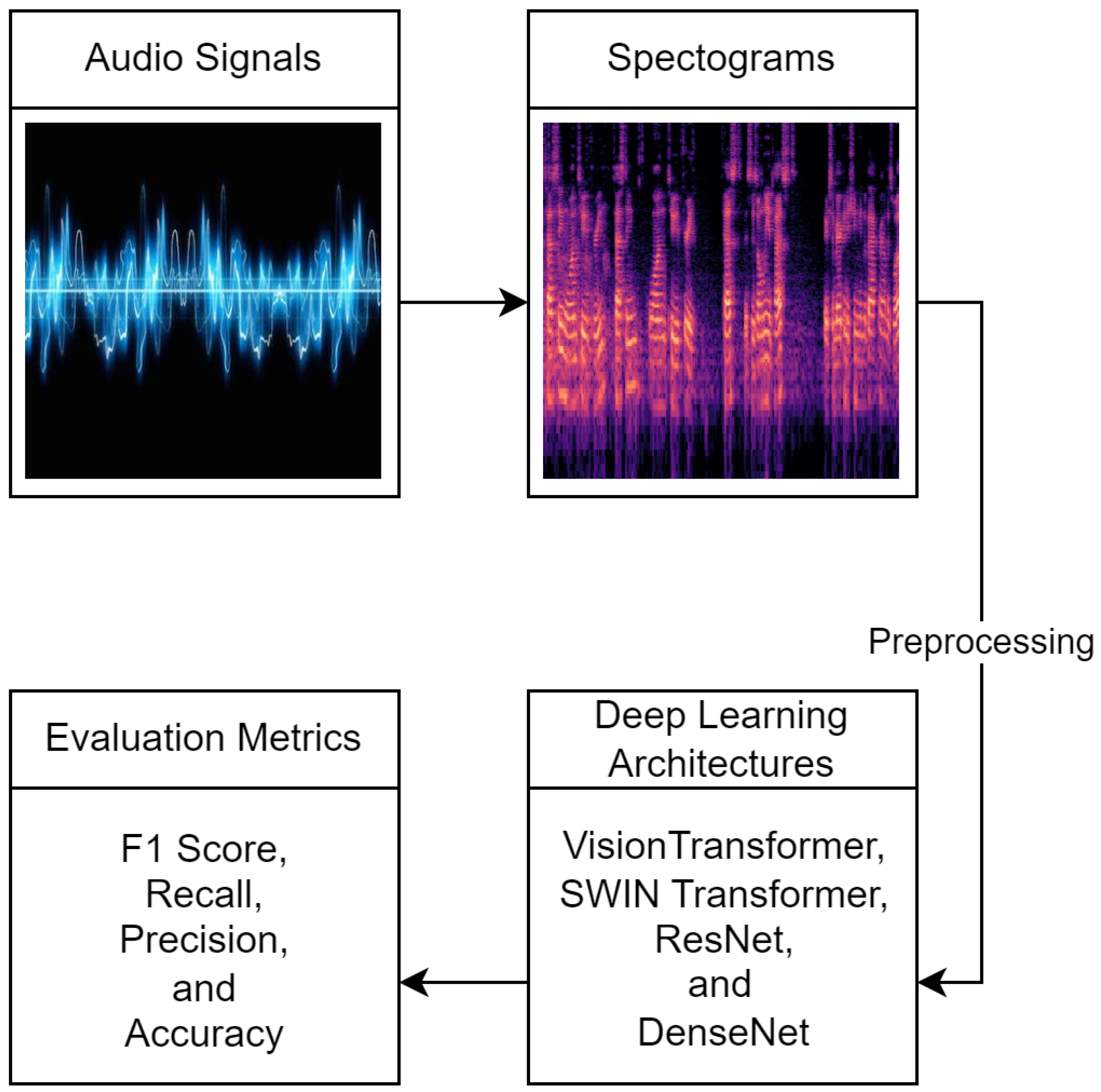
3. Methodology
3.1. Dataset
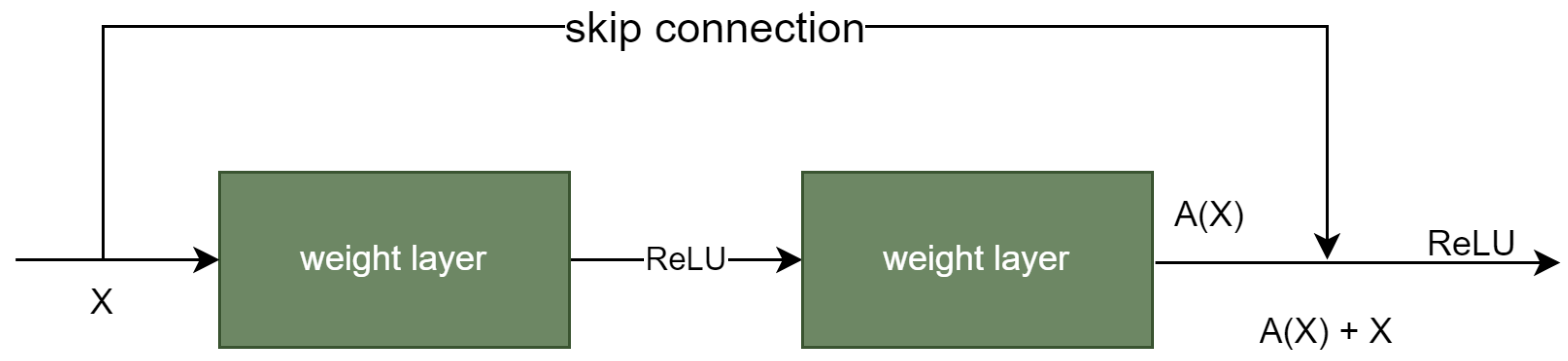
3.2. ResNet
3.3. DenseNet
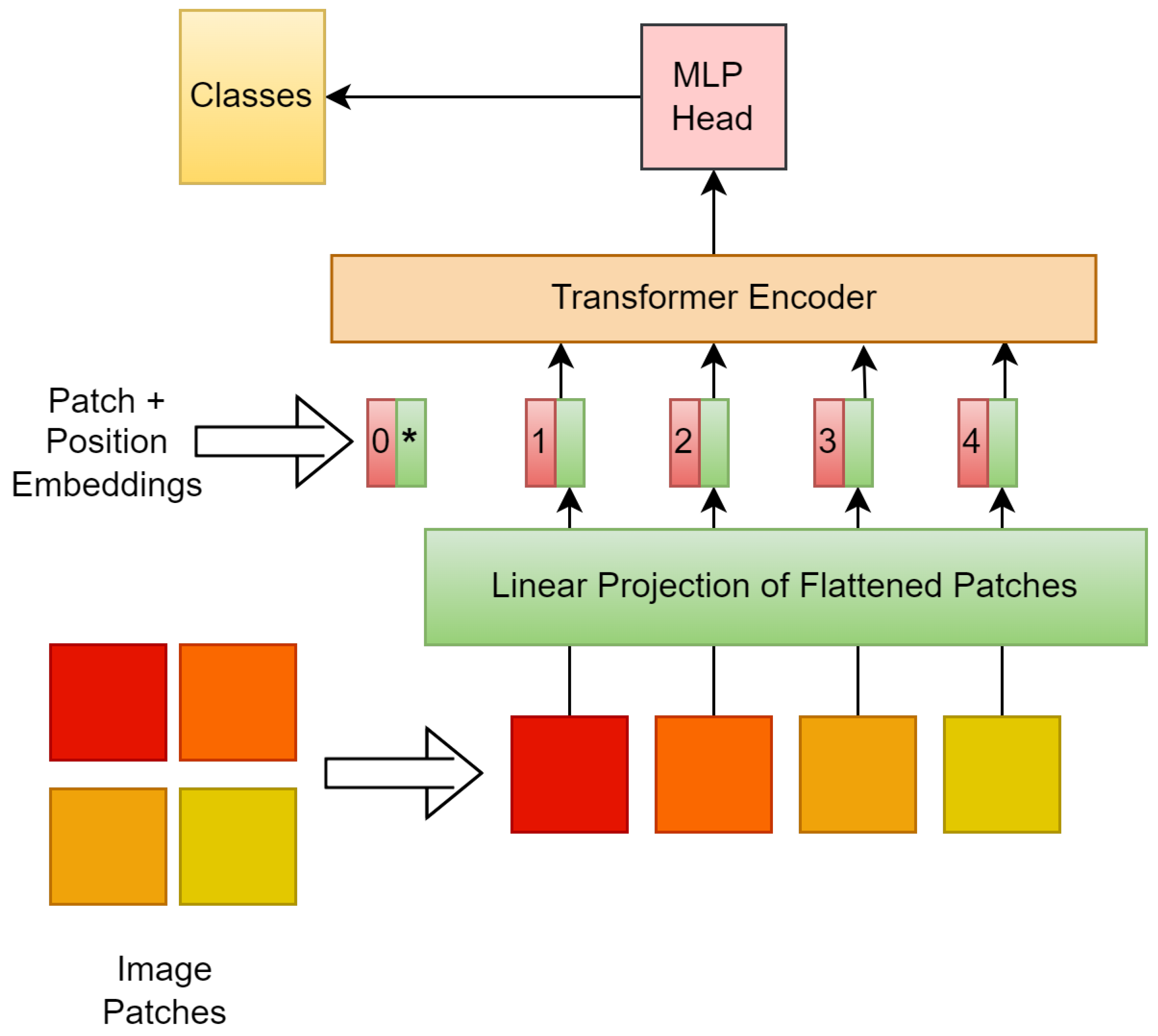
3.4. Vision Transformer
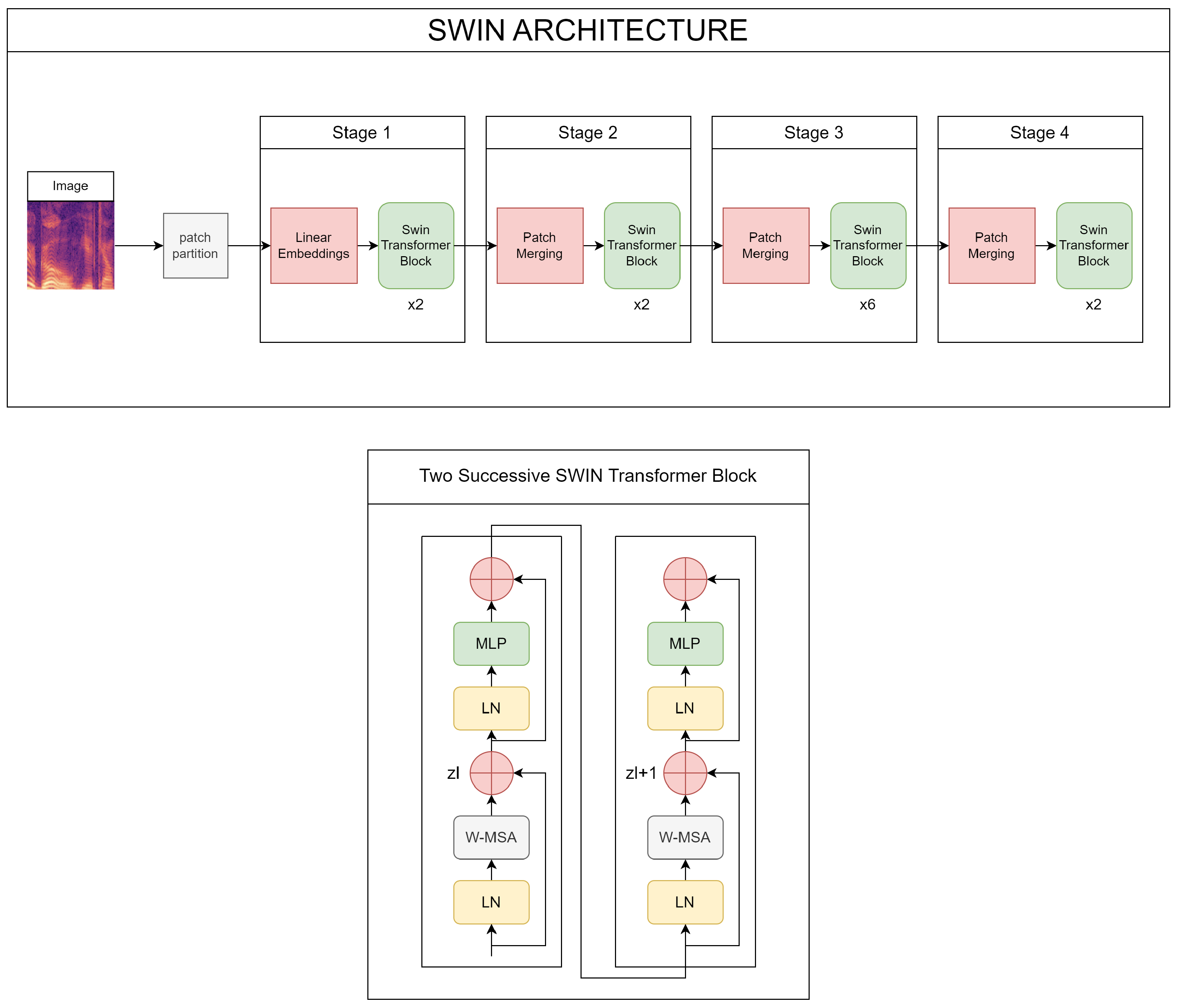
3.5. SWIN Transformer
4. Results
4.1. Performance Metrics
- Accuracy: The percentage of correctly classified images;
- Precision: The percentage of true-positive predictions among all positive predictions;
- Recall: The percentage of true-positive predictions among all actual positives;
- F1 score: The harmonic mean of precision and recall, providing a balanced measure of a model’s accuracy;
- Log loss: A measure of how well the model’s predicted probabilities align with the actual class labels.
4.2. Training and Testing Efficiency
4.3. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Humphrey, E.J.; Bello, J.P. Rethinking Automatic Chord Recognition with Convolutional Neural Networks. In Proceedings of the 11th IEEE International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 12–15 December 2012; pp. 357–362. [Google Scholar]
- Mauch, M.; Dixon, S. Approximate Note Transcription for the Improved Identification of Difficult Chords. In Proceedings of the 11th International Society for Music Information Retrieval Conference (ISMIR), Utrecht, The Netherlands, 9–13 August 2010; pp. 135–140. [Google Scholar]
- Temperley, D. The Cognition of Basic Musical Structures; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Krumhansl, C.L.; Kessler, E.J. Tracing the Dynamic Changes in Perceived Tonal Organization in a Spatial Representation of Musical Keys. Psychol. Rev. 1982, 89, 334. [Google Scholar] [CrossRef] [PubMed]
- Faraldo, Á.; Gómez, E.; Jordà, S.; Herrera, P. Key Estimation in Electronic Dance Music. In Advances in Information Retrieval, Proceedings of the 38th European Conference on IR Research (ECIR), Padua, Italy, 20–23 March 2016; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9626, pp. 335–347. [Google Scholar]
- Noland, K.; Sandler, M. Signal Processing Parameters for Tonality Estimation. In Proceedings of the Audio Engineering Society Convention 122, Vienna, Austria, 5–8 May 2007. [Google Scholar]
- Pauws, S. Musical Key Extraction from Audio. In Proceedings of the 5th International Conference on Music Information Retrieval (ISMIR), Barcelona, Spain, 10–14 October 2004. [Google Scholar]
- Temperley, D. WWhat’s Key for Key? The Krumhansl-Schmuckler Key-Finding Algorithm Reconsidered. Music Percept. 1999, 17, 65–100. [Google Scholar] [CrossRef]
- Giorgi, B.D.; Zanoni, M.; Sarti, A.; Tubaro, S. Automatic Chord Recognition based on the Probabilistic Modeling of Diatonic Modal Harmony. In Proceedings of the 8th International Workshop on Multidimensional Systems, Erlangen, Germany, 9–11 September 2013; pp. 1–6. [Google Scholar]
- Mauch, M.; Dixon, S. Simultaneous Estimation of Chords and Musical Context From Audio. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 1280–1289. [Google Scholar] [CrossRef]
- Ni, Y.; McVicar, M.; Santos-Rodriguez, R.; Bie, T.D. An End-to-End Machine Learning System for Harmonic Analysis of Music. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1771–1783. [Google Scholar] [CrossRef]
- Pauwels, J.; Martens, J.P. Combining Musicological Knowledge About Chords and Keys in a Simultaneous Chord and Local Key Estimation System. J. New Music Res. 2014, 43, 318–330. [Google Scholar] [CrossRef]
- Krumhansl, C.L. Cognitive Foundations of Musical Pitch; Oxford University Press: Oxford, UK, 2001; Volume 17. [Google Scholar]
- Harte, C. Towards Automatic Extraction of Harmony Information from Music Signals. Ph.D. Thesis, Queen Mary University of London, London, UK, 2010. [Google Scholar]
- Fujishima, T. Realtime Chord Recognition of Musical Sound: A System using Common Lisp Music. In Proceedings of the International Computer Music Conference, Beijing, China, 22–28 October 1999. [Google Scholar]
- Juslin, P.N.; Sloboda, J. Handbook of Music and Emotion: Theory, Research, Applications; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Dowling, W.J.; Harwood, D.L. Music Cognition; Academic Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Hatten, R.S. Musical Meaning in Beethoven: Markedness, Correlation, and Interpretation; Indiana University Press: Bloomington, IN, USA, 2004. [Google Scholar]
- Gómez, E. Tonal Description of Music Audio Signals. Ph.D. Thesis, Universitat Pompeu Fabra, Barcelona, Spain, 2006. [Google Scholar]
- Tzanetakis, G.; Cook, P.R. Musical Genre Classification of Audio Signals. IEEE Trans. Speech Audio Process. 2002, 10, 293–302. [Google Scholar] [CrossRef]
- Greener, J.G.; Kandathil, S.M.; Moffat, L.; Jones, D.T. A Guide to Machine Learning for Biologists. Nat. Rev. Mol. Cell Biol. 2022, 23, 40–55. [Google Scholar] [CrossRef]
- Mehta, N.; Shah, P.; Gajjar, P.; Ukani, V. Ocean Surface Pollution Detection: Applicability Analysis of V-Net with Data Augmentation for Oil Spill and Other Related Ocean Surface Feature Monitoring. In Communication and Intelligent Systems; Springer: Singapore, 2022; pp. 11–25. [Google Scholar]
- Senjaliya, H.; Gajjar, P.; Vaghasiya, B.; Shah, P.; Gujarati, P. Optimization of Rocker-Bogie Mechanism using Heuristic Approaches. arXiv 2022, arXiv:2209.06927. [Google Scholar]
- Whalen, S.; Schreiber, J.; Noble, W.S.; Pollard, K.S. Navigating the Pitfalls of Applying Machine Learning in Genomics. Nat. Rev. Genet. 2022, 23, 169–181. [Google Scholar] [CrossRef]
- Gajjar, P.; Dodia, V.; Mandaliya, S.; Shah, P.; Ukani, V.; Shukla, M. Path Planning and Static Obstacle Avoidance for Unmanned Aerial Systems. In Proceedings of the International Conference on Advancements in Smart Computing and Information Security, Rajkot, India, 24–26 November 2022; pp. 262–270. [Google Scholar]
- Bender, A.; Schneider, N.; Segler, M.; Walters, W.P.; Engkvist, O.; Rodrigues, T. Evaluation Guidelines for Machine Learning Tools in the Chemical Sciences. Nat. Rev. Chem. 2022, 6, 428–442. [Google Scholar] [CrossRef]
- Martins, R.M.; Wangenheim, C.G.V. Findings on Teaching Machine Learning in High School: A Ten-Year Systematic Literature Review. Inform. Educ. 2022, 22, 421–440. [Google Scholar] [CrossRef]
- Gajjar, P.; Mehta, N.; Shah, P. Quadruplet Loss and SqueezeNets for Covid-19 Detection from Chest-X Rays. Comput. Sci. 2022, 30, 89. [Google Scholar] [CrossRef]
- Li, X. Information Retrieval Method of Professional Music Teaching Based on Hidden Markov Model. In Proceedings of the 14th IEEE International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Changsha, China, 15–16 January 2022; pp. 1072–1075. [Google Scholar]
- Murthy, Y.V. Content-based Music Information Retrieval (CB-MIR) and its Applications Towards Music Recommender System. Ph.D. Thesis, National Institute of Technology Karnataka, Surathkal India, 2019. [Google Scholar]
- Ostermann, F.; Vatolkin, I.; Ebeling, M. AAM: A Dataset of Artificial Audio Multitracks for Diverse Music Information Retrieval Tasks. EURASIP J. Audio Speech Music Process. 2023, 2023, 13. [Google Scholar] [CrossRef]
- Khan, S.H.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in Vision: A Survey. ACM Comput. Surv. 2022, 54, 1–41. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Han, K.; Zhang, W.; Ma, S.; Gao, W. Post-Training Quantization for Vision Transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 28092–28103. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 9992–10002. [Google Scholar]
- Mao, X.; Qi, G.; Chen, Y.; Li, X.; Duan, R.; Ye, S.; He, Y.; Xue, H. Towards Robust Vision Transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 12032–12041. [Google Scholar]
- Gajjar, P.; Shah, P.; Sanghvi, H. E-Mixup and Siamese Networks for Musical Key Estimation. In International Conference on Ubiquitous Computing and Intelligent Information Systems; Springer: Singapore, 2021; pp. 343–350. [Google Scholar]
- Raphael, C. Music Plus One and Machine Learning. In Proceedings of the 27th International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 21–28. [Google Scholar]
- Purwins, H.; Li, B.; Virtanen, T.; Schlüter, J.; Chang, S.; Sainath, T.N. Deep Learning for Audio Signal Processing. IEEE J. Sel. Top. Signal Process. 2019, 13, 206–219. [Google Scholar] [CrossRef]
- Parulian, N.N.; Dubnicek, R.; Worthey, G.; Evans, D.J.; Walsh, J.A.; Downie, J.S. Uncovering Black Fantastic: Piloting A Word Feature Analysis and Machine Learning Approach for Genre Classification. Proc. Assoc. Inf. Sci. Technol. 2022, 59, 242–250. [Google Scholar] [CrossRef]
- Ghatas, Y.; Fayek, M.; Hadhoud, M. A Hybrid Deep Learning Approach for Musical Difficulty Estimation of Piano Symbolic Music. Alex. Eng. J. 2022, 61, 10183–10196. [Google Scholar] [CrossRef]
- Nagarajan, S.K.; Narasimhan, G.; Mishra, A.; Kumar, R. Long Short-Term Memory-Based Neural Networks in an AI Music Generation Platform. In Deep Learning Research Applications for Natural Language Processing; IGI Global: Hershey, PA, USA, 2023; pp. 89–112. [Google Scholar]
- Huang, H.; Zhou, X.; He, R. Orthogonal Transformer: An Efficient Vision Transformer Backbone with Token Orthogonalization. In Proceedings of the NeurIPS, New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Arnab, A.; Dehghani, M.; Heigold, G.; Sun, C.; Lucic, M.; Schmid, C. ViViT: A Video Vision Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Virtual, 11–17 October 2021; pp. 6816–6826. [Google Scholar]
- Miranda, E.R.; Shaji, H. Generative Music with Partitioned Quantum Cellular Automata. Appl. Sci. 2023, 13, 2401. [Google Scholar] [CrossRef]
- Kaliakatsos-Papakostas, M.; Velenis, K.; Pasias, L.; Alexandraki, C.; Cambouropoulos, E. An HMM-Based Approach for Cross-Harmonization of Jazz Standards. Appl. Sci. 2023, 13, 1338. [Google Scholar] [CrossRef]
- Ramírez, J.; Flores, M.J. Machine Learning for Music Genre: Multifaceted Review and Experimentation with Audioset. J. Intell. Inf. Syst. 2020, 55, 469–499. [Google Scholar] [CrossRef]
- Briot, J.; Pachet, F. Deep Learning for Music Generation: Challenges and Directions. Neural Comput. Appl. 2020, 32, 981–993. [Google Scholar] [CrossRef]
- Mao, H.H.; Shin, T.; Cottrell, G.W. DeepJ: Style-Specific Music Generation. In Proceedings of the 12th IEEE International Conference on Semantic Computing (ICSC), Laguna Hills, CA, USA, 31 January–2 February 2018; pp. 377–382. [Google Scholar]
- Schreiber, H.; Urbano, J.; Müller, M. Music Tempo Estimation: Are We Done Yet? Trans. Int. Soc. Music Inf. Retr. 2020, 3, 111. [Google Scholar] [CrossRef]
- George, A.; Mary, X.A.; George, S.T. Development of an Intelligent Model for Musical Key Estimation using Machine Learning Techniques. Multimed. Tools Appl. 2022, 81, 19945–19964. [Google Scholar] [CrossRef]
- Prabhakar, S.K.; Lee, S. Holistic Approaches to Music Genre Classification using Efficient Transfer and Deep Learning Techniques. Expert Syst. Appl. 2023, 211, 118636. [Google Scholar] [CrossRef]
- GTZAN Key Dataset. Available online: https://github.com/alexanderlerch/gtzan_key (accessed on 9 July 2023).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. CoRR. abs/1512.03385. 2016. Available online: https://openaccess.thecvf.com/content_cvpr_2016/html/He_Deep_Residual_Learning_CVPR_2016_paper.html (accessed on 20 September 2023).
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Mehta, S.; Rastegari, M. MobileViT: Light-weight, General-purpose, and Mobile-friendly Vision Transformer. arXiv 2021, arXiv:2110.02178. [Google Scholar]
- Kanavos, A.; Kounelis, F.; Iliadis, L.; Makris, C. Deep learning models for forecasting aviation demand time series. Neural Comput. Appl. 2021, 33, 16329–16343. [Google Scholar] [CrossRef]
- Lyras, A.; Vernikou, S.; Kanavos, A.; Sioutas, S.; Mylonas, P. Modeling Credibility in Social Big Data using LSTM Neural Networks. In Proceedings of the 17th International Conference on Web Information Systems and Technologies (WEBIST), Online, 26–28 October 2021; pp. 599–606. [Google Scholar]
- Savvopoulos, A.; Kanavos, A.; Mylonas, P.; Sioutas, S. LSTM Accelerator for Convolutional Object Identification. Algorithms 2018, 11, 157. [Google Scholar] [CrossRef]
- Vernikou, S.; Lyras, A.; Kanavos, A. Multiclass sentiment analysis on COVID-19-related tweets using deep learning models. Neural Comput. Appl. 2022, 34, 19615–19627. [Google Scholar] [CrossRef]

| Paper | Domain | Description |
|---|---|---|
| [46] | Genre Classification | Provides an overview of music genre classification within music information retrieval, discussing techniques, datasets, challenges, and trends in machine learning applied to music annotation, in addition to reporting a music genre classification experiment comparing various machine learning models using Audioset. |
| [47] | Music Generation | Discusses limitations in using deep learning for music generation and suggests approaches to address these limitations, in addition to highlighting recent systems that show promise in overcoming the limitations. |
| [48] | Music Generation | Introduces DeepJ, an end-to-end generative model for composing music with tunable properties based on a specific mixture of composer styles, demonstrating a simple technique for controlling the style of generated music that outperforms the biaxial long short-term memory (LSTM) approach. |
| [49] | Tempo Estimation | Explores the potential of using deep learning to improve the accuracy of global tempo estimation, considering the applications and limitations of evaluation metrics and datasets, including a survey of domain experts to understand current evaluation practices, in addition to providing a public repository with evaluation codes and estimates from different systems for popular datasets. |
| [50] | Key Estimation | Proposes a machine learning approach for determining the musical key of a song, which is important for various music information retrieval tasks, testing the model with four algorithms and achieving a maximum accuracy of 91.49% using support vector machine (SVM). |
| [51] | Genre Classification | Proposes novel approaches for music genre classification utilizing machine learning, transfer learning, and deep learning concepts, testing five approaches on three music datasets. The proposed BAG deep learning model combines bidirectional long short-term memory (BiLSTM) with an attention and graphical convolution network (GCN), achieving a classification accuracy of 93.51%. |
| Model | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) | Log Loss |
|---|---|---|---|---|---|
| DenseNet | 91.64 | 91.89 | 92.11 | 91.99 | 0.46 |
| ResNet | 86.87 | 88.12 | 87.23 | 87.67 | 0.63 |
| SWIN Transformer | 84.64 | 85.87 | 84.91 | 85.38 | 1.08 |
| ViT | 85.22 | 86.44 | 85.28 | 85.85 | 0.88 |
| Model | Training Time (min) | Testing Time (min) | Training Parameters (in 105) |
|---|---|---|---|
| DenseNet | 0.031 | 0.0068 | 69.72 |
| ResNet | 0.022 | 0.0068 | 235.77 |
| SWIN Transformer | 0.023 | 0.0084 | 2.01 |
| ViT | 0.021 | 0.0059 | 13.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garg, M.; Gajjar, P.; Shah, P.; Shukla, M.; Acharya, B.; Gerogiannis, V.C.; Kanavos, A. Comparative Analysis of Deep Learning Architectures and Vision Transformers for Musical Key Estimation. Information 2023, 14, 527. https://doi.org/10.3390/info14100527
Garg M, Gajjar P, Shah P, Shukla M, Acharya B, Gerogiannis VC, Kanavos A. Comparative Analysis of Deep Learning Architectures and Vision Transformers for Musical Key Estimation. Information. 2023; 14(10):527. https://doi.org/10.3390/info14100527
Chicago/Turabian StyleGarg, Manav, Pranshav Gajjar, Pooja Shah, Madhu Shukla, Biswaranjan Acharya, Vassilis C. Gerogiannis, and Andreas Kanavos. 2023. "Comparative Analysis of Deep Learning Architectures and Vision Transformers for Musical Key Estimation" Information 14, no. 10: 527. https://doi.org/10.3390/info14100527
APA StyleGarg, M., Gajjar, P., Shah, P., Shukla, M., Acharya, B., Gerogiannis, V. C., & Kanavos, A. (2023). Comparative Analysis of Deep Learning Architectures and Vision Transformers for Musical Key Estimation. Information, 14(10), 527. https://doi.org/10.3390/info14100527











