Abstract
This paper proposes a quantum-inspired evolutionary algorithm (QiEA) to solve an optimal service-matching task-assignment problem. Our proposed algorithm comes with the advantage of generating always feasible population individuals and, thus, eliminating the necessity for a repair step. That is, with respect to other quantum-inspired evolutionary algorithms, our proposed QiEA algorithm presents a new way of collapsing the quantum state that integrates the problem constraints in order to avoid later adjusting operations of the system to make it feasible. This results in lower computations and also faster convergence. We compare our proposed QiEA algorithm with three commonly used benchmark methods: the greedy algorithm, Hungarian method and Simplex, in five different case studies. The results show that the quantum approach presents better scalability and interesting properties that can be used in a wider class of assignment problems where the matching is not perfect.
1. Introduction
This paper considers a linear optimal service-matching task assignment problem defined by
where is the assignment matrix with N rows and M columns. We refer to as service agent set and its elements as service agent, and to as task set and its elements as task. Thus, is the cost of the assignment of service agent to task , and means that service agent is assigned to task . Without loss of generality, we assume that , i.e., the task set, is larger than the service agent set. The imposed constraint (1c) ensures that each service agent gets only one task, while constrain (1d) limits the assignment of any task to, at most, one service agent. is the adjacency matrix of the resultant matching graph after the assignment is peformed.
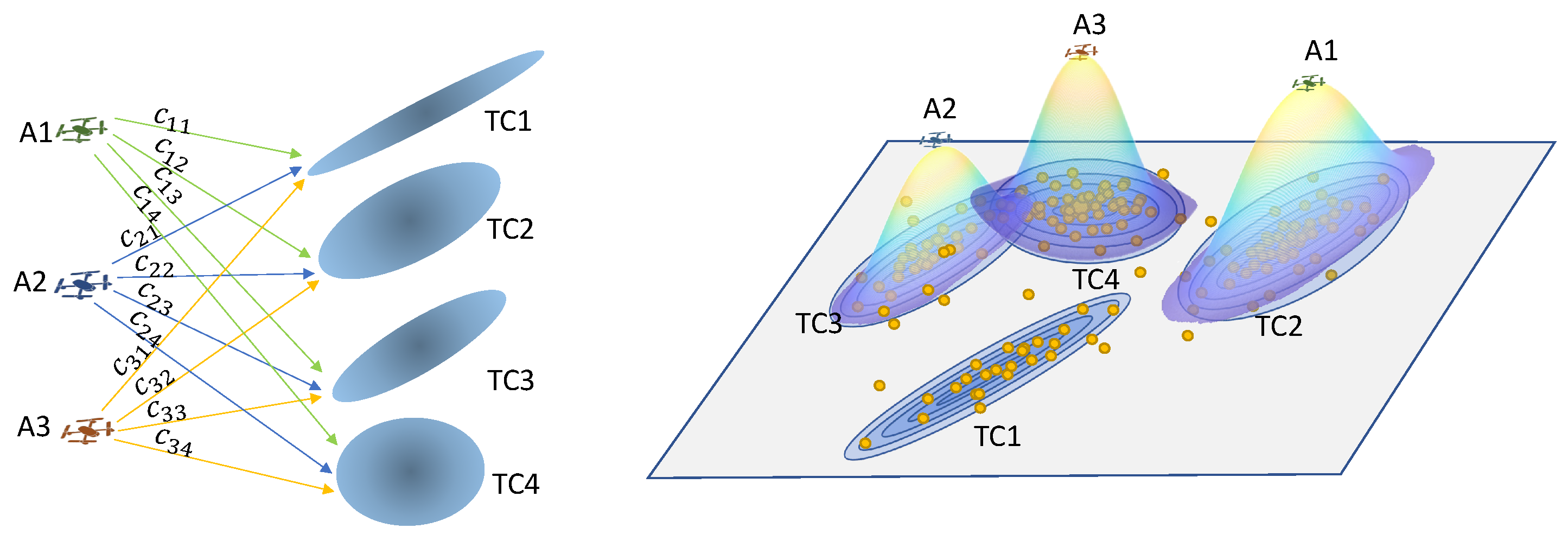
An example scenario inspired by the service-matching mobile-agent deployment for coverage over a dense set of targets studied in [1] is shown in Figure 1. In this service-matching problem, service UAVs A1, A2, A3 (flying at the same altitude), whose spatial service over the horizontal two-dimensional (2D) plane is described by a Gaussian distribution, should be deployed to provide coverage to a set of dense targets in a 2D flat plane. The targets are clustered into subgroups TC1, TC2, TC3, and TC4, each described by a Gaussian distribution of the targets. The assignment cost is the measure of similarity between the service distribution of agent Ai and the distribution of targets in subgroup TCj, measured in terms of the Kullback–Leibler divergence (KLD) ([2], p. 34). More details are provided in Section 4, where we conduct a numerical study of this service-matching task assignment.
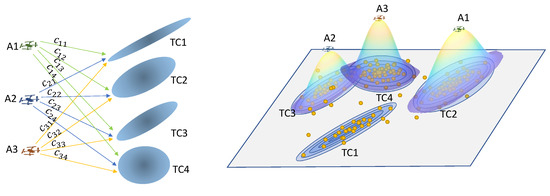
Figure 1.
An optimal service-matching UAV deployment via AP formulation. indicates the level of similarity between agent Ai’s service distribution with the target cluster TCj’s distribution. The figure depicts a case that agent A1, A3, and A3 are assigned, respectively, to TC2, TC3 and TC4.
There are many other service-matching applications which can be used with the optimal AP problem (Section 1). For example, in manufacturing, in assembly lines, where there must be a planning between the operators and the tasks [3,4]. Other situations such as in delivery tasks or ridesharing [5] can also be formulated in the same way. In addition, some social, economical or political situations are no more than an AP [6].
As in other combinatorial optimisation problems, there is a lack of methods that can achieve a good approximation factor in polynomial time with good scalability. Currently, the main algorithms still used to solve service-matching problems (Section 1) are classical methods such as the greedy algorithm, which, theoretically, ensures an approximation factor of 63% [7] with a complexity of [8]. The Hungarian method, with an approximation factor of 1 and a complexity of [8], or the Simplex method with, also, an approximation factor of 1 and a complexity of [8]. The reader should note that the aforementioned complexity bounds for the Hungarian and Simplex algorithms are based on execution of these algorithms when .
With the rise of machine learning, new techniques such as neural networks, reinforcement learning or evolutionary algorithms have been formulated to solve combinatorial optimisation problems. Related to all these techniques, the advances in quantum computation have originated a new field of study: quantum-inspired algorithms. Quantum-inspired algorithms try to formulate classical algorithms in a quantum way, using qbits and its properties, in order to increase the speed of these methods (Quantum-computing- related terminologies used here are defined in Section 2. The interested reader can find more detailed information in [9], Chapter 1.) For example, in [10], they use the superposition property in order to accelerate distribution shaping in the travelling salesman problem, or in [11], they use entanglement to prevent a two-agent autonomous system from cyber-physical attacks. In [12] is seen how quantum formulation helps in clustering problems and in [13,14] is seen how quantum properties are interesting for obtaining a better balance between exploration and exploitation in reinforcement learning. The same idea of reducing model size and increasing robustness is seen in other deep-learning techniques in [15]. One of the interesting applications of quantum-inspired algorithm development is explored in [16], where a quantum-inspired version of an evolutionary algorithm (EA) is implemented to solve a knaspack problem with a proven improvement with respect to classical EA.
This paper focuses on developing a computationally efficient suboptimal solution for the service-matching assignment problem (Section 1) using a quantum-inspired EA (QiEA) algorithm and demonstrates its application in solving a service-matching coverage problem illustrated in Figure 1. Special attention is given to the design of the collapsing procedure to make it more coherent with the real collapsing process of qbits and to speed up the process. In Section 2, preliminary notions about quantum theory are presented. The proposed method is presented in Section 3. In Section 4, a numerical study focused on a service-matching task assignment demonstrates the efficacy of our proposed algorithm. The conclusions and our plan for future work are explained in Section 5.
2. Preliminaries
This section gives the definition of the quantum formulation notion and terminologies we use throughout the paper. For the convenience of the reader, we also provide the definition of the KLD measure.
First, following [17], we introduce the notion and the definitions from the quantum formulation. In quantum computation, the basic unit of information is called a Qbit and it is neither one nor zero, but the superposition of both states. That means that, in one timestamp, there is a certain probability that the qbit is in in state zero or in state one. This can be formulated using Dirac’s notation, also known as brakets, as,
where is the qbit, and are the two possible states and and are the amplitudes of these states. The Born’s rule tells us that these amplitudes are directly related to the probability of being in state or as the probability of one state is the power of its amplitude,
One qbit remains in this superposition until it is measured or observed. When that happens, the qbit becomes fixed in one of the states in the function of the amplitudes, this process is called collapsing.
As explained in Equation (2), in the superposition state, a qbit depends on two parameters, and , that are indeed complex numbers. Therefore, qbits can be represented with spherical coordinates,
applying the Born’s rule, Equation (5),
were and . It can be demonstrated that has no observable effects [18]; therefore, effectively, we only have to consider the following equation,
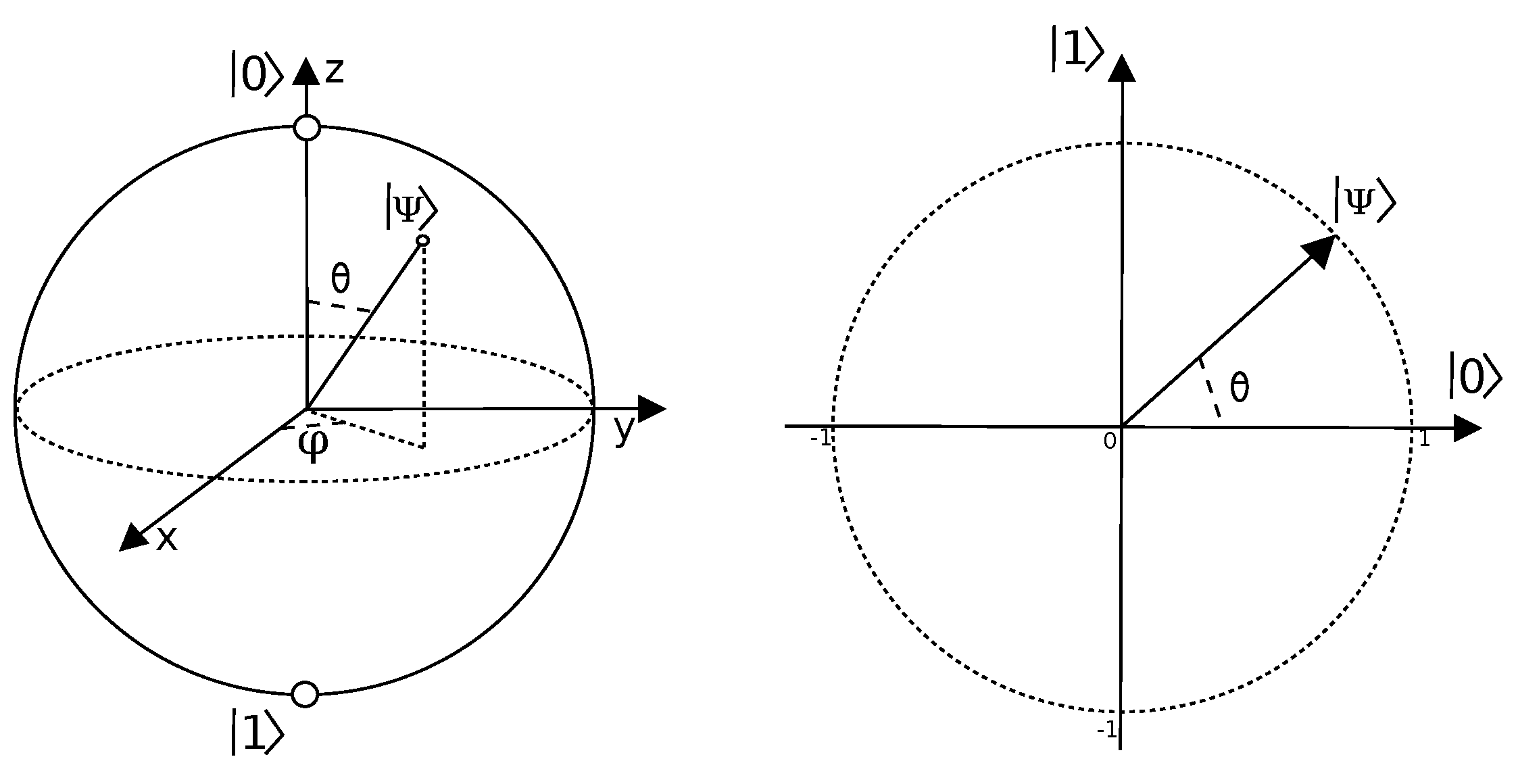
From Equation (8), it can be seen that a qbit belongs to a Hilbert space and can be represented as a sphere. This representation is known as a Bloch Sphere, Figure 2.
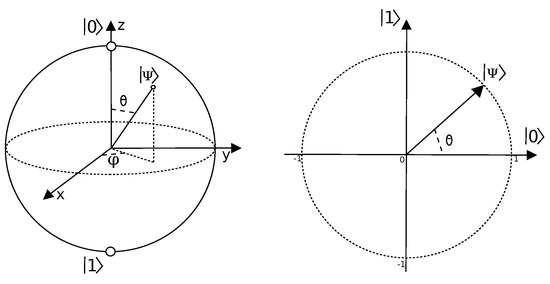
Figure 2.
Representation of a qbit: On the left, the Bloch Sphere, a spherical representation of a qbit. On the right, a circular representation of a qbit after all the assumptions.
From the Bloch Sphere, it can be seen that the state of a qbit can be modified using rotations. Indeed, in quantum computation, the logic gates used to develop circuits are no more than rotation operations. In this work, the only important rotation is the rotation, as it is the one that makes the superposition state closer or further to states or . Therefore, in this case, qbits can be represented as circles and, in order to modify them, a simple rotation matrix will be used.
KLD is a measure of similarity (dissimilarity) between two probability distributions and , where the smaller the value the more similar two distributions are. KLD is zero if and only if the two distribution are identical ([2], p.34). For Gaussian distributions, and , the KLD has a closed form expression ([19], Equation (2))
where n is the dimension of the distributions.
In what follows, we rely on a function best defined as
which, given any finite number of assignment matrices , return the assignment matrix that results in the smallest of cost , , computed according to the assignment cost (1a).
3. QiEA for Optimal Service Matching
Inspired by the concept of quantum computing of qbit representation, rotation, observation and qbit collapsing, we propose the QiEA Algorithm 1 as a suboptimal solution to the optimal service-matching problem (1). To design this algorithm, we proceeded as follows.
Consider the assignment matrix . For any given service agent , every feasible assignment consists of assigning 1 to one of the elements of , and zero to the rest, while respecting also (1d). Since we do not know which element should be 1, the idea is to start by a probabilistic approach and, for every service agent , attach a notion of probability to every , which indicates with what probability that element is 1. Then, at each iteration t of the algorithm, this probability is adjusted as we describe below. The notion of probability for each element can be realised using quantum qbits, . Thus, at each step t of the algorithm, for each individual l in population set , there is a qbit matrix
with size where each element is the mentioned probability of the assignment between agent and task .
| Algorithm 1 QiEA algorithm for service-matching assignment |
|
Evolutionary algorithms are based on the Darwinian explanation of species evolution where, step by step, there are mutations in each individual of the species and, by the end, only the individuals with better adaptation to the new environment survive. The evolutionary algorithms follow a two-step procedure [20]. First, we generate an initial population of individuals randomly. Next, we repeat the following re-generational steps until termination: (a) the fitness of each individual in the population is evaluated (lowest cost, feasibility), (b) the fittest individuals are selected as parents for reproduction, (c) new individuals are bred (from parents) through crossover and mutation operations to give birth to offspring, (d) the least-fit individuals of the population are replaced with new individuals.
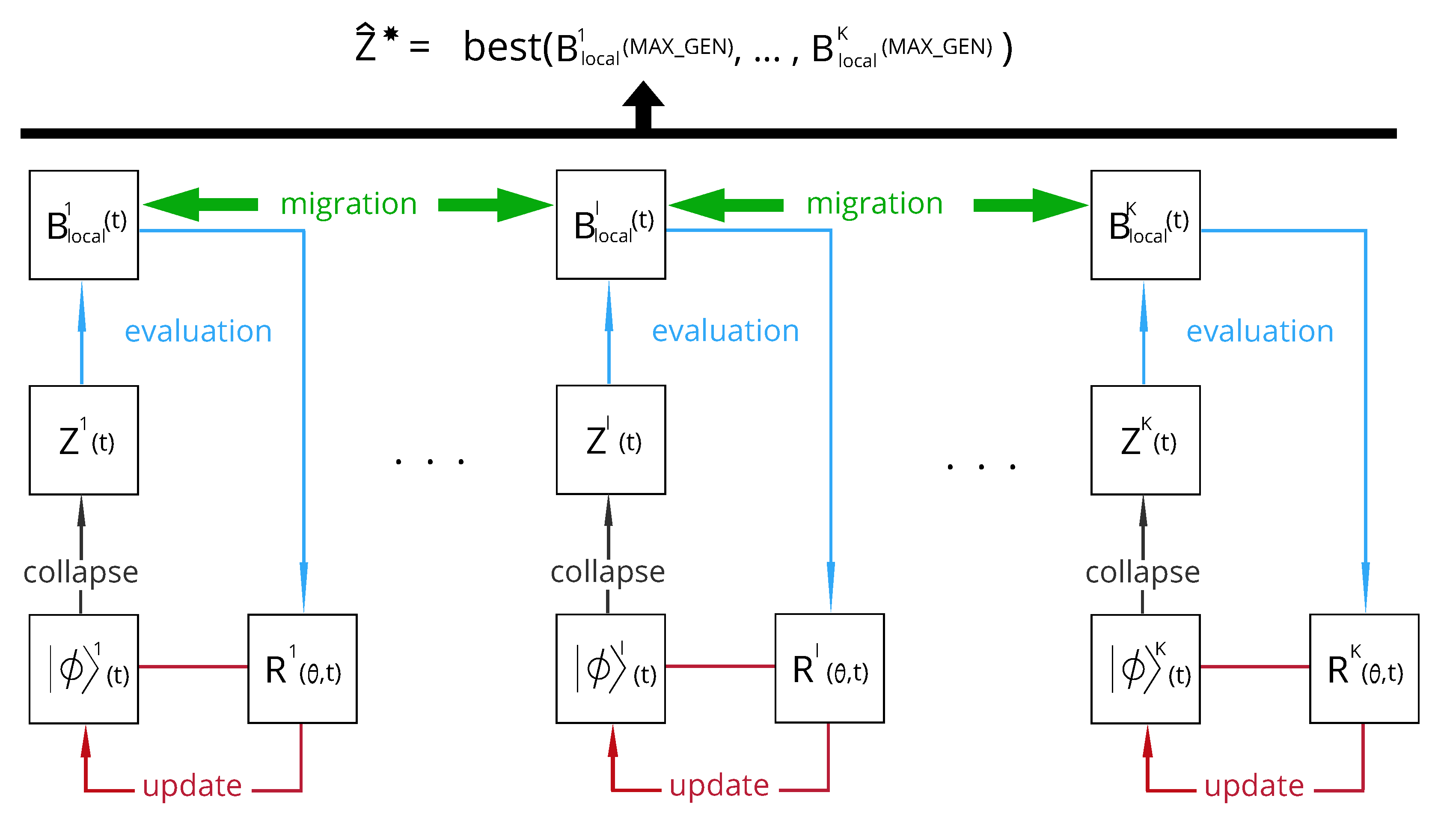
QiEA is a probabilistic algorithm similar to other evolutionary algorithms. We use an evolutionary method to go from an initial state of uncertainty to a final determined system , which is a suboptimal solution to (Section 1). The underlying concept in QiEA is that informs us on how to select individual at each step of the algorithm (an individual is selected by collapsing ). , which determines the probability of each element of being 0 or 1, is updated at each step based on the fitness of the generated individuals at step using the rotation method, which will be described below. The advantage of QiEA is, indeed, in this step of updating the probabilities of selecting future individuals based on feedback from the fitness of the generated individuals. The schematic procedure of our QiEA algorithm is shown in Figure 3. Our proposed QiEA is shown in Figure 3: there is a K parallel process to generate K individuals that constitutes the population set of the algorithm. Each individual generation process has its own , initialised at and updated at each iteration of the algorithm.
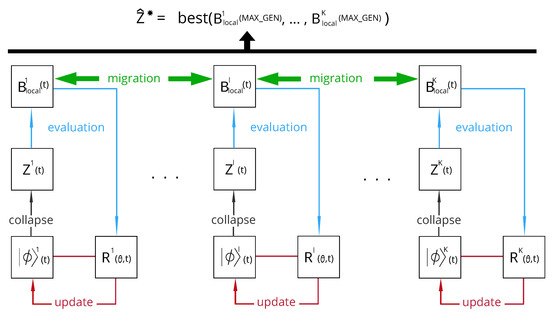
Figure 3.
Scheme of the QiEA procedure considering K initial populations.
Our proposed QiEA algorithm consists of three main procedural steps, collapsing, evaluation and updating and migration.
Collapsing procedure: This process is a novel contribution of this work and it is a faithful representation of the quantum-like collapsing of the qbit systems. With this purpose, the collapsing is performed using the maximum randomness possible. At each step t to generate individual , first, one random service i and one random target j are selected to form the agent–task pair . Then, with a uniform probability, we generate a random value . Then, is generated using the collapsing procedure below
After collapse, the agent–task pair is removed from the random selection, and the process is repeated until there is no service agent left to be selected (recall our assumption that there is more service agents than the tasks). Our collapsing procedure is summarised in Algorithm 2. It is important to note that, if a service agent is assigned to one task (qbit is collapsed to one), no other service agent can be assigned to that task and that service agent can not perform any other task. That is exactly what we formulated in constraints (1c) and (1d). That is, our individual generation procedure always generates feasible individuals , and does not need the costly and often ad-hoc repairing of the individuals that other quantum-inspired algorithms, e.g., [10,21,22], need. The elimination of the repair step also results in faster convergence.
| Algorithm 2 Collapsing |
|
Evaluation procedure: This procedure has two parts, the computation of the cost for fitness test, and the formulation/updating of the rotation matrix based on the feedback from the fitness analysis. Given the collapsed individuals , at step t, firstly, the cost of the assignment is computed. The fitness evaluation not only depends on the cost at time t due to but also has temporal information about the evolution of the system by saving the best obtained solution until that iteration, which is stored as . The variable for each individual is initialised by collapsing , as described in step 5 of Algorithm 1. The fitness analysis relies on function (11) and updates each local according to . Next, in the evaluation procedure, we update the qubit matrix according to
where rotation angle is determined from Table 1. Here, is a design parameter which normally is a very small angle. Recall that, according to the circular qbit representation (8), which is visualised in Figure 2, a positive rotation results in increasing the probability of collapsing to 1 and a negative rotation results in increasing the probability of collapsing to 0. We proposed Table 1 based on the logic that if the value of and are the same, we make no changes to the qbit corresponding to the agent–task pair , thus setting (cases 1, 2, 7 and 8 in Table 1). If changing from to results in decreasing the total cost, we want to encourage collapsing to by increasing this probability by using a positive rotation (case 3 in Table 1). On the other hand, if changing from to results in decreasing the total cost, we want to encourage collapsing to by increasing such probability by using a negative rotation (case 5 in Table 1). If the changes in the values result in increasing the total cost, we do not make any changes to , i.e., (cases 4 and 6 in Table 1). To summarise, we make an adjustment to if and the best value at step t is set to ; thus, we can interpret the change in value as a contributor to decreasing the cost. Algorithm 3 summarises our evaluation procedure.
| Algorithm 3 Evaluation |
|

Table 1.
Evaluation cases to define rotation angle.
Migration procedure: Like other evolutionary algorithms, to avoid getting stuck in local maxima or minima we perform a migration procedure when the migration condition MAX_GEN, where n is a percentage that defines when the process is completed. In the migration step, we simply replace the current best local value of all the individuals with , i.e., for all .
4. Numerical Demonstration
To demonstrate the efficacy of our proposed QiEA, consider the service-matching robot-deployment example we described in Section 1 and depicted in Figure 1. Recall that, in this example, we have a set of N service agents with spatial service distribution , with Gaussian distribution . Each target cluster , , extracted from a GMM model of the entire targets distribution, has a Gaussian distribution . According to [1], Theorm 2, the best value for is obtained when the robot is moved such that and the principle axes of the two uncertainty ellipsoids corresponding to and are parallel. Considering this configuration, for each service agent we compute to form the weighting matrix . Next, through a set of numerical simulations, we evaluate the efficacy of our QiEA algorithm in solving this optimal service-matching deployment problem.
In this work, all the simulation codes are developed with Python using well-known open-source libraries. The optimal deployment for service-matching data is randomly generated. We carry out a simulation study that compares the performance of our proposed Algorithm 1 to that of three well-known algorithms: the greedy algorithm, the Hungarian method and the Simplex linear-programming method. The greedy algorithm is an iterative method that greedily selects the smallest value of to set , eliminates the row and the column corresponding to from the weight matrix and repeats the procedure. The Hungarian method is a similar technique to the Greedy Algorithm but, instead of picking direct assignments from a static cost matrix, the cost matrix is modified at each step in the function of the minimum values of each row and column. Therefore, this method considers not only the minimum cost for each assignment, but also the rest of the assignments, which is why it can achieve the optimal solution. To have a comprehensive study, we also compare our result to that of the Simplex method, which solves the continuous relaxation of the optimal service-matching problem (Section 1).
4.1. Simulation Results
This section presents the results of our numerical experiments. The proposed algorithm is compared to the benchmark methods in five different scenarios. The simulations are conducted via Python programming on a PC with processor Intel(R) Core(TM) i7-10510U CPU @ 1.80GHz 2.30 GHz and a RAM of 16 GB.
4.1.1. Case Studies
We simulate five different scenarios, which are described in Table 2. Case 1 is the perfect-matching case, where . However, there can also be unbalanced cases where the number of target clusters is bigger than the number of the service agents. To demonstrate how our algorithm scales with respect to N and M and also their relative size, we consider various scenarios for when . The normal distributions for each target/service in each experiment are randomly created using Python.

Table 2.
Case studies.
4.1.2. Hyper-Parameters of the QiEA Algorithm 1
To execute the QiEA Algorithm 1, the set of hyper-parameters listed in the first column from the left of Table 3 should be selected. We chose three candidate values for each hyper-parameter as reported in Table 3. To tune the hyper-parameters for each case study listed in Table 2, a grid search over 81 different combinations was implemented. During this grid search, it was observed that there can be two groups of hyperparameters: the ones that make the algorithm more accurate and the ones that make the algorithm faster (compared over same number of epochs). As such, we report the simulation results for two different executions of Algorithm 1 for solving our problem of interest for the cases listed in Table 2: the accurate quantum-inspired evolutionary algorithm (AQiEA) and the fast quantum-inspired evolutionary algorithm (FQiEA). Table 4 gives the chosen hyper-parameters for each case study. Notice that the hyper-parameters are not necessarily the same for each case study.

Table 3.
Hyper-parameters of and the assigned possible values for the grid search.

Table 4.
Grid search results.
4.1.3. Metrics
In order to compare and evaluate the performance of the methods, three metrics have been considered, which include optimality gap, execution time complexity and a quality metric. The optimality gap, denoted by , is defined as
When , the Hungarian and the Simplex methods are guaranteed to produce an optimal solution; however, this guarantee is not the case when . To obtain the optimal value for , a suggested practice is adding virtual service agents whose assignment costs to task clusters are much greater than the actual service agents’. This way, a perfect matching problem is created, which we use to generate the optimal cost value for computing the optimality gap. Notice that adding virtual agents increases the computational complexity of the algorithms. The simulation results reported below for all the algorithms consider the actual matching cases when no virtual agent is added.
The execution time, measured in milliseconds (ms), is the time it took to run the algorithm. To unify both prior metrics and for the sake of the comparison, the quality metric Q was implemented in order to have a faster and easier way of comparing and discussing the algorithms. This metric is computed as
4.1.4. Simulation Results
The simulation results for the three aforementioned performance metrics are reported in Table 5, Table 6 and Table 7. Per definition (15), the best optimality result is when . Thus, for a suboptimal solution, we desire an closer to zero. For Case 1, as expected, the results in Table 5 show that the Hungarian and Simplex methods have zero optimality gap. Notice that in Case 1, AQiEA outperforms the greedy method in the optimality gap, while FQiEA delivers a close performance to that of the greedy algorithm. In the rest of the cases, the Hungarian and the Simplex methods also deliver a zero optimality gap, but as Table 6 shows, this comes with a high execution time, especially when the scale of the system grows. In Case 4, the Simplex algorithm failed to converge in a reasonable time, so no results are listed for this case in Table 5, Table 6 and Table 7. Per definition (16), the quality metric Q is designed to be 100 when the optimality gap is zero and the execution time is 1 ms. As the results in Table 7 show, both QiEA algorithms outperform the rest of the methods in terms of the quality metric.

Table 5.
Optimality gap for the case studies.

Table 6.
Execution time in ms for the case studies.

Table 7.
Quality metric for the case studies.
5. Conclusions
This work showed how a quantum-inspired evolutionary algorithm could be used as a practical solution method to solve combinatorial optimisation problems such as an optimal service-matching coverage problem. Our numerical studies showed that the quantum approach presents better scalability and interesting properties that can be used in a wider class of assignment problems where the matching is not perfect. Our future work will apply our proposed quantum-inspired evolutionary algorithm framework in solving submodular maximisation problems, particularly the optimal welfare problem. We will also study the automated tuning of the algorithm hyper-parameters using a machine-learning approach.
Author Contributions
Conceptualization, J.V. and S.K; methodology, J.V.; software, J.V.; validation, S.K.; resources, S.K.; investigation, J.V. and S.K; writing—original draft preparation, J.V.; writing—review and editing, S.K.; supervision, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by a Balsells Fellowship grant and there was no APC.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| QiEA | Quantum-inspired evolutionary algorithm |
| AQiEA | Accurate quantum-inspired evolutionary algorithm |
| FQiEA | Fast quantum-inspired evolutionary algorithm |
| EA | Evolutionary algorithm |
| AP | Assignment problem |
| KLD | Kullback–Leibler divergence |
| TC | Target cluster |
| UAV | Unmanned aerial vehicle |
References
- Chung, Y.; Kia, S.S. A distributed service-matching coverage via heterogeneous agents. IEEE Robot. Autom. Lett. 2022, 7, 4400–4407. [Google Scholar] [CrossRef]
- MacKay, D. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003; p. 34. [Google Scholar]
- Baybars, I. A Survey of exact algorithms for the simple assembly line balancing problem. Manag. Sci. 1986, 32, 909–932. [Google Scholar] [CrossRef]
- Sivasankaran, P.; Shahabudeen, P. Literature review of assembly line balancing problems. Int. J. Adv. Technol. 2014, 73, 1665–1694. [Google Scholar] [CrossRef]
- Simonetto, A.; Monteil, J.; Gambella, C. Real-time city-scale ridesharing via linear assignment problems. Transp. Res. Part C Emerg. Technol. 2019, 101, 208–232. [Google Scholar] [CrossRef]
- Siebert, H. The Assignment Problem. In Beiträge zur mikro- und zur makroökonomik; Berninghaus, S.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 1, pp. 439–448. [Google Scholar]
- Sviridenko, M. A note on maximizing a submodular set function subject to a knapsack constraint. Oper. Res. Lett. 2004, 32, 41–43. [Google Scholar] [CrossRef]
- Williamson, D.P.; Shmoys, D.B. The Design of Approximation Algorithms; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Woit, P. Introduction. In Quantum Theory, Groups and Representations: An Introduction; Department of Mathematics, Columbia University: New York, NY, USA, 2022; pp. 1–12. [Google Scholar]
- Soloviev, V.P.; Bielza, C.; Larranaga, P. Quantum-inspired estimation Of distribution algorithm to solve the travelling salesman problem. In Proceedings of the IEEE Congress on Evolutionary Computation, Kraków, Poland, 28 June–1 July 2021; pp. 416–425. [Google Scholar]
- Khoshnoud, F.; de Silva, C.W.; Ibrahim, I. Quantum entanglement of autonomous vehicles for cyber-physical security. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Banff, AB, Canada, 5–8 October 2017; pp. 2655–2660. [Google Scholar]
- Xiao, J.; Yan, Y.; Zhang, J.; Tang, Y. A quantum-inspired genetic algorithm for k-means clustering. Expert Syst. Appl. 2010, 37, 4966–4973. [Google Scholar] [CrossRef]
- Li, Y.; Aghvami, A.H.; Dong, D. Intelligent trajectory planning in UAV-mounted wireless networks: A quantum-inspired reinforcement learning perspective. IEEE Wirel. Commun. Lett. 2021, 10, 1994–1998. [Google Scholar] [CrossRef]
- Chen, C.; Yang, P.; Zhou, X.; Dong, D. A Quantum-inspired Q-learning algorithm for indoor robot navigation. In Proceedings of the IEEE International Conference on Networking, Sensing and Control, Sanya, China, 6–8 April 2008; pp. 1599–1603. [Google Scholar]
- Rajesh, V.; Parameshwar, U.; Mohana, N. Quantum Convolutional neural networks (QCNN) using deep learning for computer vision applications. In Proceedings of the International Conference on Recent Trends on Electronics, Information, Communication and Technology, Bangalore, India, 27–28 August 2021; pp. 728–734. [Google Scholar]
- Han, K.; Kim, J. Quantum-inspired evolutionary algorithm for a class of combinatorial optimization. IEEE Trans. Evol. Comput. 2002, 6, 580–593. [Google Scholar] [CrossRef]
- Combarro, E.F. A Practical Introduction to Quantum Computing: From Qubits to Quantum Machine Learning and Beyond; CERN OpenLab: Geneva, Switzerland, 2020. [Google Scholar]
- Messiah, A. Quantum Mechanics; Dover Publications Inc.: Mineola, NY, USA, 1999; Volume 1, p. 296. [Google Scholar]
- Hershey, J.R.; Olsen, P.A. Approximating the Kullback Leibler divergence between Gaussian mixture models. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, HI, USA, 15–20 April 2007; Volume 4, pp. 317–320. [Google Scholar]
- Streichert, F. Introduction to Evolutionary Algorithms. In Evolutionary Computation 1; CRC Press: Boca Raton, FL, USA; University of Tübingen: Tübingen, Germany, 2018; pp. 97–101. [Google Scholar]
- Chmiel, W.; Kwiecień, J. Quantum-inspired evolutionary approach for the quadratic assignment problem. Entorpy 2022, 20, 781. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G. Quantum-inspired evolutionary algorithms: A survey and empirical study. J. Heuristics 2011, 17, 303–351. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).