A Review of Knowledge Graph Completion
Abstract
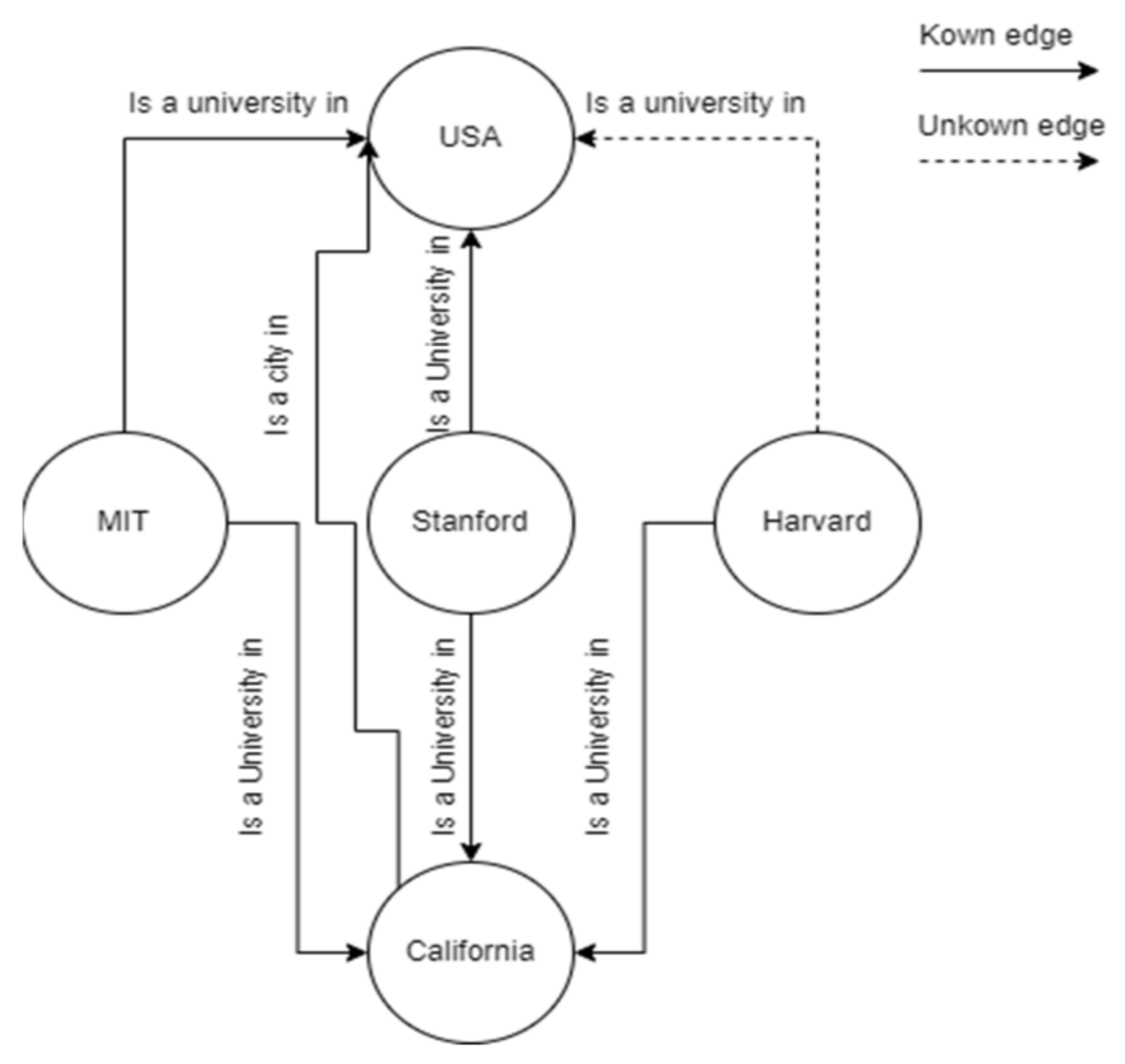
:1. Introduction
2. Conventional Knowledge Graph Completion
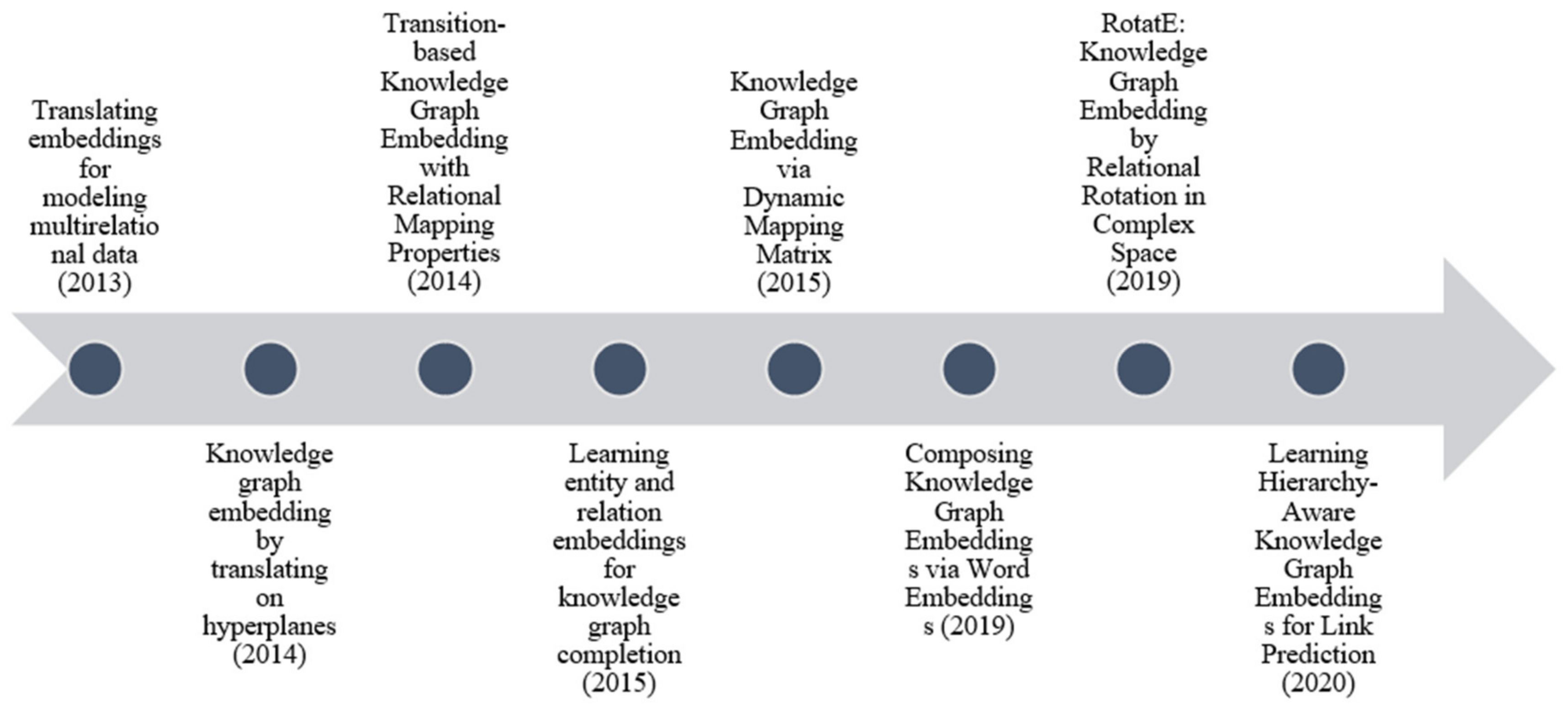
2.1. Translational Models
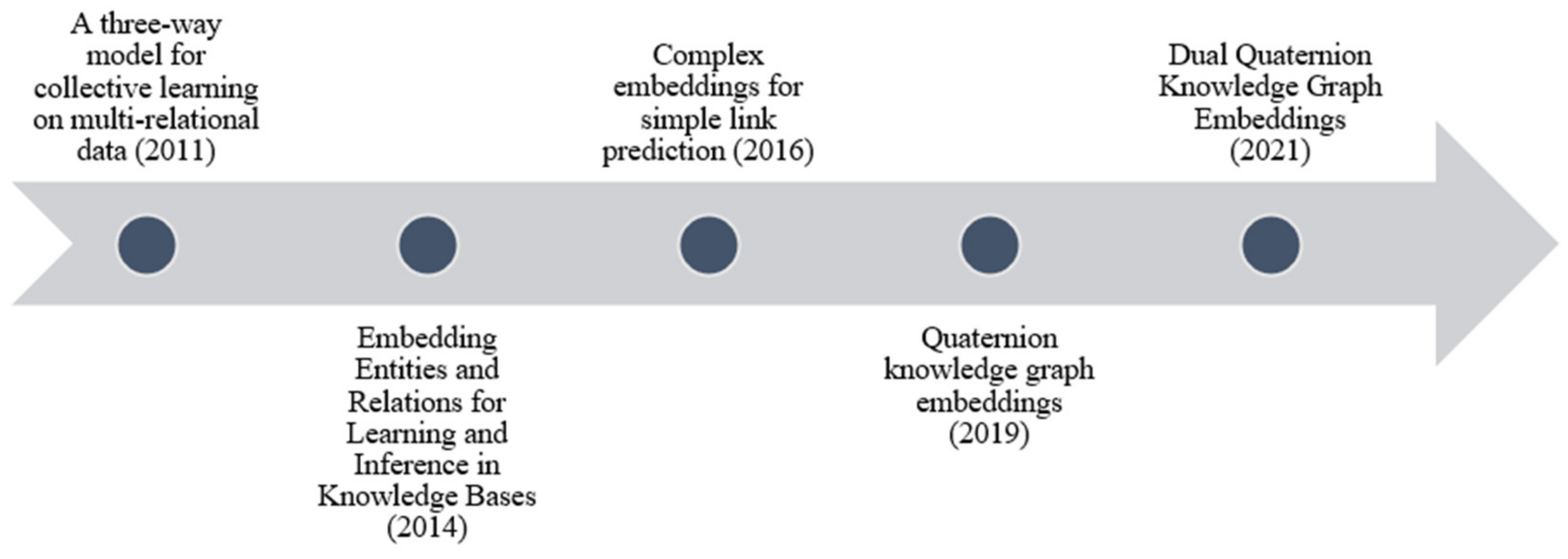
2.2. Tensor Dompositional Models
2.3. Neural Network Models
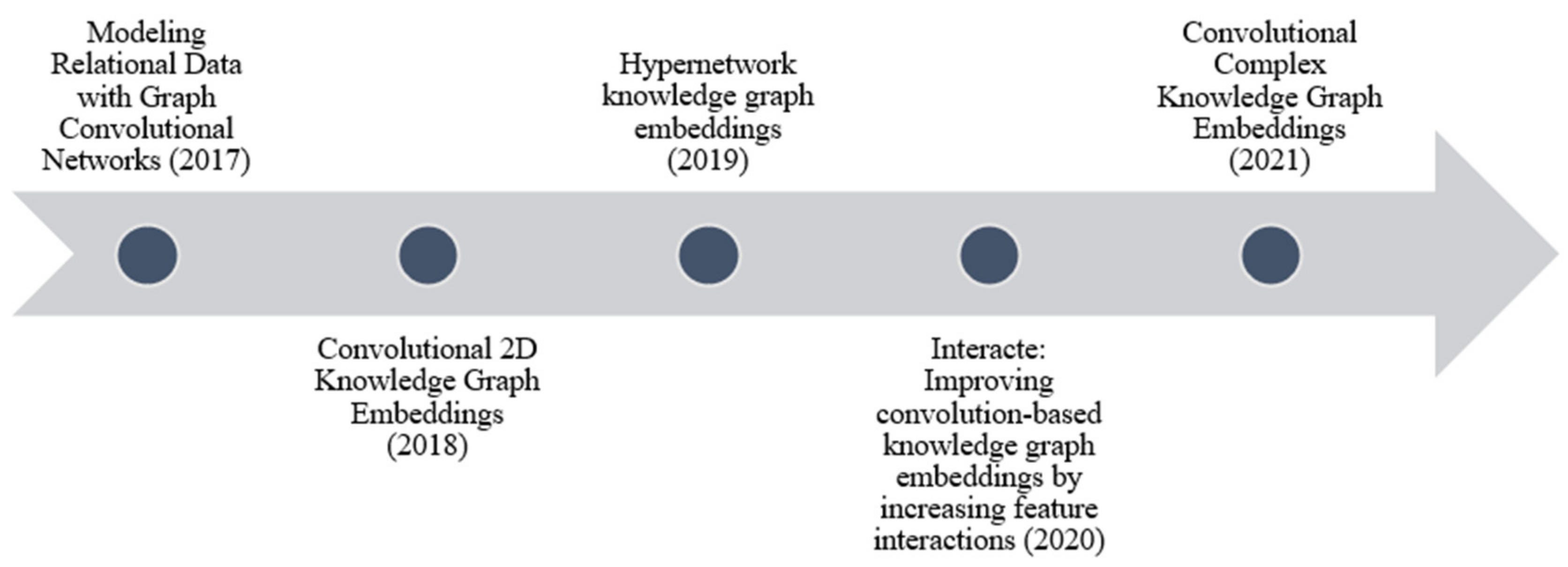
2.4. Convolutional-Based Models
3. Graph Neural Networks
3.1. Graph Convolution Network Models
3.2. Attention Neural Network Models
3.3. Pre-Trained Neural Network Models in Knowledge Graphs
4. Challenges in Knowledge Graphs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stokman, F.N.; Vries, P.H.D. Structuring knowledge in a graph. In Human-Computer Interaction; Springer: Berlin/Heidelberg, Germany, 1988; pp. 186–206. [Google Scholar]
- Noy, N.; Gao, Y.; Jain, A.; Narayanan, A.; Patterson, A.; Taylor, J. Industry-scale Knowledge Graphs: Lessons and Challenges: Five diverse technology companies show how it’s done. Queue 2019, 17, 48–75. [Google Scholar] [CrossRef]
- Lenat, D.; Guha, R. Building large knowledge-based systems: Representation and inference in the CYC project. Artif. Intell. 1993, 61, 4152. [Google Scholar]
- Auer, S.; Bizer, C.; Kobilarov, G.; Lehmann, J.; Cyganiak, R.; Ives, Z. Dbpedia: A nucleus for a web of open data. In The Semantic Web; Springer: Berlin/Heidelberg, Germany, 2007; pp. 722–735. [Google Scholar]
- Bollacker, K.; Evans, C.; Paritosh, P.; Sturge, T.; Taylor, J. Freebase: A collaboratively created graph database for structuring human knowledge. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 10–12 June 2008. [Google Scholar]
- Suchanek, F.M.; Kasneci, G.; Weikum, G. Yago: A core of semantic knowledge. In Proceedings of the 16th International Conference on World Wide Web, Banff, AB, Canada, 8–12 May 2007. [Google Scholar]
- Vrandečić, D.; Krötzsch, M. Wikidata: A free collaborative knowledgebase. Commun. ACM 2014, 57, 78–85. [Google Scholar] [CrossRef]
- Wang, S.; Huang, C.; Li, J.; Yuan, Y.; Wang, F.-Y. Decentralized construction of knowledge graphs for deep recommender systems based on blockchain-powered smart contracts. IEEE Access 2019, 7, 136951–136961. [Google Scholar] [CrossRef]
- Antoine, B.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems 2013, Lake Tahoe, NV, USA, 5–8 December 2013; Volume 26. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge graph embedding by translating on hyperplanes. In Proceedings of the AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–31 July 2014. [Google Scholar]
- Yang, B.; Yih, W.-t.; He, X.; Gao, J.; Deng, L. Embedding entities and relations for learning and inference in knowledge bases. arXiv 2014, arXiv:1412.6575. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex embeddings for simple link prediction. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Sun, Z.; Deng, Z.-H.; Nie, J.-Y.; Tang, J. Rotate: Knowledge graph embedding by relational rotation in complex space. arXiv 2019, arXiv:1902.10197. [Google Scholar]
- Yu, D.; Yang, Y.; Zhang, R.; Wu, Y. Knowledge embedding based graph convolutional network. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; van den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In European Semantic Web Conference; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Vashishth, S.; Sanyal, S.; Nitin, V.; Talukdar, P. Composition-based multi-relational graph convolutional networks. arXiv 2019, arXiv:1911.03082. [Google Scholar]
- Cai, L.; Yan, B.; Mai, G.; Janowicz, K.; Zhu, R. TransGCN: Coupling transformation assumptions with graph convolutional networks for link prediction. In Proceedings of the 10th International Conference on Knowledge Capture, Marina Del Rey, CA, USA, 19–21 November 2019. [Google Scholar]
- Nathani, D.; Chauhan, J.; Sharma, C.; Kaul, M. Learning attention-based embeddings for relation prediction in knowledge graphs. arXiv 2019, arXiv:1906.01195. [Google Scholar]
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning entity and relation embeddings for knowledge graph completion. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Ji, G.; He, S.; Xu, L.; Liu, K.; Zhao, J. Knowledge graph embedding via dynamic mapping matrix. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing, Beijing, China, 26–31 July 2015; Volume 1. [Google Scholar]
- Fan, M.; Zhou, Q.; Chang, E.; Zheng, F. Transition-based knowledge graph embedding with relational mapping properties. In Proceedings of the 28th Pacific Asia Conference on Language, Information and Computing, Phuket, Thailand, 12–14 December 2014. [Google Scholar]
- Ma, L.; Sun, P.; Lin, Z.; Wang, H. Composing knowledge graph embeddings via word embeddings. arXiv 2019, arXiv:1909.03794. [Google Scholar]
- Zhang, Z.; Cai, J.; Zhang, Y.; Wang, J. Learning hierarchy-aware knowledge graph embeddings for link prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Hogan, A.; Blomqvist, E.; Cochez, M.; d’Amato, C.; Melo, G.d.; Gutierrez, C.; Kirrane, S.; Gayo, J.E.L.; Navigli, R.; Neumaier, S. Knowledge graphs. In Synthesis Lectures on Data, Semantics, and Knowledge; Morgan & Claypool Publishers: San Rafael, CA, USA, 2021; Volume 12, pp. 1–257. [Google Scholar]
- Nickel, M.; Tresp, V.; Kriegel, H.-P. A three-way model for collective learning on multi-relational data. In Proceedings of the 28th International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Wang, Q.; Mao, Z.; Wang, B.; Guo, L. Knowledge graph embedding: A survey of approaches and applications. IEEE Trans. Knowl. Data Eng. 2017, 29, 2724–2743. [Google Scholar] [CrossRef]
- Bordes, A.; Glorot, X.; Weston, J.; Bengio, Y. A semantic matching energy function for learning with multi-relational data. Mach. Learn. 2014, 94, 233–259. [Google Scholar] [CrossRef]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2d knowledge graph embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Zhang, S.; Tay, Y.; Yao, L.; Liu, Q. Quaternion knowledge graph embeddings. In Proceedings of the Annual Conference on Neural Information Processing Systems 2019, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Cao, Z.; Xu, Q.; Yang, Z.; Cao, X.; Huang, Q. Dual quaternion knowledge graph embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021. [Google Scholar]
- Balažević, I.; Allen, C.; Hospedales, T.M. Tucker: Tensor factorization for knowledge graph completion. arXiv 2019, arXiv:1901.09590. [Google Scholar]
- Wang, Q.; Wang, B.; Guo, L. Knowledge base completion using embeddings and rules. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Guo, S.; Wang, Q.; Wang, B.; Wang, L.; Guo, L. Semantically smooth knowledge graph embedding. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing, Beijing, China, 26–31 July 2015; Volume 1. [Google Scholar]
- Lin, Y.; Liu, Z.; Luan, H.; Sun, M.; Rao, S.; Liu, S. Modeling relation paths for representation learning of knowledge bases. arXiv 2015, arXiv:1506.00379. [Google Scholar]
- Socher, R.; Chen, D.; Manning, C.D.; Ng, A. Reasoning with neural tensor networks for knowledge base completion. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems 2013, Lake Tahoe, NV, USA, 5–8 December 2013; Volume 26. [Google Scholar]
- Balažević, I.; Allen, C.; Hospedales, T.M. Hypernetwork knowledge graph embeddings. In Proceedings of the International Conference on Artificial Neural Networks, Munich, Germany, 17–19 September 2019; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Vashishth, S.; Sanyal, S.; Nitin, V.; Agrawal, N.; Talukdar, P. Interacte: Improving convolution-based knowledge graph embeddings by increasing feature interactions. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Yu, D.; Zhu, C.; Yang, Y.; Zeng, M. Jaket: Joint pre-training of knowledge graph and language understanding. arXiv 2020, arXiv:2010.00796. [Google Scholar] [CrossRef]
- Nguyen, D.Q.; Nguyen, T.D.; Nguyen, D.Q.; Phung, D. A novel embedding model for knowledge base completion based on convolutional neural network. arXiv 2017, arXiv:1712.02121. [Google Scholar]
- Demir, C.; Ngomo, A.-C.N. Convolutional complex knowledge graph embeddings. In European Semantic Web Conference; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Song, T.; Luo, J.; Huang, L. Rot-pro: Modeling transitivity by projection in knowledge graph embedding. Adv. Neural Inf. Process. Syst. 2021, 34, 24695–24706. [Google Scholar]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated graph sequence neural networks. arXiv 2015, arXiv:1511.05493. [Google Scholar]
- Guo, L.; Wang, W.; Sun, Z.; Liu, C.; Hu, W. Decentralized Knowledge Graph Representation Learning. arXiv 2020, arXiv:2010.08114. [Google Scholar]
- Hogan, A.; Blomqvist, E.; Cochez, M.; D’amato, C.; Melo, G.D.; Gutierrez, C.; Kirrane, S.; Gayo, J.E.L.; Navigli, R.; Neumaier, S.; et al. Knowledge Graphs. ACM Comput. Surv. 2021, 54, 71. [Google Scholar]
- Sperduti, A.; Starita, A. Supervised neural networks for the classification of structures. IEEE Trans. Neural Netw. 1997, 8, 714–735. [Google Scholar] [CrossRef]
- Gori, M.; Monfardini, G.; Scarselli, F. A new model for learning in graph domains. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Abboud, R.; Ceylan, I.; Lukasiewicz, T.; Salvatori, T. Boxe: A box embedding model for knowledge base completion. Adv. Neural Inf. Process. Syst. 2020, 33, 9649–9661. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Marcheggiani, D.; Titov, I. Encoding sentences with graph convolutional networks for semantic role labeling. arXiv 2017, arXiv:1703.04826. [Google Scholar]
- Shang, C.; Tang, Y.; Huang, J.; Bi, J.; He, X.; Zhou, B. End-to-end structure-aware convolutional networks for knowledge base completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Li, J.; Shomer, H.; Ding, J.; Wang, Y.; Ma, Y.; Shah, N.; Tang, J.; Yin, D. Are Graph Neural Networks Really Helpful for Knowledge Graph Completion? arXiv 2022, arXiv:2205.10652. [Google Scholar]
- Kazemi, S.M.; Poole, D. Simple embedding for link prediction in knowledge graphs. In Proceedings of the Thirty-Second Annual Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Tian, A.; Zhang, C.; Rang, M.; Yang, X.; Zhan, Z. RA-GCN: Relational aggregation graph convolutional network for knowledge graph completion. In Proceedings of the 2020 12th International Conference on Machine Learning and Computing, Shenzhen, China, 15–17 February 2020. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018. [Google Scholar]
- Liu, X.; Tan, H.; Chen, Q.; Lin, G. RAGAT: Relation aware graph attention network for knowledge graph completion. IEEE Access 2021, 9, 20840–20849. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, Y.; Kou, X.; Li, Y.; Zhang, Y. r-GAT: Relational Graph Attention Network for Multi-Relational Graphs. arXiv 2021, arXiv:2109.05922. [Google Scholar]
- Ji, K.; Hui, B.; Luo, G. Graph attention networks with local structure awareness for knowledge graph completion. IEEE Access 2020, 8, 224860–224870. [Google Scholar] [CrossRef]
- Wu, J.; Shi, W.; Cao, X.; Chen, J.; Lei, W.; Zhang, F.; Wu, W.; He, X. DisenKGAT: Knowledge Graph Embedding with Disentangled Graph Attention Network. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Gold Coast, Australia, 1–5 November 2021. [Google Scholar]
- Li, Z.; Liu, H.; Zhang, Z.; Liu, T.; Xiong, N.N. Learning knowledge graph embedding with heterogeneous relation attention networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 3961–3973. [Google Scholar] [CrossRef]
- Yao, L.; Mao, C.; Luo, Y. KG-BERT: BERT for knowledge graph completion. arXiv 2019, arXiv:1909.03193. [Google Scholar]
- Wang, X.; Gao, T.; Zhu, Z.; Zhang, Z.; Liu, Z.; Li, J.; Tang, J. KEPLER: A Unified Model for Knowledge Embedding and Pre-trained Language Representation. Trans. Assoc. Comput. Linguist. 2021, 9, 176–194. [Google Scholar] [CrossRef]
- Petroni, F.; Rocktäschel, T.; Lewis, P.; Bakhtin, A.; Wu, Y.; Miller, A.H.; Riedel, S. Language models as knowledge bases? arXiv 2019, arXiv:1909.01066. [Google Scholar]
- Wang, C.; Liu, X.; Song, D. Language models are open knowledge graphs. arXiv 2020, arXiv:2010.11967. [Google Scholar]
- Talukdar, P.P. OKGIT: Open Knowledge Graph Link Prediction with Implicit Types. arXiv 2021, arXiv:2106.12806. [Google Scholar]
- Chen, S.; Wang, J.; Jiang, F.; Lin, C.-Y. Improving entity linking by modeling latent entity type information. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]

| Notation | Description |
|---|---|
| d | Vector |
| Wr | The normal vector of hyperplane |
| r | Embedding vector of relation |
| h, t | Embedding vectors of head and tail |
| M | Projection matrix |
| 〈 〉 | Diagonal matrices |
| d | The dimensionality of an entity in embedding space |
| k | The dimensionality of relation in embedding space |
| Re | The real part of a complex value |
| ⨂ | Hamilton product |
| Model | Score Function | Memory Complexity |
|---|---|---|
| TransE | ||
| TransH | ||
| TransR | ||
| TransD | ||
| TransM | ||
| TransW | ||
| RotatE | ||
| HAKE |
| Model | Score Function | Memory Complexity |
|---|---|---|
| RESCAL | ||
| DistMult | ||
| ComplEx | ||
| Quaternion | ||
| DualE | ||
| Tucker |
| Model | Score Function | Memory Complexity |
|---|---|---|
| SME | ||
| NTN |
| Model | Score Function | Memory Complexity |
|---|---|---|
| ConvE | ||
| ConvKB | ||
| HypER | ||
| InteractE | ||
| ConEx |
| Model | Relation Update | Entity Update |
| R-GCN | - | |
| RA-GCN | - | |
| TransE-GCN | ||
| KE-GCN | ||
| CompGCN |
| Model | WN18RR | FB15k-237 | ||
|---|---|---|---|---|
| MR | Hits@10 | MR | Hits@10 | |
| TransE [13] | 3384 | 50.1 | 357 | 46.5 |
| TransH [61] | 2524 | 50.3 | 255 | 48.6 |
| TransR [61] | 3166 | 50.7 | 237 | 51.1 |
| TransD [61] | 276 | 50.7 | 246 | 48.4 |
| DistMult [61] | 3704 | 47.7 | 411 | 41.9 |
| ComplEx [61] | 3921 | 48.3 | 508 | 43.4 |
| Tucker [31] | - | 52.6 | - | 54.4 |
| ConvE [28] | 5277 | 48 | 246 | 49.1 |
| InteractE [37] | 5202 | 52.8 | 172 | 53.5 |
| ConvKB [39] | 3324 | 52.4 | 311 | 42.1 |
| ConEx [38] | - | 55 | - | 55.5 |
| LSA-GAT [49] | 1947 | 44 | 273 | 60 |
| HARN [60] | 2113 | 54.2 | 156 | 54.1 |
| R-GCN [15] | - | - | - | 41.7 |
| RotatE-GCN [17] | - | 55.5 | - | 57.8 |
| TransE-GCN [17] | - | 47.7 | - | 50.8 |
| COMPGCN [16] | 3533 | 54.6 | 197 | 53.5 |
| RotatE [13] | 3384 | 50.1 | 177 | 53.3 |
| HAKE [23] | - | 58.2 | - | 54.2 |
| KG-BERT [61] | 97 | 52.4 | 153 | 42.0 |
| QuatE [13] | 2314 | 58.2 | 87 | 55 |
| DualE [30] | 2270 | 44.4 | 91 | 55.9 |
| DisenKGAT [59] | 1504 | 57.8 | 179 | 55.3 |
| RAGAT [56] | 2390 | 56.22 | 199 | 54.7 |
| KBGAT [18] | 1921 | 55.4 | 270 | 33.1 |
| Inverse Model [28] | 13,219 | 36 | 7148 | 1.2 |
| decentRL + TransE [43] | - | - | 159 | 52.1 |
| decentRL + DistMult [43] | - | - | 151 | 54.1 |
| RGCN + TransE [43] | - | - | 325 | 44.3 |
| RGCN + DistMult [43] | - | - | 230 | 49.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamini, M.; Reza, H.; Rabiei, M. A Review of Knowledge Graph Completion. Information 2022, 13, 396. https://doi.org/10.3390/info13080396
Zamini M, Reza H, Rabiei M. A Review of Knowledge Graph Completion. Information. 2022; 13(8):396. https://doi.org/10.3390/info13080396
Chicago/Turabian StyleZamini, Mohamad, Hassan Reza, and Minou Rabiei. 2022. "A Review of Knowledge Graph Completion" Information 13, no. 8: 396. https://doi.org/10.3390/info13080396
APA StyleZamini, M., Reza, H., & Rabiei, M. (2022). A Review of Knowledge Graph Completion. Information, 13(8), 396. https://doi.org/10.3390/info13080396






