Abstract
Recently, emerging technologies have assisted the healthcare system in the treatment of a wide range of diseases so considerably that the development of such methods has been regarded as a practical solution to cure many diseases. Accordingly, underestimating the importance of such cyber environments in the medical and healthcare system is not logical, as a combination of such systems with the Metaverse can lead to tremendous applications, particularly after this pandemic, in which the significance of such technologies has been proven. This is why the digital twin of a medical microrobot, which is controlled via a stochastic model predictive controller (MPC) empowered by a system identification based on machine learning (ML), has been rendered in this research. This robot benefits from the technology of magnetic levitation, and the identification approach helps the controller to identify the dynamic of this robot. Considering the size, control system, and specifications of such micro-magnetic mechanisms, it can play an important role in monitoring, drug-delivery, or even some sensitive internal surgeries. Thus, accuracy, robustness, and reliability have been taken into consideration for the design and simulation of this magnetic mechanism. Finally, a second-order statistic noise is added to the plant while the controller is updated by a Kalman filter to deal with this environment. The results prove that the proposed controller will work effectively.
1. Introduction
The cyber-physical system (CPS) is a combination of real objects with their models, in which cyberspace and physical processes can have helpful interactions with each other. Using feedback loops, embedded computers and networks are also used to observe and regulate physical processes [1]. This way, the significance of the utilization of high-tech technologies, such as optoelectronics, mechatronic systems, and nano-technology, needs to be more noticed as the main part of physical systems is related to measurement and monitoring [2,3,4,5,6,7,8,9]. Therefore, the utilization of such methods can be constructive. Sensors collect a wide range of data kinds from the actual environment. These data are subsequently sent to cyberspace, where they are analyzed and evaluated. The CPS objective is to embed intelligence in common objects/services to perform vital functions.
Another important approach to improving the power of computing with the least knowledge of the system is artificial intelligence (AI). In this respect, machine learning (ML) and deep learning (DL) can be regarded as two important sub-techniques, presenting us with a number of models and algorithms to model and analyze a range of problems [10]. The application of ML and DL in medicine has significantly caught the attention of various fields from drug discovery to the diagnoses of diseases [11,12,13,14]. On the other hand, such techniques have appropriate performance in modeling or identifying robots. Nevertheless, the role of communication technologies such as 5G, microwave systems, and other infrastructures is very important in the deployment of such systems [15,16,17,18].
Trajectory Tracking is an important subject in order to achieve effective autonomous safe driving systems [19]. In other words, precise trajectory tracking and state estimation under uncertainty should necessarily be considered for providing intelligent vehicle control systems to operate in real environment, including neutral uncertainties. In a nutshell, a model predictive controller (MPC) is a sophisticated approach of process control that is used to govern a process while meeting a set of criteria [20,21]. An MPC algorithm with integral action is presented in [22]. Mokhtar et al., in [23], suggested an improved model predictive controller (MPC) for a grid-linked, single-phase, full-bridge, five-level, T-type inverter to maintain high reliability.
Magnetic levitation is the system investigated in this research. The magnetic levitation system has practical value in many technical applications due to the advantage of contact-less mobility. Magnetically driven robot platforms had quite a considerable influence on medical robotics throughout the last century, giving new technologies to assist noninvasive therapeutics and diagnostics in many parts of the human body. The fundamental advantage of robots which are magnetically actuated is that useful forces and torques may be applied without the requirement for additional, typically complex and large, onboard locomotion devices. These devices have been studied for use in a variety of endoscopic techniques, including colonoscopy [24,25], surgeries [26], and cardiovascular purposes [27].
An MPC consists of a wide range of variety, which is an inherent part of autonomous systems. For controlling hybrid aerial vehicles, an MPC is proposed by [28], and they made a comparison between constrained and unconstrained MPCs. The properties of a robust economic model predictive control (REMPC) algorithm in terms of rejection of disturbances in initial conditions and non-stationary disturbances, robust stabilization, and closed-loop performance in the presence of model parameter errors and the enforcement of optimal economic periodic operations are investigated by Omar Santander and colleagues in [29]. An MPC can contribute with Fuzzy logic to perform quickly and reliably [30]. A calibrated nonlinear DC motor under uncertainity [31] and a networked model predictive controller for large-scale networked control systems for collision avoidance of networked vehicles are proposed in [32].
In this paper, first, three profiles for current, position, and velocity are simulated. The system identification is then used to obtain the model’s state spaces in order to construct the MPC. The nonlinear ARX neural network is used to predict the dynamic model of the physical systems. A basic MPC was created, and the results demonstrate that the controller is functioning admirably. In order to produce a genuine model for the real environment, the statistic noise model was introduced to the plant, and then a Kalman filter approach is examined to minimize noises. The stochastic model predictive controller monitors the reference without error and reduces noise.
A real-time robust MPC in different conditions was proposed for the flight control of unmanned rotorcrafts by Kostas in [33]. In addition, a framework for the navigation of a miniature quadrotor UAV with state estimation was investigated in [34]. Moreover, for fixed-wing UAVs, multiple filters were applied to wind model estimations in [35]. Desaraju and his colleagues conducted a study on a safe, efficient, and robust model predictive controller for constrained nonlinear systems [36,37,38,39].
2. Cyber-Physical Healthcare Systems and Digital Twins
Cyber-Physical healthcare Systems have the potential to be used in social services, particularly in medical and healthcare applications [1]. In general, numerous nations have severe shortages of healthcare staff, resulting in a reduction in the efficiency of medical services and a significant increase in healthcare expenses. The ability to adapt new technologies for health monitoring systems has increased. In healthcare monitoring, data transportation via low-cost sensors and various communication mediums has become a primary issue for the existing platforms, resulting in ineffectiveness in processing vast amounts of data in real-time. As a result, infrastructure and computational frameworks are necessary to advance this industry. This results in big data processing frameworks for medical cyber-physical systems (MCPS), which merge cyber and real-world features with dynamic, completely adaptable systems for making decisions and other monitoring devices.
Robots are self-contained devices that have been designed to perform a certain activity with precision. They are artificial-intelligence-based cognition models with the ability to continually acquire information about the environment with sensors in order to function in complicated contexts and conduct pre-defined operations on a frequent basis. Medical robots that aid in surgeries and clinical services, industrial robots that execute manufacturing tasks, and surveillance robots for security and safety all play important roles in cyber-physical systems [40]. These developments are useful for monitoring patients’ health states in distant locations and delivering improved therapies. On clinical sensors, acceptable research has been conducted. The sensors are used to acquire extremely private patient information. The gathered data are sent to the access point via wireless communication means. In addition, wired sensors are used; hence, WSN provides flexibility and comfort for patients and physicians. The data collected by sensors are kept on a server and are accessible to clinicians [41].
Different criteria that are important in determining the level of autonomy in healthcare cyber-physical systems (HCPS) are roughly classified into two areas, including hardware, which is the amount of autonomy that is determined by elements such as the type of medical equipment, the style of engagement, and the length of time spent with the patient. Medical robots that provide meals and medications to coronavirus patients can operate independently to aid healthcare systems. A team of Hong Kong researchers developed ‘Grace’, a humanoid robot that interacts with isolated coronavirus patients and delivers services such as temperature tracking and response via a thermal camera installed in the chest. In order to eliminate the stress caused by seclusion, the robot will actively connect with the coronavirus patients. The type of illness and patient risk level are examples of patient-related variables. Communicable illnesses, such as coronavirus, require a high degree of autonomous cyber-physical healthcare systems, yet high patient risk levels required ongoing medical expert assistance in addition to the autonomous healthcare systems.
A digital twin is a digital twin for a real item or process. The virtual model in smart medical systems produces virtual assets in cyberspace so that digital data about resources may be utilized for planning, management, and collaboration. The digital twin for SHCPS is essentially a simulation model for medical devices and equipment, as well as behavioral analysis of the patient treatment process, to aid healthcare specialists in studying, analyzing, and predicting patients’ health conditions. The digital twin keeps a capacity graph for diverse medical devices, which are recorded as a three-tuple vector with the values resource id, allocation status, and patient id. The allocation state is active or inactive, and the anticipated redistribution may be affected by the patient’s health. A graph may be used to illustrate the patient treatment process, with nodes representing the patient’s health condition at various time intervals and edges representing the transition depending on changes in physiological data. These graphs may be used in AI techniques to compute and classify a patient’s health state.
3. Problem Description
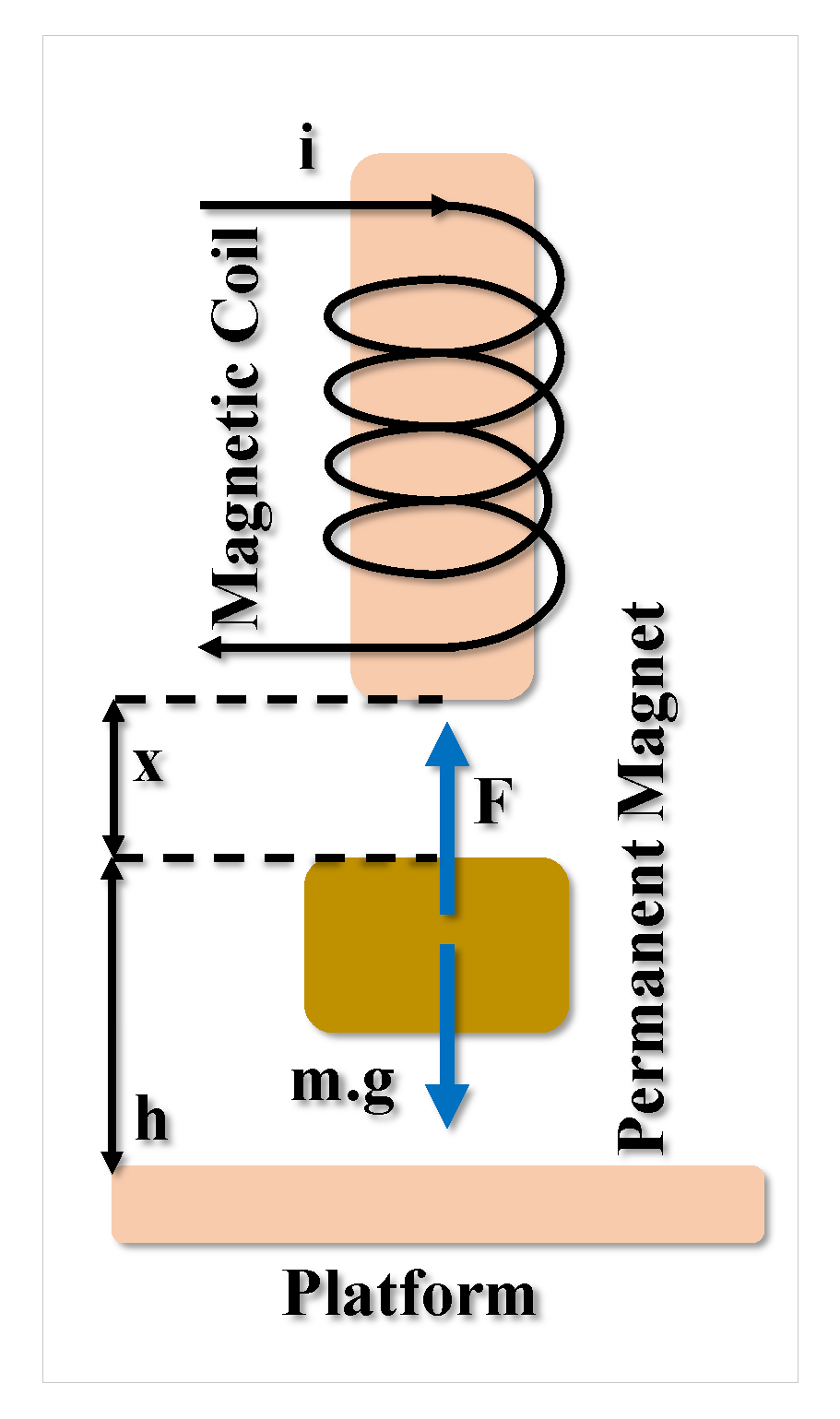
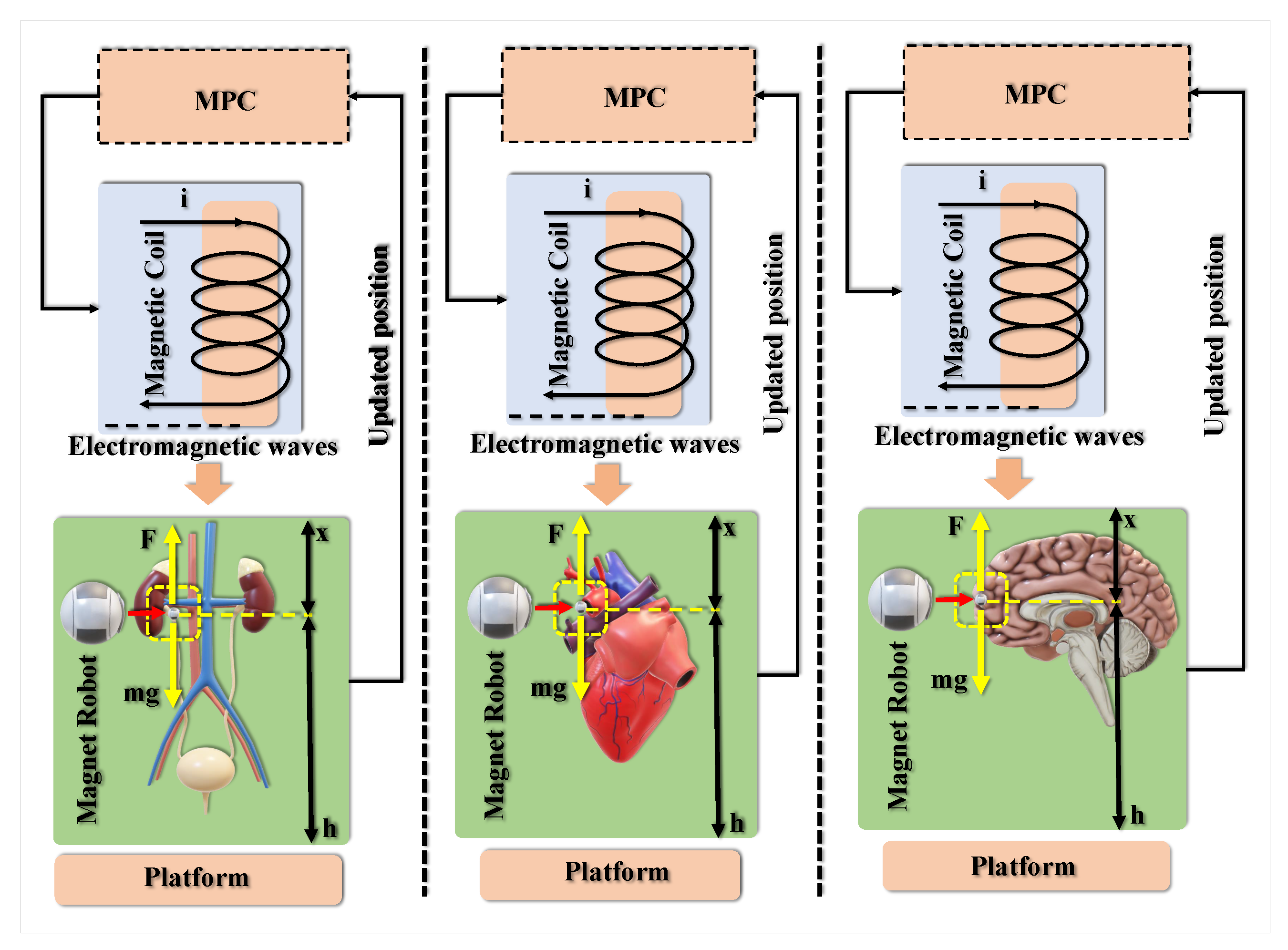
Figure 1 is a concept of the Magnetic Levitation (MAGLEV) system. The direction in the line of the lateral movement is downwards, as shown in Figure 1, with the base of the global Cartesian frame of coordinates on the electromagnetic core having a flat face. In the free space, the ball has 6 degrees of freedom (DOF), but only the vertical x-axis is controlled. Figure 2 demonstrates a comprehensive overview of the applications of the proposed system for healthcare objectives in different organs of the body. According to this figure, the proposed robot can be utilized in different sizes for different missions. However, to show some initial capabilities of the proposed robot, we try to demonstrate that it is more significant than its actual size. Nevertheless, the size of the robot can be altered for various operations, from drug delivery to invasive procedures. The proposed robot’s control system and dynamics will undoubtedly differ, but the priciple of these robots’ is based on Magnetic Levitation. It is emphasized that Figure 2 only shows an overview of the applications of the proposed robots, disregarding the size or density of the depicted organs.
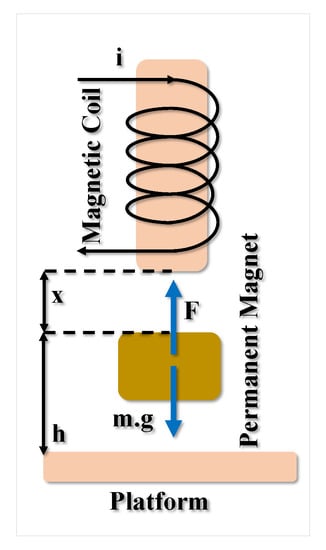
Figure 1.
Model of the system.
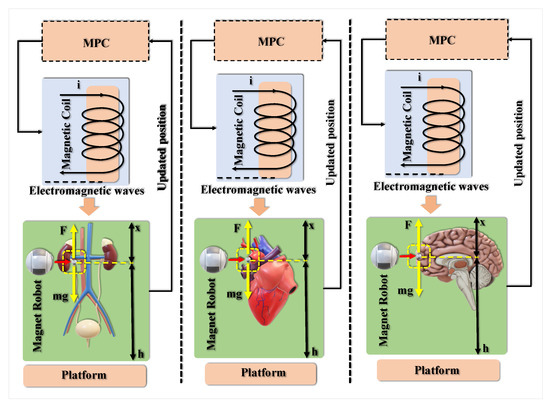
Figure 2.
The proposed magnetic microrobot for different purposes in a healthcare system.
The proposed micro-robotic technologies’ primary goals are the focused delivery of therapeutic cargo such as genetic materials, imaging agents, and medications. Functional connectivity inside the bloodstream to a specialized target site using a tunable cargo carrier is preferable to the pretty small cargo delivery. It delivers increased efficiency offered by present neutral routes of administration, such as local diffusion and intravenous delivery. This is because active navigation allows for more precise targeting of where the cargo is delivered. By using this mechanism, drivable carriers, it is feasible to achieve focused local therapy choices, reducing the likelihood of experiencing unwanted systemic consequences. For instance, administering interleukin-12 through intravenous injection resulted in fatal systemic toxicities. The total bioavailability of a single medication dosage may be increased by effective delivery and managed on-site release techniques. Since they have relatively short half-lives in blood, vulnerable cargo types such as proteins, peptides, or nucleic acids are better protected from degradation when contained inside a carrier. It is possible that the most advanced kind of in situ therapeutic and diagnostic technique would include autonomous, real-time control of the kinetics of the cargo release. To this end, microrobots can manage within the internal organs; act thoughtfully in response to discharge; deliver, carry, and shift therapeutics; and conduct complex jobs either wholly or partially autonomously might also fundamentally change several patients’ care.
We explore the challenge of controlling the motion of a permanent magnet driven by a magnetic field on a flat surface. It may be divided into a series of motion equations, much like any other motion control:
where denotes the robot’s location, and denotes its velocity.
where L is the inductance, R is the resistance, and u is the voltage of the supply source’s source (dc-link). The value of u is the average voltage during a duty cycle if the source is modulated by PWM. The switching sequence of the voltage source is the system’s ultimate control signal.
In this paper, a stochastic model predictive controller was proposed for exact positioning of the robot.
4. Methodology
4.1. Permanent Magnet Movement
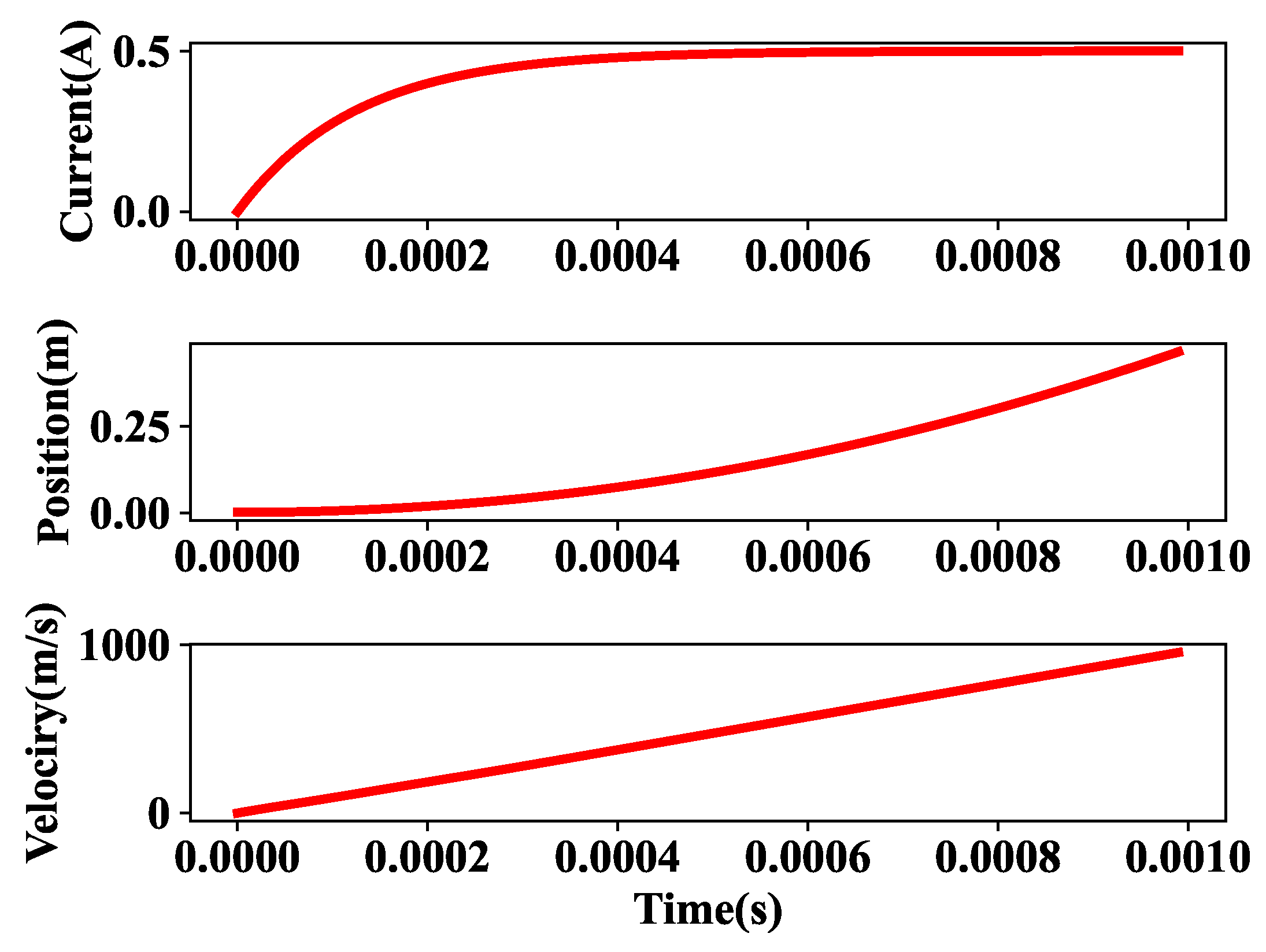
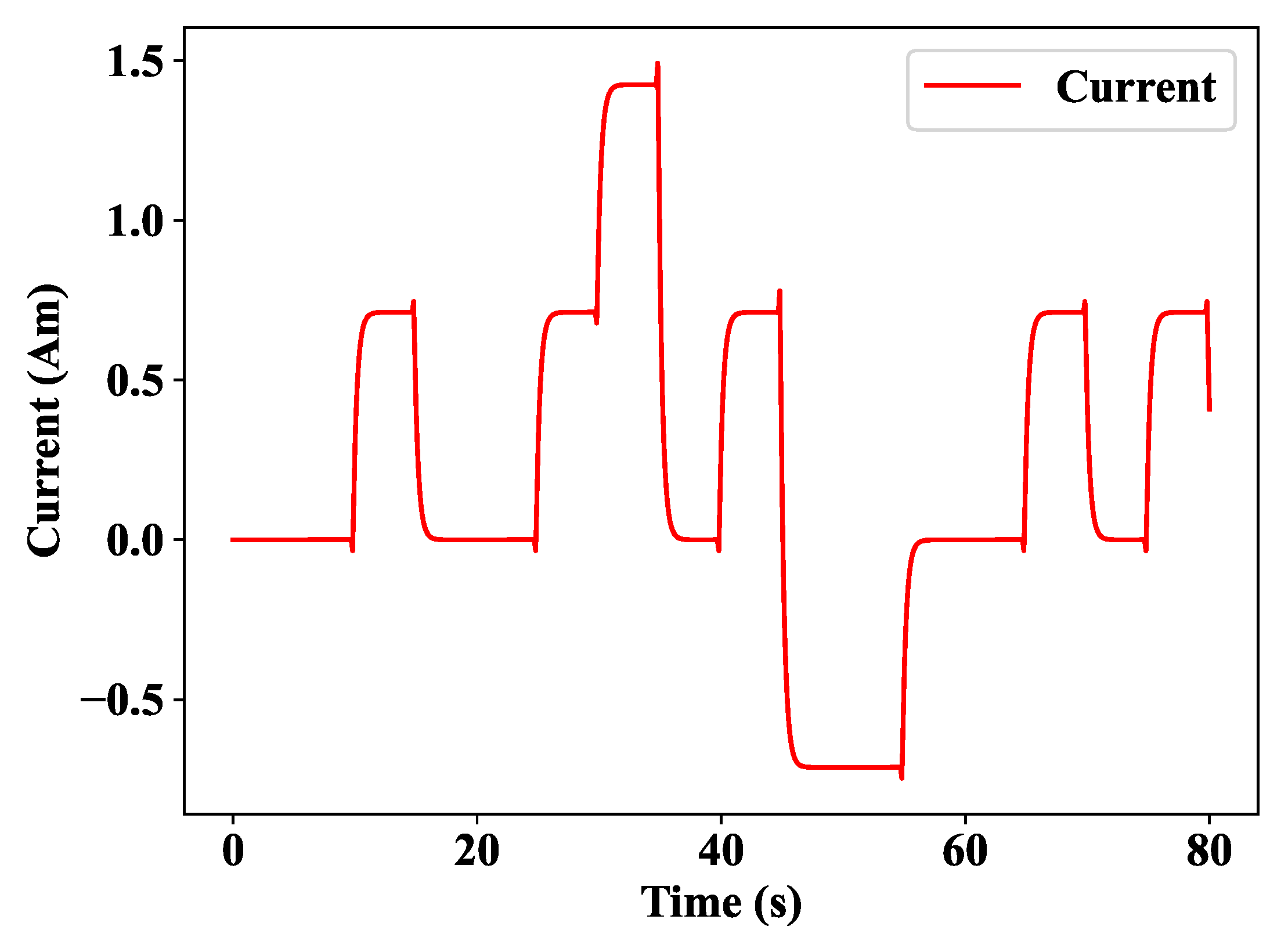
As stated in the above equations, by solving them, the movement of the permanent magnet can be achieved. As a result, in Figure 3, it can be seen how the current will change at each position of a permanent magnet. The current starts from zero, and it will converge to 0.1 Am. It is visible in the middle of the Figure how the permanent magnet will move in each phase during this time. The movement of the permanent magnet is too fast, which is show by how it reaches 0.4 m in less time. Finally, at the bottom, the Figure illustrates the speed changes.
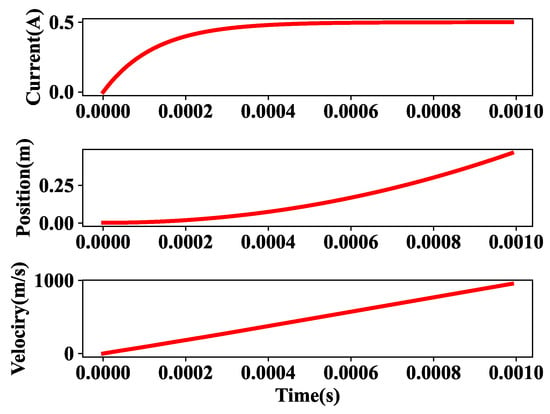
Figure 3.
Current, motion, and velocity profile.
4.2. Machine Learning System Identification
The first stage in developing a controller is to estimate the plant’s state-space, transfer function, or basically the dynamic model of the physical systems. These dynamic models are useful for analyzing, simulating, controlling, and monitoring a wide range of systems, including industrial systems, chemical processes, robotics, and aeronautical systems. There are various methods to identify the system’s model, such as state-space mode, transfer function’ polynomial methods, and nonlinear approaches.
Deep learning and system identification are two common Matlab toolboxes for determining the dynamic model of an unknown system based on input and output data. While each technical estimation can be solved via ML methods and ML techniques show suitable performance for complex systems such as the present system, ML helped to have better accuracy and brought us this opportunity to make the system more intelligent. On the other hand, since precision plays a crucial role in medical operations, ML can be helpful even if it leads to more complexity.
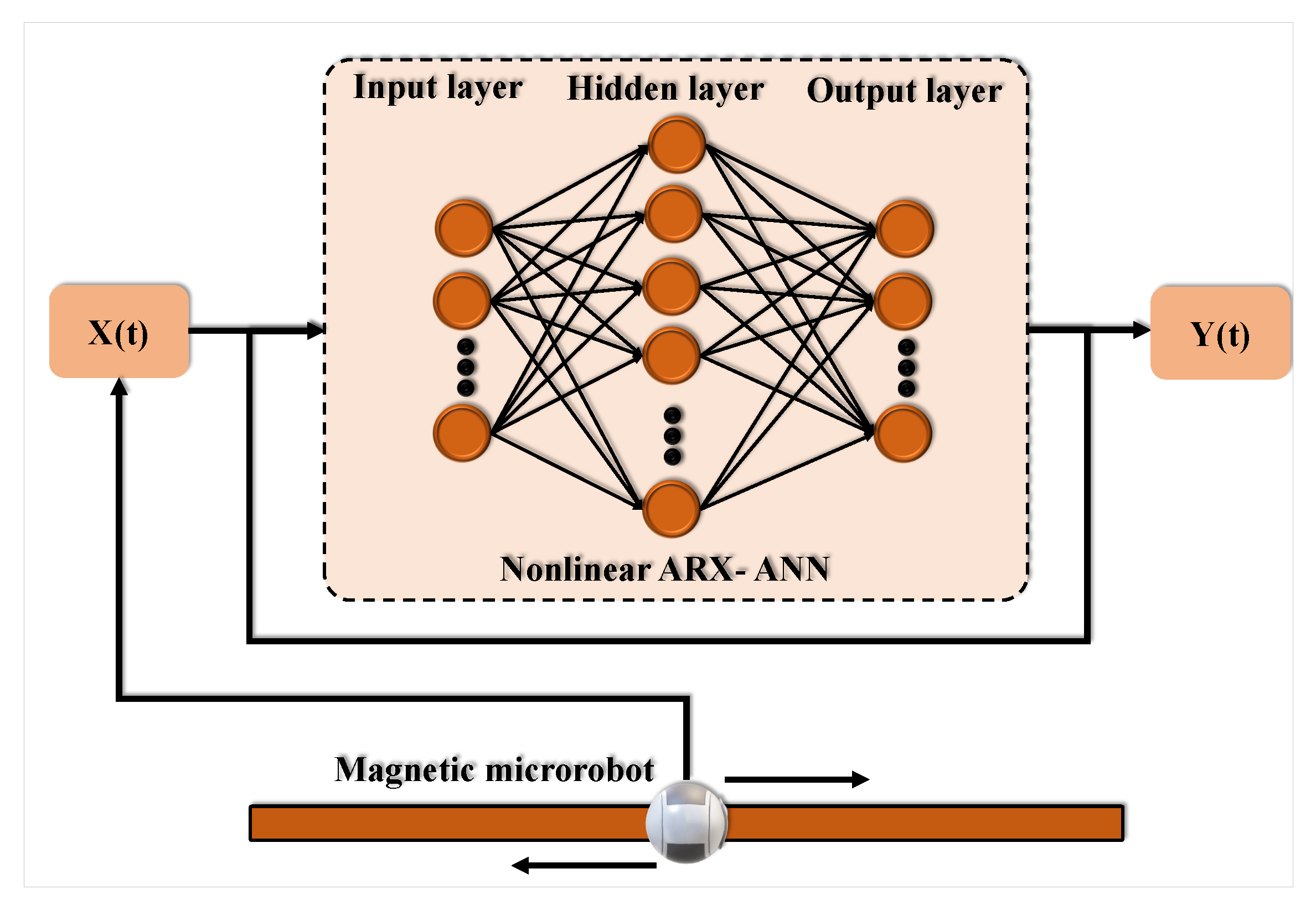
In this study, the nonlinear auto-regressive with external (exogenous) input which is known as NARX, predicts future values. These techniques have appropriate performance in the identification and analysis of the complex systems disregarding their nature and mechanisms [42,43,44,45]. Figure 4 depicts the block diagram of the dynamic deep learning nonlinear ARX, in which previous values of one or more time series are utilized to forecast future states. As indicated in Equation (4), this network predicts the series y(t) based on d previous data of y(t) and another sequence x(t):
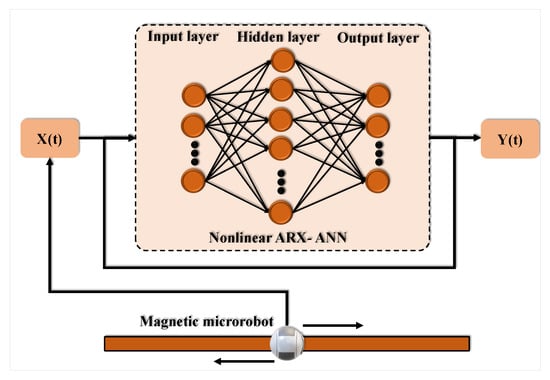
Figure 4.
Block diagrams.
In this scenario, the data generated from simulation using the mathematical model established in the previous section is fed into the neural network nonlinear ARX model, which is used to identify the model. As shown in Figure 4, the network will be built and trained in an open-loop mode. As trained, the network to create accurate current outputs may feed it correct historical outputs in an open-loop fashion. The current is utilized as input data for the identification process, while the position is used as output data to the nonlinear ARX network, and the system is considered to be an SISO system.
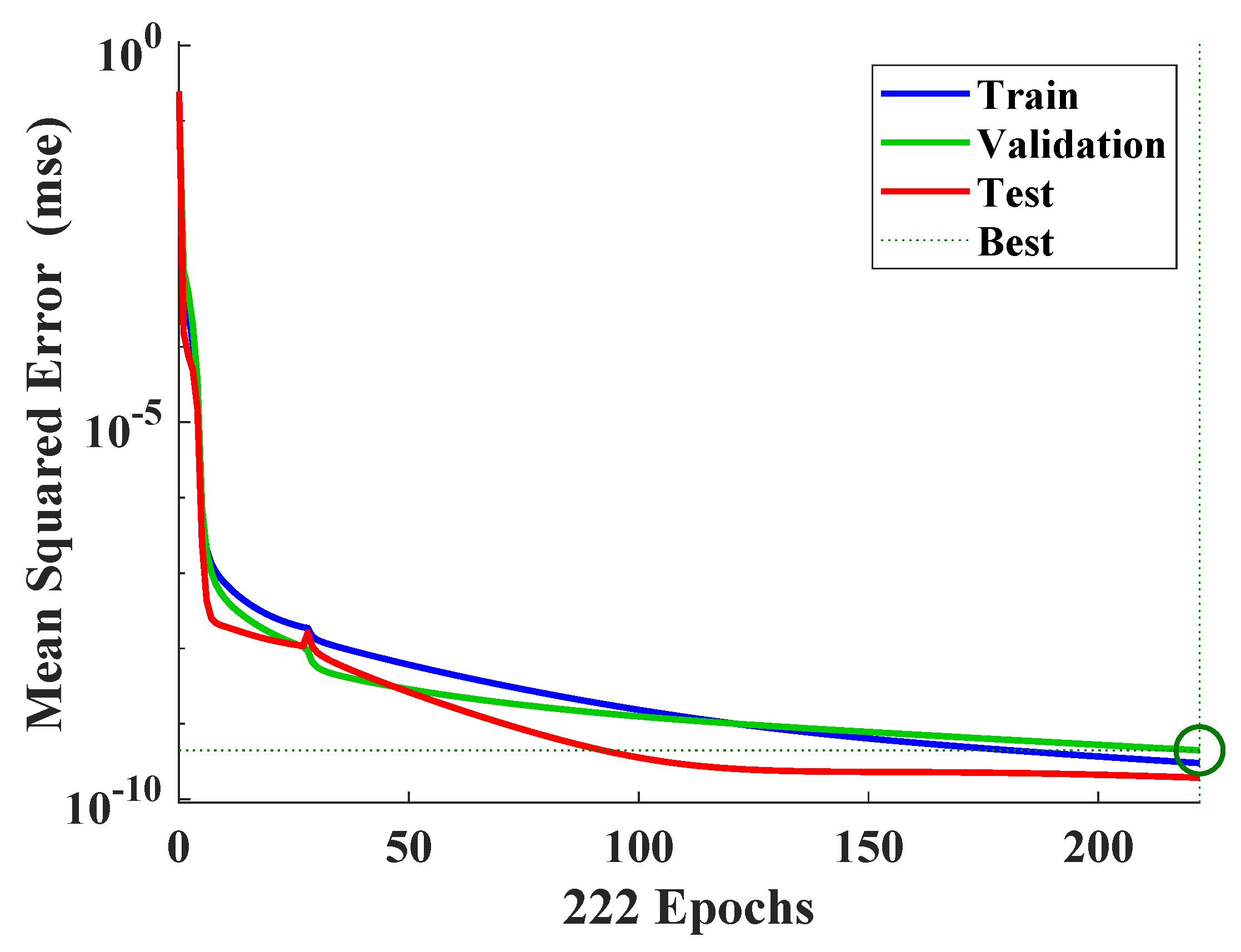
The following figures illustrate the results of the training procedure. Figure 5 displays the validation of the nonlinear ARX network’s performance based on the mean squared error over 1000 epochs. The mean squared error is the average squared discrepancy between outputs and goals, with smaller values indicating ideal performance.
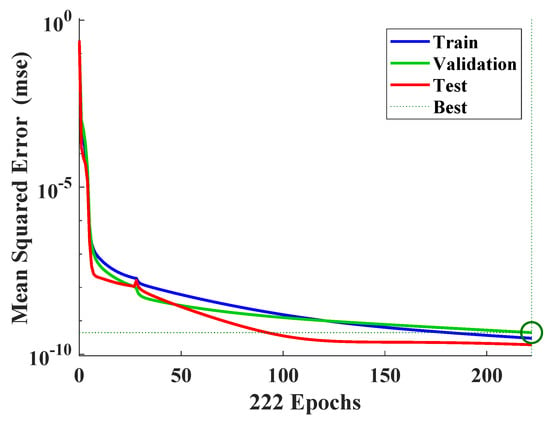
Figure 5.
Validation of the Nonlinear ARX network’s performance.
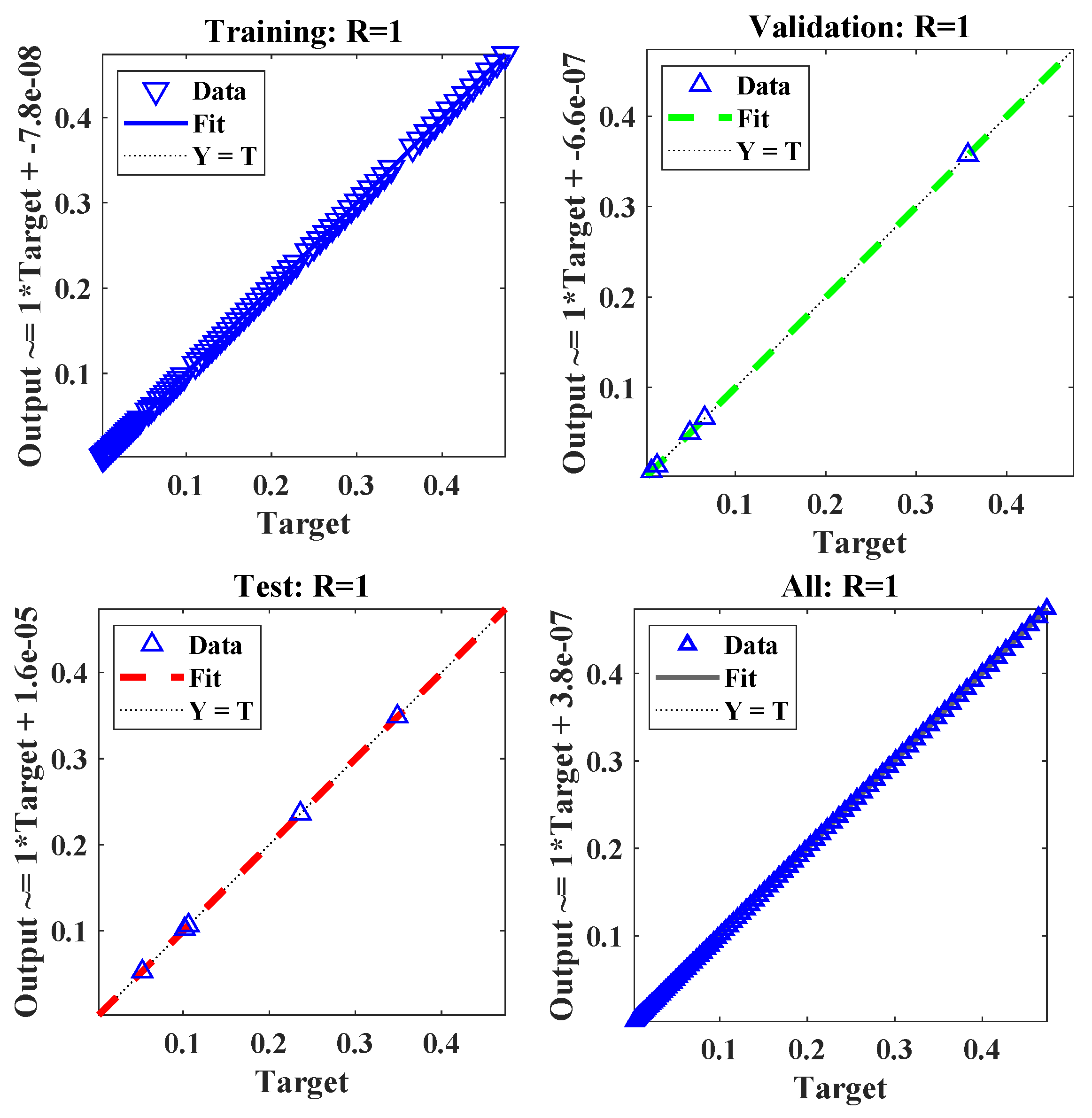
Regression R Values quantify the relationship between outputs and goals. As shown in Figure 6, a tight link is represented by a value of one for R, whereas a random relationship is represented by a value of zero.
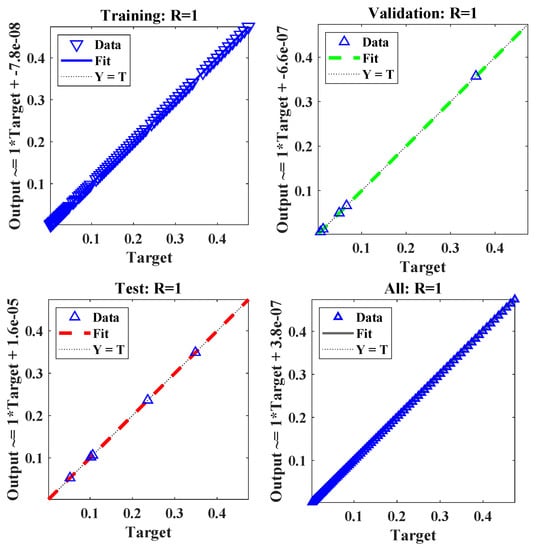
Figure 6.
Nonlinear ARX neural network regression.
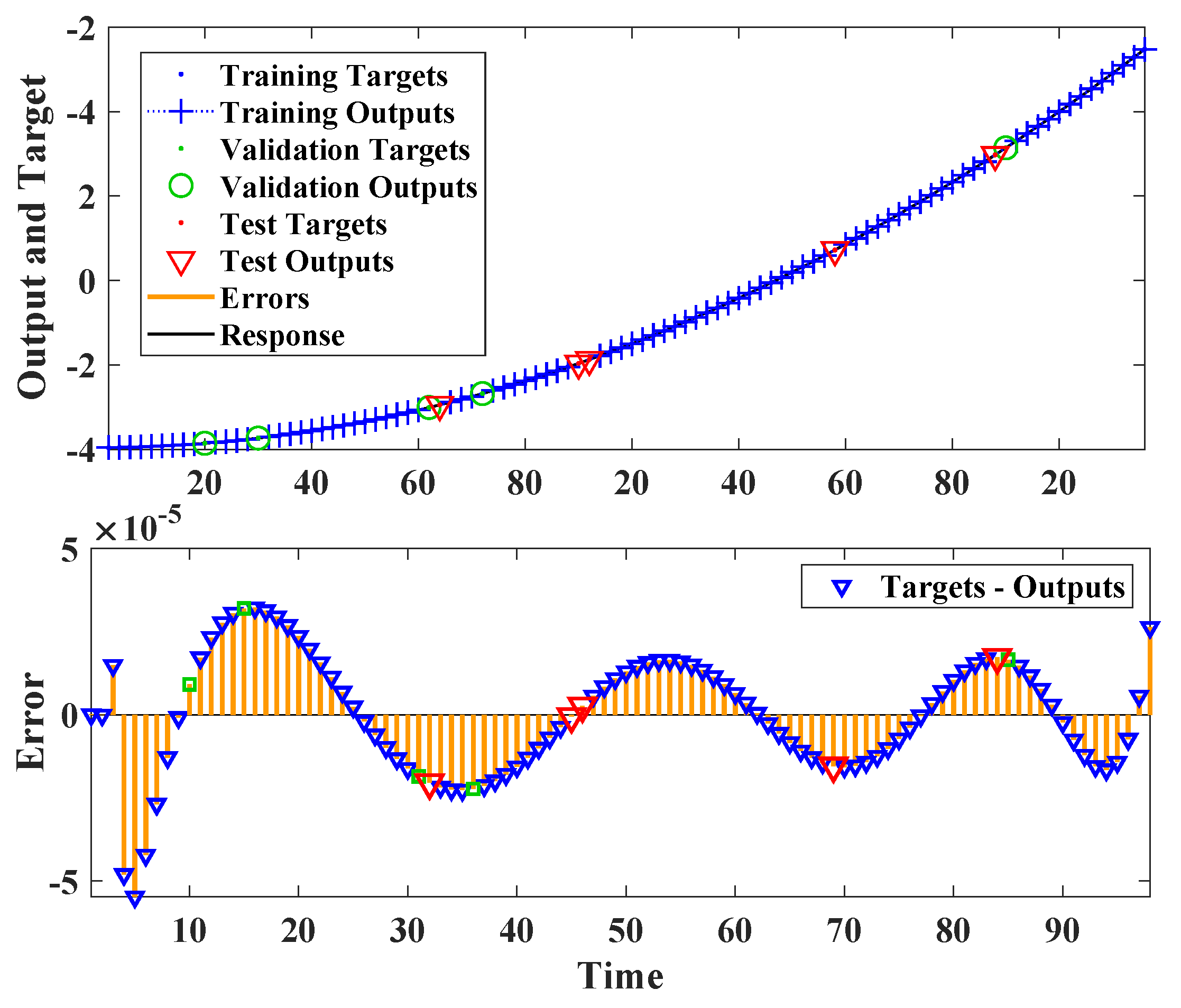
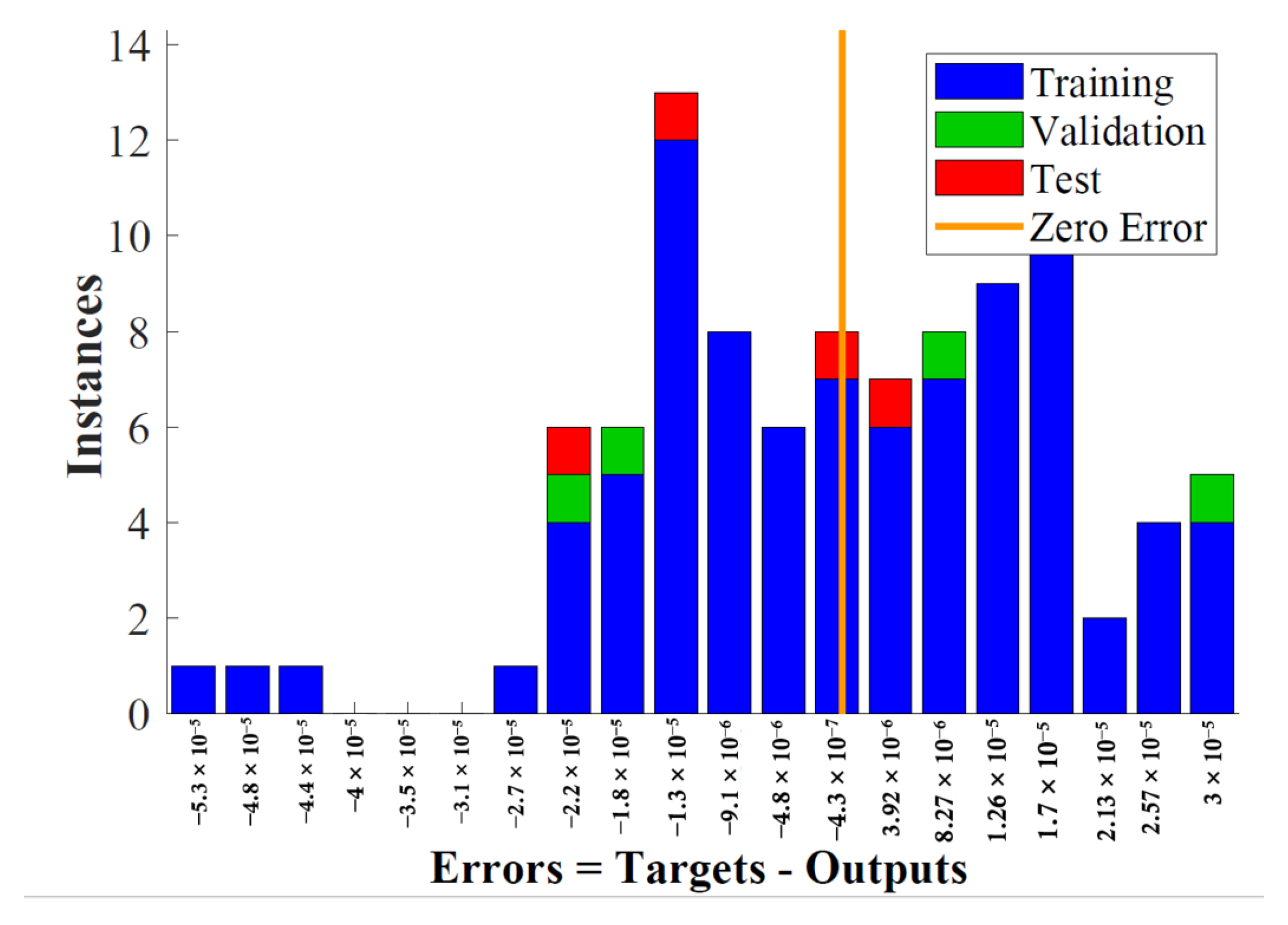
Figure 7 depicts the outputs, responses (targets), and failures as a function of time. It also specifies which time intervals were used for training, testing, and validation. Error histograms depict how the neural network’s failures on the testing examples are spread, as shown in Figure 8. In general, a normal distribution oriented at 0 is assumed for each output variable.
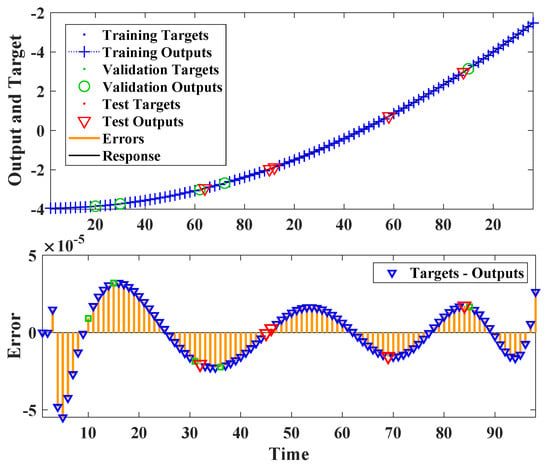
Figure 7.
Nonlinear ARX neural network’s time-series response.
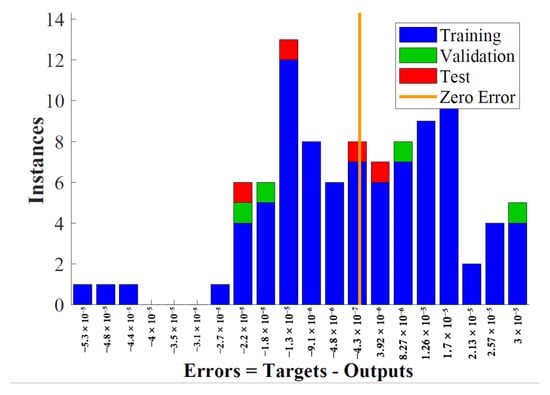
Figure 8.
Error histogram.
Following the identification procedure, the system is prepared to develop the controller. The model predictive controller, as well as the stochastic model predictive controller, are introduced in the next subsection.
4.3. Model Predictive Controller
The MPC controller computes a sequence of future control action values in order to minimize a cost function. In this cost function, we may provide weight matrices. These weight matrices alter the control action priority, rate of change in control action, and plant outputs. The MPC controller aims to minimize the following cost function J(k) for selected prediction and control horizons and :
where k denotes discrete-time, i is the index along the prediction horizon, and denotes the number of samples in the prediction horizon. Here, represents the start of the prediction horizon, represents the control horizon, Q represents the output error weight matrix, and R represents the rate of change in the control action weight matrix. ∣ is the projected plant output at time , and N is the control action error weight matrix. The output set point profile at time is represented by ∣. The expected rate of change in control action is ∣, the predicted optimal control action is ∣, and the input set-point profile is ∣.
The MPC is a technique that predicts control variables over a certain time horizon using linear system models. The following explains the control technique used:
- The value of the controlled variable is forecasted across the prediction horizon at each sampling time. This forecast is based on the future values of the control variable throughout the course of a control horizon.
- A reference trajectory is defined as , where . Specifies the intended system trajectory across the forecast horizon.
- The future control vector is computed to minimize a cost function. The cost function is a function of the differences between the reference trajectory and the anticipated output of the model.
- When the cost function has been minimized, the first optimal control action is performed in the plant, followed by an analysis of the results. The plant states analysis will be utilized as the model’s initial state for the following iteration.
A receding horizon technique involves repeating steps 1 to 4 for each sample moment. The receding horizon is only applied to the controller as the first part in the control sequence. At the next sample instant, the entire optimization method is repeated.
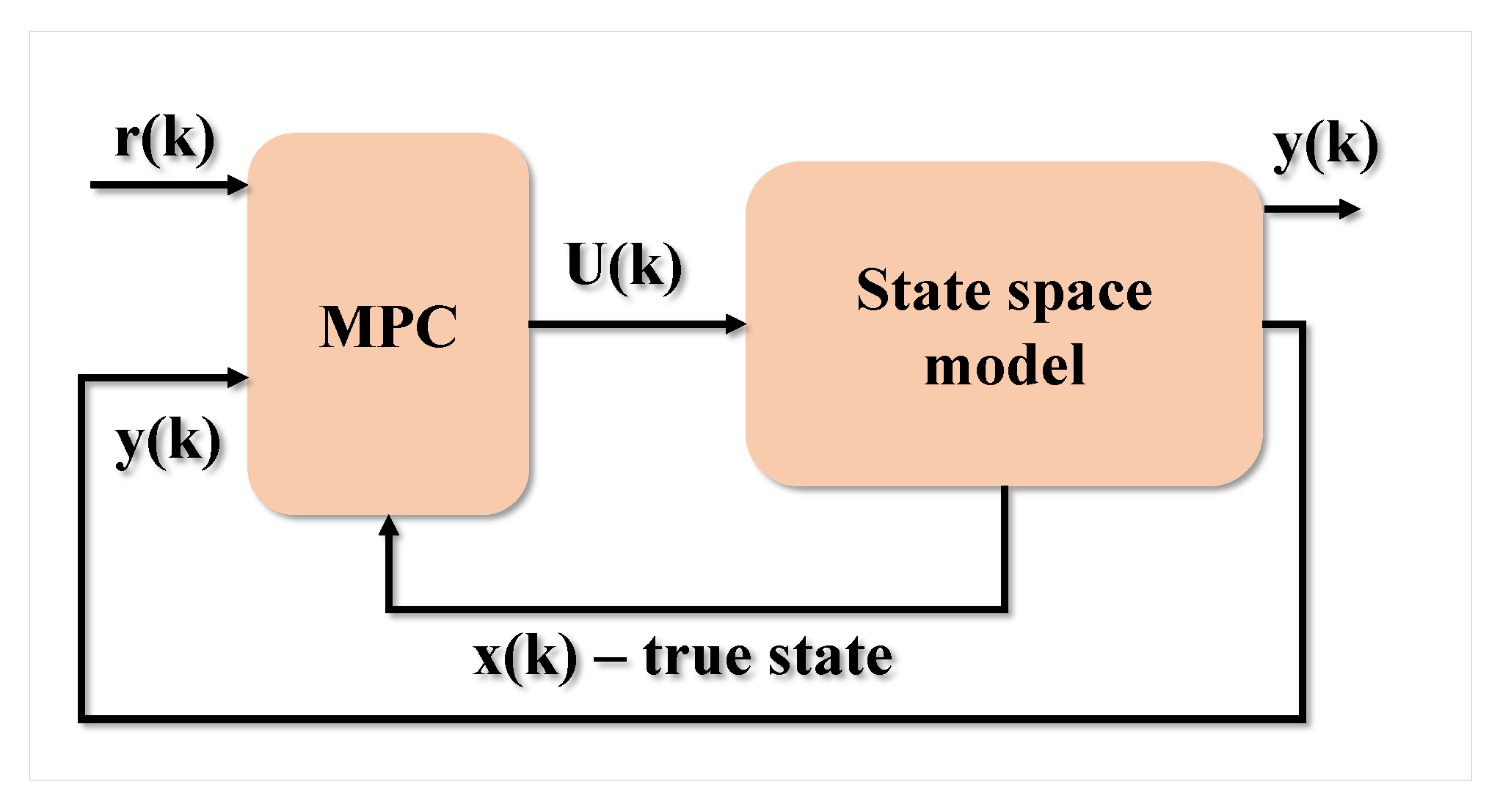
The block diagram of a simple MPC is shown in Figure 9. The control scheme is based on an open-loop process model, where A, B, C, and D are state-space models obtained from the system identification:
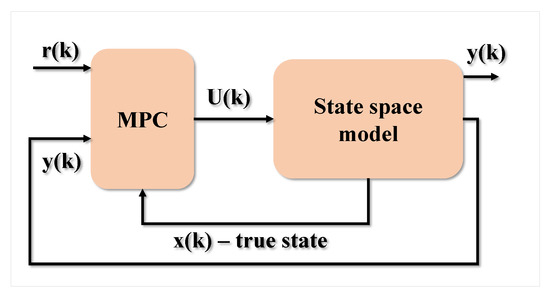
Figure 9.
MPC with true state wired.
4.4. Stochastic Model Predictive Controller
The effects of noise on the plant, actuators, and sensors are represented by stochastic system models. Random models also include the following variables in addition to the state-space matrices A, B, C, and D: Method noise is represented by the vectors w and v. G and H matrices link w to states and outputs, respectively. The following equations describe continuous random state-space models:
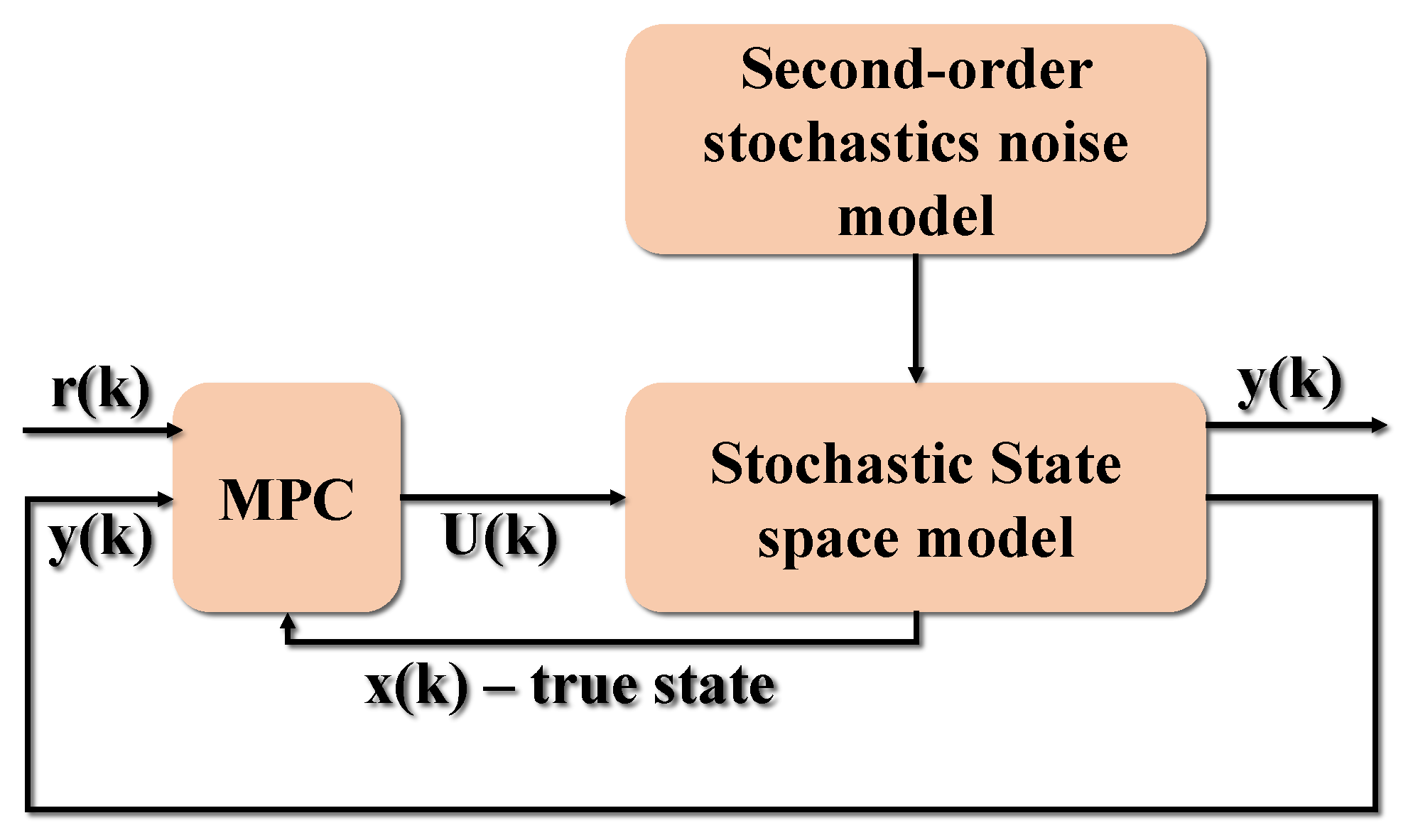
Furthermore, in order to replicate the natural and actual world, statistical noise must be added, and the stochastic model equation must be considered. The noises will then be filtered using a Kalman filter as an estimator in the feedback. One of the most significant and widely used estimate methods is the Kalman Filter. The Kalman Filter generates hidden variable estimates based on incorrect and uncertain data. In addition, the Kalman Filter predicts the future state of the system based on prior assessments. Figure 10, indicates an MPC with second-order noise model.
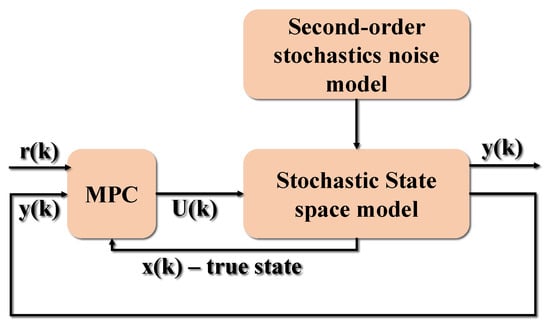
Figure 10.
Stochastic MPC with second-order statistic noise model.
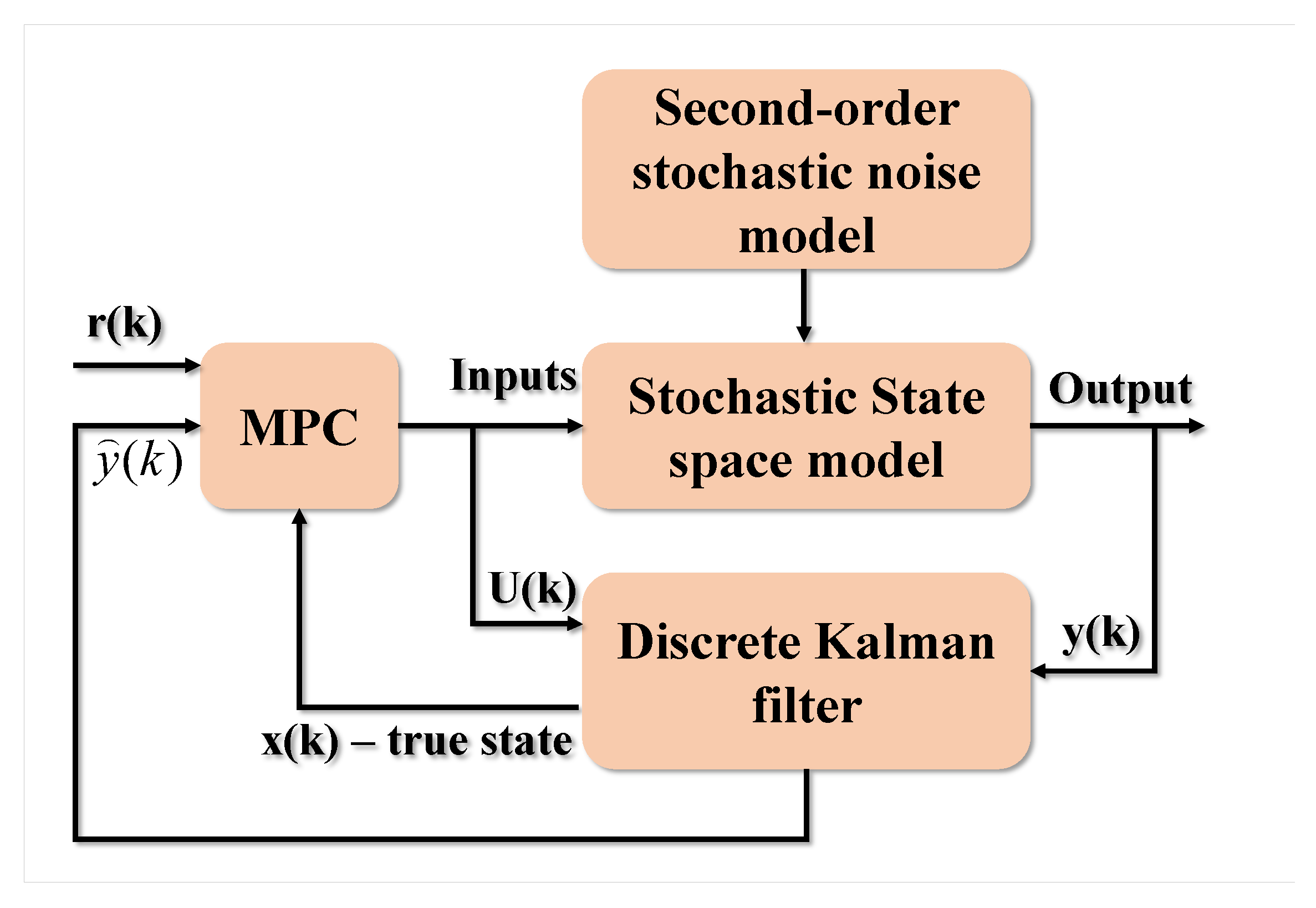
Moreover, we employ the Noise Covariance technique to build a state estimator utilizing the Q and R parameters. This approach yields a state estimator that makes use of the Kalman filter gain. The block diagram of stochastic MPC using Kalman filter is shown in Figure 11.
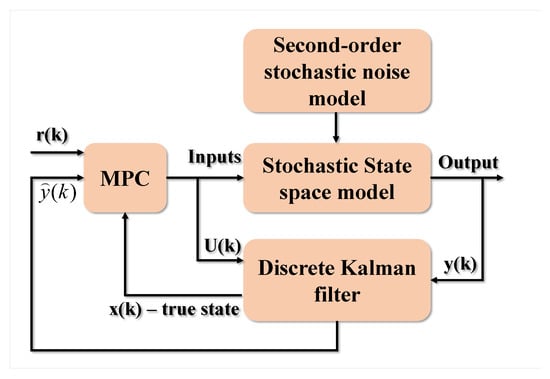
Figure 11.
Stochastic MPC with Kalman Filter.
5. Results
The project is implemented by LabVIEW using control and simulation module. First, a simple model predictive controller is designed without any noises. Prediction horizon, and control horizon were initialized as 4 and 2, respectively, as MPC parameters, and a 2D reference based on the scale of the permanent magnet was identified. By running the simulation for 80 s, the results will be as follows.
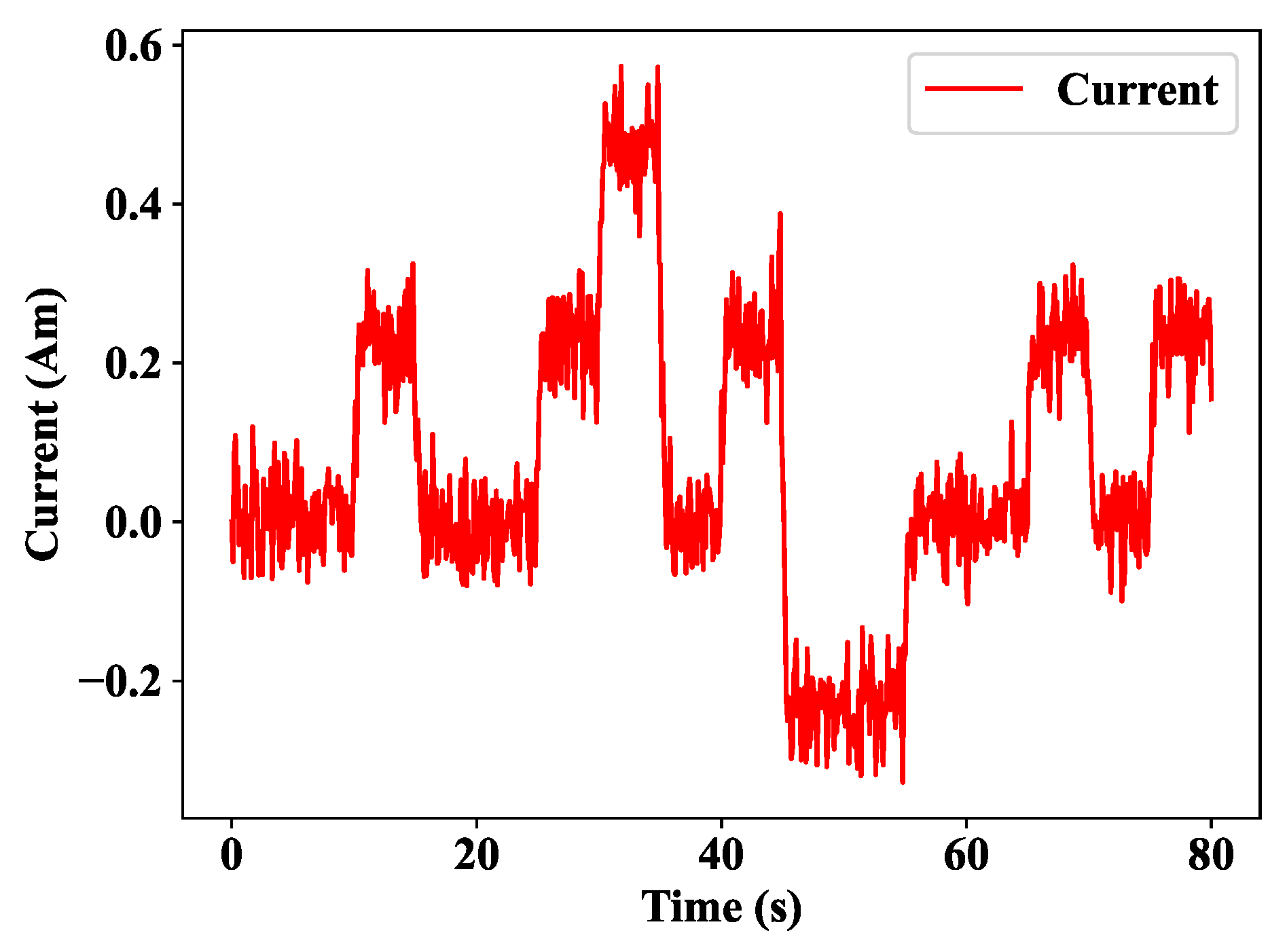
Figure 12 indicates how the control action will change based on the changes in the reference. It is obviously clear that by inflating the reference during the time, the current control action will be modified.
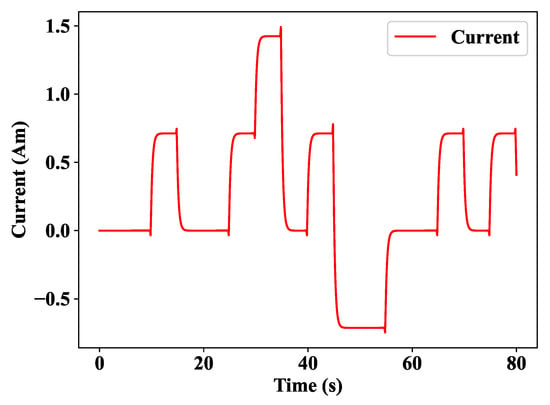
Figure 12.
Measured current control response.
The control action refers to how the automated controller generates the control signal. An automated controller measures the actual value of the system output to the desired set point (reference input), calculates the discrepancy, and generates a control signal to decrease the deviation to zero or a small quantity.
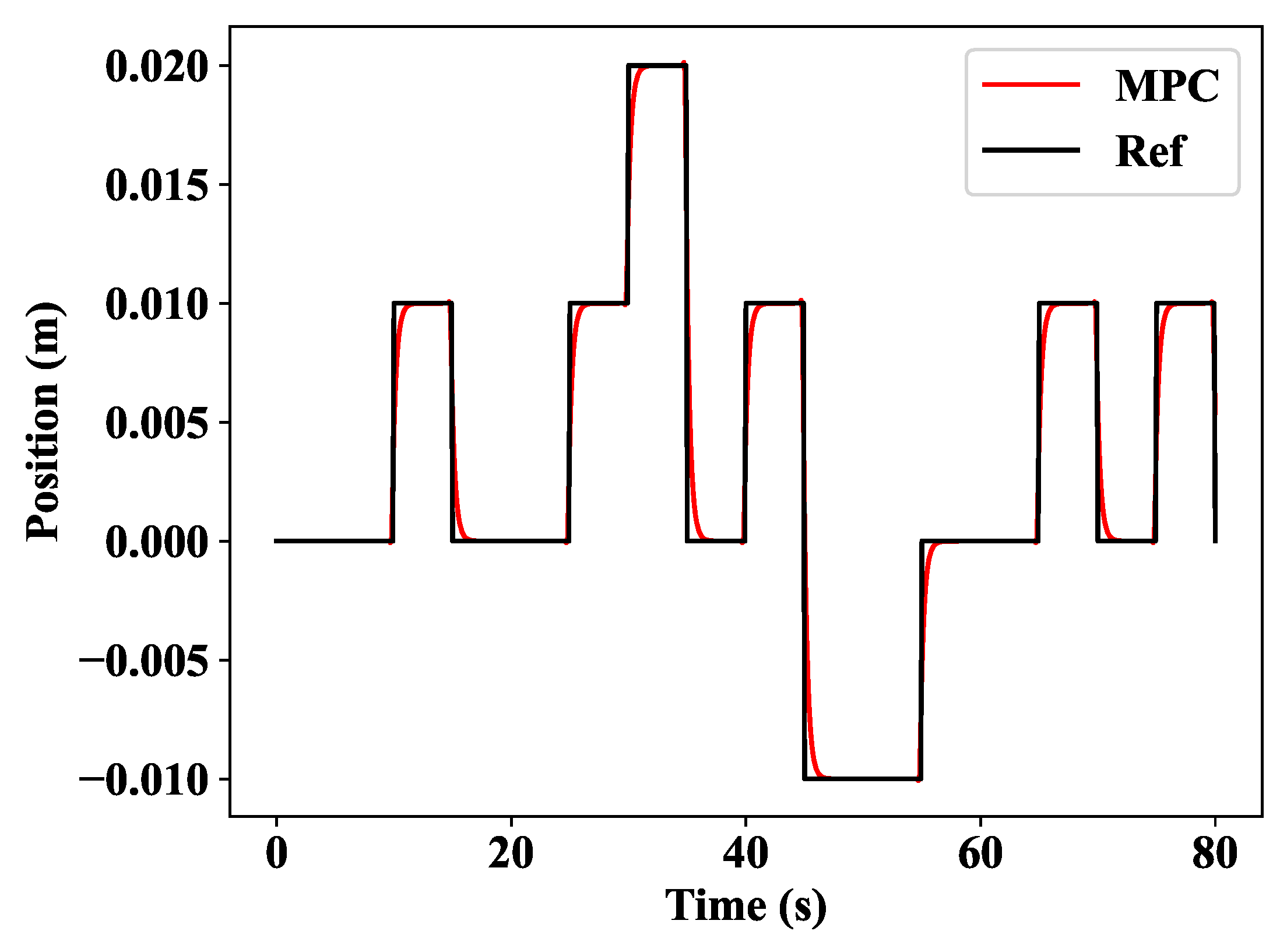
In Figure 13, it is obvious that the MPC controller performs admirably and traces the path without difficulty.
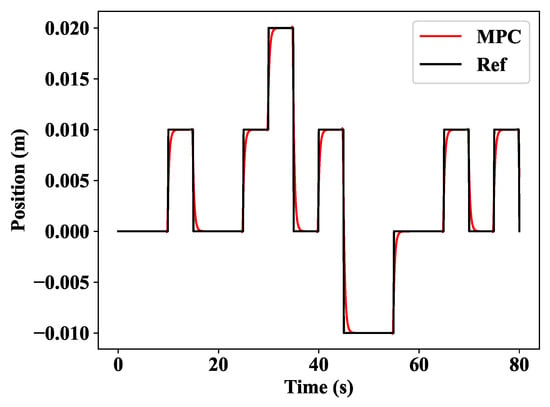
Figure 13.
MPC results.
For stochastic MPC, the plant model is the same as the model used in simple MPC, and just noise vectors will be added to complete the stochastic model predictive controller equation.
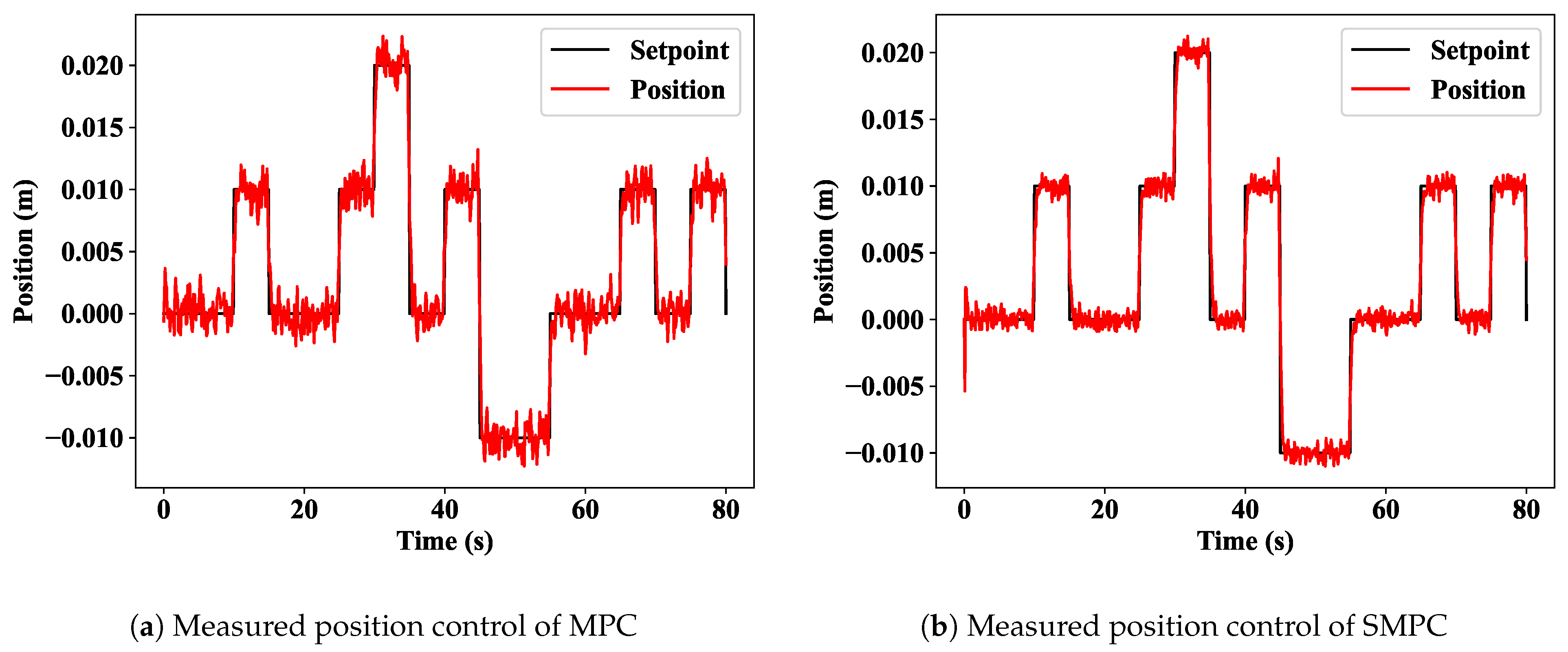
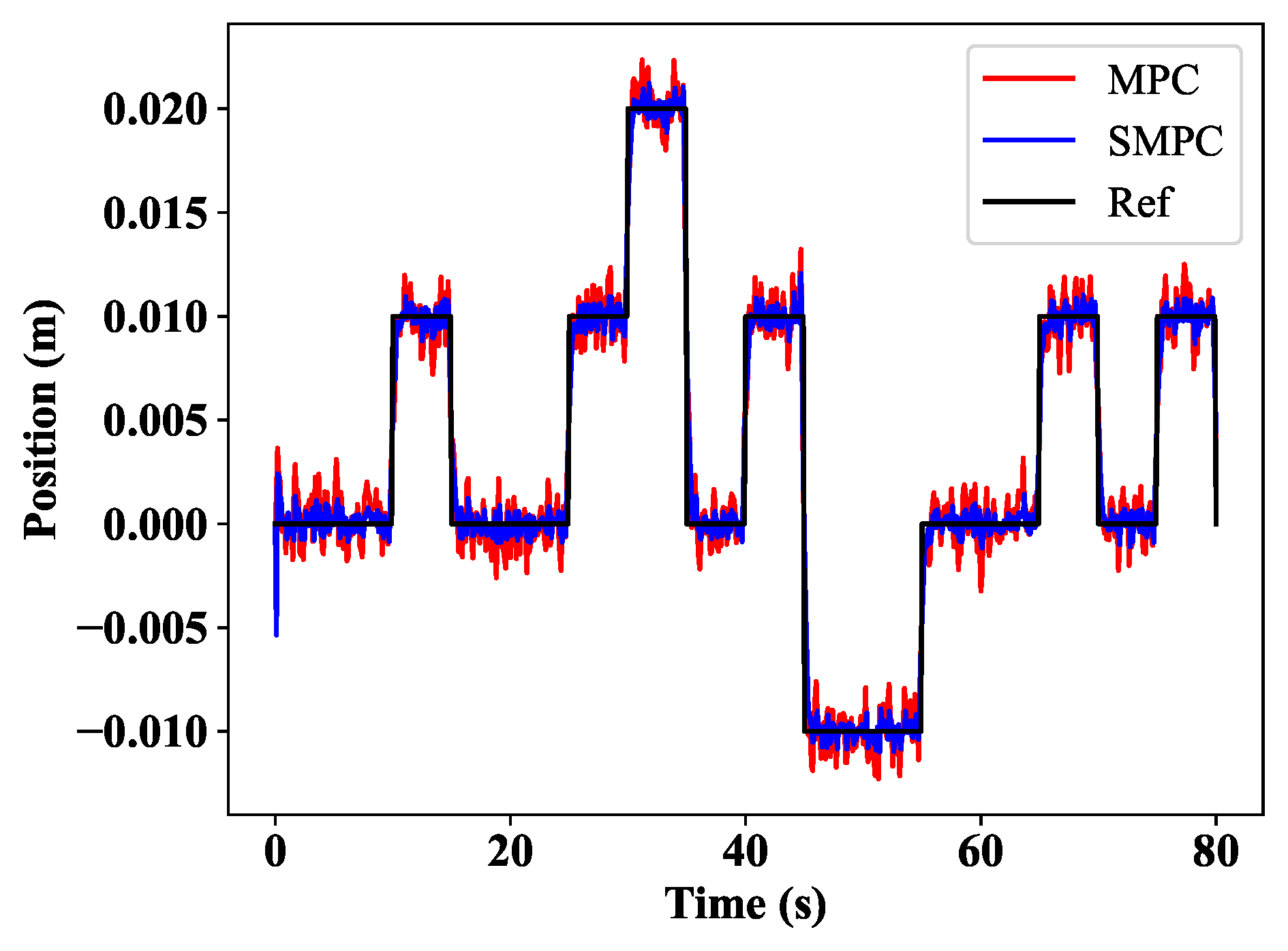
After simulation, the results are shown in Figure 14, the control action is clear, and the description is the same as the MPC, which is described above. However, it must be mentioned here that the noise which is added to the model is affecting the control action. Figure 15a indicates the stochastic MPC with severe noise. By using the Kalman filter, the noise was filtered in Figure 15b. Finally, the comparison of the SMPC and MPC is illustrated in Figure 16. It can be seen that the stochastic MPC using the Kalman filter can filter the noises in the real-world environment.
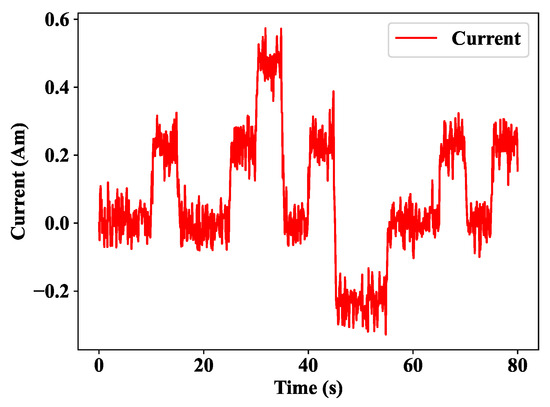
Figure 14.
Measured current control response with second-order noise.
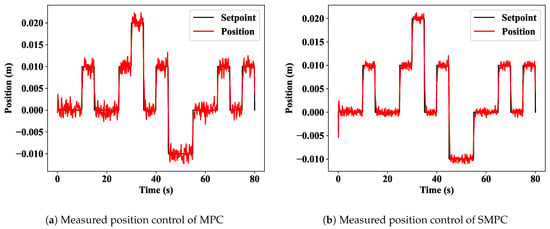
Figure 15.
MPC and Stochastic MPC results.
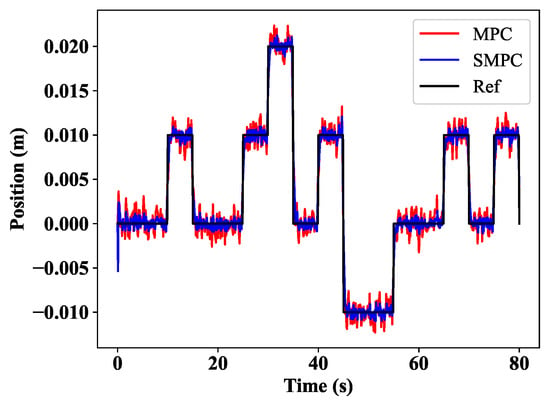
Figure 16.
Controllers comparison.
6. Conclusions
A stochastic model predictive controller based on neural network system identification is described in this work in order to regulate the location of permanent magnets. First, three profiles for current, position, and velocity were simulated. The system identification was then used to obtain the model’s state spaces in order to construct the MPC. The nonlinear ARX neural network was used to predict the dynamic model of the physical systems. A basic MPC was created, and the results demonstrate that the controller functions admirably. In order to produce a genuine model for the real environment, the statistic noise model was introduced to the plant, and then a Kalman filter approach was examined to minimize noises. As demonstrated in the results section, the stochastic model predictive controller monitors the reference without error and reduces noise.
Each model’s results are presented. Furthermore, it is demonstrated that the Model Predictive Controller with system identification is a reliable approach for trajectory tracking. It identifies the reference route quickly and does not rely on the reference path.
Author Contributions
Conceptualization, H.K.N. (Hamid Keshmiri Neghab) and M.J.; software, H.K.N. (Hamid Keshmiri Neghab) and H.K.N. (Hamed Keshmiri Neghab); validation, H.K.N. (Hamid Keshmiri Neghab), M.J. and H.K.N. (Hamed Keshmiri Neghab); writing, review and editing, H.K.N. (Hamid Keshmiri Neghab) and M.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dey, N.; Ashour, A.S.; Shi, F.; Fong, S.J.; Tavares, J.M.R. Medical cyber-physical systems: A survey. J. Med. Syst. 2018, 42, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karkhanehchi, M.M.; Parandin, F.; Zahedi, A. Design of an all optical half-adder based on 2D photonic crystals. Photonic Netw. Commun. 2017, 33, 159–165. [Google Scholar] [CrossRef]
- Parandin, F.; Sheykhian, A. Design and simulation of a 2× 1 All-Optical multiplexer based on photonic crystals. Opt. Laser Technol. 2022, 151, 108021. [Google Scholar] [CrossRef]
- Belverdi, A.R.; Jamshidi, M.B.; Taherpour, A.A.; Jamshidi, M.; Rezaei, O. Novel donor-acceptor non-fullerene metal-organic solar cells: A first DFT and TD-DFT study. Phys. B Condens. Matter 2018, 542, 37–43. [Google Scholar] [CrossRef]
- Parandin, F.; Mahtabi, N. Design of an ultra-compact and high-contrast ratio all-optical NOR gate. Opt. Quantum Electron. 2021, 53, 1–9. [Google Scholar] [CrossRef]
- Jamshidi, M.; Farhadi, R.; Jamshidi, M.; Shamsi, Z.; Naseh, S. Using a soft computing method for impedance modelling of li-ion battery current. Int. J. Adv. Intell. Paradig. 2020, 16, 18–29. [Google Scholar] [CrossRef]
- Parandin, F.; Heidari, F.; Rahimi, Z.; Olyaee, S. Two-Dimensional photonic crystal Biosensors: A review. Opt. Laser Technol. 2021, 144, 107397. [Google Scholar] [CrossRef]
- Khalaj, O.; Jamshidi, M.B.; Saebnoori, E.; Mašek, B.; Štadler, C.; Svoboda, J. Hybrid Machine Learning Techniques and Computational Mechanics: Estimating the Dynamic Behavior of Oxide Precipitation Hardened Steel. IEEE Access 2021, 9, 156930–156946. [Google Scholar] [CrossRef]
- Parandin, F.; Moayed, M. Designing and simulation of 3-input majority gate based on two-dimensional photonic crystals. Optik 2020, 216, 164930. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Gorjiankhanzad, M.; Lalbakhsh, A.; Roshani, S. A novel multiobjective approach for detecting money laundering with a neuro-fuzzy technique. In Proceedings of the 2019 IEEE 16th International Conference on Networking, Sensing and Control (ICNSC), Banff, AB, Canada, 9–11 May 2019; pp. 454–458. [Google Scholar]
- Jamshidi, M.B.; Roshani, S.; Talla, J.; Sharifi-Atashgah, M.S.; Roshani, S.; Peroutka, Z. Cloud-based Machine Learning Techniques Implemented by Microsoft Azure for Designing Power Amplifiers. In Proceedings of the 2021 IEEE 12th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 1–4 December 2021; pp. 41–44. [Google Scholar]
- Parandin, F.; Malmir, M.R.; Naseri, M.; Zahedi, A. Reconfigurable all-optical NOT, XOR, and NOR logic gates based on two dimensional photonic crystals. Superlattices Microstruct. 2018, 113, 737–744. [Google Scholar] [CrossRef]
- Jamshidi, M.; Lalbakhsh, A.; Talla, J.; Peroutka, Z.; Hadjilooei, F.; Lalbakhsh, P.; Jamshidi, M.; La Spada, L.; Mirmozafari, M.; Dehgani, M.; et al. Artificial intelligence and COVID-19: Deep learning approaches for diagnosis and treatment. IEEE Access 2020, 8, 109581–109595. [Google Scholar] [CrossRef]
- Jamshidi, M.; Lalbakhsh, A.; Talla, J.; Peroutka, Z.; Roshani, S.; Matousek, V.; Roshani, S.; Mirmozafari, M.; Malek, Z.; La Spada, L.; et al. Deep learning techniques and covid-19 drug discovery: Fundamentals, state-of-the-art and future directions. In Emerging Technologies During the Era of COVID-19 Pandemic; Springer: Berlin/Heidelberg, Germany, 2021; pp. 9–31. [Google Scholar]
- Shafiei, A.; Jamshidi, M.B.; Khani, F.; Talla, J.; Peroutka, Z.; Gantassi, R.; Baz, M.; Cheikhrouhou, O.; Hamam, H. A Hybrid Technique Based on a Genetic Algorithm for Fuzzy Multiobjective Problems in 5G, Internet of Things, and Mobile Edge Computing. Math. Probl. Eng. 2021, 2021, 9194578. [Google Scholar] [CrossRef]
- Roshani, S.; Koziel, S.; Roshani, S.; Jamshidi, M.B.; Parandin, F.; Szczepanski, S. Design of a Patch Power Divider With Simple Structure and Ultra-Broadband Harmonics Suppression. IEEE Access 2021, 9, 165734–165744. [Google Scholar] [CrossRef]
- Mohebi, Z.; Parandin, F.; Shama, F.; Hazeri, A. Highly linear wide band low noise amplifiers: A literature review (2010–2018). Microelectron. J. 2020, 95, 104673. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Roshani, S.; Talla, J.; Peroutka, Z.; Roshani, S. A novel filter-based power divider for wireless communication in intelligent transportation systems. In Proceedings of the 2020 19th International Conference on Mechatronics-Mechatronika (ME), Prague, Czech Republic, 2–4 December 2020; pp. 1–5. [Google Scholar]
- Desaraju, V.R.; Spitzer, A.E.; O’Meadhra, C.; Lieu, L.; Michael, N. Leveraging experience for robust, adaptive nonlinear MPC on computationally constrained systems with time-varying state uncertainty. Int. J. Robot. Res. 2018, 37, 1690–1712. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q.; Diehl, M. Model Predictive Control: Theory, Computation, and Design; Nob Hill Publishing: Madison, WI, USA, 2017; Volume 2. [Google Scholar]
- Raković, S.V.; Levine, W.S. Handbook of Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Di Ruscio, D.L. Model Predictive Control with Integral Action: A Simple MPC Algorithm. 2013. Available online: https://openarchive.usn.no/usn-xmlui/handle/11250/2438440 (accessed on 5 April 2022).
- Aly, M.; Ahmed, E.M.; Shoyama, M. An improved model predictive controller for highly reliable grid connected photovoltaic multilevel inverters. In Proceedings of the 2017 IEEE International Telecommunications Energy Conference (INTELEC), Broadbeach, QLD, Australia, 22–26 October 2017; pp. 450–455. [Google Scholar]
- Arezzo, A.; Menciassi, A.; Valdastri, P.; Ciuti, G.; Lucarini, G.; Salerno, M.; Di Natali, C.; Verra, M.; Dario, P.; Morino, M. Experimental assessment of a novel robotically-driven endoscopic capsule compared to traditional colonoscopy. Dig. Liver Dis. 2013, 45, 657–662. [Google Scholar] [CrossRef]
- Valdastri, P.; Ciuti, G.; Verbeni, A.; Menciassi, A.; Dario, P.; Arezzo, A.; Morino, M. Magnetic air capsule robotic system: Proof of concept of a novel approach for painless colonoscopy. Surg. Endosc. 2012, 26, 1238–1246. [Google Scholar] [CrossRef]
- Sikorski, J.; Dawson, I.; Denasi, A.; Hekman, E.E.; Misra, S. Introducing BigMag—A novel system for 3D magnetic actuation of flexible surgical manipulators. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3594–3599. [Google Scholar]
- Chautems, C.; Nelson, B.J. The tethered magnet: Force and 5-DOF pose control for cardiac ablation. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4837–4842. [Google Scholar]
- Helwa, M.K.; Esser, A.; Schoellig, A.P. Estimation-based model predictive control for automatic crosswind stabilization of hybrid aerial vehicles. arXiv 2018, arXiv:1810.00046. [Google Scholar]
- Santander, O.; Elkamel, A.; Budman, H. Robust economic model predictive control: Disturbance rejection, robustness and periodic operation in chemical reactors. Eng. Optim. 2019, 51, 896–914. [Google Scholar] [CrossRef]
- Keshmiri Neghab, H.; Pariz, N. Designing a Fuzzy Logic Controller for Automated Backward Parking Car. In Proceedings of the 2019 IEEE 4th Conference on Technology In Electrical and Computer Engineering (ETECH 2019) Information and Communication Technology, Tehran, Iran, 29 May 2019. [Google Scholar]
- Neghab, H.K.; Neghab, H.K. Calibration of a Nonlinear DC Motor under Uncertainty Using Nonlinear Optimization Techniques. Period. Polytech. Electr. Eng. Comput. Sci. 2021, 65, 42–52. [Google Scholar] [CrossRef]
- Alrifaee, B.; Abel, D.; Ament, C. Networked Model Predictive Control for Vehicle Collision Avoidance. Technical Report, Lehrstuhl und Institut für Regelungstechnik. 2017. Available online: https://d-nb.info/1158599595/34 (accessed on 5 April 2022).
- Alexis, K.; Papachristos, C.; Siegwart, R.; Tzes, A. Robust model predictive flight control of unmanned rotorcrafts. J. Intell. Robot. Syst. 2016, 81, 443–469. [Google Scholar] [CrossRef]
- Brockers, R.; Hummenberger, M.; Weiss, S.; Matthies, L. Towards autonomous navigation of miniature UAV. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Columbus, OH, USA, 23–28 June 2014; pp. 631–637. [Google Scholar]
- Sharifi, A.; Nobahari, H. Multiple model filters applied to wind model estimation for a fixed wing UAV. In Proceedings of the 2016 7th International Conference on Mechanical and Aerospace Engineering (ICMAE), London, UK, 18–20 July 2016; pp. 109–115. [Google Scholar]
- Desaraju, V.R. Safe, Efficient, and Robust Predictive Control of Constrained Nonlinear Systems. 2017. Available online: https://www.ri.cmu.edu/publications/safe-efficient-robust-predictive-control-constrained-nonlinear-systems/ (accessed on 5 April 2022).
- Desaraju, V.R.; Michael, N. Leveraging experience for computationally efficient adaptive nonlinear model predictive control. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5314–5320. [Google Scholar]
- Desaraju, V.R.; Michael, N. Fast nonlinear model predictive control via partial enumeration. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1243–1248. [Google Scholar]
- Desaraju, V.R.; Spitzer, A.; Michael, N. Experience-driven Predictive Control with Robust Constraint Satisfaction under Time-Varying State Uncertainty. In Robotics: Science and Systems; CS.cmu.edu: New York, NY, USA, 2017. [Google Scholar]
- Verma, R. Smart City Healthcare Cyber Physical System: Characteristics, Technologies and Challenges. Wirel. Pers. Commun. 2022, 122, 1413–1433. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, G.N.; Le Viet, N.H.; Elhoseny, M.; Shankar, K.; Gupta, B.; Abd El-Latif, A.A. Secure blockchain enabled Cyber–physical systems in healthcare using deep belief network with ResNet model. J. Parallel Distrib. Comput. 2021, 153, 150–160. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Rostami, S. A dynamic artificial neural network approach to estimate thermal behaviors of li-ion batteries. In Proceedings of the 2017 IEEE 2nd International Conference on Automatic Control and Intelligent Systems (I2CACIS), Kota Kinabalu, Malaysia, 21 October 2017; pp. 116–121. [Google Scholar]
- Jamshidi, M.; Lalbakhsh, A.; Lotfi, S.; Siahkamari, H.; Mohamadzade, B.; Jalilian, J. A neuro-based approach to designing a Wilkinson power divider. Int. J. Microw. Comput.-Aided Eng. 2020, 30, e22091. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Lalbakhsh, A.; Mohamadzade, B.; Siahkamari, H.; Mousavi, S.M.H. A novel neural-based approach for design of microstrip filters. AEU-Int. J. Electron. Commun. 2019, 110, 152847. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Jamshidi, M.; Rostami, S. An intelligent approach for nonlinear system identification of a li-ion battery. In Proceedings of the 2017 IEEE 2nd International Conference on Automatic Control and Intelligent Systems (I2CACIS), Kota Kinabalu, Malaysia, 21 October 2017; pp. 98–103. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).