Abstract
The typical goal of a collaborative filtering algorithm is the minimisation of the deviation between rating predictions and factual user ratings so that the recommender system offers suggestions for appropriate items, achieving a higher prediction value. The datasets on which collaborative filtering algorithms are applied vary in terms of sparsity, i.e., regarding the percentage of empty cells in the user–item rating matrices. Sparsity is an important factor affecting rating prediction accuracy, since research has proven that collaborative filtering over sparse datasets exhibits a lower accuracy. The present work aims to explore, in a broader context, the factors related to rating prediction accuracy in sparse collaborative filtering datasets, indicating that recommending the items that simply achieve higher prediction values than others, without considering other factors, in some cases, can reduce recommendation accuracy and negatively affect the recommender system’s success. An extensive evaluation is conducted using sparse collaborative filtering datasets. It is found that the number of near neighbours used for the prediction formulation, the rating average of the user for whom the prediction is generated and the rating average of the item concerning the prediction can indicate, in many cases, whether the rating prediction produced is reliable or not.
1. Introduction
Collaborative filtering (CF) [1,2] is one of the most widely used recommender systems (RSs) techniques over recent years. The overall goal of a CF system is to generate accurate predictions for items that users have not yet rated. Then, using these predictions, the RS will typically suggest, to each user, the items achieving the highest prediction value and, therefore, the highest probability that the user will actually like them [3,4]. Understandably, the more accurate these predictions are, the more reliable the final recommendations produced by the RS will be.
Initially, a typical CF system searches for users v, sharing similar tastes with user u, by comparing the known actual ratings that both u and v have given to common items j in the past. When the ratings of users u and v are (to a large extent) similar, users u and v are considered to be “near neighbours” (NNs). Then, to compute a prediction pu,i for the rating that user u would assign to item i, that u has not rated yet, the actual ratings of u‘s NN users vk to the item i are used. This idea follows the rationale that, since in the real world humans trust people close to them (e.g., family and close friends) when suggestions for a new commodity/experience are required (from making an online pizza order that costs EUR 10 to buying their next car that costs EUR 100,000) [5,6], an analogous setting would hold for computer-generated suggestions.
The accuracy of CF systems, i.e., the vicinity between the rating prediction values and the actual rating values, is a research area that has attracted a lot of research activity over the recent years. The main goal of the research in this area is to reduce the overall deviation between rating predictions and actual rating values. A CF system accuracy is experimentally determined by applying the algorithms to rating datasets, typically hiding a number of ratings, subsequently trying to predict the hidden ratings, and then assessing the closeness between hidden ratings and the respective computed predictions. Datasets may be both dense (which contain a relatively high number of ratings, compared to the number of users and items in the dataset) and sparse [7,8,9]. Typically, a sparse CF dataset suffers from lower rating prediction accuracy, since it is more difficult to find close and, hence, reliable NNs [10,11,12].
While, as mentioned before, a lot of CF research works focus on augmenting the rating prediction accuracy of CF systems, limited work has been developed on examining which features of users, items and the dataset affect the rating prediction accuracy in CF systems. The main factor that has been examined in this context is the relation between the number of NNs and the overall algorithm accuracy, generally concluding that 10–30 NNs are required to attain a good level of prediction accuracy [13,14,15]. These studies have generally been performed in the context of the examination of the performance of specific algorithms.
In this work, we aim to explore, in a broader context, the factors related to rating prediction accuracy in sparse collaborative filtering datasets, indicating that recommending the items that simply achieve higher prediction values than others, without considering other factors, in some cases, can reduce recommendation accuracy and negatively affect the success of the RS. In other words, it may be safer for an RS to recommend an item achieving a bit of a lower prediction score if, based on the factors studied in this work, this prediction is more reliable/confident than the other. We examined the effect of five features on the prediction accuracy in sparse CF systems, where the low prediction accuracy issue is more severe (because finding users’ NNs is much more difficult), by addressing the following research questions:
RQ1: What is the importance of the number of NNs for the rating prediction accuracy? If of importance, how many NNs ensure a more accurate rating prediction?
RQ2: Is there any connection between the average ratings value of users and the accuracy computed for rating predictions made to them?
RQ3: Is there any connection between the average ratings value of an item and the accuracy computed for rating predictions considering this item?
RQ4: What is the correlation between the accuracy of a rating prediction for a user and the number of items that the user has rated? If correlated, what is the number of user ratings to ensure better accuracy in the rating prediction to the user?
RQ5: Does a rating prediction formulated for an item that has been rated by several users have greater accuracy? If so, how many user ratings would ensure more accurate rating prediction for an item?
Conclusively, this work extends and completes the existing research literature in the area by (a) examining four features that have not been considered insofar, (b) considering the effect of the number of NNs outside the context of specific algorithm optimisations and (c) focusing on sparse datasets where the accuracy problem is more acute and the number of NNs is more limited. The results of this work may be used to gain deeper insight on the rating behaviour of users, while additional further research can be conducted to compute confidence levels for predictions, based on the features of each prediction, since predictions associated with smaller error margins can be deemed to be more accurate; then, confidence levels can be exploited in the recommendation generation procedure.
This work is also akin to the works presented in [16,17], which examine the features of textual reviews that affect the reliability of the review-to-rating conversion procedure. However, this method is applied during the CF rating prediction process to the ratings themselves, rather than the review-to-rating conversion procedure before the recommendation process.
The present paper will experimentally answer the aforementioned research questions by using (i) 12 widely used and acceptable sparse CF datasets, (ii) two widely used and acceptable user similarity metrics and (iii) two widely used and acceptable rating prediction error metrics to ensure the reliability of the results. In order to ascertain that the conclusions reached are not affected by particular algorithm characteristics, measurements have been obtained using six different algorithms (“plain” CF [18,19]; an algorithm that considers rating variability [20]; a CF algorithm exploiting causal relations [21]; a temporal pattern-aware CF algorithm [22]; a sequential CF recommender algorithm [23] and a CF algorithm exploiting common histories up to the item review time [24]). The rest of the paper is structured as follows: in Section 2, the related work is overviewed, while in Section 3, the prerequisites needed in our work will be analysed, considering the rating prediction process and the user similarity metrics that are used. In Section 4, the research questions are answered by experimentally evaluating the relative prediction features. Finally, in Section 5 the paper is concluded, and the future work is outlined.
2. Related Work
RS accuracy is a research field that has attracted numerous research works over the last years.
Fernández-García et al. [25] introduce a method that targets suggesting the most suitable items for each user by developing an RS using intelligent data analysis approaches. In this work, initially interaction data is gathered and the dataset is built; afterwards, the problem of transforming the original dataset from a real component-based application to an optimised one, where machine learning techniques can be applied, is addressed. By applying machine learning algorithms to the optimised datasets, the authors determined which recommender model obtains a higher accuracy, and by allowing users to find the most suitable components for them, their user experience is augmented, and thus their recommendation system achieves better results.
Forestiero [26] presents a heuristic method that exploits swarm intelligence techniques to build a recommender engine in IoT environment. In this work, real-valued vectors, obtained through the Doc2Vec model, represent smart objects. Mobile agents moving in a virtual 2D space following a bio-inspired model (namely the flocking model), in which agents perform simple and local operations autonomously obtaining a global intelligent organisation, are associated to the vectors. A similarity rule is designed to enable agents to discriminate among the assigned vectors. This work achieves a closer positioning/clustering of only similar agents, while it enables fast and effective selection operations. The validity of this approach is demonstrated in the experimental evaluations, while the proposed methodology achieves a performance increase of about 50%, in terms of clustering quality and relevance, compared to other existing approaches.
Sahu et al. [27] introduce a content-based movie RS that uses preliminary movie features (such as cast, genre director, movie description and keywords) and movie rating and voting information of similar movies. It creates a new feature set and proposes a deep learning model that builds a multiclass movie popularity prediction RS as well as proposes an RS that predicts upcoming movies popularities of different audience groups. The work uses data from IMDB and TMDB and achieves 96.8% accuracy.
Aivazoglou et al. [28] present a fine-grained RS for social ecosystems that uses the media content published by the user’s friends and recommends new ones (online clips, music videos, etc.). The design of the RS is based on the findings of an extensive qualitative user study that explores the requirements and value of a recommendation component of a social network. Its main idea is to calculate similarity scores at a fine-grained level for each social friend, by leveraging the abundance of pre-existing user information, to create interest profiles. In this paper, a proof-of-concept implementation for Facebook is developed, and the effectiveness of the underlying mechanisms for content analysis is explored. The effectiveness of the proposed approach is experimentally evaluated. A user study for exploring the usability aspects of the RS was conducted, which found that it can significantly improve user experience.
Bouazza et al. [29] present a hybrid method that recommends personalised IoT services to users by combining an ontology method with implicit CF. The ontology method models the Social IoT, while the CF method predicts the ratings and produces recommendations. The evaluation results show that the proposed technique combining the CF with Social IoT outperforms the plain CF (without the Social IoT) in terms of recommendation accuracy.
The rating prediction accuracy is a field of CF that has attracted considerable research attention over the recent years. These research works are divided into two main categories. The first one presents techniques that are based exclusively on the information contained in the user–item rating matrix (which may additionally include a timestamp), while the second presents techniques that exploit supplementary sources of information, such as item characteristics, user relations in social networks and user item reviews.
Regarding the first category, Zhang et al. [30] present an algorithm that realises an item-based CF item-variance weighting by forming a time-aware similarity computation that estimates the relationship between the items to be recommended and reduces their importance when they have not recently been rated. Furthermore, a time-related correlation degree is introduced that forms a time-aware similarity computation that estimates the relationship between products. Its experimental results show that the presented method outperforms traditional item-based CF and produces recommendations with satisfactory classification and predictive accuracy.
Zhang et al. [31] introduce a CF optimisation technique that maximises the popularity while, at the same time, maintains a low prediction accuracy reduction by optimising neighbour selection and utilising a ranking strategy that rearranges both the area the threshold controls and the top-N item list. More specifically, this work presents a two-stage CF optimisation mechanism that obtains a complete and diversified item list, where in the first stage multiple interests to optimise neighbour selection is incorporated, while the second stage uses a ranking strategy that rearranges the list of top-N items. Real-world datasets were used to evaluate the presented approach, which confirmed that the model achieved higher diversity than the conventional approaches for a given loss of accuracy.
Yan and Tang [32] use a Gaussian mixture model to cluster users and items and extracts new item features to solve the rating data sparsity problem that CF algorithms encounter. This work proposes a new similarity method by combining the Jaccard similarity with the triangle similarity. The experimental results show that the method mitigates the data sparseness, while at the same time improves the rating prediction accuracy.
Jiang et al. [33] introduce a method that is based on trusted data fusion and user similarity that can be applied to many CF systems. The proposed method includes the procedures of user similarity calculation and trusted data selection to create the final recommendation formula. The method consists of three steps. In the first one, the trusted data are selected, while in the second one the user similarity is calculated. In the last one, this similarity is added to the weight factor, and then the final recommendation equation is produced. The experimental results show that the presented algorithm has proven to be more accurate than the traditional slope one algorithm.
Rosa et al. [9] introduce a local similarity algorithm that uses multiple correlation structures between CF users. Initially, a clustering method to discover groups of similar items is employed. Afterwards, for each cluster, a user-based similarity model is used, namely the Cluster-based Local Similarity model. Two clustering algorithms are used, and the results show that the proposed algorithm achieves higher accuracy when compared to traditional and state-of-the-art CF similarity models.
Iftikhar et al. [34] introduce a triangle similarity CF product recommendation algorithm. The similarity metric of the algorithm considers the ratings of both the common rated items and the uncommon items from pairs of users, while the user rating preference behaviour is complemented by the obtained similarity in giving rating preferences. The proposed similarity metric achieves adequate accuracy when compared to existing similarity metrics.
Margaris et al. [24] introduce the Experiencing Period Criterion rating prediction CF algorithm. The algorithm combines the period that the rating to be predicted belongs to with the users’ experienced wait period in a certain product category and modifies the rating prediction value to improve the rating prediction accuracy of CF RSs. More specifically, the algorithm amplifies the prediction score when both the time of the rating to be predicted and the user’s usual experiencing time belong to same experiencing period (Late or Early) of the item and, conversely, reduces it when they belong to different ones. The algorithm achieved a considerable rating prediction quality improvement for all the datasets tested.
Although all the previous works can be applied to every CF dataset, since the information needed is located only in the user–item rating–timestamp matrix, usually their rating prediction accuracy is limited.
To this extent, Natarajan et al. [35] present an algorithm that overcomes the data sparsity and the cold start problems that CF RSs encounter. This algorithm finds information concerning the new entities by using a Matrix Factorisation Linked Open Data model. For a cold start issue, the algorithm uses a Linked Open Data knowledge base, namely DBpedia, to find information about new entities. Additionally, an improvement is made on the matrix factorisation model to handle data sparsity. The algorithm achieves improved recommendation accuracy when compared with other existing methods.
Shahbazi et al. [36] present a CF algorithm that tackles user big data by exploiting symmetric purchasing order and repetitively purchased products. This algorithm explores the purchased products based on user click patterns by combining a gradient boosting machine learning architecture with a word2vec mechanism. The algorithm improves the accuracy of predicting the relevant products to be recommended to the clients that are likely to buy them.
Yang et al. [37] present a set of NN-based and Matrix Factorisation-based RSs for online social voting. They state that information coming from both social networks and group affiliation can improve the accuracy of popularity-based voting RSs. It is also shown that group and social information is more valuable to cold rather than heavy users. The experimental results show that, in hot-voting recommendation, the metapath-based NN models outperform the computation-intensive MF models.
Jalali and Hosseini [38] introduce an algorithm that considers not only temporal user rating data for items but also temporal friendship relations among users in social networks. Furthermore, a local community detection method is presented, which, in combination with social recommendation techniques, results in improved sparsity, scalability and cold start issues of CF. The algorithm has fewer errors, as well as a higher accuracy, than previous methods in a dynamic environment and sparse rating matrix.
Zhang [39] presents a local random walk-based friend-recommendation method by combining social network information with tie strength. Initially, a weighted friend network is used to construct a friend recommendation, and then a local random walk-based similarity metric is used to compute user similarity. This method outperforms other methods using real social network data.
Guo et al. [40] present a sparsity alleviation method, which establishes enhanced trust relationships among users by using subjective and objective trust. The method uses emotional consistency for selecting each user’s trusted neighbours and predicts item ratings to obtain the final recommendations lists. In the case of data sparsity, this algorithm improves recommendation accuracy, as well as resists shilling attacks, and achieves higher recommendation accuracy than other methods for cold start users.
Herce-Zelaya et al. [41] introduce a method where data derived from social networks create a behavioural profile that is used to classify users. Then, this method creates predictions using machine learning techniques. As a result, this method alleviates the cold start problem without the need for the user to explicitly provide any additional data. The experimental results show that the algorithm obtains very satisfactory results when compared with state-of-the-art user cold-start algorithms. Margaris and Vassilakis [42] establish that a strong indication of concept drift is observed when a user abstains from submitting ratings for a long time. In this work, the authors present an algorithm that exploits the abstention interval concept, to remove ratings from the rating database that correspond to likings/preferences that are not valid anymore. From the experiments presented, it is shown that using the proposed algorithm with a rating abstention interval value of 2 months achieves the optimal results as compared not only with other settings but also with the plain CF algorithm.
Although the previous works highly improve rating prediction accuracy, they require supplementary information, which is not always available.
Margaris et al. [16] examine the features of textual reviews that affect the review-to-rating conversion procedure reliability and computes a confidence level for each produced rating, based on the uncertainty level for each conversion process. The feature that is found to be the most strongly associated with the textual review-to-rating conversion accuracy is the polarity term density. This confidence level metric is used both for the users’ similarity computation and for the prediction formulation phases in RSs. The results show that it achieves considerable accuracy improvement, while at the same time the overhead produced by the confidence level computation is relatively small.
Margaris et al. [17] present an approach that extracts social network textual information features, considering the venue category, targeted at computing a confidence metric for the ratings that are computed from texts. It uses this metric in the user similarity computation and venue rating prediction formulation process. It also proposes a venue recommendation algorithm that considers the venue QoS, similarity and spatial distance metrics, along with the generated venue rating predictions, to produce venue recommendations for social media users. The results show that the confidence level introduced improves the ability to generate personalised recommendations for users and finally increases user satisfaction.
Still, none of the aforementioned research examines the factors related to rating prediction accuracy in sparse collaborative filtering datasets, which typically suffer from lower rating prediction accuracy, since it is more difficult to find close and, hence, reliable NNs. By recommending the items that simply achieve the higher prediction values, without considering other factors, in some cases, the recommendation accuracy is reduced, and hence the success of the RS is negatively affected. Since the factors that this work examines derive from the user–item rating matrix, which all the CF datasets store, and do not need any kind of supplementary information, concerning the items and/or the users (item categories, user social relationships, etc.), the results of this study can be proven useful to any CF algorithm.
3. Prerequisites
The first step of a rating prediction in CF-based RSs is to identify the set of users having similar ratings with user U (i.e., the user whose prediction is being formulated); this set is known as U’s NNs [43,44]. A number of metrics have been proposed so as to quantify the similarity between two users, with the Pearson Correlation Coefficient (PCC) and the Cosine Similarity (CS) being the most widely used ones [45,46,47]. According to these metrics, the similarity between two users U and V is expressed as [48,49,50]:
where k iterates over the set of items that both users U and V have already entered ratings, while and denote the average value of all ratings entered by users U and V, respectively, in the ratings database.
The range of both metrics is [−1, 1], with −1 indicating complete dissimilarity and 1 indicating complete agreement. If only positive ratings are used, the CS metric range is narrowed to [0, 1], with higher values corresponding to higher similarities. For both metrics, thresholds can be set so that only users that are “close enough” to U are included in U’s NN set and thus considered in the process of formulating predictions for U. For the PCC metric, the value 0.0 is a commonly used threshold.
Then, to predict the rating value that user U would assign to item i, , the ratings given by U’s NNs to the exact same item are combined, using a prediction formula, expressed as:
where sim is the numeric similarity between users U and V, calculated in the previous step, using either the PCC or the CS.
In this work, we consider the following rating prediction features, which may affect the prediction accuracy in CF datasets:
- The number of NNs participating in the rating prediction; for this feature, we consider the NNs that have actually rated item i and not the overall number of NNs in the user’s NN set;
- The user’s U average ratings value (Uavg);
- The item’s i average ratings value (Iavg);
- The number of items user U has rated (UN);
- The number of users that have rated item i (IN).
In the following section, the performance of the aforementioned features will be assessed, in terms of prediction accuracy.
4. Exploring Rating Prediction Features
In this section, we investigate whether the rating prediction features, listed in Section 3, can be positively associated with increased rating prediction accuracy to address the RQs set in the Section 1.
Concerning the five rating prediction features, described in the previous section, the respective cases tested in the experimental procedure are as follows:
- For the exact number of NNs participating in the prediction feature (NNs features), values from 1 up to 9, plus an extra case of NNs ≥ 10, are examined.
- For the user’s U average ratings value (Uavg–feature), the values from the minimum to the maximum rating values are examined, with the increment step being equal to 0.5, i.e., the ranges of [1–1.5), [1.5–2), [2, 2.5), [2.5–3), [3–3.5), [4–4.5) and [4.5–5]. Notably, in all datasets used in this study, the ratings ranged from 1 to 5.
- For the item’s i average ratings value (Iavg–feature), the values from the minimum to the maximum rating values are again examined, with the increment step being equal to 0.5, exactly as in the previous case.
- For the number of items user U has rated (UN–feature), the smallest value used is 5 (since the datasets were 5-core), and increments with a step of 3 were considered up to the value of 25, from which point onwards all cases are classified under a range “>25”. Effectively, the following ranges are considered: [5, 7], [8, 10], [11, 13], [14, 16], [17, 19], [20, 22], [23, 25] and >25.
- For the number of users that have rated item i (IN–feature), the value ranges used are the same as with the previous case, i.e., [5, 7], [8, 10], [11, 13], [14, 16], [17, 19], [20, 22], [23, 25] and >25.
The datasets used in our experiments are widely used in CF research [33,50,51]. They vary regarding the number of ratings (from 170 K to 27 M), item domain category (sports, music, electronics, clothing, movies, etc.), number of users (17 K to 1.85 M), number of items (11 K to 685 K) and density (0.0021% to 0.08%). All are relatively sparse (dataset densities < 0.08%), where a higher deviation between the rating prediction and the factual rating is usually observed. Table 1 presents the basic information of these datasets.

Table 1.
Dataset information.
Regarding the Amazon datasets, the five-core ones are used, where each item and user have at least five ratings, to ensure that for each rating prediction formulated, at least four other ratings exist in the rating database and, hence, the application of the CF algorithm can produce valid results.
For the rating prediction accuracy to be quantified, the most widely used rating prediction error metrics in CF are used, namely the Mean Average Error (MAE) and the Root Mean Squared Error (RMSE) [56,57]. The former handles all errors uniformly, while the latter amplifies the significance of large deviations between the factual (hidden) rating and the rating prediction. The typical “hide one” technique is used (where the CF system tries to predict the value of a hidden rating in the rating database) to quantify the aforementioned errors [58,59,60,61]. In our work, all the ratings are hidden, one at a time, and their values are tried for prediction.
Measurements have been obtained using the following six different algorithms to ascertain that the conclusions reached are not affected by particular algorithm characteristics:
- The “plain” CF [18,19] algorithm, which first builds a user neighbourhood and then computes the prediction for a rating that a user would give to some item, based on the ratings given by the user’s neighbours for this particular item;
- An algorithm that considers rating variability [20] to improve rating prediction accuracy;
- A CF unveiling and exploiting causal relations between ratings [21];
- A temporal pattern-aware CF algorithm [22];
- A sequential CF recommender algorithm [23];
- A CF algorithm exploiting common histories up to the item review time [24].
The code for these algorithms was downloaded from GitHub or was obtained from authors of the respective papers. The results from all experiments were in close agreement (differences were quantified to be less than 5% in all cases). For conciseness, we report only on the results obtained for the plain CF algorithm.
Finally, when the number of samples that were tested for a specific rating value within a dataset was less than 50 (because there were few ratings with this value within the dataset and/or some rating predictions could not be formulated due to the absence of NNs that had rated the particular item), the results for the particular rating value were deemed to have reduced support and therefore are not included in the reporting and the discussion.
4.1. Number of NNs Features
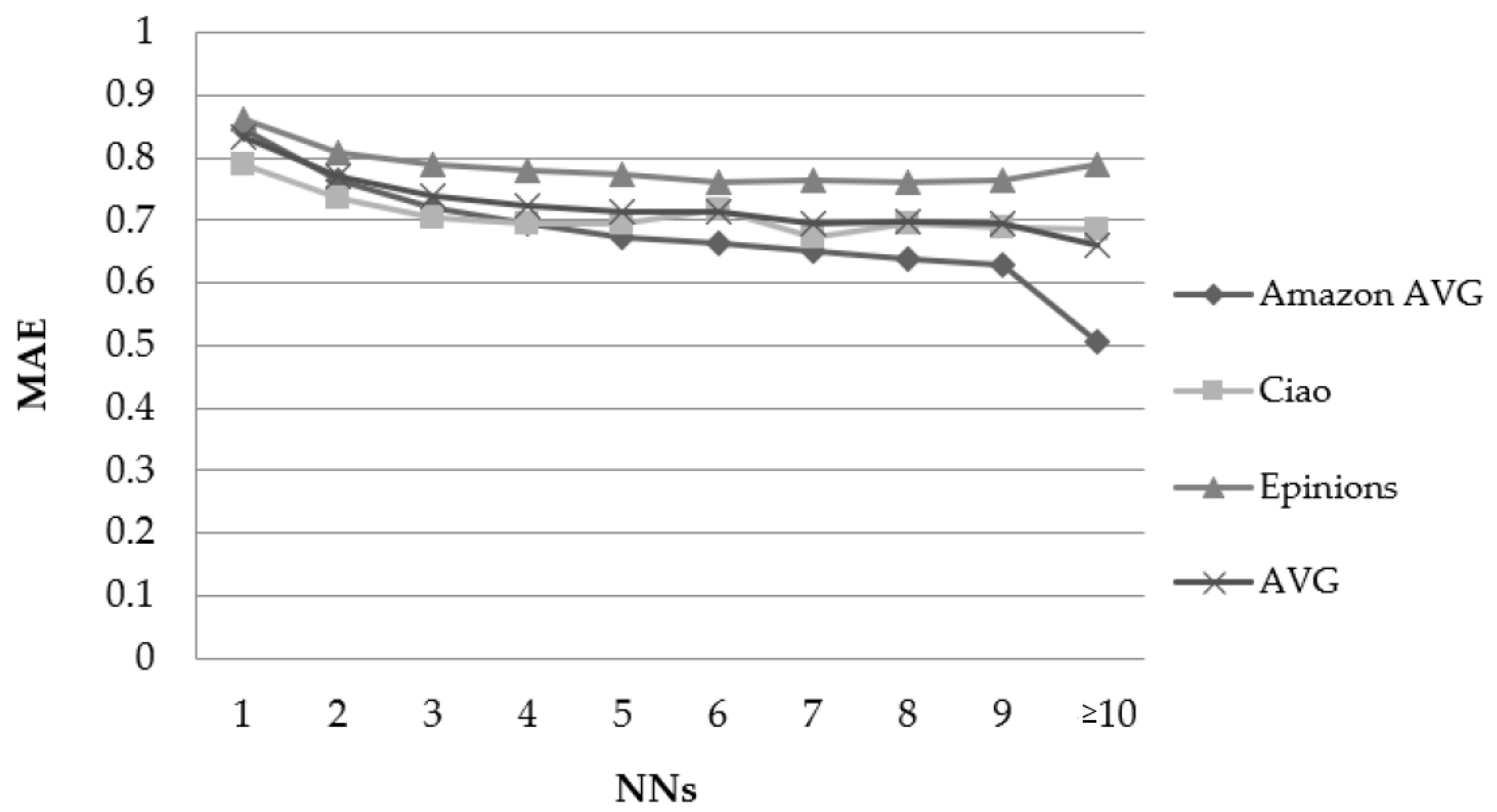
Figure 1 depicts the results obtained by running the experiments against the 10 Amazon datasets (presented by their average) and the Ciao and Epinions datasets, using the PCC user similarity metric and considering the number of NNs features.
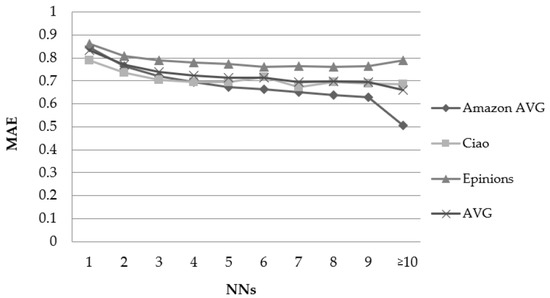
Figure 1.
Effect of the number of NNs features in the rating prediction MAE when using the PCC user similarity metric.
When the number of NNs increases, a MAE drop is observed, which grows along with the value of the “number of NNs” features, up to the point that this number reaches the value of four in all datasets. From that point forward, the datasets behave differently. Most datasets present a further reduction, ranging from 9% (Amazon CDs and Vinyl for NN ≥ 10) to 56% (Amazon Clothing for NN ≥ 10), with a notable exception of the Epinions dataset, which presents a small error decline up to the point of eight NNs and exhibits larger errors for higher NN values (1% MAE increase from NN = 4 to NN ≥ 10). The average MAE reduction from NN = 1 to NN = 4 equals to 13.3%. Similarly, the average RMSE reduction from NN = 1 to NN = 4 equals to 15.6%.
Regarding the CS user similarity metric, again, when the NN number increases, the MAE drops up to the point where the NN number reaches the value of four in all datasets. The average MAE reduction from NN = 1 to NN = 4 equals 13.7%. Similarly, the average RMSE reduction from NN = 1 to NN = 4 equals 16.9%.
Overall, we can conclude that the number of NNs features is correlated with rating prediction error reduction.
4.2. Uavg–Feature
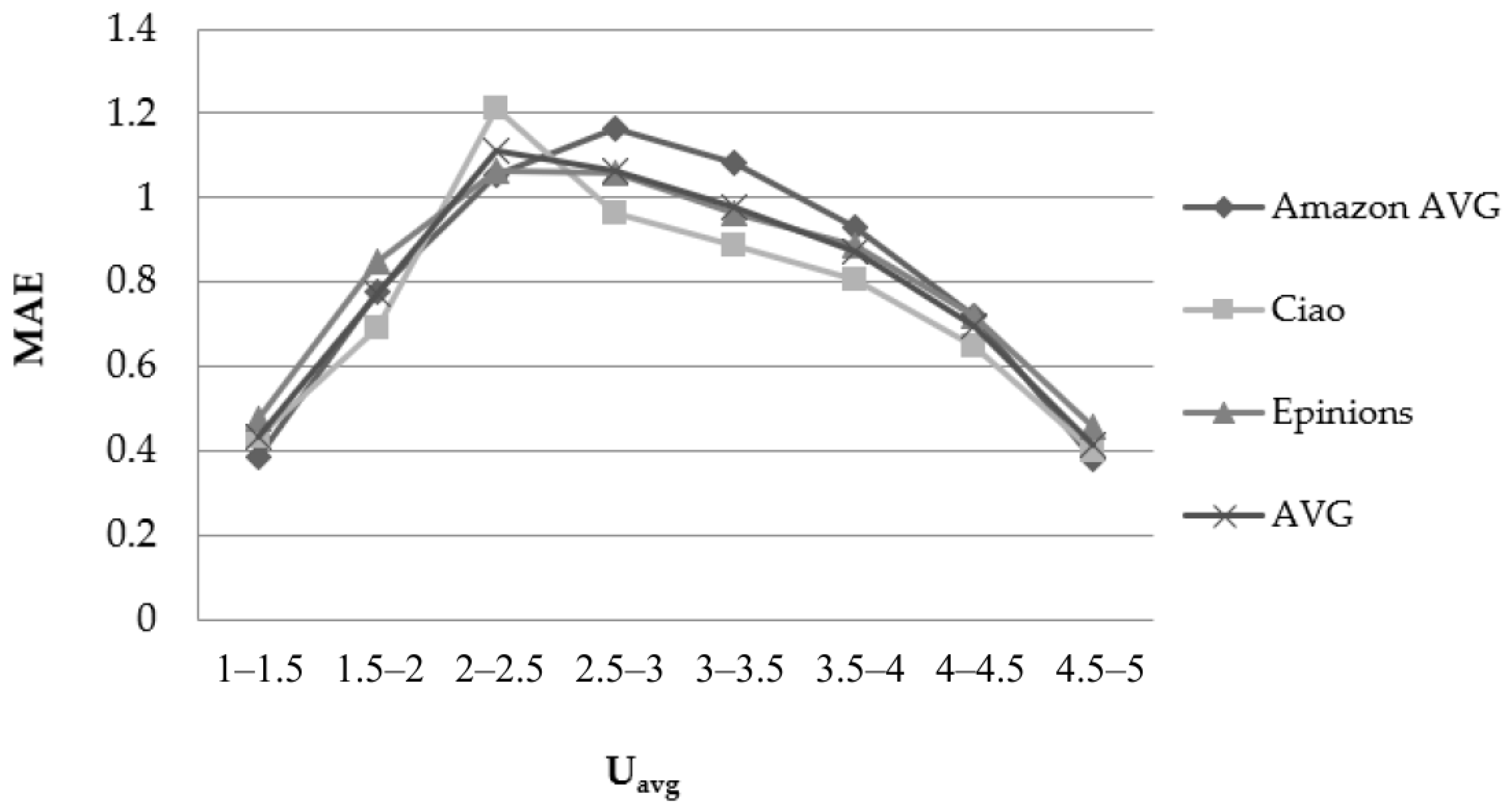
Figure 2 depicts the results obtained concerning the 10 Amazon datasets (on average) and the Epinions and Ciao datasets, using the PCC user similarity metric and considering the user rating average (Uavg) feature. It is noted that the ranges (x–axis) are not the same with the previous factor (and the next ones), since they represent metrics that take not only different values, but also types of values (for example the NNs factor represents the number of near neighbour users that take part in the rating prediction calculation—integer value, while the Uavg represents the average ratings value of the user for whom the rating prediction is being formulated—decimal value).
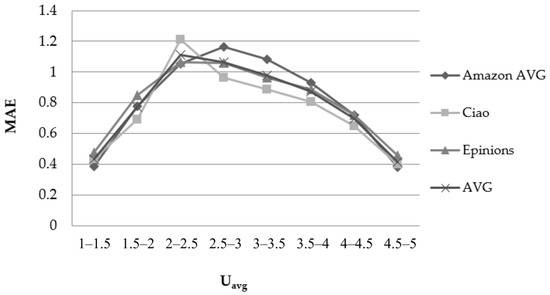
Figure 2.
Effect of the Uavg–feature in the rating prediction MAE when using the PCC user similarity metric.
When the rating average of the user for whom the prediction is being generated is close to the boundaries of the rating scale, the prediction accuracy is very high: the prediction error decreases by approximately 50%, compared to the cases where the value of the Uavg–feature is close to the middle of the rating scale. More specifically, the average MAE reduction from 2.5 ≤ Uavg ≤ 3 to 4.5 ≤ Uavg ≤ 5 equals 61.2%. The respective average RMSE reduction equals 45.2%. Correspondingly, the average MAE reduction from 2.5 ≤ Uavg ≤ 3 to 1 ≤ Uavg ≤ 1.5 is equal to 57.92%, and the relevant RMSE reduction is 68.56%.
Regarding the CS user similarity metric, again, when the rating average of the user, for whom the prediction is being generated, is close to the boundaries of the rating scale, the prediction accuracy is very high. More specifically, the prediction error decreases by approximately 50%, compared to the cases where the value of the Uavg–feature is close to the middle of the rating scale.
Overall, we can conclude that the Uavg–feature is correlated with rating prediction error reduction.
4.3. Iavg–Feature
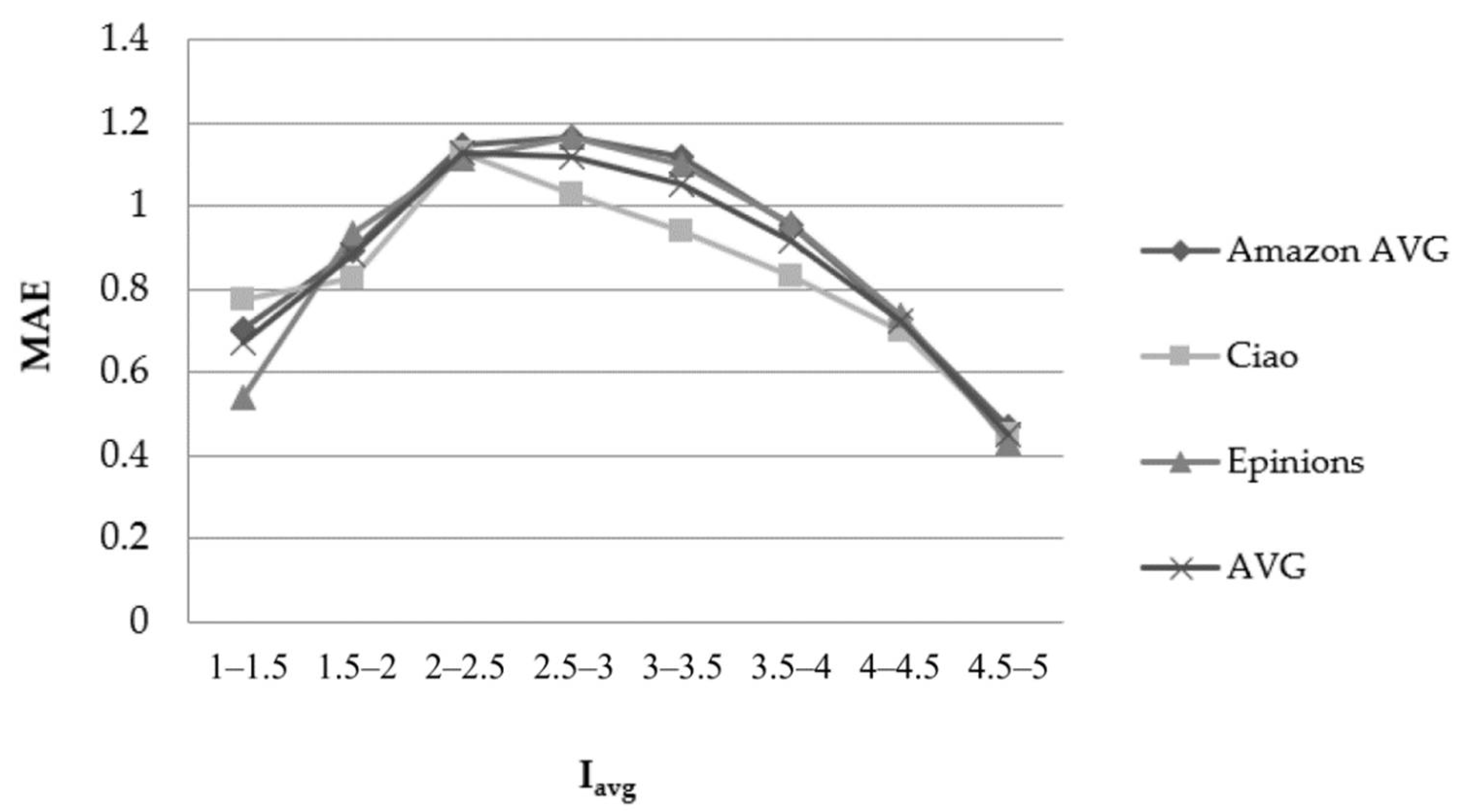
Figure 3 depicts the results obtained considering the item rating average (Iavg)–feature when using the PCC similarity metric.
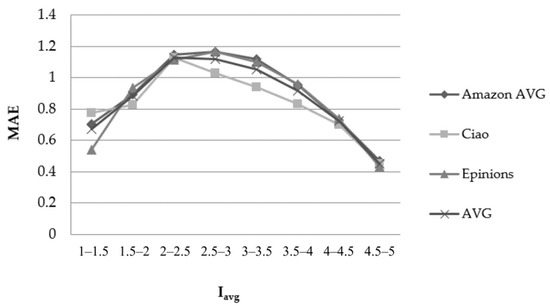
Figure 3.
Effect of the Iavg–feature in the rating prediction MAE when using the PCC user similarity metric.
When the rating average of the item for which the prediction is computed is close to the boundaries of the rating scale, the prediction accuracy is very high: the prediction error decreases by approximately 50%, compared to the cases where the value of the Uavg–feature is close to the middle of the rating scale. More specifically, the average MAE reduction from 2.5 ≤ Iavg ≤ 3 to 4.5 ≤ Iavg ≤ 5 equals to 59.8%; the respective average RMSE reduction equals to 50.1%. Correspondingly, the average MAE reduction from 2.5 ≤ Uavg ≤ 3 to 1 ≤ Uavg ≤ 1.5 is equal to 37.74%, and the relevant RMSE reduction is 30.76%.
As far as the CS user similarity metric is concerned, again, we can observe that when the rating average of the item for which the prediction is computed is close to the boundaries of the rating scale, the prediction accuracy is again very high: the prediction error decreases by approximately 50%, compared to the cases where the value of the Iavg–feature is close to the middle of the rating scale.
Overall, we can clearly conclude that the Iavg–feature is correlated with rating prediction error reduction.
4.4. UN–Feature
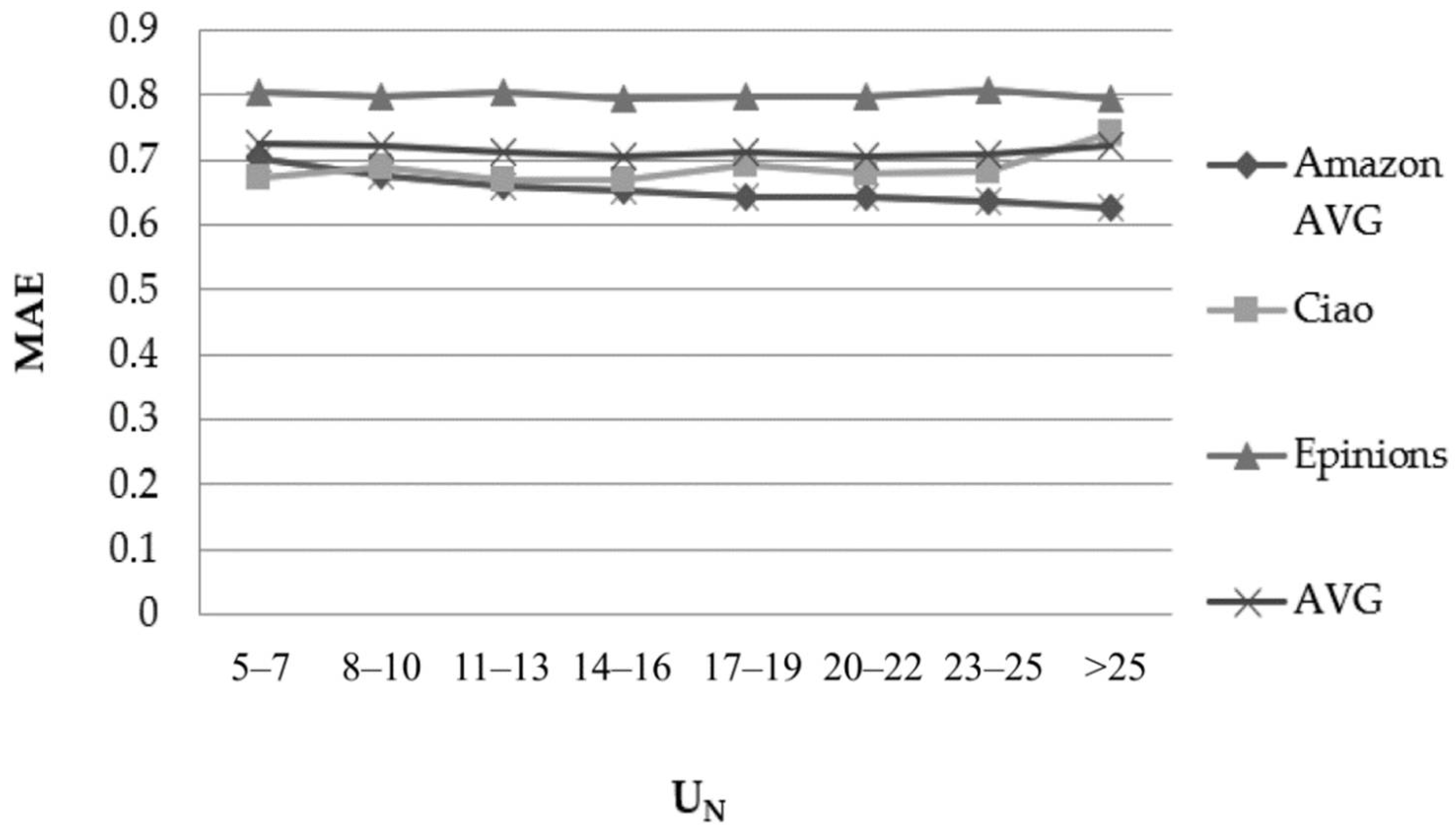
Figure 4 depicts the results obtained considering the number of items that the user U has rated (UN–feature) when using the PCC similarity metric.
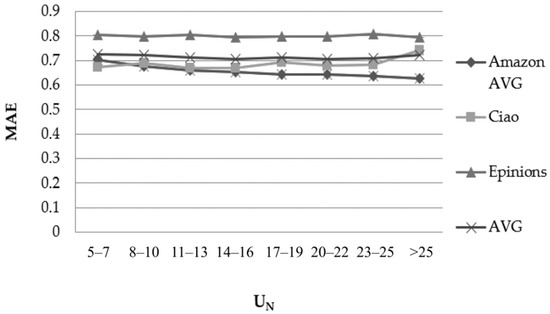
Figure 4.
Effect of the UN–feature in the rating prediction MAE when using the PCC user similarity metric.
The datasets exhibit divergent behaviour when the value of the UN–feature increases:
- For one dataset (“Digital music”), the MAE drops by more than 20% (23.82%) when UN increases from “5–7” to “>25”.
- For five datasets (“Musical instruments”, “CDs and Vinyl”, “Sports”, “Home” and “Electronics”), the MAE drops by 10–20% (10.70%, 11.26%, 11.99%, 15.03% and 14.74%, respectively).
- For five datasets (“Videogames”, “Movies and TV”, “Books”, “Clothing” and “Epinions”), the MAE drops by 1–10% (8.34%, 4.02%, 6.52%, 2.19% and 1.96%, respectively).
- For the CiaoDVD dataset, the MAE deteriorates by 10.31%.
The results obtained regarding the RMSE metric while using the PCC similarity measure, as well as the results obtained when using the CS similarity measure for both the MAE and RMSE metrics, are similar.
We can conclude that, at a global scale, no clear correlation exists between the value of the UN–feature and the rating prediction accuracy. Dataset-specific measurements need to be considered to determine whether higher confidence can be associated with predictions computed for users that have rated a higher number of items, as compared to predictions computed for users that have rated a low number of items (this issue will be investigated in our future work).
4.5. IN–Feature
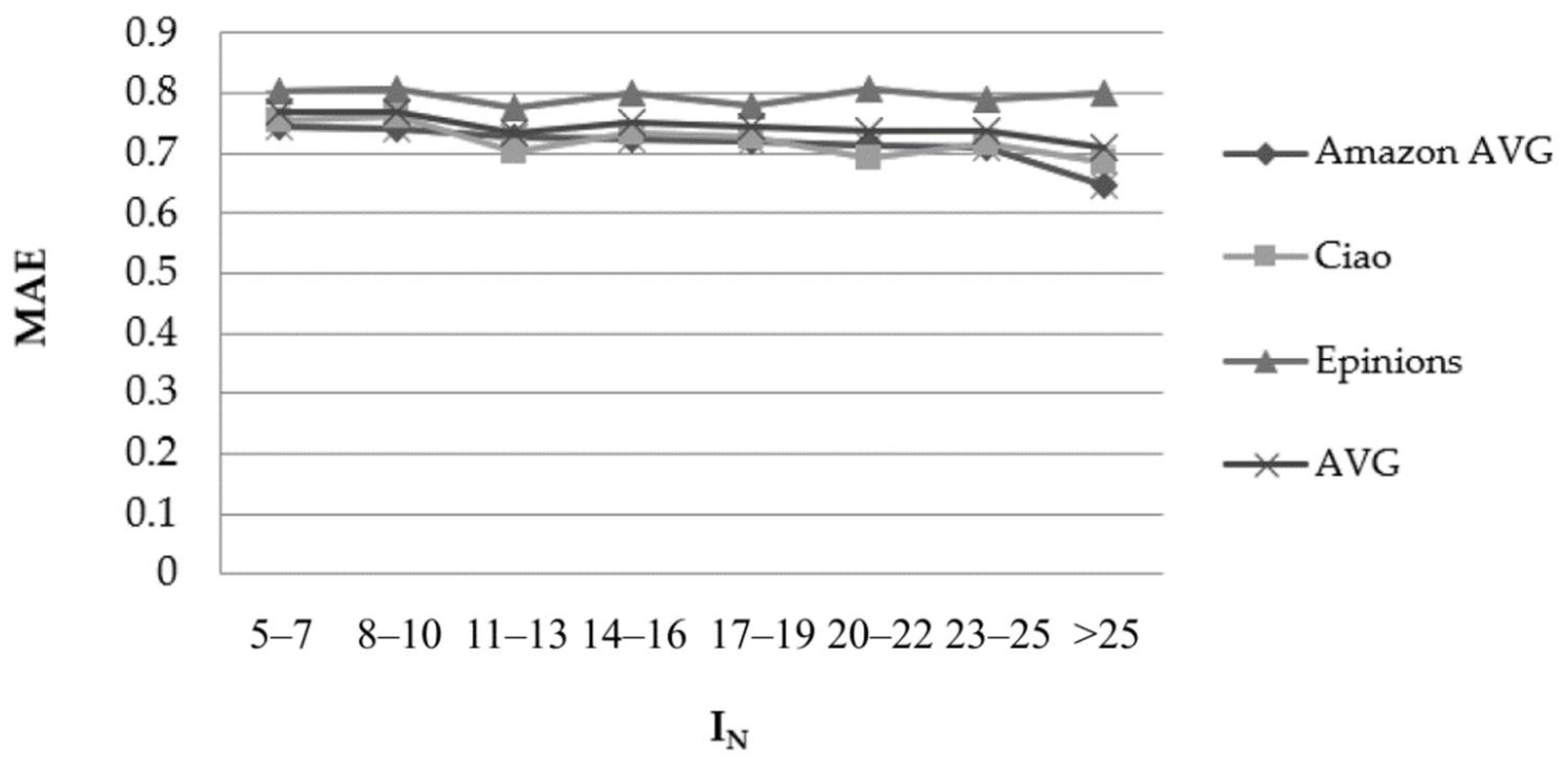
Figure 5 depicts the results obtained from the 10 Amazon datasets (on average) and the Epinions and Ciao datasets using the PCC similarity metric and considering the number of ratings that have been submitted for an item (IN)–feature.
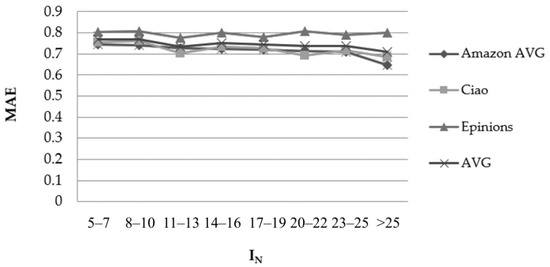
Figure 5.
Effect of the IN–feature in the rating prediction MAE when using the PCC user similarity metric.
The datasets exhibit divergent behaviour when the value of the IN–feature increases:
- For four datasets (“Digital Music”, “CDs and Vinyl”, “Home” and “Electronics”), the MAE drops by 10–20% (16.52%, 10.53%, 12.16% and 11.59%, respectively).
- For six datasets (“Videogames”, “Musical Instruments”, “Sports”, “Movies and TV”, “Books”, “Electronics” and “Epinions”), the MAE drops by 1–10% (8.98%, 8.11%, 9.42%, 5.20%, 8.98% and 3.74%, respectively).
- For two datasets, “Clothing” and “Epinions”, the MAE deteriorates by 0.25% and 2.27%, respectively.
The results obtained for the RMSE metric while using the PCC similarity measure, as well as the results obtained when using the CS similarity measure for both the MAE and RMSE metrics are similar.
We can conclude that, at a global scale, no clear correlation exists between the value of the IN–feature and the rating prediction accuracy. Dataset-specific measurements need to be considered to determine whether a higher confidence can be associated with predictions computed for items that have received a higher number of ratings as compared to predictions computed for items that have received a low number of ratings (this issue will be investigated in our future work).
4.6. Discussion of the Results and Complexity Analysis
From the experimental evaluation, we can conclude that a CF rating prediction is found to be more reliable when either:
- The number of NNs used for the formulation of the rating prediction is ≥4: a CF rating prediction formulated by taking into account ≥4 NNs is considered sounder than a prediction based on, for example, just 1 NN, since, as in real life, a recommendation based on very few opinions (friends, family members, etc.) bears a high probability of failure.
- The rating average of the user for whom the prediction is generated is close to the boundaries of the rating scale: a user with a rating average close to the maximum rating value (similarly, close to the minimum rating value) is a user who practically enters almost only excellent evaluations (similarly, bad evaluations), and hence it is easier for a rating prediction system to predict his/her next rating.
- The rating average of the item concerning the prediction is close to the boundaries of the rating scale: an item with a rating average close to the maximum rating value (or, similarly, close to the minimum rating value) is an item practically considered widely acceptable (similarly, widely unacceptable), and hence the probability that the (high value) rating prediction will be close to the (high) real user rating is relatively high.
By taking the aforementioned factors into account, the overall recommendation process can be significantly improved, since the RS will be able to know whether a rating prediction with a relatively high prediction score bears a low prediction reliability and recommends another item achieving a bit of a lower prediction score that bears high reliability, instead, and hence improves its recommendation success.
5. Conclusions and Future Work
In this work, we explored the factors related to rating prediction accuracy in sparse collaborative filtering datasets in a broader context, indicating that recommending the items that simply achieve higher prediction values than others, without considering other factors, in some cases, can reduce recommendation accuracy and negatively affect the success of the RS. In other words, it may be safer for an RS to recommend an item achieving a bit lower of a prediction score if, based on the factors studied in this work, this prediction is more reliable/confident than the other.
Five rating prediction features were examined in order to determine whether they affect the rating prediction accuracy in sparse CF systems, where the low prediction accuracy issue is more severe, since in sparse CF datasets the task of finding users’ NNs is much more very difficult when compared to dense CF datasets [10,62,63,64]. More specifically, these five features were (a) the number of NNs used for formulating the rating prediction, (b) the active user’s (i.e., the user for whom the prediction is being formulated) average ratings value, (c) the item’s average ratings value, (d) the number of items the active user has rated and (e) the number of users that have rated the item for which the rating prediction is computed (i.e., the number of ratings that the item has received).
In our experiments, 12 widely used sparse CF datasets were used from various item domain categories and having diverse numbers of users, items and ratings. Additionally, the two most commonly used CF user similarity metrics (PCC and CS) and the two most commonly used rating prediction error metrics (MAE and RMSE) were employed to ensure the reliability of the results.
The evaluation results have shown that the first three rating prediction features are correlated with a reduction in the rating prediction accuracy in all cases. More specifically:
- When the number of NNs used for the formulation of the rating prediction is ≥4, the prediction accuracy was found to be significantly higher (on average, we obtained a lower prediction error by 15%);
- When the rating average of the user for whom the prediction is generated is close to the boundaries of the rating scale, the rating prediction accuracy is very high (on average, we obtained a rating prediction error lower by 56% as compared to the accuracy obtained for users whose average is near the middle of the scale);
- When the rating average of the item concerning the prediction is close to the boundaries of the rating scale, the prediction accuracy is very high (on average, we obtain a lower rating prediction error by 57% as compared to the accuracy obtained for items whose respective average is near the middle of the scale).
On the other hand, for the two remaining features, i.e., (a) the number of items the active user has rated and (b) the number of users that have rated the item for which the rating prediction is calculated, no clear correlation between the feature value and the rating prediction accuracy could be determined. For both features, no clear correlation between the value of the feature and the rating prediction accuracy could be established at a global scale, since different datasets exhibited divergent behaviours. Therefore, dataset-specific measurements need to be taken into account in order to determine whether a higher confidence can be associated with predictions computed for objects (users or items) having low feature values as compared to predictions computed for objects having higher feature values.
Our future work will focus on quantifying the reliability of a CF rating prediction, based on the three prediction features introduced in this work, to tune the CF rating prediction algorithm. This will practically give the RS the capability to recommend an item achieving lower prediction score if, based on the three factors studied in this work, its prediction has been found to be more reliable/confident than others, and ultimately the RS will produce more successful recommendations. Furthermore, we are planning to examine additional rating prediction features in sparse CF datasets, where the low prediction accuracy issue is more acute. Finally, we are planning to explore respective rating prediction features in dense CF datasets.
Author Contributions
Conceptualization, D.M., D.S. and C.V.; methodology, D.M., D.S. and C.V.; software, D.M., D.S. and C.V.; validation, D.M., D.S. and C.V.; formal analysis, D.M., D.S. and C.V.; investigation, D.M., D.S. and C.V.; resources, D.M., D.S. and C.V.; data curation, D.M., D.S. and C.V.; writing—original draft preparation, D.M., D.S. and C.V.; writing—review and editing, D.M., D.S. and C.V.; visualisation, D.M., D.S. and C.V.; supervision, D.M., D.S. and C.V.; project administration, D.M., D.S. and C.V.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analysed in this study. These data can be found here: https://nijianmo.github.io/amazon/index.html, https://guoguibing.github.io/librec/datasets.html and http://www.trustlet.org/datasets/ (accessed on 1 April 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cui, Z.; Xu, X.; Xue, F.; Cai, X.; Cao, Y.; Zhang, W.; Chen, J. Personalized Recommendation System Based on Collaborative Filtering for IoT Scenarios. IEEE Trans. Serv. Comput. 2020, 13, 685–695. [Google Scholar] [CrossRef]
- Lara-Cabrera, R.; González-Prieto, Á.; Ortega, F. Deep Matrix Factorization Approach for Collaborative Filtering Recommender Systems. Appl. Sci. 2020, 10, 4926. [Google Scholar] [CrossRef]
- Balabanović, M.; Shoham, Y. Fab: Content-Based, Collaborative Recommendation. Commun. ACM 1997, 40, 66–72. [Google Scholar] [CrossRef]
- Cechinel, C.; Sicilia, M.-Á.; Sánchez-Alonso, S.; García-Barriocanal, E. Evaluating Collaborative Filtering Recommendations inside Large Learning Object Repositories. Inf. Process. Manag. 2013, 49, 34–50. [Google Scholar] [CrossRef]
- Herlocker, J.L.; Konstan, J.A.; Terveen, L.G.; Riedl, J.T. Evaluating Collaborative Filtering Recommender Systems. ACM Trans. Inf. Syst. 2004, 22, 5–53. [Google Scholar] [CrossRef]
- Lops, P.; Narducci, F.; Musto, C.; de Gemmis, M.; Polignano, M.; Semeraro, G. Recommendations Biases and Beyond-Accuracy Objectives in Collaborative Filtering. In Collaborative Recommendations; World Scientific: Singapore, 2018; pp. 329–368. [Google Scholar]
- Singh, P.K.; Sinha, M.; Das, S.; Choudhury, P. Enhancing Recommendation Accuracy of Item-Based Collaborative Filtering Using Bhattacharyya Coefficient and Most Similar Item. Appl. Intell. 2020, 50, 4708–4731. [Google Scholar] [CrossRef]
- Guo, J.; Deng, J.; Ran, X.; Wang, Y.; Jin, H. An Efficient and Accurate Recommendation Strategy Using Degree Classification Criteria for Item-Based Collaborative Filtering. Expert Syst. Appl. 2021, 164, 113756. [Google Scholar] [CrossRef]
- Veras De Sena Rosa, R.E.; Guimaraes, F.A.S.; Mendonca, R.; da Lucena, V.F. Improving Prediction Accuracy in Neighborhood-Based Collaborative Filtering by Using Local Similarity. IEEE Access 2020, 8, 142795–142809. [Google Scholar] [CrossRef]
- Ramezani, M.; Moradi, P.; Akhlaghian, F. A Pattern Mining Approach to Enhance the Accuracy of Collaborative Filtering in Sparse Data Domains. Phys. A Stat. Mech. Appl. 2014, 408, 72–84. [Google Scholar] [CrossRef]
- Feng, C.; Liang, J.; Song, P.; Wang, Z. A Fusion Collaborative Filtering Method for Sparse Data in Recommender Systems. Inf. Sci. 2020, 521, 365–379. [Google Scholar] [CrossRef]
- Li, K.; Zhou, X.; Lin, F.; Zeng, W.; Wang, B.; Alterovitz, G. Sparse Online Collaborative Filtering with Dynamic Regularization. Inf. Sci. 2019, 505, 535–548. [Google Scholar] [CrossRef]
- Sarwar, B.; Karypis, G.; Konstan, J.; Reidl, J. Item-Based Collaborative Filtering Recommendation Algorithms. In Proceedings of the Tenth International Conference on World Wide Web—WWW ’01, Hong Kong, 1–5 May 2001; ACM Press: New York, NY, USA, 2001; pp. 285–295. [Google Scholar]
- Li, Y.; Hu, J.; Zhai, C.; Chen, Y. Improving One-Class Collaborative Filtering by Incorporating Rich User Information. In Proceedings of the 19th ACM International Conference on Information and Knowledge Management—CIKM ’10, Toronto, ON, Canada, 26–30 October 2010; ACM Press: New York, NY, USA, 2010; p. 959. [Google Scholar]
- Herlocker, J.L.; Konstan, J.A.; Borchers, A.; Riedl, J. An Algorithmic Framework for Performing Collaborative Filtering. In Proceedings of the 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval—SIGIR ’99, Berkeley, CA, USA, 15–19 August 1999; ACM Press: New York, NY, USA, 1999; pp. 230–237. [Google Scholar]
- Margaris, D.; Vassilakis, C.; Spiliotopoulos, D. What Makes a Review a Reliable Rating in Recommender Systems? Inf. Process. Manag. 2020, 57, 102304. [Google Scholar] [CrossRef]
- Margaris, D.; Vassilakis, C.; Spiliotopoulos, D. Handling Uncertainty in Social Media Textual Information for Improving Venue Recommendation Formulation Quality in Social Networks. Soc. Netw. Anal. Min. 2019, 9, 64. [Google Scholar] [CrossRef]
- Herlocker, J.L.; Konstan, J.A.; Borchers, A.; Riedl, J. An Algorithmic Framework for Performing Collaborative Filtering. ACM SIGIR Forum 2017, 51, 227–234. [Google Scholar] [CrossRef]
- Schafer, J.B.; Frankowski, D.; Herlocker, J.; Sen, S. Collaborative Filtering Recommender Systems. In The Adaptive Web; Springer: Berlin/Heidelberg, Germany, 2007; pp. 291–324. [Google Scholar]
- Margaris, D.; Vassilakis, C. Improving Collaborative Filtering’s Rating Prediction Accuracy by Considering Users’ Rating Variability. In Proceedings of the 4th IEEE International Conference on Big Data Intelligence and Computing, Athens, Greece, 12–15 August 2018; IEEE: Athens, Greece, 2018; pp. 1022–1027. [Google Scholar]
- Zhang, J.; Chen, X.; Zhao, W.X. Causally Attentive Collaborative Filtering. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Online, 1–5 November 2021; ACM: New York, NY, USA, 2021; pp. 3622–3626. [Google Scholar]
- Chai, Y.; Liu, G.; Chen, Z.; Li, F.; Li, Y.; Effah, E.A. A Temporal Collaborative Filtering Algorithm Based on Purchase Cycle. In Proceedings of the ICCCS 2018: Cloud Computing and Security, Haikou, China, 8–10 June 2018; Xingming, S., Pan, Z., Bertino, E., Eds.; Springer: Cham, Switzerland, 2018; pp. 191–201. [Google Scholar]
- Li, J.; Wang, Y.; McAuley, J. Time Interval Aware Self-Attention for Sequential Recommendation. In Proceedings of the 13th International Conference on Web Search and Data Mining, Houston, TX, USA, 20 January 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 322–330. [Google Scholar]
- Margaris, D.; Spiliotopoulos, D.; Vassilakis, C.; Vasilopoulos, D. Improving Collaborative Filtering’s Rating Prediction Accuracy by Introducing the Experiencing Period Criterion. Neural Comput. Appl. Spec. Issue Inf. Intell. Syst. Appl. 2020. [Google Scholar] [CrossRef]
- Fernández-García, A.J.; Iribarne, L.; Corral, A.; Criado, J.; Wang, J.Z. A Recommender System for Component-Based Applications Using Machine Learning Techniques. Knowl.-Based Syst. 2019, 164, 68–84. [Google Scholar] [CrossRef]
- Forestiero, A. Heuristic Recommendation Technique in Internet of Things Featuring Swarm Intelligence Approach. Expert Syst. Appl. 2022, 187, 115904. [Google Scholar] [CrossRef]
- Sahu, S.; Kumar, R.; Pathan, M.S.; Shafi, J.; Kumar, Y.; Ijaz, M.F. Movie Popularity and Target Audience Prediction Using the Content-Based Recommender System. IEEE Access 2022, 10, 42044–42060. [Google Scholar] [CrossRef]
- Aivazoglou, M.; Roussos, A.O.; Margaris, D.; Vassilakis, C.; Ioannidis, S.; Polakis, J.; Spiliotopoulos, D. A Fine-Grained Social Network Recommender System. Soc. Netw. Anal. Min. 2020, 10, 8. [Google Scholar] [CrossRef]
- Bouazza, H.; Said, B.; Zohra Laallam, F. A Hybrid IoT Services Recommender System Using Social IoT. J. King Saud Univ. Comput. Inf. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Zhang, Z.-P.; Kudo, Y.; Murai, T.; Ren, Y.-G. Enhancing Recommendation Accuracy of Item-Based Collaborative Filtering via Item-Variance Weighting. Appl. Sci. 2019, 9, 1928. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Wei, Q.; Zhang, L.; Wang, B.; Ho, W.-H. Diversity Balancing for Two-Stage Collaborative Filtering in Recommender Systems. Appl. Sci. 2020, 10, 1257. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Tang, Y. Collaborative Filtering Based on Gaussian Mixture Model and Improved Jaccard Similarity. IEEE Access 2019, 7, 118690–118701. [Google Scholar] [CrossRef]
- Jiang, L.; Cheng, Y.; Yang, L.; Li, J.; Yan, H.; Wang, X. A Trust-Based Collaborative Filtering Algorithm for E-Commerce Recommendation System. J. Ambient Intell. Humaniz. Comput. 2019, 10, 3023–3034. [Google Scholar] [CrossRef] [Green Version]
- Iftikhar, A.; Ghazanfar, M.A.; Ayub, M.; Mehmood, Z.; Maqsood, M. An Improved Product Recommendation Method for Collaborative Filtering. IEEE Access 2020, 8, 123841–123857. [Google Scholar] [CrossRef]
- Natarajan, S.; Vairavasundaram, S.; Natarajan, S.; Gandomi, A.H. Resolving Data Sparsity and Cold Start Problem in Collaborative Filtering Recommender System Using Linked Open Data. Expert Syst. Appl. 2020, 149, 113248. [Google Scholar] [CrossRef]
- Shahbazi, Z.; Hazra, D.; Park, S.; Byun, Y.C. Toward Improving the Prediction Accuracy of Product Recommendation System Using Extreme Gradient Boosting and Encoding Approaches. Symmetry 2020, 12, 1566. [Google Scholar] [CrossRef]
- Yang, X.; Liang, C.; Zhao, M.; Wang, H.; Ding, H.; Liu, Y.; Li, Y.; Zhang, J. Collaborative Filtering-Based Recommendation of Online Social Voting. IEEE Trans. Comput. Soc. Syst. 2017, 4, 1–13. [Google Scholar] [CrossRef]
- Jalali, S.; Hosseini, M. Social Collaborative Filtering Using Local Dynamic Overlapping Community Detection. J. Supercomput. 2021, 77, 11786–11806. [Google Scholar] [CrossRef]
- Zhang, T. Research on Collaborative Filtering Recommendation Algorithm Based on Social Network. Int. J. Internet Manuf. Serv. 2019, 6, 343. [Google Scholar] [CrossRef]
- Guo, L.; Liang, J.; Zhu, Y.; Luo, Y.; Sun, L.; Zheng, X. Collaborative Filtering Recommendation Based on Trust and Emotion. J. Intell. Inf. Syst. 2019, 53, 113–135. [Google Scholar] [CrossRef]
- Herce-Zelaya, J.; Porcel, C.; Bernabé-Moreno, J.; Tejeda-Lorente, A.; Herrera-Viedma, E. New Technique to Alleviate the Cold Start Problem in Recommender Systems Using Information from Social Media and Random Decision Forests. Inf. Sci. 2020, 536, 156–170. [Google Scholar] [CrossRef]
- Margaris, D.; Vassilakis, C. Exploiting Rating Abstention Intervals for Addressing Concept Drift in Social Network Recommender Systems. Informatics 2018, 5, 21. [Google Scholar] [CrossRef] [Green Version]
- Verstrepen, K.; Goethals, B. Unifying Nearest Neighbors Collaborative Filtering. In Proceedings of the 8th ACM Conference on Recommender systems—RecSys ’14, Foster City, CA, USA, 6–10 October 2014; ACM Press: New York, NY, USA, 2014; pp. 177–184. [Google Scholar]
- Logesh, R.; Subramaniyaswamy, V.; Malathi, D.; Sivaramakrishnan, N.; Vijayakumar, V. Enhancing Recommendation Stability of Collaborative Filtering Recommender System through Bio-Inspired Clustering Ensemble Method. Neural Comput. Appl. 2020, 32, 2141–2164. [Google Scholar] [CrossRef]
- Schwarz, M.; Lobur, M.; Stekh, Y. Analysis of the Effectiveness of Similarity Measures for Recommender Systems. In Proceedings of the 2017 14th International Conference The Experience of Designing and Application of CAD Systems in Microelectronics (CADSM), Lviv, Ukraine, 21–25 February 2017; IEEE: Lviv, Ukraine, 2017; pp. 275–277. [Google Scholar]
- Sheugh, L.; Alizadeh, S.H. A Note on Pearson Correlation Coefficient as a Metric of Similarity in Recommender System. In Proceedings of the 2015 AI & Robotics (IRANOPEN), Qazvin, Iran, 12 April 2015; IEEE: Qazvin, Iran, 2015; pp. 1–6. [Google Scholar]
- Luo, C.; Zhan, J.; Xue, X.; Wang, L.; Ren, R.; Yang, Q. Cosine Normalization: Using Cosine Similarity Instead of Dot Product in Neural Networks. In Proceedings of the 2018 Conference on Artificial Neural Networks and Machine Learning—ICANN 2018, Rhodes, Greece, 4–7 October 2018; Springer: Cham, Switzerland, 2018; pp. 382–391. [Google Scholar]
- Jin, R.; Chai, J.Y.; Si, L. An Automatic Weighting Scheme for Collaborative Filtering. In Proceedings of the 27th annual international conference on Research and development in information retrieval—SIGIR ’04, Sheffield, UK, 25–29 July 2004; ACM Press: New York, NY, USA, 2004; p. 337. [Google Scholar]
- Liu, H.; Hu, Z.; Mian, A.; Tian, H.; Zhu, X. A New User Similarity Model to Improve the Accuracy of Collaborative Filtering. Knowl.-Based Syst. 2014, 56, 156–166. [Google Scholar] [CrossRef] [Green Version]
- Barkan, O.; Fuchs, Y.; Caciularu, A.; Koenigstein, N. Explainable Recommendations via Attentive Multi-Persona Collaborative Filtering. In Proceedings of the Fourteenth ACM Conference on Recommender Systems, Virtual Event, Brazil, 22–26 September 2020; ACM: New York, NY, USA, 2020; pp. 468–473. [Google Scholar]
- Wang, Q.; Yin, H.; Wang, H.; Nguyen, Q.V.H.; Huang, Z.; Cui, L. Enhancing Collaborative Filtering with Generative Augmentation. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 25 July 2019; ACM: New York, NY, USA, 2019; pp. 548–556. [Google Scholar]
- Ni, J.; Li, J.; McAuley, J. Justifying Recommendations Using Distantly-Labeled Reviews and Fine-Grained Aspects. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, 3–7 November 2019; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 188–197. [Google Scholar]
- He, R.; McAuley, J. Ups and Downs: Modeling the Visual Evolution of Fashion Trends with One-Class Collaborative Filtering. In Proceedings of the 25th International Conference on World Wide Web, Montréal, QC, Canada, 11–15 April 2016; International World Wide Web Conferences Steering Committee: Geneva, Switzerland, 2016; pp. 507–517. [Google Scholar]
- Guo, G.; Zhang, J.; Thalmann, D.; Yorke-Smith, N. ETAF: An Extended Trust Antecedents Framework for Trust Prediction. In Proceedings of the 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2014), Beijing, China, 17–20 August 2014; IEEE: Beijing, China, 2014; pp. 540–547. [Google Scholar]
- Meyffret, S.; Guillot, E.; Médini, L.; Laforest, F. RED: A Rich Epinions Dataset for Recommender Systems; LIRIS, ⟨hal-01010246⟩; HAL Open Science: Leiden, The Netherlands, 2014. [Google Scholar]
- Candillier, L.; Meyer, F.; Boullé, M. Comparing State-of-the-Art Collaborative Filtering Systems. In Machine Learning and Data Mining in Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2007; pp. 548–562. [Google Scholar]
- Candillier, L.; Meyer, F.; Fessant, F. Designing Specific Weighted Similarity Measures to Improve Collaborative Filtering Systems. In Advances in Data Mining. Medical Applications, E-Commerce, Marketing, and Theoretical Aspects; Springer: Berlin/Heidelberg, Germany, 2008; pp. 242–255. [Google Scholar]
- Yu, K.; Schwaighofer, A.; Tresp, V.; Xu, X.; Kriegel, H. Probabilistic Memory-Based Collaborative Filtering. IEEE Trans. Knowl. Data Eng. 2004, 16, 56–69. [Google Scholar] [CrossRef]
- Wang, J.; Lin, K.; Li, J. A Collaborative Filtering Recommendation Algorithm Based on User Clustering and Slope One Scheme. In Proceedings of the 2013 8th International Conference on Computer Science & Education, Colombo, Sri Lanka, 26–28 April 2013; IEEE: Colombo, Sri Lanka, 2013; pp. 1473–1476. [Google Scholar]
- Massa, P.; Avesani, P. Trust-Aware Collaborative Filtering for Recommender Systems. In Proceedings of the OTM 2004: On the Move to Meaningful Internet Systems 2004: CoopIS, DOA, and ODBASE, Agia Napa, Cyprus, 25–29 October 2004; Meersman, R., Tari, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 492–508. [Google Scholar]
- Lu, L.; Yuan, Y.; Chen, X.; Li, Z. A Hybrid Recommendation Method Integrating the Social Trust Network and Local Social Influence of Users. Electronics 2020, 9, 1496. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, J.; Gao, J.; Zhang, P. A Hybrid User Similarity Model for Collaborative Filtering. Inf. Sci. 2017, 418–419, 102–118. [Google Scholar] [CrossRef]
- Hu, R.; Pu, P. Enhancing Collaborative Filtering Systems with Personality Information. In Proceedings of the Fifth ACM Conference on Recommender Systems—RecSys ’11, Chicago, IL, USA, 23–27 October 2011; ACM Press: New York, NY, USA, 2011; p. 197. [Google Scholar]
- Lyon, G.F. Understanding and Customizing Nmap Data Files. In Nmap Network Scanning: The Official Nmap Project Guide to Network Discovery and Security Scanning; Insecure.Com LLC: Sunnyvale, CA, USA, 2009; p. 464. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).