Exploiting Incremental Virtual Full Duplex Non-Orthogonal Multiple Access Systems
Abstract
:1. Introduction
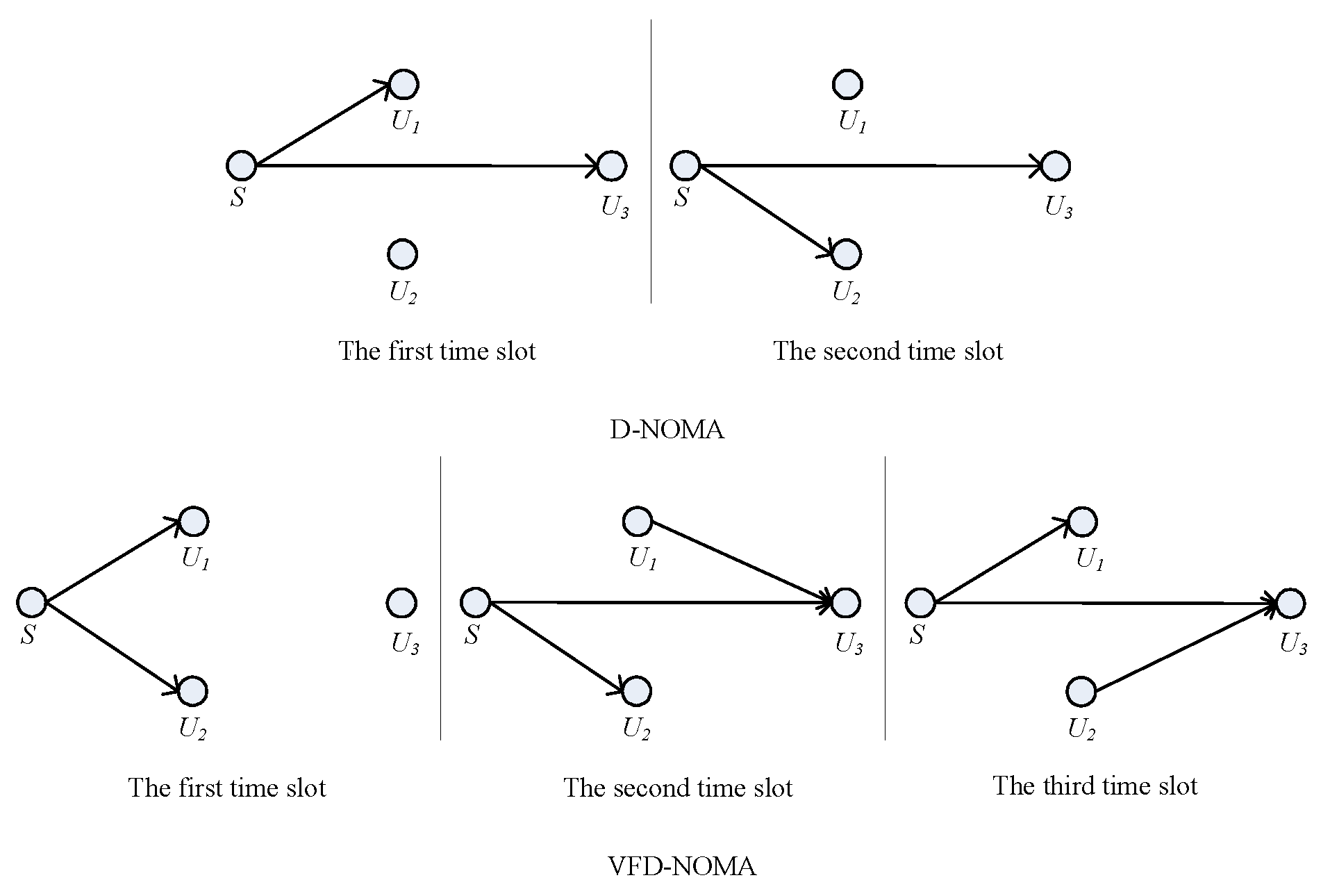
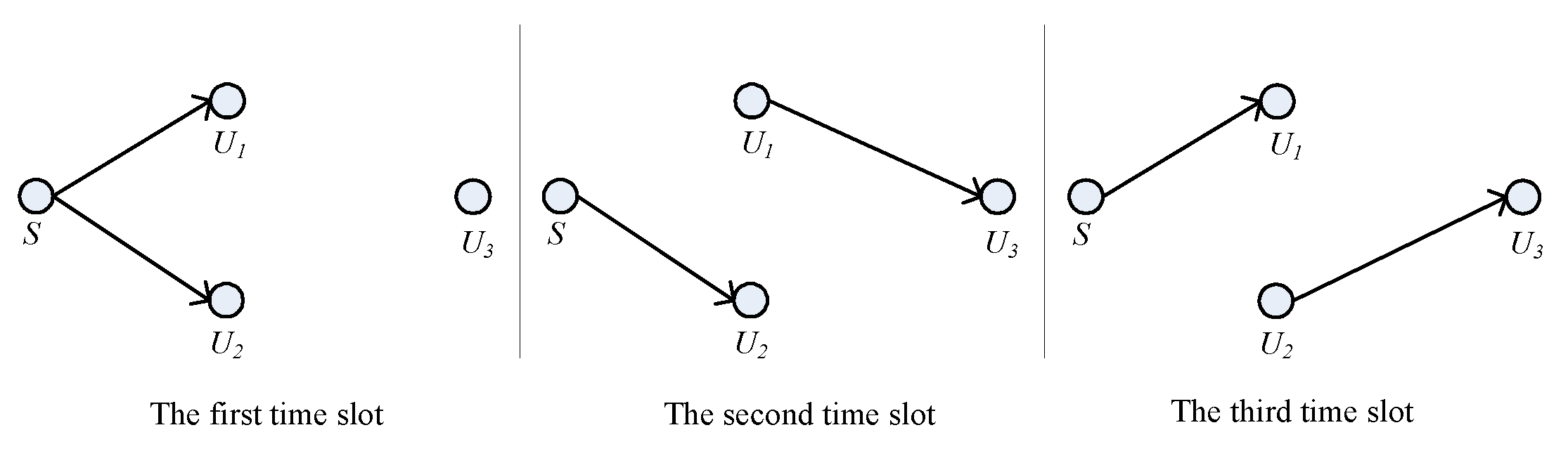
- An incremental VFD-NOMA (I-VFD-NOMA) scheme is proposed in this study. When the SINR of direct link is greater than the given threshold, direct NOMA (D-NOMA) with two time slots is used. When the SINR of this link falls below the given threshold, VFD-NOMA with three time slots is adopted. In VFD-NOMA scheme, two energy harvesting (EH) enabled near users can be considered as relays for forwarding the information successively for the far user. The analytical expression of throughput for this I-VFD-NOMA system is derived with I-SIC.
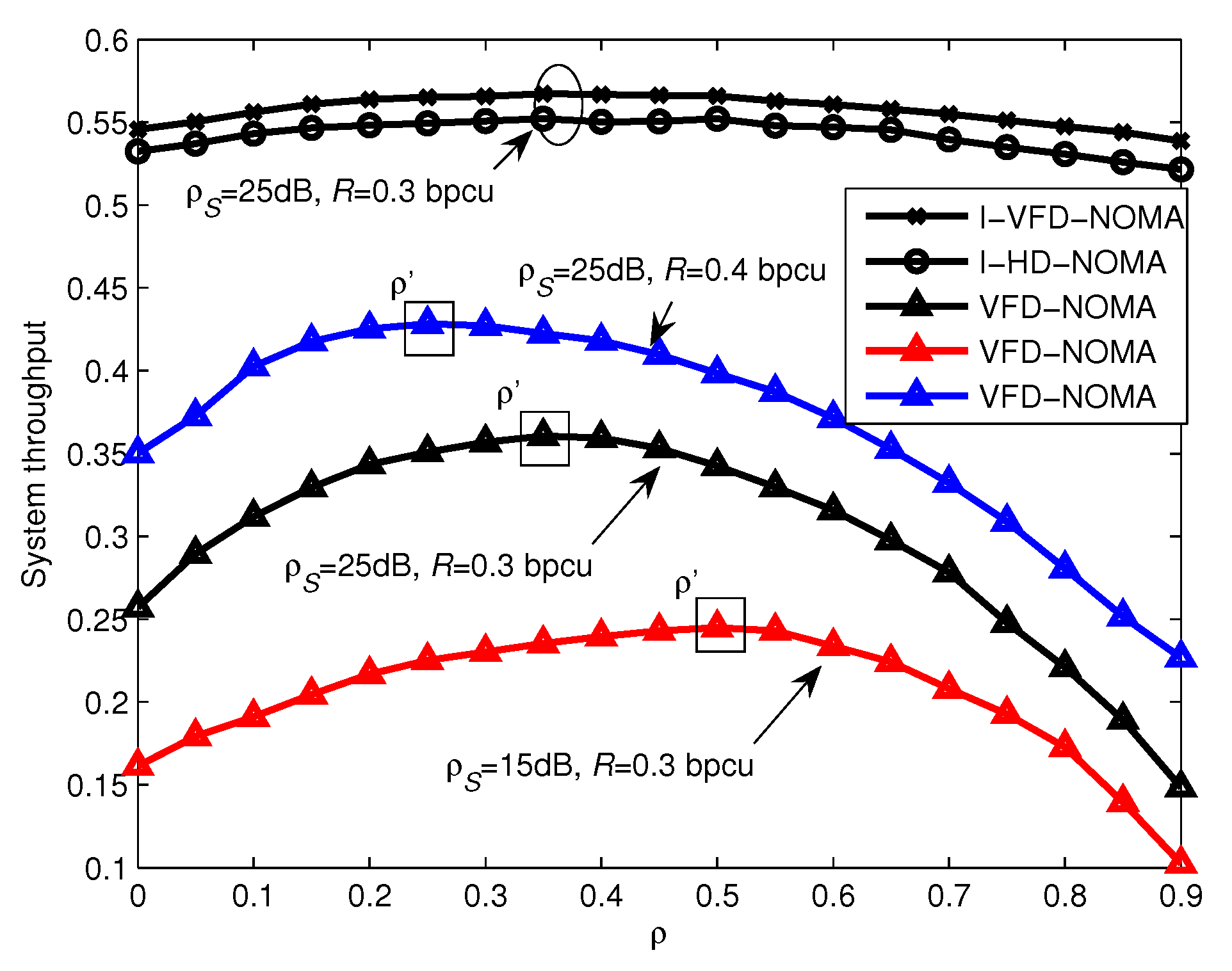
- It is well known that power splitting factor affects the performance of the EH system greatly. So the optimal power splitting factor at relay that maximizes the throughput of VFD-NOMA system without direct link is derived in this study. Numerical and simulation results show that this optimal factor can improve system performance greatly.
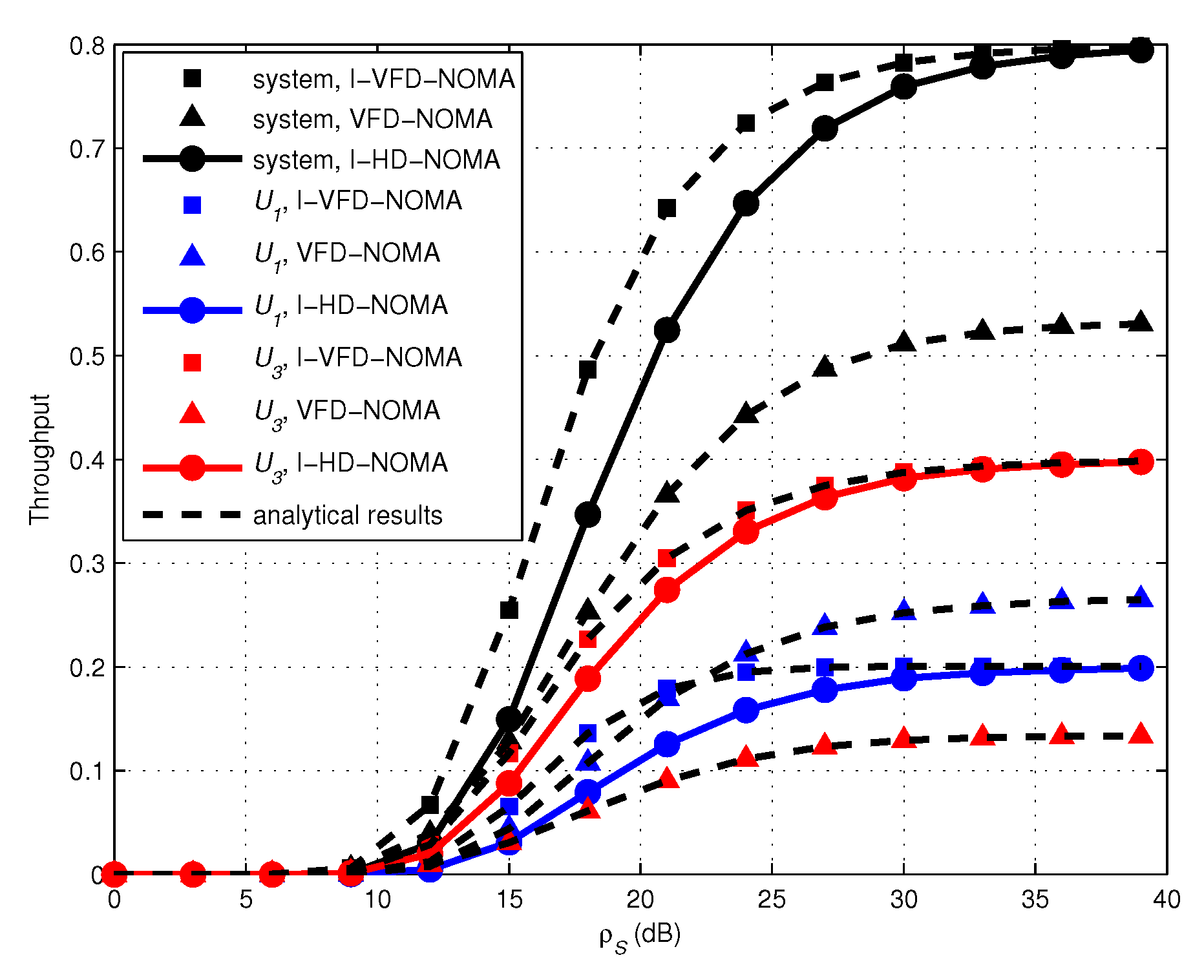
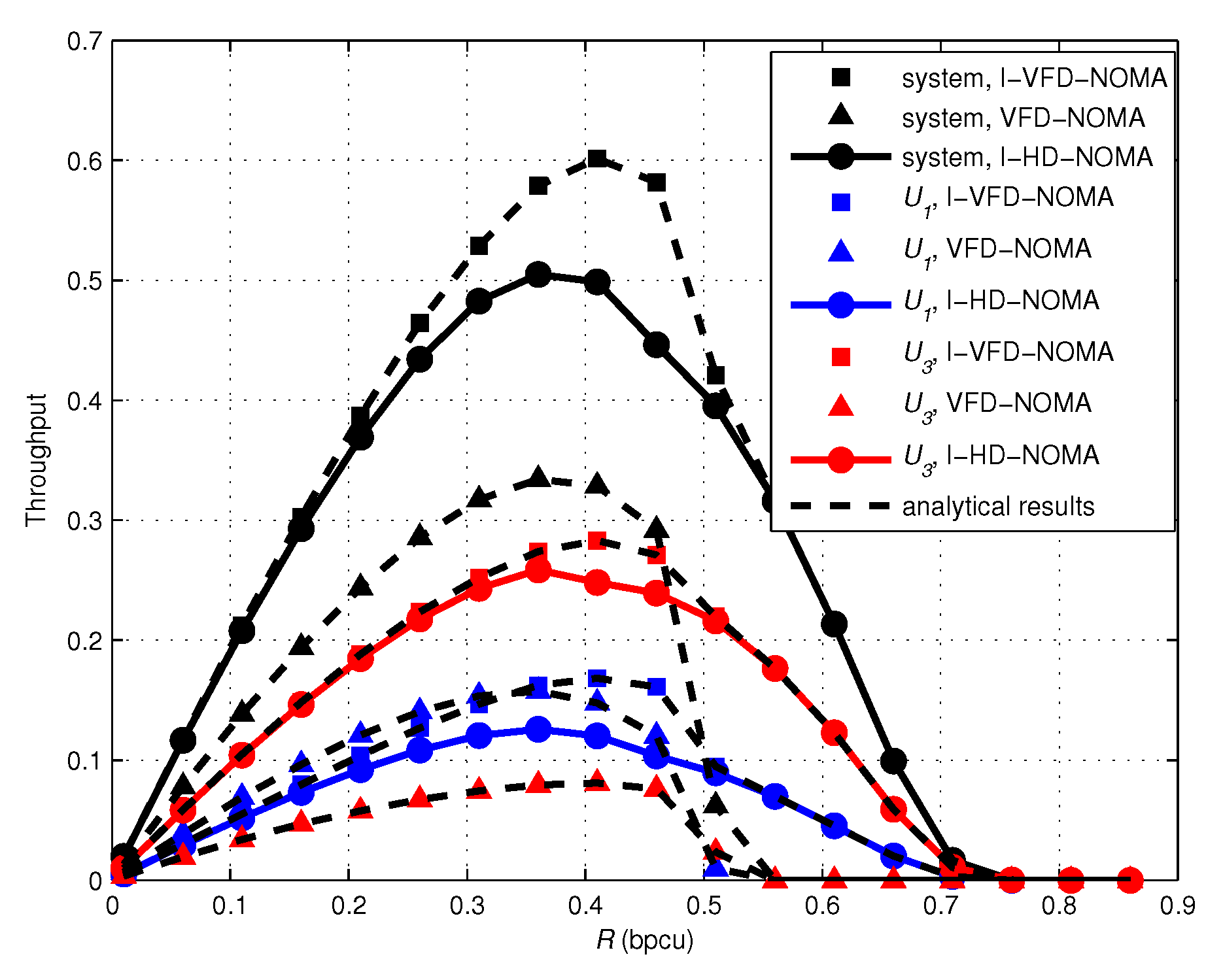
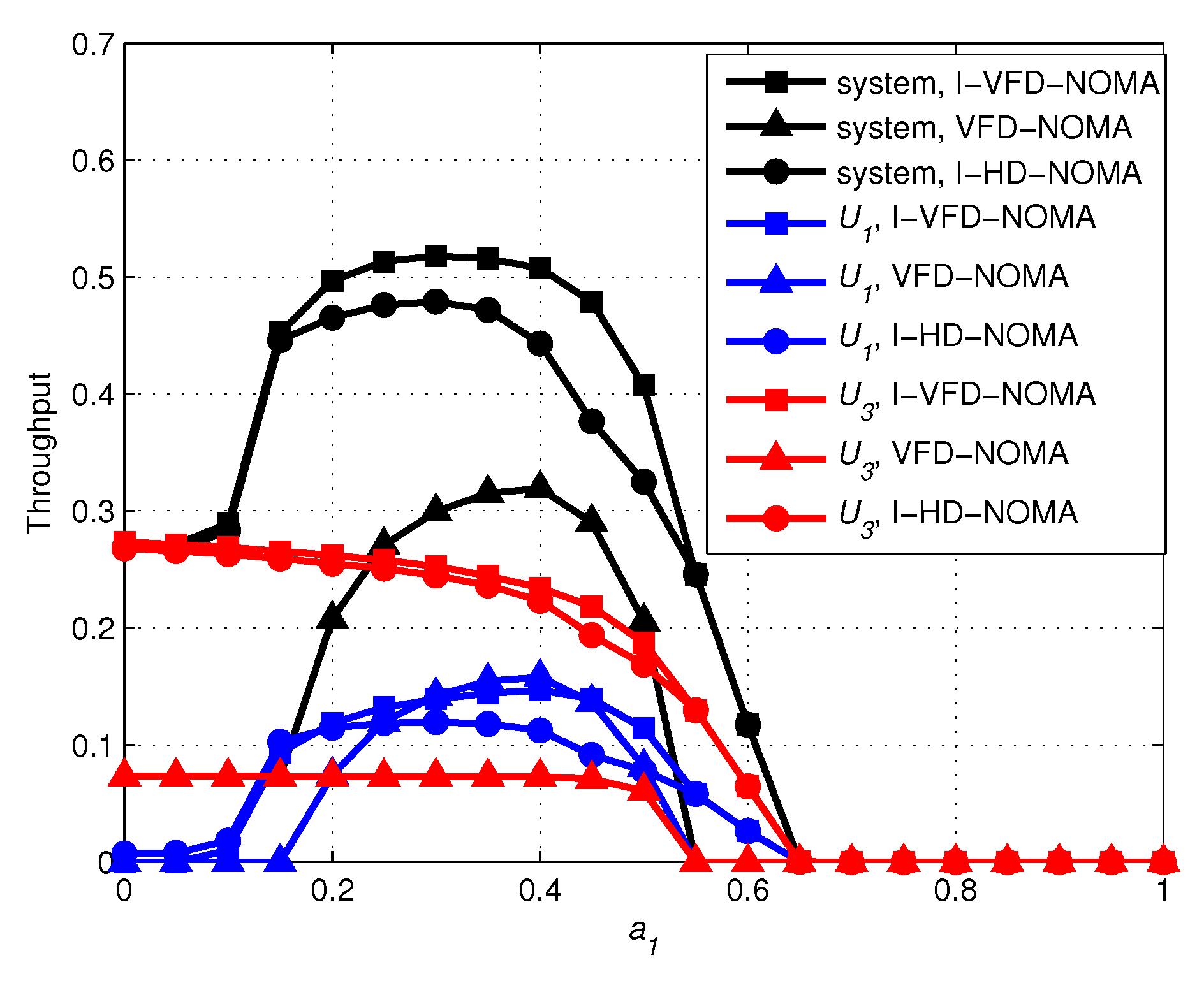
- Finally, The throughput performance of incremental HD-NOMA (I-HD-NOMA) and VFD-NOMA schemes is compared with our scheme. Numerical and simulation results show that the proposed I-VFD-NOMA scheme has better performance than existing I-HD-NOMA and VFD-NOMA schemes.
- The main novelty of this paper can be summarized as follows. (1) To the best of our knowledge, the proposed I-VFD-NOMA is the first time that the incremental relaying protocol is introduced into cooperative VFD-NOMA networks and the spectral efficiency can be further improved by this integration. (2) For the effective design of the proposed I-VFD-NOMA system, we provide an valuable insight into the I-SIC factor and optimal power splitting factor through detailed theoretical analysis and numerical results.
2. System Model
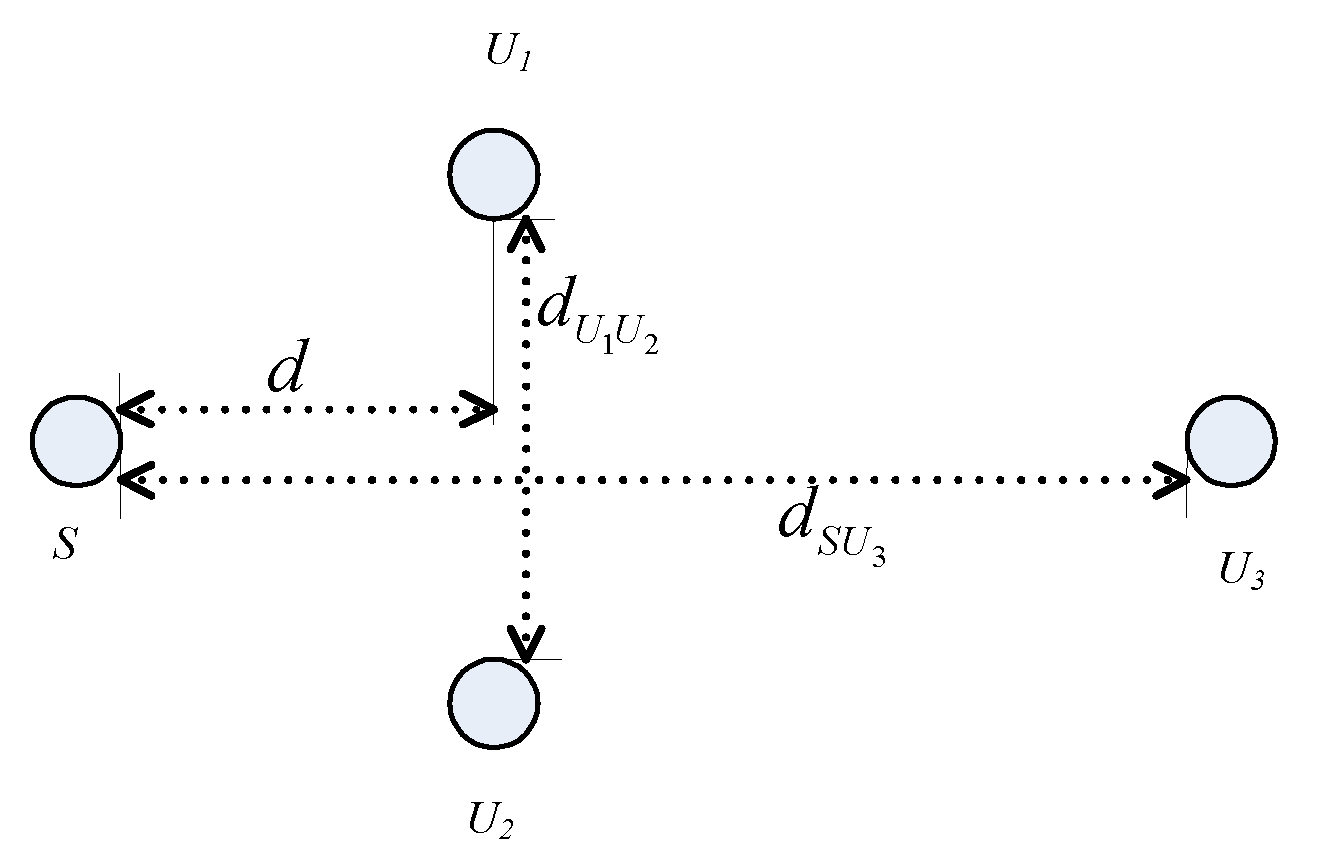
2.1. System Model for I-VFD-NOMA System
2.2. System Model for the VFD-NOMA System without Direct Link
3. Throughput Analysis
3.1. Throughput of I-VFD-NOMA System
3.2. Through of VFD-NOMA System without Direct Link
3.3. Optimal Power Splitting Factor of VFD-NOMA Mode without Direct Link
4. Numerical Results and Discussions
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| I-VFD-NOMA | Incremental virtual full-duplex non-orthogonal multiple access |
| EH | Energy harvesting |
| DF | Decode-and-forward |
| I-SIC | Imperfect successive interference cancellation |
| SC | Selection combining |
| OMA | Orthogonal multiple access |
| 5G | Fifth generation |
| HD | Half-duplex |
| SI | Self-interference |
| SINR | Signal-to-interference plus noise ratio |
| D-NOMA | Direct NOMA |
| I-HD-NOMA | Incremental HD-NOMA |
| MRC | Maximal ratio combining |
| bpcu | bits per channel use |
References
- Ding, Z.; Yang, Z.; Fan, P.; Poor, H.V. On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users. IIEEE Signal Process. Lett. 2014, 21, 1501–1505. [Google Scholar] [CrossRef] [Green Version]
- Kara, F.; Kaya, H. On the error performance of cooperative-NOMA with statistical CSIT. IEEE Commun. Lett. 2015, 23, 128–131. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Z.; Hu, J.; Ding, Z.; Fan, P. Cooperative NOMA broadcasting/multicasting for low-latency and high-reliability 5G cellular V2X communications. IEEE Internet Things J. 2019, 6, 7828–7838. [Google Scholar] [CrossRef]
- Kader, M.F.; Shin, S.Y.; Leung, V.C.M. Full-duplex non-orthogonal multiple access in cooperative relay sharing for 5G systems. IEEE Trans. Veh. Technol. 2018, 67, 5831–5840. [Google Scholar] [CrossRef]
- Wang, X.; Jia, M.; Ho, I.W.; Guo, Q.; Lau, F.C.M. Exploiting full-duplex two-way relay cooperative non-orthogonal multiple access. IEEE Trans. Commun. 2019, 67, 2716–2729. [Google Scholar] [CrossRef]
- Ren, C.; Zhang, H.; Wen, J.; Chen, J.; Tellambura, C. Successive two-way relaying for full-duplex users with generalized self-interference mitigation. IEEE Trans. Wireless Commun. 2019, 18, 63–76. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, Z.; Xiao, M.; Karagiannidis, G.K.; Ding, Z.; Fan, P. Two-timeslot two-way full-duplex relaying for 5G wireless communication networks. IEEE Trans. Commun. 2016, 64, 2873–2887. [Google Scholar] [CrossRef] [Green Version]
- Jose, J.; Shaik, P.; Bhatia, V. VFD-NOMA under imperfect SIC and residual inter-relay interference over generalized nakagami-m fading channels. IEEE Commun. Lett. 2021, 25, 646–650. [Google Scholar] [CrossRef]
- Liau, Q.Y.; Leow, C.Y.; Ding, Z. Amplify-and-forward virtual full-duplex relaying-based cooperative NOMA. IEEE Wireless Commun. Lett. 2018, 7, 464–467. [Google Scholar] [CrossRef]
- Laneman, J.N.; Tse, D.N.C.; Wornell, G.W. Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inf. Theory 2004, 50, 3062–3080. [Google Scholar] [CrossRef]
- Reshma, K.; Babu, A.V. Throughput analysis of energy harvesting enabled incremental relaying NOMA system. IEEE Commun. Lett. 2020, 24, 1419–1423. [Google Scholar] [CrossRef]
- Shukla, A.K.; Singh, V.; Upadhyay, P.K.; Kumar, A.; Moualeu, J.M. Performance analysis of energy harvesting-assisted overlay cognitive NOMA systems with incremental relaying. IEEE Open J. Commun. Soc. 2021, 2, 1558–1576. [Google Scholar] [CrossRef]
- Guo, C.; Guo, C.; Zhang, S.; Ding, Z. UAV-Enabled NOMA networks analysis with selective incremental relaying and imperfect CSI. IEEE Trans. Veh. Technol. 2020, 69, 16276–16281. [Google Scholar] [CrossRef]
- Yue, X.; Liu, Y.; Yao, Y.; Li, X.; Liu, R.; Nallanathan, A. Secure communications in a unified non-orthogonal multiple access framework. IEEE Trans. Wireless Commun. 2020, 19, 2163–2178. [Google Scholar] [CrossRef] [Green Version]
- Im, G.; Lee, J.H. Outage probability for cooperative NOMA systems with imperfect SIC in cognitive radio networks. IEEE Trans. Commun. Lett. 2019, 23, 692–695. [Google Scholar] [CrossRef]
- Bisen, S.; Shaik, P.; Bhatia, V. On performance of energy harvested cooperative NOMA under imperfect CSI and imperfect SIC. IEEE Trans. Veh. Technol. 2021, 70, 8993–9005. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Gao, Y.; Hanzo, L. Enhancing the physical layer security of non-orthogonal multiple access in large-scale networks. IEEE Trans. Wireless Commun. 2017, 16, 1656–1672. [Google Scholar] [CrossRef]
- Gradshteyn, I.; Ryzhik, I. Table of Integrals, Series and Products, 1st ed.; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]
- Kim, J.B.; Lee, I.H. Non-orthogonal multiple access in coordinated direct and relay transmission. IEEE Commun. Lett. 2015, 19, 2037–2040. [Google Scholar] [CrossRef]

| Parameters | Optimal Derived from 3.3 | |
|---|---|---|
| = 15 dB, R = 0.3 bpcu | 0.2448 | 0.2358 |
| = 25 dB, R = 0.3 bpcu | 0.3606 | 0.3722 |
| = 25 dB, R = 0.4 bpcu | 0.4284 | 0.4335 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W. Exploiting Incremental Virtual Full Duplex Non-Orthogonal Multiple Access Systems. Information 2022, 13, 216. https://doi.org/10.3390/info13050216
Guo W. Exploiting Incremental Virtual Full Duplex Non-Orthogonal Multiple Access Systems. Information. 2022; 13(5):216. https://doi.org/10.3390/info13050216
Chicago/Turabian StyleGuo, Weidong. 2022. "Exploiting Incremental Virtual Full Duplex Non-Orthogonal Multiple Access Systems" Information 13, no. 5: 216. https://doi.org/10.3390/info13050216
APA StyleGuo, W. (2022). Exploiting Incremental Virtual Full Duplex Non-Orthogonal Multiple Access Systems. Information, 13(5), 216. https://doi.org/10.3390/info13050216






