Prediction of Rainfall in Australia Using Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Data Preparation
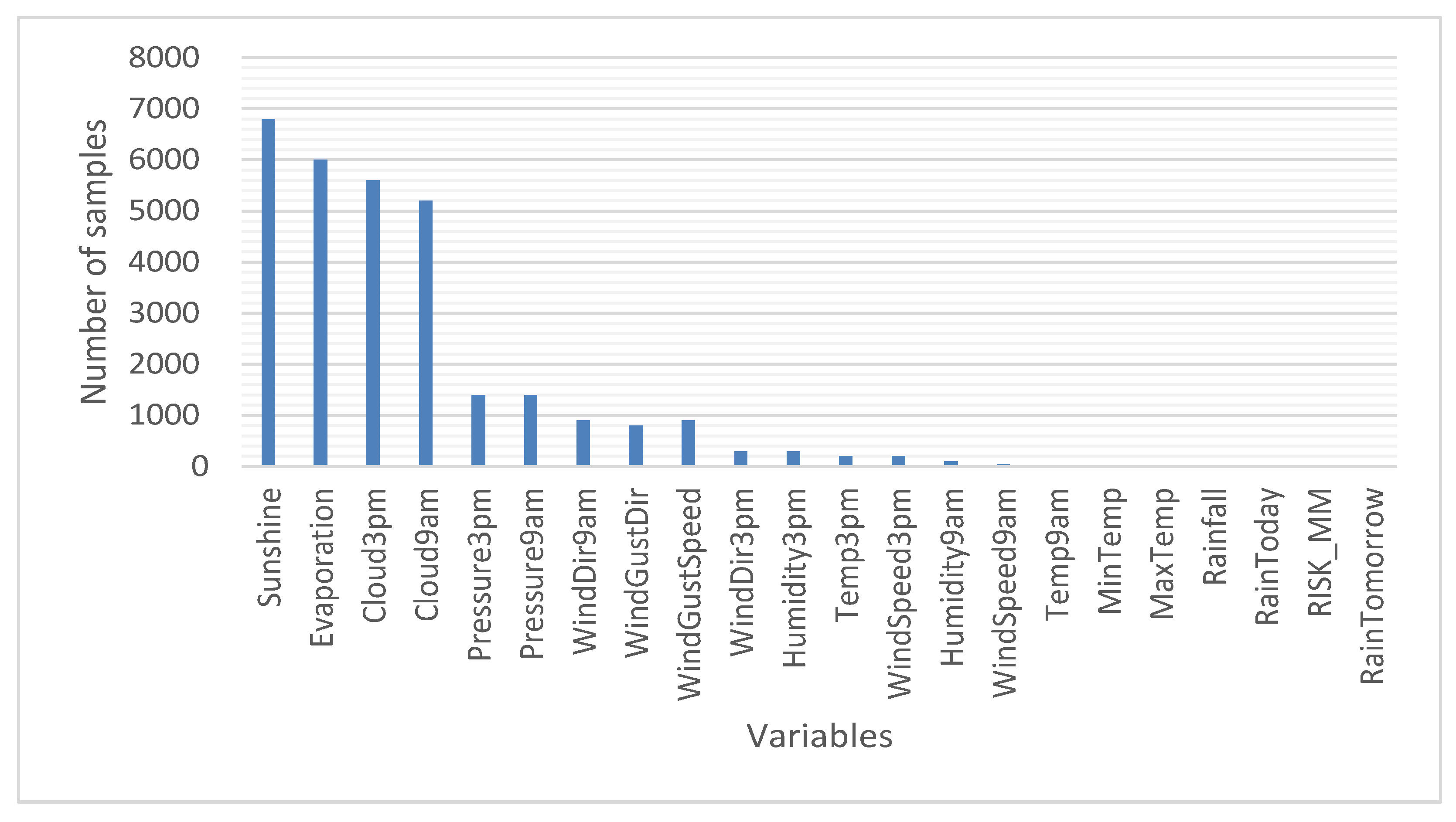
- Missing data. Figure 1 represents the number of samples of each of the variables for which there are no data. Thus, the total missing data correspond to 10% of the analyzed data (considering the total of 140,787 samples × 22 variables). Thus, if the samples that do not have data in any of their variables are eliminated, then approximately 50% of the samples would have to be eliminated. That is why the variables for which there are no data were analyzed, separating them by cities in order not to discard a large amount of data (the total number of cities for which data was available is 49). The results of the analysis of variables for which there are no data are as follows:
- There are variables that do not have a single piece of data in some of the cities. It is considered that this is because the corresponding sensor does not exist in the meteorological station of that city. For this case, the absent values werewere replaced by the monthly average [35] of said variable considering all the cities.
- There are samples for which there is no data for some of the variables. The reason could be a failure of the sensors or communication with them. Likewise, in this case, it was found that there are two different situations: data loss for one day only and data loss for several consecutive days. For this situation, it wasdecided to substitute the missing values for the monthly average [35] of said variable in the corresponding city.
- Finally, in the case of the objective variable, RainToday, the decision was made to eliminate the samples in which the variable does not exist (an “NA” appears). In this sense, 1% of the data samples were deleted, leaving a total of 140,787 samples that contain a value other than “NA” in RainToday.
- Conversion of categorical variables to numeric. It was necessary to carry out this operation on two sets of variables. On the one hand, for the wind direction and for the Boolean, this indicates whether there is rain or not. In the first case, the variables that indicate the wind direction (WindGustDir, WindDir9am, and WindDir3pm) are of type “string” and must be transformed to be used. These variables can take 16 different directions, so that, in order to convert these values to real numbers, it must be taken into account that it presents a circular distribution. That is why each of the variables was split into two, one with the sine and the other with the cosine of the angle: WindGustDir_Sin, WindGustDir_Cos, WindDir9am_Sin, WindDir9am_Cos, WindDir3pm_Sin, and WindDir3pm_Cos. With respect to the second case, the variables of type “string” that represent Booleans (they take YES/NO) are transformed into the numerical values “1/0”.
- Elimination of variables. The date and location variables were eliminated, since they contain information that can be explained using other variables (the data corresponding to each location has not been separated to construct independent subsets, since the data in the region as a whole was to be studied). For example, there are cities that, depending on their locations, have humidity and temperature conditions that more or less favor rain. Likewise, on the date the data is obtained, different meteorological conditions may occur that influence the rain.
- Data normalization. A normalization of the data of the mix–max type [35] was carried out so that all the variables would take values between 0 and 1. In this way, variables taking values of great magnitudes having a greater influence on the application of machine learning algorithms was avoided.
- Detection of outliers. For this, the “Z-score” formula [36] was used, and all those samples that have Z > 3 were discarded. As a result, 7% of the data was removed from 140,787 samples to make 131,086.
2.1.2. Correlation Analysis
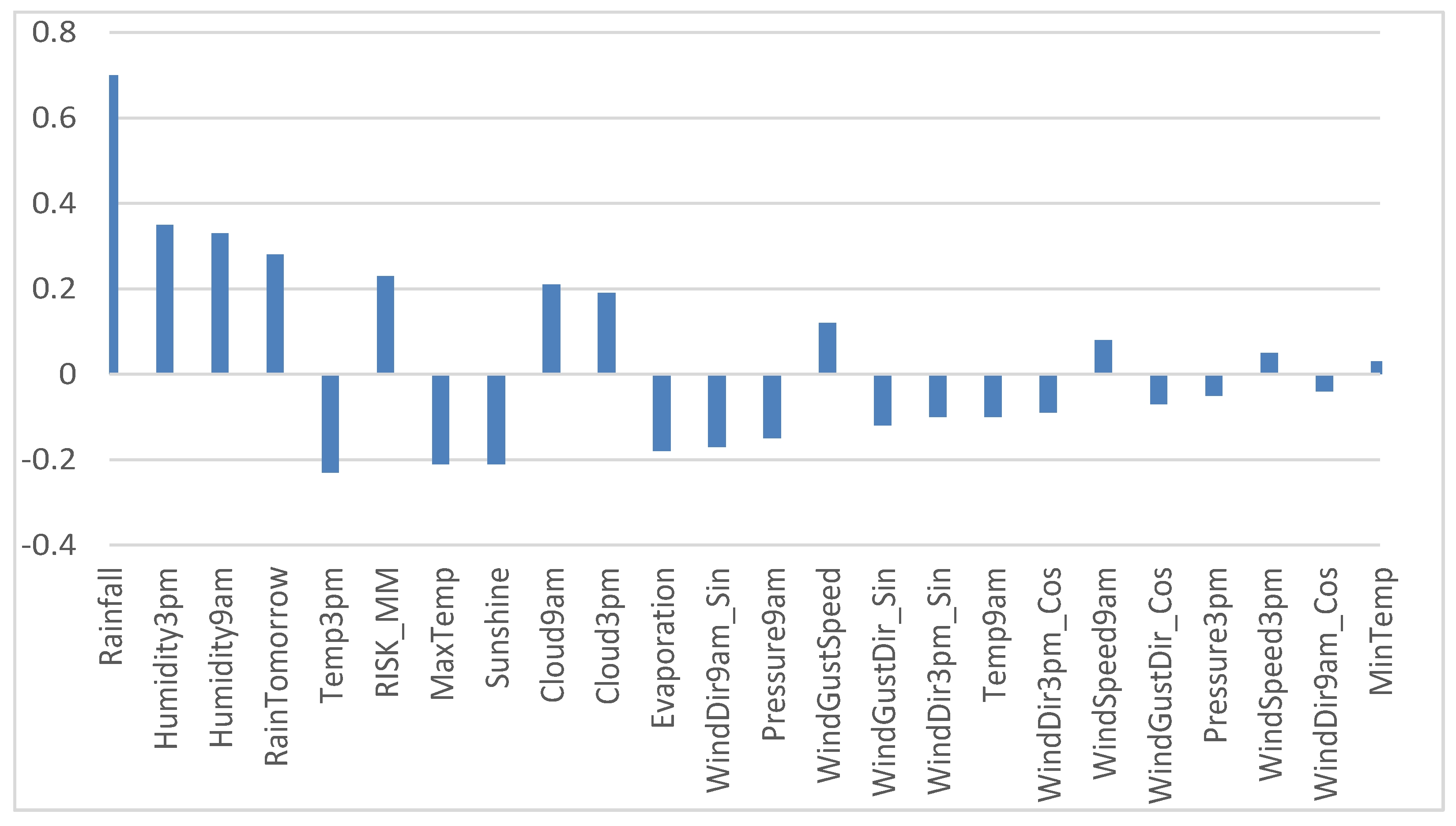
- Rainfall: It is a variable that indicates the rain that has fallen (in mm), so it is a direct measure that indicates whether it has rained or not. For this reason, it was decided to eliminate rainfall from the set of variables to be used.
- RISK_MM: It is a variable that indicates the risk of rain. This variable was eliminated as it is not a measure of something physical since its value has probably been obtained by applying some non-detailed prediction model in the dataset.
- Humidity (Humidity3pm and Humidity9am). It is reasonable that they are related, since the higher the humidity, the greater the possibility of rain.
- Cloudiness (Cloud9am and Cloud3pm). It is reasonable that they are related because the greater the number of clouds, the more likely it is that it will rain more.
- In other variables, it is observed that there was an inverse relationship. So, by increasing the values of these variables, the possibility of rain is reduced. This happens with the variables Temp3pm and MaxTemp (an increase in temperature does not favor condensation) and Sunshine (an increase in radiation from the Sun would be directly related to a less cloudy day, and, therefore, there would be less rain).
2.1.3. Results of Data Preprocessing
- Initially there were 24 variables (‘Date’, ‘Location’, ‘MinTemp’, ‘MaxTemp’, ‘Rainfall’, ‘Evaporation’, ‘Sunshine’, ‘WindGustDir’, ‘WindGustSpeed’, ‘WindDir9am’, ‘WindDir3pm’, ‘WindSpeed9am’, ‘WindSpeed3pm’, ‘Humidity9am’, ‘Humidity3pm ’, ‘Pressure9am’, ‘Pressure3pm’, ‘Cloud9am’, ‘Cloud3pm’, ‘Temp9am’, ‘Temp3pm’, ‘RainToday’, ‘RISK_MM’, ‘RainTomorrow’) with a total of 142,193 samples corresponding to measurements of rainfall and atmospheric conditions produced in 49 cities in Australia over 10 years.
- The following variables were eliminated: Location/Date (eliminated because they are string variables), Rainfall (eliminated because they are highly related to the RainToday variable), RISK_MM (artificial variable obtained to predict the rain), RainTomorrow (removed because it is a variable artificial obtained from RISK_MM), and the variables WindGustDir, WindDir9am and WindDir3pm (each is split into two variables containing the cosines and sines of the wind direction angles).
- The samples that had “NA” in the RainToday variable were eliminated (it reduced the number from 142,193 samples to 140,787), and the samples that represent outliers were also eliminated (it reduced the number from 140,787 samples to 131,086)
- As a result, 21 variables were obtained (‘MinTemp’, ‘MaxTemp’, ‘Evaporation’, ‘Sunshine’, ‘WindGustSpeed’, ‘WindSpeed9am’, ‘WindSpeed3pm’, ‘Humidity9am’, ‘Humidity3pm’, ‘Pressure9am’, ‘Pressure3pm’, ‘Cloud9am’, ‘Cloud3pm’, ‘Temp9am’, ‘RainToday’, ‘Temp3pm’, ‘WindGustDir_Cos’, ‘WindGustDir_Sin’, ‘WindDir9am_Cos’, ‘WindDir9am_Sin’, ‘WindDir3pm_Cos’, ‘WindDir3pm_Sin’) with a total of 131,086 samples.
2.2. Methods
2.2.1. K-NN Algorithm (K-Nearest Neighbors)
2.2.2. Decision Trees
2.2.3. Random Forest
2.2.4. Neural Networks
2.3. Key Performance Indicators
- Accuracy
- TP: True Positive. Result in which the model correctly predicts the positive class.
- FP: False Positive. Result in which the model incorrectly predicts the positive class.
- TN: True Negative. Result in which the model correctly predicts the negative class.
- FN: False Negative. Result in which the model incorrectly predicts the negative class.
- 2.
- Kappa statistic
- 3.
- Logarithmic Loss
- N is the number of samples.
- M is the number of classes.
- yij, indicates if the sample i belongs to the class j or not.
- pij, indicates the probability that the sample i belongs to the class j.
- 4.
- Error
- N corresponds to the total number of samples.
- corresponds to the class indicated by the classification model.
- corresponds to the actual class.
- 5.
- Sensitivity
- TP: True Positive. Result in which the model correctly predicts the positive class.
- TN: True Negative. Result in which the model correctly predicts the negative class.
- FN: False Negative. Result in which the model incorrectly predicts the negative class.
- 6.
- Specificity
- TP: True Positive. Result in which the model correctly predicts the positive class.
- FP: False Positive. Result in which the model incorrectly predicts the positive class.
- TN: True Negative. Result in which the model correctly predicts the negative class.
- 7.
- Precision
- TP: True Positive. Result in which the model correctly predicts the positive class.
- TN: True Negative. Result in which the model correctly predicts the negative class.
- FN: False Negative. Result in which the model incorrectly predicts the negative class.
- 8.
- Recall
- TP: True Positive. Result in which the model correctly predicts the positive class.
- FP: False Positive. Result in which the model incorrectly predicts the positive class.
- TN: True Negative. Result in which the model correctly predicts the negative class.
- 9.
- F-measure
3. Results
3.1. KNN
- -
- n_neighbours. Number of neighbors to be used by the algorithm.
- -
- Weights.
- uniform’: all the points considered have an identical weight.
- distance’: a weight equal to the inverse of its distance from the point to be studied is assigned. That is, the closest neighbors will have a greater influence when deciding which class to assign the point to study.
- The impact of changing the value of the chosen K closest neighbors is checked. Using a “bias–variance trade-off” it was found that the optimal results are obtained for values between 20 and 30. Observe that the calculation time increases as the number of neighbors used to make the decision of the class to which the analyzed points belong increases.
- The impact of how the weights are assigned to the K closest neighbors is checked to decide the class that corresponds to it. With the default value, it was found that more values are classified as positive. However, the overall performance does not show that of the total points 0.7% is correctly classified as positive but 0.5% were incorrectly classified as negative. The calculation times are very similar to those obtained when using the “uniform” weight assignment instead of considering the inverse of the distance.
- -
- N_neighbors: 25.
- -
- Weights assignation: distance.
3.2. Decision Tree
- -
- criterion: string.
- “entropy” for the information gain method.
- “gini” for the Gini impurity method.
- -
- splitter: string.
- “best” to choose the best partition.
- “random” to choose the best random partition.
- -
- max_depth: integral number indicating the greatest depth of the decision tree.
- -
- max_features: number of features to consider when looking for the best division.
- -
- random_state: corresponds to the seed used by the random number generator.
- -
- class_weight: weights associated with the classes; if no input is given, it is assumed that all classes have the same weight. The “balanced” option uses the value of each class to adjust the weights automatically, inversely proportional to the frequencies of each class in the data given as input.
- The impact of changing the number of max_depth was checked using the “entropy” criterion so that the optimal value was between 8 and 12. In this sense, 11 was chosen, making the best balance between the KPIs of accuracy, kappa, F1_score and error. Likewise, the impact of using the Gini information-gain criterion to perform the decision tree was verified, and the optimal numbers of tree levels match with those found when ordering according to the “entropy” criterion. Table 3 shows a comparison of the values obtained for the metrics considered according to the two criteria with a max_depth value of 11.
- The impact of changing the number of max_features (number of characteristics to consider when looking for the best division) in the results obtained was checked, setting the value of max_depth to 11 and using the entropy node division criterion. The best results were obtained if no restrictions were added to the characteristics.
- The impact of using the class_weight = “balanced” option was checked. To do this, the value of max_depth was set to 11, the entropy node division criterion was used, and a limit was not added for the max_features parameter. The weights were decided inversely proportionally to the number of these classes in the training data. As there was much less data assigned to class 1 (it does rain), this class was given much more importance, and, as a result, many values were assigned to the positive class (11,840 compared to 5090), increasing the number of TP from 3074 to 5121. At the same time, there was a significant increase in FP, from 2016 to 6719. Since the metrics obtained do not allow deciding the best value for the parameter, it was considered how many fewer false positives would be better to estimate if it rains or not, so the betterw option is “class_weight = balanced” than the default option. Table 4 shows the results of the evaluated metrics.
- The impact of using the splitter parameter was checked, so that the results were improved when it took the value of “best” instead of “random”, using the “entropy” classification criteria. The results are shown in Table 5.
- The “Random state” parameter had no impact on the performance of the results obtained.
- -
- Max_depth: 11.
- -
- Max_features: 21 (the total of the features).
- -
- Class_weight: “Balanced”.
- -
- Criterion: “entropy”.
- -
- Splitter: “best”.
3.2.1. Random Forest
- -
- n_estimators: number of decision trees to consider.
- -
- criterion: string.
- “entropy” for the information gain method.
- “gini” for the Gini impurity method.
- -
- max_depth: integral number indicating the greatest depth of the decision tree.
- -
- class_weights: weights associated with the classes, if no input is given it is assumed that all classes have the same weight. The “balanced” option uses the values to adjust the weights automatically, inversely proportionally to the frequencies of each class in the data given as input.
- The impact of the max_depth parameter that indicates the depth of the tree was checked, so that it could be seen that for the “entropy” criterion the optimal parameter was 12, and for the “gini” criterion it was 13. Table 7 shows the results for these parameter values.
- The impact of the number of estimators was checked using the “Gini” and “Entropy” criteria, so that the maximum precision was obtained when the number of estimators was 30, having reached very similar values of precision when the number of estimators was 10.
- The impact of using the class_weight = ”balanced” parameter to correct the weights according to the frequency of appearance of the different classes was verified. The results were compared with a case where the weights were not corrected. For this, 30 estimators were used, criterion = “entropy”, max_depth = 12 and max_features = 21. In conclusion, it was found that the results obtained improved (the impact of modifying the weights was inversely proportional to the number of elements in the class was greater than when the standard decision tree check was performed). The result is shown in Table 8.
- In RandomForest each tree in the set was created from a sample with replacement of the training dataset. Furthermore, when each node was separated construct a decision tree, the best split was found from all features or from a random set of size “max_features”.
- -
- N_estimators: 30.
- -
- Max_depth: 14.
- -
- Max_features: 21 (the total of the features).
- -
- Criterion: “gini”.
- -
- class_weight = ”balanced”.
3.2.2. Neural Networks
- -
- Hidden_layer_sizes: tuple, length = n_layers-2, default (100). The element i represents the number of neurons in the hidden layer i.
- -
- Activation: Activation function for hidden layers. Can be:
- ‘identity’: no-op activation, useful to implement linear bottleneck, f (x) = x.
- ‘logistic’: sigmoid activation function.
- ‘tanh’, hyperbolic tangent function.
- ‘relu’, rectified linear function.
- -
- solver: Solver used for the optimization of the weights.
- ‘lbfgs’ optimizer family of quasi-Newtonian methods.
- ‘sgd’ stochastic gradient descent optimizer.
- ‘adam’ referring to a gradient-based stochastic optimizer.
- -
- alpha: regularization parameter L2 penalty. It helps to avoid overfitting by penalizing the weights with high magnitudes.
- The impact of changing the activation function was verified so that the best results were obtained for the “relu” function, as shown in Table 10.
- The impact of the solver parameter (optimization of the weights) used to solve the algorithm weights was checked so that the best results were obtained for the “adam” function as shown in Table 11.
- The impact of changing the alpha parameter was verified (it helps to avoid overfitting by penalizing weights with high magnitudes) so that the optimum was obtained at 0.05.
- -
- Activation = ‘relu’.
- -
- Solver = ‘adam’.
- -
- Alpha = 0.05.
4. Discussion
- (a)
- City of Sydney
- -
- Max_depth = 9.
- -
- Criterion = “gini”.
- -
- Class_weight = ‘balanced’.
- -
- N_estimators = 20.
- -
- Activation = ‘relu’.
- -
- Solver = ‘lbfgs’.
- -
- Alpha = 0.0025.
- (b)
- City of Perth
- -
- Max_depth = 8.
- -
- Criterion = ‘gini’.
- -
- Class_weight = ‘balanced’.
- -
- N_estimators = 18.
- -
- Activation = ‘relu’.
- -
- Solver = ‘adam’.
- -
- Alpha = 0.025.
- (c)
- City of Darwin
- -
- Max_depth = 9.
- -
- Criterion = “gini”.
- -
- Class_weight = ‘balanced’.
- -
- N_estimators = 36.
- -
- Activation = ‘identity’.
- -
- Solver = ‘lbfgs’.
- -
- Alpha = 0.1.
5. Conclusions and Future Work
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Datta, A.; Si, S.; Biswas, S. Complete Statistical Analysis to Weather Forecasting. In Computational Intelligence in Pattern Recognition; Springer: Singapore, 2020; pp. 751–763. [Google Scholar]
- Burlando, P.; Montanari, A.; Ranzi, R. Forecasting of storm rainfall by combined use of radar, rain gages and linear models. Atmos. Res. 1996, 42, 199–216. [Google Scholar] [CrossRef]
- Valipour, M. How much meteorological information is necessary to achieve reliable accuracy for rainfall estimations? Agriculture 2016, 6, 53. [Google Scholar] [CrossRef]
- Murphy, A.H.; Winkler, R.L. Probability forecasting in meteorology. J. Am. Stat. Assoc. 1984, 79, 489–500. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Stephenson, D.B. (Eds.) Forecast Verification: A Practitioner’s Guide in Atmospheric Science; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wu, J.; Huang, L.; Pan, X. A novel bayesian additive regression trees ensemble model based on linear regression and nonlinear regression for torrential rain forecasting. In Proceedings of the 2010 Third International Joint Conference on Computational Science and Optimization, Huangshan, China, 28–31 May 2010; Volume 2, pp. 466–470. [Google Scholar]
- Tanessong, R.S.; Vondou, D.A.; Igri, P.M.; Kamga, F.M. Bayesian processor of output for probabilistic quantitative precipitation forecast over central and West Africa. Atmos. Clim. Sci. 2017, 7, 263. [Google Scholar] [CrossRef]
- Georgakakos, K.P.; Hudlow, M.D. Quantitative precipitation forecast techniques for use in hydrologic forecasting. Bull. Am. Meteorol. Soc. 1984, 65, 1186–1200. [Google Scholar] [CrossRef]
- Migon, H.S.; Monteiro, A.B.S. Rain-fall modeling: An application of Bayesian forecasting. Stoch. Hydrol. Hydraul. 1997, 11, 115–127. [Google Scholar] [CrossRef]
- Wu, J. An effective hybrid semi-parametric regression strategy for rainfall forecasting combining linear and nonlinear regression. In Modeling Applications and Theoretical Innovations in Interdisciplinary Evolutionary Computation; IGI Global: New York, NY, USA, 2013; pp. 273–289. [Google Scholar]
- Wu, J. A novel nonlinear ensemble rainfall forecasting model incorporating linear and nonlinear regression. In Proceedings of the 2008 Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008; Volume 3, pp. 34–38. [Google Scholar]
- Zhang, C.J.; Zeng, J.; Wang, H.Y.; Ma, L.M.; Chu, H. Correction model for rainfall forecasts using the LSTM with multiple meteorological factors. Meteorol. Appl. 2020, 27, e1852. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.A.; Schellart, A.N.A.; Saul, A.J. Using probabilistic radar rainfall nowcasts and NWP forecasts for flow prediction in urban catchments. Atmos. Res. 2012, 103, 80–95. [Google Scholar] [CrossRef]
- Koussis, A.D.; Lagouvardos, K.; Mazi, K.; Kotroni, V.; Sitzmann, D.; Lang, J.; Malguzzi, P. Flood forecasts for urban basin with integrated hydro-meteorological model. J. Hydrol. Eng. 2003, 8, 1–11. [Google Scholar] [CrossRef]
- Yasar, A.; Bilgili, M.; Simsek, E. Water demand forecasting based on stepwise multiple nonlinear regression analysis. Arab. J. Sci. Eng. 2012, 37, 2333–2341. [Google Scholar] [CrossRef]
- Holmstrom, M.; Liu, D.; Vo, C. Machine learning applied to weather forecasting. Meteorol. Appl. 2016, 10, 1–5. [Google Scholar]
- Singh, N.; Chaturvedi, S.; Akhter, S. Weather forecasting using machine learning algorithm. In Proceedings of the 2019 International Conference on Signal Processing and Communication (ICSC), Noida, India, 7–9 March 2019; pp. 171–174. [Google Scholar]
- Hasan, N.; Uddin, M.T.; Chowdhury, N.K. Automated weather event analysis with machine learning. In Proceedings of the 2016 International Conference on Innovations in Science, Engineering and Technology (ICISET), Dhaka, Bangladesh, 28–29 October 2016; pp. 1–5. [Google Scholar]
- Balamurugan, M.S.; Manojkumar, R. Study of short term rain forecasting using machine learning based approach. Wirel. Netw. 2021, 27, 5429–5434. [Google Scholar] [CrossRef]
- Booz, J.; Yu, W.; Xu, G.; Griffith, D.; Golmie, N. A deep learning-based weather forecast system for data volume and recency analysis. In Proceedings of the 2019 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 18–21 February 2019; pp. 697–701. [Google Scholar]
- Liu, J.N.; Lee, R.S. Rainfall forecasting from multiple point sources using neural networks. In Proceedings of the IEEE SMC’99 Conference Proceedings. 1999 IEEE International Conference on Systems, Man, and Cybernetics (Cat. No. 99CH37028), Tokyo, Japan, 12–15 October 1999; Volume 3, pp. 429–434. [Google Scholar]
- Darji, M.P.; Dabhi, V.K.; Prajapati, H.B. Rainfall forecasting using neural network: A survey. In Proceedings of the 2015 International Conference on Advances in Computer Engineering and Applications, IEEE, Ghaziabad, India, 19–20 March 2015; pp. 706–713. [Google Scholar]
- Mahabub, A.; Habib, A.Z.S.B.; Mondal, M.; Bharati, S.; Podder, P. Effectiveness of ensemble machine learning algorithms in weather forecasting of bangladesh. In Proceedings of the International Conference on Innovations in Bio-Inspired Computing and Applications, online, 16–18 December 2020; Springer: Cham, Switzerland, 2020; pp. 267–277. [Google Scholar]
- Rizvee, M.A.; Arju, A.R.; Al-Hasan, M.; Tareque, S.M.; Hasan, M.Z. Weather Forecasting for the North-Western region of Bangladesh: A Machine Learning Approach. In Proceedings of the 2020 11th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kharagpur, India, 1–3 July 2020; pp. 1–6. [Google Scholar]
- Bushara, N.O.; Abraham, A. Weather forecasting in Sudan using machine learning schemes. J. Netw. Innov. Comput. 2014, 2, 309–317. [Google Scholar]
- Ingsrisawang, L.; Ingsriswang, S.; Somchit, S.; Aungsuratana, P.; Khantiyanan, W. Machine learning techniques for short-term rain forecasting system in the northeastern part of Thailand. Proc. World Acad. Sci. Eng. Technol. 2008, 31, 248–253. [Google Scholar]
- Macabiog, R.E.N.; Cruz, J.C.D. Rainfall Predictive Approach for La Trinidad, Benguet using Machine Learning Classification. In Proceedings of the 2019 IEEE 11th International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment, and Management (HNICEM), Laoag, Philippines, 29 November–1 December 2019; pp. 1–6. [Google Scholar]
- Pham, Q.B.; Kumar, M.; Di Nunno, F.; Elbeltagi, A.; Granata, F.; Islam, A.R.M.; Anh, D.T. Groundwater level prediction using machine learning algorithms in a drought-prone area. Neural Comput. Appl. 2022, 17, 1–23. [Google Scholar] [CrossRef]
- Bagirov, A.M.; Mahmood, A.; Barton, A. Prediction of monthly rainfall in Victoria, Australia: Clusterwise linear regression approach. Atmos. Res. 2017, 188, 20–29. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Forecasting evapotranspiration in different climates using ensembles of recurrent neural networks. Agric. Water Manag. 2021, 255, 107040. [Google Scholar] [CrossRef]
- Sachindra, D.A.; Ahmed, K.; Rashid, M.M.; Shahid, S.; Perera, B.J.C. Statistical downscaling of precipitation using machine learning techniques. Atmos. Res. 2018, 212, 240–258. [Google Scholar] [CrossRef]
- Raval, M.; Sivashanmugam, P.; Pham, V.; Gohel, H.; Kaushik, A.; Wan, Y. Automated predictive analytics tool for rainfall forecasting. Sci. Rep. 2021, 11, 17704. [Google Scholar] [CrossRef]
- Feng, P.; Wang, B.; Li Liu, D.; Ji, F.; Niu, X.; Ruan, H.; Yu, Q. Machine learning-based integration of large-scale climate drivers can improve the forecast of seasonal rainfall probability in Australia. Environ. Res. Lett. 2020, 15, 084051. [Google Scholar] [CrossRef]
- Hartigan, J.; MacNamara, S.; Leslie, L.M.; Speer, M. Attribution and prediction of precipitation and temperature trends within the Sydney catchment using machine learning. Climate 2020, 8, 120. [Google Scholar] [CrossRef]
- Taylor, J.K.; Cihon, C. Statistical Techniques for Data Analysis; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Somasundaram, R.S.; Nedunchezhian, R. Evaluation of three simple imputation methods for enhancing preprocessing of data with missing values. Int. J. Comput. Appl. 2011, 21, 14–19. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, D.; Deng, Z.; Zong, M.; Deng, X. A novel kNN algorithm with data-driven k parameter computation. Pattern Recognit. Lett. 2018, 109, 44–54. [Google Scholar] [CrossRef]
- Deng, Z.; Zhu, X.; Cheng, D.; Zong, M.; Zhang, S. Efficient kNN classification algorithm for big data. Neurocomputing 2016, 195, 143–148. [Google Scholar] [CrossRef]
- Pandey, A.; Jain, A. Comparative analysis of KNN algorithm using various normalization techniques. Int. J. Comput. Netw. Inf. Secur. 2017, 9, 36. [Google Scholar] [CrossRef]
- Patel, H.H.; Prajapati, P. Study and analysis of decision tree based classification algorithms. Int. J. Comput. Sci. Eng. 2018, 6, 74–78. [Google Scholar] [CrossRef]
- Rao, H.; Shi, X.; Rodrigue, A.K.; Feng, J.; Xia, Y.; Elhoseny, M.; Yuan, X.; Gu, L. Feature selection based on artificial bee colony and gradient boosting decision tree. Appl. Soft Comput. 2019, 74, 634–642. [Google Scholar] [CrossRef]
- Fiarni, C.; Sipayung, E.M.; Tumundo, P.B. Academic decision support system for choosing information systems sub majors programs using decision tree algorithm. J. Inf. Syst. Eng. Bus. Intell. 2019, 5, 57–66. [Google Scholar] [CrossRef][Green Version]
- Schonlau, M.; Zou, R.Y. The random forest algorithm for statistical learning. Stata J. 2020, 20, 3–29. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Wu, Y.C.; Feng, J.W. Development and application of artificial neural network. Wirel. Pers. Commun. 2018, 102, 1645–1656. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed]
- Blalock, D.; Gonzalez Ortiz, J.J.; Frankle, J.; Guttag, J. What is the state of neural network pruning? Proc. Mach. Learn. Syst. 2020, 2, 129–146. [Google Scholar]
- Badawy, M.; Abd El-Aziz, A.A.; Idress, A.M.; Hefny, H.; Hossam, S. A survey on exploring key performance indicators. Future Comput. Inform. J. 2016, 1, 47–52. [Google Scholar] [CrossRef]
- KNeighborsClassifier Function. Available online: https://scikitlearn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighboursClassifier (accessed on 17 February 2022).
- DecisionTreeClassifier Function. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html (accessed on 17 February 2022).
- RandomForestClassifier Function. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html (accessed on 17 February 2022).
- MLPClassifier Function. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPClassifier.html (accessed on 17 February 2022).
| Feature Name | Description | Missing Values | Available Data | Type |
|---|---|---|---|---|
| Date | Day on which the measurement is carried out | 0 | 142,193 | string/date |
| Location | Station location name meteorological. | 0 | 142,193 | string |
| MinTemp | Minimum temperature in degrees Celsius. | 637 | 141,556 | float |
| MaxTemp | Maximum temperature in degrees Celsius. | 322 | 141,871 | float |
| Rainfall | Amount of rain recorded during the day in mm. | 1406 | 140,787 | float |
| Evaporation | “Class A pan evaporation” (mm) in 24 h until 9 a.m. | 60,843 | 81,350 | float |
| Sunshine | Number of hours of radiant sun during the day. | 67,816 | 74,377 | float |
| WindGustDir | Direction of the strongest wind gust in the 24 h to midnight. | 9330 | 132,863 | string |
| WindGustSpeed | Speed (km/h) of the strongest wind gust in the 24 h to midnight. | 9270 | 132,923 | float |
| WindDir9am | Wind direction at 9 a.m. | 10,013 | 132,180 | string |
| WindDir3pm | Wind direction at 3 p.m. | 3778 | 138,415 | string |
| WindSpeed9am | Average wind speed (km/h) in the 10 min before 9 a.m. | 1348 | 140,845 | float |
| WindSpeed3pm | Average wind speed (km/h) in the 10 min before 3 p.m. | 2630 | 139,563 | float |
| Humidity9am | Humidity (%) at 9 a.m. | 1774 | 140,419 | float |
| Humidity3pm | Humidity (%) at 3 p.m. | 3610 | 138,583 | float |
| Pressure9am | Atmospheric pressure (hpa) at the level of evil, at 9 a.m. | 14,014 | 128,179 | float |
| Pressure3pm | Atmospheric pressure (hpa) at the level of evil, at 3 p.m. | 13,981 | 128,212 | float |
| Cloud9am | Fraction of sky obscured by clouds at 9 a.m. The unit of measurement is “oktas”, which is equal to a unit of eighths. It refers to how many eighths of the sky are obscured by clouds. A value of 0 indicates a completely clear sky, while a value of 8 indicates that it is completely obscured. Temperature at 3 p.m., in degrees Celsius. | 53,657 | 88,536 | float |
| Cloud3pm | Fraction of sky obscured by clouds at 3 p.m. The unit of measurements is the same as in Cloud9am measurements. | 57,094 | 85,099 | float |
| Temp9am | Temperature at 9 a.m., in degrees Celsius. | 904 | 141,289 | float |
| Temp3pm | Temperature at 3 p.m., in degrees Celsius. | 2726 | 139,467 | float |
| RainToday | Boolean: 1 if precipitation exceeds 1 mm in the 24 h to 9 a.m., if not 0. | 1406 | 140,787 | string |
| RISK_MM | The amount of rain for the next day in mm. | 0 | 142,193 | float |
| RainTomorrow | Variable created from variable RISK_MM. A type of risk measure. | 0 | 142,193 | String |
| Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|
| 0.83 | 0.17 | 0.36 | 0.49 | 0.32 | 0.96 | 0.70 | 0.32 | 0.44 |
| Max_Depth | Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|---|
| Gini | 0.83 | 0.17 | 0.41 | 0.8 | 0.44 | 0.93 | 0.61 | 0.44 | 0.51 |
| Entropy | 0.83 | 0.17 | 0.42 | 1.02 | 0.45 | 0.92 | 0.61 | 0.45 | 0.52 |
| Class_Weight | Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|---|
| None | 0.83 | 0.17 | 0.41 | 1.03 | 0.45 | 0.92 | 0.6 | 0.45 | 0.52 |
| Balanced | 0.74 | 0.26 | 0.39 | 1.11 | 0.76 | 0.74 | 0.43 | 0.76 | 0.55 |
| Splitter | Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|---|
| Best | 0.83 | 0.17 | 0.42 | 1.02 | 0.46 | 0.92 | 0.61 | 0.46 | 0.52 |
| Random | 0.82 | 0.18 | 0.35 | 0.73 | 0.35 | 0.95 | 0.63 | 0.35 | 0.45 |
| Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|
| 0.83 | 0.17 | 0.42 | 1.02 | 0.46 | 0.92 | 0.61 | 0.46 | 0.52 |
| Max_Depth | Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|---|
| Entropy | 0.84 | 0.16 | 0.45 | 0.37 | 0.44 | 0.95 | 0.68 | 0.44 | 0.54 |
| Gini | 0.84 | 0.16 | 0.45 | 0.36 | 0.46 | 0.94 | 0.68 | 0.46 | 0.54 |
| Class_Weight | Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|---|
| None | 0.85 | 0.15 | 0.45 | 0.35 | 0.44 | 0.95 | 0.7 | 0.44 | 0.54 |
| Balanced | 0.81 | 0.19 | 0.49 | 0.41 | 0.71 | 0.84 | 0.53 | 0.71 | 0.61 |
| Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|
| 0.83 | 0.17 | 0.5 | 0.39 | 0.66 | 0.87 | 0.57 | 0.66 | 0.61 |
| Activation | Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|---|
| identity | 0.83 | 0.17 | 0.4 | 0.37 | 0.39 | 0.95 | 0.66 | 0.39 | 0.49 |
| logistic | 0.84 | 0.16 | 0.42 | 0.36 | 0.42 | 0.95 | 0.67 | 0.42 | 0.51 |
| tanh | 0.84 | 0.16 | 0.46 | 0.35 | 0.46 | 0.94 | 0.68 | 0.46 | 0.55 |
| relu | 0.85 | 0.15 | 0.47 | 0.35 | 0.47 | 0.95 | 0.69 | 0.47 | 0.56 |
| Solver | Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|---|
| Ibfgs | 0.85 | 0.15 | 0.47 | 0.35 | 0.47 | 0.95 | 0.69 | 0.47 | 0.56 |
| Sgd | 0.84 | 0.16 | 0.43 | 0.36 | 0.43 | 0.94 | 0.67 | 0.43 | 0.52 |
| adam | 0.85 | 0.15 | 0.49 | 0.34 | 0.51 | 0.93 | 0.66 | 0.51 | 0.58 |
| Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|
| 0.84 | 0.16 | 0.49 | 0.35 | 0.53 | 0.92 | 0.65 | 0.53 | 0.59 |
| Algorithm | Misclassification Rate | MSE | AUC |
|---|---|---|---|
| K-NN | 0.044 | 0.042 | 0.5 |
| Decision tree | 0.044 | 0.043 | 0.6 |
| Random forest | 0.044 | 0.041 | 0.65 |
| Neural network | 0.044 | 0.039 | 0.7 |
| Algorithm | Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|---|
| Random Forest | 0.84 | 0.16 | 0.51 | 0.42 | 0.59 | 0.91 | 0.64 | 0.59 | 0.62 |
| Neural network | 0.84 | 0.16 | 0.52 | 0.44 | 0.57 | 0.92 | 0.67 | 0.57 | 0.62 |
| Algorithm | Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|---|
| Random Forest | 0.9 | 0.1 | 0.7 | 0.3 | 0.83 | 0.92 | 0.7 | 0.83 | 0.76 |
| Neural network | 0.93 | 0.07 | 0.77 | 0.2 | 0.78 | 0.97 | 0.85 | 0.78 | 0.81 |
| Algorithm | Accuracy | Error_Rate | Kappa | LogLoss | Sensitivity | Specificity | Precision | Recall | F1_Score |
|---|---|---|---|---|---|---|---|---|---|
| Random Forest | 0.88 | 0.12 | 0.61 | 0.31 | 0.65 | 0.94 | 0.72 | 0.65 | 0.68 |
| Neural network | 0.88 | 0.12 | 0.6 | 0.31 | 0.62 | 0.94 | 0.74 | 0.62 | 0.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarasa-Cabezuelo, A. Prediction of Rainfall in Australia Using Machine Learning. Information 2022, 13, 163. https://doi.org/10.3390/info13040163
Sarasa-Cabezuelo A. Prediction of Rainfall in Australia Using Machine Learning. Information. 2022; 13(4):163. https://doi.org/10.3390/info13040163
Chicago/Turabian StyleSarasa-Cabezuelo, Antonio. 2022. "Prediction of Rainfall in Australia Using Machine Learning" Information 13, no. 4: 163. https://doi.org/10.3390/info13040163
APA StyleSarasa-Cabezuelo, A. (2022). Prediction of Rainfall in Australia Using Machine Learning. Information, 13(4), 163. https://doi.org/10.3390/info13040163






