Discrete Event Modeling and Simulation for Reinforcement Learning System Design
Abstract
1. Introduction
2. Preliminaries
2.1. Markovian Decision-Making Process Modeling
- S: corresponding to the state space.
- A: corresponding to the set of actions used to control the transitions.
- T: corresponding to the time space.
- r: corresponding to the reward function associated with state transitions.
| Algorithm 1 Q-Learning algorithm from [6]. |
|
2.2. The Discrete Event System Specification
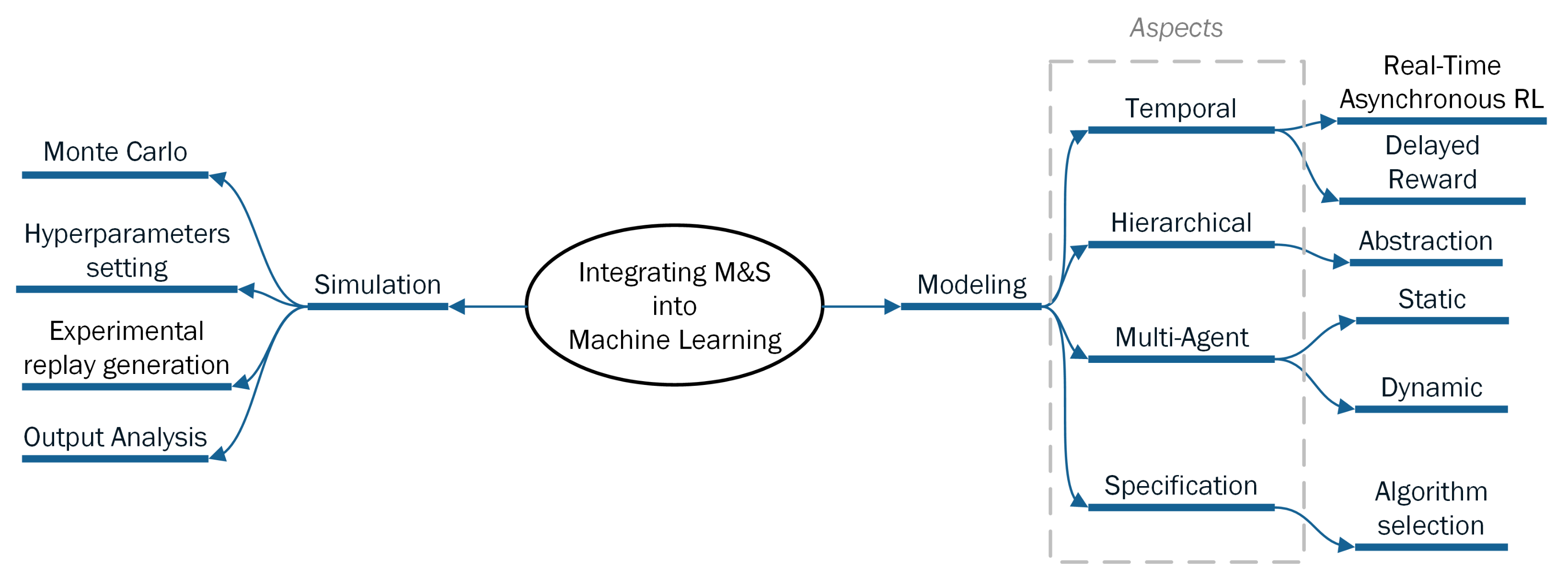
3. Modeling and Simulation and Reinforcement Learning
- the temporal feature can be found in the RL processes. For example, MDPs provide both discrete and continuous time to represent the state life time [6]. In RL processes, the time notion in the rewards consideration is used to provide a way to model the system delayed response [19]. The concept of time involved in RL systems also offers to perform asynchronous simulations.
- the abstraction hierarchy makes possible the modeling of RL elements at several levels of abstraction. This allows to define optimal solutions associated with levels of details [20].
- multi-agent definition may be introduced in RL when the best possible policy is determined according to the links between dynamic environments involving a set of agents [21].
- grouping the ML elements required to bring solutions may also be difficult [6]. A set of ML techniques can be find to have to be considered and the selection of a particular algorithm may be hard. This selection can be facilitated by introducing models libraries.
4. Discrete Event System Specification Formalism for Reinforcement Learning
- The Data Analysis phase allows to select which kind of learning methods (supervised or unsupervised or reinforcement learning) is the most appropriate to solve a given problem. Furthermore, the definition of the state variables of the resulting model is performed during this Data Analysis phase which is therefore one of the most crucial. As pointed out in Figure 2, SES [22] may be involved in order to generate a set of RL algorithms (Q-Learning, SARSA, DQN, DDQN, ...) [6].
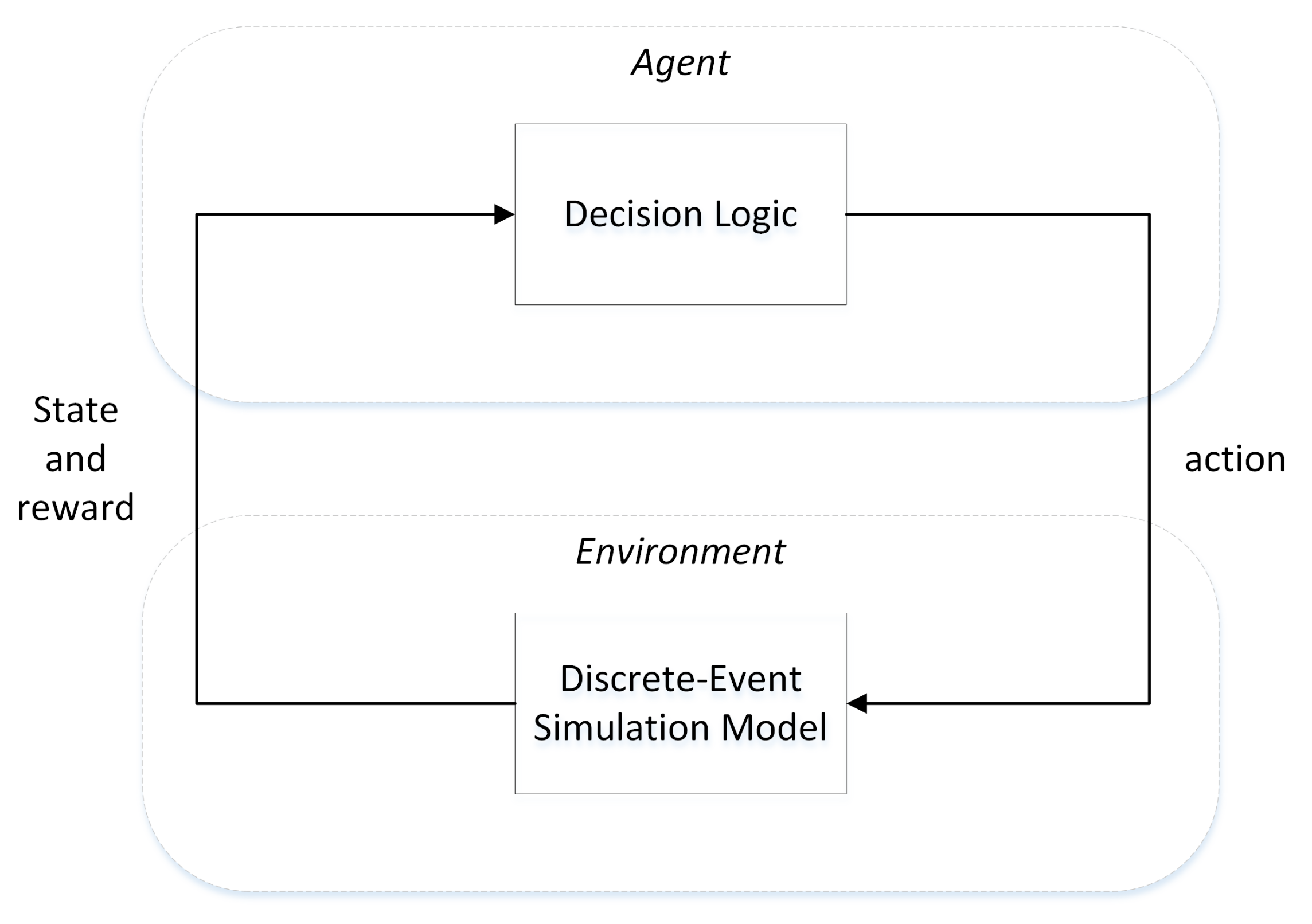
- DEVS formalism may facilitate the learning process associated with the previously defined model. Therefore DEVS is able to deal with the environment component as an atomic model. But the environment component associated to the learning agent as usual in RL approach may also be defined as a coupled model involving many atomic components. Therefore the environment may be considered as a multi-agent component modeled in DEVS whose agents may change during simulation.
- The real-time simulation phase involves both using the real clock time during simulation and exercising the model according to inputs. DEVS is a good solution to perform real time simulation of policies.
- DEVS may use RL algorithms in two ways: when performing the modeling part of the system or when considering the simulation algorithms. DEVS is able to obtain benefits from an AI for instance, in order to help the SES modeling pruning phase or enhancing simulation performance using a neural net associated with the DEVS abstract simulator.
- AI processes may use the DEVS formalism in order to perform good selection of hyper-parameters for example. The presented focuses on this last problematic.
4.1. Temporal Aspect
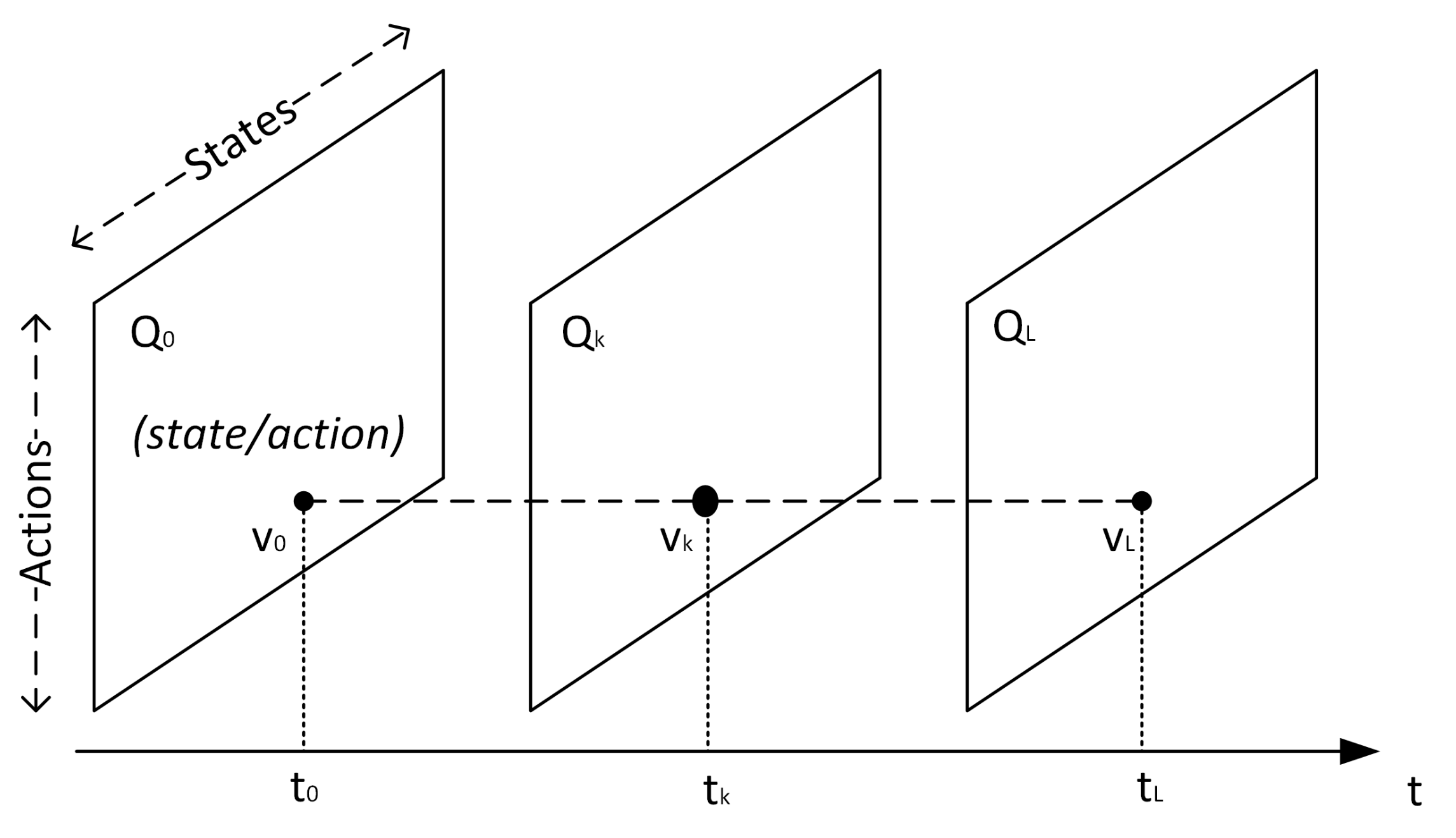
- Implicit time aspect is indeed present in the Q-learning or SARSA algorithm since it leans on the notion of reward shifted in time. However, this implicit notion of time does not refer to time unit but only to time steps involved in the algorithms. The idea is to add a third dimension in addition to the classical ones (states and actions). In this case, the time feature is introduced even if the results give an ordering of the actions involved in the chosen policy.
- The explicit time aspect is not involved in the classical Q-learning and SARSA algorithms. However, a set of work introduces the possibility to associated random continuous duration to actions [24]. Time is made explicit in these approaches.
4.1.1. Implicit Time in Q-Learning
4.1.2. Explicit Time in Q-Learning
4.2. Hierarchical Aspect
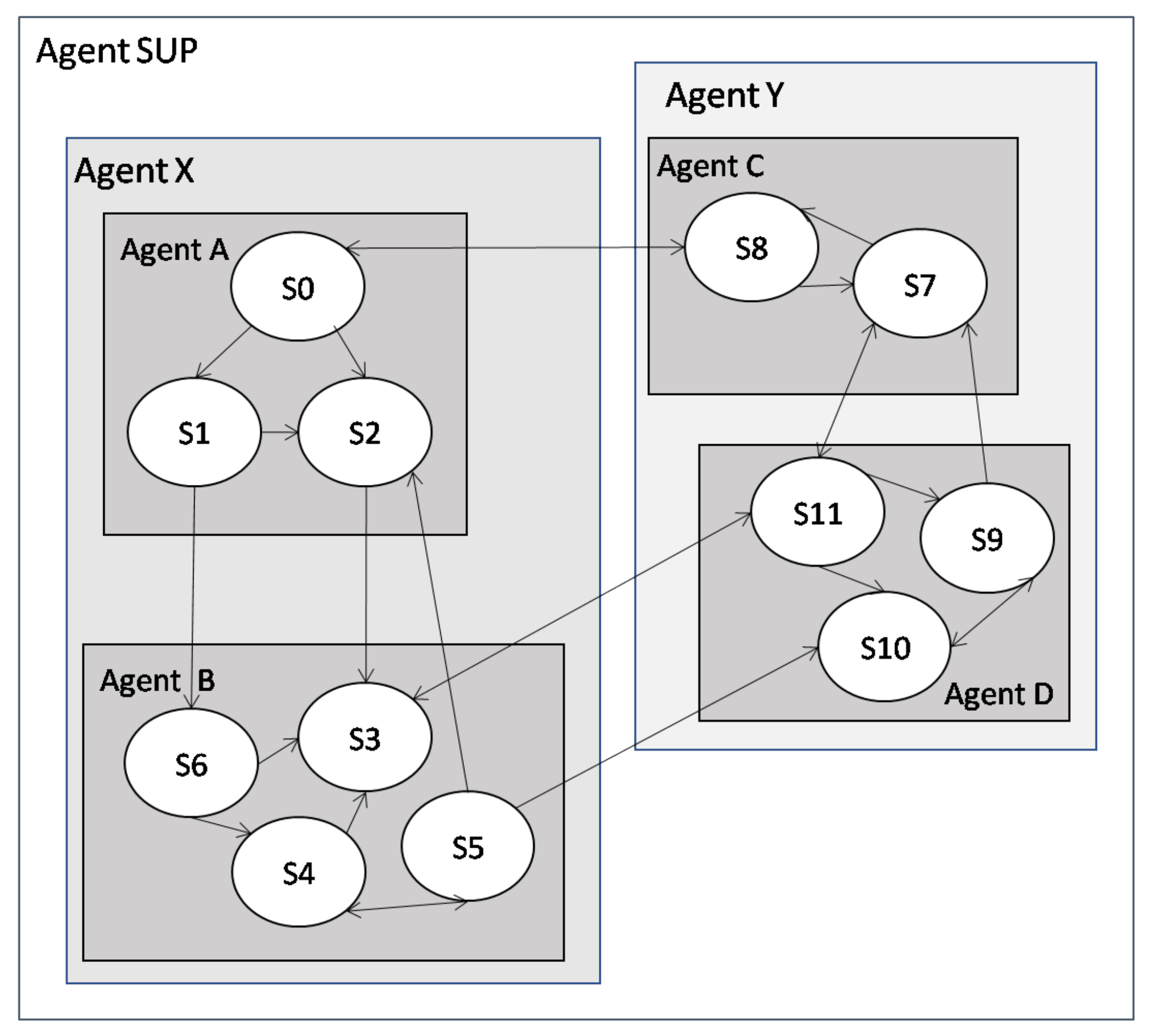
4.3. Multi-Agent Aspect
- m: the agents number;
- S: environment states;
- , : actions associated to the agents and generating the action set ;
- : transition probability function;
- , : reward functions associated with the agents.
5. Related Work
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| M&S | Modeling and Simulation |
| AI | Artificial Intelligence |
| RL | Reinforcement Learning |
| ML | Machine Learning |
| MDP | Markov Decision Process |
| DEVS | Discrete Event system Specification |
| SES | System Entity Structure |
References
- Alpaydin, E. Machine Learning: The New AI; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Busoniu, L.; Babuska, R.; Schutter, B.D. Multi-Agent Reinforcement Learning: A Survey. In Proceedings of the Ninth International Conference on Control, Automation, Robotics and Vision, ICARCV 2006, Singapore, 5–8 December 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Zeigler, B.P.; Muzy, A.; Kofman, E. Theory of Modeling and Simulation, 3rd ed.; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar] [CrossRef]
- Zeigler, B.P.; Seo, C.; Kim, D. System entity structures for suites of simulation models. Int. J. Model. Simul. Sci. Comput. 2013, 04, 1340006. [Google Scholar] [CrossRef]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; A Bradford Book: Cambridge, MA, USA, 2018. [Google Scholar]
- Bellman, R.E. Dynamic Programming; Dover Publications, Inc.: Mineola, NY, USA, 2003. [Google Scholar]
- Yu, H.; Mahmood, A.R.; Sutton, R.S. On Generalized Bellman Equations and Temporal-Difference Learning. In Proceedings of the Advances in Artificial Intelligence—30th Canadian Conference on Artificial Intelligence, Canadian AI 2017, Edmonton, AB, Canada, 16–19 May 2017; pp. 3–14. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H. Learning from Delayed Rewards. Ph.D. Thesis, King’s College, Cambridge, UK, 1989. [Google Scholar]
- Even-Dar, E.; Mansour, Y. Learning Rates for Q-learning. J. Mach. Learn. Res. 2004, 5, 1–25. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall Press: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Sharma, J.; Andersen, P.A.; Granmo, O.C.; Goodwin, M. Deep Q-Learning With Q-Matrix Transfer Learning for Novel Fire Evacuation Environment. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7363–7381. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Y.; Gao, Z.; He, X. An Improved DDPG and Its Application Based on the Double-Layer BP Neural Network. IEEE Access 2020, 8, 177734–177744. [Google Scholar] [CrossRef]
- Nielsen, N.R. Application of Artificial Intelligence Techniques to Simulation. In Knowledge-Based Simulation: Methodology and Application; Fishwick, P.A., Modjeski, R.B., Eds.; Springer: New York, NY, USA, 1991; pp. 1–19. [Google Scholar] [CrossRef]
- Wallis, L.; Paich, M. Integrating artifical intelligence with anylogic simulation. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; p. 4449. [Google Scholar] [CrossRef]
- Foo, N.Y.; Peppas, P. Systems Theory: Melding the AI and Simulation Perspectives. In Artificial Intelligence and Simulation, Proceedings of the 13th International Conference on AI, Simulation, and Planning in High Autonomy Systems, AIS 2004, Jeju Island, Korea, 4–6 October 2004; Revised Selected Papers; Springer: Berlin/Heidelberg, Germany, 2004; pp. 14–23. [Google Scholar] [CrossRef]
- Meraji, S.; Tropper, C. A Machine Learning Approach for Optimizing Parallel Logic Simulation. In Proceedings of the 2010 39th International Conference on Parallel Processing, San Diego, CA, USA, 13–16 September 2010; pp. 545–554. [Google Scholar] [CrossRef]
- Floyd, M.W.; Wainer, G.A. Creation of DEVS Models Using Imitation Learning. In Proceedings of the 2010 Summer Computer Simulation Conference, SCSC ’10, Ottawa, ON, Canada, 11–14 July 2010; Society for Computer Simulation International: San Diego, CA, USA, 2010; pp. 334–341. [Google Scholar]
- Eschmann, J. Reward Function Design in Reinforcement Learning. In Reinforcement Learning Algorithms: Analysis and Applications; Belousov, B., Abdulsamad, H., Klink, P., Parisi, S., Peters, J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 25–33. [Google Scholar] [CrossRef]
- Zhao, S.; Song, J.; Ermon, S. Learning Hierarchical Features from Deep Generative Models. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; pp. 4091–4099. [Google Scholar]
- Canese, L.; Cardarilli, G.C.; Di Nunzio, L.; Fazzolari, R.; Giardino, D.; Re, M.; Spanò, S. Multi-Agent Reinforcement Learning: A Review of Challenges and Applications. Appl. Sci. 2021, 11, 4948. [Google Scholar] [CrossRef]
- Zeigler, B.P.; Sarjoughian, H.S. System Entity Structure Basics. In Guide to Modeling and Simulation of Systems of Systems; Simulation Foundations, Methods and Applications; Springer: London, UK, 2013; pp. 27–37. [Google Scholar] [CrossRef]
- Pardo, F.; Tavakoli, A.; Levdik, V.; Kormushev, P. Time Limits in Reinforcement Learning. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Zhu, J.; Wang, Z.; Mcilwraith, D.; Wu, C.; Xu, C.; Guo, Y. Time-in-Action Reinforcement Learning. IET Cyber-Syst. Robot. 2019, 1, 28–37. [Google Scholar] [CrossRef]
- Bradtke, S.; Duff, M. Reinforcement Learning Methods for Continuous-Time Markov Decision Problems. In Advances in Neural Information Processing Systems 7; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Mahadevan, S.; Marchalleck, N.; Das, T.; Gosavi, A. Self-Improving Factory Simulation using Continuous-time Average-Reward Reinforcement Learning. In Proceedings of the 14th International Conference on Machine Learning, Nashville, TN, USA, 8–12 July 1997. [Google Scholar]
- Sutton, R.S.; Precup, D.; Singh, S. Between MDPs and semi-MDPs: A Framework for Temporal Abstraction in Reinforcement Learning. Artif. Intell. 1999, 112, 181–211. [Google Scholar] [CrossRef]
- Rachelson, E.; Quesnel, G.; Garcia, F.; Fabiani, P. A Simulation-based Approach for Solving Generalized Semi-Markov Decision Processes. In Proceedings of the 2008 Conference on ECAI 2008: 18th European Conference on Artificial Intelligence, Patras, Greece, 21–25 July 2008; IOS Press: Amsterdam, The Netherlands, 2008; pp. 583–587. [Google Scholar]
- Seo, C.; Zeigler, B.P.; Kim, D. DEVS Markov Modeling and Simulation: Formal Definition and Implementation. In Proceedings of the Theory of Modeling and Simulation Symposium, TMS ’18, Baltimore, MD, USA, 15–18 April 2018; Society for Computer Simulation International: San Diego, CA, USA, 2018; pp. 1:1–1:12. [Google Scholar]
- Dietterich, T.G. Hierarchical reinforcement learning with the MAXQ value function decomposition. J. Artif. Intell. Res. 2000, 13, 227–303. [Google Scholar] [CrossRef]
- Vezhnevets, A.S.; Osindero, S.; Schaul, T.; Heess, N.; Jaderberg, M.; Silver, D.; Kavukcuoglu, K. FeUdal Networks for Hierarchical Reinforcement Learning. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; pp. 3540–3549. [Google Scholar]
- Parr, R.; Russell, S. Reinforcement Learning with Hierarchies of Machines. In Proceedings of the 1997 Conference on Advances in Neural Information Processing Systems 10, NIPS ’97, Denver, CO, USA, 1–6 December 1997; MIT Press: Cambridge, MA, USA, 1998; pp. 1043–1049. [Google Scholar]
- Kessler, C.; Capocchi, L.; Santucci, J.F.; Zeigler, B. Hierarchical Markov Decision Process Based on Devs Formalism. In Proceedings of the 2017 Winter Simulation Conference, WSC ’17, Las Vegas, NV, USA, 3–6 December 2017; IEEE Press: Piscataway, NJ, USA, 2017; pp. 73:1–73:12. [Google Scholar]
- Bonaccorso, G. Machine Learning Algorithms: A Reference Guide to Popular Algorithms for Data Science and Machine Learning; Packt Publishing: Birmingham, UK, 2017. [Google Scholar]
- Yoshizawa, A.; Nishiyama, H.; Iwasaki, H.; Mizoguchi, F. Machine-learning approach to analysis of driving simulation data. In Proceedings of the 2016 IEEE 15th International Conference on Cognitive Informatics Cognitive Computing (ICCI*CC), Palo Alto, CA, USA, 22–23 August 2016; pp. 398–402. [Google Scholar] [CrossRef]
- Malakar, P.; Balaprakash, P.; Vishwanath, V.; Morozov, V.; Kumaran, K. Benchmarking Machine Learning Methods for Performance Modeling of Scientific Applications. In Proceedings of the 2018 IEEE/ACM Performance Modeling, Benchmarking and Simulation of High Performance Computer Systems (PMBS), Dallas, TX, USA, 12 November 2018; pp. 33–44. [Google Scholar] [CrossRef]
- Elbattah, M.; Molloy, O. Learning about systems using machine learning: Towards more data-driven feedback loops. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 1539–1550. [Google Scholar] [CrossRef]
- Elbattah, M.; Molloy, O. ML-Aided Simulation: A Conceptual Framework for Integrating Simulation Models with Machine Learning. In Proceedings of the 2018 ACM SIGSIM Conference on Principles of Advanced Discrete Simulation, SIGSIM-PADS ’18, Rome, Italy, 23–25 May 2018; ACM: New York, NY, USA, 2018; pp. 33–36. [Google Scholar] [CrossRef]
- Saadawi, H.; Wainer, G.; Pliego, G. DEVS execution acceleration with machine learning. In Proceedings of the 2016 Symposium on Theory of Modeling and Simulation (TMS-DEVS), Pasadena, CA, USA, 3–6 April 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Toma, S. Detection and Identication Methodology for Multiple Faults in Complex Systems Using Discrete-Events and Neural Networks: Applied to the Wind Turbines Diagnosis. Ph.D. Thesis, University of Corsica, Corte, France, 2014. [Google Scholar]
- Bin Othman, M.S.; Tan, G. Machine Learning Aided Simulation of Public Transport Utilization. In Proceedings of the 2018 IEEE/ACM 22nd International Symposium on Distributed Simulation and Real Time Applications (DS-RT), Madrid, Spain, 15–17 October 2018; pp. 1–2. [Google Scholar] [CrossRef]
- De la Fuente, R.; Erazo, I.; Smith, R.L. Enabling Intelligent Processes in Simulation Utilizing the Tensorflow Deep Learning Resources. In Proceedings of the 2018 Winter Simulation Conference (WSC), Gothenburg, Sweden, 9–12 December 2018; pp. 1108–1119. [Google Scholar] [CrossRef]
- Feng, K.; Chen, S.; Lu, W. Machine Learning Based Construction Simulation and Optimization. In Proceedings of the 2018 Winter Simulation Conference (WSC), Gothenburg, Sweden, 9–12 December 2018; pp. 2025–2036. [Google Scholar] [CrossRef]
- Liu, F.; Ma, P.; Yang, M. A validation methodology for AI simulation models. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 7, pp. 4083–4088. [Google Scholar] [CrossRef]
- Elbattah, M.; Molloy, O.; Zeigler, B.P. Designing Care Pathways Using Simulation Modeling and Machine Learning. In Proceedings of the 2018 Winter Simulation Conference (WSC), Gothenburg, Sweden, 9–12 December 2018; pp. 1452–1463. [Google Scholar] [CrossRef]
- Arumugam, K.; Ranjan, D.; Zubair, M.; Terzić, B.; Godunov, A.; Islam, T. A Machine Learning Approach for Efficient Parallel Simulation of Beam Dynamics on GPUs. In Proceedings of the 2017 46th International Conference on Parallel Processing (ICPP), Bristol, UK, 14–17 August 2017; pp. 462–471. [Google Scholar] [CrossRef]
- Batata, O.; Augusto, V.; Xie, X. Mixed Machine Learning and Agent-Based Simulation for Respite Care Evaluation. In Proceedings of the 2018 Winter Simulation Conference (WSC), Gothenburg, Sweden, 9–12 December 2018; pp. 2668–2679. [Google Scholar] [CrossRef]
- John, L.K. Machine learning for performance and power modeling/prediction. In Proceedings of the 2017 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), Santa Rosa, CA, USA, 24–25 April 2017; pp. 1–2. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capocchi, L.; Santucci, J.-F. Discrete Event Modeling and Simulation for Reinforcement Learning System Design. Information 2022, 13, 121. https://doi.org/10.3390/info13030121
Capocchi L, Santucci J-F. Discrete Event Modeling and Simulation for Reinforcement Learning System Design. Information. 2022; 13(3):121. https://doi.org/10.3390/info13030121
Chicago/Turabian StyleCapocchi, Laurent, and Jean-François Santucci. 2022. "Discrete Event Modeling and Simulation for Reinforcement Learning System Design" Information 13, no. 3: 121. https://doi.org/10.3390/info13030121
APA StyleCapocchi, L., & Santucci, J.-F. (2022). Discrete Event Modeling and Simulation for Reinforcement Learning System Design. Information, 13(3), 121. https://doi.org/10.3390/info13030121






