The Influence of Network Public Opinion on Audit Credibility: A Dynamic Rumor Propagation Model Based on User Weight

Abstract

Network public opinion is one of the factors that affects the credibility of audits, especially falsified network public opinion, which can easily result in the public losing trust in audits and may even impact the financial market. As users of social networks are not online 24 h a day, and their network behaviors are dynamic, in this study, we constructed a dynamic rumor-spreading model. Because the influence and authority of different user nodes in the network are different, we added user weights to the rumor propagation model, and finally, we established a dynamic rumor propagation model based on user weights. The experimental results showed that the rumor propagation model had a good monitoring effect, so it could help with managing the public opinion of audit institutions, maintaining the image of audit fairness and justice, and maintaining the stability of the capital market.

1. Introduction

At the beginning of 2021, a 55-page PPT report letter from the internal staff of Deloitte Touche Tohmatsu Huayong Certified Public Accountants sent Deloitte to the cusp of negative online public opinion. As soon as this information was released, it immediately topped the most searched list in Weibo and was news on major webpages. Even though the final results were inconclusive, the release triggered a series of effects. Two of the three companies mentioned in the PPT reported that their stock prices fell the next day. The Ministry of Finance immediately interviewed the principal person responsible for Deloitte and asked them to conduct a self-examination. For a time, Deloitte’s reporting caused the four major international accounting firms to experience a trust crisis, and the public was widely expressing opinions on the release of audit procedures and the lack of audit independence. This negative network public opinion caused the public to seriously doubt the audit’s credibility. As the gatekeepers of the capital market, audit intermediary institutions are the most important supervisory institutions in financial activities, which ensure audit credibility in a way that different from other institutions. Once problems occur with auditing, the interests of many parties can be affected, causing turbulence in the capital market.

Nowadays, the world has entered the information age, and information transmission has shifted from offline to online. The Internet provides convenient conditions for people to obtain information and express their views. More and more people who are paid to promote or criticize others are expressing their opinions and spreading what they think is the “truth” before the authenticity of information is verified. The Internet is convenient for people, but it also provides a convenient means for the spread of public opinion on the Internet, especially the spread of rumors that are later falsified. Without limitations imposed by time, space, and place, netizens hiding behind the screen create links in the chain of rumor spread. The famous social six degrees of separation law shows that in the real world, the connection between two strangers can be established through only six people, but in the online world, the connection between people may not need six people. This further shows that the strong interactivity of social networks speeds up the transmission of rumors [1,2,3,4,5].

The original infectious disease transmission model can be compared with the rumor transmission model. The population in the rumor transmission population can be divided into three categories: those who have not been infected, those who have been infected, and those who have recovered from infection and are immune to rumors. The rumor-spreading process can be described as follows: When rumors first spread, people have not heard the rumors, so they are in an uninfected state. Later, when people who were not infected received the rumors spread by other people who had heard the rumors, they become infected. At the same time, these people become rumor disseminators and begin to spread the rumors to others. Finally, when the rumor is found to be false through various channels, the person who spreads rumors no longer continues to spread rumors and turns into an immune state. Immune people do not spread rumors to others. On this basis, combined with threshold theory, the SIS transmission model was conceived, and some scholars constructed SIR [6,7], SEIR [8], SICR [9], SEIS [10], SIHR [11], SHAR [12], SPNR [13], uncertain SIR [14], and SIR-IM [15] models based on the classical infectious disease rumor transmission model.

Daley and Kendall [6] directed attention to the analogy between the spreading of an infectious disease and the dissemination of information. On the basis of it, Daley and Kendall [7] studied the variance of the fluctuations of the sample trajectory in the stochastic model about the unique trajectory in the associated deterministic approximation using the principle of the diffusion of arbitrary constants. Xia et al. [8] proposed a modified SEIR model with a hesitating mechanism by considering the attractiveness of the content of rumors. They derived mean-field equations to characterize the dynamics of the SEIR model on both homogeneous and heterogeneous networks. Zan et al. [9] studied the self-resistance feature of networks and its influence on rumor spreading, and they built two new rumor-spreading models, considering the counterattack mechanism. Zhang et al. [10] presented an SEIS epidemic model with an infective force in both the latent period and infected period, which had different general saturation incidence rates. Zhao et al. [11] extended the SIR model and proposed an SIHR model by adding a direct link from ignorants to stiflers and a new kind of people: hibernators.

Assuming that among the common mass there are three attitudes towards rumors (to like rumor spreading, to dislike rumor spreading, and to be hesitant to rumor spreading), Hu et al. [12] established an SHAR model considering individuals’ different attitudes towards rumor spreading. Jiang et al. [13] studied a two-stage rumor model to analyze rumor spread and the reversal of rumors regarding emergencies on Weibo. Sun et al. [14] proposed an uncertain SIR rumor-spreading model driven by the influence of perturbation in the transmission mechanism of rumor spreading. Qiu et al. [15] proposed a model called SIR-IM, which incorporated the number of current spreaders into the spreading probability.

In the related literature, the characteristics of rumor propagation of different models have been described in detail, and these rumor propagation models have been widely used in the study of rumor propagation in complex networks. However, most current efforts have mainly focused on static models, and dynamic models have received little attention. In addition, fuzzy concepts have not been considered in dynamic models.

Therefore, to verify the influence of network public opinion on audit credibility, in this study, we constructed a rumor dissemination model to simulate the rumor dissemination mechanism that has serious impacts on audit credibility. Through experiments and theories, we verified whether the model could reflect the real rumor dissemination mechanism. This model is needed to help control the spread of rumors and maintain the credibility of audits in the future. The main contributions are as follows:

• Proposing a dynamic rumor propagation model based on user weight.
• Incorporating a fuzzy concept and weight concept into the dynamic rumor propagation model.
• Evaluating our model to present its superiority.

The rest of this paper is organized as follows: We propose dynamic rumor propagation model in Section 2. Section 3 presents our experimental results, and Section 4 concludes the paper.

2. Dynamic Rumor Propagation Model

In this section, we use graph theory to study the spread of rumors in online social networks. E (edge) is the edge of connecting nodes in the network, and V (vertex) are the nodes in the network, and each node represents a user who logs into the online social networking platform. Therefore, an abstract binary group (V, E) can be established to represent the relationship between the edges and nodes in the network.

In a closed and uniform online social network with N independent individuals, nodes represent independent individuals, and edges represent social connections among users in the online network. Then, an undirected graph G = (V, E) is established to represent the whole online social network platform. Assuming that rumors spread through direct contact between disseminators and others, the rumor-spreading process in the dynamic rumor-spreading model UFPR is as shown in Figure 1.

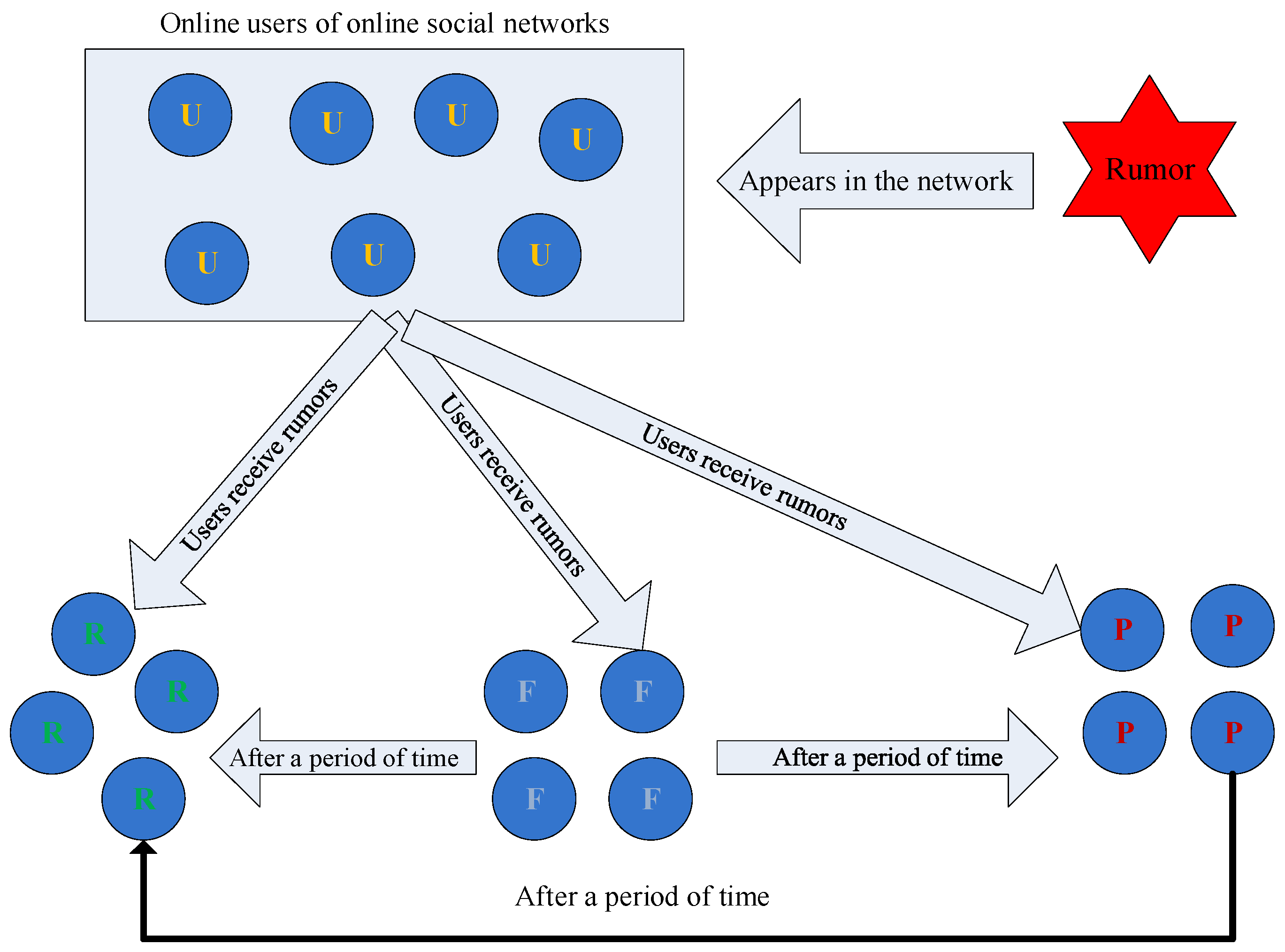
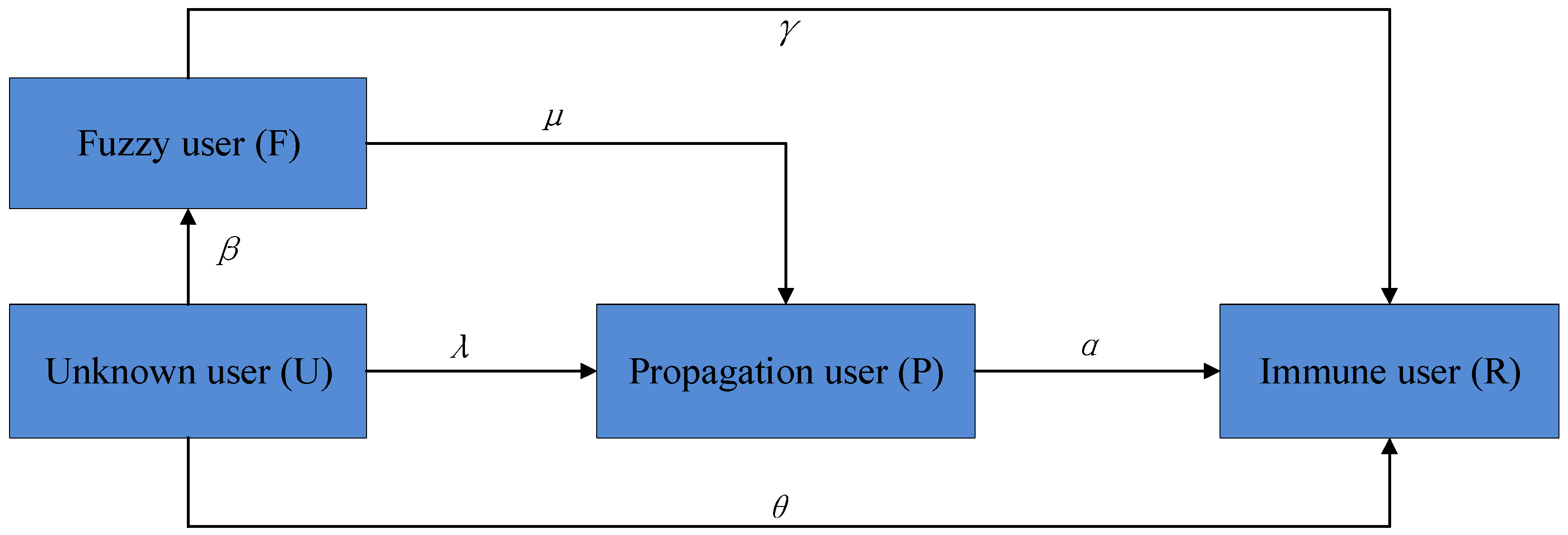
We propose a four-tuple component model to describe the state of network users when rumors spread in complex networks. The model Q = (U, F, P, R) includes four population groups: unknown people (U), fuzzy people (F), transmitted people (P), and immunized people (R). Unknown people refer to those who have not received rumors and know nothing about them. When they receive the rumors, they are more inclined to change into spreading people. Fuzzy crowds represent people who know rumors but are not sure whether they will spread them to others. Although these people are not sure whether they are interested in spreading rumors, they cannot deny the possibility of spreading rumors on online social networking platforms. Therefore, we propose using fuzziness to represent those who are not sure whether they will spread rumors, become network users who will spread rumors, are not interested in rumors, and become network users who are not immune to rumors. A spreading crowd refers to people who have received rumors and spread them to others. In this crowd, a person can make the rumor known to those who do not know it and continue to spread it when they come into contact with unknown people. Finally, the immunized population represents those who have known rumors for some time and have lost interest in rumors and will not spread them to others. These four groups of people meet the following conversion rules:

(1)

When an unknown user contacts a propagation user, the unknown user becomes a propagator with a probability of λ, which is the propagation rate;

(2)

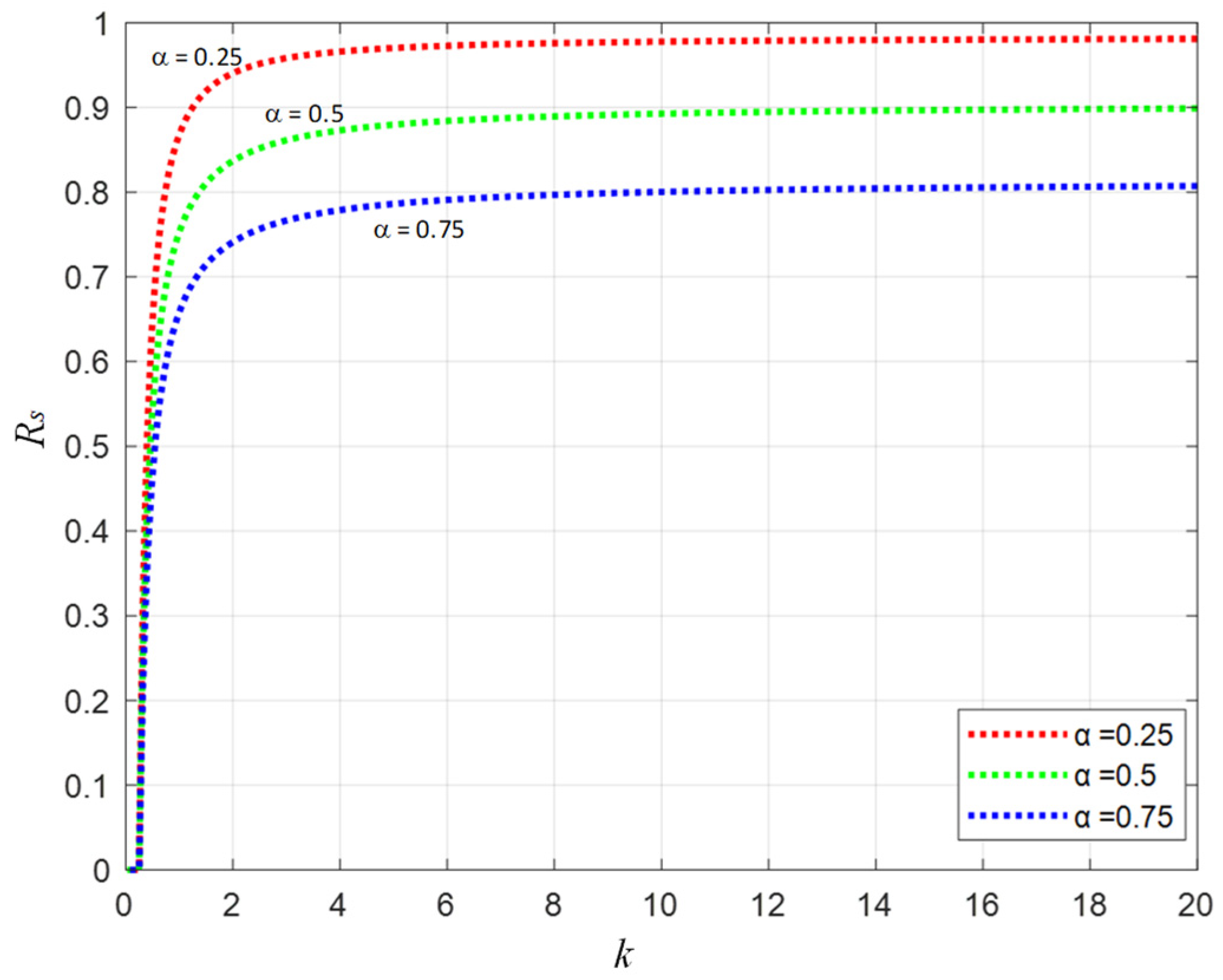
When a communication user spreads rumors for a long time, when they are immune to rumors or lose interest in rumors, or when they delete the user account on the social network platform for some reason and no longer pay attention to the rumor and related events, then the user will change from a disseminator to an immune person with a probability of α, where α is the immune rate;

(3)

When a communicating user no longer receives rumors for a long time because of the forgetting mechanism, they transition into an immune user with a probability of γ, which is the forgetting rate;

(4)

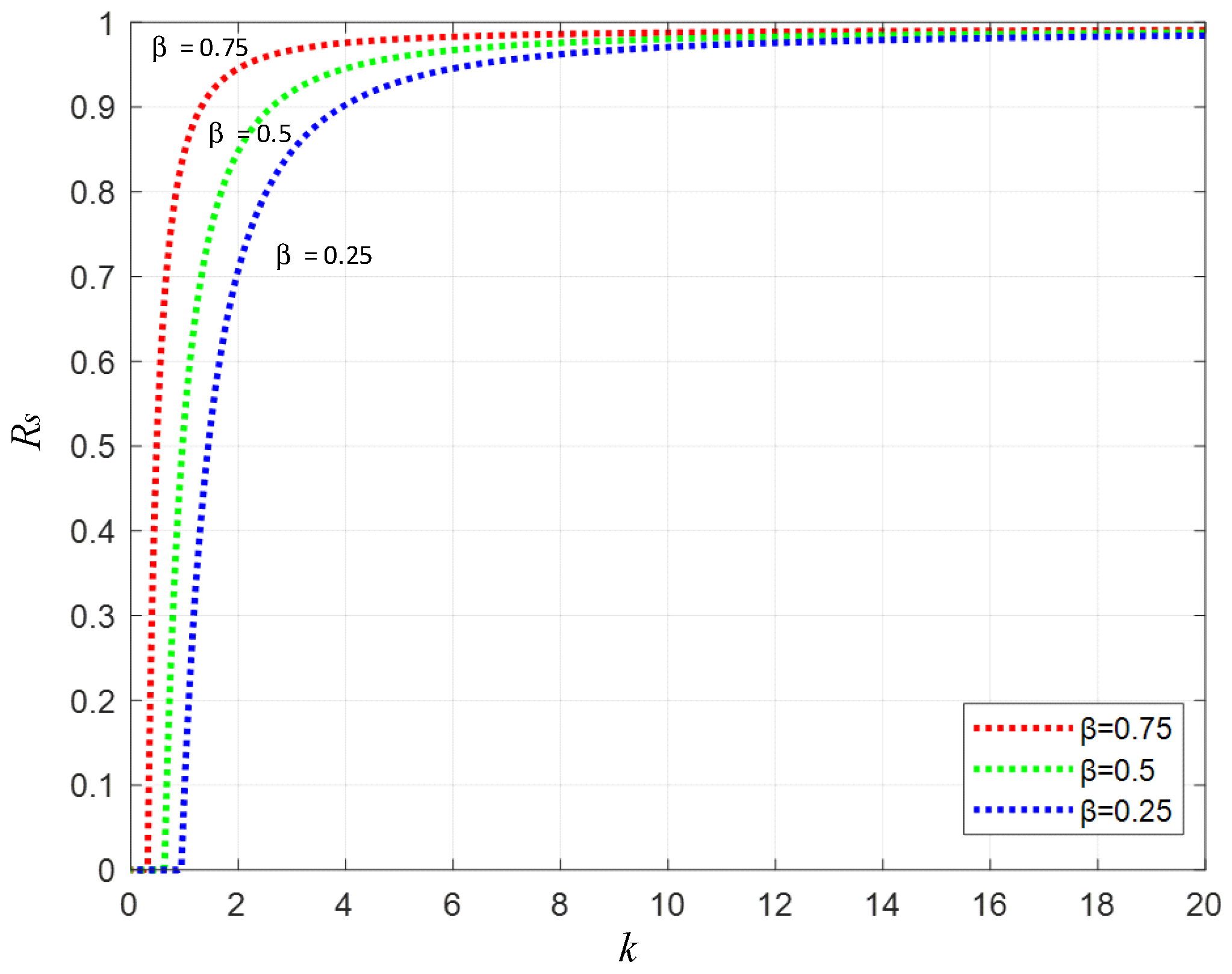
When an unknown user evolves over a period of time, it is impossible to determine their status. Assuming that the unknown user becomes a fuzzy user with a probability of β, that is, their current state is fuzzy, it is impossible to accurately judge whether they are a communicator or immune. β is called ambiguity;

(5)

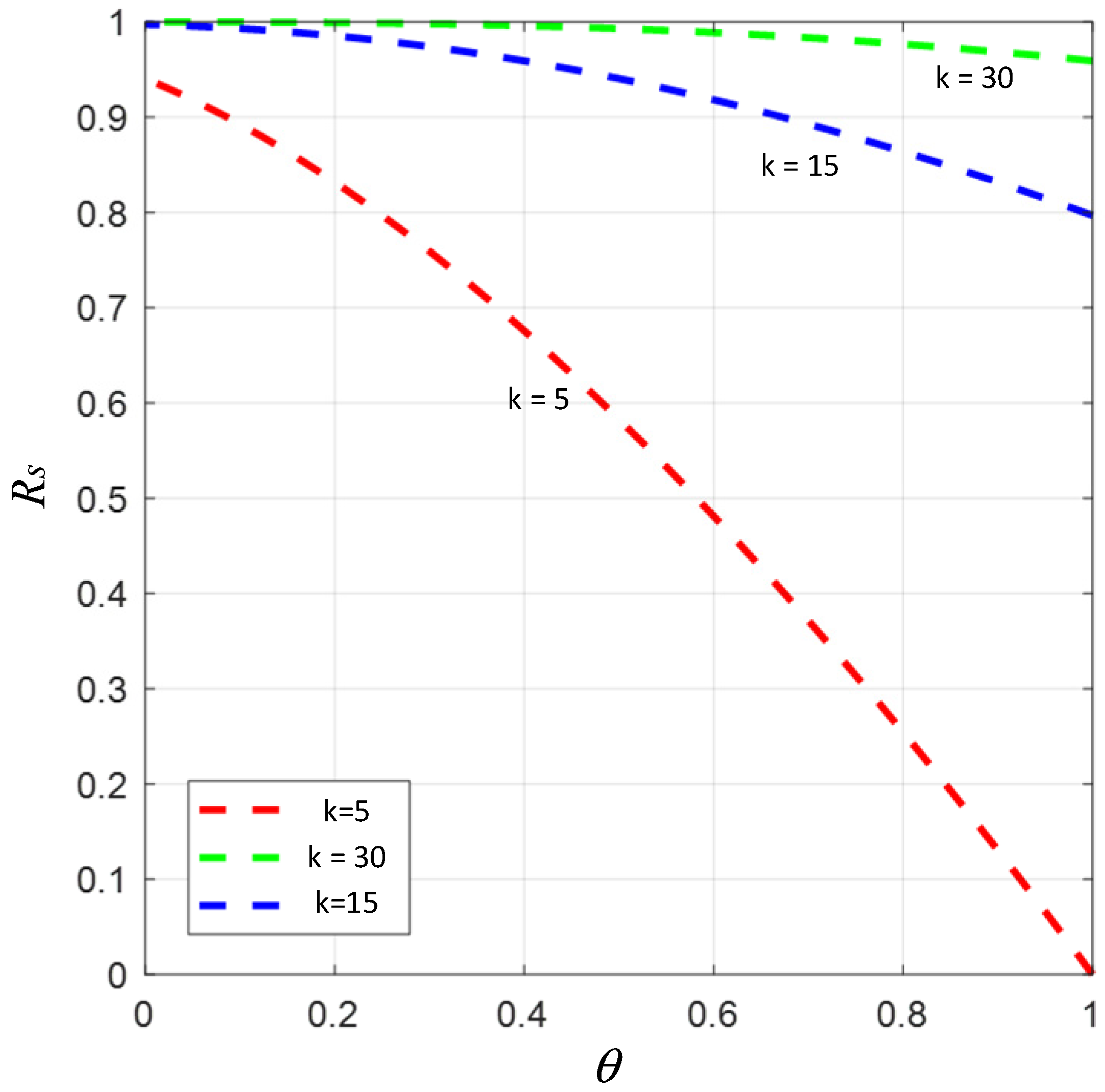
When an unknown user comes into contact with an immune user, the unknown user does not spread rumors because they do not care about the rumor content, and they will become immune with a probability of θ, which is called the rejection rate.

The state transition rules are shown in Figure 2.

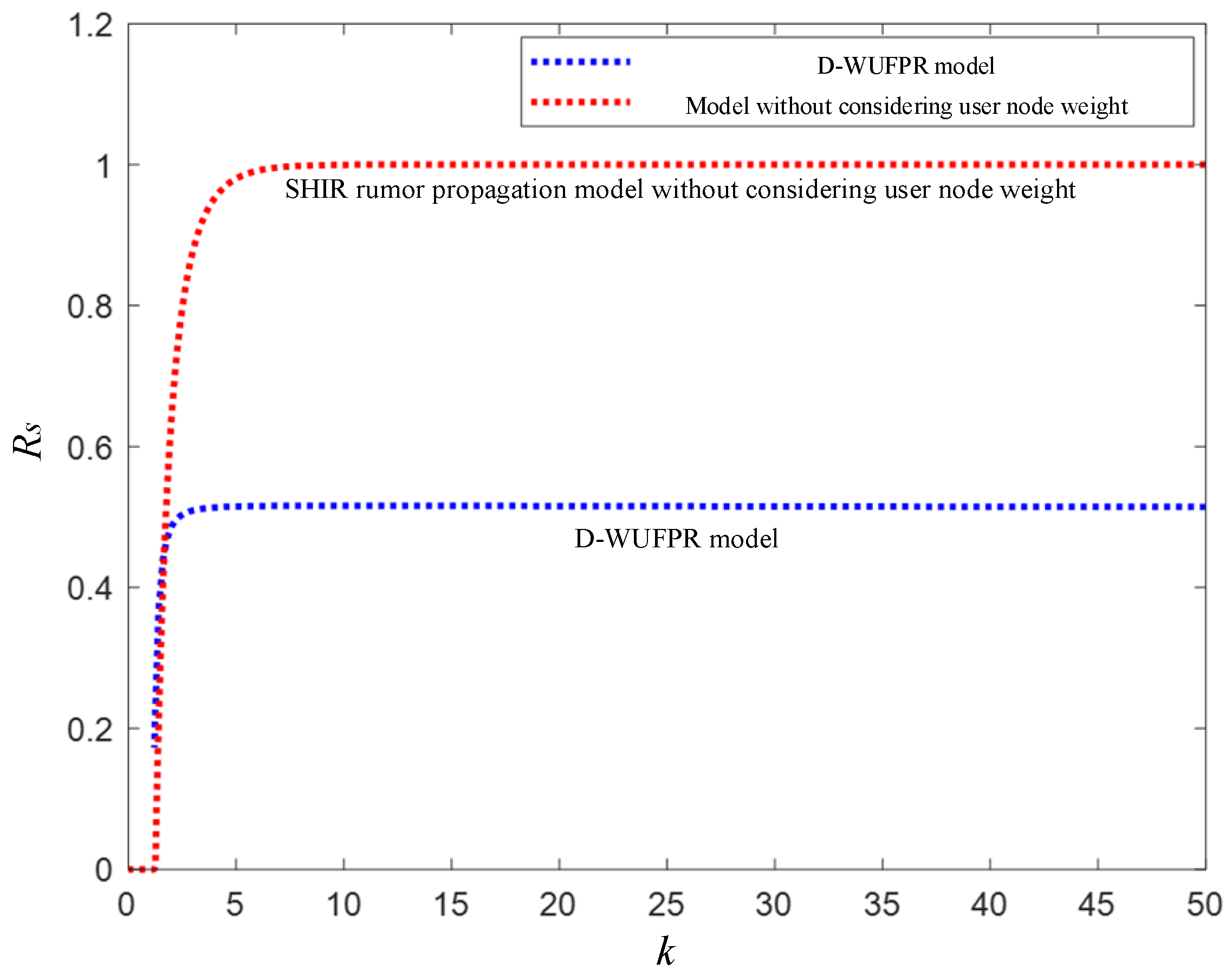
Usually, the mean field hypothesis commonly applied in application dynamics is used to study the traditional rumor propagation model. This hypothesis holds that the influence caused by the interoperation behavior between different network user nodes in a complex network is equivalent to a mean field in the whole complex network. Ignoring the operation behavior of a single network user node, it is assumed that all user nodes in the whole complex network have the same rumor infection and rumor immunity rates. This assumption can be effectively applied to uniform networks, because the topological differences in individual user nodes in uniform networks can be ignored. Under this assumption, the node degree of each single user node in the uniform network is equal to the average user node degree in the whole network; under the same network user node degree, the number of communicators in the whole network gradually decreases with the spread of rumors in the network. However, in real life, the network is uneven, and the distribution of network user node degrees is generally close to the power function in probability theory. Moreover, in actual online social networks, a huge gap exists between ordinary network users and well-known bloggers, stars, idols, and other network users in terms of influence and authority. Therefore, when establishing the rumor propagation model in complex networks, it is necessary to carefully consider the influence differences among the different network user nodes.

In addition, the traditional rumor propagation model assumes that the overall interaction effect of the network is a mean field, which ignores the specific characteristics of individual users in the network and the influence of their functions on the whole network. This is proposed under the assumption that the network has the same infection, transmission, and immunity rates, and it is only applicable to uniform networks. However, online social networks are irregular, nonuniform, and scale-free networks, and the distribution of node degrees follows the power law distribution. The preferences of online social networks create topological differences in the nodes in the network. According to a survey, the accounts of stars, experts, and celebrities on online social networking platforms have much more followers than ordinary accounts, so if they spread rumors, they will spread them several times faster than ordinary users, and people are always willing to believe what they say. Additionally, for fans, once their favorite stars, celebrities, or network celebrities distribute information on social networking platforms, they quickly learn the information and spread it to more people. Therefore, the popularity and celebrity effect of users in the network must be considered when studying rumor spread control strategies on social networking platforms. Therefore, on the basis of the previously established UFPR model, we a measure the importance of network user nodes, which is defined as the weight of user nodes.

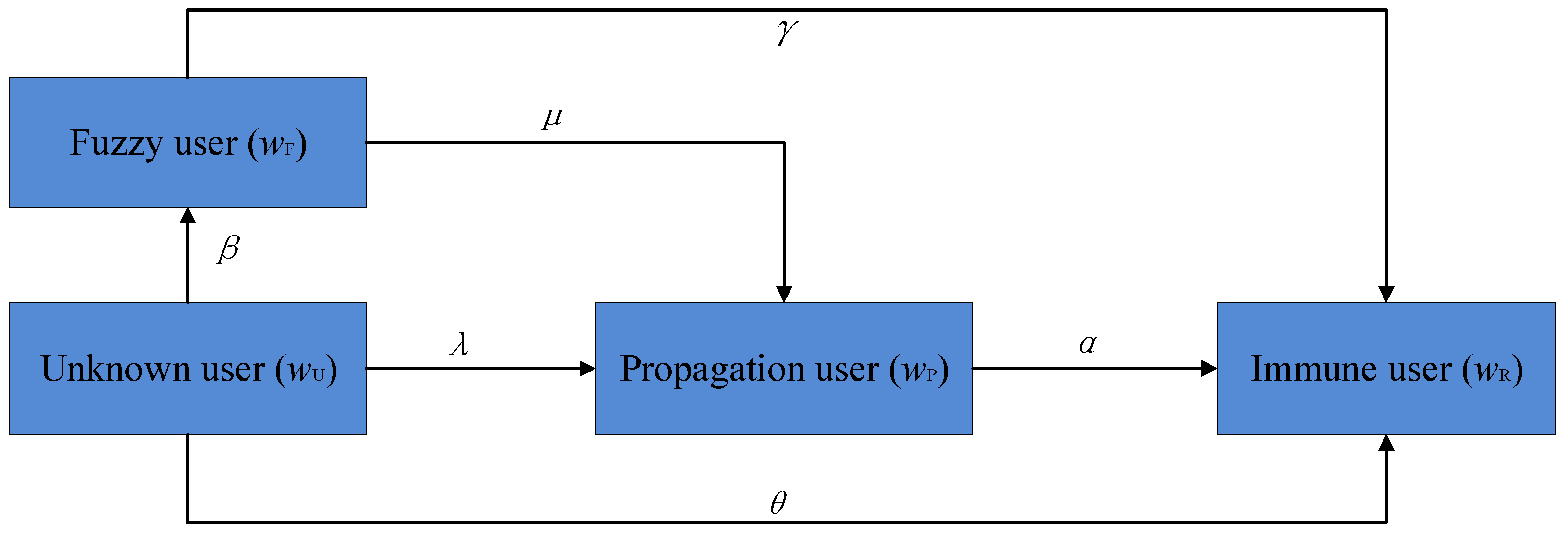
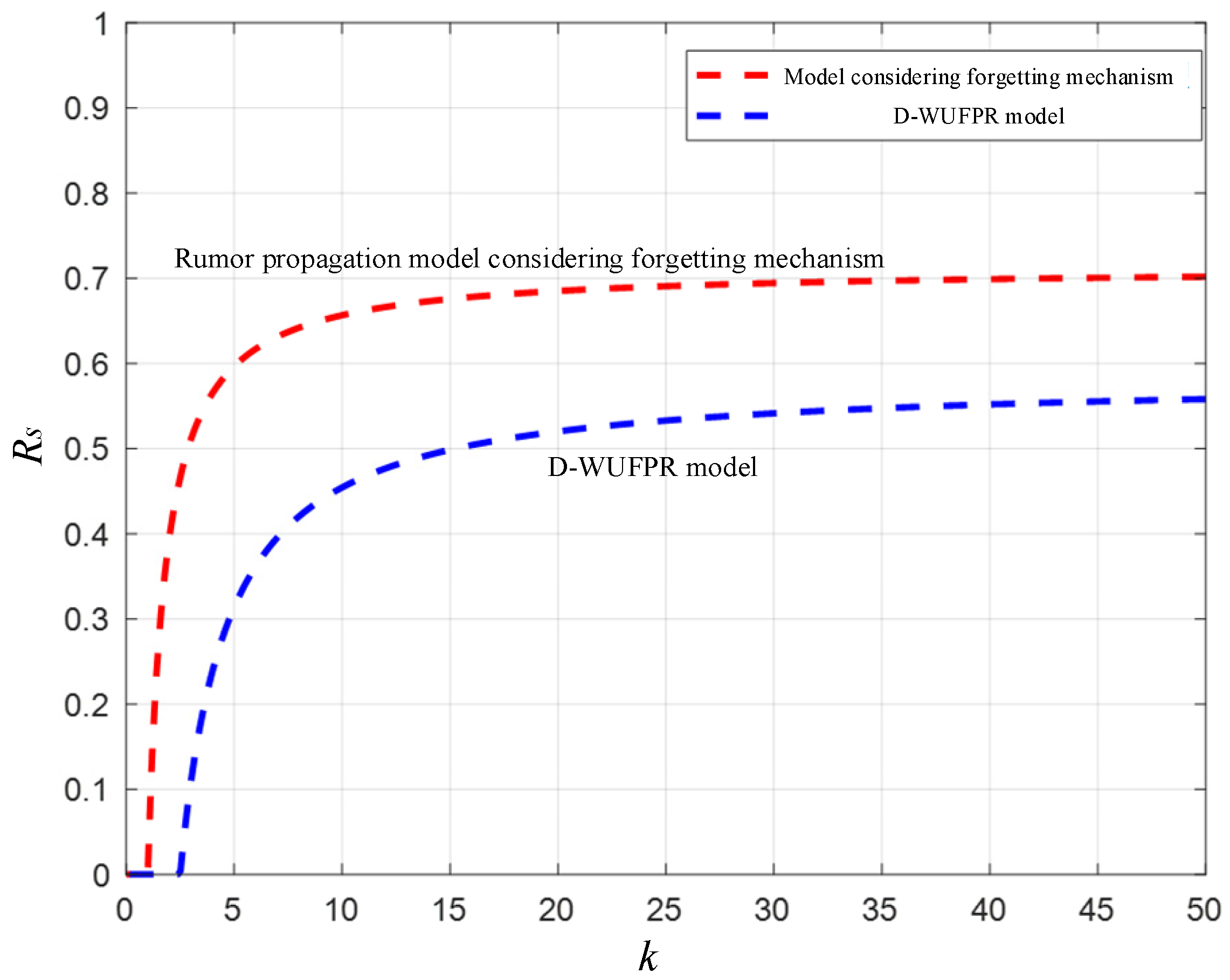
The weight of a user in an online social network is represented by w, which is defined as the sum of the node degree of the user node divided by the node degree of its adjacent user nodes. Therefore, weight w is added to the previously established rumor propagation model considering the fuzziness of the user state (UFPR model), and we establish a new model: the rumor propagation model considering the influence of user nodes and the fuzziness of the user state (WUFPR model). The rumor propagation rules in this model are the same as those in UFPR model. The state transition rules for WUFPR model are shown in Figure 3.

In addition to considering the influence of user nodes on the whole network and the fuzziness of user nodes’ states in the process of rumor spreading, the model also considers whether users are online in the process of rumor spreading. Because online social networks are dynamic and complex networks, the states of activity of network users are dynamic and autonomous. In social networks, users are not online 24 h a day. They only log on to social networking sites in their spare time, and only when they are online can they receive messages in real time. Therefore, when considering strategies for controlling rumor spreading, we can ignore the users who are not online, that is, we only consider the status and weight of users who are online in a certain period of time during the rumor-spreading stage. To improve the simulation of online social networks, a new state D is introduced to indicate whether a user is online. The probability of the user being online is ε, and the probability of the user being online to receive messages is ε. Because of the huge number of users in online social networks, the online probability of each user may be different. To simplify the calculation, the online probability ε of users is set to different constants under different experimental simulations. ε reflects the online activities of all users in the whole network. Finally, a complete online social network rumor propagation model, the D-WUFPR model, is established.

3. Experiments

In this study, we implemented all simulation and function images on MATLAB (R2017b) 64-bit software (MathWorks, Natick, MA, USA). In addition, we conducted the related experiments on an Intel^® Core™ i7-7500U processor (Santa Clara, CA, USA) with 2.90 GHz and a Windows 10 system (Microsoft, Redmond, WA, USA) with 8 GB of memory. In the modeling and simulation of user propagation state change density in the network, we used Facebook data sets with an average node degree of 29.2944, 5,284,457 user nodes, and an average of 77,402,652 connected edges.

3.1. Steady State Analysis

The final spread range of rumors in the network is related to the spread rate λ, immunity rate α, user online rate θ, and ambiguity rate β. To verify this assumption, we modeled and simulated the D-WUFPR rumor propagation model in MATLAB.

In Figure 4, we present a variation of the rumor propagation range with the average node degree of users under different propagation rates, where the horizontal axis k represents the user average node degree, and the ordinate axis R_s represents the range of rumors spreading on the Internet. Figure 4 shows that the final spread range of rumors in complex networks in the D-WUFPR rumor spread model proposed in this paper is closely related to the rumor spread rate λ. The larger the spread rate λ, the larger the final spread range of rumors in the networks.

Figure 5 shows that the fuzziness of users’ states in complex networks in the proposed D-WUFPR rumor propagation model also impacts the spread range of rumors in the network. By analyzing the images, we found that the smaller the blue rate β of the user’s state, the smaller the final range of rumors in the network. Therefore, to control the spread of rumors in complex networks, we should minimize the uncertain user nodes in the spread of rumors so as to reduce the final impact of rumors on the network.

Figure 6 shows that the immune rate α of network users in the newly proposed D-WUFPR rumor propagation model also has a strong influence on the final spread range of rumors in the network. By analyzing the three curves in Figure 6, we can see that the larger the immune rate α, the smaller the final spread range of rumors in complex networks. Only the immune and unknown people are left in the final network. If the final spread range of rumors in the network is 0.8, it means that 80% of the people in the network are immune, while the remaining 20% are unknown, that is, they have never accepted rumors.

Figure 7 shows that the rejection rate θ of spreading rumors in complex networks in the newly proposed D-WUFPR rumor propagation model impacts the final spread range of rumors. We found that the larger the rejection rate θ of users to rumors, the smaller the influence range of rumors. This shows that as the user rejection rate θ in the network increases, most users on the network receive more information because they have a larger outflow, that is, they pay attention to many other users in the same network. Therefore, they have a stronger ability to distinguish rumors, so they will not easily listen to or spread rumors. Figure 7 also shows that the smaller the average node degree k of users in complex networks, the stronger the influence of the rejection rate θ on the final spread range of rumors. When k gradually increases, the influence of the user rejection rate θ on rumor spread gradually decreases. This shows that when the average node degree of users in the network is very large, that is, the number of registered and active users in the network is very large, the attitude of some users who ignore rumors spreading in the network and will not spread rumors has no strong influence on the final spread range of rumors in the network.

Figure 8 shows that the real-time online rate ε and the immune rate α of users in the complex network of the D-WUFPR rumor propagation model have an impact on the final spread range of rumors. After simulating the dataset of 5,284,457 users on Facebook, a large online social network, the resulting final spread range of rumors in the network is shown in Figure 8, considering both the immune rate α of network users and the real-time online rate ε in the network when rumors spread. With the increase in the number of immune users in the network and the decrease in the online rate ε of users in the process of rumor spreading, the final spread range of rumors decreases and finally decreases to 0.4.

From Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, it can be concluded that the final scale of rumor propagation in complex networks is mainly related to propagation rate λ, immunity rate α, user online rate ε, user state ambiguity β, and user rejection rate θ. We verified that the proposed dynamic rumor propagation model D-WUFPR, which considers the fuzziness of user states and the influence of user nodes, is correct and can be used to control rumor propagation to achieve online public opinion rumor monitoring.

In addition, the simulation results of the number change process of the propagation user, unknown user, and immune user in the D-WUFPR model are shown in Figure 9. We found that rumors follow the following rules when spreading on social networks.

When rumors spread in social networks, the number of communicators in the network gradually increases until it reaches a maximum, and then it gradually decreases until it becomes zero. When the number of communicators in the network decreases to zero, the rumor spread is terminated.

In the process of spreading rumors on social networks, the number of immunized people is zero at first, which then gradually increases as rumors began to spread. The reason for this change is that in the beginning of the process of rumor spreading, there are only unknowns and communicators in the network, and none are immune. Unknown people turn into disseminators after receiving rumors spread by disseminators, while disseminators turn into immune people because they lose interest in rumors in the process of spreading. In addition, some unknown people also turn into immune people directly because they do not believe the rumors. Therefore, the number of immunized people in the network gradually increases from zero to a stable value, at which time rumor spread in the network tends to end.

When rumors spread in social networks, the number of unknowns gradually decreases from the peak and then tends to a stable value, because the unknown users who know nothing about the rumor at first in the network gradually change into fuzzy users, propagating users, or immune users through the user conversion rules on the proposed rumor propagation model. The number of unknown users does not decrease to zero because we considered social networks as dynamic and changing networks. Registered users are not online 24 h a day, so some network users may not be online during the whole process of spreading rumors in the network, so they never know anything about rumors, so the number of unknowns does not decrease to zero at the end of rumor spreading.

3.2. Comparative Analysis

In this subsection, we compare the proposed model D-WUFPR to the existing rumor propagation model of complex networks and the rumor propagation model of uniform networks without considering user weights to verify the advantages of the proposed model over the other models. The comparative experiments mainly focused on a uniform social network with an average node degree k of 20 and a BA scale-free network with a power law distribution P(k) = 2m²k⁻³, where the value of m is 6, which indicates the minimum node degree of the studied network. In addition, the above networks have the same network size of N = 10⁴, the same network average node degree of k = 20 in the initial state, and only one communicator in the initial state network.

As shown in Figure 10, with the increase in the average node degree of users in social networks, the final spread range of rumors gradually increases, and it finally reaches a stable value, approaching 0.52. In the SIHR complex network rumor propagation model considering the forgetting mechanism with the increase in the average node degree of users in the network, the final spread range of rumors gradually increases, and it reaches a stable value, approaching 0.7. We observed that the final spread range of rumors in the proposed D-WUFPR model is smaller than that established by the rumor-spread model considering the forgetting mechanism, which shows that the proposed model can be used to more effectively control the final spread range of rumors. In this group of experiments, we compared the proposed D-WUFPR rumor propagation model with the existing SIHR rumor propagation model, which propagates on uniform networks and considers the influence and authority of user nodes. To prove the necessity of proposing a new rumor propagation model based on user weights, we compared the rumor propagation range in the network with the increase in the average user nodes in the network when the two rumor propagation models simulate the spread of rumors.

Figure 11 compares the D-WUFPR rumor dynamic propagation model and SIHR model in terms of the change in the rumor final propagation range with the change in the user average node degree k, in which the horizontal axis of the image represents the user average node degree in complex networks and the vertical axis represents the final range of rumor propagation. Figure 11 shows that the final rumor propagation range described by the D-WUFPR model is smaller than that by the SIHR rumor propagation model, which does not consider the influence and authority of user nodes in complex networks. This shows that the weight of user nodes in the network can more effectively describe the rumor propagation process in complex networks, and the model proposed in this paper can be more effectively used to control the size of the final rumor propagation range. Therefore, we proved that this model is effective and more effective than the SIHR rumor propagation model, which does not consider the influence and authority of user nodes in complex networks. When the average node degree of users increases, it can be more effectively used to control the final spread range of rumors.

4. Conclusions

As one of the factors affecting audit credibility, network public opinion is one of the most important, especially if the opinion is later falsified. Based on this, we studied the rumor communication mechanism and constructed a new rumor communication model, D-WUFPR, on the basis of the traditional infectious disease communication model. Considering the dynamic and variability of complex networks, the user online rate in the model was increased to represent the ratio of online users to the total number of network users in the process of real-time rumor spreading. The model also considered the fuzziness of network users’ states in the process of rumor spreading, that is, it was impossible to accurately judge whether each user on the network knows the rumor, who already knows the rumor and will spread it, or who are in the immune state, where they know the rumor but do not believe it. In addition, the proposed D-WUFPR model considered the influence of those with authority and the influence of a single user on the whole network, and thus, user weights were added to the model to express the importance of user nodes in the whole network. Audit institutions should pay close attention to the management of public opinion, avoid public trust crises, and deal with any rumors that damage the credibility of audits in time, so as to maintain the image of audits and the stability of the capital market.

This study only considered the uniform online social network. Future work will further investigate the problems in an online social network that is not uniform. Another future direction is to study other key factors of our dynamic rumor propagation model on audit credibility.