1. Introduction
The world is overflowing with text. This ever-growing resource has the ability to capture thoughts, ideas, and understanding. To extract, connect, and summarize relevant electronic text records has the potential for knowledge discovery and new understandings. One example is the electronic health record which often contains important raw text information regarding a patient as documented by a physician. The electronic health record is increasing rapidly as technology is integrating itself into the patient physician interaction. To be able to deliver information quickly and accurately to a physician can help ease the burden and lesson the mistakes that a primary care physician can make when dealing with the increasing pressure from seeing too many patients in too little time.
The enormous amount of textual data makes it impossible for people to manually undertake the task of processing all the information. Computational techniques must be developed that can overcome the challenges faced by working with a very large set of free-text input. This work presents approaches that seek knowledge discovery from a large input of text documents. We focus on the task of summarizing corpora to provide a set of topics describing the general themes.
The task of extracting topics comprises the field topic modeling. In this domain different approaches exist with similar aims. Matrix-based approaches such as latent semantic analysis (LSA) may be used to reduce dimensionality of corpus and highlight more important words [
1]. A more Bayesian technique involves assuming a generative model over the corpus and then discovering the component of the generative model through Bayesian inference [
2]. More recently, the focus shifted towards deep learning-based approaches which seek to use neural networks for topic discovery. Undoubtedly combinations of these subdomains will yield improved results over running any model in isolation [
3]. For the desiderata of using topic models to convey information to an application, it is paramount that the topics be interpretable and helpful if the topics are labeled.
Although lately topic modeling research seems to be directed towards neural topic modeling (NTM) [
4,
5,
6], traditional Bayesian-based topic models (BTM) offer a viable alternative to deep learning approaches. Bayes approaches may be preferable when (1) using commodity or legacy hardware, as the NTM often requires a more complex setup (such as utilizing a graphics processing unit [GPU]), (2) a document-to-topic (
) distribution is needed, since for the NTM,
is often associated with a batch parameter and reused for multiple documents [
4,
5,
6], and (3) for more interpretable topics [
7,
8] since the high perplexity of the NTM may lead to lower interpretability [
8] and the recent work challenges the goodness of traditional pointwise mutual information (PMI) based interpretability scoring often reported in NTM results [
7,
9]. The latter scoring method [
9] may be the preferred approach to take for estimating interpretability of topic models, however we take direct human-based scoring to be a stronger approach to evaluate interpretability.
The traditional probabilistic topic model outputs a distribution of numeric topics for each document and a distribution of words for each numeric topic [
2]. These latter distributions comprise the “topics” in topic modeling. As such, a “topic” is just a distribution over words with a numeric label. However, the numeric label fails to summarize the distribution semantically. Semantically labeling each topic gives the end user a quick understanding of what each topic represents, improving the interpretability [
10]. These labels can also be used in downstream processes such as graph-based summarization systems [
11,
12], consensus building [
13] and scene identification [
14]. However, assigning an accurate label to a topic is no trivial task.
To assign semantic labels to topics, one can run an unsupervised topic model and then choose labels after inference [
15,
16,
17,
18,
19,
20,
21]. However, this can lead to problems with the topics themselves as the clusters tend to combine two or more semantically different topics [
10]. For example (Adapted from [
10] with permission), suppose a news corpus that consists of two articles is given by documents
and
each with three words:
| —pencil, pencil, umpire |
| —ruler, ruler, baseball |
Latent Dirichlet allocation (LDA) [
2], with the traditionally used collapsed Gibbs sampler, standard hyperparameters and the number of topics (
K) set as two, would output different results for different runs due to the inherent stochastic nature. It is possible to obtain the following result of topic assignments:
| —, , |
| —, , |
But these assignments to topics differs from the ideal solution that involves knowing the context of the topics in which these words come from. If the topic modeling was to incorporate prior knowledge about the topics “School Supplies” and “Baseball”, then a topic modeling process will more likely generate the ideal topic assignments of:
| —, , |
| —, , |
and assign a label of “School Supplies” to topic 1 and “Baseball” to topic 2.
A second approach to semantic topic labeling involves using a supervised input set and showed the ability to label the topic as necessary [
22,
23,
24,
25]. This approach requires many labeled input that may be time-consuming or expensive to acquire. To allow for a labeled input set that is easier to obtain, semisupervised topic models [
10,
26,
27,
28,
29] use existing knowledge sources as semisupervised input to label topics. The knowledge sources consist of articles turned into distributions and can be transformed into knowledge source topics (
). Any generative model which utilizes
is dependent on a subset of labeled data, and thus we refer to this type of topic modeling as semisupervised topic modeling. To further illustrate the concepts of the knowledge source and semisupervised topic modeling, consider the following simple example. At the time of this writing, if we open a web browser and go to Wikipedia (
https://en.wikipedia.org/w/index.php?title=Grape&oldid=908871054, accessed on 1 December 2021) and search for “grape”, the returned article (
) would start with the following text:
A grape is a fruit, botanically…
If we take the above to be the full article, then the knowledge source topic () for “grape” can be formed by taking a count of each word () in the article and dividing each word by the total number of words. For the “grape” example, the knowledge source topic is the probability vector with the index of the probability vector mapped to the word vector .
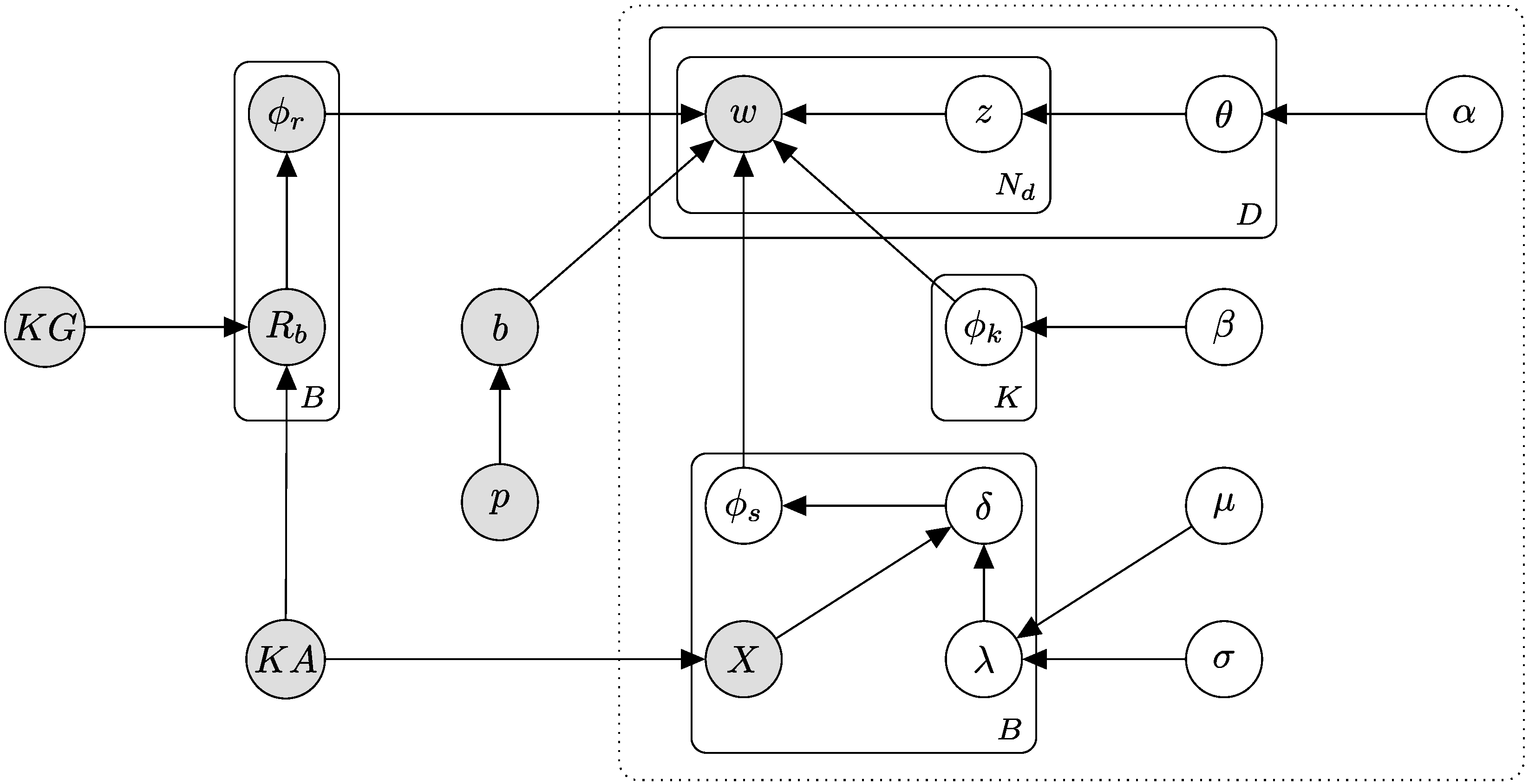
If we continue the above for a set of articles from Wikipedia, the set of articles becomes the knowledge source (). We follow the above procedure from theknowledge source to get a set of knowledge source topics. These knowledge source topics are then used in the corpus’s theoretical generative model. During inference, the topic model takes as input a set of knowledge source topics that may or may not be used in the final output of topics. Because the output is dependent on a subset of labeled data, we refer to this type of topic modeling as semisupervised topic modeling. One drawback of semisupervised topic modeling is the excess knowledge source topics used as input. Since there is a more relaxed constraint of not needing to know precisely which knowledge source topics are relevant to a corpus, there tend to be many knowledge source topics ultimately discarded. Existing approaches used to determine which topic to discard are based on counting or some form of clustering. However, counting is problematic because it is too simple and often discards importantknowledge source topics due to not having a high count. In this context, we take important topics to be topics which are used in the generative model of the corpus. Even worse is clustering, which only considers some distance metric between the topics and does not consider how many assignments of words were made to the topic. We illustrate these concepts using a simple case study.
1.1. Case Study
We are given the task of labeling patient notes from a small set of electronic health records. Given that we know we are in the medical domain, we suppose all possible and relevant topics for any patient note to be in the following set:
| —cancer, cancer, tumor, chemotherapy |
| —heart attack, heart, attack chest |
| —dementia, brain, memory, dementia |
| —diabetes, blood, sugar, insulin |
Next, we wish to obtain topics and corresponding labels for a corpus of two documents
and
, given as:
| —cancer, chest, attack |
| —tumor, heart, chemotherapy |
A good semisupervised topic model would start by considering the entire knowledge source of
but would eventually end up with document-token to topic assignments of:
| —, , |
| —, , |
With topic 1 (after the topic model interference is complete) mapped to and topic 2 mapped to . Since and are referenced in the final document-token assignment, we consider these relevant or important topics. Additionally, since and were not referenced by any document-token assignment to topic, we delegate these to be discarded topics.
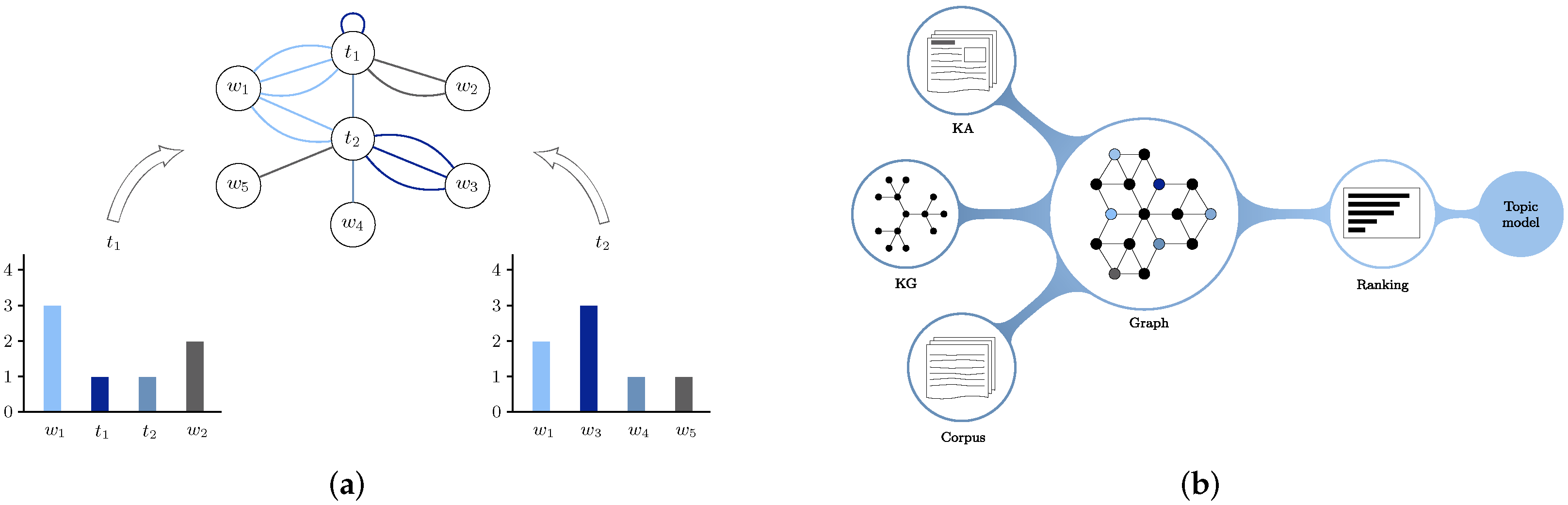
It is essential for the semisupervised topic model to determine which topics are relevant and which topics to discard. What is needed is some way to rank the topics by order of importance to a corpus. A better ranking of topics can select the relevant topics and discard the less important ones. Counting can be used for ranking, but this leads to the problems discussed previously. One method for ranking which has already shown promising results is PageRank [
30]. PageRank finds the importance of a node by considering the importance of the connecting neighbors in a recursive fashion. This approach helps determine the importance of websites in the world wide web.
With the success of PageRank in the world wide web, it is a natural approach to apply the techniques of PageRank to other ranking problems, such as the ranking of article-topics. The main obstacle of using PageRank for knowledge source rankings is representing the knowledge source as a graph consisting of nodes and edges. In most cases, a knowledge source consists of a collection of articles, i.e., Wikipedia articles corresponding to MedlinePlus (
https://www.nlm.nih.gov/medlineplus/ (accessed on 1 December 2021)) headings. However, there are knowledge sources that already take the form of a graph, such as the Unified Medical Language System (UMLS) (
https://www.nlm.nih.gov/research/umls/ (accessed on 1 December 2021)). Ontologies and other compendia exist that take the form of entities as nodes and relationships among entities as edges. For these cases we still need to determine a way to effectively rank the nodes and edges which is applicable in the context of semisupervised topic modeling.
Still, with the desiderata to increase applicability, we must consider how to rank existing article-based knowledge sources. This paper presents a novel way to aid topic models that already have a knowledge source associated with the corpus. Our technique applies to both graph-based and article-based knowledge sources. When we have both a graph and article-based knowledge source, we can take the topic labels from the article headings and emphasize these nodes in the graph-based knowledge source. When comparing the results after ranking, we can select the subset of nodes corresponding to article labels. We also formulate similar approaches for article-only and graph-only knowledge sources.
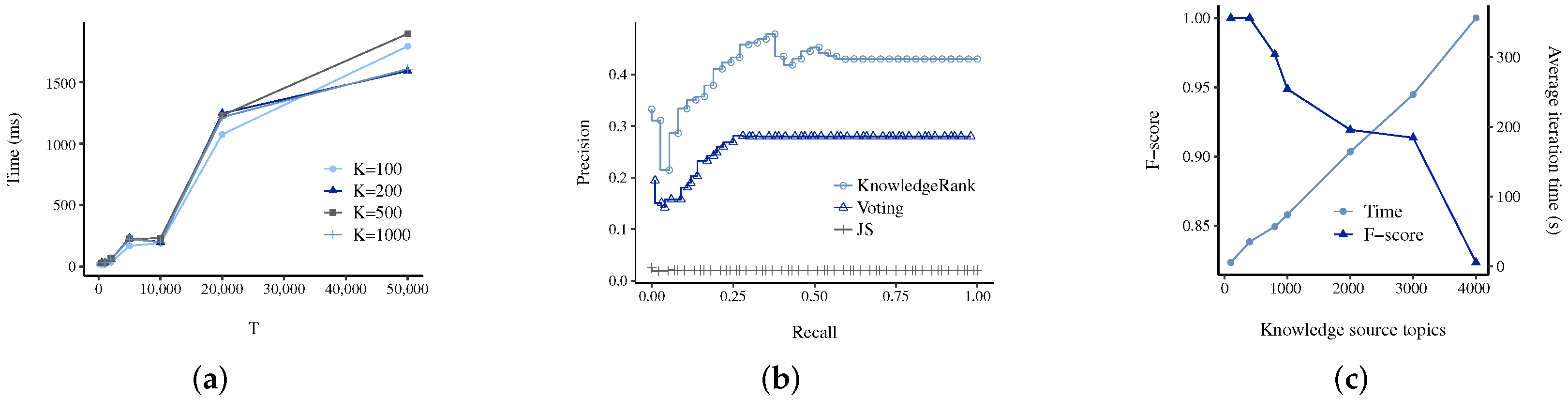
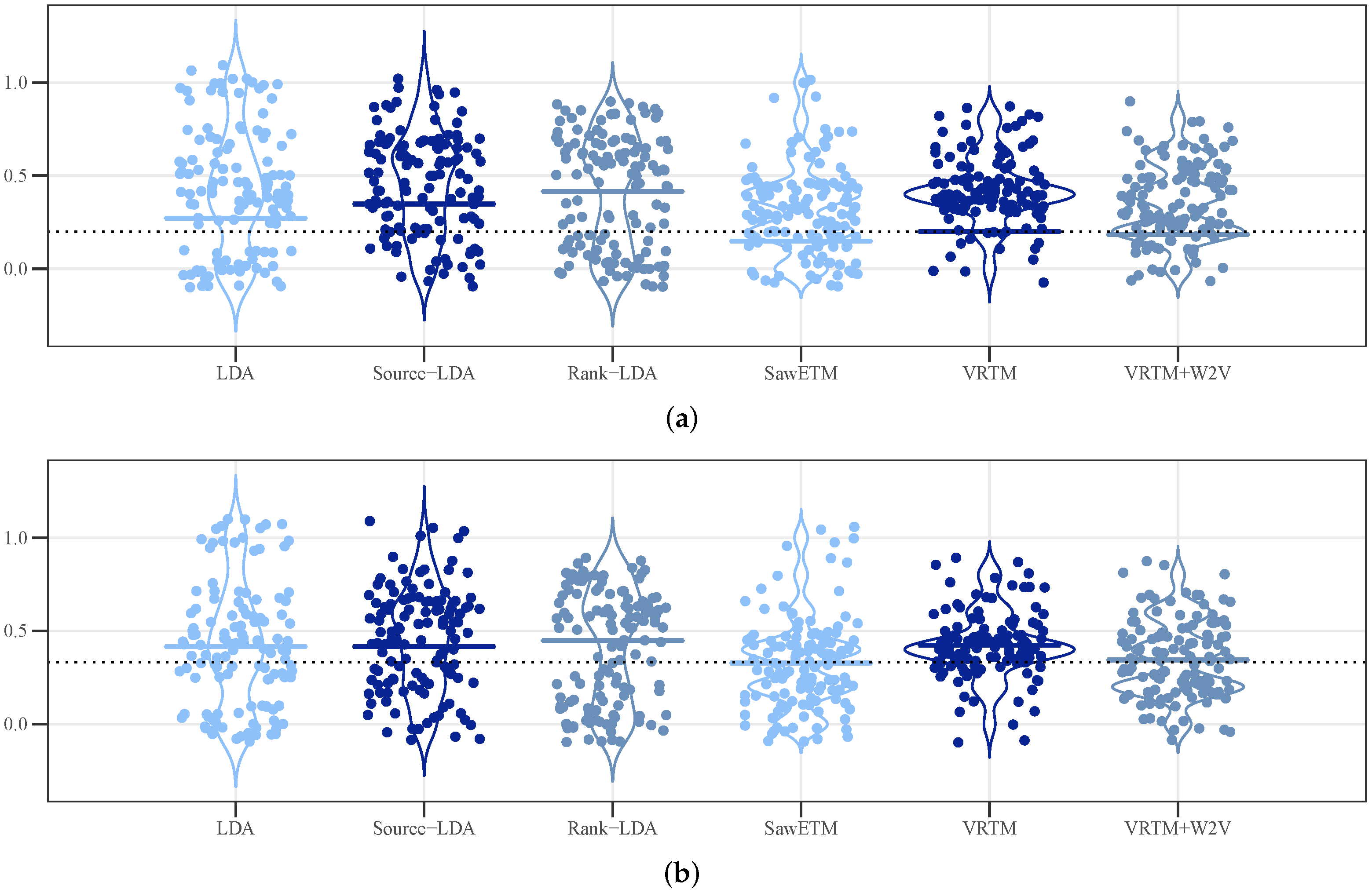
As we show in the results section, knowledge source rankings represent a significant improvement over counting for determining which topics to discard. However, even with a perfect partitioning of important and discarded topics, we are still limited in the amount of curated knowledge we can add into the semisupervised topic model [
10]. At a knowledge source size of just 1000 article-topics, the inference iteration times become too high to be practical [
10]. To further improve the applicability of our model, we aim to allow any input knowledge source regardless of size. Our solution is to rank the article-topics using our ranking method preinference and filter out low scoring article-topics. We can then input the filtered knowledge source into the semisupervised topic model and proceed as usual.
Knowledge source rankings are not only limited to preprocess filtering. The rankings are also applicable during topic modeling inference to help existing semisupervised algorithms determine which topics should be removed. We can also use knowledge source rankings in a stand-alone topic model or in the generative model alongside existing semisupervised topic models.
The intuition behind our ranking approach is like that of TextRank [
31]. This established method ranks sentences in a document to determine a sentence used to summarize the document. Similarly, and with some modifications, we should be able to develop a technique to determine a ranking of article-topics relevant to a corpus. Additionally, knowledge source preprocess filtering has already been shown to improve text-related tasks [
32]; and knowledge sources rankings utilize a graph representation to incorporate outside information. Similar outside is already established to be helpful in text classification tasks [
33,
34], while graph representations can yield improved results as well [
35].