Abstract
The mixture Rasch model is a popular mixture model for analyzing multivariate binary data. The drawback of this model is that the number of estimated parameters substantially increases with an increasing number of latent classes, which, in turn, hinders the interpretability of model parameters. This article proposes regularized estimation of the mixture Rasch model that imposes some sparsity structure on class-specific item difficulties. We illustrate the feasibility of the proposed modeling approach by means of one simulation study and two simulated case studies.
1. Introduction
In education and psychological science, multivariate data of cognitive test items such as intelligence tests are frequently analyzed. The Rasch model (RM; [1,2,3,4]) is likely the most popular statistical model in applied research for analyzing a vector of random variables of I dichotomous item responses (i.e., for ). The multivariate probability distribution in the RM is given as
where (which is also referred to as the item response function), and denotes the logistic distribution function. Moreover, is the density function of the normal distribution with mean and standard deviation . The latent variable can be thought of as an underlying unidimensional factor that represents multivariate dependencies of the discrete vector . Notably, the normal distribution assumption in the RM could be weakened [5]. The item difficulties represent a nonlinear transformation of proportion correct values of items . Note that an identification constraint in (1) in the estimation of the RM must be imposed. Frequently, the mean is set to zero, or one fixes the mean of item difficulties to zero (i.e., ).
The mixture Rasch model (MRM; [6,7,8]) models a heterogeneous distribution for . In a nutshell, it is assumed that the RM in each of C latent classes and the marginal distribution can be interpreted as a mixture distribution [9]. The distribution of the MRM with C latent classes is given by
where the non-negative mixture probabilities () add to one. The class-specific item difficulties in (2) indicate the difficulty (i.e., some nonlinear transformation of proportion correct values) of item in latent class c. The distributional differences of latent classes are captured in the mean and standard deviation . The MRM can be interpreted as a model in which subjects are allocated into one of the C latent classes. The multivariate relationships in the vector of items can differ across latent classes.
Like in the RM defined in Equation (1), identification constraints in the MRM defined in Equation (2) are required [10]. One can fix all class means to zero or set the mean of item difficulties within each of the classes to zero (i.e., for all ). The latter constraint has the advantage that differences between item parameters across latent classes can be interpreted.
After applying a standardization of class-specific item difficulties such as the above-mentioned mean centering, differences between class-specific item difficulties can be computed. The so-called latent differential item functioning (DIF; [11,12,13]) effects qualitatively describe the distinctive behavior of latent classes at the level of items [14]. Studying these latent DIF effects is an important exploratory step in understanding the differential performance of test takers on items [15].
The MRM has been extended to polytomous item responses [16,17] and more complex item response functions [18,19,20,21,22,23,24]. A disadvantage of the MRM in (2) is that all item difficulties are allowed to differ across classes. In empirical data, some parameters are likely to equal each other. This is the motivation for proposing a regularized mixture Rasch model (RMRM) that presupposes that only a subset of DIF effects differs from zero. Alternatively, to put it differently, subsets of class-specific item parameters are set to be equal to each other in model estimation. This property substantially eases the model interpretation in exploratory research.
The rest of the article is structured as follows. In Section 2, we present the estimation approach for the RMRM. In Section 3, we present a simulation study for two latent classes. In Section 4 and Section 5, we present two simulated case studies that involve two or three latent classes with a particular structure of DIF effects, respectively. Finally, the paper closes with a discussion in Section 6.
2. Regularized Mixture Models
In this section, we present the estimation of the RMRM. Regularized estimation recently became popular in psychometrics, such as item response modeling [25,26], structural equation modeling [27,28], and structured latent class analysis [29,30,31]. The MRM involves C latent classes. The allocation of persons (or subjects) to latent classes is unknown. If it were known, a multiple group RM with known (i.e., manifest) group allocation would result. The investigation of known demographic groups, such as gender or language groups, is an important topic in educational measurement. Moreover, regularization techniques were recently discussed for manifest DIF detection in the RM [32,33,34,35,36,37,38].
The main idea of using regularization techniques (see [39] for an overview) for the MRM is that by subtracting an appropriate penalty term from the log-likelihood function, some simplified structure on DIF effects is imposed. Let denote the matrix of dichotomous item responses. The marginal log-likelihood function in the MRM is given by
In practice, the integration in (3) can be substituted by a summation and evaluating at a finite grid for :
where is a discrete analog of the normal density. The latent class probabilities can be represented by logistically transformed parameters :
and one sets .
Regularization techniques use penalty functions to control the variability in subsets of model parameters. For a scalar parameter x, the lasso penalty is defined as
where is a non-negative regularization parameter. It is known that the lasso penalty induces bias in estimated parameters. To circumvent this issue, the smoothly clipped absolute deviation (SCAD; [40]) penalty has been proposed. It is defined by
with .
2.1. Two Alternative Approaches to Regularizing the Mixture Rasch Model
We can estimate the RMRM in two variants of applying regularization. In the first approach, we use overidentified item parameters and the fused regularization technique [41,42]. Let denote the vector of all class-specific item parameters and the vector of all distribution parameters. The following estimation function H (i.e., the negative of a regularized likelihood function) is minimized
Note that fused regularization (8) penalizes the presence of many nonvanishing item parameter differences . With a regularization parameter , differences in item difficulties are unpenalized. With increasing values of , the penalty contribution in the estimation function H becomes larger. Eventually, with sufficiently large values, item difficulties and are fused; that is, they receive the same estimate.
Moreover, note that sample size N is multiplied with the penalty function in (8). We prefer this choice because optimal values of the regularization parameter are less sample size dependent in this case. Moreover, optimal values can be more easily compared across different sample sizes.
It should be noted that in model estimation, the regularization parameter in (8) has to be fixed. In practice, the regularization parameter also has to be estimated. Hence, the minimization is performed on a grid of values (e.g., ), and the model that is selected is optimal with respect to some criterion. Typical criteria are the cross-validated log-likelihood, the Akaike information criterion (AIC), and the Bayesian information criterion (BIC) [39]. See [43] for model selection for the (nonregularized) MRM.
The second estimation approach relies on the ordinary regularization of latent DIF effects. The latent DIF effects are included by using an overidentified model with common item parameters and latent DIF effects by relying on the decomposition.
Note that the difference in item difficulties for classes c and are given as
Hence, latent DIF effects quantify differences between item difficulties across latent classes after introducing an implicit identification constraint for determining means of latent classes (while fixing ). Using latent DIF effects in the second approach (9) instead of considering the regularization of differences in item difficulties in (8) possesses advantages if the focus of the analysis lies in the detection and assessment of latent DIF effects.
The estimation function based on the decomposition (9) is defined by
where denotes the vector of all common item parameters .
The special case of two latent classes in the MRM requires further attention. In this case, only one DIF effect must be included in the model by relying on the decomposition
In general, fused regularization will impose a bit more structured solutions for more than three latent classes if there are clusters of latent classes with the same DIF effect at the level of each item. In contrast, SCAD regularization (11) only presupposes one item-specific cluster of latent classes with zero DIF effects, and all other DIF effects differ from zero but do not potentially merge into another cluster of latent classes with the same DIF effect. Whether the more general structure of fused regularization is advantageous in Rasch mixture with at least four classes is an empirical question in concrete applications.
2.2. Estimation
The regularized likelihood functions can be optimized using marginal maximum likelihood estimation and the expectation maximization (EM) algorithm [26,31,44]. The EM algorithm alternates between the E-step and the M-step. The E-step computation is identical to the estimation in nonregularized item response models. In the M-step, the maximization of the regularized expected log-likelihood function involving expected counts is carried out. The difference in regularized estimation is that the optimization function becomes nondifferentiable because the SCAD penalty is nondifferentiable. The optimization of nondifferentiable optimization can be performed using gradient descent [39] approaches or by replacing the nondifferentiable optimization functions with differentiable approximating functions [31,42,45,46]. In our experience, the latter approach is quite satisfactory in applications.
As usually encountered in mixture models, the maximum likelihood optimization function is often prone to local optima. Hence, it is recommended to estimate the RMRM with a sufficiently large number of random starting values to ensure that the estimated solution corresponds to the global optimum of the likelihood function (see [47]).
The sketched EM algorithm can be practically implemented in the general estimation function xxirt() in the R package sirt [48]. This function is used in the simulation study and the two case studies in this paper.
2.3. Computation of Standard Errors
The computation of standard errors in regularized ML estimation is an active area of research [39]. In the simulation and case studies in this article, standard errors are computed based on nonparametric bootstrap [49]. The estimated model parameter of interest depends on a data-driven determined regularization parameter that is determined by the AIC or the BIC criterion.
The bootstrap can either determine the optimal regularization parameter or one applies regularized ML using the optimal parameter obtained from the original sample. Typically, the former introduces additional variability. In a preliminary analysis in Simulated Case Study 2, it turned out that the average chosen parameter in bootstrap samples was substantially larger than the regularization parameter from the original sample. For this reason, we only report results of standard errors in bootstrap samples that use the fixed regularization parameter .
Furthermore, it is vital to implement a test of statistical significance for regularized latent DIF effects or differences in class-specific item difficulties. It has been suggested to report the proportion of bootstrap samples in which a regularized DIF effect was estimated equal to zero [39]. Values of that are sufficiently close to zero indicate latent DIF effects that significantly differ from zero.
3. Simulation Study 1: Simulation Study Involving Two Latent Classes
In this section, results from a simulation study of an RMRM with two latent classes are presented.
3.1. Method
The simulated datasets consisted of items with two latent classes that followed an MRM. The class-specific item difficulties were decomposed into common item difficulties and DIF effects according to Equation (12). The common item difficulties of the 20 items had equidistant values between and .
Four out of twenty items had DIF effects that differed from zero. Items 6, 8, and 17 had a positive DIF effect , while item 11 had a negative DIF effect . In the simulation study, the size of the DIF effect was either 0.5 or 1.0.
For identification, the mean of the first latent class was set to zero. The standard deviation of the first latent class was set to 1.0. For the second latent class, and were chosen throughout the simulation. The class probabilities were fixed to and .
Moreover, we varied the sample size N in the simulation. We chose sample sizes of 1000, 2500, and 5000 to cover a range of moderate to large sample sizes.
To avoid label switching issues in estimating the RMRM, we utilized a weak prior distribution on the logistically transformed the second latent class probability (i.e., ). The prior was chosen as the normal distribution , meaning that the second class was the smaller one to avoid label switching issues when estimating the mixture Rasch model. The model parameters (i.e., common item difficulties for ), (i.e., all DIF effects for ), and (i.e., , , , and ) were obtained by minimizing the penalized likelihood function:
In total, 5000 replications were simulated in the 2 (DIF effects) × 3 (sample size) conditions.
The following values of the regularization parameter were chosen in a decreasing order while using the obtained estimates from the previous estimation as starting values: 1.00, 0.95, 0.90, 0.85, 0.80, 0.75, 0.70, 0.65, 0.60, 0.55, 0.50, 0.48, 0.46, 0.44, 0.42, 0.40, 0.38, 0.36, 0.34, 0.32, 0.30, 0.29, 0.28, 0.27, 0.26, 0.25, 0.24, 0.23, 0.22, 0.21, 0.20, 0.19, 0.18, 0.17, 0.16, 0.15, 0.14, 0.13, 0.12, 0.11, 0.10, 0.09, 0.08, 0.07, 0.06, 0.05, 0.04, 0.03, 0.02, 0.01, 0.009, 0.008, 0.007, 0.006, and 0.005. DIF effect estimates were considered as zero if their absolute values did not exceed 0.02. In the Results Section 3.2, we report model estimates for fixed values of 0.05, 0.10, and 0.15, as well as parameter estimates resulting from models with minimum AIC or BIC values. The performance of parameter estimates was assessed by bias and root mean square error (RMSE).
The whole simulation was conducted in the R software [50] using the xxirt() function in the R package sirt [48]. The code for the data simulation and model estimation can be found at https://osf.io/wrs5k/ (accessed on 30 September 2022).
3.2. Results
In Table 1, the average number of detected DIF effects (i.e., estimated to be different from zero) is presented. Four out of twenty items had DIF effects different from zero. Interestingly, the number of detected DIF effects was substantially underestimated if the BIC was used as the regularization parameter selection criterion, except in the condition of large DIF effects of 1 (i.e., ) and a large sample size of with an average of 3.9 detected DIF effects. In particular, model selection based on BIC had worse performance in the case of a small DIF effect of . In contrast, the model estimated with the AIC selection criterion had, on average, 5 to 7 detected DIF effects, which was slightly higher than the number of true DIF effects.

Table 1.
Simulation Study 1: Average number of detected DIF effects .
If the RMRM is estimated with a fixed regularization parameter , the average number of detected DIF effects decreases with increasing sample sizes. Overall, model selection based on AIC might be preferred over BIC if it is more critical not to detect true DIF effects.
Table 2 presents type I error for non-DIF effects (i.e., was zero in the simulated data) and power rates for DIF effects (i.e., had values different from zero). It turned out that type I error rates were relatively high if the AIC was used as the model selection criterion (, ). Type I error rates for the model selection based on BIC ranged between 0.4 and 1.7. These low type I error rates for the BIC criterion come at the price that BIC has very low power for detecting DIF effects if the true DIF effect is small (i.e., ) or in not too large sample sizes (i.e., ). Interestingly, for the smallest sample size of and small DIF effects, type I error rates and power rates were very close to each other (i.e., based on AIC: type I error rate was 30.7 and the power rate was 38.3), but power rates improve in large sample sizes or for large DIF effects.

Table 2.
Simulation Study 1: Average type I error rates for items with no DIF effects and average power rates for items with DIF effects.
Figure 1 displays the optimal regularization parameter as a function of sample size, the size of DIF effects, and the chosen information criterion AIC or BIC. It can be seen that values were generally smaller when based on AIC instead of BIC. Moreover, the optimal regularization parameter decreases with a larger sample size. It is evident that there is substantial variability in the estimated values in repeated samples. It can be seen that the largest value was frequently obtained for BIC (i.e., for a small DIF effect of or ). In this case, all latent DIF effects were regularized.
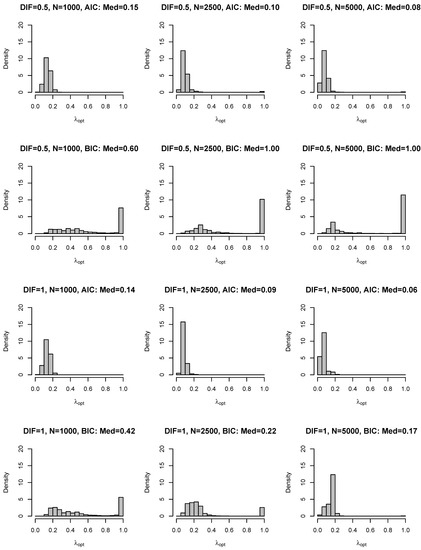
Figure 1.
Simulation Study 1: Empirical histograms of optimal regularization parameters as a function of sample size N, size of DIF effects and the chosen information criterion (i.e., AIC or BIC).
Table 3 displays average absolute biases and RMSE for different parameters or averaged across groups of parameters. In general, bias and RMSE were reduced in larger samples and were smaller in the presence of large DIF effects than for small DIF effects. Interestingly, and in coherence with a statement in [51], bias and RMSE for model parameters can be smaller for a fixed regularization parameter (i.e., for ) compared with model selection based on AIC or BIC. The property of thresholding parameter estimates to zero is helpful in parameter selection (i.e., detecting DIF effects) but has disadvantages for statistical frequentist properties of bias and RMSE. It remains to be investigated whether a noticeable increase in type I error rates for a fixed regularization parameter is of concern in applications of the RMRM. Overall, bias and RMSE were smaller if the model selection was carried out based on AIC instead of BIC.

Table 3.
Simulation Study 1: Average absolute bias (bias) and root mean square error of model parameters.
Table 3 only contains a number of selected values of the regularization parameter . In Figure 2, the RMSE of parameters , , and are displayed and compared with the RMSE based on the optimal regularization parameter obtained from AIC or BIC. It can be seen that small fixed values were competitive with optimal regularization parameters in terms of RMSE. The situation slightly differs for the parameter. For moderate sample sizes or , very large values near to one led to the lowest RMSE values.
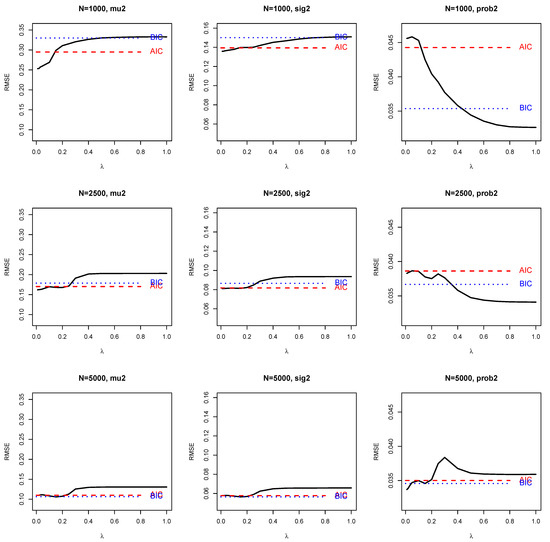
Figure 2.
Simulation Study 1: RMSE for parameters (mu2), (sig2), and (prob2) as a function of a fixed regularization parameter and optimal regularization parameters obtained from AIC or BIC.
Finally, Figure 3 presents the RMSE for parameter groups (parameters “b”), latent DIF effects with a true value of zero (i.e., non-DIF effects; parameters “e_nodif”), and latent DIF effects with a true value different from zero (parameters “e_dif”) for selected values of the regularization parameter . It can be beneficial for item difficulties in terms of RMSE if small fixed values are chosen. Obviously, using a large value for non-DIF effects is advantageous because these parameters would be correctly regularized. However, a large fixed value comes at the price of not detecting true DIF effects. To sum up, these findings illustrate that choosing a fixed value could outperform AIC- or BIC-based regularized estimation if RMSE were the statistical criterion that would drive the estimator choice.
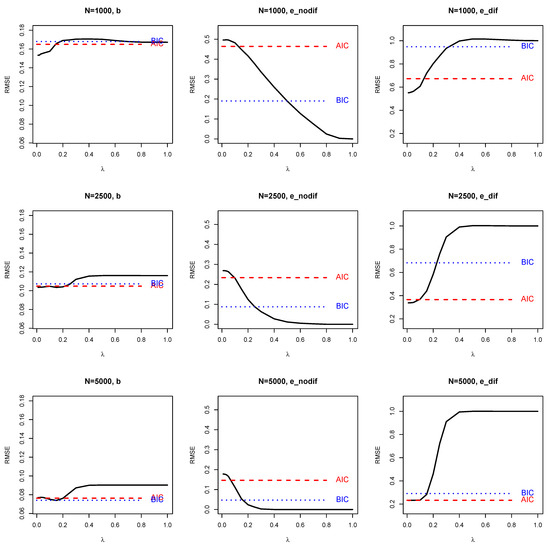
Figure 3.
Simulation Study 1: Average RMSE for parameter groups of item difficulties (b), DIF effects with true values of zero (e_nodif), DIF effects with true values different from zero (e_dif) as a function of a fixed regularization parameter and optimal regularization parameters obtained from AIC or BIC.
4. Simulated Case Study 2: Illustrative Example with a Nonspeeded and a Speeded Latent Class
In a linear fixed administered test, there is a fixed order of test items. Frequently, items at later test positions are prone to position effects; that is, they are difficultly compared with the situation if they were administered at earlier test positions. Similarly, test takers can show a performance decline [52,53,54]. This means that persons show lower performance at the end of the test compared with the beginning of the test. Importantly, the extent of performance decline can vary across persons [55,56].
Performance decline can occur if the test is speeded; that is, not all test takers reach the end of the test due to low item processing, limited testing time, or a lack of motivation. MRMs have been proposed for handling speededness effects [57]. Bolt [57] proposed to use a MRM with two latent classes. The first class refers to the nonspeeded class of test takers, while the second class refers to the speeded class of test takers. The speeded class is typically characterized by increased item difficulties for items at the end of the test [57]. In this simulated case study, we assume two latent classes in the MRM, where the class-specific item difficulties are modeled as
In the simulated dataset, we used item parameters adapted from [57]. The item difficulties are shown in Figure 4 and numerically presented in Table 4. In total, there are 26 test items. Only items 19 to 26 were prone to speeededness effects and had DIF effects larger than zero, while items 1 to 18 had equal item difficulties in the two latent classes (i.e., they had no DIF effects). The nonspeeded class had a class probability of , and the speeded class had a probability . The means of the two classes in the MRM were and , respectively. Hence, the speeded class had a lower ability on average. Moreover, the standard deviations were set to and , respectively.
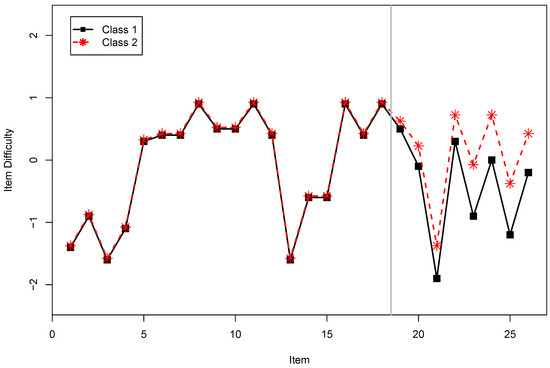
Figure 4.
Simulated Case Study 2: True item difficulties .

Table 4.
Simulated Case Study 2: True and estimated item parameters.
A dataset of a sample size was generated. We estimated an RMRM using the parameterization (14). We used the identification constraint . The regularization parameter was specified on an equidistant grid of values between 0.50 and 0.01 with decrements of 0.01. Replication material and the dataset can be found at https://osf.io/wrs5k/ (accessed on 30 September 2022).
For illustrating standard error computation, we used a nonparametric bootstrap with 500 bootstrap samples. We determined the standard error by using the robust scale parameter median absolute deviation (MAD implemented with the R function stats::mad(); [58]) of bootstrap parameter estimates to diminish the potential effect of outliers.
Figure 5 displays the AIC as a function of increasing values of the regularization parameter . It turned out that provided the least AIC value. Therefore, we report results based on this regularization parameter.
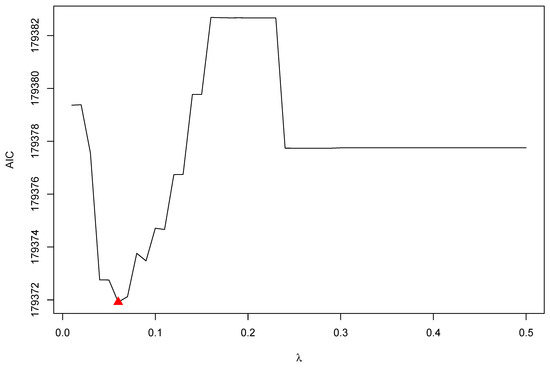
Figure 5.
Simulated Case Study 2: AIC as a function of the regularization parameter . The red triangle corresponds to the optimale value with minimal AIC.
The regularization paths for DIF effects are displayed in Figure 6. With increasing values of , fewer DIF effects were estimated as nonzero. For example, for , only one estimated DIF effect differed from zero.
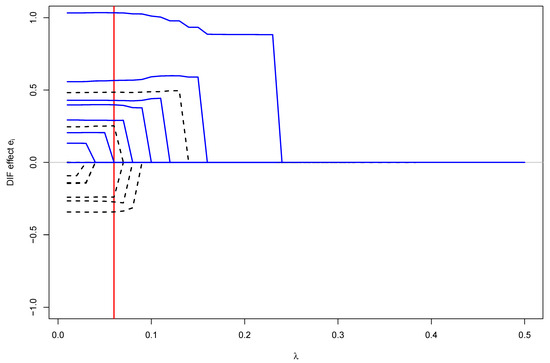
Figure 6.
Simulated Case Study 2: DIF effects as a function of the regularization parameter . Regularization paths for DIF effects are printed in blue solid lines, while paths for non-DIF effects are shown in black dashed lines.
The standard deviation of the first class was estimated as (), which somehow differed from the true value . The second speeded latent class had the following estimated parameters, which closely resembled the data-generating parameters: (, true: ), (, true: ), and (, true: ).
The estimated item parameters are shown in Table 4. It can be seen that for the 8 DIF items, 5 DIF effects were correctly estimated as different from zero, while 3 DIF items had estimated DIF effects of 0. Notably, 5 non-DIF items (i.e., items 12, 13, 14, 17, and 18) had estimated DIF effects different from zero. Overall, the estimated common item difficulties were close to the data-generating values. In accordance with findings in Simulation Study 1, the detection of DIF effects based on the BIC was less satisfactory than based on the AIC. Based on this illustrative study, it turned out that bootstrap probabilities (see Section 2.3) were substantially larger than 0.05 for true latent DIF effects that were estimated as different from zero.
5. Simulated Case Study 3: Illustrative Example Involving Three Latent Classes
In Simulated Case Study 3, we simulate data from an MRM with three latent classes. Bolt [59] presented an application in which sparse DIF effects occur. Figure 7 shows the data-generating item difficulties for the simulated dataset in this Simulated Case Study 3 that were adapted from [59]. It can be seen that many of the class-specific item difficulties were equal to each other. RMRM can be used to effectively estimate Rasch mixtures under some sparsity assumptions of DIF effects.
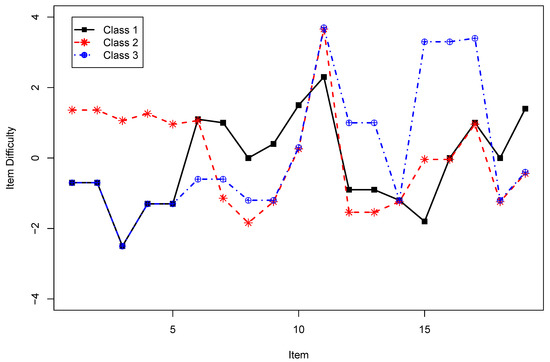
Figure 7.
Simulated Case Study 3: True item difficulties .
The simulated dataset had a sample size and items. The data-generating item parameters can be found in Table 5. The class-specific distribution parameters were , , for Class 1, , , for Class 2, and , , for Class 3.

Table 5.
Simulated Case Study 3: True and estimated item parameters.
We estimated the RMRM in two variants. First, we applied fused regularization to item parameter differences (see Equation (8)). Second, we used SCAD regularization for class-specific DIF effects based on the decomposition (9) and the regularized likelihood function (11). We used the identification constraint in model estimation. Replication material can be found at https://osf.io/wrs5k/ (accessed on 30 September 2022). We did not carry out a bootstrap to compute standard errors because it would require some computational effort, and our primary interests were only interpretational purposes.
The optimal regularization parameter was chosen using the least AIC value. It was for the two estimation approaches. Overall, it turned out that the estimated model parameters were very close in the two estimation approaches. The estimated distribution parameters for fused regularization were , , for Class 1, , , for Class 2, and , , for Class 3. The estimated distribution parameters for SCAD regularization for DIF effects were , , for Class 1, , , for Class 2, and , , for Class 3.
The estimated class-specific item difficulties are displayed in Table 5. It is evident that the pattern of true DIF effects was perfectly detected by fused and SCAD regularization. Moreover, one item (item 3) or two items (items 3 and 19) were detected to possess additional DIF effects that were not simulated for fused and SCAD regularization, respectively. Overall, the item parameter differences between the two estimation approaches were negligible.
6. Discussion
In this article, we proposed a regularized estimation approach of the mixture Rasch model. By putting a regularization penalty on differences in class-specific item difficulties or on latent DIF effects, the interpretability of latent classes in the mixture Rasch model is substantially eased. The regularization technique enables the automatic detection of latent DIF effects and provides a parsimonious model selection.
In the simulation study that involves two latent classes, model selection based on AIC tended to outperform model selection based on BIC. With AIC, there is a tendency to overestimate the number of DIF effects. At the same time, model selection based on BIC substantially underestimates the number of DIF effects. Which of the two criteria should be used in practice depends on the choice of how large type I error rates for non-DIF effects should be tolerated while guaranteeing sufficiently large power rates for the detection of DIF effects. In our view, AIC should be preferred because BIC would result in too many true DIF effects that remain undetected.
We presented two case studies to illustrate the potential of regularized mixture Rasch models. With sufficiently large sample sizes and using AIC for model selection, we successfully recovered the data-generating structure of DIF effects. Our observation that BIC should not be universally preferred over AIC was also confirmed in other research on the mixture Rasch model [43]. Moreover, we could also replicate this finding for other classes of item response models in our research [60].
We limited our simulation study only to sample sizes larger than 1000. Much smaller sample sizes might be interesting in applied research. However, we think that the maximum likelihood estimation of mixture models should involve large sample sizes (say, at least larger than 500) to ensure a sufficiently stable estimation of model parameters. Investigating the limits of applying the regularized mixture Rasch model might be an interesting topic of future research.
The computation of standard errors by nonparametric bootstrap has only been illustrated in Simulated Case Study 2. In future research, different standard error computation methods for estimating regularized mixture Rasch models might be investigated.
As with any newly proposed statistical technique, the future will tell whether the regularization approach can prove helpful in empirical applications. We think that this technique provides a means for obtaining more interpretable and less variable class-specific item parameter estimates. Likely, the regularization approach can also be applied to other classes of mixture latent variable models, such as the two- or three-parameter mixture logistic item response model or factor mixture models.
In conclusion, we believe that regularized mixture Rasch models can be used in exploratory analysis in the same way as nonregularized mixture Rasch models. We recognize the primary potential of regularization in obtaining more structured (and more stable) results if the true class-specific item difficulties follow a sparsity assumption. This assumption might not be realistic in all applications. However, one can at least include the regularized mixture Rasch model in the researcher’s toolbox for analyzing dichotomous item responses.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets can be found at https://osf.io/wrs5k/ (accessed on 30 September 2022).
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
| DIF | differential item functioning |
| EM | expectation maximization |
| MRM | mixture Rasch model |
| RM | Rasch model |
| RMRM | regularized mixture Rasch model |
| RMSE | root mean square error |
| SCAD | smoothly clipped absolute deviation |
References
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Danish Institute for Educational Research: Copenhagen, Denmark, 1960. [Google Scholar]
- von Davier, M. The Rasch model. In Handbook of Item Response Theory, Volume 1: Models; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 31–48. [Google Scholar] [CrossRef]
- Debelak, R.; Strobl, C.; Zeigenfuse, M.D. An Introduction to the Rasch Model with Examples in R; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Robitzsch, A. A comprehensive simulation study of estimation methods for the Rasch model. Stats 2021, 4, 814–836. [Google Scholar] [CrossRef]
- Xu, X.; von Davier, M. Fitting the Structured General Diagnostic Model to NAEP Data; Research Report No. RR-08-28; Educational Testing Service: Princeton, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Rost, J. Rasch models in latent classes: An integration of two approaches to item analysis. Appl. Psychol. Meas. 1990, 14, 271–282. [Google Scholar] [CrossRef]
- von Davier, M.; Rost, J. Mixture distribution item response models. In Handbook of Statistics, Vol. 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 26, pp. 643–661. [Google Scholar] [CrossRef]
- Frick, H.; Strobl, C.; Leisch, F.; Zeileis, A. Flexible Rasch mixture models with package psychomix. J. Stat. Softw. 2012, 48, 1–25. [Google Scholar] [CrossRef]
- von Davier, M. Mixture Distribution Diagnostic Models; (Research Report No. RR-07-32); Educational Testing Service: Princeton, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Paek, I.; Cho, S.J. A note on parameter estimate comparability: Across latent classes in mixture IRT modeling. Appl. Psychol. Meas. 2015, 39, 135–143. [Google Scholar] [CrossRef]
- Bulut, O.; Suh, Y. Detecting multidimensional differential item functioning with the multiple indicators multiple causes model, the item response theory likelihood ratio test, and logistic regression. Front. Educ. 2017, 2, 51. [Google Scholar] [CrossRef]
- Holland, P.W.; Wainer, H. (Eds.) Differential Item Functioning: Theory and Practice; Lawrence Erlbaum: Hillsdale, NJ, USA, 1993. [Google Scholar] [CrossRef]
- Penfield, R.D.; Camilli, G. Differential item functioning and item bias. In Handbook of Statistics, Volume 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 125–167. [Google Scholar] [CrossRef]
- Cho, S.J.; Suh, Y.; Lee, W. An NCME instructional module on latent DIF analysis using mixture item response models. Educ. Meas. 2016, 35, 48–61. [Google Scholar] [CrossRef]
- Frick, H.; Strobl, C.; Zeileis, A. Rasch mixture models for DIF detection: A comparison of old and new score specifications. Educ. Psychol. Meas. 2015, 75, 208–234. [Google Scholar] [CrossRef] [PubMed]
- Rost, J. A logistic mixture distribution model for polychotomous item responses. Br. J. Math. Stat. Psychol. 1991, 44, 75–92. [Google Scholar] [CrossRef]
- von Davier, M.; Rost, J. Polytomous mixed Rasch models. In Rasch Models; Fischer, G.H., Molenaar, I.W., Eds.; Springer: New York, NY, USA, 1995; pp. 371–379. [Google Scholar] [CrossRef]
- Choi, Y.J.; Alexeev, N.; Cohen, A.S. Differential item functioning analysis using a mixture 3-parameter logistic model with a covariate on the TIMSS 2007 mathematics test. Int. J. Test. 2015, 15, 239–253. [Google Scholar] [CrossRef]
- Formann, A.K.; Kohlmann, T. Structural latent class models. Sociol. Methods Res. 1998, 26, 530–565. [Google Scholar] [CrossRef]
- Formann, A.K.; Kohlmann, T. Three-parameter linear logistic latent class analysis. In Applied Latent Class Analysis; Hagenaars, J.A., McCutcheon, A.L., Eds.; Cambridge University Press: Cambridge, UK, 2002; pp. 183–210. [Google Scholar]
- Muthén, B.; Asparouhov, T. Item response mixture modeling: Application to tobacco dependence criteria. Addict. Behav. 2006, 31, 1050–1066. [Google Scholar] [CrossRef] [PubMed]
- Revuelta, J. Estimating the π* goodness of fit index for finite mixtures of item response models. Br. J. Math. Stat. Psychol. 2008, 61, 93–113. [Google Scholar] [CrossRef] [PubMed]
- Sen, S.; Cohen, A.S. Applications of mixture IRT models: A literature review. Meas. Interdiscip. Res. Persp. 2019, 17, 177–191. [Google Scholar] [CrossRef]
- Smit, A.; Kelderman, H.; van der Flier, H. The mixed Birnbaum model: Estimation using collateral information. Methods Psychol. Res. Online 2000, 5, 31–43. [Google Scholar]
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. Robust measurement via a fused latent and graphical item response theory model. Psychometrika 2018, 83, 538–562. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Chen, Y.; Liu, J.; Ying, Z.; Xin, T. Latent variable selection for multidimensional item response theory models via L1 regularization. Psychometrika 2016, 81, 921–939. [Google Scholar] [CrossRef]
- Huang, P.H.; Chen, H.; Weng, L.J. A penalized likelihood method for structural equation modeling. Psychometrika 2017, 82, 329–354. [Google Scholar] [CrossRef]
- Jacobucci, R.; Grimm, K.J.; McArdle, J.J. Regularized structural equation modeling. Struct. Equ. Model. 2016, 23, 555–566. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. Regularized latent class analysis with application in cognitive diagnosis. Psychometrika 2017, 82, 660–692. [Google Scholar] [CrossRef]
- Robitzsch, A.; George, A.C. The R package CDM for diagnostic modeling. In Handbook of Diagnostic Classification Models; von Davier, M., Lee, Y.S., Eds.; Springer: Cham, Switzerland, 2019; pp. 549–572. [Google Scholar] [CrossRef]
- Robitzsch, A. Regularized latent class analysis for polytomous item responses: An application to SPM-LS data. J. Intell. 2020, 8, 30. [Google Scholar] [CrossRef]
- Belzak, W.; Bauer, D.J. Improving the assessment of measurement invariance: Using regularization to select anchor items and identify differential item functioning. Psychol. Methods 2020, 25, 673–690. [Google Scholar] [CrossRef] [PubMed]
- Bauer, D.J.; Belzak, W.C.M.; Cole, V.T. Simplifying the assessment of measurement invariance over multiple background variables: Using regularized moderated nonlinear factor analysis to detect differential item functioning. Struct. Equ. Model. 2020, 27, 43–55. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Li, C.; Xu, G. DIF statistical inference and detection without knowing anchoring items. arXiv 2021, arXiv:2110.11112. [Google Scholar] [CrossRef]
- Gürer, C.; Draxler, C. Penalization approaches in the conditional maximum likelihood and Rasch modelling context. Br. J. Math. Stat. Psychol. 2022. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Jacobucci, R. Regularized structural equation modeling to detect measurement bias: Evaluation of lasso, adaptive lasso, and elastic net. Struct. Equ. Model. 2020, 27, 722–734. [Google Scholar] [CrossRef]
- Tutz, G.; Schauberger, G. A penalty approach to differential item functioning in Rasch models. Psychometrika 2015, 80, 21–43. [Google Scholar] [CrossRef]
- Schauberger, G.; Mair, P. A regularization approach for the detection of differential item functioning in generalized partial credit models. Behav. Res. Methods 2020, 52, 279–294. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical Learning with Sparsity: The Lasso and Generalizations; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Tutz, G.; Gertheiss, J. Regularized regression for categorical data. Stat. Model. 2016, 16, 161–200. [Google Scholar] [CrossRef]
- Sen, S.; Cohen, A.S.; Kim, S.H. Model selection for multilevel mixture Rasch models. Appl. Psychol. Meas. 2019, 43, 272–289. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, J.; Xu, G.; Ying, Z. Statistical analysis of Q-matrix based diagnostic classification models. J. Am. Stat. Assoc. 2015, 110, 850–866. [Google Scholar] [CrossRef]
- Battauz, M. Regularized estimation of the nominal response model. Multivar. Behav. Res. 2020, 55, 811–824. [Google Scholar] [CrossRef] [PubMed]
- Oelker, M.R.; Tutz, G. A uniform framework for the combination of penalties in generalized structured models. Adv. Data Anal. Classif. 2017, 11, 97–120. [Google Scholar] [CrossRef]
- Asparouhov, T.; Muthén, B. Random Starting Values and Multistage Optimization. Technical Report. 2019. Available online: https://bit.ly/3SCLTjt (accessed on 30 September 2022).
- Robitzsch, A. sirt: Supplementary Item Response Theory Models. R Package Version 3.12-66. 2022. Available online: https://CRAN.R-project.org/package=sirt (accessed on 17 May 2022).
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 11 January 2022).
- Liu, X.; Wallin, G.; Chen, Y.; Moustaki, I. Rotation to sparse loadings using Lp losses and related inference problems. arXiv 2022, arXiv:2206.02263. [Google Scholar] [CrossRef]
- Alexandrowicz, R.; Matschinger, H. Estimation of item location effects by means of the generalized logistic regression model: A simulation study and an application. Psychol. Sci. 2008, 50, 64–74. [Google Scholar]
- Jin, K.Y.; Wang, W.C. Item response theory models for performance decline during testing. J. Educ. Meas. 2014, 51, 178–200. [Google Scholar] [CrossRef]
- List, M.K.; Robitzsch, A.; Lüdtke, O.; Köller, O.; Nagy, G. Performance decline in low-stakes educational assessments: Different mixture modeling approaches. Large-Scale Assess. Educ. 2017, 5, 15. [Google Scholar] [CrossRef]
- Debeer, D.; Janssen, R. Modeling item-position effects within an IRT framework. J. Educ. Meas. 2013, 50, 164–185. [Google Scholar] [CrossRef]
- Hartig, J.; Buchholz, J. A multilevel item response model for item position effects and individual persistence. Psych. Test Assess. Model. 2012, 54, 418–431. [Google Scholar]
- Bolt, D.M.; Cohen, A.S.; Wollack, J.A. Item parameter estimation under conditions of test speededness: Application of a mixture Rasch model with ordinal constraints. J. Educ. Meas. 2002, 39, 331–348. [Google Scholar] [CrossRef]
- Maronna, R.A.; Martin, R.D.; Yohai, V.J. Robust Statistics: Theory and Methods; Wiley: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Bolt, D.M.; Kim, J.S.; Blanton, M.; Knuth, E. Applications of item response theory in mathematics education research. J. Res. Math. Educ. 2016, 15, 31–52. [Google Scholar]
- Robitzsch, A. Four-parameter guessing model and related item response models. Preprints 2022, 2022100430. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).