Abstract
Public organizations lack adequate models and methods to efficiently support and manage processes related to information security and IT investments. The objective is to optimize the management of strategic projects planned to improve the information security of a public organization and make efficient use of its available resources. The deductive method and exploratory research were used to review and analyze the available information. A mathematical model resulted that optimizes two objectives: (1) minimizing the costs of the strategic projects to be executed, and (2) maximizing the percentage of improvement in the organization’s information security. According to the result of the simulation, a subset of planned strategic projects was obtained that allows improving the information security of a public organization from 84.64% to 92.20%, considering the budgetary limitations of the organization. It was concluded that the proposed model is efficient, practical and can be a support tool for the IT management of a public organization.
1. Introduction
For the year 2022, Gartner forecasts that global spending on IT will be USD 4.4 trillion, equivalent to 4% more than the previous year [1]. The biggest spending will be on data analytics, cloud computing, customer management and security. Investment and spending on security was 50% more in 2021 than the previous year, justified by the high rates of security incidents and cyberattacks against the networks of organizations [2]. Despite the large investment in security, the efficiency of that spending is unknown. Organizations lack instruments to manage IT activities, mainly information security, to assess the efficient use of resources. IT governance does not solve the problem, and it is necessary to define specific metrics and indicators for each task [3]. Public organizations lack governance systems and efficient management tools to improve information security [4].
There is currently emerging research based on suitable approaches that measure the value of information security investments, but it is still difficult for professionals in the field to identify key and practical approaches that enable the optimization of information security [5]. The need to use models and optimization methods for the resolution of computer and economic security problems in a company is fundamental [6]. Organizational managers lack structured cost-benefit methods for evaluating IT security solutions [7]. Providing security and privacy must be in accordance with the limitations of the organization. The most important limitations are economic issues, and a useful scheme must consider all of these requirements [8]. A strategic planning approach is necessary to make strategic decisions about IT implementation to improve the efficiency and performance of solutions [9].
The ISO 27004 standard established a methodology that allows organizations to measure the effectiveness of the ISMS and the controls applied, but it does not determine what the specific metrics and results are, because each ISMS has a specific context and specific objectives [10]. Fundamentally, a strategic vision of information technology for organizations must be competitive and have decision support models and tools that allow the correct choice and prioritization of projects based on criteria and limitations of the organization [11]. Organizations manage a portfolio of projects that are often interconnected and share common resources, seeking to maximize the overall value generated [12]. It is important to prioritize projects in the organization to manage the use of IT investments, implementing a prioritization model to maximize profits using minimal resources [13]. Integrated decision-making about the selection and scheduling of a project portfolio can lead to a more desirable performance [14]. Organizations use IT governance to achieve their strategic goals, and one of the best practices is IT project portfolio implementation [15].
Why is it necessary to optimize the management of strategic projects using genetic algorithms in a Public Organization?
It is necessary to optimize the management of planned strategic projects to improve the information security of a public organization because the resources are limited. Generally, the allocated budget is not enough to guarantee that the organization can face all the risks and vulnerabilities that it faces in the present. For this reason, the management of strategic projects that guarantee confidentiality, integrity, and availability of information with the available resources becomes critical.
The objective was to optimize the management of strategic projects using genetic algorithms in a Public Organization.
The deductive method and exploratory analysis were used to review models and criteria that allow optimization of multiple objectives in problems related to information security management. A mathematical optimization model was proposed for the management of strategic projects planned to improve the information security of a public organization, which was implemented using the genetic algorithm based on NSGA-II with the Python programming language, and a simulation was carried out choosing a scenario originated with data from strategic projects planned to improve the information security of a public organization.
The following results were obtained: A general business architecture framework for a public organization; a mathematical optimization model for the management of strategic projects planned to improve the information security of a public organization based on a problem of multi-objective optimization; an algorithm based on NSGA-II to apply the proposed optimization mathematical model; and the application of the algorithm in Python language tested with data from a scenario created with information from a public organization, where the validity of the proposed model was verified.
It is concluded that the proposed optimization model for the management of planned strategic projects makes it possible to efficiently improve the information security of a Public Organization considering its budget limitations. In addition, it is very easy to implement, very practical and can be a powerful decision-making tool for an organization’s IT management.
2. Materials and Methods
2.1. Materials
2.1.1. IT Enterprise Architecture
Organizations must adopt a business architecture as the reference framework to optimize their processes to align all their resources with the mission, vision, strategies, objectives and organizational needs; and allows continuous improvement based on the knowledge of the organization, considering the beneficial effects of aligning the business with information systems and technologies [16,17].
Most enterprise IT architectures are based on strategic planning and the four dimensions of the TOGAF framework [16,17,18,19]. Some key factors that support enterprise architecture should be considered, such as strategic alignment and IT governance [20,21], the technological culture of the organization’s staff, efficient communication channels between business and technology specialists, managerial skills of the IT director [20,22], user satisfaction [23] and the efficiency in enterprise architecture project portfolio management [24].
Organizations must have a strategic perspective of information technologies. It is essential for organizations to be competitive, as well as have decision support models and tools that allow the correct selection and prioritization of projects based on the criteria and limitations of the organization [25]. Organizations manage a set of projects that are generally interconnected and compete for common resources, always seeking the highest profitability with the least use of resources [26]. Integrated decision-making on the management of a set of projects results in a better performance of the organization’s resources [27]. Based on these criteria, we can say that in order to meet their planned objectives, organizations need a strategic perspective, the adoption of a business architecture accompanied by the best IT governance practices and the implementation of efficient project portfolio management for success.
Figure 1 shows the proposed framework for a public organization, where we can highlight the efficient management of the project portfolio as a key factor.
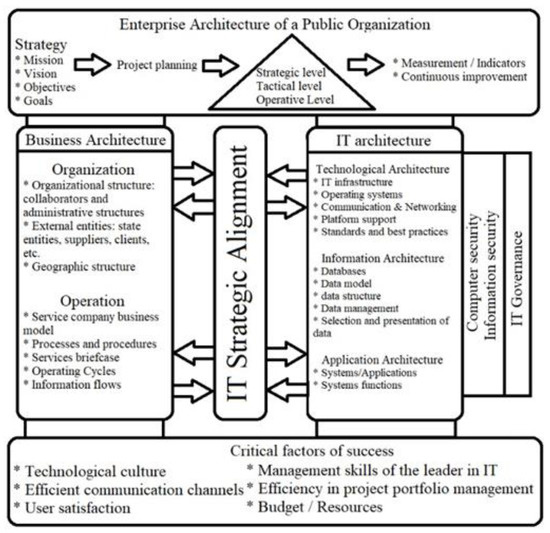
Figure 1.
Enterprise architecture of a Public Organization.
2.1.2. Project Portfolio Optimization
Various projects are generated in organizations to achieve the strategic objectives outlined by senior management and others derived from unplanned situations, which must be carried out to meet some need of the organization. The problem of selecting and scheduling a subset of projects is a complex and challenging task faced by many organizations, with budget constraints limiting the number of projects that can be selected [28,29]. In the literature, we found some methods and solutions for the prioritization of projects applied in different areas, each one with its own strengths and limitations. Researchers have identified the main advances, trends and approaches of the different scientific communities for the management and optimization of project portfolios [30,31]. They have proposed a solution for selecting the most appropriate portfolio based on the organizational resilience strategy [32,33]. They have used decision models to optimize project portfolio selection [34,35,36,37,38,39]. They have proposed an optimization model for the project portfolio selection and scheduling problem, with a personalized heuristic approach, which was improved with meta-heuristic approaches [40]. They have proposed evolutionary computation for the selection and programming of project portfolios [29,41,42,43]. The authors of [44] proposed a mixed-integer programming model for project portfolio selection and scheduling considering the resource management, cash flow, cost of delay and robustness of multiple projects [44]. The authors of [45] produced a mathematical model based on commitment scheduling and fuzzy overshooting to help decisionmakers analyze multi-criteria project portfolios quickly [45]. The authors of [46] proposed a method based on the theory of complex networks to select a robust project portfolio under strategic objectives [46]. The authors of [47] proposed a dynamic modeling of resource allocation for project management applying two strategies, static and dynamic [47]. The authors of [48] proposed a project portfolio selection method considering uncertainty through fuzzy classification based on stochastic dominance [48]. The authors of [49] proposed models and algorithms using machine learning in project portfolio management [49]. The authors of [50] developed a portfolio selection and scheduling problem formulation inspired by the Future Defense Force Design process and used genetic algorithms to simulate testing [50]. The authors of [51] exposed a mixed-integer nonlinear programming model based on the goal programming approach [51]. The authors of [52] proposed a project portfolio selection method using decision rounds with multi-criteria analysis, mathematical programming and the Monte Carlo simulation within the framework of the Iterative Trichotomic Approach [52]. The authors of [53] presented a mathematical programming model for optimal project portfolio management using a risk-adjusted net present value approach [53].
From the review of the literature, there are no published approaches that have addressed the full complexity of the project portfolio selection and scheduling problem to improve information security in public organizations. We can determine that there is a tendency to pose the problems of selection and programming of project portfolio and other applications as a multi-objective optimization scheme. In these problems, multiple objectives must be optimized simultaneously considering their criteria and constraints, resulting in a set of optimal solutions. For the present work, we used the non-dominated classification genetic algorithm NSGA-II because it is a classic algorithm, which is widely tested and used in multi-objective optimization applications.
2.1.3. Multi-Objective Optimization Problems
Most studies have focused on developing and applying variants using evolutionary algorithms because they solve the multi-objective optimization problem efficiently and practically. Currently, computational intelligence approaches have been widely used in the field of information security and have achieved good results. Research is advancing to generate, run and implement combinations of evolutionary algorithms to solve a variety of optimization problems [54]. More and more scenarios of organizations require information security. Therefore, it is necessary to develop more advanced computational intelligence approaches and techniques [55]. The authors of [56] presented = a general framework for solving large-scale MOP based on the NSGA-II algorithm [56]. The authors of [57] provided the analysis of the ant colony algorithm and Holland’s genetic algorithm, in which different laws of probability distribution of chromosomal mutations were used [57]. The authors of [58] proposed the Point-Weighted Prediction Method (WPPM) for dynamic multi-objective optimization (DMO) to predict the Pareto optimal set and to initialize the population with the appropriate diversity [58]. The authors of [59] presented an ICSBP algorithm to overcome the shortcomings of traditional neural networks, which was used as part of the information security risk assessment (ISRA) processes for a miniature IoT system [59]. The authors of [60] proposed an application model of the genetic algorithm (GA) to solve the multicriteria optimization problem in the distribution of resources destined to the cybersecurity of the protected object with the Bellman-Zade principle [60]. The authors of [61] developed an information security risk assessment model based on the GA and BP neural network to establish an information security risk assessment model [61]. The authors of [62] evaluated the performance of a restricted version of the non-dominated classification genetic algorithm 2 (NSGA II), a multi-objective evolutionary optimization algorithm, written in MATLAB [62]. The authors of [63] developed a multi-objective mathematical programming model for time-cost-quality trade-off scheduling problems in construction projects, applying three metaheuristic algorithms: the multi-objective gray wolf optimizer (MOGWO), the non-dominated genetic classification algorithm (NSGA- II) and multi-objective particle swarm optimization (MOPSO) [63]. A variety of investigations that have combined various techniques using the NSGA-II genetic algorithm, or by modifying the NSGA-II algorithm to obtain higher efficiency and better solutions [64,65,66,67,68,69]. Some works have proposed an improved multi-objective genetic algorithm, comparing it with other algorithms such as the NSGA-II to measure its effectiveness [8,70,71].
2.1.4. Criteria Used for Multi-Objective Optimization
We can categorize the most used criteria in information security optimization problems in economic criteria and technical criteria for effectiveness [8,60,72,73,74,75,76]. Other authors have used cost-benefit criteria [5,6,7,77,78]. They have also used examples of benefits, such as cost reduction, income and economic efficiency; and examples of cost, such as operating cost, opportunity cost, switching cost and total costs. Criteria widely used in this field of information security are: the threat as probability of threats, efficiency of attackers, possibility of risk; impact criteria, such as potential damage; vulnerability criteria, such as exposure factor and risk factor [5,6,59,79]. Other categories used are resources, such as fixed budgets, asset values or attacker resources; and functions as decision trees, mitigation quality parameters and fuzzy numbers [5]. The criterion considered in this work is the Information Security Management Capacity (CGSI), which considers five factors: strategic, resources and capacities, organization/management, continuous improvement and the local context, national and international. Once the five factors have been evaluated, the organization can be classified within five levels: initial, formative, managed, strategic and optimized, which is the maximum level that an organization must reach [80].
2.1.5. Multi-Objective Algorithm Metrics
There are many performance indicators to measure the quality of the Pareto front approximations produced, which allows the comparison and analysis of the results of different algorithms. Performance indicators are categorized into four groups according to their properties: cardinality, convergence, distribution and dispersion [81,82,83]. In the present work, we only mention a few indicators that found in the literature: The hypervolume indicator and the hyperarea difference are good measures of dominance and distribution properties and do not require knowledge of the Pareto front [84,85,86]; a widely used indicator to compare multi-objective algorithms is the computational time or CPU time in seconds used to execute the algorithm— the shorter the time, the better [63,87]; the number of points in the approximate front or number of non-dominated solutions are considered quality measures of the algorithms [82,88]; the Karush-Kuhn-Tucker Proximity Measure (KKTPM) [64,66]; and the non-uniformity of the solutions obtained in front of Pareto, which is measured by SPREAD [64]. Regarding the convergence metrics, the generational distance and the Inverse Generational Distance are widely used [64,82].
2.1.6. Criteria for Classifying and Prioritizing Cybersecurity Projects
There are multiple criteria to classify and prioritize cybersecurity projects which depend on each organization. These criteria are important to achieve strategic objectives. In Table 1, we can observe the most used criteria to classify and prioritize cybersecurity projects found in the literature and in the practice of public organizations.

Table 1.
Criteria for classifying and prioritizing projects.
2.2. Methods
To carry out this research, the deductive method was used, which involved exploratory research and the review of the information available from official websites, regulations and provisions related to the optimization of projects. To obtain the results, the following activities were carried out.
2.2.1. First Phase
In the first phase, the available information on business architecture models, criteria and variables to consider in an organization was analyzed to propose a general framework for public organizations. Figure 1 shows the general framework of the work proposed.
2.2.2. Second Phase
In the second phase, the information available on the most important criteria and variables related to project planning to improve information security in an organization was analyzed. In addition, the solution alternatives to multi-objective optimization problems were reviewed, as well as the main metrics and quality indicators of the results. With this analysis, we can pose the problem to solve in order to propose improvements in the information security of organizations.
Figure 2 shows the process of planning strategic projects to improve the information security of a Public Organization. The starting point is the analysis of the information security of the Public Organization to determine the current situation. For this, we considered the CGSI Information Security Management Capacity model because it gives importance to strategic planning as a starting point, which traces the route through which the organization efficiently uses all its resources and capabilities in order to preserve the continuity, integrity and availability of information. The analysis serves to highlight deficiencies and limitations in organizations, such as a lack of strategies and objectives, lack of managerial support, lack of a unified vision at all levels of the organization, lack of organizational culture and lack of resources, among others, that were related to the lack of strategic planning [80].
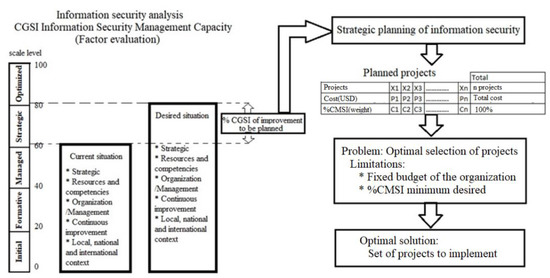
Figure 2.
Strategic project planning process for information security.
Once the current situation of information security is known, the organization proposes the desired situation; for this, a strategic planning is necessary that allows directing the resources and capacities to obtain the proposed objectives from the strategic, tactical and operational, through planned projects. The critical problem to be solved by the IT management is the optimal selection of the projects that the organization must implement considering the economic criterion that has a fixed budget that is less than the total budget of all the planned projects. In addition, for the selection of the projects, technical criteria or criteria must be considered in the prioritization of the projects. The list of criteria taken from the literature review can be seen in Table 1.
2.2.3. Third Phase
In the third phase, with the strategic projects planned and the criteria and restrictions of the organization known, a mathematical model was proposed for the optimization of the management of strategic projects to improve the information security of a Public Organization based on the generic model of multi-objective optimization problem (MOP) and through the genetic algorithm NSGA-II, considering that evolutionary computation is of the current trends to efficiently solve this type of problem according to the review of the literature. According to [91], the generic model used, considering the sets of n decision variables, k objective functions and m restrictions, is as follows:
We define x as the decision vector in a decision space X and y as the objective vector in an objective space Y. The problem lies in finding a set of optimal solutions such that one cannot be improved without deteriorating another, which we call a Pareto optimal set.
Once the optimization model has been determined with all the criteria or objectives involved in a public organization, we simplified the model, keeping only two objectives through the cost-benefit concept. According to [6], using the costs of the planned strategic projects and instead of the economic benefit, we used the technical benefit of the improvement in information security that is achieved with the implementation of the chosen projects, considering contribution of the criteria of the initial model. We considered the same weight for all the criteria that contributed to the calculation of the CMSI %. In addition, to standardize its calculation, the percentage relative frequency was used, and then the average of the frequencies of all the criteria was determined.
2.2.4. Fourth Phase
In the fourth phase, a generic algorithm was developed considering the mathematical optimization model proposed in the previous phase. According to [66], the pseudocode of the generic Algorithm 1 is as follows:
| Algorithm 1 NSGA-II |
| 1. Randomly generate the initial population 2. For counter from 1 to (number of generations defined) 3. Assess individuals for all target values 4. Non-dominated classification based on Pareto dominance 5. Generates non-dominated front sets 6. Selection by Tournament 7. Crossing 8. Mutation 9. Create the next generation of individuals 10. End For |
We chose the genetic algorithm using NSGA-II because it is one of the main multi-objective optimization methods which is widely applied, and its Pareto-based approach makes it suitable for optimization problems with few objectives. NSGA-II has been proven to be effective for two-objective functions in portfolio selection problems [66]. Simulations have shown that NSGA-II is able, for most problems, to find a much better distribution of solutions and better convergence near the true Pareto optimal front compared to other algorithms [68].
2.2.5. Fifth Phase
In the fifth phase, for the experimentation of the proposed model, the algorithm was implemented in the Python programming language to perform a simulation and obtain results to analyze the quality and robustness of the solutions.
Real data were taken from 30 strategic projects planned to improve the security of a distributed database of a public organization in order to create several test scenarios, one of which was taken to present in this investigation. We ran the program 20 times and selected one test scenario at random to display the results.
Table 2 shows data from 30 planned projects with the required cost in USD and the %CMSI that each project contributes to 100% of the strategic projects planned to improve information security.

Table 2.
List of planned strategic projects.
The parameters of the problem were the budget allocated for the planned projects P = $200,000.00 and the minimum %CMSI expected to be obtained for the planned period. For this simulation, it was E = 80%. We easily analyzed that the problem for the IT administrators of the organization was to implement a set of projects to achieve the highest %CGSI with the assigned budget, since 100% of the planned projects exceeded the budget. For this simulation, it was USD 287,446.00.
Considering the data of the problem in Table 2, the parameters of the problem and the parameters of the genetic algorithm in Table 3. A Pareto front plot was created to show the optimal, non-dominated results of the simulation performed.

Table 3.
Genetic algorithm parameters.
The execution of the algorithm implemented in Python version 3.7 was carried out on a computer with an Intel(R) Core(TM) i3-5005U CPU @ 2.00GHz, with 6.00 GB RAM and a 64-bit operating system.
2.2.6. Sixth Phase
To analyze the relationship between the variables number of planned projects, cost of projects and CMSI%, we created scatterplots and Pearson’s coefficient [92,93,94].
3. Results
3.1. Mathematical Optimization Model
3.1.1. Goal Optimization Model
Given the n decision variables, x = (x1, x2, x3, …, xn), representing all the projects planned to improve the organization’s information security, the model must obtain a subset of projects to execute, which are the optimal solutions. These solutions allow five objectives to be achieved: (1) the minimization of costs, (2) the maximization of origin of fulfillment, (3) the maximization of the profit/effort ratio, (4) the execution time maximization and (5) resource maximization. The five objectives are bounded by the constraints, which make it possible to find the subset of feasible solutions of the problem.
Optimization criteria:
Restrictions:
where
c: the costs required by the projects planned by the organization, ranging from i = 1 to “n” planned projects.
o: the information security improvement assessments added by each project due to the origin of the project’s non-compliance, expressed in percentage terms, of the “n” planned projects.
g: the valuations of the profit/effort ratio of each project, expressed in percentage terms, of the “n” planned projects.
t: the evaluations based on the execution time of each project, expressed in percentage terms, of the “n” planned projects.
r: the assessments of the types of resources required for each project, expressed in percentage terms, of the “n” planned projects.
P: the budget that the organization has allocated to execute the selected projects.
3.1.2. Simplified Cost-Benefit Optimization Model, for the Management of Planned Strategic Projects
Given the model of Formulas (5)–(15), of the five criteria, we can simplify the model using the cost-benefit criterion, where the cost defines the first objective, (1) minimization of the cost of the project, and the benefit defines the second objective, (2) maximization of the improvement of the information security CMSI. The second objective was calculated by means of the average of the four criteria of the previous model: assessment of the origin of the non-compliance, the profit/effort ratio, the execution time and the types of resources. All criteria to calculate the CMSI% had the same weight of 25%, and to standardize its calculation, the percentage relative frequency was used and then the average was determined. The result of the %CMSI calculation can be seen in Table 2.
Optimization criteria:
Restrictions:
where
c: the costs required by the projects planned by the organization, ranging from i = 1 to “n” planned projects.
b: the calculated benefits or the improvement contribution to information security of each planned project (CMSI), expressed in percentage terms, of the “n” planned projects.
P: the budget that the organization has allocated to execute the selected projects.
E: the % of CMSI that the organization expects to obtain from 100% of the n planned projects.
Models (5)–(15) and (16)–(22) meet the conditions to be considered linear programming problems, which can be solved by classical methods such as the simplex algorithm; however, we used genetic algorithms because, according to the literature review carried out, we observed a tendency to use these evolutionary methods as they overcome certain aspects and limitations of linear programming. Genetic algorithms are more efficient than linear programming algorithms [95]. In addition, they are more practical to implement, the solutions are closer to real-world problems and they can take advantage of increased computational processing power.
3.2. Genetic Algorithm Applied to the Optimization Model
The method we chose to solve the optimization problem of planned projects to improve information security for an organization was through the genetic algorithm using NSGA-II, belonging to the group of evolutionary methods that can be used to solve information security problems such as search and optimization. Figure 3 shows the application of the genetic algorithm using NSGA-II, an optimization process in which the individuals of a population of planned projects gradually improve by adapting to their environment. The environment of this evolutionary process is determined by the objective function and its restrictions.
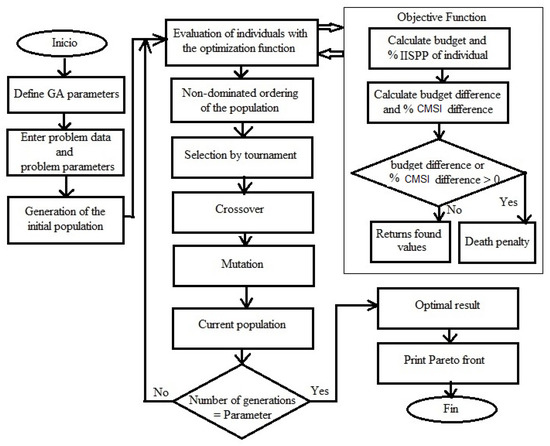
Figure 3.
Algorithm for the simplified optimization model using NSGA-II.
3.3. Experiment and Analysis
The average response time of the execution of the algorithm with the data presented was 25 s, a quite acceptable computational cost, which is an important aspect when implementing practical tools that help in the planning and optimization of the related tasks to information security in organizations.
In this simulation, the average number of solutions in the Pareto Front obtained were 43 different non-dominated ones, which are shown in Figure 4. In Table 4, we can observe the first 10 optimal solutions that meet the budget criteria and %CMSI. The results show solutions with a %CMSI from 84.64% to 92.20, higher than the 80% required, with a budget close to USD 200,000.00. The final decision will depend not only on the highest CMSI% that the set of projects contributes, but also on the number of projects to be executed and other characteristics that the IT management can compare. If the IT management has the ability to influence the senior management to achieve a larger budget, it will be able to find better solutions, which have a CMSI% close to 100%.
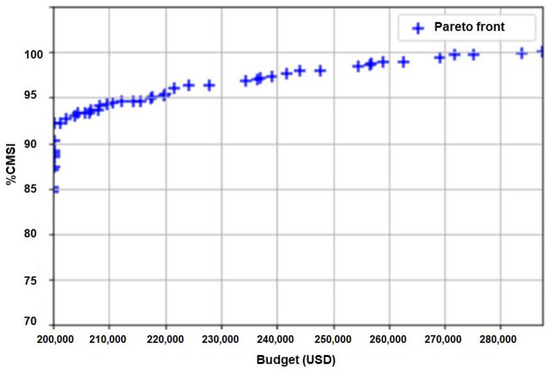
Figure 4.
Pareto Front—optimal solutions.

Table 4.
Top 10 optimal solutions from the Pareto front.
3.4. Variable Correlation Analysis
The correlation matrix in Table 5 shows the Pearson correlation values, which measure the degree of the linear relationship between each pair of variables, as well as the strength and direction of the relationship. All correlations were positive, meaning the two variables tended to increase or decrease at the same time. All variables had correlation values greater than 0.7; therefore, they are considered highly correlated. This correlation is reflected in Figure 4, Figure 5 and Figure 6, which show that the higher the budget, the greater the CMSI%; the higher the budget, the greater the number of projects to be executed; and the higher the CMSI%, the greater the number of projects to be executed.

Table 5.
Pearson correlation matrix.
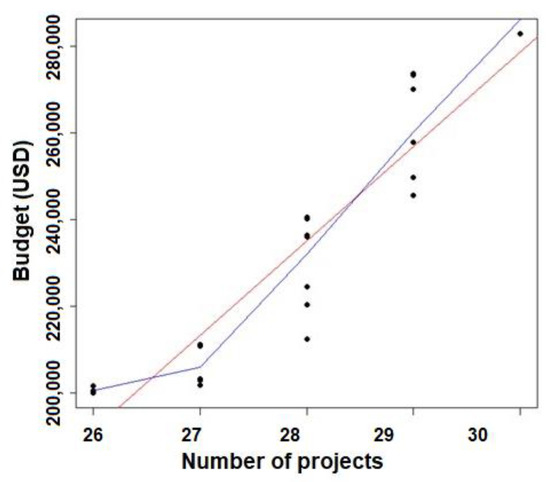
Figure 5.
Scatterplot of the number of projects and budget.
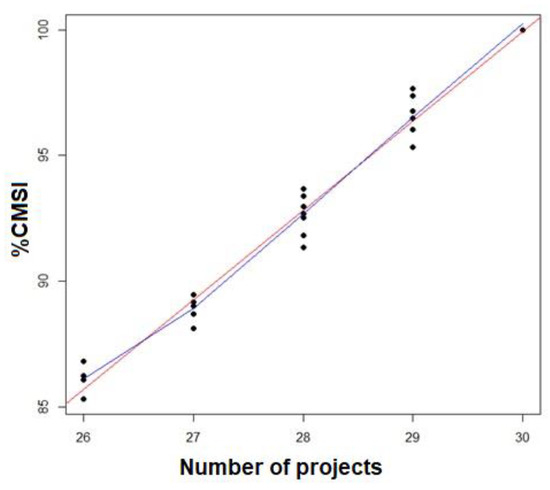
Figure 6.
Scatterplot of number of projects and %CMSI.
4. Discussion
We measured the quality and robustness of the solutions by comparing our results with other heuristic approaches considering metrics and indicators widely used in the literature. The measurements performed in the simulation, such as computation time, convergence, distribution and average number of solutions in the Pareto Front of Figure 4, show that the NSGA-II algorithm is effective for two objectives. We discarded measures that required knowing the real Pareto frontier because it was not feasible for this case.
The results obtained in the simulation demonstrate the quality and robustness of the solutions produced by the mathematical optimization Models (16)–(22) proposed. These results confirm the theoretical and practical arguments of our scientific review on project portfolio selection and scheduling issues, multi-objective optimization problems and evolutionary algorithms such as NSGA-II and decision theory, among others.
The proposed mathematical optimization Models (16)–(22) efficiently ensures the improvement of the information security of a public organization based on a strategic planning that allows directing the available resources and capacities to achieve of the objectives established for the organization; as it is a model that allows the selection of a set of security projects aligned with the strategic management objectives, better results will be achieved when organizations have more resources or higher budgets because the number of projects, the budget and the CMSI% are highly positively correlated variables.
From the review of the literature carried out, we found cases where genetic algorithms were applied both for the critical project portfolio selection problem and other multi-objective optimization problems with results similar to those of this work. The application of genetic algorithms allowed decisionmakers to have a set of optimal, quality solutions in a reasonable time that can be implemented in practical applications such as [43,62,63,64,65,66,68,69,70,71,79,84,88,96]. The proposed model is generic, so it can be implemented in any organization, whether public or private, from any line of business, from any country.
5. Future Work and Conclusions
In the future, we propose the application of the optimization model to a larger set of planned strategic projects of a public organization; it should also include all types of resources that are used in strategic project planning. The comparison must be made with other optimization algorithms, and the NSGA-II must be combined with other Artificial Intelligence methods that make it possible to obtain the solutions more efficiently.
Models (16)–(22) are a multi-objective optimization problem with two opposing criteria: the minimization of project costs and the maximization of the CMSI% of a Public Organization. The simulation carried out allowed us to verify that the model is efficient. We found a set of optimal solutions with a CMSI% from 84.64% to 92.20, which met the organization’s budget.
The mathematical model for optimizing the management of strategic projects planned to improve the information security of a Public Organization can be used as a component in the analysis and strategic planning of the information security of a Public Organization or even any type of organization.
The simulation carried out showed that the proposed model is very easy to implement, very practical and can be a powerful decision-making tool to choose the best solution considering the objectives and limitations of a Public Organization.
Among the benefits for organizations, it is worth mentioning the increase in productivity and the effectiveness of the selection process of strategic projects planned to improve information security, automation of the process, reduction of errors in the process and improvement in decision-making when have a set of optimal solutions for quality.
Author Contributions
Conceptualization, R.R.I.; methodology, R.R.I.; software, R.R.I.; validation, R.R.I.; formal analysis, R.R.I.; investigation, R.R.I.; resources, R.R.I.; writing—original draft preparation, R.R.I.; writing—review and editing, S.M.T.T.; conceptualization, methodology, S.M.T.T.; investigation, S.M.T.T.; supervision, S.M.T.T.; review, S.M.T.T. and L.J.C.M.; methodology, L.J.C.M.; supervision, M.M.B.H.; methodology, M.M.B.H.; supervision, E.Z.G.D.; validation, E.Z.G.D.; investigation, L.E.M.G.; conceptualization, L.E.M.G.; methodology; M.R.M.A.; formal analysis, M.R.M.A.; resources, J.A.O.T.; methodology, J.A.O.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the “Secretaría de Educación Superior, Ciencia, Tecnología e Innovación” (Senescyt).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gartner. Gartner Prevé que el Gasto Mundial en TI Alcanzará los 4,4 Billones de Dólares en 2022. Gartner, Inc. 2022. Available online: https://www.gartner.com/en/newsroom/press-releases/2022-04-06-gartner-forecasts-worldwide-it-spending-to-reach-4-point-four-trillion-in-2022#:~:text=WorldwideITspendingisprojected,researchvicepresidentatGartner (accessed on 22 May 2022).
- Check-Point-Research. Check Point Software’s 2022 Security Report: Global Cyber Pandemic’s Magnitude Revealed. 2022. Available online: https://pages.checkpoint.com/cyber-security-report-2022.html (accessed on 22 May 2022).
- Sönmez, F. A Conceptual Model for a Metric Based Framework for the Monitoring of Information Security Tasks’ Efficiency. Procedia Comput. Sci. 2019, 160, 181–188. [Google Scholar] [CrossRef]
- Masilela, L.; Nel, D. The role of data and information security governance in protecting public sector data and information assets in national government in South Africa. Afr. Public Serv. Deliv. Perform. Rev. 2021, 9, 10. [Google Scholar] [CrossRef]
- Schatz, D.; Bashroush, R. Economic valuation for information security investment: A systematic literature review. Inf. Syst. Front. 2016, 19, 1205–1228. [Google Scholar] [CrossRef]
- Kirenberg, A.; Medvedev, A.; Prokopenko, E. A mathematical model of information security for a mining company. E3S Web Conf. 2020, 174, 04012. [Google Scholar] [CrossRef]
- Arora, A.; Hall, D.; Piato, C.; Ramsey, D.; Telang, R. Measuring the risk-based value of IT security solutions. IT Prof. 2004, 6, 35–42. [Google Scholar] [CrossRef]
- Hashemi, S.M.; He, J.; Basabi, A.E. Multi-objective Optimization for Computer Security and Privacy. Int. J. Netw. Secur. 2017, 19, 394–405. [Google Scholar]
- Zelenkov, Y. Critical regular components of IT strategy: Decision making model and efficiency measurement. J. Manag. Anal. 2015, 2, 95–110. [Google Scholar] [CrossRef]
- ISO/IEC/27004:2016; Information Technology–Security Techniques–Information Security Management–Monitoring, Measurement, Analysis and Evaluation. International Organization for Standardization (ISO): Ginebra, Switzerland, 2016.
- Klakegg, O.J. Project delivery models—Situational or fixed design? CSIT 2017, 2, 202–206. [Google Scholar] [CrossRef]
- Bushuyev, S.; Gaydukova, N.; Bushuyeva, N.; Achkasov, I. Evaluation of the investment projects portfolio efficiency. In Proceedings of the 2021 IEEE 16th International Conference on Computer Sciences and Information Technologies (CSIT), Lviv, Ukraine, 22–25 September 2021. [Google Scholar] [CrossRef]
- Ostakhov, V.; Artykulna, N.; Morozov, V. Analysis of models for IT projects prioritization in telecommunication company portfolio. In Proceedings of the 2018 14th International Conference on Advanced Trends in Radioelecrtronics, Telecommunications and Computer Engineering (TCSET), Slavske, Ukraine, 20–24 February 2018; pp. 245–250. [Google Scholar] [CrossRef]
- Ranjbar, M.; Nasiri, M.M.; Torabi, S.A. Multi-mode project portfolio selection and scheduling in a build-operate-transfer environment. Expert Syst. Appl. 2021, 189, 116134. [Google Scholar] [CrossRef]
- Valverde-Alulema, F.; Llorens-Largo, F. Rubric for Evaluating the Alignment of the IT Project Portfolio with IT Governance in Universities. ACM SIGMIS Database Database Adv. Inf. Syst. 2021, 52, 56–76. [Google Scholar] [CrossRef]
- Saiya, A.A.; Arman, A.A. Indonesian Enterprise Architecture Framework: A Platform for Integrated and Connected Government. In Proceedings of the 2018 International Conference on ICT for Smart Society (ICISS), Semarang, Indonesia, 10–11 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Giron, C.L. Enterprise Architecture Model oriented to Architecture, Engineering and Construction Industry: Integration of Geospatial Concepts in a Specific Framework. In Proceedings of the 2020 15th Iberian Conference on Information Systems and Technologies (CISTI), Sevilla, Spain, 24–27 June 2020. [Google Scholar] [CrossRef]
- Pinheiro, C.R.; Guerreiro, S.; Mamede, H.S. Automation of Enterprise Architecture Discovery based on Event Mining from API Gateway logs: State of the Art. In Proceedings of the 2021 IEEE 23rd Conference on Business Informatics (CBI), Bolzano, Italy, 1–3 September 2021; Volume 2, pp. 117–124. [Google Scholar] [CrossRef]
- Proenca, D.; Borbinha, J. Enterprise Architecture: A Maturity Model Based on TOGAF ADM. In Proceedings of the 2017 IEEE 19th Conference on Business Informatics (CBI), Thessaloniki, Greece, 24–27 July 2017. [Google Scholar] [CrossRef]
- Makovhololo, M.L. Effects of GWEA Implementation on ICT Standardisation Across SA Government Departments. In Proceedings of the 2018 Open Innovations Conference (OI), Johannesburg, South Africa, 3–5 October 2018; pp. 339–345. [Google Scholar] [CrossRef]
- Nugroho, M.A.; Jusoh, R.; Salleh, N.A.M. The Role of Alignment between IS Strategy and Social Capital on the IS Capability and Business Performance Relationship: A Cross-Sectional Survey. IEEE Access 2020, 8, 152760–152771. [Google Scholar] [CrossRef]
- Ntsoane, M.P.; Jokonya, O. Impact of Application Development in Managerial Skills, Knowledge and Enterprise Architecture amongst SMEs in Western Cape. In Proceedings of the 2019 International Multidisciplinary Information Technology and Engineering Conference (IMITEC), Vanderbijlpark, South Africa, 21–22 November 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Almutairi, A.; Naeem, M.A.; Weber, G. Assessing User Satisfaction of Current Enterprise Systems and Their Adaptability from the Perspective of Top Management. IEEE Access 2021, 9, 153442–153455. [Google Scholar] [CrossRef]
- Sousa, P.; Carvalho, M. Dynamic Organization’s Representation. In Linking Project Management with Enterprise Architecture. In Proceedings of the 2018 IEEE 20th Conference on Business Informatics (CBI), Vienna, Austria, 11–14 July 2018. [Google Scholar] [CrossRef]
- Reis, A.C.B.; de Moraes, G.M.; de Oliveira, W.S.; Júnior, E.S.; Monteiro, S.B.S. Modelo para priorização de execução de projetos de TI em uma instituição financeira. Rev. Ibérica Sist. Tecnol. Inf. 2020, E27, 319–332. [Google Scholar]
- Tselios, D.; Ipsilandis, P. Telecommunication projects portfolio scheduling using the IFM approach. In Proceedings of the 2017 25th Telecommunication Forum (TELFOR), Belgrade, Serbia, 21–22 November 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Mylnikov, L. Efficiency management of discrete production systems under the dynamics of project portfolio. Comput. Ind. Eng. 2021, 163, 107807. [Google Scholar] [CrossRef]
- Jafarzadeh, H.; Heidary-Dahooie, J.; Akbari, P.; Qorbani, A. A project prioritization approach considering uncertainty, reliability, criteria prioritization, and robustness. Decis. Support Syst. 2022, 156, 113731. [Google Scholar] [CrossRef]
- Harrison, K.R.; Garanovich, I.L.; Weir, T.; Boswell, S.G.; Elsayed, S.M.; Sarker, R.A. Evolutionary and Memetic Computing for Project Portfolio Selection and Scheduling: An Introduction; Springer: Cham, Germany, 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Saiz, M.; Lostumbo, M.A.; Juan, A.A.; Lopez-Lopez, D. A clustering-based review on project portfolio optimization methods. Int. Trans. Oper. Res. 2021, 29, 172–199. [Google Scholar] [CrossRef]
- Liesiö, J.; Salo, A.; Keisler, J.M.; Morton, A. Portfolio decision analysis: Recent developments and future prospects. Eur. J. Oper. Res. 2020, 293, 811–825. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Abbasi, M.; Deng, X. A novel project portfolio selection framework towards organizational resilience: Robust Ordinal Priority Approach. Expert Syst. Appl. 2021, 188, 116067. [Google Scholar] [CrossRef]
- Mohagheghi, V.; Mousavi, S.M. A new multi-period optimization model for resilient-sustainable project portfolio evaluation under interval-valued Pythagorean fuzzy sets with a case study. Int. J. Mach. Learn. Cybern. 2021, 12, 3541–3560. [Google Scholar] [CrossRef]
- Kolisch, R.; Fliedner, T. A Decision Support System for Planning Portfolios of Supply Chain Improvement Projects in the Semiconductor Industry. In Evolutionary and Memetic Computing for Project Portfolio Selection and Scheduling; Springer Science and Business Media Deutschland GmbH: Cham, Germany, 2022; Volume 26, pp. 193–212. [Google Scholar] [CrossRef]
- Calbert, G.; Weir, T.; Garanovich, I.L. Kuhn, C.C.N. A Temporal Knapsack Approach to Defence Portfolio Selection. In Evolutionary and Memetic Computing for Project Portfolio Selection and Scheduling; Springer Science and Business Media Deutschland GmbH: Cham, Germany, 2022; pp. 159–191. [Google Scholar]
- De Almeida, J.A.; Vetschera, R. Bounds in Tree-Based Approaches to Generate Project Portfolios in the Presence of Interactions. Int. J. Decis. Support Syst. Technol. 2021, 13, 50–70. [Google Scholar]
- Martins, C.L.; Zaraté, P.; de Almeida, A.T.; de Almeida, J.A.; Morais, D.C. Web-Based DSS for Resource Allocation in Higher Education. Int. J. Decis. Support Syst. Technol. 2021, 13, 71–93. [Google Scholar] [CrossRef]
- Mussoi, F.L.R.; Teive, R.C.G. An integrated multicriteria decision-making approach for distribution system expansion planning. Int. J. Intell. Syst. 2021, 36, 4962–4989. [Google Scholar] [CrossRef]
- Fernández, E.; Rangel-Valdez, N.; Cruz-Reyes, L.; Gomez-Santillan, C. A New Approach to Group Multi-Objective Optimization under Imperfect Information and Its Application to Project Portfolio Optimization. Appl. Sci. 2021, 11, 4575. [Google Scholar] [CrossRef]
- Harrison, K.R.; Elsayed, S.M.; Garanovich, I.L.; Weir, T.; Boswell, S.G.; Sarker, R.A. A. A New Model for the Project Portfolio Selection and Scheduling Problem with Defence Capability Options. In Evolutionary and Memetic Computing for Project Portfolio Selection and Scheduling; Springer Science and Business Media Deutschland GmbH: Cham, Germany, 2022; pp. 89–123. [Google Scholar] [CrossRef]
- Fernández, E.; Solares, E.; Coello, C.A.C.; De-León-Gómez, V. An Overall Characterization of the Project Portfolio Optimization Problem and an Approach Based on Evolutionary Algorithms to Address It. In Evolutionary and Memetic Computing for Project Portfolio Selection and Scheduling; Springer Science and Business Media Deutschland GmbH: Cham, Germany, 2022; pp. 65–88. [Google Scholar] [CrossRef]
- Sarker, R.A.; Harrison, K.R.; Elsayed, S.M. Evolutionary Approaches for Project Portfolio Optimization: An Overview. In Evolutionary and Memetic Computing for Project Portfolio Selection and Scheduling; Springer Science and Business Media Deutschland GmbH: Cham, Germany, 2022; pp. 9–35. [Google Scholar] [CrossRef]
- Balderas, F.; Fernandez, E.; Gomez-Santillan, C.; Rangel-Valdez, N.; Cruz, L. An Interval-Based Approach for Evolutionary Multi-Objective Optimization of Project Portfolios. Int. J. Inf. Technol. Decis. Mak. 2019, 18, 1317–1358. [Google Scholar] [CrossRef]
- Zolfaghari, S.; Mousavi, S.M. A novel mathematical programming model for multi-mode project portfolio selection and scheduling with flexible resources and due dates under interval-valued fuzzy random uncertainty. Expert Syst. Appl. 2021, 182, 115207. [Google Scholar] [CrossRef]
- Rivera, G.; Florencia, R.; Guerrero, M.; Porras, R.; Sánchez-Solís, J.P. Online multi-criteria portfolio analysis through compromise programming models built on the underlying principles of fuzzy outranking. Inf. Sci. 2021, 580, 734–755. [Google Scholar] [CrossRef]
- Bai, L.; Han, X.; Wang, H.; Zhang, K.; Sun, Y. A method of network robustness under strategic goals for project portfolio selection. Comput. Ind. Eng. 2021, 161, 107658. [Google Scholar] [CrossRef]
- Khatun, M.T.; Hiekata, K.; Takahashi, Y.; Okada, I. Dynamic Modeling of Resource Allocation for Project Management in Multi-Project Environment. In Transdisciplinary Engineering for Resilience: Responding to System Disruptions, Proceedings of the 28th ISTE International Conference on Transdisciplinary Engineering, Online, 5–9 July 2021; IOS Press: Amsterdam, The Netherlands, 2021; pp. 223–232. [Google Scholar] [CrossRef]
- Wu, L.-H.; Wu, L.; Shi, J.; Chou, Y.-T. Project Portfolio Selection Considering Uncertainty: Stochastic Dominance-Based Fuzzy Ranking. Int. J. Fuzzy Syst. 2021, 23, 2048–2066. [Google Scholar] [CrossRef]
- Marchinares, A.H.; Rodriguez, C.R. Online Solution Based on Machine Learning for IT Project Management in Software Factory Companies. In Proceedings of the 2021 13th International Conference on Computational Intelligence and Communication Networks (CICN), Lima, Peru, 22–23 September 2021; pp. 150–154. [Google Scholar]
- Harrison, K.R.; Elsayed, S.; Sarker, R.A.; Garanovich, I.L.; Weir, T.; Boswell, S.G. Project portfolio selection with defense capability options. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Lille, France, 10–14 July 2021. [Google Scholar] [CrossRef]
- Mokhtari, G.; Imamzadeh, E.S.M. Balancing the Portfolio of Urban and Public Projects with Distance-Dependent Coverage Facilities. Sci. Iran. 2021, 28, 2374–2385. [Google Scholar] [CrossRef]
- Mavrotas, G.; Makryvelios, E. Combining multiple criteria analysis, mathematical programming and Monte Carlo simulation to tackle uncertainty in Research and Development project portfolio selection: A case study from Greece. Eur. J. Oper. Res. 2020, 291, 794–806. [Google Scholar] [CrossRef]
- Hesarsorkh, A.H.; Ashayeri, J.; Naeini, A.B. Pharmaceutical R&D project portfolio selection and scheduling under uncertainty: A robust possibilistic optimization approach. Comput. Ind. Eng. 2021, 155, 107114. [Google Scholar] [CrossRef]
- Abdalla, M.H.; Karabatak, M. To Review and Compare Evolutionary Algorithms in Optimization of Distributed Database Query. In Proceedings of the 2020 8th International Symposium on Digital Forensics and Security (ISDFS), Beirut, Lebanon, 1–2 June 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, R.; Ji, W. Computational Intelligence for Information Security: A Survey. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 616–629. [Google Scholar] [CrossRef]
- Yang, X.; Zou, J.; Yang, S.; Zheng, J.; Liu, Y. A Fuzzy Decision Variables Framework for Large-scale Multiobjective Optimization. IEEE Trans. Evol. Comput. 2021, 1. [Google Scholar] [CrossRef]
- Katsupeev, A.A.; Shcherbakova, E.A.; Vorobyev, S.P. Comparison of evolutionary algorithms used to solve the optimization problem of information security of distributed systems. In Proceedings of the 2016 2nd International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Chelyabinsk, Russian, 19–20 May 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Ahrari, A.; Elsayed, S.; Sarker, R.; Essam, D.; Coello, C.A.C. Weighted pointwise prediction method for dynamic multiobjective optimization. Inf. Sci. 2020, 546, 349–367. [Google Scholar] [CrossRef]
- Li, S.; Bi, F.; Chen, W.; Miao, X.; Liu, J.; Tang, C. An Improved Information Security Risk Assessments Method for Cyber-Physical-Social Computing and Networking. IEEE Access 2018, 6, 10311–10319. [Google Scholar] [CrossRef]
- Lakhno, V.; Akhmetov, B.; Adilzhanova, S.; Blozva, A.; Svitlana, R.; Dmytro, R. The Use of a Genetic Algorithm in the Problem of Distribution of Information Security Organizational and Financial Resources. In Proceedings of the 2020 IEEE 2nd International Conference on Advanced Trends in Information Theory (ATIT), Kyiv, Ukraine, 25–27 November 2020; pp. 251–254. [Google Scholar] [CrossRef]
- Song, Y.; Shen, Y.; Zhang, G.; Hu, Y. The information security risk assessment model based on GA-BP. In Proceedings of the 2016 7th IEEE international conference on software engineering and service science (ICSESS), Beijing, China, 26–28 August 2016; pp. 119–122. [Google Scholar] [CrossRef]
- Alioui, Y.; Acar, R. An evaluation of a constrained multi-objective genetic algorithm. J. Sci. Perspect. 2020, 4, 137–146. [Google Scholar] [CrossRef]
- Kebriyaii, O.; Heidari, A.; Khalilzadeh, M.; Antucheviciene, J.; Pavlovskis, M. Application of Three Metaheuristic Algorithms to Time-Cost-Quality Trade-Off Project Scheduling Problem for Construction Projects Considering Time Value of Money. Symmetry 2021, 13, 2402. [Google Scholar] [CrossRef]
- Abouhawwash, M.; Deb, K. Reference point based evolutionary multi-objective optimization algorithms with convergence properties using KKTPM and ASF metrics. J. Heurist. 2021, 27, 575–614. [Google Scholar] [CrossRef]
- Algarni, M.; Alazwari, M.A.; Safaei, M.R. Optimization of Nano-Additive Characteristics to Improve the Efficiency of a Shell and Tube Thermal Energy Storage System Using a Hybrid Procedure: DOE, ANN, MCDM, MOO, and CFD Modeling. Mathematics 2021, 9, 3235. [Google Scholar] [CrossRef]
- Awad, M.; Abouhawwash, M.; Agiza, H.N. On NSGA-II and NSGA-III in Portfolio Management. Intell. Autom. Soft Comput. 2022, 32, 1893–1904. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, N.; Li, M. Solving Many-Objective Optimization Problems by a Pareto-Based Evolutionary Algorithm with Preprocessing and a Penalty Mechanism. IEEE Trans. Cybern. 2020, 51, 5585–5594. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Chen, J.; Du, T.; Xiao, G. A multi-objective optimization for resource allocation of emergent demands in cloud computing. J. Cloud Comput. Adv. Syst. Appl. 2021, 10, 20. [Google Scholar] [CrossRef]
- Abido, M.A.; Elazouni, A. Modified multi-objective evolutionary programming algorithm for solving project scheduling problems. Expert Syst. Appl. 2021, 183, 115338. [Google Scholar] [CrossRef]
- Atta, S.; Mahapatra, P.R.S.; Mukhopadhyay, A. A multi-objective formulation of maximal covering location problem with customers’ preferences: Exploring Pareto optimality-based solutions. Expert Syst. Appl. 2021, 186, 115830. [Google Scholar] [CrossRef]
- Akhmetov, B.; Lakhno, V.; Akhmetov, B.; Myakuhin, Y.; Adranova, A.; Kydyralina, L. Models and Algorithms of Vector Optimization in Selecting Security Measures for Higher Education Institution’s Information Learning Environment. In Intelligent Systems in Cybernetics and Automation Control Theory; Springer: Berlin/Heidelberg, Germany, 2018; pp. 135–142. [Google Scholar] [CrossRef]
- Bojanc, R.; Jerman-Blažič, B. Quantitative Model for Economic Analyses of Information Security Investment in an Enterprise Information System. Organizacija 2012, 45, 276–288. [Google Scholar] [CrossRef]
- Klyaus, T.K.; Gatchin, Y.A. Mathematical Model for Information Security System Effectiveness Evaluation against Advanced Persistent Threat Attacks. In Proceedings of the 2020 Wave Electronics and its Application in Information and Telecommunication Systems (WECONF), Saint Petersburg, Russia, 1–5 June 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Ramalingam, D.; Arun, S.; Anbazhagan, N. A Novel Approach for Optimizing Governance, Risk management and Compliance for Enterprise Information security using DEMATEL and FoM. Procedia Comput. Sci. 2018, 134, 365–370. [Google Scholar] [CrossRef]
- Zeng, W.; Koutny, M. Modelling and analysis of corporate efficiency and productivity loss associated with enterprise information security technologies. J. Inf. Secur. Appl. 2019, 49, 102385. [Google Scholar] [CrossRef]
- Bai, X.; Gopal, R.; Nunez, M.; Zhdanov, D. A decision methodology for managing operational efficiency and information disclosure risk in healthcare processes. Decis. Support Syst. 2014, 57, 406–416. [Google Scholar] [CrossRef]
- Zegzhda, P.D.; Anisimov, V.G.; Suprun, A.F.; Saurenko, T.N.; Los’, V.P. A Model of Optimal Complexification of Measures Providing Information Security. Autom. Control Comput. Sci. 2020, 54, 930–936. [Google Scholar] [CrossRef]
- Stepanov, L.V.; Koltsov, A.S.; Parinov, A.V.; Dubrovin, A.S. Mathematical modeling method based on genetic algorithm and its applications. J. Phys. Conf. Ser. 2019, 1203, 012082. [Google Scholar] [CrossRef]
- Izurieta, R.R.; Morales, L.J.C.; Toapanta, S.M.T.; Gallegos, L.E.M.; Trejo, J.A.O. Analysis of the Information Security of Public Organizations in Ecuador. In Proceedings of the 2021 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 15–17 December 2021; pp. 823–829. [Google Scholar] [CrossRef]
- Audet, C.; Bigeon, J.; Cartier, D.; Le Digabel, S.; Salomon, L. Performance indicators in multiobjective optimization. Eur. J. Oper. Res. 2020, 292, 397–422. [Google Scholar] [CrossRef]
- Riquelme, N.; Von Lucken, C.; Baran, B. Performance metrics in multi-objective optimization. In Proceedings of the 2015 Latin American computing conference (CLEI), Arequipa, Peru, 19–23 October 2015; pp. 1–11. [Google Scholar] [CrossRef]
- Okabe, T.; Jin, Y.; Sendhoff, B. A critical survey of performance indices for multi-objective optimisation. In Proceedings of the 2003 Congress on Evolutionary Computation, Canberra, Australia, 8–12 December 2003. [Google Scholar] [CrossRef]
- Abedi, M.; Chiong, R.; Noman, N.; Zhang, R. A multi-population, multi-objective memetic algorithm for energy-efficient job-shop scheduling with deteriorating machines. Expert Syst. Appl. 2020, 157, 113348. [Google Scholar] [CrossRef]
- Amine, K. Multiobjective Simulated Annealing: Principles and Algorithm Variants. Adv. Oper. Res. 2019, 2019, 8134674. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Imada, R.; Setoguchi, Y.; Nojima, Y. How to Specify a Reference Point in Hypervolume Calculation for Fair Performance Comparison. Evol. Comput. 2018, 26, 411–440. [Google Scholar] [CrossRef] [PubMed]
- Nartey, C.; Tchao, E.T.; Gadze, J.D.; Yeboah-Akowuah, B.; Nunoo-Mensah, H.; Welte, D.; Sikora, A. Blockchain-IoT peer device storage optimization using an advanced time-variant multi-objective particle swarm optimization algorithm. EURASIP J. Wirel. Commun. Netw. 2022, 2022, 5. [Google Scholar] [CrossRef]
- Biswas, S.; Acharyya, S. Multi-objective Simulated Annealing Variants to Infer Gene Regulatory Network: A Comparative Study. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 18, 2612–2623. [Google Scholar] [CrossRef]
- INCIBE. 6 Criterios para Categorizar y Priorizar tus Proyectos de Ciberseguridad en la Empresa. Instituto Nacional de Ciberseguridad. 2016. Available online: https://www.incibe.es/protege-tu-empresa/blog/criterios-clasificar-y-priorizar-proyectos-ciberseguridad-en-empresa (accessed on 29 July 2022).
- Ostakhov, V.; Morozov, V. Models and Methods of IT and Infocommunications Portfolio Management Using the System of Metrics and KPIs. In Proceedings of the 2019 IEEE International Scientific-Practical Conference Problems of Infocommunications, Science and Technology (PIC S&T), Kyiv, Ukraine, 8–11 October 2019; pp. 161–164. [Google Scholar] [CrossRef]
- Van Veldhuizen, D.A.; Lamont, G.B. Genetic algorithms, building blocks, and multiobjective optimization. In Proceedings of the 1999 Genetic and Evolutionary Computation Conference, Orlando, FL, USA, 18 July 1999; Workshop Program. pp. 125–126. [Google Scholar]
- Kumar, G.P.; Jena, P. Pearson’s Correlation Coefficient for Islanding Detection Using Micro-PMU Measurements. IEEE Syst. J. 2020, 15, 5078–5089. [Google Scholar] [CrossRef]
- Yan, Q.; Wang, J.; Liu, S.; Li, D. Differentially Private Decision Tree Based on Pearson’s Correlation Coefficient. In Proceedings of the 2021 11th International Conference on Information Science and Technology (ICIST), Chengdu, China, 21–23 May 2021; pp. 77–86. [Google Scholar] [CrossRef]
- Solis, E.B.; Neto, A.M.; Huallpa, B.N. Pearson’s Correlation Coefficient for Discarding Redundant Information: Velodyne Lidar Data Analysis. In Proceedings of the 2015 12th Latin American Robotics Symposium and 2015 3rd Brazilian Symposium on Robotics (LARS-SBR), Uberlandia, Brazil, 29–31 October 2015; pp. 116–119. [Google Scholar] [CrossRef]
- Sukono; Hidayat, Y.; Lesmana, E.; Putra, A.S.; Napitupulu, H.; Supian, S. Portfolio optimization by using linear programing models based on genetic algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2018, 300, 012001. [Google Scholar] [CrossRef]
- Sadeghi, A.; Daneshvar, A.; Zaj, M.M. Combined ensemble multi-class SVM and fuzzy NSGA-II for trend forecasting and trading in Forex markets. Expert Syst. Appl. 2021, 185, 115566. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).