Dynamic Regressor/Ensemble Selection for a Multi-Frequency and Multi-Environment Path Loss Prediction
Abstract
1. Introduction
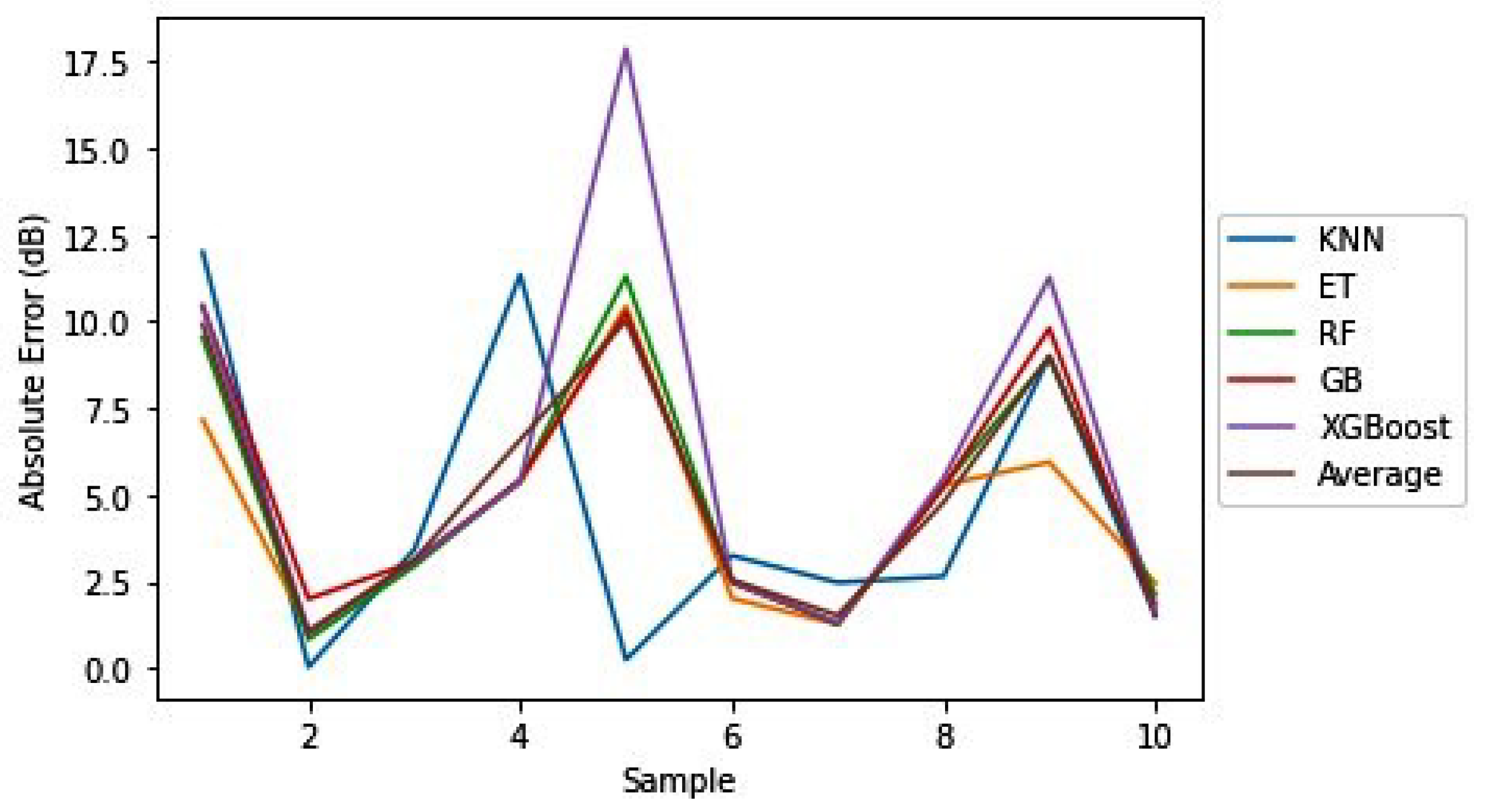
- We show that for a path loss dataset with multiple cases, a model could have the overall best accuracy but can be poor in prediction of certain data cases.
- We show that for a path loss dataset with multiple cases, a model not having the overall best accuracy could have better accuracy for cases with a low number of sample points.
- A DES scheme was developed to improve accuracy of cases with a low number of sample points.
2. Related Works
| Reference | Input Data Type | Model(s) | Environment | Frequency (MHz) |
|---|---|---|---|---|
| [17] | Numeric | RF | University campus (Suburban) | 1800 |
| [31] | Numeric | RF | Urban | 2021.4 |
| [32] | Numeric | RF | Urban (air to air interface) | 2400 |
| [33] | Numeric | RF and AdaBoost | Air craft cabin | 2400 |
| [45] | Numeric | RF | Complex environment with vegetation | 2400 |
| [34] | Numeric | RF and XGBoost | Urban | n/a |
| [46] | Numeric | RF | Urban | 900 |
| [46] | Numeric | RF | Urban | 1800 |
| [30] | Numeric | Bagging of KNN base models | Rural | 3700 |
| [22] | Numeric | RF, Gradient Boosting, and XGBoost | Rural, urban, suburban, and urban highrise | 868, 1800, 1835.2, 1836, 1840.8, 1864 |
| [23] | Numeric + Image | RF, Gradient Boosting, and XGBoost | Rural, urban, suburban, and urban highrise | 868, 1800, 1835.2, 1836, 1840.8, 1864 |
| [24] | Numeric + Image | RF, Gradient Boosting, Extreme Learning Trees, and XGBoost | Rural, urban, suburban, and urban highrise | 868, 1800, 1835.2, 1836, 1840.8, 1864 |
| [47] | Image | RF, XGBoost, and LightGBM | Urban | 900 |
| [35] | Numeric | Stacking, RF, XGBoost, LightGBM, and AdaBoost | Urban | 900 |
| [36] | Numeric | Stacking, voting, bagging with KNN base regressors, and Gradient Boosting | Rural | 3700 |
| [37] | Numeric | Bagging and Blending | Rural, suburban, and urban | 2400 |
| This study | Numeric + Image | RF, Gradient Boosting, Extreme Learning Trees, XGBoost, DRS, and DES | Rural, urban, suburban, and urban highrise | 868, 1800, 1835.2, 1836, 1840.8, 1864 |
3. Methodology
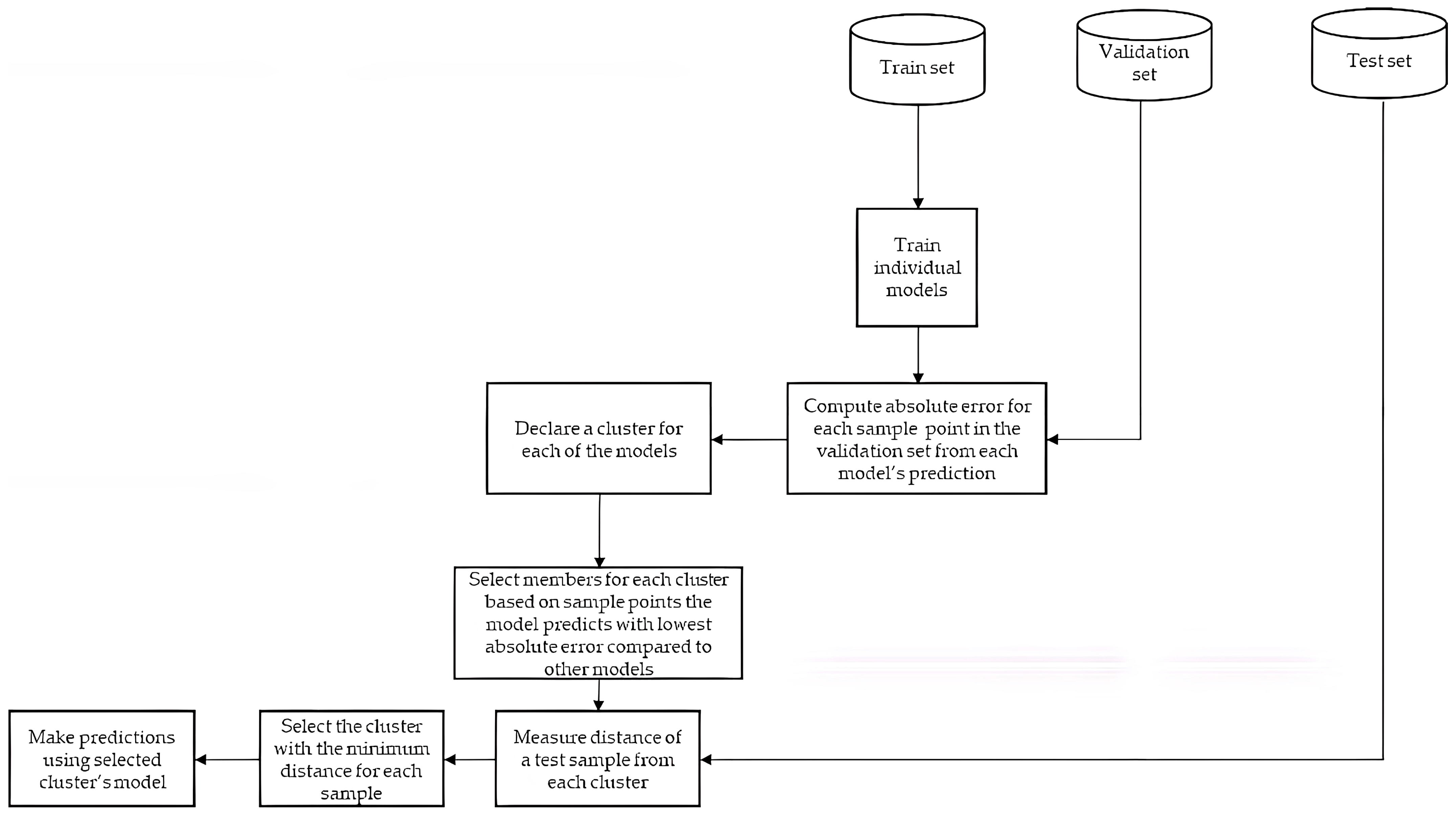
3.1. Dynamic Regressor Selection (DRS)
3.1.1. Training
- (i)
- Optimize hyper-parameters of learning algorithms (K Nearest Neighbor, Extreme Learning Trees (ET), Random Forest, Gradient Boosting (GB), and Extreme Gradient Boosting (XGBoost)).
- (ii)
- Train models with optimized hyper-parameters.
- (iii)
- Test each model with the validation set.
- (iv)
- For each validation sample point, select the model with the lowest absolute error. This is done to identify the model that predicted each validation sample point with the least error.
- (v)
- Develop a cluster for each model based on validation sample points in which they predicted with the least error. K means clustering with a K value of 1 is used for cluster formation. A value of 1 was used because the cluster members were already selected based on the minimum absolute error as shown in Figure 1, and thus, the centroids were determined by K Means. Algorithm 1, gives additional description of the DRS training phase.
| Algorithm 1 Dynamic Regressor Selection Training Phase |
|
3.1.2. Testing
- (i)
- Measure the distance of the test sample point to each cluster. This measures the similarity between the test sample point and validation samples in each cluster [57]. Euclidean distance is used for this purpose.
- (ii)
- Select the cluster with the least distance and use the model designated for the cluster to make a prediction. Further details on the DRS testing phase is presented in Algorithm 2, and description of the the whole DRS process is shown in Figure 1.
| Algorithm 2 Dynamic Regressor Selection Testing Phase |
|
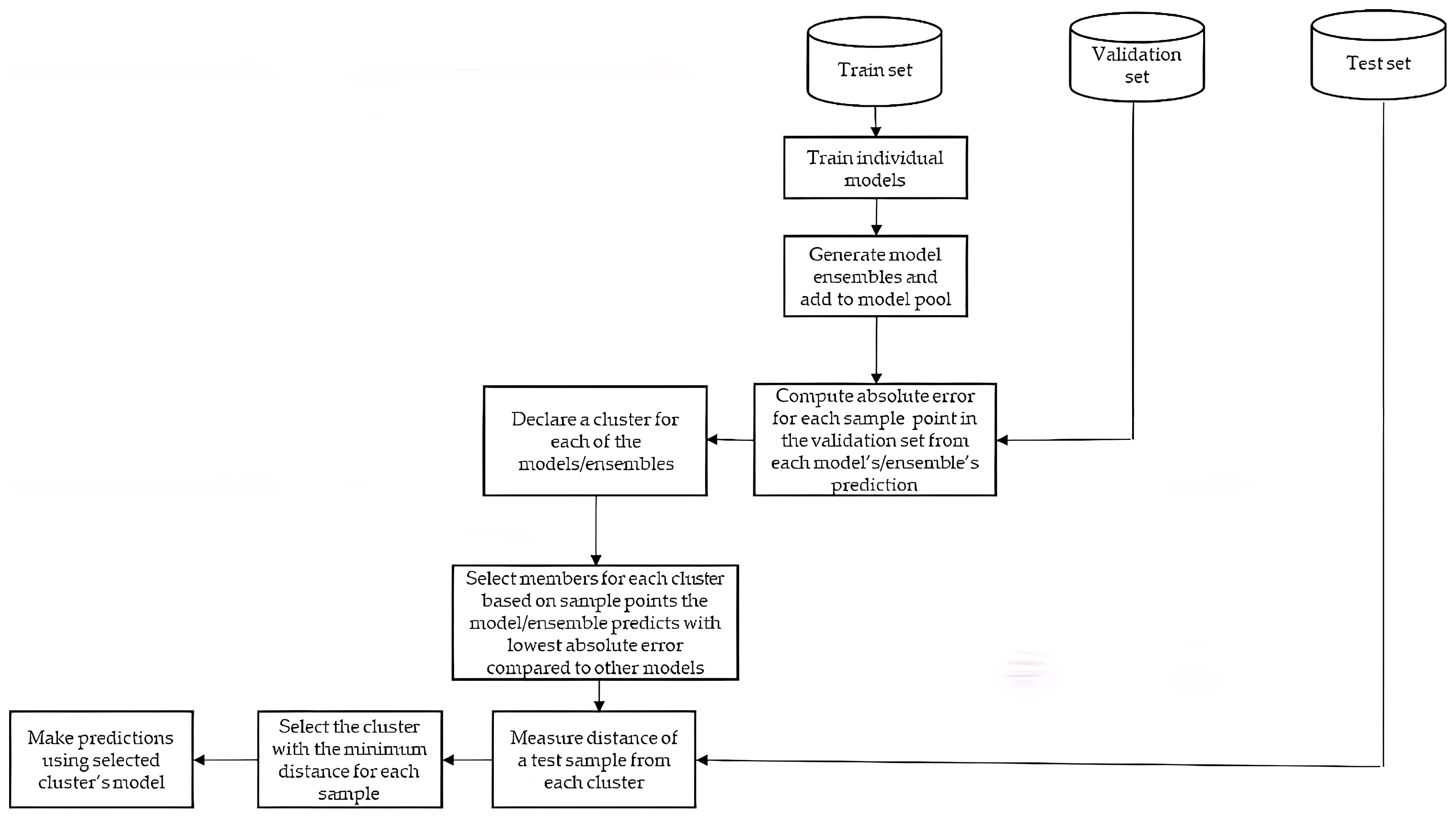
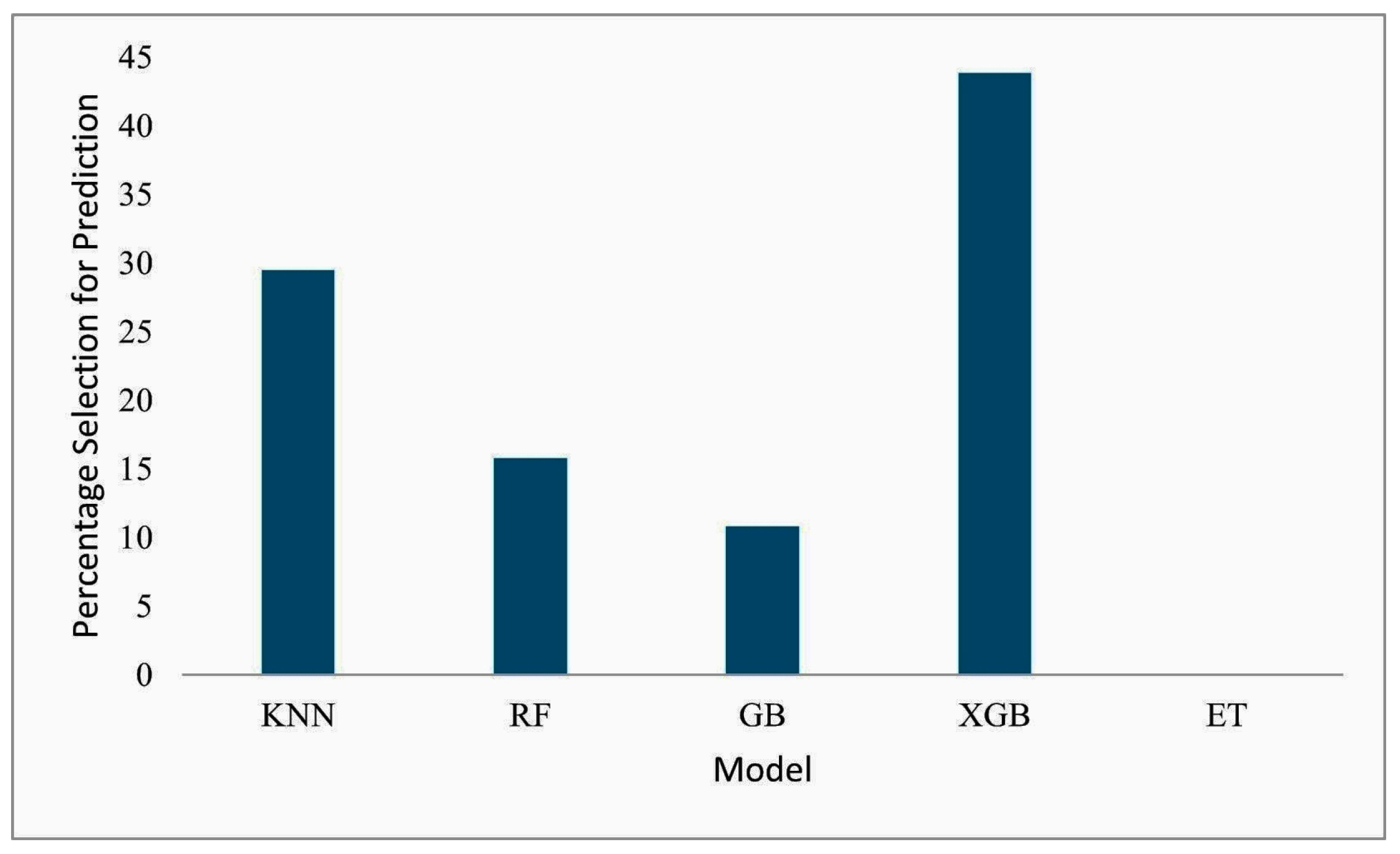
3.2. Dynamic Ensemble Selection (DES)
4. Results and Discussion
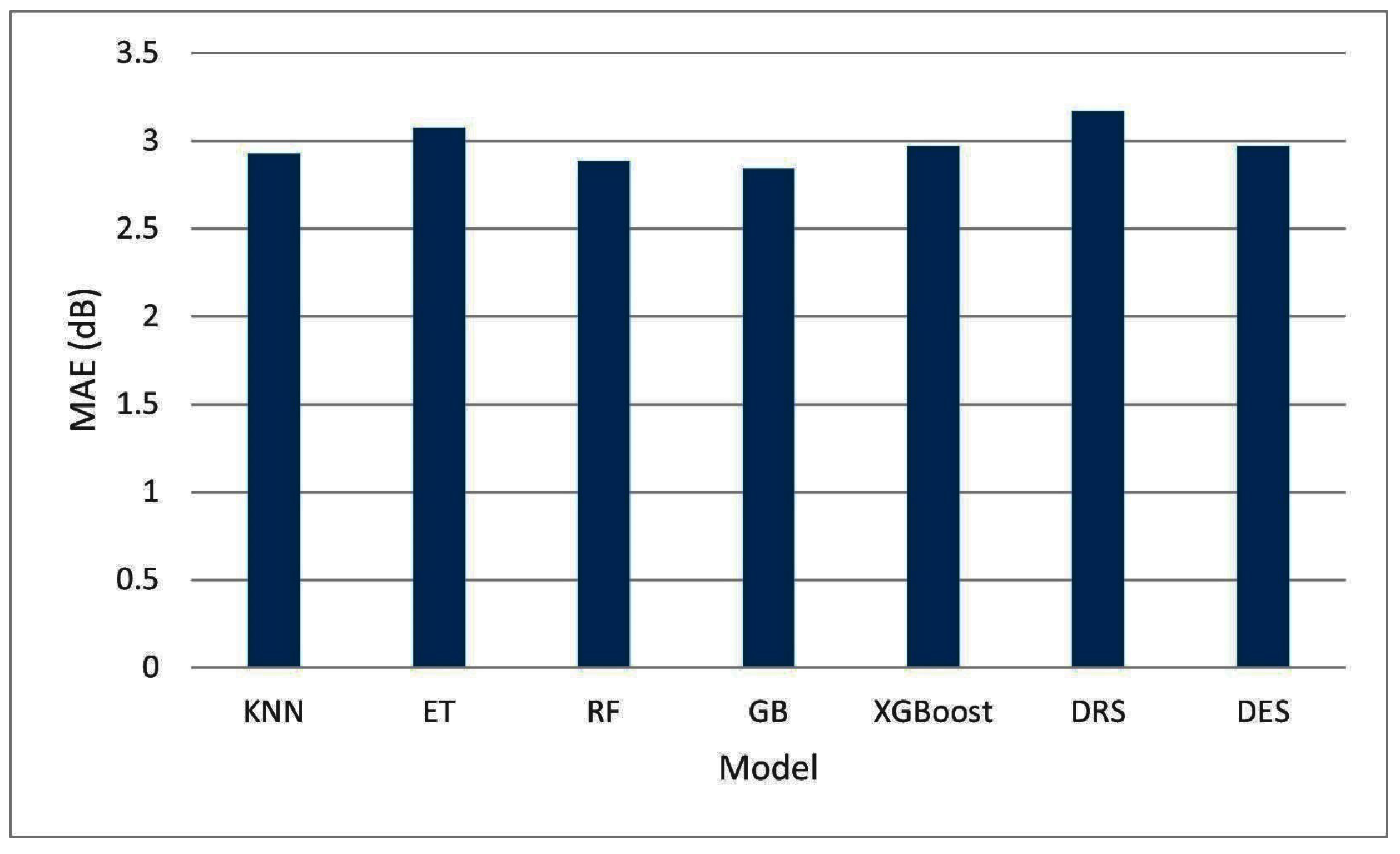
4.1. Results Based on Dataset 1
4.2. Results Based on Dataset 2
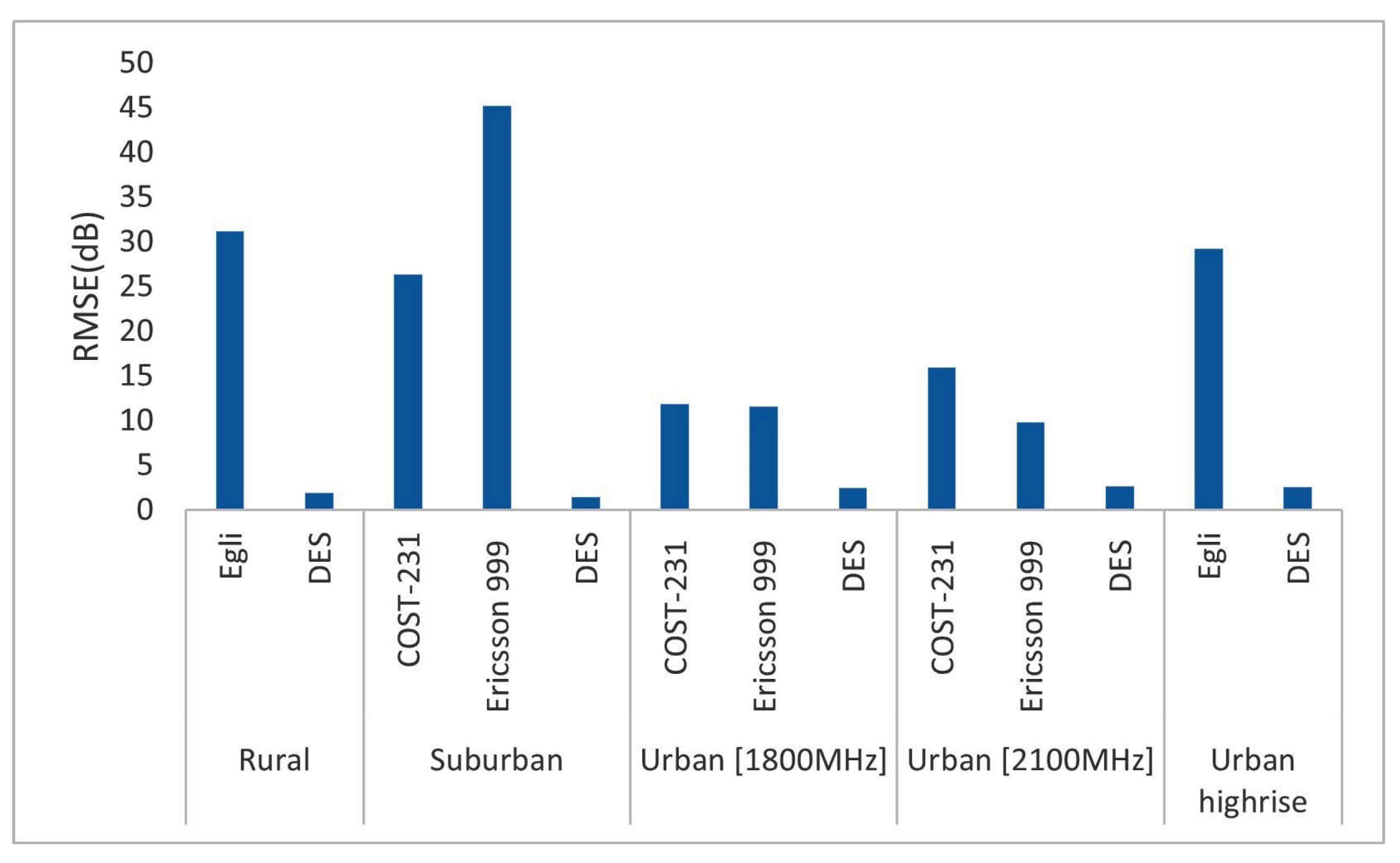
4.3. Comparison with Empirical Models
4.4. Testing on Other Datasets
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ibrahim, J.; Danladi, T.A.; Aderinola, M. Comparative Analysis Between Wired and Wireless Technologies in Communications: A Review. In Proceedings of the 9th IIER International Conference, Mecca, Saudi Arabia, 23–24 March 2017; pp. 45–48. [Google Scholar]
- Sari, A.; Alzubi, A. Path Loss Algorithms for Data Resilience in Wireless Body Area Networks for Healthcare Framework. In Security and Resilience in Intelligent Data-Centric Systems and Communication Networks, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2017; pp. 285–313. [Google Scholar]
- Faruk, N.; Popoola, S.I.; Surajudeen-Bakinde, N.T.; Oloyede, A.A.; Abdulkarim, A.; Olawoyin, L.A.; Ali, M.; Calafate, C.T.; Atayero, A.A. Path Loss Predictions in the VHF and UHF Bands within Urban Environments: Experimental Investigation of Empirical, Heuristics and Geospatial Models. IEEE Access 2019, 7, 77293–77307. [Google Scholar] [CrossRef]
- Zhang, X.; Shu, X.; Zhang, B.; Ren, J.; Zhou, L.; Chen, X. Cellular Network Radio Propagation Modeling with Deep Convolutional Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Virtual Event, CA, USA, 6–10 July 2020; pp. 2378–2386. [Google Scholar]
- Mahasukhon, P.; Sharif, H.; Hempel, M.; Zhou, T.; Wang, W.; Ma, T. Propagation path loss estimation using nonlinear multi-regression approach. In Proceedings of the 2010 IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010. [Google Scholar]
- Popoola, S.I.; Oseni, O.F. Empirical Path Loss Models for GSM Network Deployment in Makurdi, Nigeria. Int. Ref. J. Eng. Sci. 2014, 3, 85–94. [Google Scholar]
- Ogbulezie, J.; Onuu, M. Site specific measurements and propagation models for GSM in three cities in Northern Nigeria. Am. J. Sci. Ind. Res. 2013, 4, 238–245. [Google Scholar] [CrossRef]
- Popoola, S.I.; Jefia, A.; Atayero, A.A.; Kingsley, O.; Faruk, N.; Oseni, O.F.; Abolade, R.O. Determination of neural network parameters for path loss prediction in very high frequency wireless channel. IEEE Access 2019, 7, 150462–150483. [Google Scholar] [CrossRef]
- Atoll. Atoll RF Planning and Optimisation Software User Manual, Version 3.1.0. Available online: https://www.academia.edu/9190736/Atoll_Getting_Started_UMTS_Version_3_1_0_Forsk_China (accessed on 10 June 2022).
- Ates, H.F.; Hashir, S.M.; Baykas, T.; Gunturk, B.K. Path Loss Exponent and Shadowing Factor Prediction From Satellite Images Using Deep Learning. IEEE Access 2019, 7, 101366–101375. [Google Scholar] [CrossRef]
- Ahmadien, O.; Ates, H.F.; Baykas, T.; Gunturk, B.K. Predicting Path Loss Distribution of an Area from Satellite Images Using Deep Learning. IEEE Access 2020, 8, 64982–64991. [Google Scholar] [CrossRef]
- Masood, U.; Farooq, H.; Imran, A. A machine learning based 3D propagation model for intelligent future cellular networks. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 64982–64991. [Google Scholar]
- Moraitis, N.; Tsipi, L.; Vouyioukas, D. Machine learning-based methods for path loss prediction in urban environment for LTE networks. In Proceedings of the 2020 16th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Thessaloniki, Greece, 12–14 October 2020. [Google Scholar]
- Abolade, R.O.; Famakinde, S.O.; Popoola, S.I.; Oseni, O.F.; Atayero, A.A.; Misra, S. Support Vector Machine for Path Loss Predictions in Urban Environment. In Computational Science and Its Applications—ICCSA 2020; Springer: Cham, Switzerland, 2020; Volume 4, pp. 995–1006. [Google Scholar]
- Ebhota, V.C.; Isabona, J.; Srivastava, V.M. Effect of learning rate on GRNN and MLP for the prediction of signal power loss in microcell sub-urban environment. Int. J. Commun. Antenna Propag. 2019, 9, 36–45. [Google Scholar] [CrossRef]
- Ojo, S.; Imoize, A.; Alienyi, D. Radial Basis Function Neural Network Path Loss Prediction Model for LTE Networks in Multitransmitter Signal Propagation Environments. Int. J. Commun. Syst. 2021, 34, e4680. [Google Scholar] [CrossRef]
- Singh, H.; Gupta, S.; Dhawan, C.; Mishra, A. Path Loss Prediction in Smart Campus Environment: Machine Learning-based Approaches. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020. [Google Scholar]
- Gupta, A.; Ghanshala, K.; Joshi, R.C. Mobility Improvement by Optimizing Channel Model Coverage Through Fine Tuning. J. Cyber Secur. Mobil. 2021, 10, 593–616. [Google Scholar] [CrossRef]
- Omoze, E.L.; Edeko, F.O. Statistical Tuning of COST 231 Hata model in Deployed 1800MHz GSM Networks for a Rural Environment. Niger. J. Technol. 2021, 39, 1216–1222. [Google Scholar] [CrossRef]
- Ayadi, M.; Zineb, A.B.; Tabbane, S. A UHF Path Loss Model Using Learning Machine for Heterogeneous Networks. IEEE Trans. Antennas Propag. 2017, 65, 3675–3683. [Google Scholar] [CrossRef]
- Nguyen, C.; Cheema, A.A. A Deep Neural Network-based Multi-Frequency Path Loss Prediction Model from 0.8 GHz to 70 GHz. Sensors 2021, 21, 5100. [Google Scholar] [CrossRef]
- Sani, U.S.; Lai, D.T.C.; Malik, O.A. Investigating Automated Hyper-Parameter Optimization for a Generalized Path Loss Model. In Proceedings of the CECNet 2021; IOS Press: Amsterdam, The Netherlands, 2021; pp. 283–291. [Google Scholar]
- Sani, U.S.; Lai, D.T.C.; Malik, O.A. A Hybrid Combination of a Convolutional Neural Network with a Regression Model for Path Loss Prediction Using Tiles of 2D Satellite Images. In Proceedings of the 2020 8th International Conference on Intelligent and Advanced Systems (ICIAS), Kuching, Malaysia, 13–15 July 2021. [Google Scholar]
- Sani, U.S.; Lai, D.T.C.; Malik, O.A. Improving Path Loss Prediction Using Environmental Feature Extraction from Satellite Images: Hand-Crafted vs. Convolutional Neural Network. Appl. Sci. 2022, 12, 7685. [Google Scholar] [CrossRef]
- Cruz, R.M.O.; Sabourin, R. On dynamic ensemble selection and data preprocessing for multi-class imbalance learning. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1940009. [Google Scholar] [CrossRef]
- Moura, T.J.M.; Cavalcanti, G.D.C.; Oliveira, L.S. Evaluating Competence Measures for Dynamic Regressor Selection. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019. [Google Scholar]
- García-Cano, E.; Cosío, F.A.; Duong, L.; Bellefleur, C.; Roy-Beaudry, M.; Joncas, J.; Parent, S.; Labelle, H. Dynamic ensemble selection of learner-descriptor classifiers to assess curve types in adolescent idiopathic scoliosis. Med. Biol. Eng. Comput. 2018, 56, 2221–2231. [Google Scholar] [CrossRef]
- Choi, Y.; Lim, D.J. DDES: A Distribution-Based Dynamic Ensemble Selection Framework. IEEE Access 2021, 9, 40743–40754. [Google Scholar] [CrossRef]
- Shahhosseini, M.; Hu, G.; Pham, H. Optimizing Ensemble Weights and Hyperparameters of Machine Learning Models for Regression Problems. Mach. Learn. Appl. 2022, 7, 100251. [Google Scholar] [CrossRef]
- Moraitis, N.; Tsipi, L.; Vouyioukas, D.; Gkioni, A.; Louvros, S. Performance evaluation of machine learning methods for path loss prediction in rural environment at 3.7GHz. Wirel. Netw. 2021, 27, 4169–4188. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, J.; Yang, G.; He, Z.; Wang, J. Path loss prediction based on machine learning: Principle, method, and data expansion. Appl. Sci. 2019, 9, 1908. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, J.; Yang, G.; He, Z.; Luo, X. Air-to-Air Path Loss Prediction Based on Machine Learning Methods in Urban Environments. Wirel. Commun. Mob. Comput. 2018, 2018, 8489326. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, Y.; Yang, G.; He, Z.; Zhang, W. Path Loss Prediction Based on Machine Learning Methods for Aircraft Cabin Environments. IEEE Access 2019, 7, 159251–159261. [Google Scholar] [CrossRef]
- Sotiroudis, S.P.; Goudos, S.K.; Siakavara, K. Feature Importances: A Tool to Explain Radio Propagation and Reduce Model Complexity. Telecom 2020, 1, 114–125. [Google Scholar] [CrossRef]
- Sotiroudis, S.P.; Boursianis, A.D.; Goudos, S.K.; Siakavara, K. From Spatial Urban Site Data to Path Loss Prediction: An Ensemble Learning Approach. IEEE Trans. Antennas Propag. 2021, 70, 6–11. [Google Scholar] [CrossRef]
- Oroza, C.A.; Zhang, Z.; Watteyne, T.; Glaser, S.D. A Machine-Learning-Based Connectivity Model for Complex Terrain Large-Scale Low-Power Wireless Deployments. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 576–584. [Google Scholar] [CrossRef]
- Sotiroudis, S.P.; Goudos, S.K.; Siakavara, K. Neural Networks and Random Forests: A Comparison Regarding Prediction of Propagation Path Loss for NB-IoT Networks. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 13–15 May 2019. [Google Scholar]
- Fujiwara, K.; Huang, Y.; Hori, K.; Nishioji, K.; Kobayashi, M.; Kamaguchi, M.; Kano, M. Over- and Under-sampling Approach for Extremely Imbalanced and Small Minority Data Problem in Health Record Analysis. Front. Public Health 2020, 8, 178. [Google Scholar] [CrossRef]
- Torgo, L.; Ribeiro, R.P.; Pfahringer, B.; Branco, P. SMOTE for Regression. In Progress in Artificial Intelligence; Springer International Publishing: Berlin/Heidelberg, Germany, 2013; Volume 8154. [Google Scholar]
- Sotiroudis, S.P.; Athanasiadou, G.; Tsoulos, G.V.; Christodoulou, C.; Goudos, S. Ensemble Learning for 5G Flying Base Station Path Loss Modelling. In Proceedings of the 2022 16th European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022. [Google Scholar]
- Branco, P.; Torgo, L.; Ribeiro, R.P. SMOGN: A Preprocessing Approach for Imbalanced Regression. In Proceedings of the First International Workshop on Learning with Imbalanced Domains: Theory and Applications, Skopje, Macedonia, 22 September 2017. [Google Scholar]
- Misha, J.; Shweta, M. Software Effort Estimation Using Synthetic Minority Over-Sampling Technique for Regression (SMOTER). In Proceedings of the 2022 3rd International Conference for Emerging Technology (INCET), Belgaum, India, 27–29 May 2022. [Google Scholar]
- Bourou, S.; El Saer, A.; Velivassaki, T.H.; Voulkidis, A.; Zahariadis, T. A Review of Tabular Data Synthesis Using GANs on an IDS Dataset. Information 2021, 12, 375. [Google Scholar] [CrossRef]
- Sauber-Cole, R.; Khoshgoftaar, T. The use of generative adversarial networks to alleviate class imbalance in tabular data: A survey. J. Big Data 2022, 9, 98. [Google Scholar] [CrossRef]
- Sotiroudis, S.P.; Siakavara, K.; Koudouridis, G.P.; Sarigiannidis, P.; Goudos, S.K. Enhancing Machine Learning Models for Path Loss Prediction Using Image Texture Techniques. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1443–1447. [Google Scholar] [CrossRef]
- Moraitis, N.; Tsipi, L.; Vouyioukas, D.; Gkioni, A.; Louvros, S. On the Assessment of Ensemble Models for Propagation Loss Forecasts in Rural Environments. IEEE Wirel. Commun. Lett. 2022, 11, 1097–1101. [Google Scholar] [CrossRef]
- Ojo, S.; Akkaya, M.; Sopuru, J.C. An ensemble machine learning approach for enhanced path loss predictions for 4G LTE wireless networks. Int. J. Commun. Syst. 2022, 35, e5101. [Google Scholar] [CrossRef]
- Rooney, N.; Patterson, D.; Anand, S.; Tsymbal, A. Dynamic Integration of Regression Models. In Multiple Classifier Systems, MCS 2004; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Rooney, N.; Patterson, D. A weighted combination of stacking and dynamic integration. Pattern Recognit. 2007, 40, 1385–1388. [Google Scholar] [CrossRef]
- Moura, T.J.M.; Cavalcanti, G.D.C.; Oliveira, L.S. MINE: A framework for dynamic regressor selection. Inf. Sci. 2021, 543, 157–179. [Google Scholar] [CrossRef]
- de, A. Cabral, J.T.H.; Oliveira, A.L.I. Ensemble Effort Estimation using dynamic selection. J. Syst. Softw. 2021, 175, 110904. [Google Scholar] [CrossRef]
- Rooney, N.; Patterson, D.; Tsymbal, A.; Anand, S. Random subspacing for regression ensembles. In Proceedings of the Seventeenth International Florida Artificial Intelligence Research Society, Miami Beach, FL, USA, 12–14 May 2004. [Google Scholar]
- Ghoneimy, S.; Faheem, M.H.; Gamal, N. Dynamic Ensemble Modelling for Prediction of Influenza Like Illnesses: A Framework. Int. J. Adv. Technol. 2020, 11, 235. [Google Scholar] [CrossRef]
- Dias, K.; Windeatt, T. Dynamic Ensemble Selection and Instantaneous Pruning for Regression Used in Signal Calibration. In Artificial Neural Networks and Machine Learning—ICANN 2014; Springer: Cham, Switzerland, 2014; pp. 475–482. [Google Scholar]
- Sun, C.; Yan, Y.; Zhang, W.; Wang, L. A Dynamic Ensemble Selection Approach to Developing Softcomputing Models for Two-Phase Flow Metering. J. Phys. Conf. Ser. 2018, 1065, 092022. [Google Scholar] [CrossRef]
- Qiao, Z.; Wang, B. Molten Steel Temperature Prediction in Ladle Furnace Using a Dynamic Ensemble for Regression. IEEE Access 2021, 9, 18855–18866. [Google Scholar] [CrossRef]
- Irani, J.; Pise, N.; Phatak, M. Clustering Techniques and the Similarity Measures used in Clustering: A Survey. Int. J. Comput. Appl. 2016, 134, 9–14. [Google Scholar] [CrossRef]
- Quddus, J. Machine Learning with Apache Spark Quick Start Guide: Uncover Patterns, Derive Actionable Insights, and Learn from Big Data Using MLlib; Packt Publishing Limited: Birmingham, UK, 2018. [Google Scholar]
- Namoun, A.; Hussein, B.R.; Tufail, A.; Alrehaili, A.; Syed, T.A.; Benrhouma, O. An Ensemble Learning Based Classification Approach for the Prediction of Household Solid Waste Generation. Sensors 2022, 22, 3506. [Google Scholar] [CrossRef]
- Jawhly, T.; Tiwari, R.C. Characterization of path loss for VHF terrestrial band in Aizawl, Mizoram (India). In Engineering Vibration, Communication and Information Processing; Springer Nature: Singapore, 2019; pp. 53–63. [Google Scholar]
- Opio, P.; Kisolo, A.; Ireeta, T.W.; Okullo, W. Modeling the Distribution of Radiofrequency Intensities from the Digital Terrestrial Television (DTTV) Broadcasting Transmitter in Kampala. Asian J. Res. Rev. Phys. 2020, 3, 65–78. [Google Scholar] [CrossRef]
- Türke, U. Efficient Methods for WCDMA Radio Network Planning and Optimization; Deutscher Universitätsverlag: Wiesbaden, Germany, 2007. [Google Scholar]
- Thrane, J.; Zibar, D.; Christiansen, H.L. Model-aided deep learning method for path loss prediction in mobile communication systems at 2.6 GHz. IEEE Access 2020, 8, 7925–7936. [Google Scholar] [CrossRef]
- Timoteo, R.D.A.; Cunha, D.C.; Cavalcanti, G.D.C. A Proposal for Path Loss Prediction in Urban Environments Using Support Vector Regression. In Proceedings of the Tenth Advanced International Conference on Telecommunications, Paris, France, 20–24 July 2014; pp. 119–124. [Google Scholar]
- Chall, R.E.; Lahoud, S.; Helou, M.E. LoRaWAN Network Radio Propagation Models and Performance Evaluation in Various Environments in Lebanon. IEEE Internet Things J. 2019, 6, 2366–2378. [Google Scholar] [CrossRef]
- Popoola, S.I.; Adetiba, E.; Atayero, A.A.; Faruk, N.; Calafate, C.T. Optimal model for path loss predictions using feed-forward neural networks. Cogent Eng. 2018, 5, 1. [Google Scholar] [CrossRef]
- Carvalho, A.A.P.D.; Batalha, I.S.; Neto, M.A.; Castro, B.L.; Barros, F.J.B. Adjusting Large-Scale Propagation Models for the Amazon Region Using Bioinspired Algorithms at 1.8 and 2.6 GHz Frequencies. J. Microw. Optoelectron. Electromagn. Appl. 2021, 20, 445–463. [Google Scholar] [CrossRef]
- Popoola, S.I.; Atayero, A.A.; Arausi, O.D.; Matthews, V.O. Path loss Dataset for Modeling Radio Wave Propagation in Smart Campus Environment. Data Br. 2018, 17, 1062–1073. [Google Scholar] [CrossRef]
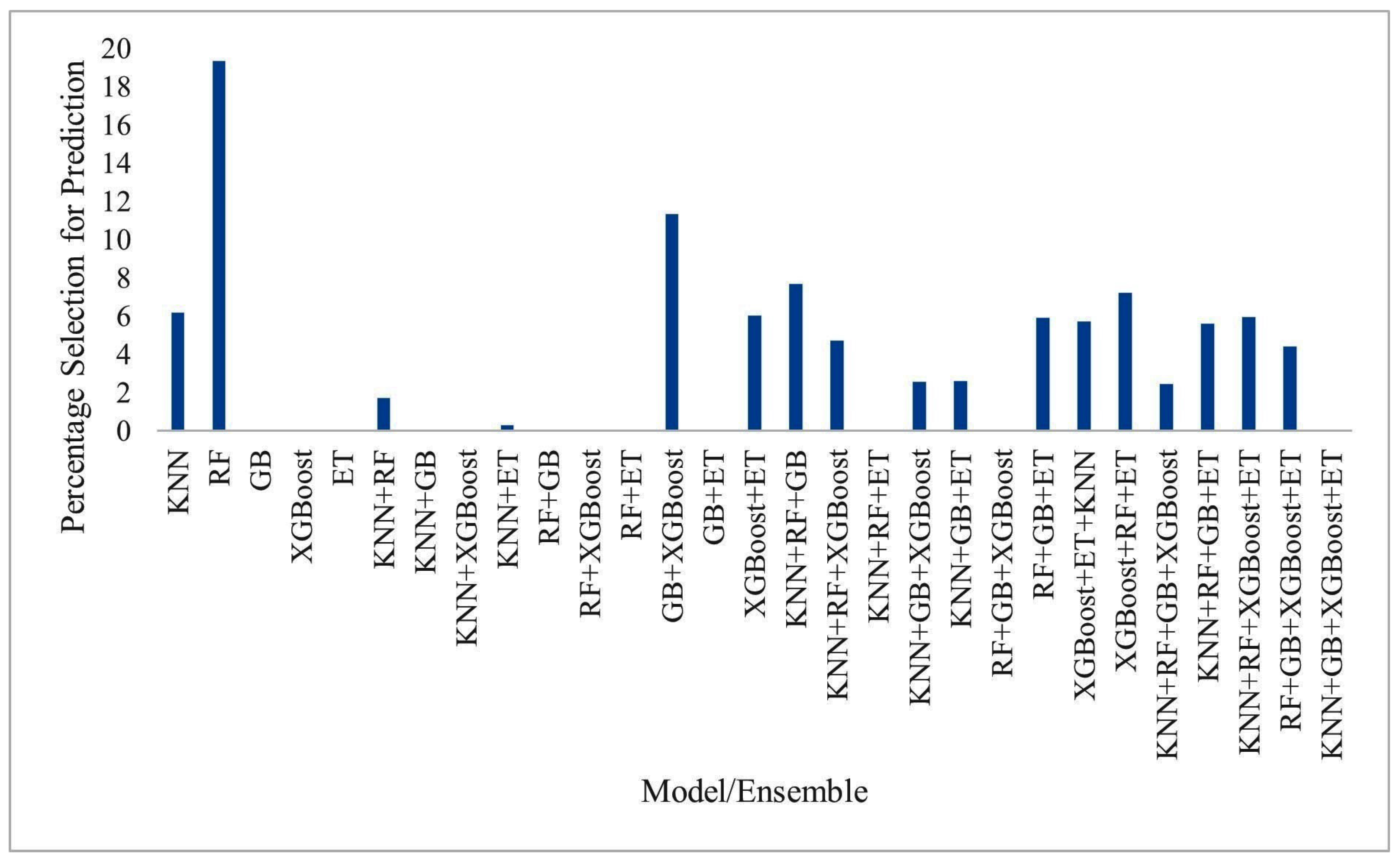


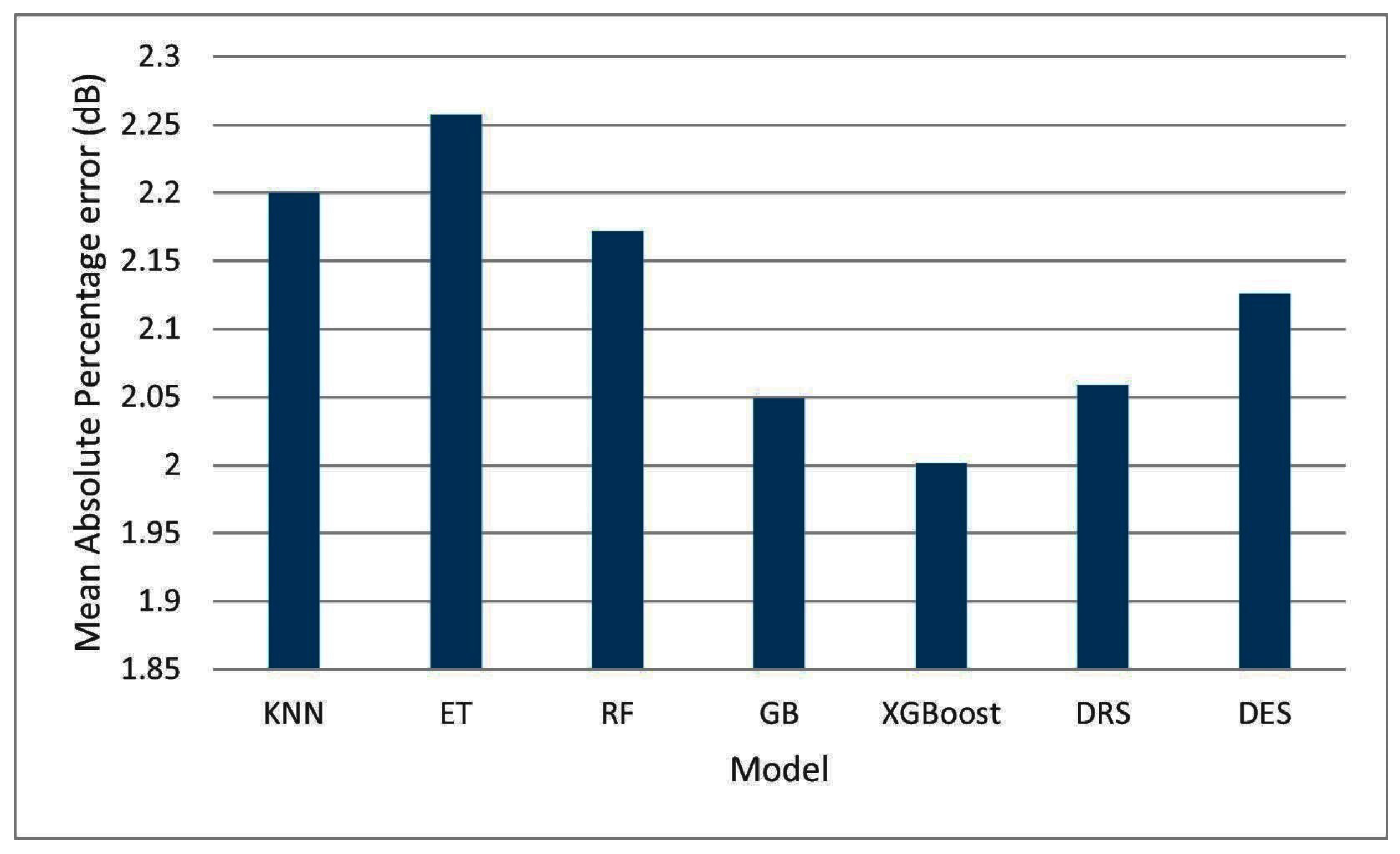
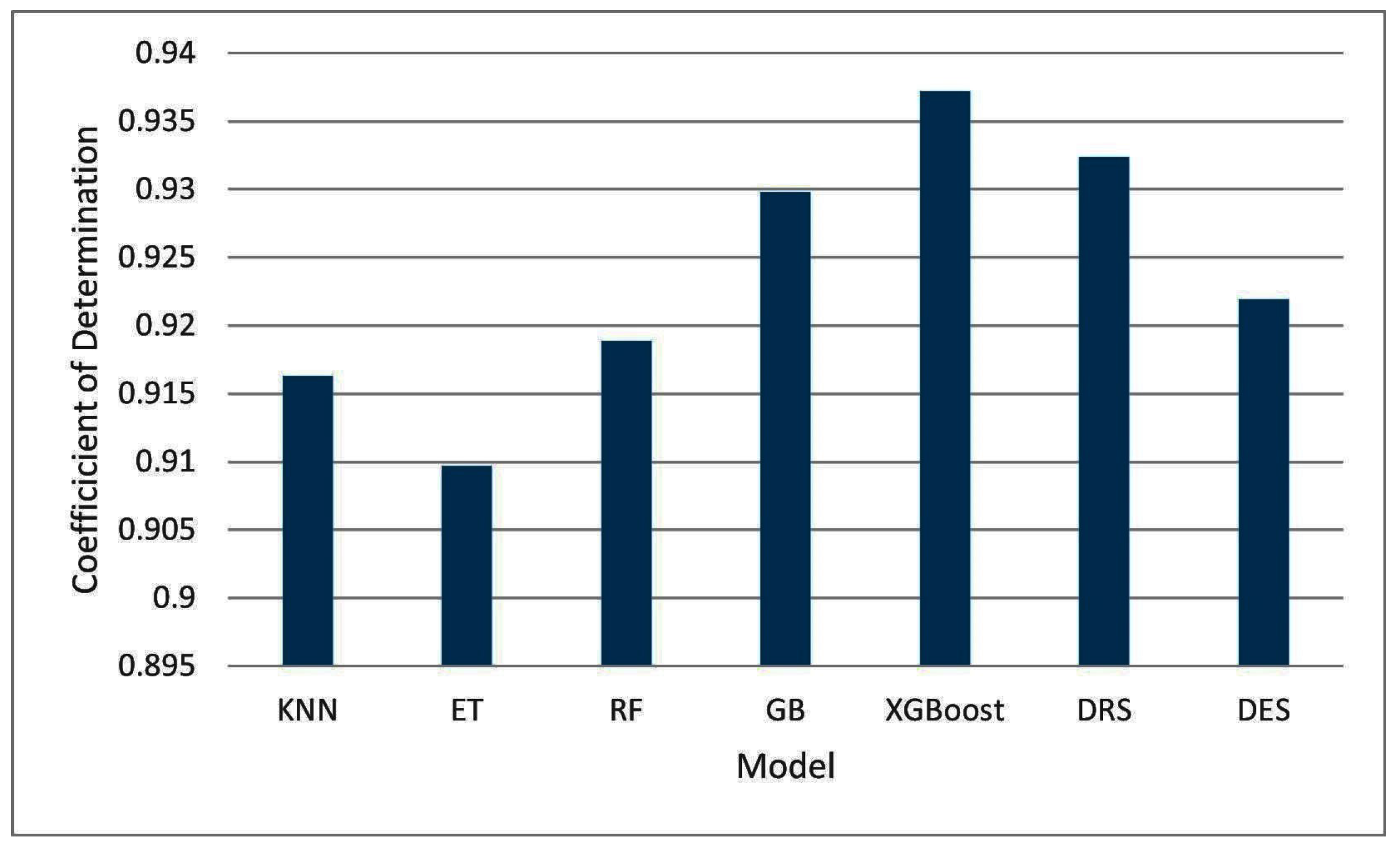
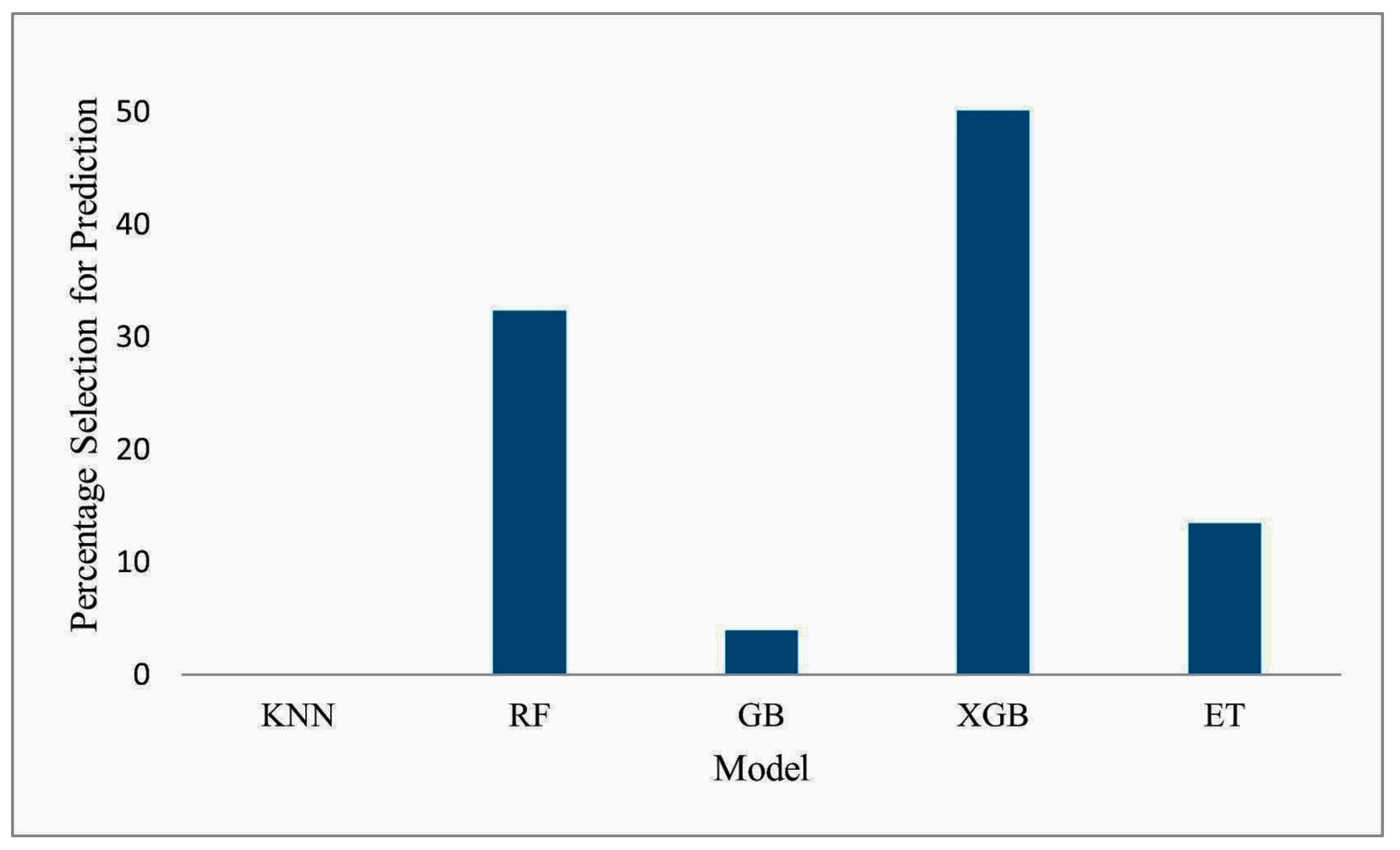
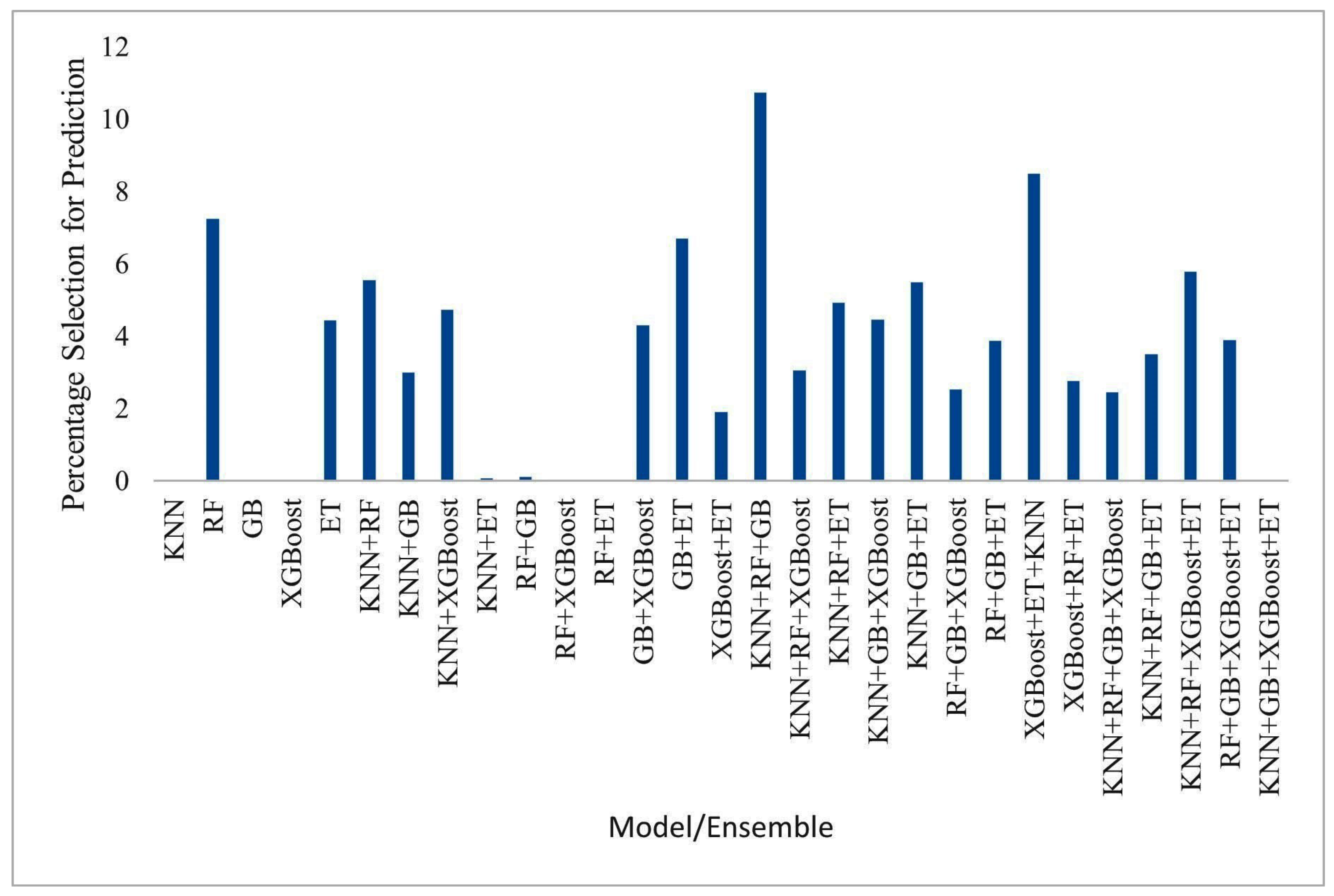


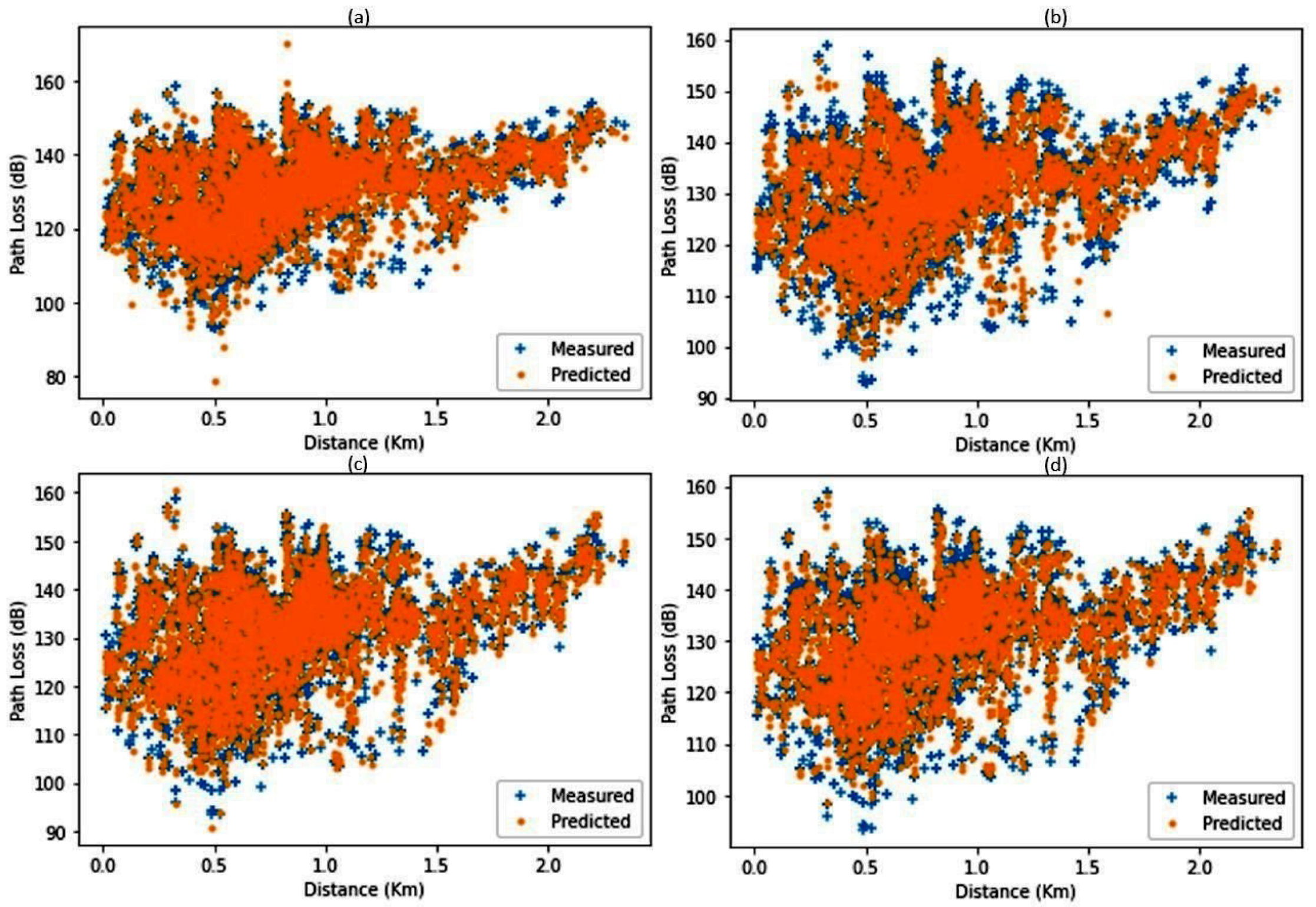
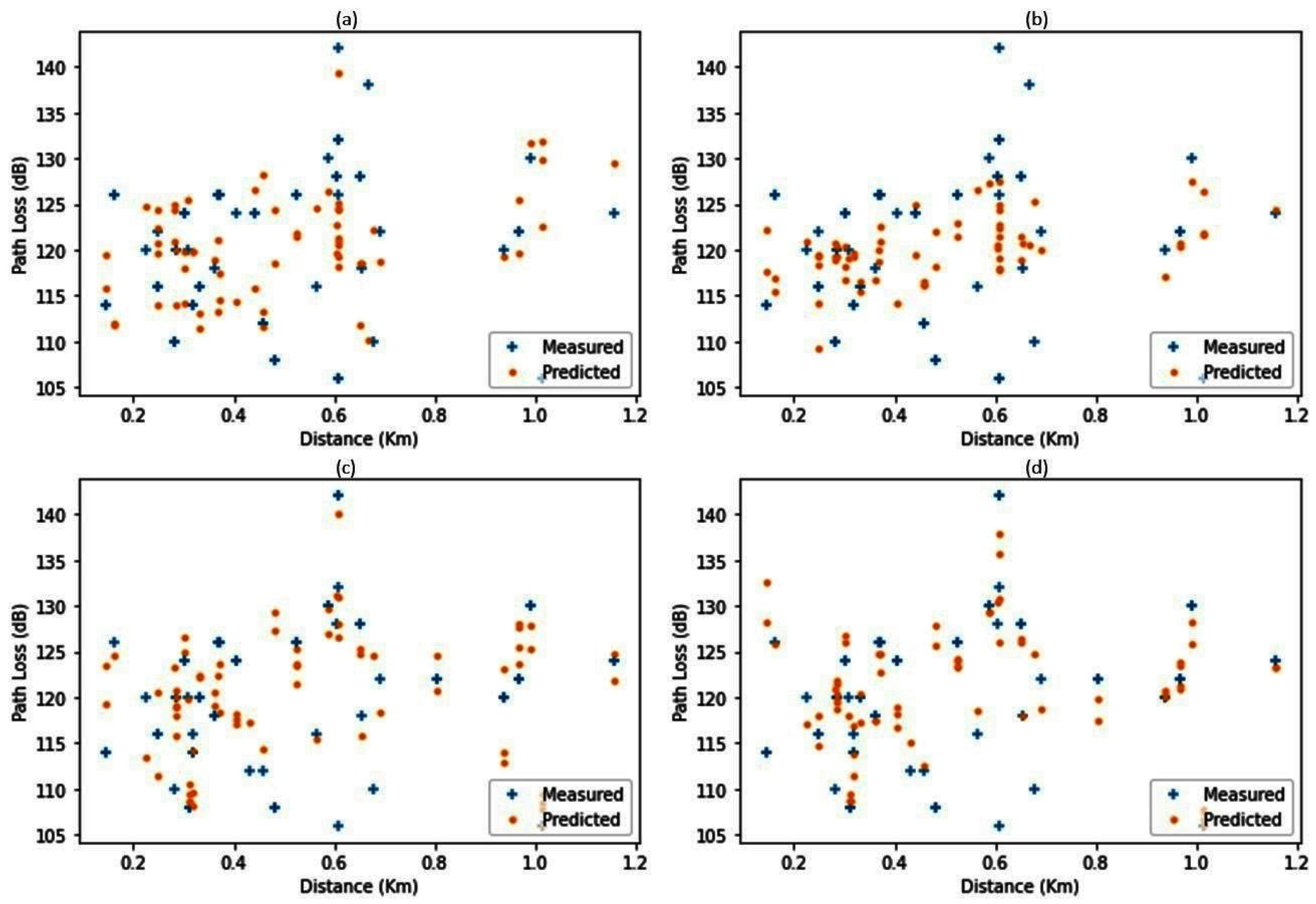
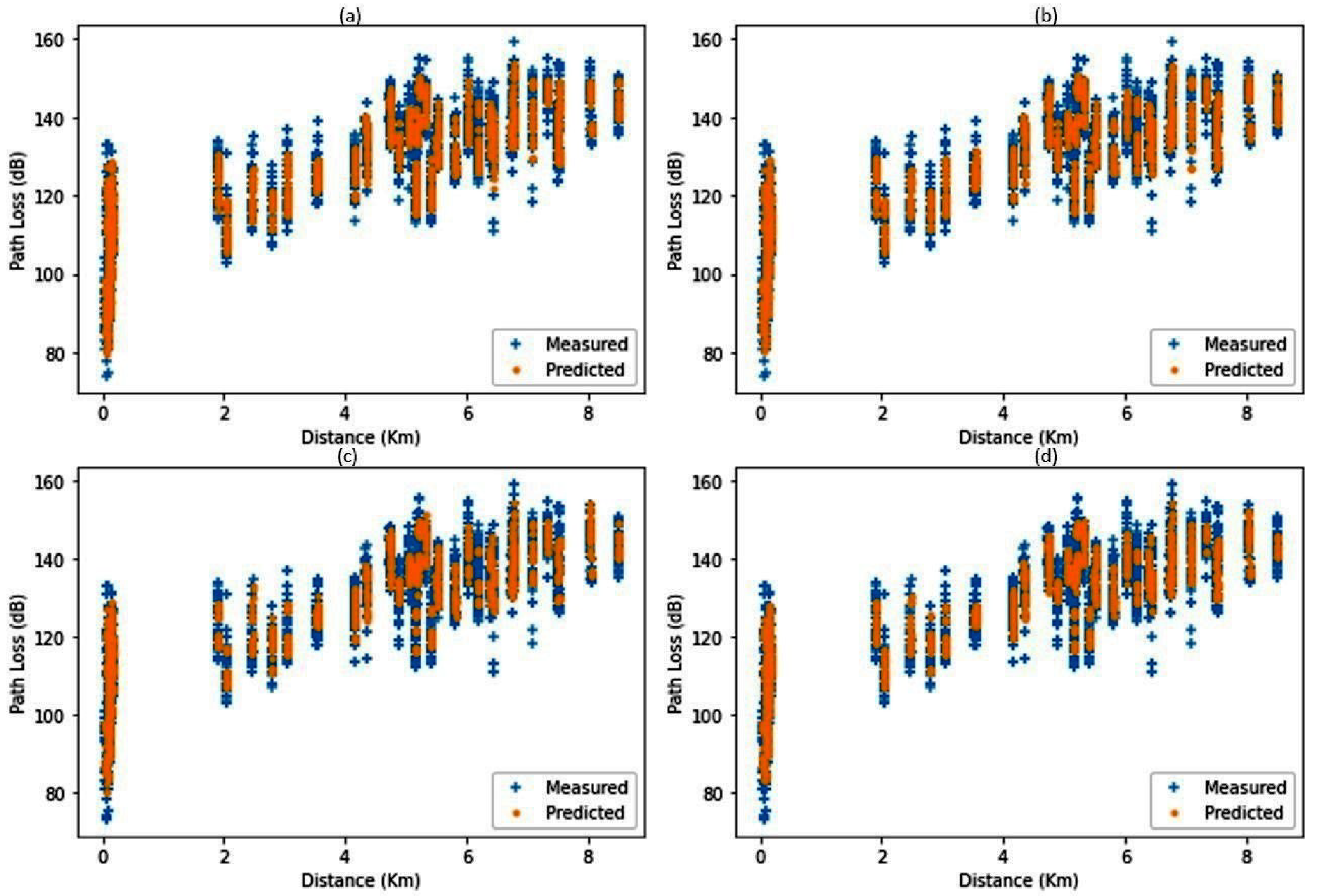
| Dataset | Size | Features |
|---|---|---|
| Dataset 1 | 12,369 | Distance, elevation of transmitter position, elevation of receiver position, frequency, height of transmitting antenna, height of receiving antenna, clutter height, latitude, longitude, distance in latitude between transmitting and receiving antenna, and distance in longitude between transmitting and receiving antenna. |
| Dataset 2 | 12,369 | Distance, elevation of transmitter position, elevation of receiver position, frequency, height of transmitting antenna, height of receiving antenna, distance in latitude between transmitting and receiving antenna, distance in longitude between transmitting and receiving antenna, and others extracted from satellite images using a CNN and GLCM. |
| Two Algorithms | Three Algorithms | Four Algorithm |
|---|---|---|
| KNN+RF | KNN+RF+GB | KNN+RF+GB+XGBoost |
| KNN+GB | KNN+RF+XGBoost | KNN+RF+GB+ET |
| KNN+XGBoost | KNN+RF+ET | KNN+RF+XGBoost+ET |
| KNN+ET | KNN+GB+XGBoost | KNN+GB+XGBoost+ET |
| RF+GB | KNN+GB+ET | RF+GB+XGBoost+ET |
| RF+XGBoost | RF+GB+XGBoost | |
| RF+ET | RF+GB+ET | |
| GB+XGBoost | XGBoost+ET+KNN | |
| GB+ET | XGBoost+RF+ET | |
| XGBoost+ET |
| Algorithm | Environment | Band | MAE (dB) | RMSE (dB) | MAPE (dB) | |
|---|---|---|---|---|---|---|
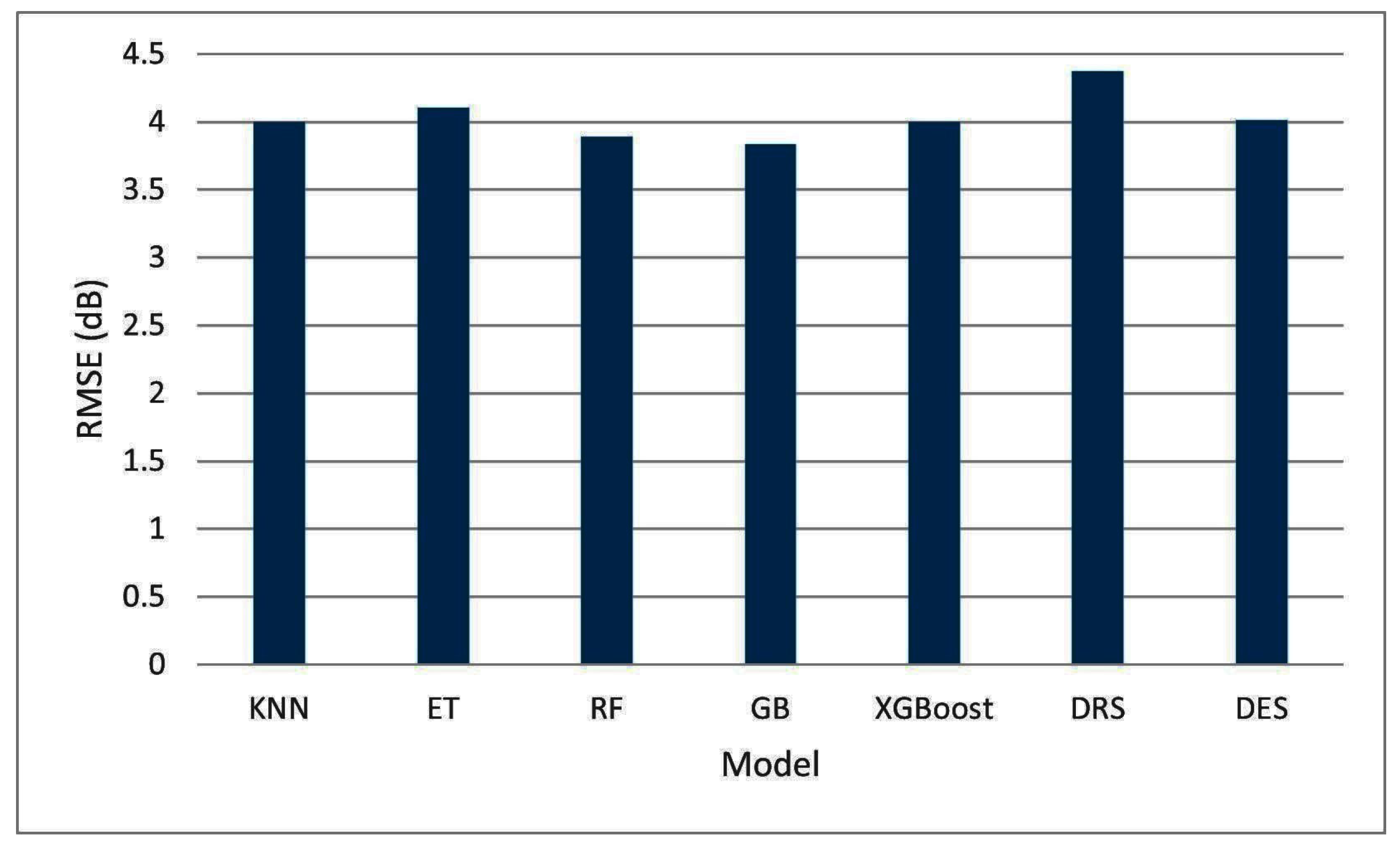
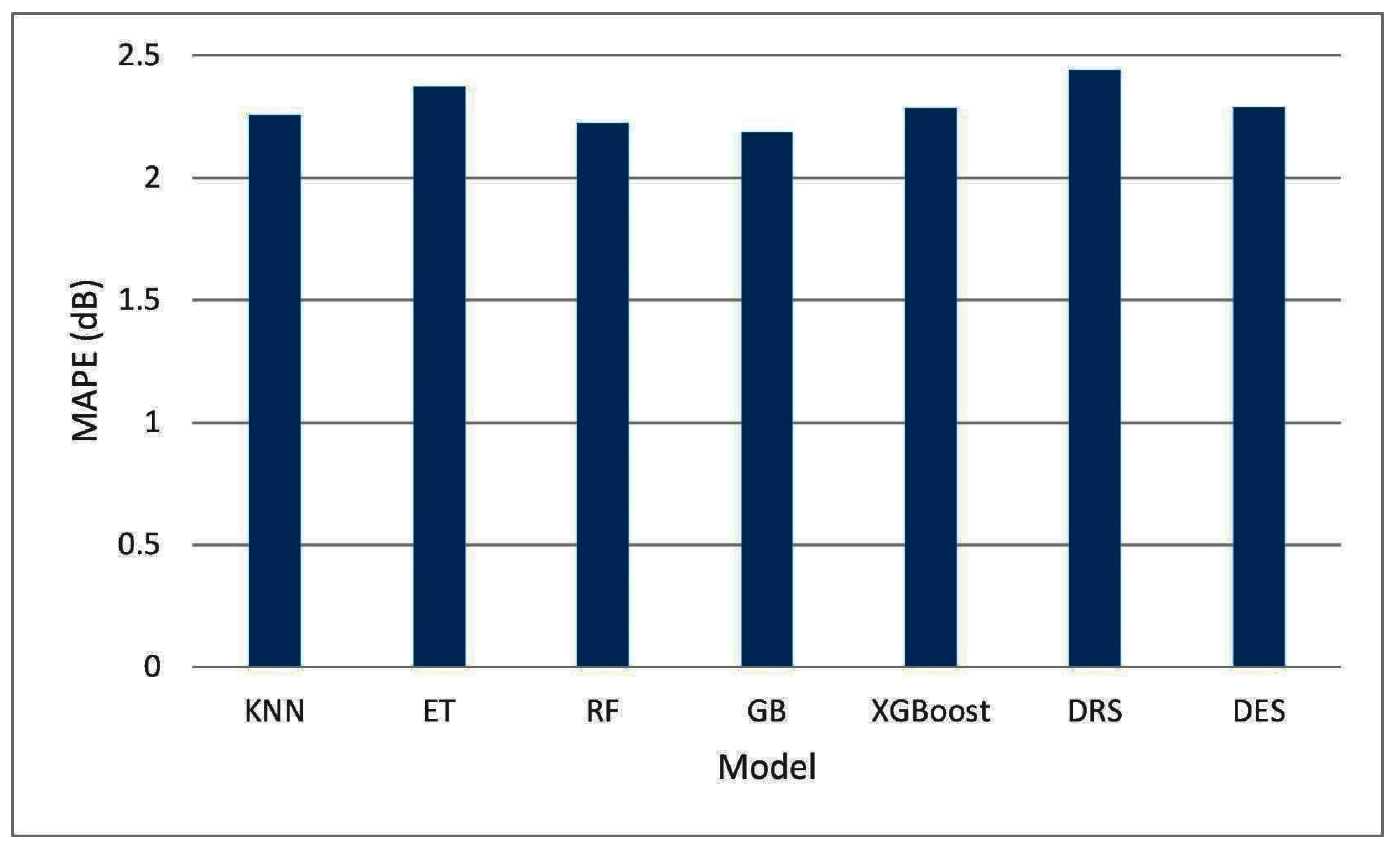
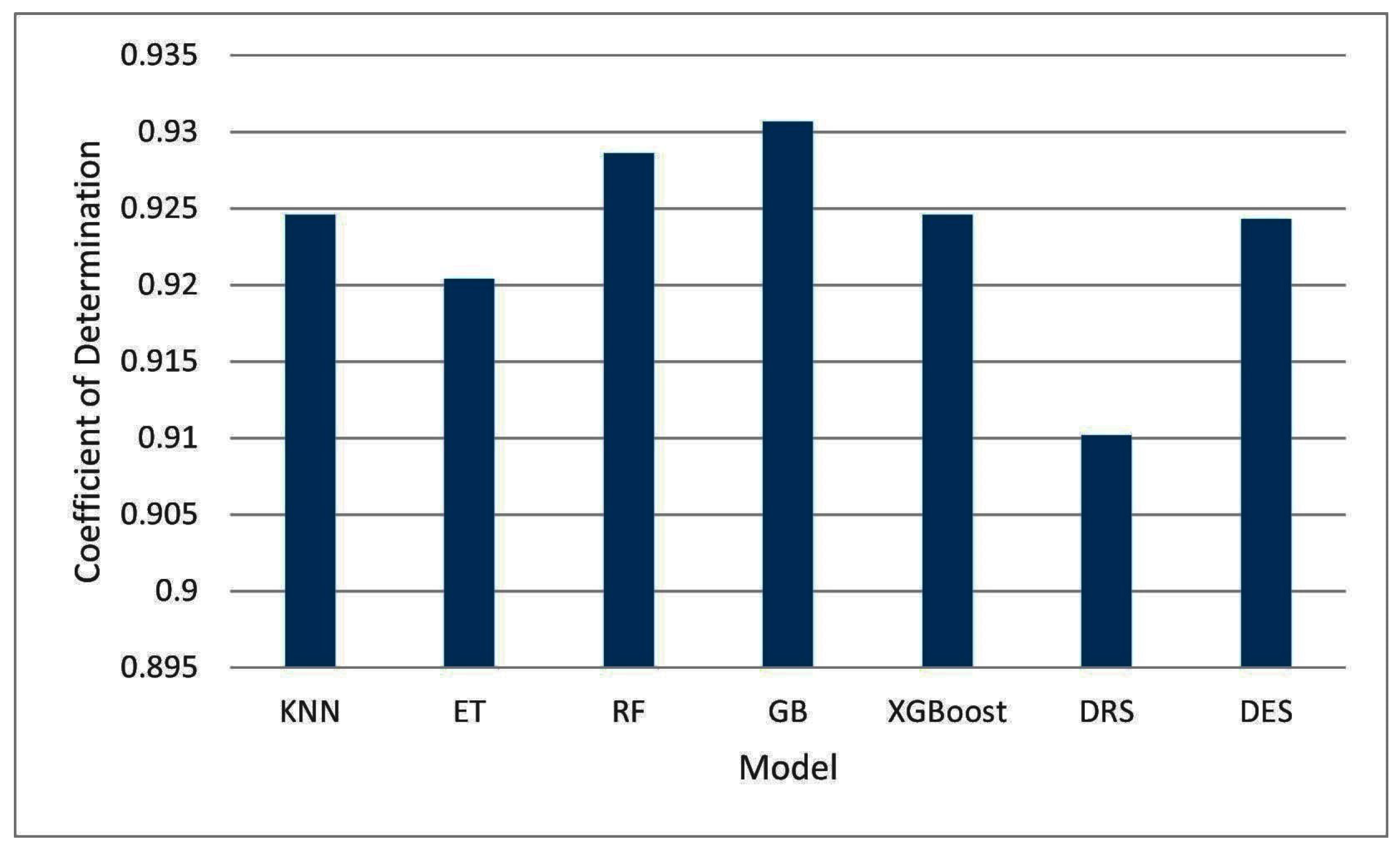
| KNN | All | All | 2.9275 | 3.9998 | 2.2583 | 0.9246 |
| Rural | 800 | 2.7144 | 3.7026 | 2.1330 | 0.9426 | |
| Suburban | 1800 | 2.2862 | 3.0839 | 1.6192 | 0.8822 | |
| Urban | 1800 | 3.4695 | 4.5189 | 2.7069 | 0.8324 | |
| Urban | 2100 | 6.5301 | 8.1102 | 5.5187 | −0.1391 | |
| Urban highrise | 800 | 3.2147 | 4.4396 | 2.5911 | 0.9164 | |
| ET | All | All | 3.0745 | 4.1078 | 2.3708 | 0.9204 |
| Rural | 800 | 2.5712 | 3.4693 | 2.0220 | 0.9496 | |
| Suburban | 1800 | 2.7102 | 3.5857 | 1.9239 | 0.8409 | |
| Urban | 1800 | 3.7666 | 4.8619 | 2.9531 | 0.8060 | |
| Urban | 2100 | 6.2294 | 7.6968 | 5.2703 | −0.0265 | |
| Urban highrise | 800 | 3.1145 | 4.2043 | 2.5288 | 0.9251 | |
| RF | All | All | 2.8815 | 3.8908 | 2.2217 | 0.9286 |
| Rural | 800 | 2.5706 | 3.4623 | 2.0231 | 0.9483 | |
| Suburban | 1800 | 2.3280 | 3.1457 | 1.6524 | 0.8775 | |
| Urban | 1800 | 3.5618 | 4.5681 | 2.7833 | 0.8287 | |
| Urban | 2100 | 6.3881 | 7.7169 | 5.3807 | −0.0317 | |
| Urban highrise | 800 | 3.0375 | 4.1677 | 2.4474 | 0.9263 | |
| GB | All | All | 2.8426 | 3.8350 | 2.1867 | 0.9307 |
| Rural | 800 | 2.5310 | 3.4443 | 1.9902 | 0.9504 | |
| Suburban | 1800 | 2.3529 | 3.1345 | 1.6669 | 0.8784 | |
| Urban | 1800 | 3.3723 | 4.3239 | 2.624 | 0.8465 | |
| Urban | 2100 | 6.6264 | 8.0565 | 5.6001 | −0.1262 | |
| Urban highrise | 800 | 3.0486 | 4.1866 | 2.4559 | 0.9257 | |
| XGBoost | All | All | 2.9690 | 3.9983 | 2.2851 | 0.9246 |
| Rural | 800 | 2.5450 | 3.4336 | 2.0023 | 0.9498 | |
| Suburban | 1800 | 2.5150 | 3.3566 | 1.7824 | 0.8605 | |
| Urban | 1800 | 3.6179 | 4.6663 | 2.8194 | 0.8212 | |
| Urban | 2100 | 6.5289 | 8.0822 | 5.5532 | −0.1364 | |
| Urban highrise | 800 | 3.1112 | 4.2227 | 0.5110 | 0.9244 | |
| DRS | All | All | 3.1692 | 4.3757 | 2.4396 | 0.9102 |
| Rural | 800 | 2.7258 | 3.7340 | 2.1339 | 0.9386 | |
| Suburban | 1800 | 2.5977 | 3.6892 | 1.8464 | 0.8342 | |
| Urban | 1800 | 4.0672 | 5.3260 | 3.1717 | 0.7665 | |
| Urban | 2100 | 8.9912 | 10.8677 | 7.5460 | −0.4363 | |
| Urban highrise | 800 | 3.2588 | 4.4808 | 2.6139 | 0.9139 | |
| DES | All | All | 2.9677 | 4.0145 | 2.2865 | 0.9243 |
| Rural | 800 | 2.5001 | 3.3901 | 1.9599 | 0.9494 | |
| Suburban | 1800 | 2.5173 | 3.4173 | 1.7887 | 0.8579 | |
| Urban | 1800 | 3.6356 | 4.7048 | 2.8484 | 0.8178 | |
| Urban | 2100 | 8.0006 | 9.6230 | 6.7360 | −0.1095 | |
| Urban highrise | 800 | 3.2326 | 4.4335 | 2.5864 | 0.9156 |
| Algorithm | Environment | Band | MAE (dB) | RMSE (dB) | MAPE (dB) | |
|---|---|---|---|---|---|---|
| KNN | All | All | 2.8328 | 4.2307 | 2.1997 | 0.9163 |
| Rural | 800 | 3.2276 | 3.2429 | 1.9116 | 0.9572 | |
| Suburban | 1800 | 3.2429 | 2.7357 | 1.4274 | 0.9085 | |
| Urban | 1800 | 3.5979 | 5.7336 | 2.8139 | 0.7278 | |
| Urban | 2100 | 3.2622 | 5.4613 | 2.8540 | 0.5099 | |
| Urban highrise | 800 | 3.2276 | 4.3935 | 2.6034 | 0.9151 | |
| ET | All | All | 2.9058 | 4.3627 | 2.2577 | 0.9097 |
| Rural | 800 | 2.5786 | 3.3885 | 2.0477 | 0.9533 | |
| Suburban | 1800 | 2.0481 | 2.7567 | 1.4506 | 0.9071 | |
| Urban | 1800 | 3.4708 | 5.8460 | 2.7077 | 0.7171 | |
| Urban | 2100 | 3.6348 | 6.0512 | 3.1511 | 0.3940 | |
| Urban highrise | 800 | 3.5089 | 4.7502 | 2.8289 | 0.9007 | |
| RF | All | All | 2.8086 | 4.1584 | 2.1721 | 0.9189 |
| Rural | 800 | 2.4753 | 3.3440 | 1.9460 | 0.9525 | |
| Suburban | 1800 | 2.1655 | 2.8948 | 1.5350 | 0.9006 | |
| Urban | 1800 | 3.3866 | 5.3520 | 2.6453 | 0.7589 | |
| Urban | 2100 | 4.4750 | 6.2959 | 3.7403 | 0.2986 | |
| Urban highrise | 800 | 3.1117 | 4.2989 | 2.4969 | 0.9199 | |
| GB | All | All | 2.6485 | 3.8459 | 2.0491 | 0.9298 |
| Rural | 800 | 2.3876 | 3.2406 | 1.8802 | 0.9573 | |
| Suburban | 1800 | 2.0517 | 2.7599 | 1.4552 | 0.9068 | |
| Urban | 1800 | 3.0806 | 4.7584 | 2.4096 | 0.8125 | |
| Urban | 2100 | 3.9586 | 6.4257 | 3.4343 | 0.3257 | |
| Urban highrise | 800 | 3.0938 | 4.2769 | 2.4810 | 0.9195 | |
| XGBoost | All | All | 2.5848 | 3.6680 | 2.0013 | 0.9372 |
| Rural | 800 | 2.4384 | 3.2622 | 1.9201 | 0.9557 | |
| Suburban | 1800 | 1.9314 | 2.6362 | 1.3675 | 0.9150 | |
| Urban | 1800 | 3.5975 | 5.4851 | 2.8129 | 0.7509 | |
| Urban | 2100 | 5.0399 | 6.7689 | 4.2441 | 0.2529 | |
| Urban highrise | 800 | 3.1088 | 4.2639 | 2.4914 | 0.9200 | |
| DRS | All | All | 2.6593 | 3.7806 | 2.0589 | 0.9324 |
| Rural | 800 | 2.5577 | 3.4003 | 2.0296 | 0.9481 | |
| Suburban | 1800 | 1.9843 | 2.6724 | 1.4027 | 0.9096 | |
| Urban | 1800 | 2.8381 | 4.1750 | 2.2091 | 0.8469 | |
| Urban | 2100 | 3.8718 | 5.6792 | 3.3268 | 0.5023 | |
| Urban highrise | 800 | 3.1815 | 4.4501 | 2.5533 | 0.9129 | |
| DES | All | All | 2.7452 | 4.0631 | 2.1262 | 0.9219 |
| Rural | 800 | 2.4446 | 3.2896 | 1.9307 | 0.9514 | |
| Suburban | 1800 | 2.0217 | 2.7029 | 1.4285 | 0.9076 | |
| Urban | 1800 | 3.1749 | 5.0792 | 2.4751 | 0.7732 | |
| Urban | 2100 | 3.0924 | 5.1577 | 2.6625 | 0.5885 | |
| Urban highrise | 800 | 3.2138 | 4.4460 | 2.5860 | 0.9131 |
| Empirical Model | Frequency Range (MHz) | Transmitting Antenna Height Range (m) | Receiving Antenna Height Range (m) | Distance Range (km) |
|---|---|---|---|---|
| Egli [60] | [40, 1000] | n/a | 10 and 10 | [1, 80] |
| Ericsson 999 [61] | [150, 1900] | [30, 300] | [1, 10] | [1, 20] |
| COST-231 Hata [62] | [1500, 2000] | [30, 200] | [1, 10] | [1, 20] |
| Dataset | RMSE in Original Work (dB) | RMSE with Proposed DES Method (dB) |
|---|---|---|
| [63] at 811 MHz | ≈4.1000 | 3.4420 |
| [63] at 2630 MHz | ≈4.2500 | 2.2058 |
| [64] | 1.7600 | 4.2061 |
| [65] for Rural | 10.2844 | 3.2203 |
| [65] for Urban highrise | 6.4300 | 4.3679 |
| [66,68] | 6.2700 | 2.6780 |
| [67] | 3.8000–6.5400 | 3.2415–5.1490 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sani, U.S.; Malik, O.A.; Lai, D.T.C. Dynamic Regressor/Ensemble Selection for a Multi-Frequency and Multi-Environment Path Loss Prediction. Information 2022, 13, 519. https://doi.org/10.3390/info13110519
Sani US, Malik OA, Lai DTC. Dynamic Regressor/Ensemble Selection for a Multi-Frequency and Multi-Environment Path Loss Prediction. Information. 2022; 13(11):519. https://doi.org/10.3390/info13110519
Chicago/Turabian StyleSani, Usman Sammani, Owais Ahmed Malik, and Daphne Teck Ching Lai. 2022. "Dynamic Regressor/Ensemble Selection for a Multi-Frequency and Multi-Environment Path Loss Prediction" Information 13, no. 11: 519. https://doi.org/10.3390/info13110519
APA StyleSani, U. S., Malik, O. A., & Lai, D. T. C. (2022). Dynamic Regressor/Ensemble Selection for a Multi-Frequency and Multi-Environment Path Loss Prediction. Information, 13(11), 519. https://doi.org/10.3390/info13110519






