Improving Map Matching of Floating Car Data with Artificial Intelligence Techniques
Abstract
1. Introduction
2. State-of-the-Art Method
Attention Mechanism
3. Materials and Methods
3.1. Case Study
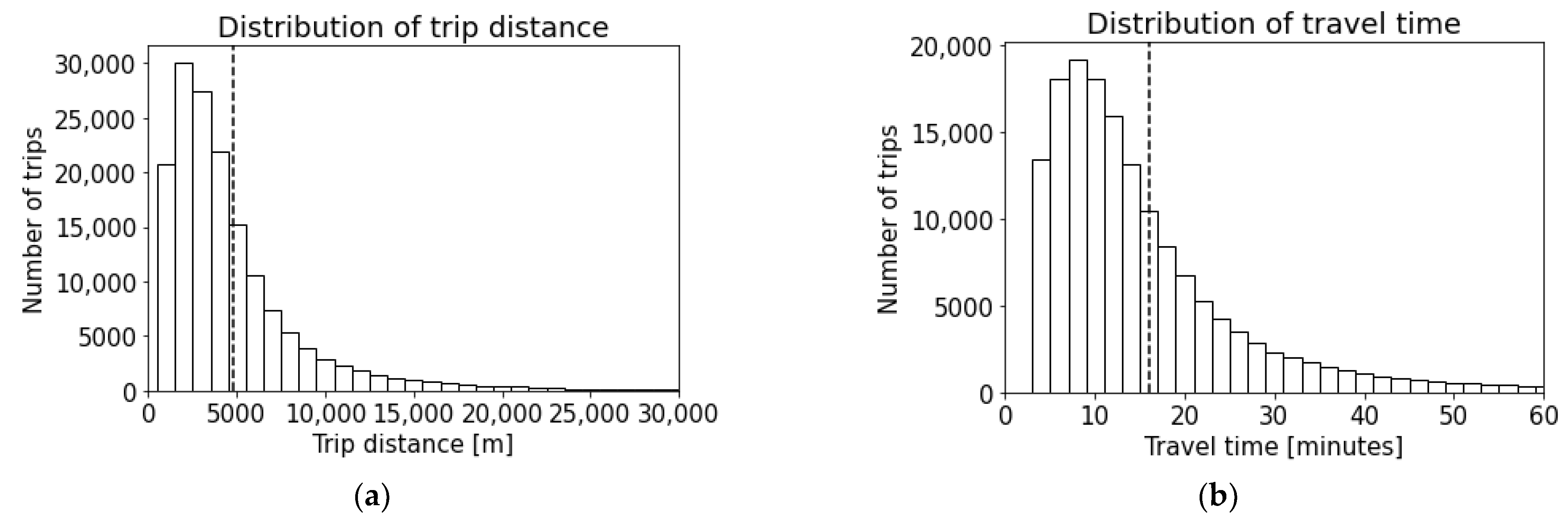
3.2. Data
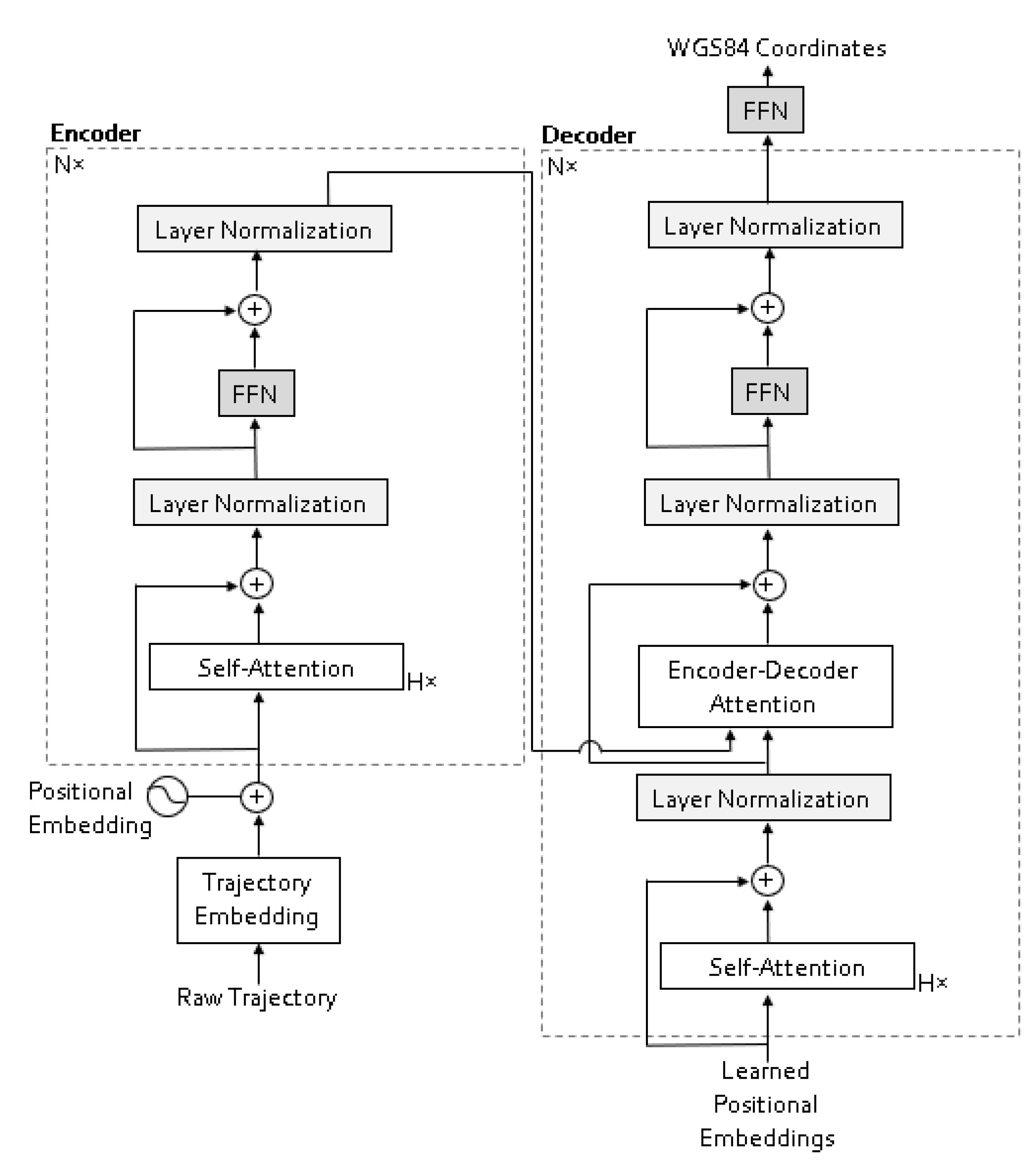
3.3. Model Architecture
3.3.1. Input Embedding
3.3.2. Encoder–Decoder
3.3.3. Regression Head
3.4. Technical Details
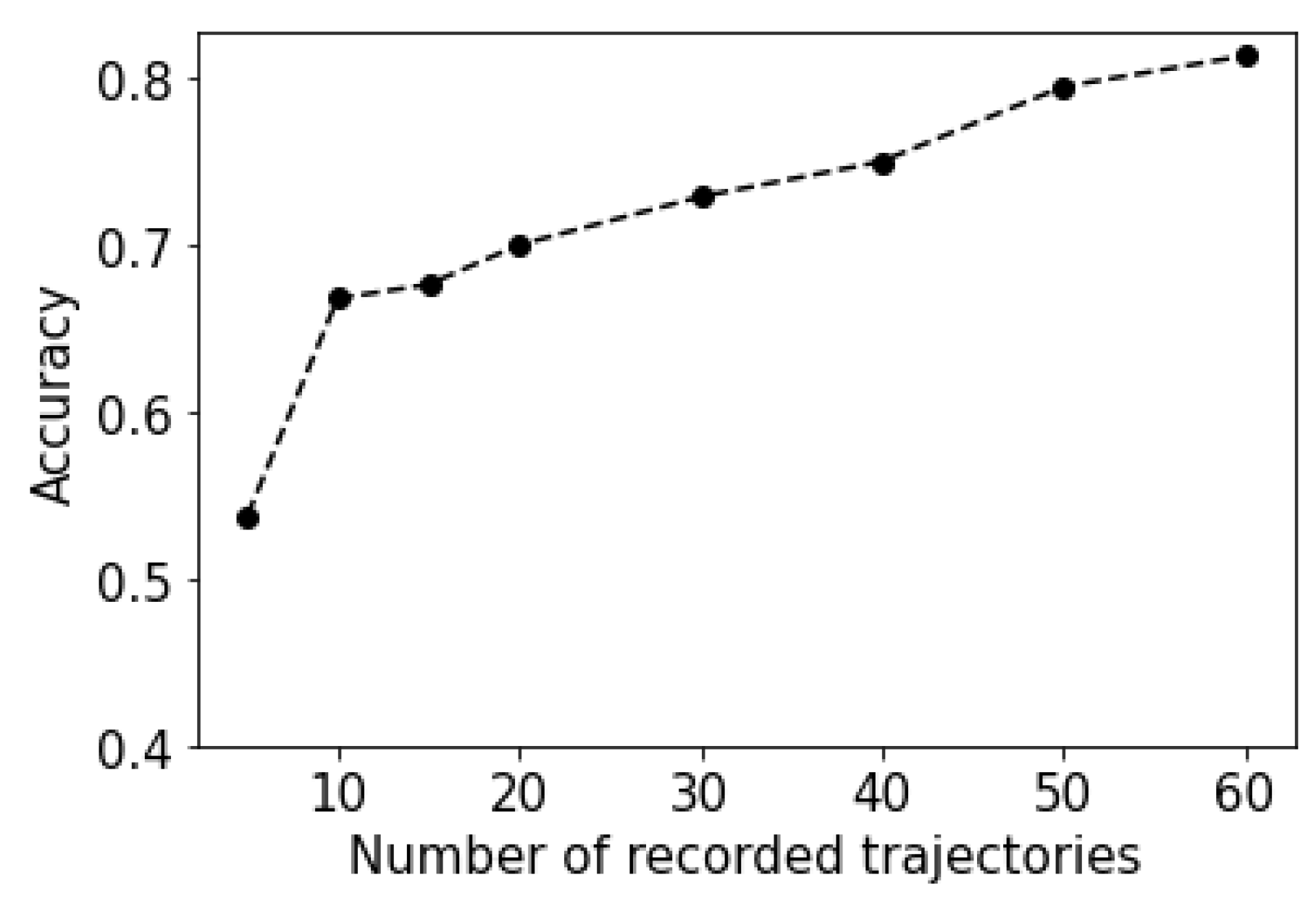
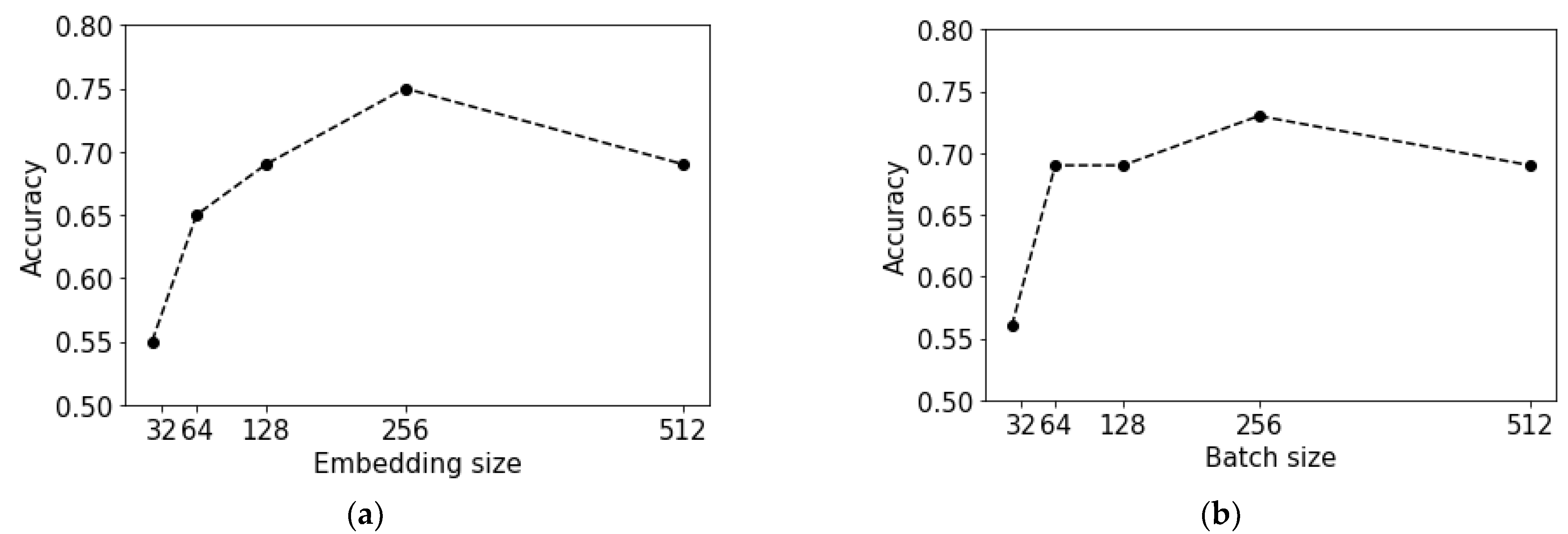
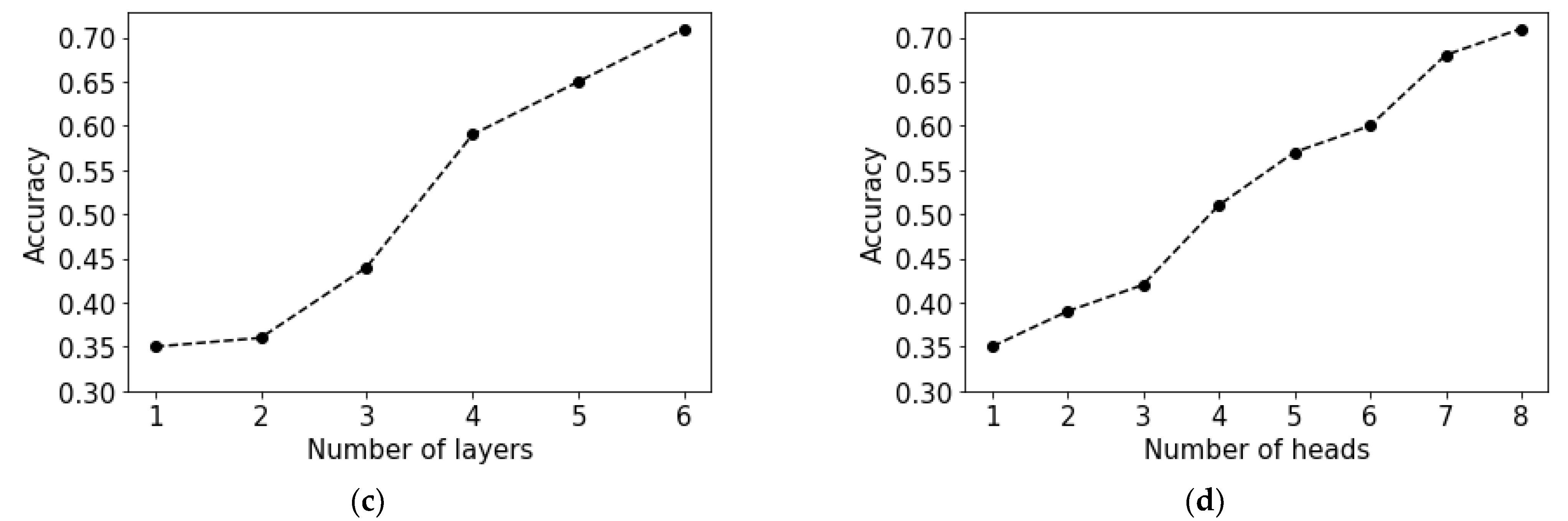
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, J.; Zheng, Y.; Xie, X.; Sun, G. T-Drive: Enhancing Driving Directions with Taxi Drivers’ Intelligence. IEEE Trans. Knowl. Data Eng. 2013, 25, 220–232. [Google Scholar] [CrossRef]
- Stenneth, L.; Wolfson, O.; Yu, P.S.; Xu, B. Transportation mode detection using mobile phones and GIS information. In Proceedings of the 19th SIGSPATIAL International Conference on Advances in Geographic Information Systems, Chicago, IL, USA, 1–4 November 2011. [Google Scholar] [CrossRef]
- Nair, R.; Miller-Hooks, E. Fleet Management for Vehicle Sharing Operations. Transp. Sci. 2011, 45, 524–540. [Google Scholar] [CrossRef]
- Rahmani, M.; Koutsopoulos, H.N.; Jenelius, E. Travel time estimation from sparse floating car data with consistent path inference: A fixed point approach. Transp. Res. Part C Emerg. Technol. 2017, 85, 628–643. [Google Scholar] [CrossRef]
- Sharath, M.; Velaga, N.R.; Quddus, M.A. A dynamic two-dimensional (D2D) weight-based map-matching algorithm. Transp. Res. Part C Emerg. Technol. 2019, 98, 409–432. [Google Scholar] [CrossRef]
- Toledo-Moreo, R.; Betaille, D.; Peyret, F. Lane-Level Integrity Provision for Navigation and Map Matching with GNSS, Dead Reckoning, and Enhanced Maps. IEEE Trans. Intell. Transp. Syst. 2010, 11, 100–112. [Google Scholar] [CrossRef]
- Merry, K.; Bettinger, P. Smartphone GPS accuracy study in an urban environment. PLoS ONE 2019, 14, e0219890. [Google Scholar] [CrossRef]
- Mohamed, R.; Aly, H.; Youssef, M. Youssef, Accurate Real-time Map Matching for Challenging Environments. IEEE Trans. Intell. Transp. 2017, 18, 847–857. [Google Scholar] [CrossRef]
- Kos, S.; Brčić, D.; Musulin, I. Smartphone application GPS performance during various space weather conditions: A preliminary study. In Proceedings of the 21st International Symposium on Electronics in Transport ISEP 2013, Ljubljana, Slovenia, 25–26 March 2013; Available online: https://www.bib.irb.hr/623174 (accessed on 30 August 2022).
- Quddus, M.A.; Ochieng, W.Y.; Noland, R.B. Current map-matching algorithms for transport applications: State-of-the art and future research directions. Transp. Res. Part C Emerg. Technol. 2007, 15, 312–328. [Google Scholar] [CrossRef]
- Lü, W.; Zhu, T.; Wu, D.; Dai, H.; Huang, J. A heuristic path-estimating algorithm for large-scale real-time traffic information calculating. Sci. China Ser. E Technol. Sci. 2008, 51, 165–174. [Google Scholar] [CrossRef]
- Teng, W.; Wang, Y. Real-Time Map Matching: A New Algorithm Integrating Spatio-Temporal Proximity and Improved Weighted Circle. Open Geosci. 2019, 11, 288–297. [Google Scholar] [CrossRef]
- Kubicka, M.; Cela, A.; Mounier, H.; Niculescu, S.-I. Comparative Study and Application-Oriented Classification of Vehicular Map-Matching Methods. IEEE Intell. Transp. Syst. Mag. 2018, 10, 150–166. [Google Scholar] [CrossRef]
- Chao, P.; Xu, Y.; Hua, W.; Zhou, X. A Survey on Map-Matching Algorithms. In Proceedings of the ADC 2020: Databases Theory and Applications, Melbourne, Australia, 3–7 February 2020. [Google Scholar] [CrossRef]
- Hashemi, M.; Karimi, H.A. A critical review of real-time map-matching algorithms: Current issues and future directions. Comput. Environ. Urban Syst. 2014, 48, 153–165. [Google Scholar] [CrossRef]
- Gong, Y.-J.; Chen, E.; Zhang, X.; Ni, L.M.; Zhang, J. AntMapper: An Ant Colony-Based Map Matching Approach for Trajectory-Based Applications. IEEE Trans. Intell. Transp. Syst. 2018, 19, 390–401. [Google Scholar] [CrossRef]
- Newson, P.; Krumm, J. Hidden Markov map matching through noise and sparseness. In Proceedings of the GIS’09: 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009. [Google Scholar] [CrossRef]
- Jo, T.; Haseyama, M.; Kitajima, H. A map matching method with the innovation of the kalman filtering. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 1996, 79, 1853–1855. [Google Scholar]
- Kim, S.; Kim, J.; Hyun, I. Development of a map matching algorithm for car navigation system using fuzzy q-factor algorithm. In Proceedings of the 5th World Congress on Intelligent Transport Systems, Seoul, Korea, 12–16 October 1998; Available online: http://worldcat.org/isbn/899500732X (accessed on 30 August 2022).
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the A 31st International Conference on Neural Information Processing Systems—NIPS, Long Beach, CA, USA, 4–9 December 2017; Available online: https://dl.acm.org/doi/proceedings/10.5555/3295222 (accessed on 31 August 2022).
- Jin, Z.; Kim, J.; Yeo, H.; Choi, S. Transformer-based map-matching model with limited labeled data using transfer-learning approach. Transp. Res. Part C Emerg. Technol. 2022, 140, 103668. [Google Scholar] [CrossRef]
- Kamath, U.; Liu, J.; Whitaker, J. Deep Learning for NLP and Speech Recognition; Springer: Cham, Switzerland, 2019; pp. 407–419. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. In Proceedings of the ICLR 2015: International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. In Proceedings of the EMNLP 2014: Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Proceedings of the NIPS’14: 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 8–13 December 2014. [Google Scholar] [CrossRef]
- Lu, K.; Grover, A.; Abbeel, P.; Mordatch, I. Pretrained Transformers as Universal Computation Engines. arXiv 2021, arXiv:2103.05247. [Google Scholar]
- CERTH-HIT. Available online: https://www.imet.gr/index.php/en/ (accessed on 31 August 2022).
- Taxiway. Available online: https://taxiway.gr/ (accessed on 31 August 2022).
- Bratsas, C.; Koupidis, K.; Salanova, J.-M.; Giannakopoulos, K.; Kaloudis, A.; Ayfantopoulou, G. A Comparison of Machine Learning Methods for the Prediction of Traffic Speed in Urban Places. Sustainability 2019, 12, 142. [Google Scholar] [CrossRef]
- Grau, J.M.S.; Maciejewski, M.; Bischoff, J.; Estrada, M.; Tzenos, P.; Stamos, I. Use of probe data generated by taxis. In Big Data for Regional Science; Routledge Advances in Regional Economics, Science and Policy; Taylor & Francis Group: Abingdon, UK; ISBN 1138282189/9781138282186.
- Grau, J.M.S.; Mitsakis, E.; Tzenos, P.; Stamos, I.; Selmi, L.G. Ayfantopoulou, Multisource Data Framework for Road Traffic State Estimation. J. Adv. Transp. 2018, 2018, 9078547. [Google Scholar] [CrossRef]
- Ahlgren, P.; Jarneving, B.; Rousseau, R. Requirements for a cocitation similarity measure, with special reference to Pearson’s correlation coefficient. J. Am. Soc. Inf. Sci. Technol. 2003, 54, 550–560. [Google Scholar] [CrossRef]
- Graves, A. Generating Sequences with Recurrent Neural Networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Oord, A.v.d.; Li, Y.; Babuschkin, I.; Simonyan, K.; Vinyals, O.; Kavukcuoglu, K.; Driessche, G.v.d.; Lockhart, E.; Cobo, L.C.; Stimberg, F.; et al. Parallel WaveNet: Fast High-Fidelity Speech Synthesis. In Proceedings of the Machine Learning Research—MLR, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Ghazvininejad, M.; Levy, O.; Liu, Y.; Zettlemoyer, L. Mask-Predict: Parallel Decoding of Conditional Masked Language Models. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 3–7 November 2019. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019. [Google Scholar]
- Chan, W.; Saharia, C.; Hinton, G.; Norouzi, M.; Jaitly, N. Imputer: Sequence Modelling via Imputation and Dynamic Programming. In Proceedings of the 37th International Conference on Machine Learning, Virtual Event, 13–18 July 2020. [Google Scholar]
- Carion, N.; Kirillov, A.; Massa, F.; Synnaeve, G.; Usunier, N.; Zagoruyko, S. End-to-end object detection with Transformers. In Proceedings of the 16th European Conference on Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Guido, V.R.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the 33rd Conference on Neural Information Processing Systems—NeurIPS2019, Vancouver, Canada, 8–14 December 2019. [Google Scholar]
- Gehring, J.; Auli, M.; Grangier, D.; Yarats, D.; Dauphin, Y.N. Convolutional Sequence to Sequence Learning. In ICML'17: Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition—CVPR, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Artificial Intelligence and Statistics—AISTATS, Sardinia, Italy, 13–15 May 2010; Available online: http://proceedings.mlr.press/v9/glorot10a.html (accessed on 29 August 2022).
- Feng, J.; Li, Y.; Zhao, K.; Xu, Z.; Xia, T.; Zhang, J.; Jin, D. DeepMM: Deep Learning Based Map Matching with Data Augmentation. IEEE Trans. Mob. Comput. 2020, 21, 2372–2384. [Google Scholar] [CrossRef]
- Jiang, L.; Chen, C.-X. L2MM: Learning to Map Matching with Deep Models for Low-Quality GPS Trajectory Data. ACM Trans. Knowl. Discov. Data 2022. [Google Scholar] [CrossRef]
- Wu, H.; Mao, J.; Sun, W.; Zheng, B.; Zhang, H.; Chen, Z.; Wang, W. Probabilistic Robust Route Recovery with Spatio-Temporal Dynamics. In Proceedings of the KDD’16: 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- Zheng, K.; Zheng, Y.; Xie, X.; Zhou, X. Reducing Uncertainty of Low-Sampling-Rate Trajectories. In Proceedings of the 2012 IEEE 28th International Conference on Data Engineering, Arlington, VA, USA, 1–5 April 2012. [Google Scholar] [CrossRef]
- Ayfantopoulou, G.; Grau, J.M.S.; Maleas, Z.; Siomos, A. Micro-Mobility User Pattern Analysis and Station Location in Thessaloniki. Sustainability 2022, 14, 6715. [Google Scholar] [CrossRef]
- Salanova, J.M.; Ayfantopoulou, G.; Magkos, E.; Mallidis, I.; Maleas, Z.; Narayanan, S.; Antoniou, C.; Tympakianaki, A.; Martin, I.; Fajardo-Calderin, J. Developing a Multilevel Decision Support Tool for Urban Mobility. Sustainability 2022, 14, 7764. [Google Scholar] [CrossRef]
- Rudskoy, A.; Ilin, I.; Prokhorov, A. Digital Twins in the Intelligent Transport Systems. Transp. Res. Procedia 2021, 54, 927–935. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. In Proceedings of the Advances of Neural Information Processing Systems 27—NIPS 2014, Montreal, Canada, 8–13 December 2014. [Google Scholar] [CrossRef]
- Valdera, S.; Ameen, S. Methods for Pruning Deep Neural Networks. arXiv 2020, arXiv:2011.00241. [Google Scholar]
- Croce, A.I.; Musolino, G.; Rindone, C.; Vitetta, A. Vitetta, Transport System Models and Big Data: Zoning and Graph Building with Traditional Surveys, FCD and GIS. ISPRS Int. J. Geo-Inf. 2019, 8, 187. [Google Scholar] [CrossRef]
- Croce, A.; Musolino, G.; Rindone, C.; Vitetta, A. Estimation of Travel Demand Models with Limited Information: Floating Car Data for Parameters’ Calibration. Sustainability 2021, 13, 8838. [Google Scholar] [CrossRef]
- Croce, A.I.; Musolino, G.; Rindone, C.; Vitetta, A. Route and Path Choices of Freight Vehicles: A Case Study with Floating Car Data. Sustainability 2020, 12, 8557. [Google Scholar] [CrossRef]

| Algorithm | Accuracy |
|---|---|
| Rule Based | 43.00% |
| Transformer | 71.00% |
| Transformer and Rule-Based | 76.00% |
| Algorithm | Accuracy |
|---|---|
| Intersections at Grade | 68.00% |
| Grade-Separated Intersections | 53.00% |
| Roundabouts | 62.00% |
| Straight Links—1 Way | 83.00% |
| Straight Links—2 Ways | 79.00% |
| Area | Accuracy |
|---|---|
| City Centre | 69.00% |
| Urban Area | 73.00% |
| Metropolitan Area | 74.00% |
| Regional Area | 76.00% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayfantopoulou, G.; Militsis, M.N.; Grau, J.M.S.; Basbas, S. Improving Map Matching of Floating Car Data with Artificial Intelligence Techniques. Information 2022, 13, 508. https://doi.org/10.3390/info13110508
Ayfantopoulou G, Militsis MN, Grau JMS, Basbas S. Improving Map Matching of Floating Car Data with Artificial Intelligence Techniques. Information. 2022; 13(11):508. https://doi.org/10.3390/info13110508
Chicago/Turabian StyleAyfantopoulou, Georgia, Marios Nikolaos Militsis, Josep Maria Salanova Grau, and Socrates Basbas. 2022. "Improving Map Matching of Floating Car Data with Artificial Intelligence Techniques" Information 13, no. 11: 508. https://doi.org/10.3390/info13110508
APA StyleAyfantopoulou, G., Militsis, M. N., Grau, J. M. S., & Basbas, S. (2022). Improving Map Matching of Floating Car Data with Artificial Intelligence Techniques. Information, 13(11), 508. https://doi.org/10.3390/info13110508









