Abstract
Owing to their high accuracy, deep convolutional neural networks (CNNs) are extensively used. However, they are characterized by high complexity. Real-time performance and acceleration are required in current CNN systems. A graphics processing unit (GPU) is one possible solution to improve real-time performance; however, its power consumption ratio is poor owing to high power consumption. By contrast, field-programmable gate arrays (FPGAs) have lower power consumption and flexible architecture, making them more suitable for CNN implementation. In this study, we propose a method that offers both the speed of CNNs and the power and parallelism of FPGAs. This solution relies on two primary acceleration techniques—parallel processing of layer resources and pipelining within specific layers. Moreover, a new method is introduced for exchanging domain requirements for speed and design time by implementing an automatic parallel hardware–software co-design CNN using the software-defined system-on-chip tool. We evaluated the proposed method using five networks—MobileNetV1, ShuffleNetV2, SqueezeNet, ResNet-50, and VGG-16—and FPGA processors—ZCU102. We experimentally demonstrated that our design has a higher speed-up than the conventional implementation method. The proposed method achieves 2.47×, 1.93×, and 2.16× speed-up on the ZCU102 for MobileNetV1, ShuffleNetV2, and SqueezeNet, respectively.
1. Introduction
In recent years, artificial intelligence and deep learning have been extensively used to solve many real-world problems. Currently, convolutional neural networks (CNNs) are one of the most advanced deep learning algorithms and are used to solve recognition problems in several scenarios. CNNs are more accurate than conventional algorithms. However, many parameters of the convolution operation require a considerable amount of computational resources and memory access [1]. This is a computational challenge for the central processing unit (CPU) as it consumes excessive power. Instead, hardware accelerators such as a graphics processing unit (GPU), field-programmable gate array (FPGA), and application-specific integrated circuit (ASIC) have been used to increase the throughput of CNNs [2,3]. When CNNs are integrated through hardware, latency is improved, and the energy consumption is reduced. GPUs are the most widely used processors and can improve the training and inference processes of CNNs. However, GPUs consume excessive power, which is a key performance metric in modern digital systems. ASIC designs achieve high throughput and low power consumption but require more development time and cost. By contrast, FPGAs increase the capacity of hardware resources, providing thousands of floating-point computing units and lower power consumption. Therefore, FPGA-based accelerators, like ASICs, are an efficient alternative that offer high throughput and configurability at low power consumption and a reasonable cost.
With the development of FPGA-based hardware accelerators, algorithms for improving the accuracy of CNNs are also evolving. Advances in CNN algorithms require many convolution operation parameters, which increase complexity and speed. Many object detection series algorithms, such as the two-stage-based R-CNN [4,5,6] and one-stage-based YOLO [7,8], have been developed to improve speed and accuracy equally. However, implementing edge computing of CNNs faces restrictions because of the complexity and the requirements associated with increased computations. To address these problems, CNN model compression methods have been attracting considerable attention.
CNN model compression technology involves simplifying the deep learning model structure, reducing the number of model parameters, reducing the number of model bits, reducing the amount of computation, improving the deep learning model inference speed, and reducing the required storage resources. In the usage environment of edge devices, fast response speed, low memory usage, and low energy consumption are required. Deep learning model compression can efficiently improve model inference speed, reduce model storage space, and reduce model energy consumption. In the application scenario of large deep learning models, model compression can improve product competitiveness by reducing edge equipment cost, increasing efficiency, and improving low-carbon environmental protection. In the existing deep learning model compression methods, the compression technique is relatively complex, and the difficulty is primarily related to the following aspects.
- Existing model compression algorithms rely on model training:
The current model compression methods rely on the learning process without considering the time cost. However, owing to a lack of raw data or algorithm complexity, users cannot obtain the training code and cannot reproduce the training process.
- 2.
- The several types of model compression algorithms and the difficulty of parameter adjustment:
Taking post-training quantization as an example, classic and commonly used offline quantization algorithms exist, including MSE, ABS_MAX, Bias Correctiony, AVG, HIST, KLD, AdaRound, and EMD. Each offline quantization algorithm has 2–4 parameters. The efficient selection of an appropriate offline quantization algorithm for a model and its parameters in a specific scenario is a significant problem in the implementation of a model compression technology project.
- 3.
- The complexity of combining the model compression of multiple strategies:
In addition to offline quantization, model compression includes various compression techniques such as pruning and distillation. A combination of various compression algorithms can also be used as the demand for model miniaturization increases. Compression algorithms affect each other and cannot simply accumulate their effects. Selecting a suitable compression algorithm set from various candidate compression algorithms is highly dependent on human experience and long-term experimentation.
- 4.
- The numerous compressed model structures and the complexity of the deployment environments:
In terms of model structure, the backbone network improves rapidly, and the active function continues to evolve. Different structures and active functions have different sensitivities and lossless compression ratios. In addition, in terms of the deployment environment, the FPGA characteristics and optimization details of the inference library are all factors to consider when compressing. Considering the model structure and deployment environment, manual compression faces difficulty in achieving the expected goal.
In this study, we develop an automatic model compression tool set that can significantly reduce the size of deep learning models by combining model optimization methods with model compression to solve the aforementioned problems. Automatic parallelization of FPGA designs such that software and hardware coordinate CNN tasks and cleaning up CNNs to better adapt to FPGA and advanced RISC machine (ARM) NEON architectures are examined. Section 2.1 and Section 2.2 discuss recent studies related to FPGA design CNNs and CNN optimization. Section 3 focuses on the proposed research method. The developed method can address several problems by focusing on the following main ideas.
- We propose a model compression method that considers memory resources to enable software and hardware acceleration through a lightweight CNN model. In the proposed model compression method, the quantization method is determined through the distillation method. Further, the pruning method also balances accuracy and speed to ensure maximum performance for CNN prediction.
- The determined pruning is grouped to achieve an appropriate balance between CNN prediction accuracy and accessing group-specific memory. The per-memory data flow varies and helps with parallel computations. To improve the computational efficiency of CNN, we propose a CPU-FPGA cooperative computation method. Based on the CNN architecture and advanced pruning method, we design software and hardware to be parallelized in CNN computation. This approach achieves high hardware parallelism, including weight groups and memory access methods. Moreover, it enables parallelism of the ARM NEON architecture and FPGAs.
- We propose an automated method to design an optimal accelerator with the performance of ARM and FPGA balanced by utilizing a space exploration model. The proposed method generates a CNN auto-accelerator through network analysis, layer decomposition, software-defined system-on-chip (SDSOC) template mapping, and long short-term memory (LSTM)-based CNN auto-generator design steps. Based on this process, an automatic CNN model optimization engine is designed by implementing a CNN model generation LSTM that satisfies the FPGA design performance suitable for CNN implementation.
2. Related Work
2.1. Related Research for Implantation of FPGA DNN
Recently, with the release of the Xilinx Zynq hyperscale board capable of quick implementation of deep neural network (DNN) inference, this technology has been compared to implementations of DNN acceleration. By all kernels in the convolutional layer, which extensively use local memory to store data and rely on parallelism, the architecture is computed flexibly in all network sizes. This technology enables reduced implementation time and power consumption when accessing external memory. It compares considerably with the performance when implemented in the CPU. The power consumption in hardware use is less than that of the CPU.
Independent and careful research is required to design a DNN model and FPGA hardware acceleration, and deep learning experts design using two methods. The first is to design deep learning models manually, and the second is to design them automatically through RNN or reinforcement learning. An example of an FPGA accelerator design is how a conventional convolution and a Winograd convolution are combined to implement a DNN in an FPGA [9]. Aidonnat et al. reported that Winograd-based solutions could reduce the DNN multiplication operation because it is FPGA-based [10].
Another study utilizes a processor-based DNN search method to implement DNN inference using a variety of processors [11]. This method is also improving and evolving over many previously published studies. However, for the studies mentioned, the authors only considered the DNN inference latency of the CPU and GPU, not the FPGA DNN inference latency.
In DNN implementation studies, new techniques such as quantization [12] and compression [13] methods of DNN models are also used in FPGA DNN accelerators. This method has the advantage of reducing the size and latency of the model while inferring the DNN. However, there are limitations because DNN models cannot use these methods.
Recent research can deploy DNN on the FPGA rapidly by researching and developing automation tools [14]. However, integrated register-transfer level (RTL) design is possible only by targeting the convolution layer, which is the main layer, and FPGA RTL design studies have not been conducted for fully connected layers. The proposed RTL design template automatically maps the DNN to the FPGA. However, it has lower computational performance than dedicated designs in other networks. This is because dynamic link libraries (DLL) use integrated computational units such as fixed-size computing engines [15]. In this study, the DNN automatic FPGA mapping method using the high-level synthesis (HLS) template was further studied, significantly improving the RTL size [16].
2.2. Related Research for Pruning DNN
Pruning is a method for reducing unnecessary operations and memory without losing accuracy. The weights of the CNN have operations that are duplicated by repeating many layers. It is a lightweight method of the CNN model, widely used recently, minimizing overlap. The two most widely used pruning methods are unstructured pruning [17,18] and structured pruning [19,20].
Unstructured pruning is possible in both the channels and filters of DNN weights without a definite shape; it is not fixed-weight pruning. Figure 1 shows the unstructured pruning method. Because the channel and filter are arbitrarily pruning, and not a fixed shape, it has high flexibility and a high compression rate. However, arbitrary matrices are randomly removed from the weights, which causes irregular sparsity and requires additional indices to find non-zero values during the operation. These methods are not suitable for hardware parallelism in FPGAs. We wished to utilize pruning to speed it up; however, DNN acceleration can be slow on FPGAs. Therefore, unstructured pruning has the advantage of having high flexibility, a high compression ratio, and a low loss of accuracy in DNN weight operations, while it has the disadvantage of reducing speed as well as difficulty in applying it to FPGA DNN acceleration.
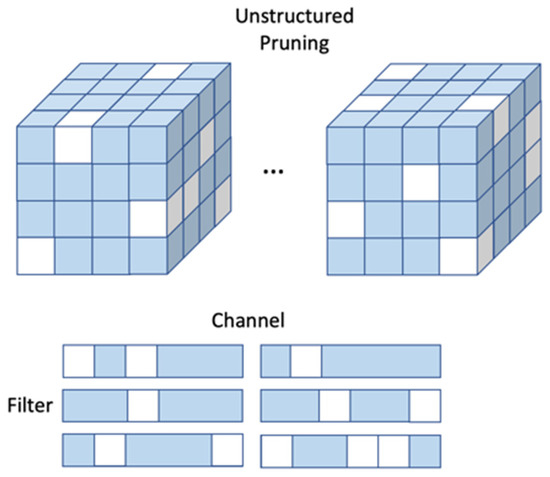
Figure 1.
Example of unstructured pruning.
Structured pruning regularly removes rows and columns or channels and filters of DNN weights. Figure 2 shows this method. It can either remove entire channels or filters. It is a method to continuously and regularly remove the channels and filters developers want to remove. Further, this method maintains a regular shape because it structurally prunes the weights continuously, which is appropriate for FPGA hardware. Hardware parallelism can be utilized when designing FPGA accelerators. However, considerable accuracy is lost owing to the continuous removal of the entire filter and channel. Therefore, structured pruning is suitable for FPGA hardware design and can apply parallel processing to weight operations; however, it has the disadvantage of a high loss of accuracy.
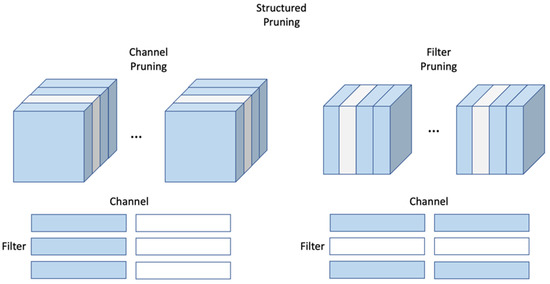
Figure 2.
Example of structured pruning.
3. Materials and Methods
3.1. Overview of Proposed Design Flow
Figure 3 shows the overall contents of a software method for optimizing CNN weights, a hardware accelerator architecture that co-designs a CNN with a CPU and FPGA, and an automatic CNN model optimization engine that can implement CNN prediction with the performance required by the user for the indicated design. We proposed an optimal automation accelerator design that balances the ARM and FPGA performances. We needed a parallel computation method as a joint design computation approach of the CPU and FPGA to efficiently utilize resources on time when processing CNN inference. Because CNN frequently uses multi-branch architecture, we optimized it through the CPU-FPGA co-design computation method.
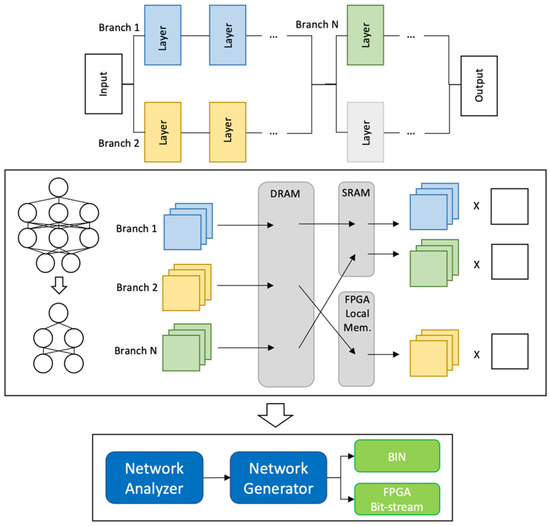
Figure 3.
Proposed system overview.
We utilized the distillation technique to proceed with quantizing the CNN inference model. The proposed quantization model compression imports the definition file of the CNN inference model, copies the inference model in the memory as a teacher model of knowledge distillation, and copies the original model as a student model. This causes the teacher model to supervise the quantization in search of a suitable layer for distillation loss addition and a layer with learnable parameters. By grouping the quantized CNN weights by branch and accessing the memory, we prevented memory conflicts in the computation process. Methods involving structured and unstructured pruning are relied on to devise grouping patterns. We first split the given weights by branch. We pruned the split weights by appropriately balancing accuracy and speed. Pruning in each group can be freely removed to suit performance requirements. This branch-by-branch memory grouping pruning has several advantages. Because the approach is segmented by branch, we can apply the sparsity of the weight differently. When groups of different pruning types are accessed simultaneously, they are transferred to static random-access memory (SRAM) and FPGA local memory to prevent access conflicts. Section 3.2 provides more details about this part.
The hardware architecture proposes an architecture that calculates the CNN weights stored in the branch-pruned format by moving them for each processor. In this method, weights belonging to the same group are moved to the same processor and calculated. In the case of an unstructured pruning group, where the speed is low when adapting to the FPGA with high flexibility, the operation is performed in the ARM. In this case, a memory copy is moved to SRAM. Conversely, in the case of structured pruning where hardware parallel processing is suitable for use, the operation proceeds in the FPGA and moves to the FPGA local memory. Section 3.3 presents the architecture and memory flow in detail.
Finally, we proposed a space exploration model to design an optimal accelerator that balances the ARM and FPGA performances. First, the developers design and train CNNs. After training, the CNN is analyzed through an analyzer, decomposed according to the configured layers, and mapped according to the SDSOC template. By extracting and implementing feature values from SDSOC C/C++ inference code and training these feature values using LSTM, designs with a high degree of parallelism are automatically generated. Section 3.4 presents the automatic CNN model optimization engine in detail.
3.2. CNN Model Compression Method through Distillation
We primarily identified the effects of automated compression in an open-source model dealing with image classification, image semantic segmentation, and image object detection. Automatic compression also supports inference models created in PyTorch and TensorFlow. In contrast to the conventional manual compression, the automatic aspect of automatic compression is primarily reflected in four areas: deep learning training code separation, offline quantized hyperparameter search, automatic algorithm combination, and hardware recognition model. Users can perform compression methods that rely on training processes such as quantitative training and sparse training by providing only an inference model and unlabeled data. Automated compression adds training logic to the inference model through distillation. Figure 4 shows the distillation process, and Figure 5 shows the compression process. First, the user-specified inference model file is loaded, the inference model is copied to the memory as the teacher model of knowledge distillation, and the original model is copied as the student model. It then automatically analyzes the model structure to find a suitable layer for adding distillation losses and finds a layer with learnable parameters. Finally, the teacher model supervises the quantization training of the original model through distillation loss.
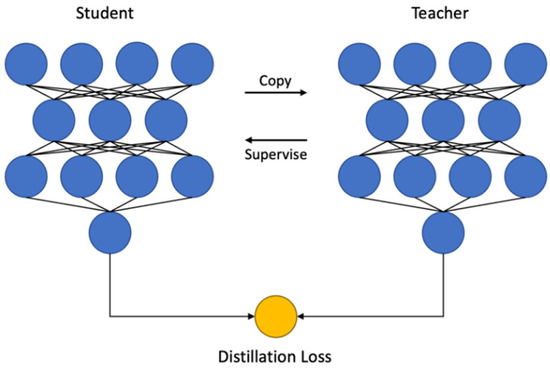
Figure 4.
Example of structured knowledge distillation.
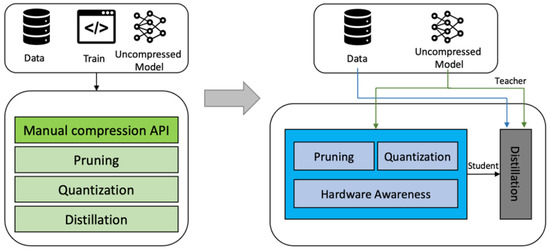
Figure 5.
Automatic compression model method flow.
Offline quantization with many models and fast iteration rates in the search scenario is the best compression method for this scenario. Various offline quantization algorithms are implemented. Offline quantization algorithms perform a few algorithms that can be used in combination.
The automatic compression function analyzes the model structure and automatically selects an appropriate combination algorithm according to the user-specified model structure characteristics and deployment environment. Determining the parameters of each compression algorithm after selecting a joint compression algorithm is challenging. Setting the parameters of the compression algorithm is closely related to the deployment environment. Various factors, such as chip characteristics and the degree of optimization of the inference library, must be considered. As an agent of the deployment environment, the hardware awareness module models and learns the characteristics of the deployment environment and provides a performance inquiry service for parameter setting.
The relationship between compression parameters and inference speed, constrained by optimizations such as inference library operator fusion, is not linear. Taking sparsity as an example, an inference library can support matrix multiplication operations where sparsity is greater than 75%. That is, 60% sparsity and 10% sparsity have no inference acceleration effect. Therefore, setting the sparsity to 60% is impractical. In addition, the sparse acceleration effect is also affected by the input form of the matrix multiplication operator. In conclusion, accurately evaluating the relationship between compression parameters and inference speed based on human experience or simple formulas in various model structures and deployment environments is impossible.
To this end, we developed a hardware delay estimation function. This feature uses data tables combined with deep learning models to model factors that affect inference speed and guide the setting of parameters for the joint algorithm. The two key modules of the hardware delay estimation function are the delay estimation table and the estimator.
Estimation table: Sample and test the inference performance of multiple operators for each deployment environment and record it in the data table. Each row in the data table contains the operator type, parameters of the operator itself (e.g., input shape stride and padding), sparsity, quantization, and other information. Estimation tables can accurately estimate the information of the target operator; however, it faces difficulty in dealing with all possible parameters of the operator.
Predictors: Use data from the estimation table to train predictors for each type of operator to predict inference performance. The predictor accuracy is not as good as the prediction table; however, it has stronger generalizability and can contain more operator parameter values.
The workflow for this function is shown in the flowchart on the right in Figure 6.
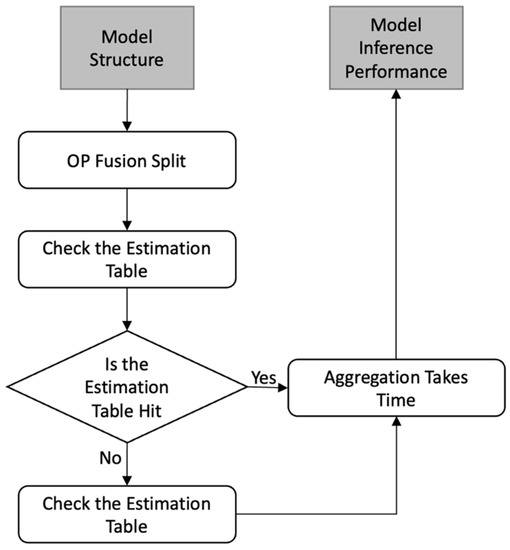
Figure 6.
Target board performance prediction method.
Step 1: Analyze the model structure and perform OP fusion on the inference model (to get the OP executed during deployment).
Step 2: Check the estimation table in turn for every OP of the inference model created in step 1, and check the estimator if it does not meet the target.
Step 3: Accumulate the time of all OPs to obtain the final inference performance of the candidate model.
By supporting the above functions, quickly obtaining model inference performance under various compression parameters and locking a small number of candidate models according to the user-specified inference acceleration multiplier on specific hardware are possible. Finally, the accuracy of the candidate models is verified individually.
The candidate model obtained after verification optimizes the CNN branch by pruning to perform parallel computation in the CPU–FPGA co-design method of the CNN. The branch optimizes with structured pruning and unstructured pruning for both CPU and FPGA processors, respectively. The CPU processor focused on unstructured pruning, which arbitrarily removed CNN weights. Unstructured pruning is a technique that can achieve high sparsity, averaging 90%, which helps reduce resources for on-chip storage needs when computing CNNs. However, high sparsity does not necessarily lead to high-performance speed-ups owing to the additional encoding and indexing overhead, workload imbalance, and poor data locality. The performance is degraded when the sparsity distribution is heavily skewed. Significant progress has recently been made in structured pruning, which aims to prune networks according to specific sparsity patterns. Starting with a strict sparsity pattern that follows particular mathematical properties, it designs the hardware to support the necessary mathematical transformations. These techniques can achieve high regularity and computational efficiency suitable for FPGA hardware designs. A typical convolutional computation is a computationally intensive kernel that traverses a multidimensional tensor (feature map, weights) to perform addition and multiplication. We must reconstruct the CNN branch weights into blocks to increase the parallelism of the CNN architecture. Multiple branches access tensors simultaneously with each processor solving memory bottlenecks and helping with parallel computing performance resistance issues during computation.
3.3. Hardware Acceleration through CPU–FPGA Co-Design
A parallel operation method is required as a joint design operation approach for the CPU and FPGA to utilize resources more efficiently in time execution during CNN inference processing. Because most of the latest CNNs use multi-branch architecture frequently, we performed hardware acceleration through the CPU–FPGA co-design computation method. Implementing CNN inference with only one processor on the system-on-chip (SOC) board wastes excessive computational resources. In particular, the CPU has excessive wasted resources when the FPGA performs the operation. Therefore, if the CPU and FPGA perform calculations simultaneously, we can obtain high efficiency and speed in resource use.
Hardware such as FPGAs are better suited for highly parallel tasks, such as convolution tasks in CNNs, than CPUs. In a CNN multi-branch structure, there is a difference in operation time between a branch structure with many convolutional layers and a branch structure with relatively few or no convolutional layers. In addition, owing to the branch-by-branch pruning previously performed, there is a structural difference between groups in addition to time. If a branch is optimized through structured pruning, it operates as an FPGA, and another branch of unstructured pruning operates as a CPU. Then, CPU and FPGA can be used simultaneously. If the convolutional layer of the branch of structured pruning is continuous, it can be operated sequentially using FPGA.
As shown in Figure 7, we stored the weights of CNNs divided into groups in DRAM for calculation. The CPU and FPGA logical spaces inside dynamic random-access memory (DRAM) can be copied between each other; therefore, arranging the weights to move to each processor memory at CNN runtime is possible. In pruning, the sort criterion takes the form of a structure copied into space on the CPU and FPGA. When the corresponding CNN branch is executed, the weight groups copied to each processor space are copied again to different memories for operation, and the weight groups of the unstructured pruning are moved from the CPU logical space to the SRAM. However, the weight group of structured pruning is moved from the FPGA logical space to the FPGA local memory.
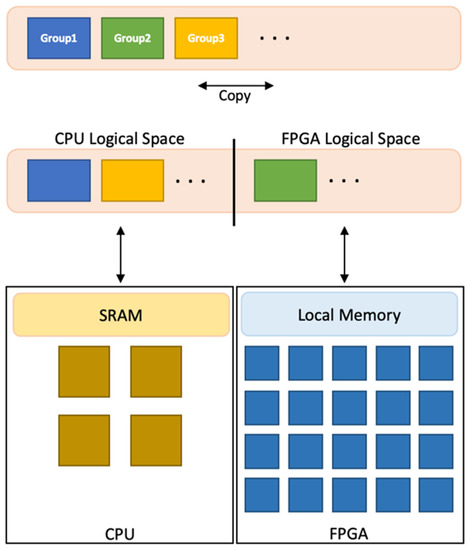
Figure 7.
Dataflow by weight group.
Branch operation time is defined as t_u for unstructured pruning and as t_s for structured pruning to measure the operation time of each CPU and FPGA in a branch of the CNN. For CNN branch architecture with various branches, the representable computing times are t_s1, t_s2, t_s3, …, t_u1, t_u2, and t_u3. When branch1 and branch2 of Figure 3 are operated simultaneously from the CPU and FPGA to different processors, the operation time is determined by the long operation time, expressed by the following equation:
T_diff = max {t_u1, t_s2}
If the processors for branch1 and branch2 are computed in CPU-CPU and FPGA-FPGA, the minimum time is calculated differently. If the two structures in the branch are identical and the operation is performed on the same processor, serial computing is performed. If each branch is computed on the same processor, the computation time is determined as follows:
T_same = min {t_s1 + t_s2, t_u1 + t_u2}
By comparing the serial operation time T_same of the same processor and the CPU-FPGA parallel operation time T_diff of different processors, the optimal processor for branch1 and branch2 can be selected as the minimum. The CPU and FPGA execution times are measured in each branch, and T_total is the total computation time for both branches.
T_total = min {T_same, T_diff}
Consequently, this calculation computes the CNN inference process with the processor combination that is the minimum value of the total computation time T_total. When running on this processor, implementing CNN inference with high speed and high hardware utilization is possible through a CPU–FPGA co-design approach.
3.4. Auto-Generator Design
We proposed a space exploration model to design an optimal accelerator that balances the constraints of the CNN and the FPGA performance. As shown in Figure 8, we developed a CNN accelerator through a procedure that includes a network analyzer and the automatic generation of ARM C/C++ and HDL. Developers use deep learning frameworks to design and train target CNNs. A CNN designed and trained by the developer generates a definition file of the CNN. We passed the definition file of the CNN to the CNN analyzer. The network analyzer decomposed the layers in the network designed by the developer. The decomposed layer comprises various layers such as the convolution layer, pooling layer, and fully connected layer. We mapped the exploded layers to fit the SDSOC template. Finally, we extracted specific values from SDSOC’s CNN inference C or C++ code, trained specific values with LSTMs, and designed an LSTM-based automatic CNN model optimization generator. These methods automatically generated designs that allowed CNN inference to be processed with a high degree of parallelism. We generated the CNN model automatically generated by the CNN model optimization generator such that it could be compiled on each processor of the CPU and FPGA to balance the user’s accuracy and speed requirements.
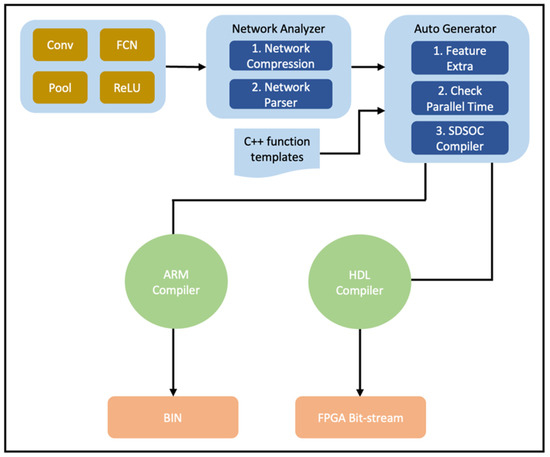
Figure 8.
Workflow of the proposed auto-generator design method.
Calculations and data communication are critical to improving throughput in accelerator designs. A deep learning network consists of various operators; however, not all operators have the same properties. Even when performing similar operations, memory usage is typically low, high, or unequal. The same operator computes by changing properties using the parameters. We can classify various operators in deep learning networks into computationally intensive and memory-access-intensive operators. Computationally intensive operators are typically convolution and FC. The time implemented to infer CNN has a linear relationship with the computation of computationally intensive operators. In addition, ReLU and Concat are representative memory-access-intensive operators. For these operators, CNN inference time has a linear relationship with memory access. A deep learning network consists of both types of operators. However, many difficulties in the design of CNNs involve fully exploiting the hardware performance using operators of two properties. Therefore, our design, based on LSTM, automatically generates the CNN model optimization design to meet the performance needs of developers. LSTM design requires extracting specific values from C/C++ code. We must train an LSTM using specific extracted values and predict a new method in SDSOC with the trained LSTM. The specific values extracted from the SDSOC code include operators, variables, parallel structures, and memory allocation sizes; we can use an abstract syntax tree to extract them. We can express an abstract syntax tree by structuring specific values into a sorted tree, as shown in Figure 9. First, it expresses a loop like a for statement and stores the range of the loop. It then transforms the matrix of loop-level variables into memory allocation patterns. At each loop level, we must add tags to distinguish loops from other loops that define buffer dimensions to avoid using duplicate loops. In addition, before hardware synthesis, the loop is optimized and added to the tag. To design an automatic CNN generator, interchange, tile, and unrolling were selected as optimization examples and extracted as specific values that determine these loops in the SDSOC pragma.
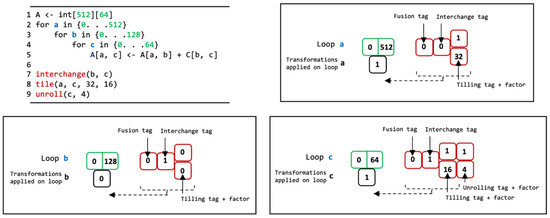
Figure 9.
Loop optimization representation and pseudocode.
We must add training via LSTM to synthesize hardware designs by extracting specific values. The structure of the LSTM architecture should consider CNN depth, layer size, and connection activation function between layers. When designing it by expressing it as a parameter, it may have good performance or overfit depending on the number of parameters. We trained it based on the regression LSTM to design the LSTM with the best performance. Regression LSTMs are modeled as regression problems when inferring CNNs by speeding up. By transforming the algorithm code with the extracted values, predicting the expected execution speed is possible, in contrast to the existing program.
4. Results
We used the proposed method to build five CNNs: ResNet-18, MobileNet, ShuffleNet, SqueezeNet, and VGG-16. ResNet-18 is a CNN composed of 18 layers and uses residual block as the basic structure [21]. In addition, MobileNet is a lightweight model using depth-wise separable convolution [22,23]. It differs from Xception by focusing on lightweighting rather than increasing performance by stacking as many layers as the number of reduced parameters using depth-wise separable convolution. ShuffleNet uses the structure of MobileNet and has a 1 × 1 convolution structure with almost all computations and parameters [24,25]. SqueezeNet uses eight fire modules and one convolutional layer each for input and output [26]; however, it does not use the fully connected layer. Finally, VGG is a model trained on a neural network in layers 16–19, using 3 × 3 filters on all convolutional layers [27]. This model succeeded in training the deep network twice more than AlexNet, and also succeeded in reducing the error rate by half.
We first used the Xilinx tool to generate RTL code from a C/C++-based CNN design for the accelerator. We prototyped the proposed method on FPGA platforms, Xilinx ZCU102. We chose the Zynq family, an example FPGA board with few gates. The Xilinx ZCU102 was configured with UltraScale FPGA, quad ARM Cortex-A53 processor, and 500 MB DDR3. We used Xilinx Vivado HLS and Xilinx SDSOC for implementation.
Auto-compression can effectively compress and work with small models designed for mobiles such as MobileNet, ShuffleNet, and SqueezeNet. After automatic compression, the inference time of various models on ARM-FPGA reduced significantly. Table 1 presents the evaluation results on the Xilinx ZCU102 platform using MobileNetV1, ShuffleNetV2, and SqueezeNet networks. ZCU102 achieves 12.88 ms for the MobileNetV1 network. The performance of the ShuffleNetV2 implementation is 5.201 ms on the ZCU102. The performance of the SqueezeNet implementation is 16.01 ms on the ZCU102.

Table 1.
Evaluation of FPGA.
Additionally, we compared the speed of the proposed method with the latest embedded GPUs, TX2 and TX1. Owing to the real-time requirements of edge applications, we tried to use the minimum batch size. Based on the experimental results summarized in Table 2, we observed that the designs of Xilinx ZCU104 and ZCU102 provided higher efficiency than Nvidia Jetson TX2-based TensorRT inference solutions.

Table 2.
Speed evaluation on FPGA.
We compared two previously studied accelerator designs, D.Wu [28] and L.Bai [29]. We measured top-1 accuracy and the overall performance of all convolution layers. Table 3 shows that our proposed method performs better than the two previously studied methods.

Table 3.
Comparison with other FPGA works.
5. Conclusions
Real-time artificial intelligence of things (AIoT) applications, which are being widely used, require improved performance. AIoT devices have difficulties in complex and real-time calculations, making it difficult to localize devices for tasks that require high precision or many variables. FPGA designs are a promising solution because of their low cost and energy efficiency. However, most FPGA development can only work with a single artificial intelligence (AI) network, and developing it is time-consuming. Therefore, we developed an automation technique by combining model compression for accelerating CNN models and methods using CPU–FPGA parallelism. We experimentally demonstrated that our design has a higher speed-up than the conventional implementation method. Moreover, we evaluated this method on the ZCU102 FPGA platforms, and it achieved 2.47×, 1.93×, and 2.16× speed-up for MobileNetV1, ShuffleNetV2, and SqueezeNet, respectively.
Author Contributions
Date curation, S.J.; Formal analysis, S.J. and W.L.; Founding acquisition, Y.C.; Methodology, W.L.; Software, S.J.; Supervision, Y.C.; Validation W.L.; Writing—original draft, S.J.; Writing—review & editing, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Evaluation Institute of Industrial Technology (KEIT) under the Industrial Embedded System Technology Development (R&D) Program 20016341. The EDA tool was supported by the IC Design Education Center (IDEC), Korea.
Institutional Review Board Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qi, X.; Liu, C. Enabling Deep Learning on IoT Edge: Approaches and Evaluation. In Proceedings of the IEEE/ACM Symposium on Edge Computing (SEC), Seattle, WA, USA, 25–27 October 2018; pp. 25–27. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, X.; Xiong, J.; Hwu, W.; Chen, D. Implementing neural machine translation with bi-directional GRU and attention mechanism on FPGAs using HLS. In Proceedings of the 24th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 23 January 2019; pp. 21–24. [Google Scholar]
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing FPGA-based accelerator design for deep convolutional neural networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; pp. 22–24. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems 28: Annual Conference on Neural Information Processing Systems 2015, Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Wang, J.; Lou, Q.; Zhang, X.; Zhu, C.; Lin, Y.; Chen, D. Design flow of accelerating hybrid extremely low bit-width neural network in embedded FPGA. In Proceedings of the 2018 28th International Conference on Field Programmable Logic and Applications (FPL), Dublin, Ireland, 27–31 August 2018; pp. 27–31. [Google Scholar]
- Aydonat, U.; OʹConnell, S.; Capalija, D.; Ling, A.C.; Chiu, G.R. An openclTM deep learning accelerator on arria 10. In Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2017; pp. 22–24. [Google Scholar]
- Cai, H.; Zhu, L.; Han, S. Proxylessnas: Direct neural architecture search on target task and hardware. In Proceedings of the 2019 7th International Conference on Learning Representation (ICLR), New Orleans, LA, USA, 6–9 May 2019; pp. 6–9. [Google Scholar]
- Qiu, J.; Wang, J.; Yao, S.; Guo, K.; Li, B.; Zhou, E.; Yu, J.; Tang, T.; Xu, N.; Song, S.; et al. Going deeper with embedded fpga platform for convolutional neural network. In Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 21–23 February 2016; pp. 21–23. [Google Scholar]
- Zhang, M.; Li, L.; Wang, H.; Liu, Y.; Qin, H.; Zhao, W. Optimized Compression for Implementing Convolutional Neural Networks on FPGA. Electronics 2019, 8, 295. [Google Scholar] [CrossRef]
- Zeng, H.; Chen, R.; Zhang, C.; Prasanna, V. A framework for generating high throughput CNN implementations on FPGAs. In Proceedings of the 2018 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 25–27 February 2018; pp. 25–27. [Google Scholar]
- Ma, Y.; Cao, Y.; Vrudhula, S.; Seo, S. An automatic RTL compiler for high-throughput FPGA implementation of diverse deep convolutional neural networks. In Proceedings of the 2017 27th International Conference on Field Programmable Logic and Applications (FPL), Ghent, Belgium, 4–8 September 2017; pp. 4–8. [Google Scholar]
- Guan, Y.; Liang, H.; Xu, N.; Wang, W.; Shi, S.; Chen, X.; Sun, G.; Zhang, W.; Cong, J. FP-DNN: An automated framework for mapping deep neural networks onto FPGAs with RTL-HLS hybrid templates. In Proceedings of the 2017 IEEE 25th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Napa, CA, USA, 30 April–2 May 2017. [Google Scholar]
- Guo, Y.; Yao, A.; Chen, Y. Dynamic network surgery for efficient dnns. In Proceedings of the Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Frankle, J.; Carbin, M. The lottery ticket hypothesis: Finding sparse, trainable neural networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wen, W.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Learning structured sparsity in deep neural networks. In Proceedings of the Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- He, Y.; Zhang, X.; Sun, J. Channel pruning for accelerating very deep neural networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 27–29 October 2017. [Google Scholar]
- Kaiming, H.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Howard, G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Iandola, F.; Han, S.; Moskewicz, M.; Ashraf, K.; Dally, W.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Wu, D.; Zhang, Y.; Jia, X.; Tian, L.; Li, T.; Sui, L.; Xie, D.; Shan, Y. A High-Performance CNN Processor Based on FPGA for MobileNets. In International Conference on Field Programmable Logic and Applications (FPL); IEEE: Piscataway, NJ, USA, 2019; pp. 136–143. [Google Scholar]
- Bai, L.; Zhao, Y.; Huang, X. A CNN Accelerator on FPGA using Depthwise Separable Convolution. In IEEE Transactions on Circuits and Systems II: Express Briefs; IEEE: Piscataway, NJ, USA, 2018; Volume 65, pp. 1415–1419. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).