Evaluation of Continuous Power-Down Schemes
Abstract
:1. Introduction
1.1. The Power-Down Problem and Online Competitive Analysis
1.2. Background and Related Work
1.3. Organization of Paper
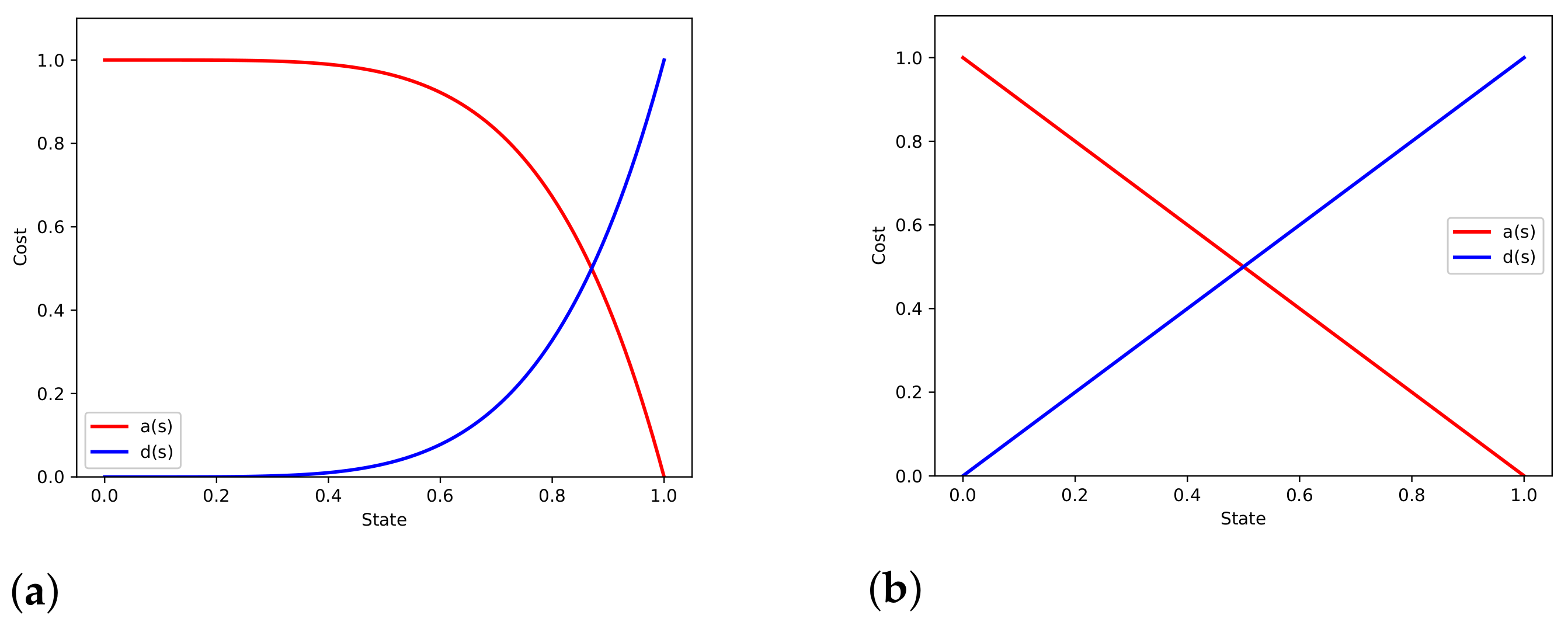
2. The Power Model
3. Offline Strategy
4. Online Strategies
5. Logarithmic Strategies
6. Exponential Strategies
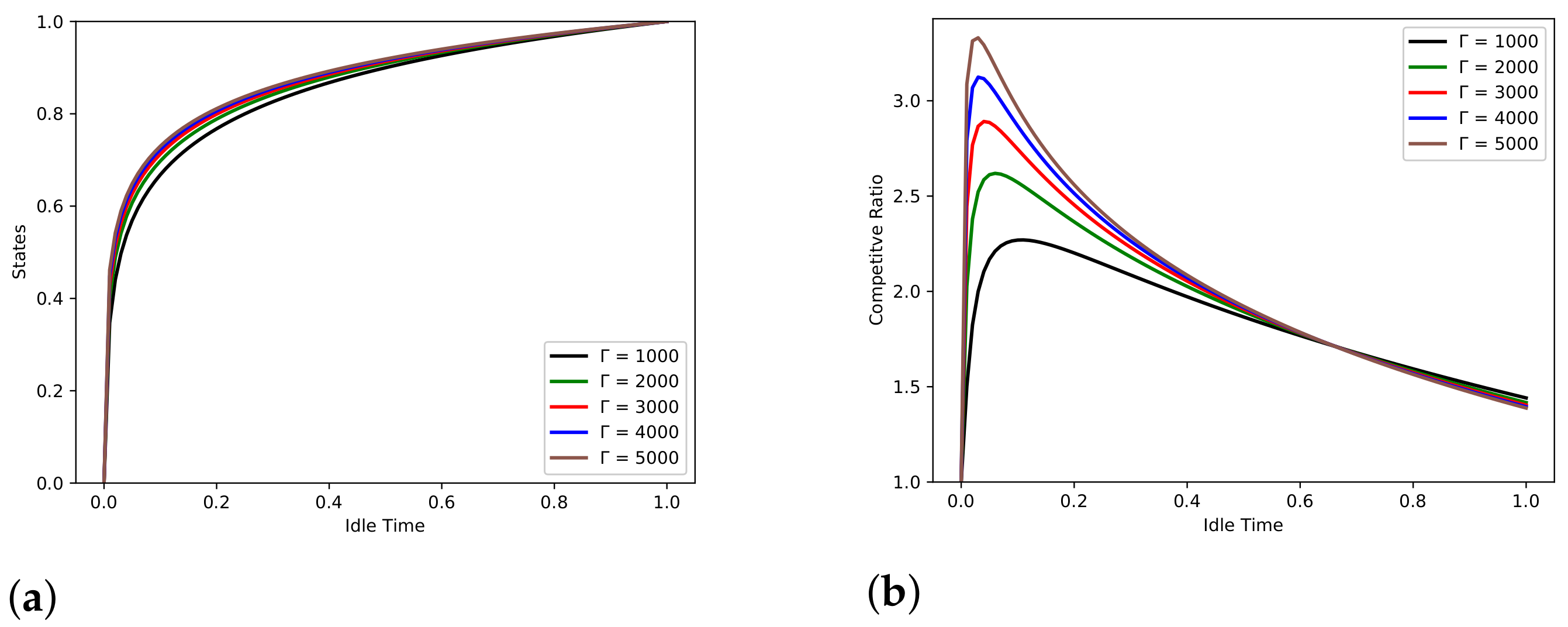
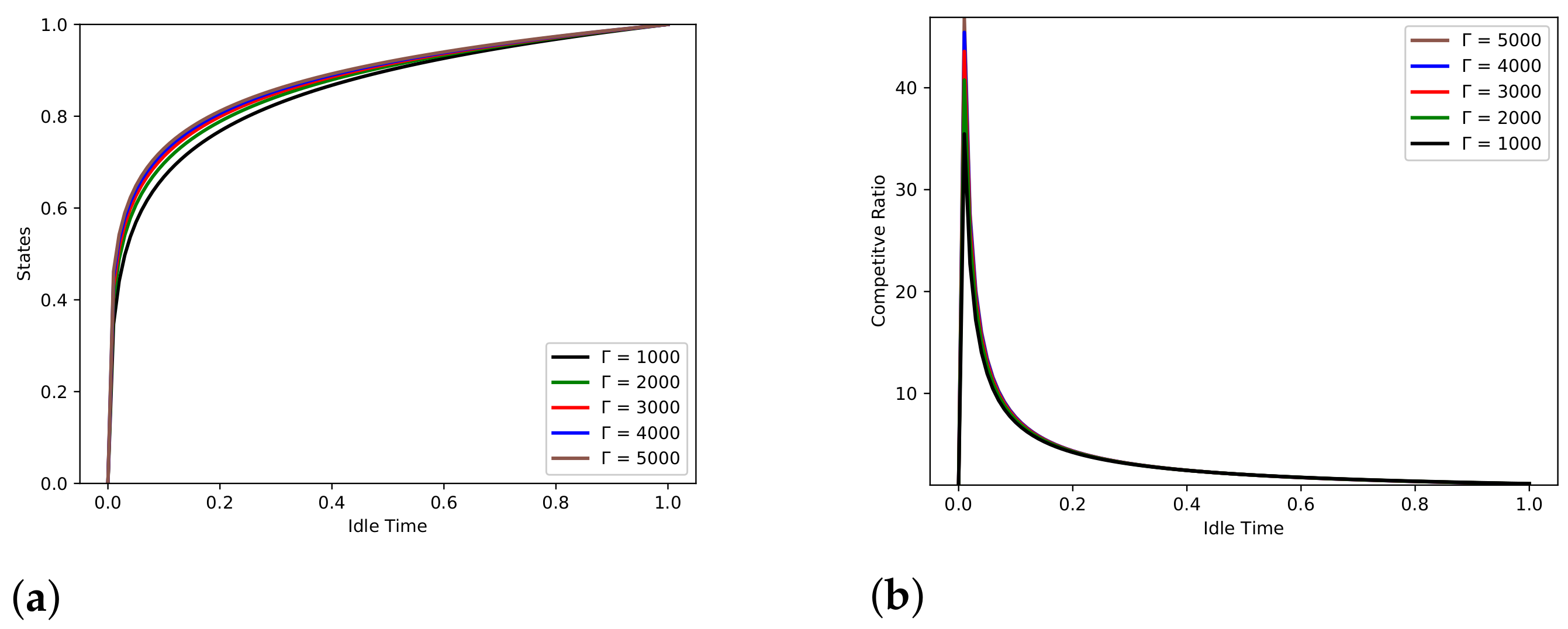
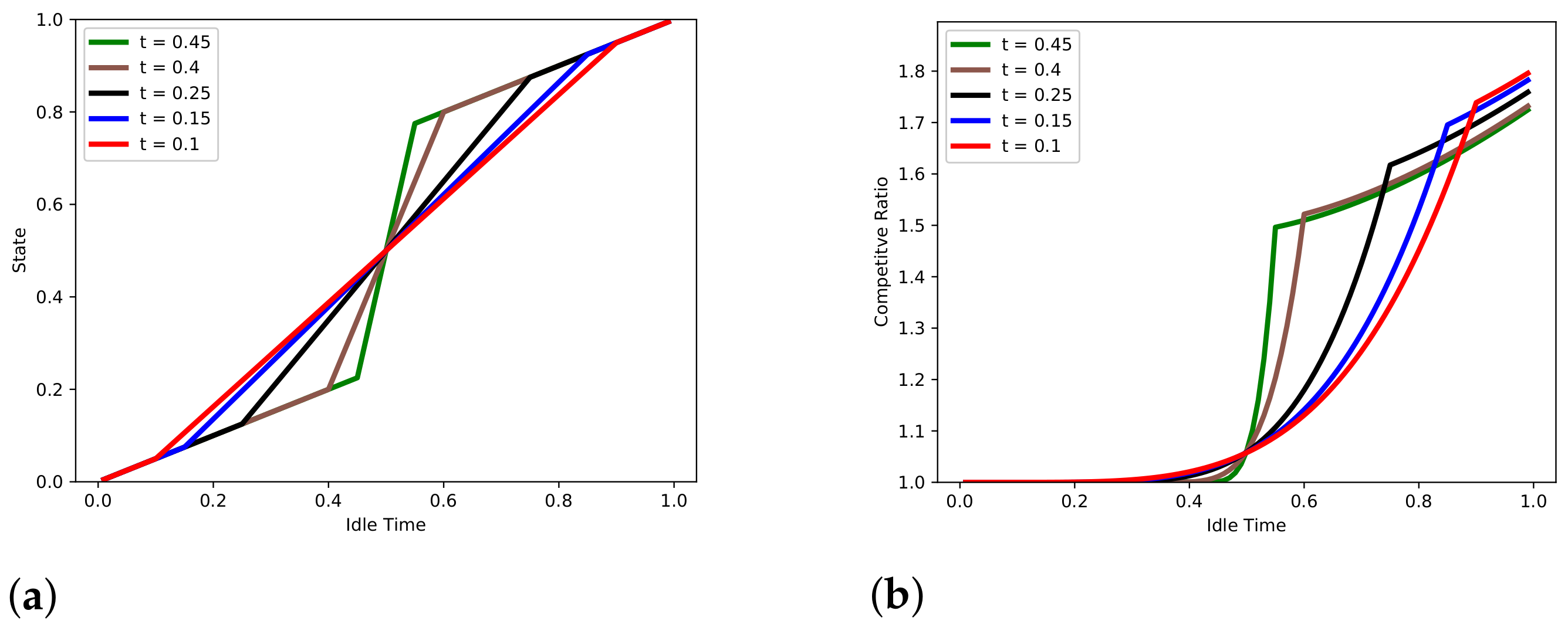
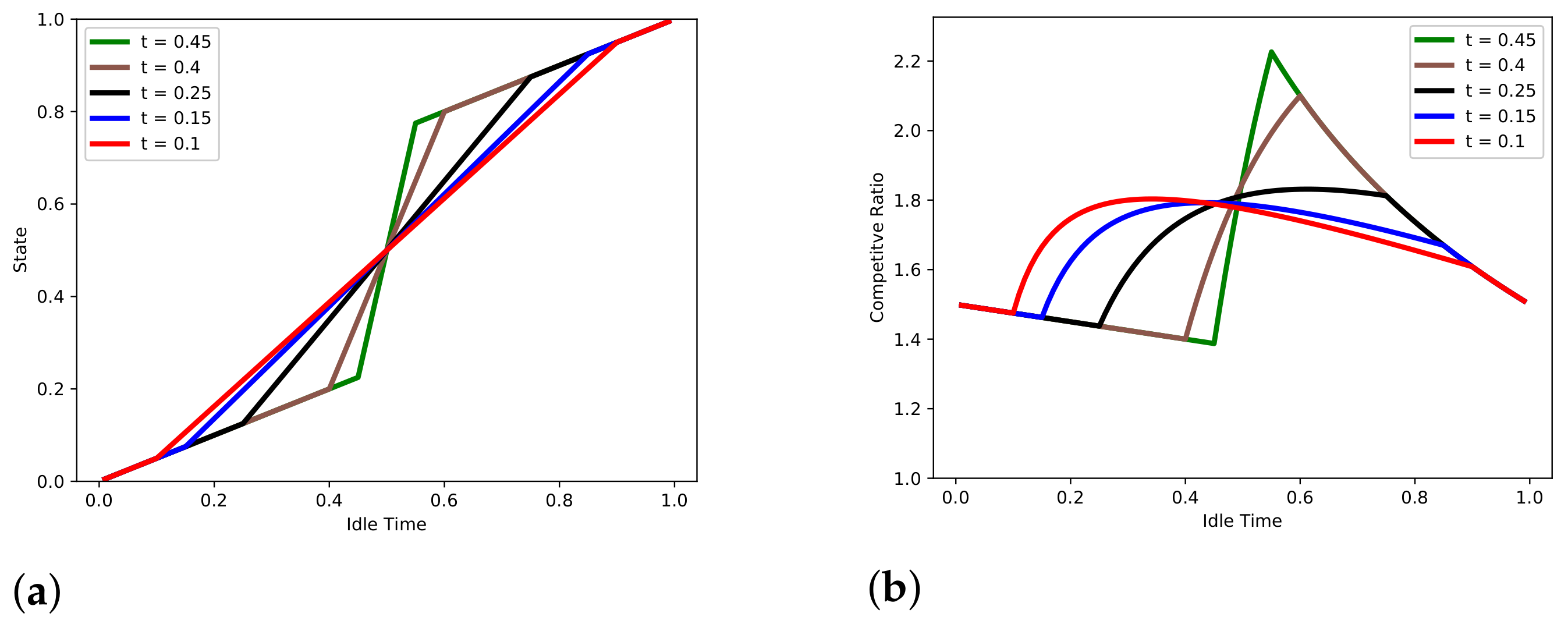
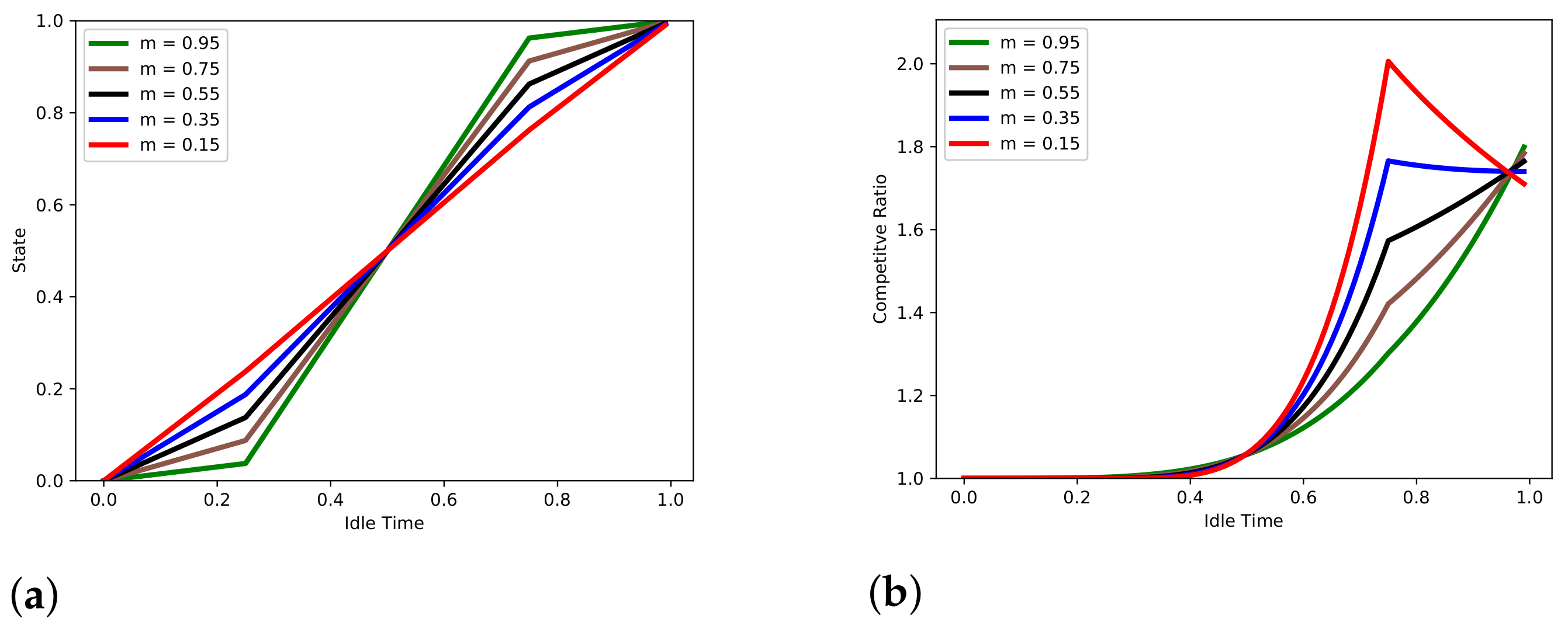
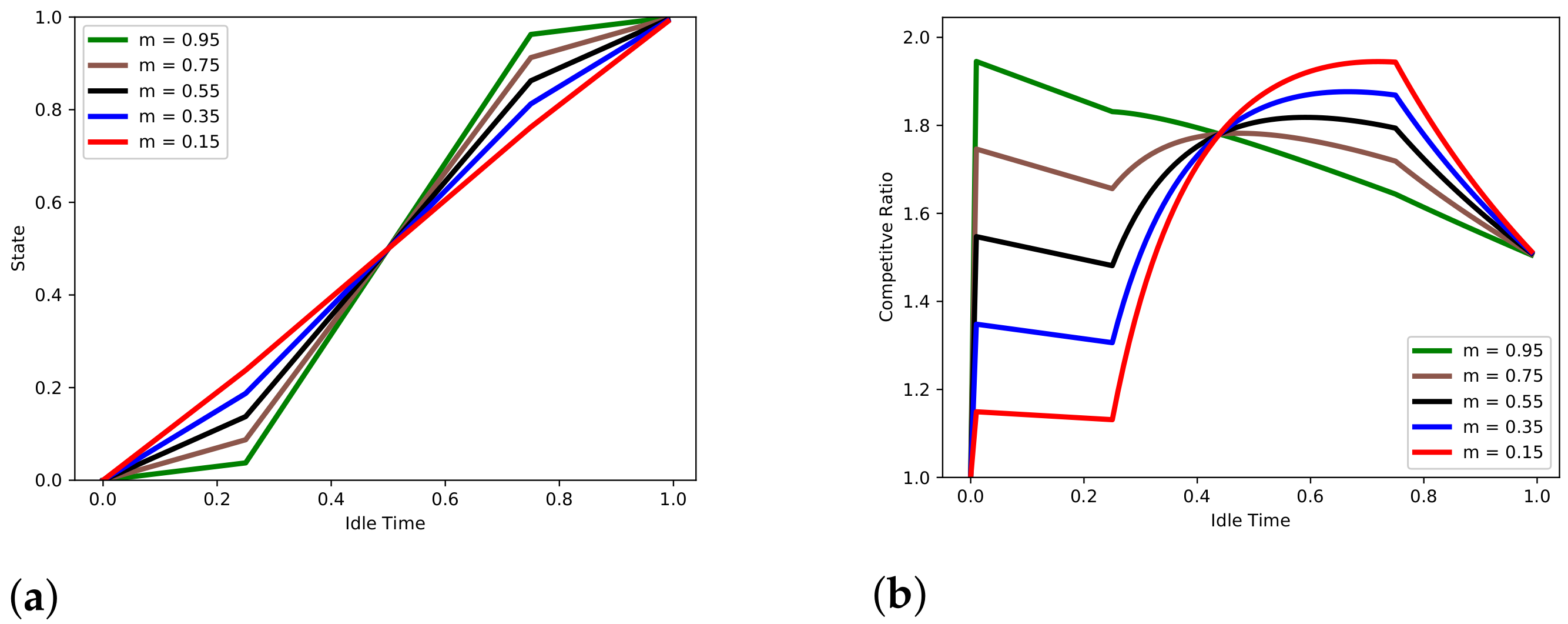
7. Piece-Wise Linear Strategies
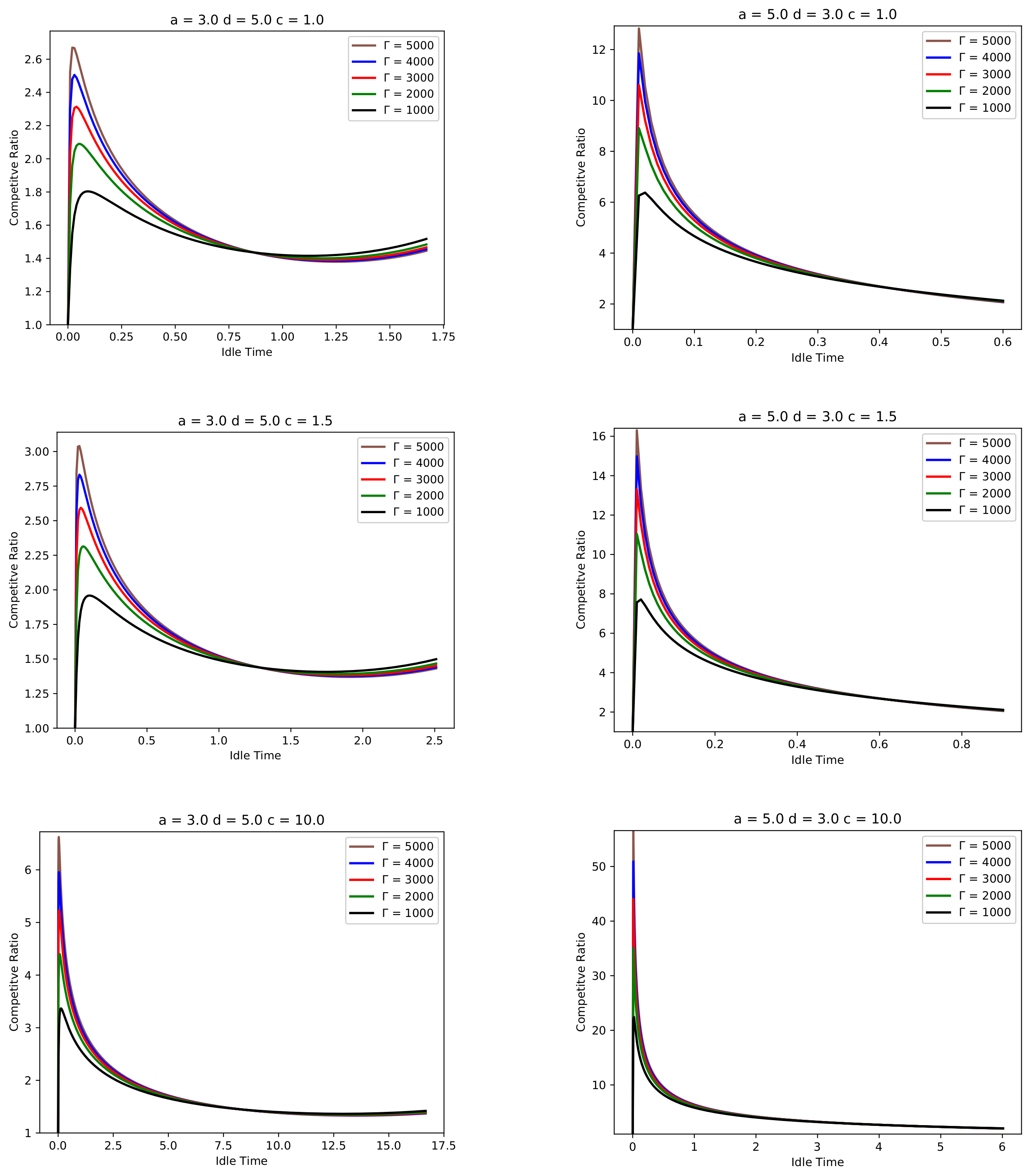
8. Comparative Analysis
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Borodin, A.; El-Yaniv, R. Online Computation and Competitive Analysis; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Agarwal, Y.; Hodges, S.; Chandra, R.; Scott, J.; Bahl, P.; Gupta, R. Somniloquy: Augmenting Network Interfaces to Reduce PC Energy Usage. In Proceedings of the USENIX Symposium on Networked Systems Design and Implementation (NSDI ’09), Boston, MA, USA, 22–24 April 2009; pp. 365–380. [Google Scholar]
- Agarwal, Y.; Savage, S.; Gupta, R. Sleepserver: A software-only approach for reducing the energy consumption of PCs within enterprise environments. In Proceedings of the 2010 USENIX Conference on USENIX Annual Technical Conference (USENIXATC’10), Berkeley, CA, USA, 22–25 June 2010. [Google Scholar]
- Nedevschi, S.; Chandrashekar, J.; Liu, J.; Nordman, B.; Ratnasamy, S.; Taft, N. Skilled in the art of being idle: Reducing energy waste in networked systems. In Proceedings of the 6th USENIX Symposium on Networked Systems Design and Implementation (NSDI ’09), Boston, MA, USA, 22–24 April 2009; USENIX Association: Berkeley, CA, USA, 2009; pp. 381–394. [Google Scholar]
- Reich, J.; Goraczko, M.; Kansal, A.; Padhye, J.; Goraczko, M. Sleepless in seattle no longer. In Proceedings of the 2010 USENIX Conference on USENIX Annual Technical Conference (USENIXATC’10), Boston, MA, USA, 22–25 June 2010; USENIX Association: Berkeley, CA, USA, 2010. [CrossRef]
- Albers, S. Energy-efficient algorithms. Commun. ACM 2010, 53, 86–96. [Google Scholar] [CrossRef] [Green Version]
- Augustine, J.; Irani, S.; Swamy, C. Optimal power down strategies. In Proceedings of the IEEE Symposium on Foundations of Computer Science, Rome, Italy, 17–19 October 2004; Cambridge University Press: Cambridge, UK, 2004; pp. 530–539. [Google Scholar]
- Bein, W.; Madan, B.; Bein, D.; Nyknahad, D. Algorithmic approaches for a dependable smart grid. In Proceedings of the Information Technology: New Generations: 13th International Conference on Information Technology (ITNG 2016), Las Vegas, NV, USA, 11–13 April 2016; Latifi, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 677–687. [Google Scholar]
- Hall, R.; Erdélyi, R.; Hanna, E.; Jones, J.M.; Scaife, A.A. Drivers of North Atlantic Polar Front jet stream variability. Int. J. Climatol. 2014, 35, 1697–1720. [Google Scholar] [CrossRef]
- Wu, D.; Zheng, X.; Xu, Y.; Olsen, D.; Xia, B.; Singh, C.; Xie, L. An Open-source Model for Simulation and Corrective Measure Assessment of the 2021 Texas Power Outage. arXiv 2021, arXiv:2104.04146. [Google Scholar]
- Maimó-Far, A.; Tantet, A.; Homar, V.; Drobinski, P. Predictable and Unpredictable Climate Variability Impacts on Optimal Renewable Energy Mixes: The Example of Spain. Energies 2020, 13, 5132. [Google Scholar] [CrossRef]
- Andro-Vasko, J.; Bein, W.; Ito, H. Energy Efficiency and Renewable Energy Management with Multi-State Power-Down Systems. Information 2019, 10, 44. [Google Scholar] [CrossRef] [Green Version]
- Andro-Vasko, J.; Bein, W. Online Competitive Control of Power-Down Systems with Adaptation. In Proceedings of the 16th International Conference on Information Technology-New Generations (ITNG 2019), Las Vegas, NV, USA, 1–3 April 2019; Advances in Intelligent Systems and Computing. Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Andro-Vasko, J.; Bein, W.; Ito, H.; Kasahara, S.; Kawahara, J. Decrease and reset for power-down. Energy Syst. 2021. in print. [Google Scholar] [CrossRef]
- Guelen, S.C. Gas Turbines for Electric Power Generation; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Winterbone, D.E.; Turan, A. Advanced Thermodynamics for Engineers, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Andro-Vasko, J.; Bein, W.; Cisneros, B.; Domantay, J. Online Competitive Schemes for Linear Power-Down Systems. In Proceedings of the 17th International Conference on Information Technology, New Generations (ITNG 2020), Las Vegas, NV, USA, April 2020; Springer: Berlin/Heidelberg, Germany, 2020. Available online: https://link.springer.com/chapter/10.1007/978-3-030-43020-7_76 (accessed on 12 October 2021).
- Andro-Vasko, J.; Bein, W. An Evaluation for Online Power Down Systems Using Piece-Wise Linear Strategies. In Proceedings of the 18th International Conference on Information Technology, New Generations (ITNG 2021), Las Vegas, NV, USA, April 2021; Springer: Berlin/Heidelberg, Germany, 2021. Available online: https://link.springer.com/chapter/10.1007/978-3-030-70416-2_34 (accessed on 12 October 2021).


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andro-Vasko, J.; Bein, W. Evaluation of Continuous Power-Down Schemes. Information 2022, 13, 37. https://doi.org/10.3390/info13010037
Andro-Vasko J, Bein W. Evaluation of Continuous Power-Down Schemes. Information. 2022; 13(1):37. https://doi.org/10.3390/info13010037
Chicago/Turabian StyleAndro-Vasko, James, and Wolfgang Bein. 2022. "Evaluation of Continuous Power-Down Schemes" Information 13, no. 1: 37. https://doi.org/10.3390/info13010037
APA StyleAndro-Vasko, J., & Bein, W. (2022). Evaluation of Continuous Power-Down Schemes. Information, 13(1), 37. https://doi.org/10.3390/info13010037






